-
Black hole thermodynamics have been developed based on an understanding of black holes and quantum physics [1-5]. In extended phase space, the cosmological constant can be considered as a thermodynamic variable [6-8]. Specifically, one can treat the cosmological constant
$ \Lambda $ as thermodynamic pressure$P = - {\Lambda}/{8\pi G}$ , which means that its conjugate quantity can be interpreted as thermodynamic volume. For a negative cosmological constant$ \Lambda $ , the pressure P is positive, which yields a well-defined equilibrium thermodynamic framework. It is worth noting that this volume is usually not equal to the geometric volume of black holes, except in some simple cases, such as AdS Schwarzschild black holes.Although the definition of thermodynamic volume has been given, its physical interpretation is still a puzzle. An early attempt to answer this question led to the conjecture that the volume satisfies the reverse isoperimetric inequality [9,10]. This conjecture was motivated by progress in studying Kerr-AdS black holes and then generalized to other black holes. The reverse isoperimetric inequality is saturated for Schwarzschild-AdS black holes, which indicates that for a black hole of a given thermodynamic volume V, the entropy is maximized for Schwarzschild-AdS black holes [9]. However, further investigations discovered that this inequality does not apply to all types of black holes. Those black holes that exceed the maximum entropy bound are called super-entropic black holes [11-15], and they rotate with non-compact event horizons of finite surface area [11]. More relevant discussions can be found in Refs. [16-29].
A black hole reduces its mass-energy via Hawking radiation. If the specific heat is negative, this shrinking leads to a higher temperature, increased radiation, and hence, more mass loss. Therefore, the system accelerates through this downward spiral instead of settling into an equilibrium state. For charged BTZ black holes, which are the simplest super-entropic black holes, it has been shown that there is a connection between the violation of the reverse isoperimetric inequality and the thermodynamical instability with the specific heat at constant volume
$ C_{V}<0 $ [23]. This result consequently leads to the natural conjecture that super-entropic black holes always have$ C_{V}<0 $ , making them unstable in extended thermodynamics. Later, it was found that this conjecture is violated for generalized exotic BTZ black holes in some parameter region [24]. However in this case, the specific heat at constant pressure$ C_{P} $ was determined to be negative whenever$ C_{V}>0 $ . Thus, a broader version of the instability conjecture was proposed [24], which states that all super-entropic black holes are in general thermodynamically unstable with either negative$ C_{V} $ or negative$ C_{P} $ . The instability conjecture was analytically verified for$ 3 $ D charged BTZ black holes [23,30,31]. As it is difficult to obtain analytical expressions for$ C_{V} $ and$ C_{P} $ , using methods described in Ref. [32], the instability conjecture was tested numerically for ultra spinning d-dimensional Kerr black holes [14], generalized exotic BTZ black holes [24], and super-entropic black holes with Immirzi, as described in Ref. [27].Here, we test the instability conjecture for EBI AdS black holes in
$ (2+1) $ -dimensional space-time. An EBI AdS black hole is the charged black hole solution in EBI theory based on non-linear electrodynamics as proposed by Born and Infeld in 1934 [33] and is an extension of the RN black hole in the Einstein-Maxwell theory. As it was found that non-linear electrodynamics, in particular Born-Infeld electrodynamics, can arise from the low-energy limit of string theory and encode the low-energy dynamics of D-branes (i.e., the low-energy effective action for a constant electromagnetic field is precisely the Born-Infeld action) [34-37], they have attracted considerable attention in recent years. After BI black hole solutions in anti-de Sitter space were obtained [38,39], their properties have been extensively investigated [40-57]. Although various aspects of 3D EBI AdS black holes have also been studied, the specific heat and instability conjecture need to be explored in more depth.The organization of the rest of this work is as follows. In section II, we discuss the thermodynamic quantities of 3D EBI AdS black holes. In section III, we first show that 3D EBI AdS black holes violate the reverse isoperimetric inequality, and hence, are super-entropic. Then, the instability conjecture is considered by calculating
$ C_{V} $ and$ C_{P} $ . We find that when non-linear electrodynamics effects are strong enough, there exists some parameter region in which$ C_{V} $ and$ C_{P} $ are both positive. This observation provides a counter example to the instability conjecture. The conclusion is given in section IV. In this paper, we use geometrical units, whereby G, c,$ \hbar $ , and$ k_{B} $ have been set to unity. -
In this section, thermodynamics of 3D EBI AdS black holes are discussed. The actions of 3D-Einstein gravity being coupled with Born-Infeld electrodynamics are
$ I = \int {\rm d}^{3}x\sqrt{-g}\left[ \frac{R-2\varLambda} {16\pi}+L(F)\right] , $

(1) $ L(F) = \frac{b^{2}}{4\pi}\left( 1-\sqrt{1+\frac{2F}{b^{2}}}\right) .$

(2) Here, constant b is the Born-Infeld parameter, g is the determinant of the metric tensor,
$ \Lambda = -1/l^{2} $ is the cosmological constant, l is the AdS radius, and$ L(F) $ is the Lagrangian of Born-Infeld electrodynamics. The metric and gauge potential are [40,41]$ {\rm d}s^{2} = -f\left( r\right) {\rm d} t^{2}+f(r)^{-1}{\rm d}r^{2}+r^{2}{\rm d}\theta^{2}, $

(3) $\begin{aligned}[b] f\left( r\right) = & -8M+\frac{r^{2}}{l^{2}}+2b^{2}r\left( r-\sqrt {r^{2}+\frac{Q^{2}}{4b^{2}}}\right)\\ & -\frac{1}{2}Q^{2}\ln\left[ r+\sqrt {r^{2}+\frac{Q^{2}}{4b^{2}}}\right] \\& +\frac{1}{2}Q^{2}\ln\left[ l+\sqrt{l^{2}+\frac{Q^{2}}{4b^{2}}}\right] -2b^{2}l\left[ l-\sqrt{l^{2}+\frac{Q^{2}}{4b^{2}}}\right] , \end{aligned} $

(4) where Q and M stand for the charge and mass of EBI black holes, respectively. In the limit of
$ b\rightarrow\infty $ , this is reduced to the charged BTZ black hole solution [23],$ f^{\text{BTZ}}\left( r\right) = -8M-\frac{Q^{2}}{2}\log\left( \frac{r} {l}\right) +\frac{r^{2}}{l^{2}}. $

The horizon is located at
$ r = r_{+} $ with$ f\left( r_{+}\right) = 0 $ , from which the mass of 3D EBI AdS black holes is obtained [40], as follows:$\begin{aligned}[b] M =& \frac{r_+^{2}}{8l^{2}}+\frac{1}{4}b^{2}r_+\left( r_+-\sqrt {r_+^{2}+\frac{Q^{2}}{4b^{2}}}\right) \\& -\frac{1}{16}Q^{2}\ln\left[ r_++\sqrt{r_+^{2}+\frac{Q^{2}}{4b^{2}}}\right] \\ & +\frac{1}{16}Q^{2}\ln\left[ l+\sqrt{l^{2}+\frac{Q^{2}}{4b^{2}}}\right] -\frac{1}{4}b^{2}l\left[ l-\sqrt{l^{2}+\frac{Q^{2}}{4b^{2}}}\right] . \end{aligned} $

(5) In extended thermodynamics, one identifies enthalpy H [6] with the mass of the black hole, and the pressure is
$ P = -\Lambda/8\pi = 1/8\pi l^{2} $ . Moreover, entropy S is$ S = \frac{A}{4} = \frac{1}{2}\pi r_+. $

(6) The first law of thermodynamics,
${\rm d}M = T{\rm d}S+ V{\rm d}P+ $ $ \Phi {\rm d}Q$ , gives the temperature and the thermodynamic volume of 3D EBI AdS black holes$ T = \left. \frac{\partial M}{\partial S}\right\vert _{P} = \frac{r_+}{2\pi l^{2}}+\frac{b^{2}r_+}{\pi}\left( 1-\sqrt {1+\frac{Q^{2}}{4b^{2}r_+^{2}} }\right) , $

(7) $ V = \left. \frac{\partial M}{\partial P}\right\vert _{S} = \pi r_+^{2}+2\pi l^{4}b^{2}\left( 1-\sqrt{1+\frac{Q^{2}}{4b^{2}l^{2}}}\right) , $

(8) respectively. It is observed that the thermodynamic volume is different from the geometric volume
$ \pi r_{+}^{2} $ . -
For an asymptotically AdS black hole in extended phase space, it was conjectured in Ref. [9] that a reverse isoperimetric inequality holds,
$ R\equiv\left( \frac{\left( d-1\right) V}{\omega_{d-2}}\right) ^{\textstyle\frac{1}{d-1}}\left( \frac{\omega_{d-2}}{A}\right) ^{\textstyle\frac {1}{d-2}}\geqslant 1, $

(9) where the isoperimetric ratio R is defined. Here, V is the thermodynamic volume, A is the horizon area,
$ \omega_{d} $ stands for a d-dimensional unit sphere,$ \omega_{d} = \frac{2\pi^{\textstyle\frac{d+1}{2}}}{\varGamma\left( \dfrac{d+1}{2}\right) }, $

(10) where
$ \omega_{1} = 2\pi $ and$ \omega_{2} = 4\pi $ . The reverse isoperimetric inequality is saturated for a Schwarzschild AdS black hole, as its thermodynamic volume is simply equal to its naive geometric volume. For some more complicated black holes, e.g., Kerr [9], STU [58] and Taub-NUT/Bolt black holes [59], thermodynamic volumes are larger than naive geometric volumes, hence resulting in$ R>1 $ . Moreover, unlike a Schwarzschild AdS black hole, these black holes have nonzero$ C_{V} $ . However, several black hole solutions were later found to violate the reverse isoperimetric inequality [11-14,60,61]. A black hole that violates the inequality is dubbed "super-entropic black hole" as its entropy is larger than the maximum entropy allowed by the reverse isoperimetric inequality. As argued in Ref. [11], this violation can be attributed to be a result of the finite-area but noncompact event horizon. It was further presented in Refs. [23,24] that a large family of super-entropic black holes has$ C_{V}<0 $ or$ C_{P}<0 $ whenever$ C_{V}>0 $ , showing that they are unstable in extended thermodynamics.In this section, we first show that 3D EBI AdS black holes are super-entropic, which means that they violate the reverse isoperimetric inequality
$ \left( 9\right) $ . In fact, according to Eqs.$ \left( 6\right) $ ,$ \left( 7\right) $ , and$ \left( 9\right) $ , the isoperimetric ratio R for 3D EBI AdS black holes can be readily computed to be$ R = \sqrt{1-\frac{l^{2}Q^{2}}{2r_+^{2}}\left( 1+\sqrt{1+\frac{Q^{2}}{4l^{2}b^{2}}}\right) ^{-1}}. $

(11) It is obvious from Eq.
$ \left( 11\right) $ that$ R<1 $ , which means that 3D EBI AdS black holes violate the reverse isoperimetric inequality as long as$ Q\neq0 $ . Note that for$ Q = 0 $ , EBI AdS black holes are reduced to Schwarzschild AdS black holes, which have$ R = 1 $ . Consequently, 3D EBI AdS black holes are super-entropic. In the remainder of this section, we discuss the behavior of$ C_{V} $ and$ C_{P} $ of 3D EBI AdS black holes and provide further investigation results of the instability conjecture.Using Eq.
$ \left( 6\right) $ , we can write thermodynamic quantities in terms of S and P,$ T = \frac{8PS}{\pi}+\frac{2Sb^{2}}{\pi^{2}}\left( 1-\sqrt{1+\frac{\pi ^{2}Q^{2}}{16b^{2}S^{2}}}\right) , $

(12) $ V = \frac{4S^{2}}{\pi}+\frac{b^{2}}{32\pi P^{2}}\left( 1-\sqrt {1+\frac{2\pi PQ^{2}}{b^{2}}}\right) . $

(13) From Eq.
$ \left( 6\right) $ , we observe that the entropy S is geometrical and only depends on the horizon radius$ r_{+} $ . Hence the entropy S and the thermodynamic volume V are independent functions, which consequently gives a nonzero$ C_{V} $ . To obtain the specific heat at constant volume$ C_{V} $ , it is easier to start with$ C_{P} $ . Using Eq.$ \left( 12\right) $ , we can express S in terms of T and P,$ S = \frac{\pi T}{16P}\left[ 1+\left( 1+\frac{2\pi P}{b^{2}}\right) ^{-1}\left( \frac{2\pi P}{b^{2}}+\sqrt{1+\frac{4P^{2}Q^{2}}{T^{2}b^{2}} +\frac{2PQ^{2}}{\pi T^{2}}}\right) \right] . $

(14) Then,
$ C_{P}\left( T\right) $ is given by$\begin{aligned}[b] C_{P}(T) =& \left. T\frac{\partial S}{\partial T}\right\vert _{P} = \frac{\pi T}{16P}\Bigg[ 1+\left( 1+\frac{2\pi P}{b^{2}}\right) ^{-1}\\&\times\left( \frac{2\pi P}{b^{2}}+\frac{1}{\sqrt{1+\dfrac{4P^{2}Q^{2}}{b^{2}T^{2}} +\dfrac{2PQ^{2}}{\pi T^{2}}}}\right) \Bigg] ,\end{aligned} $

(15) which is manifestly positive. For large T, one has
$ C_{P}(T) = \dfrac{\pi T}{8P}+\cdots $ . When$ b\rightarrow\infty $ , Eq.$ \left( 15\right) $ reduces to$ C_{P}^{\text{BTZ}} $ of charged BTZ black holes (see Eq.$ \left( 7\right) $ in Ref. [23]),$ C_{P}^{\text{BTZ}}(T) = \frac{\pi T}{16P}\left[ 1+\frac{1}{\sqrt{1+\dfrac {2PQ^{2}}{\pi T^{2}}}}\right] . $

(16) One can calculate
$ C_{V}(T) $ from$ C_{P}(T) $ via the well-known relation,$ \frac{C_{P}}{C_{V}} = \frac{1}{\kappa_{T}\beta_{S}}, $

(17) where
$ \kappa_{T}\equiv-V\partial P/\left. \partial V\right\vert _{T} $ is the isothermal bulk modulus, and$ \beta_{S}\equiv-V^{-1}\partial V/\left. \partial P\right\vert _{S} $ is the adiabatic compressibility. To be self-contained, a derivation of Eq.$ \left( 17\right) $ is given in the appendix. Substituting Eq.$ \left( 14\right) $ in Eq.$ \left( 13\right) $ yields$\begin{aligned}[b] V\left( T,P\right) =& \frac{\pi T^{2}}{64P^{2}}\Bigg[ 1+\left( \frac{2\pi P}{b^{2}}+1\right) ^{-1}\\&\times \left( \frac{2\pi P}{b^{2}}+\sqrt {1+\frac{4P^{2}Q^{2}}{T^{2}b^{2}}+\frac{2PQ^{2}}{\pi T^{2}}}\right) \Bigg] ^{2}\\& -\frac{Q^{2}}{16P}\left( \sqrt{1+\frac{2\pi PQ^{2}}{b^{2}}}+1\right) ^{-1}. \end{aligned} $

(18) From Eqs.
$ \left( 13\right) $ and$ \left( 18\right) $ ,$ \kappa_{T} $ and$ \beta_{S} $ can be readily computed,$\begin{aligned}[b] \kappa_{T} \equiv & -V\partial P/\left. \partial V\right\vert _{T} = -V\left[ \frac{-8S^{2}}{\pi P}+\frac{TS}{2P}\gamma\right.\\&\left.+\frac{1}{16P^{2}}\frac{Q^{2}}{\delta+1}+\frac{\pi Q^{4}}{16Pb^{2}}\frac{1}{\delta(\delta+1)^{2}}\right] ^{-1}, \end{aligned} $

(19) $\begin{aligned}[b] \beta_{S} \equiv & -V^{-1}\partial V/\left. \partial P\right\vert _{S} \\=& -V^{-1}\left[ \frac{Q^{2}}{8P^{2}\left( \sqrt{1+\dfrac{2\pi PQ^{2}}{b^{2}}}+1\right) }-\frac{Q^{2}}{32P^{2}\sqrt{1+\dfrac{2\pi PQ^{2}}{b^{2}}} }\right] , \end{aligned} $

(20) where
$\begin{aligned}[b] \gamma = & \frac{\dfrac{2\pi}{b^{2}}+\dfrac{\eta^{2}-1}{P\eta}-\dfrac{Q^{2}} {\eta\pi T^{2}}}{\left( \dfrac{2\pi P}{b^{2}}+1\right) }-\frac{\left( \dfrac{2\pi P}{b^{2}}+\eta\right) \left( \dfrac{2\pi}{b^{2}}\right) }{\left( \dfrac{2\pi P}{b^{2}}+1\right) ^{2}},\\ \eta = & \sqrt{1+\frac{4P^{2}Q^{2}}{T^{2}b^{2}}+\frac{2PQ^{2}}{\pi T^{2}}},\\ \delta =& \sqrt{1+\frac{2\pi PQ^{2}}{b^{2}}}. \end{aligned} $

(21) With the above results for
$ \kappa_{T} $ ,$ \beta_{S} $ , and$ C_{P}(T) $ , one can use Eq.$ \left( 17\right) $ to obtain the specific heat at constant volume$ C_{V} $ . As a check, in the limit of$ b\rightarrow\infty $ , we find that$ C_{V}(T) $ becomes$ C_{V}^{\text{BTZ}}(T) $ of charged BTZ black holes (see Eq.$ \left( 10\right) $ in Ref. [23]), where$ C_{V}^{\text{BTZ}}(T) = -\frac{Q^{2}}{32T}\left[ \frac{1+\sqrt{1+\dfrac{2PQ^{2} }{\pi T^{2}}}}{1+\sqrt{1+\dfrac{2PQ^{2}}{\pi T^{2}}}+\dfrac{3PQ^{2}}{2\pi T^{2} }}\right] . $

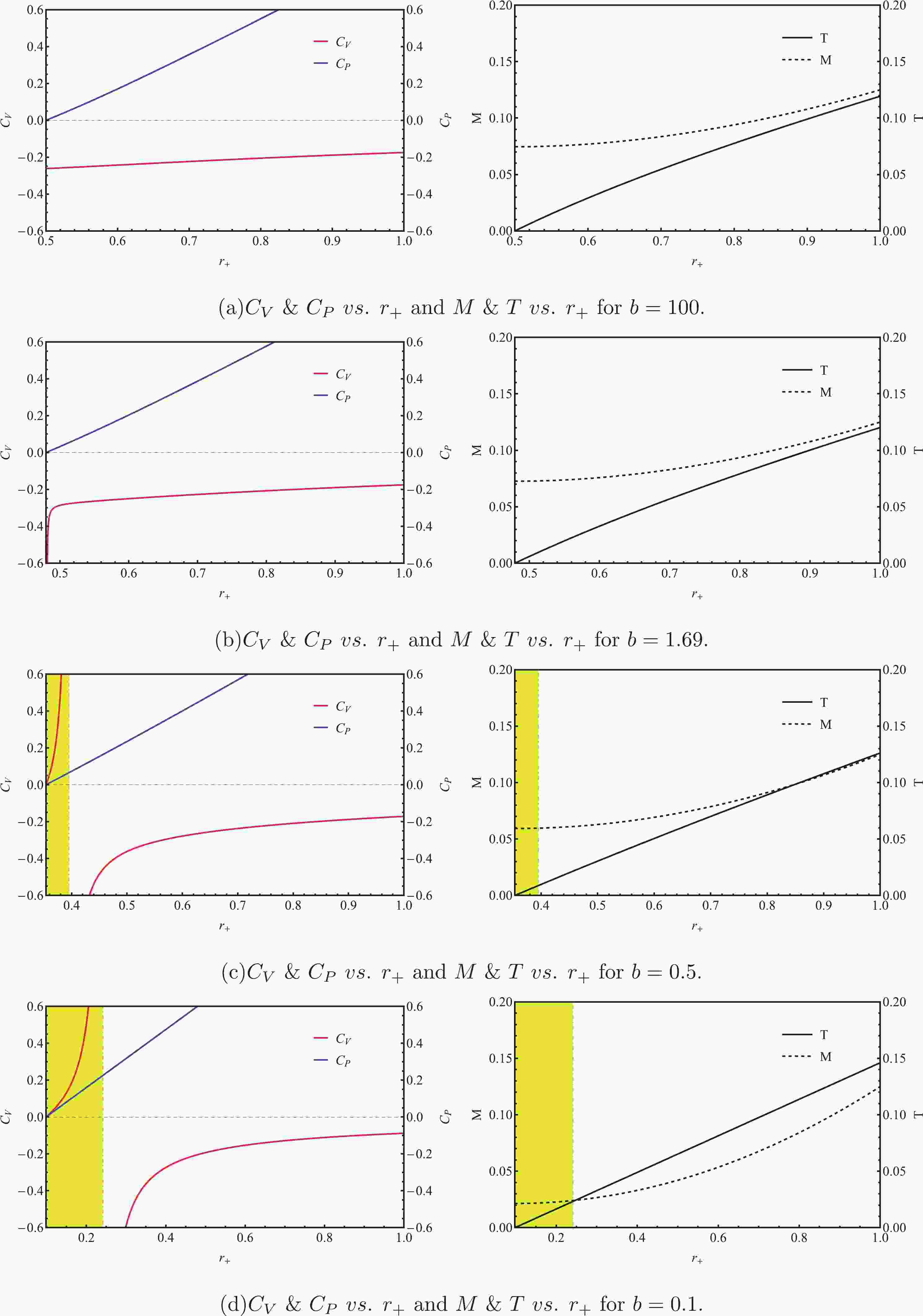
(22) In Fig. 1, we plot the specific heat at constant volume
$ C_{V} $ , the specific heat at constant pressure$ C_{P} $ , the black hole mass M and the black hole temperature T as functions of the black hole horizon radius$ r_{+} $ for 3D EBI AdS black holes with fixed pressure$ l = 1.0 $ , fixed charge$ Q = 1.0 $ and various$ b = 0.1,0.5,1.69,100 $ . For$ b = 100 $ , non-linear electrodynamics effects are negligible, and hence, the behavior of 3D EBI AdS black holes closely resembles that of charged BTZ black holes. As shown in Fig. 1(a),$ C_{P} $ is always positive, whereas$ C_{V} $ is always negative, which recovers the results of BTZ black holes [23]. As b decreases to$ b\simeq1.69 $ , Fig. 1(b) shows that$ C_{V} $ stays negative and becomes highly negative as T goes to zero. Interestingly, for small enough values of b (i.e.,$ b\lesssim 1.69 $ ), our numerical results show that$ C_{V} $ and$ C_{P} $ can both be positive in some parameter region. In fact, when$ b = 0.5 $ and$ 0.1 $ , the regions in which$ C_{V}>0 $ and$ C_{P}>0 $ are represented by yellow in Figs. 1(c) and 1(d). Note that the black hole temperature T and mass M are both positive in the yellow regions of Figs. 1(c) and 1(d), which means that the 3D EBI AdS black hole solutions with$ C_{V}>0 $ and$ C_{P}>0 $ are physical. Moreover, Figs. 1(c) & 1(d) suggest that the conjecture violation region increases in size with decreasing parameter b. In short, we find that 3D EBI AdS black holes can violate the instability conjecture.
Figure 1. (color online) Plots of heat capacity at constant volume
$ C_{V} $ , heat capacity at constant pressure$ C_{P} $ , the black hole mass M, and the black hole temperature T against the black hole horizon radius$ r_{+} $ for 3D EBI AdS black holes with$ Q = 1 = l $ and various values of b. Yellow regions denote the regions of interest, where$ C_{V} $ and$ C_{P} $ are both positive, and hence, black holes can be free of thermodynamic instability.Interestingly, Fig. 1 shows that
$ C_{V} $ has a discontinuity for a small enough b. To investigate the nature of the discontinuity in$ C_{V} $ , we plotted the horizon radius$ r_{+} $ and the Helmholtz free energy F as functions of the black hole temperature T with fixed volume V in Fig. 2, where$ Q = 1 $ and$ b = 0.1 $ . The left panel in Fig. 2 shows that, for a given T, there are two black hole solutions of different sizes, namely Large BH (red line) and Small BH (blue line). Moreover, the black hole temperature T has a maximum$ T_{\max} $ , which corresponds to$ \left. \partial r_{+}/\partial T\right\vert _{V} = 0 $ . Note that$ C_{V} $ can be rewritten as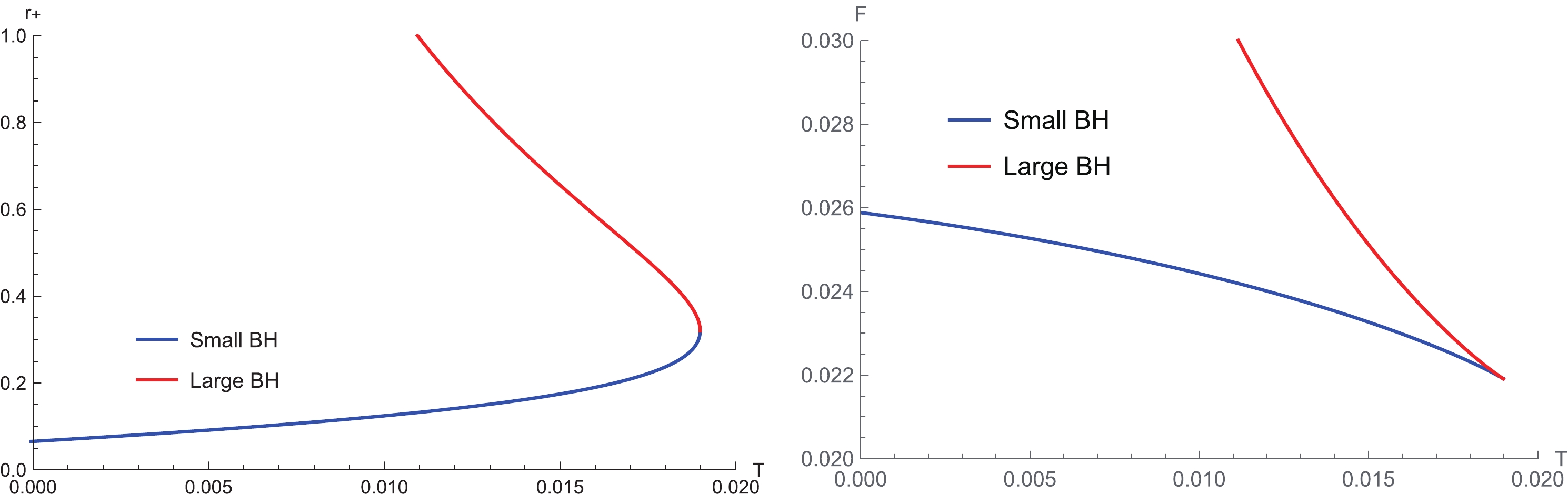
Figure 2. (color online) Plots of the horizon radius
$ r_{+} $ and the Helmholtz free energy F against the black hole temperature T for 3D EBI AdS black holes with fixed volume V. Here, we take$ Q = 1 $ and$ b = 0.1 $ . The blue and red lines represent Small BH and Large BH, respectively. The specific heat at constant volume$ C_{V} $ of Small/Large BH is positive/negative. As a result,$ C_{V} $ is discontinuous at the maximum value of T.$ C_{V} = \frac{\pi}{2}\left. \frac{\partial r_+}{\partial T}\right\vert _{V}, $

(23) where we use Eq.
$ \left( 6\right) $ for the entropy S. Therefore, Large/Small BH has a negative/positive$ C_{V} $ , which goes to negative/positive infinity as T approaches$ T_{\max} $ . In short, the discontinuity in$ C_{V} $ corresponds to the maximum value of the black hole temperature, at which the two black hole phases (i.e., Large BH and Small BH) merge. The right panel of Fig. 2 displays that the free energy of Small BH is always smaller than that of Large BH, which indicates that there is no phase transition. Our results suggest that, at a constant volume, 3D EBI AdS black holes with positive$ C_{V} $ are globally stable. -
In this paper, we tested the instability conjecture by considering 3D EBI AdS black holes: super-entropic black holes always have
$ C_{V}<0 $ or$ C_{P}<0 $ whenever$ C_{V}>0 $ , making them unstable in extended gravitational thermodynamics. This conjecture was tested and found satisfied for a large class of super-entropic solutions [11,23,24]. After showing that 3D EBI AdS black holes are super-entropic, we found that black holes satisfy the instability conjecture when b is large enough (i.e., non-linear electrodynamics effects are inessential). However, when non-linear electrodynamic effects play an important role, our numerical results (see Fig. 1) show that there exists some parameter region in which both$ C_{V}>0 $ and$ C_{P}>0 $ , and hence, this provides a counter example to the instability conjecture. In addition, it was suggested that the violation region will increase as non-linear electrodynamic effects become stronger.It is worthwhile pointing out that for
$ d\geq4 $ dimension, the thermodynamic volume of EBI AdS black holes is just the naive geometric volume$ V = \left( d-1\right) ^{-1}\omega_{d-2}r_{+}^{d-1} $ , which means that$ R = 1 $ , and hence, higher dimensional EBI AdS black holes are not super-entropic. In contrast, for higher dimensional EBI AdS black holes, entropy S and volume V are not independent, which leads to a constant volume specific heat$ C_{V} = 0 $ [62]. -
We are grateful to Wei Hong and Yucheng Huang for useful discussions and numerical analysis.
-
In this appendix, we present a derivation of Eq.
$ \left( 17\right) $ , which starts from the definition of the adiabatic compressibility and the isothermal bulk modulus. In fact, the adiabatic compressibility$ \beta_{S} $ and the isothermal bulk modulus$ \kappa_{T} $ are defined by$\tag{A1} \beta_{S}\equiv-\frac{1}{V}\left. \frac{\partial V}{\partial P}\right\vert _{S}\ \ \text{and} \ \ \kappa_{T}\equiv-V\left. \frac{\partial P}{\partial V}\right\vert _{T}, $

(A1) respectively. Using the properties of partial derivatives, one can rewrite
$ \beta_{S} $ as$ \tag{A2}\begin{aligned}[b]\beta_{S} =& -\frac{1}{V}\left. \frac{\partial V}{\partial S}\right\vert _{P}\left. \frac{\partial S}{\partial P}\right\vert _{V} = -\frac{1}{V} \frac{\left. \dfrac{\partial S}{\partial P}\right\vert _{V}}{\left. \dfrac{\partial S}{\partial V}\right\vert _{P}} \\=& -\frac{1}{V}\frac{\left. \dfrac{\partial S}{\partial T}\right\vert _{V}\left. \dfrac{\partial T}{\partial P}\right\vert _{V}}{\left. \dfrac{\partial S}{\partial T}\right\vert _{P}\left. \dfrac{\partial T}{\partial V}\right\vert _{P} }. \end{aligned} $

(A2) In contrast, the specific heat at constant pressure
$ C_{P} $ and the specific heat at constant volume$ C_{V} $ are defined by$ \tag{A3} C_{P}\equiv T\left. \frac{\partial S}{\partial T}\right\vert _{P}\ \ \text{and}\ \ C_{V}\equiv T\left. \frac{\partial S}{\partial T}\right\vert _{V}, $

(A3) respectively. Consequently, Eq.
$ \left( 25\right) $ reduces to$ \tag{A4}\begin{aligned}[b] \beta_{S} =& \frac{C_{V}}{C_{P}}\left( -\frac{1}{V}\left. \frac{\partial T}{\partial P}\right\vert _{V}\left. \frac{\partial V}{\partial T}\right\vert _{P}\right) = \frac{C_{V}}{C_{P}}\left( -\frac{1}{V}\left. \frac{\partial V}{\partial P}\right\vert _{T}\right) \\=& \frac{C_{V}}{C_{P}}\frac{1}{\kappa _{T}}, \end{aligned}$

(A4) which leads to
$ \tag{A5} \frac{C_{P}}{C_{V}} = \frac{1}{\beta_{S}\kappa_{T}}. $

(A5)
Thermodynamic instability of 3D Einstein-Born-Infeld AdS black holes
- Received Date: 2020-01-28
- Available Online: 2021-06-15
Abstract: Super-entropic black holes possess finite-area but noncompact event horizons and violate the reverse isoperimetric inequality. It has been conjectured that such black holes always have negative specific heat at constant volume





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF
















 DownLoad:
DownLoad: