-
Radiative leptonic heavy meson decay plays an important role in our understanding of strong and weak interactions and also provides a background of pure leptonic decays. It is apparent that the corresponding decay amplitudes depend on the Cabibbo-Kobayashi-Maskawa (CKM) matrix elements, the Fermi coupling constant, and non-perturbative QCD dynamics. Although we can extract CKM matrix elements from pure leptonic heavy meson decay processes, it is difficult to measure these processes due to the well-known helicity suppression effect. In contrast, radiative leptonic decays are not subject to helicity suppression due to the photon emission of the charged particles. In addition, the radiative leptonic decays are of interest on their own for exploring the factorization properties of heavy quark decays.
In the heavy quark limit, both the B- and D-meson decays could be studied within the factorization approach; the leading power (LP) predictions of
$ D\to e\,\nu_e\,\gamma $ are presented in [1, 2], where the final state photon can be either hard or soft. In 2017, the BES-III Collaboration measured the radiative leptonic$ D^+\to\gamma\, e^+\,\nu_e $ decay [3], and the upper limit on the branching fraction is approximately$ 3.0\times10^{-5} $ with$ E_{\rm cut} = 10$ MeV. This result is in agreement with the LP predictions [1, 2]. However, as the charm quark mass is not much larger than$ \Lambda_{\rm QCD} $ , the expansion of inverse$ m_c $ will work less effectively compared with B-meson decays. Therefore, a further study with more careful treatment of the power suppressed contribution is required. As the energy release in D-meson decays is not sufficiently large, some alternative methods based on the non-perturbation approach are also employed in radiative leptonic D-meson decays, such as the light-front quark model (LFQM), non-relativistic constituent quark model (NRQM), and relativistic independent quark model (RIQM) [4-7]. In addition, this process has been studied using the perturbative QCD (pQCD) approach [8]. Most of the predictions are within the upper limit of the experimental measurement.In this work, we will study radiative leptonic D-meson decay within the framework of QCD factorization (QCDF) [9-13] as well as the dispersion relation [14-16]. In the framework of QCDF, one can separate long-distance and short-distance contributions via a simultaneous expansion in the power of the strong coupling constant and
$ \Lambda_{\rm QCD}/m_Q $ , and the factorization approach has been applied to various radiative heavy meson decays [7, 8, 17-26], and other processes such as factorization of the correlation function in light-cone sum rules [27-31]. As the power suppressed contribution is expected to be very important in D-meson decay, we will perform a careful investigation on the “soft” contribution, the local contribution, and the higher-twist contribution. Although the precision of the predictions with the factorization approach is limited due to the low energy scale, the inclusion of power suppressed contributions will significantly improve the reliability of the theoretical results.Our paper is structured as follows. In Sec. II, we introduce the theoretical framework. Then, we calculate the two-particle LP and soft contributions to next-to-leading logarithm (NLL) accuracy and evaluate the higher-twist (HT) contribution from two-particle and three-particle light-cone distribution amplitudes (LCDA). Sec. III is devoted to our numerical analysis, where we discuss the NLP contributions in detail and discuss the photon energy and inverse-moment dependence of form factors. Sec. IV will be reserved for our conclusion.
-
The radiative leptonic decay amplitude for the D-meson can be written as
$\begin{aligned}[b] {\cal A}(D \to \gamma \, \ell \, \nu ) = &\frac{G_{\rm F} \, |V_{cd}|} {\sqrt{2}} \, \left \langle \gamma \, \ell \, \nu | \left [ \bar{\ell} \, \gamma_{\mu} \, (1- \gamma_5) \, \nu \right ] \,\right.\\&\times \left. \left [ \bar d \, \gamma^{\mu} \, (1- \gamma_5) \, c \right ] | D(p+q) \right \rangle , \end{aligned}$

(1) where
$ G_{\rm F} $ is the Fermi coupling constant, and$ |V_{cd}| $ is the CKM matrix element. We consider a D-meson with momentum$ p + q $ , where p and$ q = p_{\ell}+p_{\nu} $ denote the momenta of the photon and lepton pair, respectively. In the D-meson rest frame, we can decompose the four-momenta of the photon and lepton pair in the light-cone coordinate$ \begin{aligned}[b] p_{\mu} = \frac{n\cdot p}{2}\bar{n}_{\mu}\equiv E_{\gamma} \bar{n}_{\mu}, \quad q_{\mu} = \frac{n\cdot q}{2}\bar{n}_{\mu}+\frac{\bar{n}\cdot q}{2}n_{\mu}, \end{aligned}$

(2) and the velocity vector of the D-meson is
$ v_{\mu} = (p+q)_{\mu}/ $ $ m_D = (n_{\mu}+\bar{n}_{\mu})/2 $ , where$ n_{\mu} $ and$ \bar{n}_{\mu} $ satisfy$ n\cdot n = \bar{n}\cdot\bar{n} = 0 $ and$ n\cdot\bar{n} = 2 $ .One could compute the
$ D\to\gamma \,\ell\,\nu $ amplitude to the first order of the electromagnetic interaction [16]:$ \begin{aligned}[b] {\cal A}(D \to \gamma \, \ell \ \nu) =& {G_{\rm F} \, |V_{cd}| \over \sqrt{2}} \, \left ( {\rm i} \, g_{em} \, \epsilon_{\nu}^{\ast} \right ) \bigg \{ T^{\nu \mu}(p, q) \, \overline \ell \, \gamma_{\mu} \,\\&\times (1-\gamma_5) \nu + Q_{\ell} \, f_D \,\overline \ell \, \gamma^{\nu} \, (1-\gamma_5) \nu \bigg \}. \end{aligned} $

(3) Then, we rewrite the hadronic tensor in terms of
$ F_V $ and$ F_A $ $ \begin{aligned}[b] T_{\mu\nu}(p,q) =& -{\rm i}\int {\rm d}^4 x \, {\rm e}^{{\rm i} p \cdot x} \,\langle 0 | {T} \{j_{\mu, {em}}(x),\\& \left [\bar d \,\gamma_{\nu} (1-\gamma_5) c \right ] (0) \} | D(p+q) \rangle \,,\\ =& \epsilon_{\mu \nu \rho \sigma}\,p^{\rho}\,v^{\sigma}F_V-{\rm i}\big [g_{\mu\nu}\,p\cdot v-v_{\mu}\,p_{\nu} \big ]\hat{F}_A\\&-{\rm i}\frac{v_{\mu}\,v_{\nu}}{p\,v}f_D\,m_D+p_{\mu}\rm- \rm terms . . . \end{aligned} $

(4) with
$ \epsilon^{0123} = +1 $ , where$ j_{\mu,{ em}} = \sum_qQ_q\bar{q}\,\gamma_{\mu}\,q $ is the electromagnetic current, and the last term is canceled for the sake of$ \epsilon^*\cdot p = 0 $ . We can redefine$ F_A(n \cdot p) = \hat{F}_A(n \cdot p)+\frac{Q_{\ell} f_D}{v\cdot p}, $

(5) so the hadronic tensor can be written as
$ \begin{aligned}[b] T_{\nu \mu}(p, q) \rightarrow & \epsilon_{\mu \nu \rho \sigma} \, p^{\rho} \, v^{\sigma} \, F_V(n \cdot p)\\&\quad-{\rm i} \left [ g_{\mu \nu} \,v \cdot p - v_{\nu} \, p_{\mu} \right ] \,F_A(n\cdot p) +{\rm i}Q_{\ell} \, f_D \, g_{\mu \nu} \,, \end{aligned}$

(6) and the last term in the above can precisely cancel the second term in Eq. (3). Finally, we can write the differential decay rate of
$ D\rightarrow \gamma\, \ell \,\nu $ in terms of$ F_V $ and$ F_A $ $\begin{aligned}[b] \frac{{\rm d} \, \Gamma}{ {\rm d} \, E_{\rm \gamma}} \left ( D \to \gamma\, \ell \,\nu \right ) =& \frac{\alpha_{em} \, G_{\rm F}^2 \, |V_{cd}|^2}{6 \, \pi^2} \, m_D \, E_{\gamma}^3 \, \left ( 1- \frac{2 \, E_{\gamma}}{m_D} \right ) \,\\&\times \left [ F_V^2(n \cdot p) + F_A^2(n \cdot p) \right ] \,. \end{aligned}$

(7) The following task is to compute the form factors of the photon radiated from the down quark and charm quark.
-
Now we will evaluate the leading power and sub-leading power form factors in the framework of the dispersion relation. This approach was proposed in [14] for the calculation of
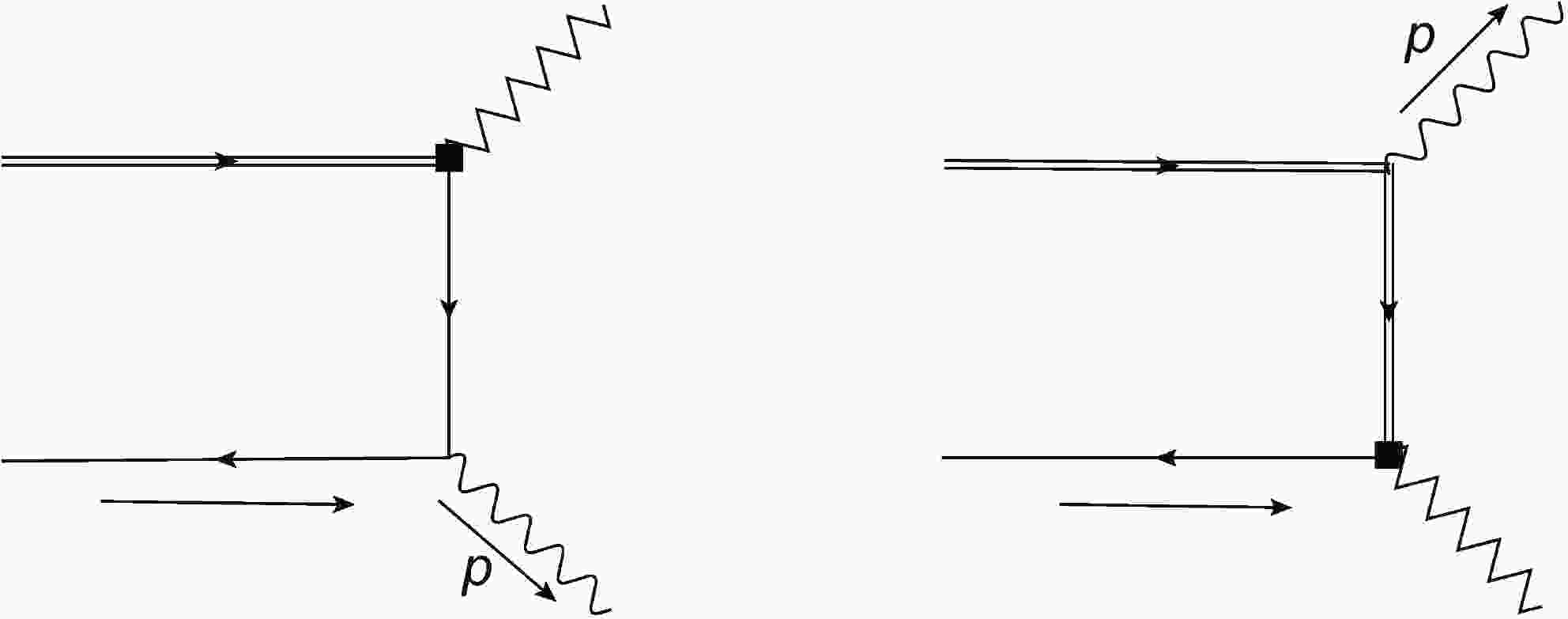
$ \gamma^*\,\gamma\to\pi $ form factors, and was applied to various processes [16, 32, 33]. In the dispersion approach, the photon in the final state of$ D\to\gamma \,\ell \,\nu $ becomes a space-like photon ($ p^2<0 $ ), and we can treat this process perturbatively. In the framework of heavy quark effective theory (HQET), the leading power form factors of two-particle tree-level contributions can be obtained by calculating the first diagram in Fig. 1 with a photon radiated from the down quark: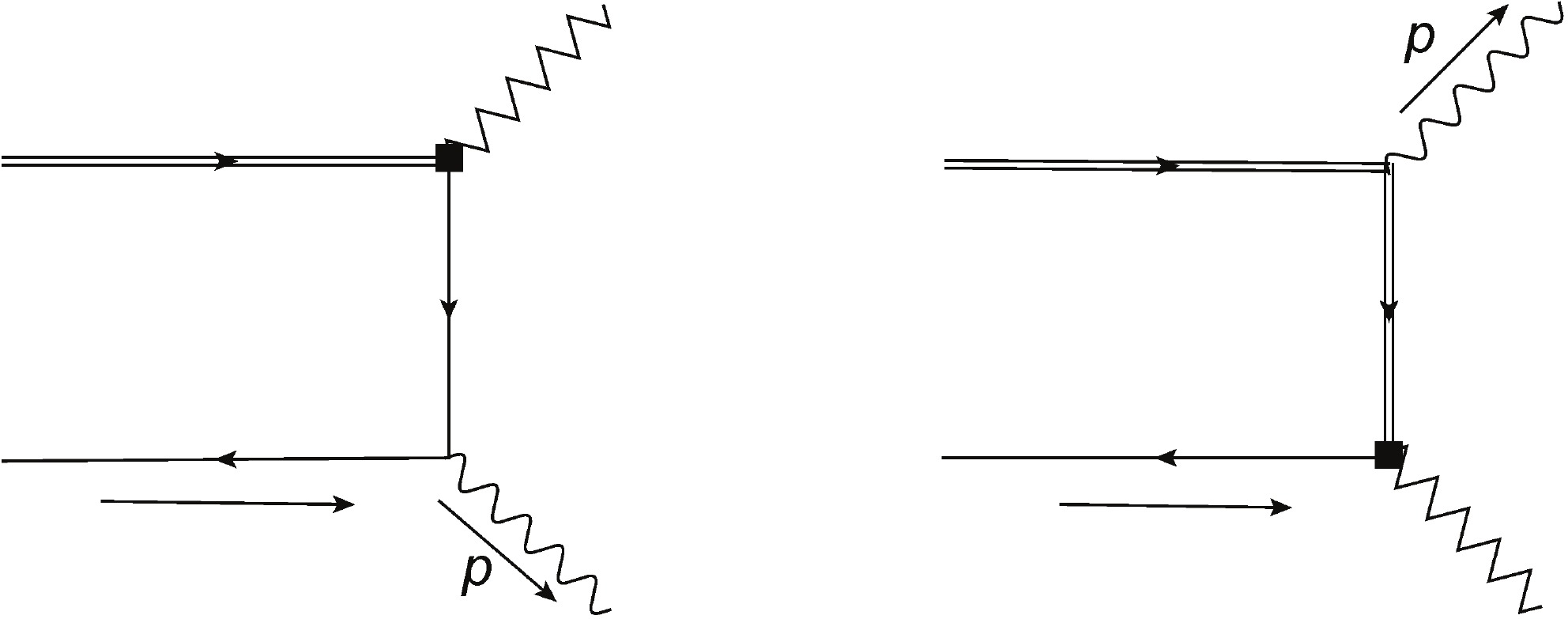
Figure 1. Feynman diagram of the two-particle contributions at tree level, where the double line represents the charm quark, the single line represents the down quark, and the square boxes refer to the weak vertex.
$ \begin{aligned}[b]& \{F_{V}^{D \to \gamma^{\ast}}(n \cdot p, \bar n \cdot p) ,\hat{F}_{A}^{D \to \gamma^{\ast}}(n \cdot p, \bar n \cdot p)\} \\ =& \frac{Q_d \, F_D(\mu) \, m_D}{n \cdot p} \, \, \int_0^{\infty} \, {\rm d} \omega \, \frac{\phi_D^+(\omega, \mu)}{\omega - \bar n \cdot p - {\rm i} 0} +{\cal O}(\alpha_s, \Lambda/m_c) \,, \end{aligned} $

(8) where
$ \phi_D^{+}(\omega, \mu) $ is the D-meson LCDA [34-36]$\begin{aligned}[b] {\rm i} \, F_D(\mu) \, m_D \, \phi_D^+(\omega, \mu) =& {1 \over 2 \, \pi} \, \int_0^{\infty} {\rm d} t \, {\rm e}^{{\rm i} \omega \, t } \, \langle 0 | (\bar q_s \, Y_s)(t \, \bar n) \\&\times\, \! \not \!\! {\bar n} \, \gamma_5 \, (Y_s^{\dagger} \, c_v)(0) | D(p+q) \rangle \,. \end{aligned}$

(9) In the above,
$ Y_s(t \, \bar n) $ is the soft Wilson line, and$ F_D(\mu) $ is the HQET decay constant:$ \begin{aligned}[b] F_D(\mu) =& [ K(\mu) ]^{-1} \, f_D \,, \\ K(\mu) =& 1 + {\alpha_s(\mu) \, C_F \over 4 \, \pi} \,\left [3\, \ln{m_c \over \mu} -2 \right ]. \end{aligned}$

(10) The QCD spectral density in our calculation is extracted from (8):
$ \begin{aligned}[b]{\rm Im}\, F_V^{D \to \gamma^{\ast}}(n \cdot p, \omega^{\prime}) =& {\rm Im}\,\hat{F}_A^{D \to \gamma^{\ast}}(n \cdot p, \omega^{\prime}) \\ =& \pi \frac{Q_d \, F_D(\mu) \, m_D}{n \cdot p} \, \phi_D^+(\omega^{\prime}, \mu)\\& +{\cal O}(\alpha_s, \Lambda/m_c) \,, \end{aligned} $

(11) and the expression (applicable to
$ F_V $ and$ F_A $ ) of the hadronic dispersion relation is given by$\begin{aligned}[b] F_{D\to\gamma^*}(n \cdot p, \bar n \cdot p) =& \frac{f_{\rho}F_{D\to\rho}(q^2)}{m_{\rho}^2-p^2}\\&+{1\over\pi} \int_{\omega_s}^{\infty}{\rm d}\omega\frac{{\rm Im}F_{D\to\gamma^*}(n \cdot p, \omega^{\prime})}{\omega_s-\bar n \cdot p}\, . \end{aligned} $

(12) According to the parton-hadron duality assumption, the spectral density
$ {\rm Im}\,F_{D\to\gamma^*}(n \cdot p, \bar n \cdot p) $ for$ F_V $ ($ F_A $ ) is the same as the QCD spectral density$ {\rm Im}\, F_V^{D \to \gamma^{\ast}}(n \cdot p, \omega^{\prime}) $ ($ {\rm Im}\, F_A^{D \to \gamma^{\ast}}(n \cdot p, \omega^{\prime}) $ ) for$ \omega>\omega_s $ . In the above, we have combined the contributions of$ \rho $ and$ \omega $ because of the assumption that$ m_\rho\simeq m_\omega $ . Equating (8) and (12) at$ \bar{n}\cdot p = 0 $ , one obtains the relation of the$ D\to\rho $ form factor$ F_{D\to\rho}(q^2) $ and the QCD spectral density. Performing the Borel transformation, we have$ \begin{aligned}[b] F_V(n \cdot p) =& {1 \over \pi} \, \int_{0}^{\infty} \,\,{\rm d} \omega^{\prime} \,\, \frac{1}{\omega^{\prime}} \, \, \left [{\rm Im}_{\omega^{\prime}} \, F_V^{D \to \gamma^{\ast}}(n \cdot p, \omega^{\prime}) \right ] \\& + {1 \over \pi} \, \int_0^{\omega_s} \,\,{\rm d} \omega^{\prime} \, \left \{ \frac{n \cdot p}{m_{\rho}^2} \, {\rm Exp} \left [{m_{\rho}^2 - \omega^{\prime} \, n \cdot p \over n \cdot p \, \omega_M} \right ]\right. \\&\left.- {1 \over \omega^{\prime}} \right \} \, \left [{\rm Im}_{\omega^{\prime}} \, F_V^{D \to \gamma^{\ast}}(n \cdot p, \omega^{\prime}) \right ] , \end{aligned} $

(13) $ \begin{aligned}[b] \hat{F}_A(n \cdot p) =& {1 \over \pi} \, \int_{0}^{\infty} \,\,{\rm d} \omega^{\prime} \,\, \frac{1}{\omega^{\prime}} \, \, \left [{\rm Im}_{\omega^{\prime}} \, \hat{F}_A^{D \to \gamma^{\ast}}(n \cdot p, \omega^{\prime}) \right ] \\ &+ {1 \over \pi} \, \int_0^{\omega_s} \,\,{\rm d} \omega^{\prime} \, \left \{ \frac{n \cdot p}{m_{\rho}^2} \, {\rm Exp} \left [{m_{\rho}^2 - \omega^{\prime} \, n \cdot p \over n \cdot p \, \omega_M} \right ]\right.\\&\left. - {1 \over \omega^{\prime}} \right \} \, \left [{\rm Im}_{\omega^{\prime}} \, \hat{F}_A^{D \to \gamma^{\ast}}(n \cdot p, \omega^{\prime}) \right ] , \end{aligned} $

(14) where
$ \omega_M $ is the Borel mass, and$ \omega_s $ is the effective threshold.Beyond tree level, the factorization formulae of the
$ D\to\gamma^* \,\ell\,\nu $ form factors at leading power are$ \begin{aligned}[b] F_{V}^{D \to \gamma^{\ast}}(n \cdot p, \bar n \cdot p) =& \hat{F}_{A}^{D \to \gamma^{\ast}}(n \cdot p, \bar n \cdot p) = \frac{Q_d \, F_D(\mu) \, m_D}{n \cdot p} \,\\&\times C_{\perp}(n \cdot p, \mu) \, \, \int_0^{\infty} \, {\rm d} \omega \, \frac{\phi_D^+(\omega, \mu)}{\omega - \bar n \cdot p - {\rm i} 0} \,\\&\times J_{\perp}(n \cdot p, \bar n \cdot p , \omega, \mu) + ... \,, \end{aligned} $

(15) where the hard function
$ C_{\perp}(n \cdot p, \mu) $ and jet function$ J_{\perp}(n \cdot p, \bar n \cdot p , \omega, \mu) $ are extracted simultaneously by perturbative matching with the method of regions. The expressions of the hard function and jet function at one loop have been calculated in [16]:$ \begin{aligned}[b] C_{\perp} =& 1- \frac{\alpha_s \, C_{\rm F}}{4 \, \pi} \bigg [ 2 \, \ln^2 {\mu \over n \cdot p} + 5 \, \ln {\mu \over m_c} -2 \, {\rm Li}_2 \left ( 1-{1 \over r} \right ) \\& - \ln^2 r + \, {3 r -2 \over 1 -r} \, \ln r + {\pi^2 \over 12} + 6 \bigg ] \,, \end{aligned} $

(16) $ \begin{aligned}[b] J_{\perp} =& 1 + {\alpha_s \, C_{\rm F} \over 4 \, \pi} \, \Bigg \{ \ln^2 { \mu^2 \over n \cdot p \, (\omega - \bar n \cdot p)} - {\pi^2 \over 6} - 1 - {\bar n \cdot p \over \omega} \,\\& \times \ln {\bar n \cdot p - \omega \over \bar n \cdot p } \, \left [ \ln { \mu^2 \over -p^2} + \ln { \mu^2 \over n \cdot p \, (\omega - \bar n \cdot p)} + 3 \right ] \Bigg \} \,, \end{aligned} $

(17) where
$ r = n\cdot p/m_c $ . Applying the Renormalization Group (RG) approach in the momentum space, we improve the factorization formulae for the form factors to NLL accuracy:$ \begin{aligned}[b]F_{V}^{D \to \gamma^{\ast}}(n \cdot p, \bar n \cdot p) =& \hat{F}_{A}^{B \to \gamma^{\ast}}(n \cdot p, \bar n \cdot p) = \frac{Q_d \, m_D\,f_D}{n \cdot p} \,\\&\!\times\! C_{\perp}(n\!\cdot\! p, \mu_{h1})K^{-1}(\mu_{h2})U(n \cdot p, \mu_{h1}, \mu_{h2}, \mu) \\ & \times \,\int_0^{\infty} \, {\rm d} \omega \, \frac{\phi_D^+(\omega, \mu)}{\omega - \bar n \cdot p - {\rm i} 0} \,\\&\times J_{\perp}(n \cdot p, \bar n \cdot p , \omega, \mu) + ... \,, \end{aligned} $

(18) where the factorization scale is chosen as a hard-collinear scale
$ \mu\sim\sqrt{\Lambda_{\rm QCD}\, m_c} $ , and hard scales$ \mu_{h1} $ and$ \mu_{h2} $ are of order$ m_c $ .$ U(n \cdot p, \mu_{h1}, \mu_{h2}, \mu) = U_1(n \cdot p, \mu_{h1}, \mu)\,U_2^{-1}(n \cdot p, $ $ \mu_{h2}, \mu) $ is the renormalization group equation of the hard function. The first factor$ U_1(n \cdot p, \mu_{h1}, \mu) $ (Appendix A) is given by solving$ \frac{{\rm d} U_1(n \cdot p, \mu_{h1}, \mu)}{{\rm d} \ln \mu} \, = \left [ \Gamma_{\rm {cusp}}(\alpha_s) \, \ln{\mu \over n \cdot p} + \gamma(\alpha_s) \right ] \, U_1(n \cdot p, \mu_{h1}, \mu) \, $

(19) with
$ U_1(\mu,\mu) = 1 $ as the initial condition, where$ \Gamma_{\rm {cusp}}(\alpha_s) $ and$ \gamma(\alpha_s) $ are the cusp anomalous dimension and anomalous dimension, respectively. The second factor$ U_2(n \cdot p,\mu_{h2}, \mu) $ is given by setting the cusp anomalous dimension in the expression of$ U_1(n \cdot p, \mu_{h1}, \mu) $ to zero. The explicit expressions of the two factors could be given by replacing$ E_{\gamma} $ of$ U_1(n \cdot p, \mu_{h1}, \mu) $ in [37] with$ n\cdot p/2 $ .Now we can obtain the dispersion relation of the
$ D\to\gamma $ form factors by setting$ \bar{n}\cdot p $ in (19) to zero and integrating the convolution integrals in the spectral representations (Appendix B):$ \begin{aligned}[b] F_{V, 2P}(n \cdot p) =& \hat{F}_{A,2P}(n \cdot p) = \frac{Q_d \, m_D\,f_D}{n \cdot p} \, C_{\perp}(n \cdot p, \mu_{h1})K^{-1}(\mu_{h2})U(n \cdot p, \mu_{h1}, \mu_{h2}, \mu) \ \ \, \, \Bigg \{ \,\int_0^{\infty} \, {\rm d} \omega \, \frac{\phi_D^+(\omega, \mu)}{\omega} \, J_{\perp}(n \cdot p, 0, \omega, \mu) \\ \ \ \,& + \int_0^{\omega_s} \,\,{\rm d} \omega^{\prime} \,\, \left [ \frac{n \cdot p}{m_{\rho}^2} \, {\rm Exp} \left [{m_{\rho}^2 - \omega^{\prime} \, n \cdot p \over n \cdot p \, \omega_M} \right ] - {1 \over \omega^{\prime}} \right ] \, \phi_{D, {\rm eff}}^+(\omega^{\prime},\mu) \, \Bigg \} \, \equiv F_{V, \rm LP}^{\rm NLL}(n \cdot p) + F_{V, \rm{NLP}}^{\rm{soft}}(n \cdot p) \,, \end{aligned} $ 
(20) where
$ F_{V, \rm LP}^{\rm NLL}(n \cdot p) $ and$ F_{V, \rm{NLP}}^{\rm{soft}}(n \cdot p) $ are expressions including the first part and second part in the brace only, respectively. The convolution integral [37] in the LP form factor is expressed as$ \begin{aligned}[b] &\int_0^{\infty} \, {\rm d} \omega \, \frac{\phi_D^+(\omega, \mu)}{\omega} \, \, J_{\perp}(n \cdot p, 0, \omega, \mu) \\ =& \lambda_D^{-1}(\mu) \, \Bigg \{ 1 + {\alpha_s(\mu) \, C_{\rm F} \over 4 \, \pi} \, \Bigg [\sigma_2(\mu) \end{aligned} $

$ \begin{aligned}[b] + 2 \, \ln {\mu^2 \over n \cdot p \, \mu_0} \, \sigma_1(\mu) + \ln^2 {\mu^2 \over n \cdot p \, \mu_0} - {\pi^2 \over 6} -1 \Bigg ] \Bigg \} \,, \end{aligned} $

(21) where the definition of the inverse moment is
$ \frac{1}{\lambda_D(\mu)} = \int_{0}^{\infty}{\rm d}\omega\frac{\phi_D^+(\omega,\mu)}{\omega}. $

(22) The effective distribution amplitude
$ \phi_{D,\rm eff}^{+} (\omega^{\prime},\mu) $ [33] in the soft form factor reads$ \begin{aligned}[b] \phi_{D,\rm eff}^+ (\omega^{\prime},\mu) = & \phi_{D}^+(\omega^{\prime},\mu) + \frac{\alpha_{s}(\mu)C_{\rm F}} {4\pi} \Bigg\{ \Bigg( \ln^{2}\frac{\mu^{2}}{n\cdot p \,\omega^{\prime}} + \frac{\pi^{2}}{6} - 1 \Bigg)\, \phi_{D,}^+(\omega^{\prime},\mu) + \, \Bigg(2\ln\frac{\mu^{2}}{n\cdot p\,\omega^{\prime}} + 3 \Bigg) \,\omega^{\prime} \int^{\infty}_{\omega^{\prime}} {\rm d}\omega \ln\frac{\omega-\omega^{\prime}}{\omega^{\prime}} \frac{\rm d}{{\rm d}\omega} \frac{\phi_{D}^+(\omega,\mu)}{\omega} \\ & - \,2\ln\frac{\mu^{2}}{n\cdot p\,\omega^{\prime}} \int^{\omega^{\prime}}_{0} {\rm d}\omega \ln\frac{\omega^{\prime}-\omega}{\omega^{\prime}} \frac{\rm d}{{\rm d}\omega} \phi_{D}^+(\omega,\mu) +\,\int^{\omega^{\prime}}_{0}{\rm d}\omega \ln^{2}\frac{\omega^{\prime}-\omega}{\omega^{\prime}} \frac{\rm d}{{\rm d}\omega} \Bigg[ \frac{\omega^{\prime}}{\omega} \phi_{D}^+(\omega,\mu) + \phi_{D}^+(\omega,\mu) \Bigg] \Bigg\}. \end{aligned} $ 
(23) -
In this section, we will compute the higher-twist contribution and the local sub-leading power contribution of radiative D-meson decay. The local sub-leading power contribution in this procedure is given by evaluating the second diagram and the local term of the first diagram in Fig. 1, which is the same as [37] by just changing the bottom quark to a charm quark according to the symmetry of heavy quarks:
$ \begin{aligned}[b] F_{V, \rm NLP}^{\rm {LC}}(n \cdot p) =& -\hat{F}_{A, \rm NLP}^{\rm {LC}}(n \cdot p) \\=& \frac{Q_d \, f_D \, m_D}{(n \cdot p)^2} + \frac{Q_c \, f_D \, m_D}{n \cdot p \, m_c} \,, \end{aligned} $

(24) where the first term and second term correspond to the photon emission from the down quark and charm quark, respectively.
The higher-twist contribution is from the non-local term of the propagator in the first diagram in Fig. 1. The hadronic tensor in the framework of HQET reads
$\begin{aligned}[b] T_{\mu\nu}(p,q) =& -{\rm i}Q_q \int {\rm d}^4x\,{\rm e}^{{\rm i}px}\langle 0 | T\{ \bar d(x) \gamma_\mu d(x),\,\\&\times \bar{d}(0)\gamma_\nu(1-\gamma_5)h_v(0)\}| D(p+q)\rangle + \ldots , \end{aligned} $

(25) where the following tree level matching of the heavy-to-light currents is used:
$ \bar{d} \gamma_{\mu} c = \bar{d}\gamma_{\mu}h_v+\ldots\,. $

(26) We will consider the contribution from two-particle twist-4 and three-particle LCDA of the D-meson. In the calculation of the contribution from three-particle LCDA of the D-meson, the light-cone expansion of the quark propagator [38] in (25) is required:
Inserting the above propagator into the correlation function (25), we can obtain the factorization formula of the higher-twist contribution. At tree level, the factorization formula can be further simplified by taking advantage of the QCD equation of motion to relating the two-particle and three-particle LCDAs. Finally, we arrive at the higher-twist contributions:
$ \begin{aligned}[b] F_{V,\rm NLP}^{\rm{HT}}(n \cdot p) =& \hat{F}_{A,\rm NLP}^{\rm{HT}}(n \cdot p) \\=& -\frac{2 Q_d f_D m_D}{(n\cdot p)^2}\left [\frac{2(\lambda_E^2+2\lambda_H^2)}{6\bar{\Lambda}^2+2\lambda_E^2+\lambda_H^2}+\frac{1}{2}\right ],\end{aligned}$

(28) where
$ \lambda_E^2 $ and$ \lambda_H^2 $ denote the higher-twist matrix elements defined by$ \begin{aligned}[b]& {\langle 0| \bar q(0) g_sG_{\mu\nu}(0)\Gamma h_v(0)|D(p+q)\rangle } \\ =& -\frac{\rm i}{6} F_D \lambda^2_H {\rm Tr}\Big[\gamma_5\Gamma P_+ \sigma_{\mu\nu}\Big] \\ & -\frac{1}{6} F_D\Big( \lambda^2_H- \lambda^2_E\Big) {\rm Tr}\Big[\gamma_5\Gamma P_+(v_\mu\gamma_\nu-v_\nu\gamma_\mu)\Big]\,, \end{aligned} $

(29) and
$ \bar{\Lambda} = m_D-m_c $ . This expression is the same as the first term in [33].Collecting the results of (20), (24), and (28) together, we obtain the form factors of D-meson decay including the NLP corrections:
$ \begin{aligned}[b] F_{V}(n \cdot p) =& F_{V,\rm LP}^{\rm NLL}(n \cdot p) +F_{V,\rm NLP}^{\rm soft}(n \cdot p) \\& + F_{V,\rm NLP}^{\rm LC}(n \cdot p)+F_{V,\rm NLP}^{\rm HT}(n \cdot p) \,, \end{aligned} $

(30) $ \begin{aligned}[b] \hat{F}_{A}(n \cdot p) =& \hat{F}_{A, \rm LP}^{\rm NLL}(n \cdot p) + \hat{F}_{A,\rm NLP}^{\rm soft}(n \cdot p)\\& + \hat{F}_{A,\rm NLP}^{\rm LC}(n \cdot p) +\hat{F}_{A,\rm NLP}^{\rm HT}(n \cdot p)\,. \end{aligned} $

(31) -
Following [39], the power counting scheme relies on the behavior of the D-meson distribution amplitude (DA):
$ \phi_D^+(\omega, \mu_0) \sim \left\{ \begin{array}{l} {1 / \Lambda} \,; \qquad \omega \sim \Lambda \\ 0 \,; \qquad \quad \omega \gg \Lambda \end{array} \right. , $

(32) implying that the power counting of the inverse moment is
$ \lambda_D(\mu_0)\sim\Lambda $ with$ \omega\sim\Lambda $ . However, the scaling of the inverse moment should be$ \lambda_D(\mu_0)\sim \Lambda^2/m_c $ with$ \lambda_D(\mu_0) \leqslant $ $ 100\; \rm MeV $ in the heavy quark limit, and this will lead to$\begin{aligned}[b] F_{V}^{\rm LP} \sim F_{V}^{\rm soft} \sim \left ( {m_c \over \Lambda} \right )^{1/2} , \;\; {\rm for} \;\; \lambda_D(\mu_0) \sim \Lambda^2/m_c \,, \end{aligned} $

(33) this region will be shown in our numerical analysis of
$ \lambda_D $ dependence. When$ \lambda_D(\mu_0)\geqslant 200\;\rm MeV $ , the power counting scheme becomes$\begin{aligned}[b]& F_{V, \rm 2P}^{\rm{LP}} \sim \left ( {\Lambda \over m_c} \right )^{1/2} \,, \;\;F_{ V,\rm 2P}^{\rm{NLP}} \sim \left ( {\Lambda \over m_c} \right )^{3/2} \,, \;\; {\rm for} \;\; \lambda_D(\mu_0) \sim \Lambda \,, \end{aligned} $

(34) which is consistent with typical power counting rules.
-
We consider two models of the two-particle D-meson DA
$ \phi_D^+(\omega,\mu_0) $ [16] in our calculation:$ \phi_{D,\rm I}^+(\omega,\mu_0) = \frac{\omega}{\omega_0^2} \, {\rm e}^{-\omega/\omega_0} \,, $

(35) $ \phi_{D,\rm II}^+(\omega,\mu_0) = \frac{1}{4 \pi \,\omega_0} \, {k \over k^2+1} \, \left[ {1 \over k^2+1} - \frac{2 (\sigma_{1}(\mu_0) -1)}{\pi^2} \, \ln k \right ] \,, $

(36) where
$ \omega_0 = \lambda_D(\mu_0) $ , and$ k = \omega/(1 \,\, \rm GeV) $ .$ \phi_{D,\rm I}^+(\omega,\mu_0) $ and$ \phi_{D,\rm II}^+(\omega,\mu_0) $ are based upon the Grozin-Neubert parametrization (left panel) and Braun-Ivanov-Korchemsky parametrization (right panel), respectively. The value of$ \lambda_D(\mu_0) $ is taken from lattice simulations [40]. From the one loop evolution equation of$ \phi_D^+(\omega,\mu) $ [41, 42], we derive the scale-dependence of the inverse moment$ \frac{\lambda_D(\mu_0)}{\lambda_D(\mu)} = 1\!+\! {\alpha_s(\mu_0) \, C_{\rm F} \over 4 \, \pi} \, \ln {\mu \over \mu_0} \, \left [2 - 2\, \ln {\mu \over \mu_0} \!-\! 4 \sigma_{1}(\mu_0) \right ] + {\cal O}(\alpha_s^2)\,. $

(37) In the above,
$ \sigma_1(\mu_0) $ ($ \sigma_2(\mu_0) $ in (21)) is the inverse-logarithmic moment. The definition of the inverse-logarithmic moment [37] is$ \sigma_n(\mu) = \lambda_D(\mu)\int_{0}^{\infty}\frac{{\rm d}\omega}{\omega}{\rm ln}^n\frac{\mu_0}{\omega}\phi_{D}^+(\omega,\mu), $

(38) where
$ \mu_0 $ is fixed at$ 1\, \rm GeV $ . One could find the other numerical values of the input parameters in Table 1; the factorization scale interval is$ \mu = 1.2\pm0.2\;\rm GeV $ , and the hard scale ($ \mu_{h1} = \mu_{h2} = {\cal O}(m_c) $ ) interval is$ m_c/2\sim 2\,m_c $ .Parameter DATA Parameter DATA $ m_D $ 

$ 1.86965\pm0.05\, \rm GeV $ 

$ n\cdot p\,\omega_s $ 

$ (1.5\pm0.2)\,\rm GeV^2 $ 

$ \tau_D $ 

$ (1.040\pm0.007)\times10^{-12}\,s $ 

$ \mu_{h1} $ 

$ 1.288\, \rm GeV $ 

$ m_c $ 

$ 1.288\pm0.020\, \rm GeV $ 

$ \mu_{h2} $ 

$ 1.288\, \rm GeV $ 

$ m_d $ 

$ 4.71\pm0.09\, \rm MeV $ 

$ \mu_0 $ 

$ 1\, \rm GeV $ 

$ |V_{cd}| $ 

0.221 $ \pm $ 0.004

$ \mu $ 

$ (1.2\pm0.2)\,\rm GeV $ 

$ \lambda_D(\mu_0) $ 

$ 0.354_{-0.03}^{+0.038}\,\rm GeV $ 

$ f_D $ 

$ 212.0\pm0.7\, \rm MeV $ 

$ \sigma_1(\mu_0) $ 

$ 1.5\pm1 $ 

$ \lambda_E^2/\lambda_H^2 $ 

$ 0.5\pm0.1\,\rm $ 

$ \sigma_2(\mu_0) $ 

$ 3\pm2 $ 

$ 2\lambda_E^2+\lambda_H^2 $ 

$ 0.25\pm0.15\,\rm GeV^2 $ 

$ n\cdot p\,\omega_M $ 

$ (1.25\pm 0.25)\,\rm GeV^2 $ 

$ \bar{\Lambda} $ 

$ 0.58\, \rm GeV $ 

We take
$ \phi_{D,\rm I}^+ $ as the default model in the following analysis. With$ \lambda_D(\mu_0) = 354\,\rm MeV $ and the kinematic region$ n\cdot p\in [ 1 \,{\rm GeV}, m_D ] $ , we evaluate the sub-leading power contributions of$ D\to\gamma \,\ell \,\nu $ . As shown in Fig. 2, the sub-leading power contributions are sizeable. The higher-twist contribution reduces the leading power contribution by approximately 35%$ \sim $ 65%, and the soft contribution$ F_{V,\rm NLP}^{\rm soft} $ leads to a 30%$ \sim $ 60% reduction in the leading power contribution$ F_{V,\rm LP}^{\rm NLL} $ . The local sub-leading power contribution is insensitive to the photon energy, and the correction to the LP form factor is approximately 20%$ \sim $ 40%. Comparing the soft vector form factor$ F_{V,\rm NLP}^{\rm soft,LL} $ with$ F_{V,\rm NLP}^{\rm soft,NLL} $ , we find the perturbative QCD correction gives rise to an approximately 12.5% shift compared to the leading logarithm (LL) contribution. From the above discussion, we conclude that the leading power contribution is mainly corrected by the soft and higher-twist contributions at low photon energy, and the local sub-leading correction to the LP form factor is enhanced at high photon energy.
Figure 2. (color online) Photon-energy dependence of various contributions to the form factor
$ F_V(2E_{\gamma}) $ , with the exponential model of$ \phi_D^{+}(\omega, \mu_0) $ and the inverse moment$ \lambda_D(\mu_0) $ = 354 MeV.Now we investigate the
$ \lambda_D(\mu_0) $ dependence of the sub-leading power contributions. As shown in Fig. 3, the form factor$ F_{V,\rm NLP}^{\rm soft,NLL} $ decreases rapidly when$ \lambda_D\leqslant $ $ 0.15 \;\rm GeV $ . With$ \lambda_D = 0.1\; \rm GeV $ , the form factor$ F_{V,\rm NLP}^{\rm soft,NLL} $ can decrease the leading power contribution by approximately 100% at$ n\cdot p = m_D $ and 130% at$ n\cdot p = 1\; \rm GeV $ . The NLL resummation gives a sizable correction to$ F_{V,\rm NLP}^{\rm soft,LL} $ , both of$ {\cal O} $ (50%) with$ \lambda_D(\mu_0) = 0.1\;\rm GeV $ and$ \lambda_D(\mu_0) = m_D $ . The higher-twist correction to the form factor$ F_V $ at$ \lambda_D = 0.1\; \rm GeV $ is approximately 10% at$ E_{\gamma} = m_D $ and 18% at$ E_{\gamma} = 1\; \rm GeV $ , and this result could be explained by the analytical expression (28). As the results are insensitive to the inverse moment of the D-meson LCDA, the higher-twist and local sub-leading power corrections to the leading power form factors are enhanced with increasing inverse moment. In short, the next-to-leading power contributions are large with small$ \lambda_D(\mu_0) $ , and the higher-twist and local sub-leading power corrections among them are insensitive to the inverse moment.
Figure 3. (color online) Dependence of the leading and subleading power two-particle contributions to the form factor
$ F_V(n\cdot p) $ on the inverse moment$ \lambda_D(\mu_0) $ at zero momentum transfer (left panel) and at$ n\cdot p $ = 1 GeV (right panel).We have discussed the
$ \lambda_D(\mu_0) $ dependence of the form factors$ F_V $ and$ F_A $ in detail, and now we will focus on the dependence on the D-meson LCDA models and the photon energy. From Fig. 4, we find that both$ F_V $ and$ F_{\rm A} $ are insensitive to the models for a large value of inverse moment. This can be easily concluded from Fig. 3, and the discrepancies of the form factor predictions from different models are enhanced at$ n\cdot p = 1\;\rm GeV $ . The photon energy dependence of the$ D\to\gamma $ form factors$ F_V $ ,$ F_A $ , and their difference$ F_A-F_V $ are shown in Fig. 5. In our calculation, the uncertainties arise from the errors of$ \mu $ ,$ \lambda_D(\mu_0) $ ,$ \sigma_1(\mu_0) $ and$ \sigma_2(\mu_0) $ , and different models of D-meson$ \phi_D^+(\omega,\mu_0) $ . It is easy to find that the soft contribution is sensitive to the shape of$ \phi_D^+(\omega,\mu_0) $ at small$ \omega $ from the analytical expression of$ F_{V,\rm NLP}^{\rm soft,NLL} $ . As the soft and higher-twist contributions are symmetry conserved, the symmetry breaking effect originates from the local sub-leading correction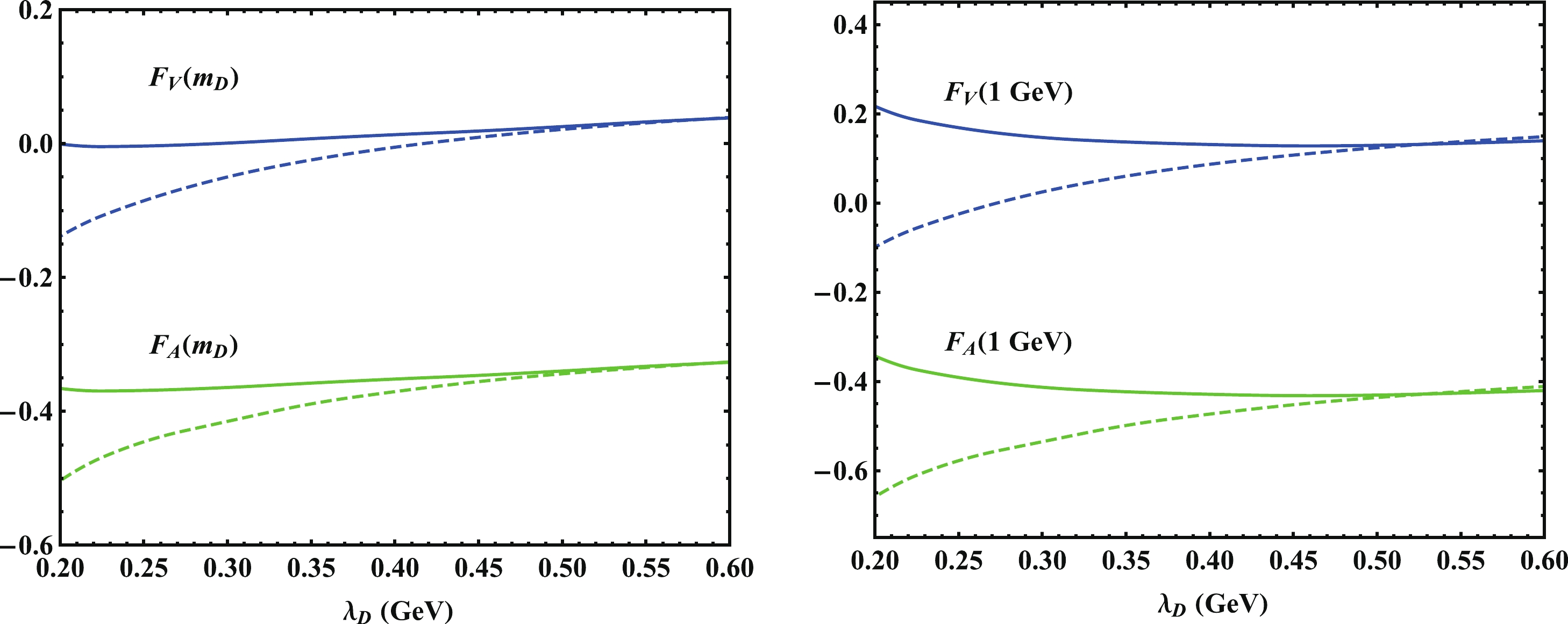
Figure 4. (color online) Dependence of the form factors on specific models for the D-meson DA at
$ n\cdot p = m_D $ and at$ n\cdot p = 1\; \rm GeV $ . The solid and dashed blue (green) curves indicate the predictions of$ F_V(F_A) $ from model$ \phi_{D,\rm I}^+ $ and model$ \phi_{D,\rm II}^+ $ , respectively.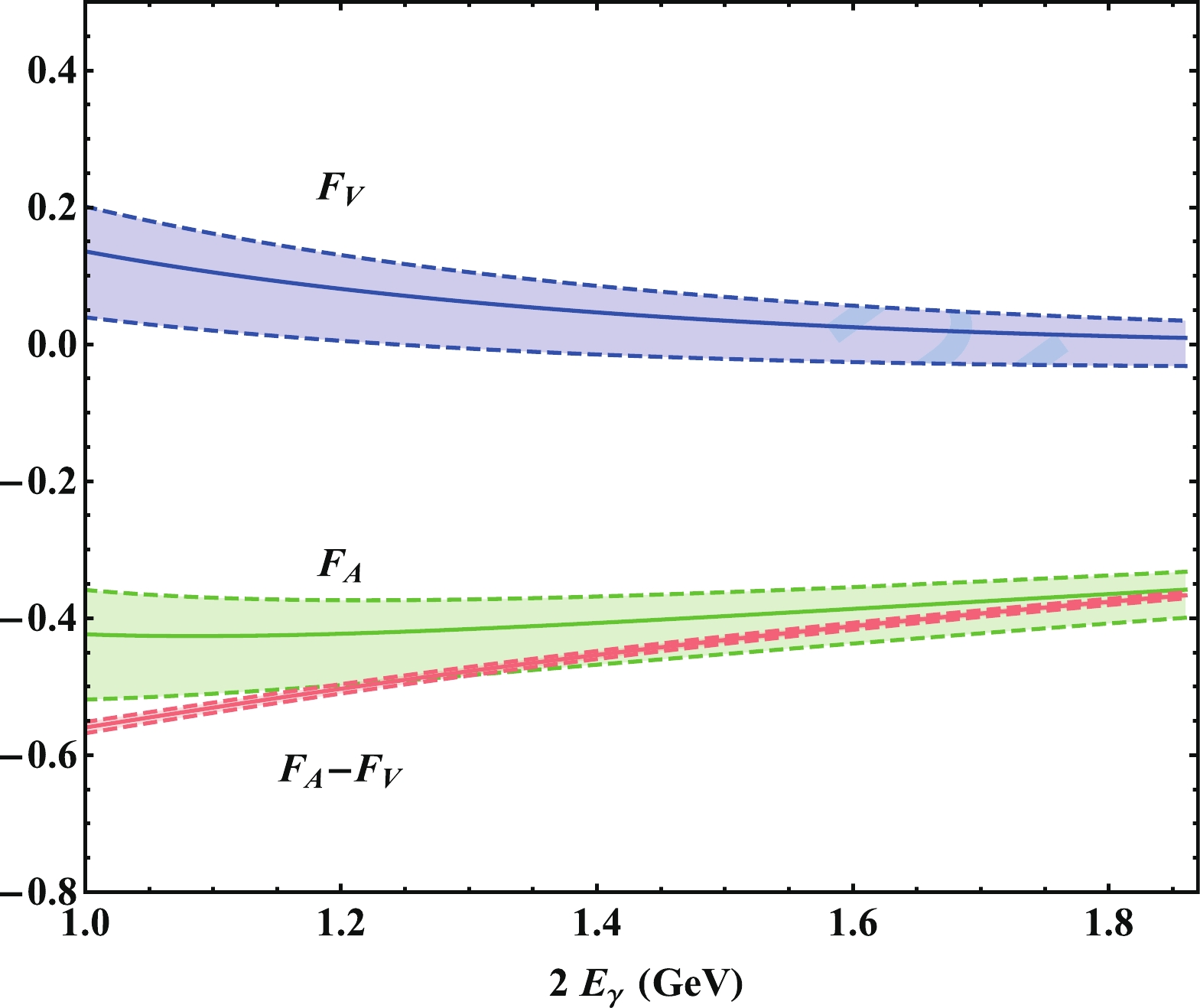
Figure 5. (color online) Photon-energy dependence of the form factors
$ F_V(2\,E_{\gamma}) $ and$ F_A(2\,E_{\gamma}) $ as well as their difference with$ \lambda_D(\mu_0) $ = 354 MeV.$ F_{ A}(n \cdot p)-F_{V}(n \cdot p) = {2 \, f_D \over n \cdot p} \, \left [Q_{\ell} - {Q_d \, m_D \over n \cdot p} - {Q_c \, m_D \over m_c} \right ] + {\cal O}(\alpha_s) \,. $

(39) We should note that the local sub-leading power correction only depends on the decay constant
$ f_D $ , and this can explain why the uncertainty of$ F_{A}-F_{V} $ is so small.We now consider the theory constraint on
$ \lambda_D(\mu_0) $ . As we have chosen the power counting scheme$ n\cdot p = 2\,E_{\gamma}\sim{\cal O}(m_D) $ in our calculation of the factorization formula, we should write the integrated decay rate as$ \Delta {\cal BR}(E_{\rm cut}) = \tau_{D} \, \int_{E_{\rm cut}}^{m_D/2} \, {\rm d} \, E_{\rm \gamma} \,\, \frac{{\rm d} \, \Gamma}{ {\rm d} \, E_{\rm \gamma}} \left ( D \to \gamma \ell \nu \right ) \,. $

(40) From the BES-III experiment, we know the upper limit on the branching ratio
$ \Delta {\cal BR}(E_{\gamma}\geqslant 10\;\rm MeV)< $ $ 3\times10^{-5} $ with photon energy larger than$ 10\; \rm MeV $ . As the photon emission off the charged particle is not a soft photon, we can choose$ E_{\rm cut} = 0.5\;\rm GeV $ . One can see from the left panel of Fig. 6 that there is no bound on$ \lambda_D(\mu_0) $ for the Grozin-Neubert mode after including the soft and higher-twist contributions. With$ \lambda_D(\mu_0) = 354\;\rm MeV $ , our prediction of the branching fraction is$ (1.88_{-0.29}^{+0.36})\times10^{-5} $ . The right panel of Fig. 6 shows that the branching ratio of the DA model$ \phi_{D,\rm II}^+(\omega,\mu_0) $ is large at small$ \lambda_D(\mu_0) $ , and the experimental result yields a bound$ \lambda_D(\mu_0)>270\;\rm MeV $ . To understand this result, we should note that the behavior of the form factors in the Braun-Ivanov-Korchemsky model is sensitive to the inverse moment of D-meson LCDA at small$ \lambda_D(\mu_0) $ . The prediction of the branching fraction from this model is$ (2.31_{-0.54}^{+0.65})\times10^{-5} $ . It is difficult to extract the inverse moment of D-meson LCDA in the$ D\to\gamma\,\nu\,\ell $ decays as the inverse moment dependence of the NLP corrections is complicated. As shown in Fig. 7, the higher-twist and local sub-leading power corrections are enhanced with increasing inverse moment, and the large correction makes it hard to extract the inverse moment.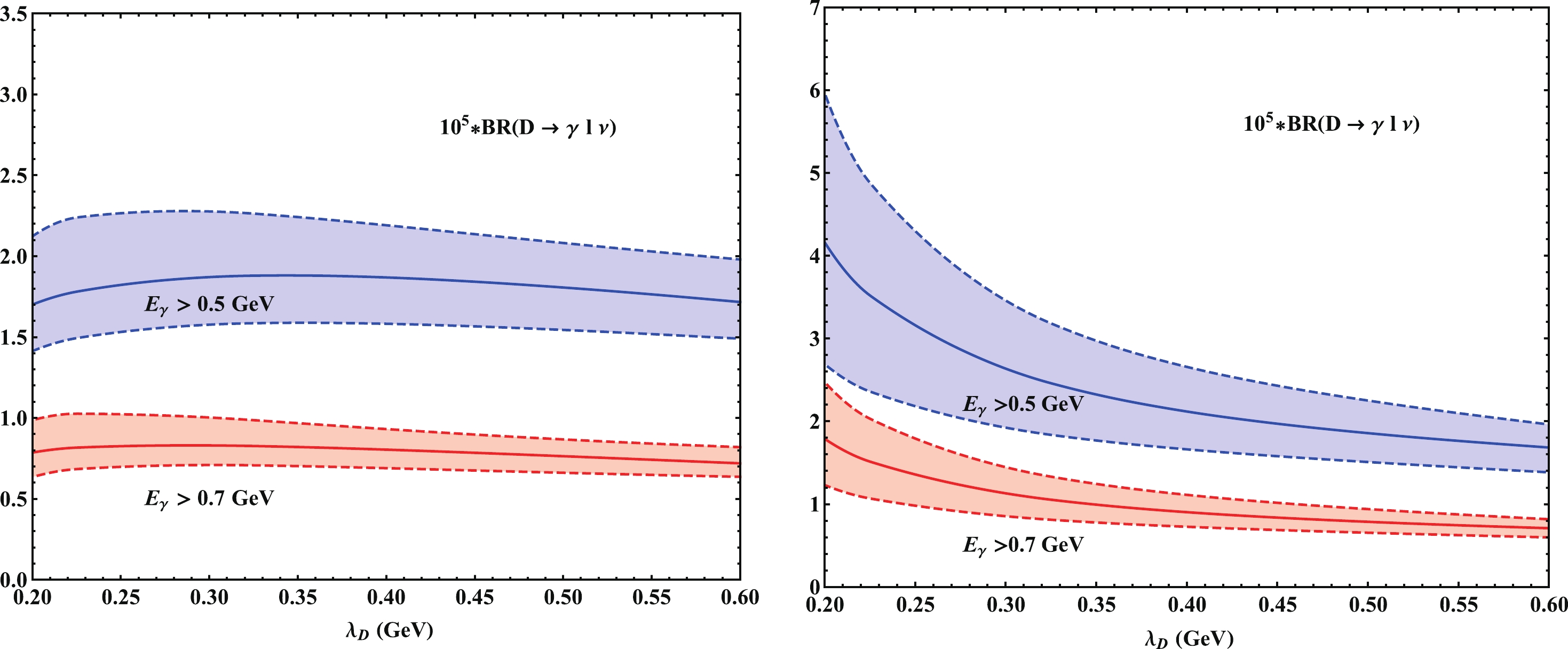
Figure 6. (color online) Blue band shows the inverse-moment
$ \lambda_D(\mu_0) $ dependence of the partial branching fractions of$ {\cal BR}(D\rightarrow\gamma l\nu,E_{\gamma}\geq E_{cut}) $ for$ E_{\rm cut} $ = 0.5 GeV with the model$ \phi_{D,\rm I}^+(\omega,\mu_0) $ based upon the Grozin-Neubert parametrization (left panel) and with the model$ \phi_{D,\rm II}^+(\omega,\mu_0) $ based upon the Braun-Ivanov-Korchemsky parametrization (right panel). The red band shows the inverse-moment$ \lambda_D(\mu_0) $ dependence of the partial branching fractions for$ E_{\rm cut} $ = 0.7 GeV with the model$ \phi_{D,\rm I}^+(\omega,\mu_0) $ (left panel) and with the model$ \phi_{D,\rm II}^+(\omega,\mu_0) $ (right panel).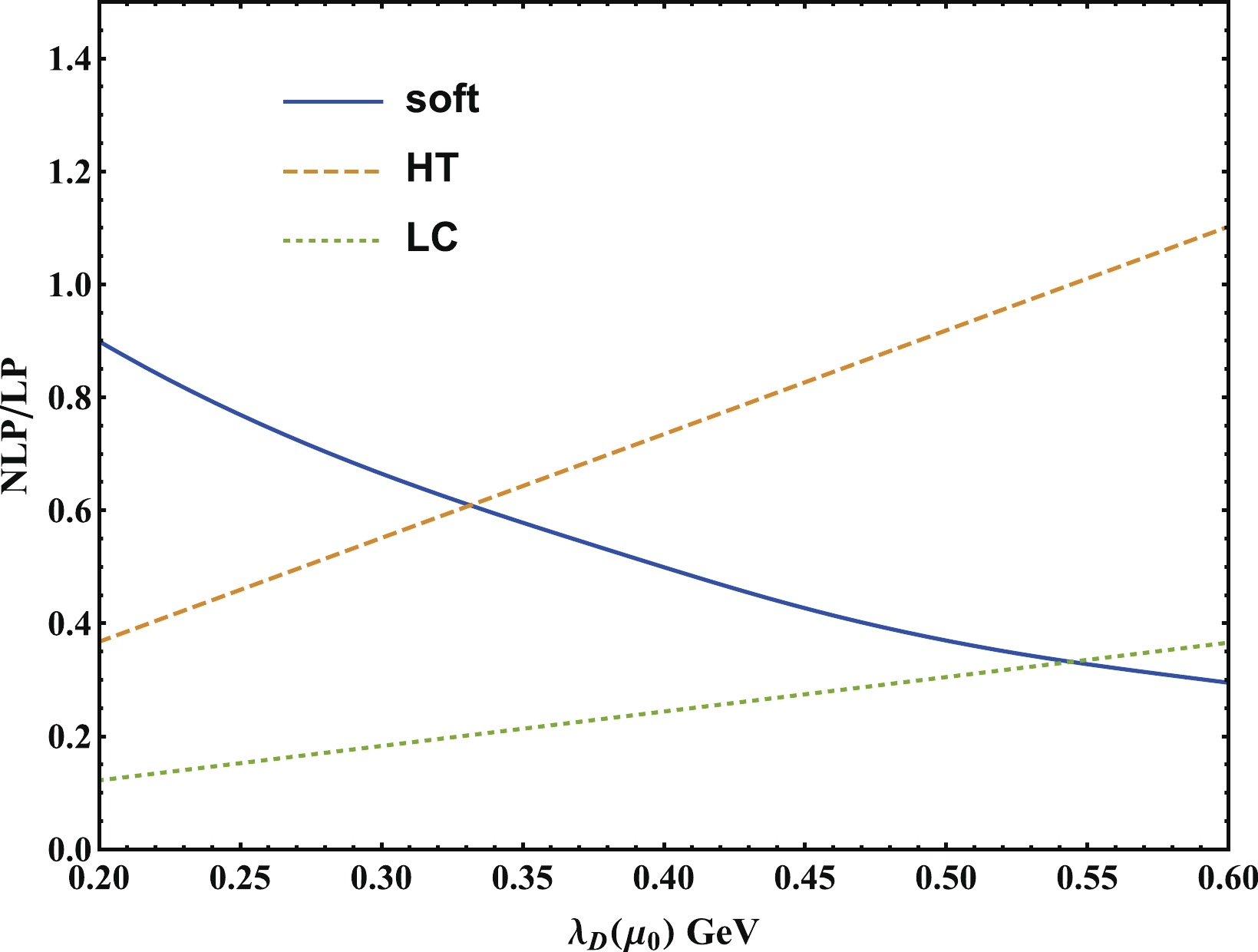
Figure 7. (color online) Dependence of the NLP corrections to the LP vector form factor from the D-meson DA model
$ \phi_{D,\rm I}^+(\omega,\mu_0) $ on the inverse moment with$ n\cdot p = 1 $ GeV.We know theoretically that the power corrections of
$ 1/m_c $ will be significant, and now we will estimate the corrections in practice. Although it is less effective to study the radiative leptonic D-meson decay by the factorization approach, we can still deepen our understanding of the factorization approach through the$ D\to\gamma\,l\,\nu $ process. If we fix the photon energy at 0.5 GeV, and adopt the D-meson LCDA as$ \phi_{D,\rm I}^+(\omega,\mu_0) $ , the NLP correction to the LP form factors is approximately 143%, and the correction is approximately 120% when the LCDA model$ \phi_{D,\rm II}^+(\omega,\mu_0) $ is adopted. The above results indicate that the power suppressed contributions play important roles in radiative leptonic D-meson decays, which is consistent with the theoretical analysis.The theoretical uncertainties from the LCDA parameters are collected in Table 2, and the errors from these parameters are approximately 10%
$ \sim $ 20%. These results suggest that the uncertainties from the inverse-logarithmic moment$ \sigma_2(\mu_0) $ are great, while the dependence of the model$ \phi_{D,\rm II}^+(\omega,\mu_0) $ on$ \sigma_1(\mu_0) $ and$ \lambda_D(\mu_0) $ is more remarkable. Comparing results evaluated from the total form factor$ F_V $ and$ F_A $ with the LP form factor$ F_{V,\rm LP}^{\rm NLL} $ and$ F_{A,\rm LP}^{\rm NLL} $ , it is manifest that sub-leading power contributions yield a correction of approximately$ {\cal O} $ (100%) to the branching fraction.$ {\rm BR}\times 10^{6} $ 

$ \lambda_D(\mu_0)[\omega_0] $ 

$ \mu $ 

$ \sigma_1(\mu_0) $ 

$ \sigma_2(\mu_0) $ 

$ \phi_{D,\rm I}^+ $ 

18.8 $ +0.0 $ 

$ +0.74 $ 

$ +0.59 $ 

$ +2.01 $ 

−0.08 −0.87 −0.36 −1.56 $ \phi_{D,\rm II}^+ $ 

23.1 +1.64 +0.53 +4.73 +2.41 −1.58 −0.9 −3.88 −2.17 $ \rm LP \ results $ 

12.5 +2.4 +0.0 +0.45 +2.45 −2.2 −0.46 −0.68 −2.44 Table 2. Branching fraction uncertainties with
$ \lambda_D(\mu_0) = 354\;\rm MeV $ associated with the inverse moment, the factorization scale, and two inverse-logarithmic moments$ \sigma_1(\mu_0) $ and$ \sigma_2(\mu_0) $ . The LP results are evaluated from$ F_{V,\rm LP}^{\rm NLL} $ and$ F_{A,\rm LP}^{\rm NLL} $ , and the others are evaluated from$ F_V $ and$ F_A $ .Now we make a comparison with other works. Numerical results of different methods have been collected in Table 3. Results from various methods are consistent with the experimental upper limit except for the pQCD and RIQM results. The work of NRQM [6] is an extension of [7] by including the diagrams of a photon emission from a heavy quark, lepton, and W-boson, which leads to a much smaller result. In [4], the LFQM was used to calculate the
$ D\to\gamma $ form factor, and gave a reliable prediction of the D-meson decay. The$ {\cal O}(\Lambda_{\rm QCD}/m_D) $ correction in the factorization method was calculated in [1], which was extended in [2] by including the soft photon region. The predictions of these two works have been verified experimentally. We improve the factorization calculation to the NLP corrections, and our predictions of the branching fraction are in agreement with the experimental upper limit. However, as shown in Table 2, the sub-leading power contributions are important in this work. From the above results, we conclude that our results are still below the upper limit of the experimental result, and predictions of the branching fraction with$ E_{\gamma}>0.5\;\rm GeV $ need further experimental verification.Method BR Method BR Model $ \phi_{D,\rm I}^+ $ 

$ (1.88_{-0.29}^{+0.36})\times10^{-5} $ 

NRQM [6] $ 4.6\times10^{-6} $ 

Model $ \phi_{D,\rm II}^+ $ 

$ (2.31_{-0.54}^{+0.65})\times10^{-5} $ 

pQCD [8] $ (0.82\pm0.65)\times10^{-4} $ 

LFQM [4] $ 2.5\times10^{-5} $ 

RIQM [5] $ 3.34\times10^{-5} $ 

QCDF [2] $ 1.92\times10^{-5} $ 

BES-III [3] $<3\times10^{-5} $ 

Table 3. Results from different methods.
-
We studied the NLP contributions of radiative leptonic D-meson decay within the framework of factorization. In the study of D-meson decay, both the QCD correction and the power correction are large because the charm quark mass
$ m_c $ is not sufficiently large. After including the NLP corrections, the theoretical prediction is highly improved. In addition, we provided the analytic expressions of the NLP form factors for$ D\to\gamma \,\ell\,\nu $ with the soft contribution, the power suppressed local contribution and the higher-twist contribution included, and the error estimate from the expansion of$ m_c $ .When using the model based on the Grozin-Neubert parametrization, the power suppressed correction is dominated by the soft and higher-twist contributions with
$ \lambda_D(\mu_0) = 354\;\rm MeV $ . The experimental upper limit yields a bound$ \lambda_D(\mu_0)>270\;\rm MeV $ according to the dependence of branching fractions of the DA model$ \phi_{D,\rm II}^+ $ on the inverse moment of D-meson LCDA, but the importance of the power corrections indicates that it is difficult to extract the appropriate inverse moment. Numerically, we found that all the sub-leading power contributions are significant at$ \lambda_D(\mu_0) = 354\;\rm MeV $ , and the next-to-leading power contributions will lead to 143% in$ \phi_{D,\rm I}^+ $ and 120% in$ \phi_{D,\rm II}^+ $ corrections to leading power vector form factors with$ E_{\gamma} = 0.5\;\rm GeV $ .To summarize, the branching fraction predictions in this work are in agreement with the experimental upper limit, though the NLP corrections are significant. The effects of the power corrections require both theoretical and experimental studies, and we hope an experiment on
$ E_{\gamma}>0.5\;\rm GeV $ can be conducted in the future. Other sources of the power correction exist, such as the power suppressed heavy quark field and the non-local power suppressed terms in the light quark propagator; they will be investigated in future studies. -
The author would like to thank Yu-Ming Wang for illuminating discussions.
-
This expression has been calculated in [37], and the second factor just requires us to set the cusp anomalous dimension to zero; details can be found in this reference.
$\tag{A1} \begin{aligned}[b] U_1(E_\gamma,\mu_h,\mu) = & \exp\left(\,\int_{\alpha_s(\mu_h)}^{\alpha_s(\mu)} {\rm d}\alpha_s\, \left[ \frac{\gamma(\alpha_s)}{\beta(\alpha_s)} + \frac{\Gamma_{\rm cusp}(\alpha_s)}{\beta(\alpha_s)} \left( \ln\frac{2 E_\gamma}{\mu_h} - \int_{\alpha_s(\mu_h)}^{\alpha_s} \frac{{\rm d}\alpha_s^\prime}{\beta(\alpha_s^\prime)} \right) \right]\right) \\ = &\,\exp\left(\, -\frac{\Gamma_0}{4\beta_0^2} \left( \frac{4\pi}{\alpha_s(\mu_h)}\left[\ln r-1+\frac{1}{r}\right] \right.\right.-\frac{\beta_1}{2 \beta_0} \,\ln^2 r \left.\left.+\left(\frac{\Gamma_1}{\Gamma_0}-\frac{\beta_1}{\beta_0}\right) \left[r-1-\ln r\right]\right) \right) \left(\frac{2 E_\gamma}{\mu_h}\right)^ {-\frac{\Gamma_0}{2\beta_0} \ln r} r^{-\frac{\gamma_0}{2\beta_0}} \\ & \times \Bigg[1 - \frac{\alpha_s(\mu_h)}{4\pi}\,\frac{\Gamma_0}{4\beta_0^2} \,\Bigg(\frac{\Gamma_2}{2\Gamma_0} \left[1-r\right]^2 +\frac{\beta_2}{2\beta_0} \left[1-r^2+2 \ln r\right] -\,\frac{\Gamma_1\beta_1}{2\Gamma_0\beta_0} \left[3-4 r+r^2+2 r \ln r\right] \\& +\frac{\beta_1^2}{2\beta_0^2} \left[1-r\right]\left[1-r-2\ln r\right] \Bigg) +\,\frac{\alpha_s(\mu_h)}{4\pi}\left( \ln\frac{2E_\gamma}{\mu_h} \left(\frac{\Gamma_1}{2\beta_0}-\frac{\Gamma_0\beta_1}{2\beta_0^2}\right) +\frac{\gamma_1}{2\beta_0}-\frac{\gamma_0\beta_1}{2\beta_0^2}\right) \left[1-r\right] + {\cal O}(\alpha_s^2)\Bigg]. \end{aligned}$ 
-
We collect this dispersion representation of various convolution integrals from [16].
$\tag{B1} \begin{aligned}[b]& {1 \over \pi} \, {\rm Im}_{\omega^{\prime}} \, \int_0^{\infty} \, \, \, \frac{{\rm d} \omega}{\omega-\omega^{\prime}-{\rm i}0} \, \ln^2{\mu^2 \over n \cdot p \, (\omega-\omega^{\prime})} \,\, \phi_D^+(\omega, \mu) \\ =& \int_0^{\infty} \, {\rm d} \omega \, \left [ {2 \, \theta(\omega^{\prime}-\omega) \over \omega - \omega^{\prime}} \, \ln {\mu^2 \over n \cdot p \, (\omega^{\prime} - \omega)} \right ]_{\oplus} \,\, \phi_D^+(\omega, \mu) + \left [ \ln {\mu^2 \over n \cdot p \, \omega^{\prime} } - {\pi^2 \over 3} \right ] \phi_D^+(\omega^{\prime}, \mu) \,, \end{aligned} $

$\tag{B2} \begin{aligned}[b]& {1 \over \pi} \, {\rm Im}_{\omega^{\prime}} \, \int_0^{\infty} \, \, \, \frac{{\rm d} \omega}{\omega-\omega^{\prime}-{\rm i}0} \,\, { \omega^{\prime} \over \omega } \,\, \ln {\omega^{\prime} - \omega \over \omega^{\prime}} \,\, \ln {\mu^2 \over - n \cdot p \, \omega^{\prime}} \,\, \phi_D^+(\omega, \mu) \\ =& -{\omega^{\prime} \over 2} \,\, \bigg \{ \int_0^{\infty} {\rm d} \omega \, \ln^2 \bigg|{\omega - \omega^{\prime} \over \omega^{\prime} } \bigg| \,\, {{\rm d} \over {\rm d} \omega} \, {\phi_D^+(\omega^{\prime}, \mu) \over \omega} + \, \int_{\omega^{\prime}}^{\infty} {\rm d} \omega \, \, \left [ 2 \, \ln{\mu^2 \over n \cdot p \, \omega^{\prime}} \, \ln {\omega - \omega^{\prime} \over \omega^{\prime} } - \pi^2 \right ] \, {{\rm d} \over {\rm d} \omega} \, {\phi_D^+(\omega^{\prime}, \mu) \over \omega} \bigg \} \,, \end{aligned} $

$\tag{B3} \begin{aligned}[b] & {1 \over \pi} \, {\rm Im}_{\omega^{\prime}} \, \int_0^{\infty} \, \, \, \frac{{\rm d} \omega}{\omega-\omega^{\prime}-{\rm i}0} \,\, { \omega^{\prime} \over \omega } \,\, \ln {\omega^{\prime} - \omega \over \omega^{\prime}} \,\, \ln {\mu^2 \over n \cdot p \, (\omega - \omega^{\prime})} \,\, \phi_D^+(\omega, \mu) \\ = &\omega^{\prime} \, \bigg \{ \int_0^{\infty} \, {\rm d} \omega \, \left [ { \theta(\omega^{\prime} - \omega) \over \omega - \omega^{\prime}} \, \ln { \omega^{\prime} - \omega \over \omega^{\prime}} \right ]_{\oplus} \, \, {\phi_D^+(\omega^{\prime}, \mu) \over \omega} + \, {1 \over 2} \, \int_{\omega^{\prime}}^{\infty} \, {\rm d} \omega \, \left [ \ln^2 {\mu^2 \over n \cdot p \, (\omega - \omega^{\prime})} - \ln^2 {\mu^2 \over n \cdot p \, \omega^{\prime}} + {\pi^2 \over 3} \right ] \, {{\rm d} \over {\rm d} \omega} \, {\phi_D^+(\omega^{\prime}, \mu) \over \omega} \bigg \} \,, \end{aligned}$

$ \tag{B4} {1 \over \pi} \, {\rm Im}_{\omega^{\prime}} \, \int_0^{\infty} \, \, \, \frac{{\rm d} \omega}{\omega-\omega^{\prime}-{\rm i}0} \,\, { \omega^{\prime} \over \omega } \,\, \ln {\omega^{\prime} - \omega \over \omega^{\prime}} \,\, \phi_D^+(\omega, \mu) = - \omega^{\prime} \, \int_{\omega^{\prime} }^{\infty} \, {\rm d} \omega \, \ln {\omega - \omega^{\prime} \over \omega^{\prime} } \,\, {{\rm d} \over {\rm d} \omega } \, {\phi_B^+(\omega, \mu) \over \omega} \,. $

Factorization of radiative leptonic D-meson decay with sub-leading power corrections
- Received Date: 2020-11-17
- Available Online: 2021-07-15
Abstract: In this work, we calculate the sub-leading power contributions to radiative leptonic





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF





















 DownLoad:
DownLoad: