-
The importance of pairing correlation in nuclear systems was realized very early [1]. In finite nuclei, neutron-neutron (n-n) and proton-proton (p-p) pairing effects are realized in several nuclear properties such as deformation, moments of inertia, alignments, and mass systematics [2-4]. In extended systems, nuclear pairing is expected to occur in the dense matter inside the neutron stars [5, 6]. This pairing is crucial for understanding various phenomena in neutron star physics, from the cooling of new born stars [7, 8] to the afterburst relaxation in X-ray transients [9], as well as in the understanding of glitches [10]. However, insufficient attention is paid to the isospin-singlet pairing, i.e., the neutron-proton (n-p) paring. Recently, it was suggested that the isospin-singlet pairing is possibly crucial in understanding some nuclear structural issues, such as the Gamow-Teller transition [11, 12]. In addition, considering the spin and isospin degrees of freedom, the nuclear Cooper pairs contain very interesting inner structures [13].
It is well-known that pair correlations crucially depend on the pairing near the Fermi surface. Because neutrons and protons share the same Fermi energy in symmetric nuclear matter, n-n (p-p) pairs compete intensely with n-p pairs. Generally, the most energetically favored excludes the others. The investigations on nuclear pairs relatively focus on the single pairing structure, i.e., either the n-n (p-p) or n-p pair only [14-23]. Nevertheless, coexistence may emerge in special cases, such as in the case of isospin asymmetric nuclear matter. In a neutron-rich system, although the isospin-singlet n-p pairing may be favored, the excess neutrons can form isospin-triplet n-n pairs coexisting with the other, and they can influence each other. Furthermore, the nuclei far from the beta-stability line, i.e. the exotic nuclei, can be obtained from heavy-ion collisions (HIC), which has been addressed as a laboratory for the dynamic evolution of the superfluid state of nuclear matter [24]. New aspects of pairing could appear in these exotic nuclei, relative to isospin asymmetries, one of which might be the interplay between n-n and n-p pairings in the nuclei owing to the significant overlap of proton and neutron orbits [13, 25].
In Ref. [13], the coexistence of isospin
$ I = 1 $ and$ I = 0 $ pairings are considered to study the inner phase structure and phase transition at low density, where the BCS-BEC crossover occurs. The result obtained indicates that including the$ I = 1 $ channel pairing significantly alters the phase structure and phase transition properties. Another challenge in nuclear matter is the interplay between the$ I = 1 $ and$ I = 0 $ pairings. Based on this motivation, to investigate the coexistence of the n-n, p-p, and n-p pairings in asymmetric nuclear matter with effective contact pairing interaction in this study, we employ the extended Nambu-Gorkov propagator, which comprises the isospin-triplet n-n and p-p pairings and the isospin singlet n-p pairing.The paper is organized as follows. In Sec. II, we briefly derive the gap equation and thermodynamics, as well as introduce the adopted effective pairing interaction. The numerical results and discussion are presented in Sec. III, where the results of the coexistence of three types of pairings are compared with the single pairing at a certain density. Finally, a summary and a conclusion are provided in Sec. IV.
-
The Nambu-Gorkov propagator at finite temperatures, including the n-n, n-p, and p-p pairings [13], is expressed as:
$ \begin{array}{l} G = \left( \begin{array}{llll} {\rm i}\omega_{\upsilon}-\varepsilon_{n} & \ \ \ \ 0 &\ \ \Delta_{np} &\ \ \Delta_{nn}\\ \\ \ \ \ \ 0 & {\rm i}\omega_{\upsilon}-\varepsilon_{p} & \ \ \Delta_{pp} & -\Delta_{np}\\ \\ \ \ \Delta_{np} &\ \ \Delta_{pp} & {\rm i}\omega_{\upsilon}+\varepsilon_{p} &\ \ \ \ 0 \\ \\ \ \ \Delta_{nn} & -\Delta_{np} &\ \ \ \ 0& {\rm i}\omega_{\upsilon}+\varepsilon_{n} \end{array} \right)^{-1}, \end{array} $

(1) where
$ \omega_{\upsilon} = (2\upsilon+1)\pi k_{B}T $ with$ \upsilon\in \mathbb{Z} $ represents the Matsubara frequencies.$ \varepsilon_{n/p} = { p}^{2}/(2m)-\mu_{n/p} $ is the single particle (s.p.) energy with chemical potential$ \mu_{n/p} $ . In addtion,$ \Delta_{nn} $ ,$ \Delta_{pp} $ , and$ \Delta_{np} $ are the isospin-triplet n-n, isospin-triplet p-p, and isospin-singlet n-p pairing gaps, respectively. -
The neutron-proton anomalous propagator, which corresponds to
$ G_{13} $ , reads$ \begin{aligned}[b] & F_{np}^{\dagger}(\omega_{\upsilon},{ p}) \\=& \frac{-\Delta_{np} [({\rm i}\omega_{\upsilon})^{2}+{\rm i}\omega_{\upsilon}(\varepsilon_{n}-\varepsilon_{p})-\varepsilon_{n}\varepsilon_{p}-\Delta_{np}^{2}-\Delta_{nn}\Delta_{pp}]} {\big[({\rm i}\omega_{\nu})^{2}-E_+^{2} \big]\big[({\rm i}\omega_{\nu})^{2}-E_-^{2} \big]}\\ =& \frac{ -\Delta_{np}\bigg\{[({\rm i}\omega_{\upsilon})^{2}-\varepsilon_+^{2}]-{\rm i}\omega_{\upsilon}(2\delta\mu)+2\delta\mu^{2}+\dfrac{(\Delta_{nn}-\Delta_{pp})^{2}}{2}\bigg\}} {\big[({\rm i}\omega_{\nu})^{2}-E_+^{2} \big]\big[({\rm i}\omega_{\nu})^{2}-E_-^{2} \big]}, \end{aligned} $

(2) where
$ E_{\pm} = \sqrt{\varepsilon_{+}^{2}\pm\sqrt{\varepsilon_{-}^{4}+\varepsilon_{\Delta}^{4}}} $ is the quasi-particle energy in the condensate with the definition$ \varepsilon_{\Delta}^{4} = $ $ \Delta_{np}^{2}[(\varepsilon_{n}-\varepsilon_{p})^{2}+(\Delta_{nn}-\Delta_{pp})^{2}] $ and$ 2\varepsilon_{\pm}^{2} = \varepsilon_{n}^{2}+\Delta_{nn}^{2}+\Delta_{np}^{2}\pm $ $ (\varepsilon_{p}^{2}+ \Delta_{pp}^{2}+\Delta_{np}^{2}) $ .$ \delta\mu = (\varepsilon_{p}-\varepsilon_{n})/2 = (\mu_{n}-\mu_{p})/2 $ represents the Fermi surface mismatch. The summation over the Matsubara frequencies provides the density matrix of particles in the condensate, i.e, the n-p pairing probabilities,$ \begin{aligned}[b] \nu_{np}({ {p}}) =& -\frac{\Delta_{np}}{2}\Bigg\{\Bigg[\frac{1-2f(E_+)}{2E_+}+\frac{1-2f(E_-)}{2E_-}\Bigg]\\ & + \frac{2\delta\mu^{2}+\dfrac{(\Delta_{nn}-\Delta_{pp})^{2}}{2}}{\sqrt{\varepsilon_-^{4}+\varepsilon_{\Delta}^{4}}}\Bigg[\frac{1-2f(E_+)}{2E_+}-\frac{1-2f(E_-)}{2E_-}\Bigg]\Bigg\}.\\ \end{aligned} $

(3) Here
$ f(E) = \left[1+\exp\left(\dfrac{E}{k_{B}T}\right)\right]^{-1} $ represents the well-known Fermi-Dirac distribution function under a temperature$ T $ . Accordingly, the n-p gap equation is expressed as$ \begin{aligned}[b] \Delta_{np} =& \int\frac{{\rm d}{ {p}}}{(2\pi)^{3}}V_{np}\frac{\Delta_{np}}{2}\Bigg\{\Bigg[\frac{1-2f(E_+)}{2E_+}+\frac{1-2f(E_-)}{2E_-}\Bigg]\\ & + \frac{2\delta\mu^{2}+\dfrac{(\Delta_{nn}-\Delta_{pp})^{2}}{2}}{\sqrt{\varepsilon_-^{4}+\varepsilon_{\Delta}^{4}}}\Bigg[\frac{1-2f(E_+)}{2E_+}-\frac{1-2f(E_-)}{2E_-}\Bigg]\Bigg\}. \end{aligned} $

(4) In the absence of the n-n and p-p pairings, the quasi-particle energy
$ E_{\pm} $ becomes$ E_{\pm} = \sqrt{[(\varepsilon_{n}+\varepsilon_{p})/2]^{2}+\Delta_{np}^{2}} $ $ \pm\delta\mu = E_{\Delta}\pm\delta\mu $ , and the gap equation is reduced to a more familiar form for the n-p pairing in asymmetric nuclear matter:$ \Delta_{np} = \int\frac{{\rm d}{ {p}}}{(2\pi)^{3}}V_{np}\frac{\Delta_{np}[1-f(E_+)-f(E_-)]}{2E_{\Delta}}. $

(5) Similarly, the n-n and p-p pairing gaps are respectively expressed as
$ \begin{aligned}[b] \Delta_{nn} =& \int\frac{{\rm d}{ {p}}}{(2\pi)^{3}}V_{nn}\frac{\Delta_{nn}}{2}\Bigg\{\Bigg[\frac{1-2f(E_+)}{2E_+}+\frac{1-2f(E_-)}{2E_-}\Bigg]\\ & + \frac{\varepsilon_-^{2}+\Delta_{np}^{2}\left(1-\dfrac{\Delta_{pp}}{\Delta_{nn}}\right)}{\sqrt{\varepsilon_-^{4}+\varepsilon_{\Delta}^{4}}}\Bigg[\frac{1-2f(E_+)}{2E_+}-\frac{1-2f(E_-)}{2E_-}\Bigg]\Bigg\}, \end{aligned} $

(6) and
$ \begin{aligned}[b] \Delta_{pp} =& \int\frac{{\rm d}{ {p}}}{(2\pi)^{3}}V_{pp}\frac{\Delta_{pp}}{2}\Bigg\{\Bigg[\frac{1-2f(E_+)}{2E_+}+\frac{1-2f(E_-)}{2E_-}\Bigg]\\& - \frac{\varepsilon_-^{2}+\Delta_{np}^{2}\left(\dfrac{\Delta_{nn}}{\Delta_{pp}}-1\right)}{\sqrt{\varepsilon_-^{4}+\varepsilon_{\Delta}^{4}}}\Bigg[\frac{1-2f(E_+)}{2E_+}-\frac{1-2f(E_-)}{2E_-}\Bigg]\Bigg\}, \end{aligned} $

(7) The occupation numbers, corresponding to the matrix elements
$ G_{11} $ and$ G_{22} $ , can be calculated by$ \begin{aligned}[b] n_{n} =& \frac{1}{2}-\frac{\varepsilon_{n}}{2}\Bigg[\frac{1-2f(E_+)}{2E_+}+\frac{1-2f(E_-)}{2E_-}\Bigg]\\ & - \frac{\varepsilon_-^{2}\varepsilon_{n}-2\delta\mu\Delta_{np}^{2}}{2\sqrt{\varepsilon_-^{4}+\varepsilon_{\Delta}^{4}}}\Bigg[\frac{1-2f(E_+)}{2E_+}-\frac{1-2f(E_-)}{2E_-}\Bigg] \end{aligned} $

(8) and
$ \begin{aligned}[b] n_{p} =& \frac{1}{2}-\frac{\varepsilon_{p}}{2}\Bigg[\frac{1-2f(E_+)}{2E_+}+\frac{1-2f(E_-)}{2E_-}\Bigg]\\ & + \frac{\varepsilon_-^{2}\varepsilon_{p}-2\delta\mu\Delta_{np}^{2}}{2\sqrt{\varepsilon_-^{4}+\varepsilon_{\Delta}^{4}}}\Bigg[\frac{1-2f(E_+)}{2E_+}-\frac{1-2f(E_-)}{2E_-}\Bigg]. \end{aligned} $

(9) The neutron and proton densities are respectively defined as
$ \rho_{n} = 2\int\frac{{\rm d}{ {p}}}{(2\pi)^{3}}n_{n}, \ \ \rho_{p} = 2\int\frac{{\rm d}{ {p}}}{(2\pi)^{3}}n_{p}. $

(10) Notably, the n-n, p-p, and n-p pairing gaps couple to each other. For asymmetric nuclear matter at the fixed neutron and proton densities, these gap equations (Eqs. (4), (6), and (7)) should be solved self-consistently with the densities (Eq. (10)) at given densities and temperatures.
-
In principle, the nucleon-nucleon pairing interaction in nuclear matter originates from the attractive component of the bare two-body potential and the three-body force, and this pairing interaction is modified by the nuclear medium, such as the polarization effect [26-32]. In this research, to obtain qualitative conclusions from the coexistence of n-n, p-p, and n-p pairs, we adopt the density-dependent contact interaction developed by Gorrido et al. [33] to model the pairing potential. For uniform nuclear matter, the potential takes the form
$ \begin{array}{l} V_{I}( {r}, {r}') = g_{I}\delta( {r}- {r}'), \end{array} $

(11) with the effective coupling constant
$ \begin{array}{l} g_{I} = v_{I}[1-\eta_{I}(\rho_{I}/\rho_{0})^{\gamma_{I}}]. \end{array} $

(12) Here,
$ v_{I} $ ,$ \eta_{I} $ , and$ \gamma_{I} $ are adjustable parameters and$ I = 0,1 $ denote the total isospin of the pairs. For the n-n (p-p) pairing,$ \rho_{I} = \rho_{n} $ ($ \rho_{I} = \rho_{p} $ ) and for the n-p pairing,$ \rho_{I} = \rho_{n}+\rho_{p} $ .$ \rho_{0} = 0.17\; \text{fm}^{-3} $ reprsents the saturation density. Taking suitable values of the parameters, the pairing gap$ \Delta(k_{\rm F}) $ can be reproduced as a function of the Fermi momentum$ k_{F} = (3\pi^{2}\rho_{I})^{1/3} $ in the channel$ L = 0 $ ,$ I = 1 $ ,$ S = 0 $ (n-n and p-p) and$ k_{F} = (3\pi^{2}\rho_{I}/2)^{1/3} $ in channel$ L = 0 $ ,$ I = 0 $ ,$ S = 1 $ (n-p). We would like to emphasize that there is also a kind of n-p pairing in the channel$ L = 0 $ ,$ I = 1 $ ,$ S = 0 $ for the symmetric nuclear matter. In this channel, the n-p pairing force is approximately the same as the n-n or p-p pairing force. As will be discussed in Sec. III, even a minor asymmetry will destroy the n-p pairing in this channel. Therefore, the$ I = 1 $ pairings only represent neutron-neutron and proton-proton pairings hereafter.In addition to the polarization effect, the self-energy effect of the medium quenches the pairing gaps [14, 17]. Because the self-energy effect for nuclear pairing remains an open question in asymmetric nuclear matter, we adopt the calculated pairing gaps [14, 18] under the Hartree-Fock approaches to calibrate the parameters presented in Fig. 1. It should be noted that the self-energy [17] and polarization [32] effects should be included to obtain a more reliable pairing interaction. As is well known, to avoid the ultraviolet divergence, an energy cut is required for the contact interaction. Here, we fix the energy at approximately
$ 80 $ MeV for both cases. The left and right panels correspond to the$ I = 1 $ and$ I = 0 $ pairings, respectively.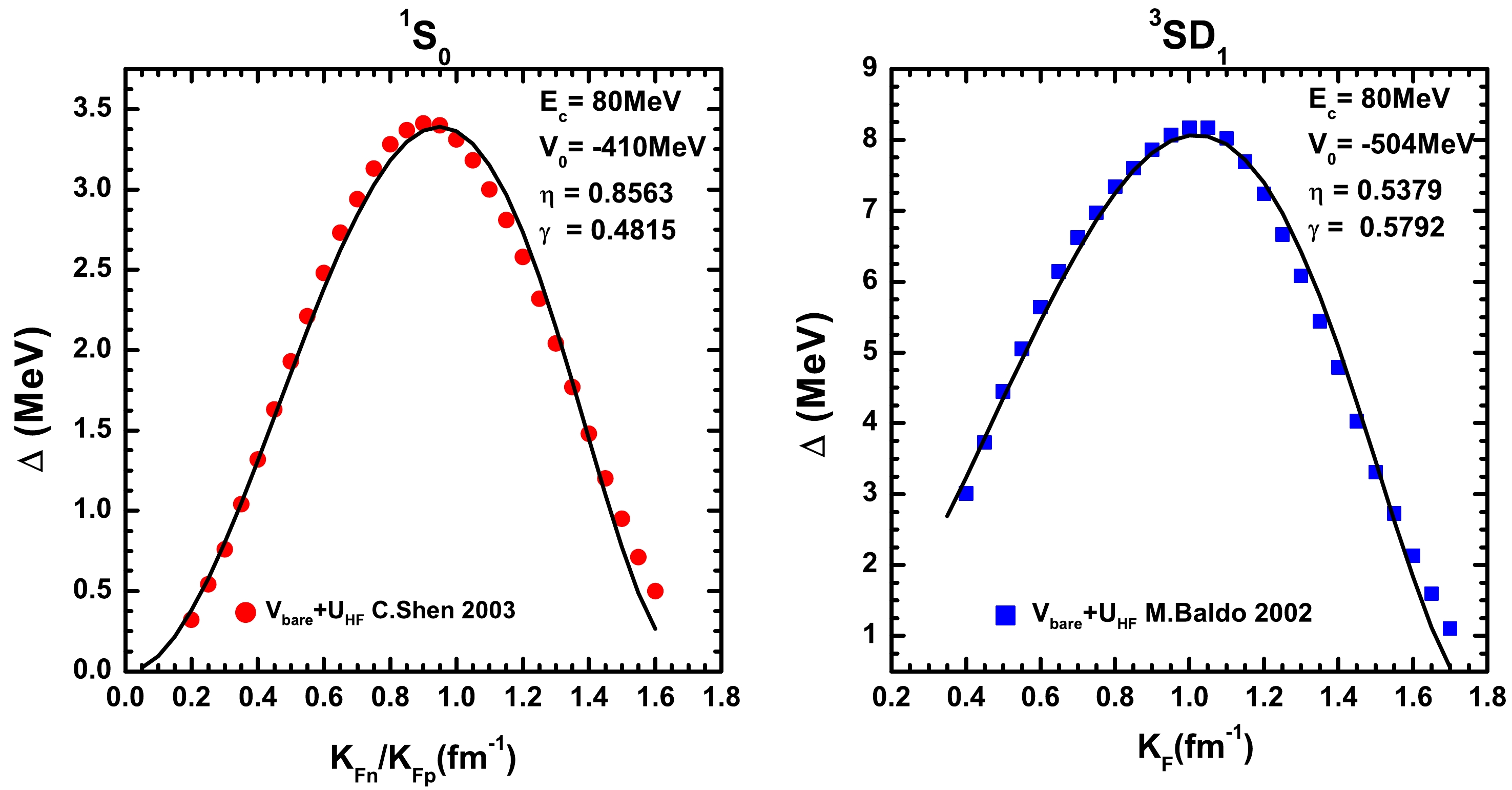
Figure 1. (color online) The density-dependent contact pairing interaction with parameters calibrated to the calculated pairing gaps. The dots represent the pairing gaps in Refs. [14, 18], whereas the lines correspond to the calculation from the effective pairing interaction. The left and right panels are related to the isospin triplet and isospin singlet channels, respectively.
-
Now, we are in a position to determine the key thermodynamic quantities. Because the occupation of the quasi-particle states is given by the Fermi-Dirac distribution function, the entropy of the system is obtained from
$ S = -2k_{B}\sum\limits_{ {p}}\sum\limits_{i}\big[f(E_{i}){\rm ln} f(E_{i})+\overline{f}(E_{i}){\rm ln} \overline{f}(E_{i})\big], $

(13) where
$ \overline{f}(E_{i}) = 1-f(E_{i}) $ and$ i = \pm $ . The internal energy of the superfluid state is expressed as$ \begin{aligned}[b] U =& 2\sum\limits_{ {p}}\big[\varepsilon_{n}n^{n}+\varepsilon_{p}n^{p}\big]\\&+\sum\limits_{ {p}}\big[g_{nn}\nu_{nn}^{2}+g_{pp}\nu_{pp}^{2}+2g_{np}\nu_{np}^{2}\big], \end{aligned}$

(14) The factor
$ 2 $ corresponds to the spin summation. The first term of Eq. (14) includes the kinetic energy of the quasi-particle as a function of the pairing gap and chemical potential. The BCS mean-field interaction among the particles in the condensate is embodied in the second term of Eq. (14). It should be noted that for asymmetric nuclear matter, the n-n and p-p pairing interactions can be different, i.e.,$ g_{nn}\neq g_{pp} $ , owing to$ \rho_{n}\neq\rho_{p} $ . Accordingly, the thermodynamic potential can be given as$ \begin{array}{l} \Omega = U-TS. \end{array} $

(15) Once the contact pairing interaction is adopted, the pairing gap is momentum independent. Therefore, the thermodynamic potential can be obtained in a simple form:
$ \begin{aligned}[b] \Omega =& 2\frac{\Delta_{np}^{2}}{g_{np}}+\frac{\Delta_{nn}^{2}}{g_{nn}}+\frac{\Delta_{pp}^{2}}{g_{pp}} +\int\frac{{\rm d} {p}}{(2\pi)^{3}}\\& \times\Bigg\{\varepsilon_{n}+\varepsilon_{p} -\sum\limits_{i = \pm}\big[E_{i}+2k_{B}T{\rm ln}(1+{\rm e}^{\frac{-E_{i}}{k_{B}T}})\big]\Bigg\}. \end{aligned}$

(16) Here, we consider the property
$f(\omega){\rm ln} f(\omega) + \overline{f}(\omega){\rm ln}\overline{f}(\omega) = $ $ -\dfrac{\omega}{k_{B}T} -{\rm ln}(1+{\rm e}^{-\omega/(k_{B}T)})$ . The gap Eqs. (4), (6), and (7) and the densities of Eq. (10) can be equivalently expressed as$ \begin{aligned}[b]& \frac{\partial\Omega}{\partial\Delta_{np}} = 0,\;\;\ \ \frac{\partial\Omega}{\partial\Delta_{nn}} = 0,\ \ \;\; \frac{\partial\Omega}{\partial\Delta_{pp}} = 0,\\& \rho_{n} = -\frac{\partial\Omega}{\partial\mu_{n}},\;\;\ \ \ \ \rho_{p} = -\frac{\partial\Omega}{\partial\mu_{p}}. \end{aligned} $

(17) It should be noted that the solution of these equations corresponds to the global minimum of the free energy
$ F = \Omega+\mu_{n}\rho_{n}+\mu_{p}\rho_{p} $ , which is the essential quantity that describes the thermodynamics of asymmetric nuclear matter. -
The numerical calculations in this study focus on the coexistence of three different types of pairs in isospin asymmetric nuclear matter with total density
$ \rho = \rho_{n}+\rho_{p} $ and isospin asymmetry$ \beta = (\rho_{n}-\rho_{p})/\rho $ . We adopt the effective contact pairing interaction at zero temperature. Fig. 2 illustrates the pairing gaps as a function of asymmetry$ \beta $ at the total density$ \rho = 0.068\; \text{fm}^{-3} $ , at which both the$ I = 1 $ and$ I = 0 $ pairing interactions are most attractive. The thick lines correspond to the results of the coexistence of three types of pairings, which include$ \Delta_{nn}\neq0, \; \Delta_{np}\neq0, \; \Delta_{pp}\neq0 $ . In the symmetric matter, neutrons and protons share the same Fermi surface, i.e.,$ k_{{\rm F}n} = k_{{\rm F}p} = k_{\rm F} $ , and the region near the Fermi surface contributes dominantly to the pairing gaps. Two neutrons and two protons near the Fermi surface can form a n-n pair and a p-p pair or two n-p pairs. Because the n-p pairing strength is significantly stronger than that of n-n and p-p, the nucleons prefer to form n-p pairs instead of n-n (p-p) pair. Equivalently, the n-p pairings severely suppress the n-n and p-p pairings for$ \beta = 0 $ . As illustraed in Fig. 2, the n-n (p-p) gap disappears in the symmetric case. In asymmetric nuclear matter, the dominant region, which contributes significantly to the n-n (p-p) pairing gap, is located at the neutron (proton) Fermi momentum$ k_{{\rm F}n} $ ($ k_{{\rm F}p} $ ), whereas the region for n-p pairing is between$ k_{{\rm F}p} $ and$ k_{{\rm F}n} $ (the average Fermi surface related to the average chemical potential of neutrons and protons). The split between neutron and proton Fermi surfaces separates the dominant regions for n-n, p-p, and n-p pairings, which enables the n-n and p-p pairings. In addition, the discrepancy between$ k_{{\rm F}p} $ and$ k_{{\rm F}n} $ increases with the increasing isospin asymmetry. Therefore the n-n and p-p pairing gaps increase with$ \beta $ .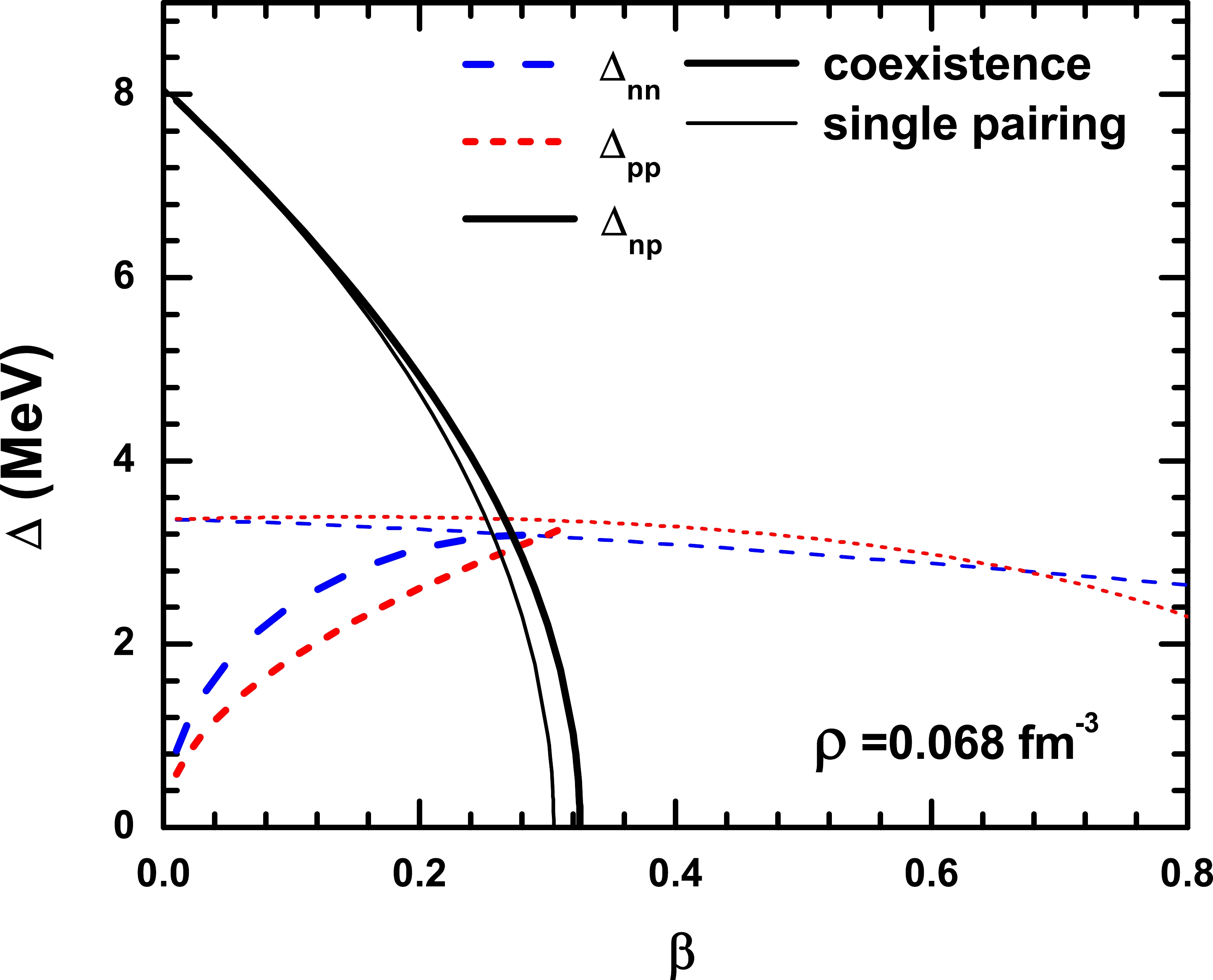
Figure 2. (color online) The n-n, p-p, n-p pairing gaps as a function of the isospin asymmetry
$ \beta $ , at a total density$ \rho = 0.068\; \text{fm}^{-3} $ . The thick and thin lines correspond to the coexistence of three types of pairings and single pairing, respectively. The dashed, short-dashed, and solid lines are related to the n-n, p-p, and n-p pairings, respectively.In addition, the results for single pairing, i.e.,
$ \Delta_{nn}\neq0, \, \Delta_{pp} = \Delta_{np} = 0 $ ,$ \Delta_{np}\neq0, \, \Delta_{nn} = \Delta_{pp} = 0, $ or$ \Delta_{pp}\neq0, $ $ \, \Delta_{nn} = \Delta_{np} = 0, $ are depicted as thin lines in Fig. 2 for comparison. Owing to the suppression from the mismatched Fermi surfaces, n-p pairing gaps decrease with$ \beta $ and disappear at certain asymmetries for both the single pairing and the coexistence of three types of pairings. In the calculation of the coexistence of three types of pairings,$ \Delta_{nn} $ and$ \Delta_{pp} $ coincide with the results obtained from the single pairing calculation when the n-p pairing disappears. In fact, if$ \Delta_{np} = 0 $ the coupled Eq. (17) degenerates into two groups of completely independent equations, which are the gap equations for$ \Delta_{nn} $ with the neutron density and the gap equation for$ \Delta_{pp} $ with proton density.Compared to single pairing, the critical isospin asymmetry, where
$ \Delta_{np} $ vanishes, is enhanced by the existence of n-n and p-p pairs, as demonstrated in Fig. 2. Unfortunately, this conclusion cannot be considered as definite, as the effective pairing interaction is simply obtained from the pairing gaps under the Hartree-Fock approximation. In addition, the effective n-p pairing interaction can be significantly reduced by the nucleon-nucleon correlation beyond the Hartree-Fock approaches [17]. Owing to the complexity of the nuclear many-body medium effects, the exact effective pairing interaction remains an open problem. To eliminate the uncertainty of the effective pairing strength, we adjust the effective neutron-proton pairing interaction artificially to obtain the qualitative conclusion. The results obtained are presented in Fig. 3. The solid and dashed lines correspond to the results obtained from the coexistence of the three types of pairings and the single pairing, respectively. For the effective interaction obtained from Ref. [18],$ g_{np}/g_{nn} = $ $ 1.3837 $ . If we reduce the n-p pairing strength$ g_{np} $ , the enhancement of the n-p pairing from the existence of the n-n (p-p) pairs is reduced. When$ g_{np}/g_{nn} $ is under a certain value, the existence of n-n (p-p) pairing might suppress the n-p pairing eventually. An interesting property is that if$ g_{np}\simeq g_{nn} $ ,$ \Delta_{np} $ decreases rapidly with$ \beta $ . As mentioned in Sec. IIB, the channel$ L = 0 $ ,$ I = 1 $ ,$ S = 0 $ embodies n-n, p-p, and n-p pairings, and the pairing interactions are approximately the same for the asymmetric case. A negligible asymmetry can destroy the n-p pairing in the$ L = 0 $ ,$ I = 1 $ ,$ S = 0 $ channel. Therefore, in general, the$ I = 1 $ pairing solely refers to the n-n and p-p pairings.
Figure 3. (color online) The n-p pairing gaps as a function of isospin asymmetry at a total density
$ \rho = 0.068\; \text{fm}^{-3} $ for different n-p pairing strengths,$ g_{np}/g_{nn} = 1.3837 $ ,$ 1.2 $ ,$ 1.12 $ ,$ 1.01 $ . The solid and dashed lines correspond to the coexistence of three types of pairings and single pairing, respectively.One straightforward way to understand the enhancement of n-p pairing from the existing n-n and p-p pairs is to investigate the n-p pairing probabilities near the average Fermi surface (related to the average chemical potentials of the neutron and proton). The results obtained are presented in Fig. 4, in the case where total density
$ \rho = 0.068\; \text{fm}^{-3} $ and isospin asymmetry$ \beta = 0.3 $ . The n-p pairing strength is set to be$ g_{np}/g_{nn} = 1.3837 $ . For the single n-p pairing, the pairing is forbidden in a window around the average Fermi surface owing to the absence of protons. Once the n-n and p-p pairings are included, the dispersion of neutron and proton Fermi surfaces can provide the kinematical phase space near the average Fermi surface for the occurence of the n-p pairing phenomena. This is a positive mechanism, such that the existence of n-n and p-p pairs enhances the n-p pairing.
Figure 4. (color online) The n-p pairing probabilities as a function of
$ k $ near the average Fermi surface with the total density$ \rho = 0.068\; \text{fm}^{-3} $ and isospin asymmetry$ \beta = 0.3 $ . Here,$ k = p/\hbar $ is the wave number. The pairing strength is set to be$ g_{np}/g_{nn} = 1.3837 $ . The solid and dashed lines correspond to the coexistence of three types of pairings and single pairing, respectively.Another effect of the existence of n-n and p-p pairs is that a n-n pair and a p-p pair ought to be broken up to form two n-p pairs. Exclusively, when the pairing energy of n-n and p-p pairs is smaller than that of the two n-p pairs, the existence of n-n and p-p pairs can enhance the n-p pairing. The pairing energy is related to the pairing strength directly. As presented in Fig. 5, when the n-p pairing strength is insufficient, the n-p pairing probability is suppressed significantly by n-n and p-p pairs.

Figure 5. (color online) The pairing probabilities vs
$ k $ near the average Fermi surface at the total density$ \rho = 0.068\; \text{fm}^{-3} $ with isospin asymmetry$ \beta = 0.15 $ . Here,$ k = p/\hbar $ is the wave number. The dashed, short-dashed, and solid lines correspond to the n-n, p-p, and n-p pairings, respectively. The n-p pairing strength$ g_{np}/g_{nn} $ is set to be$ 1.3837 $ ($ 1.12 $ ) in left (right) panel.In the calculations of this study, the temperature is set to be zero. However, for asymmetric nuclear matter, the temperature can also disperse the neutron and proton Fermi surfaces, which will eventually reduce the suppression of Fermi surface mismatch at low temperature. At high temperature, the temperature will destroy all types of pairings. Once the temperature is included, the enhanced and reduced effects on n-p paring from the existence of n-n and p-p pairings should be weakened.
In finite nuclei, the n-p pairing might be suppressed by the strong spin-orbit splitting [34, 35]. However, in nuclei where the spin-splitting becomes small, the coexistence of three types of pairings may occur. Understanding the enhanced and reduced effects on n-p paring owing to the existence of n-n and p-p pairings could be beneficial in elucidating the n-p pairing in
$ N\approx Z $ nuclei. For asymmetric nuclei, the interplay between n-n and n-p pairings might be the same as that in asymmetric nuclear matter. -
In this study, we investigated the coexistence of n-n, p-p, and n-p pairings in isospin asymmetric nuclear matter with an effective density-dependent contact pairing interaction. The three types of pairings cannot coexist in symmetric nuclear matter, only n-p pairs can survive when the n-p pairing strength is stronger than that of the n-n and p-p pairs, whereas the n-n and p-p pairs are preferred if the n-n and p-p pairing interactions become strong. Furthermore, n-n, p-p, and n-p pairs can coexist in isospin asymmetric nuclear matter when the n-p pairing interaction is stronger than that of n-n and p-p pairs.
Compared to the single pairing calculation (gap equation with only one kind of nucleon pair), the results indicate two effects of the existence of n-n and p-p pairs. On the one hand, the existence of n-n and p-p pairs can disperse the neutron and proton Fermi surfaces, which increase the phase-space overlap between neutrons and protons and eventually enhance the n-p pairing near the average Fermi surface. This positive mechanism can reduce the suppression owing to the mismatched Fermi surface of neutrons and protons in the isospin asymmetric nuclear matter. On the other hand, a n-n pair and a p-p pair should be broken up to form two n-p pairs. In this process, the pairing interaction plays a crucial role. The final results obtained are determined by these two effects. In isospin asymmetric nuclear matter, the existence of n-n and p-p pairs can enhance the n-p pairing when the n-p pairing strength is significantly stronger than that of n-n and p-p pairs. However, the existence of n-n and p-p pairs would reduce the n-p pairing probability when the n-p pairing interaction decreases in strength. Moreover, when the n-p pairing strength becomes approximately that of n-n and p-p pairs, the n-p pairing rapidly disappears with the isospin asymmetries.
In this paper, the gap solution is only thermodynamically stable. The Cooper pair momentum should also be included in the future to avoid dynamic instability [36-38]. In addition, in future works, the pairing interaction should be calibrated to the pairing gaps, including the polarization correction and the correlation effect. As a prospect, this interesting coexistence of the three types of pairings should also be applied to the studies on pairing correlations in finite nuclei.
Coexistence of isospin I = 0 and I = 1 pairings in asymmetric nuclear matter
- Received Date: 2021-03-09
- Available Online: 2021-07-15
Abstract: The coexistence of neutron-neutron (n-n), proton-proton (p-p), and neutron-proton (n-p) pairings is investigated by adopting an effective density-dependent contact pairing potential. These three types of pairings can coexist only if the n-p pairing is stronger than the n-n and p-p pairings for the isospin asymmetric nuclear matter. In addition, the existence of n-n and p-p pairs might enhance n-p pairings in asymmetric nuclear matter when the n-p pairing strength is significantly stronger than the n-n and p-p ones. Conversely, the n-p pairing is reduced by the n-n and p-p pairs when the n-p pairing interaction approaches n-n and p-p pairings.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: