-
Primordial black holes (PBHs) [1-5] have long been a subject of interest, particularly as dark matter candidates [6-10]. The abundance of PBHs that survive today is heavily constrained, and only very few narrow windows in the parameter space are still available [11-15]. Smaller PBHs could be relevant if remnants exist after evaporation [16-21]. In fact, if the initial PBH mass is sufficiently small that evaporation is completed before Big Bang nucleosynthesis (BBN), Planck mass remnants are still viable dark matter candidates [13, 22].
Alternatively, the contribution of PBHs or their remnants to dark matter could be secondary, while the main component consists of dark sector particles that have been predominantly produced by PBH evaporation [23-28]. Since PBHs could attain considerably high temperatures during the evaporation, they can efficiently emit particles in various mass ranges regardless of the background temperature of the universe. This is relevant in another important context, i.e., baryogenesis, particularly if the baryon asymmetry was produced in the early universe by heavy particle decays. Additionally, if some of the emitted particles in the dark sector remained relativistic at the time of matter-radiation equality, they could contribute to the radiation content and affect the evolution of the universe.
As a caveat, these discussions rely heavily on the fundamental properties of black holes. However, astrophysical observations only indicate strong evidences for ultracompact objects that significantly resemble black holes. Indeed, the Nobel prize for physics in 2020 [29] was awarded in this context, and much more observation work is required to confirm these objects as black holes, particularly regarding the near-horizon physics including Hawking radiation①. While it is true that general relativity (GR) is extremely successful in describing gravitational phenomena at macroscopic and cosmological scales, it is anticipated to be replaced by a more complete theory of quantum gravity below the Planck scale
$ m_{\mathrm{Pl}} $ . Unlike GR, such a theory could accommodate alternatives as dark and compact as black holes; thus, identifying these observations with black holes requires caution.Such an object, called a 2-2-hole [30-33], exists in quadratic gravity, a candidate theory of quantum gravity. As a simple extension of GR, by including all possible dimension-four terms, quadratic gravity is renormalizable and asymptotically free at the quantum level [34-37] owing to the new massive modes associated with the quadratic curvature terms. However, this theory suffers from the ghost problem at the classical level due to the new spin-2 mode. The proposed methods to deal with this pathology mostly involve modifications of the quantum prescription of the theory [38-47]. Although there is still no consensus on the resolution of this problem, the theory does provide a more tractable model to visualize near-horizon effects from the high curvature terms. The new quadratic curvature terms in quadratic gravity can be significant for ultracompact objects, and the theory predicts 2-2-holes, a new family of solutions absent in GR. A 2-2-hole is almost as compact as a black hole without an event horizon. This naturally resolves the information loss paradox and may leave distinctive imprints in gravitational wave signals that remain to be dedicatedly searched for. In contrast to other candidates, the formation of a 2-2-hole does not rely on exotic forms of matter; therefore, it may serve as the endpoint of gravitational collapse in nature.
If black holes are discovered to be ultracompact horizonless objects, the relationship between PBHs and dark matter physics deserves to be reinvestigated, and 2-2-holes serve as a good example for the study of alternatives. Since a 2-2-hole has a minimum mass
$ M_{\mathrm{min}} $ , a minimal 2-2-hole naturally serves as a stable remnant. However, a non-minimal 2-2-hole radiates like a black hole with unusual thermodynamic characteristics and could have produced strong radiation in the early universe. In an earlier paper [48], we studied the implications of 2-2-hole remnants being dark matter, and we derived the observational constraints. We observed that remnant abundance is significantly constrained by a distinctive phenomenon associated with remnant mergers owing to the evaporation of the merger product, and that only small remnants not much heavier than$ m_{\mathrm{Pl}} $ can constitute all of dark matter.In this paper, we consider the scenario in which the remnants are only subdominant in the current epoch of the universe and the main content of dark matter were produced through primordial 2-2-hole evaporation in the early universe. We investigate dark sector production and baryon asymmetry generation in this context by considering the observational constraints on the remnant abundance. In particular, we explore the available parameter space with respect to the fundamental parameter
$ M_{\mathrm{min}} $ , which not only determines the remnant mass but also appears in the evaporation rate. No such feature exists for PBH with remnants.The rest of the paper is organized as follows. The properties of the thermal 2-2-holes are reviewed in Sec. II. Dark sector production is discussed in Sec. III. Baryon asymmetry generation is studied in Sec. IV. The observational constraints and implications are discussed in Sec. V. The paper is concluded in Sec. VI.
-
The action of quadratic gravity includes two additional quadratic curvature terms, the Ricci scalar square and Weyl tensor square:
$ S_{\mathrm{QG}} = \frac{1}{16\pi}\int {\rm d}^4 x \sqrt{-g}\left(m_{\mathrm{Pl}}^2 R-\alpha\; C_{\mu\nu\rho\sigma}C^{\mu\nu\rho\sigma}+\beta R^2\right)\,, $

(1) where
$ \alpha $ and$ \beta $ are dimensionless couplings. These new terms introduce a spin-0 and a spin-2 mode with the tree level masses$m_0,\,m_2\approx m_{\mathrm{Pl}}/\!\sqrt{\beta},\,m_{\mathrm{Pl}}/\!\sqrt{\alpha}$ . As the most generic solution in the theory, the existence of 2-2-holes relies on the Weyl tensor term, and its minimum mass is determined by the mass of the spin-2 mode,$ M_{\mathrm{min}}\approx m_{\mathrm{Pl}}^2/m_2 $ . In quantum theory, the dimensionless coupling$ \alpha\gtrsim 1 $ ; hence,$ M_{\mathrm{min}}\gtrsim m_{\mathrm{Pl}} $ . In the strong coupling scenario, the Planck mass occurs dynamically through dimensional transmutation, where$ \alpha\approx1 $ and$ M_{\mathrm{min}}\approx m_{\mathrm{Pl}} $ . In contrast, in the weak coupling scenario, a large mass hierarchy is permitted and$ M_{\mathrm{min}} $ may be significantly larger than the Planck mass.2-2-holes resemble black holes closely from the exterior, while they feature a novel high curvature interior as dominated by quadratic curvature terms [31]③. A transition region relating the two distinctive behaviors exists around the gravitational radius. For a typical 2-2-hole, the transition region is extremely narrow, and it is difficult to distinguish from current observations. No exotic form of matter is required for the existence of 2-2-holes. As an example, a thermal gas that is too soft to support an ultracompact configuration in GR can source a 2-2-hole in quadratic gravity [32, 34]. This both provides a more realistic endpoint for a generic gravitational collapse and enables the study of the thermodynamics of ultracompact horizonless objects in parallel with the discussion on compact stars in GR [49]. Therefore, the thermodynamic behavior of 2-2-holes is expected to be closely related to the structure of their high-curvature interiors, and this serves as a sharp prediction of the theory. In the following, we first review the thermodynamics and evaporation of 2-2-holes, and then discuss the observational constraints from our earlier research [48].
-
Without loss of generality, we focus on 2-2-holes sourced by massless relativistic particles, with the equation of state
$ \rho = 3p $ . Following the conservation law of the stress tensor, the local measured temperature satisfies Tolman’s law, and it increases in the deep gravitational potential in the interior. When the 2-2-hole is not in thermal equilibrium with its surroundings, the temperature at spatial infinity (T) is the one at which it radiates as a black body.Depending on the mass, 2-2-holes may have distinctive thermodynamic characteristics. For a large 2-2-hole with M considerably larger than
$ M_{\mathrm{min}} $ , the interior thermal gas constitutes a high temperature firewall with a large angular proper length and a rather small radial proper length. Thus, independent of the mysterious features of the event horizon, a large 2-2-hole exhibits anomalous thermodynamics similar to that of black holes, e.g., negative heat capacity and the area law for entropy. A small 2-2-hole with M approaching$ M_{\mathrm{min}} $ behaves more like a star in GR, with a positive heat capacity and the entropy scaling trivially with the interior size. In the minimum mass limit, the temperature at infinity, entropy, and the interior size all approach zero. Thus, a large 2-2-hole begins by radiating like a black hole with increasing radiation power. After attaining the maximum temperature at approximately$ 1.5M_{\mathrm{min}} $ , it enters into the remnant stage with negligible radiation.The temperature and entropy for a large 2-2-hole can be well approximated as
$ T\approx 1.7\, \mathcal{N}^{-1/4}\hat{M}_{\mathrm{min}}^{1/2}\, T_ \mathrm{BH},\quad S\approx 0.60\, \mathcal{N}^{1/4}\hat{M}_{\mathrm{min}}^{-1/2} \,S_ \mathrm{BH}\,, $

(2) where
$ \hat{M}_{\mathrm{min}}≡M_{\mathrm{min}} /m_{Pl} $ , the Hawking temperature$ T_{BH}= $ $ m^2_{Pl}/8πM $ , and the Bekenstein-Hawking entropy$ S_{BH}= $ $ πr_H^2/ℓ^2_{Pl} $ . They differ from the black hole quantities only by an overall constant; this introduces additional dependence on the remnant mass$ M_{\mathrm{min}} $ and the number of degrees of freedom$ \mathcal{N} $ in the thermal gas. Their product remains the same, i.e.,$ T S = T_ \mathrm{BH}S_ \mathrm{BH} = M/2 $ , according to the the first law of thermodynamics.A thermal 2-2-hole evaporates when T is larger than the background temperature. Its mass evolution can be described by the Stefan-Boltzmann law, with the power being
$ -\frac{{\rm d}M}{{\rm d}t} \approx \frac{\pi^2}{120}\, \mathcal{N}_* \, 4\pi r_H^2 \,T^4\;, $

(3) which assumes
$ 4\pi r_H^2 $ as the effective emitted area.$ \mathcal{N}_* $ denotes the number of particles lighter than T [50], and it could be significantly smaller than$ \mathcal{N} $ . The time dependences of the temperature and mass assume the same form as for a black hole. Considering$ \mathcal{N}_* $ as a constant determined by the initial T, we obtain$ T(t)\approx T_{ \mathrm{init}}\left(1-\frac{\Delta t}{\tau_L}\right)^{-1/3},\quad M(t)\approx M_{\mathrm{init}}\left(1-\frac{\Delta t}{\tau_L}\right)^{1/3}, $

(4) where
$ \tau_L $ is the evaporation time for a 2-2-hole evolving from a much larger$ M_{\mathrm{init}} $ to$ M_{\mathrm{min}} $ ,$ \tau_L \,\approx \,2\times 10^{-40} \, \frac{\mathcal{N}}{\mathcal{N_*}} \, \hat{M}_{\mathrm{min}}^{-2} \, \hat{M}_{\mathrm{init}}^{3}\; {\mathrm{s}}\,, $

(5) where
$ \hat{M}_{\mathrm{init}}\equiv M_{\mathrm{init}}/m_{\mathrm{Pl}} $ . Because of the$ M_{\mathrm{min}} $ dependence,$ \tau_L $ is generally smaller than the lifetime of a black hole with the same mass. Note that (4) and (5) assume evaporation immediately after formation, while primordial 2-2-holes formed in the radiation era may initially have had a higher background temperature, and the accretion of cosmic radiation must be considered. Nonetheless, the growth in the mass is observed to be at most of order one and the effect on$ \tau_L $ is also negligible [27]. Therefore, we ignore the accretion effects in the following discussion.For a particle species j with mass
$ m_j $ , by assuming the average energy to be the temperature, the number of particles emitted through the 2-2-hole evaporation is$ N_j = g_j\int_{t_j}^{\tau_L}\frac{{\rm d}N}{{\rm d}t}{\rm d}t \approx -g_j\int_{t_j}^{\tau_L}\frac{1}{T}\frac{{\rm d}M}{{\rm d}t}{\rm d}t\,, $

(6) where
$ g_j $ is the particle species number and$ t_j $ denotes the starting time for the emission of particle j. Depending on the particle mass, two different scenarios exist:$ {\mathrm{Light}}\;{\mathrm{mass}}\;{\mathrm{case:}}\;\;\;m_j\leqslant T_{\mathrm{init}},\quad {t_j} = t_{\mathrm{init}}, $

(7) $ {\mathrm{Heavy}}\;{\mathrm{mass}}\;{\mathrm{case:}}\;\;\;{m_j} > {T_{{\mathrm{init}}}},\quad {t_j}/{\tau _L} = 1 - {({m_j}/{T_{{\mathrm{init}}}})^{ - 3}}. $

(8) Subsequently, we determine the number of emitted particles as
$ N_j\approx 7.4\, \kappa_j\, {B}_j\, \mathcal{N}^{1/4}\hat{M}_{\mathrm{min}}^{-1/2}\hat{M}_{\mathrm{init}}^{2}\,, $

(9) where
${B}_j = g_j/\mathcal{N}_*$ is the branching fraction and$ \kappa_j = \left\{ \begin{array}{ll} 1\,, & {\mathrm{for}}\quad m_j\leqslant T_{\mathrm{init}} \\ T^2_{\mathrm{init}}/m_j^2\,, & {\mathrm{for}}\quad m_j>T_{\mathrm{init}} \end{array} \right. \,. $

(10) As expected, the number of emitted particles is proportional to the effective emitted area of the hole, and for the heavy particle scenario, it is suppressed by the particle masses. Note that we ignore the spin dependence of the number of emitted particles here. Although the effective emitted area in (3) generally depends on the particle spin [51], given that
$ T\, r_H\gtrsim1 $ , the area approaches the geometrical-optics limit regardless of the spin and can be well approximated using the horizon area. Thus, the particle spin has a minimal function for our discussion of dark matter production in this paper.As a final remark, in the standard model (SM), the number of particle species varies from 107 to 11 for
$ T\gtrsim\, $ TeV, and$ T\sim $ MeV. In most of the expressions, their dependences have powers smaller than 1; hence, the selection of different numbers registers errors only on the order of 1. Even considering a large dark sector, we restrict to the scenario in which the dark sector contribution is at most in the order of the SM ones. Therefore, for the order-of-magnitude estimation, these factors are simply insignificant. In the rest of the paper, we will suppress the number of species dependence with small powers by using$ \mathcal{N}_* = \mathcal{N}\approx107 $ and$ g_{*}\approx 11 $ , unless otherwise stated. -
Assuming that the primordial 2-2-holes have already completed the evaporation and become remnants now, the mass fraction of 2-2-hole remnants in dark matter today is
$ f\equiv\frac{M_{\mathrm{min}}\,n(t_0)}{\rho_{\mathrm{DM}}(t_0)} = \frac{M_{\mathrm{min}}\,s(t_0)}{\rho_{\mathrm{DM}}(t_0)}\frac{n(t_0)}{s(t_0)}\,, $

(11) where
$ n(t) $ denotes the number density for the remnants,$ s(t_0) = 2.9\times 10^3\, \mathrm{cm}^{-3} $ ,$ \rho_{ \mathrm{DM}}(t_0)\approx 0.26\rho_c $ , and$ \rho_c = 9.5\times $ $ 10^{-30}\, \mathrm{g}\, \mathrm{cm}^{-3} $ [52]④.The relationship between f and the number density to entropy density ratio at the time of formation
$ n(t_{\mathrm{init}})/s(t_{\mathrm{init}}) $ depends on whether the primordial 2-2-holes have ever dominated the energy density or not. Considering the 2-2-hole formation in the radiation era, the initial mass faction of 2-2-holes increases with time, usually from a small value. As the leading order approximation for the cosmic evolution, we consider the evaporation as an instantaneous radiation of energy at$ t\approx \tau_L $ , with the 2-2-hole mass$ M(t) \approx M_{\mathrm{init}} $ at$ t \leqslant \tau_L $ and$ M(t) \approx M_{\mathrm{min}} $ at$ t > \tau_L $ . For a particular$ M_{\mathrm{init}} $ , we can then define a critical number density at formation:$ n_c(t_{\mathrm{init}}) = \frac{\rho_ \mathrm{rad}(t_{\mathrm{init}})}{M_{\mathrm{init}}}\sqrt{\frac{t_{\mathrm{init}}}{\tau_L}}\,, $

(12) with which the 2-2-holes and radiation have equal energy densities at
$ t\approx \tau_L $ .When
$ n(t_{\mathrm{init}})\lesssim n_c(t_{\mathrm{init}}) $ , i.e., the non-domination scenario, the 2-2-holes are always subdominant in the energy budget, and the entropy injection from evaporation is negligible. The ratio$ n(t)/s(t) $ remains constant until the present, with$ n(t_0)/s(t_0) \approx n(\tau_L)/s(\tau_L)\approx n(t_{\mathrm{init}})/s(t_{\mathrm{init}}) $ . Thus, the mass fraction of remnants today is$ f\approx 2.6\times 10^{28}\hat{M}_{\mathrm{min}} \frac{n(t_{\mathrm{init}})}{s(t_{\mathrm{init}})}\,. $

(13) When
$ n(t_{\mathrm{init}})\gtrsim n_c(t_{\mathrm{init}}) $ , i.e., the domination scenario, 2-2-holes became dominant at some earlier time and there was a new era of matter domination before$ \tau_L $ . The extra redshift of the number density introduced by this new era is canceled by the large initial density such that$ n(\tau_L) $ remains the same as the one with$ n_c(t_{\mathrm{init}}) $ . For the thermal radiation, the energy and entropy densities immediately after evaporation also remain in the same order of magnitude as the background quantities in the non-domination scenario, corresponding to the radiation temperature$ T_{\mathrm{bkg}}^{\;\tau}\approx 3.4\times 10^{16}\,\hat{M}_{\mathrm{min}} \, \hat{M}_{\mathrm{init}}^{-3/2}\; \mathrm{GeV}\,, $

(14) at
$ \tau_L $ for both scenarios. Thus, the current mass fraction has a maximum:$ f_{\mathrm{max}} \approx 2.6\times 10^{28}\hat{M}_{\mathrm{min}} \frac{n_c(t_{\mathrm{init}})}{s(t_{\mathrm{init}})} \approx 9.4\times 10^{25}\, \hat{M}_{\mathrm{min}} ^{2} \,\hat{M}_{\mathrm{init}}^{-5/2}\,, $

(15) and the bound is saturated with
$ f \approx f_ \mathrm{max} $ for the domination scenario.There is a special value of the initial mass
$ M_{\mathrm{DM}} $ corresponding to$ f_ \mathrm{max} = 1 $ , expressed as$ M_{\mathrm{DM}}\approx 5.3\times 10^5\, \hat{M}_{\mathrm{min}}^{4/5}\; \mathrm{g}\,. $

(16) Thus, for
$ M_{\mathrm{init}}\lesssim M_{\mathrm{DM}} $ , with$ f_{ \mathrm{max}} $ being greater than unity, the 2-2-hole remnants can account for all dark matter, but the 2-2-hole domination is not permitted. For$ M_{\mathrm{init}}\gtrsim $ $ M_{\mathrm{DM}} $ , even the 2-2-hole domination occurs, the remnants cannot be the majority of dark matter.For the later discussion of dark matter and baryogenesis, an important input is the 2-2-hole number density to entropy ratio immediately after evaporation. From (13) and (15), we obtain
$ \frac{n(\tau_L)}{s(\tau_L)} = \left\{\begin{array}{ll} 3.9\times 10^{-29}\,f\,\hat{M}_{\mathrm{min}}^{-1}\,, & \mathrm{non-domination} \\ 3.6\times10^{-3}\, \hat{M}_{\mathrm{min}}\, \hat{M}_{\mathrm{init}}^{-5/2}\,, & \mathrm{domination} \end{array}\right. \,. $

(17) The result for the domination scenario can be determined from the non-domination scenario by setting
$ f = f_ \mathrm{max} $ .The evaporation of primordial 2-2-holes are subject to strong constraints from BBN and cosmic microwave background (CMB) [48]. It is safe to have the evaporation end before BBN to evade the bounds, i.e.,
$ \tau_L\lesssim 1\, $ s. This imposes an upper (lower) bound on the initial mass (temperature), with$ M_ \mathrm{BBN}\approx 3.7\times 10^8 \,\hat{M}_{\mathrm{min}}^{2/3}\; \mathrm{g} \,,\quad T_ \mathrm{BBN}\approx 1.5\times 10^4\,\hat{M}_{\mathrm{min}}^{-1/6}\; \mathrm{GeV}\,. $

(18) Thus, the special values of the initial mass in (16) and (18) both increase with
$ M_{\mathrm{min}} $ but with different powers. Thus, their equality$ M_{\mathrm{DM}} = M_ \mathrm{BBN} $ defines a special value of the remnant mass:$ M_{\mathrm{min}}^ \mathrm{D} \approx 4.7\times 10^{16}\, \mathrm{g}\,. $

(19) For small remnants with
$ M_{\mathrm{min}}\lesssim M_{\mathrm{min}}^ \mathrm{D} $ , the 2-2-hole domination is permitted for the initial mass range$ M_{\mathrm{DM}}\lesssim M_{\mathrm{init}}\lesssim M_ \mathrm{BBN} $ . For large remnants with$ M_{\mathrm{min}}\gtrsim $ $ M_{\mathrm{min}}^ \mathrm{D} $ , we obtain$ M_{\mathrm{init}}\lesssim M_ \mathrm{BBN}<M_{\mathrm{DM}} $ and only the non-domination scenario is relevant.These observations can directly probe the remnant mass
$ M_{\mathrm{min}} $ . Remnants with$ M_{\mathrm{min}}\gtrsim 10^{17}\, $ GeV can be detected through gravitational interaction as in the case of PBHs. However, lighter remnants are accessible owing to a distinctive phenomenon associated with the remnant mergers. According to 2-2-hole thermodynamics, the merger product of remnant binaries with a mass of approximately$ 2M_{\mathrm{min}} $ can be considerably hot, and its temperature is approximate to the maximum permitted value, with$ T_ \mathrm{merger}\approx 1.3\times 10^{17}\hat{M}_{\mathrm{min}}^{-1/2}\, \mathrm{GeV}\,. $

(20) Thus, the evaporation of the merger product will produce high-energy particle fluxes, with the average energy ranging from the Planck scale down to the GeV scale. Considering the latest estimations for the binary merger rate and parton shower effects for the high-energy emission, we observe strong constraints from the photon and neutrino flux measurements for
$ M_{\mathrm{min}}\lesssim 10^{26}\, $ g owing to this novel phenomenon, as summarized in Fig. 1. To account for all of dark matter,$ M_{\mathrm{min}} $ has be to small and the upper bound varies from$ 10^5\, $ g to$ 10\,m_{\mathrm{Pl}} $ depending on the parton shower effects.
Figure 1. (color online) Constraints on the mass fraction of 2-2-hole remnants f as a function of
$ M_{\mathrm{min}} $ [48]. The gray lines present upper bounds from purely gravitational interactions as in the case of PBHs. The colored lines indicate the constraints on the high-energy particle fluxes particular to 2-2-hole remnants. The solid line considers only the on-shell neutrinos and serves as a conservative estimation. The dashed and dotted lines include the parton shower effects and may suffer more from the theoretical uncertainties.In the remainder of the paper, the following benchmark values of
$ M_{\mathrm{min}} $ are selected to present the results:$ M_{\mathrm{min}} \approx m_{\mathrm{Pl}},\; 10^5\, \mathrm{g},\; 10^{28}\, \mathrm{g}\,. $

(21) $ M_{\mathrm{min}} \approx m_{\mathrm{Pl}} $ corresponds to the strong coupling scenario with only one fundamental scale in the theory.$ M_{\mathrm{min}}\approx 10^5\, $ g has a large uncertainty for the constraints on f, which may range from$ 10^{-4} $ to$ 1 $ depending on whether the parton shower effects are included.$ M_{\mathrm{min}}\approx 10^{28}\, $ g is approximately the Earth mass and related to the anomalous microlensing events recently observed by OGLE with f at a percent level [53]⑤. -
Similar to that of black holes, the evaporation of primordial 2-2-holes provides a natural production mechanism for the dark sector particles that may interact only with the SM through gravity. In this section, we explore the observational implications for the production of dark matter and dark radiation. In Sec. IIIA for dark matter, we first study the requirement of the observed relic abundance and then consider the free-streaming constraints for the initially relativistic particles produced by evaporation. Light particles that remained relativistic at the time of matter-radiation equality can be considered as dark radiation, and they contribute to the effective number of relativistic degrees of freedom
$ N_{\mathrm{eff}} $ . In Sec. IIIB, we explore the dark radiation contribution to$ N_{\mathrm{eff}} $ and the possible constraints. -
Many proposals have been provided for dark matter production, including mechanisms such as freeze-out [54-56], freeze-in [57], gravitational production during inflation [58-60], misalignment mechanism [61-64], and production through out-of-equilibrium decays [65, 66]. As in the case of black holes [23-28], 2-2-hole evaporation produces particles regardless of the background temperature; hence, it provides a large viable parameter space for the dark matter mass. To obtain the strongest relic abundance constraints on the production through 2-2-hole evaporation, we focus on the simplest scenario and ignore contributions from other mechanisms.
Currently, the mass fraction of a dark matter particle
$ \chi $ is expressed as$ f_{\chi} = \frac{m_{\chi}}{\rho_{\mathrm{DM}}} \frac{n_{\chi}({t_0})}{s(t_0)} s(t_0)\;, $

(22) where
$ m_\chi $ is the particle mass and$ n_{\chi}({t_0})/s(t_0)\approx $ $ n_{\chi}({\tau_L})/s(\tau_L) = N_{\chi} n({\tau_L})/s(\tau_L) $ . Here,$ n({\tau_L})/s(\tau_L) $ denotes the number density to entropy ratio for 2-2-holes given in (17).$ N_{\chi} $ is the number of$ \chi $ particles emitted from the evaporation of a single 2-2-hole given in (9). Similar to a black hole, depending on whether the particle mass$ m_\chi $ is larger or smaller than the 2-2-hole initial temperature, the particle number differs by the factor of$ \kappa_\chi $ given in (10). For the light mass scenario,$ m_{\chi}\leqslant T_{\mathrm{init}} $ , we obtain$ f_{\chi}\approx \left\{\begin{array}{ll} 2\times 10^{-18} \dfrac{m_{\chi}}{\mathrm{GeV}}\;f \; {{B}}_{\chi}\;\hat{M}_{\mathrm{min}}^{-3/2}\;\hat{M}_{\mathrm{init}}^{2}\,, &\hspace{-2mm} \mathrm{non{\text -}domination}\\ 2\times10^{8}\; \dfrac{m_{\chi}}{\mathrm{GeV}} \; {{B}}_{\chi}\; \hat{M}_{\mathrm{min}}^{1/2}\;\hat{M}_{\mathrm{init}}^{-1/2}\,, &\hspace{-2mm} \mathrm{domination} \end{array}\right. \,. $

(23) For the heavy mass scenario,
$ m_{\chi}>T_{\mathrm{init}} $ , there is an additional mass suppression in$ \kappa_\chi $ , and we obtain$ f_{\chi}\approx \left\{\begin{array}{ll} \!\!\!\! 1.3\times10^{17}\; \left(\dfrac{m_{\chi}}{\mathrm{GeV}}\right)^{-1} \; f\; { {B}}_{\chi}\; \hat{M}_{\mathrm{min}}^{-1/2}\,, &\hspace{-3mm} \mathrm{non{\text -}domination}\\ \!\!\!1.3\times10^{43}\; \left(\dfrac{m_{\chi}}{\mathrm{GeV}}\right)^{-1} \; { {B}}_{\chi}\; \hat{M}_{\mathrm{min}}^{3/2}\;\hat{M}_{\mathrm{init}}^{-5/2}\,, &\hspace{-3mm} \mathrm{domination} \end{array}\right. \,. $

(24) As expected, the dark matter abundance
$ f_\chi $ is proportional to the 2-2-hole remnant abundance f. The domination scenario can be derived from the non-domination scenario by setting$ f = f_{\mathrm{max}} $ given in (15); therefore,$ f_\chi $ exhibits different dependences on the 2-2-hole masses. For simplicity, we assume a single particle component in the dark matter content, in addition to the contribution from 2-2-hole remnants; hence,$ f+f_{\chi} = 1 $ . In case there are other dark matter production mechanisms in play such as the ones mentioned in the beginning of this subsection, then we would obviously have$ f+f_{\chi}\leqslant1 $ in order not to overclose the universe. See [28] for discussion of PBHs (without leftover remnants) for the case where there is an additional production mechanism on the top of the production through black hole evaporation.Figure 2 depicts the constraints on the dark matter mass as a function of the initial mass
$ M_{\mathrm{init}} $ for some benchmark values of$ M_{\mathrm{min}} $ . The red dashed lines denote the boundaries of the permitted parameter space if the dark matter particle produced by 2-2-hole evaporation account for the observed abundance in the non-domination scenario. Since f can be arbitrarily small, the abundance constraint only provides an upper and lower bound for$ m_\chi> T_{\mathrm{init}} $ (heavy mass) and$ m_\chi\leqslant T_{\mathrm{init}} $ (light mass), respectively. For illustration, we select$ f\leqslant 1/2 $ to indicate the maximum permitted region, as we are interested in the scenario in which the particle dark matter is the main component. For$ M_{\mathrm{min}} = 10^5\, $ g , we also present the range for$ f\leqslant 10^{-4} $ by considering the observational constraints associated with the remnant mergers. We observe that the upper bound is independent of$ M_{\mathrm{init}} $ , while the lower bound increases for small$ M_{\mathrm{init}} $ values. At a small value of$ M_ \mathrm{HL} $ the two bounds intersect, and the$ \chi $ abundance becomes too small for a smaller$ M_{\mathrm{init}} $ regardless of the dark matter mass. In the white region, there is a one-to-one correspondence between f and$ m_\chi $ to satisfy the observed abundance. The 2-2-hole domination is permitted for$ M_{\mathrm{DM}}\lesssim M_{\mathrm{init}}\lesssim M_ \mathrm{BBN} $ when$ M_{\mathrm{min}}\lesssim M_{\mathrm{min}}^ \mathrm{D} $ given in (19), and the bounds are saturated with$ f_\chi = 1-f_ \mathrm{max} $ (solid lines). For a larger$ M_{\mathrm{init}} $ in this parameter space, the permitted range of$ m_\chi $ shrinks owing to the decreasing 2-2-holes abundance.
Figure 2. (color online) Constraints on the dark matter mass
$ m_\chi $ as a function of the 2-2-hole initial mass$ M_{\mathrm{init}} $ for the benchmark remnant masses$ M_{\mathrm{min}} $ in (21), assuming a single particle component with${B}_\chi\, (g_\chi) = 0.01\,(1)$ ,$ 0.5\, (107) $ . The white region is permitted, and the black dotted lines denote$ T_{\mathrm{init}} $ , the separation between the light mass and heavy mass scenarios. The red dashed lines indicate the upper and lower bounds derived from the observed abundance in the non-domination scenario that terminates at$ M_ \mathrm{HL} $ on the left and$ M_ \mathrm{BBN} $ on the right. For small$ M_{\mathrm{min}} $ in the first and second columns, the 2-2-hole domination is permitted for$ M_{\mathrm{DM}}\lesssim M_{\mathrm{init}}\lesssim M_ \mathrm{BBN} $ , and the thick lines indicate the relevant parameter space. For the second column, we also indicate the stronger bounds with$ f\leqslant 10^{-4} $ . For the third column, for$ f\leqslant 0.1 $ ,$ M_ \mathrm{HL} $ goes beyond$ M_ \mathrm{BBN} $ when${{B}}_\chi = 0.01$ and there is no viable parameter space. The blue shaded region is excluded by the free-streaming constraints.Therefore, the dark matter particles must be lighter for an increasing remnant mass
$ M_{\mathrm{min}} $ . The upper bound on$ m_\chi $ is independent of$ M_{\mathrm{init}} $ and it decreases as$ \hat{M}_{\mathrm{min}}^{-1/2} $ . The lower boundary is instead determined by the minimum value of the lower dashed lines in Fig. 2 with$ M_{\mathrm{init}}\approx M_{\mathrm{DM}},\,M_ \mathrm{BBN} $ for$ M_{\mathrm{min}}\lesssim M_{\mathrm{min}}^ \mathrm{D} $ and$ M_{\mathrm{min}}\gtrsim M_{\mathrm{min}}^ \mathrm{D} $ , and the remnant mass dependence becomes$ \hat{M}_{\mathrm{min}}^{-1/10} $ and$ \hat{M}_{\mathrm{min}}^{1/6} $ , respectively. Thus, the permitted parameter space shrinks in the weak coupling scenario. For$ M_{\mathrm{min}} $ as large as the Earth mass$ \sim10^{28}\, $ g, the permitted mass range is constrained such that the number of degrees of freedom for the dark matter particle can have a significant effect. For the 2-2-hole domination case,$ m_\chi $ cannot remain too close to$ T_{\mathrm{init}} $ because of a lower bound on$ f_ \mathrm{max} $ at$ M_{\mathrm{init}}\approx M_ \mathrm{BBN} $ , and the parameter space is more restricted.Next, we consider the free-streaming constraints. Dark matter particles with excessive energy can erase small scale structures; thus, they are strongly constrained by observations. In contrast to other mechanisms, particles produced by evaporation are initially relativistic and only become non-relativistic as the universe expands. For an order-of-magnitude estimation, we approximate the spectrum by emission at the average energy and then consider the constraints on the current velocity for the thermal relic [23]. Assuming dark matter particles never attain equilibrium with the thermal bath, the current average momentum is
$ p_0 = \frac{a(\tau_L)}{a(t_0)}\langle{p(\tau_L)}\rangle\,. $

(25) Up to an order one factor, the average momentum
$ \langle{p(\tau_L}\rangle\approx T_{\mathrm{init}},\, m_\chi $ for the light mass scenario ($ T_{\mathrm{init}}> m_\chi $ ) and heavy mass scenario ($ T_{\mathrm{init}}< m_\chi $ ) respectively. The redshift factor is,$ \frac{a(\tau_L)}{a(t_0)}\approx\left(\frac{s(\tau_L)}{s(t_0)}\right)^{-1/3}\approx 2.4\times 10^{-30}\,\hat{M}_{\mathrm{min}}^{-1}\,\hat{M}_{\mathrm{init}}^{3/2}\,. $

(26) For the dominant component of dark matter, its current velocity
$ v_0 = p_0/m_\chi $ is constrained to be$ v_0\lesssim 4.9\times 10^{-7} $ [67].For the light mass scenario, this imposes a lower bound on the dark matter mass with
$ m_\chi\gtrsim 1.3\times 10^{-6}\,\hat{M}_{\mathrm{min}}^{-1/2}\,\hat{M}_{\mathrm{init}}^{1/2}\, \mathrm{GeV}\,. $

(27) Because of a smaller amount of the redshift for a larger
$ M_{\mathrm{init}} $ , the bound increases with$ M_{\mathrm{init}} $ . As shown in Fig. 2, the free-streaming constraints exclude some part of the parameter space that predicts the observed relic abundance. In particular, the domination scenario for the light mass case is disfavored. For the heavy dark matter scenario, the velocity is independent of$ m_\chi $ . Thus, the maximum value is observed at$ M_{\mathrm{init}} = M_ \mathrm{BBN} $ independent of other parameters. It is observed to be significantly smaller than the demanded bound. Thus, the heavy mass scenario has no constraints. As shown in Appendix A, these simple estimates are supported by a more informative derivation by considering the momentum distribution and the relativistic fraction of dark matter particles. -
A useful method of parameterizing the effects of dark radiation is by changing the effective number of relativistic degrees of freedom
$ \Delta N_{\mathrm{eff}} $ , as defined by$ \Delta N_{\mathrm{eff}} = \frac{\rho_{\mathrm{DR}}(t_{\mathrm{EQ}})}{\rho_{\mathrm{R}}(t_{\mathrm{EQ}})}\left[N_{\nu}+\frac{8}{7}\left(\frac{11}{4}\right)^{4/3}\right]\,, $

(28) where
$ \rho_R(t_ \mathrm{EQ}), \rho_ \mathrm{DR}(t_ \mathrm{EQ}) $ are energy densities for thermal and dark radiation at the time of matter-radiation equality, respectively, and$ N_{\nu} = 3.046 $ is the standard value for the left-handed neutrinos in the SM [68]. A recent analysis by [69] estimates a slightly lower value where the difference does not cause a noticeable effect in our analysis. A nonzero$ \Delta N_{\mathrm{eff}} $ would affect the evolution of the universe, and the current upper limit is$ \Delta N_{\mathrm{eff}}\leqslant 0.28 $ at 95% C.L. [70]. It may also result in consequences for the estimation of the Hubble constant. For example,$ \Delta N_{\mathrm{eff}}\sim 0.1 $ has been suggested [26, 70-76] as a resolution for the current Hubble tension [52, 77] between the local measurements [78-80] and the CMB-inferred value from Planck data [52]. Later studies observed that changing$ \Delta N_{\mathrm{eff}} $ alone is not sufficient to fully resolve the tension, but the upper limit can be slightly relaxed,$ \Delta N_{\mathrm{eff}}\leqslant 0.52 $ [81], if the tension is considered. In the near future, CMB-S4 measurements might be able to probe$ \Delta N_{\mathrm{eff}}\sim 0.02 $ [82].To determine the contribution to
$ \Delta N_{\mathrm{eff}} $ from 2-2-hole evaporation, we relate the energy densities at the time of matter-radiation equality to the ones immediately after the end of the 2-2-hole evaporation. For dark radiation, the energy density is simply diluted by the universe expansion, with$ \rho_{\mathrm{DR}}(t_{\mathrm{EQ}})a(t_{\mathrm{EQ}})^4 = \rho_{\mathrm{DR}}(\tau_L)a(\tau_L)^4 $ . For the thermal radiation, there are additional contributions from the entropy dumps, and the relationship to the scale factor can be observed from the entropy conservation$ g_{*,\mathrm{eq}}\,a(t_{\mathrm{EQ}})^3 \,T_{\mathrm{EQ}}^3 =g_{*,\tau_L}\,a(\tau_L)^3 \,T_{\mathrm{RH}}^3 $ , where$ g_* $ denotes the number of relativistic degrees of freedom at a particular time. Thus, we obtain$ \frac{\rho_{\mathrm{DR}}(t_{\mathrm{EQ}})}{\rho_{\mathrm{R}}(t_{\mathrm{EQ}})}\approx \frac{\rho_{\mathrm{DR}}(\tau_{L})}{\rho_{\mathrm{R}}(\tau_L)}\frac{g_{*,\mathrm{eq}}^{1/3}}{g_{*,\tau_L}^{1/3}}\;, $

(29) for which we have ignored the difference in the definition of
$ g_{*} $ in entropy and energy since the corresponding error is well within$ \mathcal{O}(1) $ ; hence, it is negligible.$ \rho_{\mathrm{R}}(\tau_L) $ can be related to the energy density of 2-2-holes through the evolution of density ratios,$ \rho(\tau_L)/\rho_{\mathrm{R}}(\tau_L) = a(\tau_L)\,\rho(t_{\mathrm{init}})/ $ $ (a(t_{\mathrm{init}})\,\rho_{\mathrm{R}}(t_{\mathrm{init}})) = f/f_{\mathrm{max}} $ , where$ f_{\mathrm{max}} $ is given in (15). In the domination scenario,$ f = f_{\mathrm{max}} $ and$ \rho(\tau_L) = \rho_{\mathrm{R}}(\tau_L) $ ⑧. Finally, by using$ \rho_{\mathrm{DR}}(\tau_{L})/\rho(\tau_{L})\approx {B}_{\mathrm{DR}} $ , we obtain$ \Delta N_{\mathrm{eff}}\approx \left\{\begin{array}{ll}\!\!\!\!\! 6.6\times 10^{-26}\, {B}_{\mathrm{DR}}\,f\,g_{*,\tau_L}^{-1/12}\,\hat{M}_{\mathrm{min}}^{-2}\,\hat{M}_{\mathrm{init}}^{5/2} \,, & \!\!\!\!\!\mathrm{non{\text -}domination}\\ \!\!\!\!\!11.2\; {B}_{\mathrm{DR}}\; g_{*,\tau_L}^{-1/3} \,, &\!\!\!\!\! \mathrm{domination} \end{array}\right. \,, $

(30) where
$ g_{*,\tau_L} = g_{*,\tau_L}^{\mathrm{SM}}+g_{\mathrm{DR}} $ . In the domination scenario, since$ \rho(\tau_L) = \rho_R(\tau_L) $ ,$ \Delta N_{\mathrm{eff}} $ is identical to the black hole scenairo regardless of whether remnants exist. Thus, it is easy to achieve$ \Delta N_{\mathrm{eff}}\sim 0.1 $ for$ \mathcal{N}_*\sim 100 $ , which is still permitted by the current limit. In the non-domination scenario, there is the additional$ M_{\mathrm{min}} $ dependence and the 2-2-hole contribution generally differs from the black hole one.We depict the prediction for
$ \Delta N_{\mathrm{eff}} $ in Fig. 3 as a function of$ M_{\mathrm{init}} $ for several$ M_{\mathrm{min}} $ values. For a small$ M_{\mathrm{min}} $ value for which f is not (significantly) constrained, e.g., Fig. 3(a), the maximum contribution is achieved in the domination scenario at$ M_{\mathrm{init}}\gtrsim M_{\mathrm{DM}} $ . Owing to the simple form of contribution to$ \Delta N_ \mathrm{eff} $ , the measurements can directly constrain the degrees of freedom of dark radiation. The current observations exclude a dark sector with$ g_ \mathrm{DR}\gtrsim 15 $ or 35 if the Hubble tension is considered, while the future measurements could attain the smallest possible contribution with$ g_ \mathrm{DR}\sim 1 $ . Below$ M_{\mathrm{DM}} $ , the contribution to$ \Delta N_{\mathrm{eff}} $ in the non-domination scenario decreases rapidly with decreasing$ M_{\mathrm{init}} $ . If the domination scenario is excluded, i.e.,$ g_ \mathrm{DR}\gg10 $ , only a small range of$ M_{\mathrm{init}} $ is still currently viable and could be probed in the near future. Because of the interplay of$ g_{*,\tau_L} $ and$ {\mathrm{B}}_ \mathrm{DR} $ in (30), increasing$ g_{\mathrm{DR}} $ will increase$ \Delta N_{\mathrm{eff}} $ up to the range$ g_{\mathrm{DR}}\sim 200-300 $ , above which$ \Delta N_{\mathrm{eff}} $ will begin to decrease. Thus, the intersection between the magenta dashed line and CMS-S4 approximately indicates the smallest$ M_{\mathrm{init}} $ of interest from the$ \Delta N_{\mathrm{eff}} $ measurements.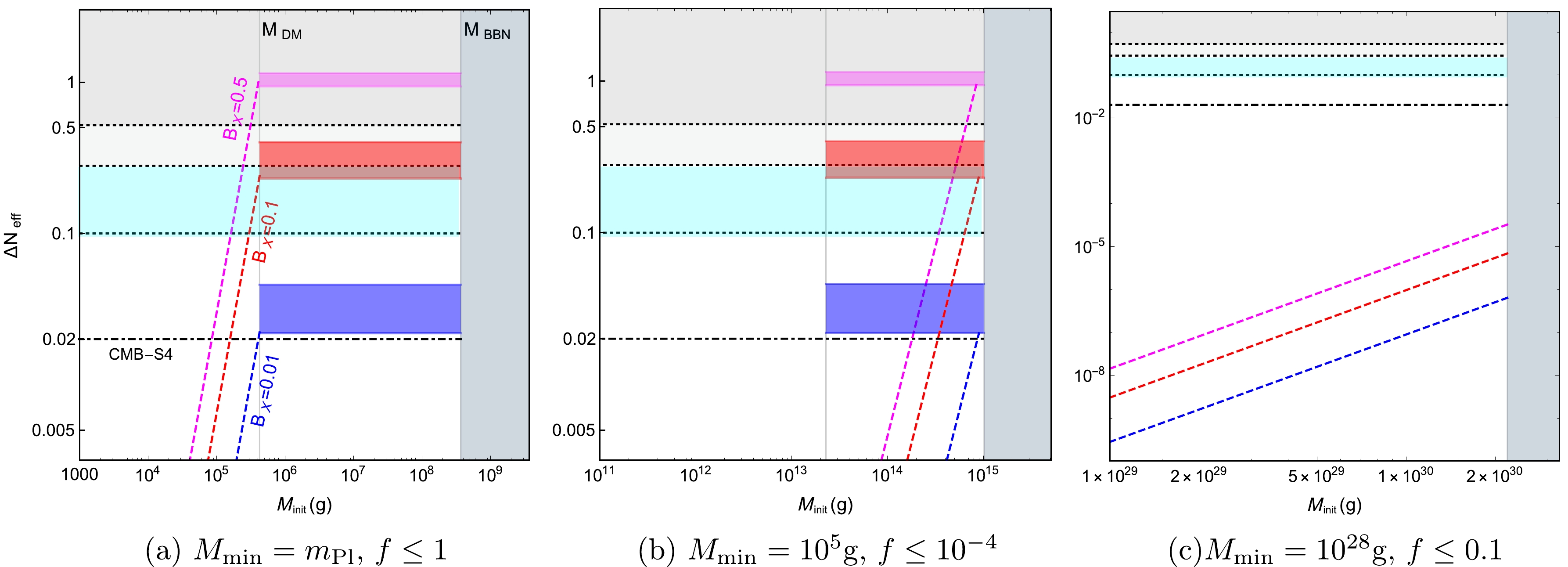
Figure 3. (color online) Several benchmark scenario demonstrating contributions to
$ \Delta N_{\mathrm{eff}} $ from the 2-2-hole evaporation in the early universe for a particular$ M_{\mathrm{min}} $ . Blue, red, and magenta lines/bands denote regions for${B}_{\mathrm{DR}}$ ($ g_{\mathrm{DR}}) = 0.01\;(1),\; 0.1\;(12) $ and$ 0.5\; (107) $ , respectively. The parameter space for the domination scenario, which can be realized only for$ M_{\mathrm{DM}}\lesssim M_{\mathrm{init}} \lesssim M_{\mathrm{BBN}} $ when$ M_{\mathrm{min}}\lesssim M_{\mathrm{min}}^ \mathrm{D} $ is indicated as shaded horizontal bands in which the upper and lower limits correspond to$ g_{*,\tau_L}^{\mathrm{SM}}\approx 11 $ and 107, respectively. The non-domination scenario corresponds to the dashed lines and connects to the domination band at$ M_{\mathrm{init}} $ where$ f_{\mathrm{max}} $ saturates the upper bound. The grey regions denote the excluded parameter space based on the Planck data, with the upper bound being$ \Delta N_{\mathrm{eff}}\leqslant 0.28 $ (or$ 0.52 $ if the Hubble tension is considered). The dot dashed line denotes the projected sensitivity of CMB-S4 measurements. The turquoise region shows the parameter space that could potentially alleviate the Hubble tension.For the larger
$ M_{\mathrm{min}} $ scenarios in which f is more strongly constrained, the lower boundary of the domination band shifts to a larger value of$ M_{\mathrm{init}} $ such that$ f_{\mathrm{max}} $ satisfies the observational bound. If this value of$ M_{\mathrm{init}} $ is larger than$ M_{\mathrm{BBN}} $ , the domination region in the parameter space cannot be reached. For instance, the dashed lines in Fig. 3(b) barely connect to the domination band. For$ M_{\mathrm{min}} > M_{\mathrm{min}}^{\mathrm{D}} $ given in (19), where the domination scenario cannot be realized, the contribution to$ \Delta N_{\mathrm{eff}} $ is generally extremely suppressed. For instance, the prediction in Fig. 3(c) is still significantly below the CMB-S4 sensitivity. This scenario persists even for a large dark sector with$ g_{\mathrm{DR}}\sim\mathcal{O}(100) $ .Finally, to consider the evaporation products as relativistic degrees of freedom and include them in
$ \Delta N_ \mathrm{eff} $ , these particles should have masses smaller than their energies at the time of matter-radiation equality,$\left\langle {{E_{{\rm{DR}}}}} \right\rangle {|_{{\rm{EQ}}}} \approx {T_{{\rm{init}}}}\;a({\tau _L})/a({t_{{\rm{EQ}}}})$ . This yields an upper bound on the dark radiation mass:$ m_{\mathrm{DR}}\lesssim 0.28\; \hat{M}_{\mathrm{init}}^{1/2}\,\hat{M}_{\mathrm{min}}^{-1/2}\;\mathrm{eV}\;. $

(31) For a particular
$ M_{\mathrm{min}} $ , since this upper bound increases with$ M_{\mathrm{init}} $ , the most conservative value can be obtained for$ M_{\mathrm{init}} = M_{\mathrm{BBN}} $ , with$ m_{\mathrm{DR}}\lesssim 1.2\; \hat{M}_{\mathrm{min}}^{-1/6}\;\mathrm{MeV}\;. $

(32) Notice the weak dependence on
$ M_{\mathrm{min}} $ . For instance, for$ M_{\mathrm{min}} = 10^{5}\, $ g the upper bound becomes$ m_{\mathrm{DR}}\lesssim 30\, $ keV, and for a much larger value$ M_{\mathrm{min}} = 10^{28\,} $ g, it is reduced to$ m_{\mathrm{DR}}\lesssim 4\, $ eV, which is slightly larger than the current limit for the SM neutrino masses. -
One of the challenges in modern physics is to understand the baryon asymmetry of the universe. Being parameterized by the baryon-to-entropy ratio
$ \mathcal{B} $ , the BBN and CMB observations require$ \mathcal{B}\approx 10^{-10} $ [83]. Since an initial contribution can be easily diluted by inflation, the observed baryon asymmetry is usually contemplated to be generated dynamically after reheating. Sakharov discovered three conditions for baryogenesis to occur in the early universe [84]: the existence of baryon number violating interactions, non-conservation of C and CP symmetries, and departure of thermal equilibrium. Depending on how these conditions are satisfied, the proposed models for baryogenesis are divided into two main categories: out-of-equilibrium decays of heavy particles [84-88] and electroweak baryogenesis [89-96].The 2-2-hole evaporation can potentially accommodate baryogenesis in both contexts, similar to black holes ([23, 25, 97-106] and [107, 108]). For particle decay, the 2-2-hole evaporation could efficiently produce the required heavy particles (accommodated in the theory beyond the SM) regardless of the background temperature. Moreover, particles emitted by 2-2-holes naturally satisfy the out-of-equilibrium condition as long as they do not rapidly attain thermal equilibrium with the background. There are other proposed mechanisms for non-thermal production for particles responsible for baryogenesis, such as production during reheating through the inflaton decay [109, 110]; the Affleck-Dine baryogenesis [111] that utilizes the flat directions of a SUSY potential along which baryon and lepton violation condensates of squarks and sleptons form and subsequently decay to regular fermions; and its Q-ball version [112-114].
In contrast to the standard scenario, in which the particles are thermally produced, the decay rates are required to range below the Hubble rate for the particles to be out-of-thermal equilibrium with the background. This usually requires the particles to be super-heavy⑩. For electroweak baryogengesis, 2-2-hole evaporation above the electroweak scale may satisfy the out-of-equilibrium condition through the domain wall formation outside the hole, without the necessity of a first order phase transition required in the standard scenario.
For both scenarios, the baryon-to-entropy ratio is expresssed as
$ \mathcal{B} = B\, \frac{n(\tau_L)}{s(\tau_L)}\,, $

(33) where B denotes the baryon number produced by each evaporating hole. Thus, we obtain
$ \mathcal{B}\approx \left\{\begin{array}{ll} 3.9\times 10^{-29}\,B\,f\,\hat{M}_{\mathrm{min}}^{-1}\,, & \mathrm{non{\text -}domination} \\ 3.6\times10^{-3}\,B\, \hat{M}_{\mathrm{min}}\, \hat{M}_{\mathrm{init}}^{-5/2}\,, & \mathrm{domination} \end{array}\right. \,. $

(34) with the 2-2-hole number density to entropy ratio
$ n(\tau_L)/s(\tau_L) $ given in (17). Since the remnant abundance is bounded from above by the observed value for dark matter, a heavier remnant is expected to have a smaller number density and then a smaller$ \mathcal{B} $ . Hence, the question becomes, what is the mass dependence for the baryon number B? In the following, we discuss the possibility of realizing the observed baryon asymmetry in both scenarios, i.e., baryogenesis through heavy particle decays and electroweak baryogenesis. -
One scenario for the baryon asymmetry generation is through direct baryon number violating decays of heavy particles, which we refer to as "direct baryogenesis." This is generally considered in grand unified theories (GUTs), referred to as GUT baryogenesis [88, 115-119], which naturally accommodates heavy gauge bosons or colored-scalars that couple to quarks and leptons simultaneously. The other scenario, known as leptogenesis [120-127], assumes the lepton-number-generation through decays of right-handed neutrinos first and then a subsequent conversion to the baryon number through sphaleron processes. Sphalerons are non-perturbative solutions in the electroweak theory that violate the accidental baryon and lepton numbers conservation at the perturbative level [89]. These processes become effective for temperatures below
$ 10^{12}\, $ GeV and above the electroweak scale. Sphalerons drive (B+L) to zero, but they do not effect (B-L). Therefore, any lepton asymmetry at appropriately high energies can be partially converted to baryon asymmetry. In either of these scenarios, if such particles that are responsible for baryogenesis exist in nature, they would have been emitted by 2-2-hole evaporation regardless of the underlying theory and their interaction strength with the SM, and the out-of-equilibrium condition would have been easily satisfied.For both scenarios, assuming the prompt decay of a heavy particle X,⑪ the baryon number produced by each evaporating hole can be expressed as
$ B = \gamma\, N_{X}\approx 24 \,\gamma \, \kappa_X\, {{B}}_X\,\hat{M}_{\mathrm{min}}^{-1/2}\,\hat{M}_{\mathrm{init}}^{2}\,, $

(35) where the particle number of X is given in (9). For direct B-violating decays,
$ \gamma $ is the parameter that quantifies CP-violation generated through the beyond SM physics and defined as$ \gamma\equiv \sum\limits_i V_i \frac{\Gamma (X\rightarrow f_i)-\Gamma (\bar{X}\rightarrow \bar{f}_i)}{\Gamma_X}\;, $

(36) where
$ V_i $ is the baryon number of the final state$ f_i $ and$ \Gamma_X $ is the decay width. For leptogenesis, X denotes the right-handed neutrino,$ V_i $ becomes the lepton number, and$ \gamma $ includes a factor of$ \sim 0.65 $ owing to the conversion from leptons to baryons through sphalerons. The value of the parameter$ \gamma $ depends on the underlying model and is usually related to the heavy particle mass$ m_X $ . Different ranges of values have been predicted in the literature, and$ \gamma $ can reach up to$ \mathcal{O} (1) $ , e.g., in resonance leptogenesis [121, 128]. Here we adopt a model-independent approach and constrain the parameter space of$ \gamma $ in the 2-2-hole evaporation picture.The baryon-to-entropy ratio is obtained from (34) as
$ \mathcal{B} = \left\{\begin{array}{ll} 9.4\times 10^{-28}\,f\,\gamma \, \kappa_X\, {B}_X\,\hat{M}_{\mathrm{min}}^{-3/2}\,\hat{M}_{\mathrm{init}}^{2}\,, & \mathrm{non{\text -}domination} \\ 8.8\times 10^{-2}\,\gamma \, \kappa_X\, {B}_X\,\hat{M}_{\mathrm{min}}^{1/2}\,\hat{M}_{\mathrm{init}}^{-1/2}\,, & \mathrm{domination} \end{array}\right. \,, $

(37) where
$ f = f_{\mathrm{max}} $ is inserted in the domination scenario. Similar to that for black holes [99], (37) indicates implicit assumptions about the background temperature after evaporation, i.e.,$ T_{\mathrm{bkg}}^{\;\tau} $ in (14). If$ T_{\mathrm{bkg}}^{\;\tau} $ is larger than the electroweak scale$ E_ \mathrm{W}\approx 100\, $ GeV, the sphaleron processes can effectively wash out the produced baryon number for direct baryogenesis; therefore,$ T_{\mathrm{bkg}}^{\;\tau}\lesssim E_ \mathrm{W} $ is required unless there is (B-L) production⑫. Moreover, sphalerons are essential for leptogenesis to transfer the lepton number to baryon number; thus, we need$ T_{\mathrm{bkg}}^{\;\tau}\gtrsim E_ \mathrm{W} $ instead.Figure 4 shows the lower limit on
$ \gamma $ required for$ \mathcal{B} \gtrsim10^{-10} $ with respect to$ M_{\mathrm{init}} $ for several benchmark$ M_{\mathrm{min}} $ ⑬. To obtain the most conservative bound, we use$ \kappa_X = 1 $ to avoid the suppression from the heavy mass$ m_X $ . We also set f to its maximum permitted value considering observational constraints. For small$ M_{\mathrm{min}} $ with$ f = 1 $ permitted, i.e., the first column, the minimum required$ \gamma $ is achieved at$ M_{\mathrm{init}}\approx M_{\mathrm{DM}} $ , the lower boundary of the domination band. In contrast to that for black holes with no remnants [98],$ \gamma $ cannot be further reduced at a smaller$ M_{\mathrm{init}} $ because of the abundance constraints on the 2-2-hole remnants. On the plots, we also highlight a special value of$ M_{\mathrm{init}} $ ,
Figure 4. (color online) Constraints on the CP-violation parameter
$ \gamma $ required for$ \mathcal{B} \gtrsim 10^{-10} $ with respect to$ M_{\mathrm{init}} $ for a particular$ M_{\mathrm{min}} $ , assuming$ \kappa_X = 1 $ and${{B}}_X\,(g_X) = 0.01\,(1)$ ,$ 0.5\,(107) $ . The grey region denotes the excluded parameter space with$ \mathcal{B} $ being too small, and the solid line indicates the region relevant for the domination scenario. For each$ M_{\mathrm{min}} $ value, we consider the observational constraints on f.$ M_ \mathrm{EW} $ denotes the value of$ M_{\mathrm{init}} $ for which the background temperature$ T_{\mathrm{bkg}}^{\;\tau} = E_ \mathrm{W} $ . The orange ($ M_{\mathrm{init}}\lesssim M_ \mathrm{EW} $ ) region indicates the relevant parameter space for leptogenesis and direct baryogenesis with (B-L) production, while the white ($ M_{\mathrm{init}}\gtrsim M_ \mathrm{EW} $ ) region is for direct baryogenesis.$ M_ \mathrm{EW}\approx 1.1\times 10^5\,\hat{M}_{\mathrm{min}}^{2/3}\; \mathrm{g} \,, $

(38) corresponding to
$ T_{\mathrm{bkg}}^{\;\tau} = E_ \mathrm{W} $ . Thus, leptogenesis only operates at$ M_{\mathrm{init}} $ below$ M_ \mathrm{EW} $ . Since$ M_ \mathrm{EW}<M_{\mathrm{DM}} $ , the minimum$ \gamma $ on the plot is relevant for direct baryogenesis, while for leptogenesis, a larger$ \gamma $ , at$ M_{\mathrm{init}}\approx M_ \mathrm{EW} $ , is required.For larger
$ M_{\mathrm{min}} $ , f is more strongly constrained as in Fig. 1, and$ \gamma $ must be enhanced to reproduce the observed asymmetry. For leptogenesis, which operates at smaller$ M_{\mathrm{init}} $ , the constraint on$ \gamma $ is always stronger for larger$ M_{\mathrm{min}} $ . For direct baryogenesis, although the smallest required value of$ \gamma $ decreases mildly for larger$ M_{\mathrm{min}} $ with unconstrained f, the final result is sensitive to the exact upper bound on f. For instance, for$ f = 1 $ , the bound at$ M_{\mathrm{init}}\approx M_{\mathrm{DM}} $ in Fig. 4(b) is smaller than that in Fig. 4(a). However, since f is actually much smaller, the lowest point is lifted to a larger value at$ M_{\mathrm{init}} $ at approximately$ M_ \mathrm{BBN} $ . For$ M_{\mathrm{min}}\gtrsim 2.8\times 10^{24}\, $ g,$ T_{\mathrm{bkg}}^{\;\tau} $ is below$ E_ \mathrm{W} $ for all possible$ M_{\mathrm{init}} $ values and leptogenesis becomes irrelevant. For such scenarios, the 2-2-hole initial temperature is also low. Thus, although the minimum required$ \gamma $ could be small, e.g., for$ M_{\mathrm{min}}\approx 10^{28\,} $ g, a considerably small$ m_X $ is required as well.To more clearly observe the dependence on heavy particle mass
$ m_X $ , we present the constraints on the$ m_X-\gamma $ plane in Fig. 5. The benchmark values selected to draw the contours correspond to several critical points in Fig. 4, for which the limit coincides with the horizontal part for the light mass scenario. The breaking point corresponds to$ m_X = T_{\mathrm{init}} $ , beyond which the lower limit of$ \gamma $ increases abruptly to compensate the suppression in the total number of particles emitted owing to$ \kappa_X<1 $ . Hence, an$ m_X $ that is exceedingly larger than the initial 2-2-hole temperature rapidly becomes disfavoured for$ \gamma\lesssim \mathcal{O}(1) $ . The lower limit of$ \gamma $ for the heavy mass scenario is observed to be independent of$ M_{\mathrm{init}} $ . Thus, different options of$ M_{\mathrm{init}} $ only change the breaking point for$ m_X $ and the minimum permitted value of$ \gamma $ . For instance, the orange and magenta solid lines indicate the most conservative constraints for leptogenesis and direct baryogengesis, respectively, for the Planck remnant scenario. Because of the smaller permitted value of$ M_{\mathrm{init}} $ , leptogenesis is subject to a stronger bound on$ \gamma $ , but with a larger breaking point for$ m_X $ . The mass$ m_X $ is more confined towards smaller values for the heavier remnant scenario. For instance, for$ M_{\mathrm{min}} = 10^{5} $ g, shown by the green line the upper limit becomes the electroweak scale, and for larger$ M_{\mathrm{min}} $ , it decreases further, forcing the decay particles to be very light.
Figure 5. (color online) Constraints on the CP-violation parameter
$ \gamma $ for$ \mathcal{B} \gtrsim 10^{-10} $ with respect to the heavy particle mass$ m_X $ , assuming${B}_X = 0.01$ . Benchmark values of$ (M_{\mathrm{min}},\;M_{\mathrm{init}},\;f) $ are selected according to Fig. 4. For each contour, the horizontal part denotes the light mass scenario with$ m_X \leqslant T_{\mathrm{init}} $ and$ \kappa_X = 1 $ , and the ascending part is for the heavy mass scenario with$ m_X > T_{\mathrm{init}} $ and$ \kappa_X <1 $ . The available parameter space is the upper left region. Only the region corresponding to the orange contour permits leptogenesis. -
Electroweak baryogengesis (EWBG) [89-96] has been an attractive scenario since it utilizes the sphaleron process in the SM for the baryon number violation, while new physics around the TeV scale is expected to satisfy the other two Sakharov conditions. In the standard scenario, the generation of baryon asymmetry proceeds through bubble nucleation during the electroweak weak phase transition. For a successful baryogenesis, new CP-violation source is required in addition to the one provided by the CKM matrix. The out-of-equilibrium condition can be realized if the electroweak phase transition is strongly first-order to prevent the washing out of the produced baryon asymmetry. This usually indicates the modification of the Higgs potential, and a large deviation of the Higgs self-interactions, which serve as an important target for the future collider. New physics models that incorporate both ingredients have been extensively studied to realize baryogenesis [129-131].
As an alternative, it was argued in [107] that primordial black holes can contribute to EWBG. If the Hawking radiation temperature is above the electroweak scale, the region surrounding the black hole is the electroweak symmetric phase, and a domain wall separating the symmetric phase from the broken one can form at some large radius. With the sphaleron process occuring in the domain wall near the symmetric region, a sufficient amount of the baryon asymmetry can be generated without the requiring a first-order phase transition since the Hawking radiation is already a non-equilibrium process. The additional CP violation should still be provided with new physics at the TeV scale. A close to the maximal CP violation is required for the simplest new physics scenario [107], while more involved models could possibly produce sufficient CP violation [108, 132]. In this subsection, we adopt the approach of [107] to investigate if the scenario could be improved for the 2-2-hole evaporation owing to the additional remnant mass
$ M_{\mathrm{min}} $ dependence.Assuming that the evaporation temperature
$ T(t) $ is significantly larger than the electroweak scale$ E_ \mathrm{W} $ , the emitted particles can attain local thermal equilibrium at a radius larger than the mean-free-path, and from the transfer energy equation, the temperature profile assumes the form$ \begin{aligned}[b] T(t, r)\approx& \left(T_{\text{bkg}}^3(t)+T_0^3(t) \, \frac{r_0}{r}\right)^{1/3}\\ \approx& \left(T_{\text{bkg}}^3(t)+1.3\times 10^{-4}\, \hat{M}_{\mathrm{min}} \, \frac{T(t)^2}{r}\right)^{1/3}\,. \end{aligned}$

(39) $ T_0(t) $ is in the order of$ T(t) $ in (4) and related to the boundary condition close to the would-be horizon, and it is typically significantly larger than the background temperature. By assuming that the total out-going energy flux equals the Hawking radiation flux, the boundary condition can be fixed as in the last expression. If the electroweak phase transition is in the second order, a domain wall forms at the radius$ r>r_ \mathrm{DW} $ , with$ r_ \mathrm{DW}\approx 1.3\times 10^{-4} \, \hat{M}_{\mathrm{min}} \,\frac{T(t)^2}{E_ \mathrm{W}^3}\, $

(40) expressed by the condition
$ T(t, r_ \mathrm{DW})\approx E_ \mathrm{W} $ . The Higgs vacuum expectation value turns nonzero at$ r_ \mathrm{DW} $ and saturates the broken phase value at$ r_ \mathrm{DW}+d_ \mathrm{DW} $ ; thus,$ d_ \mathrm{DW}\approx r_ \mathrm{DW} $ defines the width of the domain wall. The mean velocity of the out-going diffusing particles at the domain wall is$ v_ \mathrm{DW}\approx \frac{10}{3}\frac{T_0^3 r_0}{r_ \mathrm{DW}^2 E_ \mathrm{W}^4} \approx 2.6\times 10^4 \, \hat{M}_{\mathrm{min}}^{-1} \,\frac{E_ \mathrm{W}^2}{T(t)^2}\,. $

(41) Thus, for a heavier remnant, the domain wall increases and the particles diffuse more gradually.
The emitted particles passing through the domain wall can acquire a nonzero baryon asymmetry through the sphaleron process. With the domain wall properties given in (40) and (41), the production rate of the baryon number is
$ \dot{B}\approx 120\pi \, \alpha_W^5\, E_ \mathrm{W}^3\, r_ \mathrm{DW}^2\, v_ \mathrm{DW} \,\epsilon \,\Delta \theta \approx 6.1\times 10^{-11}\Delta \theta\, \hat{M}_{\mathrm{min}}\,\frac{T(t)^2}{E_ \mathrm{W}}\,, $

(42) where
$ \alpha_W\approx g^2/4\pi $ and$ \epsilon\approx 1/100 $ .$ \Delta \theta $ is the CP phase, with the typical value$ \Delta \theta \sim\pi $ . Integrating the production rate over time, the total baryon number produced during the 2-2-hole evaporation is$\begin{aligned}[b] B\approx& \int^{\tau_L}_{t_{\mathrm{init}}}\dot{B}\,{\rm d}t \approx (3\tau_L)\left(6.1\times 10^{-11}\,\Delta \theta\, \hat{M}_{\mathrm{min}}\,\frac{T_{\mathrm{init}}^2}{E_ \mathrm{W}}\right)\\ \approx& 3.8\times 10^7\,\Delta \theta\, \hat{M}_{\mathrm{init}}\,. \end{aligned} $

(43) The
$ M_{\mathrm{min}} $ dependences in the evaporation time$ \tau_L $ and in the rate$ \dot{B} $ cancel, and the total asymmetry B only depends on the initial mass. The validity of this derivation assumes two conditions: the size of the domain wall$ d_ \mathrm{DW} $ is greater than the mean-free-path$ \sim 10/E_ \mathrm{W} $ and the evaporation time$ \tau_L $ is significantly larger than the construction time of the domain wall$ \sim r_ \mathrm{DW}/v_ \mathrm{DW} $ . Consequently, these restrict$ M_{\mathrm{init}} $ within the following range:$ 7.5\times 10^{4}\,\hat{M}_{\mathrm{min}}^{6/7}\, \mathrm{g} \lesssim M_{\mathrm{init}}\lesssim 2\times 10^8\,\hat{M}_{\mathrm{min}}\, \mathrm{g}\,. $

(44) The lower bound becomes incompatible with the BBN constraints
$ M_{\mathrm{init}}\lesssim M_ \mathrm{BBN} $ for an exceedingly heavy remnant, and EWBG is relevant only for$ M_{\mathrm{min}}\lesssim $ $ 5.5\times 10^{14}\, $ g.From (34), we determine the baryon-to-entropy ratio to be
$ \mathcal{B} = \left\{\begin{array}{ll} 1.5\times 10^{-21}\,f\,\Delta \theta \,\hat{M}_{\mathrm{min}}^{-1}\,\hat{M}_{\mathrm{init}}\,, & \mathrm{non{\text -}domination} \\ 1.3\times 10^{5}\,\Delta \theta \,\hat{M}_{\mathrm{min}}\,\hat{M}_{\mathrm{init}}^{-3/2}\,, & \mathrm{domination} \end{array}\right. \,. $

(45) Because of the restriction on
$ M_{\mathrm{min}} $ from (44), the maximum permitted value$ \mathcal{B}_ \mathrm{max}\approx 3.7\times 10^{-11}\,\Delta\theta\,\hat{M}_{\mathrm{min}}^{-1/5} $ when$ f = 1 $ and$ M_{\mathrm{init}} = M_{\mathrm{DM}} $ , and it decreases for heavier remnants even without considering the stronger constraint on f. This can already be observed from the total baryon number in (43). Compared with (35) for the production through heavy particle decay, it receives smaller enhancement from the 2-2-hole mass, and this is insufficient to compensate the decrease in the 2-2-hole number density for a large$ M_{\mathrm{min}} $ . The Planck remnant scenario, similar to that of PBHs, can barely achieve the observed value$ \mathcal{B}\approx 10^{-10} $ with a significantly large CP-violating phase$ \Delta \theta\approx \pi $ . Thus, for$ M_{\mathrm{min}}\gtrsim m_{\mathrm{Pl}} $ , dependence on the additional mass scale$ M_{\mathrm{min}} $ does not improve the scenario, and EWBG is disfavored in the context of 2-2-hole evaporation. -
As a concrete example for horizonless ultracompact objects, thermal 2-2-holes not only mimic black holes in many aspects but also make distinctive predictions for the observations. In this paper, we explore the dark sector production and baryon asymmetry generation through the evaporation of primordial thermal 2-2-holes. Unlike for black holes, a cold remnant is produced at the end of the 2-2-hole evaporation. The remnant mass
$ M_{\mathrm{min}} $ is determined by the interaction strength in quadratic gravity, with$ M_{\mathrm{min}}\approx m_{\mathrm{Pl}} $ for the strong coupling scenario and$ M_{\mathrm{min}}\gg m_{\mathrm{Pl}} $ for the weak coupling scenario. The same mass parameter also affects the temperature and makes the 2-2-hole evaporation quantitatively different from a black hole counterpart. The initial mass$ M_{\mathrm{init}} $ is constrained by observations. To not contradict the abundance of light elements, 2-2-holes must evaporate prior to BBN and$ M_{\mathrm{init}}\lesssim M_ \mathrm{BBN} $ , as given in (18). For small remnant with$ M_{\mathrm{min}}\lesssim M_{\mathrm{min}}^D \approx $ $ 4.7\times 10^{16}\, $ g, a 2-2-hole domination era at early universe is permitted as for black holes for$ M_{\mathrm{init}}\gtrsim M_{\mathrm{DM}} $ , as given in (16). For a larger$ M_{\mathrm{min}} $ , a 2-2-hole domination era results in an excessively large remnant abundance f that will overclose the universe for any$ M_{\mathrm{init}}\lesssim M_ \mathrm{BBN} $ ; thus, it is forbidden. In comparison with PBH scenarios, the production through 2-2-hole evaporation predicts considerably similar parameter spaces for the strong coupling scenario. For the weak coupling scenario, f is generally more strongly constrained, and different regions of parameter space are inferred. -
For the dark sector production, we have considered the requirement from the observed abundance and the free-streaming constraints for dark matter, and the contribution to the effective number of relativistic degrees of freedom, as parameterized by
$ \Delta N_ \mathrm{eff} $ , for dark radiation.Figure 6 summarizes the permitted mass range for dark matter and dark radiation as functions of the remnant mass
$ M_{\mathrm{min}} $ . The upper white area (including the hatched region on white background) is for dark matter, for which the dotted line in the middle denotes the lowest initial temperature$ T_\mathrm{BBN} $ for the primordial 2-2-holes. The relic abundance cannot attain the observed value above or below the red solid boundary lines. For heavy dark matter, it is due to the limited number of particles produced from evaporation, while for light dark matter, it is due to a too small mass. The hatched areas indicate the relevant parameter space for the 2-2-hole domination scenario when$ M_{\mathrm{min}}\lesssim M_{\mathrm{min}}^ \mathrm{D} $ . The additional inner boundaries are related to the lower bound on the remnant abundance. The light dark matter scenario is also subject to the free-streaming constraints. Therefore, the 2-2-hole domination is completely excluded, while a large range of parameter space remains viable for the non-domination scenario.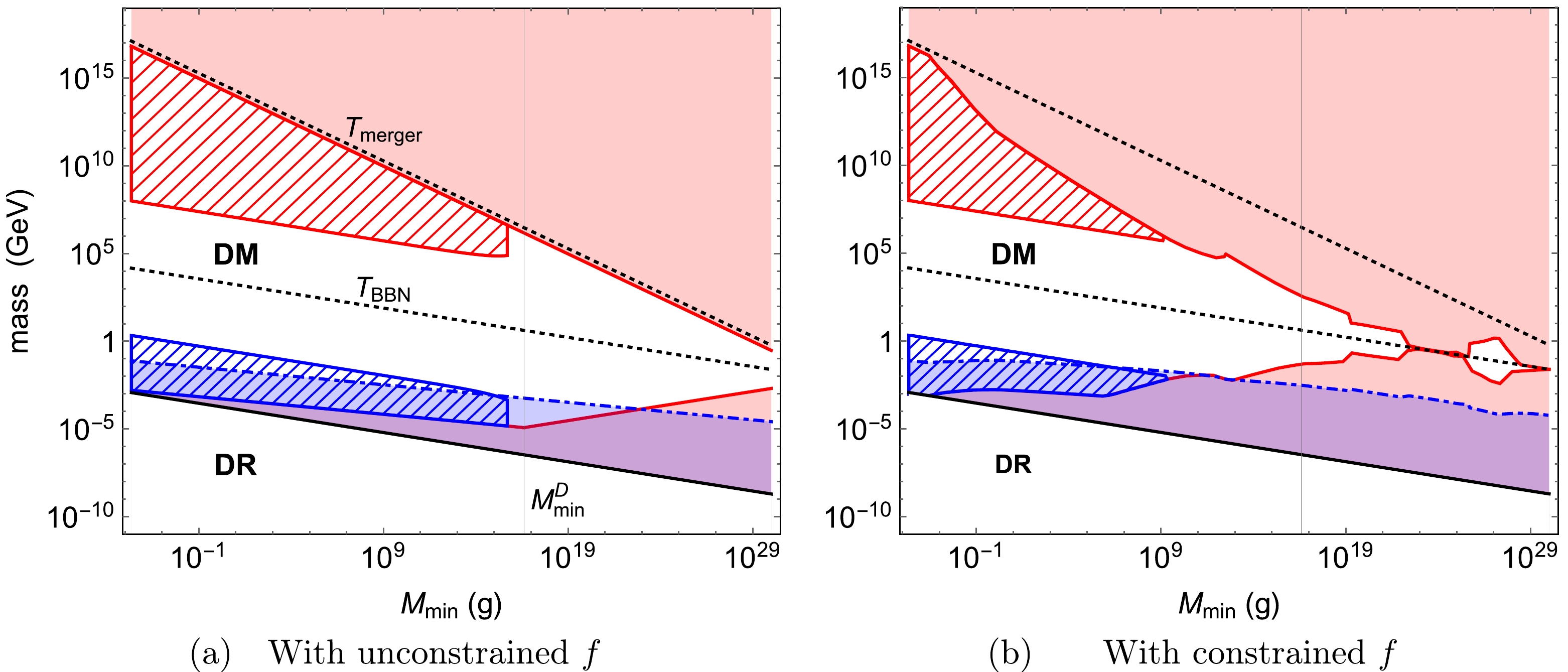
Figure 6. (color online) Permitted mass range of dark sector particles as a function of
$ M_{\mathrm{min}} $ , for the branching fraction${{B}}_\chi = 0.01-0.5$ . In 6a the remnant abundance f is considered a free parameter and$ f\leqslant 1/2 $ , whereas in 6b observational constrains in Fig. 1 are considered. The two white areas (including the red hatched region on white background) indicate the permitted parameter space for dark matter (DM) and dark radiation (DR), respectively. The red boundary lines for the upper white area denote the abundance constraints for dark matter, and the hatched regions indicate the permitted parameter space in the domination scenario in particular for$ M_{\mathrm{min}}\lesssim M_ \mathrm{min}^D $ given in (19). The blue region (including the blue hatched region) is excluded by the free-streaming constraints.$ T_{\mathrm{BBN}} $ , given in (18), sets the lowest initial temperature.$ T_{\mathrm{merger}} $ , given in (20), denotes the temperature for the merger product of a remnant binary.For the strong coupling scenario in which f is not significantly constrained, the permitted mass range for dark matter is considerably similar to that for the PBH production. Since we also consider the non-domination scenario, the dark matter mass can attain much lower scales than those considering only the domination scenario [26]. In the weak coupling scenario, as
$ M_{\mathrm{min}} $ increases, we observe that the relevant mass scale decreases and the permitted range shrinks. This is due to the decreasing initial temperature of 2-2-holes and the stronger constraints on the remnant abundance. We can observe that the viable mass range remains large for the most strongly constrained f cases, e.g.,$ M_{\mathrm{min}}\sim 10^{10}\, $ g, indicating that a small fraction of 2-2-holes can significantly enhance our understanding of dark matter. Heavy remnant scenarios with$ M_{\mathrm{min}}\gtrsim 10^{22}\, $ g are excluded, except for a small window at approximately$ M_{\mathrm{min}}\sim 10^{28}\, $ if a large dark sector is assumed. This indicates a significantly restricted mass range of dark matter that is slightly below the GeV scale.For dark radiation, the mass upper bound ranges from
$ 1\, $ MeV for the strong coupling scenario to$ 1\, $ eV for the heavy remnant scenario with$ M_{\mathrm{min}}\sim 10^{28}\, $ g. The latter is particularly comparable to the scenario in which dark radiation originates as a thermal relic. For the contribution to$ \Delta N_ \mathrm{eff} $ , as shown in Fig. 3, the 2-2-hole domination has the same prediction as for black hole evaporation, which is primarily sensitive to the number of the degrees of freedom. The current limit requires$ g_ \mathrm{DR}\lesssim 15 $ , while the future observations could probe down to$ g_ \mathrm{DR}\approx 1 $ . The contribution in the non-domination case decreases steeply for smaller$ M_{\mathrm{init}} $ values. For a large dark sector with$ g_ \mathrm{DR}\gg 10 $ , the non-domination scenario could be relevant, and a nonzero$ \Delta N_ \mathrm{eff} $ may indicate a small mass range for$ M_{\mathrm{init}} $ .Finally, in contrast to black holes, dark sector particles can be currently reproduced by the evaporation of the merger products of remnant binaries. Since the merger product acquires a very high temperature
$ T_{\mathrm{merger}} $ , heavy particles produced with a suppressed rate before can now be numerously produced. Fig. 6 shows that$ T_ \mathrm{merger} $ is generally much larger than the relevant mass scales and the emitted particles must be ultra-relativistic. Susbequently, this provides a natural realization of the boosted dark matter scenario, with the boost factor easily exceeding a few hundreds. If dark sector particles only interact with SM gravitationally, direct detection could be challenging but still possible. For instance, a recent proposal considers an array of quantum-limited mechanical impulse sensors and demonstrates the capability of detecting the Planck-scale dark matter using many sensors [133].For the lower mass range, additional interaction with the SM may be required for the direct detection. If dark sector particles interact with hadrons through some mediators, the IceCube detectors could be the optimal targets for the highly boosted flux [134]. Through deep inelastic scatterings, these energetic particles will create shower-like events as for the neutral current scattering of neutrinos [135]. Previously, the 2-2-hole remnant fraction was observed to be mostly constrained by the measurements of photon and neutrino fluxes produced by the high energy emission of the remnant mergers [47]. However, if the dark sector particles have many degrees of freedom, the dark matter flux might provide the smoking gun signal for this process as long as its scattering cross section with hadrons is not exceedingly much smaller than that for neutrinos. For such scenarios, the dark matter relic abundance may receive additional contribution from the thermal production through freeze-out. It is possible to construct a dark sector model that predicts a subdominant thermal contribution owing to a larger annihilation cross section, while being consistent with the current experimental constraints from the collider search and the direct detection. For instance, because of what we know about the well-studied Higgs-portal or Z-portal dark matter models [136], the constraints can be avoided if the dark matter mass is well above the TeV scale and the mediator mass is lighter but still considerably higher than the electroweak scale⑭. As indicated in Fig. 6, a large viable parameter space that may fulfill the requirements for a wide range of
$ M_{\mathrm{min}} $ still exists. We leave more detailed studies of particle physics models and the non-SM interactions of dark sector particles for future research. -
For the baryon asymmetry production, we have considered the out-of-equilibrium decay of heavy particles and electroweak baryogenesis. In the latter scenario, the total asymmetry produced by 2-2-holes scales with an inverse power of
$ M_{\mathrm{min}} $ , and even for the Planck mass, a considerably large CP-violating phase is required to generate the observed value. For the production through particle decays, our discussion applies to both baryogenesis through direct B-violating decays and leptogenesis, depending on whether the background temperature after evaporation is smaller or larger than the electroweak scale.Figure 7 shows the upper bound on the decay particle mass as a function of
$ M_{\mathrm{min}} $ from the requirement of baryon asymmetry generation. Similar to dark matter production, the particle must be lighter for increasing$ M_{\mathrm{min}} $ . Baryogenesis through direct B-violating decays can operate for a wide range of$ M_{\mathrm{min}} $ , while leptogenesis is only permitted in the small region around$ M_{\mathrm{min}} = m_{\mathrm{Pl}} $ since the initial mass has to take a smaller value. For the former case, the mass has to be smaller than$ \sim10^{9} $ GeV, and this is significantly lower than the expected range in the GUT framework. For leptogenesis, although the right hand neutrino can remain light, the parameter space we show assumes a considerably large CP-violating parameter and many degrees of freedom for the decay particle. For a more realistic scenario, the available parameter space may disappear.
Figure 7. (color online) Upper bound on the decay particle mass for successful baryogenesis as a function of
$ M_{\mathrm{min}} $ , assuming the CP-violating parameter$ \gamma\leqslant 1 $ and${B}_X\leqslant 0.5$ . In 7a the remnant abundance f is considered as a free parameter and$ f\leqslant 1 $ , whereas in 7b observational constrains in Fig. 1 are taken into account. The hatched region denotes the parameter space that allows leptogenesis, with the boundary value of$ M_{\mathrm{min}} $ defined by the intersection of the upper bound and the black dotted line, which shows the initial temperature for$ M_{\mathrm{init}} = M_ \mathrm{EW} $ , defined in (38).Therefore, the parameter space we obtain requires caution for the model building. For direct baryogenesis, if the baryon number violation is provided through particles that result in proton decay, we should be careful about the corresponding constraints. For instance, color-triplets in GUT models that couple to leptons and quarks are typically considered above
$ 10^{11} $ GeV in order to avoid proton decay, and are much larger than our highest upper limit$ m_X\sim10^{9} $ GeV in Fig. 7. This is generally enforced by the assumption that the triplet Yukawa couplings to the first-generation fermions are similar in magnitude to the Higgs Yukawa couplings, as the triplet and the doublet originate from the same multiplet of the SU(5). Nonetheless, their large mass hierarchy makes this assumption less motivated. Many mechanisms have been proposed to suppress the triplet Yukawa couplings, ensuring the proton stability for lighter particles, e.g., the Yukawa couplings with a suppression factor of approximately$ 10^{-7} $ enable color triplets in SUSY-SU(5) to be as light as$ 10^4 $ GeV (see the discussion in Ref. [99] and the references therein). Going beyond the GUT scenario, we can easily think of particles with appropriate quantum numbers, and express baryon number violating interactions in a simplified model, without inducing the proton decay [137, 138]. These models are subject to much weaker observational constraints, e.g., neutron electric dipole moment and neutron-antineutron oscillation, and can provide successful baryogenesis with lighter particles. For instance, a color scalar with quantum number$ \bar{6} $ can be as light as$ 10^4 $ GeV if the corresponding coupling is approximately$ 10^{-3} $ [138].For leptogenesis, our constraint
$ m_X\lesssim10^{9} $ GeV for the right-handed neutrino is significantly less challenging. In the simplest leptogenesis models for thermal production, in which the lepton asymmetry is produced primarily by the decay of the lightest right-handed neutrino, such low$ m_X $ cannot satisfy the out-of-equilibrium condition [139]; therefore, the contribution from thermal production is negligible. However, our parameter space for leptogenesis is more constrained than that for direct baryogenesis, and a relatively large CP-violation is required. The "resonant leptogenesis" scenario seems more relevant, in which two right-handed neutrinos are nearly degenerate and then a significant enhancement of CP-asymmetry can be produced. Because of the decay width suppression, the maximum value for the CP-asymmetry$ \gamma $ is approximately 1 for$ m_X $ in the TeV scale. This has a large overlap with our viable parameter space, and the relative importance of thermal production and 2-2-hole evaporation in this scenario deserves further study.Another question would be the implications of this limit in terms of the possible function of right-handed neutrinos in the seesaw mechanism. If we intend to explain the smallness of the SM neutrino masses with
$ m_X\lesssim 10^9 $ GeV, the Yukawa coupling must be smaller than$ 10^{-4} $ , which may encounter difficulties in a GUT framework if the Yukawa unification is required. However, if the UV completion of the SM only includes the three right-handed neutrinos, a model primarily motivated by hierarchy arguments and the Higgs mass stability requirement suggests an upper bound$ \sim10^6 $ GeV for the right-handed neutrino mass [140, 141]. This is not exceedingly far from our bound. -
As a generic family of classical solutions in quadratic gravity, the 2-2-hole provides a probable endpoint of gravitational collapse as an alternative to black holes. Since they are ultracompact and can be supermassive, 2-2-holes remain consistent with the current observations identified with black holes. Moreover, these objects do not possess event horizons because of the crucial roles of the quadratic curvature terms; therefore, they are free from the information-loss problem from the beginning. A typical thermal 2-2-hole radiates like a black hole with the similar peculiar thermodynamic characteristics. Thus, primordial 2-2-holes could evaporate in the early universe and produce particles of all types. The evaporation results in a 2-2-hole remnant, whose mass
$ M_{\mathrm{min}} $ is determined from the mass of the additional spin-2 mode in the theory. Thus, any information on$ M_{\mathrm{min}} $ can aid in inferring the new mass scale in quantum gravity. In a previous study [48], we considered 2-2-hole remnants as all dark matter and the constraints from various observations. The parameter space is considerably restricted, favoring toward the Planck mass remnants, namely the strong coupling scenario for quadratic gravity.In this work, we have continued our phenomenological investigation for primordial 2-2-holes. By abandoning the condition of remnants as all dark matter, we could consider remnants that are significantly heavier than the Planck mass. We have investigated the scenario in which the majority of dark matter consists of particles produced by early time evaporation, while the remnant contribution accounts for the remainder. We have also considered the possible dark radiation contribution to
$ \Delta N_ \mathrm{eff} $ and explored different mechanisms for baryon asymmetry generation from 2-2-hole evaporation. The implications can be considerably different if there was an era of 2-2-hole domination in the early universe, which can be realized only for$ M_{\mathrm{min}}\lesssim 10^{16} $ g. Throughout the paper, both domination and non-domination scenarios have been considered when necessary.We have observed that the primordial 2-2-hole picture can accommodate both dark matter production and baryogenesis through the decay of heavy particles for a large range of
$ M_{\mathrm{min}} $ , including the heavier remnant scenarios subject to strong abundance constrains. In the weak coupling scenario, the relevant particle mass scales decreases with increasing$ M_{\mathrm{min}} $ owing to the lower value of the initial temperature. The parameter space is less restricted for smaller$ M_{\mathrm{min}} $ values, which in the Planck mass limit converges to that of PBHs with Planck mass remnants. Considering the abundance requirement and the free-streaming constraints, the dark matter mass can vary from$ 10^{17}\, $ GeV to$ 0.1\, $ GeV for$ M_{\mathrm{min}}\sim m_{\mathrm{Pl}} $ –$ 10^{28} $ g. For baryon asymmetry generation, baryogenesis through direct B-violating decays can operate for a wide range of$ M_{\mathrm{min}} $ values, while leptogenesis is only permitted within a small window close to the Planck mass. The upper mass limit for the decay particle is$ 10^{9} $ GeV owing to the existence of remnants, and this requires caution in model building for direct B-violating decays. For the dark radiation contribution to$ \Delta N_ \mathrm{eff} $ , the domination scenario makes a simple prediction depending only on the number of degrees of freedom, and the current data requires it to be smaller than$ 15 $ . The contribution in the non-domination scenario is generally significantly suppressed, but it may be relevant for a small window of the 2-2-hole initial mass if there is a large dark sector. In contrast to black holes, 2-2-hole remnants can currently reproduce these particles through strong radiation from the merger products. This may provide additional opportunities to test the production mechanisms discussed in this paper. -
In this appendix, we consider another derivation for the free-streaming constraints. It involves the momentum distribution function of dark matter and constraints on the fraction of relativistic particles [24]. The final results agree with the simple estimation in Sec. IIIA up to an order one factor.
After the 2-2-hole evaporation, the particle spectrum is a superposition of the earlier time instantaneous emissions with the corresponding redshift
$\tag{A1} F(p,t) = \int_{t_\chi}^{\tau_L}{\rm d}\tau \frac{{\rm d}\dot{N}}{{\rm d}p}\left(p \frac{a(t)}{a(\tau)},\tau\right)\frac{a(t)}{a(\tau)}\,, $

(A) where
$ t_\chi $ is defined in (7). The instantaneous emissions follow the Planck distribution,$ \tag{A2} \frac{{\rm d}\dot{N}}{{\rm d}p}(p,t)\approx\frac{2M^2(t)}{\pi\, m_{\mathrm{Pl}}^4}\frac{p^2}{{\rm e}^{p/T(t)}-1}\,, $

(A2) with
$ M(t),\,T(t) $ expressed in (4). Since the distribution at$ t>\tau_L $ is simply a redshift of$ F(p,\tau_L) $ , an upper bound$ f_ \mathrm{S} $ on the fraction of relativistic particles at some later time$ t_ \mathrm{S} $ can be translated as a constraint for$ F(p,\tau_L) $ , with$ \tag{A3} \frac{\displaystyle\int_{p_ \mathrm{min}}^\infty {\rm d}p \,F(p,\tau_L)}{\displaystyle\int_0^\infty {\rm d}p \, F(p,\tau_L)}<f_ \mathrm{S},\quad p_{ \mathrm{min}} = m_{\chi}\frac{a(t_ \mathrm{S})}{a(\tau_L)}\,. $

(A3) For the light mass scenario, with the starting time
$ t_\chi = t_{\mathrm{init}} $ , we determine the momentum distribution function as$\tag{A4} F_L(p,\tau_L)\approx \frac{2\, \tau_L}{\pi\, m_{\mathrm{Pl}}^4} M_{\mathrm{init}}^2\, T_{\mathrm{init}}^2\, \tilde{F}_L(p/T_{\mathrm{init}})\,, $

(A4) where the momentum dependence is fully encoded in the dimensionless function
$ \tag{A5} \tilde{F}_L(a)\approx a^2 \int_0^1 {\rm d}x\,\frac{(1-x)^{2/3}}{x^{3/2}} \left[{\rm e}^{\textstyle a\frac{(1-x)^{1/3}}{x^{1/2}}}-1\right]^{-1}\,. $

(A5) As shown in Fig. A1,
$ \tilde{F}_L(p/T_{\mathrm{init}}) $ has a long tail in comparison to the Planck distribution. Assuming$ f_ \mathrm{S}\approx 10\% $ ,$ t_ \mathrm{S}\approx 10^6\, $ s and one dominant component of light dark matter, the free-streaming constraint (48) implies$ m_\chi\, a(t_S)/(T_{\mathrm{init}} a(\tau_L))\gtrsim 10 $ , i.e.,
Figure A1. (color online) Dimensionless momentum distribution functions for light dark matter (red) and heavy dark matter (blue). For comparison, the dot dashed line indicates the Planck distribution.
$ \tag{A6} m_\chi\gtrsim 3.1\times 10^{-5}\,\hat{M}_{\mathrm{min}}^{-1/2} \, \hat{M}_{\mathrm{init}}^{1/2}\, \mathrm{GeV}\,. $

(A6) It assumes the same form as the simpler estimation (27), and the coefficient is numerically similar.
For the heavy mass case, we obtain the momentum distribution function
$ \tag{A7} F_H(p,\tau_L)\approx \frac{2\, \tau_L}{\pi\, m_{\mathrm{Pl}}^4} M_{\mathrm{init}}^2\, T_{\mathrm{init}}^2 \,\tilde{F}_H\left(\frac{p}{T_{\mathrm{init}}}, \frac{m_\chi}{T_{\mathrm{init}}}\right)\,, $

(A7) where the form factor also depends on
$ m_\chi $ ,$\tag{A8} \tilde{F}_H(a,b)\approx a^2\!\! \int_{1-b^{-3}}^1\! {\rm d}x \,\frac{(1-x)^{2/3}}{x^{3/2}}\left[{\rm e}^{\textstyle a\frac{(1-x)^{1/3}}{x^{1/2}}}-1\!\right]^{-1} \!\approx \!b^{-3} \tilde{G}_H(a/b)\,. $

(A8) The momentum dependence now results solely from the dimensionless function
$ \tilde{G}_H(p/m_\chi) $ and is independent of$ T_{\mathrm{init}} $ . As shown in Fig. A1,$ \tilde{G}_H(x) $ approaches$ \tilde{F}_L(x) $ at large x values. Thus, the free-streaming constraint for one dominant component scenarios is$ a(t_S)/a(\tau_L)\gtrsim 10 $ . As in the simple estimation, this condition is independent of$ m_\chi $ and can be easily satisfied for$ M_{\mathrm{init}}\lesssim M_ \mathrm{BBN} $ .
Dark sector production and baryogenesis from not quite black holes
- Received Date: 2020-12-04
- Available Online: 2021-07-15
Abstract: Primordial black holes have been considered attractive dark matter candidates, whereas some of the predictions rely heavily on the near-horizon physics that remains to be tested experimentally. As a concrete alternative, thermal 2-2-holes closely resemble black holes without event horizons. Being a probable endpoint of gravitational collapse, they provide a solution to the information loss problem but also naturally result in stable remnants. Previously, we have considered primordial 2-2-hole remnants as dark matter. Owing to the strong constraints from a novel phenomenon associated with remnant mergers, only small remnants with mass approximate to the Planck mass can constitute all dark matter. In this paper, we examine the scenario in which the majority of dark matter consists of particles produced by the evaporation of primordial 2-2-holes, whereas the remnant contribution is secondary. The products with sufficiently light mass may contribute to the number of relativistic degrees of freedom in the early universe, which we also calculate. Moreover, 2-2-hole evaporation can produce particles that are responsible for the baryon asymmetry. We observe that baryogenesis through direct B-violating decays or through leptogenesis can both be realized. Overall, the viable parameter space for the Planck remnant scenario is similar to that of primordial black holes with Planck remnants. However, heavier remnants result in different predictions, and the viable parameter space remains large even when the remnant abundance is small.






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF
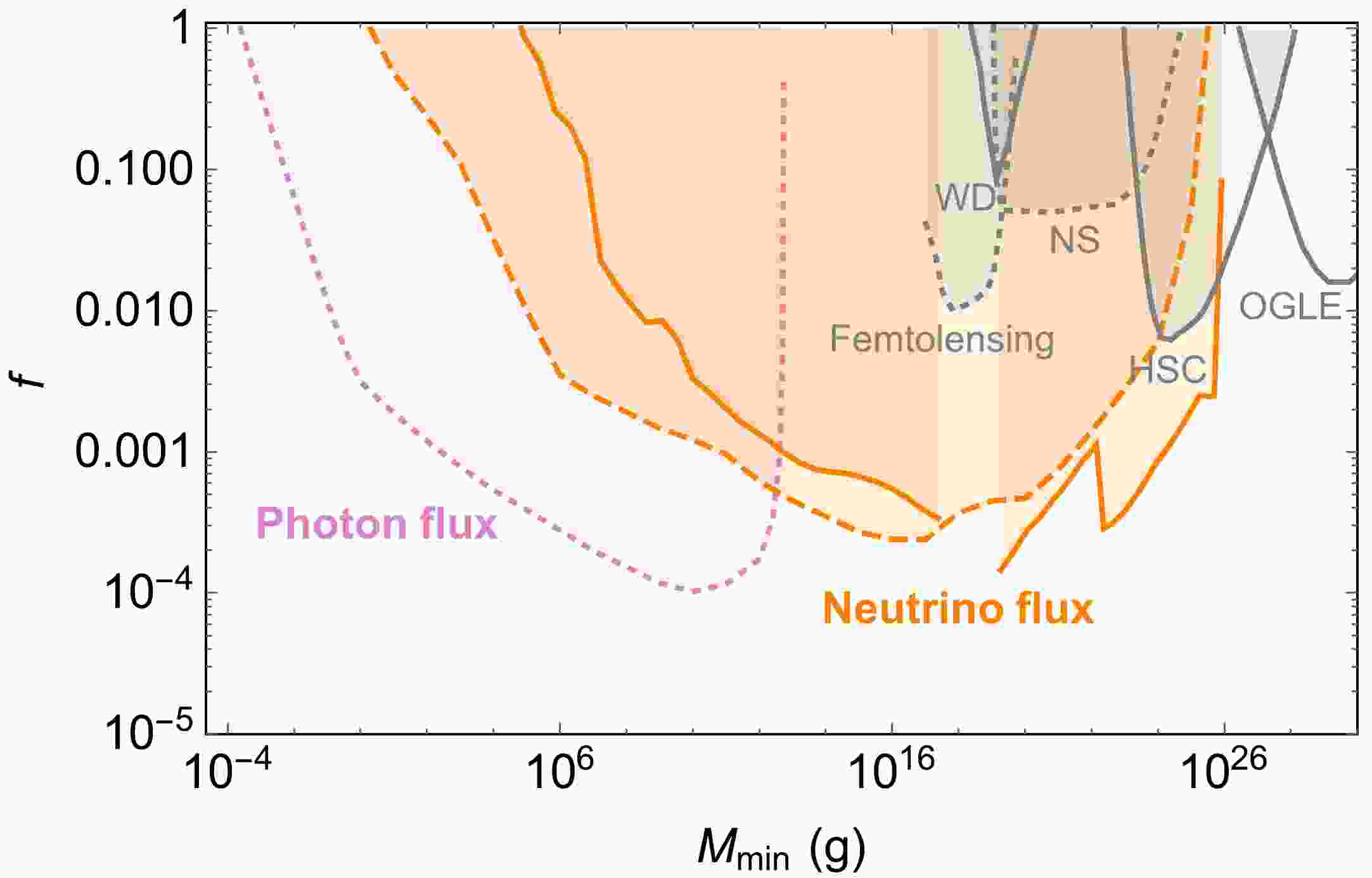













 DownLoad:
DownLoad: