-
The ground state properties of nuclei have always garnered interest in various experimental and theoretical studies [1, 2]. With the development of experimental technology, more studies have demonstrated that nuclei with larger isospin tend to exhibit a few interesting phenomena, such as neutron halo [3-5], neutron skin [6, 7], and inversion island [8, 9]. These interesting phenomena are considered important characteristics of exotic nuclei [10, 11].
Recently, owing to the shape coexistence and island of inversion phenomena of Kr, Sr, Mo, and Ru isotopes with mass number A = 90-130, the properties of these isotopes have been widely discussed [12]. In neutron-rich nuclei, deformation is correlated to the change in conventional magic numbers [13]. Conversely, the abrupt increase in the charge radii of Sr and Zr is attributed to the rapid changes in their nuclear shapes. However, the charge radius changes very gently in the Mo isotopic chain. Moreover, although the deformation process is stable for Kr isotopes, it is unstable for Zr and Sr isotopes. In addition, in the quadrupole deformation space (
$ \beta, \gamma $ ), several cases of γ-soft behavior are predicted for$ ^{98-114} {\rm{Ru}}$ and$ ^{96-112} {\rm{Mo}}$ [14-18]. Correspondingly, some of these theoretical conclusions also correspond to the experimental results [19-21]. In addition, the neutron-rich nuclei for these five isotopes are also involved in the astrophysical rapid neutron capture process (r-process). The r-process is one of the mechanisms that produce large numbers of neutron-rich unstable isotopes in the universe [22]. Consequently, both experimental and theoretical directions attempt to have some insights into the r-process. Most experiments have been devoted to measuring the ground state properties of nuclei involved in the r-process [23, 24]. In terms of theoretical research, they try to construct a suitable physical model to simulate the r-process [25].In the 1990s, Zirconium isotopes were verified to exhibit the halo phenomenon [26]. After a series of theoretical and experimental research, some features of the halo are highlighted. The large rms radii and a loose nucleon distribution, which compare to the stable nuclei, are considered the key point in confirming the halo nuclei. Simultaneously, the resonant states are determined to play an important role in the formation of exotic structures [27, 28]. In addition, the energy and lifetime of the single-particle resonant state are also important research components of the nucleosynthesis of chemical elements in the evolution of celestial bodies [29, 30]. To better study the resonant state in nuclei, several theoretical methods have been developed. Recently, the complex scaling method (CSM) has been successfully applied to the study of resonant states [31, 32]. However, we infer that the calculated values are influenced by the rotation angle. In addition, the CSM method is only applicable to the dilation analytic potentials. To improve this method, the complex-momentum-representation (CMR) method was proposed [33]. In the CMR method, the Hamiltonian matrix is solved in the complex momentum space to circumvent the various disadvantages of the CSM method. This method is a bound state type method and can be easily applied to other fields. In other words, the bound states, resonant states, and continuous spectrum can be addressed simultaneously. Furthermore, this approach has been validated to be an effective method for studying the resonant state of single particles [34-36]. The CMR method is not only suitable for spherical nuclei [37, 38] but also for deformed nuclei [39-41]. In addition, its application is successful in the RMF-CMR+BCS to describe the ground state properties and elucidate a few exotic phenomena of the neutron-rich nuclei [37, 42]. Moreover, instead of the exchange of mesons with short-distance dynamics, the zero-range point-coupling (PC) interaction could be used in the RMF framework, which simplifies several problems [43]. The current parameter sets with PC interaction include PC-PK1 [44], DD-PCX [45], and DD-PC1 [46]. Therefore, we select the RMF-CMR+BCS(DD-PC1) to research on the resonance for the isotopic chain with their proton number Z approximately 40.
This paper is organized as follows. In Sec. II, we present the derivation of theoretical formulas with the DD-PC1 parameter set. Considering four elements as examples, including Kr, Sr, Mo and Ru, numerical details are provided in Sec. III. Finally, a summary is presented in Sec. IV.
-
The Lagrangian of the density-dependent point coupling model is expressed as (see Refs. [45-47] for more details):
$ {\cal{L}} = {\cal{L}}^{\rm free}+{\cal{L}}^{4f}+{\cal{L}}^{\rm der}+{\cal{L}}^{em}, $

(1) and the expressions of each part are
$ {\cal{L}}^{\rm free} = \bar{\psi}({\rm i}\gamma_{\mu}\partial^{\mu}-m)\psi , $

(2) $ \begin{aligned}[b] {\cal{L}}^{4f} =& -\frac{1}{2}\alpha_{S}(\rho)(\bar{\psi}\psi)(\bar{\psi}\psi) -\frac{1}{2}\alpha_V(\rho)(\bar{\psi}\gamma^\mu\psi)(\bar{\psi}\gamma_\mu\psi) \\ &-\frac{1}{2}\alpha_{TV}(\rho)(\bar{\psi}\vec{\tau}\gamma^\mu\psi)\cdot(\bar{\psi}\vec{\tau}\gamma_\mu\psi), \end{aligned} $

(3) $ \begin{aligned}[b] {\cal{L}}^{\rm der} =& -\frac{1}{2}\delta_S\partial_\nu(\bar{\psi}\psi)\partial^\nu(\bar{\psi}\psi) -\frac{1}{2}\delta_V\partial_\nu(\bar{\psi}\gamma_{\mu}\psi)\partial^{\nu} (\bar{\psi}\gamma^{\mu}\psi) \\ &-\frac{1}{2}\delta_{TV}\partial_\nu(\bar{\psi}\vec{\tau}\gamma_{\mu}\psi)\cdot\partial^{\nu} (\bar{\psi}\vec{\tau}\gamma^{\mu}\psi), \end{aligned} $

(4) $ {\cal{L}}^{em} = -e\bar{\psi}\gamma^{\mu}\cdot A_{\mu}\frac{1-\tau_3}{2}\psi-\frac{1}{4}F^{\mu\nu}F_{\mu\nu}, $

(5) where m is the nuclear mass, and
$ \alpha_s,\; \alpha_V,$ and$ \alpha_{TV} $ represent the coupling constants of the four-Fermi contact terms. In addition to the free nucleus term and the point coupling term, the above Lagrangian quantity also includes the coupling between the proton and the electromagnetic field. The derivative term in the formula also explains the influence of the interaction in a limited range. We selected the following practical coupling function form to solve the self-energy of the micro-density-related scalar and vector:$ \alpha_i(\rho) = a_i+(b_i+c_ix)e^{-d_ix}\; \; \; \; \; (i\equiv S,V,TV) , $

(6) where
$x = \rho/\rho_{\rm sat}$ , and$\rho_{\rm sat}$ represents the nucleon density when the symmetrical nuclear matter is saturated.At this point, the Dirac equation can be obtained by making variations on the corresponding energy density functional:
$ \Big[{\gamma _\mu }\Big({\rm i}{\partial ^\mu } - {V^\mu } - \sum\nolimits_R^\mu \Big) - (M + S)\Big]{\psi _k}({{r}}) = 0 . $

(7) Here,
$ \sum\nolimits_R^\mu $ is expressed as$ \sum\nolimits_R^\mu = \frac{1}{2}\frac{{{j^\mu }}}{{{\rho _\upsilon }}}\left[\frac{{\partial {\alpha _S}}}{{\partial {\rho _\upsilon }}}\rho _S^2 + \frac{{\partial {\alpha _V}}}{{\partial {\rho _\upsilon }}}{j_\mu }{j^\mu } + \frac{{\partial {\alpha _{TV}}}}{{\partial {\rho _\upsilon }}}{({\vec{ j} _{TV}})_\mu }\vec {j} _{TV}^\mu \right] , $

(8) where j represents a term in the system energy density functional.
To discuss the resonant state, we convert the Dirac equation to the complex momentum representation, which can be written as
$ \int {\rm d}\vec{k}^{\prime }\left\langle \vec{k}\right\vert H\left\vert \vec{k} ^{\prime }\right\rangle \psi \left( \vec{k}^{\prime }\right) = \varepsilon \psi \left( \vec{k}\right) , $

(9) The wave function
$ \psi \left( \vec{k}\right) $ can be expressed by radial and angular parts in momentum space; hence, we assume$ \psi \left( {\vec k} \right) = \left( {\begin{array}{*{20}{c}} {f(k){\phi _{lj{m_j}}}\left( {{\Omega _k}} \right)}\\ {g(k){\phi _{\tilde lj{m_j}}}\left( {{\Omega _k}} \right)} \end{array}} \right). $

(10) Turning the potential field into the momentum representation, we obtain the following relationship with the spherical Bessel function:
$ V_+\left( k,k^{\prime }\right) = \frac{2}{\pi }\int r^{2}{\rm d} r\left[ V\left( r\right) +S\left( r\right) \right] j_{l}\left( k^{\prime }r\right) j_{l}\left( kr\right) , $

(11) $ V_-\left( k,k^{\prime }\right) = \frac{2}{\pi }\int r^{2}{\rm d}r\left[ V\left( r\right) -S\left( r\right) \right] j_{\tilde{l}}\left( k^{\prime }r\right) j_{\tilde{l}}\left( kr\right) . $

(12) By substituting Eq. (10) into Eq. (9) with the potential Eqs. (11) and (12), the expression of the Dirac equation in momentum space is
$ \left\{ {\begin{array}{*{20}{c}} {Mf(k) - kg(k) + \displaystyle\int {{k^{\prime 2}}} {\rm d}{k^{\prime} }{V_ + }\left( {k,{k^{\prime} }} \right)f({k^{\prime} }) = \varepsilon f(k),}\\ { - kf(k) - Mg(k) + \displaystyle\int {{k^{\prime 2}}} {\rm d}{k^{\prime} }{V_\_}\left( {k,{k^{\prime} }} \right)g({k^{\prime} }) = \varepsilon g(k).} \end{array}} \right. $

(13) We can obtain the resonant and bound states by solving the equation in complex momentum space. In addition, the numerical value of ground state properties for the nucleon can be investigated based on the eigenstates. More details are provided in Ref. [33].
-
Based on the theoretical formula presented in Sec. II, the even-even neutron-rich nuclei for
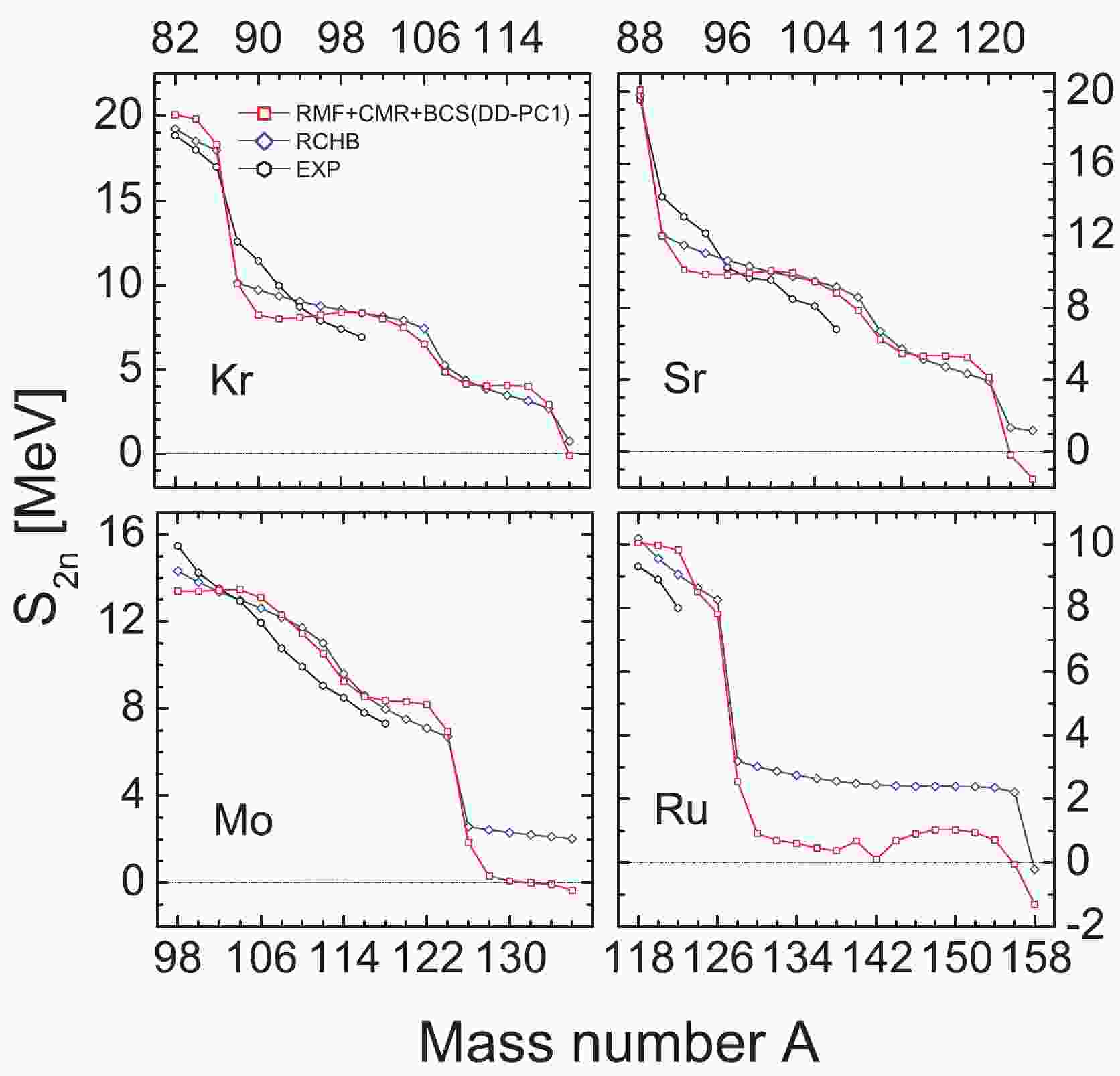
$ ^{80-120} {\rm{Kr}}$ ,$ ^{86-126} {\rm{Sr}}$ ,$ ^{96-136} {\rm{Mo}}$ , and$ ^{118-158} {\rm{Ru}}$ isotopes are investigated. As is well known, the formation of a neutron halo or neutron skin structure can be verified based on the two-neutron separation energy${S}_{2n}$ . Moreover, we can verify the drip line nuclei given the value of${S}_{2n}$ is not positive. In Fig. 1, the${S}_{2n}$ of the four isotopic chains are shown as the function with the mass number A. The calculated values with RMF-CMR+BCS (DD-PC1) are compared with the values with RCHB [48] and the experimental data [49]. The values of${S}_{2n}$ for all four isotopes decrease gradually with the increase in the mass number, and the values obtained with the two methods are closely related to the experimental data. In addition, a few differences occur in the neutron-rich region of Mo and Ru isotopes with different methods. The results with RCHB are approximately 2 MeV higher than our data in the neutron-rich area. In the Kr isotopic chain,${S}_{2n}$ decreases abruptly when the mass number A = 86, which corresponds to the magic numbers N = 50. In addition, it is determined that$ ^{120} {\rm{Kr}}$ is the first nucleus with the negative${S}_{2n}$ . Hence,$ ^{118} {\rm{Kr}}$ is predicted to be the drip line nucleus for Kr isotopes. In the Sr isotopic chain, an energy gap exists, as the neutron number is approximately N = 50, 82. Simultaneously, the value of${S}_{2n}$ is greater than 4 MeV for$ ^{120} {\rm{Sr}}$ . This does not correspond to the fact that the value of${S}_{2n}$ is low when the halo is formed. Therefore, there should be no halo phenomenon in the Sr isotopic chain. Moreover, the value of${S}_{2n}$ is less than 0 MeV in$ ^{122} {\rm{Sr}}$ ; however, it is greater than 0 MeV in$ ^{120} {\rm{Sr}}$ . This indicates that the nucleus$ ^{122} {\rm{Sr}}$ does not exist. For Mo isotopes, a few differences between Mo and Sr isotopes are illustrated in Fig. 1. The value of${S}_{2n}$ is determined to be approximately 0 MeV with the mass number A greater than 128. Consequently, the halo phenomenon occurs in$ ^{128-136} {\rm{Mo}}$ . In addition, the value of${S}_{2n}$ is less than 0 MeV when the mass number A$ \geq $ 132, but not in$ ^{130} {\rm{Mo}}$ . Similar to the Sr isotopes, the drip line should be confirmed as the mass number A = 130 for Mo isotopes. Moreover, the values for${S}_{2n}$ is inconsecutive in$ ^{124} {\rm{Mo}}$ , which corresponds to the magic number N = 82. From the observation of the Ru isotopic chain, it is evident that an energy gap appears when the neutron number N = 82. Moreover, the situation of Ru isotopes is similar to that of Mo isotopes. The value of${S}_{2n}$ is approximately 0 MeV when the mass number A$ > 130$ . This suggests that the neutron halo appears in the Ru isotopic chain. In the neutron-rich region,${S}_{2n}$ is a negative value when the mass number A$ \geqslant 156$ . Accordingly, the mass number of the drip line nucleon in Ru isotopes is A = 154.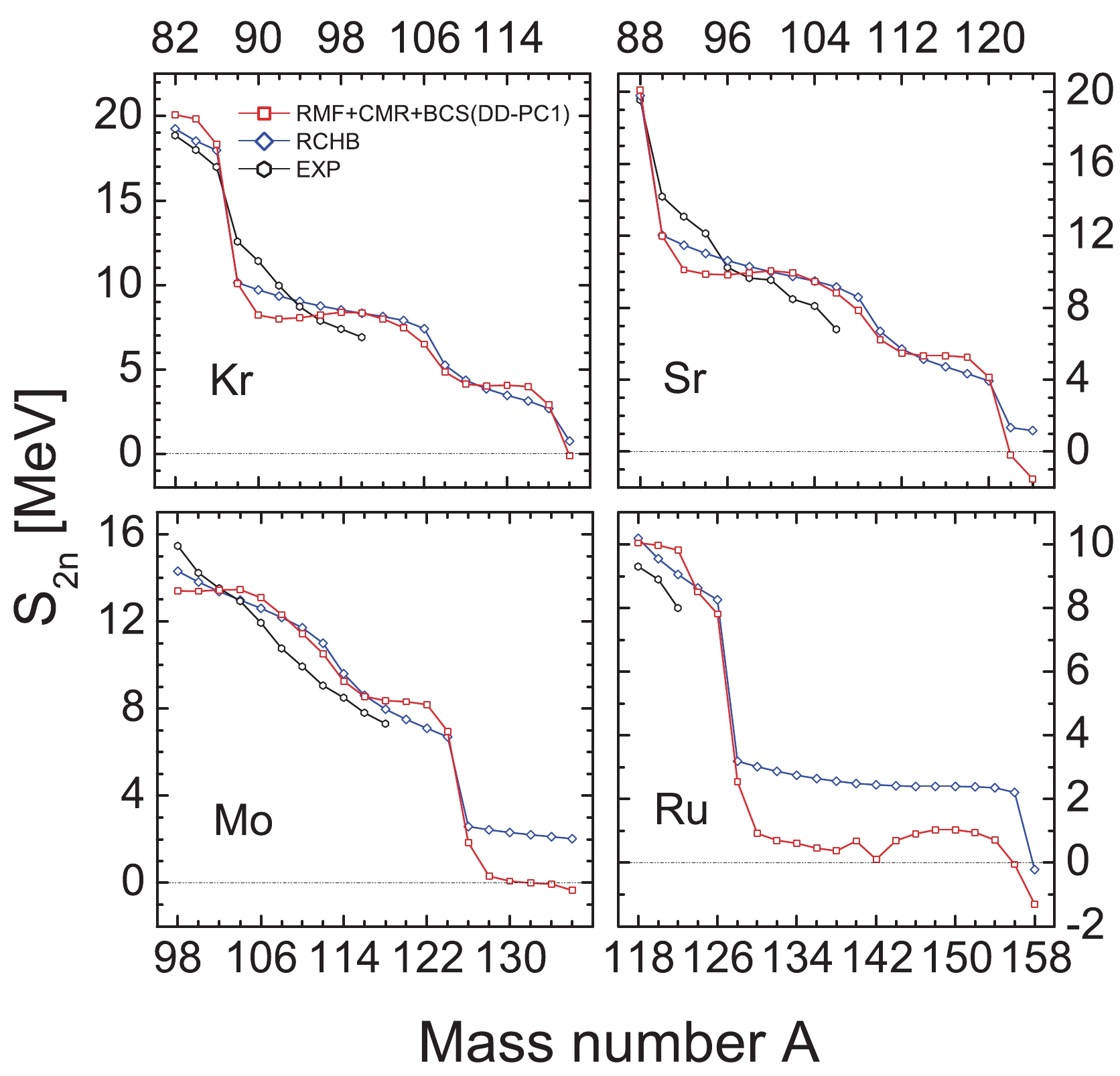
Figure 1. (color online)
${\rm{S}}_{2n}$ presented as the function of the mass number A. The red square, blue diamond, and black hexagon represent the values calculated by RMF-CMR+BCS (DD-PC1), RCHB, and experimental data, respectively.Equally, the rms radius is an important indicator in the discussion of nuclear structure. In Fig. 2, we present the relationship between the rms radii
$ \left\langle{r^2}\right\rangle^{1/2} $ of the proton and neutron and the mass number A. The calculation formula for the rms radii of neutrons and protons is expressed as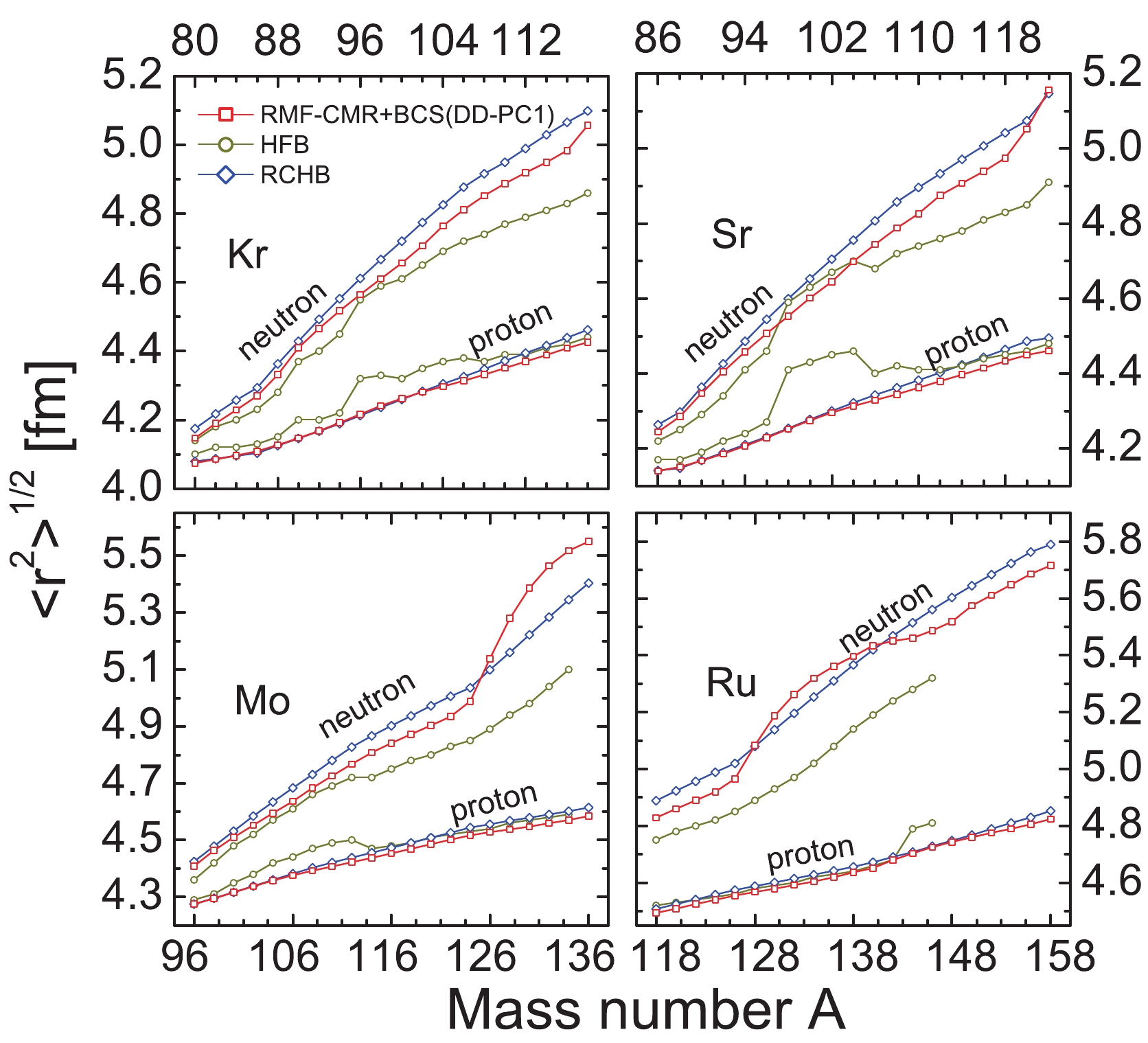
Figure 2. (color online) The rms radius presented as a function of the mass number A. The red square, dark yellow circle, and blue diamond represent the values calculated with RMF-CMR+BCS (DD-PC1), HFB, and RCHB, respectively.
$ \left\langle {r_{n(p)}^2} \right\rangle^{1/2} = \sqrt{\frac{{\displaystyle\int {{\rho _{n(p)}}{r^2}{\rm d}r } }}{{\displaystyle\int {{\rho _{n(p)}}{\rm d}r } }}}. $

(14) The calculated values of the four isotopic chains with RMF-CMR+BCS (DD-PC1), HFB [50] and RCHB [48] are plotted together to obtain a comparison. As can be observed, a few differences are obtained for the proton rms radii in
$ ^{96-106} {\rm{Sr}}$ , between the RMF-CMR+BCS and HFB calculations. These differences appear owing to the fact that the HFB method predicts an oblate axial ground state for Sr isotopes. Although some minor deviations in the numerical values of each method can be determined for the rms radii of the neutrons in Fig. 2, their growth trends are the same. Hence, it remains obvious that the Mo isotopic chains exhibit an abrupt increase in the rms radii of neutrons when the mass number A = 126-136. This agrees well with the characteristics of the neutron halo [43]. The increase in the neutron radii alternates for Ru isotopes. However, an abrupt increase remains evident provided the mass number A$ \geqslant 128$ . Accordingly, we infer that halo structures appear in$ ^{128-158} {\rm{Ru}}$ and$ ^{126-136} {\rm{Mo}}$ . In the Kr and Sr isotopic chains, the rms radii of these isotopic chains increase linearly. Therefore, we deduce that the Kr and Sr isotopic chains do not exhibit halo structures in neutron-rich regions. In addition, the neutron rms radius is determined to be greater than the proton rms radii in$ ^{80-118} {\rm{Kr}}$ and$ ^{86-122} {\rm{Sr}}$ . The difference value increases with the increase in neutron numbers. Therefore, we consider the existence of the neutron skin phenomenon in the Kr and Sr isotopic chains.The exotic phenomenon is usually related to the wide spatial distribution of nuclear density. In Fig. 3, we select four nuclei with significant neutron numbers in each isotopic chain, and we plot their neutron and proton radial density distribution. Because the ratio of the neutron to proton number in exotic nuclei is significant, the neutron-proton density distribution is different. As can be observed, the radial density distribution of both neutrons and protons are restricted within a small numerical range. It is obvious that the proton density distribution of the four isotopes converges to a radius of 9-10 fm. However, there are a few differences in the neutron density distribution. The Kr, Sr, and Mo isotopes exhibit significant long tails at the end of the radius distribution. However, in the Ru isotopic chain, only
$ ^{150} {\rm{Ru}}$ and$ ^{154} {\rm{Ru}}$ exhibit long tails, excluding$ ^{142} {\rm{Ru}}$ and$ ^{146} {\rm{Ru}}$ . These further confirm the presence of halo structures in the neutron-rich regions for Mo and Ru isotopes. Meanwhile, neutron skin structures are generated in Kr and Sr isotopic chains. Moreover, the neutron density distribution decreases slightly with the increase in the neutron number N. However, there is a deviation in Ru isotopes, the neutron density distribution is abnormal, as r$ >14$ fm. This will be explained in the analysis of the occupation probability of single-particle levels.
Figure 3. (color online) Density distributions of the neutrons and protons of Kr, Sr, Mo, and Ru isotopes presented as the function with the grid number of Gauss-Legendre quadrature. Isotopes of different mass numbers are denoted by red solid line, black short dash, orange dot-dot dash, and black dash.
To further validate the results obtained, the relationship between the ratio of neutron density to the total neutron density of the neutron single-particle level and the grid number of the Gauss-Legendre quadrature for
$ ^{118} {\rm{Kr}}$ ,$ ^{120} {\rm{Sr}}$ ,$ ^{130} {\rm{Mo}}$ , and$ ^{154} {\rm{Ru}}$ is presented in Fig. 4. As is well known, the energy level, which occupies the major density distribution on the nuclear surface, often plays an important role in the generation of the exotic phenomenon. First, almost every energy levels of the four isotopes reach its peak in Fig. 4. In other words, no single-particle level perpetually occupies a large density distribution with the extension of the radial radius. Moreover, some deep bound states, such as$ 1s_{1/2} $ , tend to occupy a large density distribution when the radius is small; however, they abruptly decrease as the radial radius increases. For$ ^{118} {\rm{Kr}}$ , it is eveident that the single-particle levels, including$ 1h_{11/2} $ ,$ 2d_{5/2} $ ,$ 3s_{1/2} $ and$ 2d_{3/2} $ , contribute to the main neutron density when r = 6-10 fm. However, their contribution continues to decline while the resonant states$ 2f_{7/2} $ ,$ 2f_{5/2} $ and$ 1h_{9/2} $ occupy most of the density distribution when r = 10-20 fm. By eliminating the energy levels that exhibit larger centrifugal barriers, the levels$ 2d_{5/2} $ ,$ 2d_{3/2} $ ,$ 3s_{1/2} $ provide the primary contribution to the formation of the neutron skin. Similarly, the density ratios for$ ^{120} {\rm{Sr}}$ are approximately the same when$ ^{118} {\rm{Kr}}$ has a radius r = 6-10 fm. The existence of level$ 3p_{3/2} $ with a large density ratio significantly contributed to the formation of the neutron skin. A similar phenomenon also appears in$ ^{130} {\rm{Mo}}$ . The proportion of density distribution for the newly emerged energy level$ 3p_{1/2} $ reaches 0.35, whereas that of the level$ 3p_{3/2} $ exceeds 0.5. With a small orbital angular momentum and low centrifugal barrier, these two energy levels play a crucial role in increasing the neutron radius and generating the halo phenomenon. For$ ^{154} {\rm{Ru}}$ , there are some differences with$ ^{130} {\rm{Mo}}$ . Owing to the existence of the$ 2g_{9/2} $ level in$ ^{154} {\rm{Ru}}$ , the sum of the ratio for the other energy levels is less than 0.1. However, the absolute density distribution of the level$ 2g_{9/2} $ is negligible, owing to the significant centrifugal barrier. Therefore, we can obtain the same conclusion as$ ^{130} {\rm{Mo}}$ .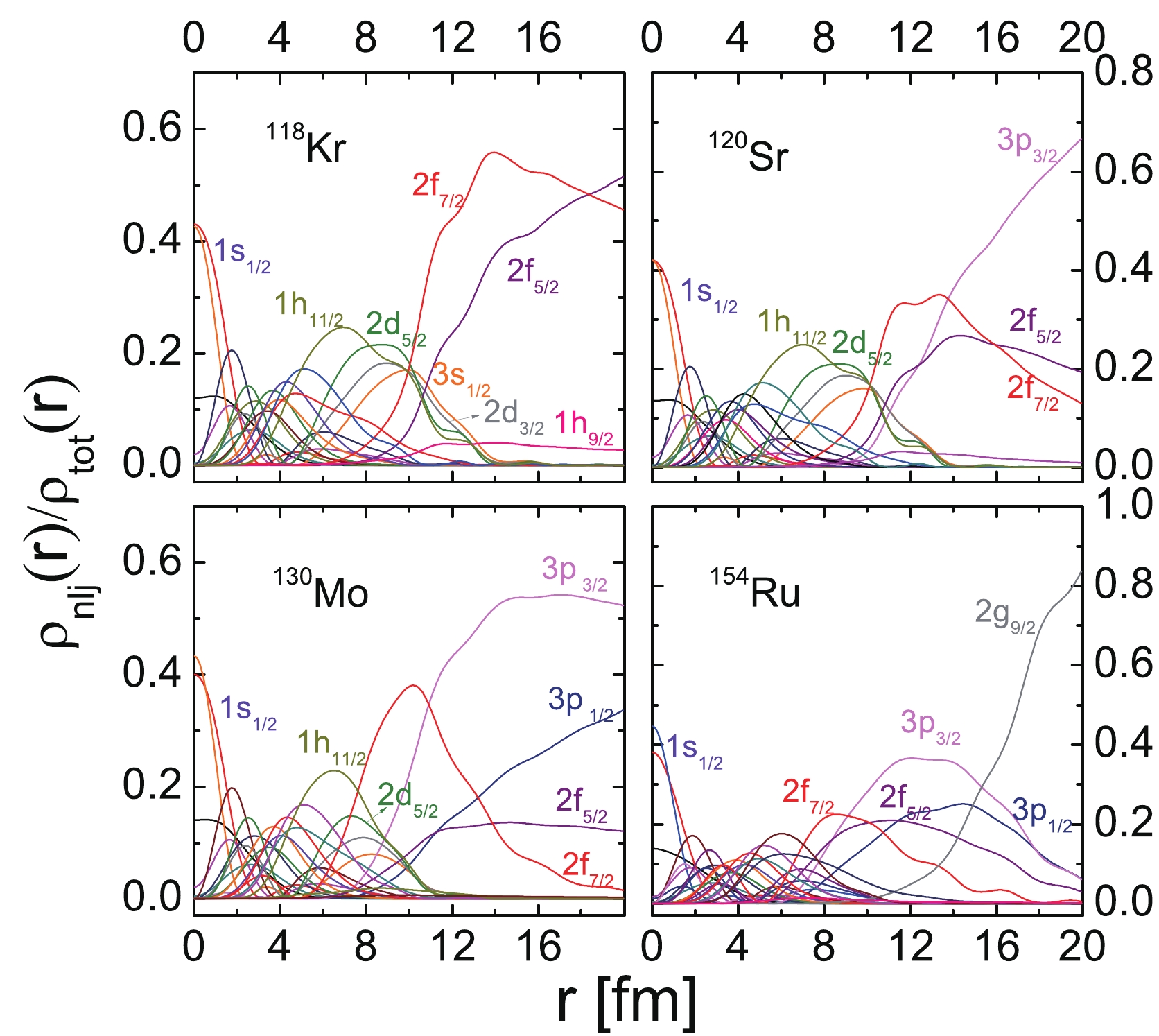
Figure 4. (color online) Density distributions in
$^{118}{\rm{Kr}}$ ,$^{120}{\rm{Sr}}$ ,$^{130}{\rm{Mo}}$ , and$^{154}{\rm{Ru}}$ . The ratios of the neutron density of the single-particle levels to the total neutron density are presented as the function with the grid number of the Gauss-Legendre quadrature.The single-particle energy level is an important property in the description of the nuclear structure. In Fig. 5, we plot the neutron single-particle levels of four isotopic chains. It can be observed that the energy values slowly decrease with the increase in the mass number. Meanwhile, the Fermi surface gradually increases and exceeds 0 MeV at the end of the isotopic chains. In addition, a significant energy gap, above the energy level
$ 1h_{11/2} $ in all of these four isotopic chains, is illustrated in Fig. 5, which corresponds to the magic number N = 82. Hence, it is difficult to occupy the level$ 1h_{11/2} $ with a neutron number N$ < 82$ . A detailed discussion will be provided in the paper. A significant energy gap was determined between$ 1h_{11/2} $ and$ 3s_{1/2} $ for Kr, Sr, and Mo isotopes. This indicates that the level$ 1h_{11/2} $ approaches$ 3s_{1/2} $ as an intruder state owing to energy splitting. Owing to its low energy value, the level$ 3s_{1/2} $ is not present in the Ru isotopic chain; hence, we do not consider it here. In the isotopic chain of Kr, the level$ 1h_{11/2} $ reduces to the bound state with the neutron number N$ > 60$ . With increasing neutrons, the levels$ 2f_{7/2} $ ,$ 1h_{9/2} $ ,$ 2f_{5/2} $ appear in turns, and these energy levels remain resonant states in the end. For Sr isotopes, it can be observed that the level$ 3p_{3/2} $ appears when the neutron number N$ \geq 74$ . Furthermore, the levels approximate to the Fermi level at the end of the isotopic chain are$ 3p_{3/2} $ and$ 2f_{7/2} $ . In fact, the levels with a small orbital angular momentums near the weakly bound state increase the feasibility of developing a halo structure. Therefore, the level$ 3p_{3/2} $ may support the formation of the halo structure. In the isotopic chain of Mo, the levels$ 2f_{7/2} $ and$ 3p_{3/2} $ are occupied by neutrons, and they reduce to bound states when the mass number A = 130, 134, whereas the resonant state$ 3p_{1/2} $ is approximately 0 MeV. Moreover, these three energy levels are determined to be approximate to the Fermi surface in the end. Similar to Sr isotopes, Mo isotopes can exhibit the halo phenomenon. Finally, for Ru isotopes, the energy gap between$ 1i_{13/2} $ and$ 2g_{9/2} $ agrees well with the magic number N = 126. In addition, these levels$ 2f_{7/2} $ ,$ 1h_{9/2} $ ,$ 3p_{3/2} $ ,$ 3p_{1/2} $ , and$ 2f_{5/2} $ are gradually occupied when mass number A = 128-158. Notably, all of these levels are approximately –1 MeV in$ ^{158} {\rm{Ru}}$ . Similarly, halo strctures can appear in the Ru isotopic chain.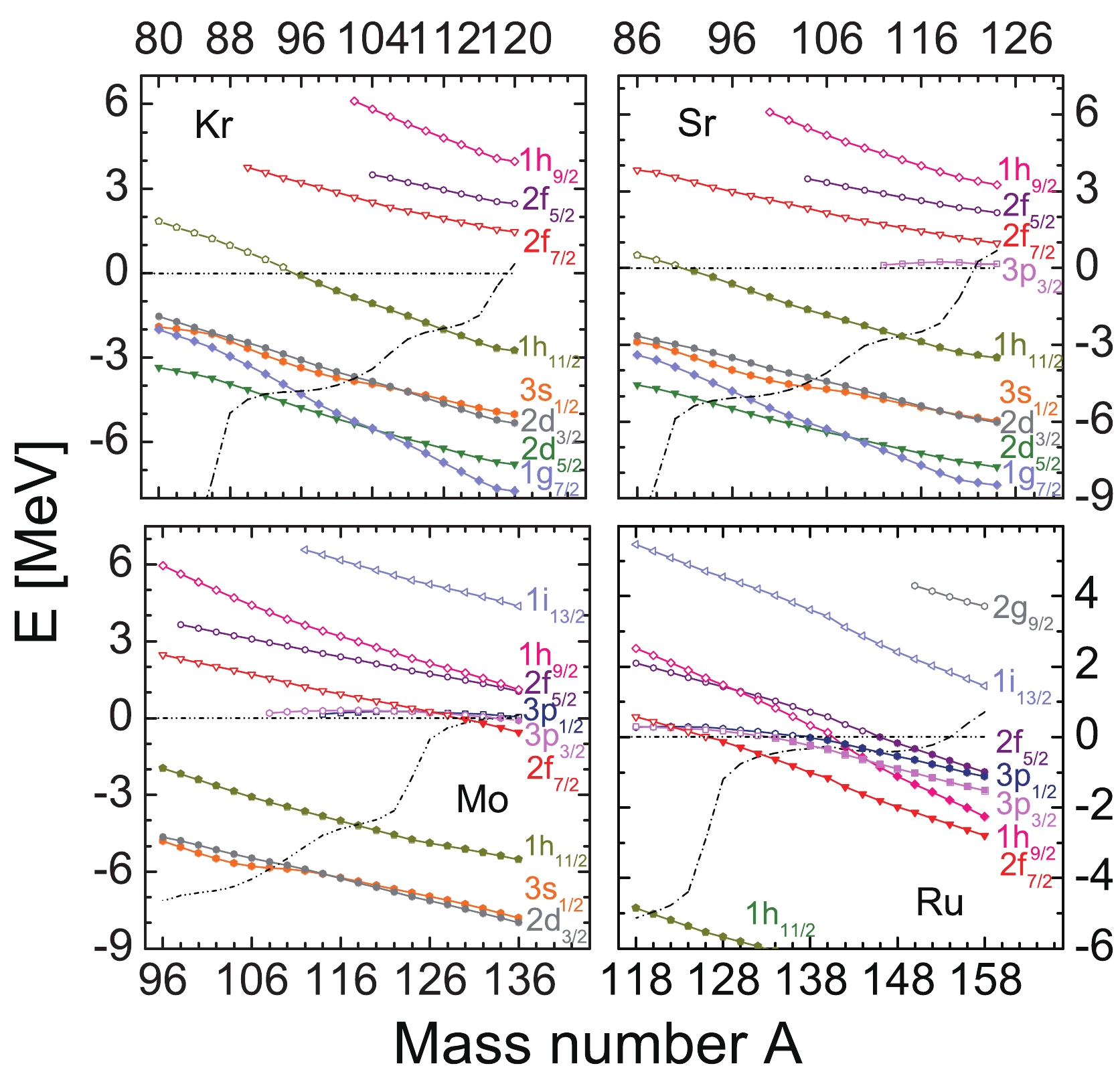
Figure 5. (color online) Neutron single-particle energies as a function of mass number for Kr, Sr, Mo, and Ru isotopes. The labels of single-particle levels are marked on the right side. The dot-dashed, solid dotted, and hollow dotted lines represent the Fermi level, bound states, and resonant states, respectively. The colors of the lines at each energy level are the same as in Fig. 4.
To better elucidate the contribution of single-particle levels to the exotic structures, the occupation probability is presented in Fig. 6. The levels, which are always occupied completely or never occupied, are ignored. As can be observed, the occupation probability of each single-particle level increases with the increase in the mass number. In the Kr isotopic chain, the relatively weak bound states
$ 2d_{5/2} $ ,$ 1g_{7/2} $ ,$ 3s_{1/2} $ ,$ 2d_{3/2} $ are determined to exhibit the maximum occupancy probability with the mass number increased in$ ^{86-110} {\rm{Kr}}$ . The single-particle levels$ 1h_{11/2} $ and$ 2f_{7/2} $ , which reduce or are close to the bound states from resonant states, are significantly occupied by neutrons when the mass number A is greater than 106. However, in the range of Kr isotopes, the single-particle levels$ 1h_{11/2} $ and$ 2f_{7/2} $ are not completely occupied by neutrons. Because the levels$ 1h_{11/2} $ and$ 2f_{7/2} $ exhibit high orbital angular momentums, we still believe that there is no halo structure in the Kr isotopes. In addition, the gap between the levels$ 3s_{1/2} $ and$ 1h_{11/2} $ refer to the energy splitting for$ 1h_{11/2} $ in Kr, Sr, and Mo isotopes. Regarding Sr isotopes, the occupation probability for relatively weak bound states$ 2d_{5/2} $ ,$ 1g_{7/2} $ ,$ 3s_{1/2} $ , and$ 2d_{3/2} $ gradually increase to saturation. With the increase in neutrons, the single-particle level$ 1h_{11/2} $ is occupied rapidly in the range of$ ^{106-126} {\rm{Sr}}$ , and its occupation probability is approximately 1 in$ ^{126} {\rm{Sr}}$ . In addition, the gap between$ 1h_{11/2} $ and$ 2f_{7/2} $ supports the magic number N = 82. In the Mo isotopic chain, the bound states, such as$ 2d_{5/2} $ ,$ 1g_{7/2} $ , and$ 3s_{1/2} $ , are gradually occupied with the increase in the neutron number N as$ 54 \leq N \leq 82 $ . In addition, the occupation probabilities for resonant states$ 2f_{7/2} $ ,$ 3p_{3/2} $ , and$ 3p_{1/2} $ , which reduce to bound states at the end of the isotopic chain, start to increase when the neutron number$ N>82 $ . Nevertheless, they are not occupied completely in$ ^{124-136} {\rm{Mo}}$ . Particularly, the occupation probabilities of the levels$ 2f_{7/2} $ ,$ 3p_{3/2} $ , and$ 3p_{1/2} $ are approximately 0.9, 0.6, and 0.5 in$ ^{136} {\rm{Mo}}$ , respectively. Similar to$ 1h_{11/2} $ , the level$ 2f_{7/2} $ exhibits a high orbital angular momentum and centrifugal barrier. Accordingly, we speculate that the levels$ 3p_{3/2} $ and$ 3p_{1/2} $ provide the major contribution to the formation of halo structures. In the Ru isotopic chain, we can obtain a large gap between the occupation probability of the levels$1{h}_{11/2}$ and$2{f}_{7/2}$ in Fig. 6. In combination with Fig. 1, the decreased value of${S}_{2n}$ is greater than 5 MeV when the neutron number N = 82. Accordingly, we infer that$ ^{126} {\rm{Ru}}$ exhibits strong stability. After the level$ 1h_{11/2} $ is occupied by neutrons, the occupation probabilities of levels$ 2f_{7/2} $ ,$ 1h_{9/2} $ ,$ 3p_{3/2} $ ,$ 2f_{5/2} $ , and$ 3p_{1/2} $ begin to increase. All the levels are close to being occupied completely in the end. Similarly, the levels$ 3p_{3/2} $ and$ 3p_{1/2} $ are inferred to play an important role in the formation of the halo phenomena. Combining Fig. 3 and Fig. 5, we analyze the deviation of density distributions for Ru isotopes because a few resonant states reduce to bound states, and their occupation probabilities reach the maximum.
Figure 6. (color online) Neutron single-particle levels occupation probability presented as the function of the mass number A for Kr, Sr, Mo, and Ru isotopes. In addition, the levels, which are occupied completely or never occupied, are not represented. The colors of the lines at each energy level are the same as in Fig. 4.
-
In this study, four isotopic chains (Kr, Sr, Mo, and Ru isotopic chains) are calculated using the RMF-CMR+BCS(DD-PC1) method. The results obtained are compared with those of RCHB, HFB, and the experimental data. From the analysis of two-neutron separation energies,
$ ^{118} {\rm{Kr}}$ ,$ ^{120} {\rm{Sr}}$ ,$ ^{130} {\rm{Mo}}$ , and$ ^{154} {\rm{Ru}}$ are predicted by RMF-CMR+BCS(DD-PC1) to be the drip line nuclei for Kr, Sr, Mo, Ru isotopes. In addition, the changes in the$ S_{2n} $ value indicate that the halo structures appear in Mo and Ru isotopic chains. Similarly, the halo is also supported by the calculated rms radii of the neutron and proton for$ ^{126-136} {\rm{Mo}}$ and$ ^{128-158} {\rm{Ru}}$ . The Kr and Sr isotopes are considered to solely form neutron skin structures in$ ^{80-120} {\rm{Kr}}$ and$ ^{86-124} {\rm{Sr}}$ . Moreover, long tails were observed in the neutron density distribution for most of the nuclei mentioned, which indicates the creation of exotic phenomena, such as neutron halo structures. The obtained density distributions for the neutron single-particle levels facilitate the determination of levels that play a vital role in creating halo structures. A conclusion can also be drawn from the neutron single-particle levels and their occupation probabilities. The resonant states with lower angular momentum, which gradually decrease to weakly bound states as the neutron number increases, provide the major contribution to the formation of exotic phenomena. This research is beneficial to theoretical and experimental studies on halo and drip line nuclei. -
We thank Quan Liu, Zhong-Ming Niu, and Xue-Neng Cao for their fruitful discussions.
Exploring the halo phenomena of medium-mass nuclei having approximately Z = 40 with point-coupled parameters in complex momentum representations
- Received Date: 2021-03-04
- Available Online: 2021-07-15
Abstract: To explore the properties of neutron-rich nuclei with approximately 40 protons, the density-dependent point coupling (DD-PC1) effective interaction parameter is adopted in the relativistic mean-field theory with the complex momentum representation (RMF-CMR). The calculated two-neutron separation energy (S2n) and root-mean-square (rms) radii support the halo structure that appear in Mo and Ru isotopic chains. Besides, the neutron skin structures appear in Kr and Sr isotopes. The conclusions drawn are also supported by the single-particle energy levels and their occupancy probability and density distribution. Particularly, the energy levels, which reduce to bound states or are approximately 0 MeV with a small orbital angular momentum, are suggested to provide the primary contribution to increasing the neutron radius. Moreover, the single-particle energy levels significantly reflect the shell structure. In addition, the neutron drip line nuclei for Kr, Sr, Mo, and Ru elements are proposed via the changes in S2n.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF













 DownLoad:
DownLoad: