AdS/Deep-Learning made easy: simple examples

Machine learning or deep learning [1] techniques have become very useful and novel tools in various research areas. Recently, an interesting machine learning idea was proposed by Hashimoto et al. in [2, 3], where the authors apply deep learning (DL) techniques to problems in gauge/gravity duality [4, 5]. They showed that the spacetime metric can be “deep-learned” by the boundary conditions of the scalar field, which lives in that space.

The essential DL idea of [2, 3] is to construct the neural network (NN) by using a differential equation structure. The discretized version of the differential equation includes the information of physical parameters such as a metric. The discretized variable plays the role of different “layers” of the NN and the dynamic variables correspond to nodes. Therefore, training the NN means training the physical parameters so that, ultimately, we can extract the trained physical parameters. This idea is dubbed AdS/DL (Deep Learning). See also [6] for an application.

In this paper, we apply the AdS/DL technique to simple classical mechanics problems such as Fig. 1. By considering simple examples, we highlight the essential idea of AdS/DL without resorting to knowledge of gauge/gravity duality. This perspective can facilitate various applications of AdS/DL: from the emergent spacetime as an NN to classical mechanics problems. Furthermore, our work will be a good starting point to learn a physics-friendly NN technique rather than the classical way from computer science.

Figure 1.  (color online) A ball goes through a “black-box” and the velocity of the ball changes from $v_i$ at $t_i$ to $v_f$ at $t_f$. It is very challenging to retrieve the information inside the black-box when the given data is limited by initial and final data.

Let us describe a prototypical problem. Suppose that we want to figure out the force in the black box shown in Fig. 1. We are given only initial and final data, for example, the initial and final position and velocity, $ (x_i, v_i) $ and $ (x_f, v_f) $, respectively. A standard method is to start with an educated guess for a functional form of the force (say, $ F(x,v) $). One can use this “trial” force to simulate the system by solving Newton's equation. After trial-and-error simulation and comparison with experimental data, we may be able to obtain the approximate functional form of the force. However, if the force is complicated enough, it will not be easy to make a good guess at first glance, and it will not be easy to modify the trial function in a simple way. In this situation, machine learning can be a very powerful method to obtain the force in the black box.

Usually, when there is a big enough input-output data set, classical DL techniques with NN, even without considering the physical meaning of NN or the structure of the problem, can reliably make a model that takes input data points and gives matching output values in a trained region, because that is the strength of DL. Having a wide and deep enough feed-forward NN with linear and nonlinear transformations can trivially make such convergence as the Universal Approximation Theorem (UAT) guarantees [7, 8]. Retrieving physical parameters from such a model is not easy because the network in general has little to do with the mathematical structures of the models we want to understand. However, if we build an NN in a way that reflects the mathematical structure of the problem as in AdS/DL, we can retrieve physical information from the model. In this case, the discretized time (t) plays the role of a layer and the dynamic variables $ (x,v) $ correspond to the nodes^①. The unknown force is encoded in the NN so it will be trained.

This paper is organized as follows. In Section II, the general framework of building and training an NN from an equation of motion (EOM) is introduced. In Sections III and IV, example problems are tackled with the methodology described in Section II. Section III covers a simpler example with one variable (one-dimensional velocity), while Section IV deals with a problem with two variables (one-dimensional position and velocity). We conclude the study in Section V.

The general framework can be divided into three major parts. First, a training data set is generated using the EOM of a system and a numeric ordinary differential equation (ODE) solver (the Euler method). Second, an NN is built from the EOM with randomly initialized parameters based on the Euler method. Third, the NN is trained with the training data sets. After these three steps, the resultant learned parameters are compared against the right parameters to see if the learning was successful. The first part, training data set generation, is trivial, and hence, we give an elaboration from the second part.

In this section, we review how to build an NN from an EOM, following the framework suggested by [3]. Figure 2 shows the basic structure of our NN of interest. It is a feed-forward network, which means the propagation of variables is one-directional without any circular feed-back. Its depth (the number of layers) is set to be $ N\!+\!1 $ (from 0 to N) excluding the input and output layers, while the width (the number of nodes for a layer) is kept as two. The propagation rule from one layer to the next layer is given by the differential equations from the EOM with learning parameters of interest.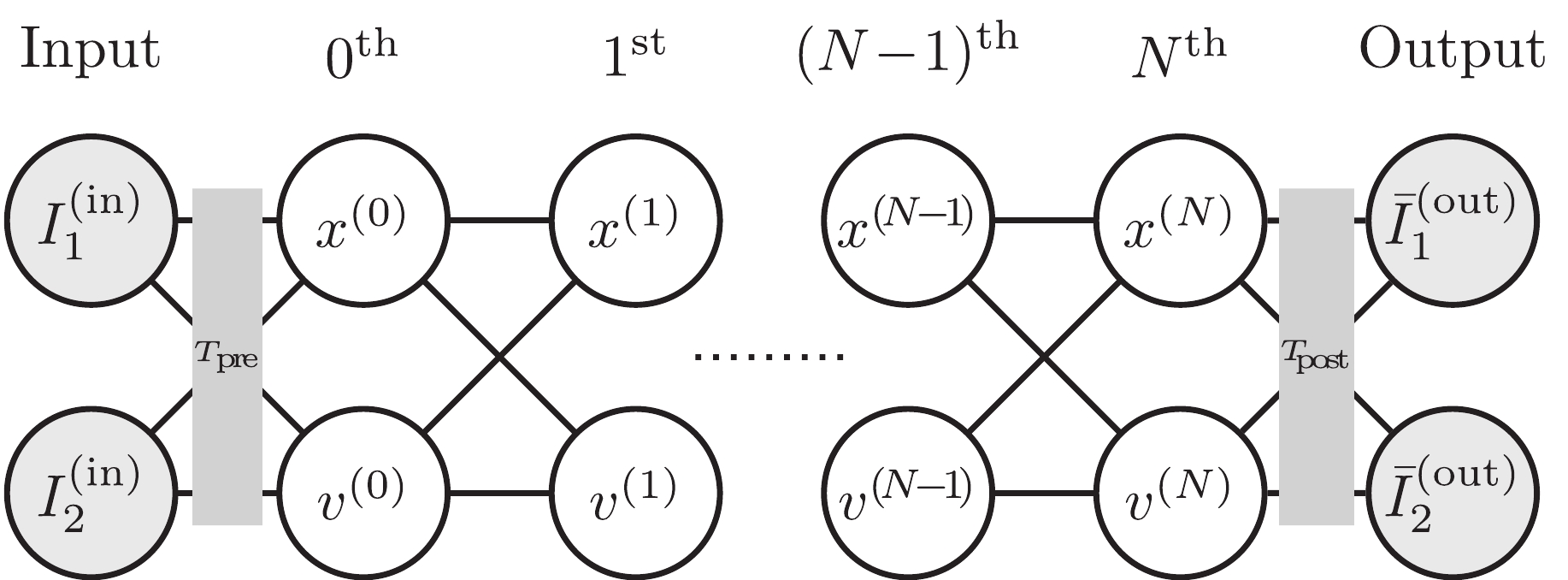

Figure 2.  NN structure with two kinematic variables, x and v. Each circular node denotes a neuron with its own variable. The lines between nodes show which nodes are directly correlated with which nodes. Their initial values $(x^{(0)},v^{(0)})$ are calculated from two input information nodes $I_1^{({\rm{in}})}$ and $I_2^{({\rm{in}})}$ by a pre-processing transformation $T_{\rm{pre}}$. The kinematic variables propagate along the NN from the $0^{\rm{th}}$ layer to the $N^{\rm{th}}$ layer with the rule given by the EOM. The final values $(x^{(N)}, v^{(N)})$ are used to calculate the model's output information nodes $\bar{I}_1^{({\rm{out}})}$ and $\bar{I}_2^{({\rm{out}})}$, which are compared against the true output values ${I}_1^{({\rm{out}})}$ and ${I}_2^{({\rm{out}})}$ given from the training data set. The number of nodes in the input and output layers can vary depending on the experimental setup.

Here, $ T_{\rm{pre}} $ is the transformation from the input layer to the $ 0^{\rm{th}} $ layer (pre-processing), which is the identity transformation in our cases, and $ T_{\rm{post}} $ is the transformation from the $ N^{\rm{th}} $ layer to the output layer (post-processing). The input layer and the pre-processing transformation is used when pre-processing of experimental data to the kinematic variables that appear in the EOM is required. If there is no need for such pre-processing, one may omit the input layer, which is the case for the rest of this paper. We, however, chose to include the input layer in this section for more general applications that require pre-processing. The output layer corresponds to a set of experimental measurements after the propagation of variables with the EOM. For our cases, it will be final variables and/or flags showing whether or not the trained data points give valid outputs^②. The details of how we set up the output layer are discussed in the following sections.

There are two main differences between the NN in our setup and a usual feed-forward NN. First, in our setup, the width of the NN stays constant, which is simply the number of kinematic variables used in the learning process. In usual cases, however, the width of the NN may vary for different layers to hold more versatility. Second, the propagation rule is set by the EOM, and there are relatively fewer learning parameters, whereas most components of the propagation rule of a usual NN are set as learning parameters. From an NN perspective, our setup may look restrictive, but from a physics perspective, it is more desirable because we may indeed obtain physical understanding of the inner structure of the NN: we want to “understand” the system rather than simply having answers.

How is the propagation rule given by the EOM? Let us assume that, as time changes from $ t_i $ to $ t_f $, the following EOM holds:

or

If we discretize the time of (2) and take every time slice as a layer, we may construct a deep NN with the structure of Fig. 2 with the following propagation rule, which is essentially the Euler method:

where $ x^{(k)} $ and $ v^{(k)} $ are variables at time $ t_i \!+\! k\,\Delta t $ (k-th layer) where $ \Delta t : = \dfrac{t_f - t_i}{N} $.

Another way of writing (3) is separating the linear part and the nonlinear part. The linear transformation can be represented by a weight matrix, $ W^{(k)} $ for the $ k^{\rm{th}} $, while the non-linear transformation is called an activation function, $ \varphi^{(k)} $ for the $ k^{\rm{th}} $, so that the $ k^{\rm{th}} $ layer variable set,

propagates to the $ (k\!+\!1)^{\rm{th}} $ layer by

where

In this way, the NN is built from the EOM and different layers mean different times, except for the input and output layers. The learning parameters, $ f(x^{(k)}, v^{(k)}) $ in our case, are randomly set within a reasonable range. The model output $ {{\bar{\bf{x}}}}^{({\rm{out}})} $ can be expressed as follows. To differentiate the true output (training data) from the model output, the model output is specified as a variable name with a bar on it, whereas the true output is without a bar.

where $ {\bf{x}}^{({\rm{in}})} = \left(I_1^{({\rm{in}})}, I_2^{({\rm{in}})}\right)^T $ and $ {\bar{\bf{x}}}^{({\rm{out}})} = \left(\bar{I}_1^{({\rm{out}})}, \bar{I}_2^{({\rm{out}})}\right)^T $. The true output from the training data is denoted as $ {\bf{x}}^{({\rm{out}})} = \left(I_1^{({\rm{out}})}, I_2^{({\rm{out}})}\right)^T $.

Note that the weight matrix $ W^{(k)} $ and the activation function $ \varphi^{(k)} $ of the NN are constructed according to the EOM as shown in (6). Thus, our goal is to train the function $ f(x^{(k)}, v^{(k)}) $ using the NN and input/output data. A single pair $ ({\bf{x}}^{({\rm{in}})}, {\bf{x}}^{({\rm{out}})}) $ is called a training data point, and a whole collection of them $ \{({\bf{x}}^{({\rm{in}})}, {\bf{x}}^{({\rm{out}})})\} $ is called a training data set. From the training data set, one can define an error function (a.k.a. loss function) as

where a batch is a part of the data set chosen for one learning cycle and $ n_{\rm{batch}} $ is the number of data points for one batch. For example, if there are 500 data points in total and 100 data points are used for one batch of the learning process, $ n_{\rm{batch}} $ is 100 and five learning cycles cover the whole data set, which is called one epoch of learning. The summation over a “batch” means that we add up the term from every data point from the batch. Dividing the data set into batches makes the learning process more efficient, especially when the data set is big. To make multiple parameters optimized with sufficient stability, many epochs of learning are required.

The first term in (8) is the ${L}^1$-norm error of the batch calculated from the difference of the output from the NN model $ \bar{{\bf{x}}}^{({\rm{out}})} $ and the true output from the training data set $ {{\bf{x}}}^{({\rm{out}})} $, which is one of the most widely-used error functions. The second term, $ E_{\rm{reg}} $, is the regularization error which makes unphysical solutions (e.g. unnecessarily zigzagging solutions) unfavorable in learning. The details on $ E_{\rm{reg}} $ are provided in the following sections. Note that the error function defined here is one example of possible choices. The structure of E can vary depending on the nature of problems. Please refer to Sec. IV for a variation.

In general, the value of E depends on both the weight matrix and the activation function^③. For our model, however, the weight matrices are constant in the sense that they are not learning parameters in the NN so that the activation functions $ \varphi^{(k)} $, or more specifically, the parameters $ f(x^{(k)}, v^{(k)}) $, are the only parameters to be learned while minimizing the value of E. As an optimizer (learning mechanism), the two most classic choices are stochastic gradient descent and Adam, where the former is more stable and the latter is faster in many cases [9]. We used the Adam method with Python 3 and PyTorch as a general machine learning environment.

In this section, we describe the basic idea of our method using one of the simplest examples. Here, we use only one kinematic variable, the one-dimensional velocity v, to extract information of the velocity-dependent drag force $ F_{1,{\rm{True}}}(v) $ of a given system. This example is very simple, but the application of DL methodology is relevant and clear. The drag force is designed to be non-trivial to fully test the capability of the methodology.

Problem definition We consider a problem setup described in Fig. 3. A ball with mass m is dropped with initial velocity $ v_i $ at time $ t_i $ through a medium with an unknown complicated drag force $ F_1(v) $ under a constant downward gravitational acceleration g. At time $ t_f $, the velocity $ v_f $ is recorded. The times $ t_i $ and $ t_f $ are fixed, whereas $ v_i $ varies as well as $ v_f $ so that we have the input-output data set $ \left\{\left(v_i,\, v_f\right)\right\} $ for training. The EOM is given as follows, and we want to find the drag force $ F_1(v) $: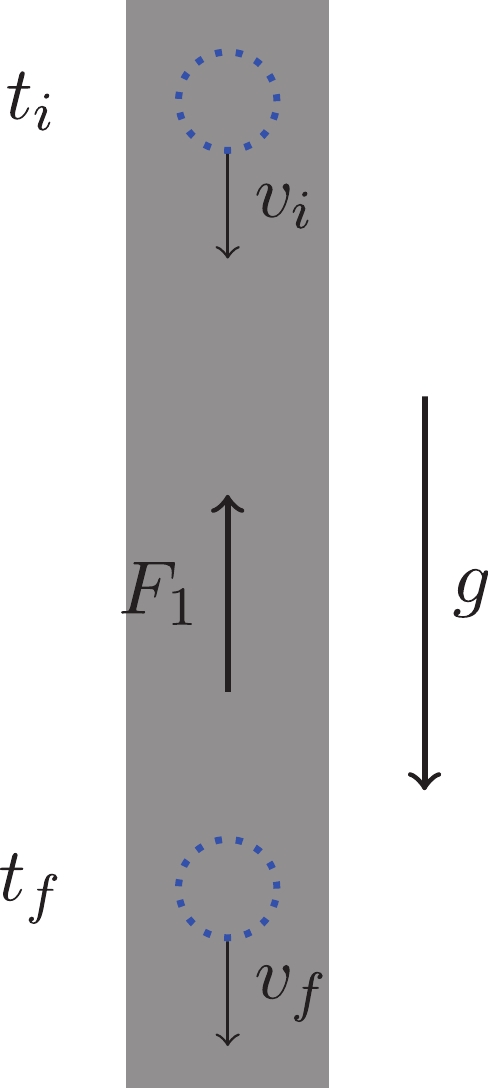

Figure 3.  (color online) Problem setup of case 1. A ball in a known constant downward gravitational acceleration g goes through a “black-box” filled with a homogeneous medium with an unknown drag force $F_1(v)$. From experiments, multiple initial and final velocity values $v_i$ and $v_f$ are recorded at fixed initial and final times $t_i$ and $t_f$.

Method Because we only have one kinematic variable v, it is enough to build an NN with one node per layer (the width of one) as described in Fig. 4. We omitted the input and output layers in Fig. 4, since the $ 0^{\rm{th}} $ and $ N^{\rm{th}} $ layer values, $ v^{(0)} $ and $ v^{(N)} $, are themselves used as the input and output layers, $ v_i $ and $ \bar{v}_f $, without any pre- or post-processing. The propagation rule of the NN is written as follows.

Figure 4.  Diagram of the deep NN for case 1.

The initial velocity values are set by $ v_i\in[-250, 0] $, evenly spaced by a gap of 5 (i.e. $ -250, -245, \cdots, 0 $) and the corresponding $ v_f $ is calculated from an ODE solver independent from the NN, which is shown as thick gray points in Fig. 5(a). Thus, the total number of collected data points ($ v_i, v_f $) is $ n_{\rm{data}} = 51 $.

Figure 5.  (color online) Case 1: comparison of trained data for different epochs and true data. With a sufficiently large epoch, for example 1000, the trained data (blue points/curve) agree with the true data (gray points/curve).

As mentioned above, it is possible to build an NN with one kinematic variable v and learn $ F_1 $ from the training data set. The depth of the NN is set by $ N = 10 $. The drag force $ F_1 $ is modeled as an array of size $ L = 251 $, where its $ i^{\rm{th}} $ element $ F_{1, i} $ corresponds to the value of the drag force when $ \left| {v} \right| = i $ ($ i = 0, 1, 2, \cdots, 250 $); $ F_{1,i} = F_1(i) $. The array can hold the information of the drag force for integer speed values $ \left| {v} \right|\in [0,250] $, where $ 250 $ is the upper limit of the speed of ball during the data collection with the true drag force $ F_{1, {\rm{true}}}(v) $^④. When the speed is not an integer, which is true for most cases, the value is linearly interpolated from the two nearest integer values. For example, if $ v = 0.4 $, the drag force value is calculated by $ F_{1} (0.4) = (1-0.4)\times $$ F_{1}(0) + 0.4 \times F_{1} (1) $.

Our goal is to train $ F_1 $ to yield $ F_{1,{\rm{True}}} $. Let us now refine our notation by adding the superscript $ (j) $ to denote the intermediate outputs by $ F_1^{(j)} $. The initial drag force $ F_1^{(0)} $ is set by $ L = 251 $ uniform random numbers between $ (10, 20) $, as a “first guess”. See the red wiggly line in Fig. 5(b). The L elements of the drag force array are learning parameters, which are updated in the direction of reducing the value of the error function. The error is minimized as learning proceeds, and the error at the j-th learning cycle $ E^{(j)} $ is

Here, the first term is the ${L}^1$-norm error to train the parameters to match the model output of final velocity values, $ \bar{v}_f = v^{(N)} $, with the true final velocity values, $ {v}_f $, for a given batch input $ v_i $. Meanwhile, the number of data points is small enough in this case, so we choose to use the whole data set for every learning cycle: $ n_{\rm{batch}}\! = $$ \!n_{\rm{data}}\! = \!51 $. To set a preference on a physically sensible profile of $ F_1 $, two regularization terms are introduced. The first term, $ \left(F_{1}(0)\right)^2 $, reflects a physical requirement: $ F_{1}(0) = 0 $, which means there should be no drag force when $ v = 0 $. The second term, $ c_{1} \sum_{i = 0}^{N-1} \left(F_{1, i+1} - F_{1, i}\right)^2 $, is a mean squared error between adjacent $ F_1 $ array values which gives a preference for smoother profiles; it is not plausible for the drag force to have a spiky zigzag profile. In our computation $ c_{1} = 0.03 $ is used, and we explain how to choose a proper value of $ c_{1} $ at the end of this section. As an optimizer, the Adam method is used^⑤. For numerical work, we choose $ m = 1 $, $ t_i = 0 $, $ t_f = 4 $, $ g = 10 $.

Examples As an example force, the following hypothetical (complicated) form of $ F_{1,{\rm{True}}} $ is assumed, and the training data set $ \left\{\left(v_i, v_f\right)\right\} $ is collected.

which is shown as the gray line in Fig. 5(b).

The learning result is shown in Fig. 5. In Fig. 5(a), the model output set $ \left\{\bar{v}_f\right\} $ is shown with the training data set $ \left\{v_f\right\} $ with different epoch numbers. The NN model learns how to match those two precisely by modifying the learning parameters $ F_1(v) $ as the number of epochs increases. How $ F_1(v) $ is trained over different epoch numbers is shown in Fig. 5(b). As these plots show, the NN model matched $ \left\{\bar{v}_f\right\} $ with $ \left\{v_f\right\} $ accurately and discovered the $ F_{1,{\rm{True}}} $ profile with high accuracy with a big enough epoch number.

To further test the capability of the NN to discover the drag force, different-shaped drag force profiles are tested with the same scheme. As Fig. 6 shows, the NN discovered the right $ F_{1,{\rm{True}}} $ profiles accurately as well at $ {\rm{epoch}} = 1000 $^⑥. From the figures, it is clear that both regularization terms (one for setting $ F_v(0) = 0 $ and the other for smoothness) are guiding the learning correctly by filtering out unphysical solutions.

Figure 6.  (color online) Learning results from different $ F_{1,{\rm{True}}}$ profiles.

We conclude this section by discussing the choice of $ c_1 $ for regularization. The value of $ c_{1} $ controls the smoothness of the $ F_1 $ profile. Figures 7(a) and 7(b) show the effect of different $ c_{1} $ values on the drag force and the error. If it is too large ($ c_1 = 3 $, yellow dots), the $ F_1 $ profile after the learning process ends up being too flat, and the error remains very high, because the learning process overly focuses on smoothing the profile, which ends up giving incorrect output $ \{\bar{v}_f\} $ values and greater error. If it is too small ($ c_1 = 0.003 $, red dots), the $ F_1 $ profile stays spiky and the error remains relatively high as well, because the regularization is not sufficient, and it becomes stuck at local minima of the error. Evidently, $ c_1 = 0.03 $ (green dots) is suitable, showing that the trained $ F_1 $ overlaps very well with $ F_{1, {\rm{True}}} $ while resulting in the minimum error. Indeed, this value of $ c_1 $ can be found by investigating how the error decreases as learning proceeds. As shown in Fig. 7(b), the $ c_1 $ value that gives the minimum error can serve as the best value for regularization^⑦.

Figure 7.  (color online) Regularization $c_1$ dependence of the training results. (a) If $c_{1}$ is too small, the force profile is not smooth enough, and if $c_{1}$ is too big, the profile becomes flat and deviates from the true profile. (b) We may choose $c_1$ such that the error saturates to the smallest value.

In the second case, two one-dimensional kinematic variables x and v come into play to retrieve the position-dependent force $ F_{2, {\rm{True}}}(x) $ of a system from the given data. Again, the force is designed to be non-trivial to fully examine the capability of the methodology. The content is divided into three subsections as well: problem definition, method, and examples.

Problem definition As shown in Fig. 8, a ball is shot at the position $ x_i $ with initial velocity $ v_i $ at time $ t_i $. The initial position $ x_i $ belongs to the range $ (x_i^{\rm{min}}, x_i^{\rm{max}}) $, and the initial velocity is also chosen in a certain range so that we can have a window of the training data set.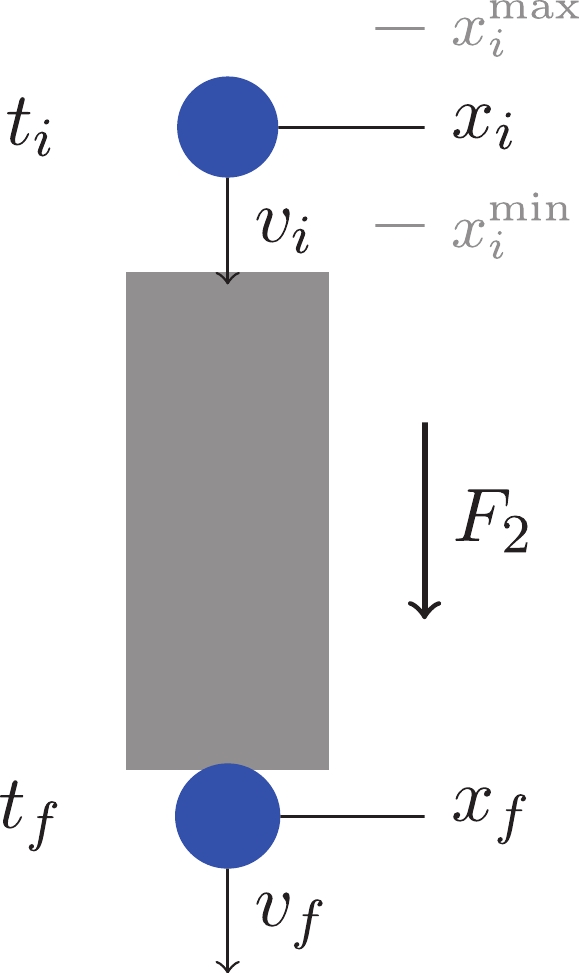

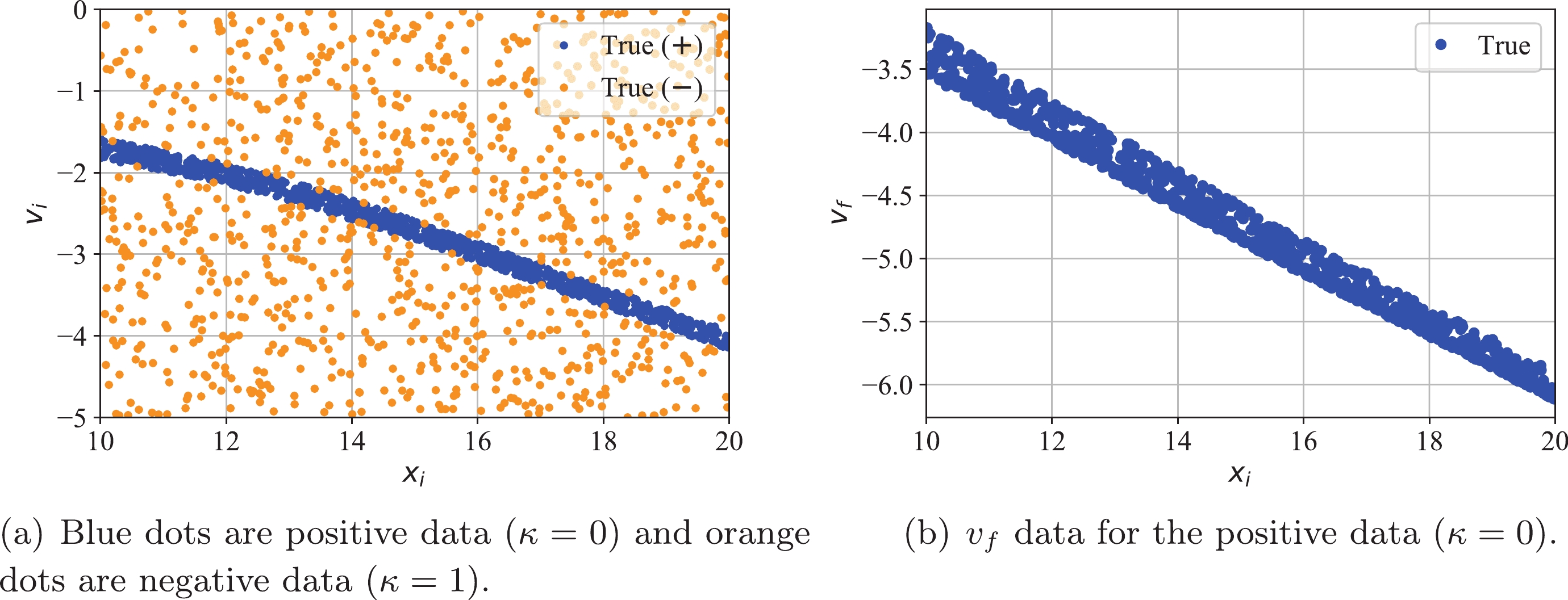
Figure 8.  (color online) Problem setup of case 2. A ball goes through a black-box with an unknown force field $F_2(x)$ without any friction. The ball is dropped with speed $v_i$ at time $t_i$ and position $x_i\in (x_i^{\rm{min}}, x_i^{\rm{max}})$. At $t_f$, if the ball is in the vicinity of $x_f$, a speedometer reads its velocity $v_f$ and the initial kinetic variable set $(x_i, v_i)$ is taken as a positive data point (kind $\kappa\!=\!0$); else, the data point is negative ($\kappa\!=\!1$).

At a fixed final time $ t_f $, if the ball is at the vicinity of $ x_f $ (within $ x_f \pm \epsilon $), the initial kinematic variable set $ (x_i, v_i) $ is taken as a positive data point (kind $ \kappa\! = \!0 $) and its velocity $ v_f $ is recorded. If the ball is not within $ x_f \pm \epsilon $ when $ t = t_f $, the data point $ (x_i, v_i) $ is taken as a negative one (kind $ \kappa\! = \!1 $) and we assume that we cannot measure a corresponding $ v_f $ value. In other words, a positive data point holds two output values, $ \kappa\! = \!0 $ and $ v_f $, while a negative point holds one output value, $ \kappa\! = \!1 $. The EOM is given as $ \ddot{x}\! = \!F_2(x)/m $ and we want to find the force $ F_2 $. The EOM can be separated into two first order differential equations as follows.

Method Because we have two kinematic variables x and v, a two nodes per layer (width of two) setup is used for building the NN, as shown in Fig. 9. The input layer is omitted while the output layer is formed using a post-processing transformation $ T_{\rm{post}} $ on $ \bar{x}_f = x^{(N)} $, which judges whether or not $ \bar{x}_f $ is in the vicinity of $ x_f $ at $ t_f $ by $ \bar{\kappa} = T_{\rm{post}}(\bar{x}_f)\simeq0 $ for $ \left| {\bar{x}_f-x_f} \right|\leqslant\epsilon $ (model-positive) and $ \simeq1 $ for $ \left| {\bar{x}_f-x_f} \right|\geqslant\epsilon $ (model-negative). More discussions about $ T_{\rm{post}} $ follow shortly. For positive data points ($ \kappa\! = \!0 $), their $ \bar{v}_f = v^{(N)} $ values are recorded as well. The propagation rule from the EOM is written as follows.

Figure 9.  Diagram of the deep NN for case 2. An input data point at the $0^{\rm{th}}$ layer $(x^{(0)}, v^{(0)})$ propagates to the $N^{\rm{th}}$ layer. Every data point gives the first output $\bar{\kappa}=T_{\rm{post}}\left( x^{(N)} \right)$ while the second output $v^{(N)}$ is given only from one of the positive data points ($\kappa=0$).

The depth of the NN is set by $ N = 20 $. As in the drag force field $ F_1 $ of case 1, the force field $ F_2 $ is modeled as an array that holds the force value for integer positions; $ F_2 $ is modeled as an array of size $ L = 21 $ covering integer position $ x \in [0, 20] $. The $ i^{\rm{th}} $ component of $ F_2 $ is the force at $ x = i $; $ F_{2, i} = F_2(i) $. When a position value is not an integer, the force is linearly interpolated from those of the two nearest integer positions.

Our goal is to train $ F_2 $ to yield $ F_{2,{\rm{True}}} $. The model's force profile at the $ j^{\rm{th}} $ learning cycle, $ F_2^{(j)} $, approaches $ F_{2,{\rm{True}}} $ as j increases, if the learning is correctly designed and performed. The initial $ F_2 $ array, $ F_2^{(0)} $, is set by normal random numbers with an average of $ -0.4 $ and a standard deviation of 0.1 as a “first guess”. See the red wiggly line in Fig. 11(e).

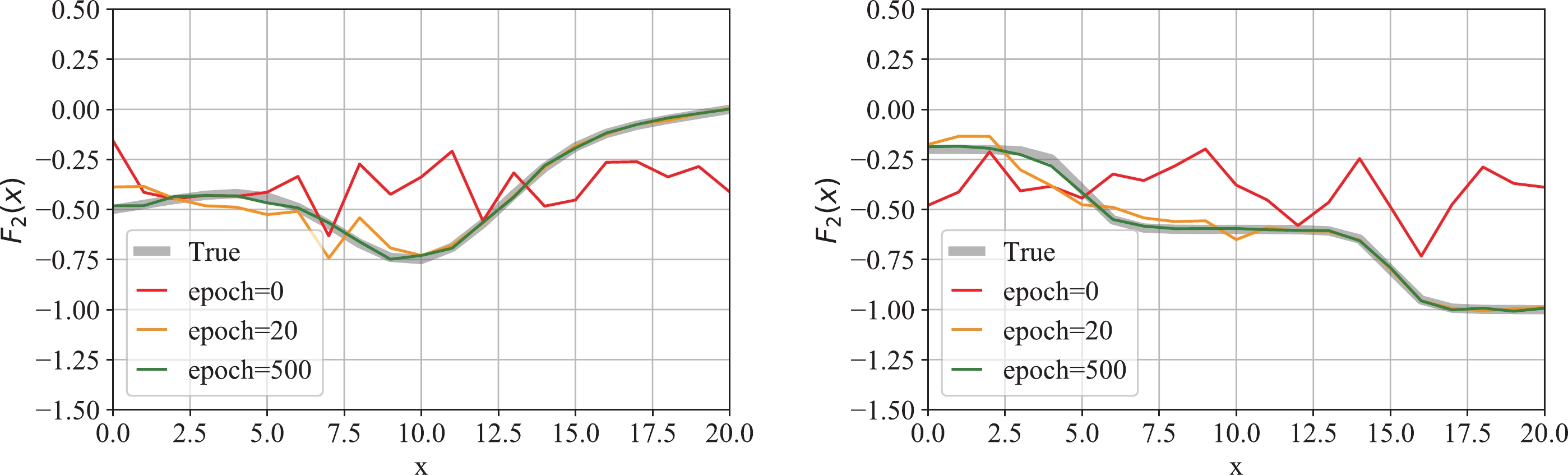
Figure 11.  (color online) Model output before (a, b) and after (c, d) learning. The learning progress of $F_2(x)$ is shown in (e). (a) $(x_{i}, v_{i})$ plot of positive and model-positive data points before learning. Most points' $\kappa$ values are incorrectly guessed as $\bar{\kappa}$ by the model NN. (b) $(x_{i}, v_{f})$ and $(x_i,\bar{v}_f)$ plots for positive data points before learning. Most $v_f$ values are incorrectly guessed as $\bar{v}_f$ by the model NN. (c) $(x_{i}, v_{i})$ plot of positive and model-positive data points after learning. Most points' $\kappa$ values are correctly learned as $\bar{\kappa}$ by the model NN. (d) $(x_{i}, v_{f})$ and $(x_i,\bar{v}_f)$ plots for positive data points before learning. Most $v_f$ values are correctly learned as $\bar{v}_f$ by the model NN. (e) As the epoch increases, the $F_2(x)$ profile approaches $F_{2,{\rm{True}}}(x)$.

There are two things for the NN model to learn. First, the model needs to distinguish positive and negative data points—it should match the $ \bar{\kappa} $ of a given data point $ (x_i, v_i) $ with its actual κ properly. Second, the model should be able to match the model's final velocity $ \bar{v}_f = v^{(N)} $ with the true final velocity $ v_f $ at positive data points $ (x_i, v_i, \kappa = 0) $.

To reflect these, we need two terms for the error function, one for $ \bar{\kappa} $ and κ and the other for $ \bar{v}_f $ and $ v_f $, in addition to the regularization error which gives a preference on smoother profiles. The error function at $ j^{\rm{th}} $ learning cycle is as follows.

where the first and second terms are ${L}^1$-norm errors normalized with their size $ n_{\rm{batch}} $ and $ n_{\rm{batch}, \kappa = 0} $, respectively, scaled by the coefficients $ {\cal{N}}_1 $ and $ {\cal{N}}_2 $ that can control relative importance between the two terms (both are set as one for our case). The third term is the regularization error for smoothness of the profile (the mean squared error between adjacent $ F_2 $ array elements) with the coefficient $ c_2 $. The model output of the kind variable $\bar{\kappa} = T_{\rm{post}} (\bar{x}_f = $$ x^{(N)})$ is calculated using the following post-processing transformation $ T_{\rm{post}} $, which gives $ T_{\rm{post}}(\left| {x-x_f} \right|\leqslant\epsilon)\simeq 0 $ and $ T_{\rm{post}}(\left| {x-x_f} \right|>\epsilon)\simeq 1 $.

The reason to use an analytic function form for $ T_{\rm{post}} $ rather than a step function is to enable the optimizer to differentiate the error function in the parameter space and find the direction to update parameters to minimize the error; if it is a step function, an optimizer would not be able to find the direction to update the parameters. For learning setup, following values are used: $ c_2 = 0.003 $, $ n_{\rm{batch}} = 200 $, and $ n_{\rm{batch}, \kappa = 0} = 100 $, $ \epsilon = 0.5 $^⑧. The termination condition is $ {\rm{epochs}} = 500 $. As an optimizer, the Adam method is used^⑨. For numerical work, we choose $ m = 1 $, $ t_i = 0 $, $ t_f = 4 $, $ (x_i^{\rm{min}}, x_i^{\rm{max}}) = (10, 20) $, $ x_f = 0 $, and $ v_i \in (-5,0) $, which is a sufficient range of velocity to collect positive data points in our setting.

Examples As an example force field, the following hypothetical (complicated) form of $ F_{2, {\rm{True}}} $ is assumed and the training data set $ \left\{ \left(x_i, v_i, \kappa, v_f \right)\right\} $ is collected:

which is shown as the gray line in Fig. 11(a). The experimental input data points $ (x_i, v_i) $ are generated uniform-randomly in their preset range, and the output data points ($ \{\kappa\! = \!0, v_f\} $ for positive data points and $ \{\kappa\! = \!1\} $ for negative data points) are collected using an ODE solver with $ F_{2, {\rm{True}}}(x) $. The number of collected data points for training is 2,000 in total (1,000 for positive, and 1,000 for negative; $ n_{\rm{data}} = 2000 $)^⑩. Figure 10 shows the training data points. Figure 10(a) shows the initial kinematic variables $ (x_i, v_i) $ where positive ($ \kappa\! = \!0 $) and negative ($ \kappa\! = \!1 $) data points are marked with blue and orange, respectively. Figure 10(b) shows the distribution of the final velocity $ v_f $ of positive data points with respect to the initial position $ x_i $.

Figure 10.  (color online) Input data for case 2.

The learning process and result are put together in Fig. 11. In Figs. 11(a) and 11(b), the before-learning training data points are put together with the model data points. Figure 11(a) shows the initial kinematic variables $ (x_i, v_i) $ of the positive data points ($ \kappa\! = \!0 $) in blue and the model-positive ($ \bar{\kappa}\!\simeq\!0 $) in orange, where their intersection is marked as green; the green portion shows the extent to which the model is correct in matching $ \bar\kappa $ with κ. Note that the intersection of negative and model-negative points ($ \kappa\! = \!1 $ & $ \bar{\kappa}\!\simeq\!1 $) are omitted for clarity. Figure 11(b) shows the distribution of the final velocity values from positive data points ($ v_f $) in blue and those from model propagation ($ \bar{v}_f $) in green, respectively; their discrepancy means the model is not matching $ \bar{v}_f $ with $ v_f $ correctly. It is clear that the NN model before learning is incorrect in matching either $ \bar{\kappa} $ with κ or $ \bar{v}_f $ with $ v_f $.

Figures 11(c) and 11(d) show the “after-learning” plots corresponding to Figs. 11(a) and 11(b), respectively. From the increased portion of green dots in Fig. 11(c) and the accurate matching between blue and green dots in Fig. 11(d), it is clear that the NN model after learning matches the outputs correctly. Meanwhile, Fig. 11(e) shows how $ F_2(x) $ is trained over different epochs. It shows how the profile of $ F_2 $ proceeds from the initial random distribution to the true profile $ F_{2,{\rm{True}}} $ by matching $ \bar\kappa $ with κ and $ \bar{v}_f $ with $ v_f $ while guided by the regularization error. From these plots, we can see that the NN model matched both sets of output variables correctly as well as accurately discovering $ F_{2,{\rm{True}}} $.

To further test the capability of the NN in discovering force fields, different-shaped force field profiles are tested with the same scheme. As Fig. 12 shows, the NN discovered the right $ F_{2,{\rm{True}}} $ profiles accurately for both cases at $ {\rm{epoch}} = 500 $^⑪. From this result, we can certify that the NN built with this methodology is capable of learning different shapes of complicated force fields.

Figure 12.  (color online) Learning results from different $F_{2,{\rm{True}}}$ profiles.

In this paper we analyzed classical mechanics problems using DL. The main idea of our problem is explained in Fig. 1: how to find the unknown force, via a DL technique, only from the initial and final data sets. When the EOM of a system is given with a set of initial conditions, calculating the propagation of variables numerically is usually not difficult. In contrast, retrieving the EOM (or the unknown force in the equations) from a given data set can be a very challenging task, especially with limited types/amounts of information (e.g., only initial and final data).

By constructing the NN reflecting the EOM (Fig. 2), together with enough input and output data, we successfully obtained the unknown complicated forces. The learning progress in estimating the unknown forces is shown in Figs. 5(b), Fig. 6, 11(e), and Fig. 12. They show that our DL method successfully discovers the right force profiles without becoming stuck at local minima, or the multiplicity of mathematically possible solutions. There are some factors that can be studied in more depth in future studies. For example, we have observed that limiting the number or range of data points (e.g., narrowing the $ (x_i^{\rm{min}}, x_f^{\rm{max}}) $ range of case 2) results in slower learning and greater deviation from the true force field. In this sense, studies on how much the number and range of data points are correlated with the quality of the learned force field can be valuable.

There are two major advantages of our method. First, the approach with DL can easily find a complicated answer, which does not allow much intuition to “correctly guess” the right form of the answer. Second, contrary to usual NN techniques, our approach trains physical quantities such as the unknown force assigned in the NN, which is important for understanding the physics.

Our framework can be generalized in a few directions. First, we can consider many particle cases and/or higher dimensional problems. In this case, the number of kinematic variables increases, which means the width of the NN increases in Fig. 2. Second, we can improve our discretization method (2) by adding higher order corrections or using the neural ODE technique developed in [10]. For better data generation we may also use more accurate ODE solvers such as the Runge-Kutta method of order 4(5) [11]. Third, we may apply our method to more complicated problems. For example, we may consider scattering experiments by unknown forces, which are not simple power-law forces or even central forces. Last but not least, this work will be pedagogical and useful for those who want to apply AdS/DL to the emergence of spacetime as an NN and other areas of physics governed by differential equations.

From a broader perspective, the examples in this paper can enhance the mutual understanding of physics and computational science in the context of both education and research by providing an interesting bridge between them.

We would like to thank Koji Hashimoto, Akinori Tanaka, Chang-Woo Ji, Hyun-Gyu Kim, and Hyun-Sik Jeong for valuable discussions and comments.