-
One of the most interesting open questions in modern physics, that can be explored within the current research, is the existence of a new type of non-luminous matter, which is possibly composed of non-baryonic particles called Dark Matter (DM). The need for a DM hypothesis arises from several astrophysical observations, and it is supposed that DM contributes to approximately 27% of the mass of the Universe [1-9]. In parallel to the evidence from astrophysical constraints, the direct search for DM at the Large Hadron Collider (LHC) is ongoing using proton-proton collision events with a signature based on large missing transverse momentum. The methodology of the direct detection of DM at the particle colliders is implemented in the "Mono-X" models, which predict the production of a visible state particle plus missing transverse momentum recoiling against that particle and is interpreted as the production of dark sector particles with the signature
$\text{X}+{\not\!\! p }_{T}$ . The visible particle could be a standard model (SM) particle, i.e., W, Z, or jets [10], a photon [11], or a Higgs boson [12]. DM particles have also been searched for in events with dileptons from Z boson decay plus large missing transverse momentum with center-of-mass energies$ \sqrt{s} $ = 8 [13] and 13 TeV [14].The same idea has been extended to beyond the standard model (BSM) particles [15, 16]. The model we study (Mono-Z
$ ^{\prime} $ ) predicts the production of DM in association with the new heavy gauge boson, denoted by$ Z' $ . These dark sector particles can be identified in the detectors located at the LHC as a large missing energy [17]. The Z$ ^{\prime} $ boson is considered a new particle in many BSM theories and some extensions of the SM, e.g., the grand unification scenarios. The Z$ ^{\prime} $ is neutral and has the same decay modes of the standard model Z boson, with a larger spectra of masses. More information can be found in [18-21]. Hence, the search for new heavy resonance in the hadronic and leptonic channels is one of the important goals of high energy physics, to investigate those BSM hypotheses that predict new types of bosons. The ATLAS collaboration [22] studied the previously mentioned Mono-Z$ ^{\prime} $ model considering the hadronic decay of the Z$ ^{\prime} $ boson. The coupling of Z$ ^{\prime} $ to electrons has been constrained previously by LEP measurements in [23]; thus, in our analysis, we consider the muonic decay of Z$ ^{\prime} $ (i.e., Z$ ^{\prime}\; \rightarrow\; \mu^{+}\mu^{-} $ ).Owing to the CMS open data project [24], the CMS collaboration has published significant amounts of recorded and simulated pp collision data at
$ \sqrt{s} = 8 $ TeV, which are available for all scientists, even if they are not members of the CMS collaboration. In our study, we use only the CMS simulated samples. These samples have great potential and offer opportunities to evaluate the cross sections of the SM processes, model the SM backgrounds for different studies, and perform further analysis, as reported in [25].Section II presents a more detailed description of the theoretical model that predicts the possible production of DM in association with the heavy gauge boson (Z
$ ^{\prime} $ ), while in section III, we briefly describe the Compact Muon Solenoid (CMS) detector. In section IV, we discuss the simulated samples for signals and SM background sources used in the analysis. That is followed, in section V, by discussion of the backgrounds in this search and the methods with which their contributions are estimated. The selection of events and the general strategy of the search are outlined in section VI. Systematic uncertainties affecting the prediction of backgrounds are presented in section VII. The results and summary of the search are respectively addressed in section VIII and section IX. -
The work reported in [17] proposed the production of DM with a resonance that comes from the heavy Z
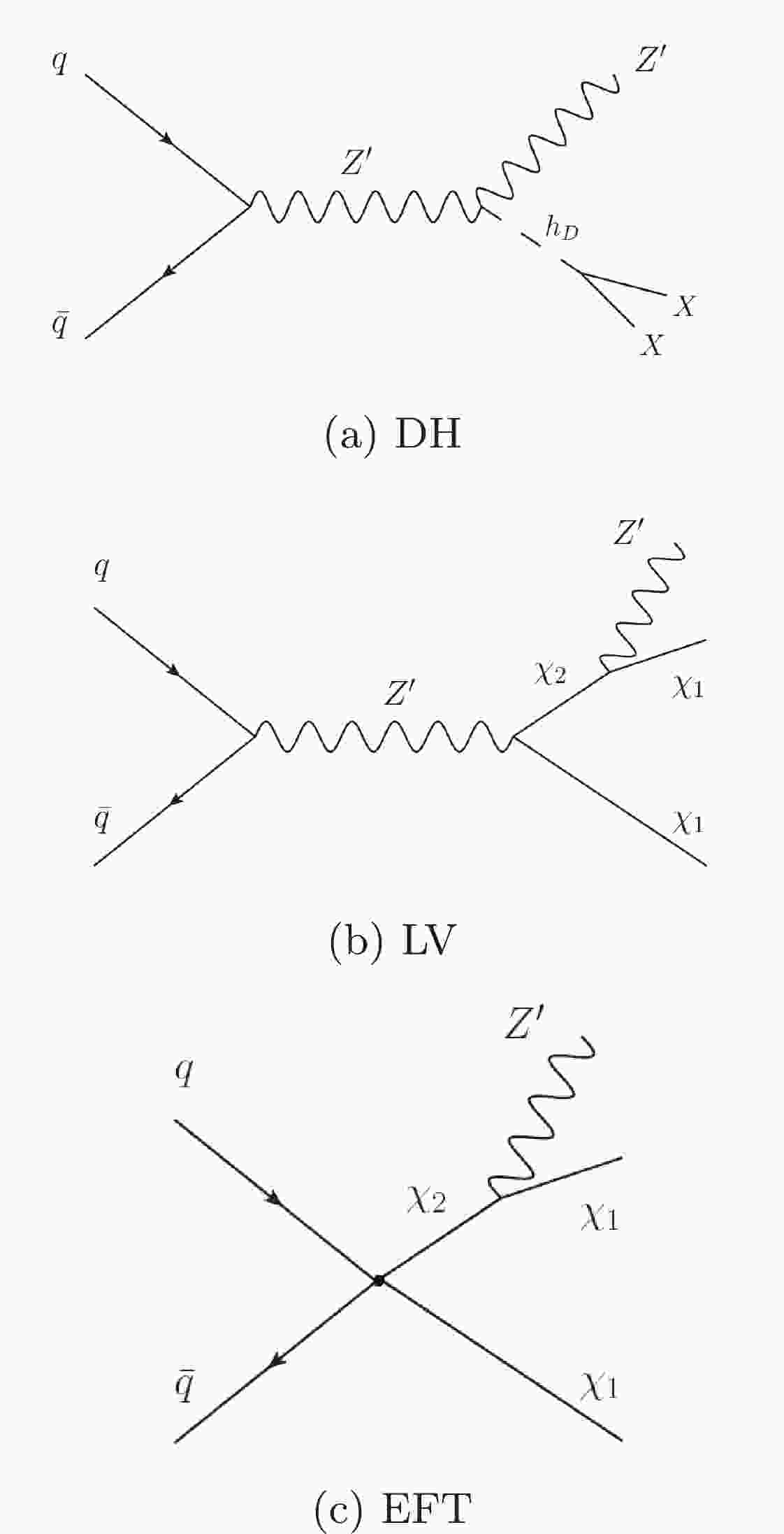
$ ^{\prime} $ gauge boson; this model is known as the Mono-Z$ ^{\prime} $ model. The model has been presented in three different possible scenarios, including two simplified models, the Dark Higgs (DH) and light vector (LV), also called the dark fermion, and a third scenario, known as an LV with an inelastic effective field theory coupling (EFT). The two simplified models are represented in Fig. 1. In the DH scenario, the mediator vector boson Z$ ^{\prime} $ is produced via the$ q\bar{q} $ annihilation process, at parton level, after which it undergoes a dark-Higgs-strahlung process analogous to the emission of the SM Higgs particle by W or Z bosons. The new scalar coupled to the Z$ ^{\prime} $ is called the Dark Higgs ($ h_{D} $ ), and it is assumed that the Dark Higgs decays rapidly into a pair of dark sector particles ($ \chi \bar{\chi} $ ). The coupling of Z$ ^{\prime} $ with$ h_{D} $ is given by ($ {\fontfamily{qcs}\selectfont{g}_{\rm DM}}M_{{Z}'}h_{D}{Z}'_{\mu}{Z}'^{\mu} $ ), and its coupling with quarks is ($ {\fontfamily{qcs}\selectfont{g}_{\rm SM}}\bar{q}\gamma^{\mu}q{Z}'^{\mu} $ ). The Feynman diagram of the process is shown in Fig. 1(a).
Figure 1. Feynman diagrams for the mono-Z
$ ^{\prime} $ simplified scenarios: Dark Higgs (a), light vector (b), and the EFT scenario (c) [17].There are two assumptions for setting masses in the DH scenario, which are illustrated for the light dark sector and the heavy dark sector in Table 1.
Scenario Mass assumptions Light dark sector $M_{h_{D}} =\begin{cases} M_{Z'}, & M_{Z'} < 125\;\text{GeV} \\ 125\;\text{GeV}, & M_{Z'} > 125\;\text{GeV} \end{cases}$ 

Heavy dark sector $M_{h_{D}} =\begin{cases} 125\;\text{GeV}, & M_{Z'} < 125\;\text{GeV} \\ M_{Z'}, & M_{h_{D}} > 125\;\text{GeV}. \end{cases}$ 

Table 1. Mass assumptions chosen in the light and heavy dark sector cases for the Dark Higgs scenario [17].
For the LV scenario, one of the dark particles is sufficiently heavier than Z
$ ^{\prime} $ , so that it can decay to Z$ ^{\prime} $ plus another light dark particle ($ \chi_{2}\rightarrow {Z'}\chi_{1} $ ), as shown in Fig. 1(b). The interaction term, in the Lagrangian, between the dark particles and Z$ ^{\prime} $ is given by$ \frac{{\fontfamily{qcs}\selectfont{g}_{\rm DM}}}{2} {Z}'_{\mu}\Big(\bar{\chi}_{2}\gamma^{\mu}\gamma^{5}\chi_{1}\; +\; \bar{\chi}_{1}\gamma^{\mu}\gamma^{5}\chi_{2}\Big), $

where
$ \chi_{1} $ is a final state dark sector stable particle. For the mass assumptions in the case of the LV scenario; the heavy dark particle ($ \chi_{2} $ ) should have a mass twice the mass of Z$ ^{\prime} $ , while the mass of the light dark particle ($ \chi_{1} $ ) is half of the mass of Z$ ^{\prime} $ .In the rest of this paper, the coupling of Z
$ ^{\prime} $ with SM fermions (quarks and leptons) will be referred to as$ {\fontfamily{qcs}\selectfont{g}_{\rm SM}} $ , and the coupling with DM particles will be denoted by$ {\fontfamily{qcs}\selectfont{g}_{\rm DM}} $ . The total decay widths of Z$ ^{\prime} $ and$ h_{D} $ (Z$ ^{\prime} $ and$ \chi_{2} $ ) in the DH (LV) cases are calculated using the mass values of Z$ ^{\prime} $ and the coupling constants, assuming that the Z$ ^{\prime} $ boson can only decay into a pair of muons and radiate an$ h_{D} $ boson in the DH scenario, and assuming that the decays$ {Z}'\rightarrow\chi_{1}\chi_{2} $ ,$ \chi_{2}\rightarrow {Z'}\chi_{1} $ and$ {Z}'\rightarrow\mu\tilde{\mu} $ are the only allowed ones for the LV scenario.In these scenarios, there are many free parameters, including mediator mass
$ M_{Z^{\prime}} $ , mass of the heavy dark particle$ M_{\chi_{2}} $ , mass of the light dark particle$ M_{\chi_{1}} $ , and coupling constants ($ {\fontfamily{qcs}\selectfont{g}_{\rm SM}} $ and$ {\fontfamily{qcs}\selectfont{g}_{\rm DM}} $ ). In this analysis, the values of couplings ($ {\fontfamily{qcs}\selectfont{g}_{\rm SM}} = 0.25 $ and$ {\fontfamily{qcs}\selectfont{g}_{\rm DM}} = 1.0 $ ) have been chosen based on the results presented in [17] and [22]. The cross section measurements times branching ratios for the two simplified models (DH and LV) for various masses of Z$ ^{\prime} $ are compared in Table 2, and were calculated using Madgraph [26] in the next-to-leading order (NLO).$ M_{{Z}'} $ / (GeV/c

$ ^{2} $ )

$ \sigma\; \times $ BR (pb) Dark Higgs

$ \sigma\; \times $ BR (pb) Light Vector

150 $ 7.086\; \; \times 10^{-2} $ 

$ 1.734\; \; \times 10^{-2} $ 

200 $ 2.366\; \; \times 10^{-2} $ 

$ 0.507\; \; \times 10^{-2} $ 

250 $ 9.555\; \; \times 10^{-3} $ 

$ 1.808\; \; \times 10^{-3} $ 

300 $ 4.368\; \; \times 10^{-3} $ 

$ 0.738\; \; \times 10^{-3} $ 

350 $ 2.100\; \; \times 10^{-3} $ 

$ 0.318\; \; \times 10^{-3} $ 

400 $ 1.040\; \; \times 10^{-3} $ 

$ 0.140\; \; \times 10^{-3} $ 

450 $ 0.569\; \; \times 10^{-3} $ 

$ 0.069\; \; \times 10^{-3} $ 

500 $ 3.283\; \; \times 10^{-4} $ 

$ 0.355\; \; \times 10^{-4} $ 

600 $ 1.191\; \; \times 10^{-4} $ 

$ 0.104\; \; \times 10^{-4} $ 

700 $ 4.725\; \; \times 10^{-5} $ 

$ 0.333\; \; \times 10^{-5} $ 

Table 2. Cross section measurements times branching ratios calculated for various masses of the Z
$ ^{\prime} $ boson with the heavy dark sector assumption for the two simplified models (DH and LV), with the coupling constants$ {\fontfamily{qcs}\selectfont{g}_{\rm SM}} = 0.25, $ $ {\fontfamily{qcs}\selectfont{g}_{\rm DM}} = 1.0 $ , at$ \sqrt{s} = 8 $ TeV.Finally, the EFT scenario reduces the interactions between the DM particles and the SM fields down to contact interaction, as given in the following interaction term
$ \frac{1}{2\Lambda^{2}}\bar{q}\gamma^{\mu}q\Big(\bar{\chi}_{2}\gamma^{\mu}\gamma^{5}\chi_{1}\; +\; \bar{\chi}_{1}\gamma^{\mu}\gamma^{5}\chi_{2}\Big). $

The Feynman diagram that illustrates this process is shown in Fig. 1(c). The assumptions for the masses are the same as those for the LV scenario. The production cross section measurements times branching ratios as a function of the scenario cutoff scale (
$ \Lambda $ ) are given in Table 3.$ \Lambda ({\rm{TeV}}) $ 

$ \sigma\; \times $ BR (pb)

1.0 0.0704 1.5 0.0139 2.0 0.0044 2.5 0.0018 3.0 0.00087 3.5 0.00047 4.0 0.000275 Table 3. EFT production cross section measurements times branching ratios as a function of the scenario cutoff scale of the EFT(
$ \Lambda $ ), for a fixed mass point of Z$ ^{\prime} $ ($ M_{Z^{\prime}} $ = 450 GeV) and center-of-mass energy$ \sqrt{s} = 8 $ TeVThe typical signature of these processes consists of a pair of opposite sign leptons or hadronic jets from the decay of Z
$ ^{\prime} $ plus a large missing transverse momentum resulting from the stable dark sector particles$ \chi $ and$ \chi_{1} $ . These two scenarios were previously studied by the ATLAS collaboration [22] with the hadronic decay of Z$ ^{\prime} $ . In our study, we have considered the heavy dark sector assumption mentioned in Table 1, in which the signal region is shifted away from the background region because of the larger missing energy assumed in this option, i.e., the signal is more distinguishable from the background for the heavy dark sector assumption compared with the light one. The muonic decay of the on-shell Z$ ^{\prime} $ is considered because the CMS detector has been optimized to this decay channel, so that our the events have the following topology:$\mu^{+}\mu^{-} +{\not\!\! E }_{T}$ .We studied one of the two simplified models, i.e., the DH scenario, as it has a higher cross section than the LV, in addition to the EFT scenario. The behavior of the cross sections times branching ratios with the mass of Z
$ ^{\prime} $ at$ \sqrt{s} $ = 8 and 13 TeV for the DH scenario is shown in Fig. 2. As expected, the cross section measurements times branching ratios decrease with an increase in the Z$ ^{\prime} $ mass. Moreover, we observe the increase in the cross section at higher$ \sqrt{s} $ (13 TeV), which is an advantage of the LHC run-II data with respect to run-I; in addition, the ratio between the cross sections in the two cases increases with the mass of Z$ ^{\prime} $ and reaches its maximum value (approximately 5 times) for the scanned range at$ M_{Z'} = 700 $ GeV, which indicates that the cross section decreases slower in the case of$ \sqrt{s} = $ 13 TeV.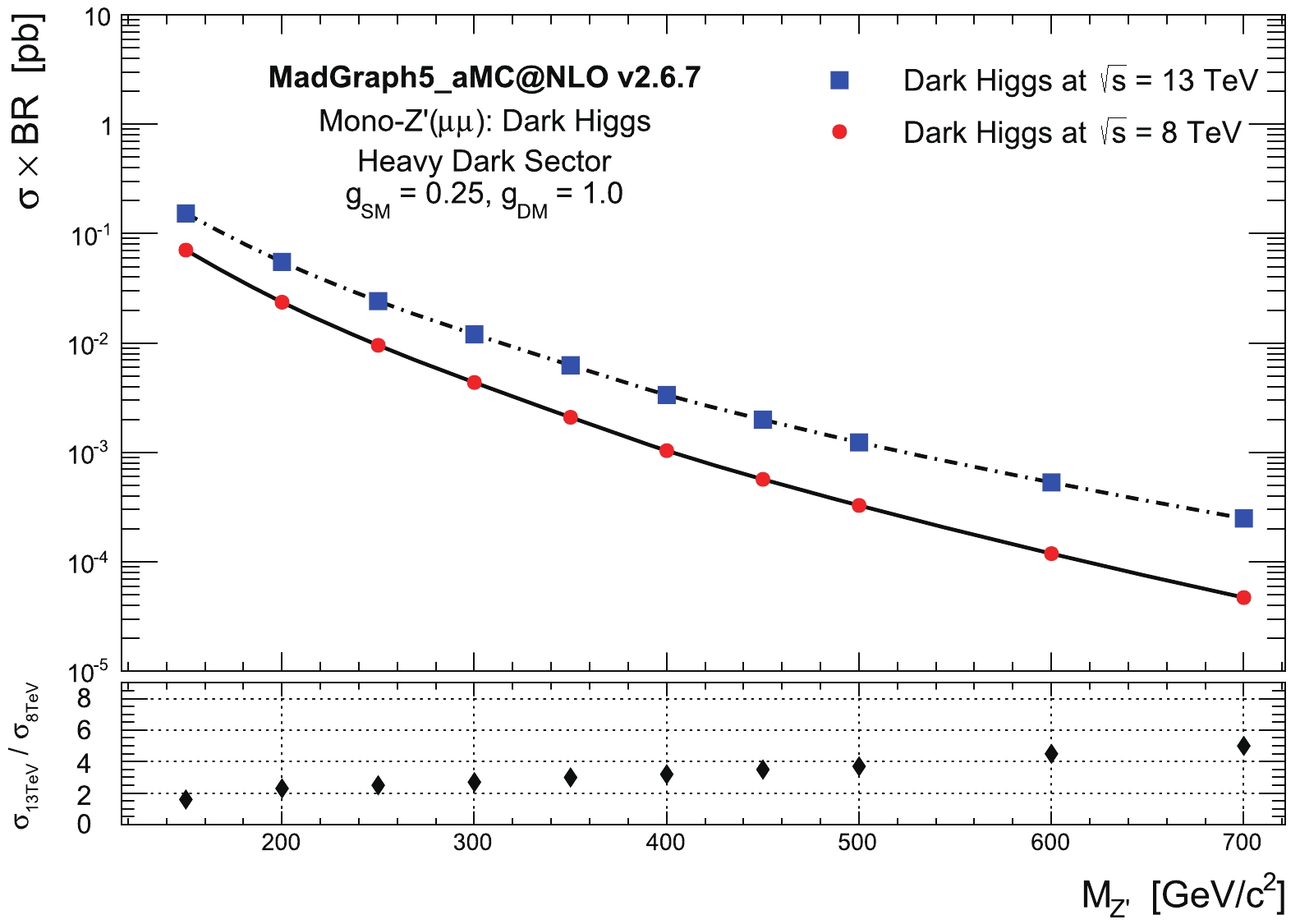
Figure 2. (color online) Behavior of the cross section measurements times branching ratios with the mass of
$ Z' $ boson for the Dark Higgs scenario at$ \sqrt{s} = 8 $ TeV, represented by red dots, and 13 TeV, represented by blue squares. The lower panel indicates the ratio of the cross sections between the two cases.Table 4 indicates the cross section measurements times branching ratios calculated for different sets of Z
$ ^{\prime} $ and$ \chi $ masses. The cross section is not sensitive to the change in the DM particle mass; for this reason, we work on the diagonal points to place a limit on this parameter, which will be discussed in the results.$M_{\chi}/{\text{GeV} }$ 

$M_{Z'} /{\text{GeV} }$ 

150 200 300 325 350 375 400 425 450 475 500 1 $7.10\times10^{-2}$ 

$2.36\times10^{-2}$ 

$0.438\times10^{-2}$ 

$0.305\times10^{-2}$ 

$0.2107\times10^{-2}$ 

$0.144\times10^{-2}$ 

$0.1036\times10^{-2}$ 

$0.764\times10^{-3}$ 

$0.568\times10^{-3}$ 

$0.428\times10^{-3}$ 

$0.328\times10^{-3}$ 

5 $ 7.08\times10^{-2} $ 

$ 2.37\times10^{-2} $ 

$ 0.437\times10^{-2} $ 

$ 0.306\times10^{-2} $ 

$ 0.210\times10^{-2} $ 

$ 0.144\times10^{-2} $ 

$ 0.104\times10^{-2} $ 

$ 0.763\times10^{-3} $ 

$ 0.569\times10^{-3} $ 

$ 0.427\times10^{-3} $ 

$ 0.3283\times10^{-3} $ 

10 $ 7.10\times10^{-2} $ 

$ 2.36\times10^{-2} $ 

$ 0.037\times10^{-2} $ 

$ 0.305\times10^{-2} $ 

$ 0.211\times10^{-2} $ 

$ 0.145\times10^{-2} $ 

$ 0.104\times10^{-2} $ 

$ 0.763\times10^{-3} $ 

$ 0.569\times10^{-3} $ 

$ 0.429\times10^{-3} $ 

$ 0.328\times10^{-3} $ 

25 $ 7.10\times10^{-2} $ 

$ 2.358\times10^{-2} $ 

$ 0.437\times10^{-2} $ 

$ 0.305\times10^{-2} $ 

$ 0.211\times10^{-2} $ 

$ 0.144\times10^{-2} $ 

$ 0.1035\times10^{-2} $ 

$ 0.763\times10^{-3} $ 

$ 0.568\times10^{-3} $ 

$ 0.429\times10^{-3} $ 

$ 0.329\times10^{-3} $ 

50 $ 7.13\times10^{-02} $ 

$ 2.36\times10^{-2} $ 

$ 0.437\times10^{-2} $ 

$ 0.306\times10^{-2} $ 

$ 0.210\times10^{-2} $ 

$ 0.144\times10^{-2} $ 

$ 0.1038\times10^{-2} $ 

$ 0.756\times10^{-3} $ 

$ 0.567\times10^{-3} $ 

$ 0.429\times10^{-3} $ 

$ 0.328\times10^{-3} $ 

75 $ 16.40\times10^{-2} $ 

$ 2.36\times10^{-2} $ 

$ 0.436\times10^{-2} $ 

$ 0.305\times10^{-2} $ 

$ 0.209\times10^{-2} $ 

$ 0.144\times10^{-2} $ 

$ 0.104\times10^{-2} $ 

$ 0.763\times10^{-3} $ 

$ 0.568\times10^{-3} $ 

$ 0.429\times10^{-3} $ 

$ 0.328\times10^{-3} $ 

100 $ 8.98 \times10^{-7} $ 

$ 5.43\times10^{-2} $ 

$ 0.436\times10^{-2} $ 

$ 0.3052\times10^{-2} $ 

$ 0.211\times10^{-02} $ 

$ 0.144\times10^{-2} $ 

$ 0.1039\times10^{-2} $ 

$ 0.764\times10^{-3} $ 

$ 0.568\times10^{-03} $ 

$ 0.428\times10^{-3} $ 

$ 0.326\times10^{-3} $ 

125 $ 1.54\times10^{-7} $ 

$ 5.01\times 10^{-7} $ 

$ 0.437\times10^{-2} $ 

$ 0.3049\times10^{-2} $ 

$ 0.209\times10^{-2} $ 

$ 0.144\times10^{-2} $ 

$ 0.104\times10^{-2} $ 

$ 0.758\times10^{-2} $ 

$ 0.567\times10^{-3} $ 

$ 0.429\times10^{-3} $ 

$ 0.327\times10^{-3} $ 

150 $ 4.09 \times10^{-8} $ 

$ 1.0 \times10^{-7} $ 

$ 1.00\times10^{-2} $ 

$ 0.3047\times10^{-2} $ 

$ 0.2094\times10^{-2} $ 

$ 0.144\times10^{-2} $ 

$ 0.1037\times10^{-2} $ 

$ 0.758\times10^{-3} $ 

$ 0.567\times10^{-3} $ 

$ 0.427\times10^{-3} $ 

$ 0.326\times10^{-3} $ 

175 $ 1.3\times10^{-8} $ 

$ 3.05\times10^{-8} $ 

$ 1.753 \times10^{-7} $ 

$ 3.766 \times10^{-7} $ 

$ 0.48\times10^{-2} $ 

$ 0.1436\times10^{-2} $ 

$ 0.1035\times10^{-2} $ 

$ 0.756\times10^{-3} $ 

$ 0.556\times10^{-3} $ 

$ 0.427\times10^{-3} $ 

$ 0.326\times10^{-3} $ 

200 $ 5.25 \times10^{-9} $ 

$ 1.0 \times10^{-8} $ 

$ 4.36 \times10^{-8} $ 

$ 6.56 \times10^{-8} $ 

$ 1.04 \times10^{-7} $ 

$ 2.08 \times10^{-7} $ 

$ 0.239\times10^{-2} $ 

$ 0.76\times10^{-3} $ 

$ 0.566\times10^{-3} $ 

$ 0.427\times10^{-3} $ 

$ 0.325\times10^{-3} $ 

Table 4. Dark Higgs cross section measurements times branching ratios (pb) calculated for different sets of masses
$ M_{\chi} $ and$ M_{Z'} $ in GeV for the heavy dark sector mass assumption, with the following couplings constants$ g_{\rm SM} = 0.25,\; g_{\rm DM} = 1.0 $ , and$ \sqrt{s} = 8 $ TeV. -
The CMS detector (described in detail in references [27, 28]) is one of the four main apparata that have been built on the LHC at CERN. The 3-m-long and 5.9-m-inner diameter superconducting conducting solenoid provides a 3.8-T magnetic field that delivers the bending power required to measure the momenta of the high energy charged particles. The solenoid accommodates the tracking system (pixel detector and silicon tracker) and two calorimeters: the Electromagnetic Calorimeter (ECAL), which has been designed to detect and measure electrons and photons, and the Hadronic Calorimeter (HCAL), used to detect and measure hadronic particles. The muon system includes the above layers, and the muon stations consist of many Drift Tube (DT) layers in the barrel part and Cathode Strip Champers (CSCs) in the endcape region. The two parts are completed by the Resistive Plate Champers (RPCs).
The interaction point is considered to be the origin of the CMS coordinate system. The x-axis points toward the center of the LHC, the y-axis points upward, and the z-axis is alongside the beam axis. The polar angle
$ \theta $ is measured from the positive direction of the x-axis, and the azimuthal angle$ \phi $ is measured from the x-y transverse plan. However, the directions of the particle yield from the collision spot are mostly expressed in terms of the pseudorapidity, defined as$ \eta = - \text{ln}[\text{tan}(\theta/2)] $ . For our purpose, we mention the reconstruction of muons and the missing transverse momentum. The muon object is identified and reconstructed from a global fit between the muon system and the inner tracker; hence, it is referred to as global muons [29, 30]. The missing transverse momentum reconstruction is based on the Particle Flow algorithm described in references [28, 31]; it is reconstructed as an imbalance in the vector sum of momenta in the transverse plan, i.e., it could be defined as the negative vector sum of the momenta of all particle flow reconstructed objects as$ \vec{{\not\!\! p }}_{T} = -\sum \vec{p}_{T}^{\; pf} $ [32]. The magnitude of$ \vec{{\not \!\!p }}_{T} $ can be affected by many factors, which can cause underestimation or overestimation of its true value. These factors are basically related to the calorimeter response, as minimum energy and$ p_{T} $ thresholds in the calorimeters, inefficiencies in the tracker, and non-linearity of the response of the calorimeter for hadronic particles. This bias can be effectively reduced by correcting for the$ p_{T} $ of the jets using jet energy corrections, as defined in the following equation, which is given in [32]$ \vec{{\not\!\! p }}_{T}^{\; \text{corr}} = \vec{{\not\!\! p }}_{T} - \sum\limits_{\rm jets} \Big(\vec{p}_{T {\rm jet}}^{\; \text{corr}} - \vec{p}_{T {\rm jet}}\Big), $

where "corr" refers to the corrected values. Thus, variables of particular relevance to the present analysis are the corrected missing transverse momentum vector
$ \vec{{\not\!\! p }}_{T}^{\; \text{corr}} $ and the magnitude of this quantity,$ {{\not\!\! p }}_{T}^{\; \text{corr}} $ . -
The model signal events were generated using MadGraph5_aMC@NLO v2.6.7 [26], which is a general purpose matrix element event generator. The cross section calculated at next to-leading-order (NLO) and the hadronizaton process were simulated with Pythia [33]. The detector simulation, simulation of read out system response (digitization), and reconstruction processes were performed using the standard CMS open data software framework (release CMSSW_5_3_32) at
$ \sqrt{s} = $ 8 TeV requirements, with the suitable triggers list used for CMS-2012 analysis. We scanned the DH production cross section at different sets of masses of the particles Z$ ^{\prime} $ and$ {\chi} $ as free parameters covering a wide range for the mass of the Z$ ^{\prime} $ boson, from 150 to 550 GeV, and from 1 to 200 GeV for the mass of$ {\chi} $ ; the production cross section of the EFT was at the range of$ \Lambda $ from 1.0 to 4 TeV, assuming$ \fontfamily{qcs}\selectfont{g}_{\rm SM} = 0.25 $ and$ \fontfamily{qcs}\selectfont{g}_{\rm DM} = 1.0 $ for all simulations. -
To simulate the SM processes that have muons and/or missing energy (because of undetected neutrinos) at the final state that could interface with our signal events, we used the CMS open Monte Carlo samples at
$ \sqrt{s} $ = 8 TeV as background processes [24]. The Drell-Yan (DY) background (the production of a virtual$ Z/\gamma^{*} $ that decays into a muon pair), which is the dominant background, was generated using Powheg [34]. Another important source of SM background with dimuons in the final state is the fully leptonic decay of$ t\bar{t} $ , which was generated using MadGraph [26]. The production of electroweak diboson channels as WW, WZ were generated with MadGraph, and the$ ZZ \rightarrow \mu^{-}\mu^{+}\mu^{-}\mu^{+} $ process was also generated with Powheg. The generation processes for the mentioned samples were interfaced with Pythia v6.4.26 [33] for modeling of the parton shower. The Monte Carlo samples used in this analysis and their corresponding cross sections, calculated at next-to-leading or next-to-next-to-leading order, are indicated in Table 5.Process Generator Data set name $ {\Large \sigma} \times\; \text{BR} $ /pb

Order $ DY \rightarrow \mu\bar{\mu} $ 

Powheg DYToMuMu_M-20_CT10_TuneZ2star_v2_8TeV. [36] 1916 NNLO $ t\bar{t} $ + jets

Madgraph TTJets_FullLeptMGDecays_8TeV. [37] 23.89 NLO WW + jets Madgraph WWJetsTo2L2Nu_TuneZ2star_8TeV. [38] 5.8 NLO WZ + jets Madgraph WZJetsTo3LNu_8TeV_TuneZ2Star. [39] 1.1 NNLO $ ZZ\rightarrow 4\mu $ 

Powheg ZZTo4mu_8TeV. [40] 0.077 NLO Table 5. CMS open MC samples used to simulate the SM background for pp collision at
$ \sqrt{s} = 8 $ TeV, their corresponding cross section times branching ratio for each process, and the order of calculations. The data set names and the used generators are provided. -
There are three main types of SM backgrounds for new physics searches in the dimuon channel. The most significant is the irreducible SM Drell-Yan process. New physics can interfere with this process, and if not mitigated, the effects can be significant. The second most important background type comes from muons from non-singularly produced W and Z bosons. The dominant source of these muons are from
$ t\bar{t} $ events, although WW events become increasingly important at high mass, as the boost of the top quark means that the b-jet enters the muon isolation cone and the muon fails isolation requirements. Other sources include WZ and ZZ events, although they are small compared with$ t\bar{t} $ and WW. This background is referred to as$ t\bar{t} $ and$ t\bar{t} $ -like background, as it is dominated by$ t\bar{t} $ . The third background is the jets background, where one or more jets are misidentified and incorrectly reconstructed as a muon, primarily arising from te W+jet and QCD multijet. The contamination of the jets background is usually estimated from data using a so called data driven method, explained in [35], which is irrelevant for our study because our analysis is based mostly on MC simulations. In this analysis, the DY background and other backgrounds from muons arising from non-singularly produced W and Z bosons are estimated directly from Monte Carlo simulation as in other, similar 8 TeV analyses [35]. The leptonic decays of$ t\bar{t} $ , WW, and WZ are generated using Madgraph, while ZZ is generated using POWHEG. The Monte Carlo samples and their cross sections are documented in Table 5, where they are normalized to their respective NLO or NNLO cross sections. Another source of background to this analysis is the cosmic muon contribution, which is suppressed by constraining the vertex position, as discussed in section VI-A, and by constraining the impact parameter of the muons relative to the vertex position, as in the high$ P_{T} $ muon identification [41, 42]; this contribution is also negligible. -
The preselection criteria are based on the high
$ p_{T} $ muon identification [41, 42], which was applied in the 2012 analysis for the search for heavy resonances in the dilepton channel [35]; in addition, the off-line muon reconstructed transverse momentum$ (p^{\mu}_{T}) $ is selected to be higher than 45 GeV so that it is fully efficient for the trigger used (HLT_Mu40_eta2p1), and the detector acceptance is restricted to the range$ |\eta^{\mu}| < 2.1 $ of the reconstructed pseudorapidity. The preselection criteria are indicated in Table 6, in which muon candidates must be reconstructed as "global" muons, i.e., standalone muon objects reconstructed in the muon system must match with an inner tracker’s track to form the global muon object used later for our analysis. The muon candidates should be isolated; thus, they have to pass a cut based on the relative tracker isolation, which is the scalar sum of the$ p_{T} $ of all other tracks within a cone of$ \Delta R = \sqrt{(\Delta\eta)^2 + (\Delta\phi)^2} < $ $ 0.3 $ around and not containing the muon’s tracker track, and this sum must be less than 10% of the muon’s transverse momentum ($ p_{T} $ ). Tracks used in the tracker isolation calculation have to originate within$ \Delta Z = 0.2 $ cm of the primary vertex, with which the muon candidate is associated [35].Table 6. Preselection selection criteria based on single muon trigger requirement (HLT_Mu40_eta2p1), muon kinematic cuts, and the high
$ P_{T} $ muon IDThe muon’s transverse impact parameter with respect to the primary vertex, as measured by the tracker-only fit, must be smaller than 0.2 cm, which is a powerful cut to reject the cosmic muons that pass at the empty time between two bunch-crossings. Another cut is provided to reject cosmic muons that pass near the interaction point in-time with a bunch-crossing, as the 3D angle between the muon pairs is selected to be less than
$ \pi - 0.02 $ rad [35]. Extra qualification cuts are applied such that the muon pairs must have two opposite-signs and the$ \chi^{2}/dof $ for the common vertex fitting is less than 10 [35], where$ \chi $ is a state vector that describe the particle's track at each point of its trajectory. This method, based on the minimization of$ \chi^{2}/dof $ using the Kalman filter technique described in references [43, 44], is implemented in the CMSSW, and this fitting is important for correct pairing of muons that originate from the same vertex and for rejection of pile-up muons. Thus, the events are selected with two opposite charge high$ p_{T} $ muons, with one of them passing the single muon trigger HLT_Mu40_eta2p1.Figure 3 illustrates the distribution of the dimuon invariant mass; the green histogram represents the Drell-Yan background, the blue histogram stands for the vector boson pair backgrounds (WW, WZ, and ZZ), and the
$ t\bar{t} $ + jets background is represented by the gray histogram. These background histograms are stacked, while the signal models with various masses of the Z$ ^{\prime} $ heavy boson are represented by different colored lines and are overlaid. The corresponding distribution of the missing transverse momentum is shown in Fig. 4. As the signal models are overwhelmed by the backgrounds, it is necessary to apply a more clever set of cuts to discriminate signals from SM backgrounds, as explained in the next section.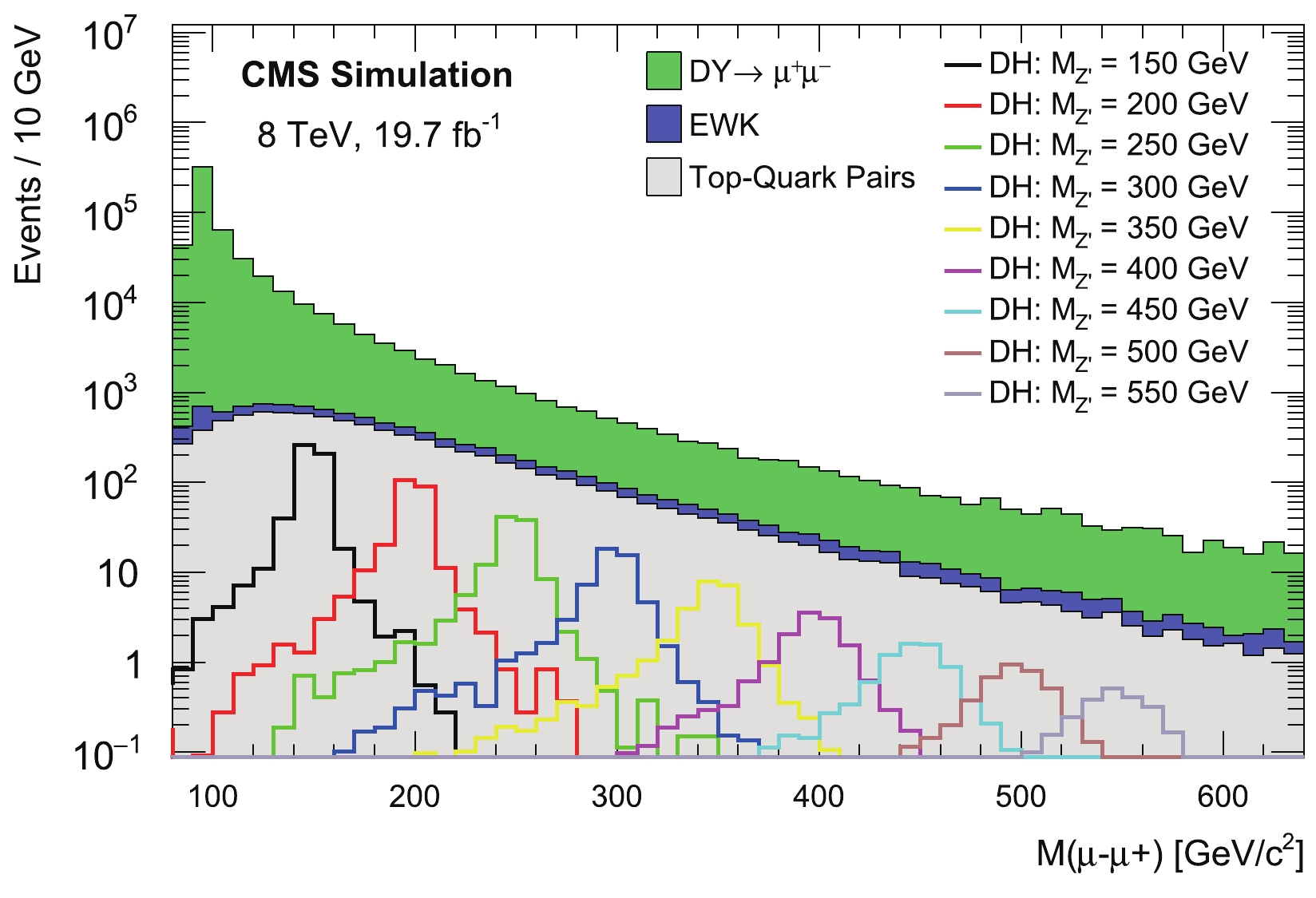
Figure 3. (color online) Measured dimuon invariant mass spectrum, after applying preselection cuts listed in Table 6, together with the estimated SM backgrounds and Z
$ ^{\prime} $ masses produced according to the Dark Higgs model.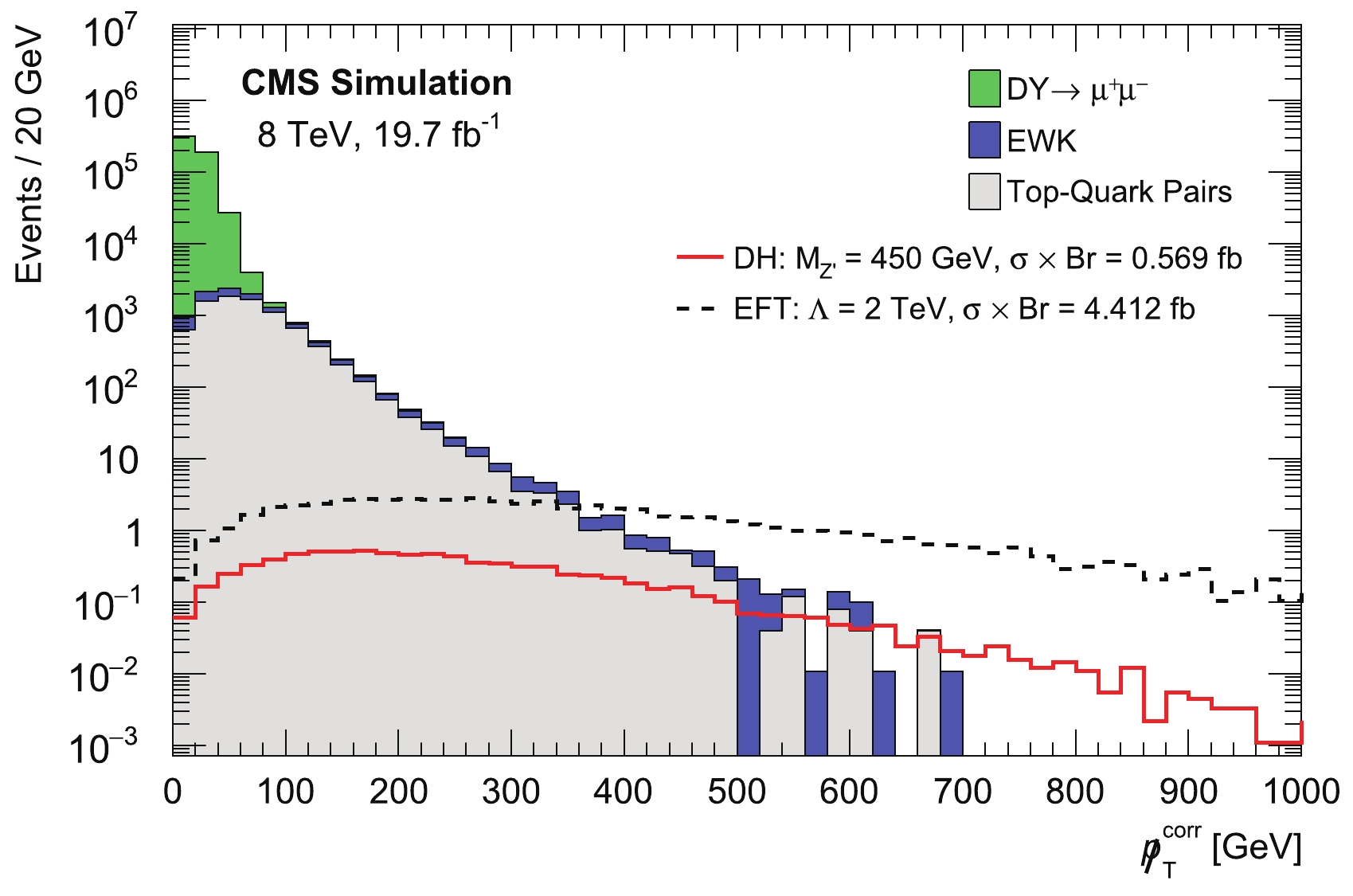
Figure 4. (color online) Missing transverse momentum distribution, after the preselection cuts listed in Table 6; the colored stacked histograms refer to the MC simulation of the SM backgrounds, where two signals representing the model corresponding to the DH scenario with
$ M_{Z^{\prime}} = 450 $ GeV and to the EFT scenario with$ \Lambda = 2 $ TeV are superimposed. The signals are normalized to the product of cross section times the Z$ ^{\prime} \rightarrow \mu^{+}\mu^{-} $ branching ratio.The number of dimuon events passing the preselection for each SM background processes and for the model signals are quoted in Table 7 for an integrated luminosity of 19.7 fb
$ ^{-1} $ . Uncertainties include both statistical and systematic components, summed in quadrature.process No. of events $ DY \rightarrow \mu^{+} \mu^{-} $ 

$ 533515\; \pm\; 127708 $ 

$ t\bar{t} + $ jets

$ 8363\; \pm\; 2004 $ 

WW + jets $ 1506\; \pm\; 362.7 $ 

WZ + jets $ 608\; \pm\; 147.8 $ 

ZZ $ \rightarrow 4\mu $ 

$ 58\; \pm\; 15.9 $ 

Sum Bkgs $ 544050\; \pm\; 130230 $ 

DH Signal (at $ M_{Z^{\prime}} $ = 450 GeV)

$ 8.2\; \pm\; 3.5 $ 

EFT Signal (at $ \Lambda $ = 2 TeV)

$ 64.2\; \pm\; 17.3 $ 

Table 7. Number of dimuon events passing the preselection for each SM background processes, the DH model, and the EFT model, corresponding to an integrated luminosity of 19.7 fb
$ ^{-1} $ . Uncertainties include both statistical and systematic components, summed in quadrature. -
After applying the preselection set of cuts, at which each event must have exactly two oppositely charged muons with
$ p^{\mu}_{T} > $ 45 GeV,$ \eta^{\mu} < $ 2.1 each and one of these two muons should pass the single muon trigger (HLT_Mu40_eta2p1), the extra tighter selection has been optimized for DM signals to distinguish them from the SM background and to obtain the best expected limit. The final selection is based on three variables: (1) the mass of the dilepton system (M$ _{\mu^{+}\mu^{-}} $ ) is required to be within$ (0.9 \times M_{Z^{\prime}}) < M_{\mu^{+}\mu^{-}} < (M_{Z^{\prime}} + 25) $ to be consistent with leptons from the heavy Z$ ^{\prime} $ boson decay; (2) the azimuthal angle difference between the dimuon system and the missing transverse energy$ \Delta\phi_{\mu^{+}\mu^{-},\vec{{\not p }}_{T}^{\text{corr}}} $ ; and (3) the relative difference between the dimuon system transverse momentum and the missing transverse momentum$ |p_{T}^{\mu^{+}\mu^{-}} - {\not p }_{T}^{\text{corr}}|/p_{T}^{\mu^{+}\mu^{-}} $ . Here,$ p_{T}^{\mu^{+}\mu^{-}} $ is the dimuon transverse momentum, and$ \Delta\phi_{\mu^{+}\mu^{-},\vec{{\not\!\! p }}_{T}^{\text{corr}}} $ is defined as the difference in the azimuth angle between the dimuon system direction and missing transverse momentum direction (i.e.,$ \Delta\phi_{\mu^{+}\mu^{-},\vec{{\not p }}_{T}^{\text{corr}}} = |\phi^{\mu^{+}\mu^{-}}-\; \phi^{\rm miss}| $ ), as indicated in Table 8.variable requirements Preselection Trigger HLT_Mu40_eta2p1 High $ p_{T} $ muon ID

[41, 42] $ p^{\mu}_{T} $ (GeV)

> 45 $ \eta^{\mu} $ (rad)

< 2.1 $ M_{\mu^{+}\mu^{-}} $ /GeV

> 50 Tight selection Mass window /GeV $ (0.9 \times M_{Z^{\prime}}) < M_{\mu^{+}\mu^{-}} < (M_{Z^{\prime}} + 25) $ 

$ |p_{T}^{\mu^{+}\mu^{-}} - {\not p }_{T}^{\text{corr}}|/p_{T}^{\mu^{+}\mu^{-}} $ 

< 0.6 $ \Delta\phi_{\mu^{+}\mu^{-},\vec{{\not p }}_{T}^{\text{corr}}} $ (rad)

> 2.6 Table 8. Summary of cut-based final event selection for analysis.
-
The selection efficiency is defined as the ratio between the number of events after applying the cut-based final event selection summarized in Table 8 and the number of events after the application of the preselection cuts, as defined in Table 6. These efficiencies are calculated for both the Dark Higgs scenario (with
$ M_{Z^{\prime}} = 450 $ GeV) simulated sample and SM background sources, while the error bars are statistical only. The selection efficiencies are listed by percentage in Table 9 and shown in Fig. 5. The cut-based final event selection criteria described above are designed to reduce background events with minimal possible effects on the signal events.signal/background efficiency (%) DH signal 67.0 $DY \rightarrow \mu^{+} \mu^{-}$ 

0.0196 $t\bar{t} +$ jets

0.24 WW + jets 0.84 WZ + jets 0.20 $ZZ \rightarrow 4\mu$ 

0.366 Table 9. Overall efficiencies of the full selection, summarized in Table 8, for the Dark Higgs scenario signal calculated at
$M_{Z'}=450$ GeV and the SM backgrounds.
Figure 5. (color online) Efficiency presented as a function of
$ {{\not \!\!p }}_{T}^{\; \text{corr}} $ for the full selection of the analysis summarized in Table 8; for the SM background, represented by solid dots with different corresponding colors, and the DH model signal, shown by hollow red dots.After applying the full selection listed in Table 8, most of the backgrounds events are strongly suppressed to less than a percent for each of the SM backgrounds, while we lose only approximately 34% of the Dark Higgs signal events. Nevertheless, in the signal region (
$ {\not\!\! p }_{T}^{\text{corr}} > 200 $ GeV), the efficiency of the DH signal is approximately 80%, which demonstrates the success of this selection criteria. -
Several sources of experimental and theoretical systematic uncertainties contribute to this analysis and affect the results. We start with the experimental systematic uncertainties; the uncertainty related to the luminosity of the CMS-2012 data is estimated to be 2.6% [45]. The uncertainty that arises from the determination of the muon detector acceptance and from the muon reconstruction efficiency (
$ A\times\epsilon $ ) has been found to be 3% [35]. The transverse muon momentum resolution uncertainty was 5%, while the misalignment in the detector geometry has an impact of 5% on the transverse momentum scale uncertainty per TeV [35]. Regarding the systematic uncertainties associated with the measurements of missing transverse momentum$ {{\not \!\!p }}_{T}^{\; \text{corr}} $ , the uncertainty in the energy scale of low energy particles, which is known as unclustered energy, was found to be 10%, while the uncertainties were 2%-10% for the jet energy scale and 6%-15% for the jet energy resolution [32]. Finally, the theoretical sources of the systematic errors are related to the uncertainties in the parton distribution function (PDF) choice. For the Drell-Yan cross section calculation, this uncertainty can be represented as a function of the invariant mass of the dimuon as$ (2.67+3.03\times $ $ 10^{-3}M_{\mu^{+}\mu^{-}}+ $ $ 2.38\times10^{-6}M_{\mu^{+}\mu^{-}}^{2}) \% $ (in GeV) [35], while PDF uncertainties for the WW and WZ processes were 5% and 6%, respectively [13].A summary of these sources of uncertainties and the corresponding values are indicated in Table 10.
Source Uncertainty (%) Luminosity ( $ {\cal{L}} $ )

2.6 [45] $ A\times\epsilon $ 

3 [35] $ P_{T} $ resolution

5 [35] $ P_{T} $ scale

5 [35] $ {\rm{Unclustered }}\;{{\not\!\! p }}_{T}^{\; \text{corr}}\;{\rm{ scale}} $ 

10 [32] Jet energy scale 2-10 [32] Jet energy resolution 6-15 [32] PDF (Drell-Yan) 4.5 [35] PDF (ZZ) 5 [13] PDF (WZ) 6 [13] Table 10. Various sources of systematic uncertainties and their corresponding estimated values.
-
For the dimuon channel, a shape-based analysis is employed. The missing transverse momentum distributions (
$ {{\not \!\!p }}_{T}^{\; \text{corr}} $ ) act as a good discriminant variable because the signal processes results in relatively larger$ {{\not \!\!p }}_{T}^{\; \text{corr}} $ values than those of the SM backgrounds.The missing transverse momentum distribution, after the final event selection, is shown in Fig. 6, which shows a significant decrease in SM background processes with the use of the final selection summarized in Table 8. The number of dimuon events passing the final selection (summarized in VIII) for each of the SM background processes, the DH model (with
$ M_{Z^{\prime}} $ = 450 GeV) and EFT model (with$ \Lambda = 2 $ TeV) corresponding to an integrated luminosity of 19.7 fb$ ^{-1} $ are shown in Table 11. Uncertainties include both statistical and systematic components, summed in quadrature.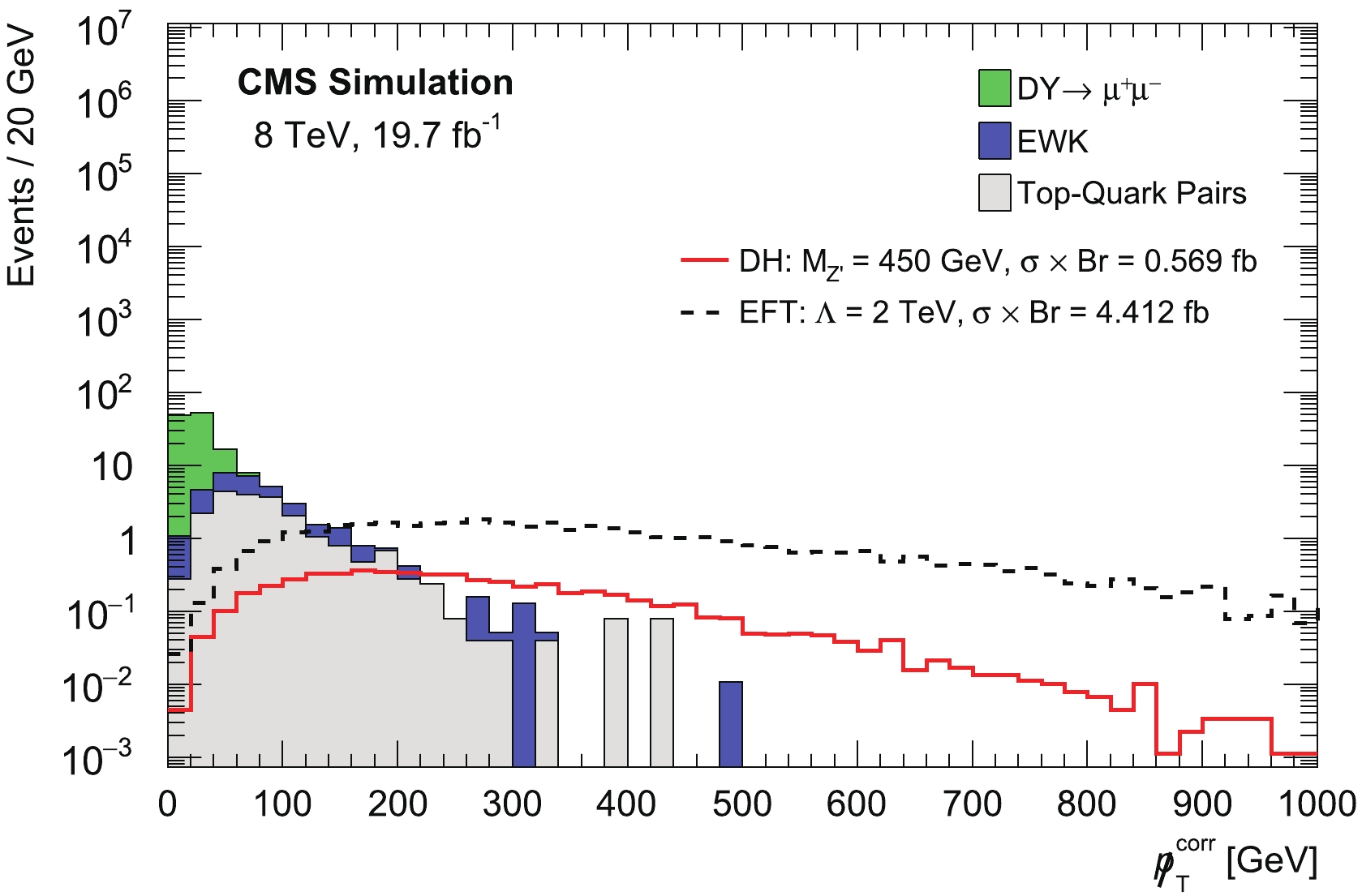
Figure 6. (color online) Distribution of the missing transverse momentum, after the final selection cuts listed in Table 8, for the SM background predictions, where the signals of the model corresponding to the DH scenario with
$ M_{Z^{\prime}} = 450 $ GeV, and the EFT scenario with cutoff scale$ \Lambda = 2 $ TeV are superimposed. The signals are normalized to the product of cross section times the Z$ ^{\prime} \rightarrow \mu^{+}\mu^{-} $ branching ratio.process no. of events $ DY \rightarrow \mu^{+} \mu^{-} $ 

$ 104.8\; \pm\; 27.1 $ 

$ t\bar{t} + jets $ 

$ 20.3\; \pm\; 6.6 $ 

$ WW + jets $ 

$ 12.7\; \pm\; 4.7 $ 

$ WZ + jets $ 

$ 1.2\; \pm\; 1.2 $ 

$ ZZ \rightarrow 4\mu $ 

$ 0.2\; \pm\; 0.5 $ 

Sum Bkgs $ 139.1\; \pm\; 35.3 $ 

Dark Higgs (at $ M_{Z^{\prime}} $ = 450 GeV)

$ 5.5\; \pm\; 2.7 $ 

EFT (at $ M_{Z^{\prime}} $ = 450 GeV)

$ 39.2\; \pm\; 11.3 $ 

Table 11. Number of dimuon events passing the analysis final selection (summarized in Table 8) for each SM background, the DH model, and the EFT model, corresponding to an integrated luminosity of 19.7 fb
$ ^{-1} $ . Uncertainties include both statistical and systematic components, summed in quadrature. -
For a statistical interpretation of our results, we use the asymptotic approximation of the distribution of the profile likelihood-based statistical test, described in detail in [46]. This approach was used to investigate the possibility of the rejection of the null hypothesis (the SM background only hypothesis) in favor of the signal hypothesis (the Dark Higgs scenario hypothesis) and used to construct the confidence intervals within 1 or 2 standard deviations, corresponding to 68% or 95% Confidence Levels (CLs). The likelihood function used to fit the data is defined as
$ {\cal{L}}(\mu,\theta) = \prod\limits_{i = 1}^{M} \frac{{(\mu s_{i} + b_{i})}^{n_{i}} \; {\rm e}^{-(\mu s_{i} + b_{i})} } {n_{i}\; !}\prod\limits_{j = 1}^{k} \frac{ u_{j}^{m_{j}} \; {\rm e}^{-u_{j}} } {m_{j}\; !}, $

where
$ \mu $ is the signal strength and defined as the ratio between the signal yield and those of the prediction from simulation, which is the parameter of interest (POI) in this analysis, and$ \theta $ represents the other nuisance parameters with an impact included in the equation on the second$ \Pi $ -product.$ s_i $ and$ b_i $ are the number of signal and background events, respectively, as estimated from MC simulation per each bin. Finally,$ u_{j} $ is a function of$ \theta $ that gives the expectation value for each bin in the control sample used to constrain the nuisance parameters. It is a shape analysis based on the missing transverse momentum distributions. -
We construct the confidence intervals for the signal strengths as a function of the mass of the new
$ Z^{\prime} $ boson ($ M_{Z^{\prime}} $ ), shown in Fig. 7, and with the mass of the stable dark sector particle$ M_{\chi} $ shown in Fig. 8 for the DH simplified scenario; the confidence intervals for the signal strengths as a function of$ \Lambda $ for the EFT approach are presented in Fig. 9. We exclude$ Z^{\prime} $ production in the mass range between 470 - 550 GeV from the expected median, as illustrated in Fig. 7. We also exclude DM particle ($ \chi $ ) production in the mass range between 170 - 200 GeV from the expected median, as shown in Fig. 8. For the EFT scenario, the range between 3670 - 3790 GeV is excluded for the model cutoff scale of the EFT($ \Lambda $ ), as shown in Fig. 9. These exclusion limits are estimated at 95% CL.
Figure 7. (color online) Limit at 95% CL of the expected
$ \sigma / \sigma_{\text{theory}} $ for the Dark Higgs scenario for the Z$ ^{\prime} $ dimuon decay of the Mono-Z$ ^{\prime} $ model. Distribution is shown as a function of$ M_{Z'} $ for the heavy dark sector mass assumption shown in Table 1. The inner and outer shaded bands show the 68% and 95% CL uncertainties in the expected limits, respectively. The horizontal red line refers to$ \sigma / \sigma_{\text{theory}} $ = 1. The vertical blue dashed line points to the intersection of expectation with the case where$ \sigma = \sigma_{\text{theory}}. $ 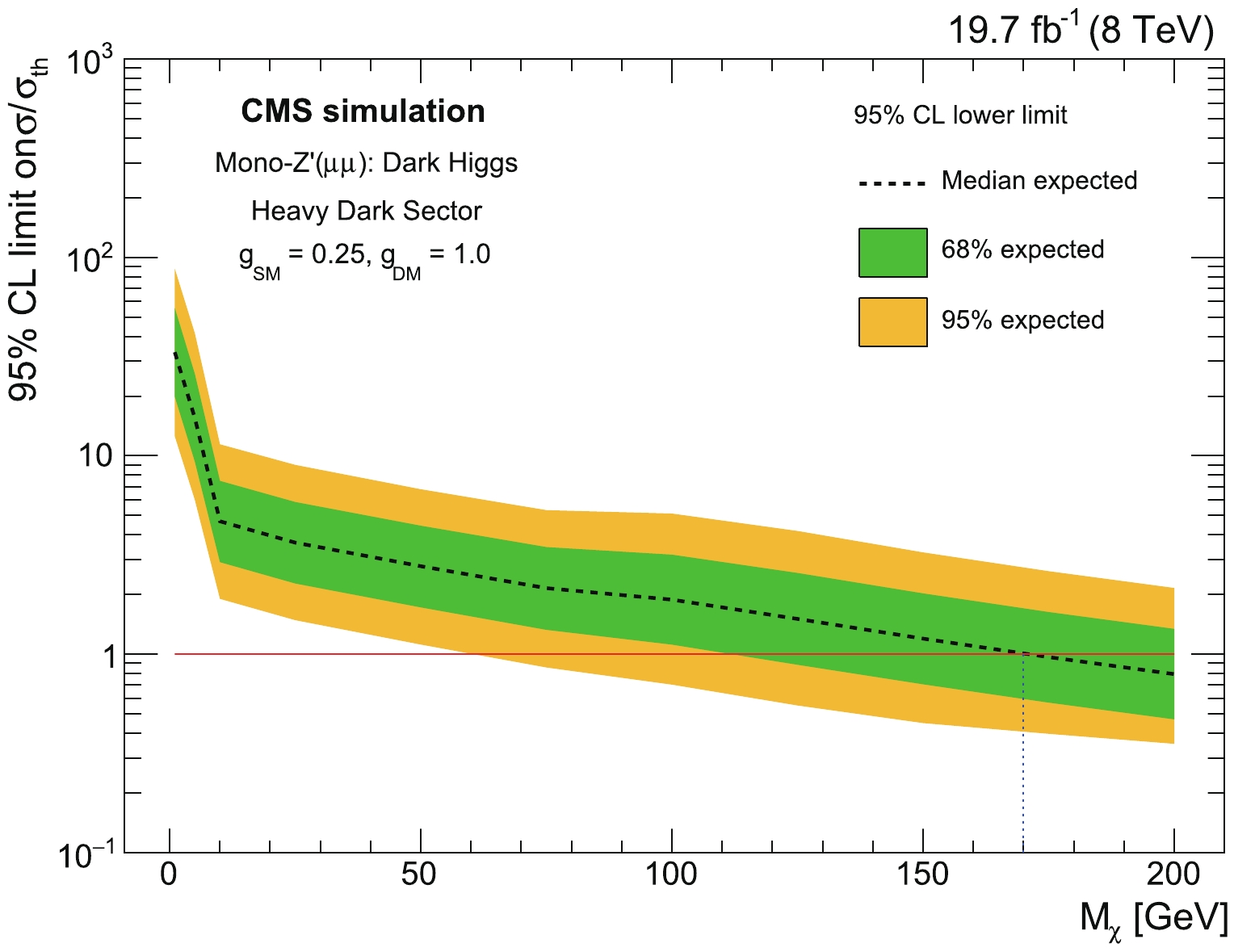
Figure 8. (color online) Limit at 95% CL of the expected
$ \sigma/\sigma_{\text{theory}} $ for the Dark Higgs scenario for the Z$ ^{\prime} $ dimuon decay of the Mono-$ {Z'} $ model. Distribution is shown as a function of$ M_{\chi} $ for various values of the Z$ ^{\prime} $ mass. The inner and outer shaded bands show the 68% and 95% CL uncertainties in the expected limits, respectively. The horizontal red line refers to$ \sigma / \sigma_{\text{theory}} $ = 1. The vertical blue dashed line points to the intersection of expectation with the case where$ \sigma = \sigma_{\text{theory}}. $ 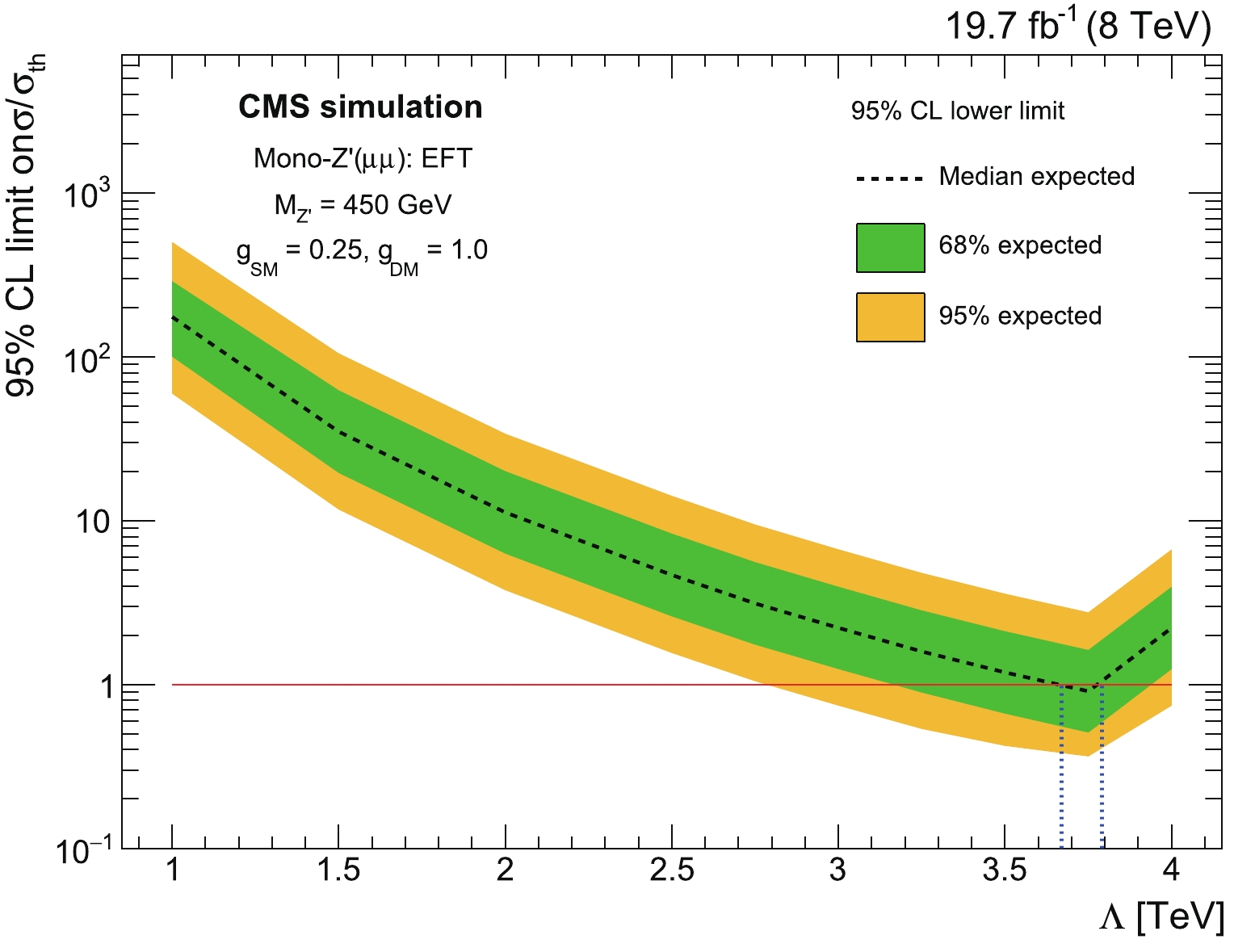
Figure 9. (color online) Limit at 95% CL of the expected
$ \sigma/\sigma_{\text{theory}} $ for the EFT scenario for the Z$ ^{\prime} $ dimuon decay of the Mono-$ {Z'} $ model. Distribution is shown as a function of the EFT cutoff scale ($ \Lambda $ ). The inner and outer shaded bands show the 68% and 95% CL uncertainties in the expected limits, respectively. The horizontal red line refers to$ \sigma / \sigma_{\text{theory}} $ = 1. The vertical blue dashed lines point to the intersection of expectation with the case where$ \sigma = \sigma_{\text{theory}}. $ -
A search for dark matter particles produced in association with the heavy gauge boson Z
$ ^{\prime} $ has been performed. In this search, we used MC samples taken from the open simulated files produced by the CMS collaboration for proton-proton collisions at$ \sqrt{s} = $ 8 TeV, and the analysis was optimized for the full LHC run-I integrated luminosity (19.7 fb$ ^{-1} $ ). Results from the muonic decay mode of Z$ ^{\prime} $ are presented, along with the statistical and systematic uncertainties. One benchmark signal corresponding to the Dark Higgs scenario was used, with different choices of the mediator (Z$ ^{\prime} $ ) mass points. The 95% CL limits on the expected$ \sigma/\sigma_{\text{theory}} $ of dark matter in a Dark Higgs scenario extended by a Z$ ^{\prime} $ boson are set. These limits constitute the most stringent limits on the parameters ($ M_{Z^{\prime}} $ and$ M_{\chi} $ ) in this model. For the mass of$ {Z'} $ ($ M_{Z^{\prime}} $ ), the ranges between 470 - 550 GeV from the expected median have been excluded, while excluding the ranges between 170 - 200 GeV from the expected median for the mass of the dark matter$ \chi $ ($ M_{\chi} $ ). In addition, the effective field theory (EFT) formalism of the mono-Z' model was used to interpret the result. A limit was set on the EFT cutoff scale ($ \Lambda $ ); thus, the$ \Lambda $ range between 3.67 - 3.79 TeV is excluded.We are planning to repeat the study with CMS full run-II data with larger center-of-mass energy (
$ \sqrt{s} $ = 13 TeV) and data integrated luminosity ($ {\cal{L}} $ = 137 fb$ ^{-1} $ ). -
The authors of this paper would like to thank Tongyan Lin, one of the authors of [17], for useful discussion about the theoretical models, crosschecking of the results, and for sharing with us the different scenarios in Madgraph cards that were used for event generation. We want to express our deepest thank to Nicola De Filippis from the Politecnico di Bari/INFN for allowing us to use the computing facilities to produce and hosting our ntuples at Bari tier 2 servers. Finally, we would like to thank Michele Gallinaro from LIP/Lisbon for useful discussion regarding our results.
Search for dark matter production in association with the Z' boson at the LHC in pp collisions at $ {{\sqrt{s}}} $ = 8 TeV using Monte Carlo simulations
- Received Date: 2021-04-13
- Available Online: 2021-08-15
Abstract: This analysis evaluates the possibility of the search for Dark Matter (DM) particles using events with a Z







 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF


























 DownLoad:
DownLoad: