-
The study on the nuclei around the
$ ^{132} $ Sn core is a crucial topic in current research [1-3]. The neutron-rich nuclei in the$ ^{132} $ Sn region lie away from the line of stability and are reported to be essential in understanding the r-process nucleosynthesis, as well as the evolution of nuclear deformation [4-11]. With the continuous development of new facilities, it has become possible to experimentally study the low-lying energy spectrum and electromagnetic properties of a few nuclei in this region. This also provides theorists with a new vision for the study on the neutron-rich nuclei.The long even-even Te isotope chain, which has two protons above the
$ Z = 50 $ shell closure, plays an important role in studying the evolution of the nuclear structure. Experimentally, the low-lying energies of Te isotopes with neutron numbers from 54 to 88 have been measured [12]. Except for the nuclei near$ N = 82 $ , the energy ratio of the first$ 4^+ $ to$ 2^+ $ state is approximately equal to 2, thereby indicating a vibration structure [13, 14]. However, the$ E2 $ transitions of a few light Te isotopes do not follow that of a typical vibrator [15-17]. The low-lying energy levels with$ N>82 $ exhibit different characteristics. Both the first$ 2^+ $ and$ 4^+ $ energies of the nuclei with$ N>82 $ are lower than those with$ N<82 $ . This suggests that the nuclei with$ N>82 $ are more collective [18]. In contrast, the ratio of$ E(6^+_1)/E(2^+_1) $ in$ N>82 $ is generally greater than that in$ N<82 $ , which is propably owing to the significant contribution of neutrons in the$ \nu f_{7/2} $ orbital, coupled with protons in the$ \pi g_{7/2} $ orbital [18].The measurement of electromagnetic properties in this nuclear region is a challenging task. To date, the heaviest Te nucleus with known reduced transition probabilities and magnetic moments is
$ ^{136} $ Te with$ N = 84 $ [19-23]. However, there is a noticeable variety in magnitudes for$ B(E2;0_1^{+}\rightarrow 2_1^{+}) $ transitions [$ B(E2)\uparrow $ for short] of$ ^{136} $ Te obtained in different experiments. The first measurement [19, 20] suggested that the$ B(E2)\uparrow $ value of$ ^{136} $ Te [0.122(18) e$ ^2 $ b$ ^2 $ ] was significantly lower than that of$ ^{132} $ Te [0.216(22) e$ ^2 $ b$ ^2 $ ], thereby indicating asymmetry with respect to the$ N = 82 $ shell closure. This result was understood as a neutron dominance in the neutron-proton exchange symmetry, generally preserved in most Te isotopes with$ N<82 $ , and broken for the nucleus$ ^{136} $ Te [24-26]. Two of the latest experiments provided different results, i.e.,$ B(E2)\uparrow = 0.181(15) $ e$ ^2 $ b$ ^2 $ in Refs. [21, 22] and$ 0.191(26) $ e$ ^2 $ b$ ^2 $ in Ref. [23]. In addition, the g factor evolution symmetry was verified via experiments [21, 22]. The resultant g factor of$ ^{136} $ Te has a similar magnitude to that of$ ^{132} $ Te, which suggests that the$ 2^+_1 $ state of$ ^{136} $ Te is not as extreme a neutron-dominant as had been thought [21, 22].The objective of this study is to investigate the low-lying band structures and electromagnetic properties of even-even Te isotopes with mass numbers from 128 to 140 via the nucleon pair approximation (NPA) of the shell model [27-30]. Recently, the NPA has been successfully applied to study low-lying states, vibration-rotation phase transitions, and regularities of nuclear structures under random interactions in the transitional region [31-48]. It has also been generalized with isospin symmetry [49], particle-hole excitations [50], m-scheme basis [51, 52], and deformation [53-55]. For a more comprehensive review, refer to Ref. [30]. The shell model configurations of the nuclei studied in this research are constructed by valence proton particles, valence neutron holes (
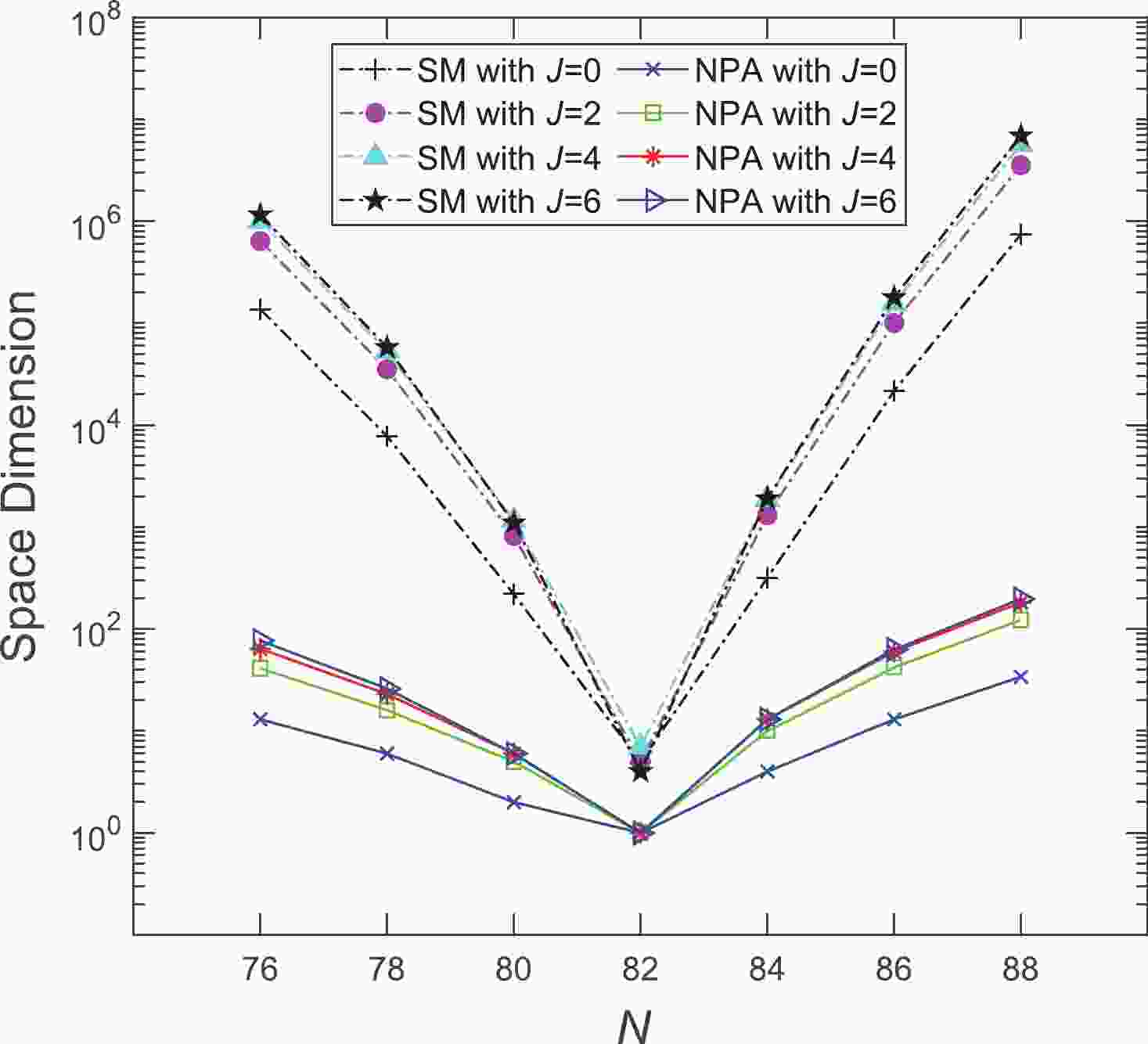
$ N<82 $ ), and valence neutron particles ($ N>82 $ ) with respect to$ ^{132} $ Sn, a doubly closed nucleus. We diagonalize a phenomenological shell model Hamiltonian in a collective pair subspace, which is an approximation of the full shell model space for low-lying states. In Fig. 1, the space dimensions of the Te isotopes between the full shell model and the NPA model space adopted in this study are compared. It can be inferred that the dimension of the SM configurations varies from the single digit at$ N = 82 $ to$ \sim 10^6 $ at$ \ N = 88 $ . The dimension of the NPA truncated space is significantly smaller, which allows us to evaluate the dominant configuration in a straightforward manner, thus providing us with a simple and clear picture of the nuclear structure.
Figure 1. (color online) Comparison of the space dimensions for the Te isotopes between the full shell model and the NPA truncated space adopted in this study. The shell model configuration space is constructed by using valence protons outside the
$Z = 50$ closed shell and valence neutrons with respect to the$N = 82$ closed shell.This paper is organized as follows. In Sec. II, we provide a brief introduction to the NPA, including the Hamiltonian, model space, and transition operators. In Sec. III, we present our results obtained from the calculations on the energy levels of low-lying states,
$ B(E2) $ transition rates between these levels, and g factors. The summary and conclusions of the study are provided in Sec. IV. -
In this study, we introduce the phenomenological Hamiltonian to describe Te isotopes, which has been wildly adopted in previous NPA calculations [31-43]. It includes the spherical single-particle energy term
$ H_{0} $ , a residual interaction containing the monopole pairing$ H_{P0} $ , the quadrupole pairing$ H_{P2} $ between similar nucleons, and the quadrupole-quadrupole interaction$ H_{Q} $ between all valence nucleons :$ H = H_{0}+H_{P0}+H_{P2}+H_{Q}, $

(1) with
$ \begin{aligned}[b] H_{0} =& \sum\limits_{j_{\sigma}} \epsilon_{j_{\sigma} }C^{\dagger}_{j_{\sigma}} C_{j_{\sigma}} , \\ H_{P0} =& \sum\limits_{\sigma} -G_{0\sigma} {\cal{P}}^{(0)\dagger}_{\sigma}\cdot {\cal{P}}^{(0)}_{\sigma}, \\ H_{P2} =& \sum\limits_{\sigma} -G_{2\sigma}{\cal{P}}^{(2) \dagger }_{\sigma} \cdot {\cal{P}}^{(2)}_{\sigma}, \\ H_{Q} =& \sum\limits_{\sigma} -\kappa_{\sigma} Q_{\sigma}\cdot Q_{\sigma}+ \kappa_{\pi\nu}Q_{\pi}\cdot Q_{\nu}. \end{aligned} $

where
$ C^{\dagger}_{j_{\sigma}} $ and$ C_{j_{\sigma}} $ are single-particle creation and annihilation operators, respectively.$ \sigma = \pi, \nu $ refers to the proton and neutron degrees of freedom.$ \epsilon_{j_{\sigma}} $ indicates the single-particle energy. The pairing and quadrupole operators are defined by:$ \begin{aligned}[b] {\cal{P}}^{(0)\dagger}_{\sigma} =& \sum\limits_{j_{\sigma}} \frac{\sqrt{2{j}_{\sigma}+1}}{2}(C_{j_{\sigma}}^{\dagger} \times C_{j_{\sigma}}^{\dagger})^{(0)}_0 , \\ {}{\cal{P}}^{(2)\dagger}_{\sigma } =& \sum\limits_{j_{\sigma} j'_{\sigma}} q(j_{\sigma} j'_{\sigma}) \left( C^{\dagger}_{j_{\sigma}} \times C^{\dagger}_{j'_{\sigma}} \right)_M^{(2)}, \\ {}Q_{\sigma } =& \sum\limits_{j_{\sigma }j'_{\sigma }} q(j_{\sigma } j'_{\sigma }) \left( C^{\dagger}_{j_{\sigma }} \times \tilde{C}_{j'_{\sigma }} \right)^{(2)}_M . \end{aligned} $

where
$ q(jj') = \dfrac{\Delta_{jj'}(-)^{l+l'+1}(-)^{j-\frac{1}{2}}\hat{ j} \hat{j'}}{\sqrt{20\pi} } C_{j\frac{1}{2}, j' -\frac{1}{2}}^{2 0}\langle n l|r^2 |n l' \rangle $ , with$ \Delta_{jj'} = \dfrac{1}{2}[1+(-)^{l+l'+2}] $ , and$ C_{j\frac{1}{2}, j' -\frac{1}{2}}^{2 0} $ is the Clebsch-Gordan coefficient.$ G_{0\sigma} $ ,$ G_{2\sigma} $ ,$ \kappa_{\sigma} $ , and$ \kappa_{\pi\nu} $ represent the two-body interaction strengths corresponding to the monopole, quadrupole pairing, and quadrupole-quadrupole interactions between all valence nucleons.The single-particle energies and two-body interaction parameters corresponding to the proton and neutron excitations in our calculations are shown in Tables 1 and 2, respectively. The nuclei with neutron number
$ N<82 $ are treated in terms of valence neutron holes, while those with$ N>82 $ are considered in terms of valence neutron particles. In Table 1, the proton single-particle energies$ d_{3/2} $ ,$ d_{5/2} $ ,$ g_{7/2} $ , and$ h_{11/2} $ are obtained from the experimental excitation energies of$ ^{133} $ Sb [12]. There are no experimental data available for the remaining orbital$ s_{1/2} $ , and we obtain its single-particle energy from a shell-model study in the$ ^{132} $ Sn region [56]. The neutron hole-like and particle-like single-particle energies are extracted from the corresponding experimental excitation energies [12] of$ ^{131} $ Sn and$ ^{133} $ Sn, respectively. The adopted two-body interaction parameters$ G_{0\sigma} $ ,$ G_{2\sigma} $ ,$ \kappa_{\sigma} $ , and$ \kappa_{\pi\nu} $ in Table 2 are obtained by fitting the experimentally excited energies and electromagnetic properties of low-lying states.$j $ 

$~$ 

$s_{1/2}$ 

$~$ 

$d_{3/2}$ 

$~$ 

$d_{5/2}$ 

$~$ 

$g_{7/2}$ 

$~$ 

$h_{11/2}$ 

$\epsilon_{j_{\pi}}$ 

2.990 2.440 0.962 0.000 2.792 $N<82$ 

$j $ 

$~$ 

$s_{1/2}$ 

$~$ 

$d_{3/2}$ 

$~$ 

$d_{5/2}$ 

$~$ 

$g_{7/2}$ 

$~$ 

$h_{11/2}$ 

$\epsilon_{j_{\nu}}$ 

0.332 0.000 1.655 2.434 0.065 $N>82$ 

$j $ 

$~$ 

$p_{1/2}$ 

$~$ 

$p_{3/2}$ 

$~$ 

$f_{5/2}$ 

$~$ 

$f_{7/2}$ 

$~$ 

$h_{9/2}$ 

$~$ 

$i_{13/2}$ 

$\epsilon_{j_{\nu}}$ 

1.363 0.8537 2.0046 0.000 1.5609 2.690 Table 1. Adopted single-particle energies
$\epsilon_{j_{\pi}}$ and$\epsilon_{j_{\nu}}$ (in MeV) for Te isotopes ($Z=52$ ) with$N<82$ and$N>82$ , respectively.$N\leqslant 82$ 

$G_{0\nu}$ 

$G_{2\nu}$ 

$\kappa_{\nu}$ 

$G_{0\pi}$ 

$G_{2\pi}$ 

$\kappa_{\pi}$ 

$\kappa_{\pi\nu}$ 

$0.17$ 

$0.021$ 

$0.04$ 

$0.18$ 

$0.018$ 

$0.039$ 

$+0.08$ 

$N>82$ 

$G_{0\nu}$ 

$G_{2\nu}$ 

$\kappa_{\nu}$ 

$G_{0\pi}$ 

$G_{2\pi}$ 

$\kappa_{\pi}$ 

$\kappa_{\pi\nu}$ 

$0.11$ 

$0.01$ 

$0.02$ 

$0.13$ 

$0.024$ 

$0.05$ 

$-0.08$ 

Table 2. Adopted two-body interaction parameters
$G_{0\sigma}$ ,$G_{2\sigma}$ ,$\kappa_{\sigma}$ , and$\kappa_{\pi\nu}$ .$\sigma=\pi, \nu$ stands for proton and neutron, respectively.$G_{0\sigma}$ is in unit of MeV;$G_{2\sigma}$ ,$\kappa_{\sigma}$ , and$\kappa_{\pi\nu}$ are in MeV/$r_{0}^{4}$ with$r_0^2=1.012A^{\frac{1}{3}}$ fm$^{2}$ .The model space in the NPA is constructed by collective nucleon-pairs, defined by
$ A^{(r)\dagger}_{\sigma} = \sum\limits_{j_{\sigma} j'_{\sigma}} y(j_{\sigma} j'_{\sigma}r) \left( C^{\dagger}_{j_{\sigma}} \times C^{\dagger}_{j'_{\sigma}} \right)_M^{(r)} \; , $

with
$ r = 0,\, 2,\, 4,\,6,\,8 $ corresponding to S, D, G, I and/or K pairs, respectively.$ y(j_{\sigma} j'_{\sigma}r) $ is called the structure coefficient of the spin-r pair. Based on the single-particle energies in Table 1 and our experience, the model space we selected is as follows. For the proton degree of freedom, collective$ S_{\pi} $ ,$ D_{\pi} $ ,$ G_{\pi} $ , and$ I_{\pi} $ pairs are taken to construct the proton nucleon-pair basis. For the neutron degree of freedom, collective$ S_{\nu}, D_{\nu}, K_{\nu} $ pairs [or$ S_{\nu}, D_{\nu}, G_{\nu}, I_{\nu} $ , and$ K_{\nu} $ pairs] are included in the neutron-hole [or neutron-particle] pair basis.The
$ E2 $ transition operator is defined by$ T(E2) = e_{\pi} Q_{\pi} + $ $ e_{\nu}Q_{\nu}, $ where$ e_{\pi} $ and$ e_{\nu} $ correspond to the effective charges of valence proton and valence neutron. The$ B(E2) $ value in units of$ \rm W.u. $ is given by$ B(E2;J_{i}\rightarrow J_{f}) = \frac{2J_{f}+1}{2J_{i}+1}\times \frac{(e_{\pi} \chi_{\pi}+e_{\nu} \chi_{\nu})^2 r_0^{4}}{5.94\times 10^{-6} \times A^{4/3}}\; \; , $

(2) with reduced matrix element
$ \chi_{\sigma} = \langle \beta_{f},J_{f}||Q_{\sigma}||\beta_{i},J_{i}\rangle $ ($ \sigma = \pi, \nu $ ) and$ r_0^2 = 1.012A^{1/3} $ fm$ ^{2} $ .$ |\beta_{i},J_{i}\rangle $ is the eigenfunction carrying angular momentum$ J_{i} $ and the symbol$ \beta_{i} $ represents all quantum numbers other than$ J_{i} $ . Our proton effective charge is taken to be$ e_{\pi} = 1.6e $ , the same as in previous calculations in this mass region [5, 31]. The neutron effective charge$ e_{\nu} = -1.20e $ for$ N<82 $ and$ e_{\nu} = 0.74e $ for$ N>82 $ are obtained by fitting to the experimental data.The
$ M1 $ transition operator is given by$ T(M1) = $ $ \sqrt{\dfrac{3}{4 \pi}}\displaystyle\sum\limits_{\sigma = \pi,\nu}g_{l\sigma} L_{\sigma} + g_{s\sigma} S_{\sigma} $ , where$ L_{\sigma} $ and$ S_{\sigma} $ represent the orbital and spin angular momenta, respectively.$ g_{l\sigma} $ and$ g_{s\sigma} $ correspond to the orbital and spin gyromagnetic ratios, respectively. The magnetic dipole moment is defined by$ \mu(J_i) = \sqrt{\frac{4\pi}{3}} C_{J_i J_i,10}^{J_i \; J_i}(\xi_{l\pi}+\xi_{s\pi}+\xi_{l\nu}+\xi_{s\nu})\; \mu_N, $

(3) with reduced matrix elements
$ \xi_{l\sigma} = \langle \beta_i,J_i||g_{l\sigma} L_{\sigma} ||\beta_i,J_i\rangle $ and$ \xi_{s\sigma} = \langle \beta_i,J_i||g_{s\sigma} S_{\sigma}||\beta_i,J_i\rangle $ ($ \sigma = \pi, \nu $ ). Here,$ \mu_N $ is the nuclear magneton. The g factor is defined by$ \dfrac{\mu(J_i)/\mu_N}{J_i} $ , and it is expressed as$ g(J_i) = \sqrt{\frac{4\pi}{3}} \frac{ C_{J_i J_i,10}^{J_i \; J_i}}{J_i}(\xi_{l\pi}+\xi_{s\pi}+\xi_{l\nu}+\xi_{s\nu}). $

(4) In the above unit convention, the g factors,
$ L_{\sigma} $ ,$ S_{\sigma} $ , and$ J_i $ are dimensionless. The effective spin gyromagnetic ratios are taken to be$ g_{s\pi} = 5.586\times 0.7 $ and$ g_{s\nu} = -3.826\times 0.7 $ . Namely, the quenching factor 0.7 is adopted. According to previous theoretical calculations in this region [21, 22, 57, 58], the orbital gyromagnetic ratio of proton$ g_{l\pi} = 1.1 $ is adopted in this study. The orbital gyromagnetic ratios of the neutron are$ g_{l\nu} = 0.025 $ for$ N<82 $ , and$ g_{l\nu} = 0.189 $ for$ N>82 $ , determined by the$ \chi^2 $ fitting of experimental g factors. -
In this section, we present the results obtained from our calculations on even-even Te isotopes with neutron numbers from 76 to 88. We discuss the low-lying structures of these nuclei and focus on the symmetric and asymmetric structural evolutions with neutron numbers. The calculated level schemes are compared with experimental ones, as presented in Fig. 2; the comparisons of
$ B(E2) $ values and g factors are presented in Table 3. As can be observed, our results agree well with the experiment, especially for the yrast states. This indicates that the NPA provides us with an appropriate theoretical framework to study low-lying states of the Te isotopes, below and above the$ N = 82 $ shell closure.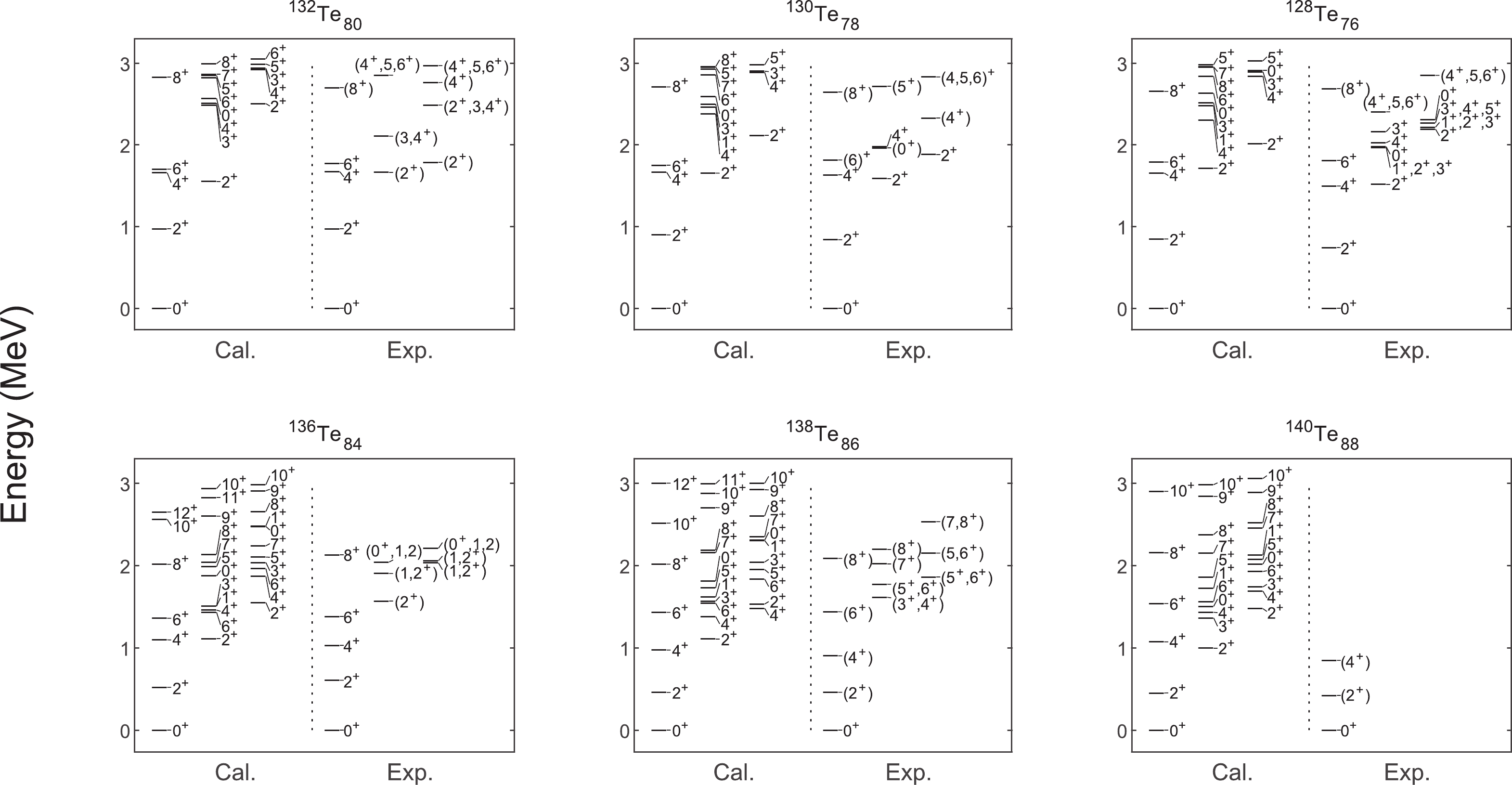
Figure 2. Low-lying states in even-even nuclei
$^{128-132}$ Te ($N<82$ ) and$^{136-140}$ Te ($N>82$ ). Experimental data are obtained from Ref. [12]. Experimental levels with "()" correspond to cases for which the spin and/or parity of the corresponding states are not well established.Nuclei State $B(E2)$ 

$g(J_i^{\pi})$ 

$J_i^{\pi}$ 

$J_f^{\pi}$ 

Exp. Cal. Exp. Cal. $^{128}$ Te

$2^+_1$ 

$0^+_1$ 

$ 19.68(18) $ 

$21.3$ 

$ +0.318(13)$ 

$+0.29$ 

$4^+_1$ 

$2^+_1$ 

$18.4$ 

$+0.63$ 

$6^+_1$ 

$4^+_1$ 

$ 9.7(6) $ 

$7.7$ 

$+0.76$ 

$8^+_1$ 

$6^+_1$ 

$<0.001$ 

$-0.22$ 

$^{130}$ Te

$2^+_1$ 

$0^+_1$ 

$ 15.1(3) $ 

$16.3$ 

$ +0.351(18) $ 

$+0.33$ 

$4^+_1$ 

$2^+_1$ 

$11.9$ 

$+0.70$ 

$6^+_1$ 

$4^+_1$ 

$ 6.1(3) $ 

$5.9$ 

$+0.77$ 

$8^+_1$ 

$6^+_1$ 

$<0.001$ 

$-0.22$ 

$^{132}$ Te

$2^+_1$ 

$0^+_1$ 

$ 10(1) $ 

$10.7$ 

$^{+0.28(15)}_{(+)0.38(4)}$ 

$+0.41$ 

$^{(+)0.46(5)}$ 

$4^+_1$ 

$2^+_1$ 

$6.6$ 

$+0.75$ 

$6^+_1$ 

$4^+_1$ 

$ 3.3(2) $ 

$3.9$ 

$+0.79(9)$ 

$+0.78$ 

$8^+_1$ 

$6^+_1$ 

$<0.001$ 

$-0.22$ 

$^{134}$ Te

$2^+_1$ 

$0^+_1$ 

$6.3(20) $ 

$4.6$ 

$+0.76(9) $ 

$+0.81$ 

$4^+_1$ 

$2^+_1$ 

$4.3(4) $ 

$4.2$ 

$ +0.70^{+0.55}_{-0.38} $ 

$+0.79$ 

$6^+_1$ 

$4^+_1$ 

$ 2.05(4)$ 

$2.3$ 

$+0.846(25)$ 

$+0.79$ 

$^{136}$ Te

$2^+_1$ 

$0^+_1$ 

$ 7.6(15) $ 

$8.9$ 

$ (+)0.34(^{+8}_{-6}) $ 

$+0.40$ 

$4^+_1$ 

$2^+_1$ 

$ 14.1(21) $ 

$9.9$ 

$+0.27$ 

$6^+_1$ 

$4^+_1$ 

$4.1$ 

$-0.04$ 

$8^+_1$ 

$6^+_1$ 

$5.6$ 

$+0.26$ 

$^{138}$ Te

$2^+_1$ 

$0^+_1$ 

$11.5$ 

$+0.28$ 

$4^+_1$ 

$2^+_1$ 

$13.1$ 

$+0.14$ 

$6^+_1$ 

$4^+_1$ 

$9.2$ 

$+0.22$ 

$8^+_1$ 

$6^+_1$ 

$9.4$ 

$+0.41$ 

$^{140}$ Te

$2^+_1$ 

$0^+_1$ 

$13.4$ 

$+0.27$ 

$4^+_1$ 

$2^+_1$ 

$18.1$ 

$+0.34$ 

$6^+_1$ 

$4^+_1$ 

$0.6$ 

$-0.14$ 

$8^+_1$ 

$6^+_1$ 

$0.4$ 

$+0.53$ 

-
First, we look at the low-lying energy levels. The energy ratio of the first
$ 4^+ $ to$ 2^+ $ state, namely$ R_{4/2} = E(4_1^+)/E(2_1^+) $ , is a well known indicator of nuclear collectivity [59]. In Fig. 2, the experimental$ R_{4/2} $ ratio is approximately$ 2.01 $ for$ N = 76,88 $ ,$ 1.95 $ for$ N = 78,86 $ , and$ 1.71 $ for$ N = 80,84 $ . This indicates that the energy ratios$ R_{4/2} $ of Te isotopes exhibit a symmetric pattern with respect to the$ N = 82 $ shell closure [13, 14]. From the values of$ R_{4/2} $ , both$ ^{128-132} $ Te with$ N<82 $ and$ ^{136-140} $ Te with$ N>82 $ exhibit vibration-like characters.The
$ E(2_1^{+}) $ energy is also a widely used structural indicator besides$ R_{4/2} $ . The experimental data and the corresponding NPA results versus the neutron number N are plotted in Fig. 3(a). From the general trend,$ E(2_1^{+}) $ energies show obvious asymmetric characteristics with respect to the$ N = 82 $ shell closure. The measured values in the$ N>82 $ region are lower than those in the$ N<82 $ region. This was explained as a reduced neutron pairing above the$ N = 82 $ shell [24]. To verify whether or not our calculation agrees with this explanation, we further investigate the contribution of different Hamiltonian interactions [i.e.,$ H_0 $ ,$ H_{P0} $ ,$ H_{P2} $ , and$ H_{Q} $ in Eq. (1)] to the$ E(2_1^{+}) $ energies presented in Fig. 3(b). It can be observed that$ H_{P0} $ dominates the evolution of$ E(2_1^{+}) $ . As illustrated in Fig. 3(c), both neutron$ H_{P0\nu} $ and proton$ H_{P0\pi} $ vary greatly after crossing$ N = 82 $ . Therefore, the drop of$ H_{P0} $ as$ N>82 $ results from the combination of both proton and neutron monopole pairings. We also note that the monopole pairing strength, i.e.,$ G_{0\sigma} $ herein, in the$ N>82 $ region is weaker than that in the$ N<82 $ region. Therefore, we suggest that this asymmetric feature of$ E(2_1^{+}) $ energies is primarily owing to the evolution of residual monopole pairing interactions across$ N = 82 $ , which is similar to the argument in Ref. [24].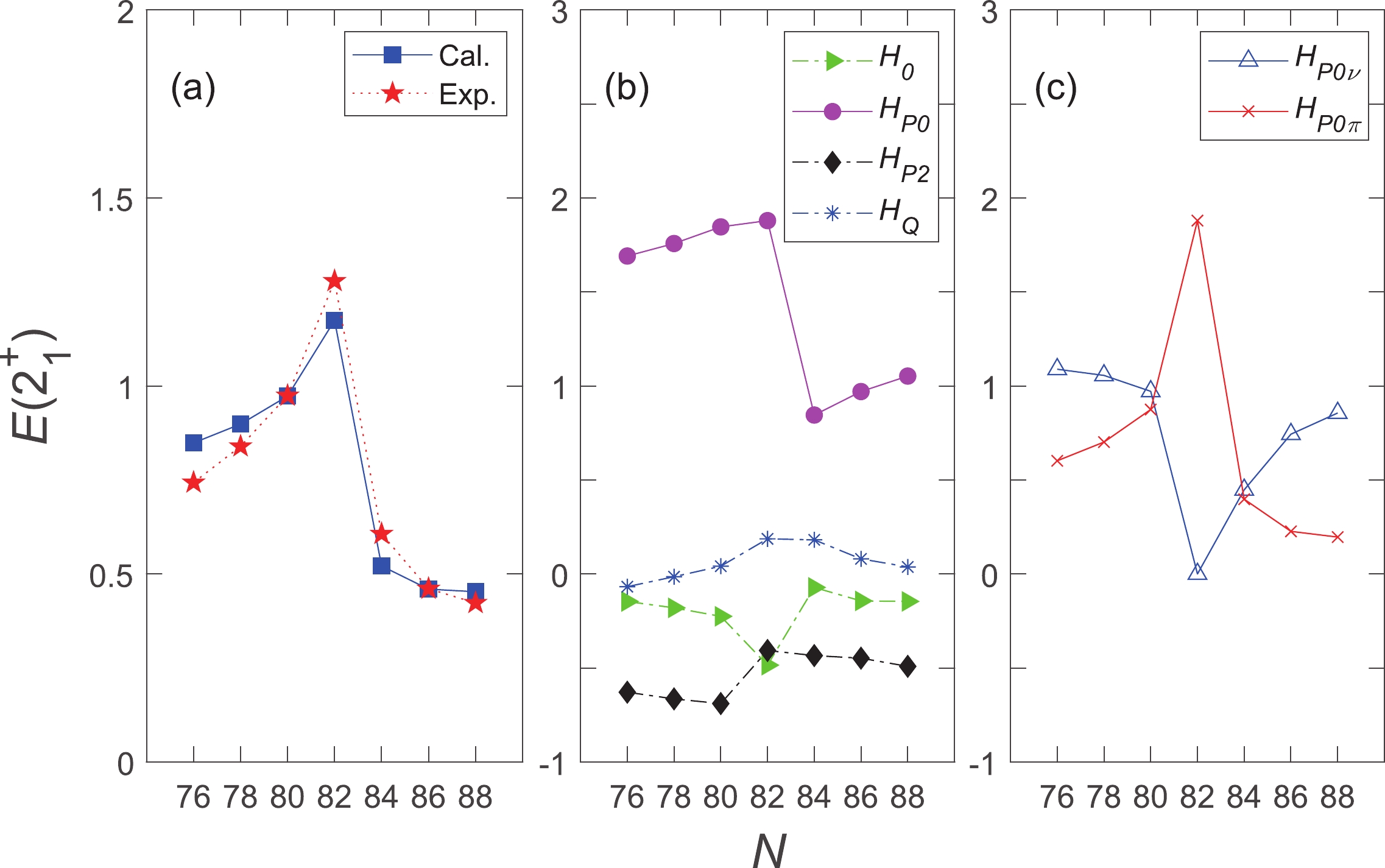
Figure 3. (color online) (a)
$E(2_1^{+})$ energies (in MeV), (b) contributions of different Hamiltonian interactions (denoted as$H_0$ ,$H_{P0}$ ,$H_{P2}$ , and$H_{Q}$ ), and (c) contributions of neutron$H_{P0\nu}$ and proton$H_{P0\pi}$ .$H_0$ is the spherical single-particle energy term.$H_{P0}$ and$H_{P2}$ refer to the residual monopole pairing and quadrupole pairing interactions between similar nucleons, respectively.$H_{Q}$ includes the quadrupole-quadrupole interactions between all valence nucleons. Our results (cal.), which include all aforementioned Hamiltonian terms, are shown as blue squares. The experimental data (exp.) are obtained from Ref. [12]. -
Nuclear electromagnetic properties, such as
$ B(E2) $ transitions and g factors, are sensitive probes for detecting quadrupole collectivity and deformation. Before the first measurement of the$ g(2_1^{+}) $ factor of$ ^{136} $ Te [21, 22], the available experimental$ B(E2;2_1^{+}\rightarrow 0_1^{+}) $ transition of$ ^{136} $ Te was approximately half that of$ ^{132} $ Te [19, 20]. This was theoretically interpreted as the neutron dominance in the$ 2_1^{+} $ -state wave function [24-26], and a negative$ g(2_1^{+}) $ factor of$ ^{136} $ Te [24, 25] was predicted as a consequence of the overestimation of the contribution of neutron excitations to the total wave function [68]. Experimentally, the sign of$ g(2_1^{+}) $ factor is suggested to be positive [$ (+)0.34(^{+8}_{-6}) $ ], thus indicating that the$ 2_1^{+} $ -state wave function of$ ^{136} $ Te is not completely dominated by the neutron configuration as previously suggested [21, 22]. To elucidate the above discussions in the literature, in this subsection, we would like to focus on the evolution trends of$ B(E2) $ transitions and g factors, as well as the dominant configuration of the$ 2_1^{+} $ state. The experimental data and the corresponding NPA results as a function of N are presented in Fig. 4(a) and 5(a), respectively. It can be inferred that our calculated results generally agree well with the experimental data.
Figure 4. (color online) (a)
$B(E2;2_1^{+}\rightarrow 0_1^{+})$ values (in W.u.) and (b) the matrix elements of proton$e_{\pi} \chi_{\pi}$ and neutron$e_{\nu} \chi_{\nu}$ . Our results with adopted effective charges ($e_{\nu} = -1.20e$ for$N<82$ and$e_{\nu} = 0.74e$ for$N>82$ ) and symmetric effective charges ($e_{\nu} = -e$ for$N<82$ and$e_{\nu} = e$ for$N>82$ ) are represented by blue squares and black asterisks, respectively. The experimental data are obtained from Refs. [12, 19-23].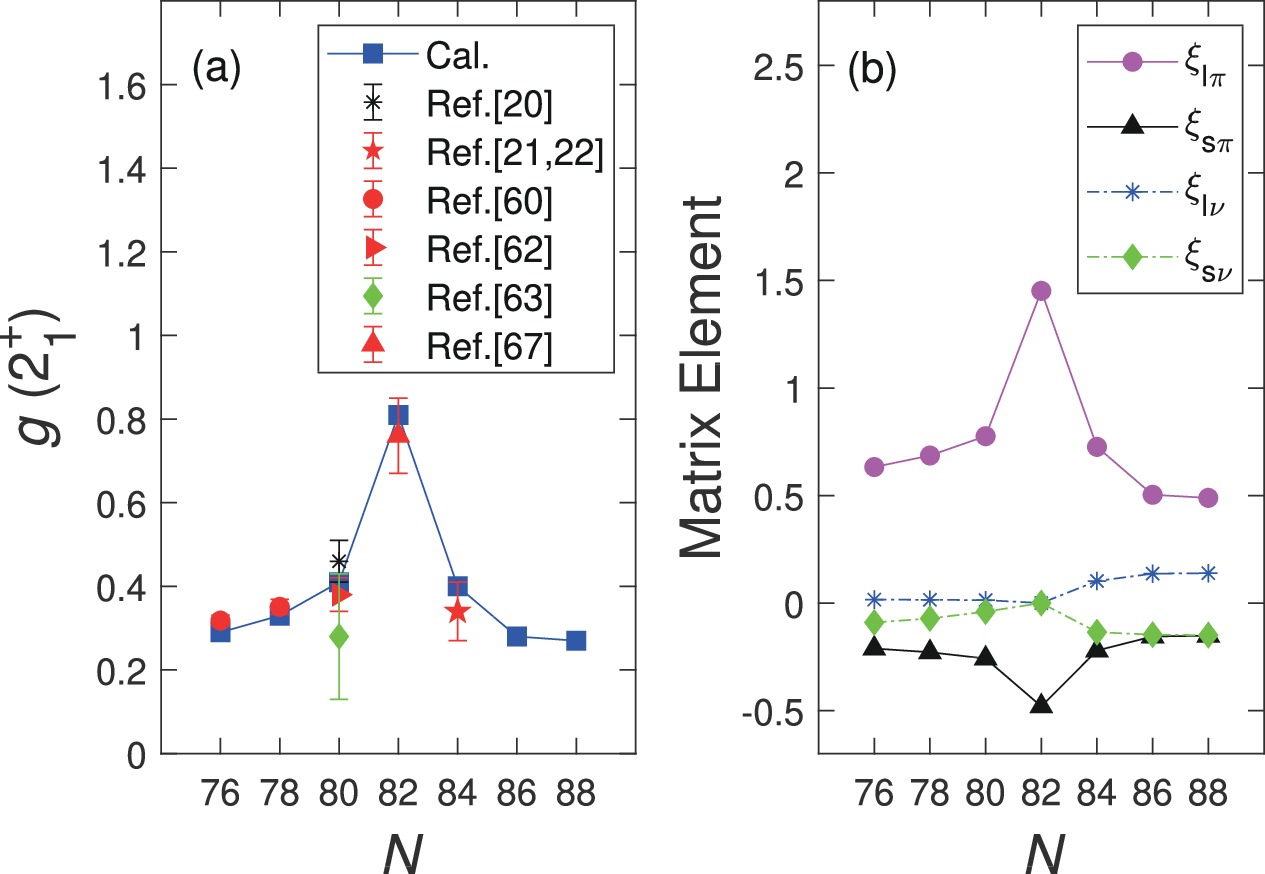
Figure 5. (color online) (a)
$g(2_1^{+})$ factors and (b) the reduced matrix elements corresponding to the proton orbital part$\xi_{l\pi}$ , proton spin part$\xi_{s\pi}$ , neutron orbital part$\xi_{l\nu}$ , and neutron spin part$\xi_{s\nu}$ . The experimental data are obtained from Refs. [20-22, 60, 62, 63, 67].As illustrated in Fig. 4(a), the measured
$ B(E2;2_1^{+}\rightarrow 0_1^{+}) $ transitions exhibit certain asymmetric patterns around the$ N = 82 $ shell. Although the$ B(E2) $ data of$ ^{136} $ Te ($ N = 84 $ ) vary slightly based on experiments, they are generally smaller than that of$ ^{132} $ Te ($ N = 80 $ ). We further study the contributions of protons and neutrons to the$ B(E2) $ values, as presented in Fig. 4(b). From Eq. (2),$ B(E2;2_1^{+}\rightarrow 0_1^{+}) = C[e_{\pi} \chi_{\pi}+e_{\nu} \chi_{\nu}]^2 $ with the coefficient$ C = \dfrac{0.2\times r_0^{4}}{5.94\times 10^{-6} \times A^{4/3}} $ . Because C varies slightly in the$ A\sim 132 $ region, it can be approximately taken as a constant (0.13 fm$ ^4 $ ). Therefore the contribution of protons and neutrons to$ B(E2) $ values only depends on the matrix elements$ e_{\pi} \chi_{\pi} $ and$ e_{\nu} \chi_{\nu} $ . It can be inferred that the evolution trend of neutron matrix elements ($ e_{\nu} \chi_{\nu} $ -adopted) in Fig. 4(b) is approximately the same as that of$ B(E2) $ values (Cal. with adopted$ e_{\nu} $ ) in Fig. 4(a). We thus suggest that the asymmetric evolution trend of$ B(E2) $ with N is primarily determined by the neutron part.To understand why the neutron part (
$ e_{\nu} \chi_{\nu} $ -adopted) is asymmetric with respect to the$ N = 82 $ shell closure, we carefully consider the dominant configurations of$ 2^+_1 $ states. For brevity, we omit S pairs and abbreviate the NPA basis$ |(D_{\pi}^{\dagger})^{n_{\pi}} (S_{\pi}^{\dagger})^{N_{\pi}-n_{\pi}} (D_{\nu}^{\dagger})^{n_{\nu}}(S_{\nu}^{\dagger})^{N_{\nu}-n_{\nu}} \rangle $ to be$ |(D_{\pi})^{n_{\pi}}(D_{\nu})^{n_{\nu}}\rangle $ . For example,$ |D_{\nu}\rangle $ represents the NPA basis$ |(S_{\pi}^{\dagger})^{N_{\pi}}D_{\nu}^{\dagger}(S_{\nu}^{\dagger})^{N_{\nu}-1}\rangle $ . Our results are as follows. For the nuclei with$ N<82 $ ,$ \begin{array}{l} |2_1^+;^{132}{\rm{Te}}\rangle: \;\;0.68|D_{\nu}\rangle, \;\;0.70|D_{\pi}\rangle, \\ |2_1^+;^{130}{\rm{Te}}\rangle : \;\; 0.72|D_{\nu}\rangle, \;\;0.64|D_{\pi}\rangle, \\ |2_1^+;^{128}{\rm{Te}}\rangle : \;\; 0.72|D_{\nu}\rangle, \;\;0.60|D_{\pi}\rangle. \end{array} $

And for the nuclei with
$ N>82 $ ,$ \begin{array}{l} |2_1^+;^{136}{\rm{Te}}\rangle : \;\;0.68|D_{\nu}\rangle,\;\; 0.69|D_{\pi}\rangle, \\ |2_1^+;^{138}{\rm{Te}}\rangle : \;\;0.71|D_{\nu}\rangle, \;\;0.54|D_{\pi}\rangle, \\ |2_1^+;^{140}{\rm{Te}}\rangle : \;\; 0.70|D_{\nu}\rangle, \;\;0.50|D_{\nu}G_{\nu}\rangle,\; \; 0.52|D_{\pi}\rangle. \label{WF} \end{array} $

Here, the coefficient in front of each configuration is the projection of the basis and the wave function, i.e.,
$ \langle {\rm basis}|2^+_1\rangle $ . The configurations with$ (\rm projection)^2 $ less than 20% are omitted. It can be observed that the$ 2_1^{+} $ state of most Te nuclei (except for$ ^{140} $ Te) is dominated by mixing$ |D_{\pi} \rangle $ and$ |D_{\nu} \rangle $ . Hence, the dominant configuration of the wave function can be approximated as symmetric at approximately$ N = 82 $ . In contrast,$ ^{140} $ Te has one more component$ |D_{\nu}G_{\nu}\rangle $ in its dominant configuration. This suggests that the configuration-mixing is enhanced in this nucleus. In the literature,$ ^{138} $ Te is located in the transitional region [69], and the shape transition from spherical in$ ^{136} $ Te to prolate in$ ^{140} $ Te is predicted to take place at$ ^{139} $ Te [4].Symmetric wave functions lead to symmetric
$ E2 $ matrix elements$ \chi_{\nu} $ . Therefore, the asymmetry of the$ B(E2) $ has to be traced back to the neutron effective charge$ e_{\nu} $ . To highlight the asymmetry of the adopted$ e_{\nu} $ , we reintroduce the symmetric effective charges with$ e_{\nu} = -e $ for$ N<82 $ and$ e_{\nu} = e $ for$ N>82 $ . Our results are denoted by "Cal. with symmetric$ e_{\nu} $ '' in Fig. 4(a) and "$ e_{\nu} \chi_{\nu} $ -symmetric'' in Fig. 4(b). Significantly large deviations from experimental data can be observed, if symmetric$ e_{\nu} $ is assumed. Therefore we suggest that the asymmetric pattern of$ B(E2) $ is related to the asymmetry of neutron effective charges (i.e., different core polarization characters below and above$ N = 82 $ ).Unlike
$ B(E2) $ transitions and$ E(2_1^{+}) $ energies, the$ g(2_1^{+}) $ factors in Fig. 5(a) are nearly symmetric. According to Eq. (4),$ g(2^+_1) \simeq 0.84(\xi_{l\pi}+\xi_{s\pi}+\xi_{l\nu}+\xi_{s\nu}) $ . In other words, the$ g(2_1^{+}) $ factor comprises proton orbital, proton spin, neutron orbital, and neutron spin parts. We calculate these four parts and present their corresponding reduced matrix elements in Fig. 5(b). One sees that the evolution trend of$ g(2_1^{+}) $ factors is primarily determined by the proton orbital part$ \xi_{l\pi} $ . The contribution of the neutron orbital part$ \xi_{l\nu} $ is close to zero, while the contributions of the proton/neutron-spin parts ($ \xi_{s\pi} $ and$ \xi_{s\nu} $ ) are negative.To this point, we have separately discussed the general trends of
$ B(E2;2_1^{+}\rightarrow 0_1^{+}) $ transitions in Fig. 4 and$ g(2_1^{+}) $ factors in Fig. 5. Next, we discuss these two simultaneously. It can be observed in Fig. 4(b) that the matrix elements of the proton and neutron contribute with the same phase in the evaluation of the$ E2 $ transition; hence, the precision of the non-dominate component is not crucial. In the corresponding calculation of$ g(2_1^{+}) $ values in Fig. 5(b), the proton/neutron orbital and spin components contribute out of phase and may lead to significant errors if they are not precisely evaluated. Therefore, the g factor is very sensitive to the details of the wave function, and in particular, the balance between proton and neutron contributes to the wave function. As we have analyzed before, the different evolution behaviors of the$ B(E2) $ transitions and g factors regarding$ N = 82 $ are primarily owing to the different roles played by the neutrons and protons. Becuase the proton component dominates the evolution of g factors, the basic symmetric distribution of g factors with$ N = 82 $ indicates that the proton contribution in the$ 2_1^{+} $ -state wave function of$ ^{136} $ Te should be equivalent to that of$ ^{132} $ Te. In other words, the$ 2_1^{+} $ -state wave function of$ ^{136} $ Te is actually not absolutely dominated by the neutron configuration, as mentioned in Refs. [21, 22]. -
Another interesting asymmetrical behavior is related to the energy level spacing between the
$ 4^+_1 $ and$ 6^+_1 $ states [$ E(6_1^+)-E(4_1^+) $ ]. Our obtained results are presented in Fig. 6. It can be observed that the spacing of nuclei with$ N<82 $ is generally smaller (the experimental values are approximately 0.10 MeV at$ N = 80 $ , 0.18 MeV at$ N = 78 $ , and 0.31 MeV at$ N = 76 $ ). After crossing the$ N = 82 $ shell, this level spacing increases rapidly to 0.35 MeV at$ N = 84 $ and then continues to 0.54 MeV at$ N = 86 $ . Possibly, owing to the emphasis on the collectivity of our calculation, there is a slightly systematic overestimation of$ E(4_1^+) $ in Fig. 6(a) and a corresponding underestimation of [$ E(6_1^+)-E(4_1^+) $ ] in Fig. 6(b).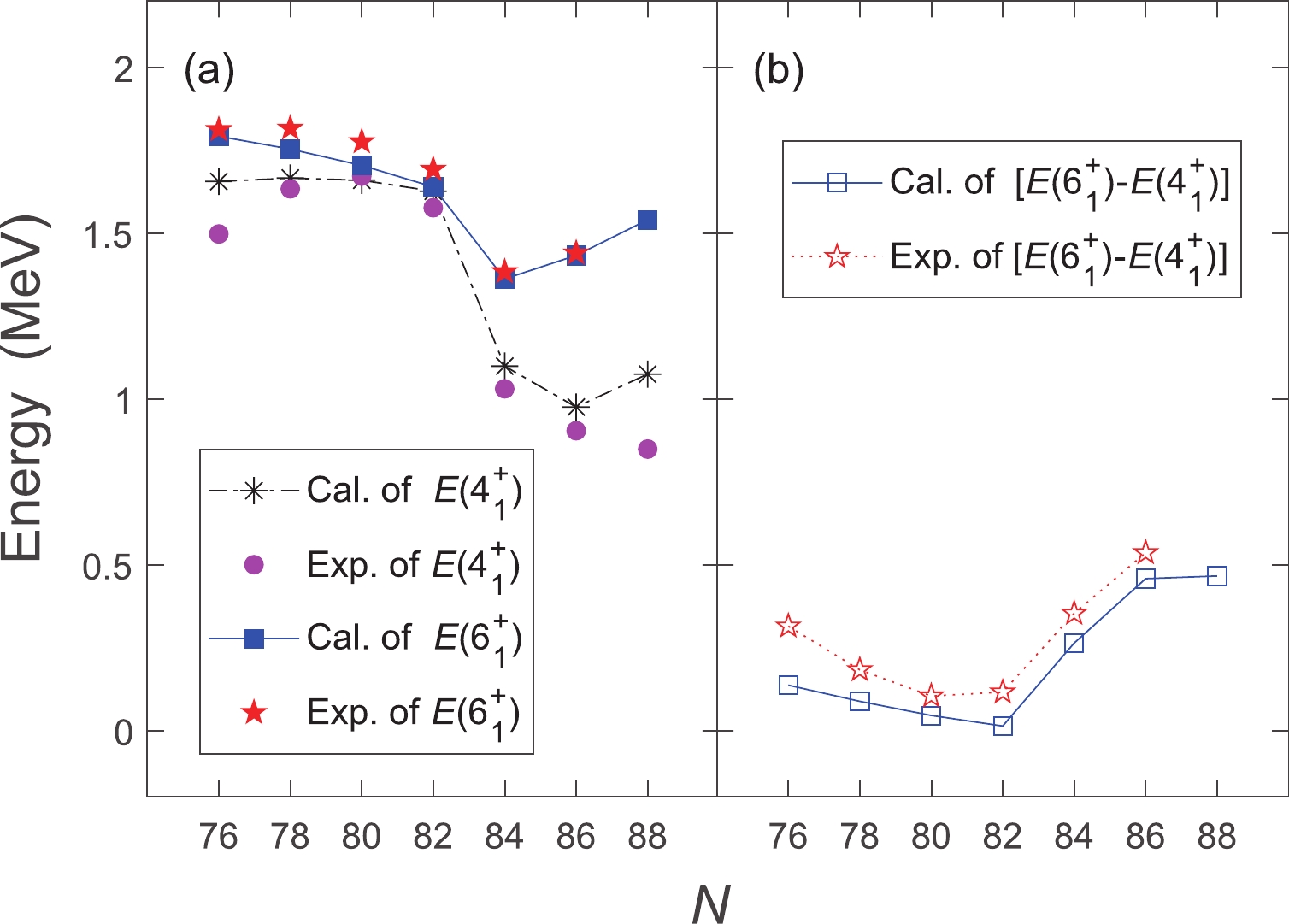
Figure 6. (color online) (a)
$E(4_1^{+})$ and$E(6_1^{+})$ energies and (b) the energy level spacing of adjacent$4^+_1$ and$6^+_1$ states [$E(6_1^+)-E(4_1^+)$ ] (in MeV). The experimental data are obtained from Ref. [12].The asymmetrical pattern of [
$ E(6_1^+)-E(4_1^+) $ ] can be explained in part by the dominant configurations of the$ 4^+_1 $ and$ 6^+_1 $ states. For the nuclei with$ N<82 $ ,$ \begin{array}{l} |4_1^+;^{132}{\rm{Te}}\rangle : \;\; 0.93|G_{\pi}\rangle ; \\ |4_1^+;^{130}{\rm{Te}}\rangle : \;\; 0.85|G_{\pi}\rangle ; \\ |4_1^+;^{128}{\rm{Te}}\rangle : \;\; 0.77|G_{\pi}\rangle,\;\;0.51|D_{\pi}D_{\nu}\rangle; \\ |6_1^+;^{132}{\rm{Te}}\rangle : \;\;0.96|I_{\pi}\rangle; \\ |6_1^+;^{130}{\rm{Te}}\rangle :\;\; 0.92|I_{\pi}\rangle; \\ |6_1^+;^{128}{\rm{Te}}\rangle : \;\;0.88|I_{\pi}\rangle. \end{array} $

It can be deduced that the
$ 4^+_1 $ (and$ 6^+_1 $ ) states of$ ^{132} $ Te and$ ^{130} $ Te are very pure proton excitations dominated by$ |G_{\pi} \rangle $ (and$ |I_{\pi}\rangle $ ) in the NPA basis. This causes the energy levels of the two nuclei to be significantly close. As presented in Table 1, the$ \pi g_{7/2} $ orbit is the lowest proton single-particle energy level. The two-valence-proton configuration$ (\pi g_{7/2})^{2} $ accounts for 99% in the collective$ G_{\pi} $ and$ I_{\pi} $ pairs. Hence, the small spacing between$ 4^+_1 $ and$ 6^+_1 $ states below$ N = 82 $ is mainly caused by the spin alignment of two protons in the$ \pi g_{7/2} $ orbit. For$ ^{128} $ Te, although its$ 6^+_1 $ state is also dominated by$ |I_{\pi}\rangle $ , its$ 4^+_1 $ state is mixed with another configuration$ |D_{\pi}D_{\nu}\rangle $ , so the$ 4^+_1 $ state is suppressed, and the spacing increases. For the nuclei with$ N>82 $ , their dominant configurations are represented as$ \begin{array}{l} |4_1^+;^{136}{\rm{Te}}\rangle : \;\;0.56|G_{\nu}\rangle, \;\;0.66|D_{\pi}D_{\nu}\rangle; \\ |4_1^+;^{138}{\rm{Te}}\rangle : \;\; 0.47|D_{\nu}^2\rangle, \;\;0.57|D_{\nu}I_{\nu}\rangle,\; \; \; 0.54|D_{\pi}D_{\nu}\rangle; \\ |4_1^+;^{140}{\rm{Te}}\rangle : \;\;0.50|D_{\nu}^2\rangle,\;\; 0.62|D_{\pi}D_{\nu}\rangle,\; \; 0.46|D_{\pi}D_{\nu}G_{\nu}\rangle; \\ |6_1^+;^{136}{\rm{Te}}\rangle : \;\; 0.81|I_{\nu}\rangle; \\ |6_1^+;^{138}{\rm{Te}}\rangle :\;\; 0.57|I_{\nu}\rangle; \\ |6_1^+;^{140}{\rm{Te}}\rangle : \;\; 0.70|I_{\nu}\rangle, \;\;0.73|D_{\nu}I_{\nu}\rangle. \end{array} $

It can be deduced that the dominant configuration of the
$ 4^+_1 $ state relatively differs from that of the$ 6^+_1 $ state. Because the configuration mixing of$ 4^+_1 $ state is significantly more complicated in the$ N>82 $ region, the$ 4^+_1 $ state is suppressed lower, which in turn causes the energy level spacing [$ E(6_1^+)-E(4_1^+) $ ] to increase. -
In summary, we calculated low-lying level schemes,
$ B(E2) $ transitions, and g factors of even-even Te isotopes with neutron numbers from 76 to 88 via the nucleon-pair approximation (NPA). The optimal agreement with experiments indicates that our theoretical framework is suitable for studying low-lying structures of the nuclei in this neutron-rich mass region.We compared the yrast band structures of
$ N<82 $ and$ N>82 $ nuclei. The energy ratio of the$ 4_1^+ $ to$ 2_1^+ $ state is symmetric at approximately$ N = 82 $ , and its value varies at approximately$ 2.0 $ . However, the$ E(2_1^{+}) $ energies in the$ N>82 $ region are lower than those in the$ N<82 $ region. This corresponds to a reduction in the contribution of residual monopole pairing interactions between similar nucleons in the$ N>82 $ region. However, a small energy spacing between the$ 4_1^+ $ and$ 6_1^+ $ state appears in nuclei with$ N<82 $ , and disappears in nuclei with$ N>82 $ . We analyzed the dominant configurations of the$ 4_1^+ $ and$ 6_1^+ $ states. Such an asymmetric behavior of$ E(6_1^+)-E(4_1^+) $ is mainly caused by the spin alignment of two protons in the$ \pi g_{7/2} $ orbit of the$ N<82 $ region.We also studied the evolution trends of
$ B(E2;2_1^{+}\rightarrow 0_1^{+}) $ transitions and$ g(2_1^{+}) $ factors with the neutron number N. We inferred that the asymmetric behavior of$ B(E2) $ with respect to$ N = 82 $ is primarily determined by the neutron contribution, which indicates different core polarization characters, below and above the$ N = 82 $ shell. In contrast,$ g(2_1^{+}) $ factors vary symmetrically at approximately$ N = 82 $ . This pattern was determined to be dominated by the proton-orbit part. Furthermore, in Table 3, we presented the theoretical predictions of$ E2 $ transitions and g factors for a few yrast states, which are still experimentally unknown. We expect our prediction to be beneficial in future studies on these nuclei.
Symmetric and asymmetric structural evolutions of Te isotopes across the N = 82 shell closure
- Received Date: 2021-04-28
- Available Online: 2021-09-15
Abstract: Systematic calculations of low-lying energy levels,





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF

















 DownLoad:
DownLoad: