-
One method of probing new physics (NP) beyond the Standard Model (SM) is the use of the bottom-up approach, i.e., describing the unknown NP effects through higher-dimensional operators constructed using the SM fields at the NP scale
$ \Lambda $ , obeying the well-established gauge structure of the SM, i.e.,$ SU(2)_{W}\otimes U(1)_Y $ . The Lagrangian of the effective field theory (EFT) is$ \mathscr{L}_{\rm EFT} = \mathscr{L}_{\rm SM}+\frac{1}{\Lambda^2}\sum\limits_i \mathcal{C}^i O_i^{(6)} +O\left(\frac{1}{\Lambda^3}\right), $

(1) where
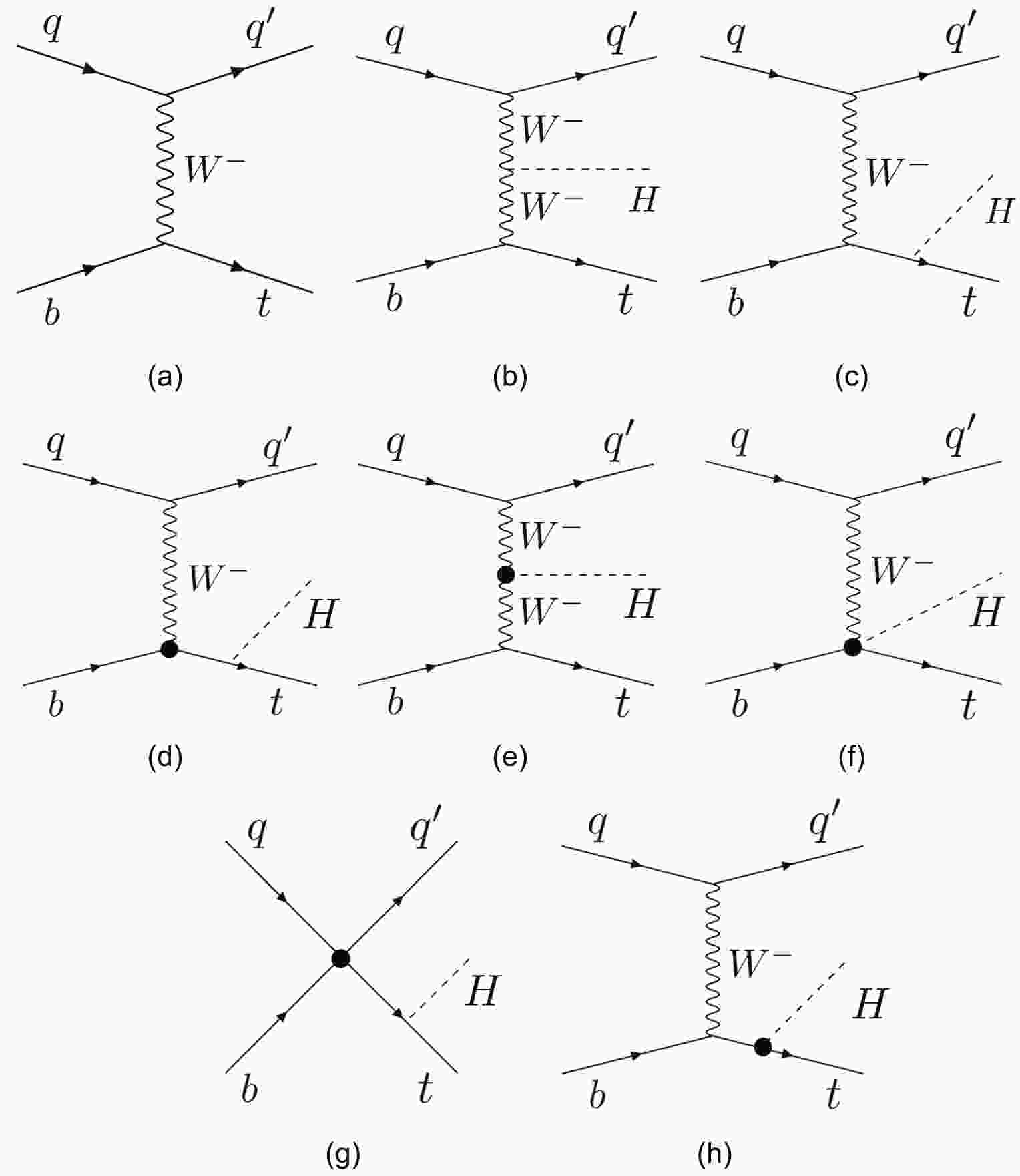
$ \mathcal{C}_i $ represents Wilson coefficients. The aim of EFT analysis is to determine nontrivial correlations among$ \mathcal{C}_i $ values as these relations would provide insights into the structure of NP models. Various bases of dimension-6 operators have been introduced in the literature, e.g., Warsaw basis [1], HISZ basis [2, 3], and SILH basis [4, 5]. However, each basis consists of 59 independent operators, and it is difficult to explore the correlations among 59 operators in practice. A method of solving the predicament is to determine independent observables that are sensitive to a small set of operators and then examine correlations among them. This has been studied for single top productions [6-12]. In this work, we explore the strong correlation between the t-channel single top (single-t) production (Fig. 1(a)) and the associated production of a single top quark with a Higgs boson (termed$ tHq $ production); see Fig. 1(b, c). The two channels primarily involve three operators that can be measured in the single-t production. This yields a strong constraint on the cross section of the$ tHq $ production.
Figure 1. Feynman diagrams of the t-channel single-t production (a), the
$ tHq $ production (b, c) in the SM, and the$ tHq $ production modified by effective operators (d-h). The operators$ O_{\phi W} $ ,$ O_{\phi q3} $ , and$ O_{uW} $ contribute to Feynman diagrams (d, e, f), and the operators$ O_{\phi D} $ ,$ O_{u\phi} $ , and$ O_{\phi\Box} $ contribute to a shift of Yukawa coupling or Higgs-gauge coupling (g, h).As some higher-dimensional operators can be absorbed by field redefinitions, various schemes of input parameters have been widely discussed in the literature [13, 14]. We select the Warsaw basis [1], in which the Higgs boson is a fundamental scalar particle created under spontaneous symmetry breaking, and follow the scheme of input parameters proposed in [15] to normalize the SM fields and masses. The assumptions made in our analysis are listed as follows: i) only diagonal elements of the CKM matrix have been considered as they are significantly larger than off-diagonal elements; ii) we ignore the masses of light quarks and maintain only the top quark mass as it is significantly larger than those of other quarks; iii) we assume the interactions of light quarks and gauge bosons are the same as the SM interaction since they are tightly constrained by the experiments such as semi-lepton decay, LEP precise measurements, and Drell-Yan process measurements [16-19]; and iv) we focus on the CP conserving effective couplings of the top quark. Therefore, the Wilson coefficients are all real.
The SMEFT analysis in the single-t channel has been conducted in the literature [6-9]. Only four independent dimension-6 operators are involved in the t-channel production:
$ \begin{aligned}[b] O_{uW} & = (\bar q_p \sigma^{\mu\nu} u_r) \tau^I \tilde\phi W^{I}_{\mu\nu} + {\rm h.c.} , \\ O_{\phi q3} & = (\phi^\dagger i \stackrel{\leftrightarrow}{D^I_\mu}\phi)(\bar q_p \tau^I \gamma^\mu q_r) + {\rm h.c.} , \\ O^{(1)}_{qq} & = (\bar q_p \gamma_\mu q_r) (\bar q_s \gamma^\mu q_t) + {\rm h.c.} , \\ O^{(3)}_{qq} & = (\bar q_p \gamma_\mu \tau^I q_r) (\bar q_p \gamma^\mu \tau^I q_r) + {\rm h.c.}\, . \end{aligned} $

(2) where
$ \phi $ denotes the SM Higgs boson doublet,$ D_{\mu} $ the covariant derivative,$ q_i $ the left-handed$ SU(2) $ doublet of the i-th generation,$ u_r $ the right-handed isosinglets [20], and$ \tau^{I} $ the usual Pauli matrices in the weak isospin space. Considering the flavor structure of four-fermion operators, flavor changing currents can occur from both the first and second generations to the third generation. However, we would ignore the contribution from the second generation, which suffers a suppression from parton distribution functions (PDFs). Using Fierz Identity, we can prove that only two independent flavored four-fermion operators contribute to the t-channel production. They are$ \begin{aligned}[b] O^{(1)}_{3113} & = (\bar q_3 \gamma_\mu q_1) (\bar q_1 \gamma^\mu q_3) + {\rm h.c.},\\ O^{(3)}_{3311} & = (\bar q_3 \gamma_\mu \tau^I q_3) (\bar q_1 \gamma^\mu \tau^I q_1) + {\rm h.c.}\, . \end{aligned} $

(3) For convenience, we still use
$ O^{(1)}_{qq} $ and$ O^{(3)}_{qq} $ to denote these two flavored operators, respectively. Indeed, the interference between$ O^{(3)}_{qq} $ and the SM is only three times as large as that of$ O^{(1)}_{qq} $ owing to a color factor. Although their contributions can be separated by quadratic terms, they can be considered to be the same degree of freedom at the leading order effects of the operators, i.e., maintaining only the interference between the SM and NP operators. Thus, hereafter, we use$ O^{(3)}_{qq} $ to denote the degree of freedom.Note that the effects of higher-dimensional operators on the branching ratio of
$ t \rightarrow W b $ can be safely neglected when considering the leading order effects of the operators. The operators can contribute to the partial decay width of$ t \to W b $ as well as the total decay width. The four fermion operators do not interfere with the top-quark decay in the SM. The modification of the operators to the W-t-b coupling tends to cancel out when one expands the operator effects in the leading order [21, 22].The cross sections of the t-channel single top-quark productions at the 13 TeV LHC are
$ \begin{aligned}[b] &\sigma_t = \left[136 - 9C_{qq}^{(3)} + 11C_{uW} + 8C_{\phi q3} \right] {\rm pb},\\ &\sigma_{\bar{t}} = \left[81 - 4 C_{qq}^{(3)} + 5 C_{uW} + 5 C_{\phi q3} \right] {\rm pb}, \end{aligned} $

(4) where
$ \begin{aligned}[b] C_{qq}^{(3)}&\equiv \mathcal{C}_{qq}^{(3)}\left(\frac{\rm TeV}{\Lambda^2}\right)^2, \\ C_{uW} &\equiv\mathcal{C}_{uW}\left(\frac{\rm TeV}{\Lambda^2}\right)^2, \\C_{\phi q3} &\equiv \mathcal{C}_{\phi q 3}\left(\frac{\rm TeV}{\Lambda^2}\right)^2, \end{aligned} $

and the first constant term denotes the SM contribution with next-to-next-to-leading-order (NNLO) QCD corrections [23]. We used FeynRules and MadGraph packages to calculate the relation between Wilson coefficients and observables. The NNPDF is used in our analysis and both the renormalization and factorization scales are set to be dynamic [24-26].
In addition to the operators affecting the single-t production, the
$ tHq $ production involves more operators as follows [1]:$ \begin{aligned}[b] O_{\phi D} & = (\phi^\dagger D^\mu \phi)^*(\phi^\dagger D_\mu \phi), \\ O_{u\phi} & = (\phi^\dagger \phi)(\bar q_p u_r \tilde\phi)+{\rm h.c.}\; , \\ O_{\phi \Box} & = (\phi^\dagger \phi)\Box(\phi^\dagger \phi), \\ O_{\phi W} & = \phi^\dagger \phi W^I_{\mu\nu} W^{I\mu\nu}. \end{aligned} $

(5) Figure 1(d-h) shows the effects of high-dimensional operators in
$ tHq $ production (thick black dots). The operators$ O_{\phi W} $ ,$ O_{\phi q3} $ , and$ O_{uW} $ contribute to the diagrams (d-f), and the operators$ O_{\phi D} $ ,$ O_{u\phi} $ , and$ O_{\phi\Box} $ contribute to a shift of Yukawa coupling or Higgs-gauge coupling as shown in diagrams (g-h). The operator$ O_{u\phi} $ is tightly constrained from gluon-gluon fusion measurements [27], and the operator$ O_{\phi W} $ is severely bounded by the combined analysis of the$ H \gamma \gamma $ ,$ HZZ $ , and$ HZ \gamma $ couplings [28]. The operators$ O_{\phi D} $ and$ O_{\phi \Box} $ are constrained by the oblique parameters [29, 30] and are also mildly sensitive to the$ tHq $ production [10]. Therefore, when maintaining only the interference effect between the SM and NP channels, we remain with only three independent operators:$ O^{(3)}_{qq} $ ,$ O_{\phi q3} $ , and$ O_{uW} $ , which affect both the single-t and$ tHq $ productions.The
$ tHq $ production has not been determined yet owing to its small production rate. We sum up both the$ tHq $ and$ \bar{t}Hq^\prime $ productions hereafter and denote the production cross section of both the$ tHq $ and$ \bar{t}Hq^\prime $ productions as$ \sigma_{tHq} $ :$ \sigma_{tHq} = \left[74.3-11.3C_{qq}^{(3)} + 22.0C_{uW} - 2.6 C_{\phi q3}\right] {\rm fb}. $

(6) -
Owing to the large rate of the single-t production, both the total cross section and the differential distributions have been measured at the LHC and can be used to search for NP beyond the SM. The leptonic decays of the top quark provide a clean collider signature at the LHC and are used widely in experimental searches. Thus, we focus on the channel
$ t\rightarrow \mu + \nu_\mu + b $ and select$ {\rm Br}(t\rightarrow b\mu \nu_\mu ) = (13.4\pm0.6)\% $ [19].Three observables are required to probe the three operators
$ O^{(3)}_{qq} $ ,$ O_{\phi q3} $ , and$ O_{uW} $ . In our analysis, we consider both the single top-quark and single antitop-quark productions. The first observable in our analysis is the total cross section of the single-t production, i.e.,$ \sigma_{t+\bar{t}}\equiv \sigma_t+\sigma_{\bar{t}}. $

(7) The second observable is the cross section ratio of the single-t and single-
$ \bar{t} $ productions, defined as$ R_{t} \equiv \frac{\sigma_{t}}{\sigma_{\bar{t}}}. $

(8) The difference in production rates primarily results from the PDFs of initial states.
The third observable is based on the spin correlation between the charged lepton and top-quark. Owing to its large production rate, the single top-quark processes have been measured at the LHC such that we can examine differential distributions of various observables. We adopt the “spectator basis” to maximize spin correlations based on the top quark produced through the single-t processes being almost 100% polarized along the direction of the spectator quark, which is the light jet produced in association with the top quark [21, 31-34]. The distribution of the cosine of the angle between the charged lepton and the spectator jet in the rest frame of top quark is
$ \frac{1}{\sigma_{t+\bar t}} \frac{\mathrm{d} \sigma_{t+\bar t}}{\mathrm{d} \cos\theta} = \frac{1}{2}\left(1+\frac{N_- -N+}{N_-+N_+} \cos\theta \right), $

(9) where
$ N_- $ ($ N_+ $ ) is the number of top quarks with polarizations against (along) the direction of the spectator jet. The third observable$ A_{FB} $ is defined as$ A_{FB} = \frac{\sigma_F-\sigma_B}{\sigma_F+\sigma_B}, $

(10) where
$ \sigma_F\equiv \int_0^1 \frac{\mathrm{d} \sigma_{t+\bar t}}{\mathrm{d} \cos\theta} \mathrm{d} \cos\theta,\; \; \sigma_B\equiv \int_{-1}^0 \frac{\mathrm{d} \sigma_{t+\bar t}}{\mathrm{d} \cos\theta} \mathrm{d} \cos\theta. $

(11) The distribution of
$ \cos\theta $ is modified by the operators as follows:$\begin{aligned}[b] \frac{\mathrm{d} \sigma_{t+\bar t}}{\mathrm{d} \cos\theta} =& \frac{1}{2}\left(\sigma_{t+\bar t}^{0} + \sum\limits_{i} C_i \sigma_{t+\bar t}^{i} \right)\\&+ \left( A^{0}_{FB} \sigma_{t+\bar t}^{0} + \sum\limits_{i} C_i A^i_{FB} \sigma^i_{t+\bar t} \right) \cos\theta,\end{aligned} $

(12) which yields
$ A_{FB} = \frac{A^{0}_{FB} \sigma_{t+\bar t}^{0} + \displaystyle\sum\nolimits_{i = 1}^{3} C_i A^i_{FB} \sigma^i_{t+\bar t}}{\sigma_{t+\bar t}^{0} + \displaystyle\sum\nolimits_{i = 1}^{3} C_i \sigma_{t+\bar t}^{i}}. $

(13) where
$ \sigma_{t+\bar t}^{i} $ and$ A_{FB}^{i} $ represent the cross section and asymmetry generated by the SM ($ i = 0 $ ) and higher-dimensional operators ($ i = O_{\phi q3} $ ,$ O_{qq}^{(3)} $ ,$ O_{uW} $ ). We consider both the single-t and single-$ \bar{t} $ in the analysis of$ \sigma_{t+\bar t} $ and$ A_{FB} $ . The numerical values of the$ \sigma_{t+\bar t}^{i} $ can be determined using Eq. (4), and the values of$ A_{FB} $ are listed as follows:$ \begin{aligned}[b] &A_{FB}^0 = 0.4596, && A_{FB}^{O_{\phi q3}} = 0.4596,\\ &A_{FB}^{O_{qq}^{(3)}} = 0.4721, && A_{FB}^{O_{uW}} = 0.3548, \end{aligned} $

(14) The operator
$ O_{\phi q3} $ modifies only the magnitude of the$ g_W $ coupling and does not affect the shape of all the differential distributions; therefore, it yields exactly the same asymmetry$ A_{FB} $ as the SM.In our analysis, we normalize the three observables by the SM predictions as follows:
$ \bar{\sigma}_{t} \equiv \frac{\sigma_{t+\bar{t}}}{\sigma_{t+\bar{t}}^0},\quad \mathcal{A} \equiv \frac{A_{FB}}{A_{FB}^0},\quad \mathcal{R} \equiv \frac{R_{t}}{R_{t}^0}. $

(15) Since the contribution of NP operators are assumed to be smaller than the SM, maintaining only the linear term of Wilson coefficients yields
$ \begin{aligned}[b] \bar{\sigma}_{t} =& 1 - 0.059 \times C_{qq}^{(3)} + 0.075\times C_{uW}+ 0.060\times C_{\phi q3},\\ {\mathcal{A}} =& 1 - 0.0033 \times C_{qq}^{(3)} - 0.0349 \times C_{uW},\\ \mathcal{R} =& 1 - 0.0308 \times C_{qq}^{(3)} + 0.0328 \times C_{uW}, \end{aligned} $

(16) from which we obtain
$ \begin{aligned}[b] C_{qq}^{(3)} & = 57 - 28\mathcal{A} - 29 \mathcal{R}, \\ C_{uW} & = 23 - 26 \mathcal{A} + 3\mathcal{R}, \\ C_{\phi q3} & = 10+ 17 \bar\sigma_{t} + 6 \mathcal{A} - 33\mathcal{R}. \end{aligned} $

(17) Note that the three observables exhibit considerably distinct sensitivities to the three operators when considering only the leading effect of NP operators. First, the operator
$ O_{\phi q 3} $ only modifies the magnitude of the W-t-b coupling and does not alter any differential distributions; therefore, it does not contribute to either the asymmetry$ \mathcal{A} $ or the charge ratio$ \mathcal{R} $ . Second,$ \mathcal{A} $ depends primarily on$ O_{uW} $ because$ O_{uW} $ flips the chirality of the top quark and yields an apparent deviation in the$ \cos\theta $ distribution. Third, both$ O_{qq}^{(3)} $ and$ O_{uW} $ yield comparable interference contributions to the single-t production; thus, they contribute equally to the$ \mathcal{R} $ , which is more sensitive to the parton distributions of valence and sea quarks in the initial state. Finally, the cross section$ \bar{\sigma}_t $ is sensitive to all the three operators.A combined analysis of the three observables can aid us in probing NP beyond the SM. For example, the relation between
$ C_{uW} $ and$ C^{(3)}_{qq} $ can be determined from the$ \mathcal{A} $ and$ \mathcal{R} $ measurements (Eq. (17)). In particular, if$ \mathcal{R}\simeq 1 $ and$ \mathcal{A}\neq 1 $ , then$ C_{uW}\simeq C_{qq}^{(3)}\neq 0 $ ; if$ \mathcal{A}\simeq 1 $ and$ \mathcal{R}\neq 1 $ , then$ C_{qq}^{(3)}\sim -10C_{uW} $ . If no deviations are observed in the$ \mathcal{A} $ and$ \mathcal{R} $ measurements, say$ \mathcal{A}\simeq \mathcal{R}\simeq 1 $ , then the only possible NP source in the single-t process will be$ O_{\phi q3} $ , which can be obtained from$ \bar{\sigma}_{t} $ .The current bound of the total cross section of the single-t production is
$ 176\; \text{pb}\leqslant \sigma_{t+\bar t}\leqslant 238\; \text{pb} $ at the$ 1\sigma $ confidence level [35], and the relative error of the cross section measurement is$ \delta \sigma_{t+\bar t} = 15\% $ . It yields$ \bar{\sigma}_{t} = 0.95\pm0.14\; . $

(18) The charge ratio [35-37] and
$ \cos\theta $ distribution [37-39] in the single-t production have been measured at the 13 TeV LHC. Utilizing the unfolding results on the charge ratio and angular distribution provided by the CMS collaboration [37, 38], we compare our parton level analysis directly to the experimental data and obtain$ \mathcal{R} = 1\pm 0.035, $

(19) $ \mathcal{A} = 0.877\pm 0.154, $

(20) where the
$ \mathcal{A} $ is obtained from the linear fitting of the$ A_\mu $ distribution in Ref. [37]. This results in the constraints on the three operators as follows:$ \begin{aligned}[b] & -1.9\leqslant C_{qq}^{(3)} \leqslant 8.8\; ,\\ & -0.9\leqslant C_{uW} \leqslant 7.3\; , \\ & -5.2\leqslant C_{\phi q3} \leqslant 3.9\; . \end{aligned} $

(21) Although the current measurements impose only crude bounds on the three operators, more accurate measurements are anticipated at the high luminosity LHC with an integrated luminosity of
$ 3000\; {\rm fb}^{-1} $ . The uncertainties are primarily due to the PDFs and systematic errors. The major uncertainties of the cross section and forward-backward asymmetry measurements are due to the systematic error, which is approximately 15% [35]. In contrast, the statistical uncertainty is approximately 1%, which can be ignored in our analysis. Therefore, we expect the uncertainties of the cross section and$ A_{FB} $ measurements to be reduced to 10% in our projection of the HL-LHC potential of measuring the single-t production.In the charge ratio measurement, the large systematic errors tend to cancel out and result in a net value comparable to the PDF uncertainty, e.g., both the PDF and systematic errors are
$ \sim 3.0\% $ in the recent CMS data [35]. According to the NNPDF study, the PDF error is expected to be less than 3% when more precision measurements are available [40]. Therefore, we optimistically expect the charge ratio to be measured with an accuracy of 3% at the HL-LHC.Assuming the central values of the three operators are the same as the SM predictions, i.e., centralizing around zero, we obtain the projected constraints on the operators at the HL-LHC as follows:
$ \begin{aligned}[b] & -3.7\leqslant C_{qq}^{(3)} \leqslant 3.7\; , \\ & -2.7\leqslant C_{uW} \leqslant 2.7\; , \\ & -3.2\leqslant C_{\phi q3} \leqslant 3.2\; , \end{aligned} $

(22) where both the cross section and
$ A_{FB} $ measurement are of 10% uncertainties, and more optimistically,$ \begin{aligned}[b] & -2.3\leqslant C_{qq}^{(3)} \leqslant 2.3\; , \\ & -1.4\leqslant C_{uW} \leqslant 1.4\; , \\ & -2.1\leqslant C_{\phi q3} \leqslant 2.1\; , \end{aligned} $

(23) when the systematic uncertainties are improved to be 5%.
-
We now examine the correlation between the single-t and
$ tHq $ productions as they both primarily depend on the three operators. A simple algebra yields$ \sigma_{tHq} = \Big[-95.1 - 44.0\bar{\sigma}_{t}- 266.0{\mathcal{A}} +479.4\mathcal{R}\Big]\; \text{fb}, $

(24) which can be used to check the consistency of the experimental measurement and operator analysis. This indicates that the information of the
$ tHq $ production rate can be inferred from the single-t production if we maintain the interference effect and neglect those sub-leading operators explained above. For example, based on the current measurement of the single-t production, our operator analysis indicates that$ \sigma_{tHq} = \Big[106.8 \pm 64.8\Big]\; {\rm fb} $

(25) at the
$ 1\sigma $ confidence level, which is exceedingly below the current upper limit$ \sigma_{tHq}\leqslant 900\; {\rm fb} $ [41, 42].When we consider only the
$ O_{uW} $ operator, it is better constrained from the measurements of$ b \rightarrow s \gamma $ , the S parameter, and the W-boson helicity fraction [43-49]. However, the above processes also involve more operators that are not related to the single-t and$ tHq $ productions; therefore, the bound on the$ O_{uW} $ can be significantly relaxed by other operators. It does not affect the correlation between the single-t and$ tHq $ productions.Figure 2 depicts the correlations among
$ \sigma_{tHq} $ and the cross section$ \bar{\sigma}_t $ (a), asymmetry$ \mathcal{A} $ (b), and charge ratio$ \mathcal{R} $ (c) at the$ 1\sigma $ confidence level at the current 13 TeV LHC (orange) and HL-LHC (black). In the study of the HL-LHC, the central values of all the three observables are set to 1, the uncertainties of the$ \sigma_{t+\bar t} $ and$ A_{FB} $ are set to 10%, and the uncertainty of$ \mathcal{R} $ is 3%. The capability of the operator analysis is highly limited by the large systematic uncertainties in$ \bar{\sigma}_t $ and$ \mathcal{A} $ . The strongest bound on$ \sigma_{tHq} $ is derived from the$ \mathcal{R} $ measurement owing to the small systematic error.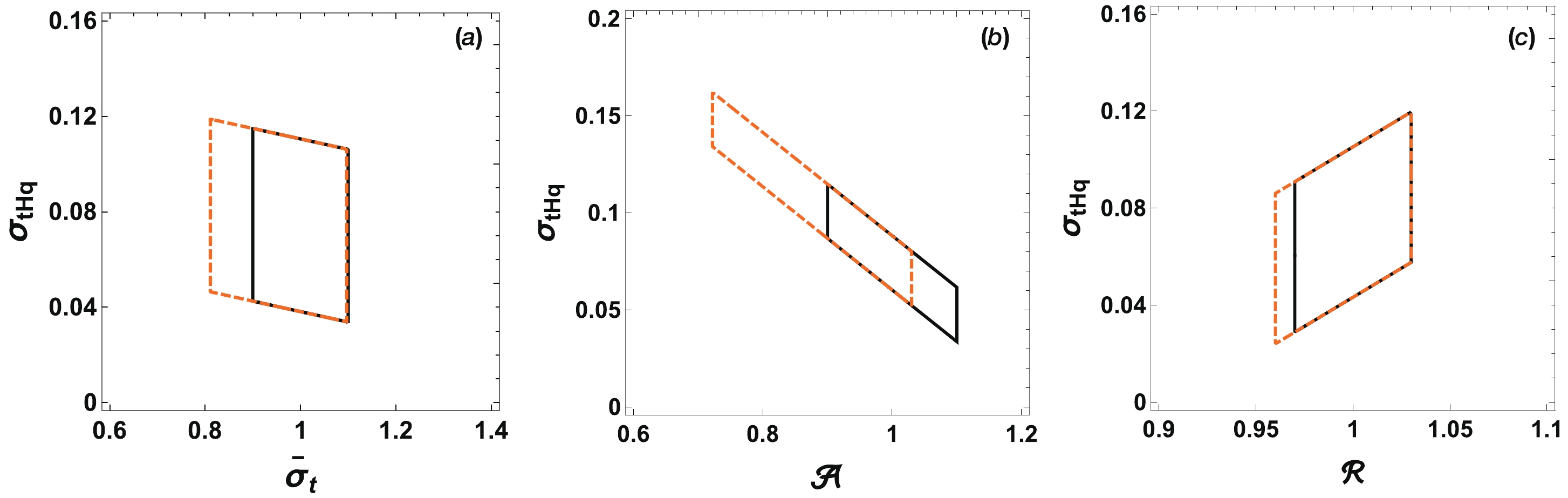
Figure 2. (color online) Correlations among
$ \sigma_{tHq} $ and the cross section$ \bar{\sigma}_t $ (a), asymmetry$ \mathcal{A} $ (b), and charge ratio$ \mathcal{R} $ (c) at the$ 1\sigma $ confidence level at the current 13 TeV LHC (orange) and HL-LHC (black). The central values of all the three observables are set to 1 at the HL-LHC.Assuming the central value of
$ \sigma_{tHq} $ is still the same as the SM prediction at the 13 TeV HL-LHC, we obtain the projected$ \sigma_{tHq} $ as follows:$ \sigma_{tHq} = \Big[74.3 \pm 45.4\; (29.9)\Big]\; {\rm fb}, $

(26) where the systematic errors of both the cross section and
$ A_{FB} $ measurements are$ 10\% $ (5%), and the error of charge ratio measurement is 3%. -
The effective field theory is an effective tool to probe new physics beyond the Standard Model in a model-independent approach. More accurate information of higher-dimensional operators are anticipated at the large hadron collider in the operation phase of high luminosity. When new physics resonances decouple from the electroweak scale, they leave their footprints in various relations among higher-dimensional operators, i.e., strong correlations among the Wilson coefficients. We demonstrate that the single-t production and the
$ tHq $ channel are highly correlated as both processes depend primarily on three dimension-6 operators. At the leading order of operator expansion, we obtain the following relation:$ \begin{aligned}[b] \sigma_{tHq} =& \bigg[ -95.1 - 44.0\times \frac{\sigma_{t+\bar{t}}}{\sigma^{\rm SM}_{t+\bar{t}}} \\ &- 266.0\times \frac{A_{FB}}{A_{FB}^{\rm SM}} +479.4\times \frac{R_t}{R_t^{\rm SM}}\bigg]\; \text{fb}, \end{aligned} $

where
$ \sigma_{t+\bar{t}} $ ,$A_{FB}$ , and$ R_t = \sigma_{t}/\sigma_{\bar t} $ denote the total cross section, asymmetry, and charge ratio measured in the single-t production, respectively. The relation predicts that, according to the current data of single-t production, the yet-to-be measured cross section of the$ tHq $ production at the 13 TeV LHC is$ \sigma_{tHq} = \Big[106.8 \pm 64.8\Big]\; {\rm fb} $

(27) at the
$ 1\sigma $ confidence level, which is exceedingly below the current upper limit$ \sigma_{tHq}\leqslant 900\; {\rm fb} $ . Assuming the central value of$ \sigma_{tHq} $ is still the same as the SM prediction at the 13 TeV HL-LHC, we obtain the projected$ \sigma_{tHq} $ as follows:$ \begin{align} \sigma_{tHq}& = \Big[74.3 \pm 45.4\Big]\; {\rm fb}, \end{align} $

(28) where the systematic errors of both the cross section and
$ A_{FB} $ measurements are$ 10\% $ , and the error of charge ratio measurement is 3%. -
We thank Yandong Liu and Rui Zhang for enlightening discussions and comments.
Single top quark production with and without a Higgs boson
- Received Date: 2021-05-20
- Available Online: 2021-09-15
Abstract: One method of probing new physics beyond the Standard Model is to check the correlation among higher-dimensional operators in the effective field theory. We examine the strong correlation between the processes






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF

















 DownLoad:
DownLoad: