-
The mass-radius trajectories of neutron stars (NSs) are closely related to the equation of state (EOS) of nuclear matter (NM). The radius of an NS with a mass of 1.4
$ M_{\odot} $ depends primarily on the properties of the symmetry energy below the central density of the NS [1], and the maximum mass is primarily determined by the nuclear EOS of isospin symmetric matter at high density. Significant research based on terrestrial experiments has been conducted to constrain the EOS, although the EOS of NM is still poorly defined at high density. In particular, the symmetry energy predicted by various models may be negative or positive at 3 times the saturation density$ \rho_0 $ [2,3]. Although collective flows [4] and Kaon production [5-10] in heavy-ion collisions provide constraints on the EOS of symmetric NM at 1.2-4.5$ \rho_0 $ , there are still uncertainties at densities greater than 4.5$ \rho_0 $ . Consequently, the radius of 1.4$ M_{\odot} $ NSs predicted by various models still contains significant uncertainty, while the maximum mass of the NS predicted by these models also suffers from large uncertainty. Fortunately, the mass-radius trajectories of NSs extracted from astrophysical observations can be used to constrain the EOS. The radius of NSs with a mass of 1.4$ M_{\odot} $ extracted from optical observations ranges from approximately 10-14 km [11-19], while the radius based on the analysis of the tidal deformability parameter of coalescence of a NS binary system was predicted to have an upper limit of 13.7 km [20-24]. The maximum mass of NSs, which is measured using the Shapiro delay, is larger than$ 2M_{\odot} $ [25,26]. The radius of 1.4$ M_{\odot} $ NSs indicates the EOS should be soft at a density below the central density of a 1.4$ M_{\odot} $ NS, and the maximum mass indicates the EOS should be stiff enough at high density to produce$ M \gtrsim2M_{\odot} $ . There are some soft models (such as IU-FSU [27,28] and XS [28]) that can satisfy the radius of 1.4$ M_{\odot} $ NSs extracted from optical observations, but these cannot produce$ M \gtrsim2M_{\odot} $ . Dark matter (DM), which may be mixed with hadronic matter in the NS, is thought to affect the mass-radius trajectories of the NS. With DM admixed NSs (DANSs), these soft models may be able to produce$ M \gtrsim2M_{\odot} $ .DM was originally proposed to explain galactic rotation velocities. Although great efforts have been made to determine the properties of DM, as the interaction between DM and visible matter is either very weak or non-existent, the mass and interactions of DM are still unknown. Therefore, many DM candidates exist, from light axions to heavy weakly interacting massive particles (WIMPs) [29,30]. These DM candidates can be divided into self-annihilating [31,32] and non-self-annihilating [33-39]. Since the self-annihilating DM will heat the host NS, this type of DM can be indrectly observed using astrophysical observations. Unlike self-annihilating DM, if non-self-annihilating DM, including the bosonic and fermionic DM candidates, has self-interaction, the non-self-annihilating DM would accumulate in the host NS and affect its mass-radius trajectories. The accumulation of bosonic DM in the host NS would lead to the formation of a small black hole [40-44]. However, due to the degeneracy pressure, fermionic DM is able to stabilize the host NS. Considering the total EOS as a simple sum of those of DM and NM, as the Fermi-gas DM will affect the total EOS strongly, both the maximum mass and the radius of the DANS with 1.4
$ M_{\odot} $ will increase or decrease simultaneously [45]. The DANS may also be described using a two-fluid system, including one NM and one DM fluid [33-38,46]. In the two-fluid system, there is only gravitational interaction between NM and DM. Considering the DM fluid as an ideal Fermi gas [33-36,38], both the maximum mass and the radius of 1.4$ M_{\odot} $ DANS become small with increasing amounts of DM. Taking into account the various interactions of the fermionic DM fluid [37,38], both the maximum mass and the radius of 1.4$ M_{\odot} $ DANS will increase or decrease at the same time. In these scenarios, the maximum mass of the NS does not increase when the radius of the 1.4$ M_{\odot} $ DANS is smaller than or close to that of one without DM. Therefore, when the soft EOS (such as the XS and IU-FSU models) is used for the NM fluid of the two-fluid system, the maximum mass and the radius of the DANS cannot satisfy the results extracted from astrophysical observations. However, when the fermionic DM is under chiral symmetry and the soft EOS of NM is taken into account, the maximum mass and the radius of DANS may correctly satisfy the results extracted from astrophysical observations.Chiral fermionic DM has been investigated previously [47,48]. Similar to the Standard Model, the gauge symmetry may be spontaneously broken via the Higgs mechanism. After spontaneous symmetry breaking, the elementary fermionic DM acquires a small mass that will softly break the chiral symmetry. The simplest model to implement this process is the chiral
$ SU(2) $ gauge theory with isospin ($ \equiv3/2 $ ) fermionic DM [48]. However, this simple model does not contain the elementary DM condensate and cannot form dark hadrons at low energy. To incorporate these aspects, one can use the chiral$ SU(3)\times SU(2) $ gauge theory [47]. It is worth noting that both the chiral$ SU(2) $ gauge theory and the chiral$ SU(3)\times SU(2) $ gauge theory can interact with the Standard Model via the Higgs portal. In this study, as there is only gravitational interaction between NM and DM, we do not consider the Higgs mechanism for the DM but take the chiral model of DM that is parallel to Quantum Hadron Dynamics (QHD). In doing so, the elementary fermionic DM is a hadron. The dynamic mass, which will break the chiral symmetry, comes naturally from the dark baryon-antibaryon condensate. This process, which was first proposed in the Nambu-Jona-Lasinio (NJL) model [49,50], is named as the spontaneous breaking of chiral symmetry.The NJL model has achieved great success as a popular chiral model. The spontaneous breaking of chiral symmetry is very important in strong interactions. Therefore, the NJL model is widely used on the nucleonic level [51-60] and on the quark level [61-70]. For quarks, since the NJL model neglects the gluon degrees of freedom, it does not confine the quarks. The NJL model is predominantly used to investigate the spontaneous breaking of chiral symmetry in low-energy quantum chromodynamics (QCD) by assuming that gluon degrees of freedom are negligible between quarks, and the confinement of quarks is not important. To describe the static properties of gluons, a popular method is to introduce a Polyakov-loop effective potential in the NJL model [64]. The Polyakov-NJL (PNJL) model allows one to describe both the chiral symmetry breaking and deconfinement phase transition. On the nucleonic level, the original NJL model cannot produce the saturation properties of NM. Similar to the non-linear
$ \sigma $ model, this problem has been solved by introducing a scalar-vector interaction in the NJL model [51]. Since then, the NJL model on the nucleonic level has been widely employed in investigating properties of NSs and nuclei [52-60].This paper is arranged as follows. In Section II, the formalism for obtaining the EOS of NM and DM is briefly introduced. The numerical results and discussions of the two-fluid system are presented in Section III. Finally, a brief summary is given.
-
The relativistic mean-field (RMF) model contains not only the interactions between nucleons but also the interactions between mesons. The nonlinear self-interactions of the
$ \sigma $ meson was introduced to reduce the incompressibility of the original RMF. The nonlinear self-interaction of the$ \omega $ meson was introduced to eliminate the scalar potential instability caused by the nonlinear self-interaction of the$ \sigma $ meson at high density. The interaction between the$ \rho $ and$ \omega $ mesons was introduced to adjust the properties of symmetry energy. The interacting Lagrangian density of the RMF is given as [27,28]:$ \begin{aligned}[b] \mathcal{L} = &\bar{\psi}[\gamma_{\mu}({\rm i}\partial^{\mu}-g_{\omega}{\omega}^{\mu}-g_{\rho}\tau_3b^{\mu})-(M'-g_{\sigma}\sigma)]\psi\\ &+ \frac{1}{2}(\partial_{\mu}\sigma\partial^{\mu}\sigma-m_{\sigma}^2\sigma^2)-\frac{1}{4}F_{\mu\nu}F^{\mu\nu}+\frac{1}{2}m_{\omega}^2{\omega}_{\mu}{\omega}^{\mu} \\ &-\frac{1}{4}B_{\mu\nu}B^{\mu\nu}+\frac{1}{2}m_{\rho}^2b_{\mu}b^{\mu}-\frac{1}{3}g_2\sigma^3-\frac{1}{4}g_3\sigma^4\\ & +\frac{1}{4}c_3({\omega}_{\mu}{\omega}^{\mu})^2+4\Lambda_Vg_{\rho}^2g_{\omega}^2{\omega}_{\mu}{\omega}^{\mu}b_{\nu}b^{\nu}, \end{aligned} $

(1) with strength tensors of
$ \omega $ and$ \rho $ mesons:$ \begin{array}{l} F_{\mu\nu} = \partial_{\mu}\omega_{\nu}-\partial_{\nu}\omega_{\mu}, B_{\mu\nu} = \partial_{\mu}b_{\nu}-\partial_{\nu}b_{\mu}. \end{array} $

(2) $ g_{i} $ and$ m_i $ ($ i = \sigma,\omega,\rho $ ) are the coupling constants and the meson masses, respectively,$ g_2 $ and$ g_3 $ are the coupling constants of the nonlinear self-interaction of$ \sigma $ meson,$ c_3 $ is the coupling constant of the nonlinear self-interaction of$ \omega $ meson, and$ M' $ is the nucleon mass in vacuum.The equations of motion for nucleons and mesons can be obtained from the Euler-Lagrange equations. Using the RMF approximation, the equations of motion are given as follows:
$ \begin{aligned}[b]& [{\rm i}\gamma^{\mu}\partial_{\mu}-g_{\omega}\gamma^{0} \omega_{0}-g_{\rho}\gamma^{0}b_{0}\tau_3-(M'-g_{\sigma}\sigma)]\psi = 0\\ m_{\sigma}^2\sigma =& g_{\sigma}\rho_S-g_2\sigma^2-g_3\sigma^3\\ m_{\omega}^2 \omega_{0} =& g_{\omega} \rho_B-c_3\omega_{0}^3-8\Lambda_Vg_{\rho}^2g_{\omega}^2b_{0}^2{\omega}_{0}\\ m_{\rho}^2 b_0 =& g_{\rho} \rho_3-8\Lambda_Vg_{\rho}^2g_{\omega}^2{\omega}_{0}^2b_{0} . \end{aligned} $

(3) The scalar density
$ \rho_S $ , the baryon density$ \rho_B $ , and the third component of the isovector density$ \rho_3 $ are given as$ \begin{aligned}[b] \rho_B =& \sum\limits_{i = p,n}\frac{k_{F,i}^3}{3\pi^2}\\ \rho_3 =& \frac{k_{F,n}^3}{3\pi^2}-\frac{k_{F,p}^3}{3\pi^2}\\ \rho_S =& \sum\limits_{i = p,n}\frac{2}{{(2\pi)^3}}\int_{0}^{k_{F,i}}{{\rm d}^3k}\frac{M^*}{\sqrt{k^2+{M^*}^2}}, \end{aligned} $

(4) where
$ k_{F,i}(i = n,p) $ is the Fermi momentum and$M^* = M'- $ $ g_{\sigma}\sigma$ is the effective mass of the nucleon. The energy density$ \epsilon $ and pressure$ P $ are obtained from the energy-momentum tensor and written as$ \begin{aligned}[b] \epsilon =& \sum\limits_{i = p,n}\frac{2}{(2\pi)^3}\int_{0}^{k_{F,i}} {\rm d}^3k\sqrt{k^2+{M^*}^2}+\frac{1}{2}m_{\omega}^2\omega_0^2\\& +\frac{1}{2}m_{\sigma}^2\sigma_0^2+\frac{1}{2}m_{\rho}^2b_0^2+\frac{1}{3}g_{2}\sigma_0^3+\frac{1}{4}g_{3}\sigma_0^4\\ &+\frac{3}{4}c_3\omega_0^4+12\Lambda_Vg_\rho^2g_\omega^2\omega_0^2b_0^2, \end{aligned} $

(5) $ \begin{aligned}[b] P =& \frac{1}{3}\sum\limits_{i = p,n}\frac{2}{(2\pi)^3}\int_{0}^{k_{F,i}}{\rm d}^3k\frac{k^2}{\sqrt{k^2+{M^*}^2}}+\frac{1}{2}m_{\omega}^2\omega_0^2\\& -\frac{1}{2}m_{\sigma}^2\sigma_0^2+\frac{1}{2}m_{\rho}^2b_0^2-\frac{1}{3}g_{2}\sigma_0^3-\frac{1}{4}g_{3}\sigma_0^4\\ &+\frac{1}{4}c_3\omega_0^4+4\Lambda_Vg_\rho^2g_\omega^2\omega_0^2b_0^2, \end{aligned} $

(6) where the scalar field
$ \sigma_0 $ , the vector field$ \omega_0 $ , and the isovector field$ b_0 $ are obtained from the equations of motion (Eq. (3)). -
The properties of DM are still open for debate. In this study, we attempt to make the interaction as simple as possible. Thus, similar to the study of Ref. [37], we do not consider the isospin degeneracy in the fermionic DM. The interaction between the fermionic DM is described via the exchange of scalar and vector mesons. The Lagrangian density for the self-interacting fermionic DM with meson exchange (DMM) can be written as [37]:
$ \begin{aligned}[b] \mathcal{L}_D =& \bar{\psi}_D[\gamma_{\mu}({\rm i}\partial^{\mu}-g_{V}{V}^{\mu})-(M_D-g_{\phi}\phi)]\psi_D\\&+ \frac{1}{2}(\partial_{\mu}\phi\partial^{\mu}\phi-m_{\phi}^2\phi^2)+\frac{1}{2}m_{V}^2{V}_{\mu}{V}^{\mu}\\& -\frac{1}{4}(\partial_{\mu}V_{\nu}-\partial_{\nu}V_{\mu})(\partial^{\mu}V^{\nu}-\partial^{\nu}V^{\mu}), \end{aligned} $

(7) where
$ M_D $ is the mass of DM in vacuum, and$ g_{i} $ and$ m_i $ ($ i = V,\phi $ ) are the coupling constant and the meson mass of DM, respectively. The energy density$ \epsilon_D $ and pressure$ P_D $ are similar to those of NM:$ \begin{aligned}[b] \epsilon_{D} =& \frac{2}{(2\pi)^3}\int_{0}^{k_{F,D}}{\rm d}^3k\sqrt{k^2+{M_D^*}^2}+\frac{g_V^2}{2m_V^2}\rho_D^2\\& +\frac{m_\phi^2}{2g_\phi^2}(M_D-M_D^*)^2, \end{aligned} $

(8) $ \begin{aligned}[b] P_{D} =& \frac{1}{3}\frac{2}{(2\pi)^3}\int_{0}^{k_{F,D}}{\rm d}^3k\frac{k^2}{\sqrt{k^2+{M_D^*}^2}}+\frac{g_V^2}{2m_V^2}\rho_D^2\\& -\frac{m_\phi^2}{2g_\phi^2}(M_D-M_D^*)^2, \end{aligned} $

(9) where
$ M_D^* = M_D-g_\phi\phi_0 $ is the effective mass of DM and$ \rho_D = \dfrac{k_{F,D}^3}{3\pi^2} $ is the DM density.This model does not include the chiral symmetry. However, as the chiral symmetry is important in strong interactions, it is relevant to introduce it for DM. Similar to baryons [51-60], the Lagrangian density for self-interacting fermionic DM with chiral symmetry (DMC) is given as follows:
$ \begin{aligned}[b] \mathcal{L}_{D} =& \bar{\psi}({\rm i}\gamma_{\mu}{\partial^{\mu}}-m_0)\psi\\&+\frac{G_S}{2}[(\bar{\psi}\psi)^2-(\bar{\psi}\gamma_5\tau\psi)^2] \\&-\frac{G_V}{2}[(\bar{\psi}\gamma_{\mu}\psi)^2+(\bar{\psi}\gamma_{\mu}\gamma_5\psi)^2], \end{aligned} $

(10) where
$ m_0 $ is the bare DM mass, which corresponds to the DM mass at the critical density of the chiral symmetry restoration, and$ G_S $ and$ G_V $ are the scalar and vector coupling constants, respectively. In the mean field approximation, the energy density$ \epsilon_{D} $ and the pressure$ P_{D} $ of DM with chiral symmetry are written as$ \begin{aligned}[b] \epsilon_{D} = -\frac{2}{{(2\pi)^3}}\int_{k_{F,D}}^{\Lambda}{{\rm d}^3k}(k^2+M_{DC}^{*2})^{1/2}+\frac{G_V\rho_D^2}{2} +\frac{G_S\rho_{SD}^2}{2}+\epsilon_0 \end{aligned} $

(11) $ \begin{aligned}[b] P_{D} =& \rho_{D}\frac{\partial\epsilon_{D}}{\partial\rho_{D}}-\epsilon_{D} = -\frac{1}{3}\frac{2}{{(2\pi)^3}}\int_{k_{F,D}}^{\Lambda}\frac{{\rm d}^3k}{(2\pi)^3}\frac{k^2}{\sqrt{k^2+M_{DC}^{*2}}}\\& +\frac{G_{V}\rho_D^{2}}{2} -\frac{G_S\rho_{SD}^{2}}{2}+\frac{\Lambda^3\sqrt{\Lambda^2+M_{DC}^{*2}}}{3\pi^2}-\epsilon_0, \end{aligned} $

(12) where
$ \Lambda $ is the momentum cutoff, and$ \epsilon_0 $ is introduced to ensure$ \epsilon_{D} = 0 $ in a vacuum. The number density$ \rho_D $ , the scalar density$ \rho_{SD} $ , and the effective mass$ M_{DC} $ are written as$ \begin{aligned}[b] \rho_D =& \frac{k_{F,D}^3}{3\pi^2}\\ \rho_{SD} =& -\frac{2}{{(2\pi)^3}}\int_{k_{F,D}}^{\Lambda}\frac{{\rm d}^3k}{(2\pi)^3}\frac{M_{DC}^*}{\sqrt{k^2+M_{DC}^{*2}}}\\ M_{DC}^* =& m_0-G_S\rho_{SD}. \end{aligned} $

(13) When the DM density
$ \rho_D $ is given, the EOSs (the energy density and the pressure) are easily obtained using Eqs. (11) and (12). -
We assume the interaction between the NM fluid and DM fluid is only gravitational. The energy-momentum tensors of NM fluid and DM fluid are conserved separately. The two-fluid Tolman-Oppenheimer-Volkoff (TOV) equation, which comprises a combination of NM fluid and DM fluid, is defined as [33-38,46]:
$ \begin{aligned}[b] \frac{{\rm d}P_N}{{\rm d}r} =& \frac{-[P_N(r)+\epsilon_N(r)][M(r)+4\pi r^3P(r)]}{r[r-2M(r)]}\\ \frac{{\rm d}P_D}{{\rm d}r} =& \frac{-[P_D(r)+\epsilon_D(r)][M(r)+4\pi r^3P(r)]}{r[r-2M(r)]}, \end{aligned} $

(14) where
$ P_{N} $ ($ P_{D} $ ) and$ \epsilon_{N} $ ($ \epsilon_{D} $ ) are the the pressure and energy density of NM (DM), respectively. The pressure$ P(r) = P_N(r)+P_D(r) $ , which resists gravity, is the sum of the pressures of NM and DM. The total gravitational mass$ M(r) = M_N(r)+M_D(r) $ is defined as$ M(r) = 4\pi\int_0^r(\epsilon_N(r')+\epsilon_D(r'))r'^2{\rm d}r'. $

(15) We have taken the value of
$ G = c = 1 $ here. When the EOS of NM and DM is given, the radius$ R $ and the total gravitational mass$ M(R) $ of the DANS are determined by taking Eqs. (14) and (15) with the condition$ P(R) = 0 $ .Aside from the mass-radius relations, the tidal deformability, which describes the deformation degree of a compact star under gravitational effects, is a prominent topic in astrophysics. The dimensionless tidal deformability of a compact star is defined as [20-24,71-74]
$ \Lambda_{CP} = \frac{2}{3}k_2C^{-5}, $

(16) where
$ C $ (defined as$ M/R $ ) is the compactness parameter, and$ k_2 $ , which depends on the structure of the compact star, is written as$ \begin{aligned}[b] k_2 =& \frac{8C_5}{5}(1-2C)^2[2+2C(y_R-1)-y_R]\{2C[6\\&-3y_R+3C(5y_R-8)] +4C^3[13-11y_R+C(3y_R-2)\\&+2C^2(1+y_R)]+3(1-2C)^2[2-y_R+2C(y_R-1)]\\& \times \ln(1-2C)\}^{-1} .\end{aligned} $

(17) The quantity of a two-fluid system
$ y_R $ (defined as$ y(R) $ ) is obtained by solving the following differential equation [74]:$ y\frac{{\rm d}y(r)}{{\rm d}r}+y(r)^2+y(r)F(r)+r^2Q(r) = 0, $

(18) with
$ F(r) = \frac{r-4\pi r^3[\epsilon_N(r)+\epsilon_D(r)-P_N(r)-P_D(r)]}{r-2M(r)}, $

(19) $ \begin{aligned}[b] Q(r) =& \frac{4\pi r[5(\epsilon_N(r)+\epsilon_D(r))+9(P_N(r)+P_D(r))]}{r-2M(r)}\\& +\frac{4\pi r\left[\dfrac{\epsilon_N(r)+P_N(r)}{\partial P_N(r)/\partial \epsilon_N(r)}+\dfrac{\epsilon_D(r)+P_D(r)}{\partial P_D(r)/\partial \epsilon_D(r)}-\dfrac{6}{4\pi r^2}\right]}{r-2M(r)}\\& -4\left[\frac{m(r)+4\pi r^3(P_N(r)+P_D(r))}{r^2(1-2M(r)/r)}\right]^2. \end{aligned} $

(20) According to the two-fluid TOV equation and the additional boundary condition
$ y(0) = 2 $ , Eq. (18) can be solved. It is worth noting that there is a small difference between the two-fluid quantity$ y_R $ and the one-fluid quantity. -
During the formation of an NS, some DM may reside in the host NS due to gravitational interactions. Then, owing to the self-interaction of DM, more non-self-annihilating DM will accumulate in the host NS. In the two-fluid system, the total radius and mass of DANSs depend not only on the EOS of NM but also the EOS of DM. Since the EOS of non-self-interacting DM is softer than the EOS of NM [33-36,38], the accumulation of non-self-interacting DM will lead to decreases of both the maximum mass and the radius of 1.4
$ M_\odot $ NSs. When the DM exhibits self-interaction [37,38], the EOS becomes more complicated. The accumulation of self-interacting DM may lead to decreases of both the maximum mass and the radius of 1.4$ M_\odot $ NSs, or it may lead to an explicit DM halo with a large radius. In previous studies, it is certain that the maximum mass of an NS does not increase when the radius of a DANS of 1.4$ M_\odot $ is smaller than that of one without DM. We have investigated whether the EOS of self-interacting DM can simultaneously produce$ M \gtrsim2M_{\odot} $ and a small radius for 1.4$ M_\odot $ NSs.The DMC model has four parameters:
$ \Lambda $ ,$ m_0 $ ,$ G_S $ , and$ G_V $ . These parameters are arbitrary, so we choose the cutoff momentum Λ as 400 MeV, and set the bare mass of DM$ m_0 $ to be 5 MeV. The scalar coupling constant$ G_S $ is adjusted to obtain the DM mass$ M_{DC}^* $ in a vacuum. Since the DM is not bound, the vector coupling constant$ G_V $ is chosen to make the EOS of DM a monotonically increasing function. The DMM model has five parameters:$ M_D $ ,$ m_\phi $ ,$ m_V $ ,$ g_\phi $ , and$ g_V $ . In this model, as the potential should be attractive at large distances and repulsive at short distances,$ m_V $ must be greater than$ m_\phi $ , and$ g_V $ must be greater than$ g_\phi $ . We set$ m_\phi $ = 500 MeV and$ m_V $ = 1000 MeV. For comparison,$ g_\phi $ and$ g_V $ are determined by$ C_S = \dfrac{g_\phi^2}{m_\phi^2} = G_S $ and$ C_V = \dfrac{g_V^2}{m_V^2} = G_V $ , respectively. When$ C_S $ and$ C_V $ are given, the DM mass of the DMM model$ M_D $ is set to that of the DMC model$ M_{DC}^* $ in vacuum.To produce the maximum mass
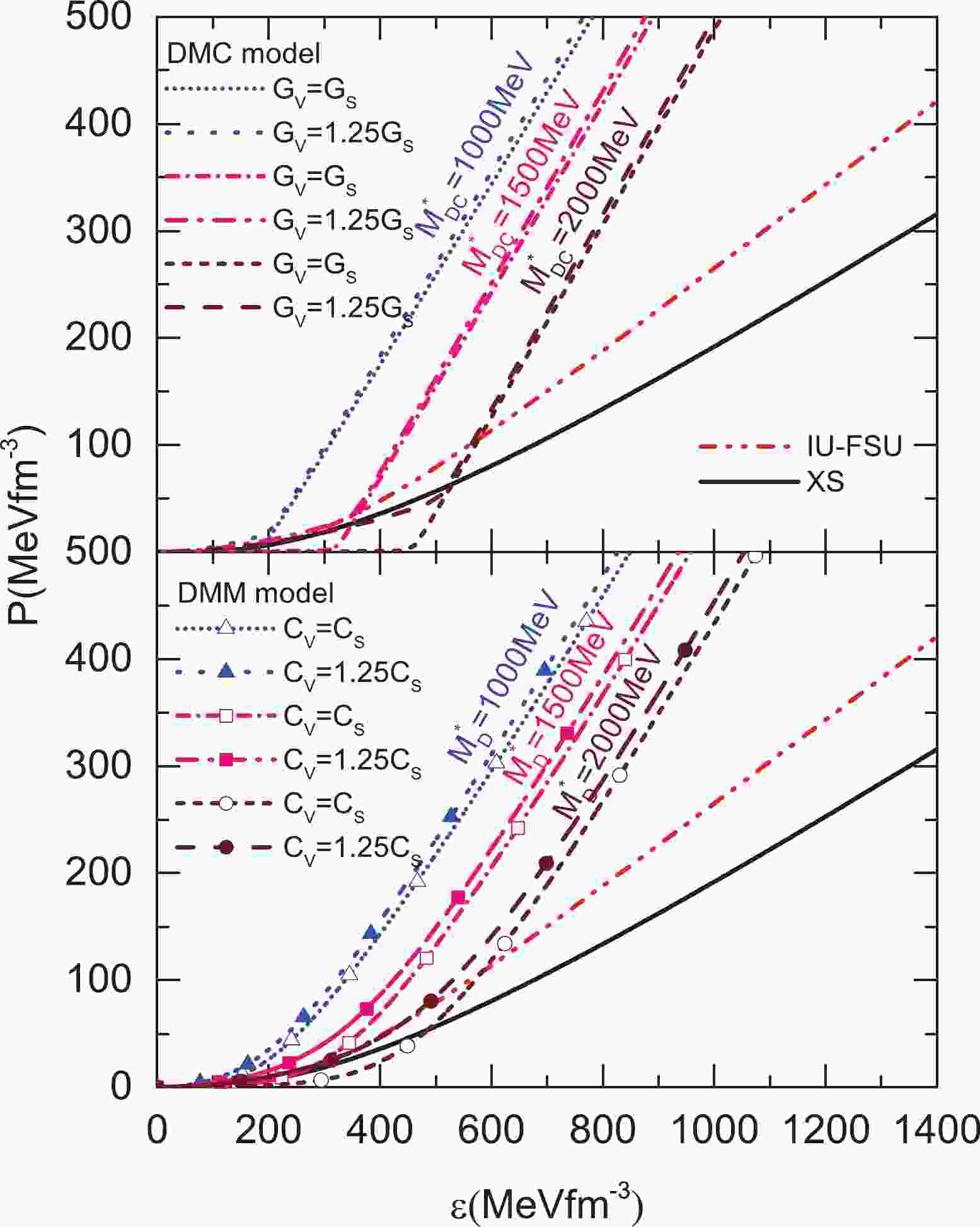
$ M \gtrsim2M_{\odot} $ with a reasonable radius for a 1.4$ M_\odot $ NS, the EOS of NM should be soft at low density and stiff at high density. However, as shown in Fig. 1, the EOSs of the IU-FSU [27, 28] and XS [28] models are soft at low density but not stiff enough at high density. Therefore, as shown in Table 1, although the EOS of NM with the IU-FSU and XS models can produce a reasonable radius for 1.4$ M_\odot $ NSs, it cannot produce$ M\gtrsim2M_{\odot} $ . In a two-fluid system, for producing$ M \gtrsim2M_{\odot} $ and a reasonable radius for a 1.4$ M_\odot $ NS, the EOS of DM should be softer or close to that of the XS and IU-FSU models at low density, but stiffer than that of the XS and IU-FSU models at high density. When the cutoff momentum$ \Lambda $ of the DMC model is fixed, the scalar coupling constant$ G_S $ is determined by the DM mass$ M_{DC}^* $ . Here, we choose the DM masses$ M_{DC}^* $ for the DMC model as 1000, 1500, and 2000 MeV. As displayed in Fig. 1, in the DMC model, the EOS for a large DM mass is softer than that for a small DM mass. For all given DM masses$ M_{DC}^* $ , the EOS of the DMC model with$ G_V = G_S $ can be softer at low density and stiffer at high density than that of NM. As the$ G_V $ increases to$ 1.25G_S $ , the EOS becomes stiff, particularly at low density. For the DMM model, the EOS for a large DM mass is also softer than that for a small DM mass. However, there are some differences between the DMM model and the DMC model. For instance, for the same DM mass in vacuum and coupling strength ($ C_S = \dfrac{g_\phi^2}{m_\phi^2} = G_S $ and$ C_V = \dfrac{g_V^2}{m_V^2} = G_V $ ), the EOS for the DMC model is softer than that for the DMM model at low density, while the EOS for the DMC model is stiffer than that for the DMM model at high density. The difference between the EOS for the DMC model and that for the DMM model is predominantly due to the chiral symmetry of the DMC model. When the chiral symmetry of the DMC model is restored, the scalar part of the EOS vanishes, and the EOS becomes stiff.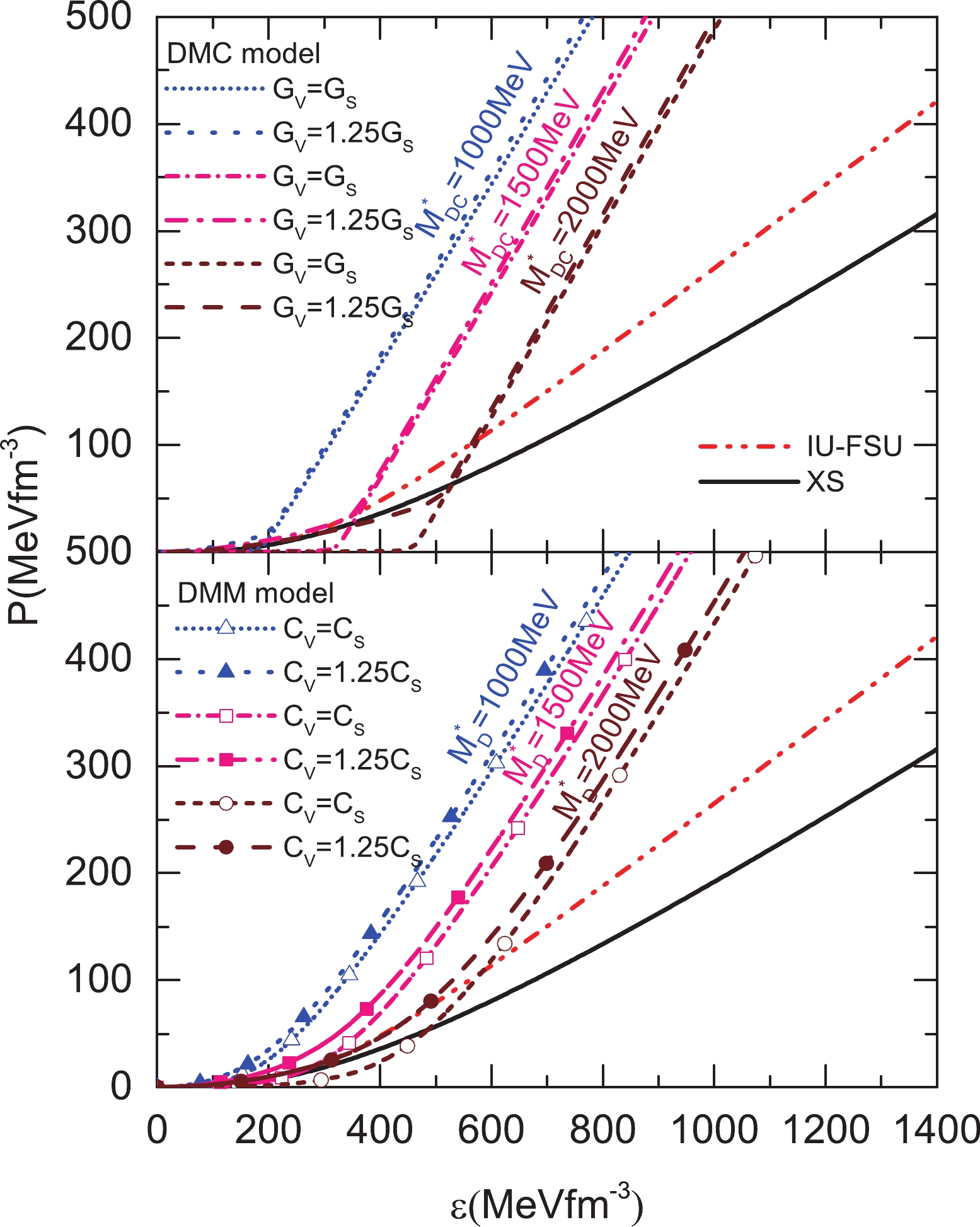
Figure 1. (color online) Pressure and energy density relationship of DM for various DM masses. Interactions with various strengths are considered. The units of
$ G_S $ ($ C_S $ ) and$ G_V $ ($ C_V $ ) are GeV$\rm fm^3$ . For comparison, the results for NM using the XS and IU-FSU models are also displayed.Model $ g_\sigma $ 

$ g_\omega $ 

$ g_\rho $ 

$ m_\sigma $ 

$ m_\omega $ 

$ m_\rho $ 

$ g_2 $ 

$ g_3 $ 

$ c_3 $ 

$ \Lambda_V $ 

$ \rho_0 $ 

$M_{\max}/M_{\odot}$ 

$ R(1.4M_\odot) $ 

IU-FSU 9.971 13.032 6.795 491.500 782.500 763.000 8.493 0.488 144.219 0.046 0.155 1.96 12.5 XS 11.446 16.066 7.314 491.500 782.500 763.000 0.030 124.114 999.268 0.040 0.148 1.61 11.9 Table 1. Parameter sets for the IU-FSU and XS models.
$M_{\max}/M_{\odot}$ is the maximum mass of an NS predicted by the IU-FSU and XS models, and$ R(1.4M_\odot) $ is the radius of an NS of$ 1.4M_\odot $ .With the EOSs in Fig. 1 and Eq. (14), the mass-radius trajectories of DANSs for various amounts of DM are easily obtained. As shown in Fig. 2, for a central energy density ratio of DM to NM of 0.5, as the EOS of DM for various interactions differs, the mass-radius trajectories of DANSs are very complicated. When the EOS for DM is very soft at a central energy density ratio of DM to NM of 0.5, the total DM mass is very small and gathers in the center of the DANS. For example, with
$ G_V = G_S $ ($ C_V = C_S $ ) and a DM mass of 2000 MeV, the mass-radius trajectory of the DANS almost coincides with that of one without DM, for a total mass below the maximum mass of the DANS. As the vector repulsion coupling constant$ G_V $ ($ C_V $ ) increases to 1.25$ G_S $ (1.25$ C_S $ ), the EOS for a DM mass of 2000 MeV becomes stiff. As a result, the total DM mass in the center of the DANS increases, and the increase of total DM mass causes the DANS to shrink earlier. When the DM mass equals 1500 MeV, the mass-radius trajectory of the DANS with various interactions is similar to that with a DM mass of 2000 MeV. The maximum mass of the DANS with a DM mass of 1500 MeV and 2000 MeV is lower than one without DM for a central energy density ratio of 0.5. However, for$ G_V = G_S $ ($ C_V = C_S $ ) and a DM mass of 1000 MeV, although the central energy density ratio of DM to NM is 0.5, the total DM mass of the DANS will surpass the total NM mass, as the EOS for the DM becomes very stiff. In this case, the total pressure$ P(r) = P_N(r)+P_D(r) $ can resist the collapse of the DANS, meaning the maximum mass is higher than one without DM, and even higher than 2$ M_\odot $ . With a DM mass of 1000 MeV, as the EOS of DM is soft at low density for$ G_V = G_S $ ($ C_V = C_S $ ), the radius of a 1.4$ M_\odot $ DANS may be less than one of pure NM. When the EOS of DM is stiff at all densities, both the maximum mass of the DANS and the radius of a 1.4$ M_\odot $ NS will surpass those of pure NM. For instance, when$ C_V = 1.25C_S $ and the DM mass equals 1000 MeV in the DMM model, the radius of the DANS will always surpass one of pure NM, and even surpass the constraint extracted from the GW170817 event. This result indicates that a clear DM halo surrounds the NM.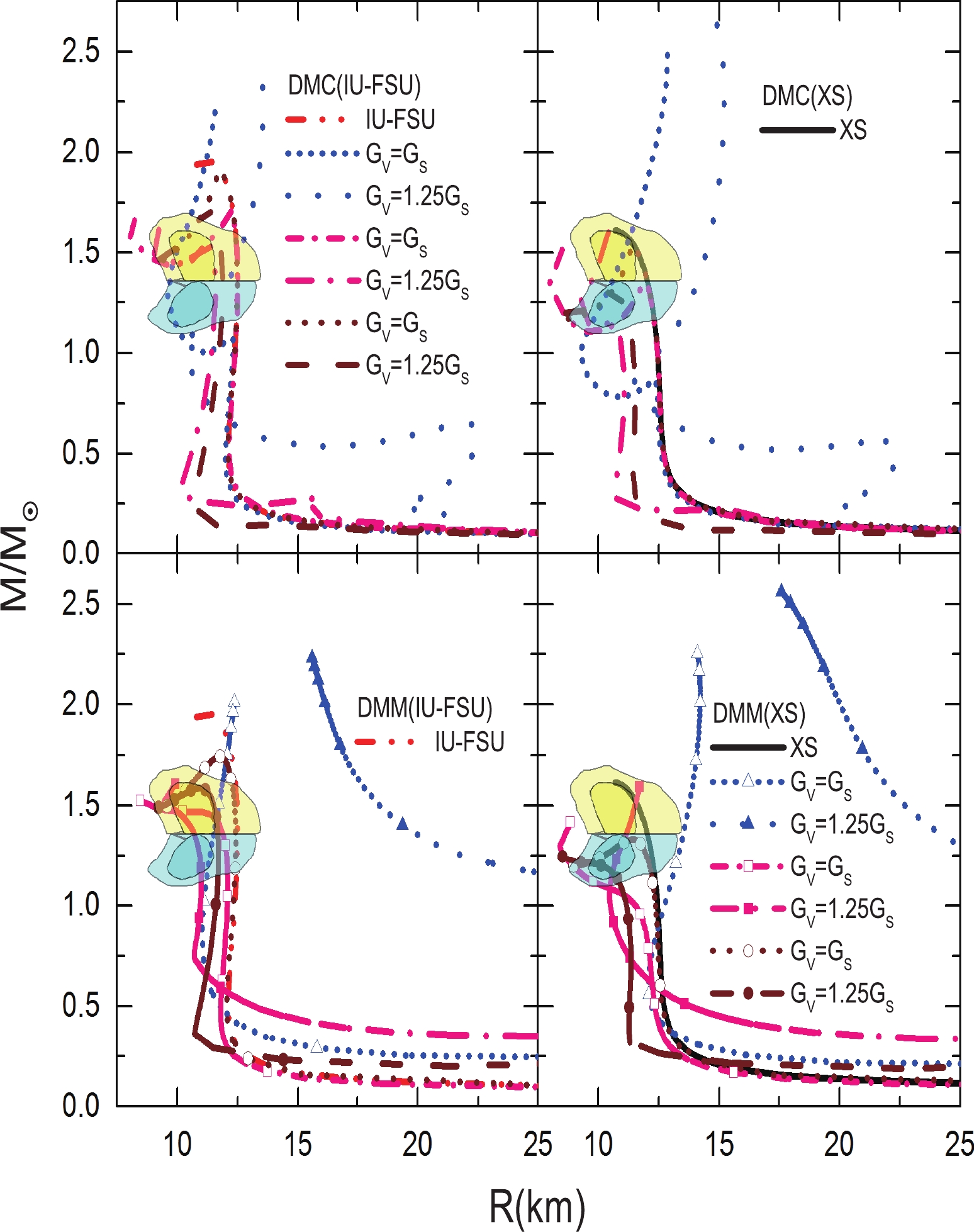
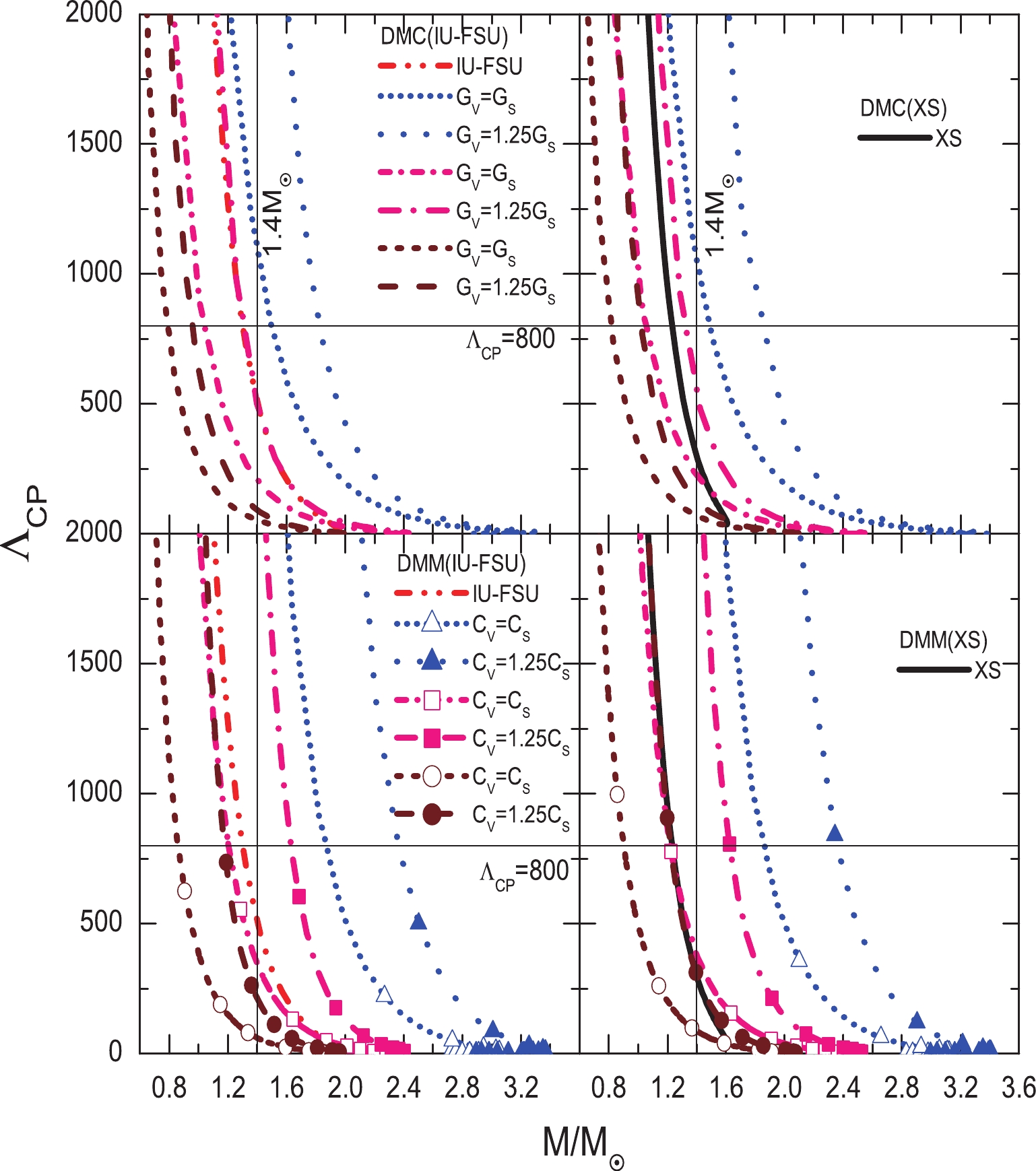
Figure 2. (color online) Mass-radius relations for a central energy density ratio of DM to NM of 0.5. DMC(IU-FSU), DMC(XS), DMM(IU-FSU), and DMM(XS) refer to the DMC model or DMM model admixed with the IU-FSU model or XS model in the two-fluid system, respectively. XS and IU-FSU denote a normal DM-free neutron star. The yellow and cyan regions represent the constraints given by using EOS-insensitive relations to analyze the GW170817 event [24].
Since there are interactions with DM, it may continue to accumulate. As shown in Fig. 3, the mass-radius trajectories of DANSs are displayed for the central energy density ratio of DM to NM of 1.0. For a DM mass of 2000 MeV, the maximum mass of the DANS is still lower than 2.0
$ M_\odot $ . When the DM mass decreases to 1500 MeV, the EOS of the DM becomes stiff at high density, and the maximum mass of the DANS surpasses 2.0$ M_\odot $ . For a DM mass of 1500 MeV and$ G_V = G_S $ ($ C_V = C_S $ ), the EOS of the DM is lower than that of NM at low density, and the radius of a 1.4$ M_\odot $ DANS is less than one without DM. When the vector coupling constant$ G_V $ ($ C_V $ ) increases to 1.25$ G_V $ (1.25$ C_V $ ), the mass-radius trajectories of the DANSs are complicated. In the DMC model, as the EOS of DM with a DM mass of 1500 MeV and$ G_V = 1.25G_S $ is still softer than that of IU-FSU at low density, the radius of a 1.4$ M_\odot $ DANS is lower than that of IU-FSU. However, since the EOS of the DMC model with a DM mass of 1500 MeV and$ G_V = 1.25G_S $ is stiffer than that of XS at low density, the radius of a 1.4$ M_\odot $ DANS surpasses that of XS. In the DMM model, the radius of a 1.4$ M_\odot $ DANS with a DM mass of 1500 MeV and$ C_V = 1.25C_S $ surpasses that of both IU-FSU and XS. For a DM mass of 1000 MeV, the maximum mass of all DANS surpasses 2.75$ M_\odot $ . For a DM mass of 1000 MeV, the radius of DANSs of various masses for the DMM model will always surpass that of pure NM and form halos around the NM. However, as the DMC model has chiral symmetry, the EOS of DM for the DMC model can be very soft at low density. As a result, for a DM mass of 1000 MeV and$ G_V = G_S $ , the radius of a 1.4$ M_\odot $ DANS for the DMC model is not very large and is close to that of pure NM. Additionally, it is still within the constraints extracted from the GW170817 event.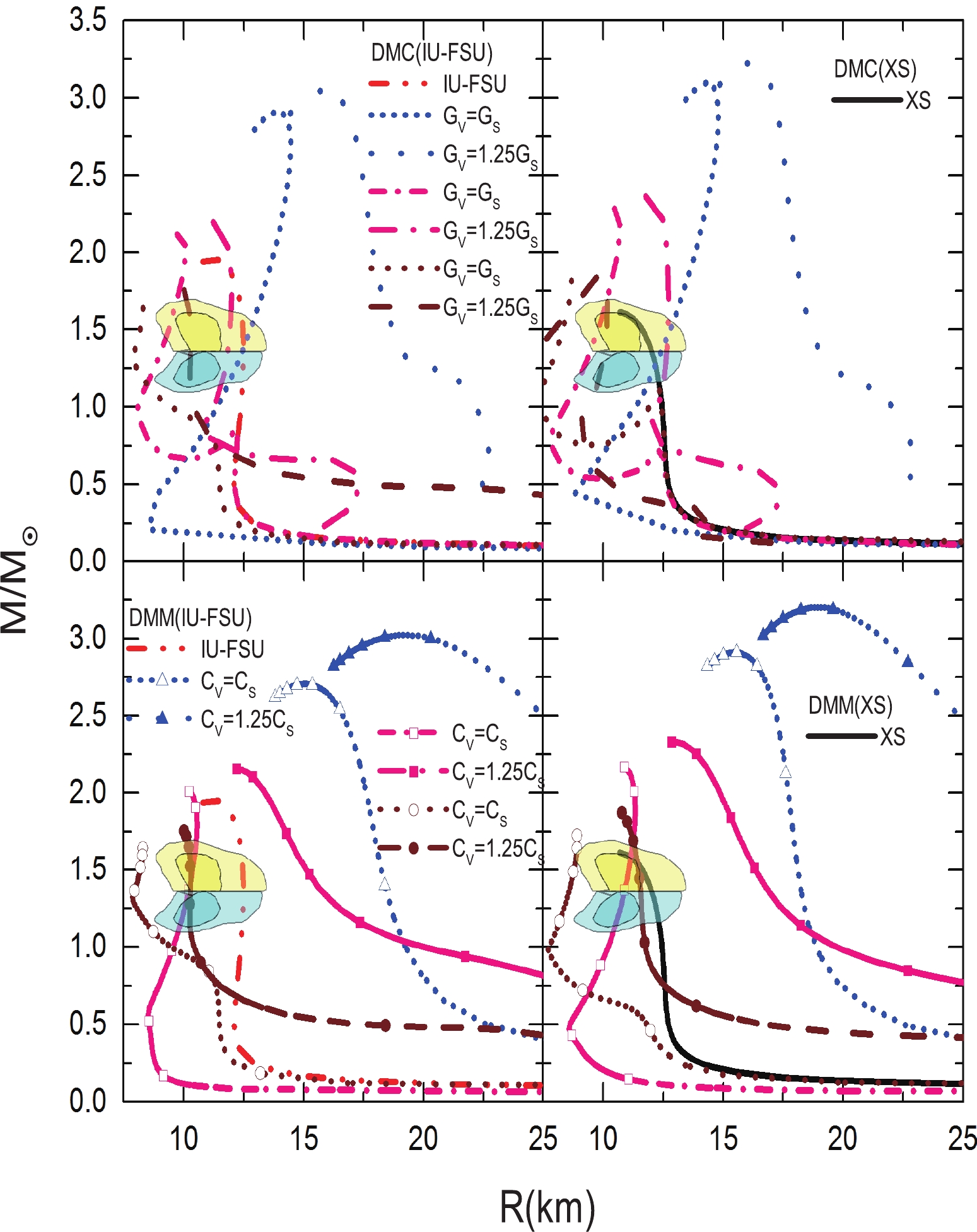
Figure 3. (color online) The same as Fig. 2 but for a central energy density ratio of DM to NM of 1.0.
As displayed in Fig. 4, the central energy density ratio of DM to NM is 1.5. Since the EOS of DM will surpass one of NM at high density, the maximum mass of the DANS will eventually surpass one of pure NM as the central energy density ratio of DM to NM increases. For a DM mass between 1500 and 2000 MeV, there are always DM interactions that can satisfy the maximum mass and radius extracted from astrophysical observations. However, when the DM mass equals 1000 MeV, the radius of the DANS for the DMM model becomes large, and cannot satisfy the radius extracted from astrophysical observations. Interestingly, for a DM mass of 1000 MeV, the radius of the DANS for the DMC model with
$ G_V = G_S $ still satisfies the constraint extracted from the GW170817 event. This is due to the EOS of the DMC model being softer than that of the DMM model at low density for a DM mass of approximately 1000 MeV.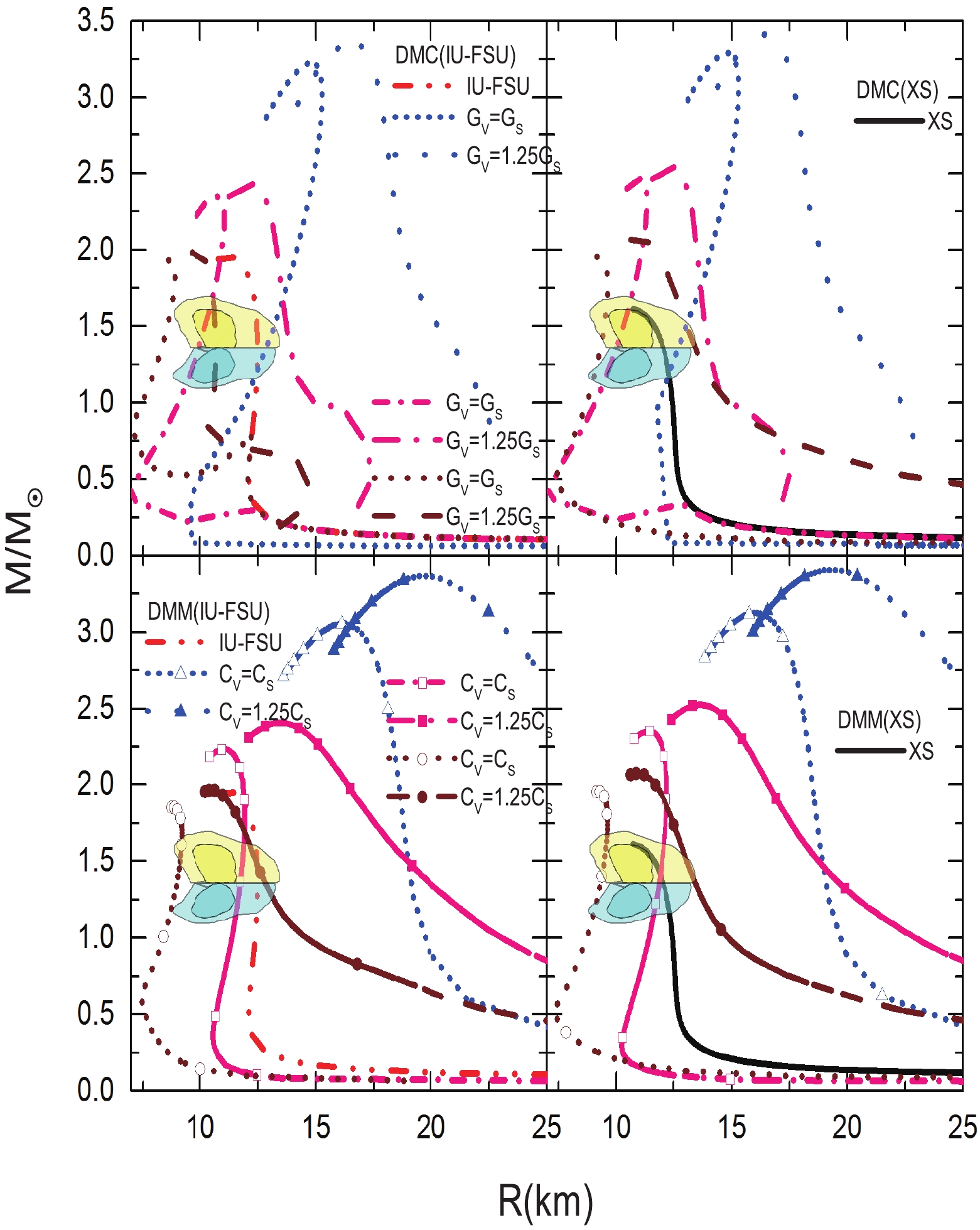
Figure 4. (color online) The same as Fig. 2 but for a central energy density ratio of DM to NM of 1.5.
In the two-fluid system, the difference in the mass-radius relationship between the DMM and DMC models becomes obvious when the central energy density of DM is greater than that of NM. Therefore, we investigated the dimensionless tidal deformability
$ \Lambda_{CP} $ for a central energy density ratio of DM to NM of 1.5. As shown in Fig. 5, similar to the case of a compact star without DM, the$ \Lambda_{CP} $ of the DANS of 1.4$ M_\odot $ depends predominantly on its radius when the maximum masses of the DANSs are close to each other. Therefore, for the same mass of the DANSs, the$ \Lambda_{CP} $ for the DMM model is always larger than that of the DMC model for the same DM mass and coupling strength. For larger differences in maximum mass, the$ \Lambda_{CP} $ of a 1.4$ M_\odot $ DANS increases for increasing maximum mass of the DANS [21,23]. For instance, for the DMC model, as the maximum mass of the DANS with a DM mass of 1500 MeV and$ G_V = 1.25G_S $ is smaller than that of a DANS with a DM mass of 1000 MeV and$ G_V = G_S $ , the$ \Lambda_{CP} $ of the DANS with a DM mass of 1500 MeV and$ G_V = 1.25G_S $ is always smaller than that of a DANS with a DM mass of 1000 MeV and$ G_V = G_S $ . Moreover, when the DMC model takes a DM mass of 1000 MeV and$ G_V = G_S $ , the radius of the DANS of 1.4$ M_\odot $ is approximately 13.0 km, however, the$ \Lambda_{CP} $ of the DANS is higher than$ \Lambda_{CP} = 800 $ . -
In this study, we introduce chiral symmetry in the DM and investigate the properties of DANSs using the two-fluid TOV approach. In the two-fluid system, early studies have shown that both the maximum mass and the radius of a 1.4
$ M_{\odot} $ DANS will decrease or increase simultaneously. These studies imply that the DM admixed soft EOS of NM (such as IU-FSU and XS) cannot produce$ M \gtrsim2M_{\odot} $ and a reasonable radius for a 1.4$ M_\odot $ DANS at the same time using the two-fluid approach. We provide a different result, that is, the maximum mass of the DANS increases, but the radius of the 1.4$ M_\odot $ DANS decreases. This provides the possibility for soft EOSs to explain astrophysical observations. In DANSs, when the the central energy density ratio of DM to NM is 0.5, with DM masses of 1500 MeV and 2000 MeV, the maximum mass of the DANS still cannot reach 2$ M_\odot $ . However, for a DM mass of 1000 MeV, there are interactions within the DMC and DMM models that can produce$ M \gtrsim2M_{\odot} $ and a reasonable radius for a 1.4$ M_\odot $ DANS. The difference between the DMC model and DMM model is not obvious for a central energy density ratio of DM to NM of 0.5. When the the central energy density ratio increases to 1.0, except for a DM mass of 2000 MeV, the DMM model and the DMC model with DM masses of 1000 MeV and 1500 MeV can produce$ M\gtrsim2M_{\odot} $ . At this central energy density ratio, only when the DM mass is 1500 MeV can the DMM model produce a reasonable radius for a 1.4$ M_\odot $ DANS. However, the DMC model with DM masses of both 1000 MeV and 1500 MeV can reproduce a reasonable radius for a 1.4$ M_\odot $ NS. For instance, the DMC model with a DM mass of 1000 MeV when admixed with NM can produce a maximum mass of 2.75$ M_\odot $ and a radius of 1.4$ M_\odot $ below 13.7 km. This is due to the EOS of the DMC model with a DM mass of 1000 MeV being very soft at low density and very stiff at high density. This is similar to the case of central energy density ratios being 1.0 and 1.5. Indeed, in the two-fluid system, increasing the maximum mass and decreasing of the radius of the 1.4$ M_\odot $ DANS can occur simultaneously. We have also investigated the dimensionless tidal deformability$ \Lambda_{CP} $ of DANSs for a ratio of DM to NM of 1.5. Similar to the previous study of DANSs, when the maximum masses of the DANSs were close to each other, the$ \Lambda_{CP} $ of the 1.4$ M_\odot $ DANS depends predominantly on its radius. However, when the maximum masses of the DANS are further apart, the$ \Lambda_{CP} $ of the 1.4$ M_\odot $ DANS largely depends on the maximum mass and increases with increasing maximum mass of the DANS.
Dark matter with chiral symmetry admixed with hadronic matterin compact stars
- Received Date: 2021-09-30
- Available Online: 2022-04-15
Abstract: Using the two-fluid Tolman-Oppenheimer-Volkoff equation, the properties of dark matter (DM) admixed neutron stars (DANSs) have been investigated. In contrast to previous studies, we find that an increase in the maximum mass and a decrease in the radius of 1.4





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF















 DownLoad:
DownLoad: