-
Direct and indirect searches for Dark Matter (DM) so far have given a lot of constraints on the DM interaction [1–9]. In particular, direct detection experiments [1–4] have constrained the DM–nucleus interaction cross section to be less than around
$ 10^{-46} $ cm2 for GeV–TeV-scale DM particles. These direct detection measurements have raised serious concerns that GeV–TeV-scale DM should have interactions much weaker than we thought, such that for the DM candidate of weakly interacting massive particles, an over-production of the relic density with thermal production mechanisms seems hard to avoid.One way out of this difficulty is to note that the dark sector particle directly involved in the thermal production mechanism may not be the DM candidate, but rather the mother particle of a decay process with the DM particle as the child particle. In such a scenario, the DM relic density is derived from the relic density of another dark sector particle obtained from the thermal production mechanism. Since the mass of the DM particle could be much smaller than the mass of other dark sector particle, one can obtain a relic density of DM much smaller than the relic density directly obtained in the thermal production mechanism. Therefore, in such a scenario, one can still have a weak-scale interaction between the dark sector and the visible sector, and yet obtain a DM relic density consistent with cosmological observations.
This possibility of light DM from dark sector decay has been explored in a previous work [10]. In this article, we further study some collider phenomenology of this DM scenario. We will focus on the potential collider signature of a DM model which can have light DM from dark sector decay. We study the feasible signatures at future lepton colliders, such as CEPC, FCC-ee and ILC. For the sake of comparison, we also study the signature and constraints from a hadron collider such as the LHC.
The article is organized as follows. In the next section, we quickly review the DM model we are considering and the various constraints on the model. Then we study the signature of the DM model at future lepton colliders. After a detailed analysis of the signature at a lepton collider, we give a brief analysis on the signature at a hadron collider. We summarize in the last section.
-
The model we consider is an extension of the Type-I seesaw model where the right-handed neutrinos
$ N_{R} $ are coupled to a dark sector consisting of a real scalar ϕ and a Dirac fermion χ [10]. The model is similar to DM models in which$ N_{R} $ works as a portal to the DM [11–15]. Previous works on this type of models have focused on the possibility that the DM relic density is achieved by the thermal freeze-out mechanism [14–16] or by the freeze-in mechanism [17–20]. Here, we consider the possibility that the DM relic density is given mainly by the decay of other heavier particles in the dark sector which were first studied in Ref. [21].We impose a
$ Z_2 $ symmetry in the Lagrangian with the dark sector particles χ and ϕ odd and SM fermions even under the$ Z_2 $ operation. This guarantees the lightest of the dark sector particles to be stable, and makes it a DM candidate. We can write the full Lagrangian as the sum of four parts$ \begin{equation} \mathcal{L} = \mathcal{L}_{\mathrm{SM}}+\mathcal{L}_{\rm {Seesaw }}+\mathcal{L}_{\mathrm{DS}}+\mathcal{L}_{\rm {int}}, \end{equation} $

(1) where the first term is the Standard Model (SM) Lagrangian and the other three terms are as follows.
$ \begin{eqnarray} \mathcal{L}_{\rm {Seesaw }}&& = -Y_{\alpha \beta} \overline{L^{\alpha}} \tilde{H} N_{R \beta}-\frac{1}{2} M_{N} \overline{N_{R}^{c}} N_{R}+\rm { h.c. } \end{eqnarray} $

(2) $ \begin{aligned}[b] \mathcal{L}_{\rm {DS }} =& \bar{\chi}\left({\rm i} \not\partial-m_{\chi}\right) \chi + \frac{1}{2} \partial_{\mu} \phi \partial^{\mu} \phi\\&-\frac{1}{2}\mu_{\phi}^{2} \phi^{2} -\frac{1}{4}\lambda_{\phi} {\phi}^4 -\lambda_{H \phi}\left(H^{\dagger} H\right)\phi^{2} . \end{aligned} $

(3) $ \begin{eqnarray} \mathcal{L}_{\rm {int }} && = -\left( y_{\rm {DS }} \phi \bar{\chi} N_{R}+\rm h.c \right). \end{eqnarray} $

(4) In these equations,
$ L^\alpha $ is the left-handed lepton doublet, H the SM Higgs doublet with$\tilde{H} = {\rm i} \tau_{2} H^{*}$ ,$ m_{\chi} $ the mass of χ,$ M_N $ the mass of the right-handed neutrinos. There are three generations of right-handed neutrinos and we consider the simplest case where the three generations of right-handed neutrinos are degenerate. After electroweak symmetry breaking, the scalar ϕ gets a further contribution to its mass and we have$ \begin{equation} m^2_{\phi} = {\mu}^2_{\phi}+\lambda_{H \phi} v_{ew}^2, \end{equation} $

(5) where
$ v_{ew}/\sqrt{2} $ is the vacuum expectation of the Higgs doublet H after electroweak symmetry breaking.As shown in Ref. [10], the right relic abundance of DM can be obtained in this model by a scenario where the dark fermion χ serves as the DM candidate and is produced mainly through the decay of the heavier dark scalar ϕ. In this scenario, the coupling
$y_{\rm DS}$ is assumed to be very small, typically of the order of$ 10^{-12} $ . For such a small value of$y_{\rm DS}$ , the fermion χ is never in thermal equilibrium. We also assume that the coupling$ \lambda_{H \phi} $ is not so small, so that the scalar ϕ is in thermal equilibrium with the SM particles at high temperature. As temperature drops down to the mass scale of ϕ, the heavier ϕ freezes out and decouples from the thermal bath. Then, ϕ after freeze-out decays into fermion χ and the right-handed neutrinos. The right-handed neutrinos would later decay to leptons and other particles, and we are left with a relic density of χ which is to be compared with the DM relic density found in cosmological observations.In the previous work [10], only the case for
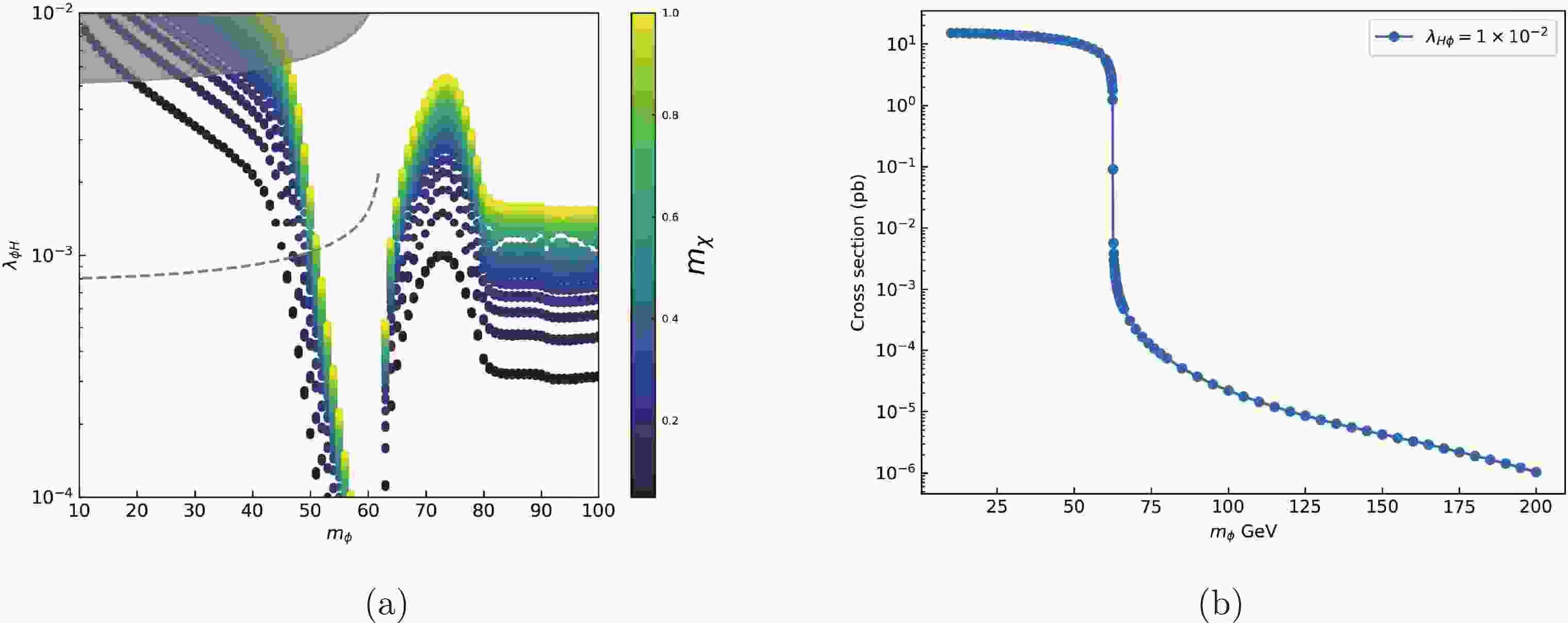
$ m_\phi > 200 $ GeV was considered for obtaining the right relic density. The right relic density of DM can also be obtained for smaller ϕ mass. In this article, we consider the parameter space with$ m_{\phi} < 100 $ GeV. The allowed parameter space of$ m_{\phi} $ and$ \lambda_{H \phi} $ for$ m_{\phi} $ below 100 GeV is shown in Fig. 1(a). We can see that we can obtain the right relic abundance, and$ \lambda_{H \phi} $ is required to be in the range$ 10^{-4} - 10^{-2} $ for$ m_{\phi} $ in the range 10−100 GeV. Here we choose$y_{\rm DS} = 10^{-12}$ ,$ m_{N} = 10 $ GeV, and$ m_{\chi} $ in the range 5−1000 MeV. Note that for these parameters, ϕ can decay sufficiently fast that the DM relic density can be produced at sufficiently high temperature, similar to the analysis given in Ref. [10]. Typically for$ m_{\phi} = 50 $ GeV and$ m_{\chi} = 1 $ GeV with chosen parameters, the lifetime of ϕ is around 0.7 s, which would not make much impact on the BBN processes. We note that the peak at around 75 GeV is due to the opening of the$ \phi \phi \rightarrow W^{+} W^{-} $ annihilation channel. The numerical results shown in the figure are obtained using the public code MicrOmegas [22,23] and CALCHEP [24] to solve the Boltzmann equation and calculate relic abundance. In numerical calculation, all the contributions from$ 2 \rightarrow 2 $ process have been taken into account. The model implementation for MicrOmegas was done using the FeynRules [25] package.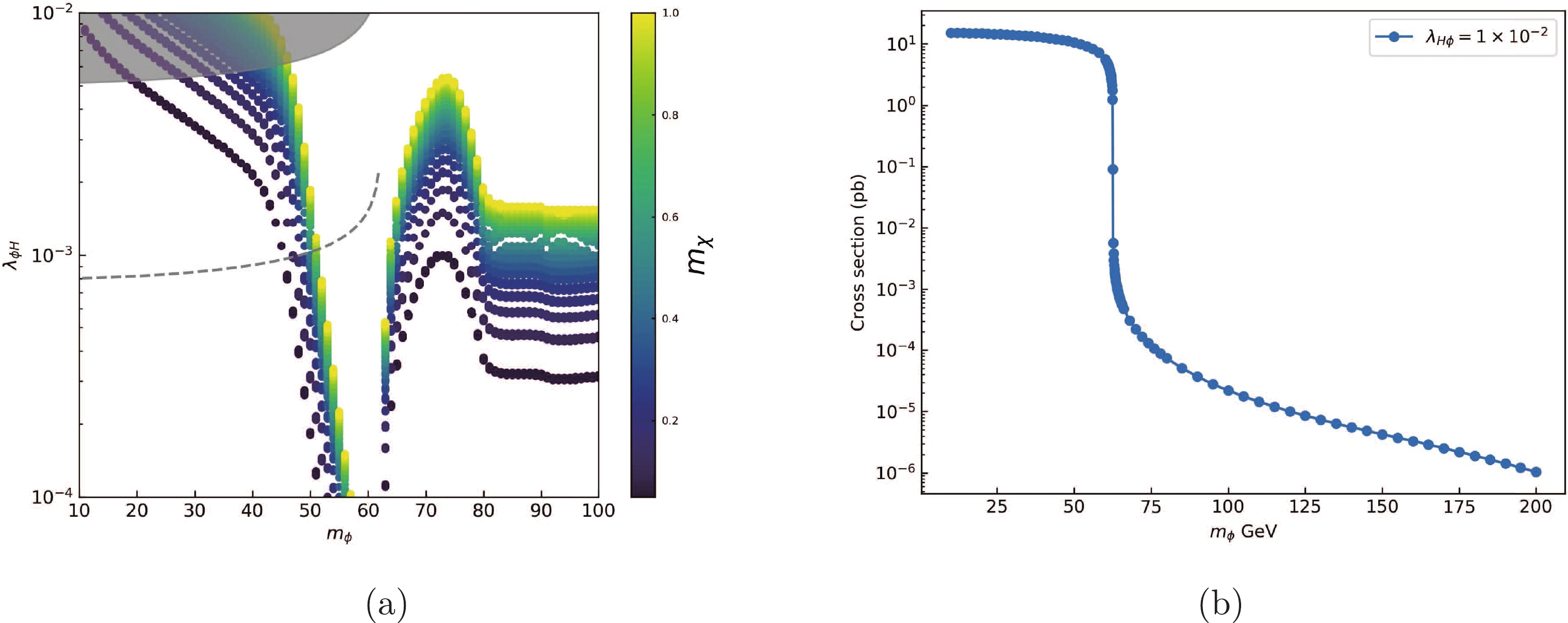
Figure 1. (color online) (a) Allowed parameter space of
$ m_{\phi} $ and$ \lambda_{H \phi} $ for$ m_{\chi} $ in the range from 5 MeV to 1000 MeV.$ M_{N} = 10 $ GeV and$y_{\rm DS} = 10^{-12}$ . The gray region is excluded by Higgs invisible decay. The gray dashed line is the limit on coupling$ \lambda_{H \phi} $ obtained by directly using the constraints on invisible Higgs decay from CEPC CDR. (b) Cross section for gluon–gluon fusion production of ϕ pairs at a pp collider, here we choose$ \lambda = 0.01 $ and center-of-mass energy 13 TeV.For
$ m_{\phi} < m_{H}/2 $ , Higgs would decay to ϕ and would contribute to the Higgs invisible decay. Experimental data will give an additional constraint on model parameters$ \lambda_{H \phi} $ and$ m_{\phi} $ . The branching ratio of Higgs invisible decay is required by the latest experiment [26] to be less than 11%. In our model$ \begin{equation} \Gamma_{h \rightarrow \phi \phi} = \frac{\lambda_{H \phi}^{2} v_{e w}^{2}}{8 \pi m_{H}} \sqrt{1-\frac{4 m_{\phi}^{2}}{m_{H}^{2}}} \end{equation}\ . $

(6) Only the parameter space for
$ \Gamma_{h \rightarrow \phi \phi} / (\Gamma_{S M}+\Gamma_{h \rightarrow \phi \phi}) \leq 11\%$ is allowed [26]. The gray region in Fig. 1(a) is excluded by the constraint from the branching ratio of Higgs invisible decay which is required to be less than 11%. The gray dashed line is the limit on coupling$ \lambda_{H \phi} $ obtained using the future constraint on Higgs invisible decay from CEPC CDR [27],$ \mathrm{BR}_{\mathrm{inv}}^{\mathrm{BSM}} <\; 0.3\% $ at 95% C.L. with integrated luminosity$5.6\ \rm ab^{-1}$ .The dark particle χ does not couple to the SM sector directly, so it's hard to find relevant signals of χ with a collider. But the scalar ϕ in the dark sector couples to the SM sector directly with a not-so-small coupling constant
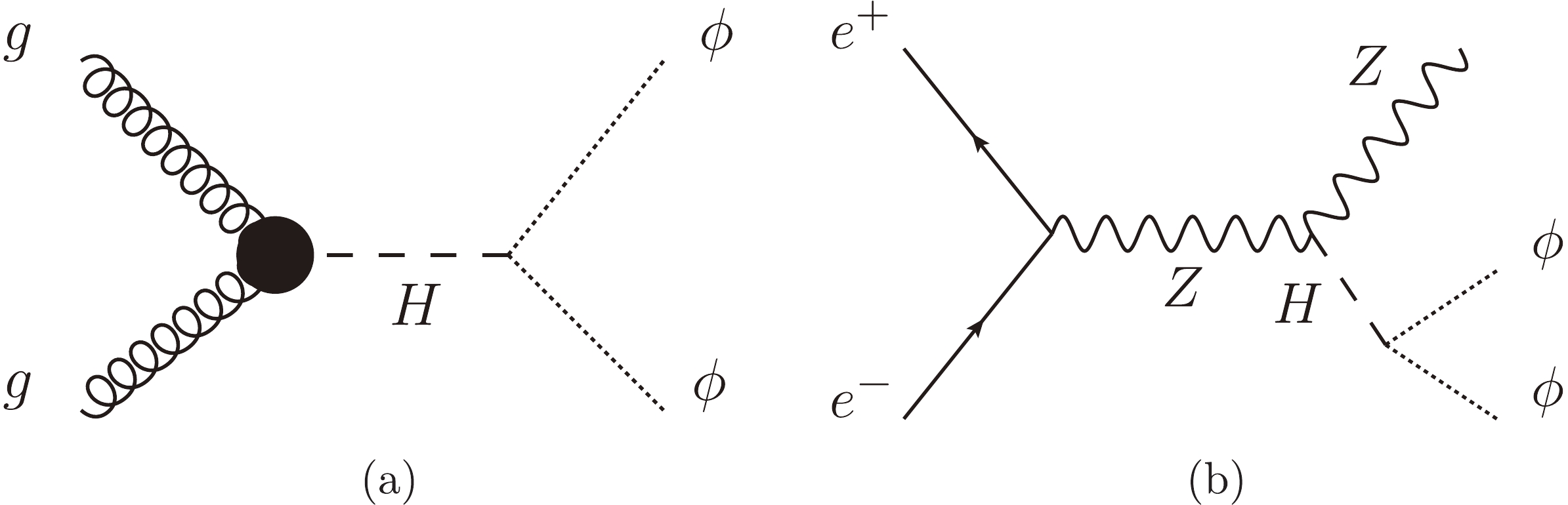
$ \lambda_{H\phi} $ , which gives us an opportunity to search for this dark scalar ϕ with colliders. In general, the production of this dark sector particle ϕ will lead to a large$ E_{\mathrm{T}}^{\mathrm{miss}} $ , which can be a good signal for dark ϕ at colliders. Note here that the dark-sector particle ϕ is a long-lived particle due to the very small coupling$y_{\rm DS}$ , which can lead to a displaced vertex signal in the collider detector or long baseline experiment such as MATHUSLA [28]; we will leave this topic for a future work.The dark-sector particle ϕ is mainly produced by the gluon–gluon fusion process through Higgs at hadron colliders, or by the ZH(
$ \rightarrow \phi \phi $ ) process at a future Higgs factory, as shown in Fig. 2. The cross section for gluon–gluon fusion production at hadron colliders can be obtained numerically by the MadGraph5_aMC@NLO package [29, 30]. The result is shown in Fig. 1(b) for$ \lambda_{H \phi} = 0.01 $ and center-of-mass energy$ \sqrt{s} = 13 $ TeV. The total cross section has been rescaled to 48.61 pb which is calculated at next-to-next-to-next-to-leading order (N3LO) in QCD [31]. We can see in Fig. 1(b) that the cross section drops sharply around$ m_{\phi} = m_{H}/2 \simeq 62.5 $ GeV. This is because for$ m_\phi \lesssim 62 $ GeV, the production process is basically a$ 2 \to 1 $ process with the Higgs produced on-shell and then decays to$ \phi \phi $ , as can be seen in the left panel in Fig. 2, while for$ m_\phi \gtrsim 63 $ GeV on-shell Higgs can not decay to$ \phi \phi $ and the production of$ \phi \phi $ shown in Fig. 2 is mediated by off-shell Higgs. So there is a transition from a$ 2 \rightarrow 1 $ gluon–gluon fusion production process to a$ 2 \rightarrow 2 $ production process at around$ m_{\phi}\simeq 62.5 $ GeV. We can see in Fig. 1(b) that the cross section for$ m_{\phi} > m_{H}/2 $ is around five orders of magnitude smaller than that for$ m_{\phi} < m_{H}/2 $ . For the integrated luminosity of$300\ \rm fb^{-1}$ , it is estimated that there are only few pairs of ϕ generated for$ m_{\phi} > m_{H}/2 $ at the LHC. For designed future$ e^{+} e^{-} $ colliders, a rapid decrease of Higgs production cross section will also happen when$ m_{\phi}\simeq 62.5 $ GeV, which is associated with a transition from a$ 2 \rightarrow 2 $ production process to a$ 2 \rightarrow 3 $ production process. Also for an$ e^{+} e^{-} $ collider running at 250–350 GeV, energy conservation will suppress the production of these events with a ϕ mass much heavier than$ m_{H} $ /2. Therefore, in this work, we mainly focus on the parameter region with$ m_{\phi} < m_{H}/2 $ . -
For the planned future Higgs factories like CEPC, FCC-ee and ILC with integrated luminosities of the order of
$\rm ab^{-1}$ , around$ 10^{6} $ Higgs bosons can be produced, which offers us an opportunity to search for the dark particle signal. In our model, the major signal process is$ e^+ e^- \to Z H $ with the Higgs boson decaying into a pair of ϕ which can fly off the detectors as missing energy. Below we provide a feasibility study for$2 \ell + {\not E}$ final states at$ e^{+} e^{-} $ colliders with a detailed Monte Carlo (MC) analysis.Before presenting our MC analysis, one remarkable aspect of
$ e^{+} e^{-} $ colliders is worthy of highlighting, i.e. the full four-momentum of the missing energy can be precisely reconstructed at$ e^{+} e^{-} $ colliders. In contrast, only the transverse momentum of the missing energy can be reconstructed at pp colliders.Another remarkable feature is that the charged leptons
$ \ell $ both in the final states and in the initial states can be measured accurately, which is crucial for reconstruction of the mass parameters of mother particles in the signal and background events. In principle, our analysis can be extended to the case of two jets plus missing energy. Due to the large errors in the jet energy reconstruction, we restrict this work to the case with two charged leptons plus missing energy.In this work, both signal and background events at the parton level are generated using MadGraph5_aMC@NLO [29,30]. The main Feynman diagrams for signal and background processes are displayed in Fig. 3. The signal process and the main background processes with decays are listed below:
$\begin{equation} \begin{aligned} &e^+ e^- \rightarrow ZH \rightarrow l^+ l^- + E^{\mathrm{miss}}(\phi \phi) \quad\ \textrm{(signal process),}\\ &e^+ e^- \rightarrow ZZ \rightarrow l^+ l^- + E^{\mathrm{miss}}(\nu \bar{\nu}) \ \quad\ \textrm{(major background process),}\\ &e^+ e^- \rightarrow ZH \rightarrow l^+ l^- + E^{\mathrm{miss}}(\nu \bar{\nu} \nu \bar{\nu} ) \ \textrm{(subdominant background process),}\end{aligned} \end{equation} $ 
(7) where the missing energy in the signal process originates from Higgs boson's invisible decay, while the missing energy in the background process comes from Z boson decay and also from the SM contribution to the Higgs invisible decay
$ H \rightarrow Z Z^{*} \rightarrow 4 \nu $ .To fully utilize the experimental precision and to generate the most relevant events, we introduce the following geometric acceptance cuts at the parton level. The leptons in the final state must be energetic, be near the central region of the detectors, and be isolated, i.e.
$p_{\rm T}(l) > 20$ GeV,$ |\eta(\ell)|<2.5 $ , and$ R(\ell)>0.4 $ . The leptons' momentum and energy in the non-central region has worse accuracy and it is better to neglect those events with leptons at the non-central region.All acceptance cuts for the final state
$ \ell \ell+E^{\rm {miss }} $ are provided in Table 1. Such acceptance cuts are introduced so as to measure the full momentum of leptons in the final state precisely and to guarantee the successful reconstruction of the masses of mother particles of missing children particles.Geometric Acceptance Cuts Energetic charged lepton $ P_{T}(l)> 20 $ GeV

Central region $ |\eta(\ell)|< 2.5 $ 

Isolation $ \Delta R_{\ell \ell} > 0.4 $ 

Table 1. Geometric acceptance cuts for the
$ 2 \ell+E^{\rm {miss }} $ final states search at Higgs factory.For signal events, we choose two benchmark points with theoretical parameters (BP1:
$ m_{\phi} = 30 $ GeV,$\lambda_{H \phi} = $ $ 0.005$ , and BP2:$ m_{\phi} = 50 $ GeV,$ \lambda_{H \phi} = 8 \times 10^{-4} $ ) as two show cases to demonstrate how the recoil mass method can work to separate signal and background events. It should be mentioned that both of these two benchmark points can lead to the correct relic density for a cosmological DM candidate.As it is known that the total energy at the center-of-mass frame for
$ e^{+} e^{-} $ colliders can be determined with a remarkable precision (say 0.5 GeV due to the beam spreading) [32], therefore the four-momentum of the mother particles (say$ H^0 $ or Z here) can be measured precisely in the central region of detectors by accurate measurements of the four-momentum of the final state lepton pair$ p(l_1) $ and$ p(l_2) $ from Z decay (say$ \frac{\delta p }{p} = 10^{-5} $ ). By using these measurements, the four-momentum of the invisible particle can be fully reconstructed via the recoil mass method.The four-momentum of the invisible mother particle denoted as
$P^\mu_{\rm inv} = q^\mu - P^\mu(Z)$ can be used to find its invariant mass, where$ q^\mu = (\sqrt{s}, 0,0,0) $ and$P^\mu(Z) = p(\ell_1)^\mu + $ $ p(\ell_2)^\mu$ . The invariant mass can be defined as$m_{\mathrm{inv}}^{\mathrm{miss}} = $ $ \sqrt{ P_{\rm inv}^2 }$ , which can be expressed as a function of collision energy and measured lepton four-momenta$ \begin{equation} m_{\mathrm{inv}}^{\mathrm{miss}} = \sqrt{(\sqrt{s} - E_{l_1} - E_{l_2})^2-(\vec{p}(l_1)+\vec{p}(l_2))^2}\,. \end{equation} $

(8) It should be stressed that the error of the observable
$ m_{\mathrm{inv}}^{\mathrm{miss}} $ depends only upon the error of$ \sqrt{s} $ and the error of ($ E_\ell $ and$ p(\ell) $ ). For the signal events, the invariant mass$P^\mu_{\rm inv}$ will yield a sharp peak at the Higgs mass. In contrast, the events of the major background process$ e^{+} e^{-} \rightarrow Z(\rightarrow l^{+} l^{-}) Z(\rightarrow \nu \nu) $ will lead to a peak at the Z mass. For a 350-GeV lepton collider, the VBF processes$ e^+ e^- \to \nu \bar{\nu} W^+ W^- \to \nu \bar{\nu} H $ and$ e^+ e^- \to e^+ e^- Z Z \to $ $ e^+ e^- H $ will give a significant contribution to Higgs production, since$\sigma_{\text{VBF-W}} = 0.030$ pb and$\sigma_{\text{VBF-Z}} = 0.002$ pb, while$\sigma_{\rm ZH} = 0.128$ pb. However, in our analysis, we have imposed the conditions that there are two energetic leptons with large missing energy events in the final state and require that the invariant mass of the sum of the four-momentum of the two leptons is on the Z pole and the recoiled mass is in the window$ 125 \pm 1 $ GeV, which will not accept events from VBF processes. With these conditions, events from VBF processes will be highly suppressed. At most 1% of events from VBF processes will be taken into account. Therefore, it is safe to neglect their contribution in our analysis.Meanwhile, it is well-known that the decay width of a Higgs boson is around 4 MeV, which is much narrower than that of a Z boson (2.49 GeV). Therefore, the signal events will enrich at a narrower Higgs boson mass window, i.e.
$ |m_{\mathrm{inv}}^{\mathrm{miss}} - m_H| \sim 2 $ GeV, as demonstrated in Fig. 4 for BP1. Therefore, it clearly shows that it is possible to distinguish a signal/background event by setting a cut around the Higgs mass window$ |m_{\mathrm{inv}}^{\mathrm{miss}}-125| = 2 $ GeV.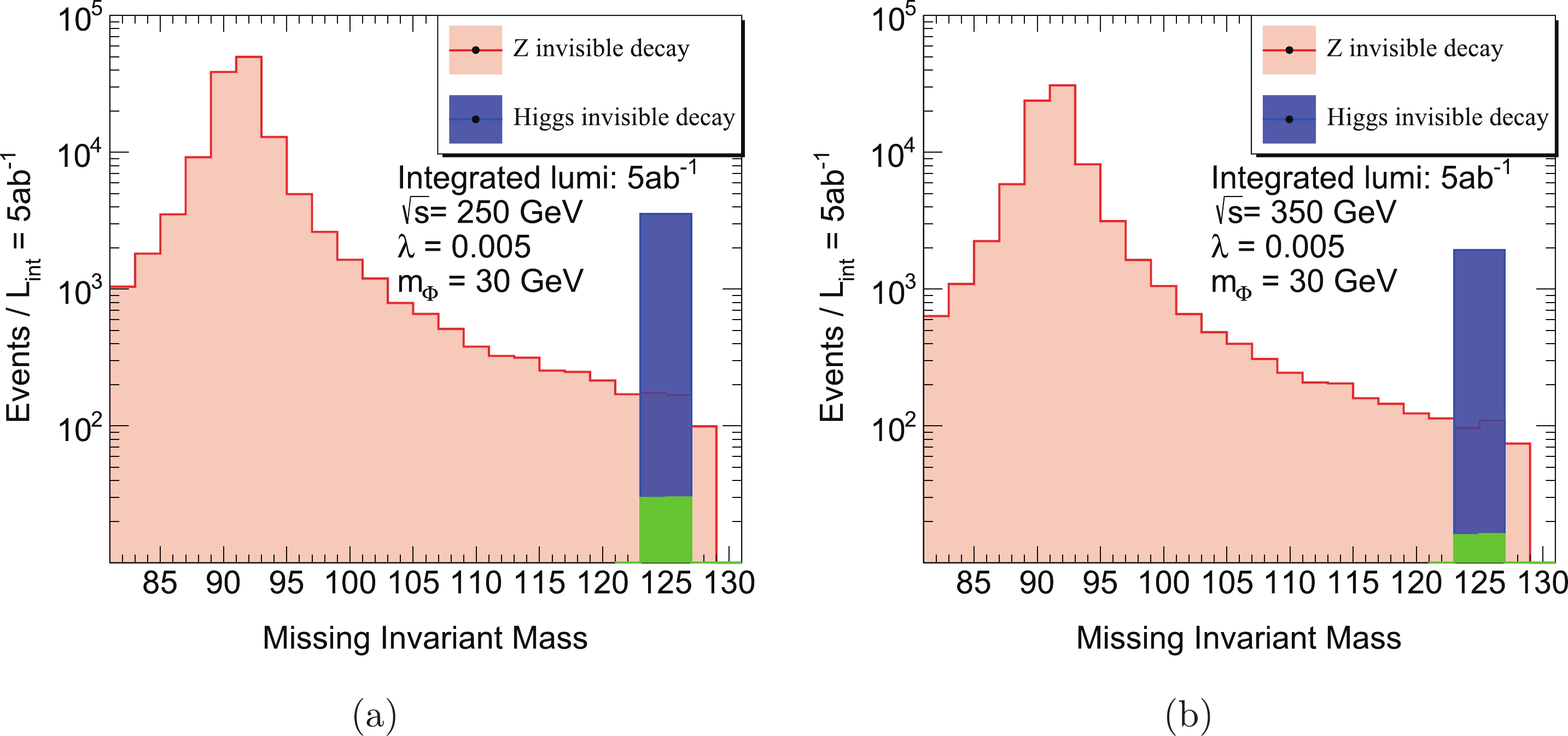
Figure 4. (color online) Missing invariant mass for different center-of-mass frame energies of the collider for BP1: (a)
$ \sqrt{s} = 250 $ GeV; around 7100 signal events and 420 background events between$ 125 \pm 2 $ GeV (b)$ \sqrt{s} = 350 $ GeV; around 3850 signal events and 250 background events between$ 125 \pm 2 $ GeV. Here the green bin is the SM contribution to Higgs invisible decay from$ h \rightarrow Z Z^{*} \rightarrow \nu \bar{\nu} \nu \bar{\nu} $ . We set the bin width to be 2 GeV, which is reasonable when the errors of the collision energy and momentum of charged leptons are considered.In Fig. 4 for BP1, even though the events via off-shell Z and γ can contribute significantly even out of the
$ m_Z $ mass window, the signal events condense in the Higgs boson mass window, and a significance$\sigma = \frac{N_{\rm S}}{\sqrt{N_{\rm B}}} = 346$ for BP1 can be established ($N_{\rm S}$ and$N_{\rm B}$ denote the number of signal and background events in the Higgs mass window). For the collision energy$ \sqrt{s} = 350 $ GeV, a significance$ \sigma = 245 $ for BP1 can be established. Compared with the$ \sqrt{s} = 250 $ GeV case, the loss of significance for$ \sqrt{s} = 350 $ GeV can mainly be attributed to the fact that the cross section of the signal process is suppressed by collision energy since the signal process is s-channel dominant, while the cross section of the background process is less suppressed since it is t/u-channel dominant.In Fig. 5 for BP2, in the case with
$ \sqrt{s} = 250 $ GeV and an assumed 1/ab dataset, a significance$ \sigma = 6.5 $ can be achieved. For the case with$ \sqrt{s} = 350 $ GeV and the 1/ab dataset, a significance$ \sigma = 4.5 $ is feasible. For both BP1 and BP2, we can arrive at the conclusion that an$ e^{+} e^{-} $ collider with$ \sqrt{s} = 250 $ GeV has a better sensitivity for signal events. Note here that we can also choose the Higgs boson mass window to be$ |m_{\mathrm{inv}}^{\mathrm{miss}}-125| = 1 $ GeV. Compared with the 2 GeV window, this scheme cuts more background events and leads to a higher background rejection rate, so a higher significance can be obtained. For the 2 GeV window, a higher signal efficiency will be achieved. If the background events can be well understood and if the side-band analysis technique can be applied, we can expect an even better result.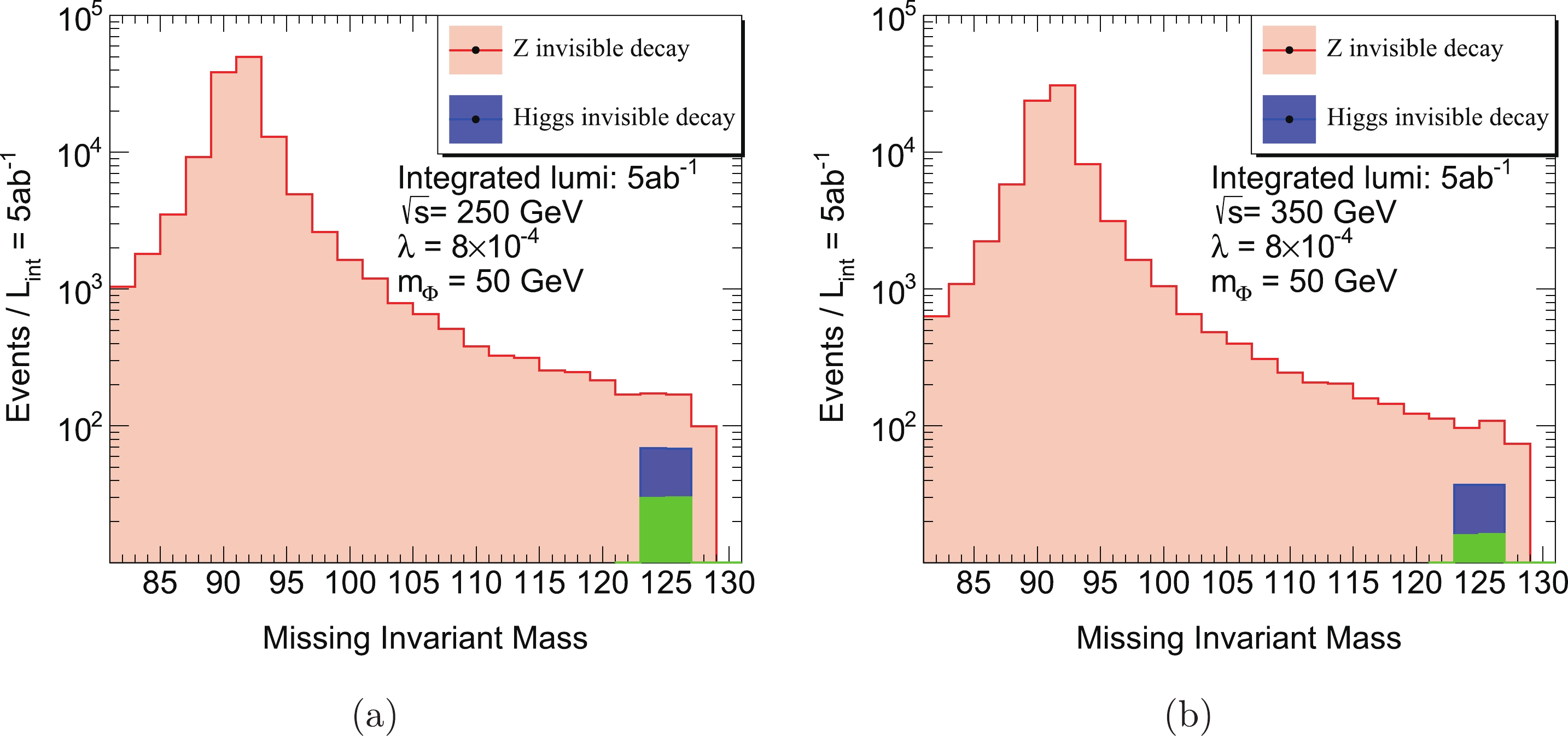
Figure 5. (color online) Recoiled mass for different center-of-mass frame energies of the collider for BP2: (a)
$ \sqrt{s} = 250 $ GeV; around 140 signal events and 420 background events between$ 125 \pm 2 $ GeV. Significance of the signal is around 6.5 σ. (b)$ \sqrt{s} = 350 $ GeV; around 75 signal events and 250 background events between$ 125 \pm 2 $ GeV. Significance of the signal is around 4.5 σ. Here the green bin is the SM contribution to Higgs invisible decay from$ h \rightarrow Z Z^{*} \rightarrow \nu \bar{\nu} \nu \bar{\nu} $ . We set the bin width to 2 GeV, which is reasonable when the errors of the collision energy and momentum of charged leptons are considered.We can extend our analysis for BP1 and BP2 to other points in the theoretical parameter space formed by
$ \lambda_{H \phi} $ and$ m_\phi $ , as demonstrated in Table 2. We can obtain the lower bounds of the values of coupling$ \lambda_{H \phi} $ which can be probed at$ 3 \sigma $ and$ 5 \sigma $ significance level for integrated luminosity of both$ \sqrt{s} = 250 $ GeV and$ \sqrt{s} = 350 $ GeV and for some different values of mass parameter$ m_\phi $ .$ \sqrt{s} = 250 $ GeV

$ m_{\phi} $ = 30 GeV

$ m_{\phi} $ = 50 GeV

$ m_{\phi} $ = 60 GeV

3 σ 5 σ 3 σ 5 σ 3 σ 5 σ 5 $\rm ab^{-1} $ 

$ 4.50 \times 10^{-4} $ 

$ 5.90 \times 10^{-4} $ 

$ 5.40 \times 10^{-4} $ 

$ 7.10 \times 10^{-4} $ 

$ 7.90 \times 10^{-4} $ 

$ 1.04 \times 10^{-3} $ 

1 $\rm ab^{-1} $ 

$ 6.90 \times 10^{-4} $ 

$ 9.00 \times 10^{-4} $ 

$ 9.30 \times 10^{-4} $ 

$ 1.09 \times 10^{-3} $ 

$ 1.22 \times 10^{-3} $ 

$ 1.59 \times 10^{-3} $ 

500 $\rm fb^{-1} $ 

$ 8.20\times 10^{-4} $ 

$ 1.10 \times 10^{-3} $ 

$ 1.01 \times 10^{-3} $ 

$ 1.32 \times 10^{-3} $ 

$ 1.45 \times 10^{-3} $ 

$ 1.93 \times 10^{-3} $ 

$ \sqrt{s} = 350 $ GeV

5 $\rm ab^{-1} $ 

$ 5.50 \times 10^{-4} $ 

$ 7.10 \times 10^{-4} $ 

$ 6.60 \times 10^{-4} $ 

$ 8.50 \times 10^{-4} $ 

$ 9.60 \times 10^{-4} $ 

$ 1.24 \times 10^{-3} $ 

1 $\rm ab^{-1} $ 

$ 8.30 \times 10^{-4} $ 

$ 1.09 \times 10^{-3} $ 

$ 1.00 \times 10^{-3} $ 

$ 1.32 \times 10^{-3} $ 

$ 1.46 \times 10^{-3} $ 

$ 1.93 \times 10^{-3} $ 

500 $\rm fb^{-1}$ 

$ 1.01\times 10^{-3} $ 

$ 1.32 \times 10^{-3} $ 

$ 1.22 \times 10^{-3} $ 

$ 1.61 \times 10^{-3} $ 

$ 1.78 \times 10^{-3} $ 

$ 2.35 \times 10^{-3} $ 

Table 2. Minimum values of coupling
$ \lambda_{H \phi} $ which can be probed at 3 σ and 5 σ confidence levels with different masses of$ m_\phi $ with collision energy$ \sqrt{s}=250 $ GeV and$ \sqrt{s}=350 $ GeV.When collision energies are fixed, the minimum integrated luminosity to obtain
$ 3 \sigma $ and$ 5 \sigma $ significance for different values of the coupling$ \lambda_{H\phi} $ and mass$ m_\phi $ are shown in Table 3.$ \sqrt{s} = 250 $ GeV

$ m_{\phi} = 30 $ GeV

$ m_{\phi} = 50 $ GeV

$ m_{\phi} = 60 $ GeV

$ \lambda_{H \phi} $ 

$ 6 \times 10^{-4} $ 

$ 8\times 10^{-4} $ 

$ 1 \times 10^{-3} $ 

$ 6 \times 10^{-4} $ 

$ 8 \times 10^{-4} $ 

$ 1 \times 10^{-3} $ 

$ 8 \times 10^{-4} $ 

$ 1\times 10^{-3} $ 

$ 1.2 \times 10^{-3} $ 

3 σ 1.64 $\rm ab^{-1} $ 

550 $\rm fb^{-1} $ 

260 $\rm fb^{-1} $ 

3.50 $\rm ab^{-1} $ 

1.14 $\rm ab^{-1} $ 

500 $\rm fb^{-1} $ 

4.95 $\rm ab^{-1} $ 

2.05 $\rm ab^{-1} $ 

1.05 $\rm ab^{-1} $ 

5 σ 4.55 $\rm ab^{-1} $ 

1.53 $\rm ab^{-1} $ 

680 $\rm fb^{-1} $ 

9.50 $\rm ab^{-1} $ 

3.13 $\rm ab^{-1} $ 

1.38 $\rm ab^{-1} $ 

13.70 $\rm ab^{-1} $ 

5.75 $\rm ab^{-1} $ 

2.84 $\rm ab^{-1} $ 

$ \sqrt{s} = 350 $ GeV

$ \lambda_{H \phi} $ 

$ 6 \times 10^{-4} $ 

$ 8\times 10^{-4} $ 

$ 1 \times 10^{-3} $ 

$ 6 \times 10^{-4} $ 

$ 8 \times 10^{-4} $ 

$ 1 \times 10^{-3} $ 

$ 8 \times 10^{-4} $ 

$ 1\times 10^{-3} $ 

$ 1.2 \times 10^{-3} $ 

3 σ 3.40 $\rm ab^{-1} $ 

1.20 $\rm ab^{-1} $ 

530 $\rm fb^{-1} $ 

6.90 $\rm ab^{-1} $ 

2.35 $\rm ab^{-1} $ 

1.00 $\rm ab^{-1} $ 

9.90 $\rm ab^{-1} $ 

4.20 $\rm ab^{-1} $ 

2.20 $\rm ab^{-1} $ 

5 σ 9.30 $\rm ab^{-1} $ 

3.10 $\rm ab^{-1} $ 

1.35 $\rm ab^{-1}$ 

19.40 $\rm ab^{-1} $ 

6.40 $\rm ab^{-1} $ 

2.70 $\rm ab^{-1} $ 

28.00 $\rm ab^{-1} $ 

10.50 $\rm ab^{-1} $ 

5.80 $\rm ab^{-1}$ 

Table 3. Minimum integrated luminosity for 3 σ and 5 σ confidence level for different masses
$ m_\phi $ and values of coupling$ \lambda_{H \phi} $ with two collision energy$ \sqrt{s} = 250 $ GeV and$ \sqrt{s} = 350 $ GeV.From the results given in Table 3, we can observe that the future
$ e^{+} e^{-} $ colliders can probe the signal process with the coupling$ \lambda_{H \phi} $ down to$ 6 \times 10^{-4} $ or so. In our work, we only demonstrate how to apply the mass recoil method in the simulation to probe the proposed model at future colliders. We have neglected some important background processes (like single Z processes), ISR (initial state radiation) and FSR (final state radiation), electroweak radiation corrections and detector effects. For the full simulation, all the effects mentioned should be taken into account, which is beyond the scope of our work. The interested reader can refer to a detailed study in Ref. [33] for Higgs invisible decay, which might be more reasonable and precise than the results given in CEPC CDR [27]. Therefore, our numerical results on the bounds of theoretical parameters should only be interpreted as a reasonable estimate.With the results of more points in theoretical parameter space, we can conclude that
$ e^+ e^- $ colliders with collision energy$ \sqrt{s} = 250 $ can have a better sensitivity to our model. -
For the sake of comparison, we study the feasibility to detect dark particle ϕ at proton–proton colliders. We focus on both mono-jet and
$ 2 \ell + E_{\mathrm{T}}^{\mathrm{miss}} $ final states at pp colliders.It is well-known that the mono-jet process serves as a unique probe to search for DM production processes which lead to a large
$ E_{\mathrm{T}}^{\mathrm{miss}} $ and one energetic jet in the final state. In our model, the signal process is$ pp \to H + j $ with Higgs boson decaying into a ϕ pair. The dominant background process is$ pp \to Z + j $ with the Z boson decaying into a neutrino pair. The detailed signal/background processes and decays are given below$ \begin{aligned}[b] &p p \rightarrow H+{\rm jet} \rightarrow E_{\mathrm{T}}^{\rm {miss }}(\phi \phi)+\rm{jet} \quad (\textrm{signal}) \\ &p p \rightarrow Z +{\rm jet} \rightarrow E_{\mathrm{T}}^{\rm {miss }}(\nu \bar{\nu})+\rm{jet} \ \quad (\textrm{background}) \end{aligned} $

(9) We generate the relevant the mono-jet events at parton level using the MadGraph5_aMC@NLO [29,30] generator for signal and background processes.
For simplicity, only one energetic jet in the final state is considered. The PDF set used for the generation is NNPDF23LO, and the cross section for the process with the hard jet in the final state is obtained using a dataset at parton level (no hadronization and no detector effects have been considered). We set the following selection cuts to the leading jet:
$p_{\rm T}(j) > 150$ GeV and$ |\eta(j)|<2.4 $ .In Fig. 6, the distributions of the transverse momentum of the leading jet
$p_{\rm T}(j)$ of signal/background events are shown. For the signal events, we have chosen the theoretical parameters$ m_{\phi} = 30 $ GeV in the left panel and$ m_{\phi} = 50 $ GeV in the right panel with$ \lambda_{H \phi} = 5 \times 10^{-3} $ . The blue (red) bins represent the distribution of signal (background) events.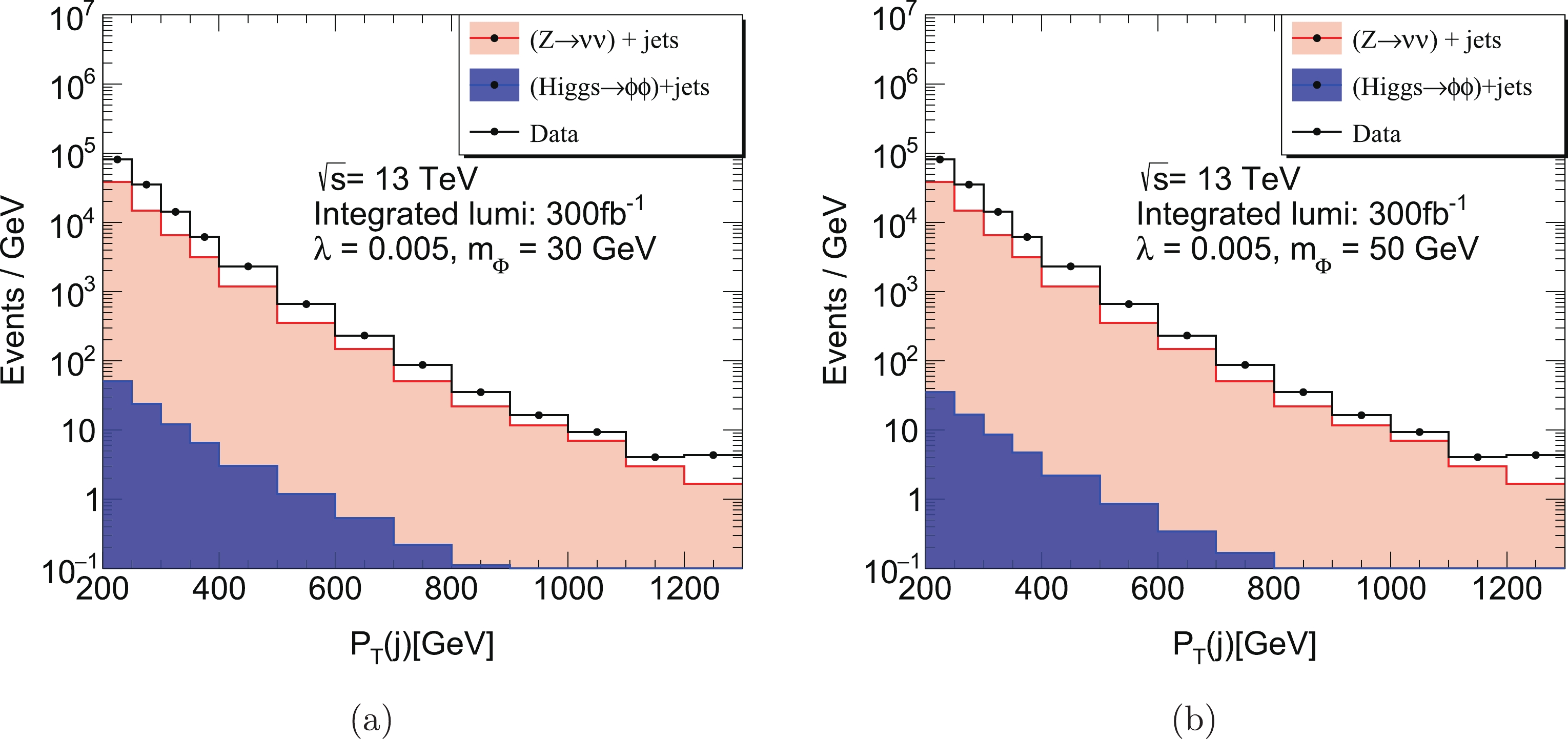
Figure 6. (color online) (a)
$p_{\rm T}(j)$ distribution of signal events and background events in the monojet processes. The black points represent the experimental data. (a)$ \lambda_{H \phi} = 5 \times 10^{-3} $ ,$ m_{\phi} = 30 $ GeV. (b)$ \lambda_{H \phi} = 5 \times 10^{-3} $ ,$ m_{\phi} = 50 $ GeV.To examine the reliability of our MC simulation, the experimental data are denoted by the black points, which is normalized to the experimental results for mono-jets searches at LHC with integrated luminosity
$139\ \rm fb^{-1}$ [34,35] and rescaled to$300\ \rm fb^{-1}$ . It is noticed that there exists a small gap between the experimental data and the results of MC simulation which can be attributed to the W+jets processes and the NLO contribution, as has been taken into account in Ref. [34].We can find in both Fig. 6(a) and Fig. 6(b) that the background events are approximately 3 orders of magnitude larger than signal events for each bin, even when the NLO correction for the
$ gg \to H^0 j $ is taken into account. This indicates that it is really challenging for the LHC to find the signal process from mono-jet events even with a total integrated luminosity of$300\ \rm fb^{-1}$ after Run 3.The process for production of the Higgs boson in association with a Z boson, with the Higgs boson invisibly decaying is also a good channel to search for new physics at pp colliders. The signal process and major background process are similar to the
$ e^{+} e^{-} $ collider case, with protons instead of electrons in the initial state.$ \begin{aligned}[b] &p p \rightarrow ZH \rightarrow l^+ l^- + E_{\mathrm{T}}^{\mathrm{miss}}(\phi \phi) \quad (\textrm{signal})\\ &p p \rightarrow ZZ \rightarrow l^+ l^- + E_{\mathrm{T}}^{\mathrm{miss}}(\nu \bar{\nu}) \ \quad (\textrm{background}) \end{aligned} $

(10) Since we can not reconstruct the full momentum of the missing particles in the final state at pp colliders, instead we can only use the transverse missing momentum
$ E_{\mathrm{T}}^{\mathrm{miss}} $ as an observable.In Fig. 7, we show the distribution of
$ E_{\mathrm{T}}^{\mathrm{miss}} $ for signal/background in blue/red at LO and compare the experimental data with the Monte Carlo results. Here the ATLAS results for an invisibly decaying Higgs boson in association with a Z boson at 36.1$\rm fb^{-1}$ [36] are quoted and scaled to 300$\rm fb^{-1}$ .
Figure 7. (color online) Distribution of
$ E_{\mathrm{T}}^{\mathrm{miss}} $ for signal process$ (H \rightarrow \phi \phi) $ +$ (Z\rightarrow l^{+} l^{-}) $ and background process$ (Z \rightarrow \nu \bar{\nu}) $ +$ (Z\rightarrow l^{+} l^{-}) $ . The black points represent the experimental data. (a)$ \lambda_{H \phi} = 5 \times 10^{-3} $ ,$ m_{\phi} = 30 $ GeV. (b)$ \lambda_{H \phi} = 5 \times 10^{-3} $ ,$ m_{\phi} = 50 $ GeV.In our analysis, we require that the leptons
$p_{\rm T}(\ell) > 20$ GeV and the leading lepton$p_{\rm T}(\ell) > 30$ GeV. Also$ E_{\mathrm{T}}^{\mathrm{miss}} > 90 $ GeV is required and the invariant mass of two charged leptons is required to be in the range$ 76 $ GeV$ < m_{\ell \ell} < 106 \; \mathrm{GeV} $ to reject background processes with two leptons that do not originate from the decay of a Z boson. All the cuts we use are shown in Table 4.Selection cuts for mono-jet final states Leading jet $p_{\rm T}(j) > 150$ GeV and

$ |\eta|<2.4 $ 

Selection cuts for $ ZH \rightarrow \ell \ell+E_{\mathrm{T}}^{\rm {miss}} $ final states

Two leptons leading (subleading) $p_{\rm T}(\ell)$ > 30 (20) GeV,

$ |\eta(\ell)|<2.5 $ 

$ m_{\ell \ell} $ 

$ 76 $ GeV

$<m_{\ell \ell}<106 $ GeV

$ E_{\mathrm{T}}^{\rm {miss }} $ 

$ E_{\mathrm{T}}^{\rm {miss }}> 90 $ GeV

$ \Delta R_{\ell} $ 

$ \Delta R_{\ell} \geq 0.4 $ 

Table 4. Selection cuts for mono-jet and
$ 2\ell + E_{\mathrm{T}}^{\rm {miss }} $ final states at pp colliders are presented.Note here that the result has a deviation of about 30% from the experimental data quantitatively. Such a difference can be attributed to higher order QCD corrections and the effects of the hadronization and detector simulation. Note that we have used a log scale for the y-axis in the plot which makes the difference between our simulation and experimental results not so obvious. We can find in the figure that the signal is two orders of magnitude smaller than the background. So the signal events for dark sector particle ϕ are also very hard to be found from ZH process at pp colliders.
Comparing these results with those at
$ e^{+} e^{-} $ colliders given in Sec. III, we can conclude that$ e^+e^- $ colliders have more advantages in searching for such a dark sector particle ϕ from Higgs invisible decay. -
In summary, we continued the research on the scenario where DM can be produced by the decay of other heavier particles in the dark sector. For the specific model which includes one singlet scalar ϕ and one singlet fermion χ in the dark sector, we have studied the possibility for a lighter dark sector particle ϕ with
$ m_{\phi} < 100 $ GeV to obtain the right relic density. We find this scenario with lower$ m_{\phi} $ is also appropriate in a wide range in parameter space.We have studied the possibility to find the signal of the dark sector particle ϕ at colliders. We mainly focus on the region where
$ m_{\phi} < m_{H}/2 $ and have studied the production rate and possible signals on the colliders. For a future Higgs factory running at 250–350 GeV, the dark particle ϕ is mainly produced from the ZH process and will result in a dilepton final state with large$ E_{\mathrm{T}}^{\mathrm{miss}} $ . This kind of signature can also be generated by SM process from diboson (ZZ) decay, which is the domant background event. By reconstructing the full missing three-momentum and energy, we can obtain the invariant mass of the missing part, which gives us a powerful tool to distinguish the signal and background events. Using the missing invariant mass as an observable, we can probe this kind of dark sector signal with the coupling of ϕ and Higgs down to$ 6\times10^{-4} $ at future Higgs factories. We have studied the signal and background processes for some benchmark points in our model and have found that the signal has strong significance for a wide range in the parameter space. We have also studied the sensitivity for searching for this dark sector particle signal at Higgs factories with different center-of-mass frame energies. We find that a center-of-mass frame energy of 250 GeV is slightly better for finding the dark sector signal.To reduce the theoretical uncertainties, ISR effects and electroweak radiation corrections should be taken into account. ISR can reduce the leading order cross-section of
$ e^{+} e^{-} \rightarrow Z h $ by about 10%, as has been studied in detail in Refs. [37,38], also electroweak correction can decrease the cross section about 9% [39]. Combining the two effects, the cross section for ZH production process is reduced to$\sigma_{\rm ZH}^{\rm N L O}(s) = 205.2\ \mathrm{fb}$ , which is 18.6% smaller than the tree-level cross section$\sigma_{\rm ZH}^{\rm L O}(s) = 252.0\ \mathrm{fb}$ for$ \sqrt{s} = 250 $ GeV [39]. So only the coupling$ \lambda_{H \phi} > 8 \times 10^{-4} $ can be probed at the 5 σ confidence level, which is close to the constraints obtained by directly using the limit for Higgs inviable decay from CEPC CDR shown in Fig. 1(a). Since the constraints from CDR are obtained by Monte Carlo simulation, and how to completely understand the uncertainties on both the theoretical and experimental sides is still under study, a better result can be expected if the side-band analysis technique can be applied to the real data for future experiments.For comparison, we have also studied the possibility of looking for the same dark sector signals with pp colliders. Higgs production and then decay to a ϕ pair associated with an energetic jet in our model will lead to mono-jet signals, for which
$ Z \rightarrow \nu \bar{\nu} + \textrm{jets}$ process is the major SM background. We have studied the$p_{\rm T}(j)$ distribution for signal and background and have found that the signal is three orders of magnitude smaller than the background. We have further studied the dark sector particle produced by ZH process at pp colliders, where$ (ZZ \rightarrow l^{+} l^{-})+E_{\mathrm{T}}^{\mathrm{miss}} $ is the major background in the SM. Since we cannot reconstruct the full missing momentum, we could only choose the transverse missing energy as an observable. We find that for some benchmark points of the model, the signal is two orders of magnitude smaller than the background in the$ E_{\mathrm{T}}^{\mathrm{miss}} $ plot. We find that for the missing energy signals considered in this article the pp collider is not a good place to detect the signal of the dark sector ϕ particle.Note that the dark sector particle ϕ may lead to signals of a displaced vertex in the detector, which depends upon the dark sector and right-handed neutrinos coupling
$y_{\rm DS}$ . We will leave this topic for a future work.
Collider search of light dark matter model with dark sector decay
- Received Date: 2021-11-27
- Available Online: 2022-06-15
Abstract: We explore the possibility that the dark matter relic density is not produced by a thermal mechanism directly, but by the decay of other heavier dark-sector particles which themselves can be produced by the thermal freeze-out mechanism. Using a concrete model with light dark matter from dark sector decay, we study the collider signature of the dark sector particles associated with Higgs production processes. We find that future lepton colliders could be a better place to probe the signature of this kind of light dark matter model than hadron colliders such as LHC. Also, we find that a Higgs factory with center-of-mass energy 250 GeV has a better potential to resolve the signature of this kind of light dark matter model than a Higgs factory with center-of-mass energy 350 GeV.






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: