-
The QCD phase diagram, especially its critical end point (CEP), is essential to deeply understand the evolution of the early universe and compact stars. Therefore, it has always been the focus of theories, such as Dyson-Shwinger Equations (DSEs) [1–3], lattice QCD [4], the Nambu-Jona-Lasinio model (NJL), and the Polyakov-Nambu-Jona-Lasinio model (PNJL) [5–9], and experiments, such as the Large Hadron Collider (LHC) at CERN [10], Relativistic Heavy-Ion Collider (RHIC) at the BNL [11], and future Facility for Antiproton and Ion Research (FAIR) at GSI [12].
Topologically non-trivial gluon configurations (instantons or sphalerons) can transform left- into right-handed quarks or vice versa via an axial anomaly [13–17]. This produces a non-zero chiral charge
$N_{5} = N_{R}-N_{L}$ , where$ N_{R} $ ,$ N_{L} $ denotes the net number of quarks (minus antiquarks) with right- or left-handed chirality. The nonvanishing$ N_{5} $ can induce an electric current along the direction of the magnetic field, which is known as the chiral magnetic effect (CME). Observation of the CME will offer direct experimental evidence for the existence of topologically non-trivial gluon configurations and event-by-event parity and charge-parity violation. Related experiments have been carried out [18–21].The QCD phase diagram becomes more colorful when the chiral chemical potential
$ \mu_{5} $ is introduced as a conjugate of$ N_{5} $ . Ref. [22] shows that the CEP in the$ T-\mu $ plane can be continuous to$ \mathrm{CEP}_{5} $ in the$ T-\mu_{5} $ plane and provides a way to obtain the approximate location of the CEP from$ \mathrm{CEP}_{5} $ . However, lattice QCD simulations [23, 24] and DSEs [2, 25] indicate that there is no$ \mathrm{CEP}_{5} $ in the$ T-\mu_{5} $ plane. In addition, chiral charge density$ n_{5} $ is closely related to CME. Correlating$ n_{5} $ and$ \mu_{5} $ helps to express the induced electric current density as a function of the chirality density [26].$ n_{5} $ at finite$ \mu_{5} $ with different system sizes is shown in Refs. [25, 27].However, it should be noted that previous studies on the QCD phase diagram with chiral chemical potential
$ \mu_{5} $ were all based on Boltzmann-Gibbs (BG) statistics. Strictly speaking, BG statistics are only valid for equilibrium systems at the thermodynamic limit. In relativistic heavy-ion collisions, because the production of quark-gluon plasma (QGP) is accompanied by strong intrinsic fluctuations and long-range correlations and volume effects, this condition is not satisfied. As a result, several quantities (such as entropy) become nonextensive and develop non-exponential probability distributions [28, 29]. Therefore, the use of BG statistics in such collisions is questionable.Nonextensive statistics, also known as Tsallis statistics, was first proposed by Tsallis [30]. Its novelty is that it replaces the usual exponential probability distribution with the corresponding q-exponential distribution [31–33],
$ \rho_{\rm BG}(x) = C\mathrm{exp}(x)\longrightarrow \rho_{q}(x) = C_{q}\mathrm{exp}_{q}(x), $

(1) where
$ \mathrm{exp}_{q}(x) = [1+(1-q)x]^{\frac{1}{1-q}}, $

(2) and correspondingly, its inverse function is
$ \mathrm{ln}_{q}(x) = \frac{x^{1-q}-1}{1-q}. $

(3) The nonextensivity parameter q represents the deviation from BG statistics. For
$ q\rightarrow1 $ ,$ \mathrm{exp}_{q}(x)\rightarrow \mathrm{exp}(x) $ ,$ \mathrm{ln}_{q}(x)\rightarrow \mathrm{ln}(x) $ , and Tsallis statistics naturally returns to BG statistics.Tsallis statistics has long been used for nonextensive descriptions of nuclear matter (e.g., the nonextensive version of the Walecka model [34–36]), hadronic matter [37, 38], and QCD matter (e.g., the nonextensive version of QCD effective models [31, 32] and nonextensive lattice simulations [39, 40]). Furthermore, it has been widely applied in high-energy physics [28, 41–50], astrophysics [51, 52], cold atoms in optical lattices [53], anomalous diffusion [54, 55], and model systems [56, 57]. In fact, for complex systems (caused by various geometrical-dynamical ingredients, including non-ergodicity, long-term memory, multifractality, and long-range correlations), BG statistics are usually difficult to describe reasonably, and the correct approach is to use Tsallis statistics [29, 52, 56, 57]. In particular, Ref. [29] shows that renormalizable field theories lead to fractal structures, which can be studied from a thermodynamical perspective using Tsallis statistics.
Therefore, in this paper, we use Tsallis statistics to study the QCD chiral phase diagram in the presence of
$ \mu_{5} $ . Within the PNJL model, this paper is organized as follows: In Sec. II, we introduce the nonextensive version of the PNJL model at finite T, μ, and$ \mu_{5} $ and its solution. In Sec. III, we study the chiral phase diagram in the presence of$ \mu_{5} $ , mainly focusing on the shift in the CEP with$ \mu_{5} $ and q. In addition, changes in$ n_{5} $ with T, μ,$ \mu_{5} $ , and q are studied. Finally, we provide a brief summary of our study in Sec. IV. -
First, we provide a brief introduction to the usual PNJL model. The Lagrangian of the two-flavor and three-color PNJL model can be written as follows [58, 59]:
$ \begin{aligned}[b] \mathcal{L}_{\rm PNJL} = & \bar{\Psi}({\rm i}\gamma_{\mu}D^{\mu}-m)\Psi +G\,[(\bar{\Psi}\Psi)^2+(\bar{\Psi} {\rm i}\gamma_5\mathit{\boldsymbol{\tau}}\Psi)^2]\\ &-\mathcal{U}(\Phi,\bar{\Phi};T), \end{aligned} $

(4) where Ψ denotes the two-flavor quark field,
$D_{\mu} = \partial_{\mu}+ {\rm i} A_{\mu}$ , with$ A_{\mu} = gA_{\mu}^{a}\lambda^{a}/2 $ describing the matrix valued gluon field configuration appropriate for this model, m is the current quark mass, and G is the effective coupling strength of the four-quark interaction.$ \mathcal{U}(\Phi, \bar{\Phi}; T) $ is a Polyakov-loop effective potential as a function of the traced Polyakov-loop expectation value Φ and its Hermitian conjugate$ \bar{\Phi} $ . For simplicity, we take the approximation$ \Phi = \bar{\Phi} $ following Refs. [22, 27, 60, 61].To reproduce pure gluonic lattice data with
$ N_{c} = 3 $ , the potential term$ \mathcal{U} $ is provided by [62]$ \frac{\mathcal{U_{L}}}{T^{4}} = -\frac{a(T)}{2}\Phi^{2}+b(T)\mathrm{ln}[1-6\Phi^{2}-3\Phi^{4}+8\Phi^{3}], $

(5) with the temperature-dependent coefficients
$ a(T) = a_{0}+a_{1}\left(\frac{T_{0}}{T}\right)+a_{2}\left(\frac{T_{0}}{T}\right)^{2}, $

(6) and
$ b_{T} = b_{3}\left(\frac{T_{0}}{T}\right)^{3}, $

(7) and the corresponding parameters are given in Table 1. Following Ref. [63], the value of
$ T_{0} $ is adjusted to account for the presence of dynamical quarks.$a_0$ 

$a_1$ 

$a_2$ 

$b_3$ 

$T_{0}/\mathrm{MeV}$ 

3.51 −2.47 15.2 −1.75 190 Table 1. Parameter set used in our study.
It should be noted that the four-fermion coupling G, as argued in Refs. [63, 64], should depend on Φ. Therefore, we use the following coupling constant:
$ G = g[1-\alpha_{1}\Phi^{2}-2\alpha_{2}\Phi^{3}]. $

(8) The numerical values of
$ \alpha_{1} $ and$ \alpha_{2} $ can be obtained by a best fit of lattice data at zero chemical potential on the coincidence between the pseudocritical temperatures of chiral and deconfinement crossover transitions [65] and at imaginary chemical potential on the bare quark mass dependence of the order of the Roberge-Weiss endpoint [66]. The best-fit procedure leads to$ \alpha_{1} = \alpha_{2} = 0.2 $ within the hard cutoff regularization scheme. Moreover, the PNJL model with$ G(\Phi) $ is consistent with all lattice QCD data at imaginary chemical potential and real and imaginary isospin chemical potentials (see Ref. [63]).When considering the chiral chemical potential
$ \mu_{5} $ , the following term is then added to the Lagrangian density [67]:$ \mu_{5}\bar{\Psi}\gamma_{0}\gamma_{5}\Psi, $

(9) which induces the chiral charge density
$ n_{5} = \langle\bar{\Psi}\gamma_{0}\gamma_{5}\Psi\rangle. $

(10) Adopting the mean-field approximation, the thermodynamic potential density function is given by Ref. [22].
$ \begin{aligned}[b] \Omega(\mu,\mu_{5},T;M,\Phi) = &\mathcal{U}(\Phi;T)+\frac{(M-m)^{2}}{4G}\\ &-2N_{c}\sum\limits_{s = \pm1}\int_{0}^{\Lambda}\frac{{\rm d}^3\vec{p}}{(2\pi)^3}\omega_{s}\\ &-2T\sum\limits_{s = \pm1}\int_{0}^{\infty}\frac{{\rm d}^3\vec{p}}{(2\pi)^3}(\mathrm{ln}\mathcal{F}^++\mathrm{ln}\mathcal{F}^-), \end{aligned}$

(11) where M represents the dynamical quark mass and relates to the quark chiral condensate
$ \sigma = \langle\bar{\Psi}\Psi\rangle $ as$ M = m-2G(\Phi)\sigma, $

(12) and
$ \begin{aligned}[b] \mathcal{F}^{\pm} = 1+3\Phi({\rm e}^{-(\omega_{s}\mp\mu)/T}+ {\rm e}^{-2(\omega_{s}\mp\mu)/T})+ {\rm e}^{-3(\omega_{s}\mp\mu)/T}, \end{aligned} $

(13) in which
$ \omega_{s} = \sqrt{(s\mid\overrightarrow{p}\mid-\mu_{5})^{2}+M^{2}} $ is the single quasi-particle energy, and s represents helicity projection. The cut-off Λ is imposed only on the vacuum term [58, 59, 68, 69]. The finite temperature contribution has a natural cut-off in itself that is specified by the temperature. The chiral charge density is$ n_{5} = -\frac{\partial\Omega}{\partial\mu_{5}}. $

(14) The parameters for the NJL model part of the effective Lagrangian
$\mathcal{L}_{\rm PNJL}$ are summarized in Table 2 [70].$\Lambda/\mathrm{MeV}$ 

$g/\mathrm{MeV^{-2} }$ 

$m/\mathrm{MeV}$ 

631.5 $5.498\times10^{-6}$ 

5.5 Table 2. Parameter set used in our study.
Finally, for any given μ,
$ \mu_{5} $ , and T, the corresponding values of M and Φ are obtained by minimizing the thermodynamic potential$ \frac{\partial\Omega}{\partial M} = \frac{\partial\Omega}{\partial\Phi} = 0. $

(15) -
When we introduce the nonextensive PNJL model and perform calculations, as in Ref. [8], we adopt the following two simplifications:
(i) Nonextensive effects, similar to finite-size effects, are not directly reflected in the pure Yang-Mills sector [71, 72]. In other words, the Polyakov-loop potential remains unchanged and experiences nonextensive effects implicitly only through saddle point equations. The reason is that in the standard Polyakov-loop potential, there is no space to introduce nonextensive effects because this potential is based on a group integral rather than a momentum integral. However, lattice QCD data within Tsallis statistics is not currently available. Otherwise, we can obtain
$ \mathcal{U}_{q} $ via fitting, similar to Refs. [58, 62]. The same simplification also appears in the linear sigma model (see Ref. [32]).(ii) The parameters of the usual PNJL model remain unchanged. Here, we treat q as a thermodynamic variable, similar to T and μ [71, 72]. In other words, we use the ansatz that the parameters determined at zero temperature and zero quark chemical potential can be used to study the finite temperature and finite quark chemical potential.
Considering nonextensive thermodynamics [32, 36], the thermodynamic potential density function of the nonextensive PNJL model can be derived as
$ \begin{aligned}[b] \Omega_{q}(\mu,\mu_{5},T;M,\Phi) = &\mathcal{U}(\Phi;T)+\frac{(M-m)^{2}}{4G}\\ &-2N_{c}\sum\limits_{s = \pm1}\int_{0}^{\Lambda}\frac{{\rm d}^3\vec{p}}{(2\pi)^3}\omega_{s}\\ &-2T\sum\limits_{s = \pm1}\int_{0}^{\infty}\frac{{\rm d}^3\vec{p}}{(2\pi)^3}(\mathrm{ln}_{q}\mathcal{F}_{q}^++\mathrm{ln}_{q}\mathcal{F}_{q}^-), \end{aligned} $

(16) where
$\begin{aligned}[b] \mathcal{F}_{q}^{\pm} = & 1+3\Phi(e_{q}(-(\omega_{s}\mp\mu)/T)+e_{q}(-2(\omega_{s}\mp\mu)/T))\\ &+e_{q}(-3(\omega_{s}\mp\mu)/T). \end{aligned} $

(17) Please see the appendix for the main steps. Here, we abbreviate
$ \mathrm{exp}_{q}(x) $ as$ e_{q}(x) $ . In this paper, we only consider$ q > 1 $ because the typical value of the nonextensivity parameter q for high-energy collisions is found to be$ 1 \leq q \leq 1.2 $ [28, 48, 73, 74]. To ensure that$ e_{q}(x) $ is always a non-negative real function, the following condition must be met:$ [1+(1-q)x]>0. $

(18) If this condition is not met, an approach with or without the Tsallis cut-off prescription can be used. However, these two schemes have corresponding problems, as mentioned in Ref. [31]. Therefore, to ensure the reliability of the results, Eq. (18) is always satisfied in our numerical calculations. Moreover, note that the nonextensive signal can only appear at a sufficiently high temperature because for
$ T\rightarrow0 $ ,$ \Omega_{q}\rightarrow \Omega $ as long as$ q > 1 $ .To study the QCD phase diagram, according to Eq. (15), the nonlinear coupling equations to be solved for M and Φ can be derived as
$ \begin{aligned}[b]\\[-5pt] M = m+2GN_{c}N_{f}\sum\limits_{s = \pm1}\int\frac{{\rm d}^3\vec{p}}{(2\pi)^3}\frac{M}{\omega_{s}}[1-n_{q}-\bar{n}_{q}], \end{aligned} $ 
(19) $ \begin{aligned}[b] 0 = & \frac{\partial\mathcal{U}}{\partial\Phi}-\frac{(M-m)^{2}}{4G^{2}}\frac{\partial G}{\partial\Phi}-N_{c}N_{f}T\sum\limits_{s = \pm1}\int_{0}^{\infty}\frac{{\rm d}^3\vec{p}}{(2\pi)^3}\\&\times\Bigg\{\frac{e_{q}(-(\omega_{s}-\mu)/T)+e_{q}(-2(\omega_{s}-\mu)/T)}{[1+3\Phi(e_{q}(-(\omega_{s}-\mu)/T)+e_{q}(-2(\omega_{s}-\mu)/T))+e_{q}(-3(\omega_{s}-\mu)/T)]^{q}}\\ &+\frac{e_{q}(-(\omega_{s}+\mu)/T)+e_{q}(-2(\omega_{s}+\mu)/T)}{[1+3\Phi(e_{q}(-(\omega_{s}+\mu)/T)+e_{q}(-2(\omega_{s}+\mu)/T))+e_{q}(-3(\omega_{s}+\mu)/T)]^{q}}\Bigg\}, \end{aligned}$

(20) where the q-version of the Fermi-Dirac distribution is
$ n_{q}(T,\mu) = \frac{e_{q}^{q}(-3(\omega_{s}-\mu)/T)+\Phi(e_{q}^{q}(-(\omega_{s}-\mu)/T)+2e_{q}^{q}(-2(\omega_{s}-\mu)/T))}{[1+3\Phi(e_{q}(-(\omega_{s}-\mu)/T)+e_{q}(-2(\omega_{s}-\mu)/T))+e_{q}(-3(\omega_{s}-\mu)/T)]^{q}}, $

(21) and
$ \bar{n}_{q}(T,\mu) = \frac{e_{q}^{q}(-3(\omega_{s}+\mu)/T)+\Phi(e_{q}^{q}(-(\omega_{s}+\mu)/T)+2e_{q}^{q}(-2(\omega_{s}+\mu)/T))}{[1+3\Phi(e_{q}(-(\omega_{s}+\mu)/T)+e_{q}(-2(\omega_{s}+\mu)/T))+e_{q}(-3(\omega_{s}+\mu)/T)]^{q}}. $

(22) According to Eq. (14), the chiral charge density is
$ n_{5q} = 2N_{c}\sum\limits_{s = \pm1}\int\frac{{\rm d}^3\vec{p}}{(2\pi)^3}\frac{-sp+\mu_{5}}{\omega_{s}}[1-n_{q}-\bar{n}_{q}]. $

(23) It should be noted that our q-version of the Fermi-Dirac distribution function is directly derived from Eq. (15), which satisfies the thermodynamic consistency condition. For
$ q\rightarrow1 $ ,$ n_{q} $ and$ \bar{n}_{q} $ return to the standard Fermi-Dirac distribution of the usual PNJL model. -
By solving Eqs. (19)–(22), we obtain QCD phase diagrams on the
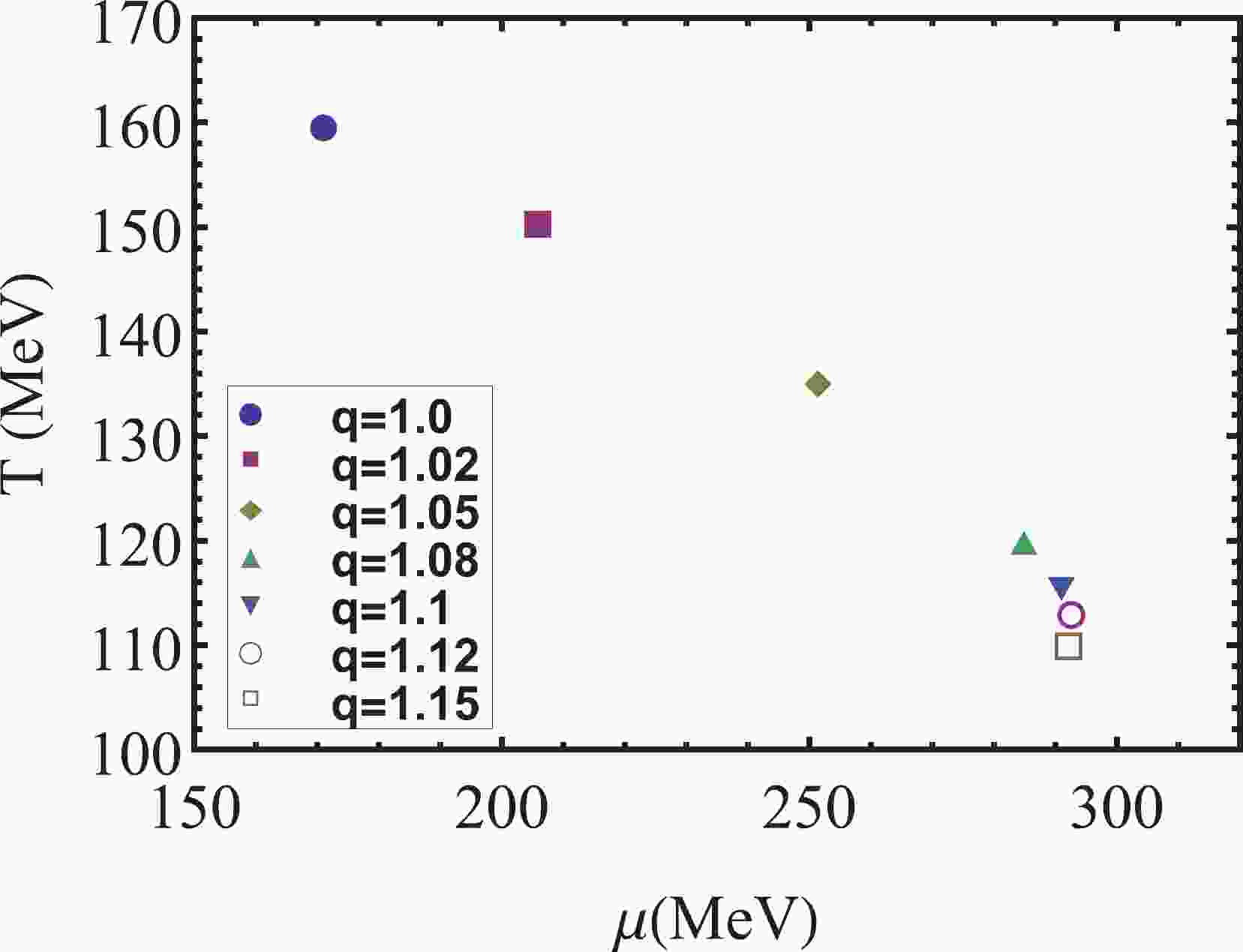
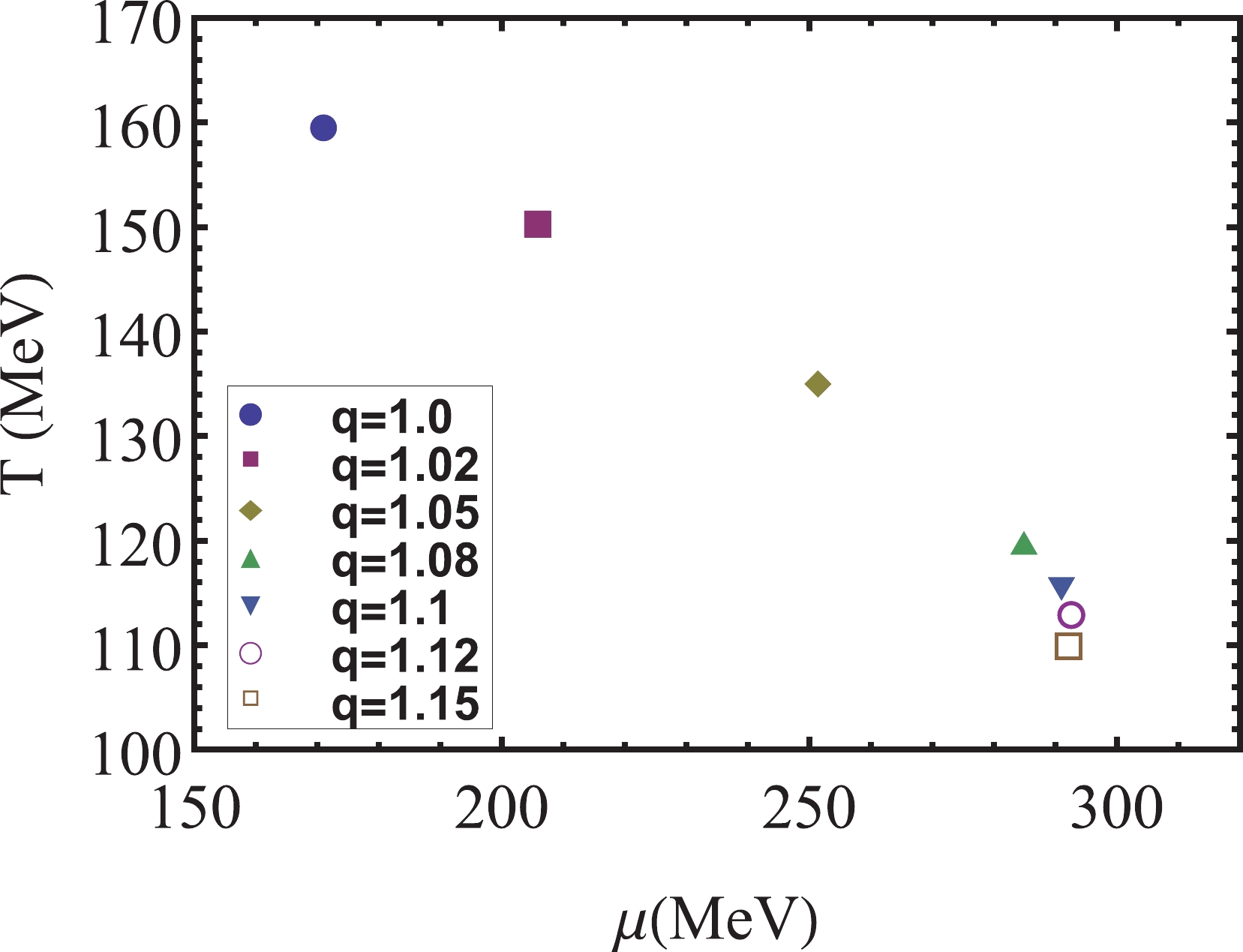
$ T-\mu $ and$ T-\mu_{5} $ plane, as shown in Figs. 1 and 2, respectively. The positions of the CEP and$ \mathrm{CEP}_{5} $ are determined by the thermal susceptibility$ \chi_{T} = \partial\sigma/\partial T $ . We find that nonextensive effects have a significant impact on the positions of the CEP and$ \mathrm{CEP}_{5} $ . For$ q = 1 $ , the positions of the CEP and$ \mathrm{CEP}_{5} $ are$ (\mu_{c}, T_{c}) =$ (171 MeV, 159.5 MeV) and$ (\mu_{c5}, T_{c5}) = $ (296 MeV, 167 MeV), respectively; however, for$ q = 1.15 $ , their positions are$ (\mu_{c}, T_{c}) = $ (290.2 MeV, 109.4 MeV) and$ (\mu_{c5}, T_{c5}) = $ (550 MeV, 118 MeV), respectively. Generally, as q increases, both the CEP and$ \mathrm{CEP}_{5} $ move in the direction of a lower temperature and larger chemical potential. However, the CEP trajectory declines so that$ \mu_{c} $ eventually remains at approximately$ 290\ \mathrm{MeV} $ , whereas the change in$ \mathrm{CEP}_{5} $ is approximately linear.
Figure 2. (color online) Trajectory of
$ \mathrm{CEP}_{5} $ position with q on the$ T-\mu_{5} $ plane.Next, we reveal the evolution from the CEP to
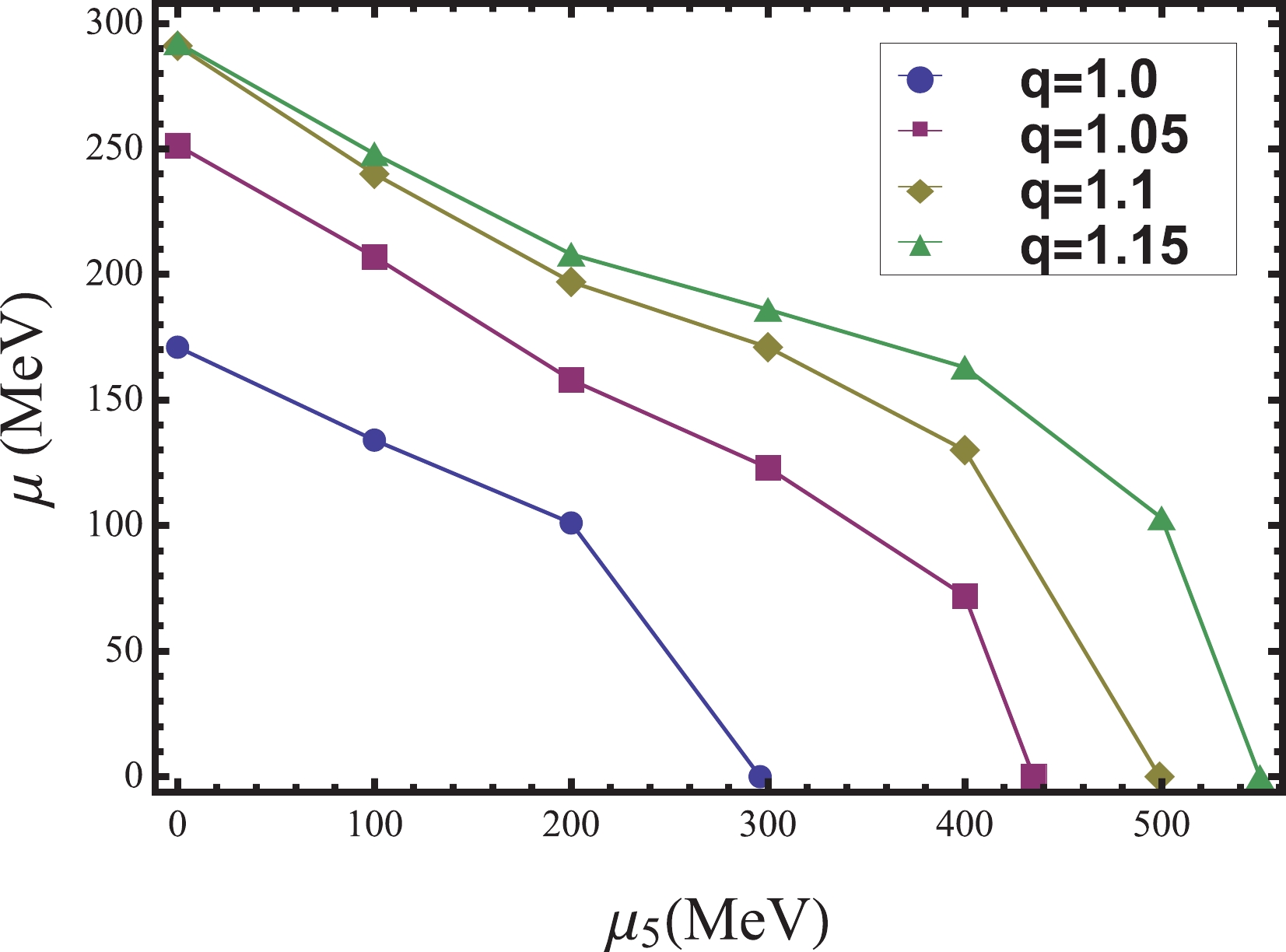
$ \mathrm{CEP}_{5} $ on the$ T-\mu_{5} $ ,$ \mu-\mu_{5} $ , and$ T-\mu $ planes. From Fig. 3, we can see that for$ q = 1 $ ,$ T_{c} $ increases as$ \mu_{5} $ increases. However, as q increases, we find that$ T_{c} $ first increases and then decreases, which is especially clear for$ q = 1.15 $ . From Fig. 4,$ \mu_{c} $ decreases to zero with$ \mu_{5} $ . It is worth noting that when q increases from 1.1 to 1.15, the changes in$ T_{c} $ and$ \mu_{c} $ are limited, whereas the changes in$ T_{c5} $ and$ \mu_{c5} $ are clear. This can also be seen in Figs. 1 and 2. This reveals that there is a situation in which two points far apart on the$ T-\mu_{5} $ plane can evolve to be close to each other on the$ T-\mu $ plane. Therefore, considering the nonextensive effects, the evolution from$ \mathrm{CEP}_{5} $ to the CEP becomes more complex. In other words, it may not be feasible to approximate the location of the CEP through$ \mathrm{CEP}_{5} $ , as in Ref. [22]. Moreover, from Fig. 5, we can see that even if$ \mu_{5} $ is considered, the movement trend of the CEP with q remains unchanged before the CEP extends to the$ T-\mu_{5} $ plane. For example, when$ \mu_{5} = 200\ \mathrm{MeV} $ , the CEP still moves in the direction of a lower temperature and larger chemical potential as q increases.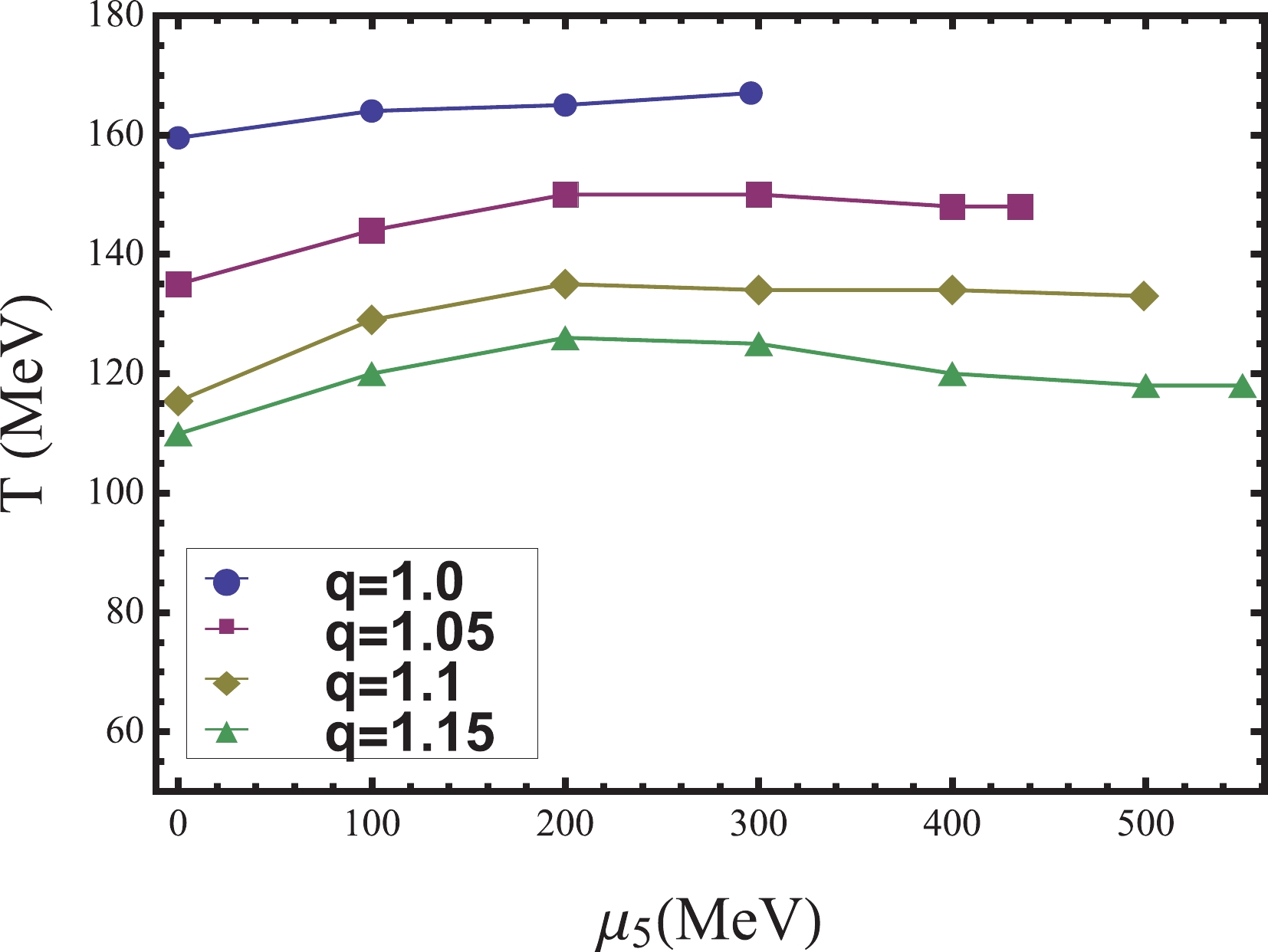
Figure 3. (color online) Projection of the evolution of the CEP on the
$ T-\mu_{5} $ plane for different parameters q. -
The non-vanishing chiral charge density
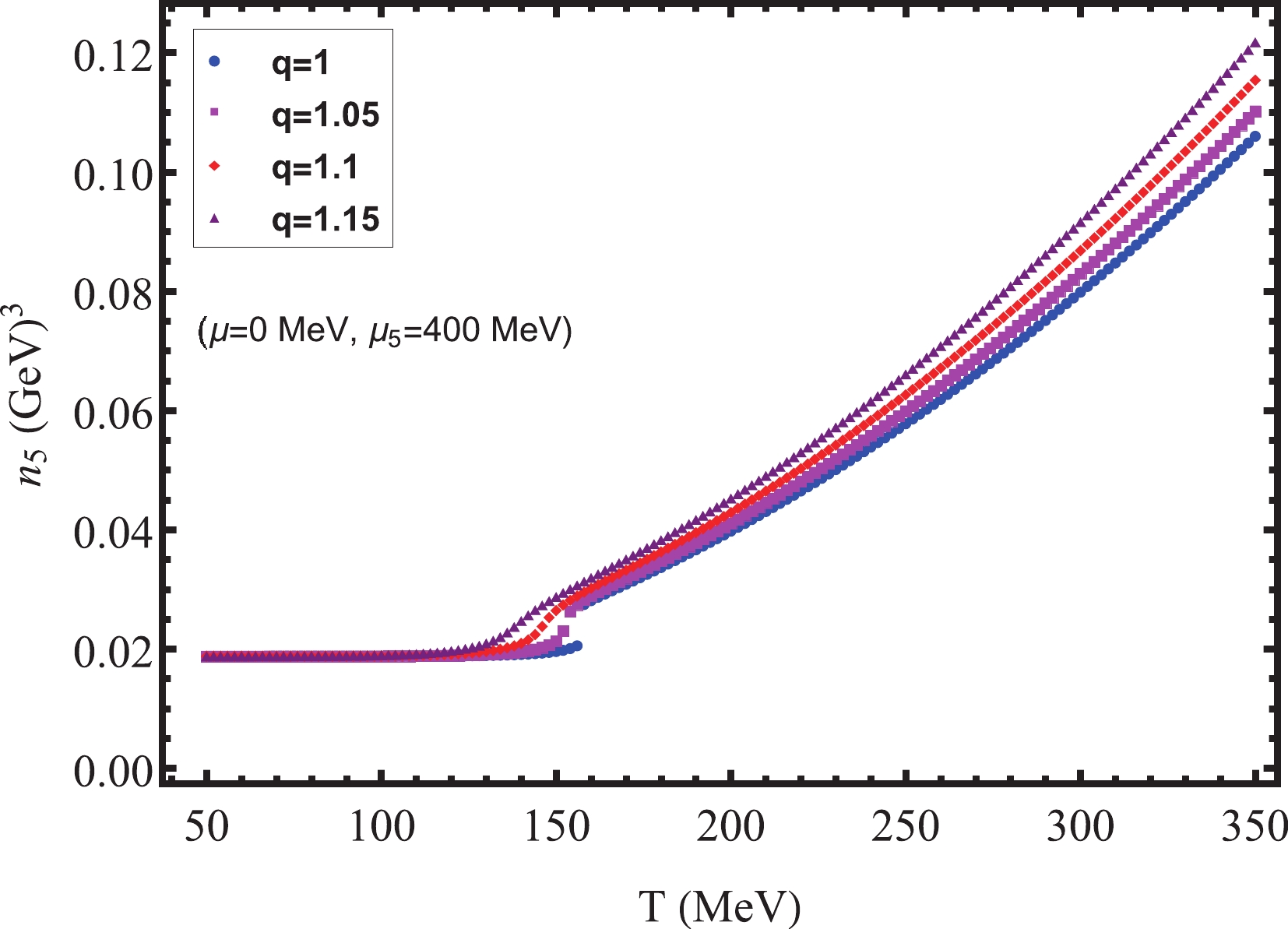
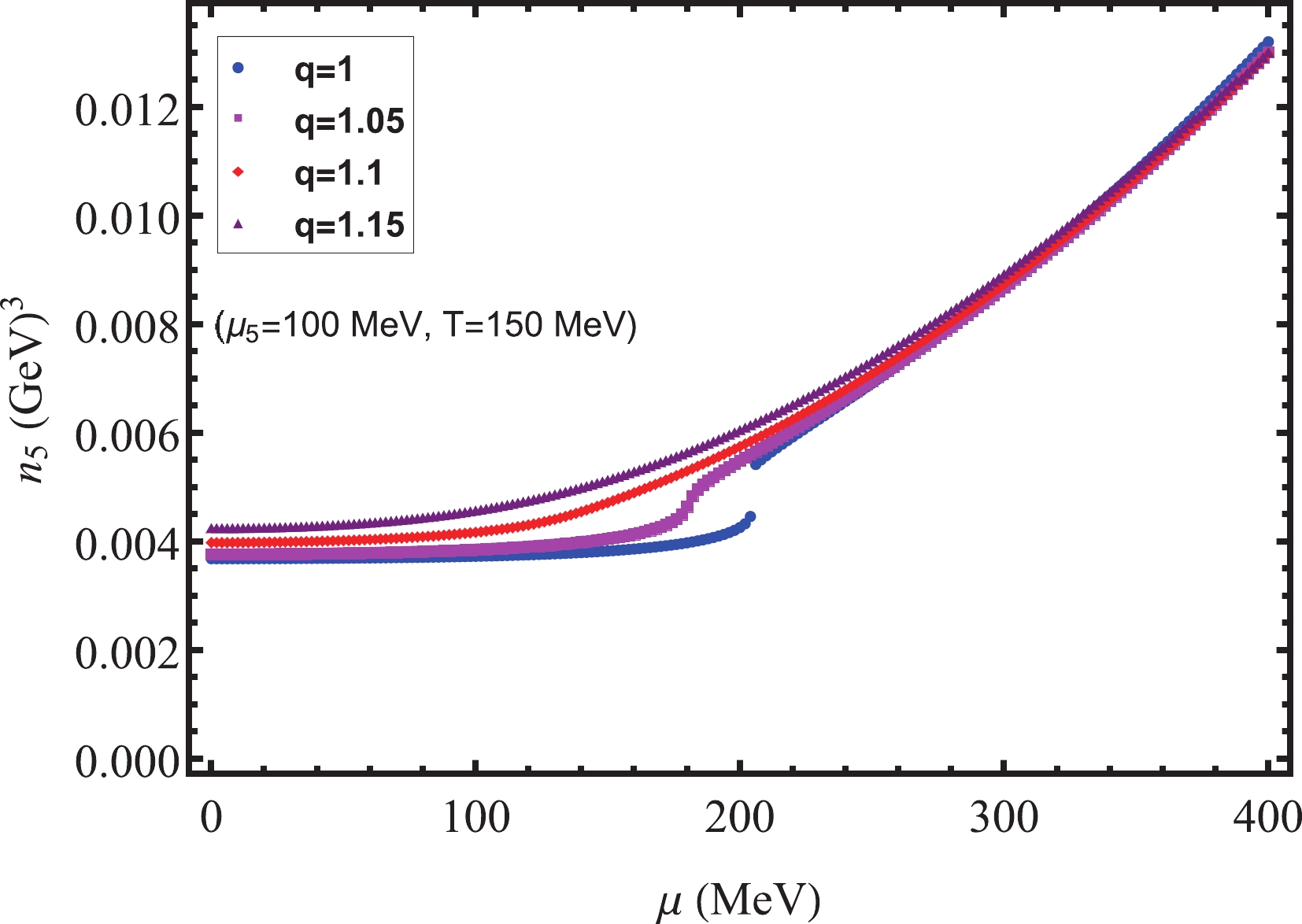
$ n_{5} $ is indispensable for the CME. Because the CME is typically investigated with peripheral collisions, the nonextensive effects are not negligible. Studying the impact of nonextensive effects on$ n_{5} $ will help better understand the CME. Therefore, in this subsection, we study changes in$ n_{5} $ with temperature T and chemical potential μ,$ \mu_{5} $ , paying special attention to the influence of nonextensive effects on$ n_{5} $ . Using Eq. (14), our numerical results are shown in Figs. 6, 7, 8, and 9. In Figs. 6 and 7, for$ q = 1 $ ,$ n_{5} $ is discontinuous because a first-order phase transition occurs. In Fig. 6, at$ \mu = 0\ \mathrm{MeV} $ ,$\mu_{5} = 400 \mathrm{MeV} > \mu_{c5} = 296\ \mathrm{MeV}$ . In Fig. 7, at$ \mu_{5} = 100\ \mathrm{MeV} $ ,$ T = 150\; \mathrm{MeV} < T_{c} = 164\ \mathrm{MeV} $ . As q increases, the phase transition behavior also changes. In addition, we find that in the Nambu phase (the phase with broken dynamical chiral symmetry),$ n_{5} $ is small and remains almost unchanged with increasing T and μ. This is because the chiral condensate couples the left- and right-handed quarks and tends to erase any asymmetry between the number of them, thereby reducing the chiral charge density. Conversely, in the Wigner phase (the phase with partially restored chiral symmetry),$ n_{5} $ increases with T and μ. The same conclusion about the change in$ n_{5} $ with μ can be found in Ref. [27].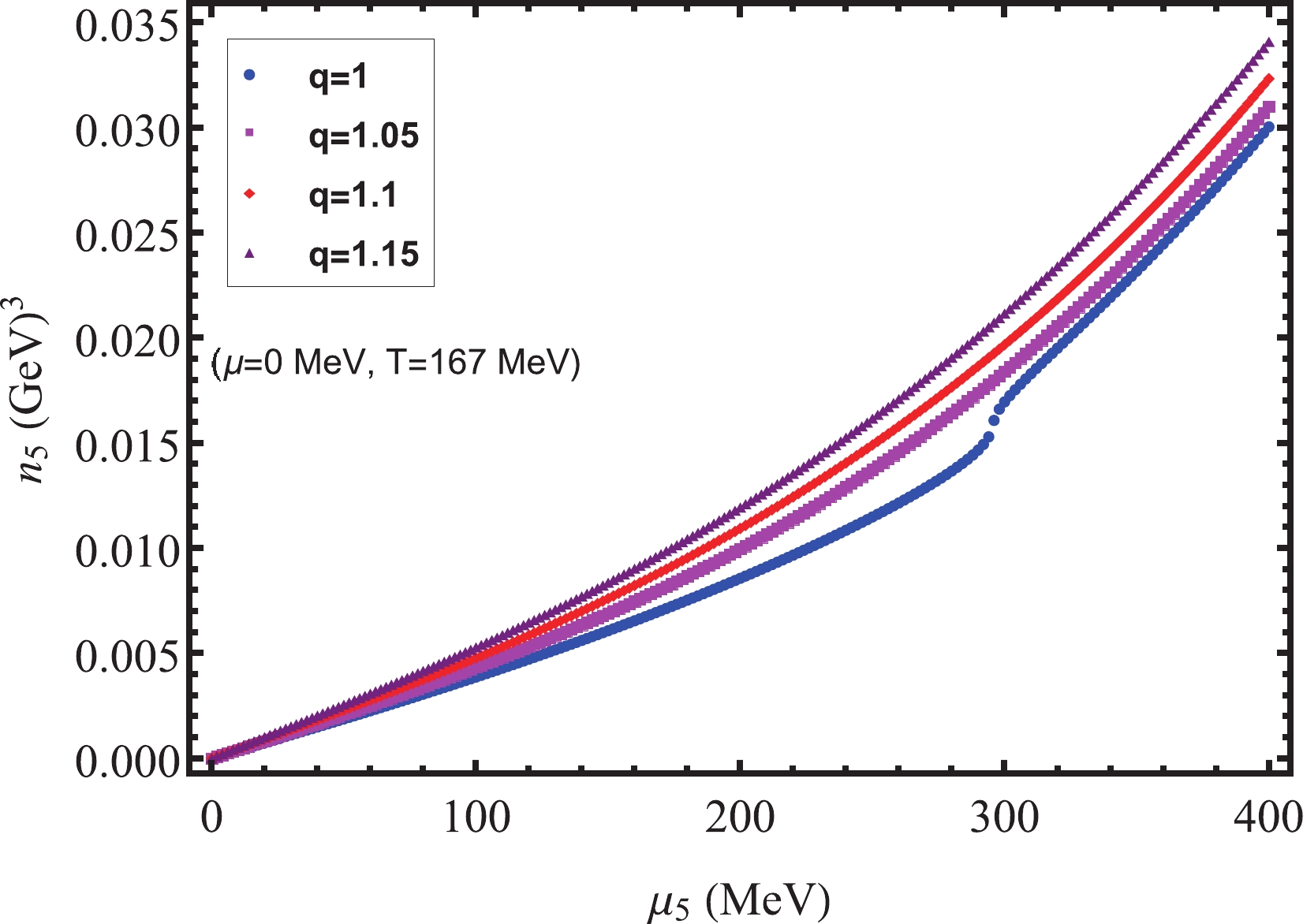
Figure 9. (color online) Chiral charge density
$ n_{5} $ at finite$ \mu_{5} $ for different parameters q.We are more concerned with the impact of nonextensive effects on
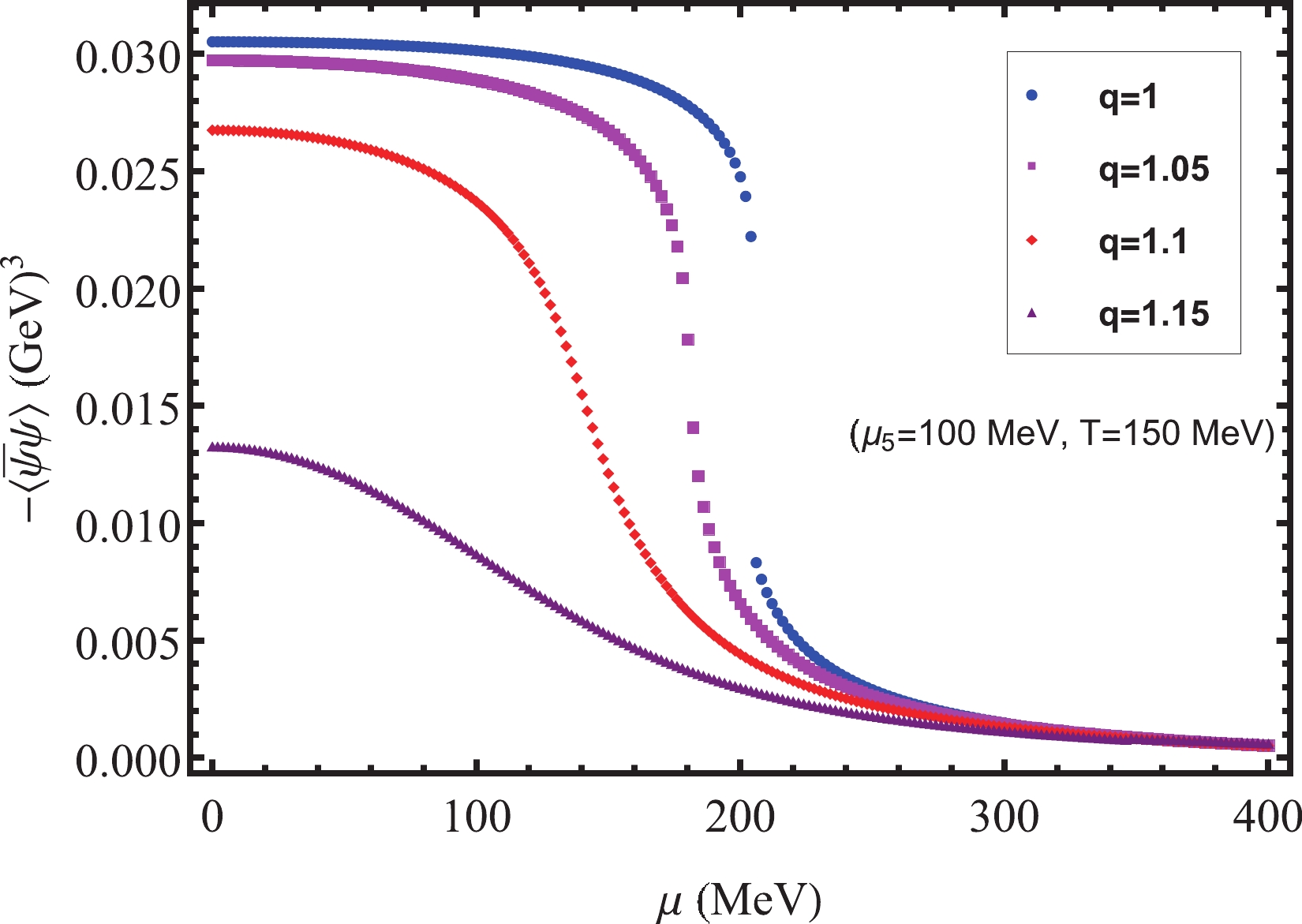
$ n_{5} $ . An interesting observed phenomenon is that the influence of the nonextensive effects on$ n_{5} $ is different on the temperature and chemical potential axes. On the temperature axis,$ n_{5} $ is barely affected by the nonextensive effects at low temperatures. However, for high temperatures,$ n_{5} $ increases with q, and as the temperature increases, the nonextensive effects become increasingly obvious. This is because for$ T\rightarrow0 $ , nonextensive effects do not exist; they only appear at sufficiently high temperatures. In contrast, on the chemical potential axes, the situation is the opposite.$ n_{5} $ is almost unaffected by the nonextensive effects at larger chemical potentials, and at lower chemical potentials,$ n_{5} $ increases significantly with q. We can explain this using Fig. 8. This is because at lower chemical potentials, especially in the critical region, the nonextensive effects significantly depress the chiral condensate, thereby clearly increasing$ n_{5} $ . The change in$ n_{5} $ with the chiral chemical potential$ \mu_{5} $ is shown in Fig. 9, where the temperature$ T = T_{c5} = 167\ \mathrm{MeV} $ is the critical temperature for$ q = 1 $ ;$ n_{5} $ increases as$ \mu_{5} $ and q increase, and the nonextensive effects become more obvious in the critical region and at larger$ \mu_{5} $ . We conclude that nonextensive effects have a significant impact on$ n_{5} $ at high T, high$ \mu_{5} $ , and low μ and in the critical region of phase transition, thereby affecting the electric current induced by the CME. -
Considering that the system is in a non-equilibrium state in relativistic heavy-ion collisions, in this study, we use nonextensive statistical mechanics to investigate chirally imbalanced hot and dense strongly interacting matter using the PNJL model. In particular, the influence of nonextensive effects on the evolution from the CEP to
$ \mathrm{CEP}_{5} $ and the chiral charge density$ n_{5} $ are studied. As q increases, both the CEP and$ \mathrm{CEP}_{5} $ move rapidly toward a larger chemical potential and lower temperature. However, for$ q\geq 1.1 $ , the CEP declines and moves in a direction in which the temperature is lower but the chemical potential is almost unchanged. In addition, we found that for$ q = 1 $ ,$ T_{c}[\mu_{5}] $ increases with$ \mu_{5} $ , whereas for$ q = 1.15 $ ,$ T_{c}[\mu_{5}] $ first increases and then decreases with$ \mu_{5} $ .$ \mu_{c}[\mu_{5}] $ decreases to zero with$ \mu_{5} $ , which is natural because$ \mathrm{CEP}_{5} $ exists based on our calculations. In fact, our focus in this paper is not whether$ \mathrm{CEP}_{5} $ exists. Different models provide different results; although lattice simulation shows that$ \mathrm{CEP}_{5} $ does not exist, this is still based on BG statistics, which only applies to equilibrium systems, and there are no simulation results based on nonextensive statistics. Furthermore, owing to the different influence of nonextensive effects on the CEP and$ \mathrm{CEP}_{5} $ in the case of$ q\geq 1.1 $ , there is a situation in which two points far apart on the$ \mathrm{CEP}_{5} $ plane can evolve to be close to each other on the CEP plane. In other words, even if$ \mathrm{CEP}_{5} $ exists, we may not obtain useful information about the location of the CEP.Chiral charge density
$ n_{5} $ , as a novel feature of chirally imbalanced matter, is indispensable for the CME. We found that in the Nambu phase,$ n_{5} $ is almost constant with T and μ, whereas in the Wigner phase,$ n_{5} $ increases with T and μ. This is because for$ n_{5} $ , chiral symmetry restoration is essential, and a large chiral condensate tends to eliminate the asymmetry between the numbers of right- and left-handed quarks. In addition,$ n_{5} $ increases with$ \mu_{5} $ . Because the CME is typically investigated with peripheral collisions, nonextensive effects are considered. We found that nonextensive effects have a significant impact on$ n_{5} $ at high T, high$ \mu_{5} $ , and low μ. In the critical region, nonextensive effects are still significant. We conclude that for chirally imbalanced hot and dense strongly interacting matter, nonextensive effects have a significant impact on the evolution from the CEP to$ \mathrm{CEP}_{5} $ and$ n_{5} $ , thereby affecting the electric current induced by the CME. Our research may provide useful hints for related experiments and other studies. The issues related to nonextensive effects deserve further study. -
Based on nonextensive thermodynamics [32, 36], the thermodynamic potential density function
$ \Omega_{q} $ is defined as$\begin{aligned}[b] \Omega_{q}& = -T {\ln_{q}}Z_{q}\\ & = -T {\ln_{q}}{\bf{Tr}}\ {\rm exp}_{q}\left(-\frac{1}{T}\int {\rm d}^{3}x(\mathcal{H}-\mu\psi^{\dagger}\psi)\right), \end{aligned} \tag{A1}$

where
$ Z_{q} $ is the nonextensive version of the grand canonical partition function,$ \mathcal{H} $ is the Hamiltonian density, and$ {\bf{Tr}} $ is a functional trace over all states of the system. Using the finite-temperature field theory method, after integrating the fermion fields in the partition function, we can express$ \Omega_{q} $ in the following three parts (in the mean-field approximation):$ \begin{aligned}[b] \Omega_{q} =& \mathcal{U}(\Phi;T)+\frac{\sigma^{2}}{2G}\\& -T\sum\limits_{n}\int\frac{{\rm d}^3p}{(2\pi)^3}\mathrm{Tr}\ \mathrm{ln_{q}}\frac{S^{-1}({\rm i}\omega_{n},\vec{p})}{T}. \end{aligned}\tag{A2}$

Here,
$ \omega_{n} = (2n+1)\pi T $ are Matsubara frequencies, and the inverse quark propagator is$ S^{-1}(p^{0},\vec{p}) = \gamma_{0}(p^{0}+\mu- {\rm i} A_{4})-\vec{\gamma}\cdot\vec{p}-M . \tag{A3}$

We use the identity
$ \mathrm{Tr}\ {\ln}_{q}X = {\ln_{q}}\ {\rm Det}_{q}X. \tag{A4}$

Take the diagonal matrix as an example,
$ \begin{aligned}[b] {\ln_{q}}\ {\rm Det}_{q}\left( \begin{array}{*{20}{c}} a&0\\ 0&b\\ \end{array} \right)& = {\ln_{q}}(a\otimes_{q}b) = {\ln_{q}}a+ {\ln_{q}}b\\ & = {\rm Tr}\ {\ln}_{q}\left( \begin{array}{*{20}{c}} a&0\\ 0&b\\ \end{array} \right). \end{aligned} \tag{A5}$

For further q-calculus, see Refs. [75, 76]. Based on Ref. [32], we obtain the approximate formula
$\begin{aligned}[b] &T\sum\limits_{n}\mathrm{ln}_{q}\left[\frac{1}{T^{2}}(\omega_{n}^{2}+(E_{p}\pm\mu)^{2})\right]\approx(E_{p}\pm\mu)\\ +&2T\mathrm{ln}_{q}[1+\mathrm{exp}_{q}(-(E_{p}\pm\mu)/T)]. \end{aligned}\tag{A6}$

Finally, we obtain the thermodynamic potential density function
$ \Omega_{q} $ of the two-flavor nonextensive PNJL model as$ \begin{aligned}[b] \Omega_{q}(\mu,T,M,\Phi) =& \mathcal{U}(\Phi;T)+\frac{(M-m)^{2}}{4G}\\ &-2N_{c}N_{f}\int_{0}^{\Lambda}\frac{{\rm d}^3\vec{p}}{(2\pi)^3}E_{p}\\ &-2N_{f}T\int_{0}^{\infty}\frac{{\rm d}^3\vec{p}}{(2\pi)^3}(\mathrm{ln}_{q}F_{q}^++\mathrm{ln}_{q}F_{q}^-), \end{aligned}\tag{A7} $

where
$\begin{aligned}[b] F_{q}^{\pm} = &1+3\Phi(e_{q}(-(E_{p}\mp\mu)/T)+e_{q}(-2(E_{p}\mp\mu)/T))\\ &+e_{q}(-3(E_{p}\mp\mu)/T), \end{aligned}\tag{A8}$

and
$ E_{p} = \sqrt{p^{2}+M^{2}} $ is the single quasi-particle energy. Introducing the chiral chemical potential$ \mu_{5} $ , Eq. (16) is obtained accordingly.
Nonextensive effects on QCD chiral phase transition with a chiral chemical potential
- Received Date: 2021-12-20
- Available Online: 2022-10-15
Abstract: In this study, we investigate the QCD chiral phase diagram in the presence of a chiral chemical potential





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF




















 DownLoad:
DownLoad: