-
Charmonium states are the bound states of a charmed quark (c) and a charmed antiquark (
$ \bar{c} $ ). Since the discovery of the first charmonium state, the$ J/\psi $ , at BNL [1] and at SLAC [2] in 1974, all the charmonium states below the open-charm threshold and a few charmonium states above the open-charm threshold have been established; the measured spectrum of the states agrees well with theoretical calculations based on QCD [3–5] and QCD-inspired potential models [6–8]. On the contrary, the decays of the charmonium states into light hadrons, which must proceed via the annihilation of the charmed quark-antiquark pair, are still poorly known, although they are governed by the same QCD theory.The first calculation by Appelquist and Politzer [9] using perturbative QCD related the hadronic decays of
$ J/\psi $ and its radial excited sibling,$ \psi(2S) $ , to their leptonic decays, and predicted$ \begin{aligned}[b] Q^V =&\frac{ {\cal B}( \psi(2S)\to {\rm hadrons})}{ {\cal B}( J/\psi\to {\rm hadrons})} \\ =&\frac{ {\cal B}( \psi(2S)\to e^+e^-)}{ {\cal B}( J/\psi\to e^+e^-)}. \end{aligned} $

The ratio was found to be around 12% using the branching fractions of the leptonic decays at that time, and this was called the "12% rule" since then, although the most recent ratio is (13.3 ± 0.3)% [10]. Extending
$ Q^V $ of inclusive decays of charmonium to light hadrons to each individual hadronic final state, h, the Mark II experiment tested$ Q^V_h $ with eight final states [11] and found two modes were severely suppressed relative to 12%, while the other six modes agreed with 12% reasonably well, and the$ \rho\pi $ mode was suppressed by more than an order of magnitude; therefore, this was referred to as the "$ \rho\pi $ puzzle." Many theoretical explanations have been put forth to decipher this puzzle [12]. Some attribute the small$ Q^V_{\rho\pi} $ to the enhanced branching fraction of$ J/\psi $ decays, some attribute it to the suppressed branching fraction of$ \psi(2S) $ decays, and some others attribute it to some dynamics that may affect both$ \psi(2S) $ and$ J/\psi $ decays but in a different way. Improved measurements from BES, CLEOc, and lately, BESIII experiments confirmed the Mark II observations and tested various theoretical models [10]. None of these models can solve the "$ \rho\pi $ puzzle" and all the newly available data satisfactorily [12].As the spin-partners of
$ J/\psi $ and$ \psi(2S) $ , respectively, the spin-singlets$ \eta_c $ and$ \eta_c(2S) $ may decay into light hadrons in a similar way as their spin-triplets partners. Anselmino, Genovese, and Predazzi assumed [13]$ \frac{ {\cal B}( \eta_c(2S)\to {\rm hadrons})}{ {\cal B}( \eta_c\to {\rm hadrons})} \approx \frac{ {\cal B}( \psi(2S)\to {\rm hadrons})}{ {\cal B}( J/\psi\to {\rm hadrons})} = Q^V, $

while Chao, Gu, and Tuan argued that [14]
$ Q^P = \frac{ {\cal B}( \eta_c(2S)\to {\rm hadrons})}{ {\cal B}( \eta_c\to {\rm hadrons})} \approx 1. $

These two predictions differ by a factor of seven and should be tested with experimental data.
The theoretical work was clearly ahead of its time since the
$ \eta_c(2S) $ was first observed in 2002 [15], and until now, only three hadronic decays of it were listed with branching fractions and the uncertainties are more than 50% [10].By examining the experimental data available for
$ \eta_c(2S) $ decays (cited by the PDG [10] and those listed in the Appendix A), we found an amazing fact that in most of the cases, both$ \eta_c $ and$ \eta_c(2S) $ were measured in an experiment at the same time; therefore, this allowed a very convenient way of determining the ratio of the branching fractions and to test the theoretical predictions. We scrutinized the experimental measurements, selected only the reliable results, and performed a global fit to extract properties related to the$ \eta_c $ and$ \eta_c(2S) $ states.There are mainly three categories of measurements related to
$ \eta_c $ and$ \eta_c(2S) $ states: two-photon processes ($ \gamma\gamma\to \eta_c\; ( \eta_c(2S)) $ ), B meson decays ($ B\to K\eta_c\; ( \eta_c(2S)) $ ), and charmonium decays ($ \psi(2S)\to \gamma \eta_c\; ( \eta_c(2S)) $ ,$J/\psi\to \gamma \eta_c$ , and$ h_c\to \gamma \eta_c $ ). In many of the cases, experimental measurements are the ratio or the product of the branching fractions or partial widths. With the help of measurements of a few absolute branching fractions and the total widths of$ \eta_c $ ($ \Gamma_{ \eta_c} $ ) and$ \eta_c(2S) $ ($ \Gamma_{ \eta_c(2S)} $ ), we were able to determine the branching fractions of$ \eta_c $ and$ \eta_c(2S) $ decays and the ratios, as well as their partial widths, of$ \gamma\gamma $ ($ \Gamma_{ \eta_c\to \gamma\gamma} $ and$ \Gamma_{ \eta_c(2S)\to \gamma\gamma} $ ).The
$ \eta_c $ -related measurements before 1995 were obtained by using$ \eta_c $ mass and width that are significantly smaller than the recent results [10]. They were not used in our analysis since the results are biased and the precision is low. The$ \eta_c $ -related measurements from$J/\psi\to \gamma \eta_c$ were biased by neglecting the interference between$ \eta_c $ and${\rm{non}}\text{-}\eta_c$ amplitudes and using unreliable line shape of$ \eta_c $ resonance in this$ M1 $ transition [16]. They were also not used in our analysis.We were left with 97 measurements from the AMY, BaBar, Belle, BESIII, CLEO, DELPHI, E760, E835, and LHCb experiments, as listed in Appendix A. We performed a least-squares fit with 29 parameters, and the
$ \chi^2 $ of the fit was 86, which corresponds to a confidence level of 5.7%, indicating a reasonable fit. The main contributor to large$ \chi^2 $ is DELPHI [17]; the uncertainties of its three measurements may have been underestimated, but there was no significant effect on the results by including these data.Table 1 and Fig. 1 show the fit results and the total uncertainties of
$ \eta_c $ and$ \eta_c(2S) $ hadronic decays. We found that the ratios of all the modes with positive$ \eta_c(2S) $ signals (upper half of Table 1) were less than one, and those of some modes with stringent$ \eta_c(2S) $ decay rates were also less than one, although those of some other modes were inconclusive (lower half of Table 1). These put the prediction of$ Q^P\approx 1 $ in question. Although each and all of the ratios agreed with the "12% rule" better than$ Q^P\approx 1 $ , we found that all central values were higher than 13%, except for$ p\bar{p} $ mode, which was lower by more than three standard deviations. These indicated that the experimental measurements do not agree with either of the two predictions.decay mode (h) $ {\cal B}( \eta_c\to h) $ (%)

$ {\cal B}( \eta_c(2S)\to h) $ (%)

$ Q^P_h $ 

$ p\bar{p} $ 

$ 0.136\pm 0.012 $ 

$ 0.0077_{-0.0021}^{+0.0028} $ 

$ 0.057_{-0.016}^{+0.022} $ 

$ K\bar{K}\pi $ 

$ 6.90_{-0.42}^{+0.44} $ 

$ 1.86_{-0.49}^{+0.68} $ 

$ 0.27_{-0.07}^{+0.10} $ 

$ K\bar{K}\eta $ 

$ 1.27_{-0.14}^{+0.15} $ 

$ 0.51_{-0.23}^{+0.31} $ 

$ 0.40_{-0.18}^{+0.25} $ 

$ \pi^+\pi^- \eta^{\prime} $ 

$ 1.20_{-0.17}^{+0.18} $ 

$ 0.25_{-0.09}^{+0.14} $ 

$ 0.21_{-0.08}^{+0.12} $ 

$ \pi^+\pi^- p\bar{p} $ 

$ 0.365_{-0.039}^{+0.042} $ 

$ 0.236_{-0.052}^{+0.076} $ 

$ 0.65_{-0.16}^{+0.22} $ 

$ K_{S}^{0} K^\pm\pi^\mp \pi^+\pi^- $ 

$ 2.39_{-0.62}^{+0.67} $ 

$ 1.00_{-0.42}^{+0.69} $ 

$ 0.42_{-0.19}^{+0.34} $ 

$ K^+K^- \pi^+\pi^-\pi^0 $ 

$ 3.50_{-0.57}^{+0.60} $ 

$ 1.36_{-0.48}^{+0.70} $ 

$ 0.39_{-0.14}^{+0.22} $ 

$ \pi^+\pi^-\eta $ 

$ 1.43^{+0.41}_{-0.38} $ 

<0.96 [18] <0.78 $ 2( \pi^+\pi^-) $ 

$ 0.86^{+0.13}_{-0.12} $ 

<0.41[19] <0.50 $ K^+K^- \pi^+\pi^- $ 

$ 0.57\pm 0.10 $ 

<0.32 [19] <0.60 $ 2( K^+K^-) $ 

$ 0.135^{+0.028}_{-0.027} $ 

<0.14 [19] 1.5 $ 3( \pi^+\pi^-) $ 

$ 1.75\pm 0.48 $ [20]

<2.9 [18] <2.0 $ K^+K^- 2( \pi^+\pi^-) $ 

$ 0.72\pm 0.37 $ [20]

<2.2 [18] <5.4 $ \phi\phi $ 

$ 0.155^{+0.018}_{-0.017} $ 

— — $ \phi K^+K^- $ 

$ 0.36^{+0.15}_{-0.14} $ 

— — $ 2( \pi^+\pi^-\pi^0) $ 

$ 15.1^{+2.0}_{-1.9} $ 

— — Table 1. The branching fractions of
$ \eta_c(2S) $ and$ \eta_c $ decays and the ratios. For the modes with upper limits only, the data are from experimental measurements directly. The upper limits of the ratios at the 90% confidence level are determined by dividing the upper limits of the$ \eta_c(2S) $ decays by the branching fractions of the$ \eta_c $ decays lowered by the corresponding uncertainties.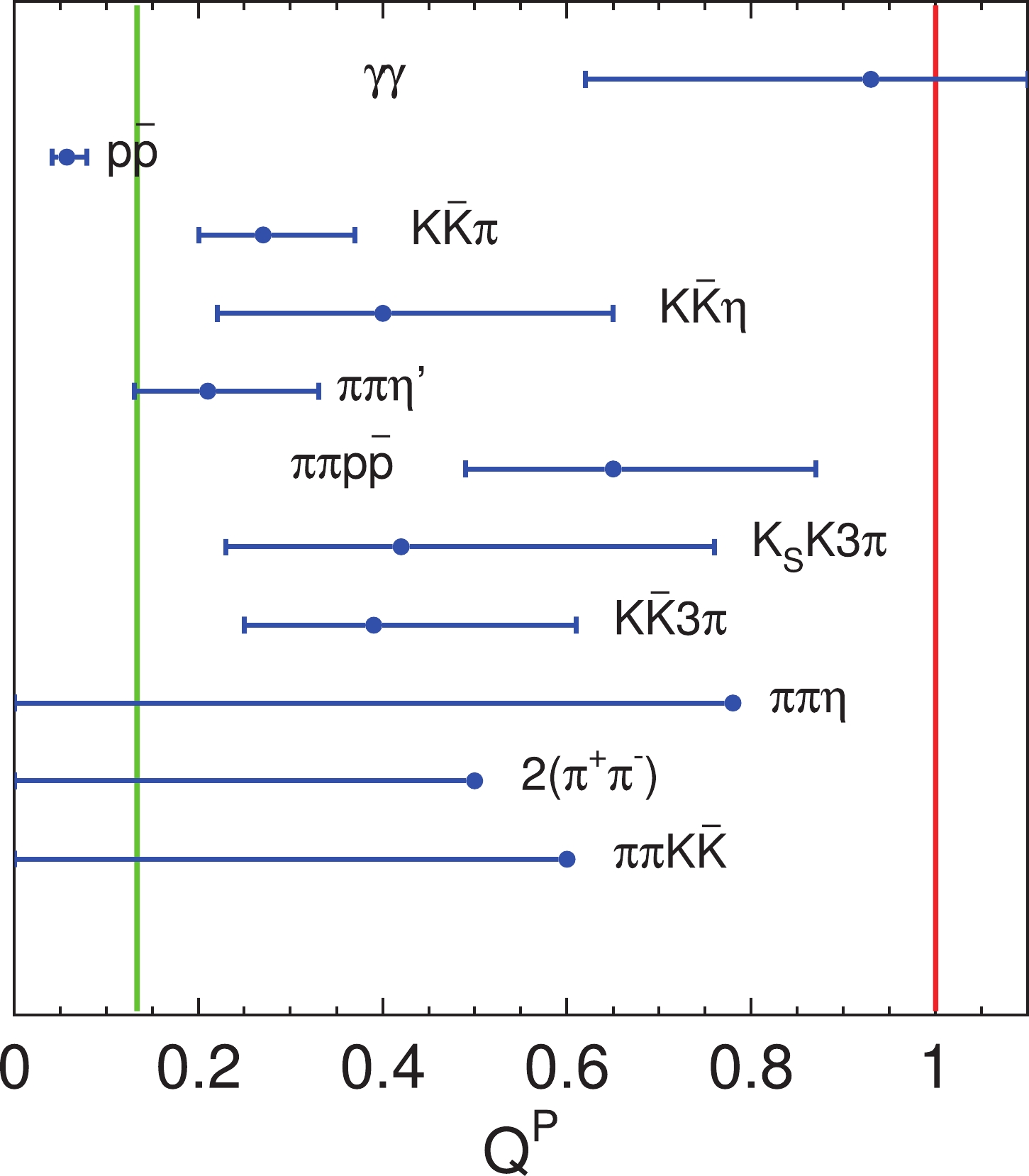
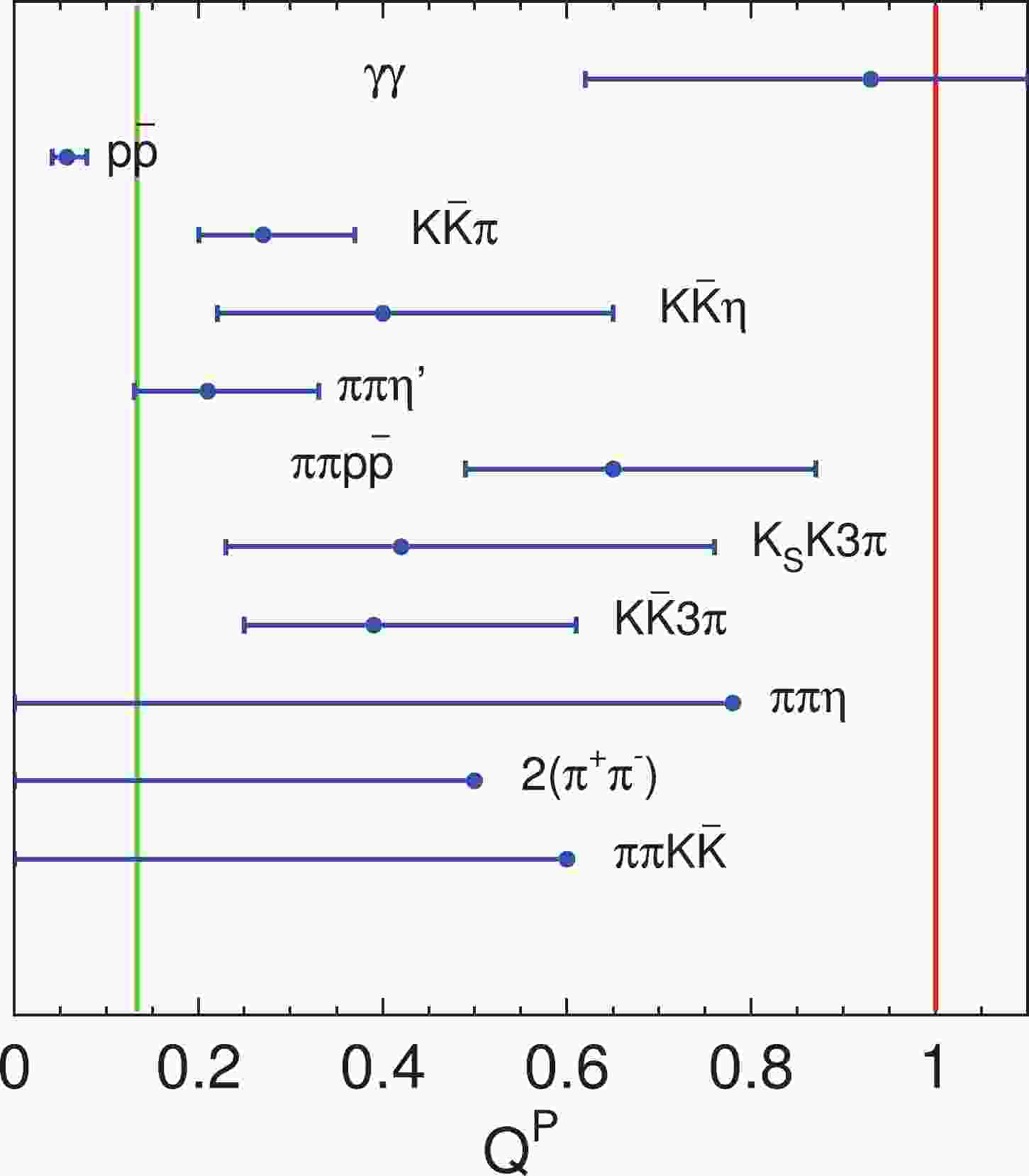
Figure 1. (color online)
$ Q^P $ from the global fit and the comparison with theoretical predictions. Dots with error bars are data and the vertical lines show$ Q^P=0.133 $ and$ Q^P=1 $ .Table 2 shows the other fit results. We found that the total widths of
$ \eta_c $ and$ \eta_c(2S) $ agreed with those obtained in Ref. [10], and the ratio$\Gamma_{ \eta_c(2S)}/\Gamma_{ \eta_c} = 0.44\pm 0.10$ agreed well with the expectation of Eq. (14) of Ref. [14], i.e.,$ \Gamma_{ \eta_c} $ 

$ 32.2\pm 0.7 $ MeV

$ \Gamma_{ \eta_c(2S)} $ 

$ 14.1\pm 3.1 $ MeV

$ \Gamma_{ \eta_c\to \gamma\gamma} $ 

$ 5.43_{-0.38}^{+0.41} $ keV

$ \Gamma_{ \eta_c(2S)\to \gamma\gamma} $ 

$ 2.21_{-0.64}^{+0.88} $ keV

$ {\cal B}( B^+\to \eta_cK^+) $ 

$ (10.8\pm 0.6)\times 10^{-4} $ 

$ {\cal B}( B^+\to \eta_c(2S)K^+) $ 

$ (4.42\pm 0.96)\times 10^{-4} $ 

$ {\cal B}( \psi(2S)\to \gamma \eta_c(2S)) $ 

$ (7.0^{+3.4}_{-2.5})\times 10^{-4} $ 

$ {\cal B}( \psi(2S)\to \pi^0 h_c\to \pi^0\gamma \eta_c) $ 

$ (5.03^{+0.52}_{-0.49})\times 10^{-4} $ 

Table 2. The fit results on
$ \eta_c(2S) $ and$ \eta_c $ related quantities.$ \frac{\Gamma_{ \eta_c(2S)}}{\Gamma_{ \eta_c}} \approx \frac{\Gamma_{ \eta_c(2S)\to {\rm hadrons}}}{\Gamma_{ \eta_c\to {\rm hadrons}}} \approx \frac{\Gamma_{ \psi(2S)\to e^+e^-}}{\Gamma_{ J/\psi\to e^+e^-}} = 0.42 \pm 0.01, $

where
$ \Gamma_{ \psi(2S)\to e^+e^-} $ and$ \Gamma_{ J/\psi\to e^+e^-} $ are the leptonic partial widths of the vector charmonium states [10].The partial width of
$ \eta_c\to \gamma\gamma $ ,$ (5.43_{-0.38}^{+0.41}) $ keV, is about one standard deviation higher than the world average [10] and is lower than the lattice QCD calculation of$ \Gamma_{ \eta_c\to \gamma\gamma}=(6.51\pm 0.20) $ keV [21] by 2.5 standard deviations. Further measurements and refined calculations are needed to clarify the tension and to develop other model calculations [22, 23].The partial width of
$ \eta_c(2S)\to \gamma\gamma $ of$ (2.21_{-0.64}^{+0.88}) $ keV is a first model-independent evaluation, to be compared with various calculations compiled in Ref. [23]. Note that the ratio of the branching fractions of$ \eta_c(2S) $ and$ \eta_c\to \gamma\gamma $ agreed fairly well with the$ Q^P=1 $ rule:$ \frac{ {\cal B}( \eta_c(2S)\to \gamma\gamma)}{ {\cal B}( \eta_c\to \gamma\gamma)} = \frac{\Gamma_{ \eta_c(2S)\to \gamma\gamma}/\Gamma_{ \eta_c(2S)}}{\Gamma_{ \eta_c\to \gamma\gamma}/\Gamma_{ \eta_c}} = 0.93^{+0.48}_{-0.31}, $

although the uncertainty was large.
As by products, we also report the best evaluation of
$ {\cal B}( B^+\to \eta_cK^+) $ ,$ {\cal B}( B^+\to \eta_c(2S)K^+) $ ,$ {\cal B}( \psi(2S)\to \gamma \eta_c(2S)) $ , and$ {\cal B}( \psi(2S)\to \pi^0 h_c)\cdot {\cal B}( h_c\to \gamma \eta_c) $ to date, as shown in Table 2. These results will be used in future measurements with these processes.In summary, we determined the ratios of the pseudoscalar charmonium states
$ \eta_c(2S) $ and$ \eta_c $ decay branching fractions and found prominent discrepancy from theoretical predictions [13, 14]. The mixing of the$ J/\psi $ with a nearby glueball has been proposed [24] to explain the "$ \rho\pi $ puzzle", and the scheme has been extended to the$ \eta_c $ case [13, 14]. As the pseudoscalar glueballs are expected to be close to$ \eta_c $ or$ \eta_c(2S) $ [25, 26], the mixing between them may also play an important role in the charmonium decays [27–29]. The different contribution of the open-charm loop in$ \eta_c $ and$ \eta_c(2S) $ decays may affect the branching fraction ratio [30] too. The fact that all the known hadronic decays of$ \eta_c(2S) $ have rates lower than$ \eta_c $ decays suggests abnormal dynamics in either$ \eta_c(2S) $ or$ \eta_c $ decays, and these may be investigated at future experiments like BESIII [31], Belle II [32], and LHCb [33] in charmonium decays, two-photon processes, and B decays.
HTML
-
Index quantity Value (%) Experiment Branching fraction 1 $ {\cal B}( \eta_c\to K^+K^-\pi^0) $ 

$ 1.15 \pm 0.12 \pm 0.10 $ 

BESIII [34] 2 $ {\cal B}( \eta_c\to K_{S}^{0} K^{\pm}\pi^{\mp}) $ 

$ 2.60 \pm 0.21 \pm 0.20 $ 

BESIII [34] 3 $ {\cal B}( \eta_c\to p\bar{p}) $ 

$ 0.120\pm 0.026\pm 0.015 $ 

BESIII [34] 4 $ {\cal B}( \eta_c\to 2(\pi^+\pi^-\pi^0)) $ 

$ 15.3 \pm 1.8 \pm 1.8 $ 

BESIII [34] 5 $ {\cal B}( B^+\to \eta_cK^+) $ 

$ 0.120\pm 0.008\pm 0.007 $ 

Belle [35] 6 $ {\cal B}( B^+\to \eta_cK^+) $ 

$ 0.096\pm 0.012\pm 0.006 $ 

BaBar [36] 7 $ {\cal B}( B^+\to \eta_c(2S)K^+) $ 

$ 0.048\pm 0.011\pm 0.003 $ 

Belle [35] 8 $ {\cal B}( B^+\to \eta_c(2S)K^+) $ 

$ 0.035\pm 0.017\pm 0.005 $ 

BaBar [36] Ratio of the branching fractions 9 $ \dfrac{ {\cal B}( \eta_c\to \phi\phi)}{ {\cal B}( \eta_c\to p\bar{p})} $ 

$ 1.79\pm 0.14\pm 0.32 $ 

LHCb [37] 10 $ \dfrac{ {\cal B}( \eta_c\to \phi\phi)}{ {\cal B}( \eta_c\to K\bar{K}\pi)} $ 

$ 0.032^{+0.014}_{-0.010}\pm 0.009 $ 

Belle [38] 11 $ \dfrac{ {\cal B}( \eta_c\to K^+K^-\eta)}{ {\cal B}( \eta_c\to K^+K^-\pi^0)} $ 

$ 0.571\pm 0.025\pm 0.051 $ 

BaBar [39] 12 $ \dfrac{ {\cal B}( \eta_c\to \phi K^+K^-)}{ {\cal B}( \eta_c\to K\bar{K}\pi)} $ 

$ 0.052^{+0.016}_{-0.014}\pm 0.014 $ 

Belle [38] 13 $\dfrac{ {\cal B}( \eta_c\to 2(K^+K^-))}{ {\cal B}( \eta_c\to K\bar{K}\pi)}$ 

$ 0.026^{+0.009}_{-0.007}\pm 0.007 $ 

Belle [38] 14 $ \dfrac{ {\cal B}( \eta_c(2S)\to K^+K^-\eta)}{ {\cal B}( \eta_c(2S)\to K^+K^-\pi^0)} $ 

$ 0.82\pm 0.21\pm 0.27 $ 

Belle [39] 15 $ \dfrac{ {\cal B}( \eta_c(2S)\to K\bar{K}\pi)\cdot {\cal B}( B^+\to \eta_c(2S)K^+)}{ {\cal B}( \eta_c\to K\bar{K}\pi)\cdot {\cal B}( B^+\to \eta_cK^+)} $ 

$ 0.096^{+0.020}_{-0.019}\pm0.025 $ 

BaBar [40] 16 $ \dfrac{ {\cal B}( \eta_c(2S)\to K_{S}^{0} K^{\pm}\pi^{\mp})\cdot\Gamma_{ \eta_c(2S)\to \gamma\gamma}}{ {\cal B}( \eta_c\to K_{S}^{0} K^{\pm}\pi^{\mp})\cdot\Gamma_{ \eta_c\to \gamma\gamma}} $ 

$ 0.18\pm 0.05 \pm 0.02 $ 

CLEO [41] Table A1. Data used in the analysis: absolute branching fractions and the ratios of the branching fractions for
$ \eta_c $ and$ \eta_c(2S) $ .Index quantity Value ( $ \times 10^{-6} $ )

Experiment 17 $ {\cal B}( \eta_c\to p\bar{p})\cdot {\cal B}( \psi(2S)\to\pi^0h_c\to \pi^0\gamma\eta_c) $ 

$ 0.65\pm 0.19\pm 0.10 $ 

BESIII [42] 18 $ {\cal B}( \eta_c\to p\bar{p})\cdot {\cal B}( \eta_c\to \gamma\gamma) $ 

$ 0.224^{+0.038}_{-0.037}\pm 0.020 $ 

E835 [43] 19 $ {\cal B}( \eta_c\to p\bar{p})\cdot {\cal B}( \eta_c\to \gamma\gamma) $ 

$ 0.336^{+0.080}_{-0.070} $ 

E760 [44] 20 $ {\cal B}( \eta_c\to p\bar{p})\cdot {\cal B}( B^+\to \eta_cK^+) $ 

$ 1.64\pm 0.41^{+0.17}_{-0.24} $ 

Belle [45] 21 $ {\cal B}( \eta_c\to p\bar{p})\cdot {\cal B}( B^0\to \eta_cK^0) $ 

$ 1.79\pm 0.68^{+0.19}_{-0.25} $ 

Belle [45] 22 $ {\cal B}( \eta_c\to p\bar{p})\cdot {\cal B}( B^+\to \eta_cK^+) $ 

$ 1.8^{+0.3}_{-0.2}\pm 0.2 $ 

BaBar [46] 23 $ {\cal B}( \eta_c\to p\bar{p})\cdot {\cal B}( B^+\to \eta_cK^+) $ 

$ 1.42\pm 0.11^{+0.16}_{-0.20} $ 

Belle [47] 24 $ {\cal B}( \eta_c\to \gamma\gamma)\cdot {\cal B}( B^+\to \eta_cK^+) $ 

$ 0.22^{+0.09}_{-0.07}\,^{+0.04}_{-0.02} $ 

Belle [48] 25 $ {\cal B}( \eta_c\to \phi\phi)\cdot {\cal B}( B^+\to \eta_cK^+) $ 

$ 4.7\pm 1.2\pm 0.5 $ 

BaBar [49] 26 $ {\cal B}( \eta_c\to \phi\phi)\cdot {\cal B}( B^0\to \eta_cK^0) $ 

$ 2.4\pm 1.4\pm 0.3 $ 

BaBar [49] 27 $ {\cal B}( \eta_c\to K\bar{K}\pi)\cdot {\cal B}( B^+\to \eta_cK^+) $ 

$ 74.0\pm 5.0\pm 7.0 $ 

BaBar [49] 28 $ {\cal B}( \eta_c\to K\bar{K}\pi)\cdot {\cal B}( B^0\to \eta_cK^0) $ 

$ 64.8\pm 8.5\pm 7.1 $ 

BaBar [49] 29 $ {\cal B}( \eta_c\to K^+K^-\pi^0)\cdot {\cal B}( \psi(2S)\to\pi^0h_c\to \pi^0\gamma\eta_c) $ 

$ 4.54\pm 0.76\pm 0.48 $ 

BESIII [42] 30 $ {\cal B}( \eta_c\to K^+K^-\pi^0)\cdot {\cal B}( B^+\to \eta_cK^+) $ 

$ 11.4\pm 2.5^{+1.1}_{-1.8} $ 

Belle [45] 31 $ {\cal B}( \eta_c\to K^+K^-\pi^0)\cdot {\cal B}( B^0\to \eta_cK^0) $ 

$ 16.6\pm 5.0\pm 1.8 $ 

Belle [45] 32 $ {\cal B}( \eta_c\to K_{S}^{0} K^{\pm}\pi^{\mp})\cdot {\cal B}( \psi(2S)\to\pi^0h_c\to \pi^0\gamma\eta_c) $ 

$ 11.35\pm 1.25\pm 1.50 $ 

BESIII [42] 33 $ {\cal B}( \eta_c\to K_{S}^{0} K^{\pm}\pi^{\mp})\cdot {\cal B}( B^+\to \eta_cK^+) $ 

$ 24.0\pm 1.2^{+2.1}_{-2.0} $ 

Belle [50] Continued on next page Table A2. Data used in the analysis: product branching fractions measured in B decays and charmonium decays.
Table A2-continued from previous page Index quantity Value ( $ \times 10^{-6} $ )

Experiment 34 $ {\cal B}( \eta_c\to K_{S}^{0} K^{\pm}\pi^{\mp})\cdot {\cal B}( B^0\to \eta_cK^0) $ 

$ 20.1\pm 4.7^{+3.0}_{-4.5} $ 

Belle [45] 35 $ {\cal B}( \eta_c\to \pi^+\pi^-\eta)\cdot {\cal B}( \psi(2S)\to\pi^0h_c\to \pi^0\gamma\eta_c) $ 

$ 7.22\pm 1.47\pm 1.11 $ 

BESIII [42] 36 $ {\cal B}( \eta_c\to K^+K^-\eta)\cdot {\cal B}( \psi(2S)\to\pi^0h_c\to \pi^0\gamma\eta_c) $ 

$ 2.11\pm 1.01\pm 0.32 $ 

BESIII [42] 37 $ {\cal B}( \eta_c\to 2(\pi^+\pi^-))\cdot {\cal B}( \psi(2S)\to\pi^0h_c\to \pi^0\gamma\eta_c) $ 

$ 7.51\pm 0.85\pm 1.11 $ 

BESIII [42] 38 $ {\cal B}( \eta_c\to 2(K^+K^-))\cdot {\cal B}( \psi(2S)\to\pi^0h_c\to \pi^0\gamma\eta_c) $ 

$ 0.94\pm 0.37\pm 0.14 $ 

BESIII [42] 39 $ {\cal B}( \eta_c\to 2(K^+K^-))\cdot {\cal B}( B^+\to \eta_cK^+) $ 

$ 2.0\pm 0.6\pm 0.4 $ 

BaBar [49] 40 $ {\cal B}( \eta_c\to 2(K^+K^-))\cdot {\cal B}( B^0\to \eta_cK^0) $ 

$ 0.9\pm 0.9\pm 0.4 $ 

BaBar [49] 41 $ {\cal B}( \eta_c\to \pi^+\pi^-p\bar{p})\cdot {\cal B}( B^+\to \eta_cK^+) $ 

$ 3.94^{+0.41}_{-0.39}\,^{+0.22}_{-0.18} $ 

Belle [51] 42 $ {\cal B}( \eta_c\to \pi^+\pi^-p\bar{p})\cdot {\cal B}( B^0\to \eta_cK_{S}^{0}) $ 

$ 1.90^{+0.32}_{-0.29}\,^{+0.13}_{-0.47} $ 

Belle [51] 43 $ {\cal B}( \eta_c\to \pi^+\pi^-p\bar{p})\cdot {\cal B}( \psi(2S)\to\pi^0h_c\to \pi^0\gamma\eta_c) $ 

$ 2.30\pm 0.65\pm 0.36 $ 

BESIII [42] 44 $ {\cal B}( \eta_c\to K^+K^-\pi^+\pi^-)\cdot {\cal B}( \psi(2S)\to\pi^0h_c\to \pi^0\gamma\eta_c) $ 

$ 4.16\pm 0.76\pm 0.59 $ 

BESIII [42] 45 $ {\cal B}( \eta_c\to K_{S}^{0} K^\pm\pi^\mp\pi^+\pi^-)\cdot {\cal B}( \psi(2S)\to\pi^0h_c\to \pi^0\gamma\eta_c) $ 

$ 12.01\pm 2.22\pm 2.04 $ 

BESIII [42] 46 $ {\cal B}( \eta_c\to 2(\pi^+\pi^-\pi^0))\cdot {\cal B}( \psi(2S)\to\pi^0h_c\to \pi^0\gamma\eta_c) $ 

$ 75.13\pm 7.42\pm 9.99 $ 

BESIII [42] 47 $ {\cal B}( \eta_c(2S)\to p\bar{p})\cdot {\cal B}( B^+\to \eta_c(2S)K^+) $ 

$ 0.0342\pm 0.0071\pm 0.0021 $ 

LHCb [52] 48 $ {\cal B}( \eta_c(2S)\to K\bar{K}\pi)\cdot {\cal B}( \psi(2S)\to \gamma\eta_c(2S)) $ 

$ 13.0\pm 2.0\pm 3.0 $ 

BESIII [53] 49 $ {\cal B}( \eta_c(2S)\to K_{S}^{0} K^{\pm}\pi^{\mp})\cdot {\cal B}( B^+\to \eta_c(2S)K^+) $ 

$ 3.1\pm 0.8\pm 0.2 $ 

Belle [50] 50 $ {\cal B}( \eta_c(2S)\to \pi^+\pi^-p\bar{p})\cdot {\cal B}( B^+\to \eta_c(2S)K^+) $ 

$ 1.12^{+0.18}_{-0.16}\ ^{+0.05}_{-0.07} $ 

Belle [51] 51 $ {\cal B}( \eta_c(2S)\to \pi^+\pi^-p\bar{p})\cdot {\cal B}( B^0\to \eta_c(2S) K_{S}^{0}) $ 

$ 0.42^{+0.14}_{-0.12}\pm 0.03 $ 

Belle [51] 52 $ {\cal B}( \eta_c(2S)\to K_{S}^{0} K^\pm\pi^\mp\pi^+\pi^-)\cdot {\cal B}( \psi(2S)\to \gamma\eta_c(2S)) $ 

$ 7.03\pm 2.10\pm 0.70 $ 

BESIII [54] Index quantity Value/eV Experiment 53 $ {\cal B}( \eta_c\to \phi\phi)\cdot\Gamma_{ \eta_c\to \gamma\gamma} $ 

$ 7.75\pm 0.66\pm 0.62 $ 

Belle [55] 54 $ {\cal B}( \eta_c\to \phi\phi)\cdot\Gamma_{ \eta_c\to \gamma\gamma} $ 

$ 6.8\pm 1.2\pm 1.3 $ 

Belle [19] 55 $ {\cal B}( \eta_c\to p\bar{p})\cdot\Gamma_{ \eta_c\to \gamma\gamma} $ 

$ 7.20\pm 1.53^{+0.67}_{-0.75} $ 

Belle [56] 56 $ {\cal B}( \eta_c\to K\bar{K}\pi)\cdot\Gamma_{ \eta_c\to \gamma\gamma} $ 

$ 386\pm 8\pm 21 $ 

BaBar [57] 57 $ {\cal B}( \eta_c\to K\bar{K}\pi)\cdot\Gamma_{ \eta_c\to \gamma\gamma} $ 

$ 374\pm 9\pm 31 $ 

BaBar [58] 58 $ {\cal B}( \eta_c\to K\bar{K}\pi)\cdot\Gamma_{ \eta_c\to \gamma\gamma} $ 

$ 600\pm 120\pm 90 $ 

DELPHI [17] 59 $ {\cal B}( \eta_c\to K_{S}^{0} K^{\pm}\pi^{\mp})\cdot\Gamma_{ \eta_c\to \gamma\gamma} $ 

$ 490\pm 290\pm 90 $ 

AMY [59] 60 $ {\cal B}( \eta_c\to K_{S}^{0} K^{\pm}\pi^{\mp})\cdot\Gamma_{ \eta_c\to \gamma\gamma} $ 

$ 142\pm 4\pm 14 $ 

Belle [60] 61 $ {\cal B}( \eta_c\to \pi^+\pi^-\eta^{\prime})\cdot\Gamma_{ \eta_c\to \gamma\gamma} $ 

$ 65.4\pm 2.6\pm 7.8 $ 

Belle [61] 62 $ {\cal B}( \eta_c\to 2(\pi^+\pi^-))\cdot\Gamma_{ \eta_c\to \gamma\gamma} $ 

$ 40.7\pm 3.7\pm 5.3 $ 

Belle [19] 63 $ {\cal B}( \eta_c\to K^+K^-\pi^+\pi^-)\cdot\Gamma_{ \eta_c\to \gamma\gamma} $ 

$ 25.7\pm 3.2\pm 4.9 $ 

Belle [19] 64 $ {\cal B}( \eta_c\to K^+K^-\pi^+\pi^-)\cdot\Gamma_{ \eta_c\to \gamma\gamma} $ 

$ 280\pm 100\pm 60 $ 

DELPHI [17] 65 $ {\cal B}( \eta_c\to 2(K^+K^-))\cdot\Gamma_{ \eta_c\to \gamma\gamma} $ 

$ 5.6\pm 1.1\pm 1.6 $ 

Belle [19] 66 $ {\cal B}( \eta_c\to 2(K^+K^-))\cdot\Gamma_{ \eta_c\to \gamma\gamma} $ 

$ 350\pm 90\pm 60 $ 

DELPHI [17] 67 $ {\cal B}( \eta_c\to K^+ K^-\pi^+\pi^-\pi^0)\cdot\Gamma_{ \eta_c\to \gamma\gamma} $ 

$ 190\pm 6\pm 28 $ 

BaBar [57] 68 $ {\cal B}( \eta_c(2S)\to K\bar{K}\pi)\cdot\Gamma_{ \eta_c(2S)\to \gamma\gamma} $ 

$ 41\pm 4\pm 6 $ 

BaBar [57] 69 $ {\cal B}( \eta_c(2S)\to K_{S}^{0} K^{\pm}\pi^{\mp})\cdot\Gamma_{ \eta_c(2S)\to \gamma\gamma} $ 

$ 11.2\pm 2.4\pm 2.7 $ 

Belle [60] 70 $ {\cal B}( \eta_c(2S)\to \pi^+\pi^-\eta')\cdot\Gamma_{ \eta_c(2S)\to \gamma\gamma} $ 

$ 5.6^{+1.2}_{-1.1}\pm 1.1 $ 

Belle [61] 71 $ {\cal B}( \eta_c(2S)\to K^+ K^-\pi^+\pi^-\pi^0)\cdot\Gamma_{ \eta_c(2S)\to \gamma\gamma} $ 

$ 30\pm 6\pm 5 $ 

BaBar [57] Table A3. Data used in the analysis: product of
$ \gamma\gamma $ partial width and branching fraction of$ \eta_c $ and$ \eta_c(2S) $ decays measured in two-photon processes.Index Process Width/MeV Experiment 72 $ \gamma\gamma\to \eta_c $ ,

$ \eta_c\to \eta^{\prime} \pi^+\pi^- $ 

$ 30.8^{+2.3}_{-2.2}\pm 2.9 $ 

Belle [61] 73 $ \gamma\gamma\to \eta_c $ ,

$ \eta_c\to K^+K^-\eta $ 

$ 34.8\pm 3.1\pm 4.0 $ 

BaBar [39] 74 $ \gamma\gamma\to \eta_c $ ,

$ \eta_c\to K^+K^- \pi^0 $ 

$ 25.2\pm 2.6\pm 2.4 $ 

BaBar [39] 75 $ \gamma\gamma\to \eta_c $ ,

$ \eta_c\to K_{S}^{0} K^{\pm}\pi^{\mp} $ 

$ 32.1\pm 1.1\pm 1.3 $ 

BaBar [57] 76 $ \gamma\gamma\to \eta_c $ ,

$ \eta_c\to K_{S}^{0} K^{\pm}\pi^{\mp} $ 

$ 24.8\pm 3.4\pm 3.5 $ 

CLEO [41] 77 $ \gamma\gamma\to \eta_c $ ,

$ \eta_c\to K_{S}^{0} K^{\pm}\pi^{\mp} $ 

$ 36.6\pm 1.5\pm 2.0 $ 

Belle [60] 78 $ \gamma\gamma^{*}\to \eta_c $ ,

$ \eta_c\to K_{S}^{0} K^{\pm}\pi^{\mp} $ 

$ 31.7\pm 1.2\pm 0.8 $ 

BaBar [58] 79 $ \gamma\gamma\to \eta_c $ ,

$ \eta_c\to K^+ K^-\pi^+\pi^-\pi^0 $ 

$ 36.2\pm 2.8\pm 3.0 $ 

BaBar [57] 80 $ \gamma\gamma\to \eta_c $ ,

$\eta_c\to \rm hadrons$ 

$ 28.1\pm 3.2\pm 2.2 $ 

Belle [19] 81 $ B^+\to \eta_c K^+ $ ,

$ \eta_c\to p\bar{p} $ 

$ 34.0\pm 1.9\pm 1.3 $ 

LHCb [52] 82 $ B^+\to \eta_c K^+ $ ,

$ \eta_c\to p\bar{p} $ 

$ 48^{+8}_{-7}\pm 5 $ 

Belle [47] 83 $ B^+\to \eta_c K^+ $ ,

$ \eta_c\to \Lambda\bar{\Lambda} $ 

$ 40\pm 19\pm 5 $ 

Belle [47] 84 $ B^+\to \eta_c K^+ $ ,

$ \eta_c\to K_{S}^{0} K^{\pm}\pi^{\mp} $ 

$ 35.4\pm 3.6^{+3.0}_{-2.1} $ 

Belle [50] 85 $ B\to \eta_c K^{(*)} $ ,

$ \eta_c\to K\bar{K}\pi $ 

$ 36.3^{+3.7}_{-3.6}\pm 4.4 $ 

BaBar [40] 86 $ b\to \eta_c X $ ,

$ \eta_c\to \phi\phi $ 

$ 31.4\pm 3.5\pm 2.0 $ 

LHCb [37] 87 $ b\to \eta_c X $ ,

$ \eta_c\to p\bar{p} $ 

$ 25.8\pm 5.2\pm 1.9 $ 

LHCb [62] 88 $ p\bar{p}\to \eta_c $ ,

$ \eta_c\to \gamma\gamma $ 

$ 20.4^{+7.7}_{-6.7}\pm 2.0 $ 

E835 [43] 89 $ p\bar{p}\to \eta_c $ ,

$ \eta_c\to \gamma\gamma $ 

$ 23.9^{+12.6}_{-7.1} $ 

E760 [44] 90 $ \psi(2S)\to\pi^0h_c\to \pi^0\gamma\eta_c $ ,

$\eta_c\to \rm hadrons$ 

$ 32.0\pm 1.2\pm 1.0 $ 

BESIII [63] 91 $ \psi(2S)\to\pi^0h_c\to \pi^0\gamma\eta_c $ ,

$\eta_c\to \rm hadrons$ 

$ 36.4\pm 3.2\pm 1.7 $ 

BESIII [63] 92 $ \gamma\gamma\to \eta_c(2S) $ ,

$ \eta_c(2S)\to K_{S}^{0} K^{\pm}\pi^{\mp} $ 

$ 13.4\pm 4.6\pm 3.2 $ 

BaBar [57] 93 $ \gamma\gamma\to \eta_c(2S) $ ,

$ \eta_c(2S)\to K_{S}^{0} K^{\pm}\pi^{\mp} $ 

$ 6.3\pm 12.4\pm 4.0 $ 

CLEO [41] 94 $ \gamma\gamma\to \eta_c(2S) $ ,

$ \eta_c(2S)\to K_{S}^{0} K^{\pm}\pi^{\mp} $ 

$ 19.1\pm 6.9\pm 6.0 $ 

Belle [60] 95 $ B^+\to \eta_c(2S) K^+ $ ,

$ \eta_c(2S)\to K_{S}^{0} K^{\pm}\pi^{\mp} $ 

$ 41.0\pm 12.0^{+6.4}_{-10.9} $ 

Belle [50] 96 $ \psi(2S)\to \gamma \eta_c(2S) $ ,

$ \eta_c(2S)\to K\bar{K}\pi $ 

$ 16.9\pm 6.4\pm 4.8 $ 

BESIII [53] 97 $ \psi(2S)\to \gamma \eta_c(2S) $ ,

$ \eta_c(2S)\to K_{S}^{0} K^\pm\pi^\mp\pi^+\pi^- $ 

$ 9.9\pm 4.8\pm 2.9 $ 

BESIII [54] Table A4. Data used in the analysis: total widths of
$ \eta_c $ (upper half in the table) and$ \eta_c(2S) $ (lower half in the table).






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF



















 DownLoad:
DownLoad: