-
In recent decades, heavy-ion collisions have served as one of the essential methods to study quantum chromodynamics (QCD). It is widely accepted that when heavy nuclei collide at high energy, a deconfinement phase transition takes place and a new state of matter is created, called quark–gluon plasma (QGP) [1, 2]. The interaction between quarks and gluons is dominated by the strong interaction, therefore by studying the properties of QGP, one could gain crucial knowledge of QCD. Various probes have been proposed for this purpose, including quarkonium. Heavy quarkonia such as charmonia can survive the QGP and have interesting phenomena including dissociation and recombination while moving in the fireball. Therefore, they are proposed as one of the sensitive probes of QGP [3].
Nuclei are positively charged, so non-centered collisions produce extremely strong magnetic fields. At the initial stage of the collision, one would expect a magnetic field at the magnitude of
$ 1\; m_\pi^2 $ at RHIC and$ 15\; m_\pi^2 $ at the LHC [4–9]. Strong magnetic fields will affect the properties of QGP. Various novel phenomena, including the chiral magnetic effect (CME), have been proposed. The quarkonia will also be affected by the magnetic field. Since some of them are created in initial collisions, they can carry the information of the magnetic field when it is strongest [10]. Therefore, it is possible to study the magnetic field using quarkonia if we quantitatively determine how they are affected by both the hot medium and the strong magnetic field.At zero temperature, the interaction between the c and
$ \bar{c} $ quark can be described by the Cornell potential. Due to the mass of the heavy quarks, the relativity correction for quarkonia is small [11], and one can safely use the Schrödinger equation to study them [12]. The Schrödinger equation has been successfully used to study the dissociation of quarkonium in the hot medium using the free energy from lattice simulation [13]. It is also used to study quarkonium properties in strong magnetic fields [10]. Therefore, it is straightforward to consider these two at the same time. -
The Schrödinger equation for a pair of particles in vacuum can be expressed as
$ \left [\frac{{\boldsymbol{p}}_{a}^{2}}{2m_{q}}+\frac{{\boldsymbol{p}}_{b}^{2}}{2m_{q}} +{\boldsymbol{V}} \right ]\Phi \left ( {\boldsymbol{R}},{\boldsymbol{r}} \right )=\left [ E-2m_{q} \right ]\Phi \left ( {\boldsymbol{R}},{\boldsymbol{r}} \right ), $

(1) where the eigenvalue
E means the total energy of the system, including static mass $ m_{m} $ and the kinetic energy E$ _{k} $ . Using minimal coupling to introduce an electromagnetic field, the Schrödinger equation becomes$ \begin{aligned}[b] &\left[ \frac{\left( {\boldsymbol{p}}_{a}-q_{a}{\boldsymbol{A}}_{a}\right) ^{2}}{2m_{q}}+ \frac{\left( {\boldsymbol{p}}_{b}-q_{b}{\boldsymbol{A}}_{b}\right) ^{2}}{2m_{q}}+{\boldsymbol{V}} -{\boldsymbol{\mu}}\cdot {\boldsymbol{B}}\right] \Phi \left( {\boldsymbol{R}}, {\boldsymbol{r}}\right) \\ =&\left[ E-2m_{q}\right] \Phi \left( {\boldsymbol{R}},{\boldsymbol{r}}\right), \end{aligned} $

(2) where
$ {\boldsymbol{\mu}}=\dfrac{q}{m_{q}}\left({\boldsymbol{S}}_{a}-{\boldsymbol{S}}_{b}\right) $ is the spin magnetic moment. As the kinetic momentum${\boldsymbol{P}}_{\rm kin}={\boldsymbol{p}}_a+{\boldsymbol{p}}_b-q_a {\boldsymbol{A}}_a-q_b{\boldsymbol{A}}_b$ is no longer conserved in such a system, we should define the kinetic energy using its expectation value, so the meson mass here should be defined as$ m_{m}=E-E_{k} $ $ =E-\dfrac{ \langle {\boldsymbol{p}}_{a}+{\boldsymbol{p}}_{b}-q_{a}{\boldsymbol{A}}_{a}-q_{b}{\boldsymbol{A}} _{b}\rangle }{4m_{q}}^{2} $ .Then we use center-of-mass coordinates and make the transformation
$ {\boldsymbol{R}}=\frac{1}{2}{\boldsymbol{r}}_{a}+\frac{1}{2}{\boldsymbol{r}}_{b}, $

(3) $ {\boldsymbol{r}}={\boldsymbol{r}}_{a}-{\boldsymbol{r}}_{b}, $

(4) and the corresponding momentum
$ {\boldsymbol{P}}={\boldsymbol{p}}_{a}+{\boldsymbol{p}}_{b}=-{\rm i}{\boldsymbol{\partial}}_{R}, $

(5) $ {\boldsymbol{p}}=\frac{1}{2}{\boldsymbol{p}}_{a}-\frac{1}{2}{\boldsymbol{p}}_{b}= -{\rm i}{\boldsymbol{\partial}}_{r}. $

(6) For a homogenous and constant magnetic field, we fix the vector potential as
$ {\boldsymbol{A}}=\dfrac{1}{2}B\times {\boldsymbol{r}} $ , and the electric charges of the quark and antiquark are opposite. In this case, we can derive that$ \frac{\left ( {\boldsymbol{p}}_{a}-q_{a}{\boldsymbol{A}}_{a} \right )^{2}}{2m_{q}}+\frac{\left ({\boldsymbol{p}}_{b}-q_{b}{\boldsymbol{A}}_{b} \right )^{2}}{2m_{q}}=\frac{{\boldsymbol{P}}_{\rm kin}^{2}}{4m_{q}}+\frac{{\boldsymbol{{p}'}}^{2}}{m_{q}}, $

(7) where
${\boldsymbol{P}}_{\rm kin}={\boldsymbol{P}}-\dfrac{1}{2}q{\boldsymbol{B}}\times {\boldsymbol{r}}$ and$ {\boldsymbol{{p}'}}={\boldsymbol{p}}-\dfrac{1}{2}q{\boldsymbol{B}}\times {\boldsymbol{R}} $ .It is easy to prove that
$ \left[ {\boldsymbol{P}}+\frac{1}{2}q{\boldsymbol{B}}\times {\boldsymbol{r}},{\boldsymbol{{p}'}}\right] =0\Rightarrow \left[ {\boldsymbol{P}}+\frac{1}{2}q{\boldsymbol{B}}\times {\boldsymbol{r}},{\boldsymbol{H}}\right] =0 . $

This shows that the quantity called pseudo-momentum
${\boldsymbol{P_{ps}}}={\boldsymbol{P}}+ \dfrac{1}{2}q{\boldsymbol{B}}\times {\boldsymbol{r}}={\boldsymbol{P_{\rm kin}}}+q{\boldsymbol{B}}\times {\boldsymbol{r}}$ [14] is a conserved quantity. Using this, we can separate the$ {\boldsymbol{R}} $ dependence from the wave function, and find that [15]$ \Psi ({\boldsymbol{R}},{\boldsymbol{r}}) ={\rm e}^{{\rm i}({\boldsymbol{P}}_{ps}-\frac{1}{2}q{\boldsymbol{B}}\times {\boldsymbol{r}} )\cdot R}\psi ({\boldsymbol{r}}), $

(8) $ {\boldsymbol{{p}'}}\Psi ({\boldsymbol{R}},{\boldsymbol{r}}) ={\rm e}^{{\rm i}({\boldsymbol{P}}_{ps}-\frac{1}{2}q{\boldsymbol{B}} \times {\boldsymbol{r}})\cdot R}{\boldsymbol{p}}\psi ({\boldsymbol{r}}), $

(9) $ {\boldsymbol{{p}'}}^{2}\Psi ({\boldsymbol{R}},{\boldsymbol{r}}) = {\rm e}^{{\rm i}({\boldsymbol{P}}_{ps}-\frac{1}{2}q{\boldsymbol{B}} \times {\boldsymbol{r}})\cdot R}{\boldsymbol{p}}^{2}\psi ({\boldsymbol{r}}). $

(10) Separating out the
$ {\boldsymbol{R}} $ -dependent part, the Schrödinger equation becomes$ \begin{aligned}[b]&\left[ \begin{array}{c} {{\boldsymbol{p}}^{2}}+m_{q}V-q({\boldsymbol{S}}_{a}-{\boldsymbol{S}}_{b})\cdot {\boldsymbol{B}}+ \\ \dfrac{-2q{\boldsymbol{P}}_{ps}\times {\boldsymbol{B}}\cdot {\boldsymbol{r}}+q^{2}({{\boldsymbol{B}}\times {\boldsymbol{r}} })^{2}}{4} \end{array} \right] \psi ({\boldsymbol{r}})\\ =&\left[ m_{q}E-2m_{q}^{2}-\frac{{\boldsymbol{P}}_{ps}^{2}}{4}\right] \psi ({\boldsymbol{r}}), \end{aligned} $

(11) and the kinetic energy can be expressed in a simpler form
$E_{k}=\dfrac{ \langle {\boldsymbol{P}}_{\rm kin}\rangle ^{2}}{4m_{q}}=\dfrac{ \langle \boldsymbol{P}_{ps}-q\boldsymbol{B}\times \boldsymbol{r} \rangle ^{2}}{4m_{q}}$ . One can see that the Hamiltonian still depends on$ {\boldsymbol{P}}_{ps} $ , or equivalently$ {\boldsymbol{P}} $ . This is because the translational symmetry is broken by the magnetic field. From the equation one can see that the effects of magnetic field include three terms. The term$ -\dfrac{q}{m_{q}}({\boldsymbol{S}}_{a}-{\boldsymbol{S}}_{b})\cdot {\boldsymbol{B}} $ is the interaction between the magnetic moment and the magnetic field. The term$ -q{\boldsymbol{P}}_{ps}\times {\boldsymbol{B}}\cdot {\boldsymbol{r}} $ reflects the Lorentz force on the two quarks. It's easy to imagine that due to the opposite charge, the effect of this term is pulling apart the quark–antiquark pair. The last term$ \dfrac{{q}^{2}}{4m_{q}}({\boldsymbol{B}}\times {\boldsymbol{r}})^{2} $ effectively adds an extra constraining potential on the plane perpendicular to the magnetic field and keeps the pair from running far away. We define$ P_{ps,\perp } $ as the projection of$ {\boldsymbol{P}}_{ps} $ perpendicular to$ {\boldsymbol{B}} $ . We set the z axis as the direction of the magnetic field, and x axis the direction of$ P_{ps,\perp } $ . It turns out that$ \langle \boldsymbol{r}\rangle =\langle y\rangle \boldsymbol{e}_{y} $ , and$\langle \boldsymbol{P}_{\rm kin}\rangle =\boldsymbol{P} _{ps}+qB\langle y\rangle \boldsymbol{e}_{x}$ .There are two competing effects from B and
$ P_{ps} $ . The first term,$ -q{\boldsymbol{P}}_{ps}\times {\boldsymbol{B}}\cdot {\boldsymbol{r}} $ can be viewed as an effective repulsive potential, tending to break the$ c\bar{c} $ pair. The other term,$ \dfrac{1}{4}q^{2}({{\boldsymbol{B}}\times {\boldsymbol{r}}})^{2} $ is an attractive potential. Also, the repulsive term depends on both the magnetic field and the total momentum, while the attractive term only depends on the magnetic field. Therefore, we expect that the magnetic field can both strengthen or weaken the bound state, depending on its magnitude, but the momentum will only weaken it. The interplay of these two effects could cause interesting results, forming a new effective$ 3-D $ "phase structure".With the external magnetic field, the angular momentum is no longer conserved. As a consequence, we cannot directly simplify the 3-dimensional equation into a 1-dimensional radial equation as usual. Nevertheless, the orbital and spin angular momentum eigenstates still form an orthogonal basis set, so we choose to expand our wave functions on them.
$ \phi ^{t\pm }({\boldsymbol{r}}) \equiv \frac{1}{r}\psi ^{t\pm }({\boldsymbol{r}} )=\sum\limits_{l,m}a_{l,m}^{t\pm }\phi _{l,m}^{t\pm }(r)Y_{l}^{m}(\theta ,\varphi ), $

(12) $ \begin{aligned}[b] \phi ^{s0,t0}({\boldsymbol{r}}) \equiv &\frac{1}{r}\psi ^{s0,t0}({\boldsymbol{r}} )=\sum\limits_{l,m}a_{l,m}^{t0}\phi _{l,m}^{t0}(r)Y_{l}^{m}(\theta ,\varphi )\\ &+\sum\limits_{l,m}a_{l,m}^{s0}\phi _{l,m}^{s0}(r)Y_{l}^{m}(\theta ,\varphi ). \end{aligned} $

(13) This procedure will simplify the later numerical calculation by converting a 3-dimensional array problem to an N-coupled one-dimensional array problem. Also, the physical meaning of the wave function is clearer when we study the behavior of different orbital angular momentum components. The spin–magnetic interaction makes the singlet and spin-zero triplet no longer eigenstates of the Hamiltonian, which yields the mixing of different spin components, e.g.,
$ \eta _{c} $ and$J/\psi $ [16, 17]. It is worth noting that the triplet states whose$ S_z =\pm 1 $ are still eigenstates, while the$ S_z = 0 $ triplet will couple with the singlet and they are no longer eigenstates. In a practical case, we cannot solve eigenfunctions with infinite dimensions, we should always make a cut-off that we just consider terms with$l \leq l_{\max } $ .We can write the Schrödinger equation as
$ \left[-\frac{\mathrm{d}^{2}}{\mathrm{d}r^{2}}+m_{q}V_{c}+\frac{1}{4} m_{q}V_{s}+\frac{1}{r^{2}}U+\frac{q^{2}B^{2}}{4}r^{2}V+\frac{qBP_{ps,\perp } }{2}rW-\lambda \right] \phi ^{\pm }(r) =0, $ 
(14) $ \left[ -\frac{\mathrm{d}^{2}}{\mathrm{d}r^{2}}+m_{q}V_{c}+\frac{1}{4} m_{q}V_{s}+\frac{1}{r^{2}}U+\frac{q^{2}B^{2}}{4}r^{2}V+\frac{qBP_{ps,\perp } }{2}rW-\lambda \right] \phi ^{t0}(r)-qB\phi ^{s0}(r) =0, $

(15) $ \left[ -\frac{\mathrm{d}^{2}}{\mathrm{d}r^{2}}+m_{q}V_{c}-\frac{3}{4} m_{q}V_{s}+\frac{1}{r^{2}}U+\frac{q^{2}B^{2}}{4}r^{2}V+\frac{qBP_{ps,\perp } }{2}rW-\lambda \right] \phi ^{s0}(r)-qB\phi ^{t0}(r) =0. $

(16) The interaction matrices U, V, W are defined as
$ U= l(l+1)\delta_{l,l'}\delta_{m,m'}, $

(17) $ \begin{aligned}[b] V=& u_{l,m} \delta_{l,l'}\delta_{m,m'} - v_{l,m} \delta_{l+2,l'}\delta_{m,m'} \\ &- v_{l-2,m} \delta_{l-2,l'}\delta_{m,m'}, \end{aligned} $

(18) $ \begin{aligned}[b] W=& w_{l-1,-m-1}\delta_{l-1,l'}\delta_{m+1,m'}-w_{l,m}\delta_{l+1,l'}\delta_{m+1,m'}\\& +w_{l-1,m-1}\delta_{l-1,l'}\delta_{m-1,m'}-w_{l,-m}\delta_{l+1,l'}\delta_{m-1,m'}, \end{aligned} $

(19) where
$ u_{l,m}=\frac{2(l^2+l-1+m^2)}{(2l-1)(2l+3)}, $

(20) $ v_{l,m}=\frac{1}{2l+3}\frac{\sqrt{[(l+1)^2-m^2][(l+2)^2-m^2]}}{\sqrt{(2l+1)(2l+5)}}, $

(21) $ w_{l,m}=\frac{\sqrt{(l+m+1)(l+m+2)}}{2{\rm i}\sqrt{(2l+1)(2l+3)}}. $

(22) For convenience, we denote
$ m_{q}E-2m_{q}^{2}-P_{ps}^{2}/4 = \lambda $ .The static potential between a
$ c\bar{c} $ pair in a QGP is calculated by lattice simulation and can be described by the color screening model [13]$ \begin{aligned}[b] &\mathrm{V}_{s}(r, T)=\frac{\sigma}{\mu}\left[\frac{\Gamma(1 / 4)}{2^{3 / 2} \Gamma(3 / 4)}-\frac{\sqrt{\mu r}}{2^{3 / 4} \Gamma(3 / 4)} K_{1 / 4}\left[(\mu r)^{2}\right]\right] ,\\ &\mathrm{V}_{c}(r, T)=-\frac{\alpha}{r}\left[{\rm e}^{-\mu r}+\mu r\right], \end{aligned} $

(23) where μ is the temperature-dependent screening mass. By fitting the lattice data [18], an analytical formula is acquired. The other parameters are
$ m_{c} = $ 1.25 GeV,$ \sqrt{\sigma }= $ 0.445 GeV and$ \alpha = \pi /12 $ for charmonium.We make a final simplification to our simulation process. At each temperature, we first solve the eigenstates at
$ {\boldsymbol{B}}=0 $ . The resulting eigenfunctions$ \phi _{nl}^{s} $ serve as another orthogonal basis set for the radial wavefunction. At any finite magnetic field, the Hamiltonian can be quantified into the following matrix form,$ H_{nn^{\prime }ll^{\prime }mm^{\prime }}^{ss^{\prime }}=\langle \phi _{n^{\prime },l^{\prime }}^{s^{\prime }}Y_{l^{\prime }}^{m^{\prime }}|H|\phi _{n,l}^{s}Y_{l}^{m}\rangle. $

(24) In the actual computation, it is found that at moderate temperatures,
$ n\leq 2 $ ,$ l\leq 7 $ can achieve quite a good accuracy. So the matrix size is of the order of 10$ ^{2} $ and can be solved by conventional methods. However, at higher temperatures, most states become scattering states, forming a very dense spectrum. Many of them will have a considerable transition amplitude with the ground state, so they should all be taken into consideration. For example, at around$ 1.15\; T_c $ , the cutoff should be extended to$ n\le 10 $ or higher. In principle, with a large enough cutoff, our method can work at even higher temperatures, although the efficiency will keep decreasing. One may instead choose to use more fundamental numerical approaches, such as in a recent related work [19], in which the authors use the same framework to study the gluon-dissociation of charmonium. Their results show that for$ P_{ps}=0 $ and a moderate B, charmonium can survive at a higher temperature. -
For simplicity, here we calculate the ground state of the
$ S_z =\pm 1 $ components of the spin triplet, namely$ J/\Psi $ , whose spin is in the direction of the magnetic field.Now we have three independent variables: the temperature, the magnetic field, and momentum. It is known that increasing temperature will cause the charmonia to dissolve. When the temperature approaches the dissociation temperature, the binding of the pair weakens and its average radius grows rapidly. In our calculation, without magnetic field, the dissociation temperature
$ T_d $ is found to be around$ 1.16\; T_c $ , where$ T_c $ is the deconfinement critical temperature.As discussed above, the magnetic field has both binding and breaking effects on charmonia and momentum has only the breaking effect. At different temperatures, we complete the calculation at different B and
$ P_{ps} $ and check whether the charmonium is dissolved. By doing so we can draw the phase diagrams at different temperatures, as shown in Fig. 1. The blue region is where the$ J/\psi $ is dissociated.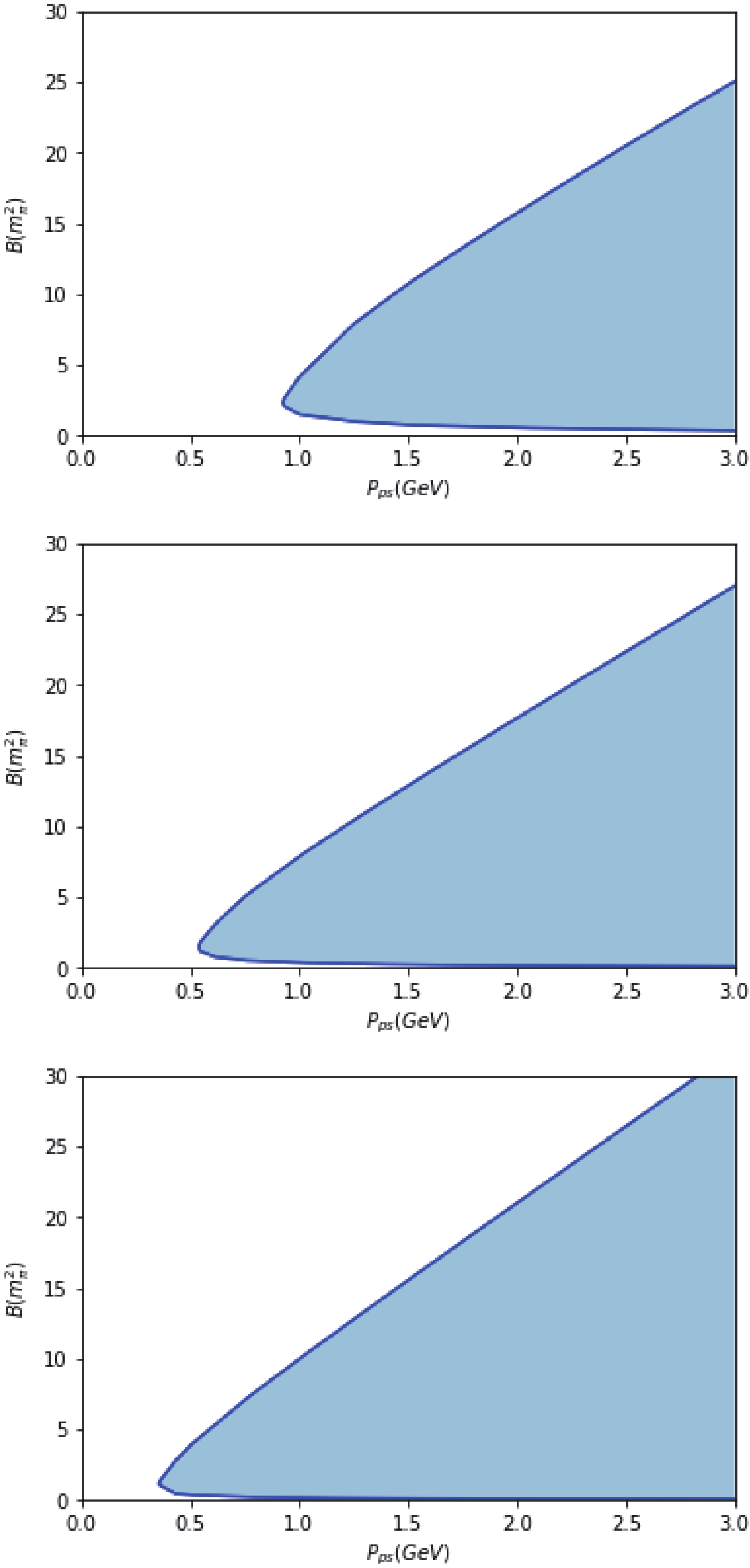
Figure 1. (color online) (From top to bottom)
$ J/\psi $ dissociation conditions at$ 1\; T_c $ ,$ 1.05\; T_c $ ,$ 1.1\; T_c $ . The blue region is where$ J/\psi $ is dissociated.We can see that, when increasing the magnetic field, the
$ J/\psi $ will first dissolve at relatively small B, but will form a bound state again when the magnetic field is strong enough. On the other hand, increasing momentum will only cause the$ J/\psi $ to dissolve. We can also notice that with increasing temperature, the region of dissociated phase expands as the$ J/\psi $ is bound more and more loosely. This matches our expectations. In addition, we check how the average radius of the bound state changes when it reaches dissociation, as shown in Fig. 2. We keep$T= 1.05\; T_c$ ,$ P_{ps}=1 $ GeV, and change the magnetic field. The average radius keeps almost constant for a wide range of B while growing rapidly when B approaches the transition value. When B reaches the second transition value, the average radius will drop sharply back to almost the same value. This rapid change of average radius is consistent with the previous result along temperature axes [11].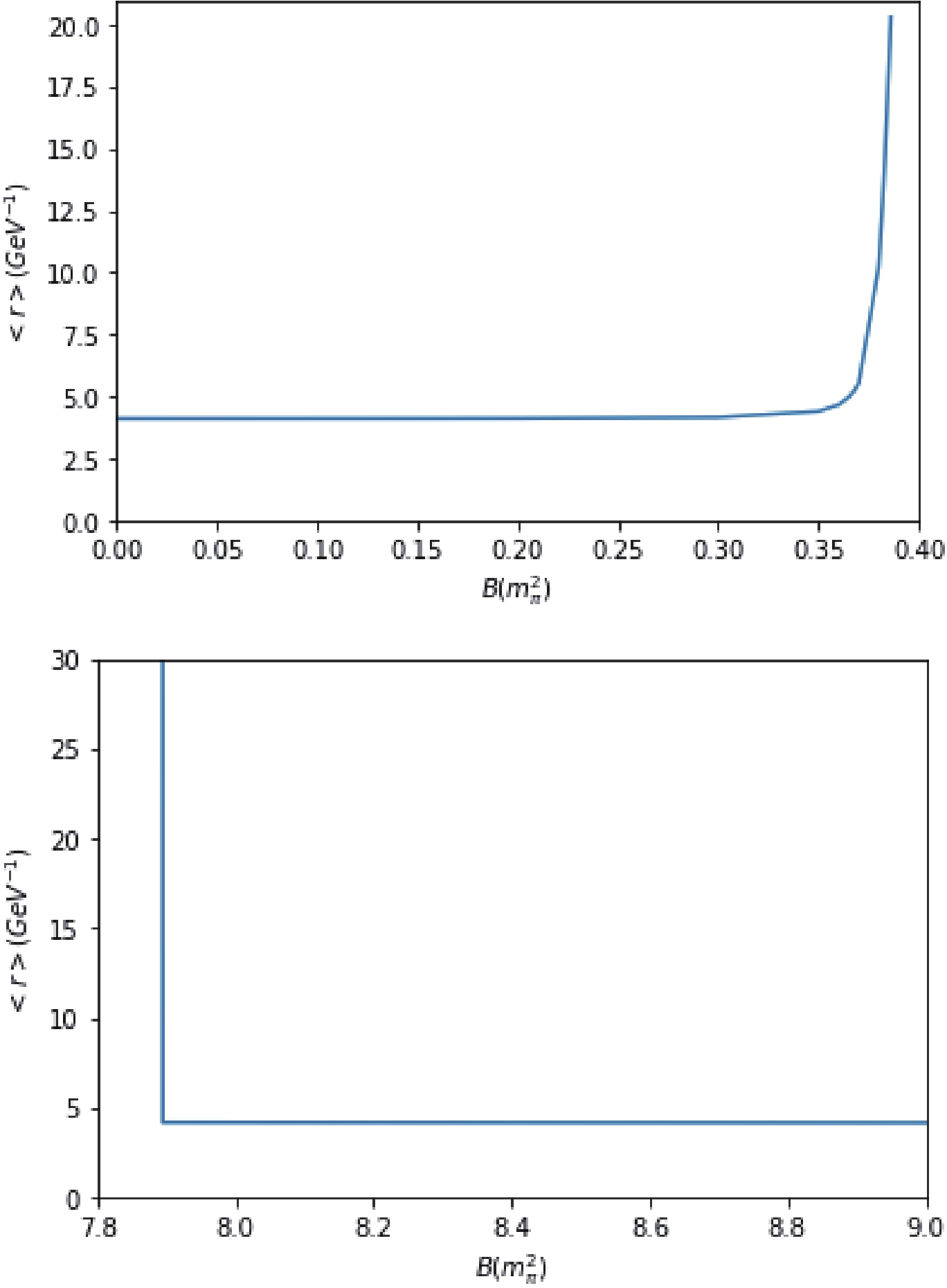
Figure 2. (color online) Average radius of the bound state as function of B at
$ T = 1.05\; T_c, P_{ps} = 1\; $ GeV.From the results above, it is clear that below
$ T_d $ , with a finite magnetic field,$ J/\psi $ are generally more likely to dissolve compared to the$ B=0 $ situation. We believe this conclusion also applies to other charmonium bound states because the mechanics are similar. This would cause an additional suppression of charmonium production in non-central nuclear–nuclear collisions. The quantitative effect remains to be calculated in the future, taking into consideration realistic fireball configurations. -
We simulated the charmonium dissociation conditions in a magnetic field using the Schrödinger equation. The dissociation of charmonium depends on temperature, magnetic field, and momentum. We plotted the phase diagram of dissociation at different temperatures. The momentum always tends to break the bound state; at lower temperatures, a strong enough magnetic field helps to bind the
$ c\bar{c} $ pair, but when the temperature raises, no new bound state can be formed due to the magnetic field.
Dissociation of J/ψ in hot medium and magnetic field
- Received Date: 2022-03-13
- Available Online: 2022-09-15
Abstract: Charmonium dissociation is an important probe of the quark–gluon plasma medium in heavy-ion collisions. The magnetic field produced in non-central collisions can affect the charmonia and their dissociation. We study the





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: