-
The phase structure of quantum chromodynamics (QCD) at finite magnetic field, temperature, and density, including chiral symmetry restoration, quark deconfinement, pion superfluids, and color superconductors, has attracted significant attention in recent years and is related to the evolution of the early universe, relativistic heavy ion collisions, and compact stars [1–3]. The mechanism behind a continuous phase transition is spontaneous symmetry breaking, and we can define an order parameter that changes from a nonzero value to zero, or vice versa, when the phase transition occurs. On the other hand, the spontaneous breaking of global symmetry manifests itself in Goldstone's theorem [4, 5], that is, whenever global symmetry is spontaneously broken, massless fields, known as Goldstone bosons, emerge. For example, under an external magnetic field, the pseudo-Goldstone (Higgs) mode of chiral symmetry breaking is the neutral pion (σ meson), and the Goldstone mode of isospin symmetry breaking is the charged pion. Modifications to hadron properties in a medium will help to understand QCD phase transitions. Different from previous studies on the QCD phase structure at the order parameter level, we focus on the meson properties and their application for determining phase transitions in a chemical potential-temperature plane under a constant external magnetic field.
Electromagnetic interactions provide a sensitive probe for hadron structure. At hadron level, without considering the inner structure, neutral hadrons are blind to electromagnetic fields, and their properties in hot and dense mediums are not directly affected by the fields. However, at quark level, the electromagnetic interactions of charged constituent quarks lead to a sensitive dependence of the neutral meson properties on external electromagnetic fields [6–40]. When the magnetic field strength is compatible with the strong interaction, such as
$ eB\sim m^2_\pi $ , the quark structure of hadrons should be considered.LQCD has a sign problem in the case of finite baryon chemical potential. In this paper, we investigate the properties of light mesons (
$ \sigma, \pi^0, \pi^\pm $ ) and the phase structures of chiral and isospin symmetry on baryon chemical potential-temperature$ (\mu_B-T) $ and isospin chemical potential-temperature$ (\mu_I-T) $ planes under external magnetic fields in the framework of the two-flavor NJL model at quark level. The NJL model [12, 41–44], which is inspired by Bardeen-Cooper-Schrieffer (BCS) theory, enables us to directly observe how the dynamical mechanisms of symmetry breaking and restoration operate. Within this model, quarks are treated on the mean field level, and mesons are the quantum fluctuations constructed from the quark bubble. On the one side, we can study the QCD phase transitions at the order parameter level [12, 41–48]. On the other side, the associated hadronic mass spectrum and the static properties of mesons are described remarkably well [12, 41–48].In the framework of the quark model, meson properties under an external magnetic field are studied, mainly in the vacuum, finite T (vanishing
$ \mu_B $ ), and finite$ \mu_B $ (vanishing T) cases [12–16, 18–40]. During chiral crossover at finite T and vanishing$ \mu_B $ , the pseudo-Goldstone mode$ \pi^0 $ exhibits a mass jump at the Mott transition because of the discrete Landau level of constituent quarks [20, 26, 28, 30, 31]. With the first order chiral phase transition at finite$ \mu_B $ and vanishing T, the pseudo-Goldstone mode$ \pi^0 $ and Higgs mode σ display a mass jump at the phase transition point, induced by the corresponding mass jump of constituent quarks [20]. The meson properties at finite temperature and baryon chemical potential, especially around the critical end point of chiral symmetry restoration, is not yet explored and is an important issue for the experimental search for the critical end point and QCD phase structure. Furthermore, chiral symmetry restoration can be defined in terms of mesons, such as the Mott transition of the Goldstone mode$ \pi^0 $ and the minimum mass of the Higgs mode σ [23, 49, 50]. For example, chiral symmetry restoration under an external magnetic field shows inverse magnetic catalysis when defined through the Mott transition of$ \pi^0 $ [50]. Here, we study the chiral phase diagram on$ \mu_B-T $ plane under an external magnetic field based on our results on$ \pi^0 $ and σ mesons.On the isospin chemical potential-temperature
$ (\mu_I-T) $ plane, except for chiral symmetry restoration, there is a pion superfluid phase transition [27, 46–48, 51–79]. With a vanishing external magnetic field, when a pion superfluid phase transition occurs at$ \mu_I>0 $ , the$ \pi^+ $ meson becomes massless, which is confirmed by both the LQCD simulation and effective theories [27, 46–48, 54, 67, 68, 74]. Owing to the predicament caused by the electromagnetic interaction between the charged pion condensate and magnetic field, there is limited research with finite magnetic field [27, 77–79]. In vacuum, it is reported that the mass of charged pions increases when the external magnetic field is not significantly strong [10, 11, 21, 22, 26, 27]. At finite temperature and vanishing$ \mu_I $ , charged pions exhibit several mass jumps induced by the discrete Landau level and different electric charges of constituent quarks [26]. Pion superfluid phase transition under an external magnetic field has been investigated using the Goldstone meson$ \pi^+ $ [27]. Much less is known about the properties of charged and neutral pions on the$ \mu_I-T $ plane under an external magnetic field. In terms of (pseudo-)Goldstone modes, the competition between chiral symmetry restoration and pion superfluid phase transition on the$ \mu_I-T $ plane has also not been explored under an external magnetic field.The rest of this paper is organized as follows. Sec. II presents the NJL framework of quarks and mesons in
$ \mu_B-\mu_I-T-eB $ space. Numerical results and physical discussions in$ \mu_B-T-eB $ and$ \mu_I-T-eB $ space are shown in Sec. III, where we focus on the phase diagram and corresponding (pseudo-)Goldstone and Higgs modes around the critical end point. Finally, we provide a brief summary and outlook in Sec. IV. -
The two-flavor NJL model is defined using Lagrangian density in terms of the quark fields ψ [12, 41–44].
$ \begin{array}{*{20}{l}} {\cal L} = \bar{\psi}\left({\rm i}\gamma_\mu D^\mu-m_0+\gamma_0 \mu\right)\psi+G \left[\left(\bar\psi\psi\right)^2+\left(\bar\psi {\rm i}\gamma_5{\vec \tau}\psi\right)^2\right], \end{array} $

(1) where the covariant derivative
$ D_\mu=\partial_\mu+{\rm i}Q A_\mu $ couples quarks with electric charge$ Q={\rm diag} (Q_u,Q_d)= {\rm diag} (2e/3, -e/3) $ to a magnetic field in the z direction,$ {\boldsymbol{B}}=(0, 0, B) $ , through the potential$ A_\mu=(0,0,Bx_1,0) $ . In our calculations, the magnetic field is not a dynamical field and is treated as an external classical field.$ m_0 $ is the current quark mass characterizing explicit chiral symmetry breaking, and the quark chemical potential$ \mu ={\rm diag}\left(\mu_u,\mu_d\right)= {\rm diag}\left(\mu_B/3 + \mu_I/2,\mu_B/3-\mu_I/2\right) $ is a matrix in flavor space, where$ \mu_u $ and$ \mu_d $ are the u- and d-quark chemical potentials,$ \mu_B $ and$ \mu_I $ are the baryon and isospin chemical potentials, and G is the coupling constant in the scalar and pseudo-scalar channels. Under an external magnetic field,$ SU(2)_{\rm L} \otimes SU(2)_{\rm R} $ chiral symmetry is explicitly reduced to$ U(1)_{\rm L} \otimes U(1)_{\rm R} $ . The order parameter of spontaneous chiral symmetry breaking is the neutral chiral condensate$ \langle\bar\psi\psi\rangle $ or the (dynamical) quark mass$ m_q=m_0- 2G\langle\bar\psi\psi\rangle $ , and the corresponding Goldstone boson is the neutral pion$ \pi^0 $ . At finite isospin chemical potential$ (\mu_I>0) $ , with spontaneous breaking of the isospin symmetry$ U(1)_I $ by the charged pion condensate$ \langle\bar\psi\gamma_5 \tau^1 \psi\rangle $ , the Goldstone boson is the$ \pi^+ $ meson. In our study, we focus on chiral and isospin symmetries, and thus neglect the interaction of the color superconductor phase transition in the NJL model, which is an interesting issue and will be studied elsewhere.The chiral condensate is charge neutral and only affected by the external magnetic field through paired quarks. However, the charged pion condensate directly interacts with the external magnetic field. This breaks both isospin symmetry in flavor space and translational invariance in coordinate space. Moreover, when one introduces a magnetic field into a pion superfluid, there is either a superconductor or magnetic vortex, both of which can completely or partially change the magnetic field. To avoid the complication and difficulty of dealing with the charged pion condensate under an external magnetic field, we begin with the normal phase only with a neutral chiral condensate and no charged pion condensate. We calculate the light meson (
$ \sigma, \pi^0, \pi^\pm $ ) mass spectra and use them to determine the chiral symmetry restoration phase boundary and pion superfluid phase transition based on Goldstone's theorem.There are two equivalent ways to manage particle propagators under an external magnetic field: the Ritus scheme [80–82] and Schwinger scheme [1–3]. For convenience in studying both neutral and charged particles, we perform derivations using the Ritus scheme in the following, where the Fourier-like transformation of the particle propagator between the conserved Ritus momentum space and coordinate space is well defined [80–82]. For example, the quark propagator
$ S_f(x,y) $ with flavor f in coordinate space can be written as$ \begin{aligned}[b] S_f(x,y) =& \sum\limits_n \int {{\rm d}^3\tilde p\over (2\pi)^3} {\rm e}^{-{\rm i} \tilde p\cdot (x-y)}\\ & \times P_n(x_1,p_2)D_f(\bar p) P_n(y_1,p_2),\\ P_n({x_1},p_2) =& {1\over 2}\left[g_n^{s_f}({x_1},p_2)+I_n g_{n-1}^{s_f}({x_1},p_2)\right]\\ &+{{\rm i}s_f\over 2}\left[g_n^{s_f}({x_1},p_2)- I_n g_{n-1}^{s_f}({x_1},p_2)\right]\gamma_1 \gamma_2,\\ D_f^{-1}(\bar p) =& \gamma \cdot \bar p-m_q, \end{aligned} $

(2) where
$ \tilde p=(p_0,0,p_2,p_3) $ is the Fourier transformed momentum,$ \bar p=(p_0,0,-s_f \sqrt{2n|Q_f B|},p_3) $ is the conserved Ritus momentum with n describing the quark Landau level in magnetic fields,$ D_f(\bar p) $ is the quark propagator in Ritus momentum space,$ s_f={\rm{{sgn}}}(Q_f B) $ is the quark sign factor,$ I_n=1-\delta_{n0} $ is governed by the Landau energy level, and the magnetic field dependent function$ g_n^{s_f}({x_1},p_2) = \phi_n(x_1-s_f p_2 /|Q_f B|) $ is controlled by the Hermite polynomial$ H_n(\zeta) $ via$ \phi_n(\zeta) = \sqrt{\dfrac{ \sqrt{|Q_f B|}}{2^n n! \sqrt{\pi}}} {\rm e}^{-{(\zeta^2|Q_f B|)}/{2}} H_n\left(\zeta\sqrt{|Q_f B|}\right) $ Throughout this paper, we use the definitions$ x^\mu=(x_0,x_1,x_2,x_3) $ and$ p^\mu=(p_0,p_1,p_2,p_3) $ .At mean field level, the quark mass
$ m_q=m_0-2G\langle\bar\psi\psi\rangle $ is controlled by the gap equation$ \begin{aligned}[b]& m_q(1-2GJ_1)-m_0=0, \\& J_1 = N_c\sum\limits_{f,n}\alpha_n \dfrac{|Q_f B|}{2\pi} \int \dfrac{{\rm d} p_3}{2\pi} \dfrac{1-F(E_f^+)-F(E_f^-)}{ E_f}, \end{aligned} $

(3) with the summation over all flavors and Landau energy levels, the spin factor
$ \alpha_n=2-\delta_{n0} $ , the quark energy$E_f=\sqrt{p^2_3+2 n |Q_f B|+m_q^2} $ and$ E_f^\pm=E_f\pm \mu_f $ . Fermi-Dirac distribution function$ F(x)=\left({\rm e}^{x/T}+1 \right)^{-1} $ , and the number of colors$ N_c=3 $ , which is trivial in the NJL model. In this paper, the terminologies for chiral crossover or first order chiral phase transition are conventionally defined by the continuous change or sudden jump in the order parameter$ m_q $ , and the connection point is the critical end point.As quantum fluctuations above the mean field, mesons are constructed through quark bubble summation in the framework of random phase approximation (RPA) [12, 41–45]. Namely, the quark interaction via meson exchange is effectively described using the Dyson-Schwinger equation
$ \begin{array}{*{20}{l}} {\cal D}_M(x,z) = 2G \delta(x-z)+\int {\rm d}^4y\ 2G \Pi_M(x,y) {\cal D}_M(y,z), \end{array} $

(4) where
$ {\cal D}_M(x,y) $ represents the meson propagator from x to y, and the corresponding meson polarization function is the quark bubble$ \begin{array}{*{20}{l}} \Pi_M(x,y) = {\rm i}\ { {{\rm{Tr}}}}\left[\Gamma_M^{\ast} S(x,y) \Gamma_M S(y,x)\right] \end{array} $

(5) with the meson vertex
$ \begin{array}{*{20}{l}} \Gamma_M = \left\{\begin{array}{ll} 1 & M=\sigma,\\ {\rm i}\tau_+\gamma_5 & M=\pi^+, \\ {\rm i}\tau_-\gamma_5 & M=\pi^-, \\ {\rm i}\tau_3\gamma_5 & M=\pi^0 , \end{array}\right. \quad \Gamma_M^* = \left\{\begin{array}{ll} 1 & M=\sigma,\\ {\rm i}\tau_-\gamma_5 & M=\pi^+, \\ {\rm i}\tau_+\gamma_5 & M=\pi^-, \\ {\rm i}\tau_3\gamma_5 & M=\pi^0. \end{array}\right. \end{array} $

(6) The quark propagator matrix
$ S={\rm diag}(S_u,\ S_d) $ in flavor space is at mean field level (see Eq. (2)), and the trace is taken in spin, color, and flavor space. -
When studying chiral symmetry, we focus on its pseudo-Goldstone mode
$ \pi^0 $ and Higgs mode σ. The neutral mesons$ \pi^0 $ and σ are affected by an external magnetic field only through the pair of charged constituent quarks. Consequently, the transformation from coordinate to momentum space is a conventional Fourier transformation, characterized by the plane wave$ {\rm e}^{-{\rm i}k \cdot x} $ [1–3, 80–82]$ \begin{aligned}[b] {\cal D}_{M}(k) =& \int {\rm d}^4 (x-y) {\rm e}^{{\rm i} k \cdot (x-y)} {\cal D}_{M}(x,y),\\ \Pi_{M}(k) =& \int {\rm d}^4 (x-y) {\rm e}^{{\rm i} k \cdot (x-y)} \Pi_{M}(x,y), \end{aligned} $

(7) for
$ M=\pi^0, \sigma $ . By taking the quark bubble summation in the RPA and considering the complete and orthogonal conditions of the plane wave$ {\rm e}^{-{\rm i} k \cdot x} $ , the neutral meson propagator in momentum space can be simplified to$ {\cal D}_M(k)=\frac{2G}{1-2G\Pi_M(k)}. $

(8) The meson pole mass
$ m_M $ is defined as the pole of the propagator at zero momentum,$ {\boldsymbol{k}}={\bf{0}} $ ,$ \begin{array}{*{20}{l}} 1-2G\Pi_M(\omega^2=m^2_{M}, {\boldsymbol{k}}^2=0)=0, \end{array} $

(9) and the polarization function can be simplified to
$ \begin{array}{*{20}{l}} \Pi_M(\omega^2,0) = J_1-(\omega^2-\epsilon_M^2) J_2(\omega^2), \end{array} $

(10) with
$ \epsilon_{\pi^0}=0 $ ,$ \epsilon_\sigma=2m_q $ and$ J_2(\omega^2) = -N_c\sum_{f,n}\alpha_n \frac{|Q_f B|}{2\pi} \int \frac{{\rm d} p_3}{2\pi}{{1-F(E_f^+)-F(E_f^-)}\over E_f (4 E_f^2-\omega^2)}. $

During chiral symmetry restoration, the quark mass decreases, and the
$ \pi^0 $ mass keeps increasing, as guaranteed by Goldstone's theorem [4, 5]. When the$ \pi^0 $ mass is beyond the threshold$ \begin{array}{*{20}{l}} m_{\pi^0} \geq 2m_q, \end{array} $

(11) the decay channel
$ \pi^0 \rightarrow q {\bar q} $ opens, which defines the pion Mott transition [83–85]. From the explicit expression of$ \Pi_M $ in Eq. (10), the factor$ 1/(4E_f^2-\omega^2) $ in the integrated function of$ J_2 $ becomes$ (1/4)/(p_3^2+2n|Q_f B|) $ at$ \omega= 2 m_q $ . When we perform the integration over$ p_3 $ ,$ p_3^2 $ in the denominator leads to infrared divergence at the lowest Landau level,$ n=0 $ . Therefore,$ m_{\pi^0}= 2 m_q $ is not a solution of the pole equation, and there must be a mass jump for the Goldstone mode at the Mott transition. The mass jump is a direct result of quark dimension reduction [20, 26, 28, 30, 31]. When the magnetic field disappears, there is no more quark dimension reduction, the integration$ \int {\rm d}^3{\boldsymbol{p}}/(4E_f^2-\omega^2)\sim \int {\rm d}p $ becomes finite at$ \omega = 2m_q $ , and there are no more mass jumps.In the chiral limit with the vanishing current quark mass
$ m_0=0 $ , by comparing the gap equation (3) of the quark mass$ m_q $ with the pole equation (9) of the neutral meson pole mass$ m_M $ , we obtain simple relations in the chiral symmetry breaking phase,$ \begin{array}{*{20}{l}} m_q \neq 0,\ \ \ \ \ m_{\pi^0} = 0,\ \ \ \ \ m_\sigma = 2m_q, \end{array} $

(12) and chiral restoration phase,
$ \begin{array}{*{20}{l}} m_q=0,\ \ \ \ \ m_{\pi^0} = m_\sigma \neq 0. \end{array} $

(13) This confirms that
$ \pi^0 $ and σ are chiral partners in an external magnetic field.$ \pi^0 $ is the Goldstone mode corresponding to spontaneous chiral symmetry breaking, and σ is the Higgs mode, which is heavier than (degenerate with)$ \pi^0 $ in the chiral breaking (restoration) phase. When chiral restoration phase transition occurs, the$ \pi^0 $ Mott transition occurs simultaneously, and the Higgs mode σ approaches the minimum mass$ m_\sigma|_{\min}=0 $ .In the physical case with a non-vanishing current quark mass,
$ m_0 \neq 0 $ , chiral restoration is no longer a genuine phase transition. We observe$ m_q \gg m_0 $ ,$ m_{\pi^0}<2m_q $ , and$ m_\sigma> 2m_q $ in the region with spontaneous chiral symmetry breaking,$ m_q > m_0 $ ,$ m_{\pi^0} \simeq 2m_q $ , and$ m_\sigma|_{\min}>0 $ in the chiral restoration process, and$ m_q \rightarrow m_0 $ and$ m_\sigma \simeq m_{\pi^0}\gg 2m_q $ in the region with (partially) restored chiral symmetry. Different definitions of chiral restoration are proposed in literature [23, 45, 49, 50], such as the maximum change in quark mass, the Mott transition of the pseudo-Goldstone mode, and the minimum mass of the Higgs mode. However, it should be noted that there is no guarantee for the coincidence of different definitions. -
When considering the pion superfluid phase transition at
$ \mu_I>0 $ , we focus on the$ \pi^+ $ meson because it acts as the Goldstone boson corresponding to the spontaneous breaking of isospin symmetry. For the charged mesons$ \pi^\pm $ , we should consider the interaction between charged mesons and magnetic fields, which is absent for neutral mesons. With the Ritus scheme, the Fourier transformation for neutral mesons (7) is extended to [22, 26, 80–82]$ \begin{aligned}[b] {\cal D}_M(\bar k) =& \int {\rm d}^4x {\rm d}^4y F^\ast_k(x){\cal D}_M(x,y) F_k(y),\\ \Pi_M(\bar k) =& \int {\rm d}^4x {\rm d}^4y F^\ast_k(x)\Pi_M(x,y) F_k(y), \end{aligned} $

(14) where
$ {\bar k}=(k_0,0,-s_M \sqrt{(2l+1)|Q_M B|},k_3) $ is the conserved four-dimensional Ritus momentum, and$ F_k(x)={\rm e}^{-{\rm i} \tilde k\cdot x}\times g^{s_M}_l(x_1,k_2) $ is the solution of the Klein-Gordon equation in a magnetic field, with the index l describing the meson Landau level, the Fourier transformed momentum$ \tilde k=(k_0,0,k_2,k_3) $ and the meson sign factor$ s_M= {\rm{{sgn}}}(Q_M B) $ .Considering the complete and orthogonal conditions of
$ F_k(x) $ and the Dyson-Schwinger equation (Eq. (4)), the$ \pi^\pm $ meson propagator in Ritus momentum space can be simplified to$ {\cal D}_M(\bar k)=\frac{2G}{1-2G \Pi_M(\bar k)}. $

(15) The pole mass
$ m_M $ of charged pions is defined through the singularity of the meson propagator$ {\cal D}^{-1}_M(\bar k)=0 $ at$ k_0=m_M, l=0 $ and$ k_3=0 $ ,$ \begin{array}{*{20}{l}} 1-2G\Pi_M \left(m_M,0,-s_M\sqrt{|Q_M B|},0 \right)=0. \end{array} $

(16) Taking the mean field quark propagator (2) and the definition (5) of a quark bubble, we obtain the
$ \pi^+ $ polarization function at the pole$ \begin{array}{*{20}{l}} \Pi_{\pi^+}(k_0,0,-\sqrt{|eB|},0) = J_1+J_3(k^2_0), \end{array} $

(17) with
$ \begin{aligned}[b] J_3(k^2_0) =& \sum\limits_{n,n'} \int \frac{{\rm d} p_3}{2\pi}\frac{j_{n,n'}(k_0)}{4E_n E_{n'}}\\ & \times \left[\frac{F(-E_{n'}-\mu_u)- F(E_n-\mu_d)}{k_0+\mu_I+E_{n'}+E_n}\right. \\ & \left.+\frac{F(E_{n'}-\mu_u)- F(-E_n-\mu_d)}{k_0+\mu_I-E_{n'}-E_n}\right],\\ j_{n,n'}(k_0) =& \left[{(k_0+\mu_I)^2/2}-n'|Q_u B|-n|Q_d B|\right]j^+_{n,n'}\\ & -2 \sqrt{n'|Q_u B|n|Q_d B|}\ j^-_{n,n'}\; , \end{aligned} $

(18) and quark energy
$E_{n'}=\sqrt{p^2_3+2 n' |Q_u B|+m_q^2} $ and$E_n=\sqrt{p^2_3+2 n |Q_d B|+m_q^2}\ . $ At nonzero magnetic field, three-dimensional quark momentum integration in the quark bubble
$ \Pi_{\pi^+} $ becomes one-dimensional momentum integration and summation over the discrete Landau levels. The quark dimension reduction leads to infrared ($ p_3\to 0 $ ) singularity of the quark bubble$ \Pi_{\pi^+}(m_{\pi^+},{\bf{0}}) $ at some Landau levels , temperature, and isospin chemical potential, and thus, mass jumps exist for the meson mass$ m_{\pi^+} $ in this case [26]. At finite temperature and isospin chemical potential, the first singularity of the polarization function$ \Pi_{\pi^+}(m_{\pi^+},{\bf{0}}) $ is not located at the lowest Landau level. Because the spins of the u and$ {\bar d} $ quarks at the lowest-Landau-level are always aligned parallel to the external magnetic field and the$ \pi^+ $ meson has zero spin, the lowest-Landau-level term with$ n=n'= 0 $ does not contribute to the polarization function, described by$ j^\pm_{0,0}=0 $ . The constituent quark and antiquark of charged mesons carry different charges and energies$ E_u= \sqrt{p_3^2+2n'|Q_uB|+m_q^2}-\mu_I/2, \;\, E_{\bar d}=\sqrt{p_3^2+2n|Q_dB|+m_q^2}- \mu_I/2. $ The threshold for the singularity of$ \Pi_{\pi^+} $ is located at Landau levels$ n'=0 $ and$ n=1 $ , where the charged pion mass jumps from$m_{\pi^+} > m_q+\sqrt{2{|Q_dB|}+m_q^2}-\mu_I. $ to$ m_{\pi^+} > m_q+\sqrt{2{|Q_dB|}+m_q^2}-\mu_I. $ Several other jumps are located at$ n'\geq 1, n\geq 0 $ .Pion superfluid phase transition at
$ \mu_I>0 $ is a genuine phase transition with the massless Goldstone mode$ \pi^+ $ . Therefore, the phase boundary is determined by the condition$ \begin{array}{*{20}{l}} m_{\pi^+}=0. \end{array} $

(19) At weak magnetic field and vanishing temperature and baryon chemical potential, by straightforwardly comparing the gap equation (3) of the quark mass and the pole equation (16) of the
$ \pi^+ $ mass, the critical isospin chemical potential for the pion superfluid phase transition$ \mu_I^\pi $ is equal to the$ \pi^+ $ mass in magnetic fields [27]. -
Because of the four-fermion interaction, the NJL model is not a renormalizable theory and requires regularization [12, 41–44]. The external magnetic field does not cause extra ultraviolet divergence but introduces discrete Landau levels and anisotropy in momentum space. To avoid unphysical oscillations and the breaking of the law of causality under the external magnetic field, we make use of the covariant Pauli-Villars regularization scheme [18, 19, 86]. In this scheme, the quark momentum and Landau level run formally from zero to infinity, and the divergence is removed by the cancellation among the subtraction terms.
We introduce the regularized quark masses
$ m_i= \sqrt{m^2_q+a_i\Lambda^2} $ for$ i=0,1,\cdots, N $ and replace$ m^2_q $ in the quark energy$ E_f=\sqrt{p^2_3+2n|Q_fB|+m^2_q} $ with$ m_i^2 $ . The summation and integration in the gap equation$ (J_1) $ and pole equations$ (J_1,J_2,J_3) $ are modified as follows:$ \begin{aligned}[b] &\sum\limits_n\int \frac{{\rm d}p_3}{2\pi} {\rm Function}(E_f)\ \ \ \longrightarrow \\ &\sum\limits_n\int \frac{{\rm d}p_3}{2\pi} \sum\limits_{i=0}^N \left[ c_i \times {\rm Function}(E_f^i) \right], \end{aligned} $

with
$ E_f^i=\sqrt{p^2_3+2n|Q_fB|+m^2_i} $ . The parameters$ N=3 $ ,$ a_1=1,~ c_1=-3 $ ,$ a_2=2,~ c_2=3 $ , and$ a_3=3, ~c_3=-1 $ are determined by the constraints$ a_0=0 $ ,$ c_0=1 $ , and$ \sum_{i=0}^N c_im_i^{2L}=0 $ for$ L=0,1,\cdots N-1 $ .The three parameters in the NJL model, namely, the current quark mass
$ m_0=5 $ MeV, coupling constant$ G=3.44 $ GeV$ ^{-2} $ , and mass parameter$ \Lambda=1.127 $ GeV, are fixed by fitting the quark condensate$ \langle\bar\psi\psi\rangle=-2 \times (250\ {\rm{MeV}})^3 $ , pion mass$ m_\pi=134\ {\rm{MeV}} $ , and pion decay constant$ f_\pi=93\ {\rm{MeV}} $ in vacuum [12, 41–44]. In the following numerical calculations with finite temperature, chemical potential, and magnetic field, the Pauli-Villars regularization is applied in all integrations$ (J_1,J_2,J_3) $ . It can be verified that our conclusions will not be changed by applying Pauli-Villars regularization in only the vacuum integrations. -
Chiral symmetry is spontaneously broken in vacuum and will be restored at finite temperature and chemical potential. Because
$ \mu_B $ and$ \mu_I $ play similar roles in chiral restoration,$ \mu_I=0 $ is fixed in this section. Associated with chiral crossover at finite temperature and zero baryon chemical potential, the$ \pi^0 $ meson shows a sudden mass jump at the Mott transition, induced by the discrete Landau level of constituent quarks, and with the first order chiral phase transition at finite baryon chemical potential and zero temperature, the$ \pi^0 $ and σ mesons display a sudden mass jump induced by the mass jump of constituent quarks [20, 28, 30, 31]. What is the situation in the region with finite temperature and baryon chemical potential? Fig. 1 plots the quark,$ \pi^0 $ , and σ meson masses with$ eB=20m^2_\pi $ around the critical end point. Here, panel$ ({\rm a}) $ is an example in the chiral crossover region with$ T=100 $ MeV, panel$ ({\rm b}) $ is an example at the critical end point with$ T=T_{\texttt{{CEP}}}=59 $ MeV, and panels$ ({\rm c}),({\rm d}) $ are in the first order chiral phase transition region with$ T=55,\ 10 $ MeV. The vertical dashed lines in Fig. 1 denote the maximum change in quark mass (black), the$ \pi^0 $ mass jump at the Mott transition (red), and the minimum value of σ mass (blue). In the chiral crossover region and at the critical end point, the quark and σ masses change continuously; however, the$ \pi^0 $ meson shows a sudden mass jump at the Mott transition. In the first order chiral phase transition region, the quark,$ \pi^0 $ , and σ meson masses all exhibit jumps. On the$ \mu_B-T $ plane, the mass jump of the pseudo-Goldstone mode$ \pi^0 $ can be induced by either the Mott transition (discrete Landau level of constituent quarks) or first order chiral phase transition (mass jump of constituent quarks), whereas the mass jump of the Higgs mode σ is only caused by the first order chiral phase transition.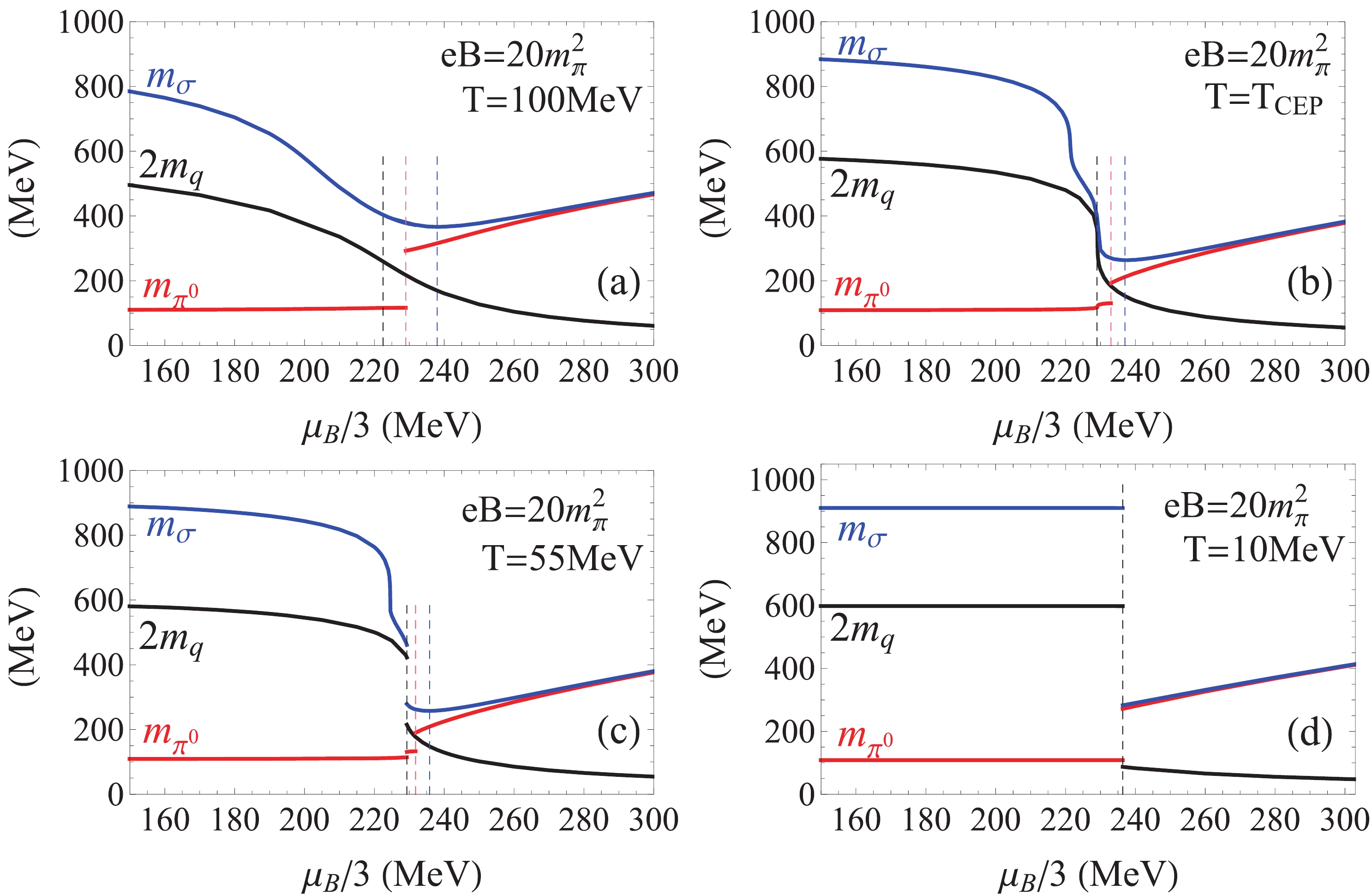
Figure 1. (color online) Quark,
$ \pi^0 $ , and σ masses with$ eB=20m^2_\pi $ and$ \mu_I=0 $ around the critical end point. Panel$ ({\rm a}) $ is an example in the chiral crossover region with$ T=100 $ MeV, panel$ ({\rm b}) $ is an example at the critical end point with$ T=T_{\texttt{{CEP}}}=59 $ MeV, and panels$ ({\rm c}),({\rm d}) $ are in the first order chiral phase transition region with$ T=55,\ 10 $ MeV. The vertical dashed lines denote the maximum change in quark mass (black), the$ \pi^0 $ Mott transition (red) and the minimum value of σ mass (blue).In the chiral crossover region, as shown by Fig. 1
$ ({\rm a}) $ , a smooth decrease in quark mass is observed, with the maximum change at$ \mu_B/3=\mu^{q}_{\texttt{pc}} $ . Owing to the discrete quark Landau level in the magnetic field, there is a mass jump for the pseudo-Goldstone mode$ \pi^0 $ at the Mott transition point$ \mu_B/3=\mu^{\pi^0}_{\texttt{mott}} $ , where the$ \pi^0 $ mass suddenly jumps from$ m_{\pi^0}<2m_q $ to$ m_{\pi^0}>2m_q $ . Except for this jump, the$ \pi^0 $ mass increases during the chiral restoration process, which is consistent with the decreasing quark mass, as guaranteed by Goldstone's theorem [4, 5]. The Higgs mode σ is always in the resonant state with$ m_\sigma>2m_q $ .$ m_\sigma $ decreases in the chiral breaking phase and reaches its minimum at$ \mu_B/3=\mu^\sigma_{\texttt{min}} $ . It then increases and becomes almost degenerate with the$ \pi^0 $ meson in the chiral restoration phase. We numerically obtain$ \mu^{q}_{\texttt{pc}}<\mu^{\pi^0}_{\texttt{mott}}<\mu^\sigma_{\texttt{min}} $ . In Fig. 1$ ({\rm b}) $ , we fix the temperature at the critical end point$ T_{\texttt{CEP}} $ and plot the quark,$ \pi^0 $ , and σ masses as functions of baryon chemical potential. At the critical end point$ T=T_{\texttt{CEP}} $ and$ \mu_B/3=\mu_{\texttt{CEP}} $ , the quark mass,$ \pi^0 $ , and σ meson masses exhibit the sharpest changes, with$ {{\rm d} m_q}/{{\rm d} \mu_B}\rightarrow \infty $ ,$ {{\rm d} m_{\pi^0}}/{{\rm d} \mu_B}\rightarrow \infty $ , and$ {{\rm d} m_{\sigma}}/{{\rm d} \mu_B}\rightarrow \infty $ , as indicated by the vertical black dashed line. In contrast to the continuous mass change of the quark and σ meson with baryon chemical potential,$ \pi^0 $ shows a sudden mass jump after the critical end point at$ \mu_B/3=\mu^{\pi^0}_{\texttt{mott}}>\mu_{\texttt{CEP}} $ , which is the Mott transition, with the mass jumping from$ m_{\pi^0}<2m_q $ to$ m_{\pi^0}>2m_q $ , as denoted by the vertical red dashed line. The σ meson, which is in the resonate state, decreases to its minimum mass at a higher baryon chemical potential, with$ \mu_B/3=\mu^\sigma_{\texttt{min}}> \mu^{\pi^0}_{\texttt{mott}}>\mu_{\texttt{CEP}} $ (see the vertical blue dashed line).Different from the single mass jump of the
$ \pi^0 $ meson in the chiral crossover region (Fig. 1$ ({\rm a}) $ ) and at the critical end point (Fig. 1$ ({\rm b}) $ ), we observe two$ \pi^0 $ mass jumps in the first order chiral phase transition region. As shown in Fig. 1$ ({\rm c}) $ , in the first order chiral phase transition region close to the critical end point, the quark mass exhibits a sudden jump at$ \mu_B/3=\mu^{q}_{\texttt{pc}} $ , which leads to mass jumps of the$ \pi^0 $ and σ mesons, as indicated by the vertical black dashed line. After this mass jump, the$ \pi^0 $ meson is still in the bound state with$ m_{\pi^0}<2m_q $ . A second mass jump is found for the$ \pi^0 $ meson at$ \mu_B/3=\mu^{\pi^0}_{\texttt{mott}}>\mu^{q}_{\texttt{pc}} $ , denoted by the vertical red dashed line, which is the Mott transition, with the mass jumping from$ m_{\pi^0}<2m_q $ to$ m_{\pi^0}>2m_q $ . For the σ meson, which is in the resonate state, after the mass jump induced by the quark mass jump, its mass continues to decrease, approaches its minimum value at$ \mu_B/3= \mu^\sigma_{\texttt{min}}>\mu^{q}_{\texttt{pc}} $ , and then begins to increase with baryon chemical potential. Nevertheless, in the first order chiral phase transition region at extremely low temperature, see Fig. 1$ ({\rm d}) $ , the$ \pi^0 $ Mott transition occurs, and the σ meson simultaneously jumps to its minimum mass, with$ \mu^{q}_{\texttt{pc}}=\mu^{\pi^0}_{\texttt{mott}}=\mu^\sigma_{\texttt{min}} $ , which is associated with the quark mass jump. The quark mass jump at the first order chiral phase transition increases with lower temperatures, and the induced mass jumps for the$ \pi^0 $ and σ mesons also increase. Comparing Fig. 1$ ({\rm c}) $ and Fig. 1$ ({\rm d}) $ , when the constituent quark has a sufficiently large mass jump, the associated$ \pi^0 $ mass jump satisfies the condition of the Mott transition, jumping from$ m_{\pi^0}<2m_q $ to$ m_{\pi^0}>2m_q $ ; therefore, we only observe a single$ \pi^0 $ mass jump in Fig. 1$ ({\rm d}) $ . For the σ meson in the resonate state, the mass jumps directly to its minimum value and then begins to increase, as shown in Fig. 1$ ({\rm d}) $ .Based on Goldstone's theorem, we can define chiral restoration not only using the order parameter, but also the
$ \pi^0 $ and σ mesons. Fig. 2 depicts the chiral phase diagram on the$ \mu_B-T $ plane at$ eB=20m^2_{\pi} $ with three characteristic phase boundaries:$ B^q_{\texttt{pc}} $ ,$ B^{\pi^0}_{\texttt{mott}} $ , and$ B^\sigma_{\texttt{min}} $ . The phase boundary$ B^q_{\texttt{pc}} $ is defined from the quark mass, and the first order chiral phase transition is denoted by the black solid line and the chiral crossover by the black dashed line, with a critical end point located at$ (T,\mu_B/3)= (T_{\texttt{CEP}},\mu_{\texttt{CEP}})=({59\ {\rm{MeV}},229\ {\rm{MeV}}}) $ . The phase boundaries$ B^{\pi^0}_{\texttt{mott}} $ and$ B^\sigma_{\texttt{min}} $ are defined by the Mott transition of the pseudo-Goldstone boson$ \pi^0 $ and the minimum mass of the Higgs mode σ, respectively. They exhibit an apparent bump structure around the critical end point. In the chiral crossover region with high temperature and low baryon chemical potential, we obtain$ \mu^{\pi^0}_{\texttt{mott}}<\mu^q_{\texttt{pc}}<\mu^\sigma_{\texttt{min}} $ for the characteristic baryon chemical potential at the phase boundaries when fixing the temperature. As we move closer to the critical end point from the crossover side, a crossing of the two phase boundaries$ B^q_{\texttt{pc}} $ and$ B^{\pi^0}_{\texttt{mott}} $ is observed; thus, we obtain$ \mu^q_{\texttt{pc}}<\mu^{\pi^0}_{\texttt{mott}}<\mu^\sigma_{\texttt{min}} $ for the characteristic baryon chemical potential with fixed temperature, which is also observed in the first order chiral phase transition region near the critical end point. In the first order chiral phase transition region with low temperature and high baryon chemical potential, the three phase boundaries become degenerate. It is noticeable that the starting point of the overlap between$ B^q_{\texttt{pc}} $ and$ B^{\pi^0}_{\texttt{mott}} $ deviates from that of$ B^q_{\texttt{pc}} $ and$ B^\sigma_{\texttt{min}} $ .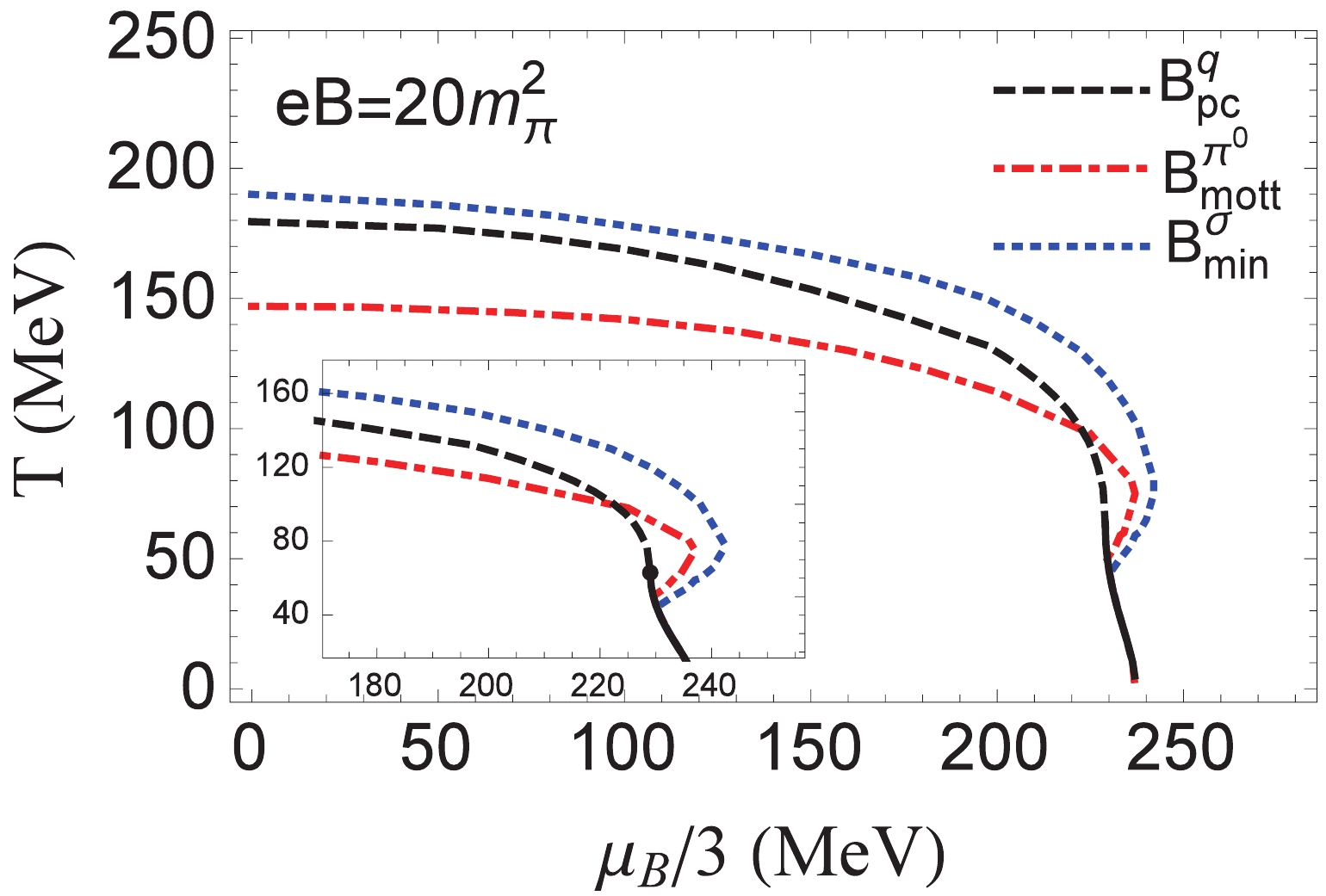
Figure 2. (color online) Chiral phase diagram on the
$ \mu_B-T $ plane at$ eB=20m^2_\pi $ and$ \mu_I=0 $ with three characteristic phase boundaries:$ B^q_{\texttt{pc}} $ , defined by the maximum change in quark mass (black line),$ B^{\pi^0}_{\texttt{mott}} $ , defined by the Mott transition of the pseudo-Goldstone boson$ \pi^0 $ (red dashed-dotted line), and$ B^\sigma_{\texttt{min}} $ , defined by the minimum mass of the Higgs mode σ (blue dotted line). Here, the terms chiral crossover (black dashed line), critical end point (black point), and first order chiral phase transition (black solid line) are conventionally defined from the continuous change in or sudden jump of the order parameter$ m_q $ .How does chiral symmetry restoration change with external magnetic field? Table 1 shows the magnetic catalysis and inverse magnetic catalysis effects of chiral symmetry restoration via the quark pseudo-critical temperature
$ T^q_{{\rm{pc}}} $ ,$ \pi^0 $ Mott transition temperature$ T^{\pi^0}_{{\rm{mott}}} $ , and the minimum mass of the σ meson$ T^{\sigma}_{{\rm{min}}} $ at vanishing baryon chemical potential and critical baryon chemical potential$ \mu_B^c/3 $ at vanishing temperature. Because quarks are treated at the mean field level,$ T^q_{{\rm{pc}}} $ is controlled by magnetic catalysis, that is, it increases with increasing magnetic field [1–3]. Mesons are quantum fluctuations constructed by quark bubble summation.$ T^{\pi^0}_{{\rm{mott}}} $ displays clearly the inverse magnetic catalysis effect, decreasing in the entire magnetic field region, and$ T^{\sigma}_{{\rm{min}}} $ first decreases with magnetic field and then increases. It is the quantum fluctuation that changes magnetic catalysis to inverse magnetic catalysis, which is consistent with the scenario of fluctuation induced inverse magnetic catalysis, discussed in Refs [17–19]. When we consider the feedback effect from mesons to quarks by including the meson contribution to the thermodynamics of the system,$ \Omega=\Omega_{mf}+\Omega_M $ , the decreasing pseudo-critical temperature$ T^q_{\rm pc} $ is observed. At vanishing temperature, the critical baryon chemical potential$ \mu_B^c=\mu^{q}_{\texttt{pc}}=\mu^{\pi^0}_{\texttt{mott}}=\mu^\sigma_{\texttt{min}} $ exhibits inverse magnetic catalysis at weak magnetic field and magnetic catalysis at strong magnetic field.$ eB/m^2_{\pi} $ 

$ T^q_{{\rm{pc}}} {\rm{/MeV}} $ 

$ T^{\pi^0}_{{\rm{mott}}} {\rm{/MeV}} $ 

$ T^{\sigma}_{{\rm{min}}} {\rm{/MeV}} $ 

$ \mu_B^c/3 {\rm{/MeV}} $ 

0 157 167 174 290 10 164 160 170 223 20 180 147 190 237 Table 1. Magnetic catalysis and inverse magnetic catalysis effects for chiral symmetry restoration shown with characteristic temperatures at vanishing baryon chemical potential and critical baryon chemical potential at vanishing temperature.
In the physical world with a non-vanishing current quark mass, chiral symmetry is an approximate symmetry and hence its restoration is not a genuine phase transition. As shown in Fig. 2, the phase boundaries from the order parameter side (
$ B^q_{\texttt{pc}} $ ) and meson side ($ B^{\pi^0}_{\texttt{mott}} $ and$ B^\sigma_{\texttt{min}} $ ) are different; however, they do not deviate significantly. The occurrence of meson mass jumps, as shown in Fig. 1, may be helpful for the experimental search for the QCD phase structure. Such mass jumps may result in some interesting phenomena within relativistic heavy ion collisions (HICs), for instance, the enhancement of pions. At the critical end point, the change from a single to two mass jumps for$ \pi^0 $ and the appearance of the σ mass jump may provide useful signals in HIC experiments. -
This section focuses on the pion superfluid phase transition and chiral symmetry restoration on the
$ \mu_I-T $ plane under an external magnetic field and vanishing baryon chemical potential, which are determined by the corresponding Goldstone mode$ \pi^+ $ and pseudo-Goldstone mode$ \pi^0 $ , respectively.Figure 3 shows a comparison between the masses of
$ \pi^+ $ and$ \pi^0 $ on the$ \mu_I-T $ plane under an external magnetic field. Here, we choose the same magnetic field,$ eB=20m^2_\pi $ , and temperatures as in Fig. 1, with the chiral crossover region with$ T=100 $ MeV in panel$ ({\rm a}) $ , critical end point with$ T=T_{\texttt{{CEP}}}=59 $ MeV in panel$ ({\rm b}) $ , and first order chiral phase transition with$ T=55,\ 10 $ MeV in panels$ ({\rm c}),(d) $ . The isospin and baryon chemical potentials play the same role in chiral symmetry restoration; thus, the$ \pi^0 $ and quark masses are the same as in Fig. 1, except for the replacement of$ \mu_B/3 $ with$ \mu_I/2 $ . Owing to the electromagnetic interaction between the$ \pi^+ $ meson and external magnetic field, the$ \pi^+ $ mass becomes heavier than the$ \pi^0 $ meson mass at zero isospin chemical potential. When increasing the isospin chemical potential$ \mu_I $ , isospin symmetry is broken, which leads to a decrease in the$ \pi^+ $ mass to zero, but the broken chiral symmetry is restored, which leads to an increase in the$ \pi^0 $ mass. Therefore, a crossing behavior is expected for the$ \pi^+ $ and$ \pi^0 $ masses, and the$ \pi^0 $ mass will become heavier than the$ \pi^+ $ meson mass with sufficiently high isospin chemical potential (as shown in Fig. 3).
Figure 3. (color online)
$ \pi^+ $ and$ \pi^0 $ masses with$ eB=20m^2_\pi $ and$ \mu_B=0 $ as functions of isospin chemical potential$ \mu_I/2 $ in the chiral crossover region with$ T=100 $ MeV (panel$ ({\rm a}) $ ), at the critical end point with$ T=T_{\texttt{{CEP}}}=59 $ MeV (panel$ ({\rm b}) $ ), and in the first order chiral phase transition region with$ T=55,\ 10 $ MeV (panels$ ({\rm c}),({\rm d}) $ ). The vertical dashed lines denote the$ \pi^0 $ mass jump (red) and$ \pi^+ $ mass jump (blue).Note that in Fig. 3, independent of temperature, both the
$ \pi^+ $ and$ \pi^0 $ masses exhibit an approximate linear behavior as functions of isospin chemical potential in the low and high$ \mu_I $ regions. In the medium$ \mu_I $ region, mass jumps are observed for both$ \pi^+ $ and$ \pi^0 $ , which depend on the temperature. For example, with$ T=100 $ MeV in Fig. 3$ ({\rm a}) $ , where the quark mass continuously decreases with isospin chemical potential, the$ \pi^+ $ meson exhibits four mass jumps induced by the discrete quark Landau levels, which differs from the single mass jump of the$ \pi^0 $ meson. In Fig. 3$ ({\rm b}) $ with$ T=T_{\texttt{{CEP}}}=59 $ MeV, the$ \pi^+ $ mass jump occurs slightly before the critical end point$ \mu_I^{\texttt{CEP}} $ and the mass jump of$ \pi^0 $ . After the mass jump, there is a sharp decrease in the mass of the$ \pi^+ $ meson (shown in the almost vertical blue solid line), which is induced by the sharp change in the constituent quark mass around$ \mu_I^{\texttt{CEP}} $ . Finally, it approaches a more gradual and constant rate of mass decrease. It should be noted that the sequence of the$ \pi^+ $ mass jump and critical end point$ \mu_I^{\texttt{CEP}} $ is dependent on the magnetic field. We numerically verify that at$ eB=10m^2_\pi $ , the$ \pi^+ $ mass jump occurs after its corresponding$ \mu_I^{\texttt{CEP}} $ . In the first order chiral phase transition region near the critical end point with$ T=55 $ MeV in Fig. 3$ ({\rm c}) $ , we observe a single$ \pi^+ $ mass jump caused by the quark mass jump, which differs from the two observed mass jumps of the$ \pi^0 $ meson, induced by the quark mass jump and discrete quark Landau levels. With a lower temperature,$ T=10 $ MeV, in Fig. 3$ ({\rm d}) $ , both the$ \pi^+ $ and$ \pi^0 $ mesons exhibit only a single mass jump due to the constituent quark mass jump at the first order chiral phase transition.The phase diagram on the
$ \mu_I-T $ plane is depicted in Fig. 4 with$ eB=10m^2_\pi $ (upper panel) and$ eB=20m^2_\pi $ (lower panel). In contrast to approximate chiral symmetry, the isospin symmetry$ U(1)_I $ is strict, and hence the pion superfluid phase transition can be defined through the Goldstone mode (massless$ \pi^+ $ meson) according to Goldstone's theorem [4, 5, 46, 54]. For chiral symmetry restoration, because the characteristic phase boundaries from the order parameter and pseudo-Goldstone boson are not far from each other, we plot the phase boundary defined through the pseudo-Goldstone mode$ \pi^0 $ , parallel to the pion superfluid phase boundary defined by the Goldstone boson$ \pi^+ $ . On the one hand, isospin chemical potential tends to break isospin symmetry and restore chiral symmetry. On the other hand, temperature tends to enhance quark thermal motion and leads to the phase transition from the pion superfluid phase to the normal phase and from chiral breaking to the restoration phase. In the low temperature and low isospin chemical potential region, the system is in the chiral breaking and normal phase, which means that chiral symmetry is spontaneously broken and isospin symmetry is intact. In the low temperature and high isospin chemical potential region, chiral symmetry is restored and isospin symmetry is spontaneously broken, indicating a chiral restored and pion superfluid phase. At medium isospin chemical potential, there is a chiral restored and normal phase. With sufficiently high temperature, the system is in the chiral restored and normal phase owing to strong quark thermal motion. In contrast to the apparent bump structure of the chiral restoration phase boundary, the phase transition temperature of the pion superfluid decreases slightly with isospin chemical potential in the low temperature region and then increases in the high temperature region. With increasing magnetic field, the separation between the two phase boundaries increases, that is, the region of the chiral restored and normal phase is enlarged. It should be noted that with a sufficiently weak magnetic field, the two phase transition lines will cross. As mentioned at the beginning of Sec.II, the coexistence of the chiral and pion condensates causes difficulty in the analytical derivations. The competition between chiral restoration and pion superfluid phase transitions under magnetic fields deserves careful investigation in future studies.
Figure 4. (color online) Phase diagram of the pion superfluid and chiral restoration on the
$ \mu_I-T $ plane at$ eB=10m^2_\pi $ and$ \mu_B=0 $ (upper panel) and$ eB=20m^2_\pi $ and$ \mu_B=0 $ (lower panel), where the pion superfluid phase transition line (blue solid line) is determined by the massless Goldstone boson$ \pi^+ $ ($ m_{\pi^+}=0 $ ), and the phase boundary of chiral symmetry restoration (red dashed-dotted line) is determined by the Mott transition of the pseudo-Goldstone boson$ \pi^0 $ ($ m_{\pi^0}=2m_q $ ). -
Light mesons
$ (\sigma, \pi^0, \pi^\pm) $ are investigated in$ \mu_B-T- eB $ and$ \mu_I-T-eB $ space using a two-flavor NJL model and are used to determine chiral symmetry restoration and the pion superfluid phase transition.On the
$ \mu_B-T $ plane, during the chiral symmetry restoration process, the mass of the pseudo-Goldstone mode$ \pi^0 $ increases and exhibits sudden jumps. In the chiral crossover region, the$ \pi^0 $ meson displays a single mass jump induced by the discrete quark Landau level. In the first order chiral phase transition region with very low temperature, the single mass jump of the$ \pi^0 $ meson is caused by the quark mass jump. At the critical end point, the$ \pi^0 $ meson shows a sharp but continuous mass increase, with a sudden mass jump at the Mott transition, In the nearby first order chiral phase transition region, we observe two$ \pi^0 $ mass jumps, one induced by the discrete quark Landau level and the other by the quark mass jump. The Higgs mode σ, which is in the resonate state, exhibits a non-monotonical mass change with a local minimum value. The σ mass continuously changes in the chiral crossover region and at the critical end point and only has a jump in the first order chiral phase transition region. We plot a chiral phase diagram on the$ \mu_B-T $ plane under an external magnetic field with three characteristic phase boundaries:$ B^q_{\texttt{pc}} $ , defined by the maximum change in quark mass,$ B^{\pi^0}_{\texttt{mott}} $ , defined by the Mott transition of the pseudo-Goldstone boson$ \pi^0 $ , and$ B^\sigma_{\texttt{min}} $ , defined by the minimum mass of the Higgs mode σ. Because of the explicit breaking of chiral symmetry in the physical world, the phase boundaries from the order parameter side ($B^q_{\texttt{pc}} $ ) and meson side ($ B^{\pi^0}_{\texttt{mott}} $ and$ B^\sigma_{\texttt{min}} $ ) are slightly different. The meson mass jump will be helpful to the experimental search for the QCD phase structure and critical end point.The competition between the pion superfluid phase transition and chiral symmetry restoration is studied on the
$ \mu_I-T $ plane in terms of the corresponding Goldstone mode$ \pi^+ $ and pseudo-Goldstone mode$ \pi^0 $ . The$ \pi^+ $ meson also exhibits a sudden mass jump caused by either the discrete quark Landau level or the mass jump of constituent quarks. In contrast to the two mass jumps of$ \pi^0 $ in the first order chiral phase transition region, several mass jumps occur for the$ \pi^+ $ meson in the chiral crossover region. At the critical end point, they both display sharp but continuous mass changes. Moreover, different from approximate chiral symmetry, the isospin symmetry is strict, and thus the pion superfluid phase transition is uniquely determined by the massless Goldstone mode$ \pi^+ $ . Isospin chemical potential tends to break isospin symmetry and restore chiral symmetry, but temperature tends to induce the phase transition from the pion superfluid phase to the normal phase and from chiral breaking to the restoration phase. In the low T case, the system is in the chiral breaking and normal phase with low$ \mu_I $ , the chiral restored and normal phase with medium$ \mu_I $ , and the chiral restored and pion superfluid phase with high$ \mu_I $ . The separation between the chiral restoration phase boundary and pion superfluid phase transition is enhanced by the external magnetic field.To obtain a comprehensive understanding of the phase diagram in
$ T-\mu_B-\mu_I $ space under an external magnetic field, studies on collective modes and phase structure in$ \mu_B-\mu_I-eB $ space are necessary, which will be reported elsewhere. This will involve competitions among chiral symmetry restoration, the pion superfluid, and color superconductor phase transitions.
Light mesons and phase structures in μB-T-eB and μI-T-eB spaces
- Received Date: 2022-02-07
- Available Online: 2022-09-15
Abstract: Light mesons





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF





















 DownLoad:
DownLoad: