-
As the number of
$ J/\psi $ events at the BESIII reaches 10 billion [1–3], a few rare decays of$ J/\psi $ may be measured, for instance, the observation of the four-lepton decay process is predicted [4] and measured [5]. In comparison with the clean property of the lepton decay process, the rare hadron decay process is more difficult to detect in experiments because of final-state quarks and gluon hadronization, small signal, and complicated background. The one-photon radiative decay channels$J/\psi \to \gamma+hadrons$ have been well studied [6], while two-photon channels$ J/\psi \to 2\gamma+ hadrons $ are much more difficult to detect. A few cases were measured in which one of the photons stems from internal hadronic resonances, such as$ \eta(1405/1475) $ [7–9]. The case with two photons directly radiated from$ J/\psi $ decay before final-state quarks and gluon hadronization has not been detected.Note that the channels of two photons radiated directly from
$ J/\psi $ decay exist but are small. With the large number of$ J/\psi $ events at the BESIII, there is a chance to measure the rare hadron decay process$ J/\psi \to 2\gamma + hadrons $ . However, detailed information on the signal and background is needed to determine optimization selection criteria for the measurements.It is well known that hadrons cannot be directly treated in perturbative calculations owing to the non-perturbative property of Quantum Chromodynamics (QCD), and a factorization scheme has to be introduced to factorize the perturbative and non-perturbative parts, where the non-perturbative parameters can be fixed in experimental measurements and the perturbative part can be calculated through perturbative expansion of QCD and other small parameter. Concerning the signal of the
$ J/\psi $ rare decay, a factorization scheme was applied in our calculations. This scheme is called non-relativistic Quantum Chromodynamics (NRQCD) [10], which was successfully applied in many other cases.In this study, we calculated the signal and background in detail, optimized the selection criteria to suppress the background, and derived estimated numerical results, which are useful for future experimental measurements.
-
The leading contribution to the two-photon radiative decay
$ J/\psi \to 2\gamma + hadrons $ stems from the processes$ J/\psi \to 2 \gamma + ggg $ and$ J/\psi \to 2 \gamma + q \bar{q} $ , where q denotes light quarks (u, d, and s flavors). The process$ J/\psi \to 2 \gamma + ggg $ contains 120 Feynman diagrams; part of them are shown in Fig. 1. The decay width is expressed as follows:$ \begin{aligned}[b] \Gamma(J/\psi \to \gamma \gamma + g g g)=\frac{1}{2M_{J/\psi}}\int {\rm d}\Pi_5\frac{1}{3} \end{aligned} $

$ \begin{aligned}[b]\quad\quad\times \sum\limits_{{\rm{polarization}}}|{\cal{M}}( J/\psi \to \gamma \gamma + g g g)|^2, \end{aligned} $

(1) where
$ {\rm d}\Pi_5 $ is the five-body phase space with possible symmetry factors due to identical final-state particles, and the polarization summation contains two transverse and one longitudinal states of$ J/\psi $ as well as polarization states of all final-state particles. The process$ J/\psi \to 2 \gamma + q \bar{q} $ contains 12 Feynman diagrams, shown in Fig. 2. The decay width can be expressed as follows:$ \begin{aligned}[b] \Gamma(J/\psi \to \gamma \gamma + q \bar{q})_{\rm fixed}=&\frac{1}{2M_{J/\psi}}\int {\rm d}\Pi_{4,{\rm fixed}}\\&\times\frac{1}{3}\sum\limits_{{\rm{polarization}}}|{\cal{M}}( J/\psi \to \gamma \gamma + q \bar{q})|^2, \end{aligned} $

(2) where
$ {\rm d}\Pi_4 $ is the four-body phase space with possible symmetry factors due to identical final-state particles. Note that there exists an evident infrared and collinear divergence problem to define two photons associated with hadron production both in theoretical calculation and experimental measurements. Therefore, hereafter a subscript "$ {\rm fixed} $ " will be added to all the decay widths to declare an infrared safety cut condition in theoretical calculations and experimental measurements.The branching ratio, defined as
$ {\cal{B}}(J/\psi \to \gamma \gamma + ggg(q\bar{q}))_{\rm fixed}=\frac{\Gamma(J/\psi \to \gamma \gamma + ggg(q\bar{q}))_{\rm fixed}}{\Gamma_{{\rm{total}}}} , $

(3) allows estimating
$ {\cal{B}}(J/\psi \to \gamma \gamma + hadrons)_{fixed} $ in our calculations. However, the absolute width entails large uncertainties in the calculations. To minimize these uncertainties from the running strong interaction coupling constant, the wave function of$ J/\psi $ at the origin, and the higher order QCD correction, the branching ratio for these two contribution processes is obtained by different bridge processes.For the process
$ J/\psi \to 2 \gamma + ggg $ , the branching ratio is expressed as follows:$ \begin{aligned}[b] {\cal{B}}(J/\psi \to \gamma \gamma + ggg)_{\rm fixed}=&\frac{\Gamma(J/\psi \to \gamma \gamma +ggg)_{\rm fixed}} {\Gamma(J/\psi \to g g g)_{\rm fixed}}\\&\times {\cal{B}}(J/\psi \to hadrons(ggg)). \end{aligned} $

(4) Note that this ratio is proportional to the electromagnetic fine structure constant
$ \alpha^2 $ . In the numerical calculations, we set$ \alpha= 1/128 $ , and the bridge branching ratio was obtained as follows [6, 11]:$ \begin{array}{*{20}{l}} {\cal{B}}(J/\psi \to hadron(ggg))=(64.1 \pm 1.0){\text{%}}. \end{array} $

(5) The leading order of the bridge process
$ J/\psi \to g g g $ contains six Feynman diagrams shown in Fig. 3, and the decay width is expressed as follows:$ \Gamma(J/\psi \to g g g) =\frac{1}{2M_{J/\psi}}\int {\rm d}\Pi_3\frac{1}{3}\sum\limits_{{\rm{polarization}}}|{\cal{M}}(J/\psi \to g g g)|^2, $

(6) where
$ {\rm d}\Pi_3 $ is the three-body phase space with possible symmetry factors due to identical final-state particles.For the process
$ J/\psi \to 2 \gamma + q \bar{q} $ , the branching ratio is expressed as follows:$\begin{aligned}[b] {\cal{B}}(J/\psi \to \gamma \gamma + q \bar{q})_{\rm fixed}=&\frac{\Gamma(J/\psi \to \gamma \gamma +q \bar{q})_{\rm fixed}} {\Gamma(J/\psi \to e^+e^-)_{\rm fixed}}\\&\times {\cal{B}}(J/\psi \to e^+e^-). \end{aligned} $

(7) This ratio is also proportional to the electromagnetic fine structure constant
$ \alpha^2 $ , and the bridge branching ratio was obtained as follows [6]:$ \begin{array}{*{20}{l}} {\cal{B}}(J/\psi \to e^+ e^-)=(5.971 \pm 0.032){\text{%}}. \end{array} $

(8) The leading order of the bridge process
$ J/\psi \to e^+e^- $ contains one Feynman diagram shown in Fig. 4, and the decay width is expressed as follows:$ \begin{aligned}[b] \Gamma(J/\psi \to e^+e^-) =&\frac{1}{2M_{J/\psi}}\int {\rm d}\Pi_2\frac{1}{3}\\&\times \sum\limits_{{\rm{polarization}}}|{\cal{M}}(J/\psi \to e^+e^-)|^2, \end{aligned} $

(9) where
$ {\rm d}\Pi_2 $ is the two-body phase space. Note the dominating contribution of$ J/\psi \to \gamma \gamma + q \bar{q} $ from Figs. 1–6 in Fig. 2. Hence, the higher order QCD correction effects in Eq. (7) could be minimized.According to Eqs. (4) and (7), the branching ratios for the rare decay of
$ J/\psi $ are obtained as follows:$ \begin{aligned}[b] {\cal{B}}(J/\psi \to \gamma \gamma +g g g)|_{\rm fixed}=&(1.20 \pm 0.02) \times 10^{-6}, \\ {\cal{B}}(J/\psi \to \gamma \gamma + q \bar{q})|_{\rm fixed}=&(2.08 \pm 0.01) \times 10^{-5}, \\ {\cal{B}}(J/\psi \to \gamma \gamma + hadrons)|_{\rm fixed}=&(2.20 \pm 0.01) \times 10^{-5}, \end{aligned} $

(10) where the infrared safety cut condition is fixed as follows: the energy for each photon is
$ E_\gamma>0.05 $ GeV and the angle between photons and gluons (quarks) is$ {\rm cos}\theta_{\gamma g, \gamma q, \gamma \bar{q}}< 0.95 $ . The hadronization requirements are expressed as follows:$ \begin{aligned}[b] m_{ggg}^2 &\equiv (\sum\limits_{{\rm{all gluon}}}p)^2 > (2 \times 0.13 \;{\rm{ GeV}})^2, \\ m_{q\bar{q}}^2 &\equiv (p_q+p_{\bar{q}})^2 > \begin{cases} (2 \times 0.13 \;{\rm{ GeV}})^2, & {\rm{for}}~~ u ~~{\rm{ or }}~~ d ~~{\rm{quarks}} \\ (2 \times 0.49 \;{\rm{ GeV}})^2, & {\rm{for }}~~ s ~~{\rm{ quark}} \end{cases} \end{aligned} $

(11) where p is the 4-momentum of gluon, 0.13 GeV is the mass of pion, and 0.49 GeV is the mass of kaon. The calculations of all decay widths for
$ \Gamma(J/\psi \to g g g) $ ,$ \Gamma(J/\psi \to \gamma \gamma + g g g) $ ,$ \Gamma(J/\psi \to \gamma \gamma + q \bar{q}) $ , and$ \Gamma(J/\psi \to e^+e^-) $ were carried out based on the leading-order NRQCD contribution using FDC package [12].There are two approaches to measure the two-photon radiative decay channel of
$ J/\psi $ . One is using$ J/\psi $ from$ \psi(3686)\rightarrow J/\psi +\pi^+ + \pi^- $ , for which there are$ N_{\psi(3686)}= (4.481\pm0.029)\times 10^8 \psi(3686) $ events, just as the recent observation of$ J/\psi $ decay to$ e^+e^-e^+ e^- $ and$ e^+ e^- \mu^+ \mu^- $ in the BESIII [5]. An estimation of the two-photon radiative decay event number can be obtained as follows:$ \begin{aligned}[b] N(J/\psi \to \gamma \gamma + hadrons)_{\rm fixed}=&N_{\psi(3686)} \times {\cal{B}}(\psi(3686) \\ & \to J/\psi \pi^+ \pi^-) \times {\cal{B}}(J/\psi \\ &\to \gamma \gamma +hadrons)_{\rm fixed}\\ =&3418, \end{aligned} $

(12) where
$ {\cal{B}}(\psi(3686) \to J/\psi \pi^+ \pi^-)=(34.68\pm 0.30)\% $ is used [6]. There is no large backgroundfrom theoretical consideration, but there are a few backgrounds in the experimental measurements.The second approach consists in searching for the two-photon radiative decay channel of
$ J/\psi $ from the data sample of$ J/\psi $ at the BESIII. In this case, the results of the branching ratio cannot be directly applied because of a special difference to be considered. For the decay width expressed by Eq. (1), the polarization summation for initial-state$ J/\psi $ should only contain the transverse polarization together with the detector coverage limitation because basically only the transverse polarization$ J/\psi $ can be produced in the electron-positron collider, while the longitudinal polarization$ J/\psi $ can be ignored. Under these conditions, the decay width for the process$ J/\psi \to \gamma \gamma + g g g $ is expressed as follows:$ \begin{aligned}[b] \Gamma(J/\psi \to \gamma \gamma + g g g)=&\frac{1}{2M_{J/\psi}}\int {\rm d}\Pi_5\frac{1}{2}\sum\limits_{{\rm{polarization}}}\\&\times|{\cal{M}}(J/\psi \to \gamma \gamma + g g g)|^2. \end{aligned} $

(13) In addition, according to the
$ J/\psi $ detector condition at the BESIII [3], the energy cut for each photon is$ 0.05 $ GeV, and the polar angle cut for each final-state particle is$ |{\rm cos}\theta|<0.93 $ , where the polar angle denotes the angle between the particle and beam direction. In the experiments, gluons cannot be detected directly; the detectable particles are hadrons, which require$ m_{ggg}^2> (2 \times 0.13 \;{\rm{ GeV}})^2 $ . Although Eq. (11) is trivial for the process$ J/\psi \to g g g $ , it really cuts the phase space for$ J/\psi \to \gamma \gamma + g g g $ . All the above considerations are also taken into consideration for$ J/\psi \to \gamma \gamma + q \bar{q} $ . In the following calculations,$ N_{{\rm{total}}}=(1.0087\pm0.0044) \times 10^{10} $ is the event number of$ J/\psi $ at the BESIII [3] with the corresponding integrated luminosity$ {\cal{L}}=3083\;{\rm pb}^{-1} $ and the center of mass energy$ \sqrt{s}=M_{J/\psi}=3.097 \;{\rm{GeV}} $ . -
To investigate rare processes, a detailed background study is crucial. For the signal of the process
$ J/\psi \to \gamma \gamma + hadrons $ , there could be a few sources for the background, such as final state radiation and resonance radiative decay. The main background is the process$ e^{+} e^{-} \to \gamma \gamma + q \bar{q} $ , where q denotes light quarks (u, d, and s flavors), with 20 Feynman diagrams, part of which are shown in Fig. 5. The cross section is expressed as follows: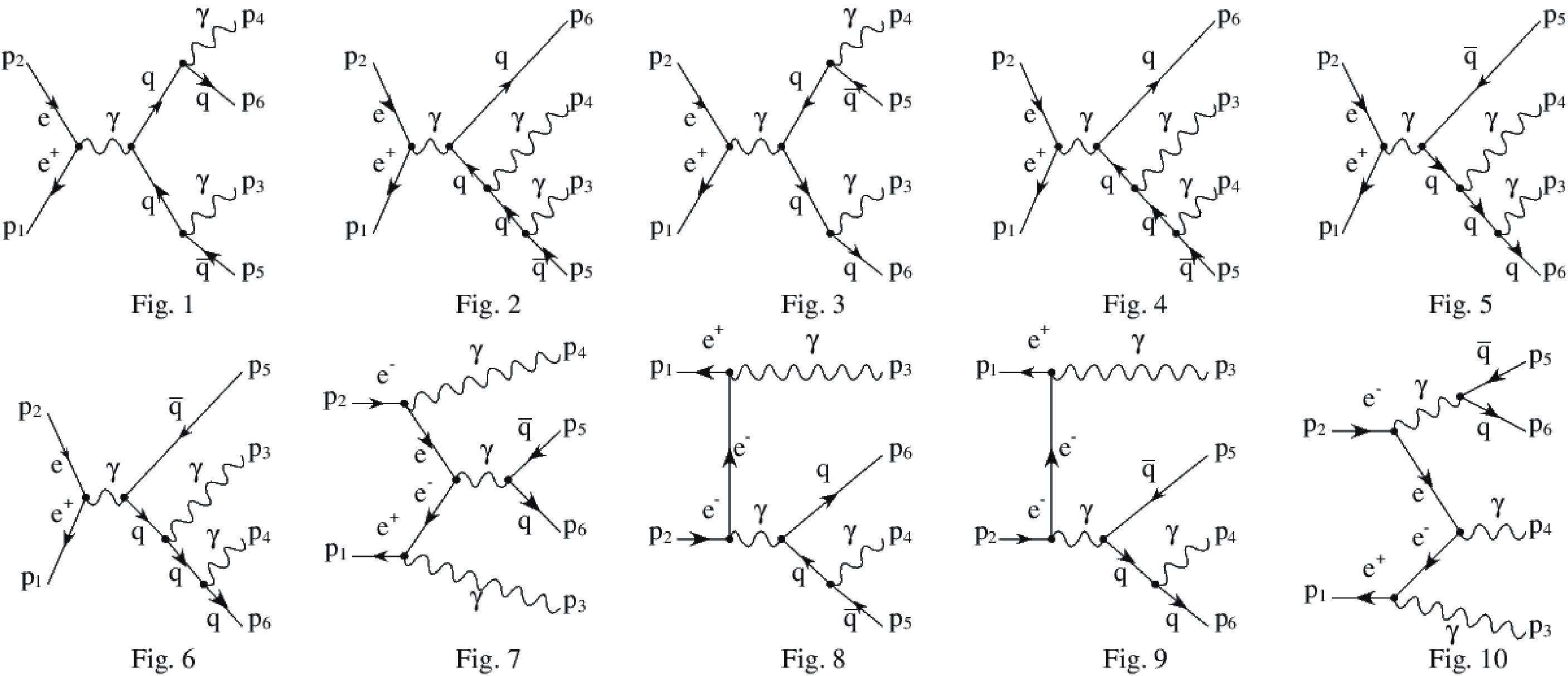
Figure 5. Part of the Feynman diagrams for the process
$ e^{+} e^{-} \to \gamma \gamma + q \bar{q}. $ $ \begin{aligned}[b] \sigma(e^+ e^- \to \gamma \gamma + q \bar{q})=&\frac{1}{2s}\int {\rm d}\Pi_4\frac{1}{4}\sum\limits_{{\rm{polarization}}}\\&\times|{\cal{M}}(e^+ e^- \to \gamma \gamma + q \bar{q})|^2, \end{aligned} $

(14) where
$ {\rm d}\Pi_4 $ is the four-body phase space with possible symmetry factors due to identical final-state particles. The calculation of the cross section was carried out by using the FDC package [12]. Thus, the event number is expressed as follows:$ \begin{array}{*{20}{l}} N(e^+ e^- \to \gamma \gamma + hadrons)=\sigma(e^+ e^- \to \gamma \gamma + q \bar{q})*{\cal{L}}. \end{array} $

(15) -
All the following optimizations are based on the event sample data generated from the signal and background calculations with the corresponding event number. There exist selection criteria for the signal
$ J/\psi \to \gamma \gamma + hadrons $ and background$ e^{+} e^{-} \to \gamma \gamma + hadrons (q \bar{q}) $ that need to be considered; they are listed in Table 1.Process $ J/\psi \to \gamma \gamma + hadrons $ 

$ e^{+} e^{-} \to \gamma \gamma + hadrons $ 

Cut of energy for each photon $ E_\gamma>E_{\gamma, {\rm cut}} $ 

$ E_\gamma>E_{\gamma, {\rm cut}} $ 

Cut of polar angle for each final-state particle $ |{\rm cos}\theta|<{\rm cos}\theta_{\rm cut} $ 

$ |{\rm cos}\theta|<{\rm cos}\theta_{\rm cut} $ 

Cut of invariant mass for hadrons production $ m_{ggg, q\bar{q}}^2 > s_{\rm cut} $ 

$ m_{q\bar{q}}^2 > s_{\rm cut} $ 

Cut of angle between photons and gluons (quarks) $ {\rm cos}\theta_{\gamma g, \gamma q, \gamma \bar{q}}<{\rm cos}\theta_{\gamma g, \gamma q, {\rm cut}} $ 

$ {\rm cos}\theta_{\gamma q, \gamma \bar{q}}<{\rm cos}\theta_{\gamma g, \gamma q, {\rm cut}} $ 

Table 1. Selection criteria for the processes
$ J/\psi \to \gamma \gamma + hadrons $ and$ e^{+} e^{-} \to \gamma \gamma + hadrons. $ The basic cut values in Table 1 are as follows:
$ \begin{aligned}[b]& E_{\gamma, {\rm cut}}=0.05 \;{\rm{ GeV}},\quad {\rm cos}\theta_{\rm cut}=0.93,\\& s_{\rm cut}= \begin{cases} (2 \times 0.13 \;{\rm{ GeV}})^2, & {\rm{for}} ~~ u ~~{\rm{ or}} ~~ d~~ {\rm{ quarks}} \\ (2 \times 0.49 \;{\rm{ GeV}})^2, & {\rm{for}}~~ s ~~{\rm{ quark}} \end{cases}, \\& {\rm cos}\theta_{\gamma g, \gamma q, {\rm cut}}=0.95, \end{aligned} $

(16) where the word 'basic' denotes the range of these values with respect to the maximum range of event selection. The basic criteria 1 and 2 are
$ J/\psi $ selection criteria at the BESIII detector [3]; the basic criterion 3 is for hadron production; and the basic criterion 4 is for avoiding the problem of collinear divergence in the processes$ e^{+} e^{-} \to \gamma \gamma + q \bar{q} $ and$ J/\psi \to \gamma \gamma +q \bar{q} $ .With these basic selection criteria, the branching ratios for the rare decay
$ J/\psi \to \gamma \gamma + g g g $ are obtained as follows:$ \begin{aligned}[b] {\cal{B}}(J/\psi \to \gamma \gamma +g g g)=&(1.01 \pm 0.02) \times 10^{-6}, \\ {\cal{B}}(J/\psi \to \gamma \gamma + q \bar{q})=&(1.74 \pm 0.01) \times 10^{-5}, \\ {\cal{B}}(J/\psi \to \gamma \gamma + hadrons)=&(1.84 \pm 0.01) \times 10^{-5}, \end{aligned} $

(17) and the numbers of events corresponding to
$ N_{{\rm{total}}}= (1.0087\pm0.0044) \times 10^{10} $ (the event number of$ J/\psi $ at the BESIII) are shown as$ \begin{aligned}[b]& N(J/\psi \to \gamma \gamma u \bar{u})=170279, \quad N(J/\psi \to \gamma \gamma d \bar{d})=2695, \\& N(J/\psi \to \gamma \gamma s \bar{s})=2465, \quad N(J/\psi \to \gamma \gamma g g g)=10180, \\& N(J/\psi \to \gamma \gamma q \bar{q})=175439, \quad N(e^+ e^- \to \gamma \gamma u \bar{u})=157382,\\& N(e^+ e^- \to \gamma \gamma d \bar{d})=25917, \quad N(e^+ e^- \to \gamma \gamma s \bar{s})=17824, \\ & N(e^+ e^- \to \gamma \gamma + hadrons)=201123, \\& N(J/\psi \to \gamma \gamma + hadrons )=185619, \quad R=92.3{\text{%}}, \\[-12pt] \end{aligned} $

(18) where
$ \begin{aligned}[b]& N(e^+ e^- \to \gamma \gamma + hadrons)\\=&N(e^+ e^- \to \gamma \gamma u \bar{u})+N(e^+ e^- \to \gamma \gamma d \bar{d})+N(e^+ e^- \to \gamma \gamma s \bar{s}), \\& N(J/\psi \to \gamma \gamma + q \bar{q})\\=&N(J/\psi \to \gamma \gamma u \bar{u})+N(J/\psi \to \gamma \gamma d \bar{d})+N(J/\psi \to \gamma \gamma s \bar{s}), \\& N(J/\psi \to \gamma \gamma + hadrons)\\=&N(J/\psi \to \gamma \gamma ggg)+N(J/\psi \to \gamma \gamma q \bar{q}), \end{aligned} $

(19) and R is a ratio:
$ R \equiv \frac{N(J/\psi \to \gamma \gamma + hadrons)}{N(e^+ e^- \to \gamma \gamma + hadrons)}. $

(20) The distributions of the two-photon invariant mass
$ m_{\gamma\gamma} $ and hadron invariant mass$ m_{ggg, q \bar{q}} $ for the signal$ J/\psi \to \gamma \gamma + hadrons $ and background process$ e^{+} e^{-} \to \gamma \gamma + hadrons $ are depicted in Fig. 6. The distributions of$ {\rm cos}\theta_\gamma $ ,$ E_\gamma $ , and$ {\rm cos}\theta_{\gamma g, \gamma q, \gamma \bar{q}} $ for signal and background are also presented in Fig. 6, where$ {\rm cos}\theta_\gamma $ and$ E_\gamma $ are the polar angle and energy of photons, respectively, and each photon is counted as 0.5 because of the presence of two indistinguishable photons in each event;$ {\rm cos}\theta_{\gamma g, \gamma q, \gamma \bar{q}} $ is the angle between photons and gluons (or quarks) and each pair is counted as 1/6 (or 1/4) for the same reason. In the distribution plots, the bin widths are 0.1 GeV for$ m_{\gamma\gamma} $ and$ m_{ggg, q \bar{q}} $ , 0.05 GeV for$ E_\gamma $ , and 0.05 for$ cos\theta_\gamma $ and$ {\rm cos}\theta_{\gamma g, \gamma q, \gamma \bar{q}} $ . Through the ratio R included in Eq. (18) and the distributions shown in Fig. 6, it can be concluded that the signal can be directly detected from the choice of basic selection criteria in Eq. (16).
Figure 6. (color online) Distributions of
$ J/\psi \to \gamma \gamma + hadrons $ and$ e^{+} e^{-} \to \gamma \gamma + hadrons $ with the basic selection criteria. The bin widths are 0.1 GeV for$ m_{\gamma\gamma} $ and$ m_{ggg, q \bar{q}} $ , 0.05 GeV for$ E_\gamma $ , and 0.05 for$ {\rm cos}\theta_\gamma $ and$ {\rm cos}\theta_{\gamma g, \gamma q, \gamma \bar{q}} $ .Concerning the quantum electrodynamics (QED) perturbative expansion, the main signal
$ J/\psi \to 2\gamma + q \bar{q} $ is a next-to-next-to-leading process while the leading process is$ J/\psi \to q \bar{q} $ . Therefore, there are double infrared and double collinear divergences in the main signal process before adding all the virtual corrections together. Although two photons must be detected in the signal, this condition can be guaranteed in experimental measurements through the condition$ E_\gamma>0.05 $ . However, the distributions of$ E_\gamma $ and$ {\rm cos}\theta_{\gamma q, \gamma \bar{q}} $ obtained in our theoretical calculations may depart signficantly from real ones in the ranges$ E_\gamma\rightarrow 0 $ and$ {\rm cos}\theta_{\gamma q, \gamma \bar{q}}\rightarrow 1 $ , and reliable results in these ranges should be obtained by resummation to all perturbative order. According to the distributions of$ E_\gamma $ and$ cos\theta_{\gamma q, \gamma \bar{q}} $ shown in Fig. 6, sharp peaks are present in these ranges. Therefore, we had to establish a set of cuts as$ E_\gamma>0.3 $ GeV and$ {\rm cos}\theta_{\gamma g,\gamma q, \gamma \bar{q}}<0.85 $ to avoid unreliable estimations in subsequent investigation. These cut values constitute an approximation without detailed calculation support.In the subsequent analysis, the basic cut values in Table 1 were modified as follows:
$ \begin{aligned}[b]& E_{\gamma, {\rm cut}}=0.30\; {\rm{ GeV}},\quad cos\theta_{\rm cut}=0.93,\\& s_{\rm cut}= \begin{cases} (2 \times 0.13 \;{\rm{ GeV}})^2, & {\rm{for}}~~ u ~~{\rm{ or }}~~ d ~~{\rm{ quarks}} \\ (2 \times 0.49 \;{\rm{ GeV}})^2, & {\rm{for}}~~ s ~~{\rm{ quark}} \end{cases} ,\\& {\rm cos}\theta_{\gamma g, \gamma q, {\rm cut}}=0.85. \end{aligned} $

(21) However, the cut values for the selection criteria can be optimized in the analysis. We can find the best cut values to suppress the background and highlight the signal. The target is to find these cut values to maximize the ratio R. The best cut values can be obtained using the following strategy:
● Step 1: Fix all the selection criteria to the basic cut values in Eq. (21).
● Step 2: Obtain the best cut value for a selection criterion from the cut value distribution of the ratio R by fixing other selection criteria.
● Step 3: Fix the best cut values from the previous criteria, and repeat Step 2 until all best selection criteria are obtained.
A specific searching process is described next:
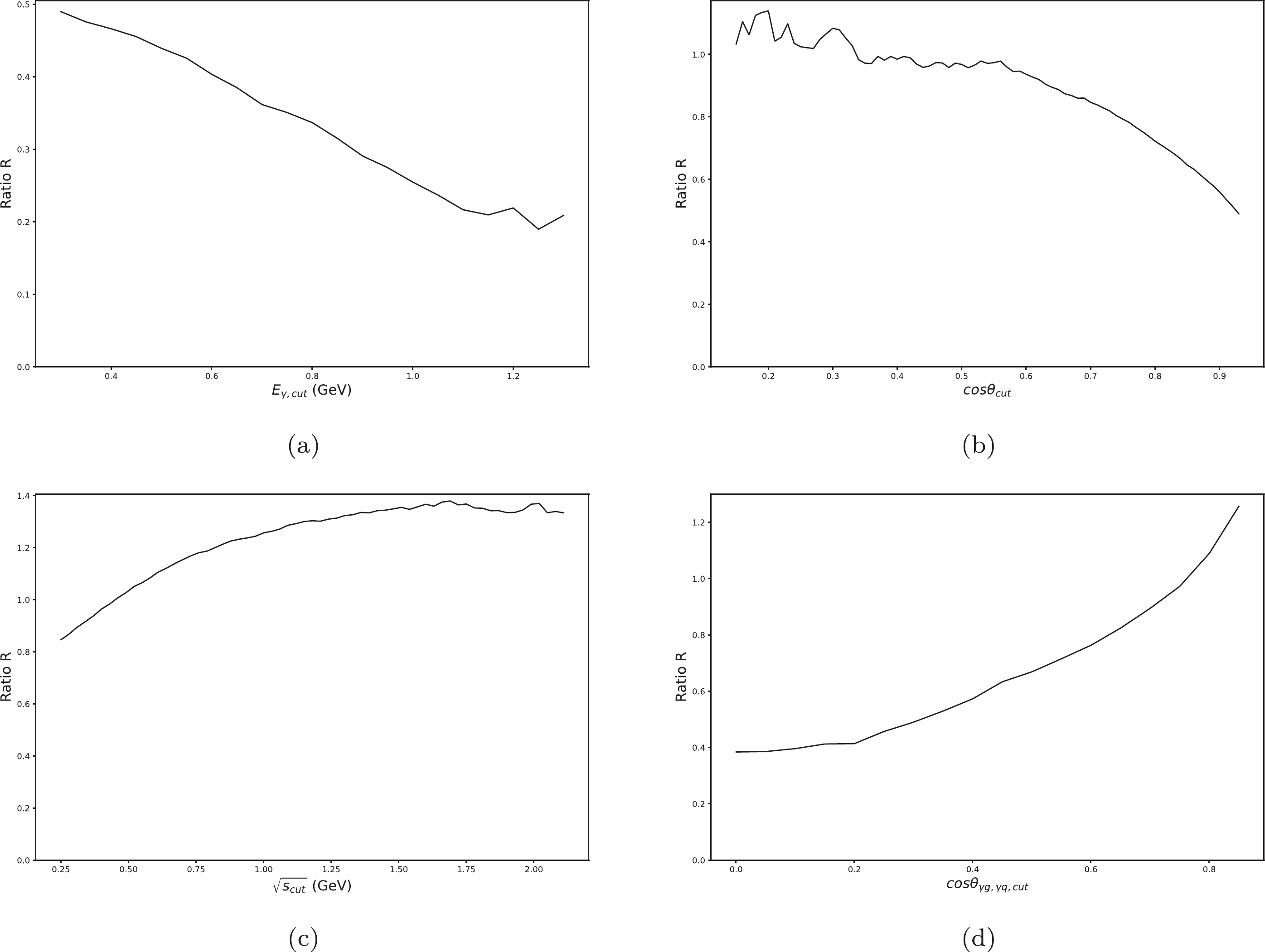
● Find the best cut value
$ E_{\gamma, {\rm cut}} $ for criterion 1: the relation of the ratio R with$ E_{\gamma, {\rm cut}} $ is shown in Fig. 7(a) with the basic cut values for criteria 2–4. The result shows that the best cut value is$ E_{\gamma, {\rm cut}}=0.30 $ GeV.● Find the best cut value
$ {\rm cos}\theta_{\rm cut} $ for criterion 2: the relation of the ratio R with$ {\rm cos}\theta_{\rm cut} $ is shown in Fig. 7(b) with$ E_{\gamma, {\rm cut}}=0.30 $ GeV and the basic cut values for criteria 3–4. In this condition, the more events are cut off, the greater the ratio R. Hence, we had to balance R and the number of events, and adopted$ {\rm cos}\theta_{\rm cut}=0.70 $ as the best cut value.● Find the best cut value
$ s_{\rm cut} $ for criterion 3: the relation of the ratio R with$ \sqrt{s_{\rm cut}} $ is shown in Fig. 7(c) with$ E_{\gamma, {\rm cut}}=0.30 $ GeV,$ {\rm cos}\theta_{\rm cut}=0.70 $ , and the basic cut value for criterion 4. Note that R only exhibits a small increase when$ s_{\rm cut}>(1.00\; {\rm{ GeV}})^2 $ . Hence, we concluded that the best cut value is$ s_{\rm cut}=(1.00\; {\rm{ GeV}})^2 $ .● Find the best cut value for criterion 4: the relation of the ratio R with
$ {\rm cos}\theta_{\gamma g, \gamma q, {\rm cut}} $ is shown in Fig. 7(d) with$ E_{\gamma, {\rm cut}}=0.30 $ GeV,$ {\rm cos}\theta_{\rm cut}=0.70 $ , and$ s_{\rm cut}=(1.00 \;{\rm{ GeV}})^2 $ . The results show that the best cut value is$ {\rm cos}\theta_{\gamma g, \gamma q, {\rm cut}}= 0.85 $ .All in all, the best cut values can be finally summarized as follows:
$ \begin{aligned}[b]& E_{\gamma, {\rm cut}}=0.30 \;{\rm{ GeV}},\\& {\rm cos}\theta_{\rm cut}=0.70,\\& s_{\rm cut}=(1.00 \;{\rm{ GeV}})^2 ,\\& {\rm cos}\theta_{\gamma g, \gamma q, {\rm cut}}=0.85, \end{aligned} $

(22) and the results are obtained as follows:
$ \begin{aligned}[b] & N(J/\psi \to \gamma \gamma u \bar{u})=3812,\quad N(J/\psi \to \gamma \gamma d \bar{d})=71, \\& N(J/\psi \to \gamma \gamma s \bar{s})=71, \quad N(J/\psi \to \gamma \gamma g g g)=928, \\& N(J/\psi \to \gamma \gamma q \bar{q})=3954, \quad N(e^+ e^- \to \gamma \gamma u \bar{u})=2974,\\& N(e^+ e^- \to \gamma \gamma d \bar{d})=485, \quad N(e^+ e^- \to \gamma \gamma s \bar{s})=485, \\& N(e^+ e^- \to \gamma \gamma + hadrons)=3944, \\& N(J/\psi \to \gamma \gamma + hadrons )=4882, \quad R=1.24. \end{aligned} $

(23) The five distributions for the signal
$ J/\psi \to \gamma \gamma + hadrons $ and background$ e^{+} e^{-} \to \gamma \gamma + hadrons $ resulting from the best cut values given in Eq. (22) are shown in Fig. 8. From these distributions, it is clear that the signal$ J/\psi \to \gamma \gamma + hadrons $ is of the same order of magnitude as the background$ e^{+} e^{-} \to \gamma \gamma + hadrons $ , and the background may be subtracted from sideband estimation in experimental measurements.
Figure 8. (color online) Distributions of
$ J/\psi \to \gamma \gamma + hadrons $ and$ e^{+} e^{-} \to \gamma \gamma + hadrons $ with the best selection criteria. The bin widths are 0.1 GeV for$ m_{\gamma\gamma} $ and$ m_{ggg, q \bar{q}} $ , 0.05 GeV for$ E_\gamma $ , and 0.05 for$ {\rm cos}\theta_\gamma $ and$ {\rm cos}\theta_{\gamma g, \gamma q, \gamma \bar{q}}. $ -
In summary, the two-photon radiative decay process
$ J/\psi \to 2\gamma+hadrons $ was studied, and the main contribution processes$ J/\psi \to 2\gamma + g g g $ and$ J/\psi \to 2\gamma + q \bar{q} $ were calculated. For the situation of the$ J/\psi $ data sample at the BESIII, the signal and main background$ e^{+} e^{-} \to \gamma \gamma + hadrons (q \bar{q}) $ were investigated. The best selection criteria for experiments were also investigated. We concluded that the ratio of signal to background can reach 1.24 with 4882 signal events. The five distributions of the signal and background were also obtained. These distributions show that the signal is large enough to be measured. It is expected that measurements on the two-photon radiative decay$ J/\psi \to 2\gamma+hadrons $ could be conducted in the future.It should be pointed out that there exist double infrared and double collinear divergences for the main signal process
$ J/\psi \to 2\gamma + q \bar{q} $ , and the$ E_\gamma $ and$ {\rm cos}\theta_{\gamma q, \gamma \bar{q}} $ distributions obtained in our fix-order perturbative calculations cannot be trusted in the ranges$ E_\gamma\rightarrow 0 $ and$ {\rm cos}\theta_{\gamma q, \gamma \bar{q}}\rightarrow 1 $ . When these distributions are obtained in future experimental measurements, further studies should be conducted to obtain reliable results in these ranges through QED resummation to all perturbative order. This was out of the scope of the present study.
Study of the rare decay ${ \boldsymbol J/\boldsymbol\psi \to {\bf 2}{\boldsymbol\gamma}{\boldsymbol{+hadrons}} }$ at the BESIII
- Received Date: 2022-04-06
- Available Online: 2022-09-15
Abstract: The two-photon radiative decay process







 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF





















 DownLoad:
DownLoad: