-
Wormhole gravity is a fascinating topic of research in cosmology. The concept of the wormhole was first proposed in 1916 by physicists Albert Einstein and Nathan Rosen, although it had not yet been discovered. They investigated the strange equations that are now known to define the unfathomable regions of space known as black holes and wondered what they truly represented. The main goals of this paper are to describe how wormholes develop and discuss different forms of wormholes. The current state of knowledge on wormholes in our universe is as follows: Einstein's general theory of relativity dramatically altered our understanding of fundamental physics concepts, such as space and time. However, it also left us with several profound mysteries. One example is black holes, which were only unequivocally discovered in the last few years. Another is the concept of "wormholes," which are bridges linking various places in space-time that, in principle, provide shortcuts for space travelers. Wormholes remain theoretical; however, experts believe that they may soon be discovered. New research has provided fascinating paths forward in recent years.
Formation of wormholes:
(i) Einstein-Rosen Bridge: In 1935, Rosen and Einstein used the general theory of relativity to propose the idea of existing "bridges" through space-time, known as Einstein-Rosen Bridges [1], by which two different locations in space-time are connected, creating a route that may decrease the time and distance of travel. Wormholes are the solutions of Einstein's field equations in which gravity acts like "tunnels," which is more intriguing. When two large materials are placed in two parallel worlds, a wormhole forms. The resistance from brane tension opposes the gravitational attraction between objects and contains negative density and a large negative pressure. Branes are then deformed, and a wormhole is created as a result of the sufficiently strong interaction [2]. Some cosmological concerns, such as dark energy, dark matter, and cosmic expansion, are used to describe the phenomena that appear to be explained by modified gravity theories. In this respect, various hypotheses proposed by certain academics claim to disclose the mystery underlying the expanding cosmos. Einstein's gravity theories, such as the special theory of relativity [3] and general theory of relativity, are based on the fundamental idea that in all inertial frames of reference, the rules of physics remain constant. Ellis [4] introduced another word for wormhole, referring to it as a "Drainhole," and "Geon" is the name given by Wheeler [5], who also predicted a form of wormhole that offers twofold space. Nonstatic Lorentzian wormholes conformally related to static wormhole geometries were found to exist for a finite (arbitrarily large) or half-infinite interval of time, with the required energy-momentum tensor satisfying the weak energy condition, as discussed by Kar [6]. Morris and Thorne [7] were the first to suggest that people may be able to travel via wormhole tunnels. They established the basic concept of traversable wormholes by applying the GR principle to static axially symmetric wormholes. Morris et al. [8] claim to have examined how the existence of exotic matter influences the development of wormhole formation. Exotic matter is a type of dark energy that has a repellent effect. Dark energy, according to recent research, is the biggest factor in the universe's rapid expansion.
(ii) Schwarzschild wormholes: The Schwarzschild wormhole was the first identified form of wormhole solution. It would appear as an infinite expanse hole in the spherically symmetric metric, but would collapse too rapidly for anything to pass through it. Only strange materials with negative energy density were considered conceivable, which may be used to create wormholes that can be traversed in both directions [9]. Some wormholes could be "traversable," allowing humans to pass through them.
(iii) Lorentzian traversable wormholes: Lorentzian traversable phenomena could allow extraordinarily fast travel in both directions, from one planet to the next. The notion of traversable wormholes was first demonstrated by Ellis in 1973 [10] using the general theory of relativity and independently studied by Bronnikov [11]. Exotic matter is used in the formation of traversable Lorentz wormholes, which violates energy conditions. There are other types of wormholes described in [12]
$ (i) $ Schwarzschild and Kerr phenomena (Horizons of Events),$ (ii) $ Morris-Thorne phenomena (Horizon-free),$ (iii) $ Reissner-Nordstrom phenomena (Charged with electricity).Investigating traversable wormhole solutions using wormhole shape functions (WSFs) is a fascinating area of research. Godani and Samanta [13] used a well defined WSF to examine the modeling of traversable wormholes. Furthermore, WSFs can be computed using the Karmarkar condition (KMc). According to Karmarkar [14], a static and spherical shape is oriented so that each line element can be of class one. Shamir and Fayyaz [15] constructed a WSF by employing the KMc for static traversable wormhole geometry. Tello-Ortiz and Contreras [16] employed the class I approach to obtain wormhole solutions in the framework of general relativity in two different ways. First, they proposed a suitable red-shift function to find its associated shape function and then imposed the well known MorrisThorne shape function to obtain the corresponding red-shift. Mustafa et al. [17] obtained wormhole solutions from the KMc in the
$ f(Q) $ gravity formalism, in which Q is a nonmetricity scalar. Rahaman et al. [18] obtained a new wormhole solution inspired by noncommutative geometry with the additional condition of allowing conformal Killing vectors. Ditta et al. [19] studied traversable wormhole solutions in the extended teleparallel theory of gravity with matter coupling using the KMc. Wang and Mustafa [20] examined embedded wormhole solutions in the modified$ f(R,T) $ theory of gravity, where T denotes the trace of the energy-momentum tensor, and R is the Ricci scalar.Inspired by literature, in this paper, our aim is to investigate wormhole solutions in
$ f(R,\phi,\chi) $ theory via the KMc, where R represents the Ricci scalar, ϕ is the scalar potential function, and χ is a kinetic term of ϕ. This theory is interesting because of the combination of the matter term, metric potential, and kinetic term, respectively. Recently, Malik and collaborators [21] investigated the behavior of anisotropic compact stars in generalized modified gravity and concluded that the behavior of compact star candidates is regular in$ f(R,\phi,\chi) $ gravity for the considered parameter. Malik [22] investigated the behavior of charged compact stars in the modified$ f(R,\phi) $ theory of gravity using the Krori and Barua technique and examined the physical properties of stellar structure. Malik et al. [23] investigated cylindrically symmetric solutions in a well known modified theory known as the$ f(R,\phi,\chi) $ theory of gravity and also examined two well-known LeviCivita and cosmic string solutions. Malik et al. [24] examined the behavior of anisotropic stellar structures in the background of$ f(R) $ modified gravity using three different stars, such as LMC X-4, Cen X-3, and EXO 1785-248. Cylindrically symmetric solutions in the background of the$ f(R,\phi) $ theory of gravity have been discussed by Malik [25], who also investigated null energy conditions for the existence of cylindrical wormholes. Several fascinating studies have been performed on the modified$ f(R) $ theories of gravity [26–29].The structure of this paper is as follows. Section II explains the formation of a traversable wormhole solution function using the KMc. Section III describes the geometry of the embedding process. In section IV, we investigate the basic formalism of the
$ f(R) $ modified theories of gravity and develop field equations. Three widely used$ f(R) $ gravity models and energy conditions are investigated in section V. In the final section, we provide a summary of the study. -
Embedding theorems have their origin in classical geometry. Both hyperbolic and elliptic non-Euclidean geometry have an intrinsic constant curvature and can be visualized as the surface of a pseudo or ordinary sphere, respectively, in Euclidean three-space. Embedding theorems have a long history in the general theory of relativity, largely aided by Campbell's theorem [30]. The resulting five-dimensional theory explains the origin of matter. More precisely, vacuum field equations in five dimensions yield the usual Einstein field equations with matter, known as induced-matter theory [31–32]. The main motivation for introducing a fifth dimension is unification; with this, our understanding of physics in four dimensions is greatly improved. Another important factor is that the extra dimension can be either spacelike or timelike. As a result, particle-wave duality can, in principle, be solved because five-dimensional dynamics has two modes depending on whether the extra dimension is spacelike or timelike [33]. Therefore, the five-dimensional relativity theory could ultimately lead to a unification of general relativity and quantum field theory.
The above discussion has shown that embedding theory based on Campbell's theorem is an effective mathematical model. Before applying this model to wormholes, we must introduce a refinement. Induced-matter theory is actually a non-compactified Kaluza-Klein theory of gravity. Matter is induced by a mechanism that locally embeds four-dimensional spacetime in a Ricci-flat five-dimensional manifold [34]. This process requires only one extra dimension. Going beyond a single extra dimension requires the concept of embedding class: recall that n-dimensional Riemannian space is said to be of embedding class m if m+n is the lowest dimension of flat space in which the given space can be embedded. It is well known that the interior Schwarzschild solution and Friedmann universe are of class one, whereas the exterior Schwarzschild solution is a Riemannian metric of class two. Because of the similarity, we can assume that wormhole spacetime is also of class two and can therefore be embedded in six-dimensional flat spacetime. However, it turns out that a line element of class two can be reduced to a line element of class one, thereby making the analysis tractable. This mathematical model has proved to be extremely useful in the study of compact stellar objects [35–40]. Moreover, a metric of class two can be reduced to a metric of class one and can therefore be embedded in five-dimensional flat spacetime,
$ {\rm d}S^2=-({\rm d}z^1)^2+({\rm d}z^2)^2+({\rm d}z^3)^2+({\rm d}z^4)^2+({\rm d}z^5)^2, $

(1) using the coordinate transformations
$z^1=\sqrt{A} {\rm e}^{a/2}{\rm Sinh}\dfrac{t}{A}$ ,$z^2=\sqrt{A}{\rm e}^{a/2}{\rm Cosh}\dfrac{t}{A}$ ,$z^3=r{\rm sin}\theta {\rm cos}\phi$ ,$z^4=r{\rm sin}\theta {\rm sin}\phi$ , and$z^5=r{\rm Cos}\theta$ . The resulting spacetime is usually referred to as anti-de Sitter space and is characterized by a negative cosmological constant. This is another important mathematical model that has been used in the study of many aspects of nuclear and condensed-matter physics, in particular the AdS/CFT correspondence (anti-de Sitter/comformal field theory correspondence) [41]. This theory has found its way into the study of entanglement, conjectured to be equivalent to the existence of another type of wormhole, the Einstein-Rosen bridge. We consider the spherically symmetric line element with Schwarzschild dimensions (coordinates) (t, r, θ, ϕ).$ {\rm d}{s}^{2} = -{\rm e}^{a(r)} {\rm d} t^{2}+{\rm e}^{b(r)}{\rm d}{r}^{2}+r^2{\rm d}{\theta}^{2}+r^2 {\rm sin}^2{\theta} {\rm d} {\phi}^{2}. $

(2) According to the above line element, the non vanishing covariant Riemannian curvature components are
$ \begin{aligned}[b]& R_{1212}=R_{2121},\quad R_{1221}=R_{2112},\quad R_{1313}=R_{3131},\\&R_{1331}=R_{3113},\quad R_{2323}=R_{3232},\quad R_{2332}=R_{3223},\\& R_{1414}=R_{4141},\quad R_{4114}=R_{1441},\quad R_{4242}=R_{2424},\\&R_{4224}=R_{2442},\quad R_{4343}=R_{3434},\quad R_{4334}=R_{3443}. \end{aligned} $

(3) Now, the Karmarkar relation is defined as
$ R_{1414}=\frac{R_{1212}R_{3434}+R_{1221}R_{4334}}{R_{2323}}. $

(4) The covariant Riemannian curvature defined in Eq. (3) satisfies the above relation. Inserting the values into Eq. (4), we get
$ \begin{aligned}[b]& \frac{1}{2}a''{\rm e}^a+\frac{1}{4}a'^2 {\rm e}^a-\frac{1}{4}a'b'{\rm e}^b\\=&\frac{\dfrac{1}{2}(rb')\left(\dfrac{1}{2}ra'{\rm e}^{a-b}\sin^{2}\theta\right)+\dfrac{1}{2}(rb')\left(\dfrac{1}{2}ra'{\rm e}^{a-b}\sin^{2}\theta\right)}{-{\rm e}^br^2\sin^{2}\theta+r^2\sin^{2}\theta}. \end{aligned} $

(5) In our current analysis,
$ a\equiv a(r) $ and$ b\equiv b(r) $ . After simplification, we obtain the following expression:$ a'b'-2a''-a'^2=\frac{2a'b'}{1-{\rm e}^b}, \quad {\rm where} \quad {\rm e}^b\neq1. $

As a result, the solution to the above differential equation is
$ {\rm e}^b=1+A{\rm e}^aa'^{2}, $

(6) where A is an integrating constant. Now, we consider the Morris-Thorne metric to construct the WSF
$ {\rm d}{s}^{2}=-{\rm e}^{a(r)}{\rm d}t^{2}+\frac{1}{1-\dfrac{\epsilon}{r}} {\rm d}{r}^{2}+r^2{\rm d}{\theta}^{2}+r^2 {\rm sin}^2{\theta}{\rm d}{\phi}^{2} . $

(7) Comparing Eq. (2) and (7), we get
$ {\rm e}^{b(r)}=\frac{1}{1-\dfrac{\epsilon}{r}}. $

(8) For this study, we consider a red shift function
$ a(r) $ [14, 42–51], expressed as$ a(r)=-\frac{2\zeta}{r} . $

(9) where ζ is an arbitrary constant. Using Eqs. (6), (8), and (9), we obtain the following WSF:
$ \epsilon(r)=r-\frac{r^5}{r^4+4A\zeta^2{\rm e}^{-\frac{2\zeta}{r}}} . $

(10) According to Morris-Throne, the shape function must satisfy the throat conditions, which are
1. At the throat:
$ \epsilon(r) $ = r at$ r=r_{0} $ .2. The condition
$ \dfrac{\varepsilon(r)-r\varepsilon'(r)}{\epsilon'(r)}>0 $ must be fulfilled at$ r=r_{0} $ .3.
$ \epsilon(r) $ must obey$ \epsilon'(r)<1 $ .4. For the maintenance of the asymptotical flatness of space time geometry,
$ \dfrac{\epsilon(r)}{r}\rightarrow0 $ at$ r\rightarrow \infty $ .Here,
$ r_{0} $ is the throat radius, and r is the radial coordinate, where$ r_{0} \leq r \leq \infty $ . When we evaluate Eq. (10) at the throat,$ \epsilon(r_{0})-r_{0}=0 $ , we obtain trivial solutions at$ r=r_{0} $ . We can add an arbitrary free parameter C to Eq. (10) to manage this issue.$ \epsilon(r)=r-\frac{r^5}{r^4+4A\zeta^2 {\rm e}^{-\frac{2\zeta}{r}}}+C. $

(11) Applying condition (1), that is,
$ \epsilon(r)-r $ = 0 at r=$ r_{0} $ , to the above equation, we get$ -\frac{r_{0}^5}{r_{0}^4+4A\zeta^2 {\rm e}^{-\frac{2\zeta}{r_{0}}}}+C=0. $

After simplifying, we obtain
$ A=\frac{r_{0}^4(r_{0}-C)}{4C\zeta^2 {\rm e}^{-\frac{2\zeta}{r_{0}}}} , $

(12) Now, substituting the value of A into Eq. (11), we get
$ \epsilon(r)=r-\frac{r^5}{r^4+r_{0}^4(r_{0}-C)}+C , $

(13) The graphical representation of
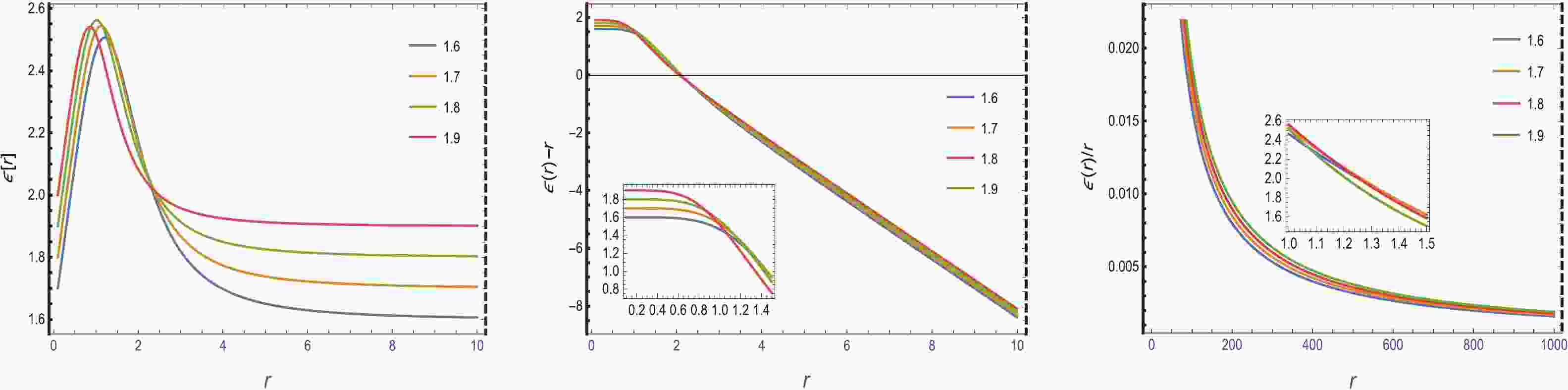
$ \epsilon(r) $ is positive and can be seen in Fig. 1. The graphical analysis of$ \epsilon(r)-r $ is initially positive and then becomes negative with the movement of the radial coordinate, as shown in the middle panel of Fig. 1. It is also noted from the right panel of Fig. 1 that$ \dfrac{\epsilon(r)}{r} $ approaches zero with the movementof the radial coordinate. The left panel of Fig. 2 shows that$ \dfrac{\varepsilon(r)-r\varepsilon'(r)}{\epsilon'(r)}>0 $ is satisfied. Thegraphicalrepresentation of$ \epsilon'(r) $ is less than one, which is also a basic condition for the WSF as shown in Fig. 2.
Figure 1. (color online) Wormhole shape function
$ \epsilon(r) $ was examined and shown in the$ 1st $ plot. The$ 2nd $ plot shows that$ \epsilon(r) - r $ = 0 at$ r = r_{0} $ , and the$ 3rd $ plot shows that$ \frac{\epsilon(r}{r}=0 $ at$ r\rightarrow \infty $ to represent the actual wormhole structure for$ r_{0} $ = 2 and C = 1.9. -
We utilize an embedding diagram to describe wormhole geometry and extract useful information. An embedding diagram is useful for understanding how gravity works in our universe. Spherically symmetric space-time allow us to set an equator slice, θ =
$ \dfrac{\pi}{2} $ and t =$ const $ , that maintains a lot of the geometric information. Using these preconceptions in Eq. (7), this then becomes$ {\rm d}{s}^{2}=\frac{r}{r-\epsilon}{\rm d}r^2+r^2{\rm d}\phi^2 . $

(14) The above embedding equation can also be written in three dimensional cylindrical coordinates
$ (r,h,\phi) $ $ \begin{aligned}[b] {\rm d}{s}^{2}={\rm d}r^2+{\rm d}h^2+r^2{\rm d}\phi^2, \;\; {\rm d}{s}^{2}={\rm d}r^2\left(1+\left(\frac{{\rm d}h}{{\rm d}r}\right)^2\right)+r^2{\rm d}\phi^2. \end{aligned} $

(15) Furthermore, by comparing Eq. (14) and Eq. (15), we get
$ \frac{r}{r-\epsilon}=\left(1+\left(\frac{{\rm d}h}{{\rm d}r}\right)^2\right). $

After simplifying,
$ \frac{{\rm d}h}{{\rm d}r}=\left(1-\frac{\epsilon}{r}\right)^\frac{-1}{2}. $

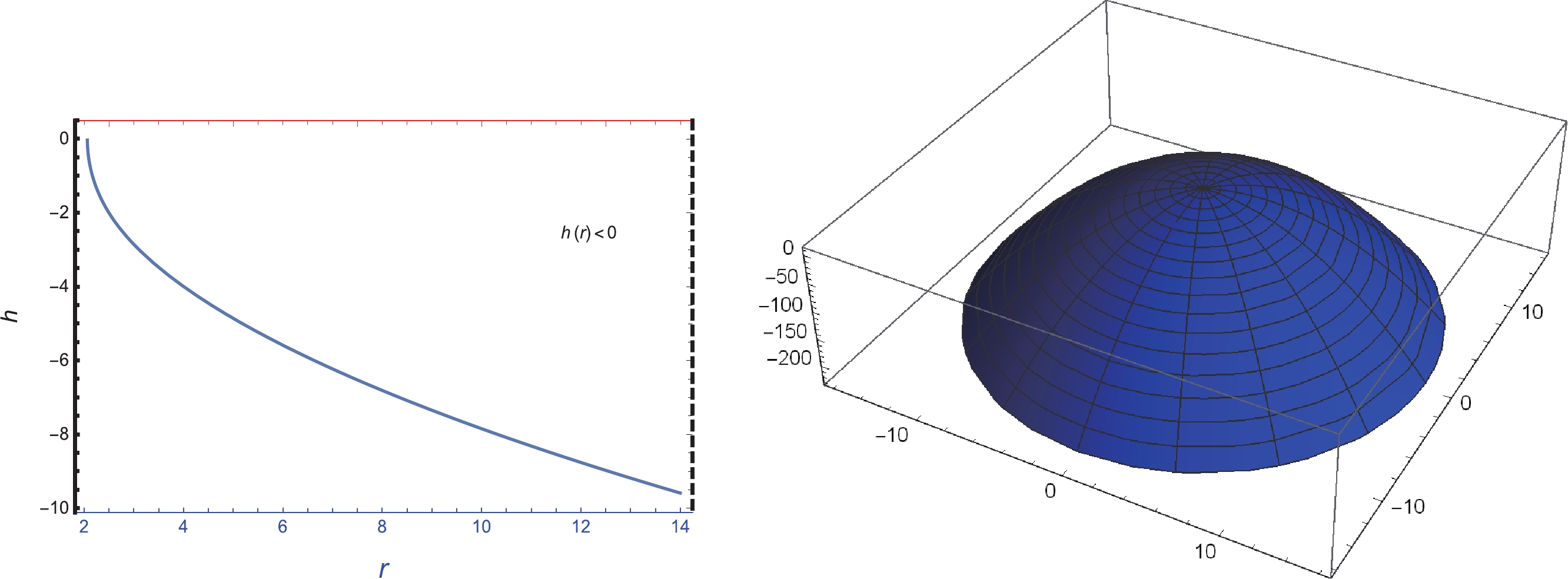
(16) An example of an embedding diagram for the bottom and top universes,
$ h(r) $ > 0 and$ h(r) < 0 $ , respectively, using a slice t =$ const $ and θ =$ \pi/2 $ with regard to the radial coordinate is shown in Fig. 3 and Fig. 4. Moreover, Eq. (16) indicates that the embedded surface at the throat is vertical because$\dfrac{{\rm d}h}{{\rm d}r}\rightarrow \infty$ . We also investigate how space is asymptotically flat away from the throat because$\dfrac{{\rm d}h}{{\rm d}r}$ approaches infinity when r approaches zero. The embedded diagram is shown in Fig. 3 and Fig. 4 for the upper and lower universes, respectively, in radial coordinates with$ 2\pi $ rotation about the h axis. -
The action of the
$ f(R, \phi, X) $ theory of gravity is defined as$ S=\int\sqrt{-g} \left(\frac{1}{16\pi G} [f(R, \phi, X)]+ L_{m} \right) {\rm d}^{4}x . $

(17) Here,
$ L_{m} $ denotes the Lagrangian field, and g represents the metric determinant. Moreover,$ f(R, \phi, X)\equiv f $ is an analytic function, which depends on R (Ricci scalar), ϕ (Scalar potential), and X (kinetic term), respectively. The field equation of the$ f(R, \phi, X) $ theory of gravity can be obtained by varying the metric tensor$ g_{\mu\nu} $ as below.$\begin{aligned}[b] f_{R}G_{\mu\nu}-&\frac{1}{2}(f-Rf_{R})g_{\nu}-\nabla_{\mu}\nabla_{\nu}f_{R}+g_{\mu\nu}\nabla_{\alpha}\nabla^{\alpha}f(R)\\-&\frac{\epsilon}{2}f_{X}(\nabla_{\mu}\phi)(\nabla_{\nu}\phi)=k^2T_{\mu\nu}, \end{aligned} $

(18) where
$ f_{R} = \dfrac{\partial f }{\partial R} $ ,$ f_{X} = \dfrac{\partial f }{\partial X} $ , and$ \nabla_{\mu} $ represents the covariant derivative. For our study, the stress energy momentum tensor is defined as$ T_{\mu\nu}=(\rho+p_{t})u_{\mu}u_{\nu}-(p_{r}-p_{t})v_{\mu}v_{\nu} , $

(19) where
$ v_{\mu} $ and$ v_{\nu} $ are four vectors defined as$ u_{\mu} $ =${\rm e}^\frac{a}{2} \delta_{\mu}^{0}$ and$ v_{\nu} $ =${\rm e}^\frac{b}{2} \delta_{\mu}^{0}$ . Moreover, ρ,$ p_r $ , and$ p_t $ are the energy density, radial pressure, and tangential pressure, respectively. Substituting these into Eq. (18), we get$ \begin{aligned}[b]& -{\rm e}^{-b}f''_{R}-2{\rm e}^{-b}\left(\frac{b'}{4} +\frac{1}{r}\right)f'_{R} \\&+\frac{{\rm e}^{-b}}{4}\Bigg(2a''+a'^{2}-a'b'+\frac{4a'}{r}\Bigg)f_{R}-\frac{1}{2}f=k^{2}\rho . \end{aligned} $

(20) $ \begin{aligned}[b]& \frac{1}{2{\rm e}^{b}}\left(a'+2b'+\frac{4}{r}\right)f'_{R}-\frac{1}{2{\rm e}^{b}}\Bigg(a''+\frac{a'^{2}}{2}\\&-\frac{a'b'}{2}-\frac{2b'}{2}\Bigg)f_{R}-\frac{1}{2}f-{\rm e}^{-b}\frac{\epsilon}{2}f_{X}'\phi^{2}=k^{2}p_{r}.\end{aligned} $

(21) $ \begin{aligned}[b]& {\rm e}^{-b}f''_{R}+\frac{1}{2{\rm e}^{b}}\left(a'+b'+\frac{2}{r}\right)f'_{R}-\frac{1}{2r{\rm e}^{b}}\Bigg(a'-b'\\&-\frac{2{\rm e}^{b}}{r}+\frac{2}{r}\Bigg)f_{R}+\frac{1}{2}f=k^{2}p_{t}. \end{aligned}$

(22) where prime is used for the derivative with respect to the radial coordinates r. For our convenience, we use
$ k^{2}=8\pi G=1 $ . The field equations can be simplified by taking the redshift factor to be a fixed value while discussing wormhole solutions in advanced theories. It is worth mentioning that Eqs. (20)–(22) are significantly more complicated, and it is very difficult to find analytical solutions. Now, we investigate generic models of$ f(R) $ gravity theories to find wormhole solutions. -
In this section, we focus on energy conditions and attempt to create methods of detecting the presence of wormhole geometries. Energy conditions are very important and helpful for explaining traversable wormhole geometry because the violation of energy conditions may predict the presence of wormholes. In this part, we consider several specific models of the
$ f(R) $ theories of gravity and observe the behavior of energy conditions using Eqs. (20)–(22). For this, we conduct a graphical analysis of energy density, pressure terms, and energy conditions for the considered$ f(R) $ gravity models.Energy conditions:
Energy conditions are very important for investigating the geometry of wormhole solutions. There are four main energy conditions: the null energy condition (NEC), strong energy condition (SEC), weak energy condition (WEC), and dominant energy condition (DEC).
1- Null Energy Condition (NEC):
According to the NEC, the sum of energy density and radial pressure and the sum of energy density and tangential pressure must be positive. In terms of mathematics, this can be depicted as
$ \rho+p_{r}\geq0 $ and$ \rho+p_{t}\geq0 $ . The NEC may be found by exploiting field equations using the Raychaudhuri equations (Raychaudhuri 1957). Furthermore, the NEC is very important because the violation of the NEC indicates the existence of exotic matter and wormholes.2- Strong Energy Condition (SEC):
The SEC states that the sum of energy density and radial pressure, the sum of energy density and tangential pressure, and the sum of energy density, radial pressure and tangential pressure should be positive. In terms of mathematics, this can be represented as
$ \rho+p_{r}\geq0 $ ,$ \rho+p_{t}\geq0 $ , and$ \rho+p_{r}+2p_{t}\geq0 $ . The violation of the SEC may predict the presence of exotic matter and will indicate the existence of wormhole geometry owing to the exotic matter.3- Weak Energy Condition (WEC):
According to the WEC, the sum of energy density and radial pressure, the sum of energy density and tangential pressure, and independent energy density must be positive. In terms of mathematics, this can be represented as
$ \rho\geq0 $ ,$ \rho+p_{r}\geq0 $ , and$ \rho+p_{t}\geq0 $ .4- Dominant Energy Condition (DEC):
The DEC is a combination of the difference of energy density and radial pressure and the difference of energy density and tangential pressure, which must be positive. In terms of mathematics, this can be represented as
$ \rho-|p_{r}|>0 $ and$ \rho-|p_{t}|>0 $ .For the above energy conditions, we investigate how energy circumstances, especially the NEC and WEC, behave to learn more about wormhole formation. The failure of the NEC is a prerequisite for the occurrence of wormholes. The violation or non-violation of energy conditions in the framework of wormhole solutions has been studied in literature employing the framework of different gravity theories [52–54]. Furthermore, we discuss wormhole solutions in the
$ f(R) $ theories of gravity in upcoming sections. -
In this case, we assume a special model of the
$ f(R) $ theory of gravity.$ f(R, \phi, X)=f_{0}*R^{\frac{3}{2}}. $

(23) where
$ f_{0} $ is a free parameter, and R is a Ricci scalar. This method is used because it has already been investigated in several research papers in which effective solutions were identified. Using the above model (23) in Eqs. (20)–(22), we get$ \begin{aligned}[b] k^{2}\rho=&-\frac{1}{2}f_{0}R^{\frac{3}{2}} +\frac{3}{8}{\rm e}^{-b} f_{0} \sqrt{R}\Bigg(\frac{4a'}{r} \\& +a'^{2}-a'b'+2a''\Bigg), \end{aligned} $

(24) $ \begin{aligned}[b] k^{2}p_{r}=&-\frac{1}{2}f_{0}R^{\frac{3}{2}}-\frac{3}{4}{\rm e}^{-b} f_{0} \sqrt{R}\Bigg(\frac{1}{2}a'^{2}\\&-\frac{2b'}{r}-\frac{1}{2}a'b'+a''\Bigg),\end{aligned} $

(25) $ k^{2}p_{t}=\frac{1}{2}f_{0}R^{\frac{3}{2}}-\frac{3}{4r}{\rm e}^{-b} f_{0} \sqrt{R}\left(\frac{2}{r}-\frac{2e^{b}}{r}+a'-b'\right). $

(26) 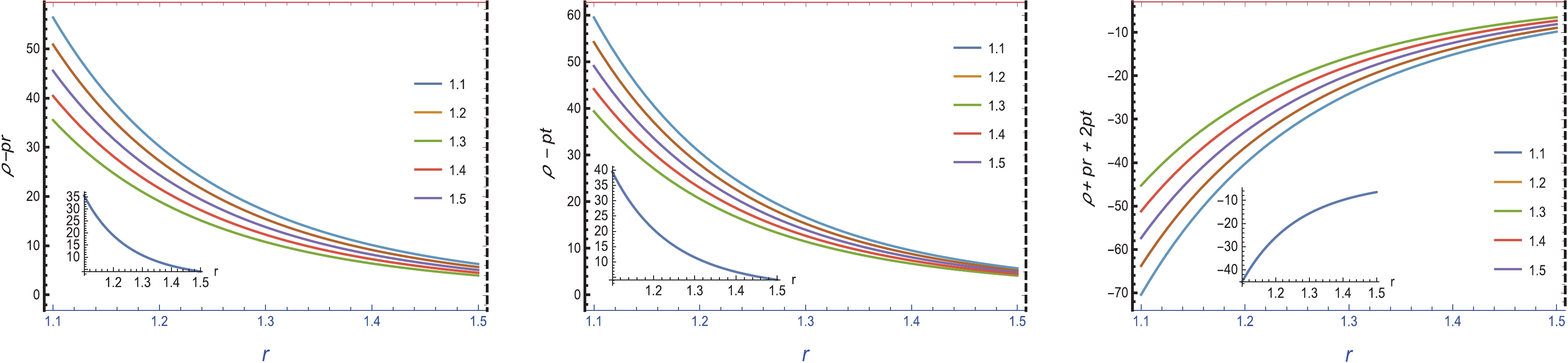
Figure 6. (color online) Graphs of the DEC (
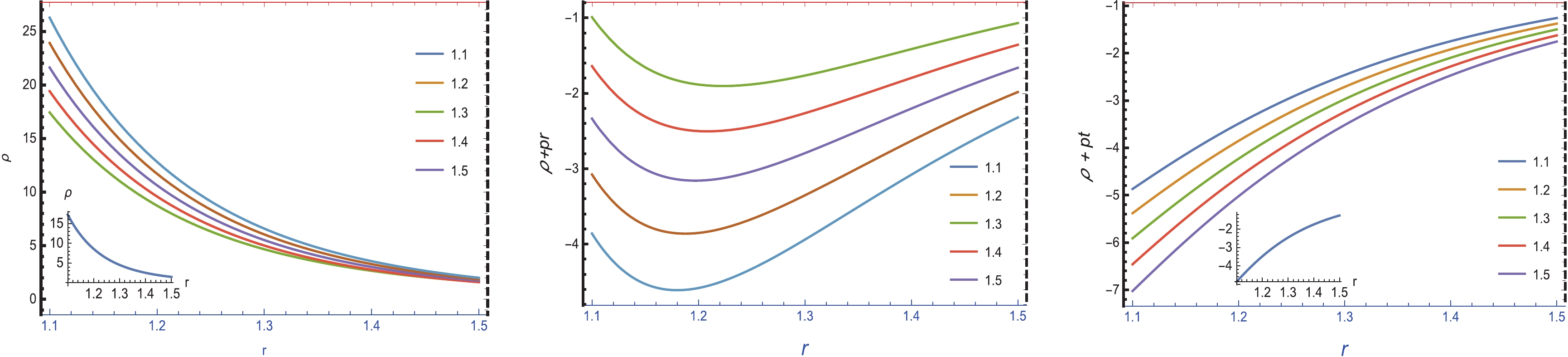
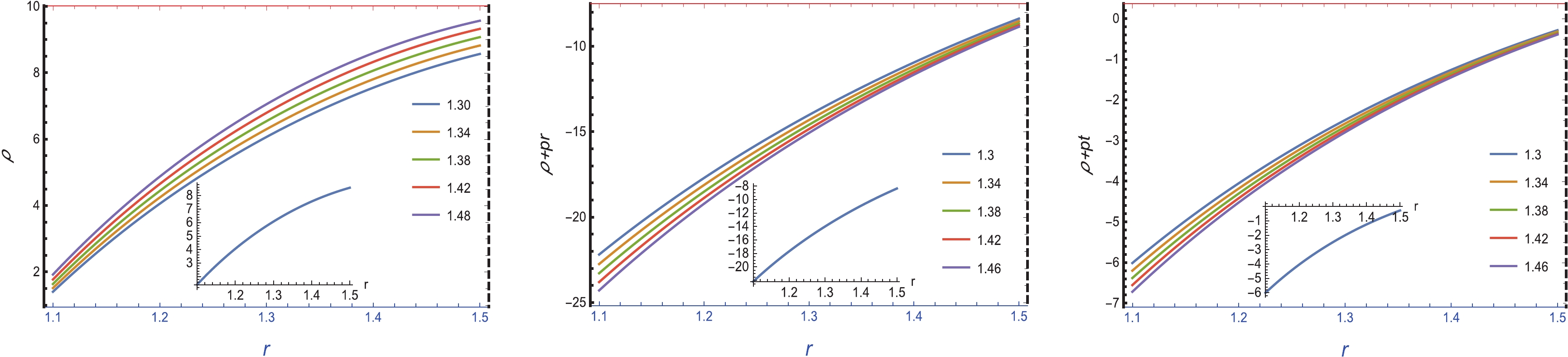
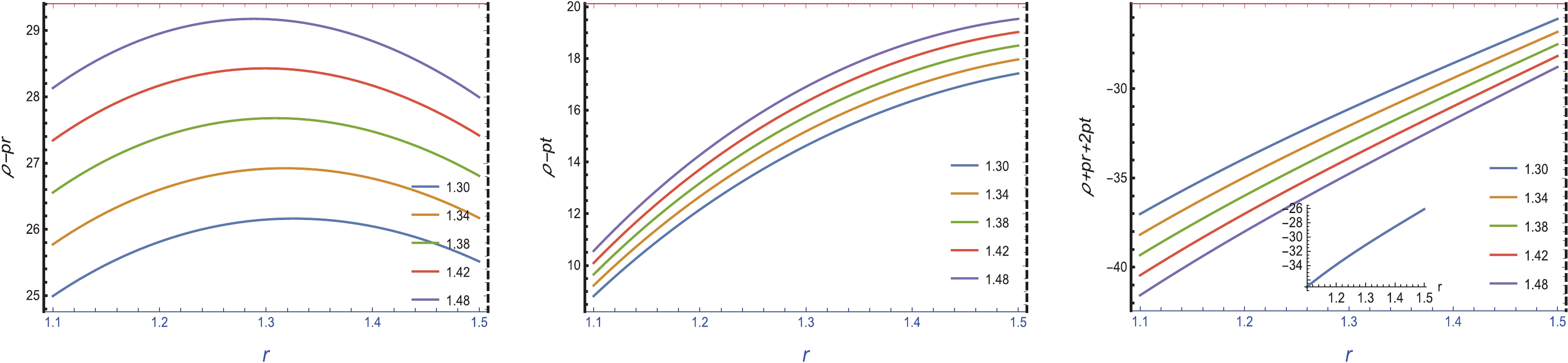
$ (\rho-p_{r})>0 $ ,$ (\rho-p_{t})>0 ) $ and SEC$ \rho+p_{r}+2p_{t}>0 $ for C = 1.1 (blue), C = 1.2 (yellow), C = 1.3 (green), C = 1.4 (orange), and C = 1.5 (pink).The graphical analysis of energy density ρ is positive and has a decreasing nature, as shown in the left part of Fig. 5. The graphical representations of
$ \rho+p_{r} $ and$ \rho+p_{t} $ are negative, which indicates that the NEC is violated, as shown in the middle and right parts of Fig. 5. We also note that the graphical representation of energy density is positive, but$ \rho+p_{r} $ and$ \rho+p_{t} $ are negative. Therefore, we can conclude that the WEC is violated. The graphical analysis of$ \rho-p_{r} $ is positive and has a decreasing nature when we move toward the boundary, as shown in the left part of Fig. 6. Similarly, the nature of$ \rho-p_{t} $ is similar to$ \rho-p_{r} $ , as shown in the middle panel of Fig. 6. Hence, it can be concluded that the DEC is satisfied in this case. The representation of$ \rho+p_{r}+2p_{t} $ exhibits negative trends, as shown in the right panel of Fig. 6. Owing to the violation of this component, we can conclude that the SEC is also violated. The significant consequences of energy condition violation, especially the violation of the NEC, may indicate the presence of exotic matter, which may justify wormhole existence in the$ f(R) $ gravity model. -
In this case, we consider the following
$ f(R,\phi) $ gravity model for discussions on wormhole geometry:$ f(R, \phi, X)=R*[\phi(r)]^{m}, $

(27) where ϕ is a scalar potential function that depends on the radial component r. If we select some power of the Ricci scalar, we are unable to obtain the required results. For our current analysis, we further consider
$ \phi(r)\ = r^{\beta} $ , where β is any arbitrary constant. Using the above model (27) in Eqs. (20)–(22), we get the following field equations:$ \begin{aligned}[b] k^{2}\rho=&-\frac{1}{2}(r^{\beta})^{m}R-{\rm e}^{-b}(mr^{-2+\beta}(r^{\beta})^{-1+m}(-1+\beta)\beta\\&+(-1+m)mr^{-2+2\beta}(r^{\beta})^{-2+m}\beta^{2})\\& -2{\rm e}^{-b}mr^{-1+\beta}(r^{\beta})^{-1+m}\beta\left(\frac{1}{r}+\frac{b'}{4}\right)\\&+\frac{1}{4}{\rm e}^{-b}(r^{\beta})^{m}\left(\frac{4a'}{r} +a'^{2}-a'b'+2a''\right), \end{aligned} $

(28) $\begin{aligned}[b] k^{2}p_{r}=&-\frac{1}{2}(r^{\beta})^{m}R+\frac{1}{2}{\rm e}^{-b}mr^{-1+\beta}(r^{\beta})^{-1+m}\\&\times\beta\left(\frac{4}{r}+a'+2b'\right)-\frac{1}{2}{\rm e}^{-b}(r^{\beta})^{m}\\&\times\left(\frac{1}{2}a'^{2}-\frac{2b'}{r}-\frac{1}{2}a'b'+a''\right),\end{aligned} $

(29) $ k^{2}p_{t}=\frac{1}{2}f_{0}R^{\frac{3}{2}}-\frac{3}{4r}{\rm e}^{-b}f_{0}\sqrt{R}\left(\frac{2}{r}-\frac{2}{r}{\rm e}^{b}+a'-b'\right). $

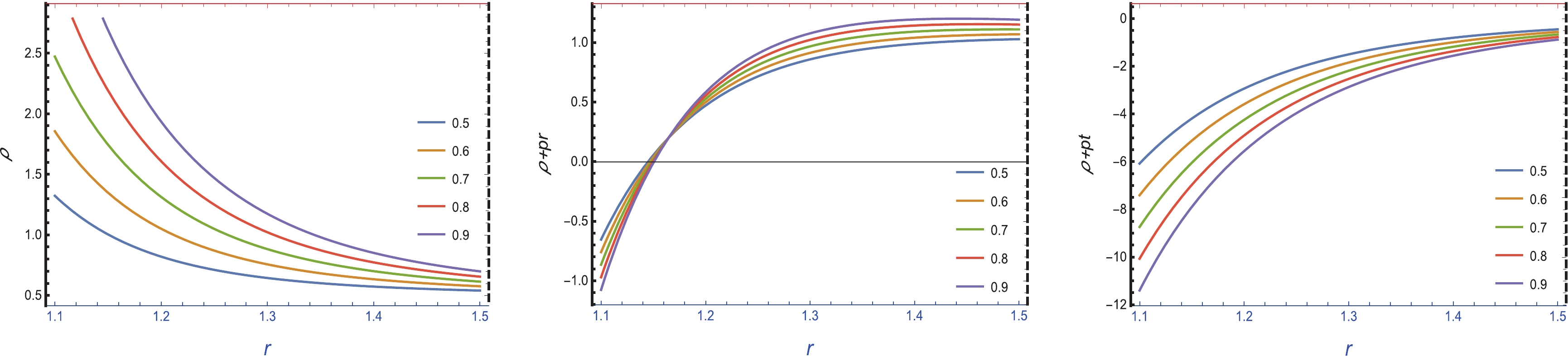
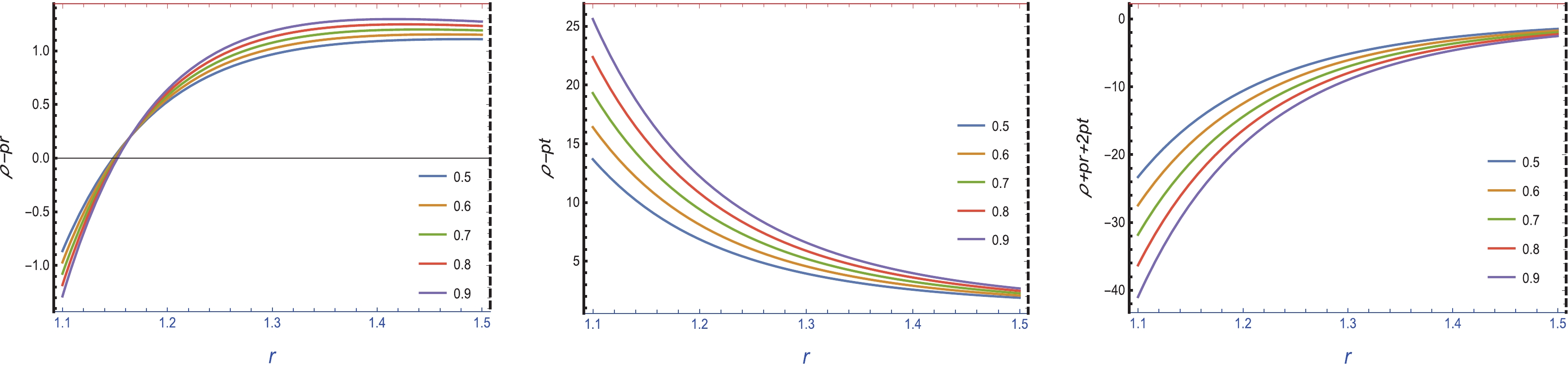
(30) By analyzing the above equations, we may examine the physical properties of wormhole geometry. The graphical analysis of energy density ρ is positive and increases when we move away from the center, as shown in Fig. 7. We know that the validation of the NEC is connected with
$ (\rho+p_{r})>0 $ and$ (\rho+p_{t})>0 $ . The middle and right panels of Fig. 7 show that the two expressions$ \rho+p_{r} $ and$ \rho+p_{t} $ are negative, which indicates that the NEC is violated. It is noted that the WEC is also violated because the WEC is connected with the NEC. Furthermore, the graphical representations of$ \rho-p_{r} $ and$ \rho-p_{t} $ are both positive, which indicates that the DEC is satisfied, as shown in the left and middle parts of Fig. 8. The components$ \rho+p_{r} $ ,$ \rho+p_{t} $ , and$ \rho+p_{r}+2p_{t} $ exhibit negative trends, which indicates that the SEC is not satisfied, as shown in right panel of Fig. 8. It is noted that the negative nature of these pressure components, especially the NEC, WEC, and SEC, indicates the presence of exotic matter, which may justify wormhole existence in the$ f(R, \phi) $ gravity model. -
In this case, the following
$ f(R, \phi, X) $ gravity model is considered for discussions on wormhole geometry:$ f(R,\phi,X)=\phi(r)+R+h(\chi), $

(31) where
$ \phi(r)=r^{\beta}, $

(32) $ h(\chi)=k_{1}\chi+k_{2}, $

(33) $ \chi=-\frac{\xi}{2}\phi^{;\mu}\phi_{;\mu}, $

(34) where
$ k_{1} $ ,$ k_{2} $ , and ξ are arbitrary constants. Now, substituting this model into Eqs. (20)–(22), we get$ \begin{aligned}[b] K^{2}\rho=&-{\rm e}^{-b}r^{-2+\beta}(-1+\beta)\beta+\frac{1}{2}\Bigg(-k_{2}-r^{\beta}R\\&+\frac{1}{2}{\rm e}^{-b}k_{1}r^{-2+2\beta}\beta^{2}\xi\Bigg)-2{\rm e}^{-b}r^{-1+\beta}\beta\left(\frac{1}{r}+\frac{b'}{4}\right)\\&+\frac{1}{4}{\rm e}^{-b}r^{\beta}\left(\frac{4a'}{r}+a'^{2}-a'b+2a''\right), \end{aligned} $

(35) $ \begin{aligned}[b] k^{2}p_{r}=&-\frac{1}{2}{\rm e}^{-b}k_{1}r^{-2+2\beta}\beta^{2}\xi+\frac{1}{2}\Bigg(-k_{2}-r^{\beta}R\\&+\frac{1}{2}{\rm e}^{-b}k_{1}r^{-2+2\beta}\beta^{2}\xi\Bigg)+ \frac{1}{2}{\rm e}^{-b}r^{-1+\beta}\beta\left(\frac{4}{r}+a'+2b'\right)\\&-\frac{1}{2}{\rm e}^{-b}r^{\beta}\left(\frac{1}{2}a'^{2}-\frac{2b'}{r}-\frac{1}{2}a'b'+a''\right), \end{aligned} $

(36) $ \begin{aligned}[b] k^{2}p_{t}=&{\rm e}^{-b}r^{-2+\beta}(-1+\beta)\beta+\frac{1}{2}\Bigg(k_{2}+r^{\beta}R\\&-\frac{1}{2}{\rm e}^{-b}k_{1}r^{-2+2\beta}\beta^{2}\xi\Bigg)- \frac{1}{2}{\rm e}^{-b}r^{-1+\beta}\Bigg(\frac{2}{r}-\frac{2{\rm e}^{b}}{r}\\&+a'-b'\Bigg)+\frac{1}{2}{\rm e}^{-b}r^{-1+\beta}\beta\left(\frac{2}{r}+a'+b'\right).\end{aligned} $

(37) Equations (35)–(37) are very important when discussing wormhole solutions in the modified
$ f(R, \phi, X) $ theory of gravity. The graphical representation of energy density ρ is increasing and has decreasing trends, as shown in Fig. 9. The graphical representation of$ \rho+p_{r} $ is negative near the origin and becomes positive when we move toward the boundary, as shown in the middle part of Fig. 9. The right panel of Fig. 9 shows that$ \rho+p_{r} $ exhibits negative trends, which is a basic reason for the violation of the NEC. We note that the WEC is also violated because validation of the WEC is linked to the validation of the NEC. The graphical analysis of$ \rho-p_{t} $ has a positive and decreasing nature, as shown in the middle panel of Fig. 10. However,$ \rho-p_{r} $ has an interesting nature; it initially exhibits negative trends before becoming positive with movement along the radial coordinate, which is shown on the left of Fig. 10. Therefore, we can conclude that the DEC is violated near the origin but satisfied when we move away from the origin. Furthermore, the SEC is also violated owing to the negative behavior of$ \rho+p_{r}+2p_{t} $ , as shown in Fig. 10. It is noted that the negative nature of these pressure components, especially the NEC, WEC, and SEC, indicates the presence of exotic matter, which may justify wormhole existence in the$ f(R, \phi, X) $ gravity model. -
The goal of this paper is to examine wormhole solutions using the framework of the
$ f(R) $ theories of gravity. The concept of wormhole geometry in cosmology attracts a large number of research specialists. As a result, several approaches to investigating wormhole geometry in various orientations are employed. In our study, we examine useful and intriguing results about the presence of genuine wormhole geometries using standard matter allocation in$ f(R,\phi, X) $ gravity models. We use three specific models of the$ f(R) $ theories of gravity and examine the energy conditions for each case. Furthermore, we observe NEC violation in all considered cases because the violation of the NEC is required for the realization of wormhole solutions.The graphical analysis of energy density ρ is positive and has a decreasing nature. The graphical representations of
$ \rho+p_{r} $ and$ \rho+p_{t} $ are negative, which indicates that the NEC is violated. It is also noted that the graphical representation of energy density is positive, but$ \rho+p_{r} $ and$ \rho+p_{t} $ are negative. Therefore, we can conclude that the WEC is violated. The graphical analyses of$ \rho-p_{r} $ and$ \rho-p_{t} $ are positive and have a decreasing nature when we move toward the boundary. Hence, it can be concluded that the DEC is satisfied in this case. The representation of$ \rho+p_{r}+2p_{t} $ exhibits negative trends, which indicates that the SEC is also violated. The significant consequences of energy condition violation, especially violation of the NEC, may indicate the presence of exotic matter, which may justify wormhole existence in the$ f(R) $ gravity model.The graphical analysis of energy density ρ is positive and increases when we move away from the center. We know that the validation of the NEC is connected with
$ (\rho+p_{r})>0 $ and$ (\rho+p_{t})>0 $ ; the expressions$ \rho+p_{r} $ and$ \rho+p_{t} $ are negative, which means that the NEC is violated. We note that the WEC is also violated because the WEC is connected with the NEC. Furthermore, the graphical representations of$ \rho-p_{r} $ and$ \rho-p_{t} $ are both positive, which indicates that the DEC is satisfied. Moreover, the components$ \rho+p_{r} $ ,$ \rho+p_{t} $ , and$ \rho+p_{r}+2p_{t} $ exhibit negative trends, which indicates that the SEC is not satisfied. It is noted that the negative nature of these pressure components, especially the NEC, WEC, and SEC, indicates the presence of exotic matter, which may justify wormhole existence in the$ f(R, \phi) $ gravity model.The graphical representation of energy density ρ is increasing and exhibits decreasing trends. The graphical representation of
$ \rho+p_{r} $ is negative near the origin and becomes positive when we move toward the boundary; however,$ \rho+p_{r} $ has negative trends, which is a basic reason behind the violation of the NEC. Furthermore, the WEC is also violated because validation of the WEC is linked to the validation of the NEC. The graphical analysis of$ \rho-p_{t} $ has a positive and decreasing nature; however,$ \rho-p_{r} $ is initially negative and becomes positive with movement along the radial coordinate. Therefore, we can conclude that the DEC is violated near the origin but satisfied when we move away from the origin. Furthermore, the SEC is also violated owing to the negative behavior of$ \rho+p_{r}+2p_{t} $ . We note that the negative nature of these pressure components, especially the NEC, WEC, and SEC, indicates the presence of exotic matter, which may justify wormhole existence in the$ f(R, \phi, X) $ gravity model. -
The authors would like to express their gratitude to the Deanship of Scientific Research at King Khalid University, Saudi Arabia for providing a funding research group under the research grant R.G.P2/130/43. Also, the authors express their gratitude to Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2022R27), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.
Traversable wormhole solutions in the f (R) theories of gravity under the Karmarkar condition
- Received Date: 2022-04-12
- Available Online: 2022-09-15
Abstract: This paper examines traversable wormhole models in the





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF
















 DownLoad:
DownLoad: