-
Energetic partons created in the early stage of heavy-ion collisions (HIC) may suffer energy loss owing to their interaction with quark-gluon plasma (QGP), a novel state of matter with deconfined quarks and gluons under an extremely high temperature and energy density. This phenomenon is referred to as jet quenching [1–3], which can provide powerful tools for studying the creation and properties of the QCD medium. In the last decade, investigations on jet quenching have been extended from leading hadron production suppression [4–16] to medium modifications of a wealth of reconstructed jet observables, such as inclusive jet production, di-jet asymmetry, correlations of gauge bosons and jets, and heavy flavor jets [17–55]. A fully reconstructed jet is a collimated spray of hadrons created in
$ e^+e^- $ collisions, p+p reactions, and nucleus-nucleus collisions with a large momentum transfer, and the existence of the QCD medium should naturally modify the yields and internal structures of full jets. Thus, the medium modifications of jet observables could be used in the tomography of QGP formed in HIC.The nuclear modifications of jet substructures have received increasing attention in the heavy-ion community. One interesting jet substructure is jet
$ p_{T} $ dispersion ($ p_{T}D $ ), which characterizes the fragmentation of a jet [56–60]. The nuclear modification of jet$ p_{T}D $ distributions may improve our understanding of jet-medium interactions and offer new insight into how jet substructures are resolved by the QCD medium. Recently, the ALICE Collaboration measured the$ p_{T}D $ distributions of small-radius ($ R=0.2 $ ) jets in heavy-ion collisions [57]. This facilitates further studies on$ p_{T}D $ in HIC distributions because the theoretical calculations may be confronted with data directly to infer crucial information on jet propagation in the QCD medium.In this paper, we present our study on the normalized
$ p_{T}D $ distributions of inclusive jets with jet radius$ R=0.2 $ both in p+p and central Pb+Pb collisions at$ \sqrt{s_{NN}}=2.76 $ TeV. We employ POWHEG+PYTHIA [61–63], a Monte Carlo model that matches next-to-leading order (NLO) matrix elements with parton showering (PS), with the hadronization process to obtain the solid baseline results of jet$ p_{T}D $ in p+p collisions, which are then served as inputs to simulate parton energy loss within the higher-twist approach [64–67] to compute the$ p_{T}D $ distribution in HIC. Our model calculations of the$ p_{T}D $ distribution of inclusive jets could provide satisfactory descriptions of ALICE data in both p+p and Pb+Pb collisions, where we observe a shift in the$ p_{T}D $ distribution toward higher values in Pb+Pb collisions relative to that in p+p collisions. We further make a comprehensive understanding of the distinct feature between quark and gluon initiated jets and the nuclear modification ratio$ p_{T}D $ distribution. We find that$ p_{T}D $ can be analytically expressed as the standard deviation and multiplicity of jet constituents. After jet quenching, more jet constituents exist further from the mean value of$ p_{T} $ .The remainder of this paper is organized as follows. In Sec. II, we introduce the framework used to calculate the normalized
$ p_{T}D $ distributions in both p+p and central Pb+Pb collisions. Our numerical results and detailed discussions on the medium modifications of the$ p_{T}D $ distributions of groomed and ungroomed jets are presented in Section II. In Sec. IV, we provide a summary. -
We study a jet substructure observable,
$ p_{T}D $ , which characterizes the second moment of the constituent$ p_{T} $ distribution inside a jet [56, 57]. This is defined as$ p_{T}D=\frac{\sqrt{\displaystyle\sum\nolimits_{i}p^{2}_{T,i}}}{p_{T,{\rm jet}}}, $

(1) where
$ p_{T,i} $ represents the transverse momentum of the ith jet ingredient inside the jet with transverse momentum$ p_{T,{\rm jet}} $ .$ p_{T}D $ is connected to how hard or soft the jet fragmentation is and whether the$ p_{T,i} $ distribution is uniform. For example, in the extreme case of very few constituents carrying the largest share of the jet momentum,$ p_{T}D $ will be close to unity, whereas in the case of jets containing a large number of constituents with soft momentum,$ p_{T}D $ may approach zero. It is noted that jet dispersion is one of a class of jet substructure observables known as the generalized jet angularities [68, 69], which are defined as$ \lambda^{\kappa}_{\beta}=\Sigma_{i}z^{\kappa}_{i}\theta^{\beta}_{i} $ , where$ z_{i}=p_{T,i}/p_{T,{\rm jet}} $ is the momentum fraction of jet constituents,$ \theta_{i}=\Delta{R_{i}}/R $ ,$ \Delta{R_{i}} $ is the opening angle from the constituent to jet axis, and κ and β are free parameters. We note that$ (p_{T}D)^2 $ is equal to$ \lambda^{\kappa}_{\beta}(\kappa=2, \beta=0) $ .In this study, we use a Monte Carlo model, POWHEG+PYTHIA, which matches NLO matrix elements with PS [61–63] to generate jet production in p+p collisions. In our simulation, the POWHEG BOX code is utilized [62, 63], which provides a computer framework for performing NLO calculations within parton shower Monte Carlo programs in accordance with the POWHEG method [70]. Previous studies have shown that the POWHEG BOX Monte Carlo program matched with PS could give a good description of the production and correlations of a variety of processes in p+p collisions, such as di-jets, gauge boson tagged jets, and heavy flavour jets [71]. We generate the NLO matrix elements for QCD di-jet events using POWHEG BOX and match them with PYTHIA6 using Perugia 2011 tunes [72] to perform PS and hadronization [73]. Subsequently, the Fastjet package [74] is employed to reconstruct final state hadrons into full jets.
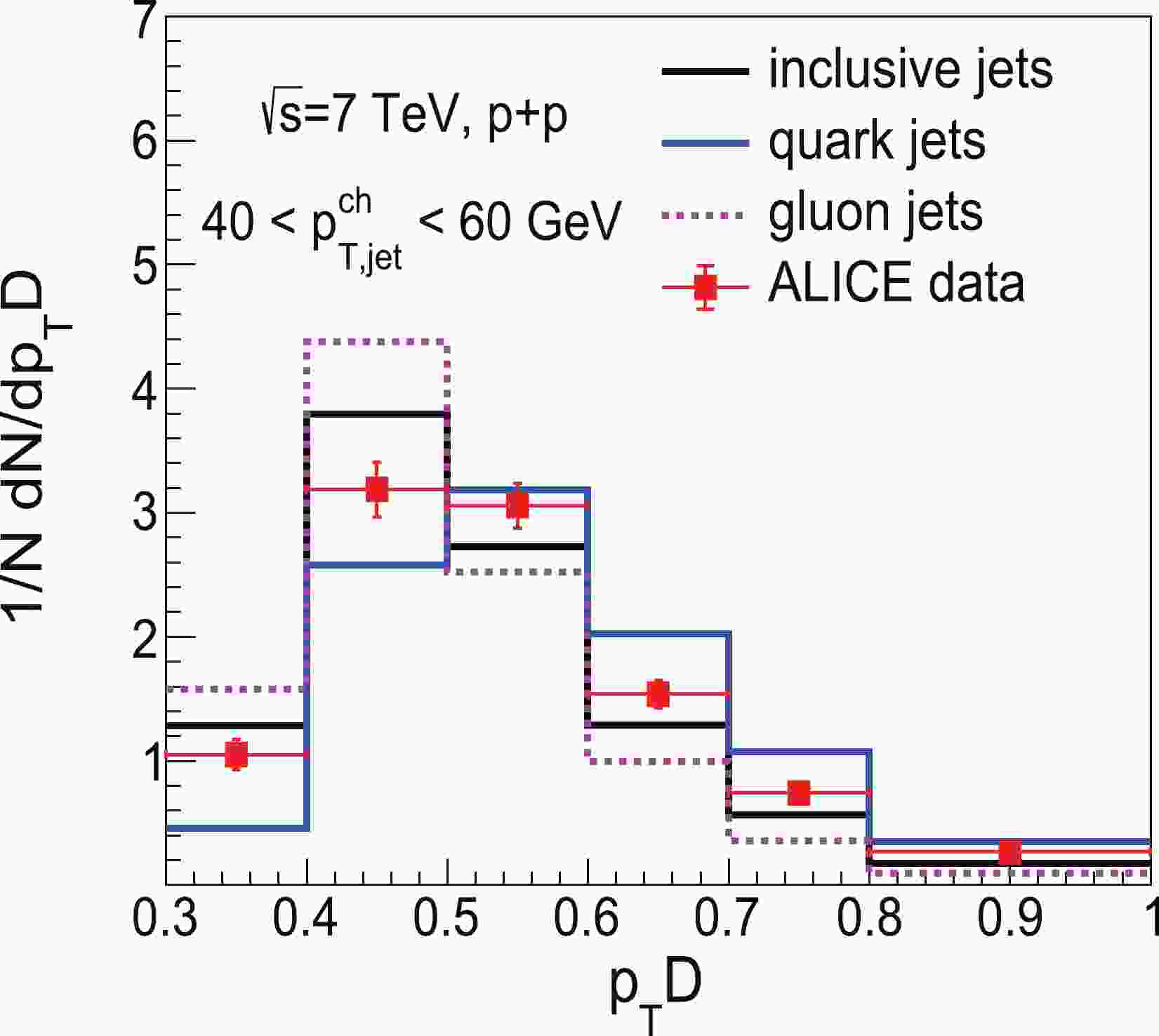
To compare with the available experimental data, we select events according to the same kinematic cuts as adopted in the experimental measurements. In ALICE Collaboration data, jets are reconstructed using an anti-
$ k_{T} $ algorithm with radius parameter$ R=0.2 $ from charged hadrons, which are required to have$ p_{T}>0.15 $ GeV. These reconstructed jets are accepted in the transverse momentum range$ 40 <p_{T, \rm jet}<60 $ GeV and rapidity range$ \left|\eta_{\rm jet}\right|<0.7 $ . Our numerical results for the normalized distributions of$ p_{T}D $ in p+p collisions at$ \sqrt{s}=7 $ TeV and their comparison with ALICE data are shown in Fig. 1. The POWHEG+PYTHIA calculations exhibit good agreement with experimental measurements in p+p collisions in the overall$ p_{T}D $ region, which is used as the input for the subsequent study of nuclear modification in HIC. The$ p_{T}D $ distributions of quark- and gluon-initiated jets are also plotted in Fig. 1. We find that, at the same jet$ p_T $ , the peak of the$ p_{T}D $ distribution of gluon jets is located in a smaller region relative to that of quark jets. This implies that compared with quark jets, gluon jets favor harder radiation, on average. To gain a comprehensive understanding of the distinct feature between quark and gluon jets, we derive$ p_{T}D $ with the standard deviation (labeled as σ) and multiplicity of jet constituents (labeled as n) below.
Figure 1. (color online) Normalized
$ p_{T}D $ distribution of inclusive jets in p+p collisions at$ \sqrt{s}=7 $ TeV from POWHEG+PYTHIA calculations compared with ALICE data [57].The standard deviation describes the average degree of a dataset. It tells us, on average, how far each value lies from the mean value. A high standard deviation signifies that values are generally far from the mean value, whereas a low standard deviation means that values are clustered near the mean value. As a result, in our study, the standard deviation of the transverse momentum of jet constituents can be written as
$ \sigma=\frac{\sqrt{\displaystyle\sum\nolimits_{i}(p_{T,i}-\langle p_{T,i} \rangle)^2}}{p_{T,{\rm jet}}}. $

(2) Then,
$ \sigma^2 $ can be expressed as$ \begin{aligned}[b] \sigma^2 =& \frac{\displaystyle\sum\nolimits_{i}(p_{T,i}-\langle p_{T,i} \rangle)^2}{(n \cdot \langle p_{T,i} \rangle)^2} = \frac{\displaystyle\sum\nolimits_{i}(p^{2}_{T,i}-2p_{T,i}\langle p_{T,i} \rangle + \langle p_{T,i} \rangle^2)}{(n \cdot \langle p_{T,i} \rangle)^2} \\ =& (p_{T}D)^2-1/n. \end{aligned} $

(3) Conversely, we have
$ (p_{T}D)^2=\sigma^2+1/n \, . $

Fig. 2 shows the normalized
$ \sigma^2 $ distributions (top) of quark and gluon jets in p+p collisions at$ \sqrt{s}=7 $ TeV as well as their gluon/quark ratios (bottom). We observe more gluon jets distributed in the lower$ p_{T}D $ region compared to quark jets. This is because gluon jets contain more fragment ingredients. Thus, at the same energy, the value of the standard deviation for gluon jets is smaller than that for quark jets.
Figure 2. (color online) (top) Normalized
$ \sigma^2 $ distribution of quark- and gluon-initiated jets in p+p collisions at$ \sqrt{s}=7 $ TeV from POWHEG+PYTHIA calculations. (bottom) Ratio of normalized$ \sigma^2 $ distribution of gluon and quark jets.In HIC, fast partons produced from hard scattering interact with medium partons and lose their energy. In our calculations, the initial jet shower partons are generated by POWHEG+PYTHIA. Then, they are arranged to have initial positions, which are sampled from the Glauber model [75]. We assume that all partons move through QGP in the same manner as classical particles. The probability of gluon radiation occurring in QGP during each time step
$ \Delta t $ can be expressed as [49, 76–78]$ \begin{array}{*{20}{l}} P_{\rm rad}(t,\Delta t)=1-{\rm e}^{-\langle N(t,\Delta t)\rangle} \, . \end{array} $

(4) Here,
$ \langle N(t,\Delta t)\rangle $ is the average number of emitted gluons, which can be integrated from the medium induced radiated gluon spectrum within the Higher-Twist (HT) method [64–67].$ \frac{{\rm d}N}{{\rm d}x{\rm d}k^{2}_{\perp}{\rm d}t}=\frac{2\alpha_{s}C_sP(x)\hat{q}}{\pi k^{4}_{\perp}}\sin^2\left(\frac{t-t_i}{2\tau_f}\right)\left(\frac{k^2_{\perp}}{k^2_{\perp}+x^2M^2}\right)^4. $

(5) Here,
$ \alpha_{s} $ denotes the strong coupling constant, x is the energy fraction of the radiated gluon, M is the mass of the parent parton, and$ k_\perp $ is the$ p_{T} $ of the radiated gluon. A lower$ p_{T} $ cut-off with$ x_{\rm min}=\mu_{D}/E $ of the emitted gluon is applied in our calculations, and$ \mu_{D} $ is the Debye screening mass.$ P(x) $ is the parton splitting function in vacuum, and$ C_s $ is the Casimir factor for gluons ($ C_A $ ) and quarks ($ C_F $ ). The formation time of the radiated gluons is$ \tau_f=2Ex(1-x)/(k^2_\perp+x^2M^2) $ .$ \hat{q} $ is a jet transport parameter, which is proportional to the local parton distribution density in the QCD medium. The jet transport parameter$ \hat{q} $ is proportional to the local parton density distribution in the QCD medium and relates to the space and time evolution of the medium relative to its initial value$ \hat{q}_0 $ in the central region when QGP formed, which controls the magnitude of energy loss due to jet-medium interactions.The number of emitted gluons is sampled from a Poisson distribution during each time step.
$ P(n_{g},t,\Delta t)=\frac{\langle N(t,\Delta t)\rangle^{n_{g}}}{n_{g}!}{\rm e}^{-\langle N(t,\Delta t)\rangle} \, . $

(6) In our calculation,
$ P_{\rm rad}(t,\Delta t) $ is first evaluated to determine whether radiation occurs during$ \Delta t $ . If accepted, the Possion distribution$ P(n_{g},t,\Delta t) $ is used to sample the number of radiated gluons. Finally, the energy fraction (x) and transverse momentum ($ k_{\perp} $ ) of the radiated gluon can be sampled based on the spectrum shown in Eq. (5).To calculate the collisional energy loss of these showered partons [46, 49], a hard thermal loop (HTL) formula is adopted [79], that is,
$\dfrac{{\rm d}E^{\rm coll}}{{\rm d}t}= \dfrac{\alpha_{s}C_{s}\mu^{2}_{D}}{2}{\rm ln}\dfrac{\sqrt{ET}}{\mu_{D}}$ . The space time evolution of the bulk medium is given by the smooth iEBE-VISHNU hydrodynamical code [80]. Jet partons stop propagating through the QGP medium when the local temperature falls below$ T_c=165 $ MeV. After all partons escape from the QGP, the PYQUEN method is used to perform the hadronization process [81, 82]. In the model, the radiated gluons are rearranged in the same string as their parent partons, and these partons may fragment into hadrons via the standard PYTHIA hadronization procedure. -
Next, we calculate the jet number normalized
$ p_{T}D $ distributions in Pb+Pb collisions at$ \sqrt{s_{NN}}=2.76 $ TeV. We use the same jet selection criterion as in p+p collisions in Sec. II. Our numerical results for the jet number normalized$ p_{T}D $ distributions of inclusive jets in p+p and Pb+Pb collisions are shown in Fig. 3, which are compared with existing experimental data in Pb+Pb collisions by the ALICE Collaboration [57]. We find that our theoretical calculations provide decent descriptions of the experimental measurements. Relative to that in p+p collisions, the observed normalized$ p_{T}D $ distribution in Pb+Pb is shifted toward higher values. In other words, the$ p_{T}D $ distribution of inclusive jets in Pb+Pb collisions is shifted toward quark jets after jet quenching. This indicates that a jet in Pb+Pb collisions may contain softer constituents than those in p+p collisions.
Figure 3. (color online) Normalized
$ p_{T}D $ distributions of inclusive jets in p+pp and central Pb+Pb (0%–10%) collisions at$ \sqrt{s_{NN}}=2.76 $ TeV compared with ALICE data [57].To investigate the deviation of jet
$ p_{T}D $ distributions in HIC from those in p+p collisions in a simpler way, it is essential to define the nuclear modification ratio ($ R_{AA}^{ p_{T}D} $ ) of$ p_{T}D $ distributions as$ \begin{array}{*{20}{l}} R_{AA}^{p_{T}D}={\dfrac{1}{N_{AA}} \dfrac{{\rm d}N_{AA}}{{\rm d}p_{T}D}}\Bigg/{\dfrac{1}{N_{pp}} \dfrac{{\rm d}N_{pp}}{{\rm d}p_{T}D}} \,\, . \end{array} $

(7) Figure 4 shows
$ R_{AA}^{ p_{T}D} $ of the normalized$ p_{T}D $ distributions for inclusive jets compared with ALICE ratio [57]. Our calculated results provide a good description of the ALICE ratio within the overall$ p_{T}D $ region. Note that the ALICE ratio is preformed from Pb+Pb measurements scaled by MC simulation in p+p collisions owing to a lack of p+p data. It is normal practice to utilize MC simulations in p+p collisions as reference in the study of nuclear modification ratios when the corresponding p+p baseline is not available [83–86]. Of course, experimentally measured$ R_{AA} $ results are more favorable because we could compare our simulations directly with the experimental data.$ R_{AA}^{ p_{T}D} $ of quark and gluon jets as the components of inclusive jets are also plotted in Fig. 4. We find that there is a suppression of the$ p_{T}D $ distribution of both quark and gluon jets in the low$ p_{T}D $ region, whereas an enhancement is observed in the high$ p_{T}D $ region. The nuclear corrections of the gluon jet$ p_{T}D $ distribution are significantly stronger than those of quark jets. The curve of$ R_{AA}^{ p_{T}D} $ for inclusive jets is observed between the curves of$ R_{AA}^{ p_{T}D} $ for quark and gluon jets because inclusive jets are a combination of quark and gluon jets.
Figure 4. (color online) Nuclear modification ratio of the
$ p_{T}D $ distribution of inclusive jets as well as quark and gluon jets. The ratio from the ALICE Collaboration is preformed using Pb+Pb measurements scaled by MC simulation in p+p collisions [57].To further understand the nuclear modification mechanism of the
$ p_{T}D $ distribution of inclusive jets, we begin with the modifications of the relative fraction of quark and gluon jets due to jet quenching. In our calculations, as in most jet quenching models, gluons may lose more energy than quarks in QGP with their larger color charge. Therefore, we generally should observe an enhancement in the contribution fraction of quark jets in A+A collisions relative to that in p+p collisions. Qualitatively, such enhancement will naturally lead inclusive jet$ p_{T}D $ distributions to larger value regions because quark jets peak at larger values of$ p_{T}D $ than gluon jets. This is illustrated in Fig. 4, where the curve labeled "inclusive jet (q/g)" represents our numerical$ R_{AA}^{ p_{T}D} $ result by only considering the effect of quark/gluon jet fraction alterations due to jet quenching while assuming there are no medium modifications for the$ p_{T}D $ distributions of pure quark and gluon jets in HIC.Next, we explore why, for normalized jet
$ p_{T}D $ distributions,$ R_{AA}^{ p_{T}D} < 1 $ in the small$ p_{T}D $ region and$ R_{AA}^{ p_{T}D} > 1 $ in the large$ p_{T}D $ region, as shown in Fig. 4. Eq. (3) indicates that the nuclear modification of$ p_{T}D $ distributions has a strong correlation with the nuclear correction of the standard deviation of$ p_{T,i} $ . Thus, we investigate the standard deviation of$ p_{T,i} $ for jets in p+p and Pb+Pb collisions. Fig. 5 presents the normalized distribution of the variance ($ \sigma^{2} $ ) of$ p_{T,i} $ in p+p and Pb+Pb collisions at$ \sqrt{s_{NN}}=2.76 $ TeV. We find that the distributions of jet variance is also shifted to the higher value region in HIC compared with those in p+p collisions, which indicates that after jet quenching, the value of$ p_{T,i} $ lies further from the mean value in HIC relative to p+p collisions. Note that the changes in the mean multiplicities of Pb+Pb relative to p+p are rather small, and the estimated mean values of the jet constituent number ($ \bar{n} $ ) in p+p and Pb+Pb collisions are$ \bar{n}_{pp}=6.72 $ and$ \bar{n}_{\rm PbPb}=6.54 $ , respectively.
Figure 5. (color online) (top) Normalized
$ \sigma^2 $ distribution of inclusive jets in central Pb+Pb (0%–10%) and p+p collisions at$ \sqrt{s_{NN}}=2.76 $ TeV. (bottom) Ratio of normalized$ \sigma^2 $ distribution in central Pb+Pb (0%–10%) and p+p collisions.We also plot the nuclear modification ratio of the momentum fraction of jet constituents (
$ z=p_{T,i}/p_{T, \rm jet} $ ) in Fig. 6. As shown, our model calculations provide a good description of ATLAS data for jets with$ p_T>100 $ GeV [23]. For jets with$ 40<p_T<60 $ GeV, the nuclear modification ratios of charged-particle transverse momentum distributions in Pb+Pb collisions to those measured in p+p collisions exhibit an enhancement in fragment yield within central collisions for$ 0.02<z<0.05 $ , a reduction in fragment yields for$ 0.05<z<0.3 $ , and an enhancement in fragment yield for$ 0.3<z<1 $ . This indicates that the number of jet constituents with lower and higher values of$ p_{T} $ is enhanced, that is, more constituents lie further from the mean value. Therefore, the jet standard deviation is shifted to a higher region in HIC.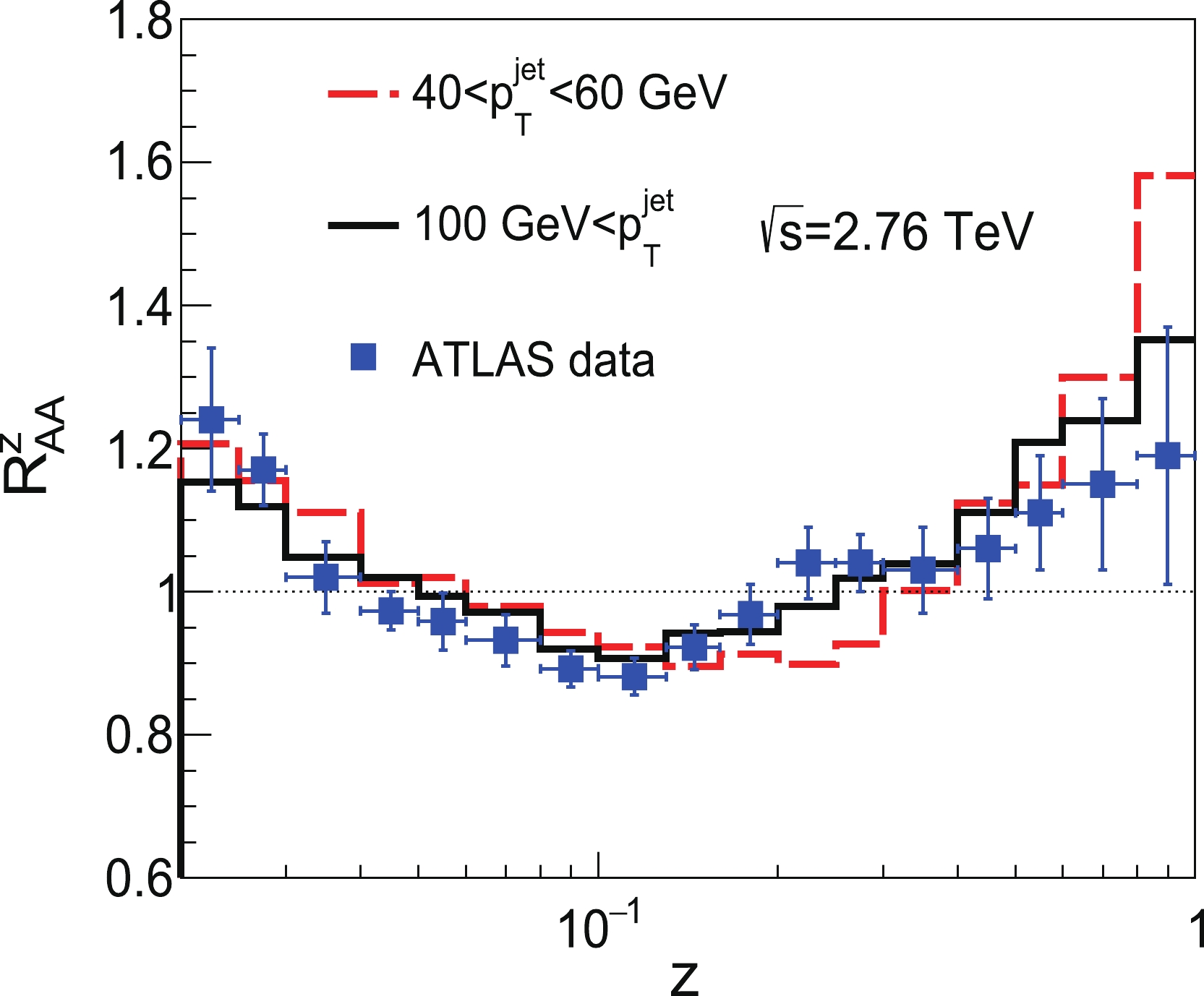
Figure 6. (color online) Nuclear modification ratio of z distributions for inclusive jets at
$ \sqrt{s_{NN}}=2.76 $ TeV compared with ATLAS data [23]. -
In this section, we study the
$ p_{T}D $ distributions of groomed jets in central Pb+Pb collisions. Jet grooming techniques have been of particularly great interest from both the experimental and theoretical perspectives [87, 88]. They are designed to remove soft wide-angle radiation from the jet, allowing for a more direct comparison between experimental data and purely perturbative QCD calculations because hadronization and underlying event contributions are significantly reduced during the grooming procedure. A full jet constructed with radius R via the anti-$ k_{T} $ algorithm is first re-clustered using the Cambridge-Aachen (C/A) algorithm [89, 90] until two hard branches are found to satisfy the following condition:$ \frac{{\rm min}(p_{T1},p_{T2})}{p_{T1}+p_{T2}}\equiv{z_{g}}>z_{\rm cut}\left (\frac{\Delta R}{R} \right)^{\beta}, $

(8) where
$ \left ({\Delta R}/{R} \right) $ is an additional parameter of the relative angular distance between the two sub-jets, and$ z_{\rm cut} $ and β are free parameters, which can be used to control how strict the soft drop condition is. For heavy-ion studies conducted so far,$ z_{\rm cut} $ has been set to$ 0.1 $ , and β has been set to zero.In the top panel of Fig. 7, we plot the nuclear modification ratio of the
$ p_{T}D $ distributions of groomed and ungroomed jets. We find that the nuclear modification pattern of the$ p_{T}D $ distributions of groomed jets is similar to that of ungroomed jets, and the$ p_{T}D $ distribution of groomed jets is also shifted to a higher$ p_{T}D $ region. Moreover, compared with that of ungroomed jets, the nuclear modification of groomed jets becomes weaker. This implies that the grooming procedure cannot only remove soft radiation from the jet in QCD vacuum, but also reduce soft radiation in the QCD medium. In the bottom panel of Fig. 7, we present the ratios of the$ p_{T}D $ distributions of the groomed jet to those of the ungroomed jet in both p+p and Pb+Pb collisions. It is shown that these ratios are below unity at small$ p_{T}D $ and larger than one at large$ p_{T}D $ . To further understand the alteration of$ p_{T}D $ distributions originating from the jet grooming procedure, in the following, we investigate the differences in the standard deviation of jet constituents$ p_{T,i} $ and jet constituent number between groomed and ungroomed jets in Pb+Pb collisions.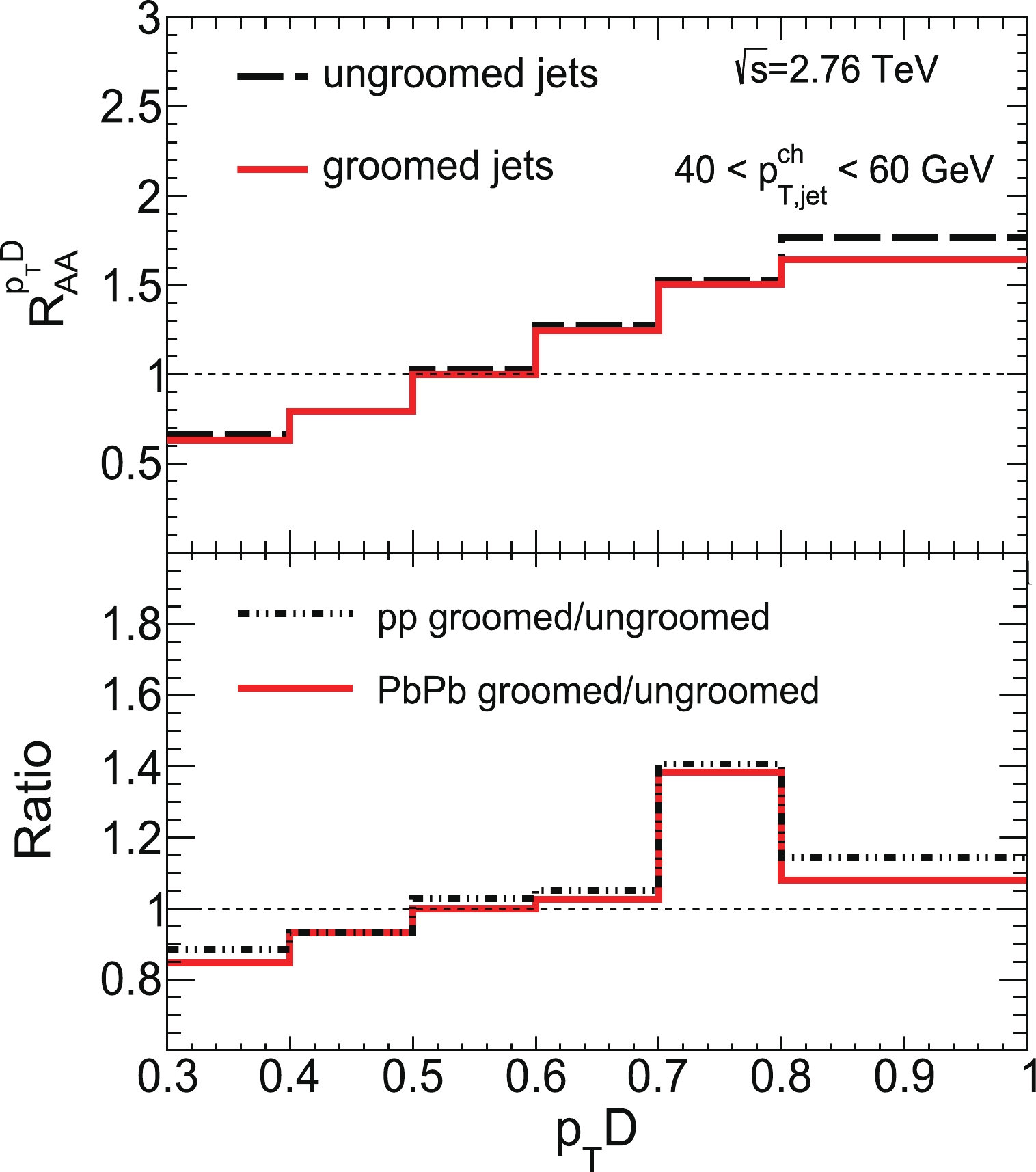
Figure 7. (color online) (top) Nuclear modification factor of the
$ p_{T}D $ distribution of groomed and ungroomed jets. (bottom) Ratio of the$ p_{T}D $ distribution of groomed and ungroomed jets in p+p and central Pb+Pb (0%–10%) collisions.First, in Fig. 8, we plot the variance (
$ \sigma^{2} $ ) distributions of the jet constituents$ p_{T,i} $ of groomed and ungroomed jets in central Pb+Pb collisions. The distributions of jet$ \sigma^{2} $ are shifted to the lower region for groomed jets compared with those for ungroomed jets, which is in contrast with the alteration of$ p_{T}D $ distributions. This indicates that after the jet soft-drop procedure, the values of$ p_{T,i} $ in groomed jets lie closer to the mean value relative to those in ungroomed jets. This is because, during grooming, some particles with low$ p_{T,i} $ are removed from the jet constituents.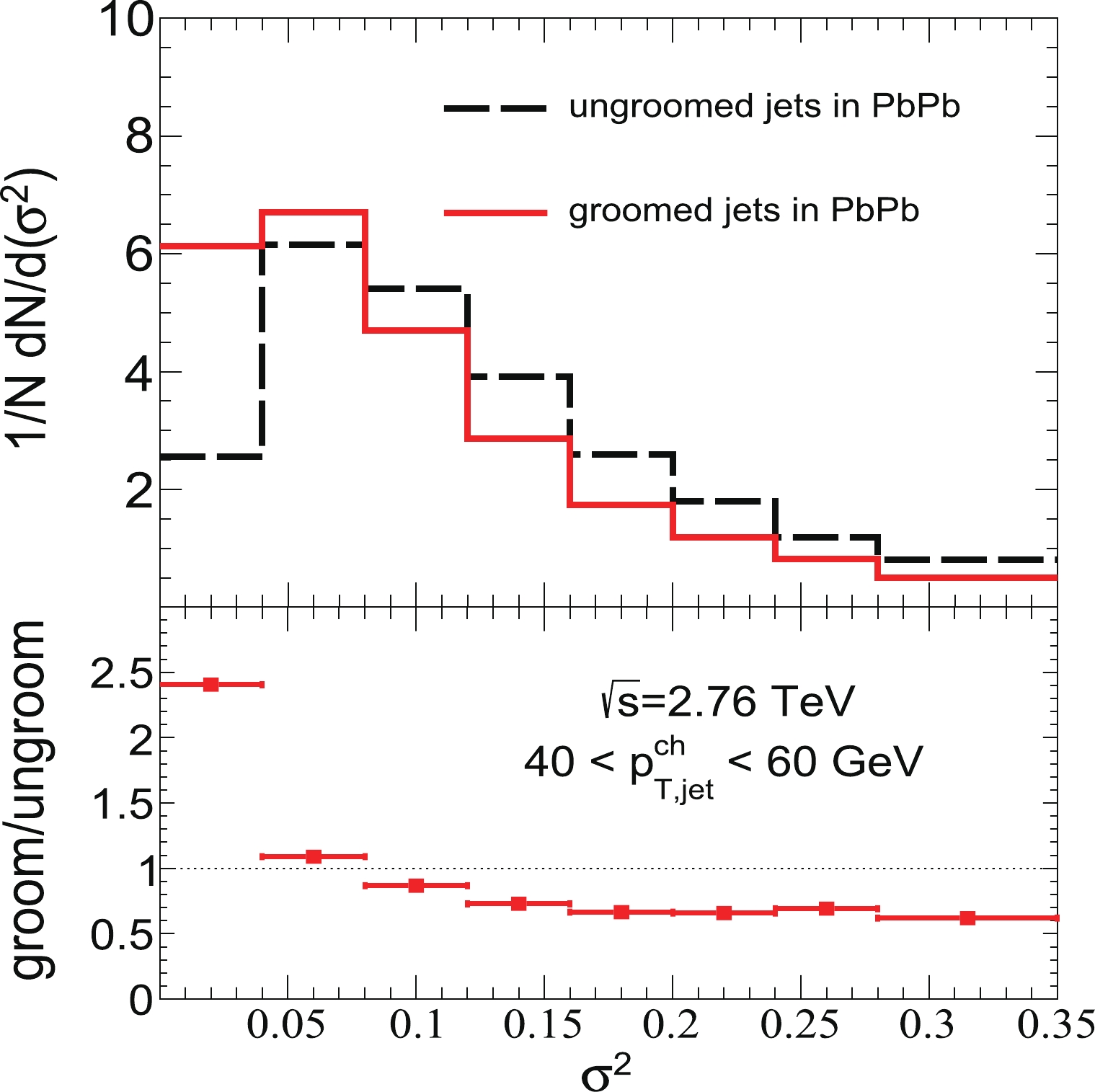
Figure 8. (color online) (top) Normalized
$ \sigma^2 $ distribution of groomed and ungroomed jets in central Pb+Pb (0%–10%) collisions at$ \sqrt{s_{NN}}=2.76 $ TeV. (bottom) Ratio of normalized$ \sigma^2 $ distribution of groomed and ungroomed jets in central Pb+Pb (0%–10%) collisions.Second, the number of jet constituents is modified during the soft drop grooming process, which contributes to the correction of the
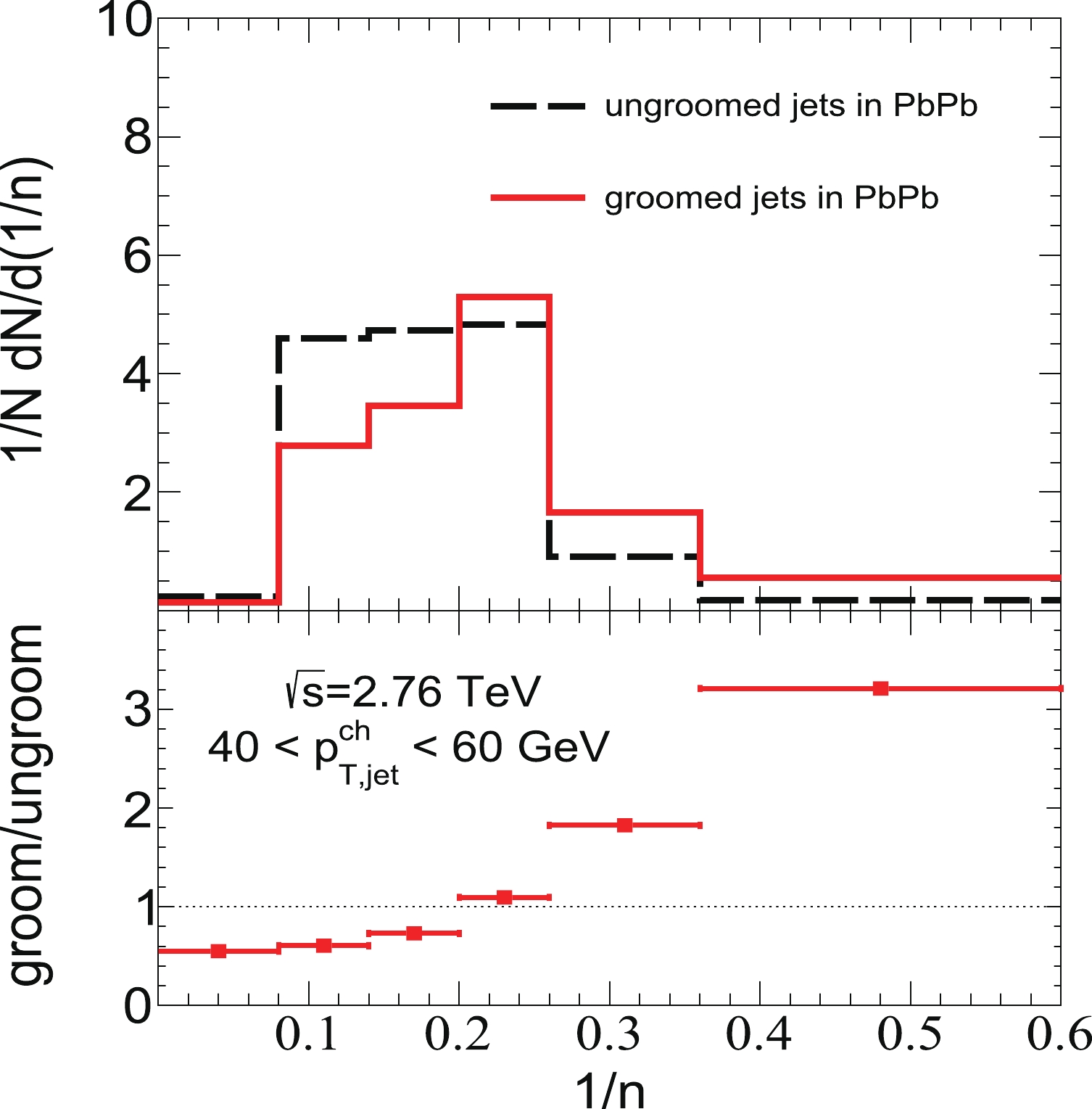
$ p_{T}D $ distributions. Fig. 9 shows the number of jet constituent distributions for groomed and ungroomed jets in p+p and central Pb+Pb collisions. We note that the value of$ 1/n $ is enhanced after the grooming process. As shown in Eq. (3), the value of$ p_{T}D $ is equivalent to the standard deviation added by$ 1/n $ . Therefore, even though the grooming process leads to a lower value of standard deviation for jet constituent transverse momenta, it enhances the value of$ 1/n $ . Although these two effects offset each other, the correction of$ 1/n $ is more pronounced, which results in an increase in the ratio of the$ p_{T}D $ distributions of groomed jets to those of ungroomed jets with$ p_{T}D $ (as shown in the bottom panel of Fig. 7), a trend similar to the increase in the ratio of the normalized ($ 1/n $ ) distribution of groomed to ungroomed jets with$ 1/n $ (as demonstrated in the bottom panel of Fig. 9). -
In this study, using an NLO
$ + $ PS event generator POWHEG$ + $ PYTHIA for a p+p baseline and HT parton energy loss approach to jet quenching, we investigate the nuclear modifications of the$ p_{T}D $ distributions of inclusive jets with a small radius$ R=0.2 $ in central Pb+Pb collisions at$ \sqrt{s_{NN}}=2.76 $ TeV. Our simulated results for inclusive jets provide a decent description of ALICE measurements. The$ p_{T}D $ distributions of inclusive jets are shifted toward the higher$ p_{T}D $ region in central Pb+Pb collisions compared to those in p+p collisions, and a similar trend has also been found for quark and gluon jets. Furthermore, we find that two elements may contribute to the nuclear modifications of$ p_{T}D $ distributions: a more uneven$ p_T $ of the jet constituents, and an enhanced fraction of quark-initiated jets after jet-medium interactions in HIC. The observed nuclear modifications of the$ p_{T}D $ distributions of gluon jets are stronger than those of quark jets in HIC because gluons may lose more energy than quarks in our model. Additionally, we investigate the medium modifications of the$ p_{T}D $ distributions of groomed jets in central Pb+Pb collisions. We observe weaker nuclear modifications of the$ p_{T}D $ distributions of groomed jets compared to those of ungroomed jets. -
The authors would like to thank P Ru, S L Zhang, S Wang, and Q Zhang for helpful discussions.
pT dispersion of inclusive jets in high-energy nuclear collisions
- Received Date: 2022-04-07
- Available Online: 2022-10-15
Abstract: In this study, we investigate the impact of jet quenching on the






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF


















 DownLoad:
DownLoad: