-
With the running of the Large Hadron Collider (LHC), the exploration of the heavy resonance, such as additional scalars, new gauge bosons, and charged fermions, has currently reached the TeV-scale. Vectorlike quarks (VLQs) are predicted to provide a dynamical explanation for the large top quark mass in some popular new physics scenarios beyond the standard model (SM) [1], such as little Higgs models [2], composite Higgs models [3], and other new physics theories [4–7]. These new particles do not receive mass through a Yukawa coupling term and thus are not excluded by current searches [8]. Based on their electric charges, such VLQs might appear in
$S U(2)$ singlets or multiplets, which can provide rich phenomenology at the current and future high-energy colliders (see, e.g., [9–33]).Many experimental searches for the VLQs and the constraints on their masses have been conducted. Current searches by the ATLAS and CMS collaborations using LHC Run-II data primarily focus on the quantum chromodynamics (QCD)-induced pair-production modes of VLQs and lead to lower bounds on the vector-like quark masses of approximately 1–1.5 TeV [34–43], depending on the assumed VLQ decay pattern. In this paper, we focus on the VLQ-B with an electric charge of
$ -1/3 $ , which is the$S U(2)$ singlet and couple exclusively to third-generation SM quarks. Very recently, the CMS collaboration presented a search for VLQ-B pair production in the fully hadronic final state [43] and excluded the masses up to 1570 and 1450 GeV for 100%$ B\to bh $ and 100%$ B\to tZ $ cases, respectively.Given the range of these exclusions, this analysis considers a VLQ-B with a mass greater than 1.3 TeV [44]. For such heavy VLQs, the single production process becomes more important owing to a reduced phase-space and has the added advantage of providing a window to the ultraviolet completion [45–49]. A particularly interesting set of couplings that this may probe are the transition magnetic moments, whether of electroweak nature or chromomagnetic. Simple strategies to probe this were developed in Refs. [50–53]. For transition chromomagnetic moments, an excited bottom quark
$ b^{\ast} $ can be single produced at the LHC via the b-gluon fusion process,$ bg\to b^{\ast} $ [52, 53]. Searches for such$ b^{\ast} $ quark have been performed at the LHC by the ATLAS and CMS collaborations at$ \sqrt{s} = 7, \; 8 $ and 13 TeV [54–57]. The future high-luminosity phase of the LHC (HL-LHC) is expected to extend the sensitivity in searching for the bounds on the VLQ mass and couplings. In this paper, we focus on the VLQ-B being the$S U(2)$ singlet and coupling exclusively to third-generation SM quarks. We consider the s-channel-resonant production of the VLQ-B at the 14 TeV LHC via the considered chromomagnetic moment and present a careful simulation of the signals and SM backgrounds for the subprocess$ bg\to B\to tW^{-} $ via the dilepton final state.The remainder of this paper is organized as follows. In Section II, we briefly describe the most general Lagrangian, which is related to the couplings of VLQ-B with the SM particles, and we discuss the decay width in narrow scenarios, the branching ratio, and its single production at the 14 TeV LHC. Section III describes a detector simulation of the signal and the relevant backgrounds at the LHC and its high-luminosity operation phase. We perform a detailed collider analysis to extract the projected sensisitivity of the HL-LHC in probing the parameter space through direct searches in the
$ B\to tW $ decay channel. Finally, we summarize our results in Section IV. -
The general Lagrangian describing the effective interaction of VLQ-B can be expressed as [52]
$ \begin{aligned}[b] {\cal{L}}=&\frac{g_s}{2\Lambda}G_{\mu\nu}\overline{b}\sigma^{\mu\nu}\Big(\kappa^b_L P_L+\kappa^b_R P_R\Big)B\\&+\frac{g_2}{\sqrt{2}}W_{\mu}^- \overline{t} \gamma^{\mu}\Big(Y_LP_L+Y_RP_R\Big)B \\ &+\frac{g_2}{2c_W}Z_{\mu}\overline{b}\gamma^{\mu}\Big(F_L P_L+F_R P_R\Big)B\\&+\frac{m_b}{\upsilon}h\overline{b}\Big(y_L P_L+y_R P_R\Big)B+ {\rm H.c.}. \end{aligned} $

(1) Here, Λ is the cutoff scale, often set to the VLQ-B mass;
$ g_s $ is the strong coupling constant;$ G_{\mu\nu} $ is the field strength tensor of the gluon;$ g_2 $ is the$S U(2)_L$ coupling constant; and$ \upsilon= 246 $ GeV is the electroweak scale. The factors$ \kappa^b_{L,R} $ ,$ Y_{L,R} $ ,$ F_{L,R} $ , and$ y_{L,R} $ parameterize the chirality of the VLQ-B couplings with the different SM particles. When the singlet VLQ-B mixes only with the left-handed bottom quark, we obtain$ Y_R\; (F_R) \simeq 0 $ and$ y_R \simeq \dfrac{M_B}{m_b} y_L $ . For simplicity, we consider a benchmark scenario with couplings$ Y_L =F_L = y_{L}=s_L= {\upsilon}/{M_B} $ . For our objectives, only the magnitude of$ \kappa^{b}= \kappa^b_{L,R} $ is relevant (for more details see Ref. [52] and the references therein), and in the absence of any theoretical knowledge, we consider a phenomenologically guided limit$ |\kappa^b|\leq 0.5 $ .Very recently, the CMS collaboration has searched for a heavy resonance decaying into a top quark and a W boson in the all-hadronic final state [56] and lepton+jets final state [57], respectively. For a benchmark value of the chromomagnetic transition moments (
$ \kappa^{b} =1 $ ), the hypotheses of B quarks with left-handed, right-handed, and vector-like chiralities are excluded at the 95% confidence level for masses below 2.6 (3.0), 2.8 (3.0), and 3.1 (3.2) TeV, respectively. Certainly, for a smaller value of coupling parameter$ \kappa^{b} $ , such mass limits should be reduced accordingly. -
From Eq. (1), we observe that the VLQ-B decays are dominated by two-body final states, namely
$ B\to bg $ ,$ B\to tW $ ,$ B\to Zb $ , and$ B\to\; hb $ . The first of these proceeds through the chromomagnetic moment$ \kappa^b $ . The remaining three are driven by the mixing parameters, and for a very large$ M_B $ , they have nearly equal partial widths, which is a consequence of the Goldstone equivalence theorem [58–63]. The partial decay widths of the VLQ-B can be expressed as$ \Gamma (B \to b\, Z) = \frac{g_2^2}{128\pi c_W^2} \frac{M_{B}^3}{M_Z^2} (F_L^2 + F_R^2) (1 - x_Z^2 )^2 ( 1 + 2 x_Z^2 ), $

(2) $ \Gamma (B \to t \,W^- ) = \frac{g_2^2}{64\pi} \frac{M_{B}^3}{M_W^2} (Y_L^2 + Y_R^2) (1 - x_t^2)^3 + {\cal O}(x_W^2) \, , $

(3) $ \Gamma (B \to b \,h ) = \frac{g^2}{128\pi} \frac{M_{B}^3}{M_W^2} (y_L^2 + y_R^2) (1 - x_h^2)^2 \, , $

(4) $ \Gamma (B \to b \,g ) = \frac{g_s^2}{12\pi} M_{B} (\kappa_L^2 + \kappa_R^2) \, . $

(5) Here,
$ x_Z = M_Z/M_{B} $ ,$ x_W = M_W/M_{B} $ ,$ x_h = M_h/M_{B} $ , and$ x_t = M_t/M_{B} $ .For the fixed coupling parameters
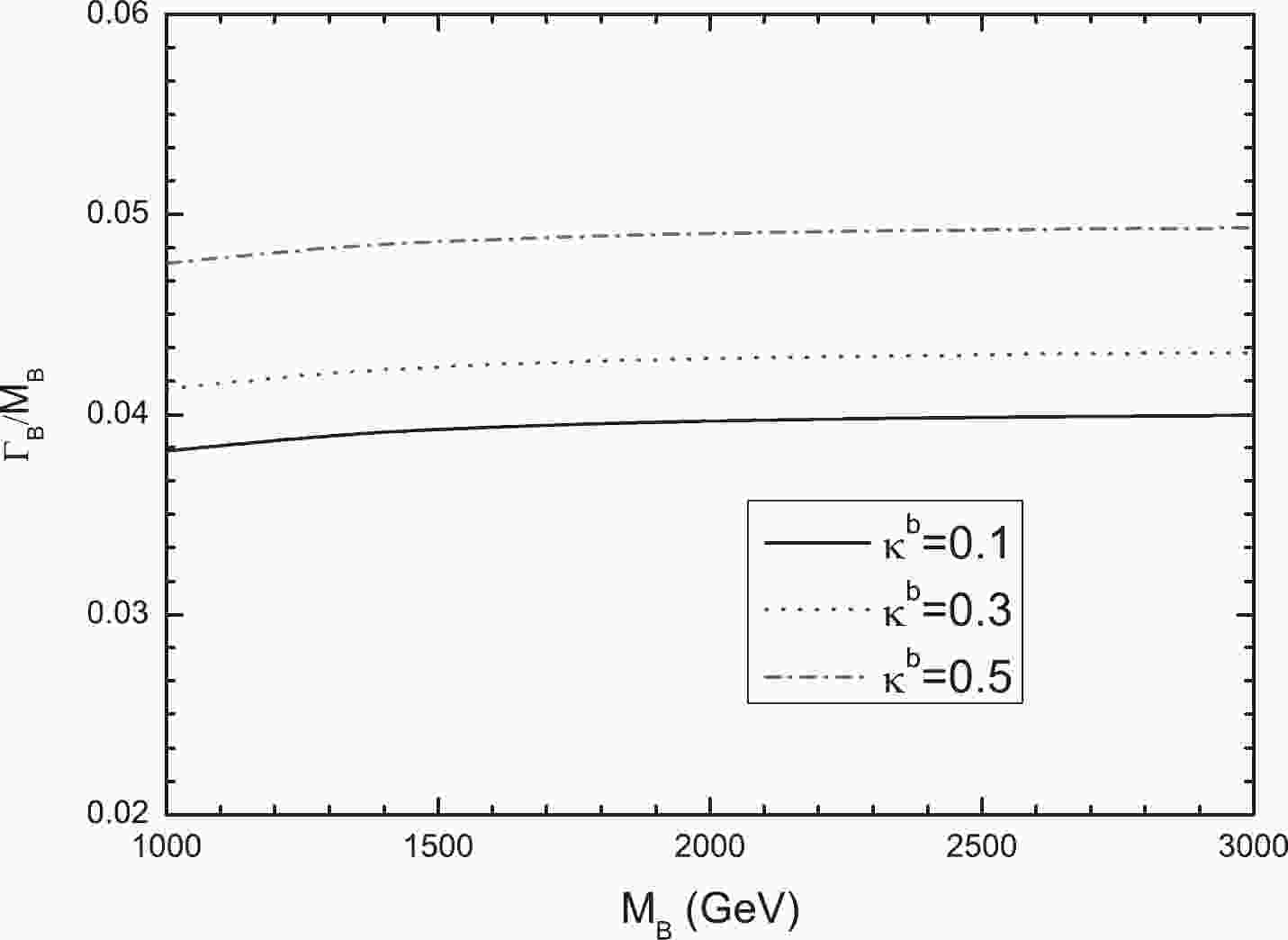
$ Y_L =F_L = y_{L}= {\upsilon}/{M_B} $ , the decay width of the VLQ-B depends on the coupling parameter$ \kappa^b $ and its mass$ M_B $ . In Fig. 1, we depict the dependence of width-over-mass ratio$ \Gamma_{B}/M_B $ on$ M_B $ for three values of$ \kappa^b $ . We can observe that, even for a very large value of$ \kappa^b $ , the ratio$ \Gamma_{B}/M_B\lesssim0.05 $ , thereby validating the narrow width approximation.
Figure 1. (color online) Width-over-mass ratio
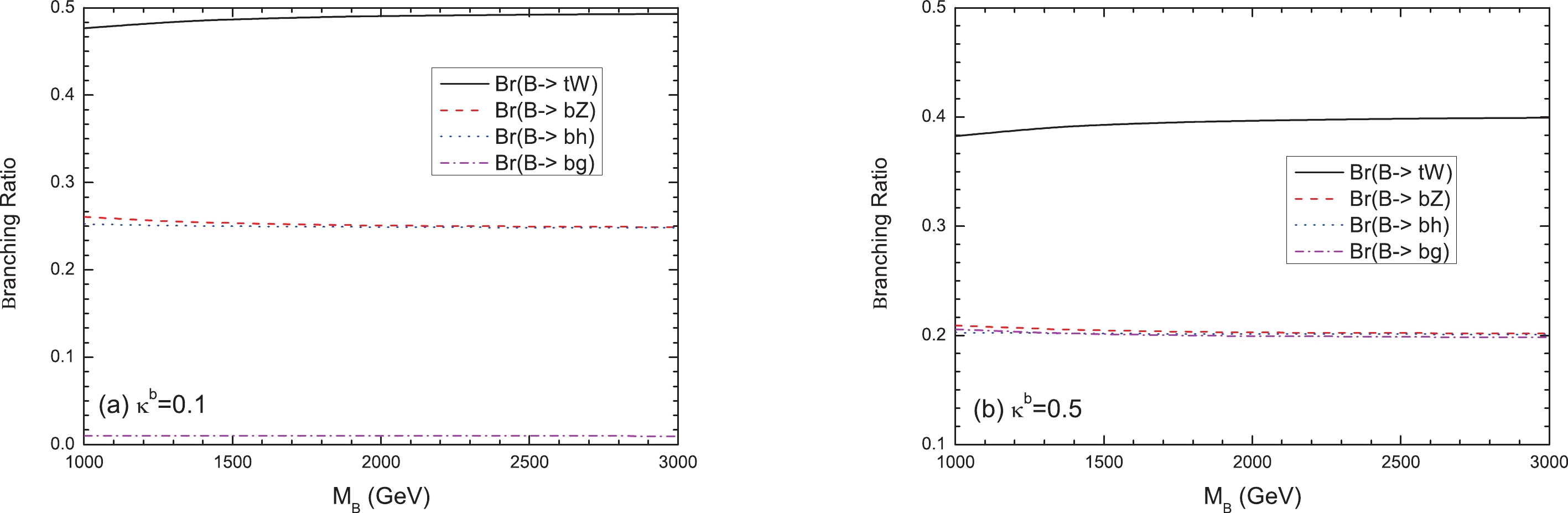
$ \Gamma_{B}/M_{B} $ as a function of$ M_B $ for different coupling strengths$ \kappa^b $ .The branching ratios for these decay channels are plotted as functions of the mass parameter
$ M_B $ in Fig. 2 for$ \kappa^b= 0.1 $ and$ \kappa^b= 0.5 $ . We can observe from Fig. 2 that, for$ \kappa^b= 0.1 $ , the branching ratio of the decay mode$ Wt $ will increase to approximately 50%, and we obtain$ Br(B \rightarrow Zb) \simeq Br(B \rightarrow hb) $ . Certainly, if we take a large value$ \kappa^b=0.5 $ , the value of the branching ratio$ Br(B \rightarrow bg) $ will be increased to approximately 20%. This is because for a fixed VLQ-B mass, the partial decay width$ \Gamma_{B\to bg} $ is always proportional to$ (\kappa^{b})^{2} $ . -
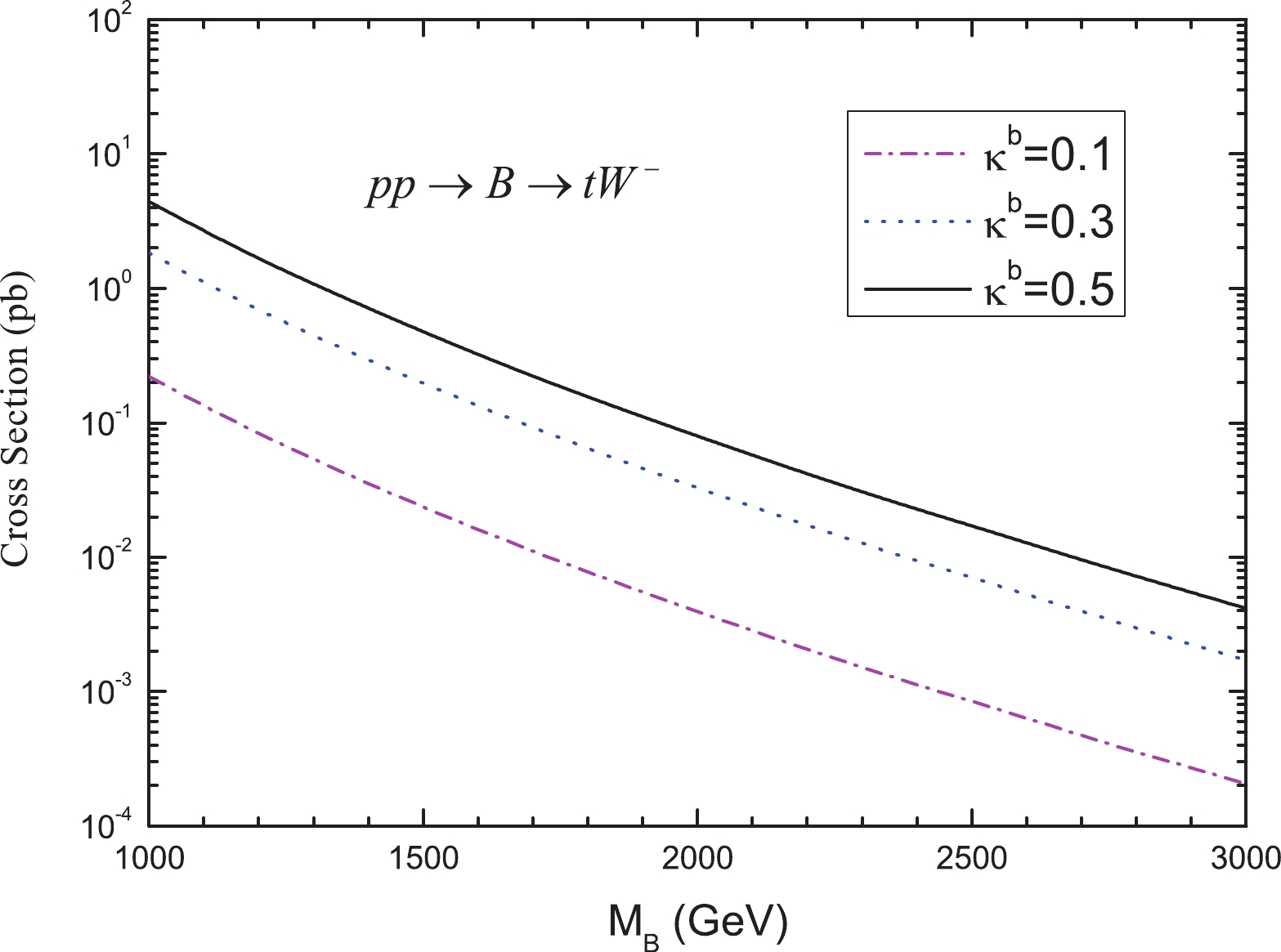
Depending on the strength of the chromomagnetic interactions
$ \kappa^b $ , the produced VLQ-B can dominantly decay into a$ tW $ system, the Feynman diagram for such resonance VLQ-B production and decay to$ tW $ is shown in Fig. 3. The production cross section$ \sigma(pp\rightarrow B \rightarrow tW) $ is plotted in Fig. 4 as a function of the mass$ M_B $ for three typical values of the parameter$ \kappa^b $ at the 14 TeV LHC. The leading-order (LO) cross sections are obtained by using MadGraph5-aMC$ @ $ NLO [64] with NNPDF23L01 parton distribution functions (PDFs) [65] for the renormalization and factorization scales of$ \mu_R=\mu_F= \mu_0/2=M_B $ . For$ 0.1\leq\kappa^b \leq0.5 $ and 1000 GeV$ <M_B< $ 3000 GeV, the values of the cross section$ \sigma(pp\rightarrow B \rightarrow tW) $ are in the range of$ 2.1\times10^{-4} \sim 4.4\; $ pb. For$ \kappa^b=0.3 $ and$ M_B $ = 1500, 1800, 2000 GeV, their values are 0.2, 0.064, 0.032$ \rm pb $ , respectively. Certainly, increasing$ \kappa^b $ would enhance the partial decay width$ \Gamma(B \to b g) $ , thereby suppressing the branching fraction for others. -
Next, we explore the discovery potentiality of the singlet VLQ-B through the final states in which both the top quark and W boson originating from the initial VLQ-B decay leptonically.
$ \begin{array}{*{20}{l}} pp\to B \to t(\to b\ell^+\nu)W^-(\to \ell^-\bar{\nu}), \end{array} $

(6) where
$ \ell= e, \mu $ . Note that the analysis has included the charge-conjugate process. As a reference point, we set a benchmark value of$ \kappa = 0.1 $ . Analogously, our benchmark points (BPs) in the mass-axis read$ M_B= $ 1500, 1800, and 2000 GeV. However, later, we will present the reach in the$ M_B $ –$ \kappa^b $ plane.For the above dilepton final states, the main backgrounds are top pair production, the associated
$ tW $ production, and diboson ($ WW $ ,$ WZ $ , and$ ZZ $ ) production in association with jets ($ VV $ +jets). Here, we do not consider multijet backgrounds in which jets can fake electrons as they are generally negligible in multilepton analyses [66].We calculated the leading order (LO) production cross sections and events of signal and backgrounds at parton level using MadGraph5-aMC
$ @ $ NLO. The relevant SM input parameters were obtained from [67]. We then transmitted the parton-level events to Pythia 8 [68] for showering and hadronization. All produced jets were forced to be clustered using FASTJET 3.2 [69] assuming the anti-$ k_{t} $ algorithm with a cone radius of$ R=0.4 $ [70]. Detector effects were simulated with Delphes 3.4.2 [71], using the standard HL-LHC detector parameterization shipped with the program. Finally, event analysis was performed using MadAnalysis5 [72]. To consider inclusive QCD contributions, we generated the hard scattering of backgrounds with up to one or two additional jets in the final state, followed by matrix element and parton shower merging with the MLM matching scheme [73]. For the SM backgrounds, we generated LO samples renormalized to the NLO or next-to-NLO (NNLO) cross sections, which are listed in Table 1.Table 1. K-factors of the leading SM background processes for our analysis.
The basic cuts at parton level for the signal and SM backgrounds were set as follows:
$ \begin{equation} \begin{aligned} p_{T}^{\ell}>\; 20\; {\rm GeV},\quad p_{T}^{j}>\; 25\; {\rm GeV},\quad |\eta_{\ell/j}|<\; 2.5, \quad \Delta R_{ij}>&\; 0.4 \\ \end{aligned} \end{equation} $

(7) where
$ \Delta R=\sqrt{\Delta\Phi^{2}+\Delta\eta^{2}} $ is the separation in the rapidity-azimuth plane, and$ p_{T}^{\ell, j} $ are the transverse momentum of leptons and jets, respectively.For the signal, the final state is required to have exactly two leptons with opposite charges and one central jet. No b-tagging is required because the dominant background from
$ t\bar{t} $ production also contains b quarks. In Fig. 5, we plot some differential distributions for signals and SM backgrounds after the basic cuts at the 14 TeV LHC, such as the transverse momentum distributions of the leading and sub-leading leptons ($ p_{T}^{\ell_{1},\ell_{2}} $ ), missing transverse momentum$\not E_T^{\rm miss}$ , separations$ \Delta R_{j,\ell} $ , scalar sum of the transverse energy of all final-state jets$ H_{T} $ , and transverse mass distribution$ M_T(j\ell_{1}\ell_{2}\not E_T) $ . Here, to reconstruct the VLQ-B mass, we use a cluster transverse mass, defined as [78]
Figure 5. (color online) Normalized distributions for the signals (with
$ M_{B} $ =1500, 1800, and 2000 GeV) and SM backgrounds at the 14 TeV LHC.$ \begin{aligned}[b] M_{T}^{2}(j\ell_{1}\ell_{2}\not E_T)=&\Big(\sqrt{p_{T}^{2}(j\ell_{1}\ell_{2})+M^{2}_{j\ell_{1}\ell_{2}}}+\not E_T\Big)^{2}\\&-(\vec{p}_{T}(j\ell_{1}\ell_{2})+\not E_T)^{2}, \end{aligned} $

(8) where
$ \vec{p}_{T}(j\ell_{1}\ell_{2}) $ is the total transverse momentum of all visible particles, and$ M_{j\ell_{1}\ell_{2}} $ is their invariant mass. Owing to the larger mass of VLQ-B, the decay products of VLQ-B are highly boosted. Therefore, the$ p_{T}^{\ell} $ peaks of the signals are larger than those of the SM backgrounds, and the angular distance between the jet and the lepton is smaller than that in background process events.Based on these kinematical distributions, we can impose the following set of cuts to enhance the signal significance.:
● Cut-1: There are exactly two isolated leptons with
$ p_{T}^{\ell_{1}}> 150 \rm \; GeV $ and$ p_{T}^{\ell_{2}}> 60 \rm \; GeV $ , and at least one jet is required$ p_T> 30 $ GeV.● Cut-2: The missing transverse momentum
$\not E_T^{\rm miss}$ is required to be larger than 60 GeV.● Cut-3: The separations
$ \Delta R_{j,\ell} $ and$ \Delta R_{\ell_{1},\ell_{2}} $ are required to have$ \Delta R_{j,\ell}< 1.0 $ and$ \Delta R_{\ell_{1},\ell_{2}}> 2.5 $ .● Cut-4: The scalar sum of the transverse energy of all final-state jets is required
$H_T > 300 \rm \; GeV$ .● Cut-5: The transverse mass is required
$M_{T} > $ 1000 GeV.We present the cross sections of three typical signals (
$ M_B=1500, 1800, 2000 $ GeV) and the relevant backgrounds after imposing the cuts in Table 2. We can observe that, at the end of the cut flow, the backgrounds are suppressed very efficiently, and the largest SM background is the$ t\bar{t} $ process with the cross section of approximately 1.17 fb.Cuts Signals Backgrounds 1500 GeV 1800 GeV 2000 GeV $ t\bar{t} $ 

$ tW $ 

$ VV $ +jets

Z+jets Basic 0.57 0.17 0.077 11700 990 940 41760 Cut-1 0.35 0.11 0.05 520 68 54 1012 Cut-2 0.31 0.094 0.044 302 39 24 136 Cut-3 0.17 0.056 0.026 82 7.8 2.2 0.005 Cut-4 0.10 0.036 0.017 26 1.75 0.54 0.002 Cut-5 0.051 0.024 0.013 1.17 0.26 0.29 0.0002 Table 2. Cut flow of the cross sections (in fb) for the signals and SM backgrounds at the 14 TeV LHC with
$ \kappa^{b}=0.1 $ and three typical B quark masses.To analyze the observability, we use the median significance to estimate the expected discovery and exclusion significance [79]:
$ \begin{aligned}[b] {\cal{Z}}_\rm{disc} &= \sqrt{2\left[(s+b)\ln\left(\frac{(s+b)(1+\delta^2 b)}{b+\delta^2 b(s+b)}\right) - \frac{1}{\delta^2 }\ln\left(1+\delta^2\frac{s}{1+\delta^2 b}\right)\right]} \\ {\cal{Z}}_\rm{excl} &=\sqrt{2\left[s-b\ln\left(\frac{b+s+x}{2b}\right) - \frac{1}{\delta^2 }\ln\left(\frac{b-s+x}{2b}\right)\right] - \left(b+s-x\right)\left(1+\frac{1}{\delta^2 b}\right)}, \end{aligned} $ 
(9) with
$ \begin{equation} \begin{aligned} x=\sqrt{(s+b)^2- 4 \delta^2 s b^2/(1+\delta^2 b)}. \end{aligned} \end{equation} $

(10) Here, s and b are the expected events of the signal and total SM background after all cuts, respectively, and δ is the percentage systematic error. To illustrate the effect of systematic uncertainty on the significance, we select three cases: no systematics (δ=0) and two typical systematic uncertainties (δ=5% and δ=10%). In the limit of
$ \delta \to $ 0, these expressions can be simplified as$ \begin{aligned}[b] {\cal{Z}}_\rm{disc} &= \sqrt{2[(s+b)\ln(1+s/b)-s]}, \\ {\cal{Z}}_\rm{excl} &= \sqrt{2[s-b\ln(1+s/b)]}. \end{aligned} $

(11) In Fig. 6 and Fig. 7, the
$ 2\sigma $ and$ 5\sigma $ lines are plotted as a function of$ \kappa^{b} $ and the VLQ-B mass$ M_B $ with the aforementioned three systematic error cases of δ=0, 5%, and 10%, for two fixed values of integrated luminosity 300 and 3000 fb$ ^{-1} $ , respectively. We observe that our signals are rather robust against the systematic uncertainties on the background determination. For$ \kappa_{b}=0.5 $ and$ \delta=0 $ , VLQ-B can be probed at the$ 5\sigma $ level with a mass of approximately 1950 (2300) GeV with the integral luminosity of 300 (3000) fb$ ^{-1} $ , while the$ 2\sigma $ exclusion limits are approximately 2230 (2600) GeV with the integral luminosity of 300 (3000) fb$ ^{-1} $ . When a realistic 5% systematic uncertainty is considered, the$ 5\sigma $ sensitivity decreases to 1800 (1900) GeV with the integral luminosity of 300 (3000) fb$ ^{-1} $ . Meanwhile, the$ 2\sigma $ exclusion limits decreases to 2100 (2200) GeV with the integral luminosity of 300 (3000) fb$ ^{-1} $ . Altogether, the higher systematic uncertainty of background can decrease the discovery capability and the excluded region.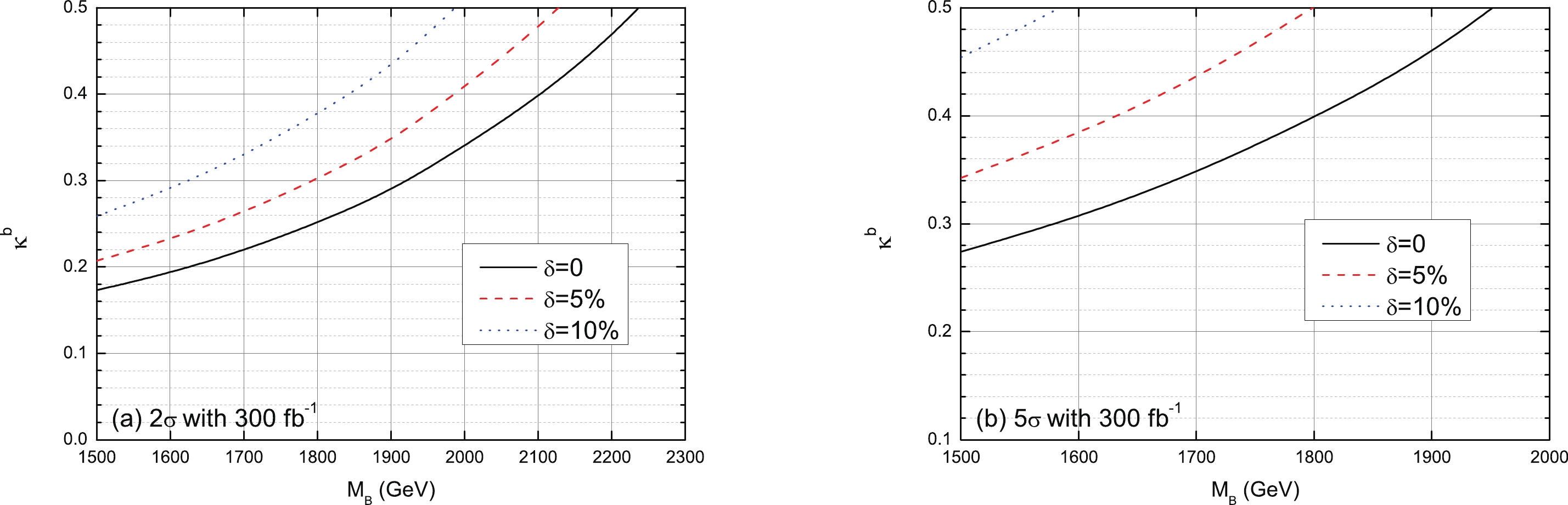
Figure 6. (color online) Exclusion limit (at
$ 2\sigma $ ) and discovery prospects (at$ 5\sigma $ ) contour plots for the signal in$ \kappa^{b}-M_{B} $ planes at 14 TeV LHC with an integral luminosity of 300 fb$ ^{-1} $ .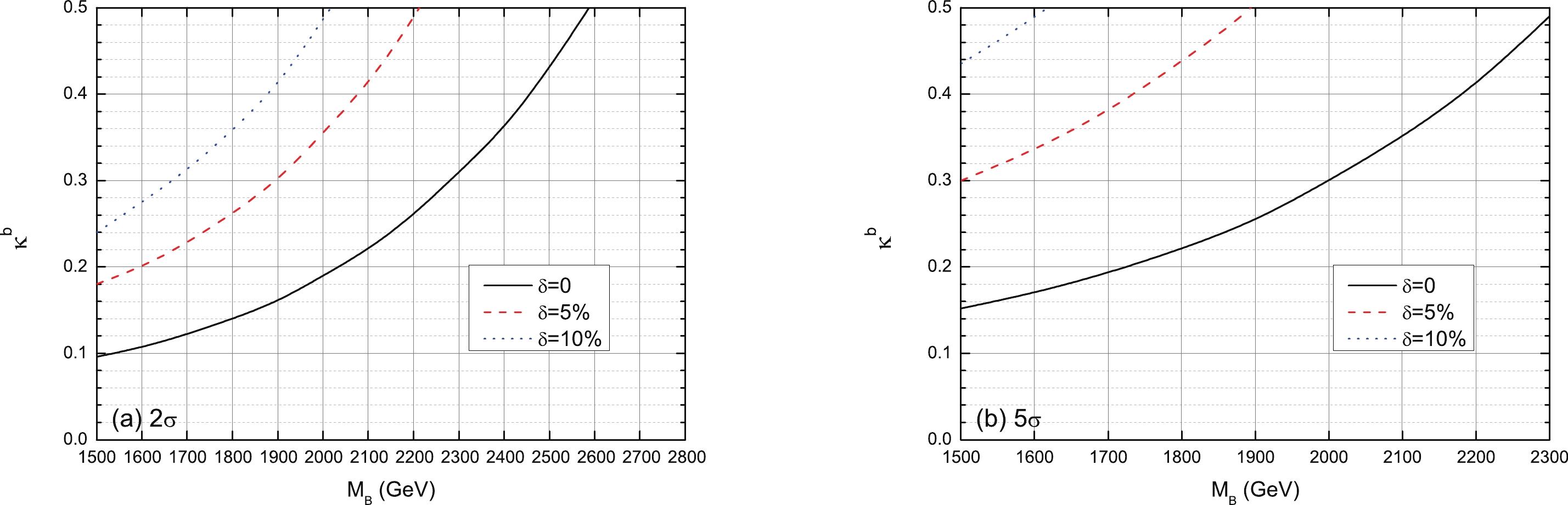
Figure 7. (color online) Same as Fig. 6, but for the integral luminosity of 3000 fb
$ ^{-1} $ .We can now perform a comparison with other complementary studies for searches at the LHC run II involving a resonant VLQ-B. In Ref. [31], the authors use the same assumption on the parameters and design a dedicated search strategy for the
$ pp\to B\to bZ $ process via the$ B\to Zb $ decay mode with$ Z\to \ell^{+}\ell^{-} $ at$ \sqrt{s }= 14 $ TeV with an integrated luminosity of 300 fb$ ^{-1} $ , and the numerical results show that for$ \kappa_{b}=0.5 $ , VLQ-B can be probed at the$ 5\sigma $ level with a mass of approximately 1620 GeV and an integral luminosity of 300 fb$ ^{-1} $ . Using the model that includes a topless vectorlike doublet$ (B, Y) $ , the author of [33] investigates the single production of a VLQ-B①, with the$ B \to b + Z/H $ subsequent decay channel and the fully hadronic final states using a jet substructure at the 13 TeV LHC with an integrated luminosity of 300 fb$ ^{-1} $ ; a modest value of the chromomagnetic transition moments ($ \kappa =0.5 $ ) enables the exclusion of$ M\lesssim 1.8 \, (2.2) \; \rm TeV $ in the Z and H channels, respectively. Therefore, our analysis is competitive with the results of the existing literature and represents a complementary candidate to search for a possible VLQ-B.Note that to avoid having to reject the overwhelming QCD multi-jet background, we do not consider other types of final events, such as the lepton+jets channel (where only one W boson decays leptonically and the other one decays hadronically) and all hadronic channel (where both of W bosons decay hadronically). Because these channels are dependent on different tagging algorithms for the identification of boosted, hadronically decaying, heavy particles [80–82], i.e., to reconstruct the top quark, a new tagging technique, such as the heavy object tagger with variable R (HOTVR) [81] algorithm, can be used to identify jets from the collimated top quark decay, which is beyond the scope of this paper.
-
Based on a simplified model to describe the interactions
$ Bgb $ , we have investigated the potential for the 14 TeV LHC to discover the vectorlike bottom quark partner produced via its chromomagnetic moment interaction,$ pp\to bg\to B $ , with the subsequent decay channel$ B\to tW $ and leptonic decay mode for the top quark and W boson. This production mechanism complements the traditional searches, which have relied on pair-production of vectorlike quark states or single production of these states through electroweak interactions. Our numerical results show that, with a benchmark coupling parameter$ \kappa^b=0.5 $ , the VLQ-B can be probed at the$ 5\sigma $ level with a mass of approximately 1950 (2300) GeV and an integral luminosity of 300 (3000) fb$ ^{-1} $ . Meanwhile, the 2σ excluded region is of approximately 2230 (2600) GeV with an integral luminosity of 300 (3000) fb$ ^{-1} $ . We expect that our analysis can represent a complementary candidate to search for such singlet VLQ-B quark at the upgraded LHC.
Search for single production of vectorlike B-quarks at the LHC
- Received Date: 2022-05-18
- Available Online: 2022-10-15
Abstract: New vectorlike quarks have been proposed in many scenarios of new physics beyond the Standard Model, which address the hierarchy problem and may be potentially discovered at the Large Hadron Collider (LHC). Based on a model-independent framework, we propose to search for the vectorlike B-quark (VLQ-B) and focus on resonant production via b-gluon fusion through chromomagnetic interactions. We then explore the possible signals of the VLQ-B through the





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF



























 DownLoad:
DownLoad: