-
The medium of deconfined gluons and light quarks, known as quark-gluon plasma (QGP) [1], can be produced in ultrarelativistic heavy-ion collisions (URHICs). Charmonium, as a bound state of a charm (c) and anti-charm (
$ \bar{c} $ ) quark pair, has been proposed as a clean probe to study the formation of QGP in heavy-ion collisions [2]. Different charmonium states bound by a$ c\bar{c} $ potential with color screening from in-medium light partons sequentially melt as the temperature of the QGP medium increases [3]. Moreover, charmonium states suffer a direct dissociation from in-medium parton inelastic scattering [4–8], which corresponds to an additional imaginary part of the$ c\bar{c} $ potential [9, 10]. In nucleus-nucleus (AA) collisions at the Large Hadron Collider (LHC), the initial temperature of QGP can be far above the dissociation temperature$ T_d $ of the charmonium ground state$ J/\psi $ [11, 12]. Most primordially produced charmonia are dissociated in the medium, and the final production is dominated by the coalescence of abundant charm and anti-charm quarks in the regions where medium local temperature becomes smaller than the dissociation temperature of charmonium [13–15]. The final spectrum of the charmonia are affected by charm quark diffusion in the medium and their coalescence probability below the dissociation temperature [16–20].In p-Pb collisions at
$ \sqrt{s_{NN}}=5.02 $ TeV, a small deconfined medium is also believed to be generated [21], where the medium temperature is slightly above the critical temperature$ T_c $ but still below the dissociation temperature$ T_d\simeq 2T_c $ of$ J/\psi $ , which is of the order of its binding energy$ T_d\simeq E_{b} $ . If the mass and typical momentum of a charm quark are considered to be larger than the charmonium binding energy,$ m > p > 3T >T_d \simeq E_b $ , one can integrate out the hard scale m and soft scale p and arrive at a non-relativistic potential description [22].Furthermore, the recombination of charmonium production becomes negligible in pA collisions [23, 24] owing to small
$ c\bar{c} $ production. This excludes contamination from the coalescence of$ c\bar{c} $ pairs and the correlation between different$ c\bar{c} $ pairs, which leads to the recombination contribution of charmonium. These features make the Schrödinger equation, which evolves only one$ c\bar{c} $ pair in a potential, viable for a quantum description of charmonium in pA collisions.With similar considerations, the recombination of bottomonia in URHICs is negligible [25–29], and an open quantum system (OQS) description of bottomonium evolution in a QCD medium, which tracks one bottom/anti-bottom (
$ b\bar{b} $ ) pair, has been constructed by various models in recent years①. The QCD medium environment can be encoded in the Hamiltonian of the heavy quark/antiquark ($ Q\bar{Q} $ ) subsystem as additional terms equivalent to real and imaginary parts of the potential. These studies begin with solving the Schrödinger equation with a complex potential [32–34], then a stochastic potential [35], and a Schrödinger-Langevin type equation [36]. More involved calculations tend to evolve the density matrix of the$ Q\bar{Q} $ subsystem with the Lindblad formalism [37], whose different terms represent color screening, primordial dissociation, and the recombination of one pair [38]. One such calculation incorporated with the quantum trajectory method can be found in [39].In this paper, we do not conduct a complicated quantum treatment, as discussed for bottomonium, but solve the Schrödinger equation with a complex potential. We parameterize the in-medium temperature dependent complex potential of a
$ c\bar{c} $ dipole according to lattice QCD data. Then, we evolve a$ c\bar{c} $ pair wave-function by solving the time-dependent Schrödinger equation in position space using the Crank-Nicolson [40] implicit method. The final production of$ J/\psi $ and$ \psi(2S) $ are obtained by projecting the wave-functions of$ c\bar c $ dipoles to the charmonium wave-function (by solving the time-independent Schrödinger equation with vacuum potential) after they leave the hot medium along different trajectories. Because the geometric sizes of different charmonium wave-functions are different,$ J/\psi $ and$ \psi(2S) $ experience different magnitudes of the screening effect and inelastic collisions with thermal partons. This results in different dissociations of$ J/\psi $ and$ \psi(2S) $ .Because the suppressions of
$ J/\psi $ and$ \psi(2S) $ are clearly distinguished, as shown by experimental data, it is essential to employ different scenarios of potential in the Schrödinger equation and understand the potential at play behind the data, especially their overall and relative suppression. To understand the role of color screening, we implement a strong and weak screening scenario with and without the imaginary part of the potential.This paper is organized as follows: In Sec. II, the Schrödinger equation model and parametrizations of the heavy quark potential are introduced. Medium evolution, which provides the space-time dependent temperature profile, is described using hydrodynamic equations. In Sec. III, we discuss the application of the model to p-Pb collisions at LHC energies, and
$R_{ pA}$ s of$ J/\psi $ and$ \psi(2S) $ are calculated with different in-medium potentials and compared with the experimental data. We conclude in Sec. IV. -
Heavy quark dipoles are produced in initial parton hard scatterings and then evolve into charmonium eigenstates. The momentum distribution of
$ c\bar c $ dipoles is approximated to be the$ J/\psi $ momentum distribution in proton-proton (pp) collisions. Therefore, in p-Pb collisions, the initial distribution of primordially produced$ c\bar c $ dipoles can be obtained through a superposition of the effective pp collisions [23],$ \begin{aligned}[b] f_{\Psi}({\boldsymbol p},{\boldsymbol x}|{\boldsymbol b}) =& (2\pi)^3\delta(z)T_{p}({\boldsymbol x}_{T})T_{A}({\boldsymbol x}_{T}-{\boldsymbol b}) \\ &\times {\cal R}_{g}(x_g,\mu_{F},{\boldsymbol x}_{T}-{\boldsymbol b}) {{\rm d} \bar \sigma^\Psi_{pp}\over {\rm d}^3{\boldsymbol p}}, \end{aligned} $

(1) where
$\boldsymbol b$ is the impact parameter,${\boldsymbol x}_{T}$ is the transverse coordinate,$T_A({\boldsymbol x}_{T})=\int {\rm d}z\rho_A({\boldsymbol x}_{T},z)$ is the nuclear thickness function, and the nuclear density is taken as the Woods-Saxon distribution.$T_p({\boldsymbol x}_{T})$ is the proton thickness, where proton density is taken as a Gaussian distribution [23]. The width of the Gaussian function is determined with the proton charge radius$ \langle r\rangle_p=0.9 $ fm [41]. The shadowing effect is included with the inhomogeneous modification factor${\cal R}_{g}$ [42] for gluons with the longitudinal momentum$x_g=e^{y}\ E_{T}/\sqrt{s_{NN}}$ and factorization factor$\mu_{F}=E_{T}$ . Transverse energy and momentum rapidity are defined as$E_{T}=\sqrt{m_\Psi^2+{\boldsymbol p}_{T}^2}$ and$y=1/2\ln((E+p_{z})/(E- p_{z}))$ , respectively. The values ofthe gluon shadowing factor$ \mathcal{R}_g $ are obtained using the EPS09model [43]. The effective initial momentum distribution$\dfrac{{\rm d} \bar \sigma^\Psi_{pp}}{ {\rm d}^3{\boldsymbol p}}$ of charmonium in p-Pb collisions includes the Cronin effect [44]. Before two gluons fuse into a heavy quark dipole, they obtain additional transverse momentum via multi-scatterings with the surrounding nucleons. The extra momentum will be inherited by the produced$ c\bar c $ dipole or charmonium states. With the random walk approximation, the Cronin effect is included with the modification in the momentum-differential cross section measured in pp collisions,$ \begin{align} {{\rm d}\bar \sigma_{pp}^{\Psi}\over {\rm d}^3{\boldsymbol p}} = {1\over \pi a_{gN}l}\int {\rm d}^2{\boldsymbol q}_{T} {\rm e}^{-{\boldsymbol q}_{T}^2\over a_{gN}l} {{\rm d}\sigma_{pp}^{\Psi}\over {\rm d}^3{\boldsymbol p}} , \end{align} $

(2) where
$l({\boldsymbol x}_{T})=0.5T_A({\boldsymbol x}_{T})/\rho_A({\boldsymbol x}_{T},z=0)$ is the average path length of a gluon in the nucleus travelling through before scattering with another gluon in the proton to produce a heavy quark dipole at the position${\boldsymbol x}_{T}$ .$ a_{gN} $ represents the extra transverse momentum square in a unit of length of nucleons before the fusion process. Its value is taken to be$ a_{gN}=0.15\ \rm{GeV^2/fm} $ [45]. The charmonium distribution in pp collisions has been measured by the ALICE Collaboration at 2.76 TeV and 7 TeV [46, 47]. With these data, we parametrize the normalized$p_{T}$ distribution of charmonium at$ \sqrt{s_{NN}}=5.02 $ TeV and obtain$ \begin{align} {{\rm d} N_{J/\psi}\over 2\pi p_T {\rm d}{ p_T}} = {(n-1)\over \pi (n-2) \langle p_T^2\rangle_{pp}}\left[1+{p_T^2\over (n-2)\langle p_T^2\rangle_{pp}}\right]^{-n}, \end{align} $

(3) where
$ n=3.2 $ , and the mean transverse momentum square of charmonium is parametrized as$ \langle p_T^2\rangle_{pp}(y)=12.5\times [1- (y/y_{\rm max})^2] \rm{(GeV/c)^2} $ , in which the maximum rapidity of charmonium is defined with$ y_{\rm max}=\ln(\sqrt{s_{NN}}/m_\Psi) $ [48].$ m_\Psi $ is the charmonium mass. -
The heavy quark potential of the
$ c\bar c $ dipole is modified by a hot medium, which affects the evolution of charmonium wave functions [49–51]. Hot medium effects can be included in the Hamiltonian of$ c\bar c $ dipoles. Because a charm quark is heavy compared with the inner movement of charmonium bound states, the relativistic effect is ignored when considering the inner structure of a charmonium. We employ the time-dependent Schrödinger equation to describe the evolution of$ c\bar c $ dipole wave functions with in-medium complex potentials. Assuming the heavy quark-medium interaction is spherical without angular dependence, there is no mixing between charmonium eigenstates with different angular momenta in the wave function of the$ c\bar c $ dipole. The radial part of the$ c\bar c $ dipole wave function in the center of mass frame is separated as follows:$ \begin{align} {\rm i}\,\hbar {\partial \over \partial t}\psi( r, t) = \Bigg[-{\hbar^2\over 2m_\mu}{\partial ^2\over \partial r^2} +V( r, T) + {L(L+1)\hbar^2\over 2 m_\mu r^2}\Bigg]\psi(r,t), \end{align} $

(4) where r is the relative distance between charm and anti-charm quarks, and t is the proper time in the center of mass frame.
$ m_\mu=m_1m_2/(m_1+m_2)=m_c/2 $ is the reduced mass, and$ m_c $ is the charm quark mass.$ \psi(r,t) $ is defined as$ \psi(r,t)=r R(r,t) $ , where$ R(r,t) $ is the radial part of the$ c\bar c $ dipole wave function. The complete wave function of the$ c\bar c $ dipole can be expanded in the eigenstates of the vacuum Cornell potential,$ \Psi(r,\theta, \phi)= \sum_{nlm}c_{nlm}R_{nl}(r)Y_{lm}(\theta, \phi) $ .$ Y_{lm} $ is the spherical harmonics function, and$ L=(0,1,...) $ is the quantum number of the angular momentum. In an ideal fluid with zero viscosity, the heavy quark potential$ V(r,T) $ is radial. There are no transitions between charmonium eigenstates with different angular momenta L. The potential depends on the local temperature of the medium, which is given by the hydrodynamic model in the next section. The radial Schrödinger equation (Eq. (4)) is solved numerically using the Crank–Nicolson method (taking natural units$ \hbar=c=1 $ ). The numerical form of the Schrödinger equation is simplified to$ \begin{align} {\boldsymbol T}_{j,k}^{n+1}\psi_{k}^{n+1} = \mathcal{V}_{j}^{n}. \end{align} $

(5) Here, j and k are the index of rows and columns in the matrix
$\boldsymbol T$ , respectively. The non-zero elements in the matrix are$ \begin{aligned}[b] &{\boldsymbol T}^{n+1}_{j,j}= 2+2a+bV_j^{n+1}, \\ &{\boldsymbol T}^{n+1}_{j,j+1}={\boldsymbol T}^{n+1}_{j+1,j}= -a, \\ &\mathcal{V}_j^n= a\psi_{j-1}^n +(2-2a-bV_j^n)\psi_j^n +a\psi_{j+1}^n , \end{aligned} $

(6) where i is an imaginary number,
$a= {\rm i} \Delta t/(2m_\mu (\Delta r)^2)$ , and$b= {\rm i}\Delta t$ . The subscript j and superscript n in$ \psi_j^n $ represent the coordinate$ r_j=r_0 +j\cdot \Delta r $ and time$ t^n=t_0 +n\cdot\Delta t $ , respectively.$ \Delta r $ and$ \Delta t $ are the steps of the radius and time in the numerical simulation, respectively, and their values are taken to be$ \Delta t=0.001 $ fm/c and$ \Delta r=0.03 $ fm, respectively.$ t_0 $ is the start time of the Schrödinger equation. The matrix${\boldsymbol T}^{n}$ at each time step depends on the in-medium heavy quark potential$ V(r,T) $ , which is given later.The Schrödinger equation (Eq. (4)) describes the evolution of the wave function of the
$ c\bar c $ dipole from$ t\ge t_0 $ . The initial wave function of the$ c\bar c $ dipole is taken to be one of the charmonium eigenstates. After traveling through the hot medium, the fractions$ |c_{nl}(t)|^2 $ of each charmonium eigenstate (1S, 1P, 2S, etc.) in the$ c\bar c $ dipoles change with time.$ c_{nl}(t) $ is defined as$ \begin{align} c_{nl}(t) &= \int R_{nl}(r) {\rm e}^{-{\rm i}E_{nl} t} \psi(r,t) r {\rm d} r , \end{align} $

(7) where the radial wave function
$ \psi(r,t) $ is given by Eq. (5). The ratio of the final and initial fractions of a certain charmonium state in one$ c\bar c $ dipole is expressed as$ R^{\rm direct}(t) ={|c_{nl}(t)|^2\over |c_{nl}(t_0)|^2} $ . In p-Pb collisions, the initial spatial and momentum distributions of primordially produced$ c\bar c $ dipoles are given by Eq. (1). After averaging over the position and momentum bins of different$ c\bar c $ dipoles in p-Pb collisions, we can obtain the ensemble-averaged fractions of a certain charmonium state in the$ c\bar c $ dipole$ \langle |c_{nl}(t)|^2\rangle_{\rm en} $ . The direct nuclear modification factor of the charmonium eigenstate ($ n,l $ ) is written as$ \begin{aligned}[b] R_{pA}^{\rm direct}(nl) &={\langle |c_{nl}(t)|^2\rangle_{\rm en}\over \langle |c_{nl}(t_0)|^2\rangle_{\rm en}} \\ &={\displaystyle\int {\rm d}{\boldsymbol x}_{\Psi}{\rm d}{\boldsymbol p}_{\Psi} |c_{nl}(t, {\boldsymbol x}_{\Psi}, {\boldsymbol p}_{\Psi})|^2{{{\rm d}N^{\Psi}_{pA}}\over{\rm d}{\boldsymbol x}_{\Psi} {\rm d}{\boldsymbol p}_{\Psi}} \over \displaystyle\int {\rm d}{\boldsymbol x}_{\Psi} {\rm d} {\boldsymbol p}_{\Psi} |c_{nl}(t_0,{\boldsymbol x}_0, {\boldsymbol p}_{\Psi})|^2 {\overline {{\rm d}N^{\Psi}_{pA}}\over {\rm d}{\boldsymbol x}_{\Psi}{\rm d}{\boldsymbol p}_{\Psi}}}, \end{aligned} $

(8) where
${\boldsymbol x}_{\Psi}$ and${\boldsymbol p}_{\Psi}$ are the position and total momentum of the correlated$ c\bar c $ dipole, respectively. Without the hot medium effects, these correlated$ c\bar c $ dipoles are simply charmonium eigenstates without dissociation.${{\rm d}N_{pA}^{\Psi}\over {\rm d}{\boldsymbol x}_{\Psi}{\rm d}{\boldsymbol p}_{\Psi}}$ is the initial spatial and momentum distributions of primordially produced charmonium in p-Pb collisions and is given by Eq. (1). Note that in the denominator,${\overline{{\rm d}N_{pA}^{\Psi}}\over {\rm d}{\boldsymbol x}_{\Psi}{\rm d}{\boldsymbol p}_{\Psi}}$ is calculated using Eq. (1) excluding cold nuclear matter effects.After considering feed-down contributions from excited states, the nuclear modification factor of
$ J/\psi $ can be obtained (which is given in the experimental data),$ \begin{align} R_{pA}(J/\psi) = {\sum_{nl} \langle |c_{nl}(t)|^2\rangle_{\rm en} f_{pp}^{nl} \mathcal{B}_{nl\rightarrow J/\psi}\over \sum_{nl} \langle |c_{nl}(t_0)|\rangle^2\rangle_{\rm en} f_{pp}^{nl} \mathcal{B}_{nl\rightarrow J/\psi}} ,\end{align} $

(9) where
$ \mathcal{B}_{nl\rightarrow J/\psi} $ is the branching ratio of charmonium eigenstates with the quantum number$ (n,l) $ decaying into the ground state$ J/\psi $ . We consider the decay channels$ \chi_c\rightarrow J/\psi $ and$ \psi(2S)\rightarrow J/\psi $ .$ f_{pp}^{nl} $ is the direct production of the charmonium eigenstate ($ J/\psi $ ,$ \chi_c $ ,$ \psi(2S) $ ) without the feed-down process in pp collisions. The ratio of direct charmonium production is extracted to be$ f_{pp}^{J/\psi}:f_{pp}^{\chi_c}:f_{pp}^{\psi(2S)} =0.68:1:0.19 $ [52]. -
In vacuum, the heavy quark potential in the quarkonium can be approximated as the Cornell potential. At finite temperature, the Cornell potential is screened by thermal light partons. The real part of the in-medium heavy quark potential is between the limits of the free energy F and internal energy U of charmonium. The in-medium potential has been studied using lattice QCD calculations and potential models [53–56]. We parametrize the temperature and coordinate dependence of free energy using the formula
$ \begin{aligned}[b] F(T,r) =& -{\alpha\over r}[e^{-\mu r}+\mu r] \\ & -{\sigma \over 2^{3/4}\Gamma[3/4]}\left({r\over \mu}\right)^{1/2} K_{1/4}[(\mu r)^2] +{\sigma\over 2^{3/2}\mu }{\Gamma[1/4]\over \Gamma[3/4]}, \end{aligned} $

(10) where
$ \alpha=\pi/12 $ and$ \sigma=0.2\ \rm{GeV^2} $ are given in the Cornell potential$ V_c(r)={-\alpha/r}+\sigma r $ . The Γ and$ K_{1/4} $ are the Gamma function and modified Bessel function, respectively. The screened mass in Eq. (10) is taken as [54]$ \begin{aligned}[b] {\mu(\bar T)\over \sqrt{\sigma}} = s\bar{T} +a \sigma_t \sqrt{\pi \over 2} \left[\mathrm{erf}\left({b\over \sqrt{2}\sigma_t}\right) - \mathrm{erf}\left({b-\bar{T}\over \sqrt{2}\sigma_t}\right)\right], \end{aligned} $

(11) with
$ {\bar T}\equiv T/T_c $ , where$ T_c $ is the critical temperature of the deconfined phase transition. Other parameters are taken as$ s=0.587 $ ,$ a=2.150 $ ,$ b=1.054 $ , and$ \sigma_t=0.07379 $ .$ \mathrm{erf}(z) $ is the error function. The internal energy of a heavy quarkonium can be obtained via the relation$ U(T,r)= F+ T(-\partial F/\partial T) $ . When the slope of the line becomes flat, this indicates that there is no attractive force to restrain the wave function at the distance r. At temperatures of approximately$ T_c $ , there is a sudden shift in the screened mass$ \mu(\bar T) $ [54]. The internal energy may become slightly larger than the vacuum Cornell potential. This behavior can be seen in$ U(T,r) $ at$ r\sim 0.4 $ fm in Fig. 1 and becomes more evident at$ T\rightarrow T_c $ . To avoid this subtlety, for the heavy quark potential, we take the free energy as the limit of strong color screening and the vacuum Cornell potential as the limit of extremely weak color screening. The realistic potential is between these two limits. Different heavy quark potentials in Fig. 1 are inserted into the Schrödinger equation to calculate the nuclear modification factors of$ J/\psi $ and$ \psi(2S) $ in the next section.
Figure 1. (color online) Different parametrizations of the real part of heavy quark potentials as a function of r at
$ T=1.5T_c $ . The free energy$ F(r,T) $ , internal energy$ U(r,T) $ , and Cornell potential$ V_c(r) $ are plotted with different colored lines.In the hot medium, quarkonium bound states can also be dissociated by inelastic scatterings with thermal light partons. This process contributes an imaginary part to the potential
$ V(T,r) $ . We parameterize the temperature and spatial dependence of the imaginary potential using$ \begin{align} &V_I(T,\bar r)= -{\rm i}\,T(a_1\, {\bar r} + a_2 {\bar r}^2)\,, \end{align} $

(12) where i is the imaginary unit, and
$ \bar r\equiv r/{\rm fm} $ is a dimensionless variable. The dimensionless coefficients$ a_1 $ and$ a_2 $ are obtained by invoking Bayesian inference to fit the lattice QCD calculations [57]. We focus on the temperature relevant to p-Pb collisions,$ T_c <T< 1.9\; T_c $ . The results are shown in Fig. 2, where the gray band represents the$ 95\% $ confidence interval, and the black curve corresponds to the parameter set$ a_1=-0.040 $ and$ a_2=0.50 $ , which maximizes the posterior distribution. In$ V_I $ , the magnitude of the imaginary potential becomes smaller at smaller distances. This results in a weaker reduction in the$ J/\psi $ component than the$ \psi(2S) $ component in the wave function of the$ c\bar c $ dipole. Because the imaginary potential in Fig. 2 is calculated in the gluonic medium, we take the same formula for QGP in heavy-ion collisions, which contributes some uncertainty to the suppression of charmonium in p-Pb collisions [56, 58]. The uncertainty on the imaginary potential is partially considered with the theoretical band in Fig. 2, which will be reflected in the charmonium$ R_{pA} $ .
Figure 2. (color online) Imaginary part of the heavy quark potential as a function of distance. The gray band represents the
$95$ % confidence region, whereas the black curve corresponds to the maximum a posteriori parameter set. The data is cited from [57]. Symbols from purple to red correspond to results from low to high temperature.In the hot medium produced in p-Pb collisions, heavy quark dipoles experience different local temperatures as they move along different trajectories. The real and imaginary parts of the potential, depending on the local temperatures, also change with time. The wave package at each time step is obtained from the Schrödinger equation, while its normalization is reduced by the imaginary part of the Hamiltonian. Therefore, the fractions of charmonium eigenstates in the wave package change with time owing to in-medium potentials.
-
The dynamical evolution of the hot medium produced in p-Pb collisions at
$ \sqrt{s_{NN}}=5.02 $ TeV is described by hydrodynamic equations [21].$ \begin{align} \partial_{\mu\nu} T^{\mu\nu}=0 ,\end{align} $

(13) where
$ T^{\mu\nu}=(e+p)u^\mu u^\nu-g^{\mu\nu}p $ is the energy-momentum tensor, e and p are the energy density and pressure, respectively, and$ u^\mu $ is the four velocity of the medium. The equation of state is required to close the hydrodynamic equations. The deconfined phase is treated as an ideal gas of gluons and massless u and d quarks plus s quarks with the mass$ m_s=150 $ MeV. The confined phase is treated using the hadron resonance gas model (HRG) [59]. Two phases are connected with a first-order phase transition, and the critical temperature of the phase transition is determined as$ T_c=165 $ MeV by choosing the mean field repulsion parameter and bag constant to be$ K=450 \ \rm{MeV\,fm^3} $ and$ B^{1/4}=236 $ MeV [60], respectively. With the multiplicity of light hadrons measured in p-Pb collisions and theoretical simulations from other hydrodynamic models [21, 61], we take the maximum initial temperature of the hot medium to be$T_0({\boldsymbol x}_T=0|b=0)= 248$ MeV in forward rapidity and$ 289 $ MeV in backward rapidity. Event-by-event fluctuations in hydrodynamic evolution are not yet included. The profile of the initial energy density is also consistent with the results from a multiple phase transport (AMPT) model [62].Hydrodynamic equations begin evolution from
$ \tau_0=0.6 $ fm/c, where the hot medium is assumed to reach local equilibrium. The time evolution of the local temperature at$ { x}_T=0 $ in forward and backward rapidity at most central collisions with the impact parameter b =0 is plotted in Fig. 3. Medium evolution with other impact parameters can be obtained via the scale of initial entropy, which depends on$ N_p(b) $ and$N_{\rm coll}(b)$ . -
We apply the Schrödinger equation to charmonium dynamical evolution in
$ \sqrt{s_{NN}}=5.02 $ TeV p-Pb collisions. In Fig. 5,$ R_{pA}s $ of$ J/\psi $ and$ \psi(2S) $ in forward rapidity (defined as the proton-going direction) are plotted. The shadowing effect modifies the parton densities in the colliding nucleus, which changes the gluon density and charmonium production in nucleus collisions compared with those in pp collisions. Because the shadowing effect exists before the initial production of a heavy quark pair in parton hard scatterings, it gives the same modification factor of$ J/\psi $ and$ \psi(2S) $ , shown as the black dotted line in Fig. 5. However, the experimental data show different degrees of suppression of the production of$ J/\psi $ and$ \psi(2S) $ , which indicates different strengths of final state interactions on different charmonium states. The magnitude of the color screening effect on charmonium deserves further investigation.To study the color screening effect on charmonium observables, we first test a scenario without an imaginary potential, as shown in Fig. 4. The calculations for a strong screening scenario with the F potential and a weak screening scenario with vacuum potential are presented in the figure. In the strong color screening scenario with the F potential, the wave function of the
$ c\bar c $ dipole expands outside owing to the weak attractive force between c and$ \bar c $ . This reduces the overlap of the wave-function between the$ c\bar{c} $ pair and charmonium eigenstate. This suppresses$ R_{pA} $ of$ J/\psi $ and$ \psi(2S) $ . The color screening effect is not strong enough to explain the strong suppression of$ \psi(2S) R_{pA} $ , which indicates the necessity of including the imaginary potential from a phenomenological perspective.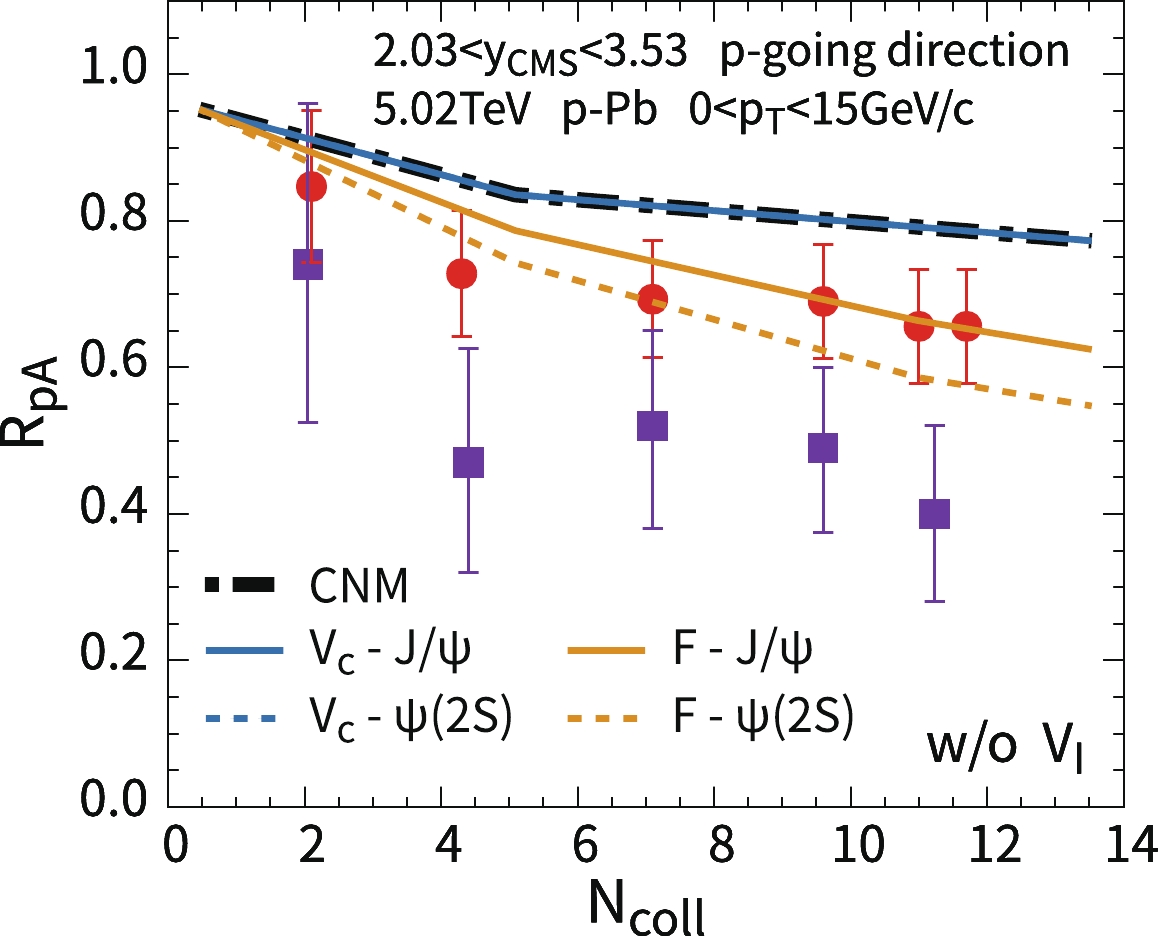
Figure 4. (color online) Nuclear modification factors of
$ J/\psi $ and$ \psi(2S) $ as a function of the number of binary collisions$ N_{\rm coll} $ in the forward rapidity of$ \sqrt{s_{NN}}=5.02 $ TeV p-Pb collisions. Only the real part of the heavy quark potential is included. The black dashed-dotted line is the calculation with only cold nuclear matter effects. The strong and weak limits of the potential are taken as the vacuum Cornell potential$ V=V_c(r) $ and free energy$ V=F(r,T) $ , respectively. The experimental data are from the ALICE Collaboration [63, 64]. The red circles and blue squares correspond to$ J/\psi $ and$ \psi(2S) $ , respectively.In Fig. 5, both color screened real and imaginary potentials are included. In the upper panel of Fig. 5, only the imaginary potential is considered without the color screening effect. The theoretical band in
$ R_{pA} $ represents the uncertainty on the parametrization of$ V_I $ . As shown, the imaginary potential can effectively explain both$ R_{pA} $ s of$ J/\psi $ and$ \psi(2S) $ . A lower$ R_{pA} $ corresponds to the upper limit of$ V_I $ parametrization. As the magnitude of$ V_I $ increases with distance, the$ \psi(2S) $ component in the$ c\bar c $ dipole wave function is more suppressed. As shown in the lower panel of Fig. 5, in a strong screening scenario, the real part of the heavy quark potential is taken as free energy,$ V_R=F(T,r) $ .
Figure 5. (color online) Nuclear modification factors of
$ J/\psi $ and$ \psi(2S) $ as a function of the number of binary collisions$N_{\rm coll}$ in the forward rapidity of$ \sqrt{s_{NN}}=5.02 $ TeV p-Pb collisions. The black dashed-dotted line is the calculation with only cold nuclear matter effects. The in-medium potential is taken to be$ V=V_c(r)+V_I(T,r) $ in the upper panel and$ V=F(T,r)+V_I $ in the lower panel. The red and blue bands are the results of$ J/\psi $ and$ \psi(2S) $ , respectively. The experimental data are from the ALICE Collaboration [63, 64]. The red circles and blue squares correspond to$ J/\psi $ and$ \psi(2S) $ , respectively.The charmonium wave function is loosely bound in the
$ c\bar{c} $ wave function. The wave function expands outside, which reduces the overlap of the wave function between the$ c\bar c $ wave package and the$ J/\psi $ eigenstate. This results in a transition of the final yields from the$ J/\psi $ to$ \psi(2S) $ states and scattering states. The value of$ R_{pA} $ is strongly reduced with$ V=F+V_I $ . The feed-down process ($ \chi_c,\psi(2S)\rightarrow J/\psi X $ ), which occurs after the charmonium escapes the hot medium, has been included in$ R_{pA} $ . Comparing the model calculated$ R_{pA}s $ with the experimental data, the vacuum potential is favored, and the color screening effect appears to be weak for charmonium at the temperatures available in p-Pb collisions. The imaginary potential is essential to explain the difference between$ R_{pA}^{J/\psi} $ and$ R_{pA}^{\psi(2S)} $ because the real potential in vacuum alone does not change the final projection of the wave-function of the$ c\bar{c} $ pair into different charmonium species.The
$ p_T $ dependence of$ J/\psi $ and$ \psi(2S) R_{pA} $ is also studied in Fig. 6. The black dashed-dotted line is the calculation with only cold nuclear matter effects. In the forward rapidity of p-Pb collisions, the shadowing effect reduces charmonium production. The value of$ R_{pA} $ from cold nuclear matter suppression alone increases with transverse momentum owing to a weaker shadowing effect at larger transverse energies. The dashed-dotted line and bands increase with$ p_T $ . Moreover,$ c\bar c $ dipoles with large velocities move rapidly out from the hot medium, where$ R_{pA} $ becomes larger owing to weaker hot medium suppression. In the upper panel of Fig. 6, theoretical calculations with only the imaginary potential can explain$ R_{pA}^{J/\psi} $ and$ R_{pA}^{\psi(2S)} $ better than with the case of the strong color screening effect in the lower panel of Fig. 6. The theoretical bands correspond to the uncertainty on$ V_I $ .
Figure 6. (color online)
$ p_T $ dependence of the$ J/\psi $ and$ \psi(2S) $ nuclear modification factors in forward rapidity in minimum-bias$ \sqrt{s_{NN}}=5.02 $ TeV p-Pb collisions. The other conditions are similar to those in Fig. 5. The experimental data are from the ALICE Collaboration [65]. The red circles and blue squares correspond to$ J/\psi $ and$ \psi(2S) $ , respectively.In backward rapidity, defined as the Pb-going direction, the anti-shadowing effect can increase
$ R_{pA} $ of$ J/\psi $ and$ \psi(2S) $ , as shown by the black dashed-dotted line in Fig. 7. Owing to the uncertainty on the anti-shadowing effect, we consider an upper-limit anti-shadowing effect, where$ R_{pA} $ is approximately 1.27 in most central collisions.$ R_{pA} $ with only the cold nuclear matter effect is greater than unity. After considering the imaginary potential, production of charmonium excited states are suppressed, and$ R_{pA}^{\psi(2S)} $ is below unity. Because approximately 40% of the final$ J/\psi $ originated from the decay of excited states ($ \chi_c $ ,$ \psi(2S) $ ) to$ J/\psi $ , the suppression of excited states affect$ R_{pA}^{J/\psi} $ via the feed-down process. As shown in the upper panel of Fig. 7, theoretical calculation of$ J/\psi R_{pA} $ reproduces the experimental data in peripheral and semi-central collisions, whereas in central collisions$N_{\rm coll}\sim 12$ , the theoretical band is at the edge of the experimental data. This discrepancy between the theoretical results and the experimental data is also reflected in the semi-classical transport model [23] and comover model [66], where$ R_{pA}^{J/\psi}\lesssim 1 $ at$N_{\rm coll}\sim 12$ . In a strong color screening scenario with the F-potential,$ J/\psi $ theoretical bands strongly underestimate the experimental data. This observation is consistent in both backward and forward rapidities.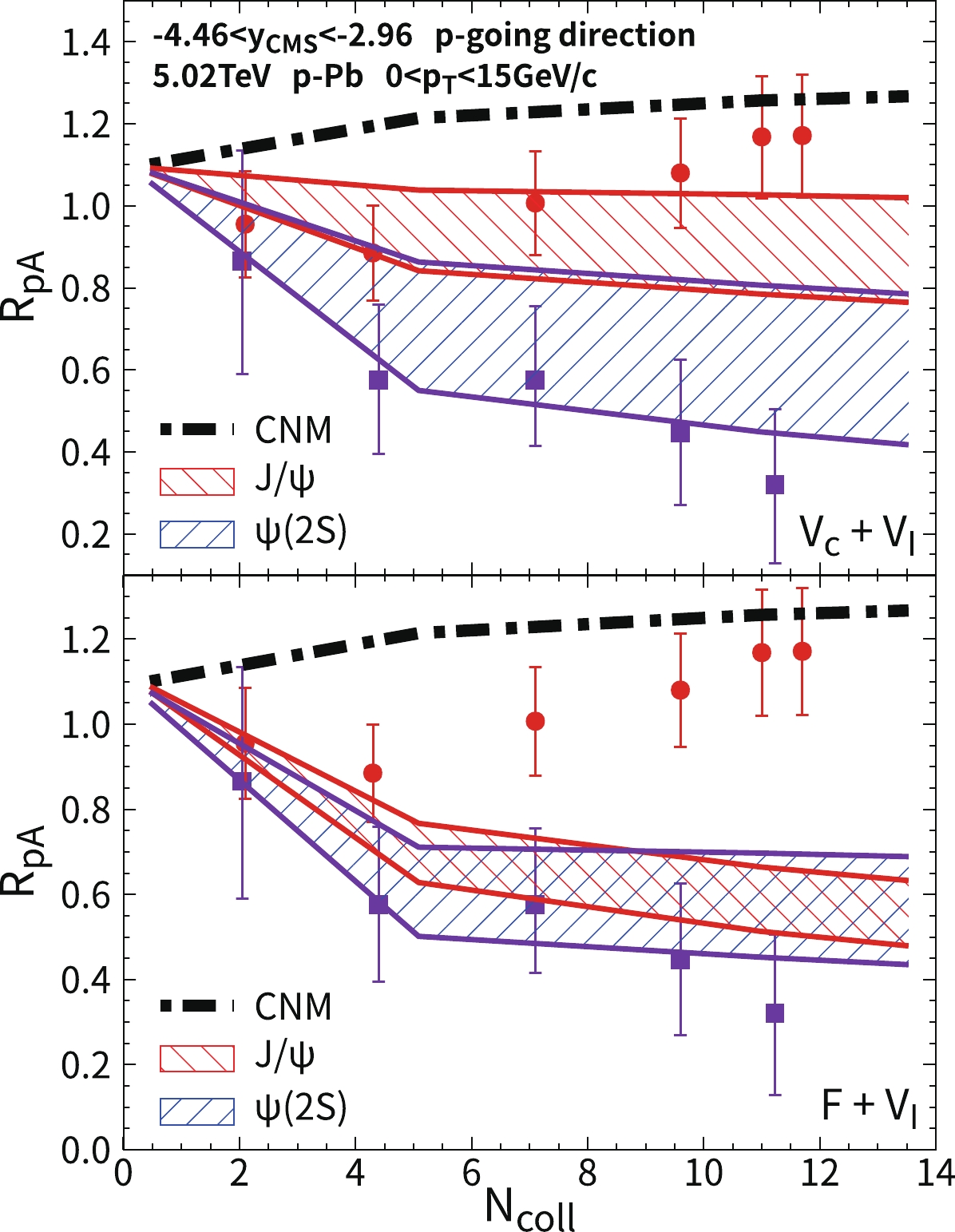
Figure 7. (color online) Nuclear modification factors of
$ J/\psi $ and$ \psi(2S) $ as a function of the number of binary collisions$ N_{coll} $ in the backward rapidity of$ \sqrt{s_{NN}}=5.02 $ TeV p-Pb collisions. The red and blue bands are the results of$ J/\psi $ and$ \psi(2S) $ , respectively. The bands originate from the uncertainty on$ V_I $ . In-medium heavy quark potentials are taken as$ V=V_c(r)+V_I(T,r) $ in the upper panel and$ V=F(T,r)+V_I(T,r) $ in the lower panel. The experimental data are from the ALICE Collaboration [63, 64]. The red circles and blue squares correspond to$ J/\psi $ and$ \psi(2S) $ , respectively.The
$ p_T $ dependence of charmonium$ R_{pA} $ is also calculated in the backward rapidity and presented in Fig. 8. The black dashed-dotted line only includes cold nuclear matter effects. Hot medium effects reduce$ R_{pA} $ of$ J/\psi $ and$ \psi(2S) $ in the low$ p_T $ region. At high$ p_T $ , the anti-shadowing effect causes$ R_{pA}^{J/\psi} $ to become larger than unity. When the real part of the heavy quark potential is taken as the vacuum potential, theoretical bands describe the data well in the upper panel of Fig. 8, whereas calculations with the F potential in the lower panel give small$ R_{pA} $ of$ J/\psi $ owing to the expansion of the$ c\bar c $ wave package.
Figure 8. (color online)
$ p_T $ dependence of the$ J/\psi $ and$ \psi(2S) $ nuclear modification factors in backward rapidity in minimum-bias$ \sqrt{s_{NN}}=5.02 $ TeV p-Pb collisions. The other conditions are similar to those in Fig. 7. The experimental data are from the ALICE Collaboration [65]. The red circles and blue squares correspond to$ J/\psi $ and$ \psi(2S) $ , respectively. -
In this study, we employ a time-dependent Schrödinger model to investigate hot medium effects on charmonium observables in proton-nucleus collisions at
$ \sqrt{s_{NN}}=5.02 $ TeV. We initialize a$ c\bar{c} $ distribution with cold nuclear matter effects, including the (anti-)shadowing and Cronin effects. Both color screening and parton scattering encodes in the real and imaginary parts of the potential, which is further incorporated into the Hamiltonian utilized in quantum evolution. To probe the strength of the color screening effect, the imaginary part of the potential is constrained by a statistical fit to lattice QCD data, while two scenarios of the real potential are considered. In the simulation, a$ c\bar{c} $ dipole, initialized with different positions and momenta, moves along different trajectories in the hydrodynamic medium, and its internal evolution is described by the Schrödinger equation. A comparison of the simulated results with experimental data favors a weak screening scenario or a strong binding scenario. Meanwhile, the imaginary potential is crucial to consistently describe the suppression of the$ J/\psi $ and$ \psi(2S) $ states and the gap between their suppressions due to the different widths of their wave-functions, indicating the importance of parton scattering for different charmonium species.The essential phenomenological results of quantum evolution presented in this paper are consistent with those from thoroughly studied semi-classical transport approaches. In semi-classical approaches, color screening affects the in-medium binding energies of charmonium states, leading to different dissociation widths, whereas in the potential model discussed in this paper, color screening broadens the
$ c\bar{c} $ wave-function, leading to a transfer of bound states to scattering states. The non-Hermitian imaginary part of the potential directly eliminates the tracking of a$ c\bar{c} $ pair, corresponding to the dissociation width. Both effects lead to different suppression strengths; however, the imaginary part (dissociation) is shown to be crucial for suppression within both the potential approach and other semi-classical approaches.There are limitations to this approach. Because the size of the
$ c\bar{c} $ pair is not significantly smaller than the size of the medium produced in pA collisions, screening at different positions of the potential may vary. Thus, a potential model may not be well-defined in this case. However, this approach is only one angle of investigating charmonium production in small systems. A potential model for bottomonium would be favored as a subject of study. Statistical extraction of the in-medium heavy quark potential has been conducted using a semi-classical transport approach [67], which incorporates the potential in the binding energies and dissociation widths of bottomonium states. Within this potential approach, direct extraction of the in-medium heavy-quark potential can be performed for bottomonium in AA collisions. We leave this to further publications. -
We appreciate inspiring discussions with Pengfei Zhuang, Ralf Rapp, Shuai Liu, and Yunpeng Liu.
Investigating color screening in proton-nucleus collisions with complex potentials
- Received Date: 2022-05-23
- Available Online: 2022-11-15
Abstract: Color screening and parton inelastic scattering modify the heavy-quark antiquark potential in mediums consisting of particles from quantum chromodynamics (QCD), leading to the suppression of quarkonium production in relativistic heavy-ion collisions. Owing to the small charm/anti-charm (





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF





















 DownLoad:
DownLoad: