-
α decay has always been a hot topic in nuclear physics because it can provide abundant nuclear structure information such as ground state [1], nuclear shell effect [2], energy levels [3], nuclear shape coexistence [4–6], low lying states [7] and so on. As one of the most important decay modes of superheavy nuclei [8], α decay was first explained by Rutherford in 1908 in terms of a process where a parent nucleus emits a
$ ^{4} $ He particle [9]. Following the foundation and development of quantum mechanics, Gamow [10] and Condon and Gurney [11] in 1928 intepreted the theory of α decay as a quantum penetration of α particles via tunneling.Up to now, based on Gamow theory, a great deal of models and/or approaches have been put forward to study α decay. The commonly used models are the cluster model [12–18], the Coulomb and proximity potential model (CPPM) [19, 20], the two-potential approach (TPA) [21–27], the density dependent M3Y (DDM3Y) effective interaction [28–33], the shell model [34], the generalized liquid drop model (GLDM) [35–37], the fission-like model [38–40] and so on. These models, with their own merits and failures, have been in acceptable agreement with experimental data. Moreover, there are lots of efficient and useful empirical formulas to calculate the α-decay half-lives such as the Viola–Seaborg formula (VS) [41], the universal decay law (UDL) [42, 43], the Royer formula [44], the Hatsukawa formula [45] and Qian et al. formula (YQZR) [46, 47] while their improvements are the Viola–Seaborg–Sobiczewski formula (VSS) [48] and the modified Viola–Seaborg formula (MVS) [49], the modified universal decay law (MUDL) [50], the unitary Royer formula (DZR) [51], the modified Hatsukawa formula (XLZ) [52] and the modified Yibin et al. formula (MYQZR) [53], respectively. From the experimental aspect, the development of radioactive beams and low temperature detector technology make it possible to synthesize new superheavy nuclei [54] and search new α-emitters in artificially occurring nuclides [55, 56].
Recently, we were intrigued by a series of reports on the synthesis of uranium isotopes. In 2015, the new neutron-deficient isotope
$ ^{215} {{\rm{U}}}$ was produced in the complete-fusion reaction$^{180} {{\rm{W}}} ( ^{40} {{\rm{Ar}}}, 5{{n}})^{215} {{\rm{U}}}$ [57]. Evaporation residues recoiled from the target were separated in flight from the primary beam by the gas-filled recoil separator SHANS [58] and subsequently identified on the basis of energy–position–time correlation measurement. The α-particle energy and half-life of$ ^{215} {{\rm{U}}}$ were determined to be 8.428(30) MeV and 0.73$^{+1.33}_{-0.29}$ ms, respectively. In 2016, Zhang et al. identified two α-decaying states in$^{216} {{\rm{U}}} $ , one for the ground state and the other for the isomeric state with 8$ ^{+} $ ($\pi h_{9/2} \pi _{7/2}$ ) configuration. The α-decay properties for$^{215,216} {{\rm{U}}} $ and the systematics of 8$ ^{+} $ isomeric state in N = 124, 126 isotones were also investigated [59, 60]. In 2021, a new α-emitting isotope$ ^{214} {{\rm{U}}}$ , produced by the fusion–evaporation reaction$^{182} {\rm W} (^{36}{\rm Ar}, 4n)^{214} {\rm U}$ was identified by employing the gas-filled recoil separator SHANS and the recoil-α correlation technique. More precise α-decay properties of even–even nuclei$ ^{216,218} {{\rm{U}}}$ were also measured in the reactions of$^{40}$ Ar and$^{40}$ Ca beams with$^{180,182,184}$ W targets [61].In addition, taking into account the electrostatic screening effect caused by the superposition of the involved charges, Budaca et al. recently proposed a simple analytical model based on the Wentzel–Kramers–Brillouin (WKB) approximation to systematically study the half-lives of proton radioactivity [62]. The results show that with the increase of proton number Z, the difference between the outer turning point radii increases, corresponding to whether the electrostatic screening effect is included in the Coulomb barrier or not. Because the penetration probability is very sensitive to outer turning point radii, it is necessary to introduce the screened electrostatic barrier, i.e. Hulthen potential [63], in the process of dealing with the decay problem. In recent years, the Hulthen potential has been widely used to study the half-lives of α decay, proton radioactivity and two-proton radioactivity [64–66], and the calculated results reproduce the experimental data well.
In 2005, Tavares et al. first evaluated the α-decay half-lives of bismuth isotopes with angular momentum l=5 carried away by the emitted α particle, based on the Gamow model [67]. Since then, it has been successfully generalized to calculate the α-decay half-lives of platinum isotopes with l=0 [68] and neptunium isotopes with l=0 and l=1 [69]. The calculations of these works are in good agreement with experimental data. Based on this model, considering the screened electrostatic barrier, in this work we systematically calculate the α-decay half-lives of uranium isotopes and explore the robustness of N = 126 shell closure at Z = 92 with the experimental data taken from the latest evaluated nuclear properties table NUBASE2020 [70].
This article is organized as follows. In Section II, the theoretical frameworks of the Gamow model and the screened electrostatic barrier are described in detail. The calculations and discussion are presented in Section III. Finally, Section IV gives a brief summary.
-
The α-decay half-life, an important indicator of nuclear stability, is calculated by
$ \begin{eqnarray} \label{1} T_{1/2} = \frac{{{\rm{ln2}}}}{\lambda}, \end{eqnarray} $

(1) where the decay constant λ can be obtained by
$ \begin{eqnarray} \label{2} \lambda=\nu_{0}S_{\alpha}P_{se}. \end{eqnarray} $

(2) Here the frequency factor
${\nu}_0$ , which represents the number of assualts on the barrier per unit of time [71, 72], is usually estimated as$ \begin{eqnarray} \label{3} {\nu}_0=\frac{v}{2a}=\frac{1}{2a}\sqrt{\frac{2Q_{\alpha}}{{\mu}}}, \end{eqnarray} $

(3) where v is the velocity of the α particle inside the parent nucleus.
$S_{\alpha}$ is the spectroscopic factor (also known as α particle preformation probability at the nuclear surface) and$P_{se}$ is the penetrability factor through the external barrier region [73]. They can be expressed as$ \begin{aligned}[b] & \label{4} S_{\alpha}={\rm e}^{-G_{ov}}, G_{ov}=\frac{2}{\hbar}\int_{a}^{b} \sqrt{2\mu[V(r)-Q_{\alpha}]}{\rm d} r,\\ &P_{se} = {\rm e}^{-G_{se}}, G_{se}=\frac{2}{\hbar}\int_{b}^{c} \sqrt{2\mu[V(r)-Q_{\alpha}]}{\rm d}r, \end{aligned} $

(4) where
$\hbar$ is the reduced Planck constant, μ denotes the reduced mass of α particle and daughter nucleus in the center-of-mass coordinate with$m_d$ and$m_{\alpha}$ being the mass of the daughter nucleus and α particle, and$V(r)$ is the total interaction potential between the emitted α particle and daughter nucleus which is depicted in Fig. 1.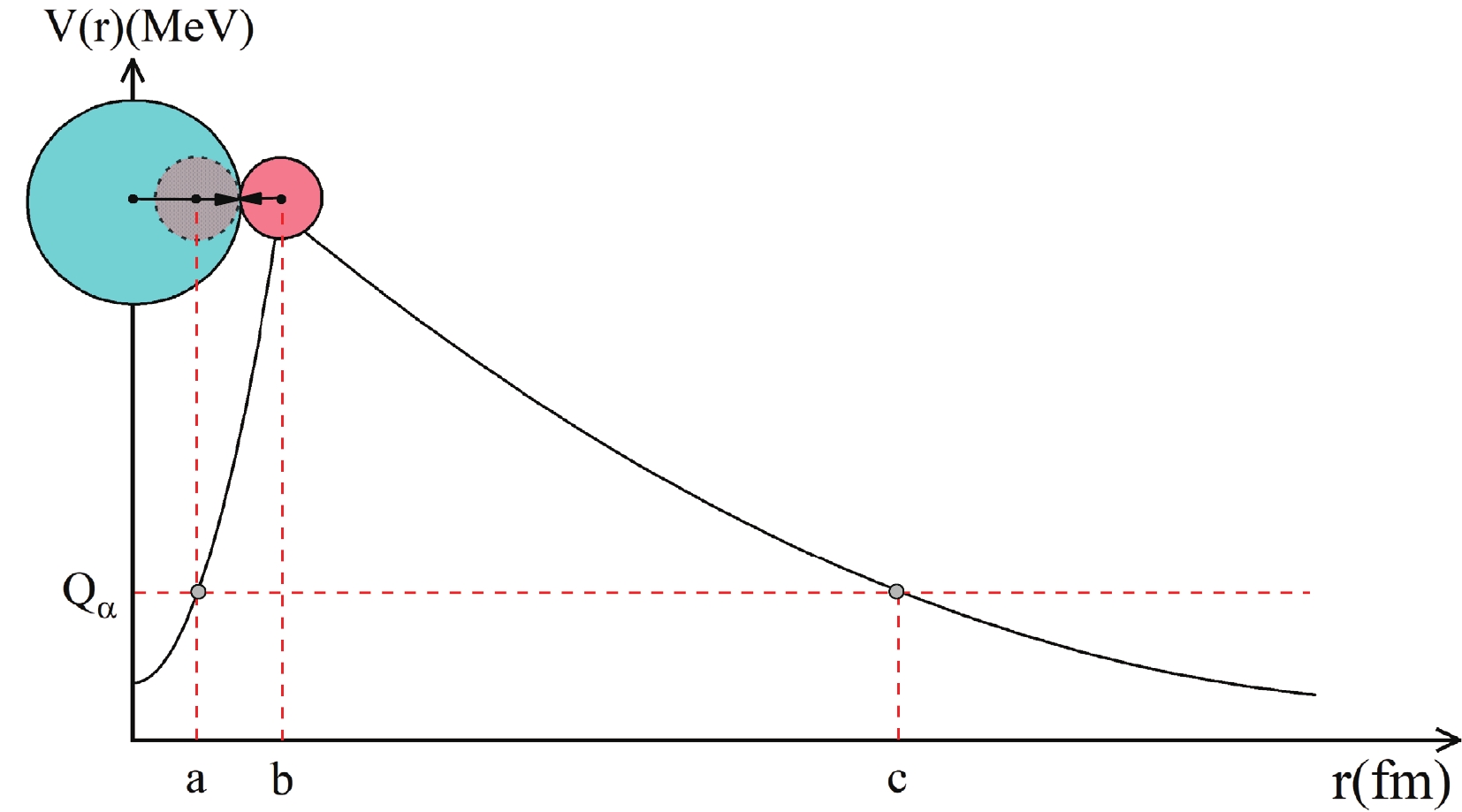
Figure 1. (color online) Schematic diagram of one-dimensional α-daughter nucleus interaction potential potential
$V(r)$ . a, b and c are the three turning points of the potential energy while the barrier from a to b is the overlapping region and b to c is the separation region.In general,
$V(r)$ is composed of the nuclear potential$V_n(r)$ , the Coulomb potential$V_c(r)$ and centrifugal potential$V_l(r)$ by default. It can be expressed as$ \begin{eqnarray} \label{5} V(r) = V_n(r) + V_c(r) + V_l(r). \end{eqnarray} $

(5) Here, the Coulomb potential
$V_c(r)$ is written as$ \begin{eqnarray} \label{6} V_{c}(r)=\frac{Z_{\alpha}Z_de^2}{r}, \end{eqnarray} $

(6) where
$Z_{\alpha}$ and$Z_d$ represent the proton numbers of α particle and daughter nucleus, respectively, and$e^2$ is the square of the electronic elementary charge. In the process of α decay, for the superposition of the involved charges, movement of the emitted particle which generates a magnetic field and the inhomogeneous charge distribution of the nucleus, the emitted α-daughter nucleus electrostatic potential behaves as a Coulomb potential at short distance and drops exponentially at large distance, i.e. the screened electrostatic effect [63–66]. This behaviour of electrostatic potential can be described as the Hulthen type potential which is defined as$ \begin{eqnarray} \label{7} V_{h}(r)=\frac{tZ_{\alpha}Z_de^2}{e^{tr}-1}, \end{eqnarray} $

(7) where t is the screening parameter. The centrifugal potential
$V_{l}(r)$ can be expressed as$ \begin{eqnarray} \label{8} V_{l}(r)=\frac{l(l+1){\hbar}^2}{2{\mu}r^2}. \end{eqnarray} $

(8) where l is the orbital angular momentum taken away by the emitted α particle. l=0 for the favored α decays, while
$l \neq $ 0 for the unfavored α decays. On the basis of conservation laws of angular momentum and parity, the minimum angular momentum$ l_{{{\rm{min}}}} $ taken away by the α particle can be obtained by$ \begin{eqnarray} l_{{{\rm{min}}}}=\left\{\begin{array}{llll} \Delta_j, & {\rm{for}}\;\;{\rm{even}} ~~ \Delta_j ~~{\rm{and}}~~ \pi_p=\pi_d, \\ \Delta_j+1, & {\rm{for}}\;\;{\rm{even}}~~ \Delta_j ~~{\rm{and}}~~ \pi_p\neq\pi_d,\\ \Delta_j, & {\rm{for}}\;\;{\rm{odd}} ~~ \Delta_j ~~{\rm{and}}~~ \pi_p\neq\pi_d,\\ \Delta_j+1, & {\rm{for}}\;\;{\rm{odd}} ~~\Delta_j ~~{\rm{and}}~~ \pi_p=\pi_d, \end{array}\right. \end{eqnarray} $

(9) where
$ \Delta_j=|j_p-j_d| $ with$ j_p $ ,$ \pi_p $ ,$ \pi_d $ ,$ j_d $ being the spin and parity values of parent and daughter nuclei, respectively.In addition,
$ G_{ov} $ and$ G_{se} $ are the Gamow factors obtained by the integral from a to b in the overlapping barrier region and from b to c in the separation barrier region in Fig. 1. Here$ b =R_d+R_{\alpha} $ is the separating radius, with$ R_d $ and$ R_{\alpha} $ being the radii of the daughter nucleus and the emitted α particle respectively.$ a =R_p-R_{\alpha} $ and c are the inner and outer classical turning points of potential barrier, with$ R_p $ being the radius of the parent nucleus. The turning points satisfy the conditions$ V(a)=V(c)=Q_{\alpha} $ . The α-decay energy$ Q_{\alpha} $ is calculated by$ \begin{eqnarray} Q_{\alpha}=\Delta{M_p}-(\Delta{M_d}+\Delta{M_{\alpha}})+10^{-6}{k}({Z_p}^{\beta}-{Z_d}^{\beta})\ {\rm MeV}, \end{eqnarray} $

(10) where
$ \Delta{M_p} $ ,$ \Delta{M_d} $ and$ \Delta{M_{\alpha}} $ represent the mass excess of parent nuclues, daughter nucleus and α particle, respectively, and the quantity$ kZ^{\beta} $ is the total binding energy of Z electrons in the atom, where k =$ 8.7 $ eV,$ {\beta} $ =2.517 for$ Z \geq $ 60 and k=$ 13.6 $ eV,$ {\beta} $ =$ 2.408 $ for$ Z < $ 60 [74]. Based on the above, the α-decay half-life can be expressed as$ \begin{eqnarray} T_{1/2} =1.0\times 10^{-22}a \left(\frac{\mu}{Q_{\alpha}}\right)^{1/2}{S_{\alpha}}^{-1}{P_{se}}^{-1}. \end{eqnarray} $

(11) In the overlapping region, since the α particle is still in the parent nucleus, the reduced mass μ can not be simply treated as a two-body problem. Duarte and Poenaru et al. have successfully dealed with this problem in α particle emitter
$ ^{222} {\rm{Rn}} $ by using$ \mu(r) = [m_{\alpha}m_d/(m_{\alpha}+ $ $ m_d)][(r-a)/(b-a)]^3$ and$ V(r) = $ $ Q_{\alpha}+ (V(b) - $ $ Q_{\alpha} $ )$ [(r-a)/ (b-a)]^2 $ [38, 75]. Encouraged by these two descriptions, the power functions of both$ \mu(r) $ and$ V(r) $ in the overlapping region can likewise be expressed by the following forms [67]$ \begin{eqnarray} \mu{(r)} = \left(\frac{m_{\alpha}m_d}{m_{\alpha}+m_d}\right)\left(\frac{r-a}{b-a}\right)^{p} , \quad {p\ge0} \ , \end{eqnarray} $

(12) $ \begin{eqnarray} V(r) = Q_{\alpha}+\left(V(b)-Q_{\alpha}\right)\left(\frac{r-a}{b-a}\right)^{q}, \quad {q\ge1}, \end{eqnarray} $

(13) with
$ \begin{eqnarray} V(b)=V_{h}(b)+V_{l}(b)=\frac{tZ_{\alpha}Z_de^2}{e^{tb}-1}+ \frac{l(l+1){\hbar}^2}{2{\mu}b^2}. \end{eqnarray} $

(14) Using Eqs. (4), (12) and (13),
$ G_{ov} $ can be obtained as$ \begin{aligned}[b] G_{ov} =& 0.4374702(b- a)\left(1+\frac{p+q}{2}\right)^{-1} \\& \left\{\mu\left[\frac{2tZ_de^2}{e^{tb}-1}+\frac{20.9008l(l+1)}{{\mu}b^2}-Q_{\alpha}\right]\right\}^{1/2}, \end{aligned} $

(15) where
$\left(1+\dfrac{p+q}{2}\right)^{-1}$ is defined as g with 0$ \le g \le {\dfrac{2}{3}} $ .In the separation region, the parent nucleus has separated into two free individuals, the daughter nucleus and the α particle. We can deal with the reduced mass
$ \mu(r) $ as the reduced mass of the final decay system$\mu=m_{\alpha}m_d/ (m_{\alpha}+m_d)$ . Meanwhile, the potential energy V(r) including the Hulthen type potential and centrifugal potential can be calculated by$ V(r)=V_{h}(r)+V_{l}(r) $ . From the above,$ G_{se} $ can be obtained as$ \begin{eqnarray} G_{se} = 1.25988794Z_d\left(\frac{\mu}{Q_{\alpha}}\right)^{1/2}\times{F}, \end{eqnarray} $

(16) where
$ \begin{aligned}[b] F=&\frac{x^{1/2}}{2y}\times\ln \left\{\frac{\left[x(x+2y-1)\right]^{1/2}+x+y}{(x/y)\left[1+(1+x/y^2)^{1/2}\right]^{-1}+y}\right\}\\& +\arccos{\left\{{\frac{1}{2}\left[1-\frac{1-1/y}{(1+x/{y}^2)^{1/2}}\right]}\right\}^{1/2}}\\& -\left[\frac{1}{2y}\left(1+x/{2y}-1/{2y}\right)\right]^{1/2}, \end{aligned} $

(17) with
$ \begin{eqnarray} x=\frac{20.9008l(l+1)}{{\mu}b^2Q_{\alpha}} \ ,\quad y=\frac{\ln\left(tZ_{\alpha}Z_de^2/{Q_{\alpha}}+1\right)}{2tb}. \end{eqnarray} $

(18) -
Based on the Gamow model, considering the screened electrostatic effect and introducing the Hulthen type potential, we propose an improved model to evaluate the α-decay half-lives of uranium isotopes. According to Eq. (9), we select as our database 14 nuclei with experimental α-decay half-lives of the ground-state to ground-state α transition with orbital angular momentum l=0, namely
$ ^{216,218,221,222,224,226,228,229,230,232,233,234,236,238} {\rm{U}} $ , excluding the newly synthesized nucleus$ ^{214} {\rm{U}} $ , and 5 cases with l=2, namely$ ^{217,223,225,227,231} {\rm{U}} $ . Based on this database, using a genetic algorithm with an optimal solution of σ i.e. the deviation between the experimental data and calculated values as the objective function, we can obtain the values of the adjustable parameters t and g. In this work, σ is defined as follows$ \begin{eqnarray} \sigma = \sqrt{\sum{({\rm{log}}_{10}{T_{1/2}^{{\rm{calc}}}}-{\rm{log}}_{10}{T_{1/2}^{{\rm{exp}}}})^2}/n}, \end{eqnarray} $

(19) where
$ {\rm{log}}_{10}{T_{1/2}^{{\rm{exp}}}} $ and$ {\rm{log}}_{10}{T_{1/2}^{{\rm{calc}}}} $ are the logarithmic form of experimental and calculated α-decay half-lives respectively, and n is the number of nuclei involved for each case. The detailed results of the corresponding σ, t and g for the 14 α transitions with l=0 and the 5 with l=2 are listed in Table 1.σ/t/g l l = 0 l = 2 cases 14 5 σ 0.141 0.340 t $5.5239\times10^{-4}$ 

$3.0519\times10^{-8}$ 

g 0.0693 0.1549 Table 1. Standard deviations between the experimental α-decay half-lives and calculated values using our improved Gamow model for l=0 and l=2 uranium isotopes, along with the corresponding parameters t and g.
Using our improved Gamow model and the obtained values of parameters t and g, we calculate the α-decay half-lives for these uranium isotopes, 14 with l=0 and 5 with l=2. The detailed calculations are listed in Table 2. In this table, the first five columns denote the α transition, decay energy
$ Q_{\alpha} $ , spin–parity transformation, the minimum angular momentum taken away by the α particle, and the spectroscopic factor, respectively. The sixth column is the logarithm of the experimental α-decay half-life. The last five columns represent α-decay half-lives in logarithmic form of the uranium isotopes, calculated by our improved Gamow model, the modified Hatsukawa formula (XLZ) [52], the unified Royer formula (DZR) [51], the universal decay law (UDL) [42, 43] and the Viola–Seaborg–Sobiczewski formula (VSS) [48], respectively. As can be seen from this table, the calculated results of our model are close to the experimental values for most of the nuclei.$\mathcal{\alpha}$ transition

$Q_{\alpha}$ 

$j_p^{\pi}\to{j_d}^{\pi}$ 

l $S_{\alpha}$ 

${\rm{lg}}{{T}}_{1/2}^{{\rm{\,exp}}}$ 

${\rm{lg}}{{T}}_{1/2}^{{\rm{\,cal}}}$ 

${\rm{lg}}{{T}}_{1/2}^{{\rm{\,XLZ}}}$ 

${\rm{lg}}{{T}}_{1/2}^{{\rm{\,DZR}}}$ 

${\rm{lg}}{{T}}_{1/2}^{{\rm{\,UDL}}}$ 

${\rm{lg}}{{T}}_{1/2}^{{\rm{\,VSS}}}$ 

Part I: α tansitions with l=0 $ ^{216} $ U

$ \to ^{212} $ Th

8.37 $ 0 ^{+} \to 0 ^{+} $ 

0 $ 0.42 $ 

$ -2.65 $ 

$ -2.42 $ 

$ -2.35 $ 

$ -2.21 $ 

$ -2.18 $ 

$ -2.57 $ 

$ ^{218} $ U

$ \to ^{214} $ Th

8.61 $ 0 ^{+} \to 0 ^{+} $ 

0 $ 0.42 $ 

$ -3.19 $ 

$ -3.14 $ 

$ -3.07 $ 

$ -2.96 $ 

$ -2.91 $ 

$ -3.26 $ 

$ ^{221} $ U

$ \to ^{217} $ Th

9.93 $ 9/2 ^{+}\# \to 9/2 ^{+}\# $ 

0 $ 0.43 $ 

$ -6.18 $ 

$ -6.49 $ 

$ -6.19 $ 

$ -6.12 $ 

$ -6.36 $ 

$ -5.70 $ 

$ ^{222} $ U

$ \to ^{218} $ Th

9.52 $ 0 ^{+} \to 0 ^{+} $ 

0 $ 0.43 $ 

$ -5.33 $ 

$ -5.56 $ 

$ -5.47 $ 

$ -5.50 $ 

$ -5.40 $ 

$ -5.63 $ 

$ ^{224} $ U

$ \to ^{220} $ Th

8.67 $ 0 ^{+} \to 0 ^{+} $ 

0 $ 0.42 $ 

$ -3.40 $ 

$ -3.39 $ 

$ -3.33 $ 

$ -3.24 $ 

$ -3.19 $ 

$ -3.42 $ 

$ ^{226} $ U

$ \to ^{222} $ Th

7.74 $ 0 ^{+} \to 0 ^{+} $ 

0 $ 0.41 $ 

$ -0.57 $ 

$ -0.58 $ 

$ -0.56 $ 

$ -0.36 $ 

$ -0.36 $ 

$ -0.61 $ 

$ ^{228} $ U

$ \to ^{224} $ Th

6.84 $ 0 ^{+} \to 0 ^{+} $ 

0 $ 0.41 $ 

$ 2.75 $ 

$ 2.72 $ 

$ 2.72 $ 

$ 2.99 $ 

$ 2.94 $ 

$ 2.66 $ 

$ ^{229} $ U

$ \to ^{225} $ Th

6.52 $ 3/2 ^{+} \to 3/2 ^{+} $ 

0 $ 0.40 $ 

$ 4.24 $ 

$ 4.07 $ 

$ 4.26 $ 

$ 4.71 $ 

$ 4.28 $ 

$ 4.89 $ 

$ ^{230} $ U

$ \to ^{226} $ Th

6.03 $ 0 ^{+} \to 0 ^{+} $ 

0 $ 0.40 $ 

$ 6.24 $ 

$ 6.31 $ 

$ 6.30 $ 

$ 6.61 $ 

$ 6.50 $ 

$ 6.19 $ 

$ ^{232} $ U

$ \to ^{228} $ Th

5.45 $ 0 ^{+} \to 0 ^{+} $ 

0 $ 0.39 $ 

$ 9.34 $ 

$ 9.39 $ 

$ 9.36 $ 

$ 9.68 $ 

$ 9.51 $ 

$ 9.19 $ 

$ ^{233} $ U

$ \to ^{229} $ Th

4.95 $ 5/2 ^{+} * \to 5/2 ^{+} * $ 

0 $ 0.39 $ 

$ 12.70 $ 

$ 12.53 $ 

$ 12.70 $ 

$ 13.17 $ 

$ 12.59 $ 

$ 13.12 $ 

$ ^{234} $ U

$ \to ^{230} $ Th

4.90 $ 0 ^{+} \to 0 ^{+} $ 

0 $ 0.39 $ 

$ 12.89 $ 

$ 12.86 $ 

$ 12.83 $ 

$ 13.13 $ 

$ 12.91 $ 

$ 12.56 $ 

$ ^{236} $ U

$ \to ^{232} $ Th

4.61 $ 0 ^{+} \to 0 ^{+} $ 

0 $ 0.39 $ 

$ 14.87 $ 

$ 14.87 $ 

$ 14.84 $ 

$ 15.12 $ 

$ 14.87 $ 

$ 14.51 $ 

$ ^{238} $ U

$ \to ^{234} $ Th

4.31 $ 0 ^{+} \to 0 ^{+} $ 

0 $ 0.39 $ 

$ 17.15 $ 

$ 17.24 $ 

$ 17.21 $ 

$ 17.46 $ 

$ 17.17 $ 

$ 16.80 $ 

Part II: α tansition with l=2 $ ^{217} $ U

$ \to ^{213} $ Th

8.47 $ 1/2 ^{-}\# \to 5/2 ^{-} $ 

2 $ 0.12 $ 

$ -1.71 $ 

$ -1.81 $ 

$ -2.43 $ 

$ -1.84 $ 

$ -2.47 $ 

$ -1.95 $ 

$ ^{223} $ U

$ \to ^{219} $ Th

9.21 $ 7/2 ^{+}\# \to 9/2 ^{+}\# $ 

2 $ 0.12 $ 

$ -4.19 $ 

$ -3.93 $ 

$ -4.53 $ 

$ -4.04 $ 

$ -4.63 $ 

$ -3.96 $ 

$ ^{225} $ U

$ \to ^{221} $ Th

8.05 $ 5/2 ^{+} \to 7/2 ^{+}\# $ 

2 $ 0.11 $ 

$ -1.21 $ 

$ -0.65 $ 

$ -1.33 $ 

$ -0.69 $ 

$ -1.34 $ 

$ -0.69 $ 

$ ^{227} $ U

$ \to ^{223} $ Th

7.28 $ (3/2 ^{+}) \to (5/2) ^{+} $ 

2 $ 0.11 $ 

$ 1.82 $ 

$ 1.98 $ 

$ 1.25 $ 

$ 1.96 $ 

$ 1.27 $ 

$ 1.90 $ 

$ ^{231} $ U

$ \to ^{227} $ Th

5.62 $ 5/2 ^{+}\# \to (1/2 ^{+}) $ 

2 $ 0.10 $ 

$ 9.95 $ 

$ 9.49 $ 

$ 8.66 $ 

$ 9.45 $ 

$ 8.62 $ 

$ 9.19 $ 

Part III: other α emitters in uranium isotopes $ ^{219} $ U

$ \to ^{215} $ Th

9.99 $ 9/2 ^{+}\# \to (1/2 ^{-}) $ 

5 $ - $ 

$ -4.22 $ 

$ - $ 

$ -6.29 $ 

$ -4.68 $ 

$ -6.47 $ 

$ -5.84 $ 

$ ^{235} $ U

$ \to ^{231} $ Th

4.72 $ 7/2 ^{-} * \to 5/2 ^{+} $ 

1 $ - $ 

$ 16.35 $ 

$ - $ 

$ 14.28 $ 

$ 14.84 $ 

$ 14.13 $ 

$ 14.66 $ 

Part IV: Predictions $ ^{214} $ U

$ \to ^{210} $ Th

8.53 $ 0 ^{+} \to 0 ^{+} $ 

0 $ 0.42 $ 

$ -3.28 $ 

$ -2.85 $ 

$ -2.77 $ 

$ -2.64 $ 

$ -2.61 $ 

$ -3.04 $ 

$ ^{215} $ U

$ \to ^{211} $ Th

8.63 $ 5/2 ^{-}\# \to 5/2 ^{-}\# $ 

0 $ 0.42 $ 

$ - $ 

$ -3.13 $ 

$ -2.85 $ 

$ -2.58 $ 

$ -2.90 $ 

$ -2.41 $ 

$ ^{220} $ U

$ \to ^{216} $ Th

10.33 $ 0 ^{+} \to 0 ^{+} $ 

0 $ 0.43 $ 

$ - $ 

$ -7.34 $ 

$ -7.23 $ 

$ -7.37 $ 

$ -7.24 $ 

$ -6.58 $ 

$ ^{237} $ U

$ \to ^{233} $ Th

4.27 $ 1/2 ^{+} \to 1/2 ^{+} $ 

0 $ 0.39 $ 

$ - $ 

$ 17.56 $ 

$ 17.73 $ 

$ 18.15 $ 

$ 17.48 $ 

$ 17.98 $ 

$ ^{240} $ U

$ \to ^{236} $ Th

4.08 $ 0 ^{+} \to 0 ^{+} $ 

0 $ 0.39 $ 

$ - $ 

$ 19.25 $ 

$ 19.21 $ 

$ 19.44 $ 

$ 19.12 $ 

$ 19.64 $ 

$ ^{242} $ U

$ \to ^{238} $ Th

3.71 $ 0 ^{+} \to 0 ^{+} $ 

0 $ 0.38 $ 

$ - $ 

$ 22.86 $ 

$ 22.81 $ 

$ 22.97 $ 

$ 22.59 $ 

$ 23.08 $ 

$ ^{239} $ U

$ \to ^{235} $ Th

4.17 $ 5/2 ^{+} \to 1/2 ^{+}\# $ 

2 $ 0.10 $ 

$ - $ 

$ 19.54 $ 

$ 18.59 $ 

$ 19.30 $ 

$ 18.32 $ 

$ 18.84 $ 

$ ^{241} $ U

$ \to ^{237} $ Th

3.86 $ 7/2 ^{+}\# \to 5/2 ^{+}\# $ 

2 $ 0.10 $ 

$ - $ 

$ 22.42 $ 

$ 21.44 $ 

$ 22.11 $ 

$ 21.08 $ 

$ 21.58 $ 

$ ^{243} $ U

$ \to ^{239} $ Th

3.60 $ 9/2 ^{-}\# \to 7/2 ^{+}\# $ 

1 $ - $ 

$ - $ 

$ - $ 

$ 24.18 $ 

$ 24.59 $ 

$ 23.72 $ 

$ 24.20 $ 

Table 2. α-decay half-lives in logarithmic form of uranium isotopes calculated by our improved Gamow model, the modified Hatsukawa formula (XLZ), the unified Royer formula (DZR), the universal decay law (UDL) and the Viola–Seaborg–Sobiczewski formula (VSS), which are denoted as
${\rm{lg}}{{T}}_{1/2}^{{\rm{\,cal}}}$ ,${\rm{lg}}{{T}}_{1/2}^{{\rm{\,XLZ}}}$ ,${\rm{lg}}{{T}}_{1/2}^{{\rm{\,DZR}}}$ ,${\rm{lg}}{{T}}_{1/2}^{{\rm{\,UDL}}}$ and${\rm{lg}}{{T}}_{1/2}^{{\rm{\,VSS}}}$ , respectively. The experimental α-decay half-lives, spin and parity are taken from the latest evaluated nuclear properties table NUBASE2020 [70] except for$^{216}$ U and$^{218}$ U, whose accurate experimental α-decay half-lives are taken from [Phys. Rev. Lett.${\boldsymbol{126}}$ , 152502 (2021)]. The$Q_{\alpha}$ values are taken from the latest evaluated atomic mass table AME2020 [76, 77]. The α-decay energies and half-lives are in units of MeV and s, respectively.To intuitively display the accuracy of our results, in Fig. 2, we plot in logarithmic form the deviations between the experimental half-lives and the calculated values for α emitters of uranium isotopes with l=0 and l=2 using our improved Gamow model, XLZ, DZR, UDL and VSS. They are denoted as red sphere, gray square, blue pentagon, pink triangle and orange star, respectively. From this figure, we find that the differences for our improved Gamow model are basically concentrated near zero. This indicates that the calculated α-decay half-lives using our model can reproduce the experimental values well. It should be emphasized that the experimental α-decay half-lives are taken from the latest evaluated nuclear properties table NUBASE2020 [70] except for
$ ^{216} $ U and$ ^{218} $ U, because the work [Phys. Rev. Lett.$ {\boldsymbol{126}} $ , 152502 (2021)] in 2021 provides us with more accurate experimental data.
Figure 2. (color online) Deviations in logarithmic form between the experimental and calculated α-decay half-lives for uranium isotopes with l=0 and l=2. The red sphere, gray square, blue pentagon, pink triangle and orange star represent the deviations calculated by our improved Gamow model, XLZ, DZR, UDL and VSS, respectively.
In the following, we extend the improved Gamow model to predict the α-decay half-lives of uranium isotopes with α transition l=0 and l=2 whose α decay is energetically allowed or observed but not yet quantified in NUBASE2020. The predicted α-decay half-lives are listed in Part IV of Table 2, along with the values calculated by XLZ, DZR, UDL and VSS for comparision.
The XLZ model was proposed by Xu et al. [52] to calculate the favored α-decay half-lives in 2022. It is expressed as
$ \begin{aligned}[b] {{\rm{log}}_{10}} {T}_{1/2} =& F(Z)\times\left(\frac{A_d}{A_pQ_{\alpha}}\right)^{1/2}\times\left[\arccos\sqrt{X}\right.\\& \left. -\sqrt{X(1-X)}\right]-20.446+C(Z,N)+h, \end{aligned} $

(20) where the coefficient
$ F(Z)=28.274\sqrt{Z}+2920.347/Z- 204.086 $ , and$ C(Z,N) $ represents the effect of shells on α-decay half-lives. This can be written as$ \begin{eqnarray} C(Z,N)=\left\{\begin{array}{llll} 1.547-0.077(82-Z)-0.050(126-N),\\ 78\leq{Z}\leq{82} ~~{\rm{and}}~~ {100}\leq{N}<126,\\ 1.397-0.116(Z-82)-0.061(126-N),\\ {82}<{Z}\leq{90} ~~{\rm{and}}~~ {110}\leq{N}\leq{126}. \end{array}\right. \end{eqnarray} $

(21) The last term h represents the blocking effect of unpaired nucleons, whose values for different parent nuclei are expressed as
$ \begin{eqnarray} h=\left\{\begin{array}{llll} 0, & {\rm{for }}\;\;{\rm{even - even }}\;{\rm{nuclei}} , \\ h_p=h_n=0.2018, & {\rm{for }}\;{{\rm odd} - A}\;{\rm{ nuclei}} ,\\ h_p+h_n=0.4036, & {\rm{for }}\;\;{\rm{odd - odd }}\;\;{\rm{nuclei}} . \end{array}\right. \end{eqnarray} $

(22) The DZR model for α decay was proposed by Deng et al. [51], and can be expressed as
$ \begin{eqnarray} {{\rm{log}}_{10}} {T}_{1/2} = a+bA^{1/6}\sqrt{Z}+c\frac{Z}{\sqrt{Q_{\alpha}}}+dl(l+1)+h, \end{eqnarray} $

(23) where A, Z,
$ Q_{\alpha} $ and l represent the mass number, proton number, α decay energy of parent nuclei and the angular momentum taken away by the emitted α particle, respectively. By fitting the experimental data, the values of adjustable parameters are a = –26.8125, b = –1.1255, c = –1.6057, and d = 0.0513. The values of h for different α decay cases are expressed as$h_{\rm log }= \begin{cases}0, & \text { for even-even nuclei, } \\ 0.2812, & \text { for odd } Z \text {-even } N \text { nuclei, } \\ 0.3625, & \text { for even } Z \text {-odd } N \text { nuclei, } \\ 0.7486, & \text { for odd-odd nuclei. }\end{cases} $

(24) The UDL model for α decay and cluster radioactivity modes was proposed by Qi et al. [42, 43], and can be expressed as
$ \begin{eqnarray} {{\rm{log}}_{10}} {T}_{1/2} = aZ_cZ_d\sqrt{\frac{A}{Q_{c}}}+b\sqrt{AZ_cZ_d(A_d^{1/3}+A_c^{1/3})} +c, \end{eqnarray} $

(25) where
$ A=A_cA_d/(A_c+A_d) $ , with$ A_c $ and$ A_d $ being the mass of cluster and daughter nucleus. The constants a = 0.4314, b = –0.4087 and c = –25.7725 are determined by fitting the experimental data of both α and cluster decays.The VSS formula is a five-parameter formula put forward by Viola and Seaborg for calculating α-decay half-lives [41]. It can be expressed as
$ \begin{eqnarray} {{\rm{log}}_{10}} {T}_{1/2} = (aZ+B)Q_{\alpha}^{-1/2}+cZ+D+h_{\rm log}, \end{eqnarray} $

(26) where Z is the atomic number of the parent nucleus and a, b, c and d are equal to 1.66175, –8.5166, –0.20228 and –33.9069, respectively [48]. The last term
$ h_{log} $ is expressed as$ h_{\rm log }= \begin{cases}0, & \text { for even-even nuclei, } \\ 0.772, & \text { for odd } Z \text {-even } N \text { nuclei, } \\ 1.066, & \text { for even } Z \text {-odd } N \text { nuclei, } \\ 1.114, & \text { for doubly odd nuclei. }\end{cases}$

(27) For l=0, there are seven nuclei i.e.
$ ^{214,215,220,237,240,242} $ U, among which$ ^{214} $ U was newly synthesized in 2021 and its measured α-decay half-life value is 0.52$ ^{+0.95}_{-0.21} $ ms [61]. It can be well reproduced by the present model as$ 1.41 $ ms, which also checks the reliability of our improved Gamow model. Meanwhile, the predicted α-decay half-lives of$ ^{215,220,237,240,242} $ U are$ 7.42\times10^{-4} $ ,$ 4.61\times10^{-8} $ ,$ 3.63\times10^{17} $ ,$ 1.77\times10^{19} $ and$ 7.20\times10^{22} $ s, respectively. For l=2, there are two nuclei,$ ^{239,241} $ U, with the predicted α-decay half-lives being$ 3.44\times10^{19} $ and$ 2.64\times10^{22} $ s. In order to test the reliability of predictions calculated by our model, we plot the relationship between${{\rm log_{10}} T_{1/2}}$ and$ Q_{\alpha}^{-1/2} $ , i.e. the Geiger–Nuttall law [78], in Fig. 3. From this figure, we can clearly see that our predicted α-decay half-lives for these eight nuclei$ ^{214,215,220,237,239,240,241,242} {\rm{U}} $ fit the linear relationship well. This indicates that our predicted results may be useful for future study of α-decay half-lives in newly synthesized uranium isotopes. In addition, there are two other α emitters of uranium isotopes$ ^{219} {\rm{U}} $ and$ ^{235} {\rm{U}} $ with l=5 and l=1 which can not be calculated by this work. We list them in Part III of Table 1.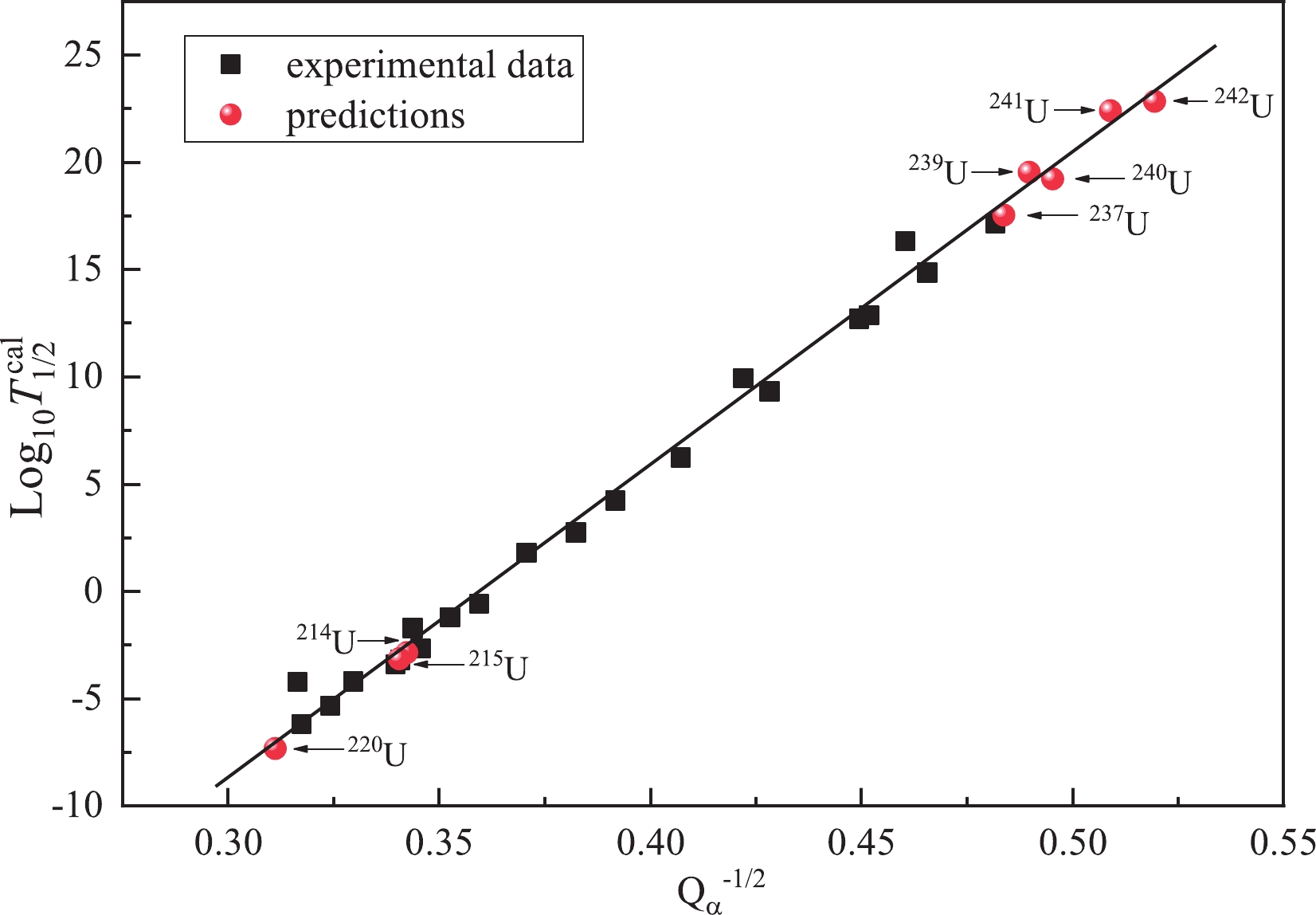
Figure 3. (color online) Logarithmic form of α-decay half-life
$\log_{10}{T_{1/2}}$ vs$Q_{\alpha}^{-1/2}$ for uranium isotopes. The line represents the Geiger–Nuttall law, black squares and red spheres denote the experimental and calculated half-lives, respectively.To verify whether the shell closure N = 126 is robust or not at Z = 92, in Fig. 4 we plot the logarithmic form of α-decay half-lives
$ \log_{10}{T_{1/2}} $ and α-decay energy$ Q_{\alpha} $ against the neutron number N of the parent nuclei. From this figure, it can be clearly seen that$ \log_{10}{T_{1/2}} $ and$ Q_{\alpha} $ present completely opposite trends with the change of N. Particularly, when N is less than 126,$ \log_{10}{T_{1/2}} $ generally shows a slow trend to fluctuate, and drops sharply after 126 until N = 128. A similar phenomenon can be seen on$ Q_{\alpha} $ , where the values of$ Q_{\alpha} $ increase dramatically to N = 128 when the neutron number is greater than 126. The above phenomena reflect strong shell effects at N = 126.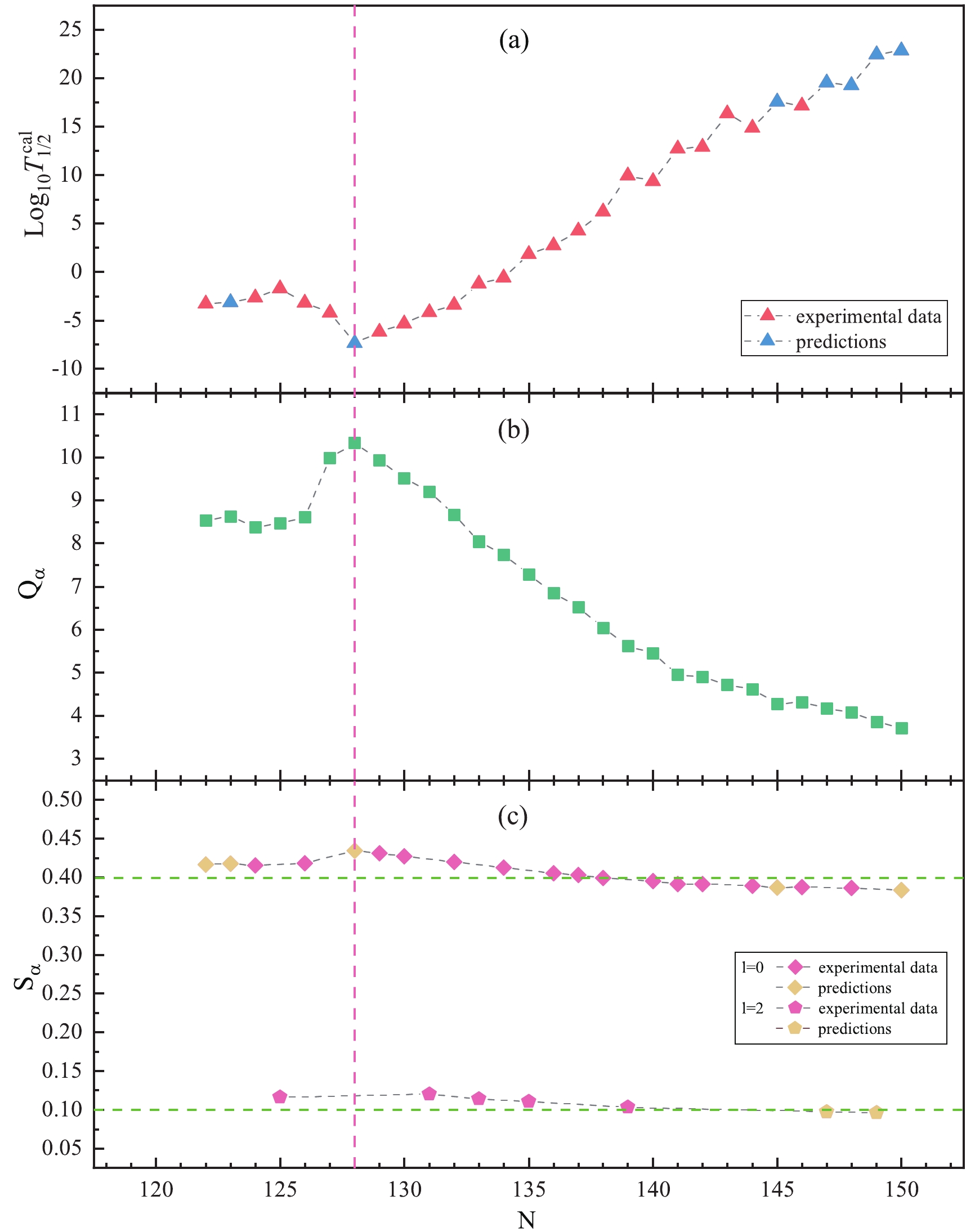
Figure 4. (color online) Relationship between the logarithmic form of α-decay half-lives
$\log_{10}{T_{1/2}}$ , α-decay energy$Q_{\alpha}$ , spectroscopic factor$S_{\alpha}$ and neutron number N of the parent nucleus : (a) for the logarithmic form of α-decay half-lives$\log_{10}{T_{1/2}}$ , the red and blue triangle represent the experimental half-lives$T^{{\rm{exp}}}_{1/2}$ and predicted values$T^{{\rm{cal}}}_{1/2}$ , respectively; (b) for the α-decay energy$Q_{\alpha}$ ; (c) for$S_{\alpha}$ with l=0 and l = 2 in neptunium isotopes, where rhombus and pentagon represent l = 0 and l = 2 while pink and pale yellow denote experimental data and predicted values, respectively.Finally, we extract the spectroscopic factor
$ S_{\alpha} $ in two cases with l = 0 and l = 2, then plot them versus the neutron number N of the parent nuclei in Fig. 4. From this figure, we find a amazing phenomenon that the$ S_{\alpha} $ values are basically the same for α transitions with the same orbital angular momentum l, with the extracted values$ S_{\alpha}\approx $ 0.406 for l = 0 and$ S_{\alpha}\approx $ 0.112 for l = 2. It shows that high angular momentum will hinder the spectroscopic factor and α-decay half-life [79–81]. Meanwhile, its small variation trend can also reflect the robustness of N = 126 at Z = 92. The above phenomena are worthy of further study in the future. -
In this work, based on the Gamow model, considering the effect of electrostatic screening, we systematically study the α-decay half-lives of uranium (Z = 92) isotopes. The calculated results are in reasonable agreement with the experimental data. In addition, we extend this model to predict α-decay half-lives of uranium isotopes whose α decay is energetically allowed or observed but not yet quantified in NUBASE2020, along with the predictions of XLZ, DZR, UDL and VSS for comparision. The predicted results of our model and these three formulas are close and consistent in trend. In addition, the robustness of the shell closure N = 126 is also verified at Z = 92. Finally, we find the values of spectroscopic factor
$ S_{\alpha} $ are basically the same for α transitions with the same orbital angular momentum l. The results of this work will prompt inquiries about nuclear structure and provide information for future experiments. -
We would like to thank J. G. Deng, H. M. Liu, X. Pan and H. F. Gui for useful discussion.
Systematic study on α-decay half-lives of uranium isotopes with a screened electrostatic barrier
- Received Date: 2022-05-24
- Available Online: 2022-11-15
Abstract: In the present work, we systematically study the α-decay half-lives of uranium (Z=92) isotopes based on the Gamow model with a screened electrostatic barrier. There are only two adjustable parameters in our model i.e. the parameter g and the screening parameter t in the Hulthen potential for considering the screened electrostatic effect of the Coulomb potential. The calculated results are in good agreement with experimental data, and the corresponding root-mean-square (rms) deviations of uranium isotopes with α transition orbital angular momentum l=0 and l=2 are 0.141 and 0.340, respectively. Moreover, we extend this model to predict α-decay half-lives of uranium isotopes whose α decay is energetically allowed or observed but not yet quantified in NUBASE2020. For comparison, the modified Hatsukawa formula (XLZ), the unified Royer formula (DZR), the universal decay law (UDL) and the Viola–Seaborg–Sobiczewski formula (VSS) are also used. The predictions are basically consistent with each other. Meanwhile, the results also indicate that N=126 shell closure is still robust at Z=92 and the spectroscopic factor





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF



















 DownLoad:
DownLoad: