Roles of tensor and isoscalar pairing interactions in β-decay calculations for possible r-process waiting point nuclei with N ~ 82 and 126

Almost half of the heavy elements beyond ⁵⁶Fe are synthesized using a process called rapid neutron capture (r-) [1, 2], whose sites are still unclear. If there are sufficient neutrons, very neutron-rich nuclei are produced; meanwhile, $ \beta^- $ decay pushes the matter flow to the stability line. Then, the competition between neutron capture and β-decay shapes the isotopic abundance of the universe. In this sense, accurate reaction rates such as neutron capture rates, β-decay rates, and β-delayed neutron emission probabilities are crucial for the final abundance pattern. With the recent experimental improvement, β-decay rates of some isotopes near the r-process paths have been updated (such as those around ¹³²Sn [3–5] and the neutron-rich rare earth nuclei [6]), but most of the remaining nuclei are still beyond the scope of current experiments or those in the near future. As an alternative, theoretical calculations with modern nuclear many-body methods can be used.

For decades, the efforts from the nuclear theory community have been focused on evaluating the β-decay half-life of nuclei relevant to the r-process. The pioneer work on quasi-particle random phase approximation (QRPA) methods with separable forces was conducted in the 1990s [7, 8] and its evolved versions are now widely used. The self-consistent density functional theory (DFT) calculations with Skyrme forces were introduced [9, 10] later on. The non-relativistic Hartree-Fock-Bogoliubov (HFB)+QRPA calculations using the finite-amplitude-method (FAM) procedure based on Skyrme interactions have also been performed for $ \beta^- $ decays of even-even or other nuclei with axial deformation [11, 12]. QRPA methods with other type of nucleon-nucleon interactions have also been adopted. In Refs. [13–17], a residual realistic force was used in both the BCS and QRPA calculation for deformed or spherical nuclei and, with a carefully modified Woods-Saxon potential, the β-decay half life of the observed nuclei could be well reproduced as well as those based on Gogny force [18]. In Refs. [19, 20] the self-consistent relativistic HFB+QRPA with meson-exchange interactions was applied. Efforts have also been made from the continuum-QRPA methods [21]. In Refs. [22, 23] the shell model approach was introduced, providing very good results with limited nuclei near magicity. However, some uncertainties arose from either the nucleon-nucleon interactions or the many-body models. Besides, recent works suggest that the simple Fermi function treatment of the phase space factor could overestimate the transition rates for light, medium, and heavy nuclei with the magnitude of the error depending on the atomic numbers and decay Q values [24, 25].

What are the major factors that may produce an obvious strong effect on the β-decay half-life in the QRPA calculation? As the nucleon-nucleon interaction is very complicated and not well determined, one of the answers should be the isoscalar spin-triplet (T = 0, S = 1) (IS) pairing interaction. As the most involved factor, it has been introduced to study the β-decay in Refs. [9, 26]. As the residual central force usually pushes the excited states upwards to the high energy region, one need to take the IS pairing into account in the particle-particle channel so as to draw the excited states downward to the low energy region. However, this raises another question about the widely accepted IS pairing force and its strength. The second answer to the above question might be the tensor interactions, which might shift the low energy excited states, especially the Gamow-Teller (GT) and charge-exchange spin-dipole (SD) states, obviously upwards or downwards, and produce a strong effect on the β-decay half-life [27–30]. Unfortunately, the strength of tensor interaction has not been well determined thus far. The third answer might be the correlations beyond the QRPA model such as the particle vibration coupling or quasi-particle vibration coupling, which also shifts the low energy states downwards [31]. In this work, we devote our interest to the study of the effects of the strength variation of IS pairing and tensor interactions on the β-decay half-lives for possible r-process waiting point nuclei with N ~ 82 and 126 so as to explore which interaction plays an important role in the β-decay of these nuclei.

In this work, we apply the HFB+proton-neutron QRPA (pnQRPA) model based on the Skyrme force to study the effects of Skyrme tensor interaction together with IS pairing on the β-decay half-life for the r-process path vicinity nuclei with neutron number N = 80, 82, 84, 124, 126, 128. We also examine how the variation in strength of the two components of the nuclear interaction in a reasonable range affects the β-decay rates. Further, we examine how the tensor force affects the detailed decay branches, which has not been addressed before. In addition, the interplay between the two components on the weak process are investigated. This article is arranged as follows. In Sec. II, a brief description of the QRPA models with canonical basis and the formula of GT and first-forbidden (FF) transitions are presented. The detailed parameters adopted in the calculations, inluding the cut-off, parameters of interaction, and determination of the quenching factor, are provided in Sec. III. In Sec. IV, we study how the β-decay half-lives in these nuclei change with the variation in strength of the IS pairing and tensor interaction. In Sec. V, the effects of the tensor force on the detailed decay branches, i.e., allowed and first forbidden decay, are examined. Sec. VI presents the summary.

The zero-range two-body tensor force employed in this study was originally proposed by Skyrme [32, 33]:

The parameters T and U denote the strengths of the triplet-even (TE) and triplet-odd (TO) tensor terms, respectively. The density-dependent contact (i.e., zero-range) surface pairing interactions are given as follows [29, 34]:

where $ {\boldsymbol{r = (r_1-r_2)}}/2 $, $ \rho_0 $ is assumed to be $ \rho_0 $ = 0.16 fm^-3, and $ P_\sigma $ is the spin exchange operator. As the iso-scalar (IS) pairing strength is not yet well constrained, factor f represents the ratio between the strengths of the IS and iso-vector (IV) pairing forces.

We start the calculation by solving the HFB equation in coordinate-space [35, 36]. The solved HFB wavefunctions are expanded on the canonical basis [37]. We then solve the pnQRPA equations:

where

In the p-p channel, both the IS and IV pairing interactions are included, with $ V_0 = (V_{0n}+V_{0p})/2 $ in $ V_{pn,p'n'}^{pp} $. After the above equations are solved by diagonalizing the QRPA matrix, the transition amplitudes in the $ \beta_- $ channel with the operator $ \hat{O} $ can then be expressed as

The $ \beta^- $ decay rates λ are defined as follows [38–41]:

with the phase space factor $ f_\beta $ of the form

where w is the electron energy in units of the electron mass, and $ w_0 $ is the maximum electron energy that can be released from the decay in units of the electron mass. It is defined following Ref. [9]:

with $ \Delta M_{n-H} = 0.78227 $ MeV, and $ \lambda_p $, $ \lambda_n $ being the fermi energy of proton and neutron, respectively.

$ F(Z,w) $ is the Fermi function as expressed in Ref. [38], and $ k,\;ka,\;kb $, and $ kc $ are the nuclear matrix elements depending on the respective nuclear structure following the expressions in Eq. (7). The detailed expressions of the respective operators are presented in [22, 23, 38]. The log$ ft $ values can be defined as

with $ f_0 $ is the phase space factor for the allowed GT decays

In this study, we use the Skyrme force $ {\rm{SKO}}^\prime $ [42], which adopted the s-wave time-odd Landau-Migdal parameter $ g_0^\prime = 0.79 $. The tensor interaction is then added on the top of $ {\rm{SKO}}^\prime $ perturbatively. For HFB, we choose the maximum angular momentum of the quasi-particle states $ J_{\rm max} $ = 19/2, for N ~ 126 nuclei, and $ J_{\rm max} $ = 15/2 for other nuclei. The cut-off of quasi-particle energy is set at 180 MeV. At the HFB level, the IS pairing is not included as we neglect the proton-neutron mixing for the ground states, and the strength of the IV pairing is separately determined to reproduce the odd-even mass staggering of protons and neutrons, i.e., we actually use different IV pairing strengths $ V_{0p} $ and $ V_{0n} $ for protons and neutrons, respectively, to obtain better fits. The values of $ V_{0p} $ and $ V_{0n} $ for different isotopic and isotonic chains are listed in Table 1.

	Cd			N=80			N=82			N=84			N=124			N=126			N=128
	$V_{0n}$	$V_{0p}$		$V_{0n}$	$V_{0p}$		$V_{0n}$	$V_{0p}$		$V_{0n}$	$V_{0p}$		$V_{0n}$	$V_{0p}$		$V_{0n}$	$V_{0p}$		$V_{0n}$	$V_{0p}$
w/o	−380.0	−590.0		−380.0	−590.0		−380.0	−590.0		−420.0	−590.0		−450.0	−660.0		−450.0	−680.0		−420.0	−680.0
w/i	−380.0	−590.0		−380.0	−590.0		−440.0	−590.0		−440.0	−590.0		−480.0	−660.0		−450.0	−680.0		−420.0	−700.0

Table 1.  $V_{0n}$ and $V_{0p}$strengths used in HFB for different isotopic or isotonic chains, with (w/i) or without (w/o) tensor force.

The IS pairing p-p interaction was the most concerned interaction in the previous calculations of β-decay half life [9, 26]. However, due to the fact that no observables are directly related to the proton-neutron IS pairing and its strength is still not well constrained, different IS pairing strengths are used in various ocassions. One straightforward constraint for IS pairing might be the low-energy super GT states observed in N = Z+2 pf shell nuclei, especially in ⁴²Ca, ⁴⁶Ti, and ⁵⁰Cr, whose formations are supposed to be directly triggered by IS pairing [43–46]. This leaves a constraint of $ f = 1.0\sim1.05 $ [34]. In this work, we hence use $ f = 1.05 $ for IS pairing.

The tensor interaction has been reported to produce a strong effect on the β-decay for closed-shell nuclei [30] because the it strongly affects the low energy GT states [27, 28]. In Ref. [11], the tensor interaction was included in the FAM-QRPA calculation to carry out global calculations in even-even nuclei. In that case, the tensor interaction is carefully fitted to reproduce the GT and SD main peak energies, as well as the β-decay half-lives in some chosen nuclei. In the previous work, the tensor interaction was constrained by the GT and SD main peak energies in ⁹⁰Zr and ²⁰⁸Pb, as performed in Ref. [47], together with the energy differences between $ 1h_{11/2} $ and $ 1g_{7/2} $ single-proton states along the Z = 50 isotopes [48]. $ {\rm{SKO}}^\prime $ is well fitted for β-decay with reasonable $ g_0^\prime $ value. Thus, a rather wide acceptable range of tensor interaction can be obtained by the GT and SD data, while a much stronger constraint comes from the single-particle energies. Finally, the strength of the TO tensor interaction is constrained to the interval from −350 to −270 MeV·fm⁵, and that of TE tensor interactions from approximately 270 to 600 MeV·fm⁵ [49]. In this section, we adopt (T, U) = (500.00, −320.00) MeV·fm⁵ as the baseline parameter, which is close to the centre of the optimized region.

In this subsection, the decay scheme of nuclei in Cd isotopes will be investigated to adjust the quenching factor. To understand the effect of tensor force and to adjust the parameter better, detailed studies of β-decay beyond half-lives are needed. As performed in [14], we investigate the detailed decay scheme and compare both decay energies as well as log$ ft $ values (the equivalence of nuclear matrix elements). The decay energies can be compared directly with those from the experiments, while the log$ ft $ value comparison is less straightforward, as there always exists the problem of axial-vector coupling constant ($ g_A $) quenching, which has an empirical value of approximately $ g_A = 0.75g_{A0} $, and its origin is still being debated. A recent study suggests that it may come from the many-body weak current [50]. In spite of such common quenching effect from nuclear medium, the many-body approximations may also bring certain quenching. As pointed out in Ref. [14], the QRPA method is in a sense an approximation to the exact shell model calculations. The calculated peak may be further broadened by multi-phonon effects beyond this approach, and this approximation may introduce an effective quenching in addition to the previous quenching for $ g_A $ mentioned above, namely, $ g_A = q g_{A}^{m} $, where $ g_A^{m}\approx 0.7-0.8g_{A0} $ is the $ g_A $ in nuclear medium extracted from various shell model calculations. Given that both $ {\rm GT} $ and $ {\rm FF} $ decay branches are studied in this article, we should also take into account an effective quenching of $ g_V $ due to the lack of strength spreading of the QRPA method, in the same manner as that of $ g_A $, that is, $ g_V = q $ instead of 1.

The allowed (GT) decays are relatively simple. Meanwhile, the measurements suggest that β-decays of Cd isotopes are dominated by GT decays, so one could fix the quenching factors by the decay schemes of the Cd isotopic chain. In Table 2, we present a comparison of GT branches for Cd isotopes with $ g_A = 0.5g_{A0} $. Our observation is that without tensor force, the decay energies of the specific decay channels are underestimated. This can be ignored if the detailed decay scheme information is not included. In that case, one would either simply resort to a larger $ g_A $, which could correctly produce the half-lives, or increase the IS pairing strength to obtain a larger decay energy; the necessity of the introduction of the tensor force may be neglected.

	SKO$^\prime$			SKO$^\prime$+T			Exp. [51]
	$Q_i$	log$ft$		$Q_i$	log$ft$		$Q_i$	log$ft$
120Cd	1.211	4.17		2.171	4.03		2.281	4.10
122Cd	1.922	4.21		2.973	4.05		3.431	3.95
124Cd	2.579	4.25		3.761	4.06
126Cd	3.191	4.29		4.538	4.08
128Cd	3.769	4.33		5.312	4.09		6.241	4.17
130Cd	4.328	4.39		6.083	4.11		6.741	4.10
132Cd	4.700	4.49		6.401	4.12

Table 2.  Decay energies and log$ft$ values of the largest GT branches for Cd isotopes using a quenching of $g_A=0.5g_{A0}$.

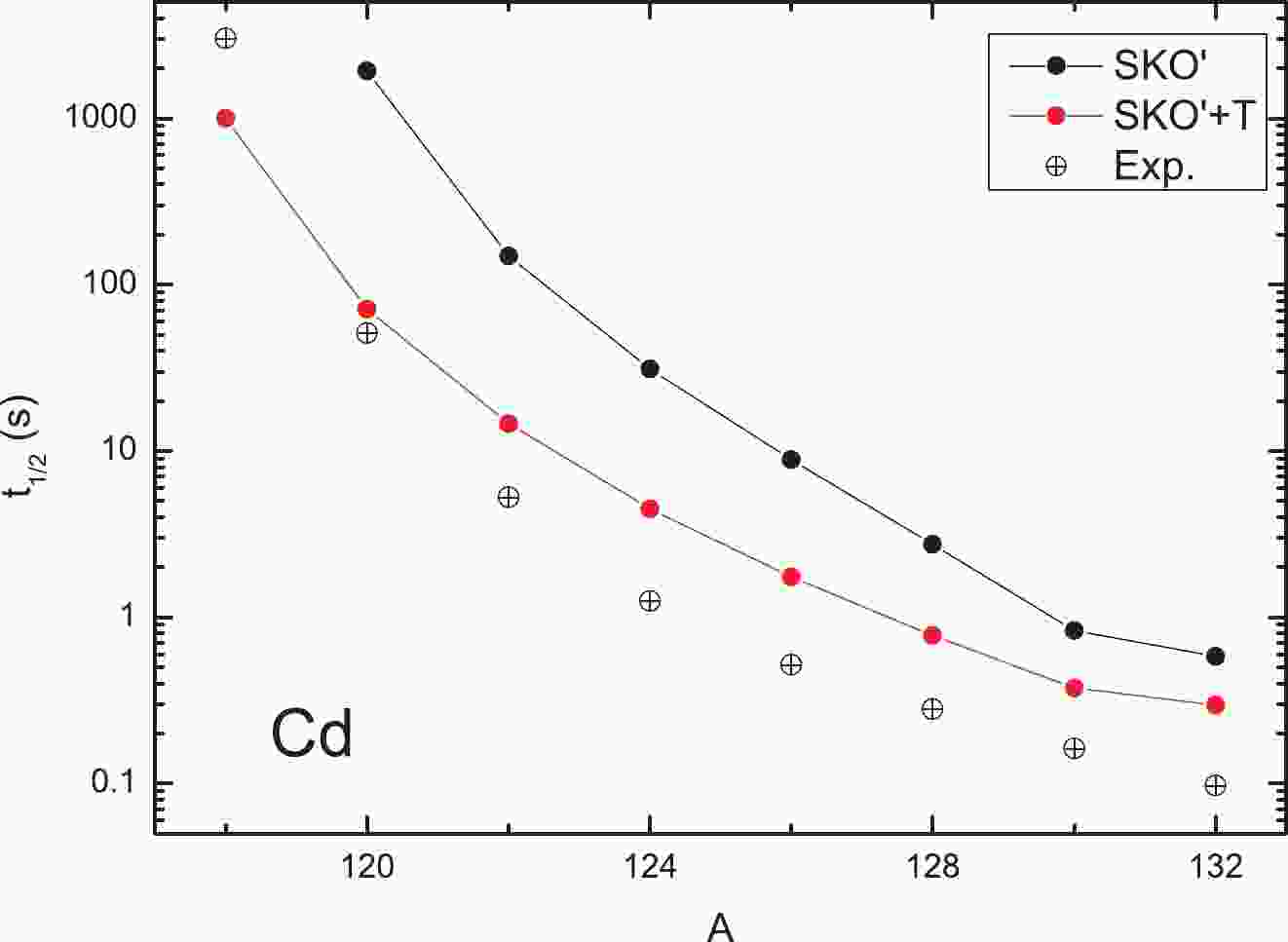
The inclusion of the tensor force becomes a better option, as it can give a much better agreement for the decay energy for most of the Cd isotopes and, with a proper quenching, it also gives better agreement to the log$ ft $ values. The inclusion of the tensor force thus provides simultaneous agreements of decay energies and log$ ft $ values of specific decay channels with proper IS pairing and $ g_A $ quenching, which are difficult to achieve without it. Moreover, these results agree well with those obtained by the QRPA with realistic forces [14].

Accordingly, the β-decay half lives for the Cd isotopic chain are displayed in Fig. 1, in which the strength of the tensor terms is set as (T,U) = (500, −320) MeV·fm⁵, the IS pairing strength is set at f = 1.05, and $ g_A = 0.5g_{A0} $. For the Cd isotopes, it is shown in Fig. 1 that without tensor force, the deviation of the calculations from the measurements can be as large as one order of magnitude. The introduction of the tensor force helps improve the situation, achieving qualitative improvements in the results, not only regarding the half-lives but also the excitation energies and matrix elements, as can be observed in Table 2.

Figure 1.  (color online) β-decay half lives for the Cd isotopic chain, calculated by HFB+QRPA with $ {\rm{SKO}}^\prime $. The strength of the tensor terms is selected as (T,U) = (500, −320) MeV·fm⁵. The IS pairing strength is set at f = 1.05. The experimental data are taken from Ref. [51].

In this section, the effects of strength variation of tensor and IS pairing interactions on the β-decay half-lives for N ~ 82 and 126 isotonic chains are presented.

In this subsection, we study the effect of strength variation of IS pairing on the β-decay half-lives. The IS pairing strength is not well constrained, and in Ref. [34] it is suggested to be f = 1.0 to 1.05, i.e., 1.0 to 1.05 times that of the average IV pairing. To study the effect of IS pairing on β-decay half-life, we vary the IS pairing interaction by taking f = 0.90 and 1.15 respectively, which means the strength of IS pairing is changed by approximately 100 MeV·fm⁵ around $ V_0 $.

The half lives in N ~ 82 chains are exhibited in Fig. 2. The calculations are carried out with or without tensor interaction. The results labelled by $ {\rm{SKO}}^\prime $ are without tensor interaction, while the curves labelled by $ {\rm{SKO}}^\prime $+T are the results with tensor interaction. It is shown in the figure that the difference caused by the strength variation of IS pairing by approximately 20% is hardly visible in the three isotonic chains, regardless of the presence of the tensor force. Comparatively, the tensor interaction with the selected strength systematically reduces the half-lives except for semi-magic ¹³⁰Sn and ¹³⁴Sn. In the N = 80 isotonic chain, the tensor interaction reduces the half lives by approximately 50% to 70%, except for ¹³⁰Sn. In the N = 82 isotonic chain, the half-lives are reduced by approximately 60% to 80%. For the N = 84 isotonic chain, they are decreased by approximately 40% to 60%, except for ¹³⁴Sn. In short, in the above N ~ 82 isotonic chains, the variation in IS pairing strength by approximately 20% does not substantially change the half-lives, while the tensor interaction plays a very strong effect and systematically reduces the half-lives by approximately 40% to 80%. This signifies the role of tensor force. Without tensor force, our calculations show that there is no way to decrease the half-lives by nearly an order of magnitude while the decay energies and log$ ft $ values simultaneously fulfill the measurements.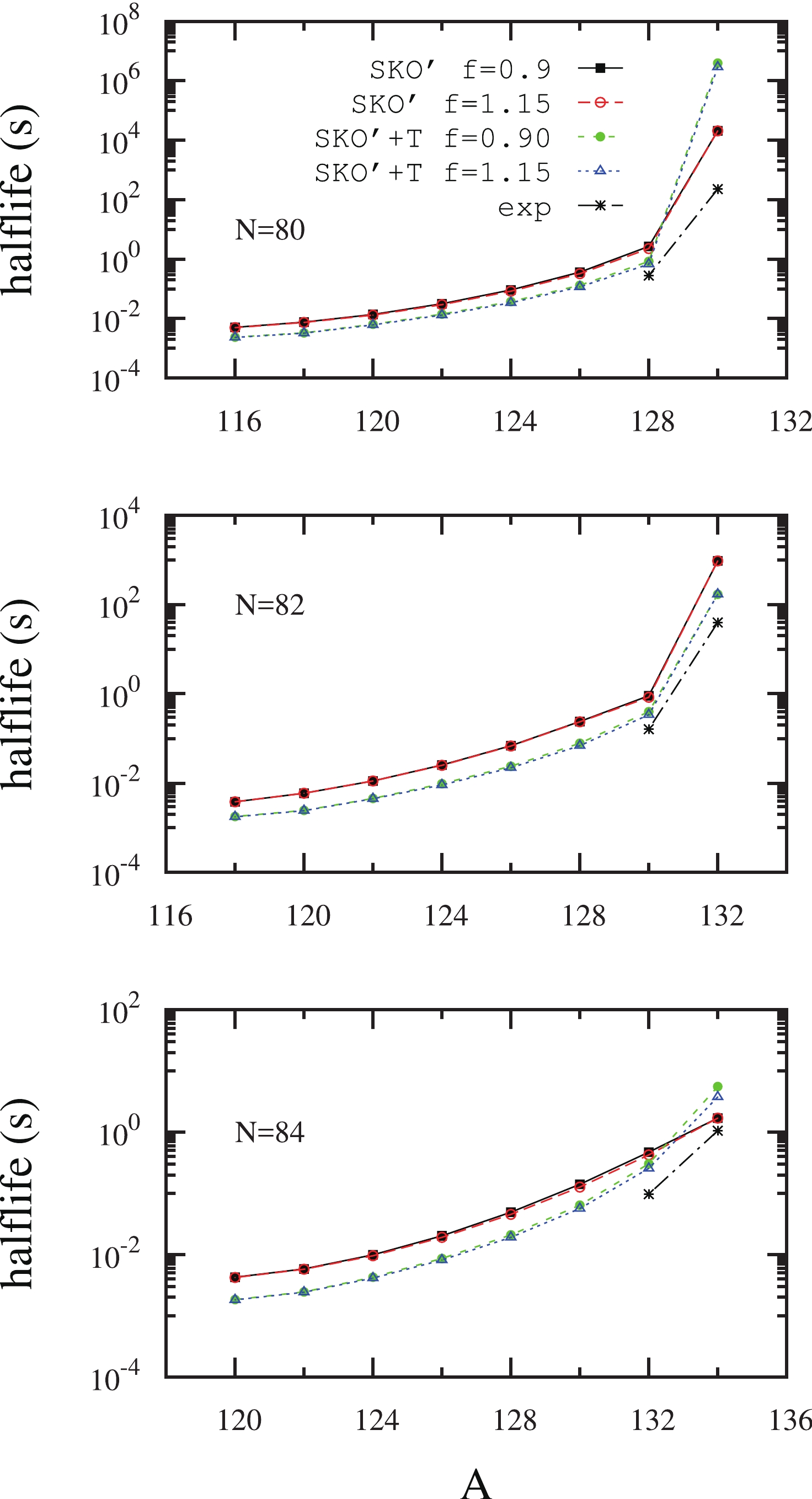

Figure 2.  (color online) β-decay half lives for the N = 80, 82, and 84 isotonic chains, calculated by HFB+QRPA with $ {\rm{SKO}}^\prime $. $ {\rm{SKO}}^\prime $ labels the results calculated without including tensor interaction, while $ {\rm{SKO}}^\prime $+T labels the results calculated with tensor interaction (T,U) = (500, −320) MeV·fm⁵. In our calculations, the IS pairing strength is set to be f = 0.90 and 1.15 times $ V_0 $. The experimental data are taken from Ref. [51].

The β-decay half lives of the nuclei in N = 124, 126, and 128 isotonic chains calculated by HFB+QRPA are shown in Fig. 3 and we have limited experimental data in this region. For the nuclei with big neutron excess in these three chains near N = 126, the results are similar to the case in N ~ 82 chains, where the variation in IS pairing strength by approximately 20% makes only an invisible change in the half-lives in the calculations with or without tensor interaction, whereas the tensor interaction produces consistently shorter half-lives. For these nuclei in the N = 124 chain, the half-lives are reduced by approximately 40%. Meanwhile, in the other two isotonic chains, the effect of the tensor interaction becomes even stronger, and the half-lives are reduced by approximately 50% to 60% in the N = 126 chain, and by approximately 40% to 50% for the N = 128 nuclei, respectively. In the region of the N = 124 chain with smaller neutron excess, the variation in IS pairing strength leads to visible differences, similar to the ones caused by the inclusion of tensor interaction. For nuclei in the N = 128 chain with smaller neutron excess, the IS pairing plays a dominant role, hence the results with the same f value are almost the same either with or without tensor interactions. However, in the N = 126 chain, IS pairing makes almost no contribution because 126 is a magic number.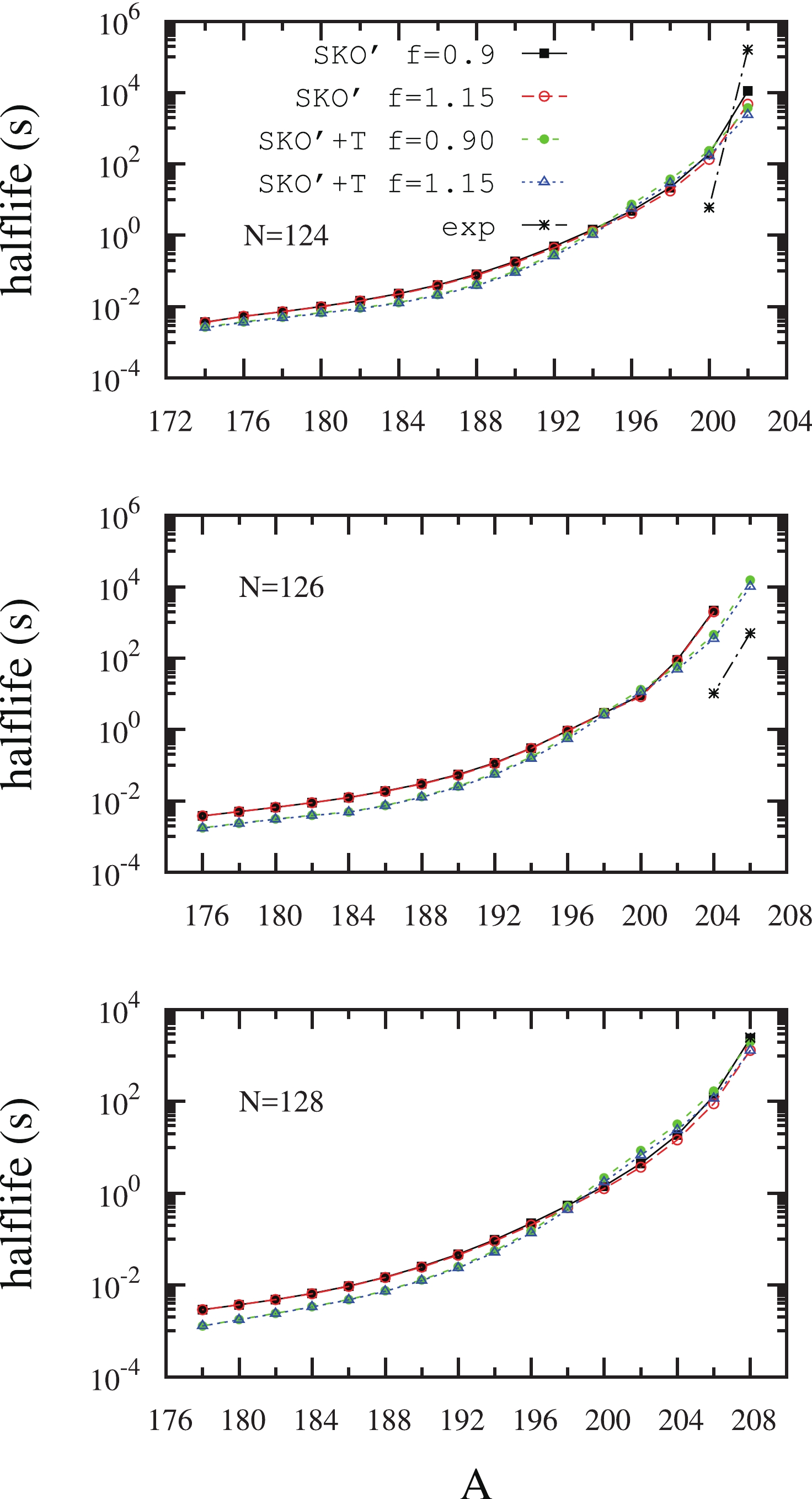

Figure 3.  (color online) Same as Fig. 2 but for the N = 124, 126, and 128 isotonic chains.

From the above analysis, we come to the conclusion that the effects of IS pairing tends to agree for the cases with or without the presence of tensor force. In both cases, the 20% changes of IS pairing around f = 1.0 barely affect the decay rates especially for neutron-rich nuclei. In general, our investigation shows that the QRPA solutions for the N ~ 82 and 126 nuclei are stable against the changes of a properly selected IS pairing strength. This guarantees the accuracy of the calculated half-lives, making it possible the future utilization of these rates for various occasions. For the later calculations, it is safe to set the value of f at 1.05.

The strong impact of the tensor interaction on β-decay half lives has been shown in the above studies, whereas it is necessary to study the half-life differences caused by the variation in strength for the tensor force. In this subsection, we will study the half lives calculated with different strengths of tensor force, namely the TE (T) and TO (U) components, in a constrained region from the GT and SD main peak energies in ⁹⁰Zr and ²⁰⁸Pb, together with the energy differences between $ 1h_{11/2} $ and $ 1g_{7/2} $ single-proton states along the Tin isotopes [49]. We provide the boundaries of T and U and also determine quantitatively the half-life errors brought by this uncertainty of tensor force. For the standard baseline tensor parameter set, we simply select the central values of the allowed parameter region, that is (T,U) = (500, –320) MeV·fm⁵. For T, 20% (T = 400 to 600) variation is allowed and for U, the deviation is 60 (U = –260 to –380).

The β-decay half-lives of the nuclei in the N = 80, 82, and 84 isotonic chains calculated by HFB+QRPA within the allowed region of the tensor parameters are shown in Fig. 4. As a first glance, we find that the effect of the TO component is much more significant than that of the TE component. In most cases, the effect caused by the change in the TE component can be negligible, while the changes in the TO strength can lead to an uncertainty as large as a factor of two for nuclei close to the stability line. Even for very neutron rich nuclei, the variation in TO strength could produce a difference of approximately 50%., whereas for the TE component, for very neutron rich nuclei, the effect is really small and we can barely see the changes.

Figure 4.  (color online) β-decay half lives for N = 80, 82, and 84 isotonic chains, calculated by HFB+QRPA with $ {\rm{SKO}}^\prime $. The numbers in parentheses are the values of T and U strength, respectively. Different values of T are distinguished by the colors, while the different U values are distinguished by the line styles as well as the shapes of the symbols. The IS pairing strength here is set to be f = 1.05. For each graph, the lower panel gives the ratio of the calculated half-lives to the baseline calculation, which adopts T = 500 and U = –320.

If we look into the detailed decay scheme, we find that the main change is in the decay energies, while the matrix elements or log$ ft $ values change more mildly. The difference between the TO and TE components is that the decay energies are much more sensitive for the former than for the latter. This means that the transition rates from the even-even to the odd-odd states are less sensitive to the changes in tensor force, but the relative energy intervals (Q) are more related, especially for the TO part.

Meanwhile, we find that at the large Z end of each isotonic chain the effect of the TE component becomes larger. The effects on the decay half-lives may be slightly reversed when we go from the large Z end to the small Z end. Except for the semi-magic nuclei, the enhanced TE strength increases the half-life at a large Z but reduces it at a small Z. As we will discuss in the next section, we find that such a reversion is closely related to the proportions of FF decays.

The half-lives for the N = 124, 126, and 128 isotonic chains are similar to those for the N ~ 82 chains, which are also presented in Fig. 5. From the figure, we see that the TE component also produces a more pronounced effect for nuclei in the chains with smaller neutron excess, as explained above. The effect of the TO component is still generally stronger than that of the TE component, especially in the region with big neutron excess. Only the difference caused by the variation in TO strength is visible, and it is of several tens of percentages. The TO strength will affect the nuclei with less neutron excess by more than a factor of two, and these nuclei usually have smaller Q values.

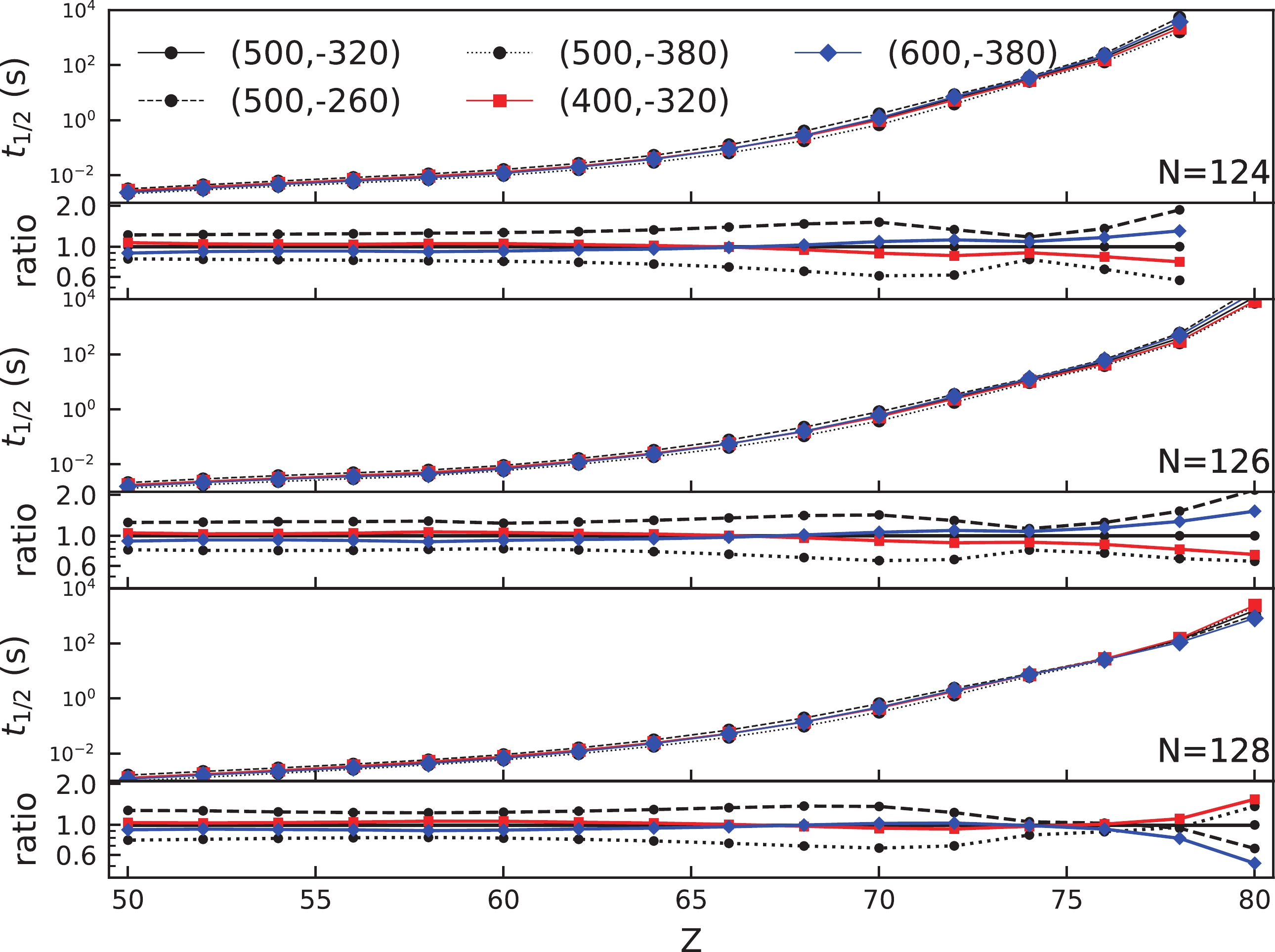
Figure 5.  (color online) Same as Fig. 6 but for N = 80, 82, and 84 isotonic chains.

Similar reversion effects are observed for these isotonic chains. The decay half-lives are more likely to be reduced by an enhanced TO strength for nuclei with a large neutron excess, and the opposite applies for a small neutron excess.

Various calculations [13, 22, 23] show that FF decays may be important for N~126 chains, and therefore, in this section, we also study the ratios of the width of FF to the total ones, $ \lambda_{\rm FF}/\lambda_{\rm tot} $, for the Cd isotopes and the $ N\sim 82 $ and $ \sim 126 $ isotonic chains.

The ratios of FF for Cd isotopes are shown in Fig. 6. It is shown in the figure that the existence of tensor force largely increases the ratios of allowed decays in Cd isotopes. This suggests that the effect of the tensor force on FF decay is not as pronounced as that for allowed decay. If we combine the results in Fig. 6 and Table 2, we find that the speed-ups of β-decays brought by the tensor force are dominated by allowed decays, whereas FF decay, although altered by the tensor force too, will not contribute that much. A careful investigation suggests that for the Cd isotopic chain, the tensor force will shift the negative parity states to higher excitation energies and the transition strength may also be reduced. This leads to the reduction in the FF ratios with the increase in the neutron excess. As an example, for the very neutron rich ¹³²Cd, we show the details of different decay channels. With the inclusion of tensor interaction, the $ 0^- $ states are shifted to high energy and they will not contribute any more. For example, a lowlying state with log$ ft $ 5.7 is now shifted out of the decay window. For $ 1^- $ states, our observation is that most states are shifted down slightly by several hundred keV and the transition slightly enhanced, but the magnitude is much smaller than that for GT decay. The same may apply to $ 2^- $ states. However, we also observe that this phenomenon is not universal.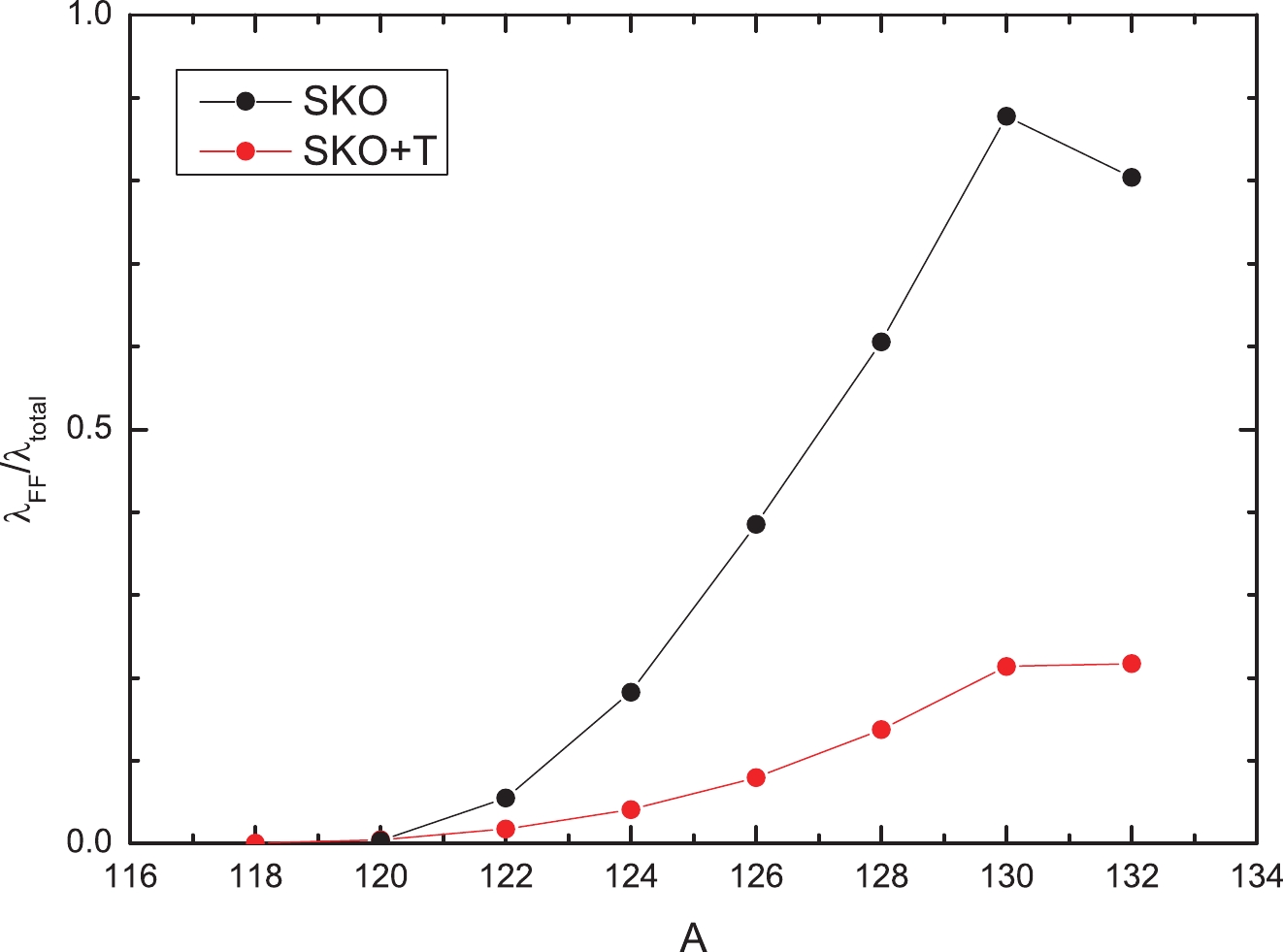

Figure 6.  (color online) Ratios of FF decay to the total decay width for Cd isotopes, calculated by HFB+QRPA with $ {\rm{SKO}}^\prime $. The strength of the tensor terms is set to be (T,U) = (500, −320) MeV·fm⁵. The IS pairing strength is set at f = 1.05.

For the decays in $ N\sim 82 $ and $ \sim 126 $ isotonic chains, the ratios of FF decay are shown in Figs. 7, 8. We find that, in general, for all these isotonic chains, the ratio of FF decay branches will be reduced by the inclusion of tensor forces with the increase in neutron excess. This occurs because GT decay is more sensitive to the tensor force. Meanwhile, the effects of tensor force on FF decays are much more complicated, and they depend on the detailed excited states and the types of FF transition. However, they are less sensitive to the tensor force. This finding is similar to that in Ref. [13] for IS pairing, where the excitation energies and transition strength of the allowed decay are very sensitive to IS pairing, while FF decay displays different patterns.

Figure 7.  (color online) Same as Fig. 6but for N = 124, 126, and 128 isotonic chains.

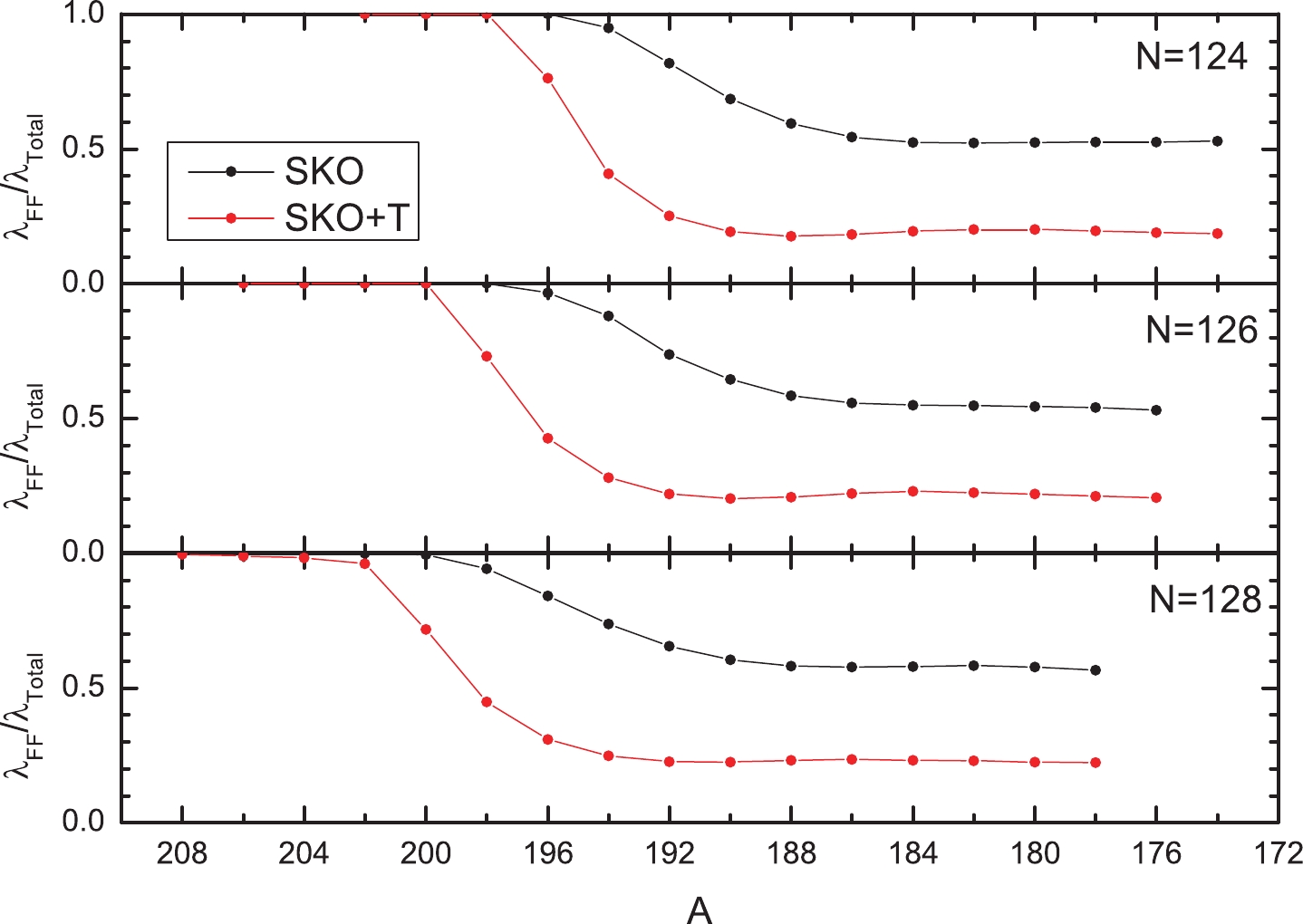
Figure 8.  (color online) Same as Fig. 4 but for N = 124, 126, and 128 isotonic chains.

For all these isotonic chains, if the neutron is rich enough, then with the inclusion of tensor force, GT transitions will become dominant. Meanwhile, without tensor force, we find that GT and FF decays contribute equally. In this sense, future experimental data on very neutron-rich nuclei will perhaps give us more evidence of the importance on the tensor force in the nuclear structure.

In summary, we have calculated the $ \beta^- $ decay half-lives of N ~ 82 and 126 isotones, with GT and FF transitions being taken into account. The effects produced by the tensor and IS pairing interactions are studied intensively. The tensor interaction applied in the calculation is well constrained by the main peak energies of GT and charge-exchange SD transition in ⁹⁰Zr and ²⁰⁸Pb, together with the single-particle energy gaps in Tin isotopes. In the chains with smaller neutron excess, when the IS pairing strength is varied from 0.9 to 1.15 times that of IV pairing, our study shows that both the tensor and IS pairing interactions may contribute to the half-lives. Meanwhile, in the nuclei with large neutron excess, a strength variation of IS pairing by approximately 20% causes invisible changes. Only the strength variation of the TO tensor interaction leads to an obvious difference, and the uncertainties for the half-lives can be evaluated. Further, the different roles of different tensor components on different decay channels are investigated. In addition, the contribution of the GT and FF decays are also discussed. If the neutron is rich enough, with the inclusion of the tensor force, GT transitions will become dominant. Without the tensor force, we find that GT and FF decays contribute equally.

DLF would like to acknowledge the support from CAS for the "Light of West" Program and "From Zero to One" Program.