-
The nucleonic equation of state (EOS) at finite temperature provides basic knowledge on the study of nuclear structure [1], compact stars [2, 3], and heavy-ion collisions [4–6]. In particular, the liquid-gas phase transition [7–11] calculated using the EOS of symmetric nuclear matter at finite temperature is required to analyze the properties of nuclear matter in different phases [12–14], such as phenomena related to the evolution of neutron stars and heavy ion collisions [15].
At comparatively low temperatures
$ T\lesssim10{\;\mathrm{MeV}} $ and densities$ \rho\lesssim0.1{\;\mathrm{fm}^{-3}} $ , the coexistence of liquid and vapor phases occurs in nuclear matter, resulting from the properties of the nucleon-nucleon interaction [16], which is similar to the van-der-Waals behavior in condensed matter physics. The thermodynamic quantities of liquid-gas coexistence, such as critical temperature$ T_{\rm c} $ , critical pressure$ p_{\rm c} $ , and critical density$ \rho_{\rm c} $ , are generally referred to as critical parameters. In the past, they have been investigated both in heavy-ion-collision experiments [17–19] and different theoretical models [20–43], and the results have been extrapolated to finite nuclei. Critical temperatures in the range$ T_{\rm c}\approx13-22{\;\mathrm{MeV}} $ were deduced.In different experiments, critical parameters have been studied by measuring caloric curves and analyzing the multi-fragment distribution of heavy-ion collisions. The limiting temperature
$ T_\mathrm{lim} $ is the maximum temperature that can be observed in experiments. It is not equal to$ T_{\rm c} $ owing to the existence of the Coulomb repulsion and surface tension of finite nuclei. However, there is still a relatively stable ratio between$ T_{\rm c} $ and$ T_\mathrm{lim} $ [28]. In a combined analysis of several experiments [35], under different excitation energies and extrapolation using the droplet model, the critical parameters were estimated as$ T_{\rm c}=17.9\pm0.4{\;\mathrm{MeV}} $ ,$ \rho_{\rm c}=0.06\pm0.02{\;\mathrm{fm}^{-3}} $ , and$p_{\rm c}=0.31\pm 0.07 { \;{\rm{MeV}}\, {\rm{fm}}^{-3}}$ for infinite symmetric nuclear matter, in agreement with an earlier analysis giving$T_{\rm c}=16.6\pm 0.9$ MeV [27].In this theoretical study of the liquid-gas phase, we employ the Brueckner-Hartree-Fock (BHF) model [1, 44–46] extended to finite temperature [47, 48]. Previously[24, 26], a critical temperature of
$ T_{\rm c}\approx20{\;\mathrm{MeV}} $ was obtained using this method with the bare Paris potential [49] or the Argonne$ V_{14} $ potential [50] supplemented with phenomenological three-body forces (TBF) [51]. The liquid-gas transition disappeared at isospin asymmetry of approximately 0.9. A slightly lower value$ T_{\rm c}\approx18{\;\mathrm{MeV}} $ was found in [28] with the Bonn B potential [52], and$ T_{\rm c}\approx13{\;\mathrm{MeV}} $ was obtained with the${\rm V}_{18} $ potential and updated TBF in [29, 53]. All these BHF values are significantly higher than$ T_{\rm c}\approx10{\;\mathrm{MeV}} $ deduced with the Dirac-Brueckner-Hartree-Fock (DBHF) approach in Refs. [22, 25]. In the BHF approach, the inclusion of suitable TBF is essential to obtain a realistic saturation point for nuclear matter and thus produce well-founded predictions for$ T_{\rm c} $ .The liquid-gas phase transition has also been investigated using other theoretical methods. The first Skyrme [20] and variational [21, 26] calculations reported values in the range
$ T_{\rm c}\approx16-19{\;\mathrm{MeV}} $ . In the framework of covariant-density-functional theory, values of 20 different models were recently compared and predicted as$ T_{\rm c}\approx13-16{\;\mathrm{MeV}} $ [38], in agreement with those of several relativistic-mean-field models [30, 32–34, 41–43]. Self-consistent Green function (SCGF) calculations with the${\rm V}_{18}$ potential predicted$ T_{\rm c}=11.6{\;\mathrm{MeV}} $ [54], and a recent comparison of SCGF [39] and BHF results using different chiral interactions yielded$ T_{\rm c}=16\pm2{\;\mathrm{MeV}} $ [37], with the difference between the two methods using the same chiral interaction being less than 2 MeV. In the framework of in-medium chiral perturbation theory [55],$ T_{\rm c}\approx15{\;\mathrm{MeV}} $ was obtained for isospin-symmetric nuclear matter. Finite nuclei with isospin asymmetry of approximately 0.13 were analyzed within an isospin-dependent quantum molecular dynamics model [40]. Extrapolating the critical temperature to infinite nuclear matter yielded a value of$ T_{\rm c}\approx13.3\pm1.2{\;\mathrm{MeV}} $ .In this paper, we employ the BHF method based on several realistic nucleon-nucleon (
$ NN $ ) interactions, namely Argonne$ {\rm V}_{18} $ (V18) [56], Bonn B (BOB) [52], and Nijmegen 93 (N93) [57] potentials, supplemented by compatible microscopically-derived TBF [58–61] and a combination of the$ {\rm V}_{18} $ potential and the phenomenological Urbana-type TBF [51, 62], which is labeled as UIX. The compatibility of the resulting zero-temperature EOSs with nuclear-structure phenomenology [63–65] and recent astronomical observation constraints [66–68] has been studied in several publications.The paper is organized as follows. In Sec. II, we briefly review the BHF method at finite temperature and the computation of thermodynamic quantities. In Sec. III, we present the results of the procedure used in this study and compare them with previous results in detail, regarding, in particular, the critical parameters. Finally, conclusions are drawn in Sec. IV.
-
Calculations for infinite symmetric nuclear matter are based on Brueckner-Bethe-Goldstone (BBG) theory [44, 45, 69–71] and its extension to finite temperature [26, 29, 47, 48, 72, 73]. In this study, we adopt the four types of interaction V mentioned above to obtain the free energy per particle to analyze the liquid-gas phase transition of hot nuclear matter. The fundamental ingredient of BBG theory is the K matrix, which represents the effective interaction between nucleons in nuclear matter and obeys the integral equation
$\begin{aligned}[b] K(\rho,x_p;E) = & V + V \;\mathrm{Re} \sum\limits_{1,2} \frac{|12 \rangle (1-n_1)(1-n_2) \langle 1 2|} {E - e_1-e_2 +{\rm i}0}\\&\times K(\rho,x_p;E) \:, \end{aligned}$

(1) where E is the starting energy, and the multiple indices 1, 2 represent momentum, isospin, and spin. Along with the equations for single-particle (s.p.) energy and potential,
$ e_1 = \frac{k_1^2}{2m_1} + U_1 , $

(2) $ U_1(\rho,x_p) = \sum\limits_2 n_2 \langle 1 2| K(\rho,x_p;e_1+e_2) | 1 2 \rangle_a , $

(3) the K matrix can be obtained self-consistently for a given baryon density ρ and proton fraction
$ x_p $ . The numerical diagonalization of the BBG equation (1) keeps track of the total and relative momenta and starting energy E while retaining the excellent angle-average approximation [74–76].The TBF are reduced to an effective, density-dependent, two-body force by averaging over the third nucleon in the medium [61],
$ \begin{equation} \overline{V}_{ 12}({\boldsymbol r}_{12}) = \rho \int {\rm d}^3 {\boldsymbol r}_3 \sum\limits_{\sigma_3,\tau_3} g_{13}(r_{13})^2 g_{23}(r_{23})^2\, V_{132} \:, \end{equation} $

(4) the average being weighted by the BHF correlation function
$ g_{\alpha}(r) = 1-\eta_{\alpha}(r) $ , related to the r-space defect functions in the partial waves$ {\alpha} $ ,$ \begin{equation} \eta_{\alpha}(r) = j_{\alpha}(r) - u_{\alpha}(r) \:, \end{equation} $

(5) with the free wave function (Bessel function)
$ j_\alpha $ , and the correlated wave function$ u_\alpha $ , which consider nucleon-nucleon in-medium correlations [26, 58–60, 77–81]. The result is an effective two-nucleon potential with the operator structure$\begin{aligned}[b] \overline{V}_{ 12}({\boldsymbol r}) =& {({\boldsymbol\tau}_1\cdot {\boldsymbol\tau}_2)}{({\boldsymbol\sigma}_1\cdot{\boldsymbol\sigma}_2)} V_C(r) + {({\boldsymbol\sigma}_1\cdot {\boldsymbol\sigma}_2)} V_S(r) + V_I(r)\\& +\, S_{ 12}({\hat{\boldsymbol{r}}}) \big[ {(\boldsymbol{\tau}_1\cdot \boldsymbol{\tau}_2)} V_T(r) + V_Q(r) \big] ,\end{aligned} $

(6) where
$S_{ 12}({\hat{\boldsymbol{r}}}) = 3({\mathit{\boldsymbol{\sigma}}}_1 \cdot \hat{\boldsymbol{r}})({\mathit{\boldsymbol{\sigma}}}_2 \cdot \hat{\boldsymbol{r}}) - {\mathit{\boldsymbol{\sigma}}}_1 \cdot {\mathit{\boldsymbol{\sigma}}}_2$ is the tensor operator, and the five components$ V_O,\; O=C,S,I,T,Q $ depend on the nucleon densities$ \rho_n, \;\rho_p $ . These are all added to the bare two-nucleon potential in the Bethe-Goldstone equation.Eqs. (1)–(3) involve the Fermi distribution
$ n(k) $ and must be solved self-consistently along with the equation for the auxiliary chemical potentials$ \tilde{\mu}_i\ (i=n,p) $ fixing the density,$ \begin{equation} \rho_i = 2\sum\limits_k n_i(k) = 2\sum\limits_k {\left[\exp{\Big(\frac{e_i(k)-\tilde{\mu}_i}{T}\Big)} + 1 \right]}^{-1} \:. \end{equation} $

(7) The results of this iterative procedure are temperature-dependent s.p. potentials
$ U_i(k) $ , which are then used to compute the free energy density for a given temperature and density.$ \begin{equation} f = \rho\frac{F}{A} = \sum\limits_{i=n,p} \left[ 2\sum\limits_k n_i(k) \left(\frac{k^2}{2m_i} + \frac12 U_i(k) \right) - Ts_i \right] \;, \end{equation} $

(8) where
$ \begin{equation} s_i = - 2\sum\limits_k \Big( n_i(k) \ln n_i(k) + [1-n_i(k)] \ln [1-n_i(k)] \Big) \end{equation} $

(9) is the entropy density of a free Fermi gas with the s.p. spectrum
$ e_i(k) $ .In previous studies, a further "frozen-correlations" approximation (FCA) was sometimes employed [26, 82–84], in which the temperature dependence of the s.p. potential
$ U_i(k) $ is neglected and the free energy in Eq. (8) is computed using the zero-temperature s.p. potential. In the following, we compare the results of the full procedure (termed BHF) and the FCA.The free energy density allows us to compute, in a thermodynamically consistent manner, other thermodynamic quantities of interest, namely chemical potentials
$ \mu_i $ , pressure p, and internal energy density$ {\varepsilon} $ ,$ \mu_i = \frac{\partial f}{\partial \rho_i} \:, $

(10) $ p = \rho^2 {\partial{(f/\rho)}\over \partial{\rho}} = \sum_i \mu_i \rho_i - f \:, $

(11) $ {\varepsilon} = f + Ts \:,\quad s = -{{\partial f}\over{\partial T}} \:. $

(12) In particular, the pressure is analyzed in the following discussion of the critical point.
-
We now discuss the results of our numerical calculations following the BHF and FCA procedures. The latter entirely disregards the T dependence of the s.p. properties and is thus a good reference for the quantitative importance of these effects.
-
To illustrate the iterative BHF procedure that fully includes Fermi distributions at finite temperature in the computation of the K matrix, Eq. (1), and the s.p. potential U (Eqs. (2) and (3)), we now discuss the temperature dependence of several physical quantities of interest.
In Fig. 1, we display the five TBF components in Eq. (6) obtained at normal density
$ \rho=0.17{\;\mathrm{fm}^{-3}} $ ,$ T=0 $ , and$ 50{\;\mathrm{MeV}} $ with different interactions. The (π, ρ)-exchange TBF contribute to the attractive central ($ V_C $ ) and tensor ($ V_T $ ) components, whereas the (σ,\;ω) TBF are mainly represented by the repulsive scalar ($ V_I $ ) component [60]. The other two parts,$ V_S $ and$ V_Q $ , are less important. For the phenomenological UIX that only involve 2π exchange, the contributions from these two parts are zero. One can clearly see that the five components depend quantitatively on the EOS and are all weakened at finite temperature.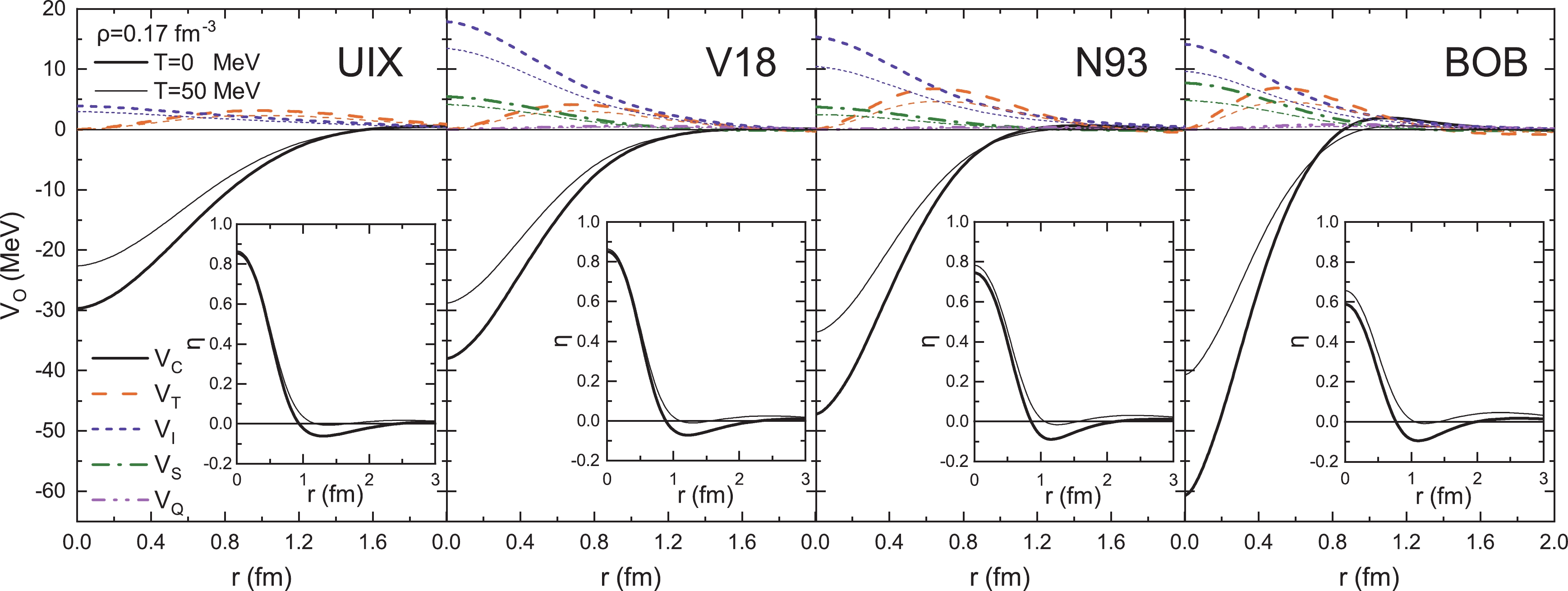
Figure 1. (color online) TBF components (Eq. (6)) for
$ \rho=0.17{\;\mathrm{fm}^{-3}} $ ,$ T=0 $ and$ 50{\;\mathrm{MeV}} $ with different EOSs. The insets show the defect functions in the$ ^1 S_0 $ channel.The only way finite temperature affects the effective TBF in our formalism is via the correlation functions
$ g_{\alpha}=1-\eta_{\alpha} $ in Eq. (4) that are obtained consistently from the K matrix [80, 81]. For illustration, the insets of Fig. 1 show the defect functions$ \eta_{^1 S_0} $ for the same conditions as the TBF in the figure. We can see that (for the 'soft-core' EOSs N93 and BOB in particular [80]) finite temperature increases the defect function and thus decreases the correlation functions g in Eq. (4), which explains the decrease in the average TBF. In other words, at finite T, interacting nucleons are maintained at larger distances, and the effective 'core' of the$ NN $ interaction increases.This repulsive effect is also observed in the s.p. potentials, which are shown in Fig. 2(a) at
$ T=0 $ and$ 20{\;\mathrm{MeV}} $ for$ \rho=0.06 $ (left panels) and$ \rho=0.17{\;\mathrm{fm}^{-3}} $ (right panels), with the four EOSs. The change due to finite temperature ($ \Delta U \equiv U_T - U_0 $ ) is shown in the central panels (b), and the Fermi distributions for the BHF and FCA procedures are shown in the lower panels (c) only for V18. It is evident that finite temperature generally increases U and$ \Delta U $ (the FCA corresponds to$ \Delta U=0 $ ), thus providing effective repulsion and increasing the free energy (Eq. (8)). However, there are exceptions, such as N93 at$ \rho=0.17{\;\mathrm{fm}^{-3}} $ , which becomes more attractive at$ T=20{\;\mathrm{MeV}} $ . This temperature effect is due to the use of Fermi functions in Eqs. (1), (2), and (3), as well as the T dependence of the TBF (see Fig. 1), which weakens the individual components. We verify that the particular behavior of N93 is due to the finite-T modification of the TBF, which provides more attraction in this case, in contrast to the other EOSs.
Figure 2. (color online) (a) Self-consistent s.p. potential at
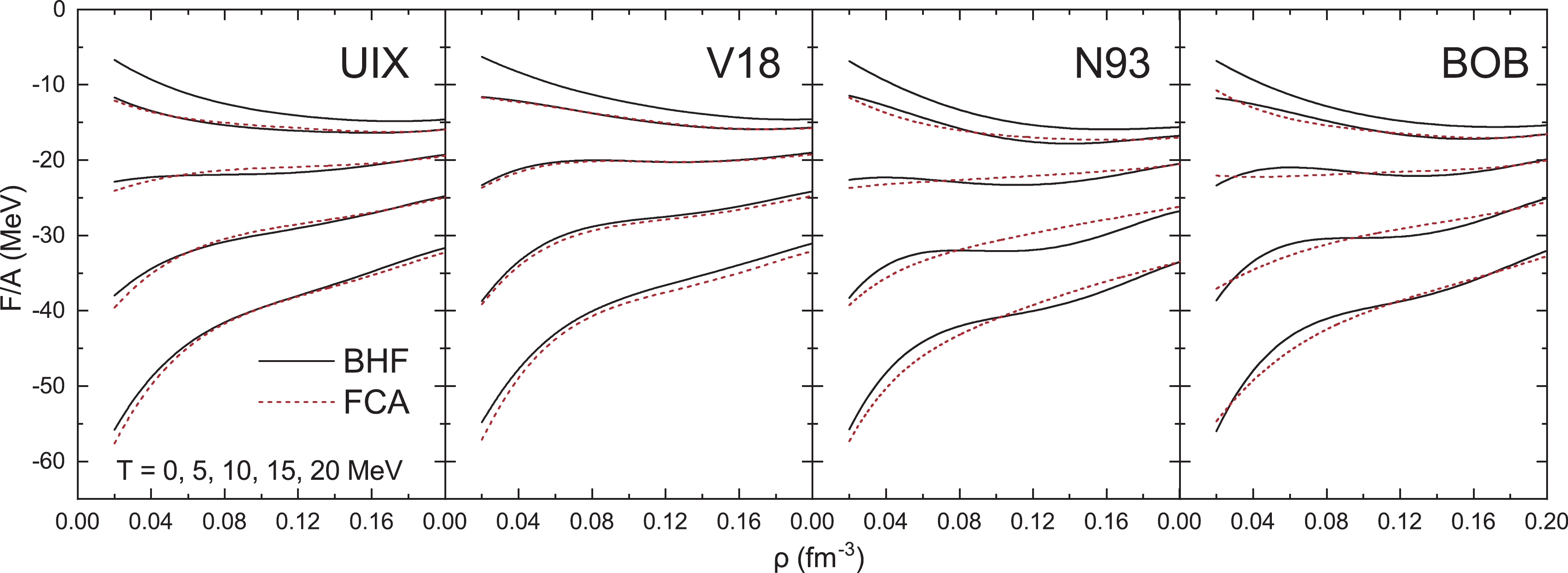
$ T=0 $ and$ 20{\;\mathrm{MeV}} $ for$ \rho=0.06 $ and$ \rho=0.17{\;\mathrm{fm}^{-3}} $ with different EOSs. (b) Differences in U between$ T=20{\;\mathrm{MeV}} $ and$ T=0{\;\mathrm{MeV}} $ . (c) Momentum distributions from the BHF and FCA procedures for the V18 EOS.However, there are several delicate effects from the different momentum distributions involved in the BHF and FCA procedures, which are caused by the use of s.p. spectra at (non)zero temperature, respectively. Note that in Fig. 2(c), the momentum distribution in the BHF procedure is slightly less extended; therefore, the kinetic-energy contribution
$ E_c/A $ to$ F/A $ (first term in Eq. (8)) is smaller than that in the FCA. This counteracts the general increase in the potential contribution$ E_U/A $ (second term in Eq. (8)) in the BHF discussed above. Furthermore, the entropy contributions$ TS/A $ (third term in Eq. (8)) are slightly different in the BHF and FCA procedures, which is summarized in Table 1 at$ \rho=0.17{\;\mathrm{fm}^{-3}} $ and$ T=20{\;\mathrm{MeV}} $ . Under these conditions, the decrease in the kinetic-energy contribution in the BHF procedure is less than 1 MeV for all EOSs, which is compensated in all cases by a comparable opposite change in the entropy contribution. In contrast, the potential contribution is EOS dependent, varying from repulsive (V18) to attractive (N93), as shown in Fig. 2(b). In the end, the overall change in$ F/A $ under the BHF procedure ranges from slightly repulsive (UIX,V18) to attractive (N93), which is the result of a delicate compensation between different contributions and changes with density and temperature.$ {F/A} $ 

$ {E_c/A} $ 

$ {E_U/A} $ 

$ {TS/A} $ 

UIX BHF −34.0 33.6 −35.9 31.7 FCA −34.5 34.3 −36.2 32.6 V18 BHF −33.1 33.9 −34.9 32.1 FCA −34.2 34.4 −35.8 32.8 N93 BHF −35.9 33.1 −38.0 31.0 FCA −35.4 34.0 −37.2 32.2 BOB BHF −34.9 32.9 −37.1 30.7 FCA −34.9 33.7 −36.8 31.8 Table 1. Contributions to
$ F/A $ (in MeV) at$ \rho=0.17{\;\mathrm{fm}^{-3}} $ and$ T=20{\;\mathrm{MeV}} $ in the BHF and FCA procedures.The final results of the free energy per particle for a given temperature and density with different EOSs are shown in Fig. 3, comparing the BHF and FCA procedures. We may conclude that the difference between both procedures is rather small over the full range of parameters and may have either sign owing to the various compensation mechanisms stated above. These results allow the computation of the pressure (Eq. (11)) and thus the following analysis of the critical point.
-
In the study of the liquid-gas phase transition, the critical parameters
$ T_{\rm c} $ ,$ \rho_{\rm c} $ , and$ p_{\rm c} $ determine the properties in the vicinity of the phase transition. The pressure$ p(\rho) $ determined by the BHF procedure is depicted in Fig. 4 for different values of temperature (dashed green curves), comprising the proper value$ T_{\rm c} $ for each EOS (solid black curves). The results range from$ T_{\rm c}=14.4{\;\mathrm{MeV}} $ for V18 to$ T_{\rm c}=19.2{\;\mathrm{MeV}} $ for the N93 EOS and are also listed in Table 2 along with the corresponding values of$ \rho_{\rm c} $ and$ p_{\rm c} $ . The results of the BHF and FCA procedures are similar, as also evidenced in Fig. 3, but reflect qualitatively the different behaviors for$ \Delta U $ shown in Fig. 2(b), that is,$ T_{\rm c} $ in the BHF is higher (lower) than in the FCA for the N93 (UIX, V18, and BOB) EOS. In any case, these values compare well with the recent experimental and theoretical results discussed in the Introduction. However, the results for$ p_{\rm c} $ are not well constrained, ranging from 0.25 to$ 0.63{ \;{\rm{MeV}}\, {\rm{fm}}^{-3}} $ .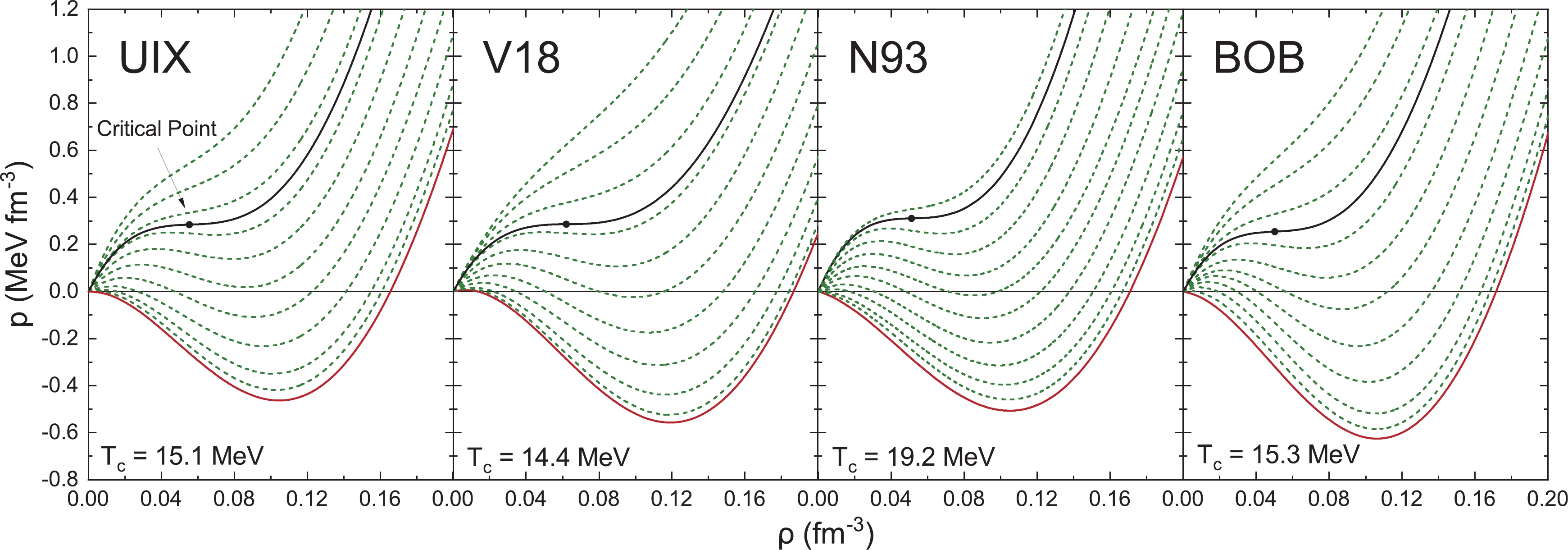
Figure 4. (color online) Pressure of symmetric nuclear matter as a function of density for various temperatures
$ T=0,2,4,\ldots,20{\;\mathrm{MeV}} $ (rising curves) with different EOSs and the BHF procedure. The solid black curves correspond to the critical temperatures$ T_c $ , and the critical points are denoted by markers.${T_{\rm c} {\;\mathrm{/MeV} } }$ 

$ {\rho_{\rm c} {\;\mathrm{/fm}^{-3}}} $ 

$ {p_{\rm c}/ ( {\;\mathrm{MeV}} {\;\mathrm{fm}^{-3}})} $ 

UIX BHF 15.1 0.053 0.29 FCA 15.2 0.067 0.39 V18 BHF 14.4 0.062 0.29 FCA 15.6 0.065 0.41 N93 BHF 19.2 0.051 0.31 FCA 17.2 0.076 0.63 BOB BHF 15.3 0.050 0.25 FCA 15.9 0.070 0.52 Table 2. Parameters of the critical point for symmetric nuclear matter with different EOSs from the BHF and FCA procedures.
-
We compute the critical parameters of symmetric nuclear matter in the BHF formalism with several realistic EOSs, comparing in detail two procedures with and without consideration of the temperature dependence of s.p. energies.
Considering all cases, the critical temperatures are found in the range
$ T_{\rm c} \approx 14-19{\;\mathrm{MeV}} $ , and critical densities are found in the range$ \rho_{\rm c} \approx 0.05-0.08{\;\mathrm{fm}^{-3}} $ , which are in good agreement with the available experimental results and the results of other theoretical approaches, apart from the DBHF model, which has predicted significantly smaller values. In our case, the variation in results is due to different two- and three-body forces used as the input to the BHF scheme. Although all of them provide similar realistic saturation properties for nuclear matter, the wide range of results for the critical properties may be considered as a current theoretical uncertainty regarding the construction of many-body input forces for the BHF scheme.The finite-T extension of the BHF formalism used here comprises temperature effects arising from the Fermi distribution functions in the Pauli operator and momentum integrals, whereas the input two- and three-body forces are assumed temperature independent. A consistent inclusion of temperature effects in these quantities has not yet been attempted and is a serious theoretical challenge for the future, because we show that the predicted critical point depends on the two- and three-body forces employed.
Nuclear liquid-gas phase transition within a Brueckner-Hartree-Fock approach
- Received Date: 2022-06-16
- Available Online: 2022-11-15
Abstract: The critical parameters of the liquid-gas phase transition of symmetric nuclear matter are computed using the Brueckner-Hartree-Fock method at finite temperature by employing different realistic nucleon-nucleon potentials. Temperature effects on single-particle potentials, defect functions, and three-body forces are discussed in detail. Results obtained from the full procedure and frozen-correlations approximation are compared. We find critical temperatures of approximately 14 to 19 MeV and critical densities in the range of





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF















 DownLoad:
DownLoad: