-
Most of the data on cross-sections for photonuclear reactions are important for many fields of science and technology, as well as for various data files (EXFOR, RIPL, ENDF, etc.), which were obtained in experiments using quasi-monoenergetic annihilation photons within the energy range of the giant dipole resonance (GDR). As a rule, such experiments were conducted with the direct detection of neutrons from the output channel of the reaction. However, when measuring the neutron yield, it becomes difficult to separate neutrons registered from various reactions, such as
$ (\gamma,n) $ ,$ (\gamma,pn) $ ,$ (\gamma,2n) $ ,$ (\gamma,p2n) $ , and$ (\gamma,3n) $ . This can lead to inaccuracies in both the values of the GDR cross-sections in the high-energy region and cross-sections with a higher reaction threshold.In Ref. [1], attention was drawn to the discrepancy between the data on the partial cross-sections for the
$ (\gamma,n) $ ,$ (\gamma,2n) $ , and$ (\gamma,3n) $ reactions of$ ^{181}{\rm{Ta}} $ from different laboratories [2, 3]. It is also shown that the sum of the cross-sections for the$ (\gamma,n) $ ,$ (\gamma,2n) $ , and$ (\gamma,3n) $ reactions obtained in different laboratories agree satisfactorily. Varlamov's works [4–6] noted systematic discrepancies between the cross-sections of partial photoneutron reactions$ (\gamma,n) $ ,$ (\gamma,2n) $ , and$ (\gamma,3n) $ and concluded that the experimental data for many nuclei are not sufficiently reliable owing to large systematic errors associated with the multiplicity method used to separate neutrons. Based on experimental data and postulates of a combined model in Refs. [7, 8], an experimentally-theoretical method was proposed for evaluating the values of reaction cross-sections, and corrections were made between the partial photoneutron reactions on several nuclei, for example, see Refs. [5, 9].An experimental study of photonuclear reactions on stable isotopes of copper was conducted in some works [10–17] and the values of the cross-sections for the reactions
$ (\gamma,n) $ and$ (\gamma,2n) $ were obtained. The discrepancy between data of different laboratories was observed both in the shape of the energy dependence of the cross-sections (the width of the distribution and the position of the maximum), and in the absolute value of the cross-section maxima. It was shown in Ref. [18] that Fultz's data [10] are systematically lower than Varlamov's data [4], and that it is necessary to introduce a multiplying factor of 1.17 to the Ref. [10] data on the$ (\gamma,n) $ reactions for the$ ^{63}{\rm{Cu}} $ and$ ^{65}{\rm{Cu}} $ nuclei. In the review paper [19] the cross-section maxima [4, 5] for reactions$ {^{63}{\rm{Cu}}}(\gamma,n)^{62}{\rm{Cu}} $ and$ {^{65}{\rm{Cu}}}(\gamma,n)^{64}{\rm{Cu}} $ are given as 79.79 and 86.38 mb, respectively, which differ significantly from the results of Ref. [10]. An analysis of the experimental cross-sections on copper isotopes for the$ (\gamma,2n) $ reaction from Ref. [10], conducted in Ref. [5] using the experimentally-theoretical procedure [7, 8], showed the need for a significant correction of these data. The authors of [7, 8] believe corrections should be introduced, not only in the case of the Cu nuclei, but also for all photonuclear cross-sections obtained by the method of direct neutron detection.Thus, we can conclude that there is a spread in the values of photonuclear cross-sections for Cu isotopes in the GDR region obtained in different laboratories. Considering that data on photonuclear reactions on copper isotopes are sometimes used to monitor the flux of bremsstrahlung quanta, for example, reaction
${^{63}{\rm{Cu}}}(\gamma,n) ^{62}{\rm{Cu}}$ in Ref. [14] and$ {^{65}{\rm{Cu}}}(\gamma,n)^{64}{\rm{Cu}} $ in Ref. [20], it is necessary to introduce more certainty into the experimental values of the cross-sections using other methods.In this work, using the γ-activation and off-line γ-ray spectrometric techniques, we study photonuclear reactions
$ {^{65}{\rm{Cu}}}(\gamma,n)^{64}{\rm{Cu}} $ ,$ {^{63}{\rm{Cu}}}(\gamma,n)^{62}{\rm{Cu}} $ ,$ {^{63}{\rm{Cu}}}(\gamma,2n)^{61}{\rm{Cu}} $ , and$ {^{63}{\rm{Cu}}}(\gamma,3n)^{60}{\rm{Cu}} $ in the bremsstrahlung end-point energy range$ E_{\rm{\gamma{max}}} $ = 35–94 MeV. The experimental results on the average cross-sections$ \langle{\sigma(E_{\rm{\gamma{max}}})}\rangle $ of reactions will enable the data of different laboratories to be supplemented for the case of the reactions$ (\gamma,n) $ and$ (\gamma,2n) $ . The cross-sections for the reaction$ {^{63}{\rm{Cu}}}(\gamma,3n)^{60}{\rm{Cu}} $ have not been measured before. The analysis of the experimental$ \langle{\sigma(E_{\rm{\gamma{max}}})}\rangle $ is conducted using the cross-sections$ \sigma(E) $ from the TALYS1.95 code [21] and the data available in the literature. -
An experimental study of copper photodisintegration cross-sections has been conducted through measurements of the residual γ-activity of the irradiated sample, which enabled one to simultaneously obtain the data from different channels of photonuclear reactions. This well known technique has been described in a variety of papers concerned with the investigation of multiparticle photonuclear reactions, e.g., on the nuclei
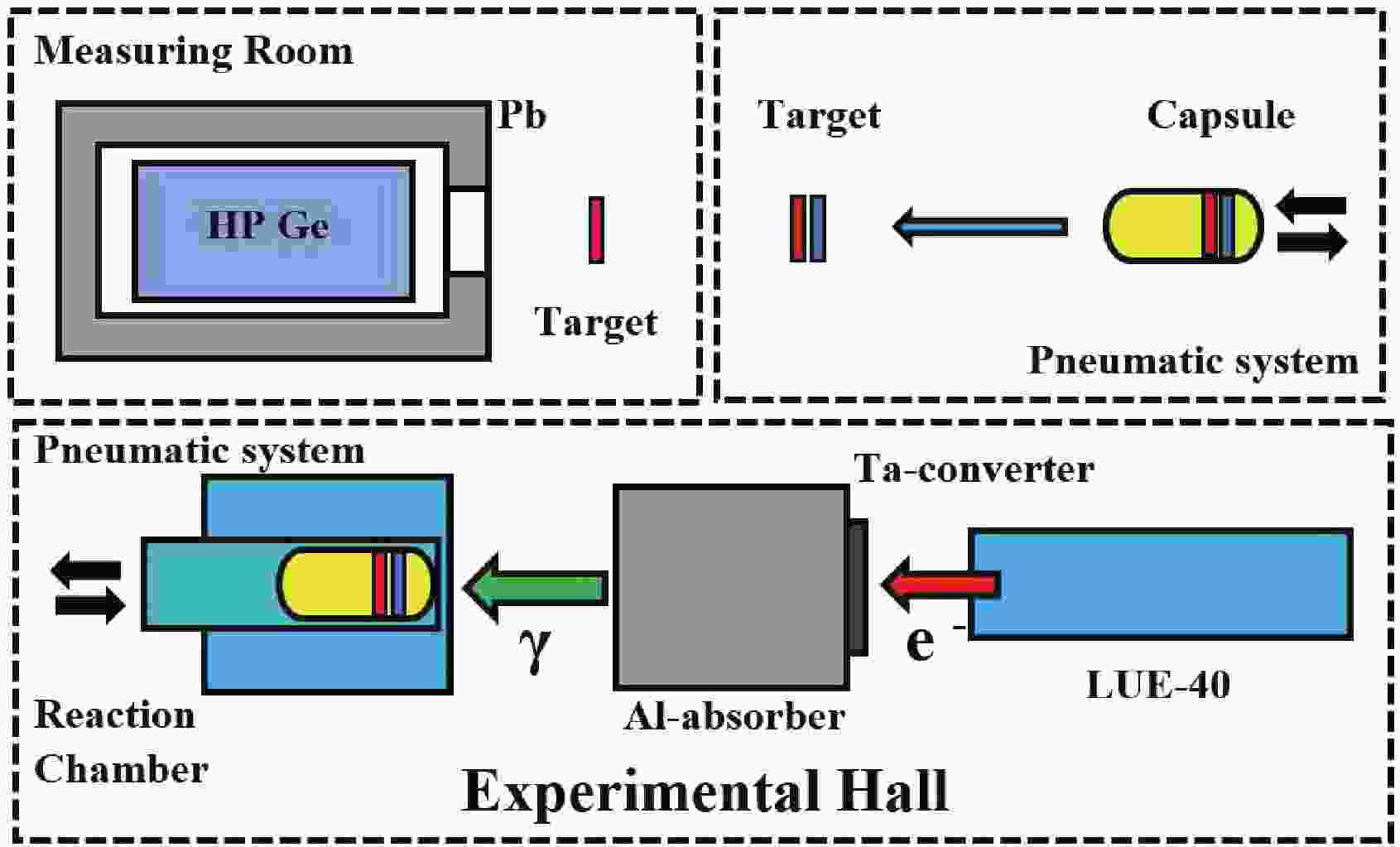
$ {^{27} {\rm{Al}}} $ [22, 23],$ {^{93}{\rm{Nb}}} $ [24–28] and$ {^{181}{\rm{Ta}}} $ [1, 29].The schematic block diagram of the experimental setup is presented in Fig. 1. The γ-ray bremsstrahlung beam was generated by means of the NSC KIPT electron linac LUE-40 RDC “Accelerator” [30, 31]. Electrons of the initial energy
$ E_e $ were incident on the target-converter made from a 1.05 mm thick natural tantalum plate, measuring 20 by 20 mm in size. To remove electrons from the bremsstrahlung flux, a cylindrical aluminum absorber was used, which measured 100 mm in diameter and 150 mm in length. The 8 mm diameter targets were placed in the aluminum capsule and arranged behind the Al-absorber on the electron beam axis. The pneumatic tube transfer system was used to transport the targets to the irradiation area and back, to induce activity registration. After the irradiated targets were delivered to the measuring room, the samples were extracted from the aluminum capsule and individually transferred to the detector for measurement.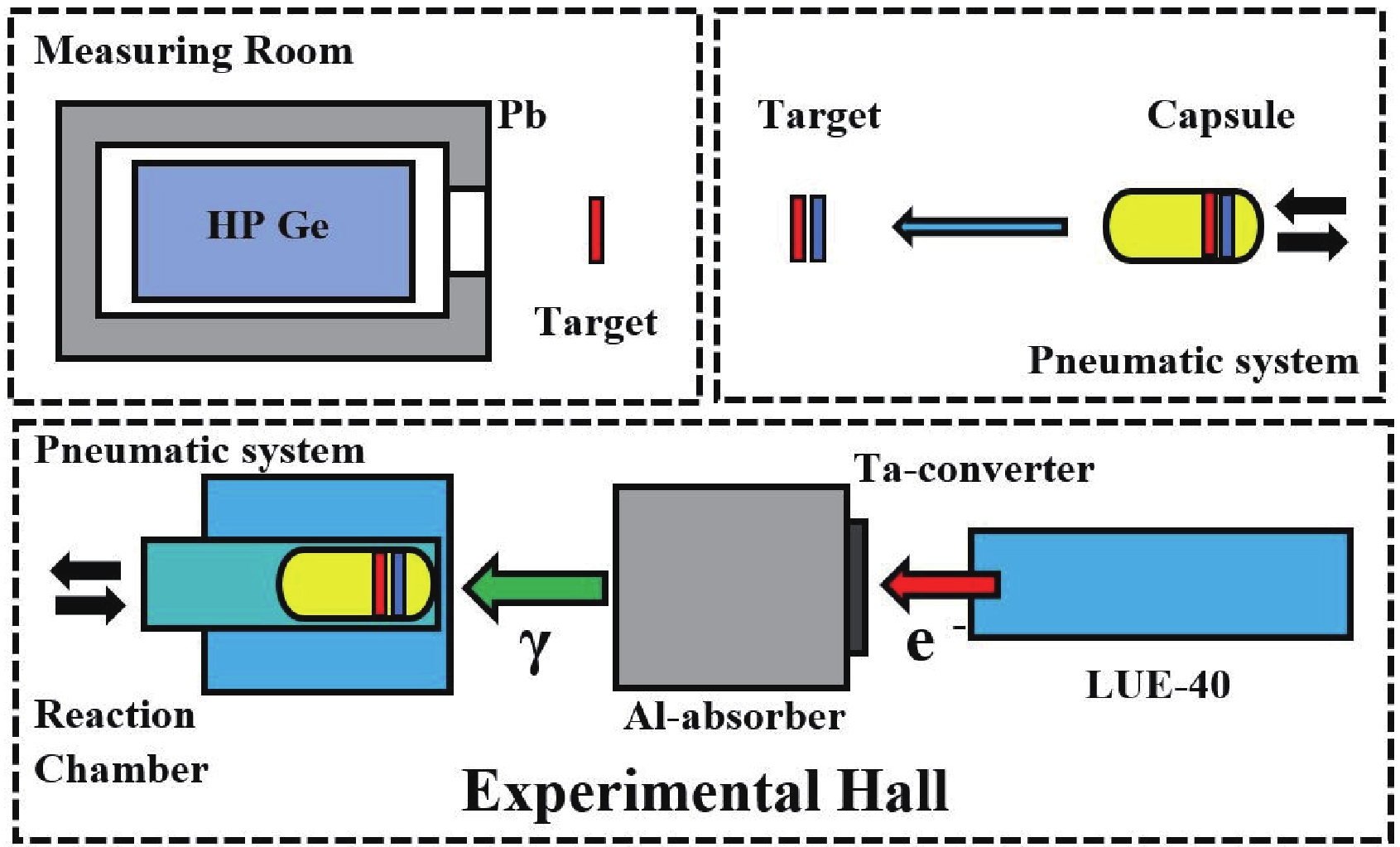
Figure 1. (color online) The schematic block diagram of the experimental setup. The upper part shows the measuring room, where the exposed target (red color) and the target-monitor (blue color) are extracted from the capsule and are arranged by turn before the HPGe detector for induced γ-activity measurements. The lower part shows the accelerator LUE-40, Ta-converter, Al-absorber, and exposure reaction chamber.
The induced γ-activity of the irradiated targets was registered by the semiconductor HPGe detector Canberra GC-2018 with resolutions of 0.8 and 1.8 keV (FWHM) for the γ-quanta energies
$ E_\gamma $ = 122 and 1332 keV, respectively. Its efficiency was 20% relative to the NaI(Tl) detector, measuring 3 inches in diameter and 3 inches in thickness. The absolute registration efficiency of the HPGe detector was calibrated with a standard set of gamma-ray radiation sources:$ ^{22} {\rm{Na}}$ ,$ ^{60}{{\rm{Co}}} $ ,$ ^{133}{\rm{Ba}} $ ,$ ^{137} {\rm{Cs}}$ ,$ ^{152} {\rm{Eu}}$ , and$ ^{241} {\rm{Am}}$ .The bremsstrahlung spectra of electrons were calculated using the GEANT4.9.2 code [32], with due regard for the actual geometry of the experiment, by considering the spatial and energy distributions of the electron beam. The program code GEANT4.9.2, PhysList G4LowEnergy, allows consideration of all physical processes during the calculation process for an amorphous target. Similarly, GEANT4.9.2PhysList QGSP-BIC-HP, allows for calculation of the neutron yield, due to photonuclear reactions from targets of different thicknesses and atomic charges. In addition, the bremsstrahlung gamma fluxes were monitored through the yield of the
$ ^{100}{\rm{Mo}}(\gamma,n)^{99}{\rm{Mo}} $ reaction. For this purpose, the natural molybdenum target-witness was placed close to the study target, simultaneously exposing it to radiation.The natCu and natMo targets were used in the experiment. The isotopic composition of copper is a mixture of two stable isotopes:
$ ^{63}{\rm{Cu}} $ (isotopic abundance 69.17%) and$ ^{65}{\rm{Cu}} $ (isotopic abundance 30.83%). We used the percentage value of isotope abundance equal to 9.63% in our calculations for$ ^{100}{\rm{Mo}} $ (see Ref. [32]). The admixture of other elements in the targets did not exceed 0.1% by weight.In the experiment, Cu and Mo samples were exposed to radiation at end-point bremsstrahlung energies
$ E_{\rm{\gamma{max}}} $ ranging from 35 to 94 MeV, with an energy step of$ \sim $ 5 MeV. The masses of the Cu and Mo targets were 22 and 60 mg, respectively. The time of irradiation$ t_{\rm{irr}} $ was 30 min for each energy$ E_{\rm{\gamma{max}}} $ value; the time of residual γ-activity spectrum measurement$ t_{\rm{meas}} $ ranged from 30 min to 17–60 h.The yield and bremsstrahlung flux-averaged cross-sections
$ \langle{\sigma(E_{\rm{\gamma{max}}})}\rangle $ of the$ ^{100}{\rm{Mo}}(\gamma,n)^{99}{\rm{Mo}} $ ,$ {^{65}{\rm{Cu}}}(\gamma,n)^{64}{\rm{Cu}} $ ,$ {^{63}{\rm{Cu}}}(\gamma,n)^{62}{\rm{Cu}} $ ,$ {^{63}{\rm{Cu}}}(\gamma,2n)^{61}{\rm{Cu}} $ , and$ {^{63}{\rm{Cu}}}(\gamma,3n)^{60}{\rm{Cu}} $ reactions were obtained. Table 1 lists the nuclear spectroscopic data of the radionuclide's reactions according to data from Ref. [33], where$ E_{\rm{th}} $ denotes reaction thresholds,$ T_{1/2} $ is the half-life period of the nuclei-products,$ E_{\gamma} $ are the energies of the γ-lines under study, and their intensities are denoted by$ I_{\gamma} $ .Nuclear reaction $ E_{\rm{th}} $ /MeV

$ T_{1/2} $ 

$ E_{\gamma} $ /keV

$ I_{\gamma} $ (%)

$ {^{65}{\rm{Cu}}}(\gamma,n)^{64}{\rm{Cu}} $ 

9.91 12.700 ± 0.002 h 1345.84 0.473 ± 0.010 $ {^{63}{\rm{Cu}}}(\gamma,n)^{62}{\rm{Cu}} $ 

10.86 9.74 ± 0.02 min 1172.9 0.34 875.68 0.150 ± 0.007 $ {^{63}{\rm{Cu}}}(\gamma,2n)^{61}{\rm{Cu}} $ 

19.74 3.333 ± 0.005 h 1185.23 3.75 ± 0.07 282.96 12.2 ± 0.3 656.01 10.77 ± 0.18 $ {^{63}{\rm{Cu}}}(\gamma,3n)^{60}{\rm{Cu}} $ 

31.44 23.7 ± 0.4 min 1332.5 88 $ ^{100}{\rm{Mo}}(\gamma,n)^{99}{\rm{Mo}} $ 

8.29 $ 65.94 \pm 0.01 $ h

739.50 $ 12.13 \pm 0.12 $ 

The error of intensity $ I_{\gamma} $ for the 1172.9 keV γ-line was determined as half-value spreads according to the databases of Refs. [33] and [34]. In the case of the 1332.5 keV γ-line, the

$ I_{\gamma} $ -error is absent in Refs. [33, 34], and therefore, it was taken to be 0.5%.

Table 1. Nuclear spectroscopic data of the radio-nuclides reactions from Ref. [33].
Measuring the yield of photoneutron reactions on copper isotopes immediately after irradiation is hampered by the high intensity of the 511 keV γ-line to positron annihilation. This can lead to random coincidences in the detection system, which can distort the result of target activity measurements. Thus, the presence of the positron line reduces the ease of measuring, which is considered a disadvantage of using the Cu nuclei as a monitor target.
Therefore, it is necessary to either significantly increase the distance between the detector and the irradiated target (up to 400 mm) or wait several hours for the intensity of short-lived residual radiation lines to weaken. We adopted both measurement variants.
To process the spectra and estimate the number of counts of γ-quanta in the full absorption peak
$ \triangle A $ , we used the InterSpec v.1.0.9 program [35]. Figure 2 shows the typical gamma-spectrum from reaction products of the copper target in the$ E_{\gamma} $ range from 800 to 1500 keV.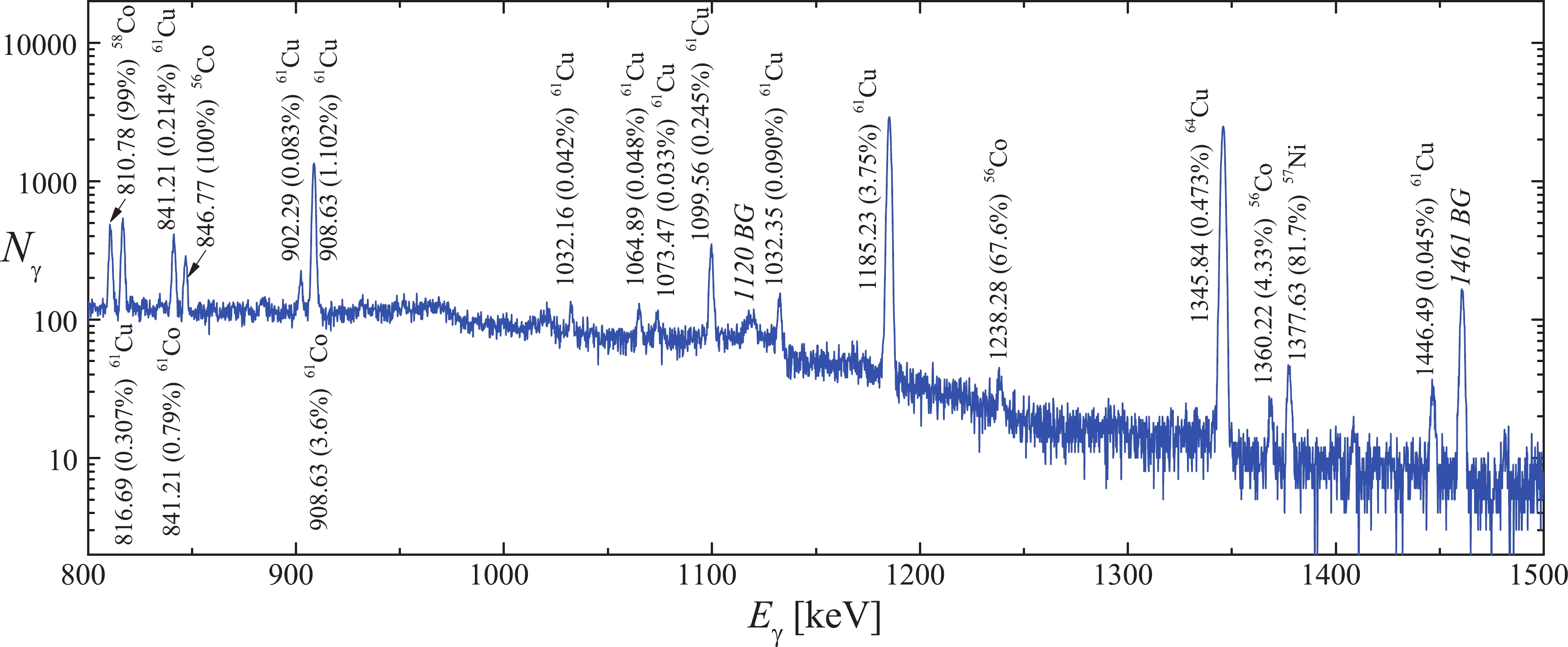
Figure 2. (color online) Gamma-ray spectrum of the reaction products from the natCu target measured for the following parameters:
$t_{\rm{meas}}$ = 63218 s,$t_{\rm{cool}}$ = 19015 s,$E_{\rm{\gamma max}}$ = 94 MeV, and m = 21.815 mg. The spectrum fragment ranges from 800 to 1500 keV. The background γ-lines peaks are indicated by the letters$\rm BG$ .The bremsstrahlung gamma-flux monitoring against the
$ ^{100}{\rm{Mo}}(\gamma,n)^{99}{\rm{Mo}} $ reaction yield was performed by comparing the experimentally obtained average cross-section values with computational data. To determine the experimental$ \langle{\sigma(E_{\rm{\gamma{max}}})}\rangle $ values, we used the$ \triangle A $ activity value for the$ E_{\gamma} $ = 739.50 keV γ-line, and the absolute intensity$ I_{\rm{\gamma}} $ = 12.13% (see Table 1). The theoretical values of the average cross-section$ \langle{\sigma(E_{\rm{\gamma{max}}})}\rangle_{\rm{th}} $ were calculated using the cross-sections$ \sigma(E) $ from the TALYS1.95 code, run with default options. The normalization (monitoring) factor$ k_{\rm{monitor}} $ , derived from the ratios of$ \langle{\sigma(E_{\rm{\gamma{max}}})}\rangle_{\rm{th}} $ to$ \langle{\sigma(E_{\rm{\gamma{max}}})}\rangle $ , represent the deviation of the GEANT4.9.2-computed bremsstrahlung γ-flux from the actual flux falling on the target. The determined$ k_{\rm{monitor}} $ values were used for normalizing cross-sections for other photonuclear reactions. The monitoring procedure has been detailed in Refs. [24, 25].The Ta-converter and Al-absorber used in the experiment, generate neutrons that can cause the
$ ^{100}{\rm{Mo}}(n,2n)^{99}{\rm{Mo}} $ reaction. Calculations were made of the neutron energy spectrum, as well as the fraction of neutrons with energies above the threshold of this reaction, similar to Ref. [36]. The contribution of the$ ^{100}{\rm{Mo}}(n,2n)^{99}{\rm{Mo}} $ reaction to the value of the induced activity of the$ ^{99} {\rm{Mo}}$ nucleus has been estimated and shown to be negligible compared to the contribution of the$ ^{100}{\rm{Mo}}(\gamma,n)^{99}{\rm{Mo}} $ reaction. The contribution of the reaction$ ^{100}{\rm{Mo}}(\gamma,p)^{99}{\rm{Nb}} $ ,$ ^{99}{\rm{Nb}} \xrightarrow{\beta^-} $ $ ^{99}{\rm{Mo}} $ is also negligible. -
The uncertainty in measurements of experimental values of the average cross-sections
$ \langle{\sigma(E_{\rm{\gamma{max}}})}\rangle $ was determined as a quadratic sum of statistical and systematical errors. The statistical error in the observed γ-activity is mainly due to statistics in the total absorption peak of the corresponding γ-line, which varies within 1 to 10%. This error varies depending on the γ-line intensity and the background conditions of spectrum measurements. The observed activity$ \triangle A $ of the investigated γ-line depends on the detection efficiency, the half-life period, and the absolute intensity$ I_{\rm{\gamma}} $ . The background is governed by the contribution of the Compton scattering of quanta.The systematic errors are associated with the uncertainties of the 1. irradiation time (
$ \sim $ 0.5%); 2. electron current ($ \sim $ 0.5%); 3. detection efficiency of the detector (2%–3%), which is mainly associated with the error of the reference sources of γ-radiation and the choice of the approximation curve; 4. half-life$ T_{1/2} $ of the reaction products and absolute intensity$ I_{\rm{\gamma}} $ of the analyzed γ-quanta as noted in Table 1; 5. normalization of experimental data to the$ ^{100}{\rm{Mo}}(\gamma,n)^{99}{\rm{Mo}} $ monitor reaction yield up to 5%; and 6. error in calculating the contribution from competing γ-lines (described in the text).Thus, the statistical and systematical errors are considered variables, as they differ for different
$ {^{65}{\rm{Cu}}}(\gamma,n)^{64}{\rm{Cu}} $ and$ {^{63}{\rm{Cu}}}(\gamma,xn)^{63-x}{\rm{Cu}} $ reactions. The total uncertainty of the experimental data is given in figures with experimental results. -
The cross-sections
$ \sigma(E) $ , averaged over the bremsstrahlung γ-flux$ W(E,E_{\rm{\gamma{max}}}) $ from the threshold$ E_{\rm{th}} $ of the reaction under study to the end-point energy of the spectrum$ E_{\rm{\gamma{max}}} $ , were calculated with the use of the theoretical cross-section values computed with the TALYS1.95 code [21], installed on Ubuntu20.04. The bremsstrahlung flux-averaged cross-section$ \langle{\sigma(E_{\rm{\gamma{max}}})}\rangle_{\rm{th}} $ in a given energy interval was calculated by the formula$ \langle{\sigma(E_{\rm{\gamma{max}}})}\rangle_{\rm{th}} = \frac {\int\limits_{E_{\rm{th}}}^{E_{\rm{\gamma{max}}}}\sigma(E)\cdot W(E,E_{\rm{\gamma{max}}}){\rm d}E} {\int\limits_{E_{\rm{th}}}^{E_{\rm{\gamma{max}}}}W(E,E_{\rm{\gamma{max}}}){\rm d}E}. $

(1) These theoretical average cross-sections were compared with the experimental values calculated by the formula:
$ \begin{aligned}[b]& \langle{\sigma(E_{\rm{\gamma{max}}})}\rangle \\=& \frac{\lambda \triangle A {\rm{\Phi}}^{-1}(E_{\rm{\gamma{max}}})}{N_x I_{\gamma} \ \varepsilon (1-\exp(-\lambda t_{\rm{irr}}))\exp(-\lambda t_{\rm{cool}})(1-\exp(-\lambda t_{\rm{meas}}))}, \end{aligned} $

(2) where
$ \triangle A $ is the number of counts of γ-quanta in the full absorption peak (for the γ-line of the investigated reaction),$ \lambda $ is the decay constant ($ {\rm{ln}}2/T_{1/2} $ ),$ N_x $ is the number of target atoms,$ I_{\gamma} $ is the absolute intensity of the analyzed γ-quanta,$ \varepsilon $ is the absolute detection efficiency for the analyzed photon energy, and$ {\rm{\Phi}}(E_{\rm{\gamma{max}}}) = $ $ {\int\limits_{E_{\rm{th}}}^{E_{\rm{\gamma{max}}}}W(E,E_{\rm{\gamma{max}}}){\rm d}E} $ is the integrated bremsstrahlung flux in the energy range from the reaction threshold$ E_{\rm{th}} $ up to$ E_{\rm{\gamma{max}}} $ ;$ t_{\rm{irr}} $ ,$ t_{\rm{cool}} $ , and$ t_{\rm{meas}} $ are the irradiation time, cooling time, and measurement time, respectively. A more detailed description of all the calculation procedures necessary for the determination of$ \langle{\sigma(E_{\rm{\gamma{max}}})}\rangle $ can be found in Refs. [24, 25]. -
In the
$ {^{65}{\rm{Cu}}}(\gamma,n) $ reaction the$ ^{64} {\rm{Cu}}$ nucleus is formed with half-life$ T_{1/2} $ = 12.700$ \pm $ 0.002 h. The$ ^{64} {\rm{Cu}}$ nucleus undergoes$ \beta^- $ -decay (39%) with the formation of the$ ^{64} $ Zn nucleus, and$ \varepsilon^+\beta^+ $ -decay (61%) with the formation of the$ ^{64} $ Ni nucleus. In the latter case, a gamma-line emission with$ E_{\rm{\gamma}} $ = 1345.84 keV of low-intensity$ I_{\gamma} $ = 0.473% is observed.An experimental study of the cross-section for the reaction
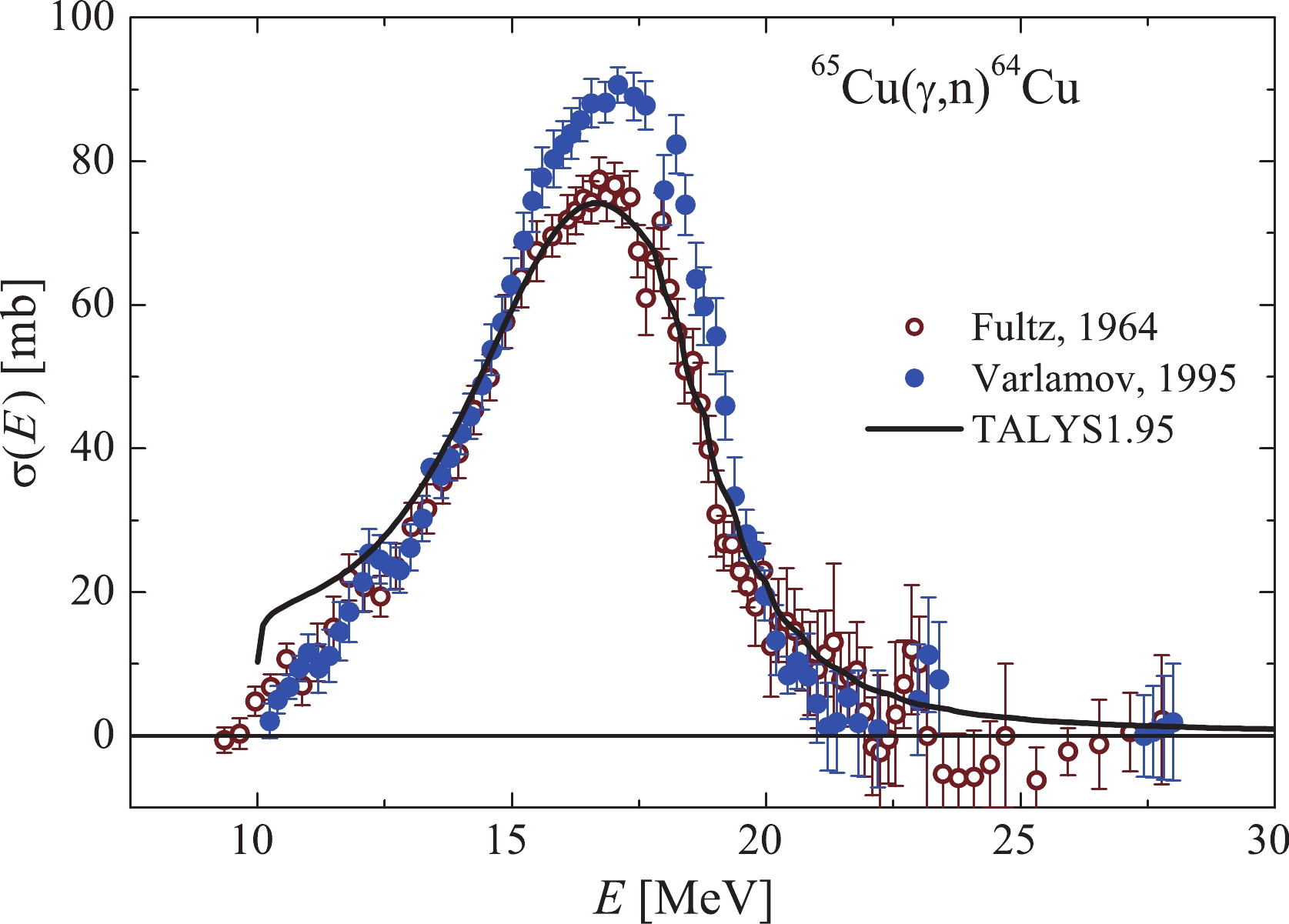
$ {^{65}{\rm{Cu}}}(\gamma,n)^{64}{\rm{Cu}} $ was conducted in several works [4, 10, 19]. The results of these works show significant differences in the value of the GDR maxima: 75$ \pm $ 7 mb [10], 86.38 mb [19] (see Fig. 3). These data were matched in the region of the GDR maximum in Ref. [4] by introducing a coefficient of 1.17 into the data of Ref. [10].The calculation of the cross-section
$ \sigma(E) $ for this reaction were conducted using the TALYS1.95 code with default parameters. As can be seen from Fig. 3, the calculated cross-section at the maximum is very close to the experimental values of$ \sigma(E) $ from Ref. [10], but significantly lower than Varlamov's data [4, 19]. Moreover, the leading edge of the calculated distribution does not coincide with the data of the two experiments.The average cross-sections
$ \langle{\sigma(E_{\rm{\gamma{max}}})}\rangle $ calculated using the cross-section from TALYS1.95, and our experimental data for the reaction$ {^{65}{\rm{Cu}}}(\gamma,n)^{64}{\rm{Cu}} $ are shown in Fig. 4. All experimental points are located noticeably higher (~15%–20%) than the calculated curve , which supports the data of Refs. [4, 19].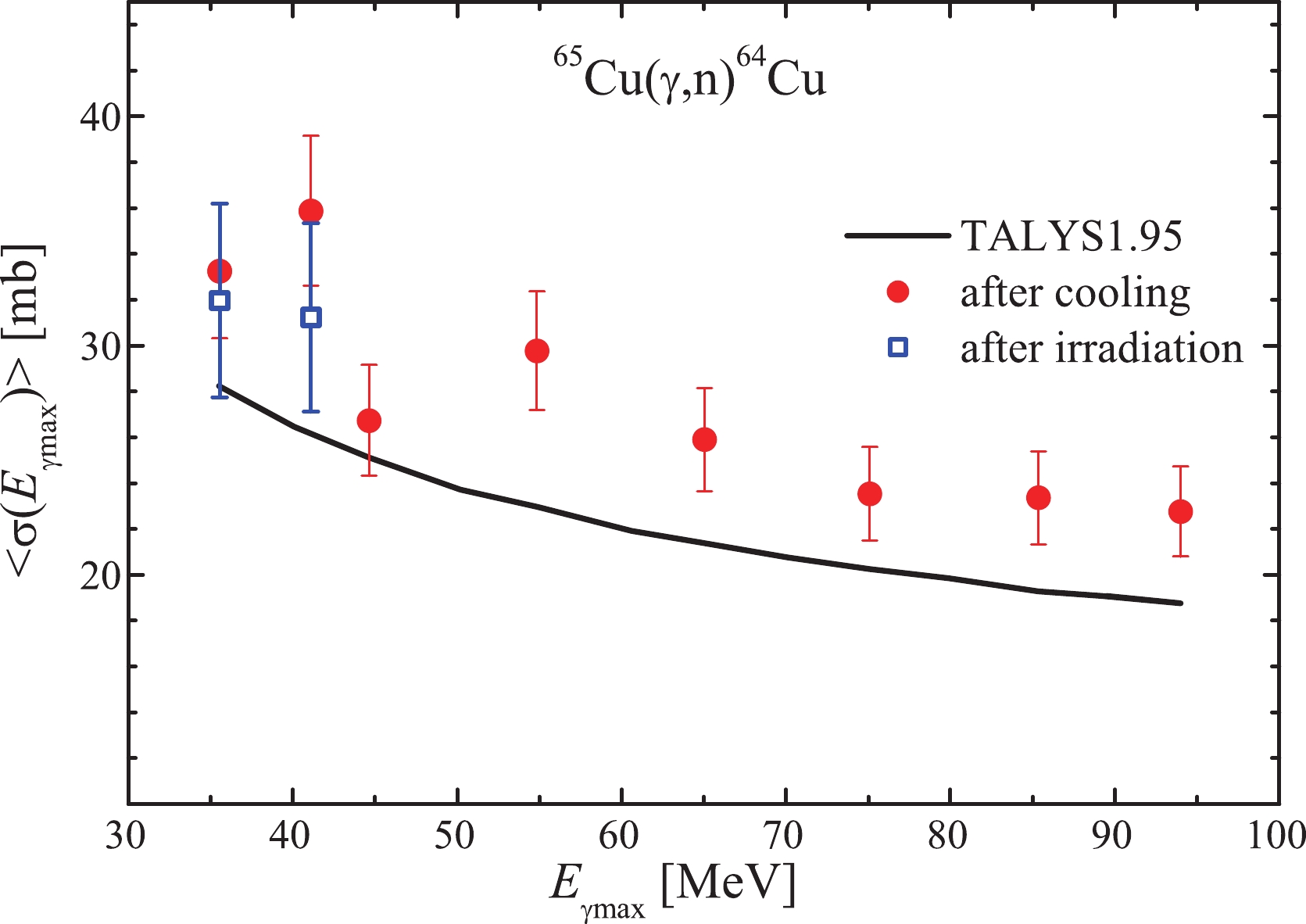
Figure 4. (color online) Flux-average cross-section
$\langle{\sigma(E_{\rm{\gamma max}})}\rangle$ of the reaction${^{65}{\rm{Cu}}}(\gamma,n)^{64}{\rm{Cu}}$ . The curve is calculated using the TALYS1.95 code. Experimental results: squares – measurements immediately after irradiation, circles – measurements after cooling. -
As a result of the
$ {^{65}{\rm{Cu}}}(\gamma,2n) $ reaction, the stable isotope$ ^{63} {\rm{Cu}}$ is formed. The induced activity method does not allow us to measure the yield of this reaction. For completeness of the analysis, Fig. 5 shows the data from [10], and calculation from TALYS1.95 with default parameters. A noticeable difference between the experimental and calculated cross-sections can be seen. The experimental values exceed the theoretical cross-sections from the TALYS1.95 code by approximately 1.3 times at energies of 19–24 MeV.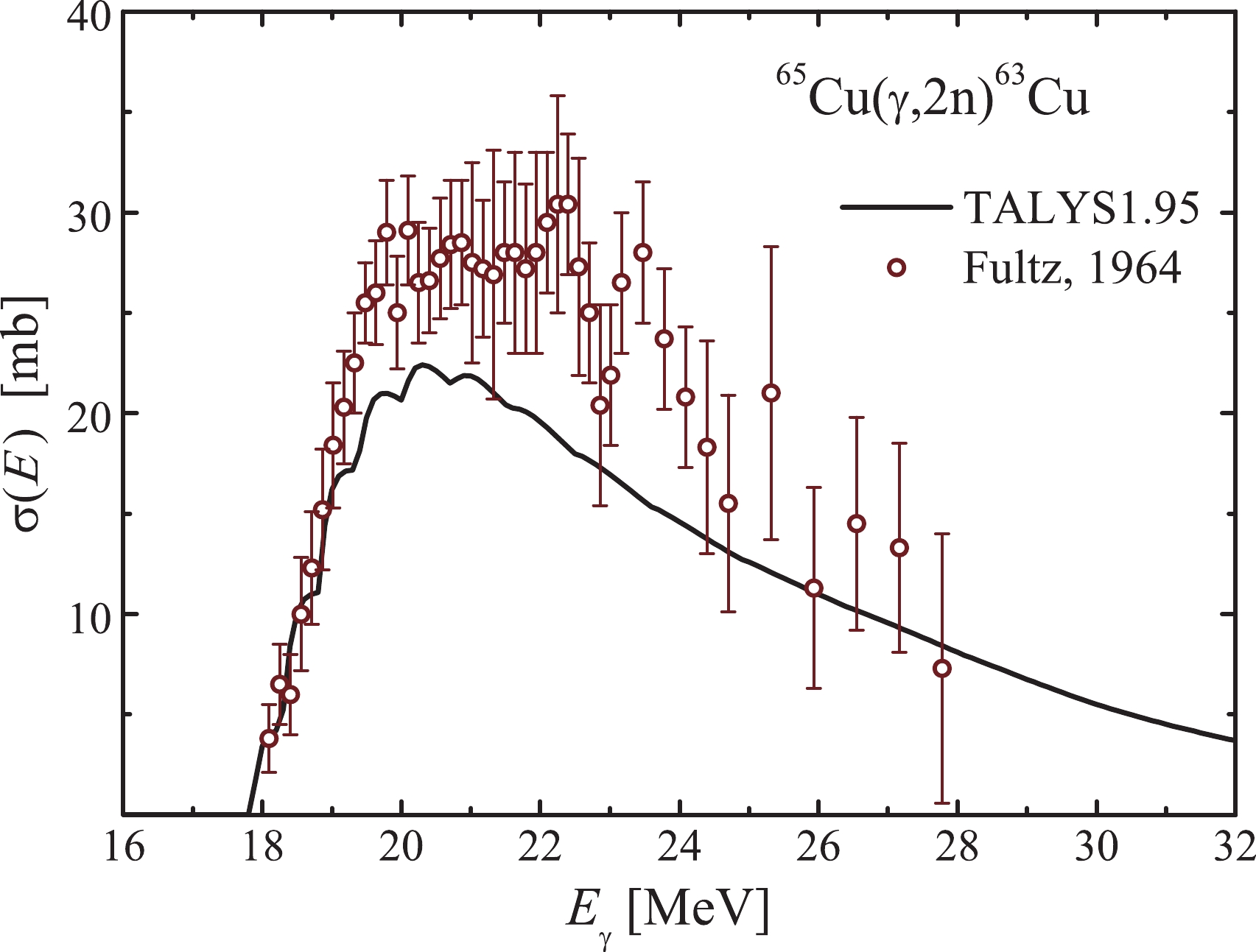
Figure 5. (color online) The
${^{65}{\rm{Cu}}}(\gamma,2n)^{63}{\rm{Cu}}$ reaction cross-section. Curve – calculation in the TALYS1.95 code, empty circles – experimental data from Ref. [10].In Ref. [5], using the experimental-theoretical approach [7, 8], the reliability of data on the cross-sections for the reaction
$ {^{65}{\rm{Cu}}}(\gamma,2n)^{63}{\rm{Cu}} $ from Ref. [10] was verified. It is shown that the estimated (recalculated) values of the cross-sections are significantly lower than the experimental ones, and the difference was up to 30% in the energy range$ E_{\rm{\gamma}} $ = 19–25 MeV. This value is very close to the discrepancy between the TALYS1.95 cross-section and the result of Ref. [10].Such a notable change (correction) in the cross-section for the
$ {^{65}{\rm{Cu}}}(\gamma,2n)^{63}{\rm{Cu}} $ reaction leads to corrections in the GDR cross-section for energies above 18 MeV. -
In the
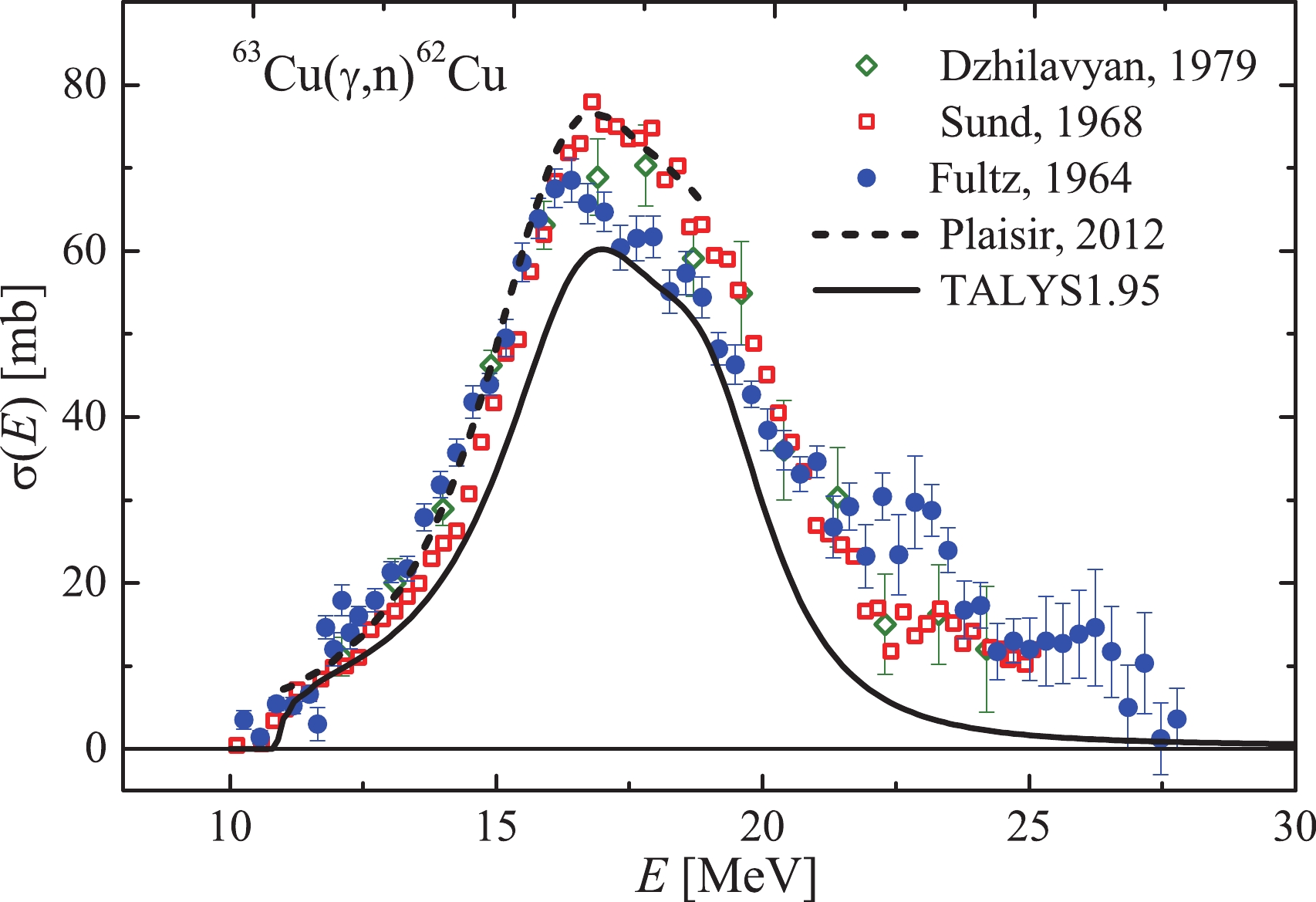
$ {^{63}{\rm{Cu}}}(\gamma,n) $ reaction, the$ ^{62}{\rm{Cu}} $ nucleus is formed with half-life$ T_{1/2} $ = 9.74 m. The$ ^{62}{\rm{Cu}} $ nucleus undergoes$ \varepsilon^+\beta^+ $ -decay (the$ ^{62}{\rm{Ni}} $ nucleus is formed) with the emission of several low-intensity gamma-lines. The line of γ-radiation with$ E_{\rm{\gamma}} $ = 1172.9 keV and intensity$ I_{\rm{\gamma}} $ = 0.34% was used in this study.An experimental study of this reaction was conducted in several works [4, 10–14, 19] in the energy range 10–28 MeV. These data show different GDR maximum heights: the data of [10] are lower than the results of other laboratories, as in the case of the
$ {^{65}{\rm{Cu}}}(\gamma,n)^{64}{\rm{Cu}} $ reaction. The disagreement in the GDR maxima between Refs. [10] and [4, 19] was 14%, i.e., 70$ \pm $ 7 mb and 79.8 mb, respectively.The calculation of cross-sections in the TALYS1.95 code run with default parameters is shown in Fig. 6. In the region of the maximum, there is good agreement between the TALYS1.95 calculation and the data of Ref. [10]. All other experimental results of Refs. [11–14], including Ref. [19], are located above the theoretical estimate. Note that the calculated distribution widths
$ \sigma(E) $ are noticeably smaller than any experimental data set.Fig. 7 shows the average cross-sections
$ \langle{\sigma(E_{\rm{\gamma{max}}})}\rangle $ of the$ {^{63}{\rm{Cu}}}(\gamma,n)^{62}{\rm{Cu}} $ reaction calculated in the TALYS1.95 code run with default parameters, and the obtained experimental data in the energy range$ E_{\rm{\gamma{max}}} $ = 35–94 MeV. An excess of experimental$ \langle{\sigma(E_{\rm{\gamma{max}}})}\rangle $ values over the calculation for the entire energy range was found to be 15%–20%. This result agrees with that observed in Fig. 6, which represents the discrepancy between data from [11–14] and cross-sections from TALYS1.95.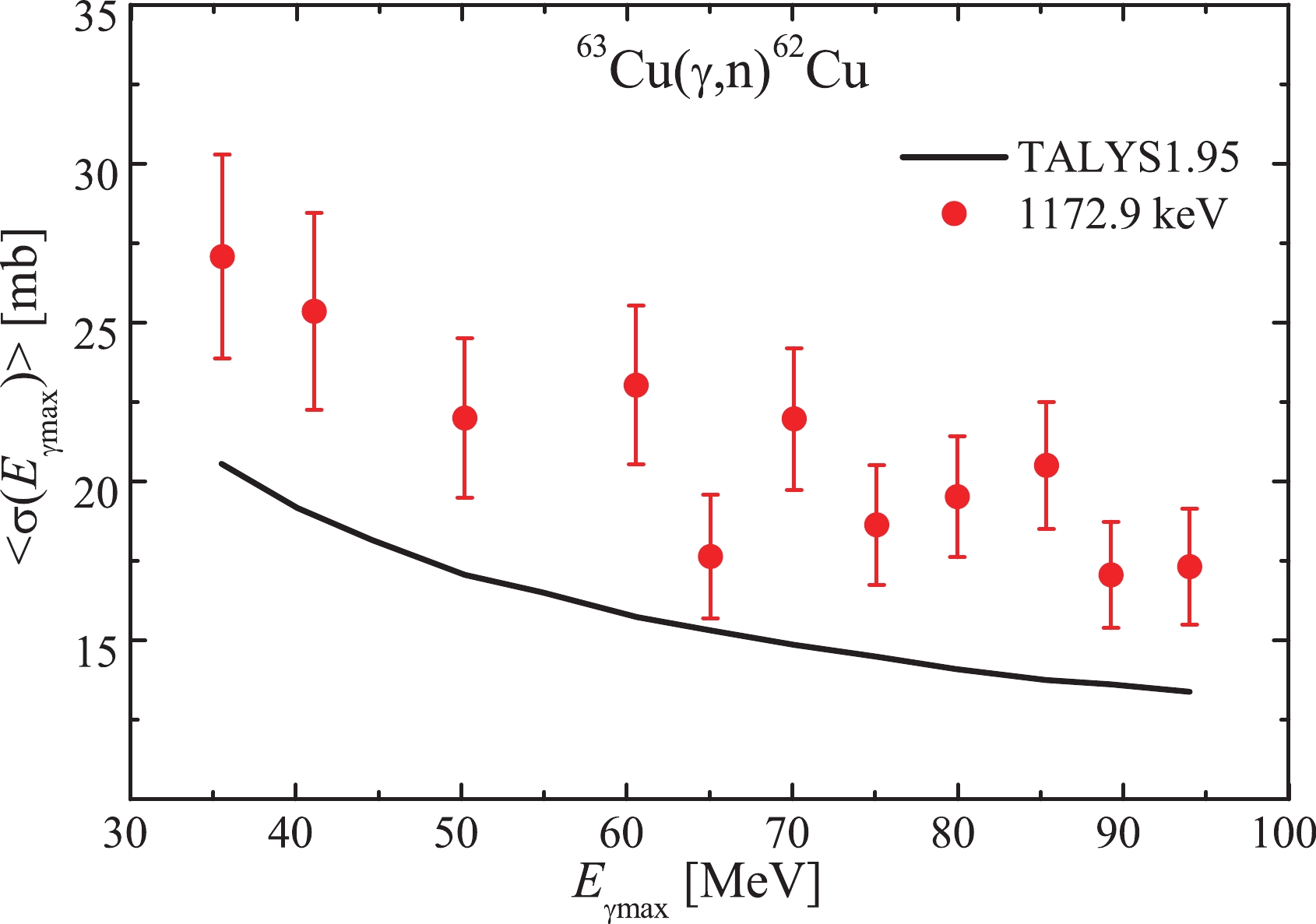
Figure 7. (color online) Flux-average cross-sections
$\langle{\sigma(E_{\rm{\gamma max}})}\rangle$ for the reaction${^{63}{\rm{Cu}}}(\gamma,n)^{62}{\rm{Cu}}$ . Curve – calculation using Talys1.95, filled circles – our experimental data.Because natural copper targets were used in the study, the effect of the
$ {^{65}{\rm{Cu}}}(\gamma,3n)^{62}{\rm{Cu}} $ reaction on the yield of the$ {^{63}{\rm{Cu}}}(\gamma,n)^{62}{\rm{Cu}} $ reaction was estimated. For this purpose, the values of the cross-section from the TALYS1.95 code were used to calculate the yield. It was found that the contribution of$ {^{65}{\rm{Cu}}}(\gamma,3n)^{62}{\rm{Cu}} $ increases with increasing energy$ E_{\rm{\gamma{max}}} $ from 0.16% at 35 MeV to 1.32% at 94 MeV.In the natCu target, under the impact of high-energy bremsstrahlung, isotopes of cobalt and copper are also formed, which have γ-radiation with
$ E_{\rm{\gamma}} $ value close to that used in the study. Thus,$ ^{62} {{\rm{Co}}}$ ($ E_{\rm{\gamma}} $ = 1172.9 keV,$ I_{\rm{\gamma}} $ = 84%,$ T_{1/2} $ = 1.5 min),$ ^{62m} {{\rm{Co}}}$ ($ E_{\rm{\gamma}} $ = 1172.9 keV,$ I_{\rm{\gamma}} $ = 98%,$ T_{1/2} $ = 13.91 min),$ ^{60} {{\rm{Co}}}$ ($ E_{\rm{\gamma}} $ = 1173.24 keV,$ I_{\rm{\gamma}} $ = 99.974%,$ T_{1/2} $ = 5.27 years), and$ ^{60} {\rm{Cu}}$ ($ E_{\rm{\gamma}} $ = 1173.24 keV,$ I_{\rm{\gamma}} $ = 0.26%,$ T_{1/2} $ = 23.7 min).The contributions of such γ-radiation were estimated using the cross-sections from the TALYS1.95 code, considering the half-lives, intensities of the competing lines, and the experimental conditions (irradiation, cooling, and measurement times). The calculated total activity of
$ ^{62} {{\rm{Co}}}$ and$ ^{62{\rm m}} {{\rm{Co}}}$ nuclei ranged from 0 to 1.72% in the range of studied$ E_{\rm{\gamma{max}}} $ . The radiation contribution from radionuclides$ ^{60} {\rm{Cu}}$ and$ ^{60} {{\rm{Co}}}$ is insignificant.The total amount of corrections ranged from 0.24%–3.28% and was accounted for in the data.
-
In the reaction
$ {^{63}{\rm{Cu}}}(\gamma,2n) $ the$ ^{61}{\rm{Cu}} $ nucleus is formed with half-life$ T_{1/2} $ = 3.333 h. The$ ^{61}{\rm{Cu}} $ nucleus undergoes$ \varepsilon^+\beta^+ $ -decay with the formation of the$ ^{61}{\rm{Ni}} $ nucleus. Three lines with$ E_{\rm{\gamma}} $ = 282.96, 656.01, and 1185.23 keV and an intensity$ I_{\rm{\gamma}} $ of 12.2, 10.77, and 3.75% were used for the study.The calculation of cross-sections for the
$ {^{63}{\rm{Cu}}}(\gamma,2n) $ reaction, performed in the Talys1.95 code with default parameters, are shown in Fig. 8. All experimental results of Refs. [10, 13, 15] are significantly higher than the theoretical estimates: the variation between the data of Ref. [10] and the calculated cross-sections is threefold at the cross-section maximum. Moreover, the energy dependence of the calculated curve is wider than the experimental results.The experimental average cross-sections
$ \langle{\sigma(E_{\rm{\gamma{max}}})}\rangle $ for the reaction$ {^{63}{\rm{Cu}}}(\gamma,2n)^{61}{\rm{Cu}} $ in the energy range$ E_{\rm{\gamma{max}}} $ = 35–94 MeV are shown in Fig. 9. The data found for the three gamma lines agree within the experimental error tolerance. To account for the contribution of the$ {^{65}{\rm{Cu}}}(\gamma,4n)^{61}{\rm{Cu}} $ reaction to the yield of the$ {^{63}{\rm{Cu}}}(\gamma,2n)^{61}{\rm{Cu}} $ reaction, calculations were conducted similar to the$ {^{63}{\rm{Cu}}}(\gamma,n)^{62}{\rm{Cu}} $ reaction. The yield for$ {^{65}{\rm{Cu}}}(\gamma,4n)^{61}{\rm{Cu}} $ was calculated and showed that this contribution increased with energy: for 50 MeV, it does not exceed 0.7%, and for 94 MeV, it reaches 3.2%. The cross-section for the$ {^{63}{\rm{Cu}}}(\gamma,2n)^{61}{\rm{Cu}} $ reaction was corrected (reduced) by the corresponding values at each energy$ E_{\rm{\gamma{max}}} $ .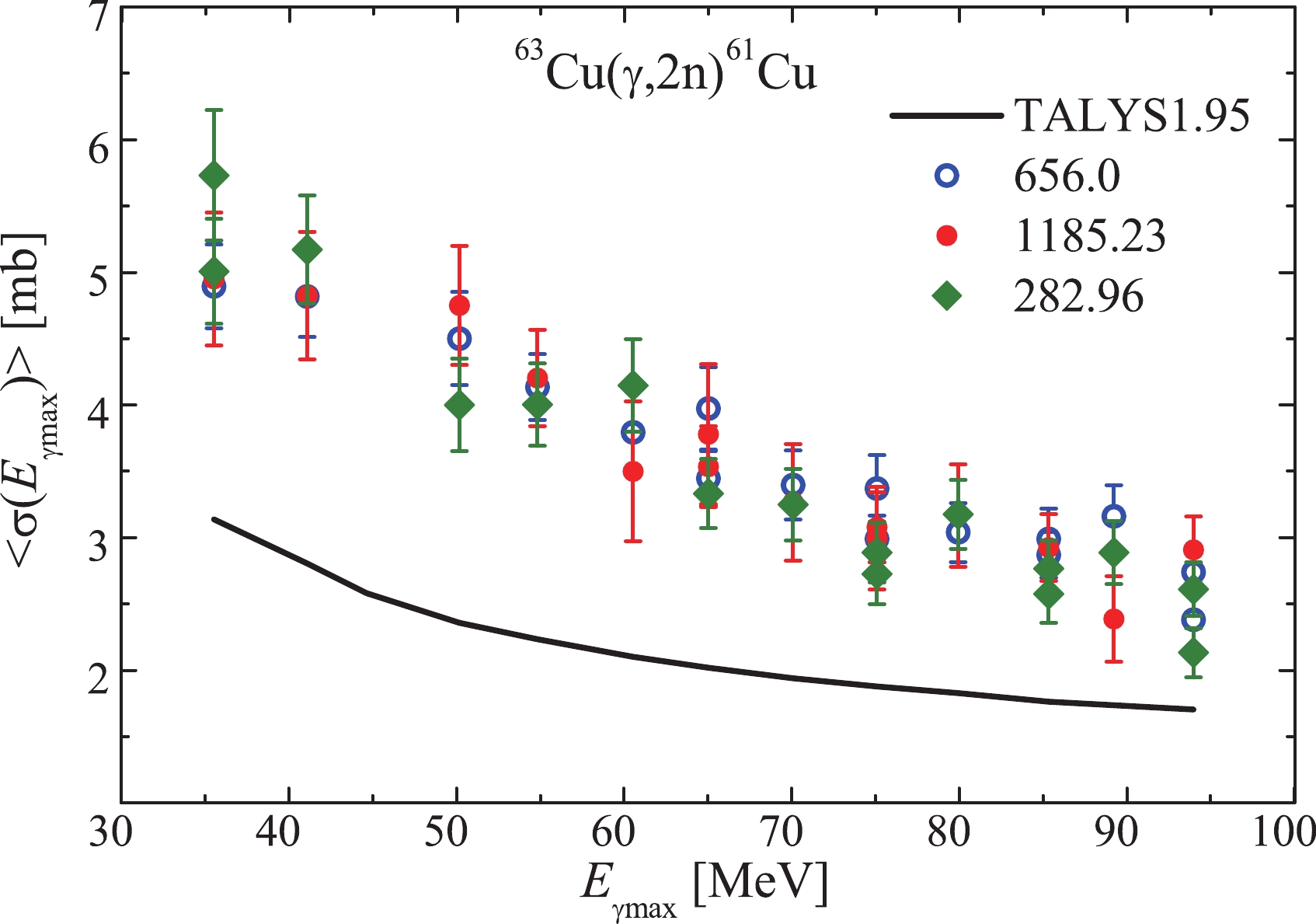
Figure 9. (color online) Flux-average cross-sections
$\langle{\sigma(E_{\rm{\gamma max}})}\rangle$ of the${^{63}{\rm{Cu}}}(\gamma,2n)^{61}{\rm{Cu}}$ reaction. The calculation using Talys1.95 code is denoted by the solid curve. Our experimental data: filled diamonds –$E_{\rm{\gamma}}$ = 282.96 keV, empty circles – 656.01 keV, filled circles – 1185.23 keV.A comparison of the experimental cross-sections
$ \langle{\sigma(E_{\rm{\gamma{max}}})}\rangle $ and the calculation with the Talys1.95 code is shown in Fig. 9. The experimental$ \langle{\sigma(E_{\rm{\gamma{max}}})}\rangle $ exceeded the calculated values over the entire$ E_{\rm{\gamma{max}}} $ range, by an average of$ \sim $ 100%, as shown.In Ref. [5], the validity of the data for the
$ {^{63}{\rm{Cu}}}(\gamma,2n)^{61}{\rm{Cu}} $ reaction from [10] was verified. As in the case of the$ {^{65}{\rm{Cu}}}(\gamma,2n)^{63}{\rm{Cu}} $ reaction, it was shown that the estimated (recalculated) data are significantly lower than the experimental data [10], by an approximate factor of 1.5 at the energy E = 23 MeV. However, such a notable change in the data from Ref. [10] does not lead to their agreement with the calculation in Talys1.95; the difference between the calculation and the recalculated data was approximately two-fold. This value is very close to the discrepancy between the calculation and the data found in this work. -
In the reaction
$ {^{63}{\rm{Cu}}}(\gamma,3n) $ , the$ ^{60}{\rm{Cu}} $ nucleus is formed with a half-life of$ T_{1/2} $ = 23.7 min. The$ ^{60}{\rm{Cu}} $ nucleus undergoes$ \varepsilon^+\beta^+ $ -decay with the formation of the$ ^{60}{\rm{Ni}} $ nucleus. To study this reaction, a γ-line with$ E_{\rm{\gamma}} $ = 1332.5 keV and intensity of$ I_{\rm{\gamma}} $ = 88% is used.Fig. 10 shows the calculated average cross-sections
$ \langle{\sigma(E_{\rm{\gamma{max}}})}\rangle $ for reaction$ {^{63}{\rm{Cu}}}(\gamma,3n)^{60}{\rm{Cu}} $ from the Talys1.95 code, using experimental data measured in this work. As can be seen at$ E_{\rm{\gamma{max}}} $ = 50–70 MeV, the experimental values of$ \langle{\sigma(E_{\rm{\gamma{max}}})}\rangle $ show an excess over the calculated ones.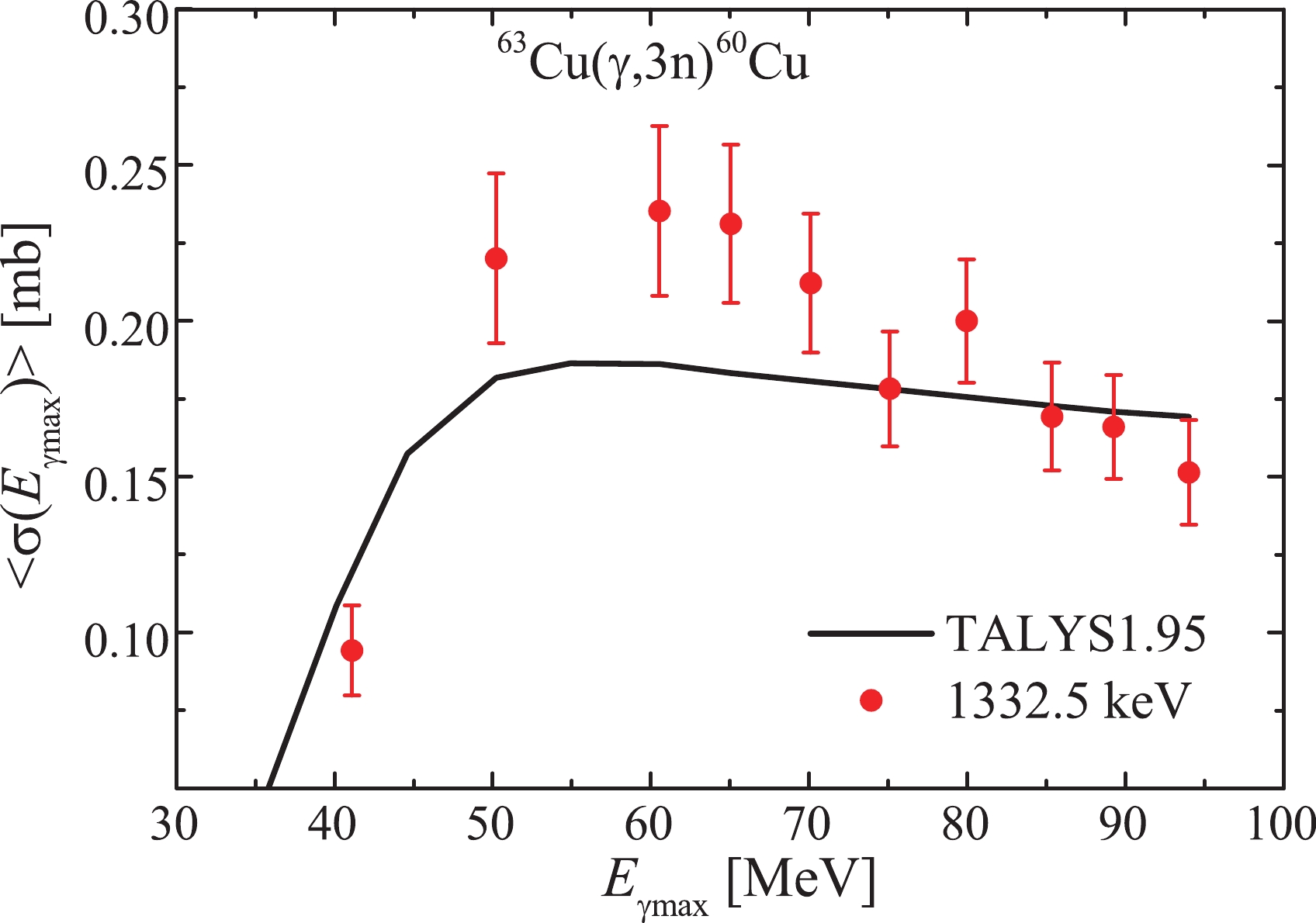
Figure 10. (color online) The calculated average cross-sections
$\langle{\sigma(E_{\rm{\gamma max}})}\rangle$ for reaction${^{63}{\rm{Cu}}}(\gamma,3n)^{60}{\rm{Cu}}$ from the Talys1.95 code (curve) and the experimental data measured in this work (filled circles).The yield values for
$ {^{65}{\rm{Cu}}}(\gamma,5n)^{60}{\rm{Cu}} $ was calculated, and their contribution was shown to increase with energy: for 60 MeV, it does not exceed 0.7%, and for 94 MeV, it reaches 5.1%. As in the case of the$ {^{63}{\rm{Cu}}}(\gamma,n)^{62}{\rm{Cu}} $ reaction, the contribution of γ-radiation from competing lines needs to be considered from$ {^{60}{\rm{Co}}} $ ($ E_{\rm{\gamma}} $ = 1332.5 keV,$ I_{\rm{\gamma}} $ = 99.986%,$ T_{1/2} $ = 5.27 years) and$ {^{60m}{\rm{Co}}} $ ($ E_{\rm{\gamma}} $ = 1332.5 keV,$ I_{\rm{\gamma}} $ = 0.24%,$ T_{1/2} $ = 10.47 min). The calculated total activity of$ {^{60}{\rm{Co}}} $ and$ {^{60m}{\rm{Co}}} $ nuclei ranged from 0.1 to 0.15% in the range of studied$ E_{\rm{\gamma{max}}} $ .The value of total corrections increased with energy and amounted to 0.1%–5.3%. The cross-section for the
$ {^{63}{\rm{Cu}}}(\gamma,3n)^{60}{\rm{Cu}} $ reaction was corrected (reduced) by the corresponding values at each energy$ E_{\rm{\gamma{max}}} $ . -
The total bremsstrahlung flux-averaged cross-sections
$ \langle{\sigma(E_{\rm{\gamma{max}}})}\rangle $ for the photonuclear reactions$ {^{65}{\rm{Cu}}}(\gamma,n)^{64}{\rm{Cu}} $ ,$ {^{63}{\rm{Cu}}}(\gamma,n)^{62}{\rm{Cu}} $ ,$ {^{63}{\rm{Cu}}}(\gamma,2n)^{61}{\rm{Cu}} $ , and$ {^{63}{\rm{Cu}}}(\gamma,3n)^{60}{\rm{Cu}} $ have been measured in the range of end-point energies$ E_{\rm{\gamma{max}}} $ = 35–94 MeV. The experiments were performed using the beam from the NSC KIPT electron linear accelerator LUE-40, as well as the activation and off-line γ-ray spectrometric techniques. The calculation of flux-average cross-sections$ \langle{\sigma(E_{\rm{\gamma{max}}})}\rangle_{\rm{th}} $ and yields were conducted using the cross-section values computed with the TALYS1.95 code, run with default options.The experimental bremsstrahlung flux-averaged cross-sections
$ \langle{\sigma(E_{\rm{\gamma{max}}})}\rangle $ for the reactions$ {^{65}{\rm{Cu}}}(\gamma,n)^{64}{\rm{Cu}} $ ,$ {^{63}{\rm{Cu}}}(\gamma,n)^{62}{\rm{Cu}} $ , and$ {^{63}{\rm{Cu}}}(\gamma,2n)^{61}{\rm{Cu}} $ are systematically higher than theoretical TALYS1.95 estimates. The experimental results obtained for$ \langle{\sigma(E_{\rm{\gamma{max}}})}\rangle $ supplement literature data for the case of$ (\gamma,n) $ and$ (\gamma,2n) $ reactions of$ {^{63}{\rm{Cu}}} $ and$ {^{65}{\rm{Cu}}} $ . These data can be used to analyze the discrepancies in the results of different laboratories, when analyzing possible corrections for reaction cross-sections obtained by direct neutron detection.It is shown that the experimental data obtained for reactions
$ {^{65}{\rm{Cu}}}(\gamma,n)^{64}{\rm{Cu}} $ and$ {^{63}{\rm{Cu}}}(\gamma,n)^{62}{\rm{Cu}} $ satisfactorily agree with the results of Ref. [19], and in the case of reaction$ {^{63}{\rm{Cu}}}(\gamma,2n)^{61}{\rm{Cu}} $ , with that of data recalculated from Refs. [5, 10].The data for the
$ \langle{\sigma(E_{\rm{\gamma{max}}})}\rangle $ reaction$ {^{63}{\rm{Cu}}}(\gamma,3n)^{60}{\rm{Cu}} $ was measured for the first time. -
The authors would like to thank the staff of the linear electron accelerator LUE-40 NSC KIPT, Kharkiv, Ukraine, for their cooperation in the realization of the experiment.
Cross-sections of photonuclear reactions 65Cu(γ, n)64Cu and 63Cu(γ, xn)63−xCu in the energy range Eγmax = 35–94 MeV
- Received Date: 2022-05-31
- Available Online: 2022-12-15
Abstract: The flux-averaged cross-sections





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF


























 DownLoad:
DownLoad: