-
The study of the hadron structure is one of the key problems in modern physics. Some time ago, while analyzing exclusive processes, a new object was proposed, Generalized Parton Distributions (GPDs) [1–3]. It was found that the exclusive processes at a large photon virtuality
$ Q^2 $ , such as the deeply virtual Compton scattering (DVCS) [4–6] and deeply virtual meson production (DVMP) [7–9], factorize into hard subprocesses that can be calculated perturbatively and GPDs [4–6]. Generally, this factorization was proved in the leading-twist amplitude with a longitudinally polarized photon.GPDs are complicated nonperturbative objects that depend on 3 variables, i.e., x - the momentum fraction of a proton carried by the parton, ξ - skewness, and t - momentum transfer. GPDs contain information about the longitudinal and transverse distributions of the partons inside the hadron. They give information on its 3D structure; see, e.g., [10].
In the forward limit (
$ \xi=0, t=0 $ ), GPDs become equal to the corresponding parton distribution functions (PDFs). The form factors of hadrons can be calculated from GPDs through integration over x [4]. Using Ji sum rules [4], the parton angular momentum can be extracted. More information on GPDs can be found e.g. in [7, 11, 12].The study of exclusive meson electroproduction is one of the most effective ways of accessing GPDs. An experimental study of
$ \pi^0 $ production was performed by CLAS [13] and COMPASS [14]. These experimental datasets can be adopted to constrain the models of GPDs. Electron-Ion Colliders (EICs) are the next generation of colliders for investigating the nucleon structure in the future. USA and China both plan to build EICs in the next 20 years [15–17]. The GPDs are one of the most important aspects that need to be studied for the EICs [18].The theoretical study of DVMP in terms of GPDs is often based on the handbag approach, in which, as mentioned before, the amplitudes factorize into the hard subprocess and GPDs [2–5]; see Fig. 1. This amplitude contains another non-perturbative object distribution amplitude, which can be used to probe the two-quark components of the meson wave function. One of the popular ways of constructing GPDs is using the so-called Double Distribution (DD) [19], which constructs ξ dependencies of GPDs and connects them with PDFs, modified by a t- dependent term. The handbag approach with the DD form of GPDs was successfully applied to light vector meson (VM) leptoproduction at high photon virtualities
$ Q^2 $ [20–22] and pseudoscalar meson (PM) leptoproduction [23]. In this work, we compute the$ \pi^0 $ production by applying the handbag approach to the kinematics for EIC in China (EicC). Our prediction for$ \pi^0 $ production is helpful for estimating the meson cross section at EicC in the future.In the leading twist approximation, the amplitudes of the pseudoscalar meson leptoproduction are sensitive to the GPDs
$ \widetilde{H} $ and$ \widetilde{E} $ . It was found that these contributions to the longitudinal cross section$ \sigma_{\rm L} $ are not sufficient for describing the physical observables in the$ \pi^0 $ production at sufficiently low$ Q^2 $ [23]. The essential contributions from the transversity GPDs$ H_{\rm T} $ ,$ \bar E_{\rm T} $ are needed [24] to be consistent with the experiment. Within the handbag approach, the transversity GPDs together with the twist-3 meson wave function [24] contribute to the amplitudes of transversely polarized photons, which produce the transverse cross section$ \sigma_{\rm T} $ , which is much larger with respect to the leading twist$ \sigma_{\rm L} $ .We discuss the handbag approach and the properties of meson production amplitudes in Section II. We show that the transversity GPD contributions, which have the twist-3 nature, lead to a large transverse cross section.
In beginning of Section III, we investigate the role of transversity GPDs in the cross sections of the
$ \pi^0 $ leptoproduction at CLAS and COMPASS energies and show that our results are in good agreement with the experiment. Subsequently, we perform predictions for$ \pi^0 $ cross sections at EicC energies. -
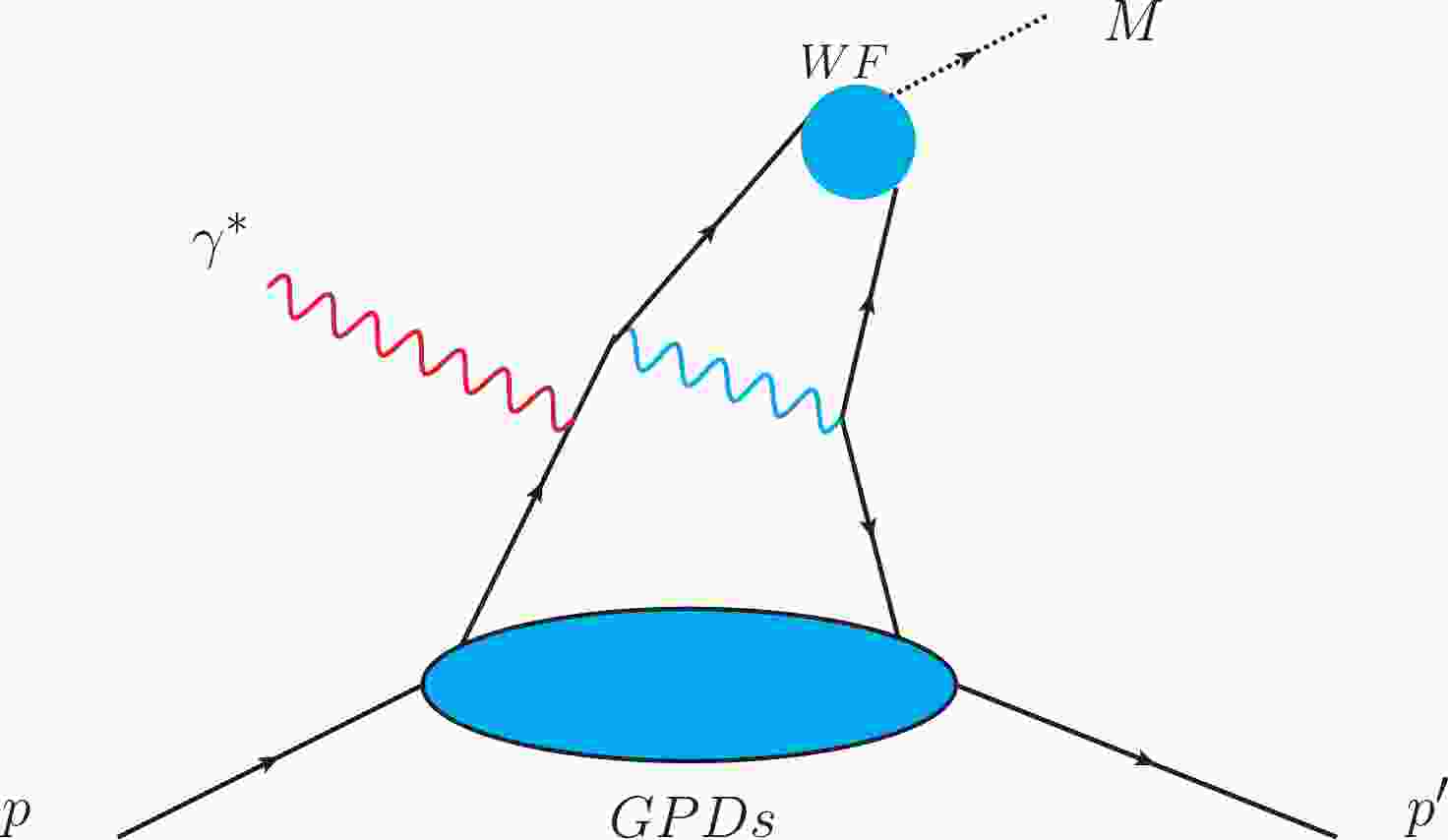
In the handbag approach, the meson photoproduction amplitude is factorized into a hard subprocess amplitude
$ {\cal H} $ and GPDs F, which include information on the hadron structure at sufficiently high$ Q^2 $ . Note that for the leading twist amplitudes with longitudinally polarized photons the factorization was proved [2, 3]. In what follows, we consider the twist-3 contributions from transversity GPDs$ H_{\rm T} $ and$ \bar {E}_{\rm T} $ as well. Factorization of these twist-3 amplitudes is an assumption. The process of the handbag approach is shown in Fig. 1.The subprocess amplitude is computed employing the modified perturbative approach (MPA) [25]. The power
$ k_\perp^2/Q^2 $ corrections are considered in the propagators of the hard subprocess$ {\cal H} $ together with the nonperturbative${ {\boldsymbol{k}}_{\perp}}$ -dependent meson wave function [26, 27]. The power corrections can be treated as an effective consideration of the higher twist contribution. The gluonic corrections are regarded in the form of the Sudakov factors. Resummation of the Sudakov factor can be done in the impact parameter space [25].The unpolarized
$ e p\to e\pi^0p $ cross section can be decomposed into a number of partial cross sections, which are observables of the process$ \gamma^*p\to\pi^0p $ $ \begin{aligned}[b] \frac{{\rm d}^2\sigma}{{\rm d}t{\rm d}\phi} =& \frac{1}{2 \pi} \bigg(\frac{{\rm d}\sigma_{\rm T}}{{\rm d}t} +{\epsilon} \frac{{\rm d}\sigma_{\rm L}}{{\rm d}t} + {\epsilon}\cos{2\phi}\,\frac{{\rm d}\sigma_{{\rm TT}}}{{\rm d}t} \\& +\sqrt{2{\epsilon}(1+{\epsilon})}\cos{\phi}\frac{{\rm d}\sigma_{{\rm LT}}}{{\rm d}t}\bigg). \end{aligned} $

(1) The partial cross sections are expressed in terms of the
$ \gamma^* p\to\pi^0 p $ helicity amplitudes. When we omit the small$ M_{0-,-+} $ amplitude, they can be written as follows$ \begin{aligned}[b] \frac{{\rm d}\sigma_{\rm L}}{{\rm d}t} =& \frac{1}{\kappa} \left[\mid {M}_{0+,0+}\mid^2 +\mid {M}_{0-,0+}\mid^2\right]\,,\\ \frac{{\rm d}\sigma_{\rm T}}{{\rm d}t}=& \frac{1}{2 \kappa}\left(\mid { M}_{0-,++}\mid^2 +2 \mid {M}_{0+,++}\mid^2 \right)\,, \\ \frac{{\rm d}\sigma_{{\rm LT}}}{{\rm d}t} =& -\frac{1}{\sqrt{2} \kappa} {\rm Re}\Big[{M^*}_{0-,++}{M}_{0-,0+}\Big] \,,\\ \frac{{\rm d}\sigma_{{\rm TT}}}{{\rm d}t} =& -\frac{1}{\kappa} \mid {M}_{0+,++} \mid^2\,. \end{aligned} $

(2) with
$ \begin{equation} \kappa=16 \pi (W^2-m^2)\sqrt{\Lambda(W^2,-Q^2,m^2)}. \end{equation} $

(3) Here,
$ \Lambda(x, y, z) $ is defined as$ \Lambda(x, y, z) = (x^2 + y^2 + z^2) - 2xy - 2xz - 2 yz $ .The amplitudes can be written as
$ \begin{aligned}[b] {M}_{0-,0+}=&\frac{e_0}{Q}\frac{\sqrt{-t'}}{2m}\langle \tilde E\rangle,\\ {M}_{0+,0+}=&\sqrt{1-\xi^2}\frac{e_0}{Q}[\langle \tilde H\rangle - \frac{\xi^2}{1-\xi^2}\langle \tilde E\rangle],\\ {M}_{0-,++}=& \frac{e_0}{Q}\sqrt{1-\xi^2}\langle {H_{\rm T}}\rangle,\\ {M}_{0+,++}=& -\frac{e_0}{Q}\frac{\sqrt{-t'}}{4m}\langle {\bar E_{\rm T}}\rangle, \end{aligned} $

(4) where
$ e_0 = \sqrt{4\pi \alpha} $ with$ \alpha=\dfrac{1}{137} $ is the fine structure constant.$ \xi=\frac{x_{\rm B}}{2-x_{\rm B}}\left(1+\frac{m_P^2}{Q^2}\right),\;\; t'=t-t_0,\;\;\;\; t_0=-\frac{4 m^2\xi^2}{1-\xi^2}. $

(5) $x_{\rm B}$ is the Bjorken variable with$x_{\rm B} = Q^2/(W^2 + Q^2 - m^2)$ . m is the proton mass and$ m_P $ is the meson mass.At the leading-twist accuracy, the PM production is only sensitive to the polarized GPDs
$ \widetilde{H} $ and$ \widetilde{E} $ , which contribute to the amplitudes of longitudinally polarized virtual photons [23]. The$ \langle F\rangle $ in Eq. (4) with$ F=\widetilde{H}, \widetilde{E} $ are the convolutions of the hard scattering amplitude$ {\cal H}_{0 \mu',0 +} $ and GPDs F$ \begin{equation} \langle F\rangle = \int_{-1}^1 {\rm d}x {\cal H}_{0 \mu' ,0 +} F(x,\xi,t). \end{equation} $

(6) The hard part is calculated employing the k-dependent wave function [26, 26], describing the longitudinally polarized mesons. The amplitude
$ {\cal H} $ is represented as the contraction of the hard part M, which can be computed perturbatively, and the non-perturbative meson wave function$ \phi_M $ , which can be found in Ref. [23]$ \begin{equation} {\cal H}_{\mu'+,\mu +}\,= \,\frac{2\pi {\alpha_s}(\mu_R)} {\sqrt{2N_c}} \,\int_0^1 {\rm d}\tau\,\int \frac{{\rm d}^{\,2} {{\boldsymbol k}_{\perp}}}{16\pi^3} \phi_{M}(\tau,k^2_\perp)\; M_{\mu^\prime\mu} . \end{equation} $

(7) The GPDs are constructed adopting the double distribution representation [19]
$ \begin{equation} F(x,\xi,t) = \int_{-1} ^{1}\, {\rm d}\rho \int_{-1+|\rho|} ^{1-|\rho|}\, {\rm d}\gamma \delta(\rho+ \xi \, \gamma - x) \, \omega(\rho,\gamma,t), \end{equation} $

(8) which connects GPDs F with PDFs h via the double distribution function ω. For the valence quark double distribution, it is
$ \begin{equation} \omega(\rho,\gamma,t)= h(\rho,t)\, \frac{3}{4}\, \frac{[(1-|\rho|)^2-\gamma^2]} {(1-|\rho|)^{3}}. \end{equation} $

(9) The t- dependence in PDFs h is presented in the Regge form
$ \begin{equation} h(\rho,t)= N\,{\rm e}^{(b-\alpha' \ln{\rho}) t}\rho^{-\alpha(0)}\,(1-\rho)^{\beta}, \end{equation} $

(10) and
$ \alpha(t)=\alpha(0)+\alpha' t $ is the corresponding Regge trajectory. The parameters in Eq. (10) are fitted from the known information about PDFs [28] e.g., or from the nucleon form factor analysis [29]. We consider the$ Q^2 $ evolution of GPDs through the of evolution of the gluon distribution, as in Eq. (9); see [20]. The evolution was tested for valence quarks as well. It is approximately calculated for the kinematical range in this work. We are working in the range 2$ < $ Q$ ^2< $ 7 GeV$ ^2 $ . The parameters of GPDs are determined at the middle point$ Q^2 $ = 4 GeV$ ^2 $ . In these very limited$ Q^2 $ range, the explicit form of the GPDs evolution is not so essential.It was found that at low
$ Q^2 $ , data on the PM leptoproduction also requires the contributions from the transversity GPDs$H_{\rm T}$ and$\bar E_{\rm T}=2 \tilde H_{\rm T}+E_{\rm T}$ , which determine the amplitudes$ M_{0-,++} $ and$ M_{0+,++} $ , respectively. Within the handbag approach, the transversity GPDs are accompanied by a twist-3 meson wave function in the hard amplitude$ {\cal H} $ [24] which is the same for both the$ {M}_{0\pm,++} $ amplitudes in Eq. (4). For the corresponding transversity convolutions, we have forms similar to (6), as follows:$ \begin{aligned}[b] \langle H_{\rm T}\rangle =&\int_{-1}^1 {\rm d}x {\cal H}_{0-,++}(x,...)\,H_{\rm T};\; \\ \langle \bar E_{\rm T}\rangle =&\int_{-1}^1 {\rm d}x {\cal H}_{0-,++}(x,...)\; \bar E_{\rm T}. \end{aligned} $

(11) There is a parameter
$ \mu_P $ in the twist-3 meson wave function which is large and enhanced by the chiral condensate. In our calculation, we adopt$ \mu_P $ = 2 GeV at a scale of 2 GeV.The
$ H_{\rm T} $ GPDs are connected with the transversity PDFs as follows:$ \begin{equation} h_{\rm T}(\rho,0)= \delta(\rho);\;\;\; \rm{and}\;\;\; \delta(\rho)=N_{\rm T}\, \rho^{1/2}\, (1-\rho)\,[q(\rho)+\Delta q(\rho)], \end{equation} $

(12) by employing the model [30]. We define the t -dependence of
$h_{\rm T}$ as in Eq. (10).The information on
$\bar E_{\rm T}$ can be obtained now only in the lattice QCD [31]. The lower moments of$\bar E_{\rm T}^u$ and$\bar E_{\rm T}^d$ were found to be quite large, have the same sign and be of a similar size. As a result, we have large$\bar E_{\rm T}$ contributions to the$ \pi^0 $ production. This is parameterized by the form as in Eq. (10). -
In this section, we present our results on
$ \pi^0 $ leptoproduction based on the handbag approach. In the calculation, we adopt the leading contribution Eq. (2) together with the transversity effects described in Eq. (11), which are essential at low$ Q^2 $ . The amplitudes are calculated based on the PARTONS collaboration code [32] that was modified in Fortran employing results of the GK model for GPDs [24].In Fig. 2, we present the model results for the
$ \pi^0 $ production cross section compared with the CLAS experimental data [13]. The transverse cross section, in which the$\bar E_{\rm T}$ and$H_{\rm T}$ contributions are important [24] dominates at low$ Q^2 $ . At small momentum transfer, the$H_{\rm T}$ effects are visible and provide a nonzero cross section. At$|t'| \sim 0.3 {\;{{\rm{GeV}}}}^2$ , the$\bar E_{\rm T}$ contribution becomes essential in$ \sigma_{\rm T} $ and results in a maximum for the cross section. A similar contribution from$\bar E_{\rm T}$ is observed in the interference cross section$\sigma_{{\rm TT}}$ [24]. For the calculations we use the parameters in Table 1. Details for$ \tilde H $ parameterization can be found in [24]. The fact that we describe well both unseparated$\sigma=\sigma_{{\rm T}}+\epsilon \sigma_{{\rm T}}$ and$\sigma_{{\rm TT}}$ cross sections indicates that the transversity$H_{\rm T}$ and$\bar E_{\rm T}$ effects were observed at CLAS [13]. Note that in this experiment it was not possible to separate$\sigma_{{\rm L}}$ and$\sigma_{{\rm T}}$ . The model produces at CLAS kinematics the leading twist$\dfrac{{\rm d} \sigma_{{\rm L}}}{{\rm d}t}(|t| = 0.3 {\;{{\rm{GeV}}}}^2) \sim \rm{few nb/GeV}^2$ . This is about two orders of magnitude smaller with respect to σ. Thus, we see that$\sigma_{{\rm T}}$ determined by the twist 3 effects gives a dominant contribution to unseparated σ. This prediction of the model [24] was confirmed by the JLab Hall A collaboration [33] by using the Rosenbluth separation of the$ \pi^0 $ electroproduction cross section.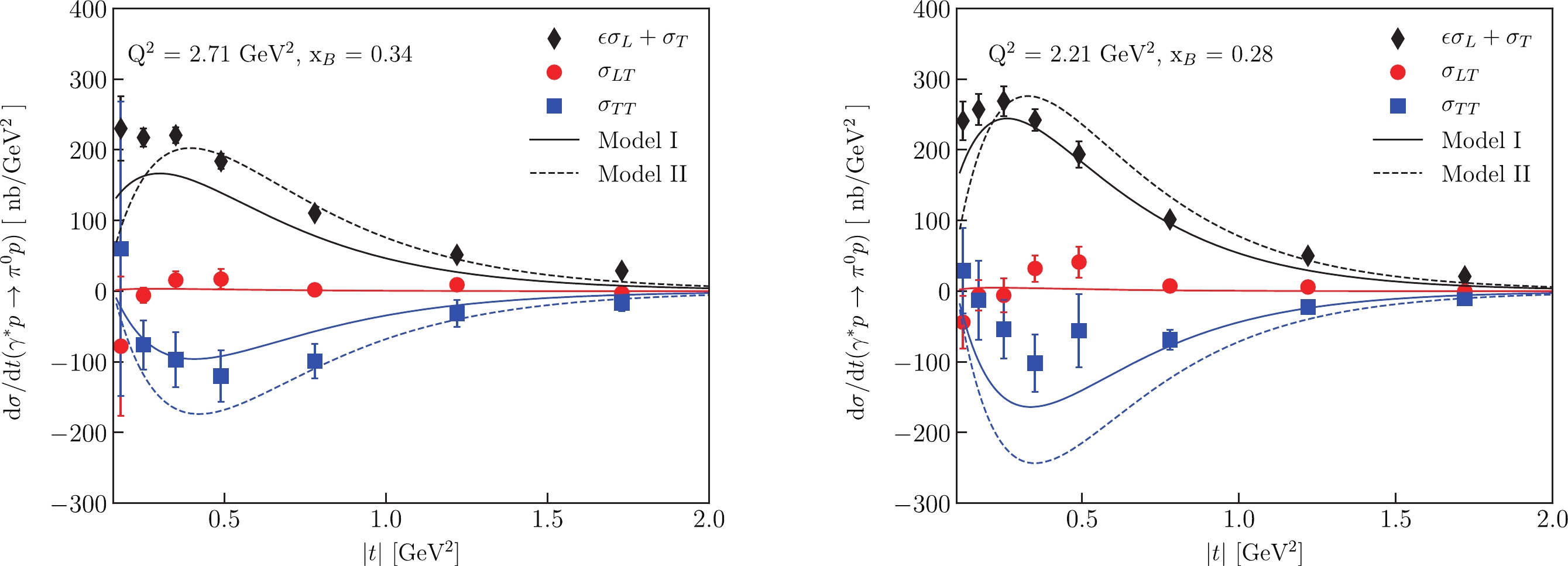
Figure 2. (color online) Cross section of
$ \pi^0 $ production in the CLAS energy range together with the data [13]. Black lines describe$\sigma=\sigma_{{\rm T}}+\epsilon \sigma_{{\rm L}}$ , red lines represent$\sigma_{{\rm LT}}$ , blue lines depict$\sigma_{{\rm TT}}$ .GPD $\alpha(0)$ 

$\beta^u$ 

$\beta^d$ 

$\alpha^\prime /{ {\rm{GeV} } }^{-2}$ 

$b /{ {\rm{GeV} } }^{-2}$ 

$N^u$ 

$N^d$ 

$\widetilde{E}$ 

0.48 5 5 0.45 0.9 14.0 4.0 $\bar{E}_{\rm T}$ 

0.3 4 5 0.45 0.5 6.83 5.05 $H_{\rm T}$ 

− − − 0.45 0.3 1.1 -0.3 Table 1. Regge parameters and normalizations of the GPDs at a scale of
$ 2\,{\,{{\rm{GeV}}}} $ . Model I.Our results for COMPASS kinematics are shown in Fig. 3. It can be seen that Model I gives results about two times larger with respect to the COMPASS data [14]. That was the reason for changing to model parameters that permit describing both CLAS and COMPASS data. New parameters for Model II are exhibited in Table 2 [34]. Because
$\bar E_{\rm T}$ contribution is essential in the$ \sigma_{{\rm T}} $ and$ \sigma_{{\rm TT}} $ cross sections, parameterization changes mainly the energy dependence of this GPD. Other GPDs are slightly changed to be consistent with experiments; see Fig. 2 and Fig. 3, in which both model results are shown.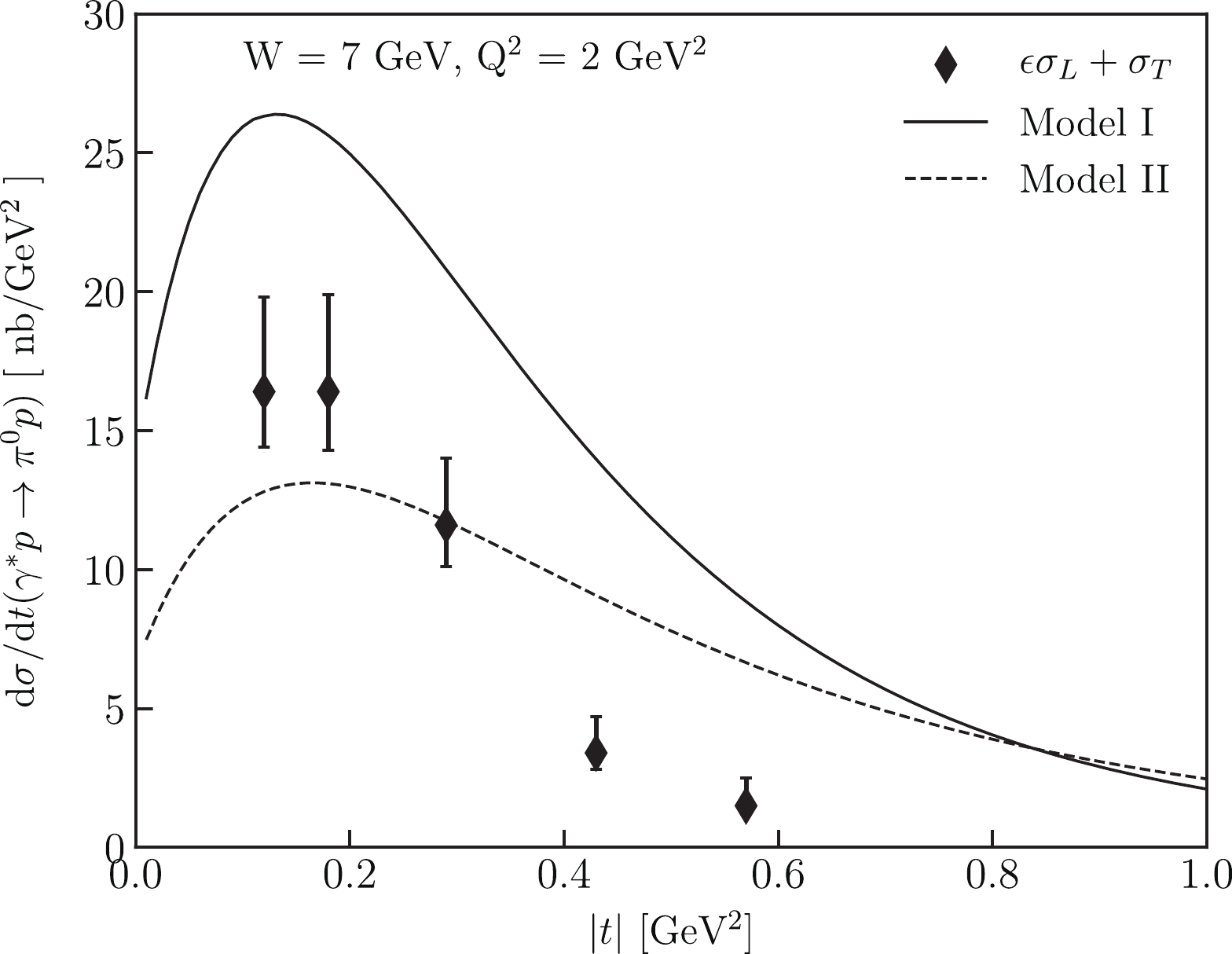
Figure 3. Models results at COMPASS kinematics. Experimental data are from [14], solid curve is the prediction of Model I and dashed line presents the results of Model II.
GPD $\alpha(0)$ 

$\alpha^\prime /{ {\rm{GeV} } }^{-2}$ 

$b /{ {\rm{GeV} } }^{-2}$ 

$N^u$ 

$N^d$ 

$\widetilde{E}_n.p.$ 

0.32 0.45 0.6 18.2 5.2 $\bar{E}_{\rm T}$ 

−0.1 0.45 0.67 29.23 21.61 $H_{\rm T}$ 

− 0.45 0.04 0.68 −0.186 Table 2. Regge parameters and normalizations of the GPDs at a scale of
$2 {\;{{\rm{GeV}}}}$ . Model II.The average COMPASS kinematics results for the cross sections are [14]
$ \begin{aligned}[b] \langle \frac{{\rm d} \sigma_{{\rm TT}}}{{\rm d}t} \rangle =& -(6.1 \pm 1.3 \pm 0.7) \;\rm{nb/GeV}^2, \\ \langle \frac{{\rm d} \sigma_{{\rm LT}}}{{\rm d}t} \rangle =& (1.5 \pm 0.5 \pm 0.3)\; \rm{nb/GeV}^2. \end{aligned} $

(13) Model II gives the following results at the same kinematics
$ \begin{aligned}[b] \langle \frac{{\rm d} \sigma_{{\rm TT}}}{{\rm d}t} \rangle =& -6.4 \;\rm{nb/GeV}^2, \\ \langle \frac{{\rm d} \sigma_{{\rm LT}}}{{\rm d}t} \rangle =& 0.1 \;\rm{nb/GeV}^2, \end{aligned} $

(14) which is close to the COMPASS results in Eq. (13). Model I gives cross sections that are about two times larger with respect to Model II. This is the same effect as we see in Fig. 3. This means that COMPASS provides essential constrains on the
$\bar E_{\rm T}$ contribution.Using new GPDs parameterization may be important at EicC because its energy range lies not far from that of COMPASS. In future analyzes, we will give predictions for both GPDs models I and II, as at higher energies, a detailed study of transversity GPDs can be done.
In Fig. 4 and Fig. 5 we show the W and
$ Q^2 $ dependencies of the σ and$\sigma_{{\rm TT}}$ cross sections in the EicC energy range. We show results for$ W=8,12,16\; \rm{GeV} $ and$ Q^2=2,5,7\; \rm{GeV}^2 $ that are typical for EicC kinematics. The cross sections$\sigma_{{\rm LT}}$ are rather small and difficult to distinguish on these figures. Thus we separate them into individual Fig. 6 and Fig. 7, where the W and$ Q^2 $ dependencies of$\sigma_{{\rm LT}}$ are shown in pb/GeV$ ^2 $ . We use the same W and$ Q^2 $ values as for Fig. 4 and Fig. 5. One can see that all cross sections decrease with increasing W and$ Q^2 $ . Model II gives typically smaller results with respect to Model I. At EicC kinematics, we get a rather small leading twist cross section$\sigma_{\rm L}$ , which is about one order of magnitude smaller with respect to$\sigma_{\rm T}$ . This means that the dominance of twist-3 transversity effects observed at low energy [24, 33] is valid up to high EicC energies. Our predictions on$ \pi^0 $ production give the possibility of performing a more detailed test on the energy dependencies of the transversity GPDs in future EicC experiments.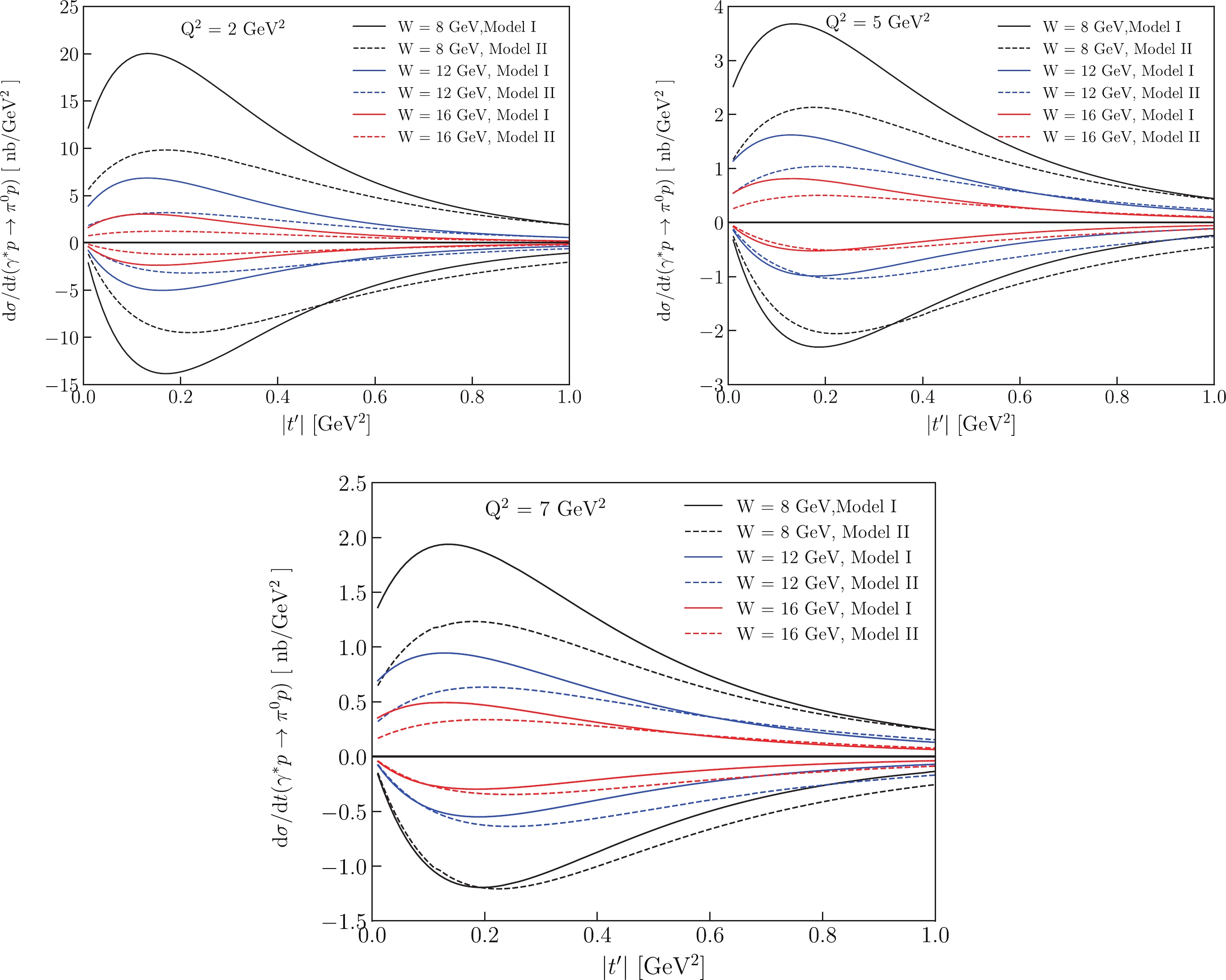
Figure 4. (color online) Models results for
$\sigma = \sigma_{\rm T}+{\epsilon} \sigma_{\rm L}$ and$\sigma_{{\rm TT}}$ cross section at EicC kinematics. W dependencies at fixed$ Q^2 $ are shown. The curves above the X-axis are predictions of σ, and the curves below the X-axis are predictions of$\sigma_{{\rm TT}}$ .
Figure 5. (color online) Models results for
$\sigma = \sigma_{\rm T}+{\epsilon} \sigma_{\rm L}$ and$\sigma_{{\rm TT}}$ cross sections at EicC kinematics.$ Q^2 $ dependencies at fixed W are shown. The curves above the X-axis are predictions of σ, and the curves below the X-axis are predictions of$\sigma_{{\rm TT}}$ .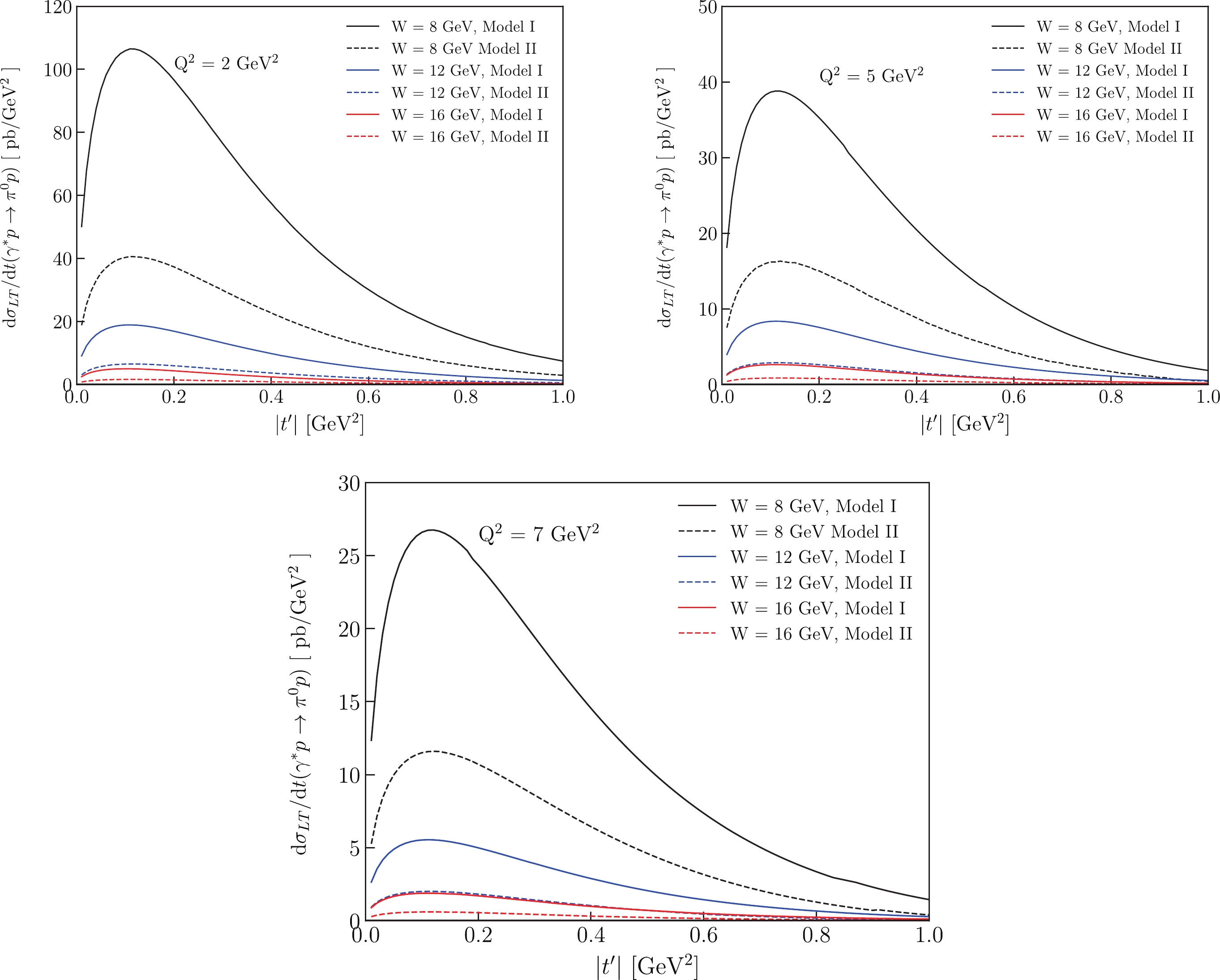
Figure 6. (color online) Models predictions for
$\sigma_{{\rm LT}}$ cross sections (in pb/GeV$ ^2 $ ) at EicC kinematics as a function of W at fixed$ Q^2 $ .
Figure 7. (color online) Models results for
$\sigma_{{\rm LT}}$ cross sections (in pb/GeV$ ^2 $ ) at EicC kinematics as a function of$ Q^2 $ at fixed W.Now, we shall briefly discuss whether it is really possible to analyze the energy dependencies of transvesity GPDs
$H_{\rm T}$ and$\bar E_{\rm T}$ from experimental data on cross sections. In experiments (see, e.g., [13]) usually, the unseparated cross sections$\sigma={\epsilon} \sigma_{\rm L}+\sigma_{\rm T}$ ,$\sigma_{{\rm LT}}$ and$\sigma_{{\rm TT}}$ are measured.$\sigma_{\rm L}$ is determined by the twist-2 contribution. It is rather small and can be omitted in our estimations. Thus$\sigma \propto \sigma_{\rm T}$ here. We will not discuss here$\sigma_{{\rm LT}}$ here.We see that if
$ \frac{{\rm d}\sigma_{\rm T}}{{\rm d}t} \sim -\frac{{\rm d}\sigma_{{\rm TT}}}{{\rm d}t}, $

this means that in this range the essential contribution comes from the
$ M_{0+++} $ amplitude (see (2). At CLAS and COMPASS energies, this approximately happened at$ |t'| = 0.3 {\;{{\rm{GeV}}}}^2 $ . This means that at this momentum transfer the$ <\bar E_{\rm T}> $ contribution dominates. At$ |t'|=0 {\;{{\rm{GeV}}}}^2 $ the$\bar E_{\rm T}$ is equal to zero. This means that at this point the$< H_{\rm T} >$ contribution is essential.Thus, using Eqs. (2)–(4), we can determine two quantities
$ \begin{aligned}[b]& <H_{\rm T}> \propto \sqrt{\kappa \frac{{\rm d}\sigma_{\rm T}}{{\rm d}t}(|t'|=0 {\;{{\rm{GeV}}}}^2)},\\& <\bar E_{\rm T}> \propto \sqrt{\kappa \frac{{\rm d}\sigma_{\rm T}}{{\rm d}t}(|t'| = 0.3{\;{{\rm{GeV}}}}^2)}, \end{aligned} $

(15) and one more in addition
$ \begin{equation} <\bar E_{\rm T} ({\rm TT})> \propto \sqrt{\kappa \Big|\frac{{\rm d}\sigma_{{\rm TT}}}{{\rm d}t}(|t'| = 0.3{\;{{\rm{GeV}}}}^2)\Big|}. \end{equation} $

(16) Eq. (15) is a some approximation based on
$\bar E_{\rm T}$ dominance near$ |t'|\sim 0.3 {\;{{\rm{GeV}}}}^2 $ . Eq. (16) gives direct information on$\bar E_{\rm T}$ , but$\dfrac{{\rm d}\sigma_{{\rm TT}}}{{\rm d}t}$ is more difficult to study.Thus, one can try to analyze the W dependencies of the cross sections at
$ |t'| \sim 0 {\;{{\rm{GeV}}}}^2 $ and$ |t'|\sim 0.3 {\;{{\rm{GeV}}}}^2 $ to determine the energy dependencies of$H_{\rm T}$ and$\bar E_{\rm T}$ .The results of the model calculations for the quantities in Eq. (15) for the GPDs models I and II can be parameterized as follows:
$ \begin{equation} <H> \sim A\, W^n. \end{equation} $

(17) We shall estimate n power using the results from Eq. (15) and
$n_{ H}$ - directly from the energy dependencies of the GPDs in the$ W=3\sim 15 {\;{{\rm{GeV}}}} $ interval. The results are$ \begin{eqnarray} <\bar E_{\rm T}^{{\rm Model}-{\rm II}}>:\;\;\;\;\;\;\; n=0.53,\;\;\;\;\;\;\;\;n_H=0.5; \end{eqnarray} $

(18) $ \begin{eqnarray} <\bar E_{\rm T}^{{\rm Model}-{\rm I}}>:\;\;\;\;\;\;\;\;n=0.72,\;\;\;\;\;\;\;\;n_ H=0.7; \end{eqnarray} $

(19) $ \begin{eqnarray} <H_{\rm T}>:\;\;\;\;\;\;\; n=0.8,\;\;\;\;\;\;\;\;\;n_ H=0.75. \end{eqnarray} $

(20) We see that the energy dependencies of models II and I are rather different. From (16) we find the same power as in Eq. (19).
Thus, we find very closed powers n from cross section analyzes and directly from GPDs. This mean that we can really estimate the energy (
$ x_{\rm B} $ ) dependencies of the GPDs from experimental data. -
The exclusive electroproduction of
$ \pi^0 $ mesons was analyzed here within the handbag approach, in which the amplitude was factorized into two parts. The first one are the subprocess amplitudes, which are calculated using$ k_\perp $ factorization [25]. The other essential ingredients are the GPDs, which contain information about the hadron structure. The results on the cross sections based on this approach were found to be in good agreement with data at HERMES, COMPASS energies at high$ Q^2 $ [24].The leading-twist accuracy is not sufficient to describe
$ \pi^0 $ leptoproduction at low$ Q^2 $ . It was confirmed [24] that rather strong transversity twist-3 contributions are required by the experiment. In the handbag approach, they are determined by the transversity GPDs$ H_{\rm T} $ and$ \bar E_{\rm T} $ in convolution with a twist-3 pion wave function. The transversity GPDs lead to a large transverse cross section for$ \pi^0 $ production.Here, we consider two GPDs parameterizations. Model I was proposed in [24] to obtain a good description of the CLAS collaboration [13]. Later on the COMPASS experiment produced
$ \pi^0 $ data at higher energies [14]. Model I predictions at COMPASS energies are higher with respect to the experiment by a factor of 2. The energy dependencies of the transversity GPDs were modified in Model II [34], which describes properly both CLAS and COMPASS data.In this analysis we perform predictions for unseparated σ,
$\sigma_{{\rm LT}}$ and$\sigma_{{\rm TT}}$ cross sections for EicC kinematics for both models I and II. We confirm that the transversity dominance$\sigma_{\rm T}\gg \sigma_{\rm L}$ , observed at low CLAS energies is valid up to the EicC energies range. Our results can be applied in future EicC experiments to give additional essential constraints on the transversity GPDs in the EicC energy range. -
S. G. expresses his gratitude to P. Kroll for long-time collaboration on GPD studies.
Exclusive π0 production at EIC of China within handbag approach
- Received Date: 2022-06-15
- Available Online: 2022-12-15
Abstract: Exclusive






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF


















 DownLoad:
DownLoad: