-
The phenomena and mechanism of nuclear fission have been continuously studied for more than eighty years since its discovery; however, a comprehensive model for describing a variety of fission observables has not yet been presented owing to the extremely complicated fission process. To date, many methods, such as the phenomenological approach [1–3], scission point model [4–6] and dynamical models [7–28], have been proposed for calculating the mass yields as well as the total kinetic energy (TKE) distribution of the fission fragments, and most of these methods have a high predictive power for calculating mass yields in the large region of nuclides. Nevertheless, the TKE distribution has not yet been calculated with comparable accuracy, as the TKE of fragments is quite sensitive to the scission configuration, which is still far from being completely understood.
The dynamical process of a fissioning nucleus evolving from the ground state to the scission point can be viewed as an evolution of the nuclear shape, which is usually described with the multidimensional Langevin equation [7–22], where the generalized coordinates represent the deformation parameters of the nuclear shape. A few powerful shape parametrizations [29] were developed for describing the shape of a fissioning nucleus, including the two-center shell model (TCSM) parametrization [30 ]. Based on the TCSM, the three and four dimensional Langevin approach were adopted by several groups in most dynamical calculations [12, 13, 16, 18, 20, 21] for studying fission dynamics at low excitation energies with a fixed neck parameter for a certain fissioning system. It is known that the neck parameter is considerably correlated with the shape of the fissioning system when the system is largely elongated, and consequently, the parameter influences the neck radius by which the scission point is defined in the Langevin approach. Accordingly, the neck parameter will possibly influence the fission observables, such as the mass and the total kinetic energy dependence of the fragments. However, knowledge about the influence of the neck parameter on the fission dynamics, scission configuration, and fission observables is still lacking.
In our previous work, the three-dimensional Langevin approach within the TCSM parametrization was applied to study the fission dynamics at low excitation energies [21, 31], in which the generalized coordinates are the elongation
$ Z_0/R_0 $ , the mass asymmetry η and the fragment deformation δ with a fixed$ \epsilon $ such as$ \epsilon $ =0.35. Based on this model, the influence of the neck parameter$ \epsilon $ on the fission dynamics is investigated in the present work by setting$ \epsilon $ to different values within a reasonable range in the Langevin calculations. We first study the influence of the neck parameter on the scission configuration. We then investigate the influence of the neck parameter$ \epsilon $ on the mass distribution and the TKE distribution of the fission fragments, taking the case of 14 MeV n+$ ^{235} $ U fission as an example. Based on calculated pre-neutron emission fragment distributions with$ \epsilon $ =0.35, we further calculate the post-neutron fragment mass distributions of 14 MeV n+$ ^{233,235,238} $ U and$ ^{239} $ Pu fission by taking prompt neutron emission into account, and the results can reproduce the experimental data well.This paper is organized as follows. In Sec. II, a brief introduction of the model is provided. The calculated results and discussions are presented in Sec. III. Finally, a summary of the present work and future prospects are presented in Sec. IV.
-
In this work, the shape of the nuclear surface is described with the two-center shell model (TCSM) proposed by J. Maruhn and W. Greiner [ 30], in which the nuclear surface is an equipotential surface retaining the same potential and enclosing the same volume as the spherical nucleus throughout nuclear fission under the assumption of volume conservation. The shape of the nuclear surface could be obtained by setting the potential
$ V(\rho,z) $ equal to the constant potential$ \dfrac12m_0\mathring{\omega}_0^2R_0^2 $ ($ \hbar\mathring{\omega} $ = 41 MeV$ \cdot A^{-\frac13} $ ). In the TCSM, the central potential$ V(\rho,z) $ is expressed in cylinder coordinates as$ \begin{equation} V(\rho,z)=\left\{ \begin{array}{*{20}{l}} \dfrac12m_0\omega_{z1}^2z'^{2}_1+\dfrac12m_0\omega_{\rho1}^2\rho^2,& z<z_1,\\ \dfrac12m_0\omega_{z1}^2z'^{2}_1(1+c_1z'_1+d_1z'^{2}_1)\\ \quad+\dfrac12m_0\omega_{\rho1}^2\rho^2(1+g_1z'^{2}_1),& z_1<z<0,\\ \dfrac12m_0\omega_{z2}^2z'^{2}_2(1+c_2z'_2+d_2z'^{2}_2)\\ \quad+\dfrac12m_0\omega_{\rho2}^2\rho^2(1+g_2z'^{2}_2),& 0<z<z_2,\\ \dfrac12m_0\omega_{z2}^2z'^{2}_2+\dfrac12m_0\omega_{\rho2}^2\rho^2,& z>z_2, \end{array} \right. \end{equation} $

(1) with
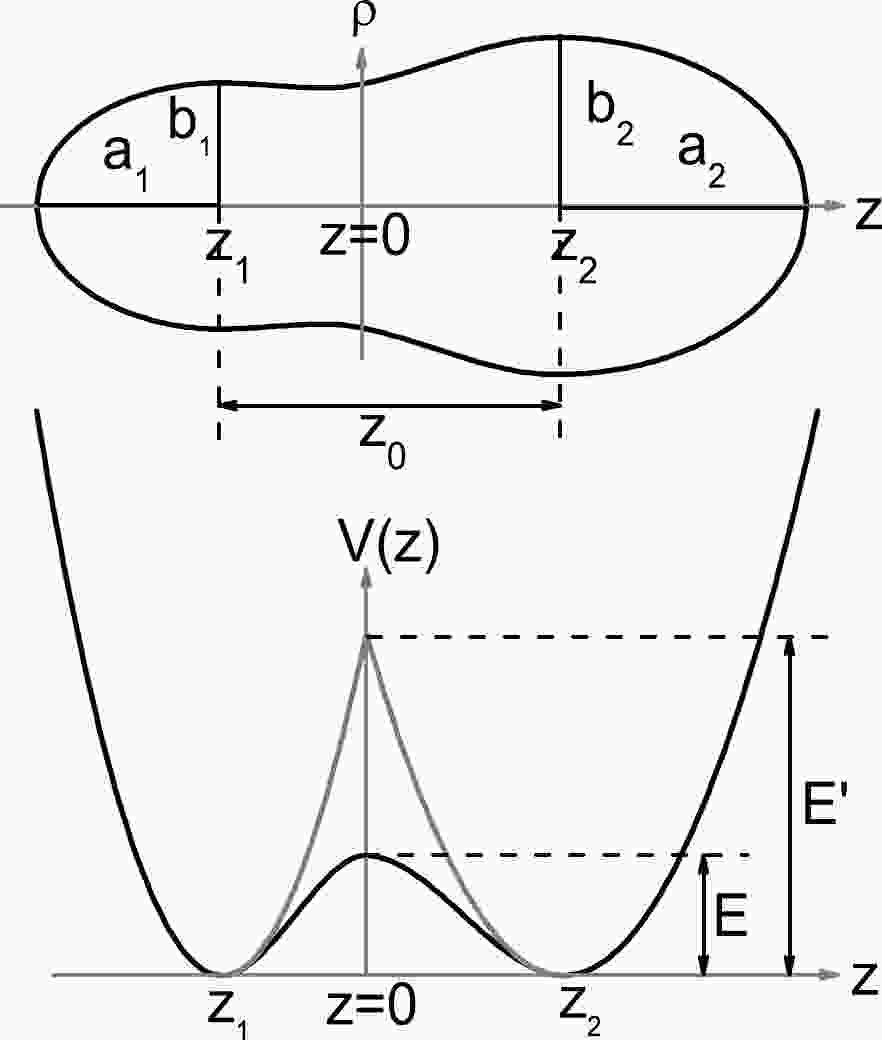
$ z'_i=z-z_i,i=1,2 $ . The above potential consists of two smoothly connected oscillator potentials, where the positions of the centers are located at$ z_1 $ and$ z_2 $ , and a modified oscillator potential between the centers with considerable deviations caused by the introduction of a variable barrier and by the need for joining the fragments continuously. Figure 1 shows the nuclear shape within the TCSM and the corresponding potential along the symmetry axis z. There are in total 5 free deformation parameters introduced in the model: the elongation parameter$ Z_0/R_0=(z_2-z_1)/R_0 $ , where$ R_0 $ denotes the radius of the spherical compound nucleus, the fragment deformation parameter$\delta_i=(3\beta_i-3)/(1+2\beta_i) (\beta_i=a_i/b_i,~ i=1,2$ ), the mass asymmetry η defined by$ \eta=(V_2-V_1)/(V_2+V_1) $ ($ V_1 $ and$ V_2 $ are the volumes of the left and right part separated by$ z=0 $ ), and the neck parameter$ \epsilon $ , which is defined as the ratio of the actual barrier height E to the fixed barrier$ E' $ of the deformed oscillator potential located at$ z=0 $ , as shown in Fig. 1. In the present work, the left and right fragment deformation are assumed to be the same, i.e.,$ \delta_1=\delta_2=\delta $ .
Figure 1. The nuclear shape described within the TCSM parametrization (top), where
$ a_i $ and$ b_i $ are the semi-axes of the left part of$ z_1 $ and the right part of$ z_2 $ . The bottom figure shows the corresponding actual potential and the deformed oscillator potential along the symmetry axis z.A series of nuclear shapes corresponding to different elongation
$ Z_0/R_0 $ and fragment deformation δ are shown in Fig. 2, in which both the mass asymmetry and neck parameter are fixed. It can be seen that the negative value of the fragment deformation δ corresponds to the oblate shape for the prefragment and that the positive δ corresponds to the prolate shape. With an increase in the elongation$ Z_0/R_0 $ , for large δ cases, such as δ=0.2 and 0.4, the neck radius decreases slowly and the more elongated shape is generated in the scission region. As is seen from Fig. 2, when δ=0.4, the system is assumed to correspond to the superlong channel, i.e., the symmetric fission channel for major actinide nuclei. In contrast, for the cases with δ=0.0, –0.2, –0.4, the system corresponds to the more compact shape in the scission region and separates into two fragments with smaller elongation depending on δ.
Figure 2. The nuclear shapes for different values of elongation
$ Z_0/R_0 $ and fragment deformation δ within the TCSM parametrization (η=0.0,$ \epsilon $ =0.35)Figure 3 shows a series of nuclear shapes corresponding to different elongation
$ Z_0/R_0 $ and neck parameter$ \epsilon $ . One can see that the nuclear shape is insensitive to the neck parameter$ \epsilon $ for the smaller elongation; however, the shape of the neck part changes largely with$ \epsilon $ for$ Z_0/R_0 $ larger than 2.0. Consequently, the neck radius decreases very fast, and correspondingly, the system separates quickly into fragments with increasing$ \epsilon $ , when the elongation$ Z_0/R_0 $ is larger than 2.5. This indicates that the nuclear shape for smaller$ \epsilon $ will be more elongated at the scission point than that for larger$ \epsilon $ . -
The time evolution of the collective degrees of freedom of a fissioning nucleus can be viewed as that of a Brownian particle in a heat bath in the stochastic approach. In this work, the multi-dimensional Langevin equation is adopted to describe the dynamics of the collective coordinates and has the following form:
$ \begin{aligned}[b] \frac{{\rm d}q_i}{{\rm d}t}&=(m^{-1})_{ij}p_j,\\ \frac{{\rm d}p_i}{{\rm d}t}&=-\frac{\partial{V}}{\partial{q_i}} - \frac12\frac{\partial{(m^{-1})_{jk}}}{\partial{q_i}}p_jp_k - \gamma_{ij}(m^{-1})_{jk}p_k + g_{ij}\Gamma_j(t), \end{aligned} $

(2) where the collective coordinates
$ \{q_i\} $ represent$ \{Z_0/R_0, \delta,~\eta\} $ within the TCSM parametrization, and$ p_i $ is the generalized momentum conjugate to$ q_i $ . In Eq. (2) and in the following equations the summation convention for repeated indices is used. In the above equation, V denotes the potential energy of deformation,$ (m^{-1})_{ij} $ is the inverse of the inertia tensor$ m_{ij} $ , and$ \gamma_{ij} $ is the friction tensor. For the random force term, the normalized random force$ \Gamma_j(t) $ is obtained by using a Gaussian random generator under the assumption of white noise, and the strength$ g_{ij} $ is calculated via the fluctuation-dissipation theorem:$ \begin{equation} g_{ik}g_{jk}=\gamma_{ij}T^*, \end{equation} $

(3) where the effective temperature
$ T^* $ is related to the general nuclear temperature T [32],$ \begin{equation} T^*=\frac{\hbar\varpi}{2}\coth\frac{\hbar\varpi}{2T}, \end{equation} $

(4) and we use the value 2 MeV for
$ \hbar\varpi $ , as suggested in Ref. [16]. The temperature T is obtained from the intrinsic excitation energy$E_{\rm int}$ , which is calculated at each step along the Langevin trajectory based on conservation of energy, as follows:$ \begin{equation} E_{\rm int}(q)=E^*-\frac12(m^{-1})_{ij}p_ip_j-V(q,T=0)=aT^2, \end{equation} $

(5) where
$ E^* $ denotes the excitation energy at the initial state, which is the sum of the incident neutron energy and the binding energy, and a is the level density parameter. Based on the deformation-dependent potential energy, the inertia tensor, the friction tensor and the random force simulation, the above Langevin equation could be solved by the second-order Runge-Kutta numerical method. Thus, the generalized coordinates and momenta at each time$ t=n\Delta{t} $ , i.e., the Langevin trajectory, are calculated when an initial condition and scission condition are given. In this work, we take the initial condition to be$ \{Z_0/R_0=0.5,\delta=0.2,\eta=0.0\} $ around the first saddle point, and the scission point is determined by a fixed neck radius to be 0.5 fm. In the Langevin calculations, we use the neck parameters$ \epsilon $ =0.25, 0.35, and 0.45 in order to study the influence of the neck parameter on the fission dynamics. The number of the Langevin trajectories reaches at least 2.5$ \times $ 10$ ^5 $ per fissioning system in order to guarantee sufficient statistics for the calculated results.In the Langevin calculations, the potential energy, the inertia tensor and the friction tensor are obtained based on the prepared meshes to save on computation time. The mesh values
$ \{Z_0/R_0,\delta,\eta\} $ are taken to be$ \begin{equation} \nonumber \begin{split} Z_0/R_0 =&-0.32 (0.1) 4.02,\quad \delta=-0.45 (0.03) 0.81,\\ \eta=&-0.62 (0.04) 0.62. \end{split} \end{equation} $

-
The potential energy is calculated with the macroscopic-microscopic model in the present work, in which the finite range liquid drop model [33, 34] is used to calculate the macroscopic energy. The microscopic energy contains the shell correction and the pairing correction, which are evaluated using the Strutinsky method [35] and the BCS method [36], respectively, based on the single-particle levels obtained from the TCSM. In addition, the potential energy is dependent on the nuclear temperature, as given in Ref. [37],
$ \begin{equation} V(q,T)=V_{\rm mac}(q)+V_{\rm mic}(q,T=0)\phi(T), \end{equation} $

(6) $ \begin{equation} \phi(T)=\exp(-aT^2/E_d), \end{equation} $

(7) with the level density parameter
$ a = A_{CN} $ /10 MeV$ ^{-1} $ . In order to describe the ratio of the contribution of the asymmetric fission to the symmetric fission well, we use the value of 60 MeV for the shell damping parameter$ E_d $ in the present work.The Werner-Wheeler method [38] is adopted to calculate the inertia tensor, which is expressed in the following form:
$ \begin{equation} m_{ij}(q)=\pi\rho_m\int_{z_{\rm min}}^{z_{\rm max}} \rho_s^2(z,q)(A_iA_j + \frac18\rho_s^2(z,q)A'_iA'_j){\rm d}z, \end{equation} $

(8) $ \begin{equation} A_i=\frac{1}{\rho_s^2(z,q)}\frac{\partial}{\partial{q_i}}\int_z^{z_{\rm max}}\rho_s^2(z',q){\rm d}z', \end{equation} $

(9) where
$ \rho_s(z,q) $ is the transverse extension of the nucleus at position z along the symmetry axis, and$ q = \{qi\} $ represents the deformation parameter within the TCSM.$ \rho_m $ denotes the mass density of the fissioning nucleus and$ A'_i $ is the differentiation of$ A_i $ with respect to z.The wall-and-window model [39–41] is applied to obtain the friction tensor. For the compact nuclear shape without neck, the wall friction tensor is written as follows:
$ \begin{equation} \gamma_{ij}^{\rm wall}(q)=\frac12\pi\rho_m\overline{\upsilon}\int_{z_{\rm min}}^{z_{\rm max}}{\rm d}z\frac{\partial{\rho_s^2}}{\partial{q_i}}\frac{\partial{\rho_s^2}}{\partial{q_j}}\left[\rho_s^2+\frac14\left(\frac{\partial{\rho_s^2}}{\partial{z}}\right)^2\right]^{-1/2}, \end{equation} $

(10) where the average velocity of the inner nucleons
$ \overline{\upsilon} $ is related to the Fermi velocity by$ \overline{\upsilon}=\frac34\upsilon_f $ . When the nucleus is highly deformed and the neck becomes obviously identified, the window dissipation needs to be taken into account. Thus, the corresponding friction tensor is$ \begin{equation} \gamma_{ij}^{W+W}(q)=\gamma_{ij}^{\rm wall 2}(q)+\gamma_{ij}^{\rm window}(q) , \end{equation} $

(11) $ \begin{aligned}[b] \gamma_{ij}^{\rm wall2}(q)=&\frac12\pi\rho_m\overline{\upsilon}\int_{z_{\rm min}}^{z_{\rm max}} {\rm d}z\left(\frac{\partial{\rho_s^2}}{\partial{q_i}}+\frac{\partial{\rho_s^2}}{\partial{z}} \frac{\partial{D_{\nu}}}{\partial{q_i}}\right)\\ &\times\left(\frac{\partial{\rho_s^2}}{\partial{q_j}}+\frac{\partial{\rho_s^2}}{\partial{z}}\frac{\partial{D_{\nu}}}{\partial{q_j}}\right)\left[\rho_s^2+\frac14\left(\frac{\partial{\rho_s^2}}{\partial{z}}\right)^2\right]^{-\frac12}, \end{aligned} $

(12) $ \begin{equation} \gamma_{ij}^{\rm window}(q)=\frac{\rho_m\overline{\nu}}{2}\Delta\sigma\frac{\partial{R_{12}}}{\partial{q_i}}\frac{\partial{R_{12}}}{\partial{q_j}}, \end{equation} $

(13) where
$ D_{\nu} $ (ν = L, R for the left and right part, respectively) is the position of the mass center of the prefragment relative to the mass center of the whole system.$ \Delta{\sigma} $ is the area of the window located at the position of the smallest neck radius.$ R_{12} $ denotes the distance between the centers of mass of the two parts.A smooth transition between the pure wall friction and the wall-and-window friction proposed by Nix and Sierk [42] is used for the whole fission process and expressed as
$ \begin{equation} \gamma_{ij}=\cos^2\left(\frac{\pi}{2}\frac{r_N^2}{b^2}\right)(\gamma_{ij}^{W+W})+\sin^2\left(\frac{\pi}{2}\frac{r_N^2}{b^2}\right)\gamma_{ij}^{\rm wall}, \end{equation} $

(14) where
$ r_N $ is the neck radius and b denotes the lesser of the transverse semi-axes of the two prefragments. -
The scission configuration is of fundamental importance for understanding fission dynamics and the calculation of fission observables. Moreover, knowledge of the scission configuration could be helpful for improving the scission-point model to a certain extent. In the present work, the scission configuration is studied within the TCSM parametrization, especially the influence of the neck parameter on the scission configuration. The upper panel of Fig. 4 shows the distributions of the elongation
$ Z_0/R_0 $ at the scission point, which is obtained by a fixed neck radius to be 0.5 fm, defined as the same as that in previous works [21, 31], with the neck parameter$ \epsilon $ fixed at 0.25, 0.35, and 0.45. With$ \epsilon $ increasing, the distribution of$ Z_0/R_0 $ is shifted towards the left side, and the overall elongation of the fissioning nucleus becomes evidently smaller.
Figure 4. (color online) The distribution of the elongation
$ Z_0/R_0 $ at the scission point (top) and the correlation between the elongation and mass asymmetry at the scission point with the neck parameter$ \epsilon $ fixed at 0.25, 0.35, and 0.45 (bottom).In addition, the correlations between the elongation
$ Z_0/R_0 $ and the mass asymmetry η at the scission point for three different$ \epsilon $ cases are shown in the bottom panel of Fig. 4. It can be seen that$ Z_0/R_0 $ decreases with increasing$ \epsilon $ , but the shapes of the correlation for the three$ \epsilon $ cases are similar, which results in an overall increase of the TKE for the entire fragment mass region with increasing$ \epsilon $ . Moreover, we find that there is a hollow near η = 0.10–0.25, and the depth of the hollow increases with increasing$ \epsilon $ , especially, the depth for$ \epsilon $ =0.25 is obviously shallower than for the other two cases. Consequently, a bump around η=0.10–0.25 (corresponding to the heavy fragment mass region around A=130–147) appears in the TKE distribution with its height and peak depending on the$ \epsilon $ .The correlations between the elongation
$ Z_0/R_0 $ and the fragment deformation δ and that between δ and η at the scission point with$ \epsilon $ fixed at 0.25, 0.35, and 0.45 are shown in the upper and middle panels of Fig. 5, respectively. It can be seen that the averaged$ Z_0/R_0 $ increases nearly linearly with δ at the scission point for fixed$ \epsilon $ , and that the correlation between δ and η is not linear but is similar to that of$ Z_0/R_0 $ and η, as there is a linear relationship between$ Z_0/R_0 $ and δ. More significantly, the figure shows that with$ \epsilon $ increasing, the curve shifts downwards with a similar slope, and this means that the net effect is an increase in TKE with increasing$ \epsilon $ . Moreover, we show in the bottom panel of Fig. 5 the averaged nuclear shapes for δ=0.0, 0.15, and 0.3 at the scission point with$ \epsilon $ fixed at 0.35, and the corresponding shape parameters$ \{Z_0/R_0, \delta, \eta\} $ =$ \{2.558, ~0, ~0.187\} $ ,$\{2.826,~ 0.15,~ 0.171\}$ , and$ \{3.143, ~0.3, ~0.097\} $ . The scission shapes for different values of δ are consistent with the behavior of the correlation between$ Z_0/R_0 $ and δ.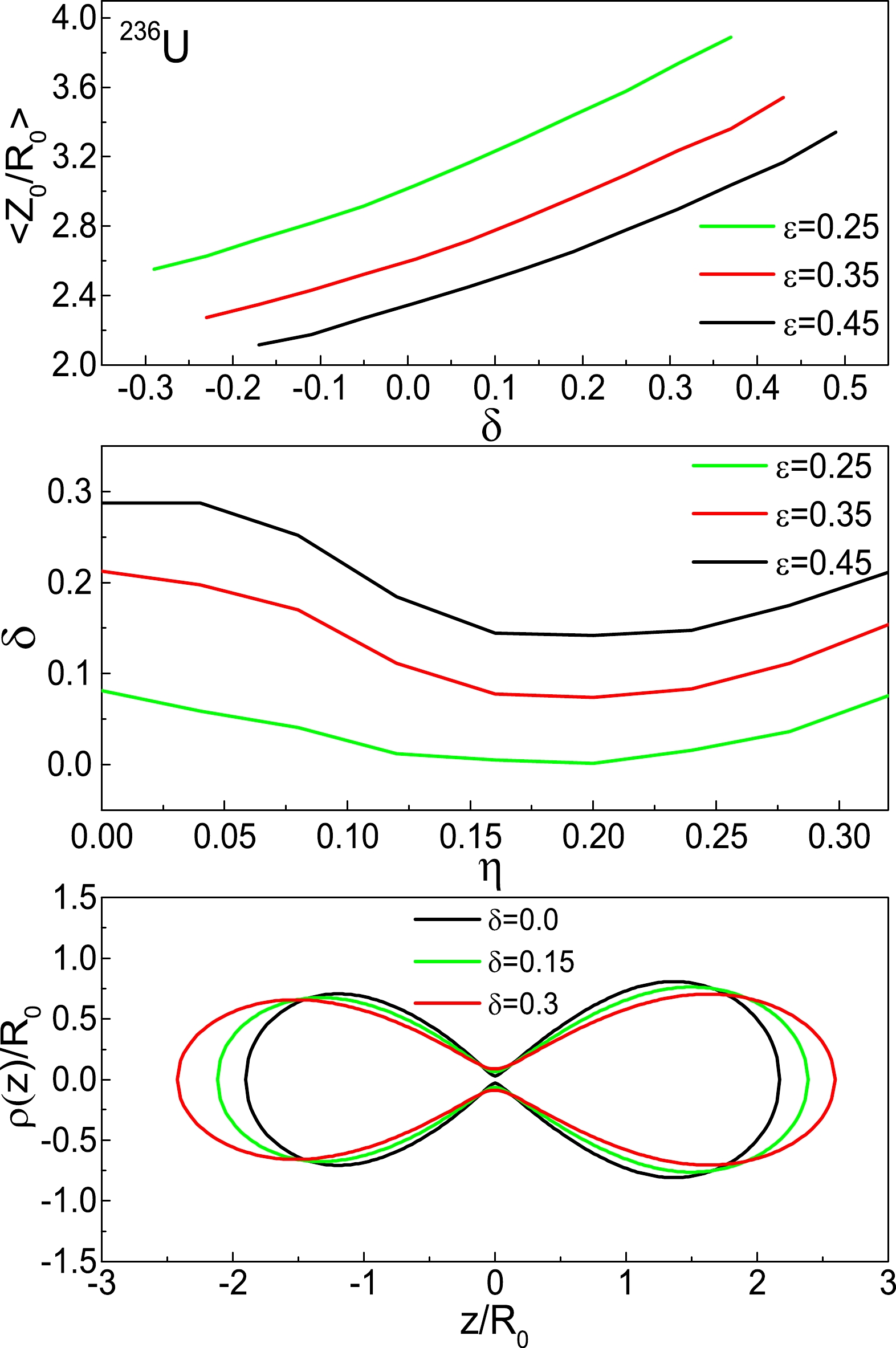
Figure 5. (color online) The correlation between the elongation and the fragment deformation (upper panel) and the correlation between the the fragment deformation and the mass asymmetry (middle panel) at the scission point with the neck parameter
$ \epsilon $ fixed at 0.25, 0.35, and 0.45. The bottom panel shows the averaged nuclear shape of$ ^{236} $ U for δ=0.0, 0.15, and 0.3 at the scission point ($ \epsilon $ =0.35).The neck radius is an important input for defining the scission point. In order to understand the dynamical effect of
$ \epsilon $ on the evolution of the neck radius, we further study the evolution of the neck radius of the fissioning nucleus from the ground state to the scission point. Figure 6 presents the contour plot of the neck radius as a function of$ Z_0/R_0 $ and$ \epsilon $ with η=0.0 and δ=0.2. It shows that the neck radius is insensitive to$ \epsilon $ for$ Z_0/R_0 $ smaller than 2.0 which is consistent with the results shown in Fig. 3, however, the neck radius decreases obviously with increasing$ \epsilon $ when the elongation is larger than 2.0. Moreover, with the elongation increasing, the neck radius becomes more sensitive to$ \epsilon $ , especially around the scission line, as shown by the white dotted curve, where the elongation reduces with increasing$ \epsilon $ , which causes the dependence of TKE on$ \epsilon $ , as discussed previously. We have also made calculations of the neck radius with the other η and δ and we find that the behavior of the neck radius as a function of$ Z_0/R_0 $ and$ \epsilon $ is similar for η and δ fixed at other values. Similar to Fig. 6, we show the results for η=0.17 and η=0.35 in Fig. 7, the behaviors of which are similar to the case of η=0.0 shown in Fig. 6. This implies that there is no obvious impact of$ \epsilon $ on the fragment mass distribution.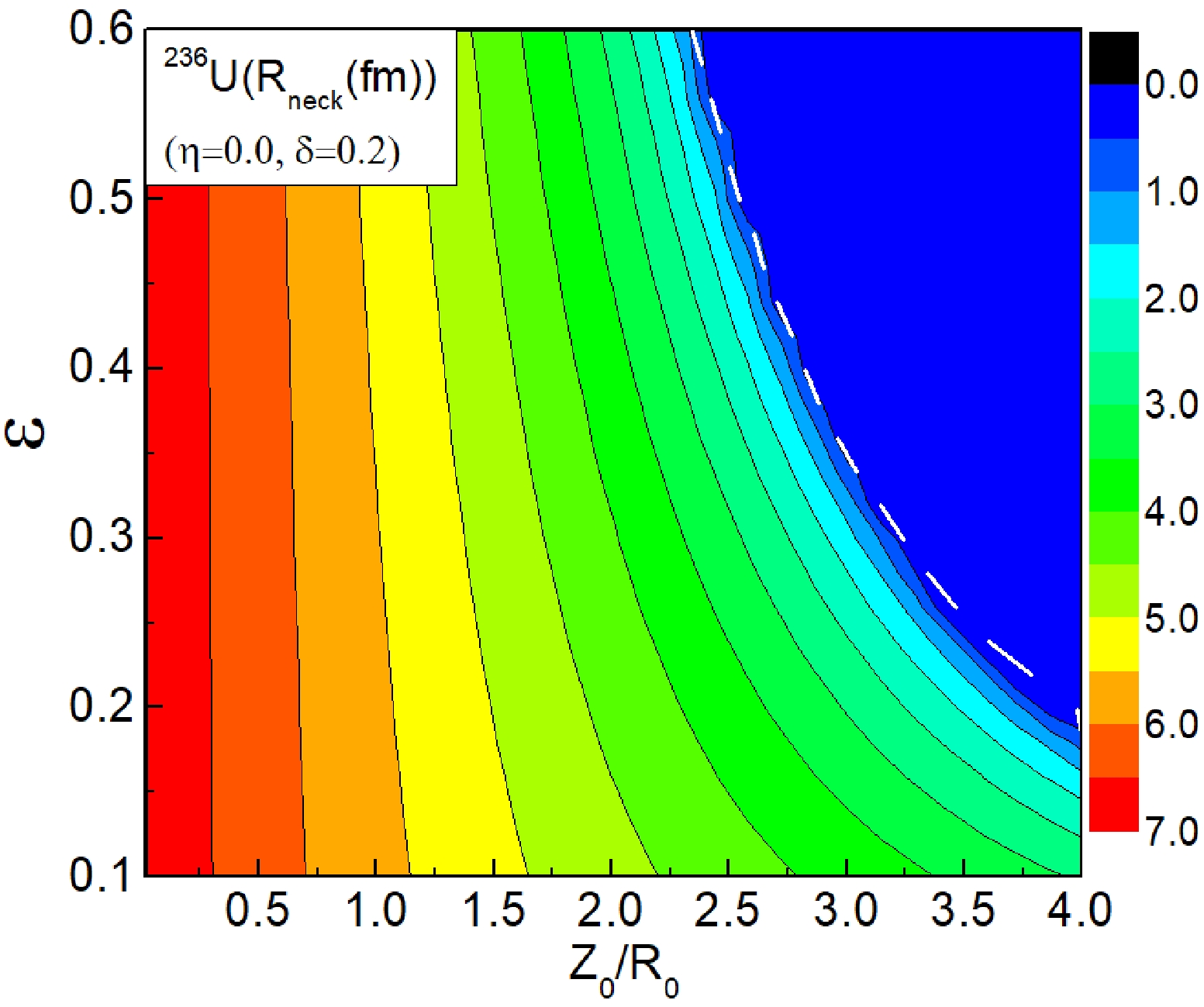
Figure 6. (color online) The contour plot of the neck radius of
$ ^{236} $ U with η=0.0 and δ =0.2. The white dotted line denotes the scission line.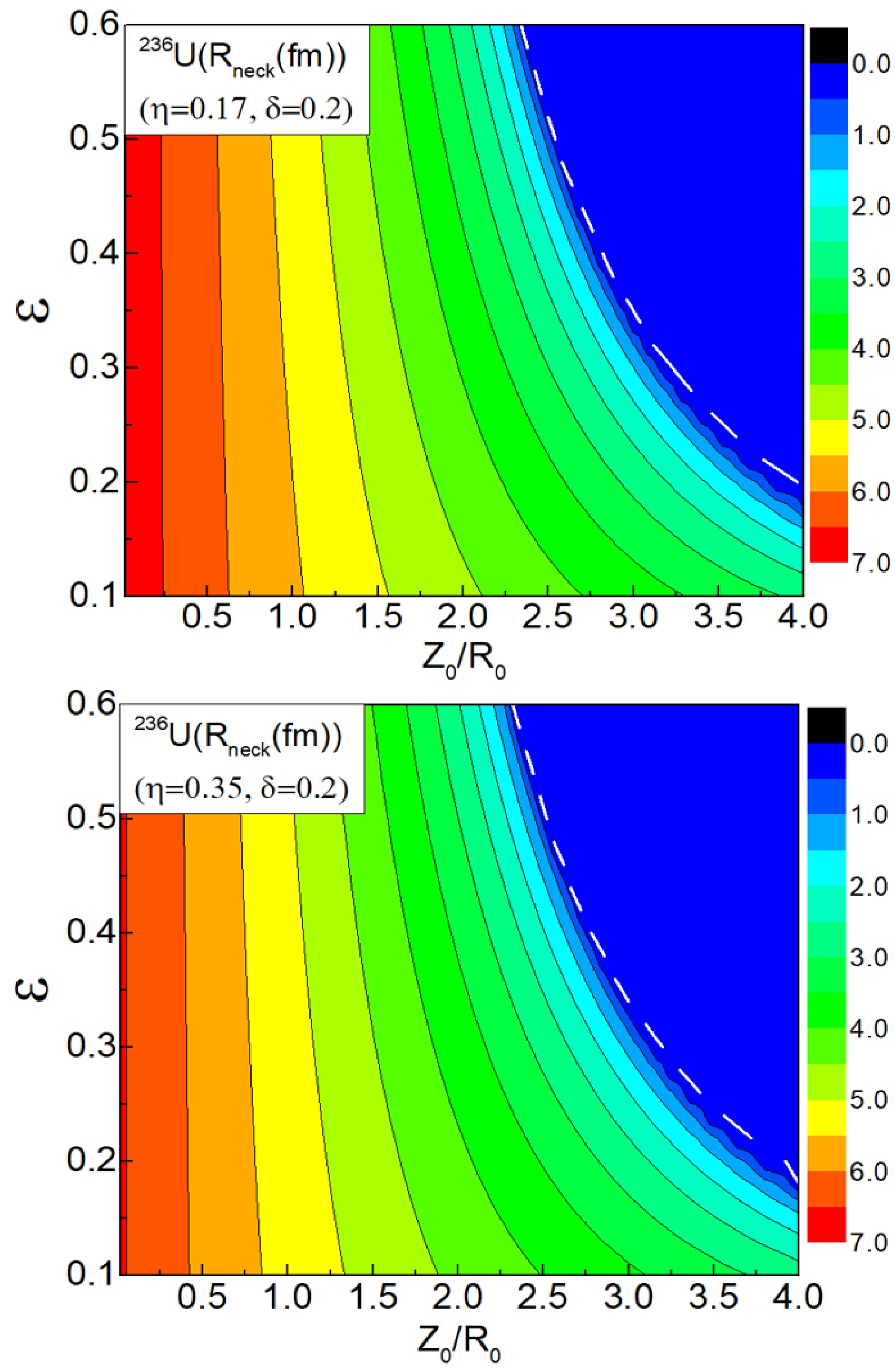
Figure 7. (color online) Similar to Fig. 6 but with η=0.17 and δ=0.2 (top) and η=0.35 and δ=0.2 (bottom).
-
In this section, we investigate the influence of the neck parameter
$ \epsilon $ on the mass distribution and the total kinetic energy (TKE) distribution of fission fragments, taking the case of 14 MeV n+$ ^{235} $ U fission as an example. Figure 8 shows the calculated fission fragment mass distributions using the Langevin approach with$ \epsilon $ taken to be 0.25, 0.35, and 0.45, and there is little difference between these results, as is expected from the study in the previous section. However, a little better fit to ENDF/B-VIII.0 [43] for$ \epsilon $ =0.35 is seen in Fig. 8 compared with the other two cases. Using the 3D Langevin model with$ \epsilon $ fixed at 0.35 as used in previous works, we calculate the pre-neutron fragment mass distributions of 14 MeV n+ $ ^{233,235,238} $ U and$ ^{239} $ Pu fission, based on which the post-neutron fragment mass distributions are obtained by taking the experimental data of prompt neutron emission ν(A) into account, if they are available. Here, the experimental data of ν(A) at$ E_n $ =14.5 MeV [44] are directly adopted for n+$ ^{238} $ U fission. For the 14 MeV n+$ ^{233,235} $ U and$ ^{239} $ Pu cases, due to a lack of enough experimental data, we adopt the experimental data$ \nu_{th} $ (A) of thermal neutron induced fission [45–48], which could cover almost the whole fragment mass region, and then evaluate ν(A) for$ E_n $ =14 MeV by assuming$ \nu(A)=\nu_{th}(A)\cdot\frac{\overline{\nu}}{\overline{\nu}_{th}} $ , in which the averaged neutron multiplicity$ \overline{\nu} $ ($ E_n $ =14 MeV) and$ \overline{\nu}_{th} $ are from ENDF/B-VIII.0. The calculated pre-neutron and post-neutron fragment mass distributions in 14 MeV n+$ ^{233,235,238} $ U and$ ^{239} $ Pu fission are shown in Fig. 9 together with the evaluated post-neutron mass yields from ENDF/B-VIII.0. One can see that the calculated post-neutron fragment mass distributions with$ \epsilon $ =0.35 (red curve) are overall consistent with the evaluated data both in peak position and peak width, indicating the power of the present model in describing the fission fragment mass distribution for major actinides. It should be noted that the calculated mass yields are those of first-chance fission, which are found to be similar to those of multi-chance fission at an excitation energy of 20 MeV [49]. In the present study, only the fission of major actinides is involved, and the fission of superheavy nuclei will be investigated in future work.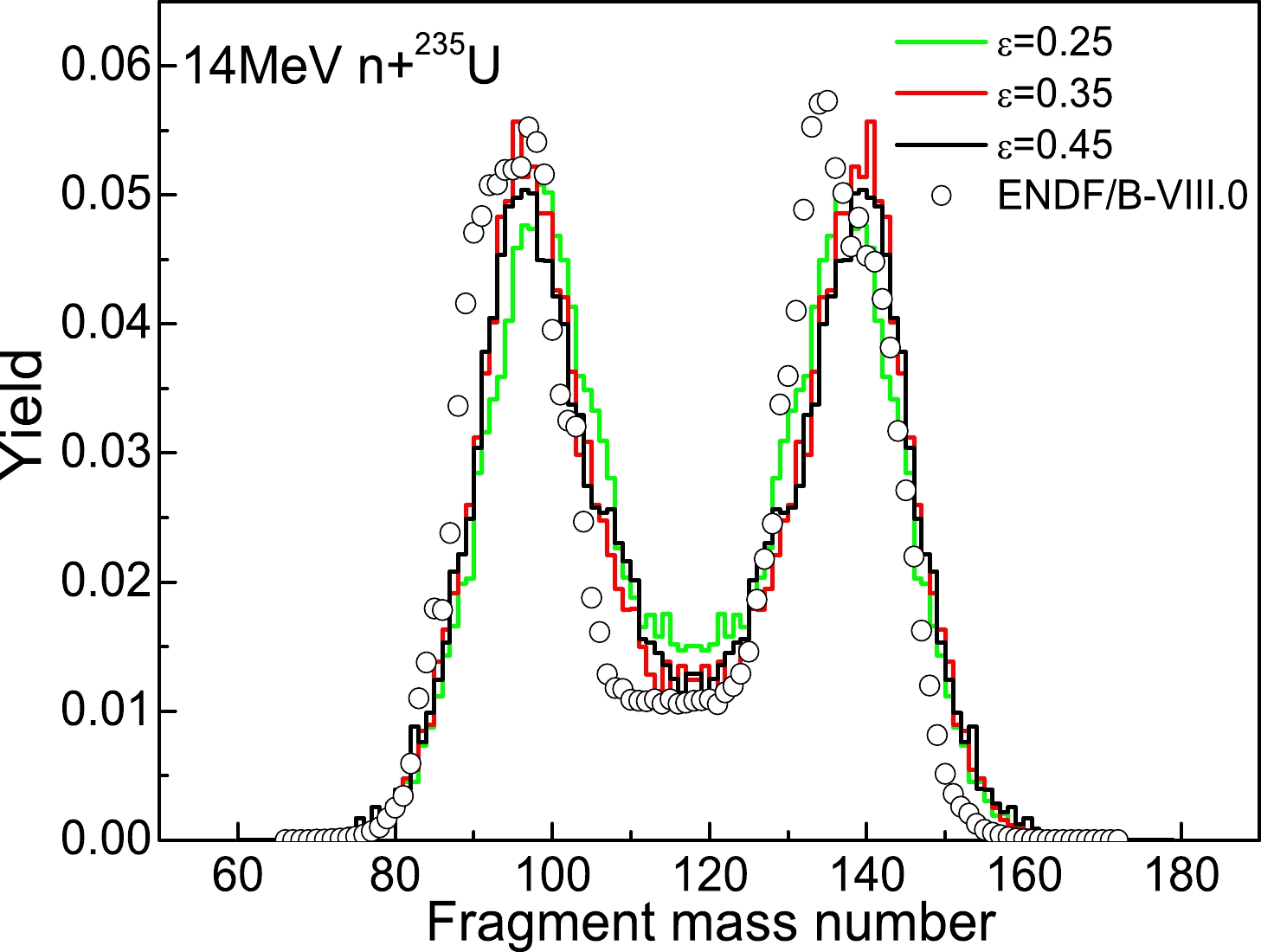
Figure 8. (color online) The fragment mass distributions in 14 MeV n+
$ ^{235} $ U fission with the neck parameter$ \epsilon $ fixed at 0.25, 0.35, and 0.45 compared with the evaluated data from ENDF/B-VIII.0 [ 43].
Figure 9. (color online) The fragment mass distribution calculations without the neutron emission (green line) and with the neutron emission from fragments (red line) in 14 MeV n+
$ ^{233,235,238} $ U and$ ^{239} $ Pu fission compared with the evaluated data from ENDF/B-VIII.0.In this work, the TKE of fragments consists of the prescission kinetic energy defined as the collective kinetic energy of the fissioning system in the fission direction at the scission point, and the Coulomb repulsion energy between two fragments, which is approximately treated as that between two charged point particles located at the centers of mass of two fragments. Figure 10(a) shows the TKE distribution with the
$ \epsilon $ fixed at 0.25, 0.35, and 0.45 compared with the experimental data. The calculated TKE with$ \epsilon $ =0.35 agrees with the experimental data to a certain extent, however, the calculated results are several MeV lower when the heavy fragment mass number$ A_H $ is around 130, and are several MeV higher around$ A_H $ =140. One can see that$ \epsilon $ has a significant influence on the TKE calculation, which shows that with an increase in$ \epsilon $ , TKE increases, and even the peak position of the TKE distribution is shifted toward the right side. In order to further study the dependence of TKE on$ \epsilon $ , the corresponding Coulomb repulsion energy at the scission point and the prescission kinetic energy are shown in Figs. 10(b) and 10(c), respectively. It can be seen that the overall behavior of the dependence of the Coulomb repulsion energy on$ \epsilon $ is similar to that of the dependence of the TKE distribution on$ \epsilon $ , and that$ \epsilon $ has a very slight influence on the prescission kinetic energy, which indicates that the influence of$ \epsilon $ on TKE mainly results from the Coulomb repulsion energy, which is quite sensitive to the scission configuration. The behavior of the TKE distribution and its dependence on the neck parameter$ \epsilon $ can be understood very well by the results about the scission configuration given in the previous section. The slight increase in the prescission kinetic energy with decreasing$ \epsilon $ may be due to an increase in the elongation of the fissioning nucleus around the scission point and a simultaneous decrease in the Coulomb energy, which leads to a larger collective kinetic energy.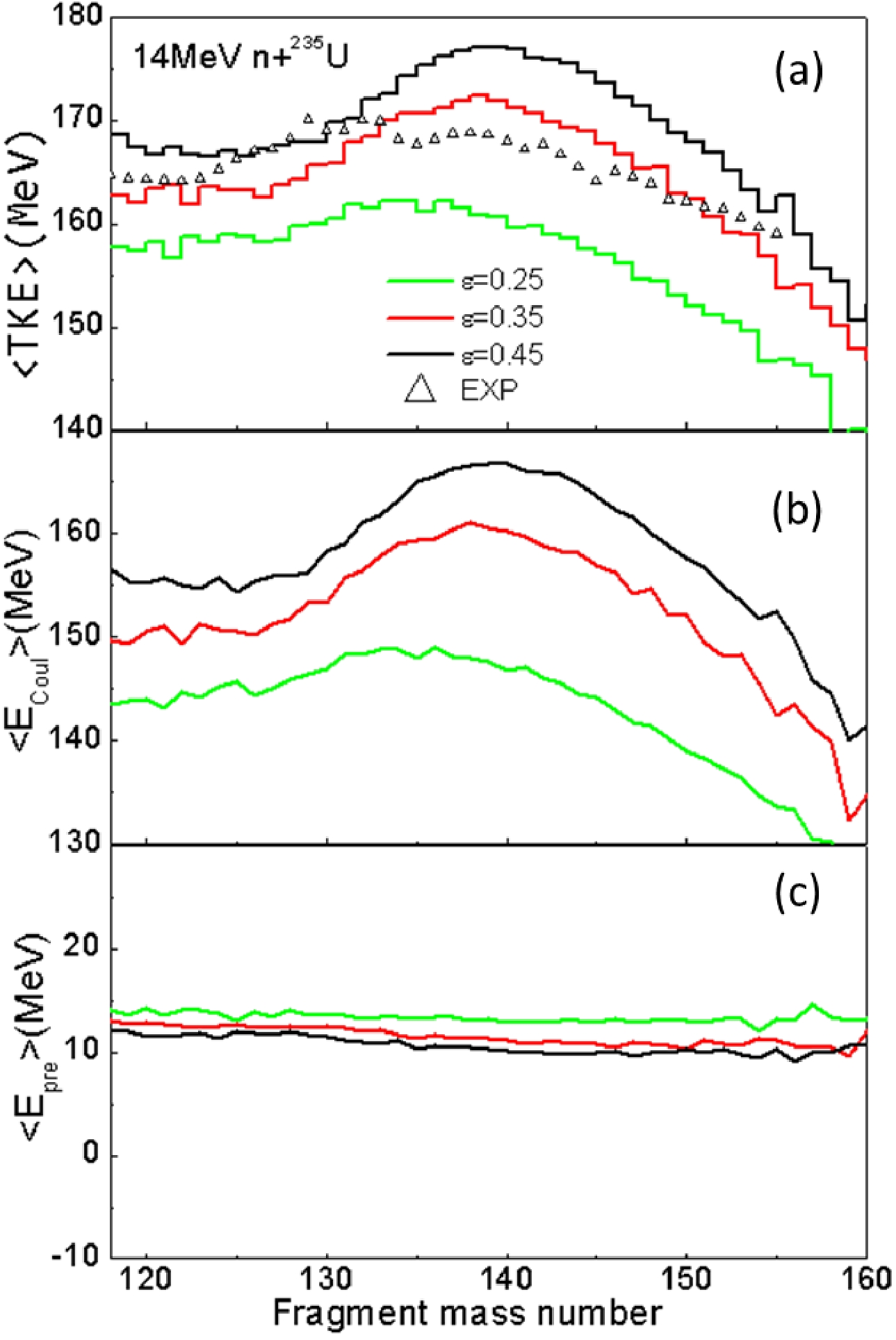
Figure 10. (color online) The TKE distribution of fragments in 14 MeV n+
$ ^{235} $ U fission with the neck parameter$ \epsilon $ fixed at 0.25, 0.35, and 0.45, respectively, together with the experimental data [50] (a). The corresponding Coulomb repulsion energy at the scission point (b) and the prescission kinetic energy as a function of heavy fragment mass number (c) for different values of$ \epsilon $ . -
In the present study, the influence of the neck parameter on the fission dynamics at low excitation energy is investigated based on the three-dimensional Langevin approach within TCSM parametrization.
We first study the influence of the neck parameter on the scission configuration. We find that there is almost no obvious correlation between the neck parameter
$ \epsilon $ and the mass asymmetry parameter η at the scission point, which clearly indicates that$ \epsilon $ has no obvious impact on the fragment mass distribution. However, the elongation$ Z_0/R_0 $ and its correlation with the mass asymmetry η at the scission point are obviously influenced by the neck parameter$ \epsilon $ , which leads to an increase in the fragment total kinetic energy (TKE) and a change in the shape of the TKE distribution with increasing$ \epsilon $ .We then investigate the influence of the neck parameter
$ \epsilon $ on the mass distribution and the TKE distribution of the fission fragments, taking the case of 14 MeV n+$ ^{235} $ U fission as an example. The fragment mass distribution is found to be insensitive to$ \epsilon $ within a reasonable range, as expected. Based on the calculated pre-neutron emission fragment distributions with$ \epsilon $ =0.35, we further calculate the post-neutron fragment mass distributions of 14 MeV n+$ ^{233,235,238} $ U and$ ^{239} $ Pu fission by taking the experimental data of prompt neutron emission from the fragments into account. The results obtained are overall consistent with the post-neutron mass yields from ENDF/B-VIII.0, indicating the power of the present model in describing the fission fragment mass distribution for major actinides.$ \epsilon $ has an important influence on the calculation results of the TKE distribution, which can be understood very well by the influence of$ \epsilon $ on the scission configuration, as it is well know that the TKE mainly contributed from the Coulomb repulsion energy strongly depends on the scission configuration. However, there are large deviations between the TKE calculated using the present model and the experimental data. It seems to us that a perfect description of the TKE distribution cannot be obtained by a simple fitting of$ \epsilon $ , and more effort is needed by increasing the dimension of the Langevin calculations and improving the shape description of the potential well for the TCSM.
Influence of the neck parameter on the fission dynamics within the two-center shell model parametrization
- Received Date: 2022-05-17
- Available Online: 2022-12-15
Abstract: The influence of the neck parameter on the fission dynamics at low excitation energy is studied based on the three-dimensional Langevin approach, in which the nuclear shape is described with the two-center shell model (TCSM) parametrization, and the elongation, mass asymmetry, and fragment deformation are set to be the generalized coordinates of the Langevin equation. We first study the influence of the neck parameter on the scission configuration. We find that there is almost no obvious correlation between the neck parameter





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF





















 DownLoad:
DownLoad: