Observational Hubble parameter data constraints on the interactive model of ${\boldsymbol f(\boldsymbol T) }$ gravity with particle creation

In the late twentieth century, by measuring cosmic distances and observing cosmic objects beyond the Milky Way, we realized that the universe is rapidly expanding, and this event occurs when there is a force greater than gravity but in the opposite direction in the universe. However, the origin of this mysterious force is introduced by an unknown energy called dark energy, which is supposed to surround the entire space and increase the expansion rate of the universe. In fact, this energy was first discovered in type-Ia supernovae and then reconfirmed by two approaches to the cosmic microwave background radiation and the large-scale structure of the universe [1–4]. The problem of dark energy originates from a fundamental theoretical framework such as string theory and quantum gravity. However, despite the existence of evidence for the fact that the universe is accelerating, these observations do not fit the standard model of cosmology within the framework of general relativity. To resolve this contradiction, we introduce a factor called negative pressure for the dark energy source, which can describe the observed accelerated expansion of the universe. Extensive studies of dark energy have been explored with models such as the cosmological constant, scalar fields, modified gravity, agegraphic, holography, and teleparallel gravity [5–46].

In addition, another scenario called teleparallel gravity, first proposed by Einstein, was introduced for the unification of electromagnetism and gravity. In this theory, space-time is characterized by a linear connection without curvature by a metric tensor field called the dynamical tetrad field. Therefore, the geometry of the teleparallel theory uses the linear Weitzenböck connection to represent a torsion connection without curvature. However, the geometry of general relativity is based on the Levi-Civita connection to represent a curvature connection without torsion [47–54].

As mentioned above, current observations with different scenarios suggest that the universe is undergoing accelerated expansion, which leads to the crossing of the phantom divided-line (equation of state (EoS) is less than –1). Furthermore, the particle creation mechanism is an appropriate alternative to describe the current acceleration of the universe, so that it can successfully mimic standard cosmology. In that case, from the point of view of the first law of thermodynamics, the creation of a dynamical number of particles, N, leads to a modified continuity equation for a system called the adiabatic universe [55–63]. Note that the corresponding continuity equation is also obtained via Einstein's equation in standard cosmology as $ \dot \rho + 3 H (\rho + p) = 0 $, in which ρ, p, and H are the energy density, pressure, and Hubble parameter, respectively. An important point that should be noted in the mechanism of particle creation is that its continuity equation, in addition to standard terms, also has the term of the rate of the number of particles as $({\dot N}/{N}) (\rho+p) $. A number of papers attribute the origin of particle number rate to the bulk viscosity. In this event, an open thermodynamic system in which the number of fluid particles is not conserved leads to a modified particle conservation equation, known as the equilibrium equation for particle flow. Hence, we consider that the corresponding particle flow is related to the energy flow between the dark components of the universe. Then, the particle flux resulting from particle creation depends on the energy transfer between dark energy and dark matter. In that case, we consider this issue as energy transfer, the so-called interaction between the dark components of the universe.

It should be noted that the particle creation in a black hole and the expanding universe was also studied [64, 65]. For this purpose, in this work, we intend to implement the mechanism of the particle creation to describe the accelerated expansion of the universe. This motivated us to make a correspondence between the particle creation mechanism and the $ f(T) $ gravity model. Therefore, using this correspondence and a power-law model for the scale factor, we expect to examine the accelerated expansion of the universe with observational data.

This paper is organized as follows:

In Sec. II, we implement the fundamental formation of viscous $ f(T) $ gravity in the flat-FRW metric. In Sec. III, we consider that the universe is dominated by a bulk viscosity fluid, and also obtain the Friedmann equations and EoS in an interacting model. In Sec. IV, we first explain the mechanism of particle creation, and then using the interaction term, we correspond the particle creation with the viscous $ f(T) $ gravity model. In what follows, in Sec. V, we investigate the present model by observational constraints with Hubble data, and then the cosmological parameters are plotted in terms of the redshift parameter. In Sec. VI, we explore the stability conditions for the corresponding model. Finally, in Sec. VII, we present a conclusion for the present model.

In this section, we review teleparallel gravity. For this purpose, we can write the corresponding action for $ f(T) $ gravity in the following form:

where $ \kappa^2=8 \pi G $, and $ e^i_{\,\,\mu} $ is a vierbein field from which the determinant of the vierbein field is obtained as $ e={\rm det}\left(e^i_{\,\,\mu}\right) $, and $ \mathcal{L}_m $ is the matter Lagrangian density. For a more complete explanation, we write the basis of the vierbein field $ e_i(x^\mu) $ as the tangent vectors at point $ x^\mu $ of a manifold as $ e_i. e_j = \eta_{ij} $, in which we consider the corresponding signature of Minkowski space-time as $ \eta_{ij}={\rm diag}(+1,-1,-1,-1) $. In this case, by using the relationship $ e_i = e_i\,^\mu \partial_\mu $, we can obtain metric tensor $ g_{\mu \nu} $ by the tetrad or vierbein field $ e^i_{\,\,\mu} $ as $ g_{\mu \nu}=\eta_{\mu \nu} e^i_{\,\,\mu} e^i_{\,\,\nu} $, which in turn leads to the relationships $ e_i\,^\mu e^i\,_\nu=\delta_\nu^\mu $ and $ e_i\,^\mu e^j\,_\mu=\delta_i^j $. It should be noted that the Greek and Latin letters denote components of space-time coordinates and tangent space-time coordinates, respectively.

As we know, we use the Weitzenböck connection in teleparallel gravity instead of the Levi-Civita connection in general relativity as

By using this connection, we can introduce the torsion tensor and the torsion scalar in the following form:

where

to be known as the antisymmetric tensor and the contortion tensor, respectively. We can also obtain the Ricci tensor and the Ricci scalar by the aforesaid relations in the following form:

By taking variation of action (1) with respect to the tetrad field, the field equations are obtained as

where index T represents the derivative with respect to torsion scalar, and $ \mathcal{T}_{\lambda}{}^{\nu} $ is the energy-momentum tensor. Here, we consider the background manifold as a flat Friedmann-Robertson-Walker (FRW) metric as

where $ a(t) $ is the scale factor. Then, one can immediately obtain the tetrad field as $ e_{\mu}^a=\mathrm{diag}(1,a,a,a) $ or $ e^{\mu}_a= \mathrm{diag}(1,a^{-1},a^{-1},a^{-1}) $, and the torsion scalar is obtained in the following form:

where $ H = \dfrac{\dot{a}}{a} $ is introduced as the Hubble parameter.

In this section, we intend to consider that the current universe is dominated by an anisotropic fluid with the view that the universe is in a more realistic form. This means that we would like to describe the corresponding universe by $ f(T) $ gravity in the presence of a bulk viscous fluid. Considering that the fluid viscosity indicates its resistance to flow as a dissipative phenomenon, the pressure within the universe becomes negative. Then, the presence of bulk viscosity causes the accelerated expansion of the universe [66]. In this case, we can write the energy-momentum tensor in the presence of bulk viscosity as follows:

where $ \rho_{\rm tot} $, $ p_{\rm tot} $, and $ p_{\rm b} $ are introduced as the total energy density, total pressure, and pressure of bulk viscosity of fluid within the universe, respectively. We use the $ 4 $-velocity $ u_\mu $ notation as $ u^i $ = (+1,0,0,0), which gives rise to $ u_i u^j $ = 1. Therefore, we can acquire the non-zero energy-momentum tensor elements as

where by substituting the aforesaid energy-momentum tensor elements and FRW metric into Eq. (6), the Friedmann equations are obtained as

where the dot and index T indicate the derivative with respect to time evolution and the torsion scalar, respectively. Note that the Friedmann Eqs. (14) and (15) are written in the standard form in general relativity by applying condition $ f(T) = T $ in a perfect fluid ($ p_{\rm b} = 0 $). Therefore, we consider that the components of the universe include matter and dark energy in an anisotropic fluid ($ p_{\rm b} \neq 0 $). In this case, we write the total energy density and total pressure in terms of the components of the universe in the following form:

where ρ and p are the energy density and pressure of matter, and $ \rho_{\rm de} $ and $ p_{\rm de} $ are the energy density and pressure of dark energy. However, from Eqs. (14), (15) and (16), (17), we obtain relations $ \rho_{\rm de} $ and $ p_{\rm de} $ in the following form:

where $ \omega_m = p/\rho $ is the matter equation of state (EoS), which is a constant, and the term $ 3 \xi H $ is substituted with the pressure of bulk viscosity, $ p_{\rm b} $, in which the coefficient ξ is a positive constant. Afterward, we can introduce the EoS of dark energy as follows:

where the corresponding EoS of dark energy describes the dynamic of the universe in late time and depends on the modified gravity, matter, and viscous fluid.

In what follows, we can obtain the total continuity equation for the total fluid inside the universe as

which can be written separately in terms of the universe components in the presence of an interacting term in the form

where $ \mathcal{Q} $ is introduced as an interaction term. Note that the interaction term appears when the energy flow is transferred between the dark components of the universe. It is evident that the quantity $ \mathcal{Q} $ should be positive, that is, energy transfer from dark energy to dark matter occurs. Therefore, the positivity of the interaction term guarantees that the second law of thermodynamics is realized [67]. In that case, since the unit $ \mathcal{Q} $ is the inverse of the time evolution, it is natural to choose this value as the product of the Hubble parameter and energy density. Herein, we consider $ \mathcal{Q} = 3 b^2 H \rho $, in which $ b^2 $ is the coupling parameter or transmission intensity.

In the next section, we discuss the thermodynamic study of the particle creation in an open system. Then, the corresponding open system is considered an adiabatic universe, so we see how the particle creation is related to the interaction term between the dark parts of the universe.

As we know, the first law of thermodynamics, or in other words, the Gibbs equation, with the dynamic number of particles N and enthalpy density $ h = \rho + p $ in an open system is written as follows:

where $ \rho = \dfrac{E}{V} $ and $ n = \dfrac{N}{V} $ are the energy density and density of particles, respectively, where E and V are the internal energy and volume of the system, respectively.

Now, we consider the open system as an adiabatic FRW universe model as $ {\rm d}Q = 0 $ with the creation or elimination of the number of particles in the corresponding system. In order to realize the creation of the particles, we consider the volume of the universe as a sphere with a radius of the scale factor $ a(t) $ in the form of the relationship $ V = \dfrac{4 \pi}{3}a^3 $, so that Eq. (24) yields

By taking the derivative from the relationship $ N = n V $ with respect to time evolution, we can clearly obtain the following relation:

where we will immediately have

and this equation is introduced as the modified continuity equation by particle creation. In this case, the third sentence provides negative pressure for matter inside the universe, which causes the present accelerated expansion. Then, we clearly obtain the solution of Eq. (27) as below:

where C is an integral constant.

Now, we can consider that the matter component within the universe is dominated by the dynamical number of particles N; therefore, the matter creation is related to theories of gravity and cosmology. It is interesting to note that researchers consider the negative pressure for Eq. (27) by a viscous fluid, but in this study, we tackle this issue with the interacting model. The existence of interaction between dark energy and dark matter affects the formation of the structure and evolution of the universe. Therefore, the coupling between dark energy and dark matter leads to the evolution of a uniform distribution of baryons in the formation of the structure of the universe and instability in the dark parts from the early era to the dominance of dark energy in the late era [68, 69]. This means that particle creation is considered as an interaction term between the universe components, that is, particle creation is expressed by the conditions $ \mathcal{Q} > 0 $ and $ \mathcal{Q} < 0 $, for the source and sink of energy flow, respectively. In this case, by applying $ \mathcal{Q} > 0 $ and comparing Eqs. (22) and (27), we find the interaction term $ \mathcal{Q} $ with particle creation in the following form

where the rate of matter production is immediately obtained as

where N is given as follows:

where c is an integral constant, assumed to be equal to 1. By substituting Eq. (31) into Eq. (28), we obtain the energy density in terms of the scale factor as follows:

which shows that, by applying $ b = 0 $ and $ \omega_m = 0 $, we reach the dominated universe with dust-like matter. Note that Eq. (32) satisfies Eq. (22). However, Eq. (32) is directly derived from (22), but with the particle creation approach, we can obtain the number of particles, N, as an explicit function in the form of Eq. (31). In contrast, we write the density parameter, $ \Omega_m $, as follows:

where $ \rho_c = 3 H^2 / \kappa^2 $ is the critical density. We describe the present density parameter as

where $ H_0 = 67.4 \pm 0.5 \; {\rm km\,s^{-1}\,Mpc^{-1}} $ is the current Hubble parameter, and here, we take $ \Omega_{m_0} = 0.315 \pm 0.007 $ [70]. The matter energy density, ρ, is given by Eqs. (32) and (34) as

where $ a_0 = 1 $ is the current scale factor.

As mentioned in the previous section, we considered an open system from the thermodynamic point of view for an adiabatic FRW universe model, where there is no heat exchange with the outside universe but the number of particles within the system is created. Therefore, the presence of particles within the universe leads to a modified continuity equation that is related to the interaction term compared to the continuity equation of $ f(T) $ gravity. With this perspective, we treat the number of particles N as a function of the scale factor in the form of Eq. (31). Therefore, in this work, the perspective of the particle creation from the point of view of $ f(T) $ gravity is considered.

In what follows, we insert Eq. (32) into Eqs. (18), (19) and then we have

In order to solve the aforesaid Friedmann equations, we need to find the form of the function $ f(T) $ in terms of the torsion scalar. For this purpose, if we compare the Friedmann Eq. (14) with the standard form of the Friedmann equation, we find function $ f(T) $ as $ f(T) = T - \alpha \sqrt{T} $. Since we are dealing with the modified Friedmann equation (14), the form of function $ f(T) $ is expected to be different from the form of function $ f(T) = T - \alpha \sqrt{T} $. For this purpose, we take the form of function $ f(T) $ as follows:

where α and β are dimensionless parameters, and $ T_0 = -6 H_0^2 $ is the current amount of the torsion scalar which arises from Eq. (11). The above particular model is expected to demonstrate the crossing of the phantom divided-line, which can solve dark energy as a serious challenge in cosmology. It should be noted that this choice is mentioned in Refs. [71, 72].

In order to solve the current system, we substitute Eqs. (11), (31), and (38) into Eqs. (36), (37) and then we have

where the dot symbol demonstrates the derivative with respect to time evolution, and we have $ \eta = b^{2} - 1 - \omega_{m} $, $ \delta = (1 + \omega_m)/3 b^2 $, and $ \sigma = \beta H_0^2/\delta^2 $. Here we can see that the Friedmann equations depend on the number of particles, N, and its corresponding derivatives with respect to time evolution.

Now we intend to reconstruct the aforesaid cosmological quantities in terms of the redshift parameter, z, which is written in terms of the scale factor by the relation $ a(t) = 1/(1+z) $. We can write down the transformation between the derivative with respect to z and the derivative with respect to time evolution as $ {\rm d}/{\rm d}t = -H (1+z) {\rm d}/{\rm d}z $. Therefore, Eq. (31) is written in terms of the redshift parameter as

and we write $ \dot{N} $ and $ \ddot{N} $ in terms of the redshift parameter in the following form

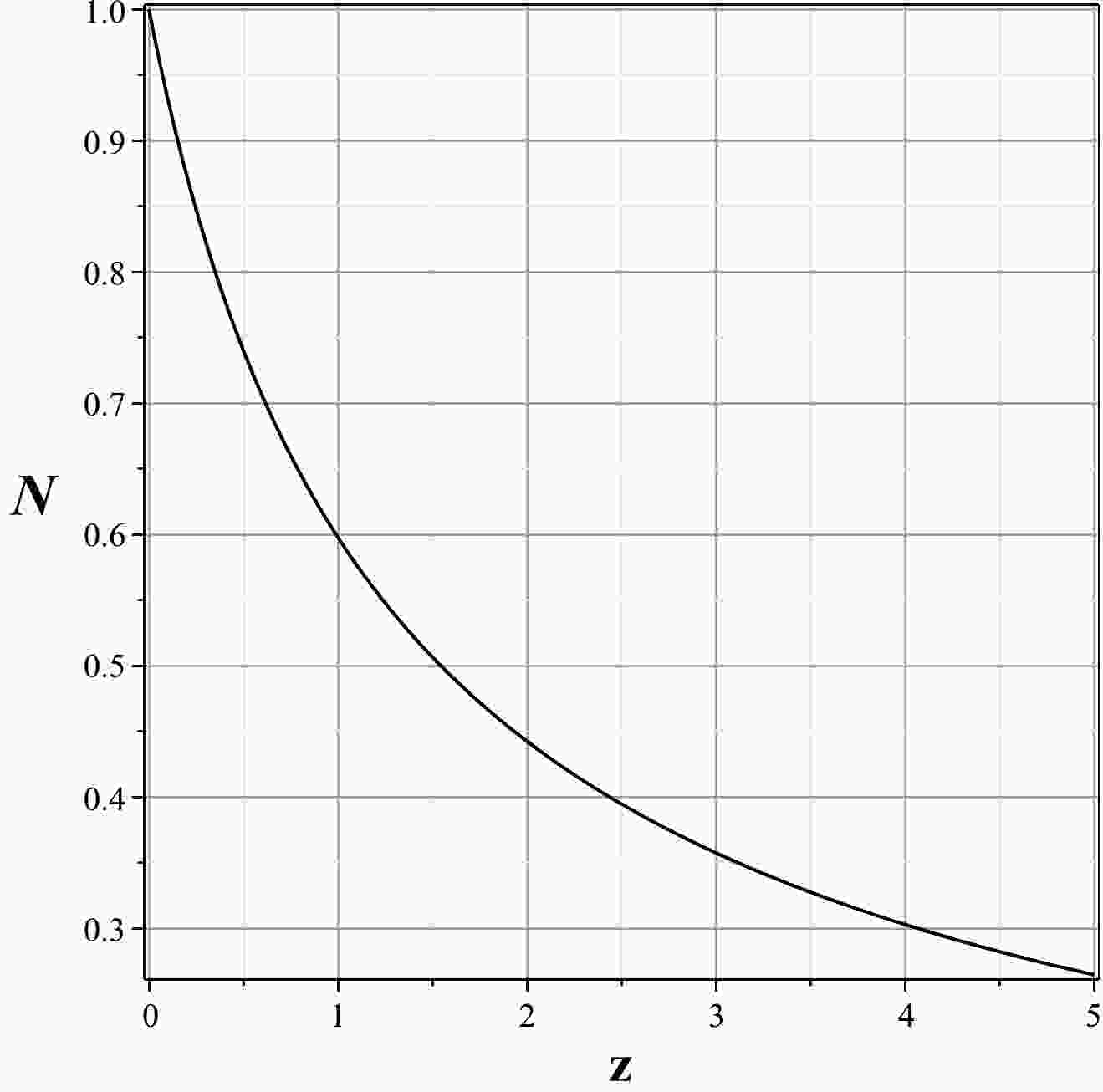
where the prime symbol indicates the derivative with respect to the redshift parameter. We can see the variation in the number of particles in terms of the redshift parameter in Fig. 1. Figure 1 shows that the value of the number of particles increases from the early universe to the late universe.

Figure 1.  Number of particles in terms of redshift parameter for $ \alpha = 0.001 $, $ \beta = 0.5 $, $ b = 0.5 $, and $ \omega_m = 0.01 $.

In what follows, in order to solve the above scenario, we take a particular model called the power-law cosmology model as below:

where $ t_0 $ is the present age of the universe, and m is a dimensionless positive coefficient [73, 74]. It should be noted that if $ t =t_0 $, we will have $ a(t_0) = a_0 =1 $, which has already been mentioned. The Hubble parameter yields

where the present age of the universe in terms of the present Hubble parameter, $ H_0 $, is written as

where the coefficient m is introduced as a correction factor. In this case, the Hubble parameter is obtained in terms of the redshift parameter in the following form:

where only one free parameter is included, which in turn is less complicated and can be easily calculated with observational constraints.

Since Eq. (47) is acquired by the power-law model in terms of the redshift parameter, we have to deliberate the correctness of using it in our model. For this purpose, we fit the power-law model with 51 supernova data points from observational Hubble parameter data [75–82], and then, by using the likelihood analysis (the chi-square value, $ \chi_{\rm min}^2 $), we obtain the value of $ m = 0.95 $ for these data. In this case, by using Eq. (46), the age of the universe is obtained as $ t_0 = 13.78 \;{\rm Gyr} $ (note that the results presented in this paragraph are the same as those in Ref. [83], and we will not go into detail in writing).

Now, we can obtain $ \dot{N} $ and $ \ddot{N} $ in terms of the pure redshift parameter in the form

By inserting Eqs. (48), (49) into Eqs. (39), (40) we have

which shows that $ \rho_{\rm de} $ and $ p_{\rm de} $ are explicit functions of the redshift parameter. We note that these obtained relationships, i.e., those of the energy density and pressure of dark energy, depend on a few free parameters that arise from scenarios of the $ f(T) $gravity, matter, particle number, and viscous fluid.

The variations of relationships $ \rho_{\rm de} $ and $ p_{\rm de} $ are plotted in terms of the redshift parameter as shown in Fig. 2. It should be noted that free parameters play an important role in drawing the corresponding graphs. For this purpose, we try to choose them by applying conditions such as $ \rho_{\rm de} > 0 $ and $ p_{\rm de} < 0 $, especially in the late time ($ z = 0 $). However, we consider the values of the free parameters for the corresponding graphs as $ \alpha = 0.001 $, $ \beta = 0.5 $, $ b = 0.5 $, $ \omega_m = 0.01 $, and $ \xi = 26, 30, 34 $. Fig. 2 shows that the energy density decreases from a very high positive value in the early time to a much lower positive value in the late time ($ z = 0 $), and the pressure decreases from a very large negative value in the early time to a much lower negative value in the late time ($ z = 0 $).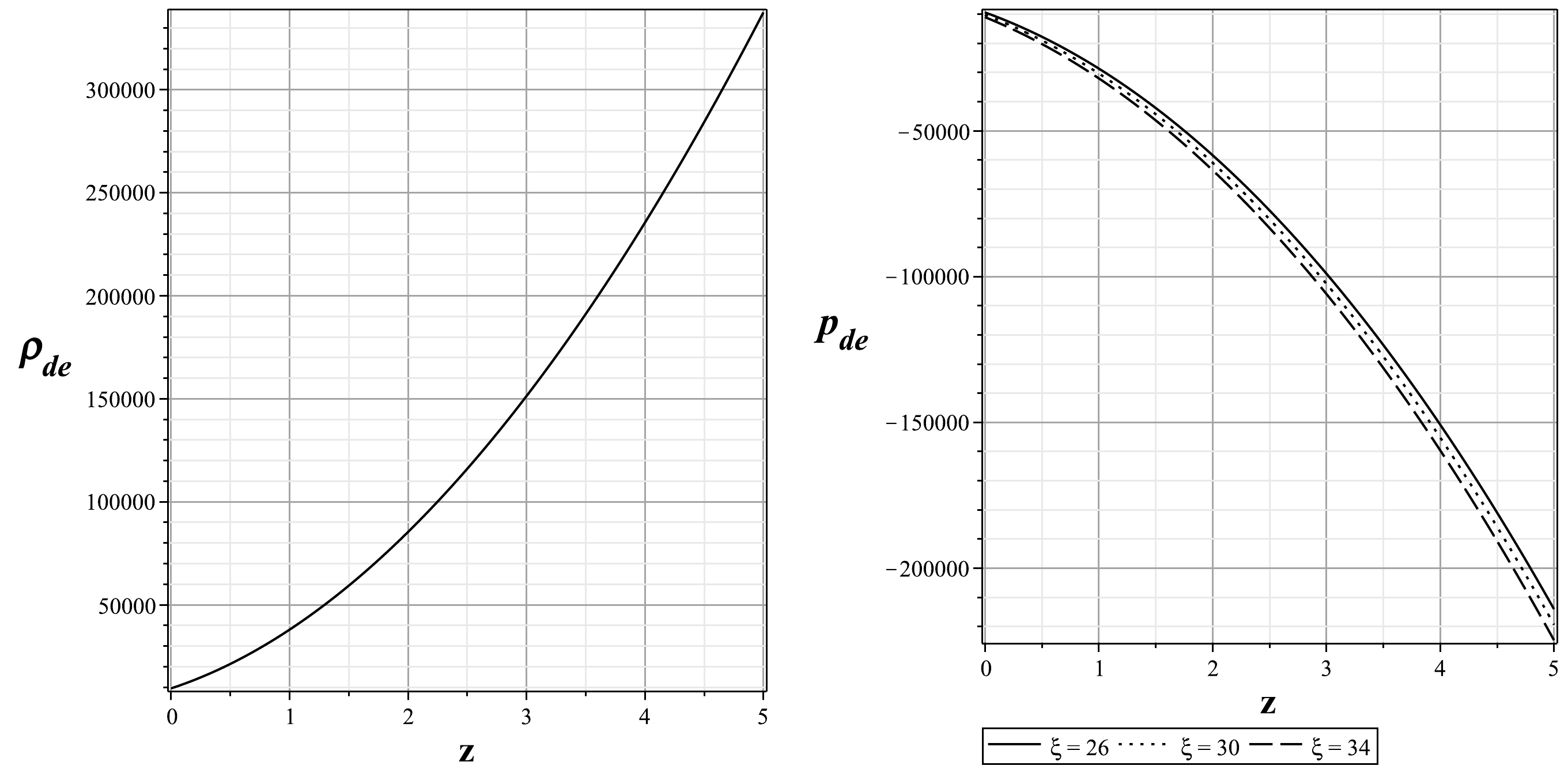

Figure 2.  Energy density and pressure of dark energy in terms of redshift parameter for $ \alpha = 0.001 $, $ \beta = 0.5 $, $ b = 0.5 $, $ \omega_m = 0.01 $, $ \xi = 26 $ (line), $ \xi = 30 $ (dot), and $ \xi = 34 $ (dash).

Since the dark energy EoS is one of the most practical cosmic parameters, it can describe the nature of dark energy and dark matter for different eras of the universe from the Big Bang to the late time. Now, using $ \rho_{\rm de} $ and $ p_{\rm de} $, we clearly find the dark energy EoS as $ \omega_{\rm de} = p_{\rm de}/\rho_{\rm de} $ by Eqs. (50), (51) (we avoid writing the corresponding EoS because it is long). In that case, we can plot the variation in the dark energy EoS, $ \omega_{\rm de} $, in terms of the redshift parameter as shown in Fig. 3. Figure 3 shows that the amount of EoS decreases from early time to late time, i.e., the evolution of the universe changes from the matter era ($ \omega_{\rm de} > -1 $) to the phantom era or dark energy era ($ \omega_{\rm de} < -1 $). Interestingly, the amount of EoS depends on the effect of the viscous fluid; hence, from Fig. 3, we can see that, when the amount of the viscosity coefficient increases, the dark energy period occurs with more growth. Therefore, this result indicates that the universe is undergoing an accelerated expansion phase, which is compatible with the obtained results in Ref. [84] for EoS.

Figure 3.  EoS of dark energy in terms of redshift parameter for $ \alpha = 0.001 $, $ \beta = 0.5 $, $ b = 0.5 $, $ \omega_m = 0.01 $, $ \xi = 26 $ (line), $ \xi = 30 $ (dot), and $ \xi = 34 $ (dash).

In this section, we study the stability and instability of the present model from the thermodynamic perspective. In this case, we employ a useful function called the sound speed parameter, $ c_s^2 $. Since the universe is an adiabatic thermodynamic system, heat energy or mass is not transferred from the inside to outside of the universe. This means that the entropy perturbation is zero, and the pressure changes in terms of the energy density. Therefore, we introduce the pressure-to-density ratio with the below sound speed parameter:

where symbol $ \partial_z $ represents the derivative with respect to the redshift parameter. Now, the parameter $ c_s^2 $ helps us find the range of the redshift parameter wherein the universe is in a state of stability or instability. It should be noted that the stability and instability analyses are expressed with conditions $ c_s^2 > 0 $ and $ c_s^2 < 0 $, respectively. The variation in the sound speed parameter is plotted in terms of the redshift parameter as shown in Fig. 4. Figure 4 shows that the universe is in a phase of instability in all eras, even with the existence of viscous fluid. This instability indicates that the energy density of dark energy does not exhibit a controllable growth.

Figure 4.  Sound speed parameter in terms of redshift parameter for $ \alpha = 0.001 $, $ \beta = 0.5 $, $ b = 0.5 $, $ \omega_m = 0.01 $, $ \xi = 26 $ (line), $ \xi = 30 $ (dot), and $ \xi = 34 $ (dash).

Now, for a more complete description of our model, we attempt to calculate the present values of the density parameters for dark energy and dark matter. According to the density parameter for dark matter (33), the density parameter for dark energy is introduced in the form

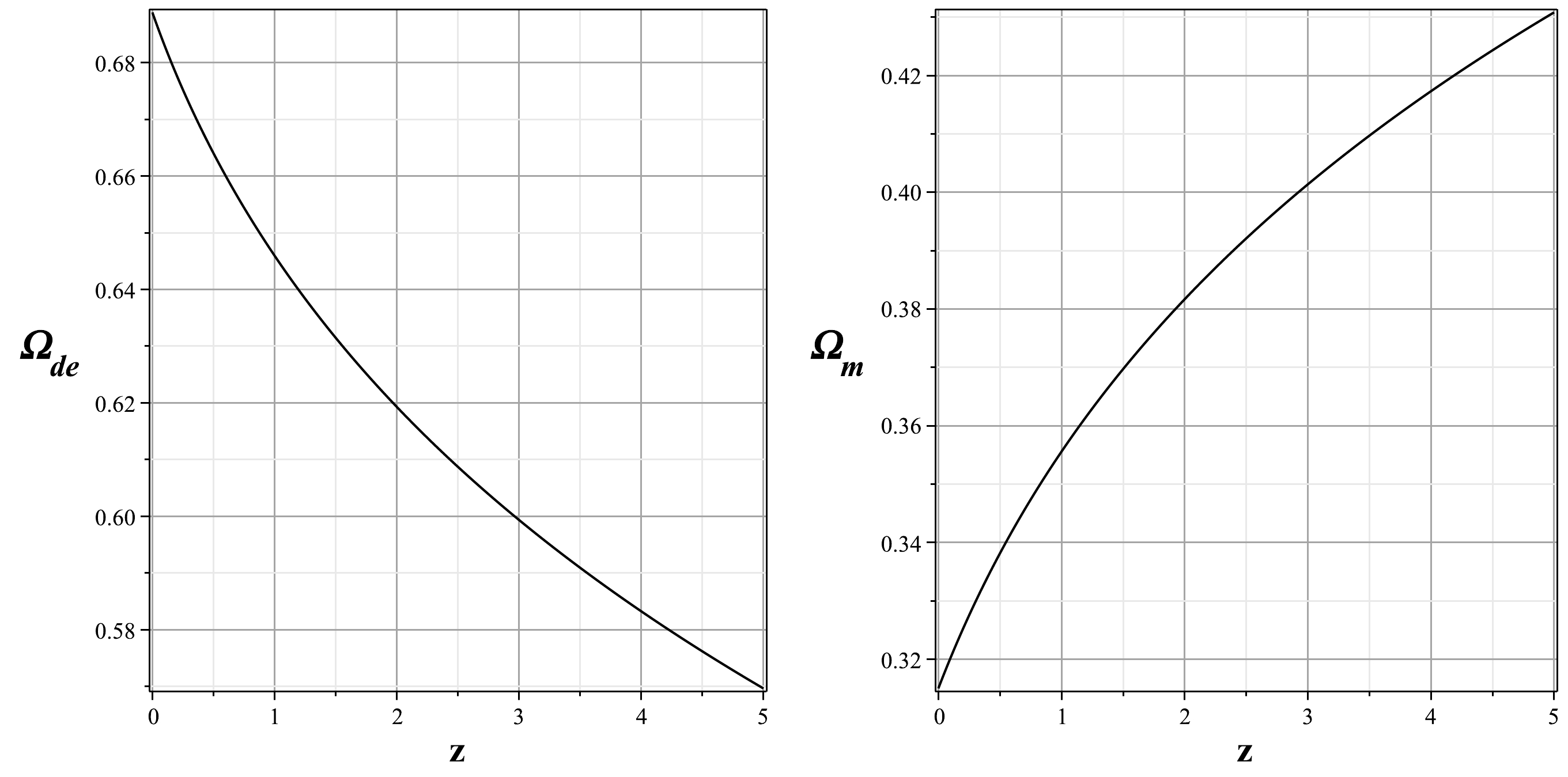
where $ \rho_{\rm c} $ is the critical density. By inserting Eq. (35) into Eq. (33), the variation in the density parameter for dark matter is plotted in terms of the redshift parameter as shown in Fig. 5(right side). Similarly, we plot the variation in the density parameter for dark energy in terms of the redshift parameter by substituting Eq. (51) into Eq. (53) as shown in Fig. 5(left side). Figure 5 shows that the value of $ \Omega_m $ decreases from the early universe to the late universe, eventually reaching the current value of $ 0.315 $. In contrast, the value of $ \Omega_{\rm de} $ increases from the early time to the late time, reaching the present value of $ 0.689 $. Therefore, these calculations show that the proportion of dark energy is increasing, which means that the universe is under a phase of accelerated expansion.

Figure 5.  Density parameters of dark energy and dark matter in terms of redshift parameter for $ \alpha = 0.001 $, $ \beta = 0.5 $, $ b = 0.5 $, and $ \omega_m = 0.01 $.

In this study, we explored particle creation from the perspective of $ f(T) $ gravity using the flat-FRW metric in the universe, which contains a viscous fluid. First, to obtain the Einstein equation in $ f(T) $ gravity, we used the Weitzenböck connection in teleparallel gravity instead of the Levi-Civita connection in general relativity. The energy-momentum tensor was considered in terms of the total energy density, total pressure, and pressure of bulk viscosity of fluid within the universe. Next, we acquired the Friedmann equations and EoS of dark energy in terms of a function of torsion scalar T and its first and second derivatives. Then, the continuity equations for the universe components were obtained by considering the interaction model. The interaction term $ \mathcal{Q} $ was considered as $ \mathcal{Q} = 3 b^2 H \rho $, in which $ b^2 $ is the transfer strength from dark matter to dark energy.

Another significant aspect of this paper is that the universe should be considered as an adiabatic system from the perspective of the first law of thermodynamics. For this purpose, we considered the creation of the number of particles in this universe, and thus, we obtained the modified continuity equation for particle creation. An interesting point is that the obtained continuity equation for matter creation has a negative pressure, which causes the present accelerated expansion. Next, we acquired the energy density of matter in terms of the number of particles, N, as shown in Eq. (28). Another interesting point is that Eq. (27) is equivalent to Eq. (22). This means that we consider particle creation to be equivalent to the exchange of energy between the components of the universe (same as the interaction term $ \mathcal{Q}) $. The result of this equivalency leads to obtaining the number of particles and energy density of matter in terms of the scale factor.

Subsequently, we related the obtained energy density of matter to Friedmann equations of $ f(T) $ gravity with a specified function $ f(T) $ of Eq. (38), which is exponential and logarithmic. In this case, we obtained the energy density (39) and pressure (40) of dark energy in terms of the number of particles N. Then, we reconstructed the number of particles in terms of the redshift parameter; the benefit of this reconstruction is that the cosmological parameters can be evaluated for late time ($ z = 0 $). For evaluations in this study, we took the power-law for the scale factor, and thus, we immediately acquired the Hubble parameter (47) in terms of the redshift parameter. After that, we used the result of Ref. [83] to fit the Hubble parameter by the minimum chi-square value with $ 51 $ observational Hubble parameter data points. Then, we plotted the graphs of the cosmological parameters such as the energy density, pressure, and EoS of dark energy in terms of the redshift parameter. These graphs indicated that the universe is in a phase of accelerated expansion. Further, stability analysis of the present model was investigated using sound speed, and the corresponding graph showed that the universe is in an instability phase during late time, i.e., the growth of the energy density of dark energy is not controlled in the present universe. Finally, in order for the results to be consistent with the observational data, we calculated the density parameter values for dark energy and dark matter, which were $ 0.689 $ and $ 0.315 $, respectively, and also plotted them against the redshift parameter.