-
In general relativity (GR), there is a theorem for the properties of black holes, known as the "no-hair theorem" [1–4], which states that no more than three characteristic parameters affect black holes: mass, angular momentum, and charge. However, in recent years, with intensifying exploration of the universe and black holes, it has been discovered that there may be other physical quantities that affect the properties of black holes. For example, black holes may contain quantum hairs [5] when other charges associated with inner gauge symmetries (and fields) are present, and black holes with scalar hair have also been discussed in scalar-tensor theories [6–10], where scalar fields play a pivotal role within particle physics and early universe cosmology [11, 12]. With the recent release of black hole images and the discovery of gravitational waves, the scope to test the no-hair theorem has been further enhanced [13]. Nevertheless, it is typically difficult (and impossible in many cases) to find analytical hairy solutions describing general matter configurations.
It is worth noting that a new and elegant method known as gravitational decoupling, which allows us to obtain new exact solutions starting from a known solution, has recently received considerable attention. This approach by means of minimal geometric deformation (MGD) was developed to deform Schwarzschild spacetime in the context of the braneworld [14, 15]. Subsequently, many applications of this method and its extension (hereafter referred to as EGD) have been studied for stellar systems in the braneworld framework [16–23]. MGD is a highly successful theory that allows the study of nonlinear gravity in braneworlds to obtain the effective action at low energies using the anti-de Sitter/conformal field theory (AdS/CFT) correspondence [24, 25].
Beyond the braneworld, this gravitational decoupling approach has also been used to generate solutions of Einstein field equations in GR and other modified gravitational theories because it has following advantages: (a) it can decouple a complex energy-momentum tensor into various relatively simpler components, (b) it can be used to extend some known seed solutions into more complex solutions, and (c) it can be used to find the solutions of gravitational theories other than GR. The procedure of the gravitational decoupling approach can be described as follows: "Suppose there are two non-interacting gravitational sources in spacetime, a seed source
$ T_{\mu\nu} $ and an extra source$ \theta_{\mu\nu} $ . The standard Einstein equations are first solved for$ T_{\mu\nu} $ , and then another set of quasi-Einstein equations are solved for$ \theta_{\mu\nu} $ . Subsequently, the two solutions can be combined to derive the complete solution for the total system." Mathematically, the total energy-momentum tensor of the gravitational system is given by$ \begin{eqnarray} \tilde{T}_{\mu\nu}=T_{\mu\nu}+\theta_{\mu\nu}. \end{eqnarray} $

(1) Here,
$ \theta _{\mu\nu} $ may be a scalar field, a vector field, etc. By applying the algorithm to previously known seed solutions, this method has been adopted to derive several new solutions of gravitational systems in GR, such as stellar distributions [26–28] and black holes [29]. Through the gravitational decoupling approach, Ovalle derived the anisotropic solutions of the Einstein field equations for self-gravitating systems from perfect fluid solutions using the MGD technique [30]. More recently, gravitational decoupling via MGD was used to investigate higher dimensional compact structures [31] and was extended to the context of the Horndeski [32], Lovelock (Gauss-Bonnet) [33–36], Rastall [37], and$ f(R,T) $ [38] gravity theories and the cosmological scenario [39].However, the MGD technique has several limitations because it only deforms the radial metric potential by leaving the temporal coordinate as an invariant quantity. As a result, the considered sources do not exchange energy in this scenario. Fortunately, EGD was presented in [40], where Ovalle considered the decoupling of two spherically symmetric and static gravitational sources in GR and found the exchange of energy between decoupled sources. Moreover, the corresponding metrics possessed a well-defined event horizon and reproduced the Reissner-Nordstrom solution. Sharif et al. [41, 42] obtained astrophysical and cosmological solutions in the context of SBD theory using the MGD and EGD techniques, respectively. Contreras et al. [43] successfully decoupled field equations in
$ (1+2) $ -dimensional gravity to obtain the exterior charged BTZ model from the corresponding vacuum solution through the EGD technique.Now, let
$ g_{\mu\nu} $ be any metric. After calculating its Einstein tensor$ G_{\mu\nu} $ ,$ g_{\mu\nu} $ can be regarded as the metric corresponding to the dynamic tensor$T_{\mu\nu} = \dfrac{G_{\mu\nu}}{8 \pi}$ . The problem is that such an arbitrary$ T_{\mu\nu} $ is not necessarily an excessive amount of motion for some material fields. Therefore, such a " solution " is not necessarily physically meaningful. It is generally believed that the dynamic tensor of any material field must satisfy a number of "reasonable" conditions, collectively known as energy conditions [44]. The energy conditions imposed on the energy-momentum tensor can be generally considered sensible guidelines to avoid classically unphysical configurations and exotic matter sources apart from the Einstein field equations in the context of a wide class of spacetime theories [45]. Considering the deformation of seed Schwarzschild vacuum spacetime, Ovalle et al. [46] recently formulated new hairy black holes through the EGD technique for the first time, where the additional source is described by a conserved energy-momentum tensor$ \theta_{\mu\nu} $ , which satisfies either the strong (SEC) or dominant energy condition (DEC) in the region outside the event horizon. Subsequently, hairy black holes were discussed from the perspective of conformal anomalies [47]. From a spherically symmetric seed solution, the solutions of rotating hairy black holes were also constructed using the EGD technique [48, 49], including in studies of the strong field gravitational lensing effects [50] and thermodynamic properties [49] of these black holes. It is well known that AdS/CFT duality generally states that weakly-coupled gravity in$ (d+1) $ -dimensional AdS space is the dual theory to strongly-coupled CFT. It is interesting to explore the applications of the gravitational decoupling approach in asymptotic AdS spacetimes. Note that several new solutions of the Einstein field equations in asymptotic (A-)dS spacetimes are also presented in Refs. [51–53] using the MGD technique. Moreover, the AdS/CFT correspondence setup has been employed to compute Bose-Einstein condensates (BCS) [54] and holographic entanglement entropy (HEE) corrections [55, 56] for spherically symmetric spacetimes in the context of MGD and EGD. Retaining the energy conditions, we adopt the EGD technique to derive the solutions of hairy black holes in asymptotic AdS spacetimes. We expect that the obtained hairy AdS black holes can be investigated to explore aspects of gravity in the strong nonlinear regime and compare any deviation from the GR setup in the gravitational wave astrophysical scenario.The paper is organized as follows: In Sec. II, we review the gravitational decoupling approach via EGD in asymptotic AdS spacetime. In Sec. III, we separately adopt the SEC and DEC to derive two new families of hairy black hole solutions. Finally, we summarize the results of our study in Sec. IV.
-
We consider the Einstein field equations
$ \begin{eqnarray} G_{\mu\nu}=R_{\mu\nu}-\frac{1}{2}R g_{\mu\nu}+\Lambda g_{\mu\nu}=\kappa^2 \tilde{T}_{\mu\nu}, \end{eqnarray} $

(2) and assume that the total energy-momentum tensor is given by
$ \begin{eqnarray} \tilde{T}_{\mu\nu}=T_{\mu\nu}+\theta_{\mu\nu}, \end{eqnarray} $

(3) where Λ is a negative cosmological constant,
$ T_{\mu\nu} $ is the four-dimensional energy-momentum tensor of a perfect fluid,$T_{\nu}^{\; \mu}={\rm diag}(-\rho,p,p,p)$ , and$ \theta_{\mu\nu} $ describes an additional source whose coupling to gravity is proportional to the constant α. Because the Einstein tensor$ G_{\mu\nu} $ is divergence free, the total energy-momentum tensor$ \tilde{T}_{\mu\nu} $ satisfies the conservation equation$ \begin{eqnarray} {\nabla _\nu }{\tilde{T}^{\mu \nu }} = 0. \end{eqnarray} $

(4) From the expression of the energy-momentum tensor in Eq. (3), we define the effective density
$ \begin{eqnarray} \tilde{\rho} =-\tilde{T}_0^{\; 0}=\rho-\theta _0^{\; 0}, \end{eqnarray} $

(5) effective radial pressure
$ \begin{eqnarray} \tilde{p}_r=\tilde{T}_1^{\; 1}=p_r+\theta _1^{\; 1}, \end{eqnarray} $

(6) and effective tangential pressure
$ \begin{eqnarray} \tilde{p}_{\bot}=\tilde{T}_2^{\; 2}=p_{\bot}+\theta _2^{\; 2}. \end{eqnarray} $

(7) In this study, we investigate the static and spherically symmetric metric
$ \begin{eqnarray} {\rm d}{s^2}=-{{\rm e}^{\nu (r)}}{\rm d}{t^2}+{{\rm e}^{\lambda (r)}}{\rm d}{r^2}+{r^2}({\rm d}{\theta ^2}+{\sin ^2}\theta {\rm d}{\phi ^2}), \end{eqnarray} $

(8) where
$ \nu =\nu(r) $ and$ \lambda=\lambda(r) $ are functions of the areal radius r only. Substituting the above metric into the Einstein field equations (Eq. (2)), we get$ \begin{aligned}[b] \kappa ^2 \left(-\rho+\theta _0^{\; 0}\right)=&-\frac{1}{r^2}+{\rm e}^{-\lambda } \left(\frac{1}{r^2} -\frac{\lambda '}{r}\right)+\Lambda, \\ \kappa ^2 \left(p_r+\theta _1^{\; 1}\right)=&-\frac{1}{r^2}+{\rm e}^{-\lambda } \left(\frac{1}{r^2} +\frac{\nu '}{r}\right)+\Lambda, \\ \kappa ^2 \left(p_{\bot}+\theta _2^{\; 2}\right)=&\frac{1}{4} {\rm e}^{-\lambda } \left(-\lambda ' \nu ' +2 \nu ''+\left(\nu '\right)^2+\frac{2 \left(\nu '-\lambda '\right)}{r}\right)\\ &+\Lambda. \end{aligned} $

(9) We further consider the seed source for the perfect fluid
$ T_{\mu\nu} $ (i.e.,$ \theta_{\mu\nu}=0 $ in Eq. (2)) and assume that the new metric ansatz takes the following form:$ \begin{eqnarray} {\rm{ds}}^2=-{\rm e}^{\xi\left(r\right)}{\rm{dt}}^2+{\rm e}^{\mu\left(r\right)}{\rm{dr}}^2+r^2{\rm{d \Omega }}^2, \end{eqnarray} $

(10) which implies new forms of the Einstein field equations,
$ \begin{aligned}[b] {\kappa ^2}\rho =& \frac{1}{{{r^2}}} - {{\rm e}^{ - \mu }}\left(\frac{1}{{{r^2}}} - \frac{{\mu '}}{r}\right)-\Lambda,\\ {\kappa ^2}p_r =&-\frac{1}{{{r^2}}}+{{\rm e}^{ - \mu }}\left(\frac{1}{{{r^2}}} + \frac{{\xi '}}{r}\right)+\Lambda,\\ {\kappa ^2}p_{\bot} =& - \frac{{{{\rm e}^{ - \mu }}}}{4}\left(2\xi " + \xi {'^2} - \mu '\xi ' + 2\frac{{\xi ' - \mu '}}{r}\right)+\Lambda. \end{aligned} $

(11) To obtain information on the additional source
$ \theta_{\mu}^{\; \nu} $ , we must apply some distortion of this metric, namely [30],$ \begin{aligned}[b]\xi \to \nu =&\xi+\alpha * g\left(r\right),\\ {\rm e}^{-\mu }\to {\rm e}^{-\lambda }=&{\rm e}^{-\mu }+\alpha * f\left(r\right). \end{aligned} $

(12) With two Einstein field equations (Eqs. (9) and (11)) and the metric deformation (Eq. (12)), the quasi-Einstein field equations for
$ \theta_{\mu}^{\; \nu} $ can be obtained as$ \begin{aligned}[b] \kappa ^2 \theta _0^{\; 0} =&\alpha \frac{f}{r^2}+\alpha\frac{ f'}{r},\\ \kappa ^2 \theta _1^{\; 1}=&\alpha f \left(\frac{1}{r^2}+\frac{\nu '}{r}\right)+\alpha \gamma _1,\\ \kappa ^2 \theta _2^{\; 2}=&\alpha \frac{f}{4}\left(2 \nu ''+\nu '^2+\frac{2 \nu '}{r}\right) +\alpha \frac{f'}{4} \left(\nu '+\frac{2}{r}\right)+\alpha\gamma_2, \end{aligned} $

(13) with
$ \begin{eqnarray} {\gamma _1}{{\rm{ = }}}\frac{{{{\rm e}^{ - \mu }}g'}}{r},\quad {\gamma _2} = \frac{{{{\rm e}^{ - \mu }}}}{4}(2g'' + g{'^2} + \frac{{2g'}}{r} + 2\xi 'g' - \mu 'g'). \end{eqnarray} $

Clearly, the two sources
$ T_{\mu\nu} $ and$ \theta_{\mu\nu} $ are successfully decoupled using the EGD method.Considering the conservation equations for the total energy-momentum tensor
$ \tilde{T}^{\mu\nu} $ , the tensors$ T^{\mu\nu} $ and$ \theta^{\mu \nu } $ satisfy$ \begin{eqnarray} {\nabla _\nu }{T^{\mu \nu }} = 0,\quad {\nabla _\nu }{{\theta}^{\mu \nu }} = 0, \end{eqnarray} $

(14) because the tensors
$ T_{\mu\nu} $ and$ \theta_{\mu\nu} $ are non-interacting. Then, we can obtain the conservation equation for the additional energy-momentum tensor$ \theta_{\mu\nu} $ $ \begin{eqnarray} (\theta_1^{\; 1})'-\frac{{\nu'}}{2}(\theta_0^{\; 0}-\theta_1^{\; 1})-\frac{2}{r}(\theta_2^{\; 2}-\theta_1^{\; 1}) -\frac{{\alpha g'}}{2}(T_0^{\; 0} - T_1^{\; 1})=0. \end{eqnarray} $

(15) -
Now, we construct hairy black holes. For simplicity, we can assume the energy-momentum
$ T_\mu^{\; \nu} $ (seed source) to satisfy$ T_\mu^{\; \nu}=0 $ , namely,$ \rho=p_r=p_{_\bot}=0 $ . From the Einstein field equations (Eq. (11)), we can easily obtain the analytical solutions for the seed metric,$ \begin{eqnarray} {{\rm e}^\xi}={{\rm e}^{-\mu}}=1-\frac{{2M}}{r}-\frac{{{r^2}\Lambda}}{3}, \end{eqnarray} $

(16) which are exactly Schwarzschild AdS black hole solutions. Substituting the above metric solution into Eq. (12), we can obtain
$ \begin{aligned}[b]{{\rm e}^{ - \xi (r)}} \to {{\rm e}^{ - \nu (r)}} =& \left(1-\frac{{2M}}{r}-\frac{{{r^2}\Lambda }}{3}\right)*{{\rm e}^{\alpha g(r)}},\\ {{\rm e}^{ - \mu (r)}} \to {{\rm e}^{ - \lambda (r)}} =& \left(1-\frac{{2M}}{r}-\frac{{{r^2}\Lambda }}{3}\right) + \alpha f(r). \end{aligned} $

(17) In order to obtain black hole solutions with a well defined horizon structure, we set
$ \begin{eqnarray} {{\rm e}^{\nu}} = {{\rm e}^{-\lambda}}. \end{eqnarray} $

(18) Then, the killing and causal horizons of the hairy black hole will be in the same position,
$ \begin{eqnarray} {{\rm e}^{\nu (r_h)}} = {{\rm e}^{ - \lambda (r_h)}} = 0. \end{eqnarray} $

(19) From Eqs. (12) and (18), the metric deformations
$ f(r) $ and$ g(r) $ can be rewritten as$ \begin{eqnarray} \alpha f(r)=\left(1-\frac{{2M}}{r}-\frac{{{r^2}\Lambda }}{3}\right)*({{\rm e}^{\alpha g(r)}} - 1). \end{eqnarray} $

(20) The metric line element of the hairy black hole then becomes
$ \begin{aligned}[b] {\rm d}{s^2}=&-\left(1-\frac{{2M}}{r}-\frac{{{r^2}\Lambda}}{3}\right)*{{\rm e}^{\alpha g(r)}}\\&+{\left(1-\frac{{2M}}{r} -\frac{{{r^2}\Lambda}}{3}\right)^{-1}}*{{\rm e}^{-\alpha g(r)}}+{r^2}{\rm d}{\Omega^2}. \end{aligned} $

(21) Therefore, the event horizon
$ r_h $ of this hairy black hole is given by$ \begin{aligned}[b] {r_h}=&-\frac{1}{{\left({3M{\Lambda ^2}+\sqrt{9{M^2}\Lambda^4-\Lambda ^3} } \right)}^{1/3}} \\&-\frac{{\left({3M{\Lambda^2}+\sqrt{9{M^2}\Lambda^4-\Lambda ^3} } \right)}^{1/3}}{\Lambda}. \end{aligned} $

(22) Note that the horizon radius
$ r_h>0 $ of hairy black holes is always satisfied on account of the positive mass ($ M>0 $ ) of black holes and the negative cosmological constant ($ \Lambda<0 $ ).According to the new metric ansatz of hairy black holes (21) and the seed solutions (16), the quasi-Einstein field equations (13) for
$ \theta_{\mu}^{\; \nu} $ become$ \begin{aligned}[b] \kappa ^2 \theta _0^{\; 0} =&\Lambda-\frac{1}{r^2}+{\rm e}^{\alpha g(r)}\left(\Lambda-\frac{1}{r^2} +\alpha \left(\frac{1}{r}-\frac{2M}{r^2}-\frac{\Lambda r}{3}\right)\right)g(r),\\ \theta _1^{\; 1}=&\theta _0^{\; 0},\\ \kappa ^2 \theta _2^{\; 2}=&\Lambda+{\rm e}^{\alpha g(r)}\Big[\alpha\left(\frac{1}{2}-\frac{M}{r} -\frac{\Lambda r^2}{6}\right)\left(\alpha g'(r)^2+g''(r)\right)\\ &+\alpha\left(\Lambda r-\frac{1}{r}\right)g'(r)-\Lambda\Big]. \\[-5pt] \end{aligned} $

(23) It is clear that the deformation metric
$ g(r) $ is only determined by the additional source$ \theta _\mu^{\; \nu} $ . We can then further derive the quasi-Einstein system to obtain the solutions of hairy black holes by assuming that the source$ \theta _\mu^{\; \nu} $ satisfies some physically motivated equations of state. We first consider the simple case of isotropic pressure,$ \begin{eqnarray} \theta _0^{\; 0}=\theta _1^{\; 1}=\theta _2^{\; 2}. \end{eqnarray} $

(24) Eq. (23) then yields a differential equation,
$ \begin{eqnarray} 6(h(r)-1)+4(r^3\Lambda-3M)h'(r)+(6 M r+r^4\Lambda-3 r^2)h''(r)=0, \end{eqnarray} $

(25) where the function
$ {{\rm{h}}}(r) $ denotes${{\rm e}^{\alpha g(r)}}$ . Then, we have$ \begin{eqnarray} {{\rm{h}}}(r)={{\rm e}^{\alpha g(r)}}=1+\frac{C_1+ r^3 C_2}{{6M-3r + {r^3}\Lambda }}, \end{eqnarray} $

(26) where
$ C_1 $ and$ C_2 $ are integration constants. Finally, we obtain the solution of the hairy black hole,$ \begin{eqnarray} {{\rm e}^\nu}={{\rm e}^{-\lambda }}=1-\frac{2M}{r}-\frac{{{r^2}\Lambda}}{3}-\frac{{{C_1}}}{3r} -\frac{C_2 r^2}{9}. \end{eqnarray} $

(27) Note that it takes the same form as the solution of a Schwarzchild AdS black hole by adopting the redefinition of the asymptotic mass
$ M\rightarrow M=M+C_1/6 $ and cosmological constant$ \Lambda\rightarrow \Lambda=\Lambda+C_2/3 $ .Moreover, considering the previous seed source
$ T_{\mu\nu}=0 $ , the effective density, effective radial pressure, and effective tangential pressure are obtained as$ \begin{eqnarray} \tilde{\rho}=-\theta_0^{\; 0}=\frac{C_2}{3},\quad \tilde{p}_r=\tilde{p}_{_\bot}=-\frac{C_2}{3}. \end{eqnarray} $

(28) This implies that it is an exact isotropic fluid.
Now, let us consider the linear equation of state and assume that the components of the source
$ \theta _\mu^{\; \nu} $ satisfy$ \begin{eqnarray} \theta _0^{\; 0}= a\theta _1^{\; 1} + b\theta _2^{\; 2}, \end{eqnarray} $

(29) where a and b are arbitrary constants. From the quasi-Einstein field equations (Eq. (23)), we can easily obtain
$ \begin{aligned}[b] &6[a-1-(a+b-1){r^2}\Lambda]+6[1-a+(a+b-1){r^2}\Lambda ]h(r)\\ &+2[6(a-1)M-3(a+b-1)r+(a+3b-1){r^3}\Lambda]h'(r) \\ &+br(6M-3r+{r^3}\Lambda )h''(r)=0. \end{aligned} $

(30) Then, the solution can be written as
$ \begin{eqnarray} {{\rm e}^{\alpha g(r)}}=h(r) = \frac{{-3r + {r^3}\Lambda + {C_1} + \dfrac{{b{r^{\frac{{2 - 2a + b}}{b}}}{C_2}}}{{2 - 2a + b}}}}{{6M-3r + {r^3}\Lambda }}. \end{eqnarray} $

(31) Here,
$ C_1 $ and$ C_2 $ are constants with dimensions of length.Considering the line element of the hairy black hole (21), we obtain the solution of the hairy black hole,
$ \begin{eqnarray} {{\rm e}^\nu}={{\rm e}^{-\lambda }}=1-\frac{{{r^2}\Lambda}}{3}-\frac{{{C_1}}}{3r} -\frac{{b{r^{\frac{{2-2a}}{b}}}{C_2}}}{6-6a+3b}. \end{eqnarray} $

(32) Because
$ T_{\mu\nu}=0 $ was defined previously, the corresponding components of$ \theta_{\mu\nu} $ are obtained as the effective density$ \begin{eqnarray} \tilde{\rho }=-\theta _0^{\; 0} = - \frac{1}{3}{C_2}{r^{ - \frac{{2\left( { - 1 + a + b} \right)}}{b}}}, \end{eqnarray} $

(33) effective radial pressure
$ \begin{eqnarray} \tilde{p}_r=\theta _1^{\; 1}=\theta _0^{\; 0} = - \rho, \end{eqnarray} $

(34) and effective tangential pressure
$ \begin{eqnarray} \tilde{p}_{_\bot}=\theta _2^{\; 2}=-\frac{{\left({-1 + a}\right)C_2{r^{-\frac{{2\left({-1+a+b}\right)}}{b}}}}}{3b}. \end{eqnarray} $

(35) The anisotropy is thus given by
$ \begin{eqnarray} \Pi=\tilde{p}_r-\tilde{p}_{_\bot}=-\frac{{\left({-1+a+b}\right)C_2{r^{-\frac{{2\left({-1+a+b}\right)}}{b}}}}}{3b} \ne 0. \end{eqnarray} $

(36) If setting
$ n=\dfrac{{2-2a}}{b} $ and$ C_1=6M $ , this solution (36) reduces to the Kiselev-AdS black hole with quintessence. In addition, we check several other scenarios when the additional source$ \theta_{\mu}^{\; \mu} $ satisfies the conformal equations of state$ \theta_{\mu}^{\; \mu}=0 $ or the polytropic$ \alpha\theta_{1}^{\; 1}=K\left(\alpha\theta_{0}^{\; 0}\right)^\Gamma $ . However, these hairy black hole solutions have already been studied in Refs. [57–60].It is worth noting that the energy conditions are generally considered as sensible guidelines to avoid classically unphysical configurations. In Ref. [45], energy conditions are usually imposed on the energy-momentum tensor to avoid exotic matter sources in the context of a wide class of spacetime theories. In the next sections, we discuss black holes in asymptotic AdS spacetime when energy conditions are imposed on the source
$ \theta_{\mu\nu} $ . -
In energy condition theory, there is an important condition known as the SEC, which arises from proving the singularity theorem. It can be written as follows [44]:
$ \begin{eqnarray} \tilde{\rho} + \tilde{p}_r + 2\tilde{p}_{_\bot } \ge 0, \end{eqnarray} $

(37) $ \begin{eqnarray} \tilde{\rho} + \tilde{p}_r \ge 0, \end{eqnarray} $

(38) $ \begin{eqnarray} \tilde{\rho} + \tilde{p}_{_\bot } \ge 0. \end{eqnarray} $

(39) Considering the choice of metric ansatz,
$ {{\rm e}^{\nu}} = {{\rm e}^{-\lambda}} $ (18), Eqs. (37)–(39) become$ \begin{eqnarray} \theta _2^{\; 2} \ge 0, \end{eqnarray} $

(40) $ \begin{eqnarray} \theta _0^{\; 0} \le \theta _2^{\; 2}. \end{eqnarray} $

(41) According to the quasi-Einstein field equations for the additional source
$ \theta_{\mu}^{\; \nu} $ (Eq. (23)), conditions (40) and (41) lead to the inequalities$ \begin{aligned}[b] {G_1}(r)\equiv&6h'(r)-6Mh''(r)+3rh''(r)-\Lambda\Big(-6r+6rh(r)\\ &+6{r^2}h'(r)+{r^3}h''(r)\Big)\ge 0 , \end{aligned} $

(42) $ \begin{aligned}[b] {G_2}(r)\equiv&6-6h(r)+12Mh'(r)-6Mrh''(r)\\ &+3{r^2}h''(r)-\Lambda(4{r^3}h'(r)+{r^4}h''(r))\ge 0 , \end{aligned} $

(43) where the function
$h(r)$ denotes${{\rm e}^{\alpha g(r)}}$ .Let us first compute the corresponding boundary solution of the above two expressions. From
$ {G_1(r)=0} $ , we can easily obtain$ \begin{eqnarray} h(r) = \frac{{{r^3}\Lambda + C_{11}+ r C_{12} }}{{6M-3r+{r^3}\Lambda}}. \end{eqnarray} $

(44) Then, we can obtain the black hole solution from metric (21),
$ \begin{eqnarray} {{{\rm{e}}}^\nu } = {{\rm e}^{ - \lambda }} =-\frac{{{r^2}\Lambda }}{3}-\frac{1}{3} \left( \frac{{{C_{11}}}}{r} + {C_{12}} \right). \end{eqnarray} $

(45) For the inequality of
$ {G_2(r)} $ (43), the corresponding boundary solution can also be obtained from$ {G_2(r)=0} $ $ \begin{eqnarray} h(r) = 1 + \frac{{{C_{21}} + \frac{1}{3}{r^3}{C_{22}}}}{{6M-3r+{r^3}\Lambda }}, \end{eqnarray} $

(46) and
$ \begin{eqnarray} {{{\rm{e}}}^\nu } = {{\rm e}^{ - \lambda }} = 1 - \frac{{2M}}{r}-\frac{{{r^2}\Lambda }}{3} -\frac{{{C_{21}}}}{3r}-\frac{1}{9} {r^2}{C_{22}}. \end{eqnarray} $

(47) To agree on Eqs. (45) and (47), we can set
$ C_{11}=C_{21}+6M $ ,$ C_{12}=-3 $ , and$ C_{22}=0 $ . The metric then becomes$ \begin{eqnarray} {{{\rm{e}}}^\nu}={{\rm e}^{-\lambda }}=1 - \frac{{2M}}{r}-\frac{{{r^2}\Lambda }}{3}-\frac{{{C_{21}}}}{3r}. \end{eqnarray} $

(48) This is actually the Schwarzschild AdS black hole. In other words, the black hole solution derived from the boundary conditions is mediocre.
Now let us look for a nontrivial solution of the function
$ h(r) $ . From Eq. (42), we can choose a simple model, i.e.,$ \begin{eqnarray} G_1(r)\equiv{G_\alpha (r)}=\frac{\alpha }{A_1}\left(r-2M-\frac{{{r^3}\Lambda}}{3}\right){{\rm e}^{\frac{{-r}}{B_1}}}, \end{eqnarray} $

(49) where
$ A_1 $ and$ B_1 $ are pending parameters. The function$ G_{\alpha} (r) $ clearly satisfies$ {G_1}(r) = 0 $ near the horizon$ r = r_h $ and at infinity$ r \to \infty $ and also meets$ \begin{eqnarray} {G_1}(r)>0, \quad r_h<r<\infty, \end{eqnarray} $

(50) when
$ A_1>0 $ . After substituting Eq. (49) into Eq. (42), we get$ \begin{aligned}[b] h(r)=&\frac{1}{3A_1(6M-3r+{r^3}\Lambda )}\Big({B_1^2\alpha {\rm e}^{-\frac{r}{B_1}}}\Big(24{B_1^3}\Lambda+6M-3r+{r^3}\Lambda\\ & +18{B_1^2}r+6B_1({r^2}\Lambda-1)\Big)+3{A_1}({r^3}\Lambda+{C_1}+r{C_2})\Big). \end{aligned} $

(51) Then, the solution of the hairy black hole is obtained as
$ \begin{aligned}[b] {\rm e}^\nu={{\rm e}^{-\lambda}}=&-\frac{{{r^2}\Lambda}}{3}-\frac{{{C_1}+r{C_2}}}{{3r}} +{{\rm e}^{-\frac{r}{B_1}}}\alpha\left(\frac{{B_1^2}(-2M+2B_1+r)}{3{A_1}r}\right.\\ &\left.- \frac{{(24{B_1^5} + 18{B_1^4}r + 6{B_1^3}{r^2} + {B_1^2}{r^3})\Lambda }}{{9{A_1}r}}\right) . \\[-6pt]\end{aligned} $

(52) If setting
$ A_1=B_1^2 $ , Eq. (52) reduces to$ \begin{aligned}[b] {{\rm e}^\nu }={{\rm e}^{-\lambda}}=&{{\rm e}^{-\frac{r}{B_1}}}\alpha\Bigg(\frac{-2M+2B_1+r}{3r}\\&-\frac{{(24{B_1^3}+18{B_1^2}r+6B_1{r^2}+{r^3})\Lambda }}{{9r}}\Bigg)\\ \end{aligned} $

$ \begin{aligned}[b] \quad\quad-\frac{{{r^2}\Lambda}}{3}-\frac{1}{3}\left(\frac{{{C_1}}}{r}+{C_2}\right) . \end{aligned} $

(53) Furthermore, if we continue to set
$ B_1=M $ ,$ C_1=6M $ , and$ C_2=-3 $ , Eq. (53) reduces to$ \begin{aligned}[b] {{\rm e}^\nu}={{\rm e}^{-\lambda }}=&1-\frac{2M}{r}-\frac{1}{3}\alpha\Bigg(\frac{(24M^3+18M^2r+6Mr^2+r^3)\Lambda}{3r} \\ &+1\Bigg){\rm e}^{-\frac{r}{M}}-\frac{r^2\Lambda }{3}. \end{aligned} $

(54) In addition, we must check that the function
$ h(r) $ satisfies the inequality of Eq. (43). By substituting Eq. (51) into Eq. (43), we can get$ \begin{aligned}[b] \Delta=&-6{M^2}+3{r^2}-(12{M^4} + 12{M^3}r + 6{M^2}{r^2}\\& + 2M{r^3} + {r^4})\Lambda\ge 0. \end{aligned} $

(55) In AdS space-time (
$ \Lambda<0 $ ), Δ is a monotonically increasing function of r. Therefore, as long as the value of the function is positive at the horizon, it must also be positive outside the horizon. Because the analytic solution of the event horizon (22) of the black hole is complicated, we use the numerical simulation method to analyze the value of Δ. The behavior of this function at the event horizon of the black hole is plotted in Fig. 1. The figures show that no matter how the values of Λ and M change, Δ is always positive. Therefore, the inequality of Eq. (43) is always true at$ r \ge r_h $ .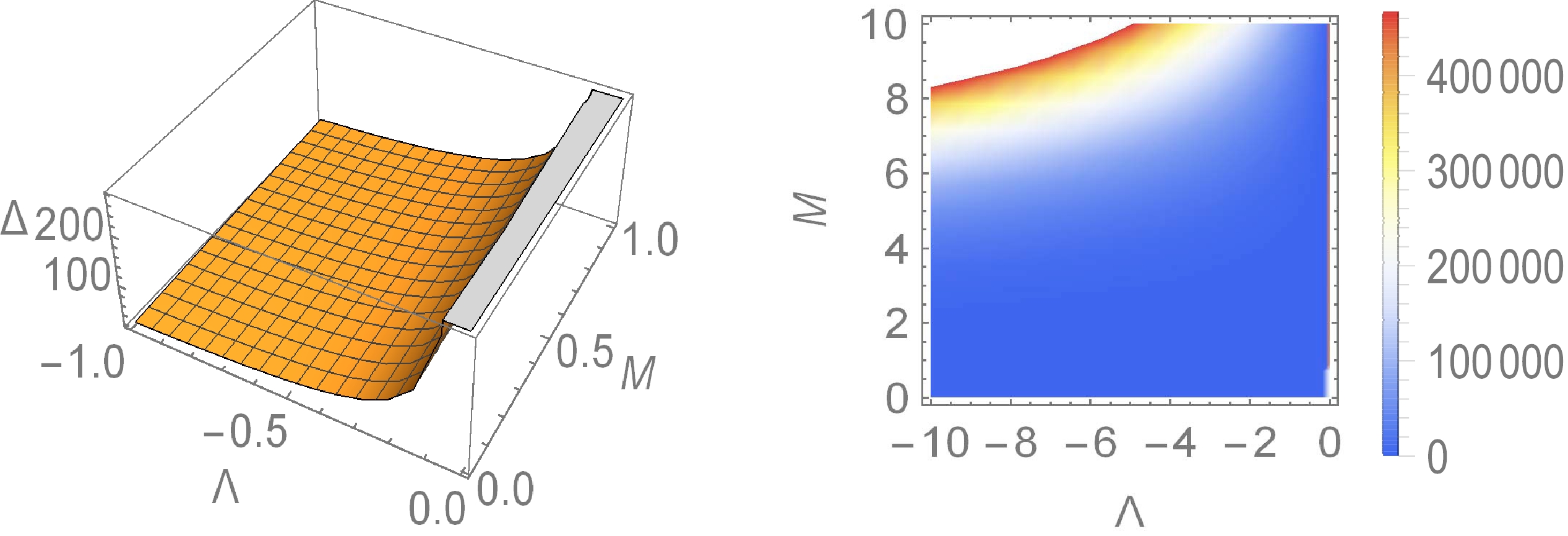
Figure 1. (color online) Value of Δ at the horizon. The left graph is a surface diagram of Δ with respect to Λ and M, where the corresponding values of Λ and M are
$ -1 $ to$ 0 $ and$ 0 $ to$ 1 $ , respectively. The right graph is a density map of Δ, and the value ranges of Λ and M are$ -10 $ to$ 0 $ and$ 0 $ to$ 10 $ , respectively.For the line element in Eq. (54), we can also find its effective density,
$ \begin{aligned}[b] -\tilde{\rho} = \theta _0^{\; 0} = \tilde{p}_r = & \frac{{{{{\rm{e}}}^{ - \frac{r}{M}}}\alpha }}{{9M{r^2}}}(3M-3r+6{M^3}\Lambda+6{M^2}r\Lambda \\+& 3Mr^2\Lambda + r^3\Lambda ), \end{aligned} $

(56) and the effective tangential pressure
$ \begin{eqnarray} \tilde{p}_{_ \bot } = \theta _2^{\; 2}= \frac{{{{{\rm{e}}}^{ - \frac{r}{M}}}\alpha \left( { - 6M + 3r - {r^3}\Lambda } \right)}}{{18{M^2}r}}. \end{eqnarray} $

(57) Note that when
$ \Lambda\to 0 $ , Eqs. (54), (56), and (57) degenerate into the results in Ref. [29]. -
Now let us consider another condition. The DEC requires that the four-momentum density measured by any instantaneous viewer is a time-like or light-like vector. Its physical interpretation is that the energy flow rate of the material field is less than or equal to the speed of light, which is equivalent to [44]
$ \begin{eqnarray}\tilde \rho \ge \left| {{{\tilde p}_r}} \right|, \end{eqnarray} $

(58) $ \begin{eqnarray} \tilde \rho \ge \left| {{{\tilde p}_t}} \right|, \end{eqnarray} $

(59) in the system of Eq. (21). These two inequalities reduce to
$ \begin{aligned}[b]& -\theta _0^{\; 0} - \theta _2^{\; 2} \ge 0, \quad -\theta _0^{\; 0} + \theta _2^{\; 2} \ge 0, \end{aligned} $

(60) which yield the differential inequalities
$ \begin{aligned}[b] {H_{{\rm{1}}}}(r) = &2 - 2h(r) + \left( {4M - 4r} \right)h'(r) + \left( {2Mr - {r^2}} \right){h^{\prime \prime }}(r)\\ &+ \Lambda \left( {4{r^2} - 4{r^2}h(r) + \frac{8}{3}{r^3}h'(r) + \frac{1}{3}{r^4}{h^{\prime \prime }}(r)} \right)\ge 0, \end{aligned} $

(61) $ \begin{aligned}[b] {H_{{\rm{2}}}}(r) = & 2 - 2h(r) + 4Mh'(r) + \left( { - 2Mr + {r^2}} \right){h^{\prime \prime }}(r)\\ & - \Lambda \left( {\frac{4}{3}{r^3}h'(r) + \frac{1}{3}{r^4}{h^{\prime \prime }}(r)} \right)\ge 0, \end{aligned} $

(62) respectively, for which we use Eq. (23) again. Now, choosing the same model as for the SEC (Eq. (49)),
$ \begin{eqnarray} H_1(r)\equiv{H_\alpha(r)}=\frac{\alpha }{A_1}\left(r-2M-\frac{{{r^3}\Lambda }}{3}\right){{\rm e}^{\frac{{-r}}{B_1}}}, \end{eqnarray} $

(63) we can solve Eq. (61) and obtain
$ \begin{aligned}[b] h(r)=&\frac{{\rm{e}}^{-\frac{r}{{{B_1}}}}}{{r({6M-3r+{r^3}\Lambda }){A_1}}}\Big((-\alpha B_1^2(6M-3r+{r^3}\Lambda\\&+6(-1+{r^2}\Lambda){B_1}+18r\Lambda B_1^2+24\Lambda B_1^3))\\&+(-3{r^2}+{r^4}\Lambda+{C_1}+r{C_2}){A_1}\Big). \end{aligned} $

(64) Similarly, let us take the same approach as Eq. (53), that is,
$ A = B^2 $ ,$ \begin{aligned}[b] h(r)=&\frac{{\rm{e}}^{-\frac{r}{B_1}}}{r({6M-3r+{r^3}\Lambda })}\Big(-\alpha(6M-3r+{r^3}\Lambda\\&+6({-1+{r^2}\Lambda}){B_1}+18r\Lambda B_1^2\\ & + 24\Lambda B_1^3) + (-3{r^2} + {r^4}\Lambda + C_1 + r C_2 )\Big). \end{aligned} $

(65) Furthermore, setting
$ B = M $ ,$ C_1 = - 3 Q^2 $ , and$ C_2 =6M $ , the metric can finally be written as$ \begin{aligned}[b] {\rm e}^\nu = {\rm e}^{ - \lambda } = & \alpha {{{\rm{e}}}^{ - \frac{r}{M}}}\left( { - \frac{1}{r} - \frac{{\left( { - 24{M^3} - 18{M^2}r - 6M{r^2} - {r^3}} \right)\Lambda }}{{3{r^2}}}} \right)\\& + 1 - \frac{{2M}}{r} + \frac{{{Q^2}}}{{{r^2}}} - \frac{{{r^2}\Lambda }}{3}. \end{aligned} $

(66) As with the SEC, we must check whether
$ h(r) $ (65) satisfies the other inequality for the DEC (62), and we get the inequality$ \begin{aligned}[b] \frac{{4{Q^2}}}{{{r^2}}} &- {{{\rm{e}}}^{ - \frac{r}{M}}}\alpha \frac{1}{{3{r^2}}}\Big( \frac{{6{r^2}}}{M} + \frac{{3{r^3}}}{{{M^2}}} - ( 96{M^3} + 96{M^2}r \\ & + 48M{r^2} + 16{r^3} + \frac{{4{r^4}}}{M} + \frac{{r^5}}{{M^2}} )\Lambda \Big) \ge 0. \end{aligned} $

(67) The inequality of Eq. (67) is not guaranteed to be satisfied at any point. The necessary condition is that
$ \begin{aligned}[b] \frac{{12{Q^2}}}{\alpha }&\ge \frac{{6{r^2}}}{M}+\frac{{3{r^3}}}{{{M^2}}}-\Bigg( 96{M^3} + 96{M^2}r + 48M{r^2}\\& + 16{r^3} + \frac{{4{r^4}}}{M} + \frac{{{r^5}}}{{{M^2}}} \Bigg)\Lambda . \end{aligned} $

(68) On the premise that the above condition is satisfied, if we treat Q as the electric charge, it is clear that this black hole is a deformation of a charged black hole in asymptotic AdS spacetime. Moreover, the effective density can be written as
$ \begin{aligned}[b] \tilde{p}_r = \theta _1^{\; 1} = & \frac{1}{{{r^4}}}\Bigg( - (24{{{\rm{e}}}^{ - \frac{r}{M}}}{M^3}\alpha + 24{{{\rm{e}}}^{ - \frac{r}{M}}}{M^2}r\alpha + 12{{{\rm{e}}}^{ - \frac{r}{M}}}M{r^2}\alpha \\& + 4{{{\rm{e}}}^{ - \frac{r}{M}}}{r^3}\alpha + \frac{{{{{\rm{e}}}^{ - \frac{r}{M}}}{r^4}\alpha }}{M}\Bigg)\Lambda + \frac{{{{{\rm{e}}}^{ - \frac{r}{M}}}{r^2}\alpha }}{M} - {Q^2}\Bigg), \end{aligned} $

(69) and the effective tangential pressure is
$ \begin{aligned}[b] \tilde{p}_{_\bot} =& \theta_2^{\; 2}=\frac{1}{{{r^4}}}\Bigg(\frac{1}{6}(48{{{\rm{e}}}^{ - \frac{r}{M}}}{M^3}\alpha + 48{{{\rm{e}}}^{ - \frac{r}{M}}}{M^2}r\alpha \\& + 24{{{\rm{e}}}^{ - \frac{r}{M}}}M{r^2}\alpha + 8{{{\rm{e}}}^{ - \frac{r}{M}}}{r^3}\alpha \\& + \frac{{2{{{\rm{e}}}^{ - \frac{r}{M}}}{r^4}\alpha }}{M} + \frac{{{{{\rm{e}}}^{ - \frac{r}{M}}}{r^5}\alpha }}{{{M^2}}}\Lambda \Bigg) + {Q^2} - \frac{{{{{\rm{e}}}^{ - \frac{r}{M}}}{r^3}\alpha }}{{2{M^2}}}\Bigg). \end{aligned} $

(70) Then, we can obtain
$ \begin{aligned}[b] \tilde{p}_r - \tilde{p}_{_ \bot } =&\frac{1}{{r^4}}\Bigg(\frac{{{{{\rm{e}}}^{ - \frac{r}{M}}}{r^2}\left( {2M + r} \right)\alpha }}{{2{M^2}}} - 2{Q^2} - \frac{1}{6}\Bigg(48{{{\rm{e}}}^{ - \frac{r}{M}}}{M^2}\left( {2M + r} \right)\alpha \\& + 24{{{\rm{e}}}^{ - \frac{r}{M}}}Mr\left( {2M + r} \right)\alpha + 12{{{\rm{e}}}^{ - \frac{r}{M}}}{r^2}\left( {2M + r} \right)\alpha \\& + \frac{{2{{{\rm{e}}}^{ - \frac{r}{M}}}{r^3}\left( {2M + r} \right)\alpha }}{M} + \frac{{{{{\rm{e}}}^{ - \frac{r}{M}}}{r^4}\left( {2M + r} \right)\alpha }}{{{M^2}}}\Bigg)\Lambda \Bigg). \end{aligned} $

(71) Therefore, the source
$ \theta_{\mu\nu} $ under the DEC is also anisotropic. -
For two non-interacting gravitational sources in the gravitational system, we adopt the gravitational decoupling approach via EGD to present how the Schwarzschild AdS black hole is modified when the vacuum is filled by the new fields
$ \theta_{\mu\nu} $ . The EGD technique is devised for describing deformations of known solutions of GR induced by adding extra sources. We first consider several scenarios, where the source term$ \theta_{\mu\nu} $ satisfies the case of isotropic pressure or the linear equation of state. Then, we obtain the corresponding solutions of hairy black holes by deriving quasi-Einstein field equations for an additional source$ \theta _\mu^{\; \nu} $ . However, these black hole solutions are mediocre and have already been extensively studied in many papers.The SEC and DEC are adopted as constraint conditions for the construction of hairy black holes because the energy conditions are generally considered as sensible guidelines to avoid exotic matter sources in the context of a wide class of spacetime theories. We find two new families of hairy black holes in the asymptotic AdS spacetime. In addition, if we regard the black hole spacetime as a fluid system, the fluid under each conditions is anisotropic.
Finally, let us comment on some concrete prospects of this study. Currently, black hole thermodynamics in the presence of a negative cosmological constant is becoming even more appealing because they allow a gauge duality description through thermal field theory via the AdS/CFT correspondence [61]. The gravitational decoupling method has been applied to discuss the thermodynamics of spherically symmetric black holes in asymptotically flat spacetime [62], where the first law of thermodynamics was decoupled into two sectors: the standard first law of thermodynamics and the quasi first law of thermodynamics. Therefore, it is interesting to investigate the thermodynamics and phase transitions of hairy black holes in asymptotically AdS spacetime.
On the other hand, entanglement entropy is a versatile tool and may provide us with new insights into a rich variety of physical phenomena, ranging from the confining phase of large-N gauge theories [63] to topological phases in condensed matter systems [64] and tachyon condensation [65] in light of the AdS/CFT correspondence. Ryu and Takayanagi [66, 67] proposed a holographic description of entanglement entropy in quantum (conformal) field theories via the AdS
$ _{d+2} $ /CFT$ _{d+1} $ correspondence and computed entanglement entropy at finite temperature employing AdS black hole geometry. It is worth discussing HEE for the hairy AdS black holes obtained using the EGD approach. In addition, the stability and quasinormal modes (QNMs) of hairy black holes caused by gravitational decoupling under various field perturbations have been investigated in Refs. [68, 69]. QNMs play a fundamental role in characterizing gravitational wave signals detected by LIGO and VIRGO [70, 71]. We will investigate the stability and QNMs of hairy AdS black holes in future studies. The final results could be expected to provide some direction for observing hairy black holes caused by gravitational decoupling in future experiments. -
We thank Xiao-Mei Kuang and Sheng-Yuan Li for helpful discussions.
Gravitational decoupling for hairy black holes in asymptotic AdS spacetimes
- Received Date: 2022-08-16
- Available Online: 2023-01-15
Abstract: In this study, the gravitational decoupling approach via extended geometric deformation is utilized to generate analytical black hole solutions owing to its simplicity and effectiveness. Considering the external fields surrounding Schwarzschild AdS black holes, we derive hairy black hole solutions in asymptotic AdS spacetime, satisfying the strong and dominant energy conditions. Moreover, we find that if the black hole spacetime is a fluid system, the fluid under each of these conditions is anisotropic.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF













 DownLoad:
DownLoad: