-
The research undertaken by Hawking and Bekenstein laid a firm foundation for the study of black hole thermodynamics. Notably, phase transition and critical phenomena are important characteristics of usual thermodynamic systems. Therefore, one may naturally consider the corresponding properties of black holes. Davies found that the heat capacities of some black holes diverge at certain points according to the Ehrenfest classification, which is a feature associated with a second-order phase transition [1–3]. These divergent points of heat capacities are now known as Davies points.
In general, the heat capacities of black holes can be expressed in the following form:
$ \begin{array}{*{20}{l}} C_X=\left.T\displaystyle \frac{\partial S}{\partial T}\right|_X=\left.T\displaystyle \frac{\partial S/\partial r_h}{\partial T/\partial r_h}\right|_X, \end{array} $

(1) where X represents a certain thermodynamic quantity, and
$ r_h $ is the radius of the event horizon. Therefore, the divergent heat capacity is equivalent to$ \partial T/\partial r_h=0 $ . According to this result, Davies points can be further classified into two types. For the first type, the Davies points correspond to extreme points of temperature, where the temperatures may have maximal or minimal values, whereas for the second type, a Davies point lies at the infection point of temperature, which is also the critical point of black holes.So far, the properties of various black holes near critical points have been studied extensively. On the basis of AdS/CFT, the phase structures of charged AdS black holes have been reported in Ref. [4, 5]. The thermodynamic stability and phase transition of several charged black holes have been analyzed by placing them in a finite box [6–8]. Using thermodynamic geometry, the thermodynamic curvature can be obtained, and based on this, one can ascertain the phase transition of black holes near the critical points [9–14]. Inspired by the idea of [15] treating the cosmological constant as pressure and its conjugate quantity as the thermodynamic volume, an extended phase space can be constructed. Analogous to a liquid–gas system, the
$ P-V $ criticality and phase structures of several AdS black holes have been analyzed [16–28]. In all the related studies, the authors concluded that the phase transition occurring at the critical point is of the second order.Hilfer proposed a type of generalized Ehrenfest classification that classified the phase transition according to the continuity of the fractional derivatives of free energy [29, 30]. Inspired by Hilfer's research, we reanalyze the phase transition of the RN-AdS black hole using the generalized Ehrenfest classification and determine that the order of phase transition at the critical point should be
$ 4/3 $ and not$ 2 $ [31]. At present, the generalized Ehrenfest classification is primarily used to deal with the phase transition at critical (Davies) points; hence, these do not affect the original phase structure of black holes. Chabab and Iraoui further studied AdS black holes in higher dimensions and without spherical symmetry and discovered that the order of fractional phase transition can be dependent on the geometry of spacetime [32, 33].Notably, both types of Davies points correspond to a divergent heat capacity. In other words, we cannot discriminate between Davies points of the two types based on the heat capacity. By employing fractional derivatives, we can generalize the Ehrenfest classification to include phase transitions of the fractional order. This finer-grained classification may reflect richer phase structures of thermodynamic systems. Here, we consider the RN-AdS black hole as an example to analyze the phase structure at its Davies points. Considering that the temperatures of the RN-AdS black hole exhibit different behaviors at the two types of Davies points, we expect to observe different phase structures. Therefore, we consider whether the phase structures at the two types of Davies points can be distinguished using this generalized Ehrenfest classification. We also aim to understand whether the order of phase transition at the critical point is the same in the extended phase space and non-extended phase space.
The paper is organized as follows: We first briefly review the RN-AdS black hole and describe several thermodynamic quantities in Section I. In Section II, we analyze the phase structures at the first type of Davies point, referring to two Davies points on the left-hand side and right-hand side. In Section III, we discuss the phase structures of the RN-AdS black hole at the critical point. Finally, we summarize our results and discuss possible future studies.
-
The RN-AdS black hole represents a static spherically symmetric spacetime, and its line element is
$ \begin{array}{*{20}{l}} {\rm d}s^2=-f(r){\rm d}t^2+f^{-1}(r){\rm d}r^2+r^2{\rm d}\Omega^2. \end{array} $

(2) The metric function is
$ \begin{array}{*{20}{l}} f(r)=1-\displaystyle \frac{ {2M}}{ {r}}+\frac{ {Q^2}}{ {r^2}}-\frac{ {\Lambda r^2}}{ {3}}, \end{array} $

(3) where the parameters M, Q, and
$ \Lambda=-3/L^2 $ denote the black hole mass, electric charge, and cosmological constant, respectively.Using
$ f(r_h)=0 $ , we can determine the position of the event horizon. We do not consider the extended phase space in this paper. The first law of thermodynamics does not include the thermodynamic volume and pressure and is described as follows:$ \begin{array}{*{20}{l}} {\rm d}M=T{\rm d}S+\phi {\rm d}Q. \end{array} $

(4) In this case, M is the internal energy. Through the Legendre transformation, we can obtain the Helmholtz free energy
$ F=M-TS $ , which satisfies the following differential relation:$ \begin{array}{*{20}{l}} {\rm d}F=-S{\rm d}T+\phi {\rm d}Q. \end{array} $

(5) Thus,
$ F=F(T,Q) $ is a thermodynamic characteristic function, based on which we can derive all other thermodynamic quantities. We consider a canonical ensemble and assume$ (T,Q) $ as the thermodynamic variables.The temperature of the RN-AdS black hole is
$ \begin{array}{*{20}{l}} T=\displaystyle \frac{L^2 r_h^2+3 r_h^4-L^2 Q^2}{4 \pi L^2 r_h^3}. \end{array} $

(6) The entropy satisfies the area law, that is,
$ S=A/4=\pi r_h^2 $ , and the electric potential at the horizon measured at infinity is$ \phi=Q/r_h $ .The heat capacity at constant charge is defined as
$ \begin{aligned}[b]C_Q&= \displaystyle \left.\frac{ {\partial M}}{ {\partial T}}\right|_Q=T\left.\frac{ {\partial S}}{ {\partial T}}\right|_Q=T\left.\frac{ {\partial S/\partial r_h}}{ {\partial T/\partial r_h}}\right|_Q\\&=\frac{2 \pi r_h^2 \left(L^2 r_h^2+3 r_h^4-L^2 Q^2\right)}{-L^2 r_h^2+3 r_h^4+3 L^2 Q^2}. \end{aligned} $

(7) Using the denominator, we can derive the position of the Davies points as follows:
$ \begin{array}{*{20}{l}} r_h=\displaystyle\sqrt{\frac{L^2}{6}\pm \frac{1}{6} \sqrt{L^4-36 L^2 Q^2}}. \end{array} $

(8) When
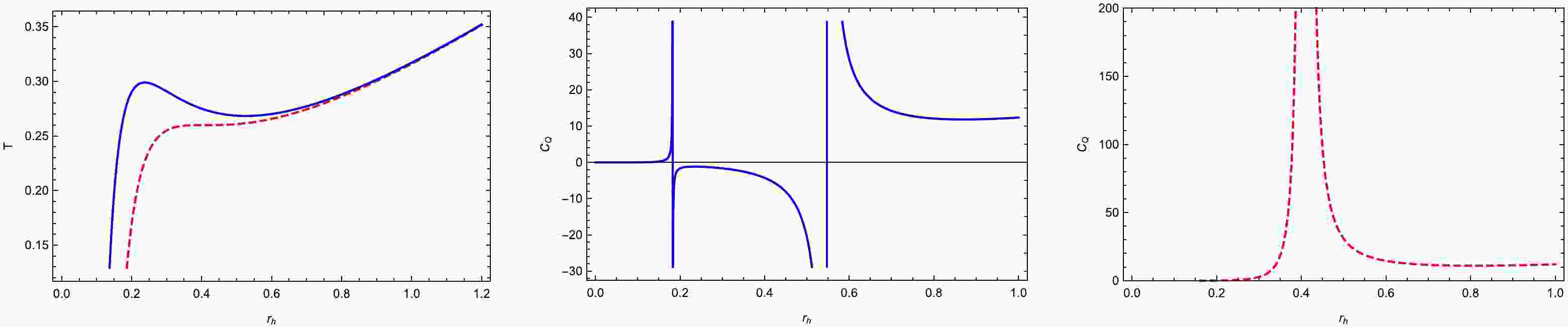
$ L>6Q $ , two different roots, which correspond to the first type of Davies point, can be observed, whereas when$ L=6Q $ , the two roots coincide, which denotes the critical point and belongs to the second type of Davies point.As depicted in Fig. 1, two Davies points of the first type can be noted on the blue curve. Each Davies point separates the temperature into two branches. The heat capacity has opposite signs on the two branches. As the two Davies points coincide on the red curve, it transforms into a critical point. We also depict the heat capacity in this figure. At the two types of Davies points, the heat capacities both diverge. According to the standard Ehrenfest classification, the phase transitions are both of the second order. In the following sections, we attempt to distinguish between these phase structures using our generalized Ehrenfest classification.
-
According to Eq. (6), for smaller
$ r_h $ , the temperature of the RN-AdS black hole is dominated by the electric charge Q, rather than L, whereas for larger$ r_h $ , the temperature is dominated by L. Therefore, the behavior of temperature near the left Davies point is different from that near the right Davies point. Thus, we should analyze the phase structures at the two Davies points separately.For simplicity, we set
$ L=1 $ in this section.The left Davies point lies at
$ \begin{aligned}[b] T_c=&\displaystyle-\frac{\sqrt{\displaystyle\frac{3}{2}} \left(12 Q^2+\sqrt{1-36 Q^2}-1\right)}{\pi \left(1-\sqrt{1-36 Q^2}\right)^{3/2}}, \\ r_c=&\frac{\sqrt{1-\sqrt{1-36 Q^2}}}{\sqrt{6}}. \end{aligned}$

(9) We define several dimensionless quantities as
$ \begin{array}{*{20}{l}} T=T_c(1+t), \quad r_h=r_c(1+\rho). \end{array} $

(10) In this case, the Davies point lies at
$ t=\rho=0 $ . In this manner, we can perform a series expansion near the Davies point. Because this left Davies point corresponds to the maximal value of temperature,$t\leqslant 0$ at all times.After setting
$ Q=1/8 $ , we can obtain a dimensionless equation of state from Eq. (6):$ \begin{aligned}[b] & 0.057 \rho ^4-\rho ^3 (0.302 t+0.0729)\\ -&\rho ^2 (0.906 t+0.224)-0.906 \rho t-0.302 t=0. \end{aligned} $

(11) Near the Davies point, we solve Eq. (11) to obtain a series solution of ρ as a function of t:
$ \begin{aligned}[b] \rho=&-1.162 (-t)^{1/2}-1.804 t -3.270 (- t)^{3/2}+6.633 t^2 \\&-14.616 (-t)^{5/2} +O(t^3), {} \\ \rho=&-1.162 (-t)^{1/2}-1.804 t +3.270 (- t)^{3/2}+6.633 t^2 \\&+14.616 (-t)^{5/2} +O(t^3). \end{aligned} $

(12) The two series solutions correspond to the two branches on both sides of the Davies point. The most notable feature of this result is that it contains terms with fractional exponents.
According to the definition above, we can obtain the free energy
$ \begin{array}{*{20}{l}} \displaystyle F=\frac{(\rho +1)^2 \left(\rho ^2+2 \rho -2\right) \left(\sqrt{1-36 Q^2}-1\right)+18 \left(\rho ^4+4 \rho ^3+6 \rho ^2+4 \rho +4\right) Q^2}{12 (\rho +1) \sqrt{6-6 \sqrt{1-36 Q^2}}}, \end{array} $ 
(13) where
$ \rho=\rho(t) $ is given by Eq. (12).Substituting the results obtained from Eq. (12) into the free energy, we have the following:
$ \begin{aligned}[b] F=& 0.105 -0.053 t -0.082 (-t)^{3/2} + 0.13 t^2 \\&-0.227 (-t)^{5/2} +O(t^3), \end{aligned} $

(14) $ \begin{aligned}[b] F=& 0.105 -0.053 t +0.082 (-t)^{3/2} + 0.13 t^2 \\&+0.227 (-t)^{5/2} +O(t^3). \end{aligned} $

(15) We should note the presence of terms with fractional exponents. In particular, the coefficients before the term
$ (-t)^{3/2} $ have opposite signs.We now compute the derivatives of the free energy. We use Caputo's definition of fractional derivatives [34–36]. The main formulae needed are as follows:
$ \begin{aligned}[b]&D^\alpha_x x^n =0, \; \; \; \text{with} ~~ n\text{ integer and}~~ \alpha>n ;\\ & D^\alpha_x x^a \propto x^{a-\alpha}, \; \; \; \text{with a real}. \end{aligned} $

(16) For additional properties of the fractional derivatives, refer to the appendix of [31].
The α-order fractional derivative of the free energy with
$1 < \alpha \leqslant 2$ has the following form:$ \begin{array}{*{20}{l}} D_{ t}^{\alpha}F(t)=(-t)^{1-\alpha}\left[A(-t)^{1/2}\pm B t+C(-t)^{3/2} \pm D t^2+\cdots \right], \end{array} $

(17) where
$ A,B,C,D $ are several constant coefficients. The "+" sign corresponds to the case of approaching the Davies point from the left-hand side, and the "-" sign corresponds to approaching the point from the other side.Owing to
$t\leqslant 0$ , the$ D_{ t}^{\alpha}F-t $ curves all turn up on the left hand-side of the$ t=0 $ axis. We can also express$ D_{ t}^{\alpha}F $ as a function of ρ. In this case,$ D_{ t}^{\alpha}F $ can occur on both sides of the$ \rho=0 $ axis.Substituting concrete values of α into Eq. (17) and considering the
$ t\rightarrow 0^{-} $ limit, we can obtain$ \begin{array}{*{20}{l}} \lim\limits_{ t\rightarrow 0^-}D_{ t}^{\alpha}F(t)=\left\{ \begin{array}{lr} 0, \; & \; \alpha<3/2,\\ \pm 0.291, \; \; & \alpha=3/2,\\ \pm \infty, \; \; & \alpha>3/2. \end{array} \right. \end{array} $

(18) Observing the behaviors of
$ D_{ t}^{\alpha}F(t) $ displayed in Fig. 2 reveals that when$ \alpha<3/2 $ ,$ D_{ t}^{\alpha}F(t) $ is continuous at the Davies point; when$ \alpha=3/2 $ ,$ D_{ t}^{\alpha}F(t) $ has a finite jump; and when$ \alpha>3/2 $ ,$ D_{ t}^{\alpha}F(t) $ is divergent. According to the generalized classification, a$ 3/2 $ -order phase transition occurs at this Davies point.
Figure 2. (color online) Behaviors of
$ D_{ t}^{\alpha}F(t) $ near the left Davies point for the RN-AdS black hole. The left panel depicts the$ D_{ t}^{\alpha}F-t $ curves. The black arrows indicate the direction of increasing$ r_h $ . The right panel displays the$ D_{ t}^{\alpha}F-\rho $ curves.Next, we analyze the phase structure of the RN-AdS black hole at the right Davies point. The procedure here is also similar. In this case, the Davies point occurs at
$ \begin{array}{*{20}{l}} T_c= \displaystyle \frac{\sqrt{\displaystyle\frac{3}{2}} \left(1-12 Q^2+\sqrt{1-36 Q^2}\right)}{\pi \left(1+\sqrt{1-36 Q^2}\right)^{3/2}}, \ \ r_c=\frac{\sqrt{1+\sqrt{1-36 Q^2}}}{\sqrt{6}}. \end{array} $

(19) With the dimensionless quantities, the equation of state is reduced to
$ \begin{aligned}[b] & 1.380 \rho ^4+(2.573-2.948 t)\rho ^3 +(1.099 -8.844 t)\rho ^2\\&\quad-8.844 \rho t-2.948 t=0. \end{aligned} $

(20) It should be noted that the right Davies point of the RN-AdS black hole corresponds to the minimal value of temperature; thus, we have
$t\geqslant 0$ at all times.Similarly, we solve Eq. (20) to obtain
$ \rho=\rho(t) $ in series form and substitute the values into the free energy. Finally, we can derive the free energy in the following form:$ \begin{aligned}[b] F=& 0.117-0.233 t-0.510 t^{3/2}-0.519 t^2\\&-0.397 t^{5/2} +O(t^3), \end{aligned} $

(21) $ \begin{aligned}[b] F=& 0.117-0.233 t+0.510 t^{3/2}-0.519 t^2\\&+0.397 t^{5/2} +O(t^3). \end{aligned}$

(22) Except for the values of the coefficients and
$t\geqslant 0$ , these free energies have forms similar to those near the left Davies point. Therefore, their fractional derivatives are also analogous. However, they are not shown here. In Fig. 3, we directly depict the behaviors of the fractional derivatives of free energy as functions of t or ρ. The$ t \rightarrow 0^{+} $ limit values of the fractional derivatives are as follows: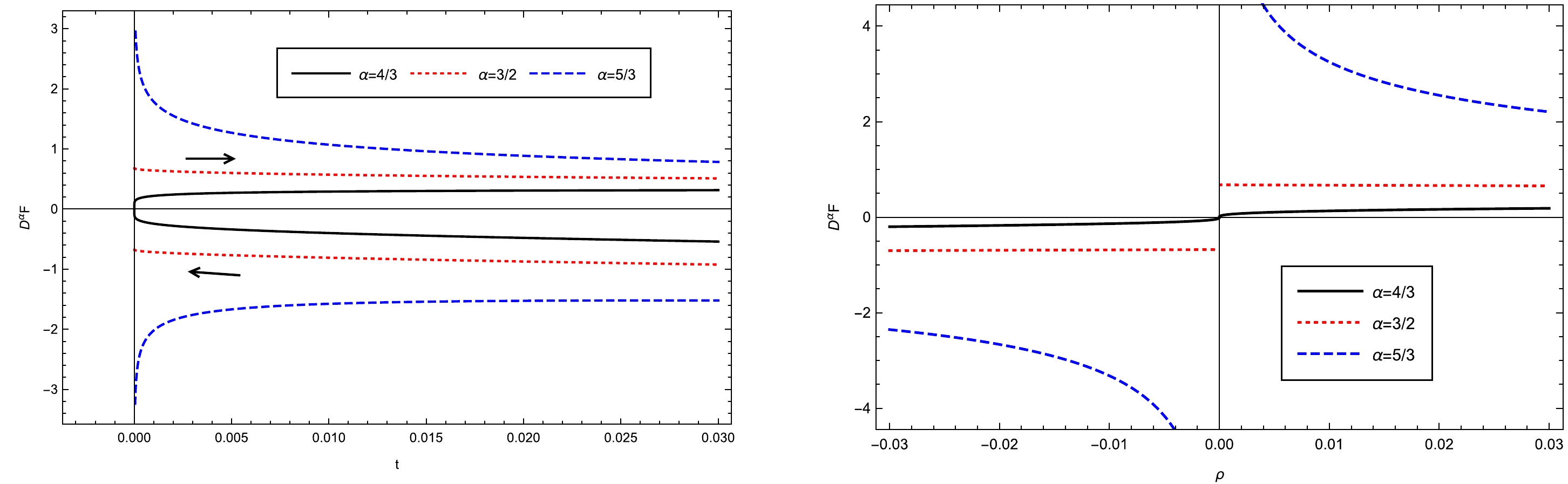
Figure 3. (color online) Behaviors of
$ D_{ t}^{\alpha}F(t) $ near the right Davies point for the RN-AdS black hole. The left panel depicts the$ D_{ t}^{\alpha}F(t)-t $ curves. The black arrows indicate the direction of increasing$ r_h $ . The right panel displays the$ D_{ t}^{\alpha}F(t)-\rho $ curves.$ \begin{array}{*{20}{l}} \lim\limits_{ t\rightarrow 0^+}D_{ t}^{\alpha}F(t)=\left\{ \begin{array}{lr} 0, & \alpha<3/2,\\ \pm 0.678, \; \; & \alpha=3/2,\\ \pm \infty, \; \; & \alpha>3/2. \end{array} \right. \end{array} $

(23) In summary, although the temperatures exhibit different behaviors at the left and right Davies points, the phase structures at the two points are similar. However, the phase transitions at these points both belong to the order of
$ 3/2 $ rather than the second-order as previously assumed. Based on our knowledge, in usual thermodynamic systems, temperatures are generally monotonic and are not analogous to the first type of Davies point. -
Next, we consider the second type of Davies point, namely the critical point, where
$ \begin{array}{*{20}{l}} {\rm d}T/{\rm d}r_h=0, \quad {\rm d}^2T/{\rm d}r_h^2=0. \end{array} $

(24) The critical point lies at
$ \begin{array}{*{20}{l}} r_c=L/\sqrt{6}, \quad Q_c=L/6, \quad T_c=\sqrt{\displaystyle\frac{ {2}}{ {3}}} \displaystyle \frac{ {1}}{ {\pi L}}. \end{array} $

(25) We also use the dimensionless quantities defined above. Because the critical point is an infection point, the dimensionless temperature t can now be greater or smaller than zero.
Based on the definition in Eq. (10), we also define
$ Q=Q_c(1+q) $ . The equation of state is simplified to$ \begin{array}{*{20}{l}} 2q+q^2+8t+24 t \rho+24 t\rho ^2+(8t-4)\rho^3-3 \rho ^4=0. \end{array} $

(26) This is a quartic equation about ρ. In principle, we can analytically solve this equation. However, the exact solutions are too lengthy and unnecessary.
Near the critical point, the free energy has the following form:
$ \begin{array}{*{20}{l}} F= \displaystyle \frac{L \left(-\rho ^4-4 \rho ^3+3 q^2+8 \rho +6 q+8\right)}{24 \sqrt{6} (\rho +1)}. \end{array} $

(27) For simplicity, we introduce the reduced free energy
$ \begin{aligned}[b] \tilde{F}= &\displaystyle \frac{ {24\displaystyle\sqrt{6}}}{ {L}}F\\=&\frac{ -\rho ^4-4 \rho ^3+3 q^2+8 \rho +6 q+8}{ \rho +1}. \end{aligned} $

(28) Next, two potential methods can be adopted for further calculations. The first involves the use of the same procedure as in the previous section: first, solve the equation of state to obtain
$ \rho=\rho(t,q) $ and then substitute it into Eq. (28) to obtain the free energy as a function of$ (t,q) $ . However, here, we choose another method used by Hilfer [30]. In the$ (t,q) $ plane, the critical point can be accessed through an infinite number of possible pathways. We can reparameterize the dimensionlessquantities as follows:$ \begin{aligned}[b] \displaystyle t=x \cos\theta, \quad\quad q=x \sin\theta, \end{aligned} $

(29) where θ controls the direction of approach to the critical point, and
$ x \rightarrow 0 $ leads to$ t \rightarrow 0 $ and$ q \rightarrow 0 $ .Correspondingly, in this new coordinate
$ (x,\theta) $ , we have the following:$ \begin{array}{*{20}{l}} \tilde{F}=\tilde{F}(t,q)=\hat{F}(x,\theta). \end{array} $

(30) In this manner, we can solve Eq. (26) to obtain
$ \begin{aligned}[b] \rho=&\rho(x,\theta)=\frac{x^{1/3} (\sin \theta+4 \cos \theta)^{1/3}}{2^{1/3}}+\frac{x}{32} (3 \sin \theta+28 \cos \theta)+\frac{x^{2/3} (12 \cos \theta-\sin \theta)}{4\times 2^{2/3} (\sin \theta+4 \cos \theta)^{1/3}} \\ &+\frac{x^{4/3} \left(29 \sin ^3\theta+2368 \cos ^3\theta+1136 \sin \theta \cos ^2\theta-4 \sin ^2\theta \cos \theta\right)}{384 \times 2^{1/3} (\sin \theta+4 \cos \theta)^{5/3}}+O(x^{5/3}). \end{aligned} $ 
(31) However, it should be noted that this series solution is valid for
$ \sin \theta+4 \cos \theta \neq 0 $ , namely$ q+4t \neq 0 $ . Substituting Eqs. (29) and (31) into Eq. (28), we obtain$ \begin{aligned}[b] \hat{F}(x,\theta)=&8+(4 \sin \theta -8 \cos \theta)x-\frac{3 (\sin \theta +4 \cos \theta )^{4/3}x^{4/3}}{2^{1/3}} \\& +\frac{3 (\sin \theta -4 \cos \theta ) (\sin \theta +4 \cos \theta )^{2/3}x^{5/3}}{2^{2/3}}\\ &+\frac{[8 \sin (2 \theta )-309 \cos (2 \theta )-299]x^2}{32}{} + O(x^{7/3}). \end{aligned}$

(32) Next, we can calculate the fractional derivatives of the free energy and consider the
$ x\rightarrow 0^{+} $ limit. The results obtained are as follows:$ \begin{array}{*{20}{l}} \lim\limits_{ x\rightarrow 0^+}D_{ x}^{\alpha}\hat{F}(x,\theta) = \left\{ \begin{array}{lr} 0, \; & \alpha < 4/3,\\ \displaystyle -\frac{4 \times 2^{2/3} \pi (\sin \theta + 4 \cos \theta )^{4/3}}{3 \displaystyle\sqrt{3} \Gamma \left(\frac{2}{3}\right)}, \; & \alpha = 4/3,\\ \pm \infty, \; & \alpha > 4/3. \end{array} \right. \end{array} $

(33) Except for the values of θ satisfying
$\sin \theta+ 4 \cos \theta =0$ , the$ 4/3 $ -order derivative of the free energy is discontinuous, which is a signature of the$ 4/3 $ -order phase transition. For clarity, we can choose a concrete direction to depict the fractional derivative. We consider$ \theta=0 $ and$ \theta=\pi $ , which correspond to the t-axis, and thus,$ q=0 $ . Substituting these values into Eq. (32), we can obtain$ \begin{aligned} \tilde{F}(t)=\left\{ \begin{array}{l} &8-8t-12\times 2^{1/3} t^{4/3}-12\times 2^{2/3} t^{5/3}\\&-19 t^2 +O(t^{7/3}), \quad\quad\quad t>0,\\ &8-8t-12\times 2^{1/3} (-t)^{4/3}+12\times 2^{2/3} (-t)^{5/3}\\&-19 t^2 +O(t^{7/3}),\quad\quad\quad t<0. \end{array} \right. \end{aligned} $

(34) Owing to the
$ (\pm t)^{4/3} $ terms, a finite jump can be noted for$ \alpha=4/3 $ :$ \begin{array}{*{20}{l}} \lim\limits_{t\rightarrow 0^-}\displaystyle\frac{ {d^\alpha \tilde{F}}}{ {dt^\alpha}}=\frac{32 \sqrt[3]{2} \pi }{3 \displaystyle\sqrt{3} \Gamma(2/3)} \neq\lim\limits_{t\rightarrow 0^+}\frac{ {d^\alpha \tilde{F}}}{ {dt^\alpha}}=-\frac{32 \sqrt[3]{2} \pi }{3 \sqrt{3} \Gamma(2/3)}. \end{array} $

(35) According to the generalized classification, the phase transition at the critical point is of the order of
$ 4/3 $ . The corresponding result is shown in Fig. 4.
Figure 4. (color online) Behaviors of
$ D_{ t}^{\alpha}\tilde{F}(t) $ near the critical point for the RN-AdS black hole.Further, we must deal with the exceptional case
$ t+4q=0 $ , which selects a special direction in the$ (t,q) $ plane. The critical point must be approached along this direction from both sides.In this case, the equation of state becomes
$ \begin{array}{*{20}{l}} -3 \rho ^4+\rho ^3 (8 t-4)+24 \rho ^2 t+24 \rho t+16 t^2=0. \end{array} $

(36) Its series solution is as follows:
$ \begin{array}{*{20}{l}} \rho(t)=\displaystyle-\frac{2 t}{3}-\frac{40 t^2}{81}-\frac{470 t^3}{729}+O(t^4). \end{array} $

(37) In this special case, no terms with fractional exponents are present, which naturally leads to a free energy without fractional exponents:
$ \begin{array}{*{20}{l}} \tilde{F}(t)=8-24t+32 t^2+\displaystyle\frac{32 t^3}{3}+O(t^4). \end{array} $

(38) Clearly, in the
$ t\rightarrow 0 $ limit, the arbitrary fractional order derivatives of this free energy are zero, and the integral order derivatives are constants; thus, the free energy is always continuous. This exceptional direction is known as the phase boundary at the critical point, but there exists a second-order phase transition along this phase boundary in Ref. [30]. -
Herein, based on the generalized Ehrenfest classification of phase transition, we analyze the phase structure of the RN-AdS black hole at its Davies points. Generally, two types of Davies points must be observed, corresponding to the extreme and infection points of temperature. According to the standard Ehrenfest classification, second-order phase transitions occur at these points. However, using fractional derivatives, we determine that at the first type of Davies point, the phase transition is of the order of
$ 3/2 $ . At the second type of Davies point, a$ 4/3 $ -order phase transition is observed, which is the same as the result obtained in the extended phase space [31]. Therefore, this generalized classification can indeed offer additional details on the critical behaviors of black holes.Notably, RN and Schwarzschild-AdS (SAdS) black holes can be considered as the
$ \Lambda \rightarrow 0 $ and$ Q \rightarrow 0 $ limits of the RN-AdS black hole, respectively. These two black holes have the first type Davies point. We also study the fractional phase transitions of these black holes and determine that they are both of the$ 3/2 $ order. Indeed, if we divide the temperature curve of the RN-AdS black hole into two parts, the left part exhibits a behavior similar to that of the RN black hole, and the right part exhibits a behavior similar to the temperature of SAdS. Therefore, it is not surprising that they have the same order of phase transition.The equations of state were originally thought to determine the order of fractional phase transition. However, according to Ref. [32], the symmetry of black hole spacetimes appears to influence the order of phase transition. In the present study, we identify that the equations of state near the first and second types of Davies points are both quartic equations. To clarify this problem, we must further consider other black holes. Although a
$ 3/2 $ -order phase transition is observed at the first type of Davies point for the RN-AdS black hole, we cannot ascertain whether the order is the same for other black holes with the first type of Davies point. Until now, the generalized Ehrenfest classification has only been used to deal with phase transitions at the Davies points of black holes. However, it should also be available for reanalyzing the original first-order phase transition. The orders of phase transitions at critical points are related to critical exponents. In a real physical system, these exponents can be explored in a laboratory. The critical exponents corresponding to the fractional order phase transitions of black holes should also be examined. These interesting problems should be considered in future studies. -
We are grateful to the reviewers for their suggestions on improving the content of the paper.
Fractional phase transitions of RN-AdS black holes at their Davies points
- Received Date: 2022-10-31
- Available Online: 2023-03-15
Abstract: In this study, we investigate the phase transitions of the RN-AdS black hole at its Davies points according to the generalized Ehrenfest classification of phase transition established based on fractional derivatives. Notably, Davies points label the positions at which the heat capacity diverges. According to the usual Ehrenfest classification, second-order phase transitions occur at these points. For the RN-AdS black hole, the Davies points can be classified into two types. The first type corresponds to extreme values of the temperature, and the second type corresponds to the infection point (namely the critical point) of temperature. Employing the generalized Ehrenfest classification, we determine that the orders of phase transition at the two types of Davies points are different, that is, we note an order of 3/2 for the first type and 4/3 for the second type. Thus, this finer-grained classification can discriminate between phase transitions that are expected to lie in the same category, providing new insights leading toward a better understanding of black hole thermodynamics.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: