-
The deuteron is a proton and neutron molecular state, which is well explained by the one boson exchange model [1, 2]. Along this line, we may wonder whether a heavy baryon pair can also form a deuteron-like bound state by exchanging virtual light mesons. Intuitively, the larger mass of the heavy baryons can reduce the kinetics of the systems and easily form bound states. Therefore, it is interesting to study whether one boson exchange interactions are sufficiently strong to bind two heavy baryons (dibaryon) or a heavy baryon and an anti-baryon (baryonium).
$ \Lambda_c $ is the lightest charmed baryon, which contains a charm quark and two light quarks, and the composition is similar to that of a proton. Having more knowledge about$ \Lambda_c $ is helpful when studying the properties of other charmed baryons. To date, our understanding of$ \Lambda_c $ behavior is limited. The Belle Collaboration first reported a charmonium-like state$ Y(4630) $ in the$ \Lambda_c \bar{\Lambda}_c $ invariant mass spectrum from the$e^+e^- \to \gamma_{\rm ISR} \Lambda_c \bar{\Lambda}_c$ process, where$\gamma_{\rm ISR}$ is the emitted photon from the initial leptons, the related parameters are mass$ M = 4634^{+8+5}_{-7-8} $ MeV, width$ \Gamma = 92^{+40+10}_{-24-21} $ MeV, and quantum number$J^{PC}=1^{--}$ [3].After the observation of
$ Y(4630) $ , various theoretical interpretations were proposed, such as the conventional charmonium state [4, 5], tetraquark state [6–8],$ \Lambda_c \bar \Lambda_c $ baryonium [9, 10], and threshold effect [11]. Simonov proposed a mechanism to study baryon-antibaryon production, which can explain why the$ Y(4630) $ enhancement structure appears in the electroproduction of$ \Lambda_c \bar\Lambda_c $ [12]. Recently, a series of investigations on strong decay behaviors were proposed, which intended to reveal the inner structure of$ Y(4630) $ [13–15].Resonance is one of the most striking phenomena across the entire range of scattering experiments and appears widely in atoms, molecules, nuclei, and chemical reactions. Based on conventional scattering theory, the R-matrix method [16, 17], K-matrix method [18], scattering phase shift method, continuous spectrum theory, and J-matrix method [19] have been developed. For the convenience of calculation, several bound-state-like methods have been developed, such as the real stabilization method (RSM) [20], the analytic continuation method of the coupling constant (ACCC) [21], and the complex scaling method (CSM) [22, 23]. The CSM can describe the bound state, resonant state, and continuum in a consistent way and is widely used to explore the resonance in atomic, molecular, and nuclear physics. The CSM has been extended from the nonrelativistic to relativistic framework [24–28] and from spherical to deformed nuclei [29], which has been applied in halo nuclei. In Ref. [30], the authors first extend the CSM from atomic, molecular, and nuclear physics to hadron physics to explain the hadron molecular state. Recently, the CSM has been increasingly used in hadronic physics [31–33].
Among various explanations, hadronic molecules gain the most attention because Y(4630) is close to the thresholds of two hadrons. The bound state of the S wave is easier to form, but higher excited states also have a certain probability of formation. For example, the heavy quarkonium has not only found the ground state
$ J/\psi $ , but the excited states$ h_c(1P) $ ,$ \chi_{c2}(2P) $ , and$ \Upsilon(1^3D_2) $ have also been observed in experiments. The higher excited states of hadrons provide a unique way to study the structure of hadron states. In the framework of the one-boson-exchange model, if hadrons can bind to hadron molecular states, they can form resonant states with high angular momentum. In Ref. [30], the authors calculated the resonant states for the$ DD(\bar{D}) $ ,$ \Lambda_cD(\bar{D}) $ , and$ \Lambda_c\Lambda_c(\bar{\Lambda}_c) $ systems in heavy quark effective theory. The bound state of the$ \Lambda_c\bar{\Lambda}_c $ system has been investigated in several previous studies [9, 34–36]. In this paper, we consider the spin-orbit coupling effect and further investigate whether the$ \Lambda_c \bar{\Lambda}_c $ system can form a resonant state consistent with the quantum number, mass, and width of Y(4630).This paper is organized as follows. We present the theoretical framework and calculation method in Section II. The numerical results and discussion are given in Section III. A short summary is given in Section IV.
-
In this study, we calculate the effective interaction potential for the
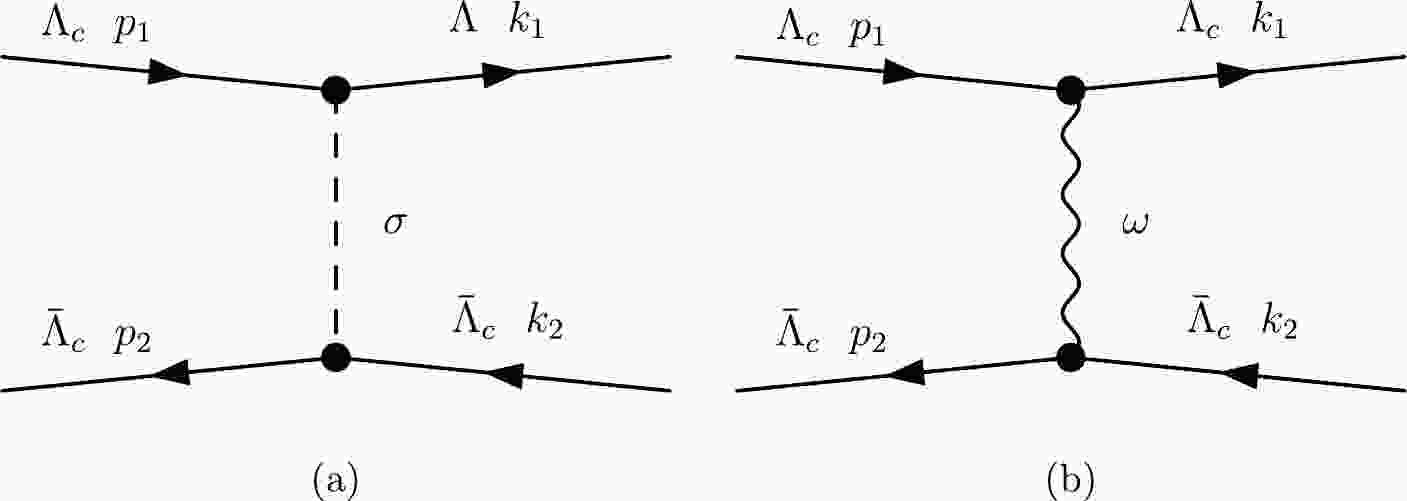
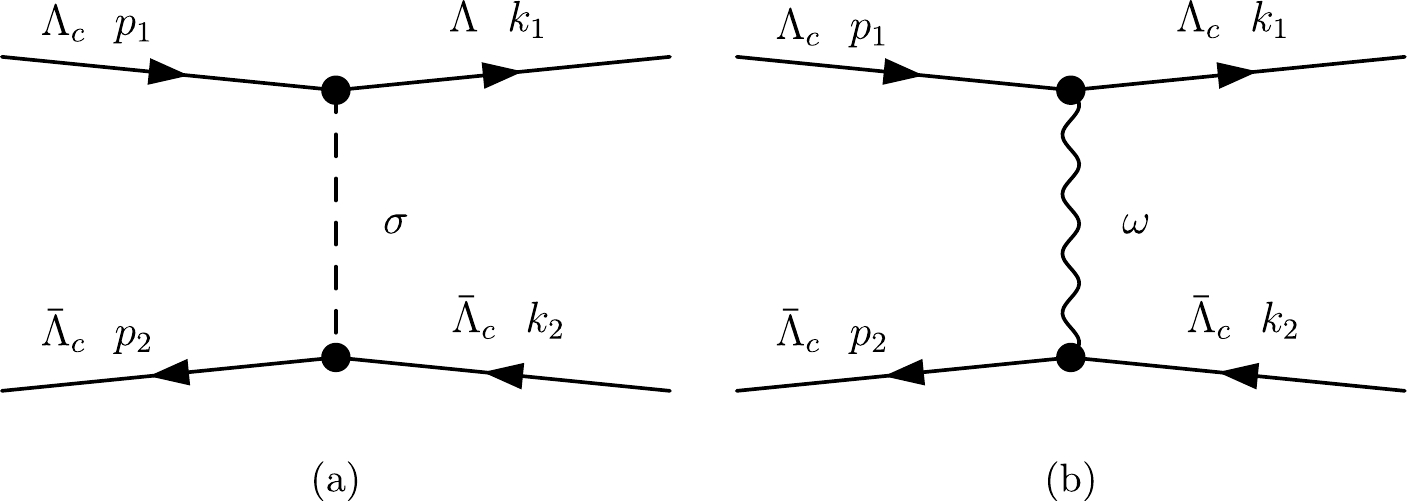
$ \Lambda_c\bar{\Lambda}_c $ system in the Bonn meson-exchange model. Owing to spin and isospin conservation in hadron systems, the contributions of the π, η, and ρ meson exchanges are forbidden or heavily suppressed. The interactions of the$ \Lambda_c\bar{\Lambda}_c $ system are mainly mediated by the σ and ω mesons, and the effective Lagrangian densities for one-σ-exchange and one-ω-exchange are expressed.$ \begin{array}{*{20}{l}} \mathcal{L} = g_{\sigma \Lambda_c \Lambda_c}\bar\psi\sigma \psi -g_{\omega \Lambda_c \Lambda_c}\bar\psi \gamma_{\mu} \omega^{\mu}\psi +\dfrac{f_{\omega \Lambda_c \Lambda_c}}{2m_{\Lambda_c}}\bar\psi\sigma_{\mu\nu}\psi \partial^{\mu}\omega^{\nu}, \end{array} $

(1) where ψ is the Dirac-spinor for the spin-
$ \dfrac{1}{2} $ particle of$ \Lambda_c $ . In the tensor coupling term, the constant$ f_{\omega \Lambda_c \Lambda_c}= -g_{\omega \Lambda_c \Lambda_c} $ in Ref. [9]; hence, the tensor coupling coefficient is$ 2m_{\Lambda_c} $ lower than the vector coupling coefficient. Moreover, the tensor term is proportional to the relative momentum$ q^\nu $ , which is small, and thus, the contribution of the tensor term can be ignored.Although there are no definite values for the coupling strengths
$ g_{\omega/\sigma \Lambda_c \Lambda_c} $ in experiments, they can be estimated using the quark model. Because the exchange of σ and ω mesons occurs mainly between light quarks in heavy hadrons, the interactions of light quarks$ (q=u,d) $ and$ \sigma/\omega $ can be written as$ \begin{array}{*{20}{l}} \mathcal{L}_{qq\sigma/\omega} = -g_{\sigma}^{q}\bar{\psi}_q\sigma\psi_q-g_{\omega}^{q}\bar{\psi}_q\gamma^{\mu}\omega_{\mu}\psi_q. \end{array} $

(2) Compared with the vertices of
$ \bar{\Lambda}_c\Lambda_c\sigma/\omega $ and$ \bar{q}q\sigma/\omega $ in Eqs. (1)$ - $ (2), the coupling constants can be related via$ \begin{aligned}[b]& g_{\sigma \Lambda_c \Lambda_c} = 2 g_{\sigma}^{q}, \\& g_{\omega \Lambda_c \Lambda_c} = 2 g_{\omega}^{q}. \end{aligned} $

(3) In a σ model [37], the value of
$ g_{\sigma}^{q} $ is taken as$ g_{\sigma}^{q}= 3.65 $ . For the ω coupling$ g_{\omega}^{q} $ , in the Nijmegen model,$ g_{\omega}^{q}= 3.45 $ , whereas it is equal to 5.28 in the Bonn model [38]. In Ref. [39],$ g_{\omega}^{q} $ was roughly assumed to be 3.00.Based on the Lagrangians in Eq. (1), we can obtain the scattering Feynman amplitudes for
$ \Lambda_c\bar{\Lambda}_c \to \Lambda_c\bar{\Lambda}_c $ in Fig. 1. The annihilation effect from the S-channel is not considered in the calculation. In the center-of-mass frame, the initial four-momenta are$ p_1(E_1,\vec{p}) $ and$ p_2(E_2,-\vec{p}) $ , and the final four-momenta are$ k_1(E_1,\vec{p'}) $ and$ k_2(E_2,-\vec{p'}) $ , as shown in Fig. 1. Thus, the four-momenta of the propagator are$ \begin{equation} q=k_1-p_1=p_2-k_2=(0,\vec{p'}-\vec{p})=(0,\vec{q}). \end{equation} $

(4) For convenience of calculation, we make the substitution for the following four-momenta:
$ \vec{q}=\vec{p'}-\vec{p}, \; \; \; \vec{k}=\frac{1}{2}(\vec{p}+\vec{p'}). $

(5) In the nonrealistic approximation, we keep the terms up to the order of
$ \dfrac{1}{m_{\Lambda_c}^2} $ . The scattering amplitudes are$ \begin{aligned}[b] {\rm i} M_{\sigma}&=-g_{\sigma \Lambda_c \Lambda_c}^2\bar{u}(k_1)u(p_1) \frac{\rm i}{q^2-m_{\sigma}^2} \bar{\upsilon}(p_2)\upsilon(k_2) \\ &= {\rm i}\frac{g_{\sigma \Lambda_c \Lambda_c}^2}{\vec{q}^{2}+{m_\sigma}^2} \left[1 - \frac{\vec{k}^{2}}{2 m_{\Lambda_c}^2} + \frac{\vec{q}^{2}}{8 m_{\Lambda_c}^2} + {\rm i}\frac{\vec{S}\cdot(\vec{k}\times \vec{q})}{2m_{\Lambda_c}^2}\right], \end{aligned} $

(6) and
$ \begin{aligned}[b] {\rm i} M_\omega =& -g_{\omega \Lambda_c \Lambda_c}^2\bar{u}(k_1)\gamma^{\mu}u(p_1) {\rm i}\frac{-g_{\mu\nu}+\dfrac{q_{\mu}q_{\nu}}{m_{\omega}^2}}{q^2-m_{\omega}^2}\bar{\upsilon}(p_2)\gamma^{\nu} \upsilon(k_2)\\ = & {\rm i}\frac{g_{\omega \Lambda_c \Lambda_c}^2}{\vec{q}^2+m_{\omega}^2} \Bigg[1-\frac{\vec{q}^{2}}{8m_{\Lambda_c}^2} + \frac{3\vec{k}^{2}}{2 m_{\Lambda_c}^2}+ {\rm i}\frac{3\vec{S}\cdot\left(\vec{k}\times\vec{q}\right)}{2m_{\Lambda_c}^2}\\ &-\frac{(\vec{\sigma_1}\cdot\vec{\sigma_2})\cdot\vec{q}^2}{4m_{\Lambda_c}^2} +\frac{(\vec{\sigma}_1\cdot\vec{q})(\vec{\sigma}_2\cdot\vec{q})}{4m_{\Lambda_c}^2}\Bigg], \end{aligned} $

(7) where
$ \vec{S}=\dfrac{1}{2}(\vec{\sigma}_1+\vec{\sigma}_2) $ is the total spin of the$ \Lambda_c\bar{\Lambda}_c $ system.Inthe Breit approximation, the relation between the effective potential in the momentum space
$ \mathcal{V}_{fi} $ and the scattering amplitude$ \mathcal{M}_{fi} $ in the momentum space is expressed as$ \begin{array}{*{20}{l}} \mathcal{V}_{fi}({\boldsymbol{q}}) = -\dfrac{\mathcal{M}_{fi}(\Lambda_c\bar{\Lambda}_c \to \Lambda_c\bar{\Lambda}_c)}{\sqrt{\prod_i2m_i\prod_f2m_f}}. \end{array} $

(8) Here,
$ m_i $ and$ m_f $ are the masses of the initial ($ \Lambda_c $ ,$ \bar{\Lambda}_c $ ) and final particles ($ \Lambda_c $ ,$ \bar{\Lambda}_c $ ), respectively.In the above, hadrons are directly treated as point particles without considering the internal structure of the hadrons. To regularize the off shell effect of the exchanged meson, it is necessary to introduce a monopole form factor
$ \mathcal{F}(q^2) $ at every vertex, which has the form$ \begin{array}{*{20}{l}} \mathcal{F}(q^2) = \dfrac{\Lambda^2-m^2}{\Lambda^2-q^2}, \end{array} $

(9) where Λ is the cutoff parameter, and m and q correspond to the mass and momentum of the exchanged meson, respectively. In Refs. [1, 2], Λ is related to the root-mean-square radius of the source hadron, which propagates the interaction through the intermediate boson (σ or ω). According to previous experience of the deuteron, the cutoff Λ is taken at approximately 1.0 GeV.
After adding the monopole form factor
$ \mathcal{F}(q^2) $ , the effective potential in the coordinate space$ \mathcal{V}(r) $ is obtained by performing a Fourier transformation,$ \begin{array}{*{20}{l}} \mathcal{V}({\boldsymbol{r}}) = \displaystyle\int\dfrac{{\rm d}^3{\boldsymbol{q}}}{(2\pi)^3}{\rm e}^{{\rm i}{\boldsymbol{q}}\cdot{\boldsymbol{r}}}\mathcal{V}({\boldsymbol{q}})\mathcal{F}^2(q^2). \end{array} $

(10) The detailed Fourier transformations for different types of effective potentials are shown below [40, 41].
$ \begin{aligned}[b] \mathcal{F}\left\{\frac{1}{\vec{q}^2+m^2}\left(\frac{\Lambda^2-m^2} {\Lambda^2+\vec{q}^2}\right)^2\right\} = &Y\left(\Lambda,m,r\right),\\ \mathcal{F}\left\{\frac{\vec{q}^2}{\vec{q}^2+m^2}\left(\frac{\Lambda^2-m^2} {\Lambda^2+\vec{q}^2}\right)^2\right\}=&-\nabla^2Y\left(\Lambda,m,r\right),\\ \mathcal{F}\left\{\frac{\vec{k}^2}{\vec{q^2}+m^2}\left(\frac{\Lambda^2-m^2} {\Lambda^2+\vec{q}^2}\right)^2\right\}=&\frac{1}{4}\nabla^2Y\left(\Lambda,m,r\right) \\ &-\frac{1}{2}\left\{\nabla^2,Y\left(\Lambda,m,r\right)\right\},\\ \mathcal{F}\left\{\frac{\left(\vec{S}\cdot(\vec{q}\times\vec{k})\right)} {\vec{q}^2+m^2}\left(\frac{\Lambda^2-m^2}{\Lambda^2+\vec{q}^2}\right)^2\right\} = & -{\rm i}\vec{S}\cdot\vec{L}\frac{1}{r}\frac{\partial}{\partial r}Y\left(\Lambda,m,r\right),\\ \mathcal{F}\left\{\frac{\left(\vec{\sigma}_1\cdot\vec{q}\right) \left(\vec{\sigma}_2\cdot\vec{q}\right)}{\vec{q}^2+m^2} \left(\frac{\Lambda^2-m^2}{\Lambda^2+\vec{q}^2}\right)^2\right\} =& -\frac{1}{3}\left(\vec{\sigma}_1\cdot\vec{\sigma}_2\right) \nabla^2Y\left(\Lambda,m,r\right)\\ & -\frac{1}{3}S\left(\vec{\hat{r}},\vec{\sigma}_1, \vec{\sigma}_2\right)T\left(\Lambda,m,r\right).\\ \end{aligned} $

(11) As shown in Ref. [9], owing to the cancellation of the coupling constants
$ f_{\omega \Lambda_c \Lambda_c} $ and$ g_{\omega \Lambda_c \Lambda_c} $ in the tensor terms, there is no mixing of the S and D states. Therefore,$ \Lambda_c\bar{\Lambda}_c $ systems do not need to consider S-D coupling. The$ \vec{k}^2 $ term is referred to as the recoil correction term, and the function$ Y\left(\Lambda,m,r\right) $ is defined as$ \begin{array}{*{20}{l}} Y\left(\Lambda,m,r\right) = \dfrac{1}{4\pi r}\left({\rm e}^{-mr}-{\rm e}^{-\Lambda r}\right)-\dfrac{\Lambda^2-m^2}{8\pi\Lambda}{\rm e}^{-\Lambda r}. \end{array} $

(12) The one-σ-exchange and one-ω-exchange interactions correspond to intermediate- and short-range forces; therefore, they are suppressed when the radius r reaches 1.0 fm or larger. For the
$ ^1S_0 $ state, both ω-exchange and σ-exchange provide an attractive force. For the$ ^3S_1 $ state, the vector meson ω provides a repulsive force in the short range but an attractive force in the medium range, whereas the scalar meson σ always provides an attractive force.After the interaction potential
$ \mathcal{V}(r) $ in the coordinate space is obtained, the eigenvalue and eigenfunction of the bound state for the$ \Lambda_c\Lambda_c $ system can be obtained by solving the non-relativistic Schrödinger equation. In this paper, we extend the CSM to solve the Schrödinger equation in the complex energy plane. The Aguilar-Balslev-Combes (ABC) theorem [42] proved that, under the complex scaling transformation, the energy spectrum has three parts: (i) the bound states are a discrete set of real points on the negative energy axis and remain unchanged under complex scale transformation; (ii) the resonant states correspond to the discrete set of points in the lower half of the complex energy plane, which does not change with the coordinate transformation; and (iii) the continuous spectrum is rotated at$ 2\theta $ around the origin of the coordinates. In the CSM, bound states, resonant states, and continuous spectra can be described uniformly. As θ increases, the resonant states are exposed in the fourth quadrant of the complex energy plane and do not change with the rotation of the continuous spectrum. We solve the complex scaled Schrödinger equation using the basis expansion method, where the radial function uses the spherical harmonic oscillator basis. For the detailed calculation scheme, refer to our previous paper [30]. -
In this section, we discuss and analyze the effects of the one-σ-exchange and one-ω-exchange interactions for the
$ \Lambda_c \bar{\Lambda}_c $ system. The total boson exchange potentials are used to calculate the numerical solution of the Schrödinger equation in the CSM. The related parameters are given in Table 1. The corresponding eigenvalues can be obtained by diagonalizing the Hamiltonian. Then, we can obtain information on the resonant state.Hadron $ I(J^P) $ 

Mass/MeV σ $ 0(0^+) $ 

600 ω $ 0(1^-) $ 

782.65 $ \Lambda_c $ 

$0\left(\dfrac{1}{2}^+\right)$ 

2286.46 Table 1. Related parameters used in this study [43].
The eigenvalues of the transformed Hamiltonian
$ H_\theta $ are shown in Fig. 2. We can clearly see that all the eigenvalues of$ H_\theta $ have three parts; the dark blue square, deep yellow triangle, and green circle represent the bound state, resonant state, and continuum, respectively. The bound state is located on the negative energy axis, whereas the continuous spectrum rotates clockwise with an angle of$ 2\theta $ , and the resonant state in the lower half of the complex energy plane, which is surrounded by the positive energy axis and the rotated continuum line and becomes isolated.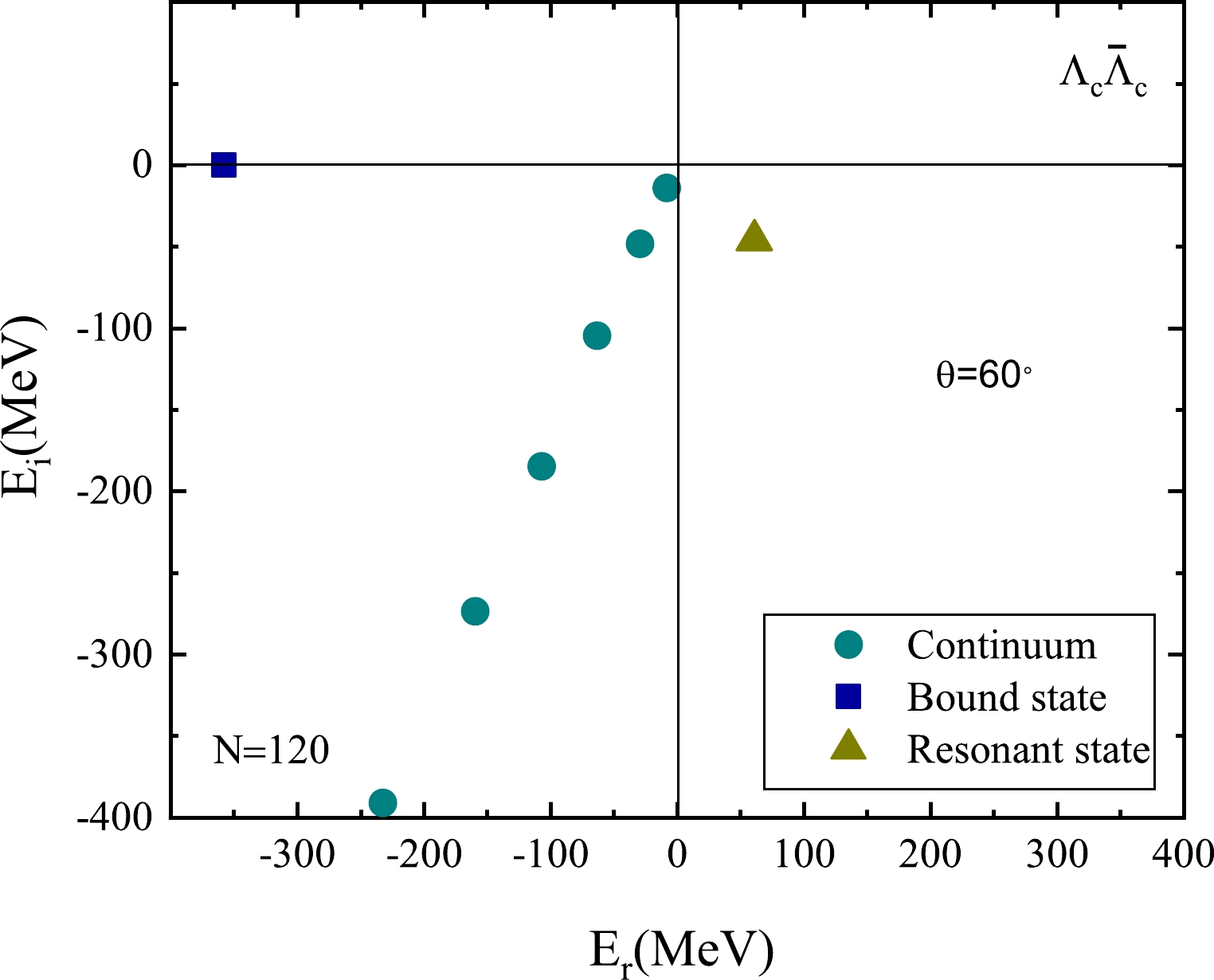
Figure 2. (color online) Resonant state is presented with
$ \theta = 60^{\circ} $ . Here, the cutoff parameter$ \Lambda=1.2 $ GeV,$ g_{\sigma \Lambda_c \Lambda_c} $ =7.3, and$ g_{\omega \Lambda_c \Lambda_c} $ =10.57. The result is obtained by expanding the basis function with N=120.To show how the resonant state is separated from the continuum via complex rotation, the eigenvalues of
$ H_\theta $ with different complex scale angles θ are plotted in Fig. 3, and the other parameters are the same as those in Fig. 2. In Fig. 3(a), when$ \theta = 20^{\circ} $ , we can only see the continuous spectrum, and it is difficult to observe the resonant state in the complex energy plane. In Fig. 3(b), when the rotation angle increases to$ \theta = 30^{\circ} $ , the resonant state begins to gradually separate from the continuum spectrum. When$ \theta = 40^{\circ} $ , it is clear that the resonant state is completely separated from the continuum in Fig. 3(c). Overall, from Fig. 3(b) to Fig. 3(d), no matter how the complex scale angle rotates, the position of the resonant state is almost unchanged in the complex energy plane. The above results suggest that the resonant state can be determined as long as the selected rotation angle is sufficiently large.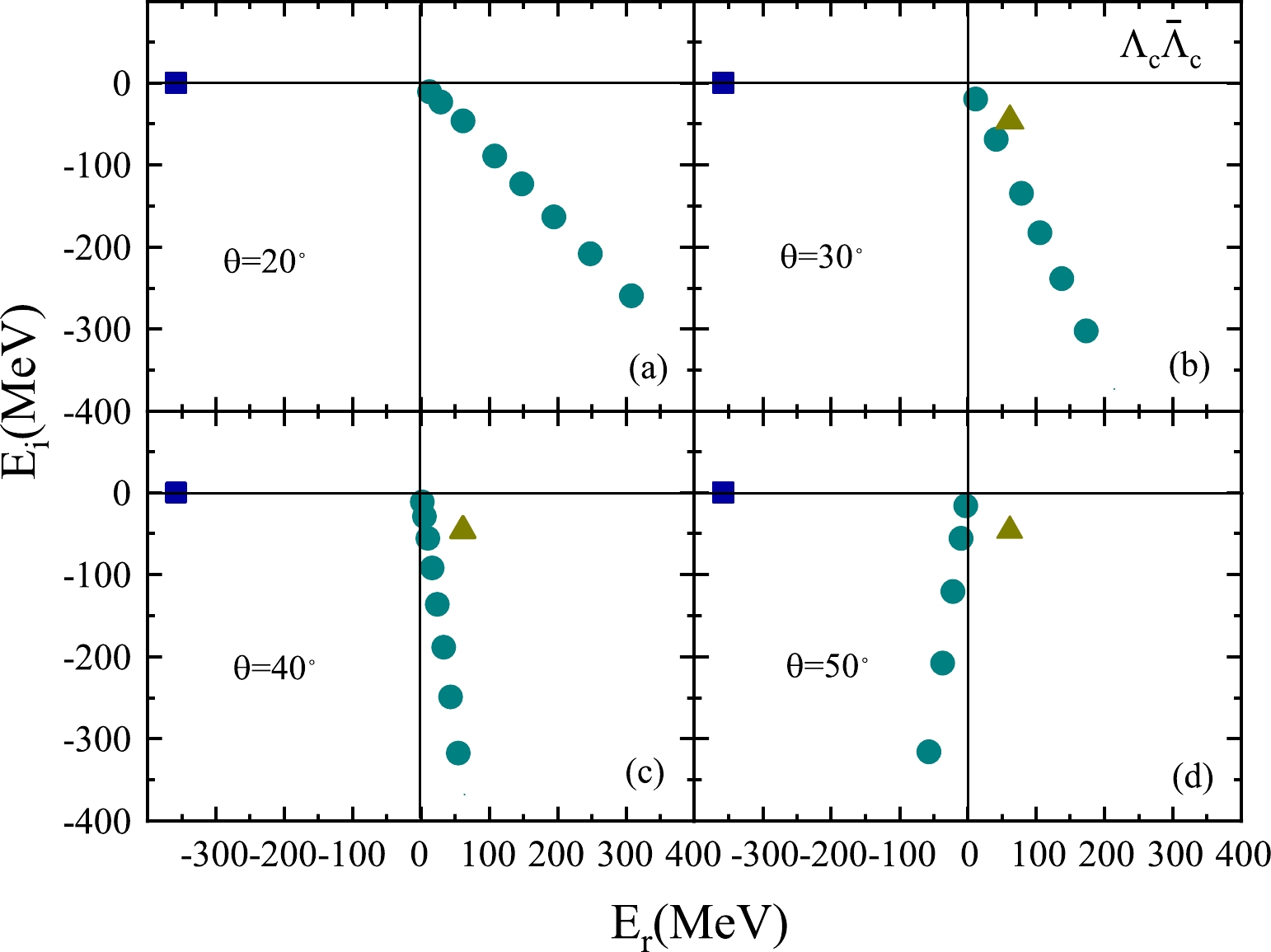
Figure 3. (color online) Resonant and continuous spectra varying with the complex rotation angle in the complex energy plane. Except for the complex rotation angle, the parameters are set the same as those in Fig. 2.
The total potentials of the
$ \Lambda_c\bar{\Lambda}_c $ system in the one boson exchange model with different orbit angular momenta, L = 0, 1, 2, are plotted in Fig. 4. The black and red lines correspond to the potential with$ g_{\omega\Lambda_c \Lambda_c} =6.9 $ and$ g_{\omega \Lambda_c \Lambda_c} =10.56 $ in Fig. 4, respectively. The centrifugal force term$ L(L+1)/2 \mu r^2 $ is a repulsive force, and the potential energy term provides an attractive force; these two parts are competitive. From Fig. 4(a), we can see that under the reasonable parameters, the potential becomes sufficiently large to bind two heavy baryons. In Fig. 4(b), the depth of the potential well becomes smaller and a lower potential barrier appears compared with those in Fig. 4(a), which only has the center potentials. In Table 2, we find that when$ g_{\omega\Lambda_c \Lambda_c} =6.9 $ , the energy and width of the P resonant state are small, and there is no P wave resonant state for the$ \Lambda_c\bar{\Lambda}_c $ system when$ g_{\omega \Lambda_c \Lambda_c} =10.56 $ . In Fig. 4(c), the total potentials are larger than those in Fig. 4(b), and they can relatively easily form resonant states.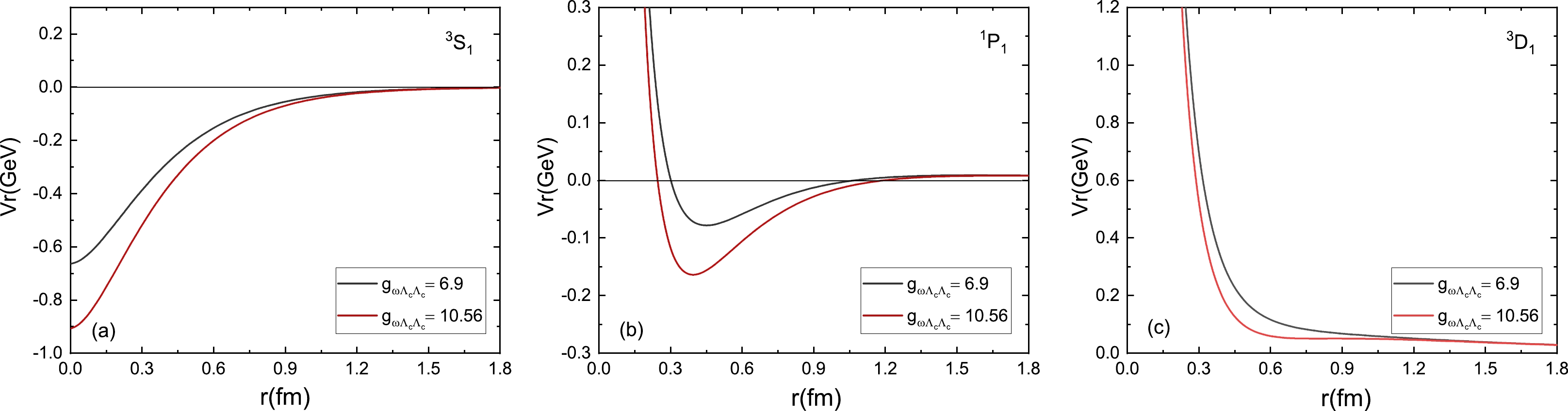
Figure 4. (color online) Total potentials in the one boson exchange model with different orbit angular momenta, L = 0, 1, 2, for the
$ \Lambda_c\bar{\Lambda}_c $ system dependence on r. The cutoff Λ is set as 1.1 GeV, and the value of the coupling constant$ g_{\omega}^{q} $ is set as 3.45 in the Nijmegen model and 5.28 in the Bonn model [38].$ g_{\sigma}^{q} $ is set as$ g_{\sigma}^{q} $ = 3.65. The relation between$ g_{\omega/\sigma \Lambda_c \Lambda_c} $ and$ g_{\omega/\sigma}^{q} $ is$ g_{\omega/\sigma \Lambda_c \Lambda_c} =2 g_{\omega/\sigma}^{q} $ .L E Γ L E Γ $ ^1S_0 $ 

−131.66 $\ldots$ 

$ ^3D_1 $ 

38.86 183.82 $ ^3S_1 $ 

−126.13 $\ldots$ 

$ ^1D_2 $ 

32.71 192.12 6.9 $ ^3P_0 $ 

7.15 8.28 $ ^3D_2 $ 

34.94 188.42 $ ^1P_1 $ 

9.16 13.82 $ ^3D_3 $ 

28.78 193.7 $ ^3P_2 $ 

9.90 17.0 $ ^1S_0 $ 

−240.84 $\ldots$ 

$ ^3D_1 $ 

54.61 131.8 $ ^3S_1 $ 

−224.53 $\ldots$ 

$ ^1D_2 $ 

49.66 152.64 10.56 $ ^3P_0 $ 

$\ldots$ 

$\ldots$ 

$ ^3D_2 $ 

51.23 144.34 $ ^1P_1 $ 

$\ldots$ 

$\ldots$ 

$ ^3D_3 $ 

44.79 160.1 $ ^3P_2 $ 

$\ldots$ 

$\ldots$ 

Table 2. Energy and width of the bound and resonant states for the
$ \Lambda_c\bar{\Lambda}_c $ system. E and Γ represent the energy and width of the resonant states in units of MeV, respectively. The cutoff Λ is set as 1.1 GeV. The value of the coupling constant$ g_{\omega}^{q} $ is set as 3.45 in the Nijmegen model and 5.28 in the Bonn model [38].$ g_{\sigma}^{q} $ is set as$ g_{\sigma}^{q} $ = 3.65. The relation between$ g_{\omega/\sigma \Lambda_c \Lambda_c} $ and$ g_{\omega/\sigma}^{q} $ is$ g_{\omega/\sigma \Lambda_c \Lambda_c} =2 g_{\omega/\sigma}^{q} $ . The notation$ \ldots $ denotes no bound or resonant state solutions.We extend the complex scale method to solve the Schrödinger equation and obtain the bound state and resonant state for the
$ \Lambda_c\bar{\Lambda}_c $ system numerically. The solution for the resonant state has the form$E-{\rm i}\Gamma /2$ , where E is the resonance energy and Γ is its decay width. The coupling strength$ g_{\omega \Lambda_c \Lambda_c} $ is twice that of$ g_{\omega}^{q} $ in heavy quark effective theory. The coupling constant$ g_{\omega}^{q} $ is set as 3.45 in the Nijmegen model and 5.28 in the Bonn model as the input benchmark parameter. We can obtain the energies of the bound states, and the energies and widths of the resonant states for the$ \Lambda_c\bar{\Lambda}_c $ system with different angular momenta L, which are listed in Table 2.In Table 2, we find that there is an S wave bound state in each case with
$ \Lambda=1.1 $ GeV, whose binding energy is approximately hundreds of MeV, and the difference in energy between the$ ^1S_0 $ and$ ^3S_1 $ states is approximately 10 MeV. For the case with$ g_{\omega \Lambda_c \Lambda_c}=6.9 $ , the$ \Lambda_c\bar{\Lambda}_c $ system can form P wave resonant states, and the energies and widths are approximately several to more than a dozen MeV. In addition, the$ \Lambda_c\bar{\Lambda}_c $ system can form D wave resonant states, and the energies are dozens of MeV, while the widths are more than 100 MeV. The resonance widths increase with increasing angular momentum L for the$ \Lambda_c\bar{\Lambda}_c $ system, which indicates that the resonant states become more and more unstable. We find that the quantum number of the resonant state$ ^3D_1 $ agrees with the quantum number$ J^{PC}=1^{–} $ of Y(4630). We then aim to discover whether there is a suitable parameter consistent with the energy and width of Y(4630).In Fig. 5, we show radial density distributions for the bound state
$ ^3S_1 $ and the resonant states$ ^1P_1 $ and$ ^3D_1 $ with the coupling constants$ g_{\sigma \Lambda_c \Lambda_c}=7.3 $ and$ g_{\omega \Lambda_c \Lambda_c}= $ 10.56 and the cutoff parameter$ \Lambda=1.1 $ GeV. The black, red, and blue lines represent the bound state$ ^3S_1 $ and resonant states$ ^1P_1 $ and$ ^3D_1 $ , respectively. The black bound state converges when the radius is approximately 0.25 fm, whereas the red and blue resonant states begin to converge when the radius is approximately 0.75 and 1.25 fm, respectively, which indicates that compared with the bound state, the resonant states are more dispersed.
Figure 5. (color online) Radial density distributions in the coordinate space for the bound state
$ ^3S_1 $ and the resonant states$ ^1P_1 $ and$ ^3D_1 $ with$ g_{\sigma \Lambda_c \Lambda_c}=7.3 $ ,$ g_{\omega \Lambda_c \Lambda_c}=10.56 $ , and$ \Lambda=1.1 $ GeV.The coupling constants
$ g_{\sigma \Lambda_c \Lambda_c} $ and$ g_{\omega \Lambda_c \Lambda_c} $ in the Lagrangians are difficult to extract from experiments. In Ref. [9], the coupling constants of the heavy charmed baryons and light mesons can be approximately determined by nucleon-meson coupling the obtained numerical values$ g_{\sigma \Lambda_c \Lambda_c}= $ 5.64 and$ g_{\omega \Lambda_c \Lambda_c}= $ 10.57. However, the coupling constant$ g_{\sigma \Lambda_c \Lambda_c} $ is 7.3 in a σ model [37],$ g_{\omega \Lambda_c \Lambda_c}= $ 6.9 in the Nijmegen model, and$ g_{\omega \Lambda_c \Lambda_c}= $ 10.56 in the Bonn model [38]. Therefore, the value of these two coupling strengths have large uncertainties. Considering the width uncertainties of Y(4630) from 60 to 133 MeV, we show the different values of$ g_{\omega \Lambda_c \Lambda_c} $ and$ g_{\sigma \Lambda_c \Lambda_c} $ , which satisfy the mass of Y(4630) in Fig. 6. When$ g_{\sigma \Lambda_c \Lambda_c}= 7.2 $ and$ g_{\omega \Lambda_c \Lambda_c}=9.13 $ , there is a resonant state for the$ \Lambda_c\bar{\Lambda}_c $ system, with an energy of 61.08 MeV and a width of 91.24 MeV. The width of Y(4630) reported by the Belle Collaboration is its total width, and$ \Lambda_c\bar{\Lambda}_c $ is simply one of its partial decay channels; thus, the decay width of the$ \Lambda_c\bar{\Lambda}_c $ resonant state should be less than the width of Y(4630). In Fig. 6, the orange dots represent widths less than the 92 MeV width of Y(4630), whereas the gray dots represent widths greater than 92 MeV. We can see that the range covered by the orange dots can satisfy the requirements of the experiment.
Figure 6. (color online) Values of
$ g_{\omega \Lambda_c \Lambda_c} $ and$ g_{\sigma \Lambda_c \Lambda_c} $ for the decay width of the$ \Lambda_c\bar{\Lambda}_c $ system varying from 60 to 133 MeV, with$ \Lambda=1.25 $ GeV.To clarify the dependence of energy and width on the coupling strength
$ g_{\omega \Lambda_c \Lambda_c} $ , we present the energy and width as a function of the coupling strength$ g_{\omega \Lambda_c \Lambda_c} $ for the resonant state$ ^3D_1 $ in Fig. 7. As shown in Fig. 7(a), the energy of the resonant state increases slowly and then gradually decreases with increasing$ g_{\omega \Lambda_c \Lambda_c} $ . It reaches a maximum value when$ g_{\omega \Lambda_c \Lambda_c} $ is approximately 9.0. Unlike the change in energy, in Fig. 7(b), the width decreases significantly with the change in the coupling constant$ g_{\omega \Lambda_c \Lambda_c} $ .
Figure 7. (color online) Variation in the energy and width of the
$ ^3D_1 $ wave resonant state with the change in the coupling constant$ g_{\omega \Lambda_c \Lambda_c} $ for the$ \Lambda_c\bar{\Lambda}_c $ system with$ \Lambda=1.25 $ GeV.The cutoff parameter Λ is related to the size of hadrons and has a significant impact on the results of energy and width. For the nucleon-nucleon interaction, the cutoff parameter Λ is usually from 0.8 to 1.5 GeV. For the heavy hadron state, this value should be slightly larger. In Fig. 8(a) and (b), we present the energy and width of the resonant state
$ ^3D_1 $ for the$ \Lambda_c\bar{\Lambda}_c $ system as a function of Λ. From Fig. 8(a), we can see that the energy of the resonant state$ ^3D_1 $ increases from 25 to 60 MeV and then decreases to 40 MeV when the cutoff parameter Λ varies from 1.0 to 1.4. The corresponding width decreases from 200 to 20 MeV, as shown in Fig. 8(b). The energies and widths are related to the potential functions, which depend on the coupling constants and cutoff parameter. The dependence of the potential function on the coupling constants and cutoff is similar, and thus we present the potential functions for the different cutoff parameters in Fig. 9. When the cutoff parameter increases, the depth of the potential well becomes deeper, the barrier effect is more obvious, the formed resonant state is more stable, and the decay width is smaller.
Figure 8. (color online) Energy and width of the
$ ^3D_1 $ wave resonant state as a function of the cutoff parameter Λ for the$ \Lambda_c\bar{\Lambda}_c $ system with$ g_{\omega \Lambda_c \Lambda_c}=9.13 $ .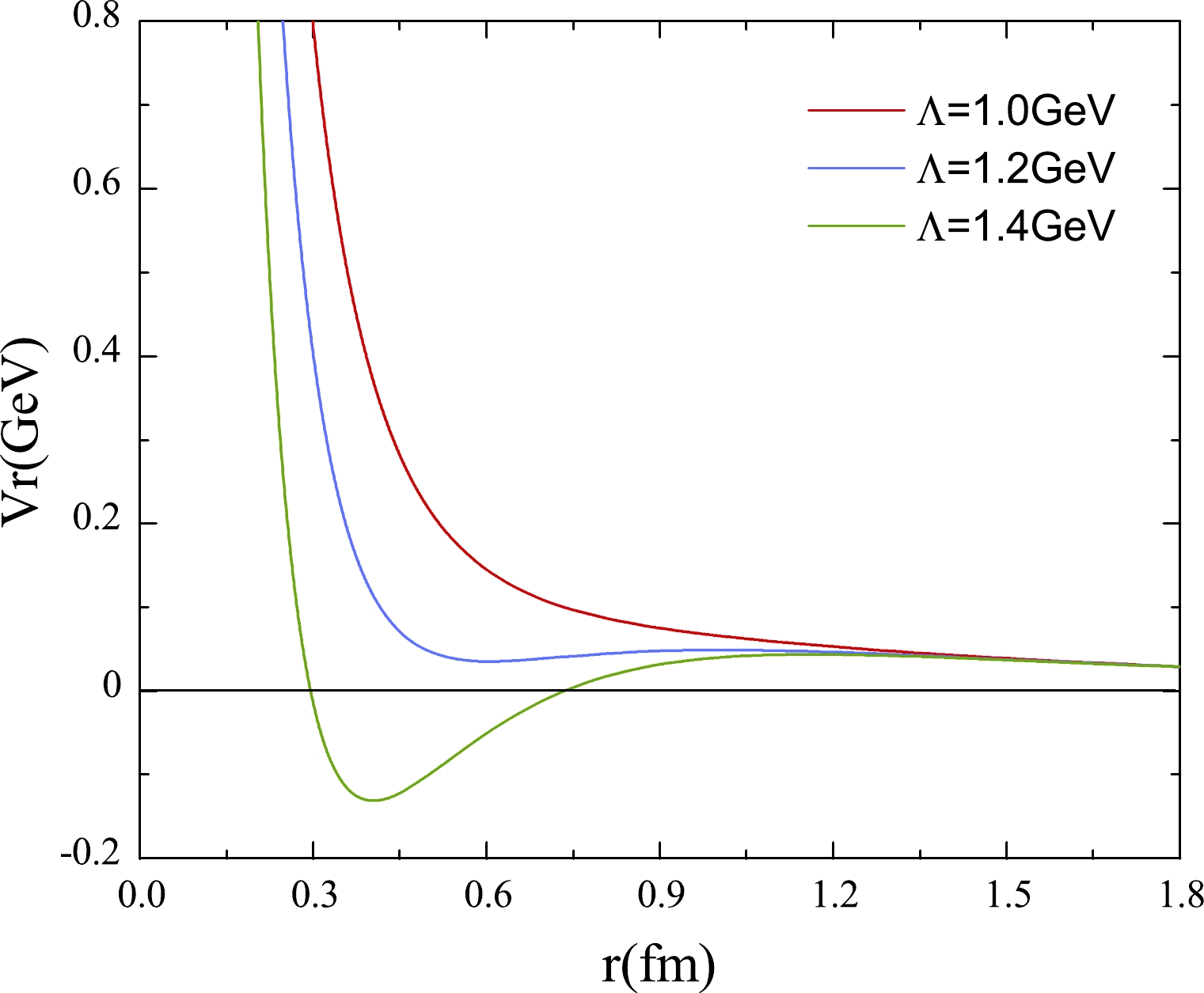
Figure 9. (color online) Total potentials in the one boson exchange model with different values of the cutoff parameter Λ for the
$ ^3D_1 $ wave resonant state dependence on r. The coupling constants are set as$ g_{\sigma \Lambda_c \Lambda_c}= 7.2 $ and$ g_{\omega \Lambda_c \Lambda_c}=9.13 $ .In Table 3, we list the bound and resonant states for the
$ \Lambda_c\bar{\Lambda}_c $ systems. When the cutoff Λ is 1.25 GeV, the coupling constants are set as$ g_{\sigma \Lambda_c \Lambda_c}= 7.2 $ and$ g_{\omega \Lambda_c \Lambda_c}= 9.13 $ . As shown in Table 3, if the$ ^3D_1 $ resonant state is a reasonable explanation for Y(4630), there may also be$ ^1D_2 $ ,$ ^3D_2 $ , and$ ^3D_2 $ resonant states around Y(4630), as well as$ ^1S_0 $ and$ ^3S_1 $ deeper bound states; however, the P resonant state cannot be formed. These states can be investigated in future experiments. Although the angular momentum of the P state is lower than that of the D state, the height of the potential barrier is smaller, and it is not easier to form a resonant state than with the D state. It can be seen that the P state can be formed when$ g_{\omega \Lambda_c \Lambda_c} $ =6.9 (Table 2), and there are no resonant states when$ g_{\omega \Lambda_c \Lambda_c} $ =10.56 (Tables 2 and 3). Therefore, the P-wave resonant state can be formed within a certain parameter range. The P-wave resonant state is not observed in the experiment, probably because it does not form a resonant state or the researchers need to analyze additional data.L E Γ L E Γ $ ^1S_0 $ 

−408.9 $\ldots$ 

$ ^3D_1 $ 

61.08 91.24 $ ^3S_1 $ 

−376.27 $\ldots$ 

$ ^1D_2 $ 

60.41 125.06 $ ^3P_0 $ 

$\ldots$ 

$\ldots$ 

$ ^3D_2 $ 

60.69 112.68 $ ^1P_1 $ 

$\ldots$ 

$\ldots$ 

$ ^3D_3 $ 

55.99 140.98 $ ^3P_2 $ 

$\ldots$ 

$\ldots$ 

Table 3. Energy and width of the bound and resonant states for
$ \Lambda_c\bar{\Lambda}_c $ systems when the cutoff Λ is 1.25 GeV, and the coupling constant are set as$ g_{\sigma \Lambda_c \Lambda_c}= 7.2 $ and$ g_{\omega \Lambda_c \Lambda_c}=9.13 $ . E and Γ represent the energy and width of the resonant states in units of MeV, respectively. The notation$ \ldots $ denotes no bound or resonant state solutions. -
In recent years, many new exotic hadrons have been discovered, some of which can be explained via hadronic molecular states in the one-boson-exchange model. In this paper, we investigate the
$ \Lambda_c\bar{\Lambda}_c $ system using the CSM in the one boson exchange model. The numerical results indicate that the$ \Lambda_c\bar{\Lambda}_c $ system can form not only an S wave bound state but also higher angular momentum L resonant states. When the coupling constants are taken as$ g_{\sigma \Lambda_c \Lambda_c}=7.2 $ and$ g_{\omega \Lambda_c \Lambda_c}=9.13 $ , there is a$ ^3D_1 $ wave resonant state with energy$ E=61.08 $ MeV and decay width$ \Gamma=91.24 $ MeV, which is consistent with the exotic hadron stateY(4630) with the quantum number $J^{PC}=1^{--}$ , a mass of 4634 MeV, and a width of 91.24 MeV. If the$ ^3D_1 $ resonant state is a reasonable explanation for Y(4630), there may also be other bound and resonant states around Y(4630), which remains to be verified experimentally in future.
Explanation of Y(4630) as a hadronic resonant state
- Received Date: 2022-09-18
- Available Online: 2023-03-15
Abstract: Theorists have given various explanations for the discovery of Y(4630). We find that if Y(4630) is interpreted as the D-wave resonant state of the






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF
















 DownLoad:
DownLoad: