-
Research on CP asymmetry in the field of particle physics has received considerable attention and dates back to 1964 [1]. The terms C and P refer to charge conjugation transformation and parity inversion transformation, respectively [2]. CP asymmetry is a crucial platform for discovering new physical signals and exploring the standard model (SM). Over the years, researchers have made significant progress in understanding CP asymmetry through experiments conducted at various particle accelerators around the world. Exciting discoveries in such experiments help us better understand how particles behave under different conditions. However, there are still unknown modules when studying CP asymmetry. Nowadays, studies on the B meson from both the theoretical and experimental perspectives play an increasingly important role and are considered established. These studies can help explore the SM and reveal the quality of interactions between mesons. Meanwhile, the B meson contains a heavy b quark, which makes its decay processes highly suitable for detecting CP asymmetry owing to significant perturbation effects. In this study, we investigate the novel
$ V\rightarrow K^{+}K^{-} (V=\phi, \rho, \omega) $ resonance, which generates a strong phase associated with vector meson resonance and can result in significant CP asymmetry within the interference range. The resonances of vector mesons can not only offer rich physical mechanisms for research on particle characteristics but also provide valuable information on intermediate mesons in multi-body decay processes [3].To theoretically investigate the popular non-leptonic weak decay of the B meson, methods such as perturbative QCD (PQCD) [4] and QCD factorization (QCDF) [5] have been fully explored and widely used by researchers. The PQCD method is employed to extract the hard component attributed to transverse momentum, where QCD correction is involved and treated as perturbative theory. The Sudakov factor is introduced to mitigate the non-perturbative effects. The hadron wave function incorporates the contribution of non-perturbative effects. In the framework of QCDF, we can take the limit to infinity and neglect high-order
$ 1/ m_b $ contributions when the quark mass is extremely large (e.g., b quark) in weak decay processes under the heavy quark limit. The amplitude of two-body non-leptonic decay can be expressed as the product of the form factor from the initial state meson to the final state meson and the light cone distribution amplitude of the other final state meson in the heavy quark limit. The non-leptonic three-body decay of the B meson has been successfully resolved and widely adopted by researchers in recent years. Studying CP asymmetry in B meson decay processes with final states of π and K under QCDF via resonance effects is a highly effective approach [6, 7].The vector meson dominant model (VMD) predicts that the vacuum polarization of the photon is composed of the vector mesons
$ \rho^{0}(770) $ ,$ \omega(782) $ , and$ \phi(1020) $ [8]. The neutral vector meson is predominantly coupled to the two-pion state when$ e^{+}e^{-} $ decay into the pair$ \pi^{+}\pi^{-} $ . The decays of$ \omega(782)(\phi(1020)) $ and$ \rho^{0}(770) $ transition to the$ \pi ^+\pi ^- $ pair and originate from isospin breaking and conservation related to the mixings of$ \rho^{0}(770)-\omega(782) $ and$ \rho^{0}(770)-\phi(1020) $ [9]. Through the unitary matrix, the physical and isospin states of the intermediate resonance hadrons can be combined, yielding a dynamics mechanism that arises from interference among$ \phi(1020) $ ,$ \rho^{0}(770) $ , and$ \omega(782) $ mesons. The presence of new strong phases may impact CP asymmetry in hadron decay within this framework.As a whole, this paper provides a brief introduction to the research background and situation. In the Section II, we analyze the resonance effect in the three-body decay process by examining both the physical mechanisms and detailed formalisms in Subsection A. Then, we conduct a comprehensive analysis of CP asymmetry in the decay processes
$ \bar{B}^{0}\rightarrow K^{+}K^{-} \bar K^{0}(\pi^{0}) $ and$ B^{-}\rightarrow K^{+}K^{-}K^{-}(\pi^{-}) $ under the vector meson resonance mechanisms$ \phi \rightarrow K^{+}K^{-} $ ,$ \rho\rightarrow K^{+}K^{-} $ , and$ \omega \rightarrow K^{+}K^{-} $ in Subsections B and C, respectively, which are the main parts of this study. We then take the decay process$ \bar B^{0}\rightarrow \phi\bar K^{0}\rightarrow K^{+}K^{-}\bar K^{0} $ as an example to illustrate the form of the decay amplitude after considering the above resonance effect and present the typical three-body decay amplitude in Section III. The numerical results of the analysis of CP asymmetry and the localized form are given in Section IV. We present the summary and conclusions in Section V. -
Based on the model dominated by vector mesons, the polarization of the
$ \phi(1020) $ ,$ \rho^{0}(770) $ , and$ \omega(782) $ vector mesons is induced by photons generated from the annihilation of positron-electron pairs. These mesons can subsequently decay into$ K^{+}K^{-} $ pairs. Then, we are able to construct physical particle states by utilizing the isospin fields$ \phi_{I} $ ,$ \rho^{0}_{I} $ , and$ \omega_{I} $ . The two representations are related through a unitary matrix R [9].Because the resonance effect is not a physical field, the unitary matrix R is required to transform the isospin field into a physical field. A relationship between the isospin field (
$ \phi_{I} $ ,$ \rho_{I}^{0} $ ,$ \omega_{I} $ ) and the physical field ((ϕ,$ \rho^{0} $ , ω) can be established using the unitary matrix R, which can be expressed as follows [10]:$ \begin{aligned}[b] R =& \left( {\begin{array}{*{20}{c}} { \lt {\rho _I}|\rho \gt }&{ \lt {\omega _I}|\rho \gt }&{ \lt {\phi _I}|\rho \gt}\\ { \lt {\rho _I}|\omega \gt }&{ \lt {\omega _I}|\omega \gt }&{ \lt {\phi _I}|\omega \gt }\\ { \lt {\rho _I}|\phi \gt }&{ \lt {\omega _I}|\phi \gt }&{ \lt {\phi _I}|\phi \gt } \end{array}} \right) \\=& \left( {\begin{array}{*{20}{c}} 1&{ - {F_{\rho \omega }}(s)}&{ - {F_{\rho \phi }}(s)}\\ {{F_{\rho \omega }}(s)}&1&{ - {F_{\omega \phi }}(s)}\\ {{F_{\rho \phi }}(s)}&{{F_{\omega \phi }}(s)}&1 \end{array}} \right), \end{aligned} $

(1) where
$ F_{\rho\omega}(s) $ ,$ F_{\rho\phi}(s) $ , and$ F_{\omega\phi}(s) $ are of the order$ \mathcal{O}(\lambda) $ ,$ (\lambda\ll 1) $ [9]. The physical manifestation of this transformation can be articulated as$\rho^{0}\;=\;\rho^{0}_{I}-F_{\rho\omega}(s)\omega_{I}-F_{\rho\phi}(s)\Phi_{I}$ ,$\omega\;=\;F_{\rho\omega}(s)\rho^{0}_{I}\;+\; \omega_{I}\;-\;F_{\omega\phi}(s)\Phi_{I}$ , and$\Phi\;=\;F_{\rho\Phi}(s)\rho^{0}_{I}\;+ F_{\omega\phi}(s)\omega_{I}+\Phi_{I}$ .Using the representation forms of the physics and isospin, we establish the following definitions for propagators:
$ D_{V_1V_2}=\left< 0|TV_1V_2|0 \right> $ and$ D_{V_1V_2}^{I}=\left< 0|TV_{1}^{I}V_{2}^{I}|0 \right> $ .$ V_{1} $ and$ V_{2} $ of$ D_{V_{1}V_{2}} $ denote one of the mesons belonging to$ \rho^{0} $ , ω, and ϕ. In fact,$ D_{V_{1}V_{2}} $ is equal to zero owing to the absence of three-vector meson mixing in the physical representation. Furthermore, based on the expression of three-vector meson mixing under physical states, the parameters$ F_{\rho\omega} $ ,$ F_{\rho\phi} $ , and$ F_{\omega\phi} $ are ordered by$ \mathcal{O}(\lambda) (\lambda\ll 1 )$ .There are higher order terms resulting from the contributions of two or more terms, which can be safely disregarded [9]. Consequently, we obtain
$ F_{\rho\omega}=\frac{\Pi_{\rho\omega}}{S_{\rho}-S_{\omega}},\; \; F_{\rho\phi}=\frac{\Pi_{\rho\phi}}{S_{\rho}-S_{\phi}}, \; \; F_{\omega\phi}=\frac{\Pi_{\omega\phi}}{S_{\omega}-S_{\phi}}, $

(2) where
$ \Pi_{\rho\omega} $ ,$ \Pi_{\rho\phi} $ , and$ \Pi_{\omega\phi} $ are the mixing parameters, and$ S_{V} $ and$ m_{V} $ denote the inverse propagator and mass of the vector meson V$ (V=\phi, \rho, \omega) $ , respectively. The propagator$ S_{V} $ is associated with the invariant mass$ \sqrt s $ , which serves as a reliable indicator of CP asymmetry.The mixing parameters
$ \rho-\omega $ ,$ \rho-\phi $ , and$ \omega-\phi $ are extracted from the$ e^{+}e^{-}\rightarrow \pi^{+}\pi^{-} $ experimental data [11−14].Then, we define
$ \widetilde{\Pi}_{\rho\omega}=\frac{S_{\rho}\Pi_{\rho\omega}}{S_{\rho}-S_{\omega}}, \; \; \widetilde{\Pi}_{\rho\phi}=\frac{S_{\rho}\Pi_{\rho\phi}}{S_{\rho}-S_{\phi}}, \; \; \widetilde{\Pi}_{\omega\phi}=\frac{S_{\omega}\Pi_{\rho\omega}}{S_{\omega}-S_{\phi}}, $

(3) where the mixing parameters
$ \widetilde{\Pi}_{\rho\omega}(s) $ ,$ \widetilde{\Pi}_{\rho\phi}(s) $ , and$ \widetilde{\Pi}_{\omega\phi}(s) $ are the momentum dependence for the$ \rho-\omega $ ,$ \rho-\phi $ , and$ \omega-\phi $ interferences, respectively [15].From the above equations, we obtain
$ \tilde{\Pi}_{\rho \omega} $ ,$ \tilde{\Pi}_{\rho \phi} $ , and$ \tilde{\Pi}_{\omega \phi} $ according to the definition$ \tilde{\Pi}_{V_1V_2}=\dfrac{S_{V_1}\Pi _{V_1V_2}}{S_{V_1}-S_{V_2}} $ . For example, we can use$ \dfrac{S_{\rho}\Pi_{\rho\omega}}{S_{\rho}-S_{\omega}} (\dfrac{S_{\omega}\Pi_{\omega\rho}}{S_{\omega}-S_{\rho}} )$ to define$ \widetilde{\Pi}_{\rho\omega} (\widetilde{\Pi}_{\omega\rho} )$ , which is also available for the conversion of the mixing parameters$ \widetilde{\Pi}_{\omega\phi(\phi\omega)} $ and$ \widetilde{\Pi}_{\rho\phi(\phi\rho)} $ . The mixing parameter depends on the momentum, including both the resonant and non-resonant contributions. We expect to search for the contribution of this mixing mechanism in the resonance region of the ω and ϕ mass.Then, we can present
$\mathfrak{Re}\widetilde{\Pi}_{\rho\omega}(m_{\omega}^2)=(-4760\pm440) {\rm{MeV}}^2$ ,${\mathfrak{Im}}\widetilde{\Pi}_{\rho\omega}(m_{\omega}^2)=(-6180\pm3300)~ {\rm{MeV}}^2$ ;$\mathfrak{Re}\widetilde{\Pi}_{\rho\phi}(m_{\phi}^2)= (796\pm 312)~ {\rm{MeV}}^2$ ,${\mathfrak{Im}}\widetilde{\Pi}_{\rho\phi}(m_{\phi}^2)=(-101\pm67)~ {\rm{MeV}}^2$ ;$\mathfrak{Re}\widetilde{\Pi}_{\omega\phi}(m_{\phi}^2)= 19000 ~{\rm{MeV}}^2$ ,${\mathfrak{Im}}\widetilde{\Pi}_{\omega\phi}(m_{\phi}^2)\;=\;(2500\;\pm 300) \; {\rm{MeV}}^2$ , on the basis of$ \widetilde{\Pi}_{\rho\omega}(s)={\mathfrak{Re}}\widetilde{\Pi}_{\rho\omega}(m_{\omega}^2)+{\mathfrak{Im}}\widetilde{\Pi}_{\rho\omega}(m_{\omega}^2) $ ,$ \widetilde{\Pi}_{\rho\phi}(s)= {\mathfrak{Re}}\widetilde{\Pi}_{\rho\phi}(m_{\phi}^2)+{\mathfrak{Im}}\widetilde{\Pi}_{\rho\phi}(m_{\phi}^2) $ , and$ \widetilde{\Pi}_{\omega\phi}(s)= {\mathfrak{Re}}\widetilde{\Pi}_{\omega\phi}(m_{\phi}^2)+ {\mathfrak{Im}}\widetilde{\Pi}_{\omega\phi}(m_{\phi}^2) $ . -
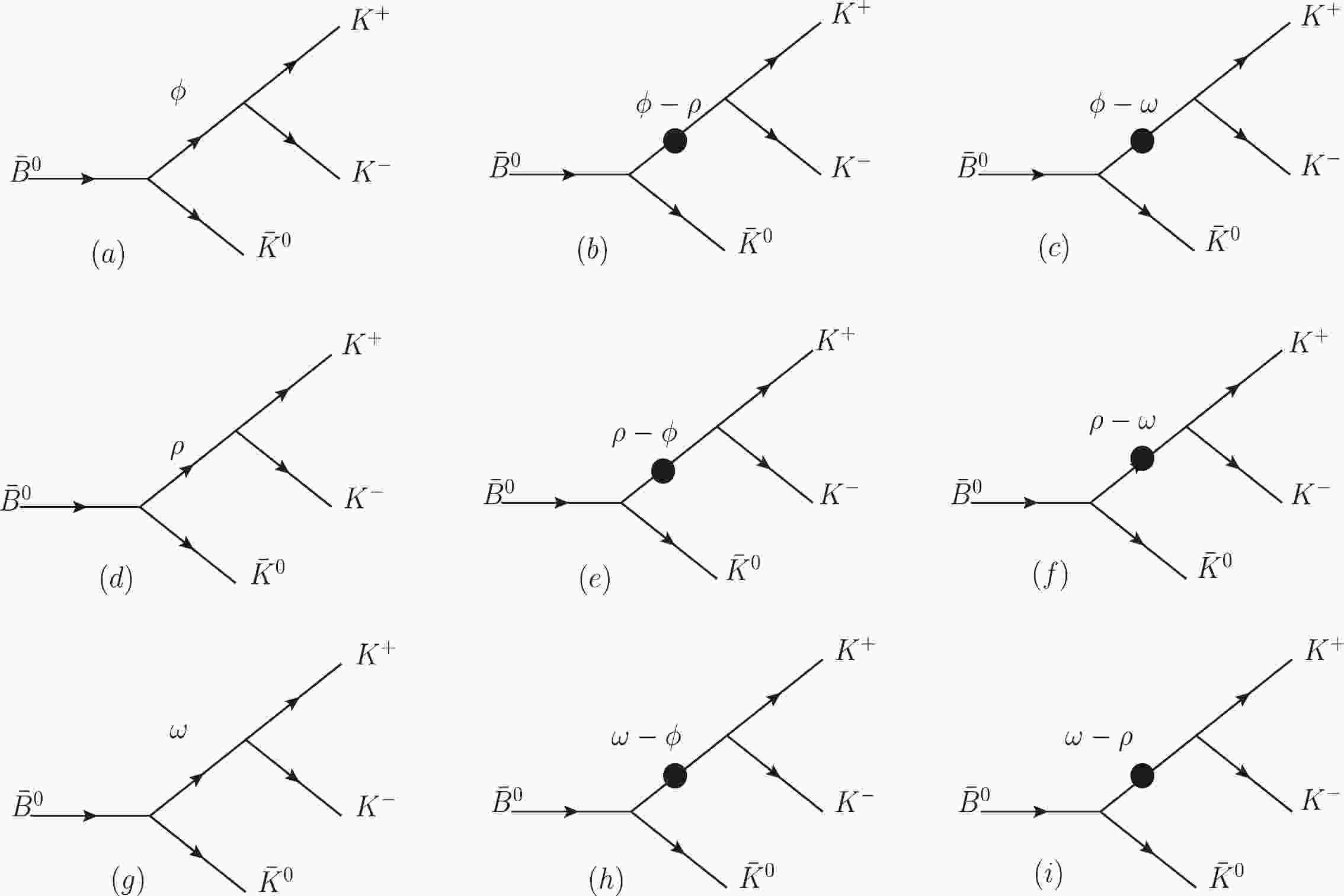
We take the
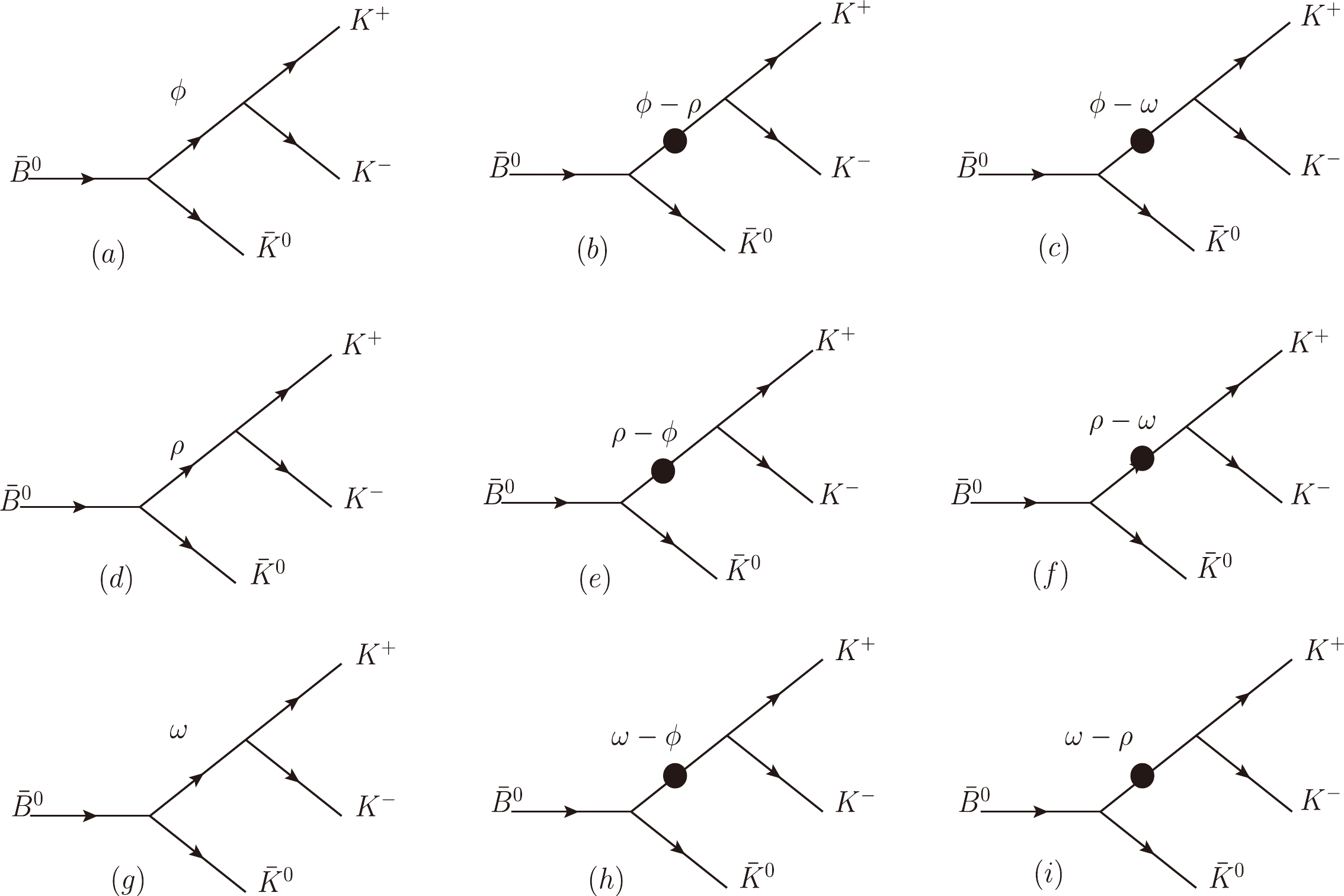
$ \bar B^{0}\rightarrow \phi(\omega,\rho^0) \bar K^{0}\rightarrow K^{+}K^{-} \bar K^{0} $ decay channel as an example to study CP asymmetry. In Fig. 1(a), the$ \bar B^{0} $ meson decays into$ \bar K^{0} $ and a$ K^{+}K^{-} $ pair, which is produced directly by the ϕ resonance effect. Meanwhile, it is known that a$ K^{+}K^{-} $ pair can also exist from the intermediate state of the ω or ρ meson. Therefore, we also consider the processes of ρ and ω decay into$ K^{+}K^{-} $ , which are shown in Fig. 1(d) and (g). Fig. 1 (b) differs from the above decay processes because the ϕ meson decays into$ K^{+}K^{-} $ through ρ resonance, and the mixing parameter$ \rho-\phi $ is given here. Fig. 1 (c), (e), (f), (h), and (i) are similar to Fig. 1 (b). However, we find that there are the resonance effects$ \rho-\phi ( \phi-\rho )$ ,$ \omega-\phi (\phi-\omega) $ , and$ \rho-\omega ( \omega-\rho) $ , which produce the$ \Pi_{\rho\phi(\phi\rho)} $ ,$ \Pi_{\omega\phi(\phi\omega)} $ , and$ \Pi_{\rho\omega(\omega\rho)} $ mixing parameters, respectively.The amplitude A of the three-body decay process of
$ \bar B^{0}\rightarrow K^{+}K^{-} \bar K^{0} $ can be expressed as$ A=\big<K^+K^- \bar K^{0}|H^T|\bar B^{0}\big>+\big<K^+K^- \bar K^{0}|H^P|\bar B^{0}\big>, $

(4) where
$ \big<K^{+}K^{-} \bar K^{0}|H^T|\bar B^{0}\big> $ and$ \big<K^{+}K^{-} \bar K^{0}|H^P|\bar B^{0}\big> $ refer to the amplitude from the tree and penguin contributions, respectively. To obtain the formalism of CP asymmetry, we set a definition$ A=\big<K^+K^- \bar K^{0}|H^T|\bar B^{0}\big>[1+r{\rm e}^{{\rm i}(\delta+\phi)}], $

(5) where
$r\equiv\Bigg|\frac{\big<K^+K^- \bar K^{0}|H^P|\bar B^{0}\big>}{\big<K^+K^- \bar K^{0}|H^T|\bar B^{0}\big>}\Bigg|. $

(6) The strong phase δ is generated through the Wilson coefficient and resonance effect in this three-body decay process. The weak phase ϕ is associated with the CKM matrix. They can affect the CP asymmetry of this decay process. Furthermore, we can present the detailed formalisms of the tree and penguin amplitudes by combining the decay diagrams in Fig. 1:
$ \begin{aligned}\\[-6pt] \big<K^+K^- \bar K^{0}|H^T|\bar B^{0}\big>=\frac{g_{\rho}}{s_{\rho}}t_{\rho} +\frac{g_{\phi}}{s_{\phi}s_{\rho}}\widetilde{\Pi}_{\rho\phi}t_{\rho} +\frac{g_{\omega}}{s_{\omega}s_{\rho}}\widetilde{\Pi}_{\rho\omega}t_{\rho} +\frac{g_{\omega}}{s_{\omega}}t_{\omega} +\frac{g_{\phi}}{s_{\phi}s_{\omega}}\widetilde{\Pi}_{\omega\phi}t_{\omega} +\frac{g_{\rho}}{s_{\rho}s_{\omega}}\widetilde{\Pi}_{\rho\omega}t_{\omega}, \end{aligned}$ 
(7) $ \begin{aligned}[b] \big<K^+K^- \bar K^{0}|H^P|\bar B^{0}\big>= & \frac{g_{\phi}}{s_{\phi}}p_{\phi} +\frac{g_{\rho}}{s_{\rho}s_{\phi}}\widetilde{\Pi}_{\rho\phi}p_{\phi} +\frac{g_{\omega}}{s_{\phi}s_{\omega}}\widetilde{\Pi}_{\omega\phi}p_{\phi} +\frac{g_{\rho}}{s_{\rho}}p_{\rho} +\frac{g_{\phi}}{s_{\rho}s_{\phi}}\widetilde{\Pi}_{\rho\phi}p_{\rho} \\ & +\frac{g_{\omega}}{s_{\rho}s_{\omega}}\widetilde{\Pi}_{\rho\omega}p_{\rho} +\frac{g_{\omega}}{s_{\omega}}p_{\omega} +\frac{g_{\phi}}{s_{\omega}s_{\phi}}\widetilde{\Pi}_{\omega\phi}p_{\omega} +\frac{g_{\rho}}{s_{\rho}s_{\omega}}\widetilde{\Pi}_{\rho\omega}p_{\omega}, \end{aligned} $

(8) where
$ t_{\phi}(p_{\phi}) $ ,$ t_{\rho}(p_{\rho}) $ , and$ t_{\omega}(p_{\omega}) $ are the tree (penguin) contributions for the$ \bar B^{0}\rightarrow \phi \bar K^{0} $ ,$ \bar B^{0}\rightarrow \rho^{0} \bar K^{0} $ , and$ \bar B^{0}\rightarrow \omega \bar K^{0} $ decay processes, respectively. The term$ t_{\phi} $ in Eq. (7) is ignored because it is zero during our calculation. The coupling constant$ g_{V} (V=\phi, \rho, \omega) $ is from the decay process$ V\rightarrow K^{+}K^{-} $ . We quote an article to describe the value of$ g_{V} $ by assuming the$S U(3) $ relations with ideal mixing [16]:$ g_{\rho K \bar K} = g_{\omega K \bar K} = \dfrac{1}{\sqrt{2}}g_{\phi K \bar K} $ and$ g_{\phi K \bar K} =4.46\; {\rm{GeV}}^2 $ . Then, we can obtain$ \begin{aligned}[b] \\[-5pt] r{\rm e}^{{\rm i}\delta}{\rm e}^{{\rm i}\phi}=& \frac{g_{\omega}p_{\omega}s_{\rho}s_{\phi}+g_{\phi}p_{\phi}s_{\rho}s_{\omega}+ g_{\rho}p_{\rho}s_{\phi}s_{\omega}+g_{\phi}p_{\rho}s_{\omega}\widetilde{\Pi}_{\rho\phi} +g_{\rho}p_{\phi}s_{\omega}\widetilde{\Pi}_{\rho\phi}} {g_{\rho}s_{\phi}s_{\omega}t_{\rho}+g_{\omega}s_{\rho}s_{\phi}t_{\omega}+g_{\phi}s_{\omega}t_{\rho}\widetilde{\Pi}_{\rho\phi} +g_{\rho}s_{\phi}t_{\omega}\widetilde{\Pi}_{\rho\omega}+g_{\phi}s_{\rho}t_{\omega}\widetilde{\Pi}_{\omega\phi}+ g_{\omega}s_{\phi}t_{\rho}\widetilde{\Pi}_{\rho\omega}} \\ &+\frac{g_{\rho}p_{\omega}s_{\phi}\widetilde{\Pi}_{\rho\omega} +g_{\phi}p_{\omega}s_{\rho}\widetilde{\Pi}_{\omega\phi}+g_{\omega}p_{\rho}s_{\phi}\widetilde{\Pi}_{\rho\omega} +g_{\omega}p_{\phi}s_{\rho}\widetilde{\Pi}_{\omega\phi}} {g_{\rho}s_{\phi}s_{\omega}t_{\rho}+g_{\omega}s_{\rho}s_{\phi}t_{\omega}+g_{\phi}s_{\omega}t_{\rho}\widetilde{\Pi}_{\rho\phi} +g_{\rho}s_{\phi}t_{\omega}\widetilde{\Pi}_{\rho\omega}+g_{\phi}s_{\rho}t_{\omega}\widetilde{\Pi}_{\omega\phi}+ g_{\omega}s_{\phi}t_{\rho}\widetilde{\Pi}_{\rho\omega}}. \end{aligned} $ 
(9) Define
$\frac{p_{\omega}}{t_{\rho}}\equiv r_{1} {\rm e}^{{\rm i}(\delta_\lambda+\phi)}, \quad\frac{p_{\phi}}{t_{\rho}}\equiv r_{2}{\rm e}^{{\rm i}(\delta_\chi+\phi)}, \quad\frac{t_{\omega}}{t_{\rho}}\equiv r_{3} {\rm e}^{{\rm i}\delta_\alpha}, \quad\frac{p_{\rho}}{p_{\omega}}\equiv r_{4} {\rm e}^{{\rm i}\delta_\beta}, $

(10) where
$ \delta_\lambda $ ,$ \delta_\chi $ ,$ \delta_\alpha $ , and$ \delta_\beta $ are strong phases. Then, we can substitute them into Eq. (9) and perform some simplifications:$ \begin{aligned}[b] r{\rm e}^{{\rm i}\delta}=& \frac{r_{1}{\rm e}^{{\rm i}\delta_\lambda}s_{\phi}s_{\rho}g_{\omega} +r_{2}{\rm e}^{{\rm i}\delta_\chi}s_{\omega}s_{\rho}g_{\phi} +r_{1}{\rm e}^{{\rm i}\delta_\lambda}r_{4}{\rm e}^{{\rm i}\delta_\beta}s_{\omega}s_{\phi}g_{\rho} +r_{2}{\rm e}^{{\rm i}\delta_\chi}s_{\omega}g_{\rho}\widetilde{\Pi}_{\rho\phi} +r_{1}{\rm e}^{{\rm i}\delta_\lambda}r_{4}{\rm e}^{{\rm i}\delta_\beta}s_{\omega}g_{\phi}\widetilde{\Pi}_{\rho\phi}} {r_{3}{\rm e}^{{\rm i}\delta_\alpha}s_{\phi}s_{\rho}g_{\omega}+s_{\phi}s_{\omega}g_{\rho} +s_{\omega}g_{\phi}\widetilde{\Pi}_{\rho\phi} +r_{3}{\rm e}^{{\rm i}\delta_\alpha}s_{\phi}g_{\rho}\widetilde{\Pi}_{\rho\omega} +r_{3}{\rm e}^{{\rm i}\delta_\alpha}s_{\rho}g_{\phi}\widetilde{\Pi}_{\omega\phi} +s_{\phi}g_{\omega}\widetilde{\Pi}_{\rho\omega}}\\ & +\frac{r_{1}{\rm e}^{{\rm i}\delta_\lambda}s_{\phi}g_{\rho}\widetilde{\Pi}_{\rho\omega} +r_{1}{\rm e}^{{\rm i}\delta_\lambda}s_{\rho}g_{\phi}\widetilde{\Pi}_{\omega\phi} +r_{1}{\rm e}^{{\rm i}\delta_\lambda}r_{4}{\rm e}^{{\rm i}\delta_\beta}s_{\phi}g_{\omega}\widetilde{\Pi}_{\rho\omega} +r_{2}{\rm e}^{{\rm i}\delta_\chi}s_{\rho}g_{\omega}\widetilde{\Pi}_{\omega\phi}} {r_{3}{\rm e}^{{\rm i}\delta_\alpha}s_{\phi}s_{\rho}g_{\omega}+s_{\phi}s_{\omega}g_{\rho} +s_{\omega}g_{\phi}\widetilde{\Pi}_{\rho\phi} +r_{3}{\rm e}^{{\rm i}\delta_\alpha}s_{\phi}g_{\rho}\widetilde{\Pi}_{\rho\omega} +r_{3}{\rm e}^{{\rm i}\delta_\alpha}s_{\rho}g_{\phi}\widetilde{\Pi}_{\omega\phi} +s_{\phi}g_{\omega}\widetilde{\Pi}_{\rho\omega}}, \end{aligned} $

(11) where
$ r{\rm cos\delta} $ is defined as the real part of$r{\rm e}^{{\rm i}\delta}$ associated with the mixing parameter, and$ r{\rm sin\delta} $ is defined as the imaginary part of$r{\rm e}^{{\rm i}\delta}$ associated with the mixing parameter; hence, the real and imaginary parts of the mixing parameters act here. ϕ is related to$\dfrac{V_{\rm tb}V_{\rm ts}^{*}}{V_{\rm ub}V_{\rm us}^{*}}$ from the CKM matrix. Therefore, we can get${\rm sin}\phi =-\dfrac{\eta}{\sqrt{\rho^2+\eta^2}}$ and${\rm cos}\phi = -\dfrac{\rho}{\sqrt{\rho^2+\eta^2}}$ through the Wolfenstein parameters. Thus, the definition of CP asymmetry is as follows:$ A_{\rm cp} = \frac{\left| A \right|^2-\left| \overline{A} \right|^2}{\left| A \right|^2+\left| \overline{A} \right|^2}= \frac{-2r{\rm sin\delta}{\rm sin\phi}}{1+2r{\rm cos\delta}{\rm cos\phi}+r^2}. $

(12) -
In previous experimental measurements, large localized CP asymmetry has been observed from the decay mode
$ B^{\pm}\rightarrow \phi K^{\pm}\rightarrow K^{+}K^{-}K^{\pm} $ in the region$ m_{K^+ K^-} < 1.04 $ GeV and the decay mode$ B^{\pm}\rightarrow \phi \pi^{\pm}\rightarrow K^{+}K^{-}\pi^{\pm} $ in the region$ m^2_{K^+ K^-} < 1.5 \; {\rm{GeV}}^2 $ under the range of ϕ [17−19]. To simplify, we take the$ \bar B^{0}\rightarrow \phi(\omega,\rho^0) \bar K^{0}\rightarrow K^{+}K^{-} \bar K^{0} $ decay channel as an example to introduce the localized CP asymmetry in a certain energy region by integrating$ A_{ CP} $ . First, the total amplitude of$ \bar B^{0}\rightarrow K^{+}K^{-} \bar K^{0} $ can be regarded as two components. We can obtain their forms in the decay process$ \bar B^{0}\rightarrow \phi \bar K^{0}\rightarrow K^{+}K^{-} \bar K^{0} $ as follows:$ M_{\bar B^{0}\rightarrow \phi \bar K^{0}}^{\lambda}=\alpha p_{\bar B^{0}} \cdot \epsilon^{*}(\lambda), $

(13) $ M_{\phi \rightarrow K^+ K^-}^{\lambda}=g_{\phi}\epsilon(\lambda)\left(p_{1}-p_{2}\right), $

(14) where
$ \epsilon $ is the polarization vector of ϕ, λ represents the direction of polarization for$ \epsilon $ ,$ p_{\bar B^{0}} $ is the momentum of the$ \bar B^{0} $ meson, α refers to the part of the amplitude that is independent of λ,$ p_{1} $ and$ p_{2} $ are the momentum of$ K^{+} $ and$ K^{-} $ produced by ϕ in the decay process$ \phi\rightarrow K^{+}K^{-} $ ,$ g_{\phi} $ is introduced to the effective coupling constant, and$ s_{\phi} $ refers to the gluon propagator. Therefore, the total amplitude of the$ \bar B^{0}\rightarrow \phi \bar K^{0}\rightarrow K^{+}K^{-} \bar K^{0} $ decay process can be expressed as$ \begin{aligned}[b] A =&\alpha p_{\bar B^{0}}^{\mu} \frac{\sum_{\lambda} \epsilon_{\mu}^{*}(\lambda) \epsilon_{\nu}(\lambda)}{s_{\phi}} \frac{g_{\phi}}{s_{\phi}}\left(p_{1}-p_{2}\right)^{\nu} \\ =&-\frac{g_{\phi} \alpha}{s_{\phi}} \cdot p_{\bar B^{0}}^{\mu}\left[g_{\mu \nu}-\frac{\left(p_{1}+p_{2}\right)_{\mu}\left(p_{1}+p_{2}\right)_{\nu}}{m_{\phi}^{2}}\right]\left(p_{1}-p_{2}\right)^{\nu}, \end{aligned} $

(15) where
$ \sqrt{s} $ is the low invariant mass of the$ K^{+}K^{-} $ pair. If$ \sqrt{s^{\prime}} $ is the high invariance mass of the$ K^{+} K^{-} $ pair,$ s_{\max }^{\prime} $ is the maximum values of$ s^{\prime} $ for a fixed s and$ s_{\min }^{\prime} $ is the minimum values of$ s^{\prime} $ for a fixed s [20]. We get$ m^{2}_{ij} = p^{2}_{ij} $ via the conservation of energy and momentum in the three body decay process. Thus, the amplitude is expressed as$A =\frac{g_{\phi}}{s_{\phi}} \cdot \frac{M_{\bar B^{0}\rightarrow \phi \pi^{0}( \bar K^{0})}^{\lambda}}{p_{\bar B^{0}} \cdot \epsilon^{*}} \cdot\left(\Sigma-s^{\prime}\right)=\left(\Sigma-s^{\prime}\right)\cdot \mathcal{N}, $

(16) We can integrate the denominator and numerator of
$ A_{CP} $ within the range$ \Omega \left(s_{1}<s<s_{2}, s_{1}^{\prime}<s^{\prime}< s_{2}^{\prime}\right) $ .$ \mathcal{N} $ is the substitution of the previous formula. Through the kinematic analysis of three-body decay in the region$ \Omega \left(s_{1}<s<s_{2}, s_{1}^{\prime}<s^{\prime}< s_{2}^{\prime}\right) $ , it can be concluded that$\Sigma=\left(s_{\max }^{\prime}+s_{\min }^{\prime}\right)/2$ is related to the value of s. In this case, Σ is generally considered a constant because s varies only at the smallest scale. It follows that$ \int_{s_{1}^{\prime}}^{s_{2}^{\prime}} \mathrm{d}s^{\prime}\left(\Sigma-s^{\prime}\right) $ is canceled out, and we also believe that the$A_{CP}^{\Omega}$ obtained in this way is independent of the invariant mass of the positive and negative meson pairs. We obtain the localized integrated CP asymmetry, which takes the form [21]$ A_{CP}^{\Omega}=\frac{\displaystyle\int_{s_{1}}^{s_{2}} \mathrm{\; d} s \displaystyle\int_{s_{1}^{\prime}}^{s_{2}^{\prime}} \mathrm{d} s^{\prime}\left(\Sigma-s^{\prime}\right)^{2}\left(|\mathcal{N}|^{2}-|\overline{\mathcal{N}}|^{2}\right)}{\displaystyle\int_{s_{1}}^{s_{2}} \mathrm{\; d} s \displaystyle\int_{s_{1}^{\prime}}^{s_{2}^{\prime}} \mathrm{d} s^{\prime}\left(\Sigma-s^{\prime}\right)^{2}\left(|\mathcal{N}|^{2}+|\overline{\mathcal{N}}|^{2}\right)}.$

(17) It is assumed that
$ s_{\min}^{'}<s^{'}<s_{\max}^{'} $ represents the integral interval of the high invariant mass of$ K^{+}K^{-} $ , and$ \int_{s_{1}^{\prime}}^{s_{2}^{\prime}} \mathrm{d}s^{\prime}\left(\Sigma-s^{\prime}\right) $ represents the factor dependent on s. In our calculation, we consider an s dependence between the values of$ s_{\max}^{'} $ and$ s_{\min}^{'} $ . -
We compute the CP asymmetry using the quasi-two-body decay process, wherein both tree-level and penguin-level contributions are involved. In the two-body decay of the B meson, the form factor governing its transition to final hadrons is primarily determined by non-perturbative effects. The non-factorizable contribution of the hadron matrix element arises mainly from hard gluon exchange. We employ the QCDF approach to compute the amplitudes of quasi-two-body decays and complete the calculation of associated hard-scattering kernels. In our phenomenological analysis, we evaluate both the chirality-enhancement term and weak annihilation contributions [5]. Based on the CKM matrix elements of
$V_{\rm ub}V^{*}_{\rm us}$ and$V_{\rm tb}V^{*}_{\rm ts}$ , the decay amplitude of$\bar{B}^{0}\rightarrow \phi(\rho^0,\omega) \bar K^{0}\rightarrow K^+ K^-\bar K^{0}$ in the QCDF approach can be written as$ \begin{aligned}[b] \\[-5pt] A\left(\bar{B}^{0}\rightarrow \phi \left( \phi \rightarrow K^+ K^- \right) \bar K^{0} \right) =&{\sum_{\lambda =0,\pm 1}}{\frac{G_FP_{\bar{B}^{0}}\cdot \epsilon ^*\left( \lambda \right) g_{\phi}\epsilon \left( \lambda \right) \cdot \left( p_{K ^+}-p_{K ^-} \right)}{s_{\phi}}} \times \left\{V_{\rm tb}V_{\rm ts}^{*} \left[-\sqrt{2}m_{\phi} (\epsilon \cdot p_{K})f_{\phi}F_{1}^{B\rightarrow K}\left( a_3+a_5+a_4\right.\right.\right. \\ &-\frac{1}{2}a_{10}\left.\left.\left.-\frac{1}{2}a_7-\frac{1}{2}a_9\right)-\frac{\sqrt{2}}{2}f_B f_K f_{\phi}b_{3}(\phi,K)-\frac{\sqrt{2}}{4}f_B f_K f_{\phi}b_{3}^{e\omega}(\phi,K)\right]\right\}, \end{aligned} $ 
(18) $ \begin{aligned}[b] A\left(\bar{B}^{0}\rightarrow \rho^0 \left(\rho^0 \rightarrow K^+ K^- \right) \bar K^{0} \right) ={\sum_{\lambda =0,\pm 1}}{\frac{G_FP_{\bar{B}^{0}}\cdot \epsilon ^*\left( \lambda \right) g_{\rho}\epsilon \left( \lambda \right) \cdot \left( p_{K ^+}-p_{K ^-} \right)}{s_{\rho}}} \times \left\{V_{\rm ub}V_{\rm us}^{*}m_{\rho}(\epsilon \cdot p_{K})f_{\rho}F_{1}^{B\rightarrow K}a_2+V_{\rm tb}V_{\rm ts}^{*}\left[m_{\rho}(\epsilon \cdot p_{K})f_{K} \right.\right. \end{aligned} $

$ \begin{aligned}[b] & \left.\left. A_{0}^{B\rightarrow \rho}\left( a_4-\frac{1}{2}a_{10}+a_6Q -\frac{1}{2}a_8Q\right)-m_{\rho}(\epsilon \cdot p_{K})f_{\rho}F_{1}^{B\rightarrow K}\right.\right. \Bigg(\frac{3}{2}a_{7}+\frac{3}{2}a_9\Bigg)\\&+\frac{1}{2}f_B f_K f_{\rho} b_{3}(K,\rho)-\frac{1}{4}f_B f_K f_{\rho}b_{3}^{e\omega}(K,\rho)\Bigg]\Bigg\}, \end{aligned} $

(19) $ \begin{aligned}[b] A\left(\bar{B}^{0}\rightarrow \omega \left(\omega \rightarrow K^+ K^- \right) \bar K^{0} \right) =&{\sum_{\lambda =0,\pm 1}}{\frac{G_FP_{\bar{B}^{0}}\cdot \epsilon ^*\left( \lambda \right) g_{\omega}\epsilon \left( \lambda \right) \cdot \left( p_{K ^+}-p_{K ^-} \right)}{s_{\omega}}} \times \left\{V_{\rm ub}V_{\rm us}^{*}m_{\omega} (\epsilon \cdot p_{K})f_{\omega}F_{1}^{B\rightarrow K}a_2+V_{\rm tb}V_{\rm ts}^{*}\left[-m_{\omega} (\epsilon \cdot p_{K})f_{K}\right.\right. \\ &\left.\left.A_{0}^{B\rightarrow \omega}\left(a_4-\frac{1}{2}a_{10}+a_6Q-\frac{1}{2}a_8Q \right)-m_{\omega} (\epsilon \cdot p_{K})f_{\omega}F_{1}^{B\rightarrow K}\Bigg(2a_3\right.\right. +2a_5+\frac{1}{2}a_{7}+\frac{1}{2}a_9\Bigg)\\&-\frac{1}{2}f_B f_K f_{\omega}b_{3}(K,\omega)-\frac{1}{4}f_B f_K f_{\omega}b_{3}^{e\omega}(K,\omega)\Bigg]\Bigg\}. \end{aligned} $

(20) where
$ f_{\pi} $ ,$ f_{B} $ , and$ f_{\phi(\rho, \omega)} $ represent the decay constants, and$ a_{n} $ (n = 1, 2, 3...) is related to the Wilson coefficient$ C_{n} $ under QCDF theory [22],$ A_{0}^{B\rightarrow \rho} $ ,$ A_{0}^{B\rightarrow \omega} $ , and$ F_{1}^{B\rightarrow \pi} $ are the form factors from the non-perturbative contribution,$ b_{1(\rho,\pi)} $ and$ b_{3,4}^{e\omega}(\rho,\pi) $ are the contributions from the annihilation process [23],$ \epsilon $ is the polarization vector of the vector meson$ (V=\phi, \rho, \omega) $ , and$ p_{K} $ is the momentum of the K meson. To simplify the calculation, we define the operator Q$ (Q=\dfrac{-2m_{K^{0}}^{2}}{(m_b+m_d)(m_d+m_s)}) $ [24, 25].Phenomenological parameters are used to express the end point integrals of these logarithmic divergences in hard scattering processes involving the spectator quark. The investigation of the annihilation amplitude involves the contribution from the twist-3 distribution amplitude of the final pseudo-scalar meson [25]. In the annihilation decay process, b represents the annihilation coefficient, where
$ b_{1,2} $ ,$ b_{3,4} $ , and$ b_{3,4}^{e\omega} $ correspond to the effective operator$ Q_{1,2} $ , QCD penguin operator$ Q_{3-6} $ , and weak electric penguin operator$ Q_{7-10} $ , respectively . The amplitude is parameterized and depends on the contributions of tree-level and penguin-level, where the parameters$ X_H $ and$ X_A $ are introduced. We define$X_{H}=\int_{0}^{1} \dfrac{{\rm d}{y}}{1-y}$ and$X_{A}=\int_{0}^{1} \dfrac{{\rm d}{x}}{x}$ to deal with the contribution from the annihilation process, which cannot be ignored [26]. We also consider the hard scattering of the spectator quark and the contribution from the annihilation process, which provide valuable information regarding the strong phase. -
The numerical results clarify the relationship between CP asymmetry (r and strong phase δ) and
$ \sqrt{s} $ under the resonance effect of the three vector mesons, which are shown in Fig. 2 to Fig. 7. In our study, we observe the figures of CP asymmetry and consider the threshold for$ K^+ K^- $ to be around 0.98 GeV from the PDG (2022) [27]. We find that the decay channel$ \phi(\rho,\omega)\rightarrow K^{+}K^{-} $ will produce large CP asymmetry around 0.98 GeV. For a simpler observation, we choose the region 0.96−1.06 GeV under our theoretical framework, which is the main region of resonance for the decay process$ B\rightarrow K^{+}K^{-}\pi(K) $ , to construct the figures. We find that CP asymmetry changes sharply for the decay processes$\bar{B}^{0}\rightarrow $ $ K^{+}K^{-}\bar K^{0}(\pi^{0})$ and$ B^{-}\rightarrow K^{+}K^{-}K^{-}(\pi^{-}) $ from the$\phi\rightarrow K^{+}K^{-}$ ,$ \rho\rightarrow K^{+}K^{-} $ , and$ \omega\rightarrow K^{+}K^{-} $ resonances in Figs. 2 and 3, where ϕ is the main contribution.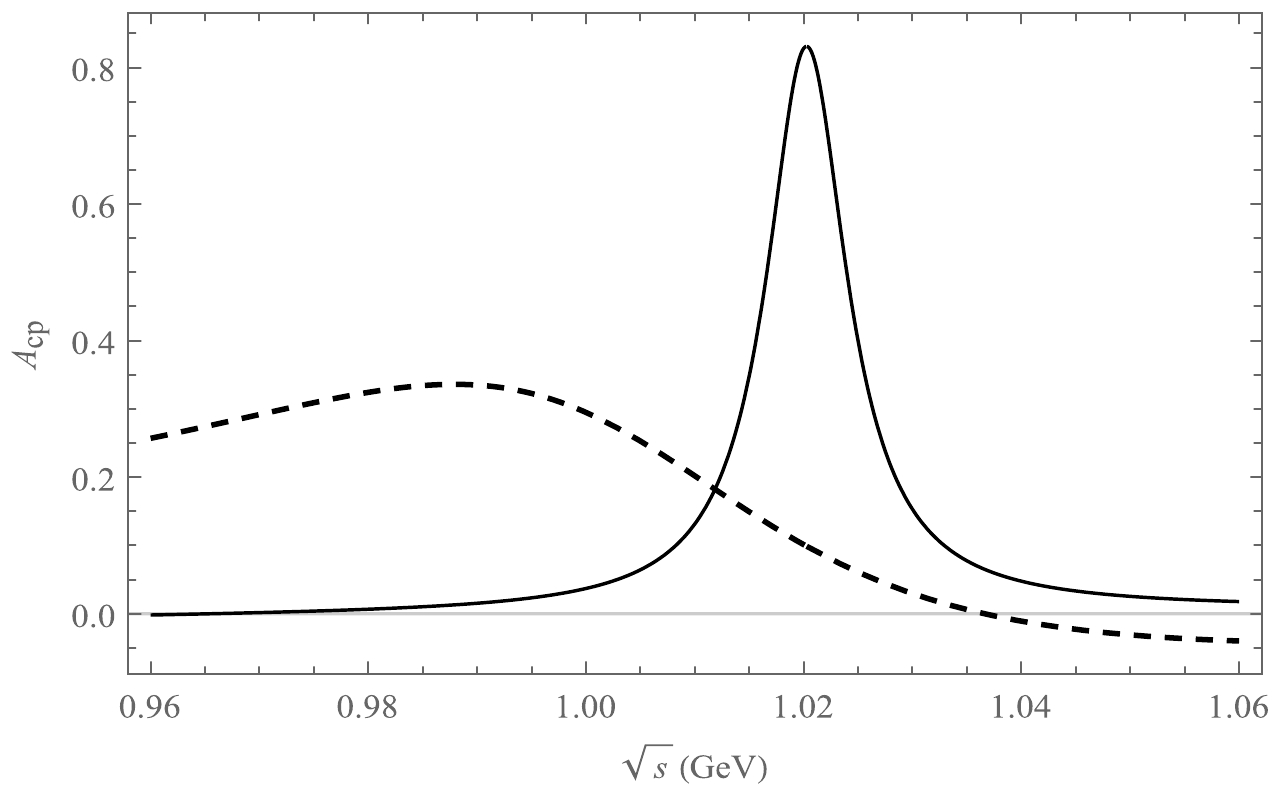
Figure 2.
$A_{ CP}$ as a function of$ \sqrt{s} $ , where the solid line corresponds to the decay channel$ \bar B^{0}\rightarrow K^{+}K^{-}\pi^{0} $ , and the dotted line refers to the decay channel$ \bar B^{0}\rightarrow K^{+}K^{-} \bar K^{0} $ .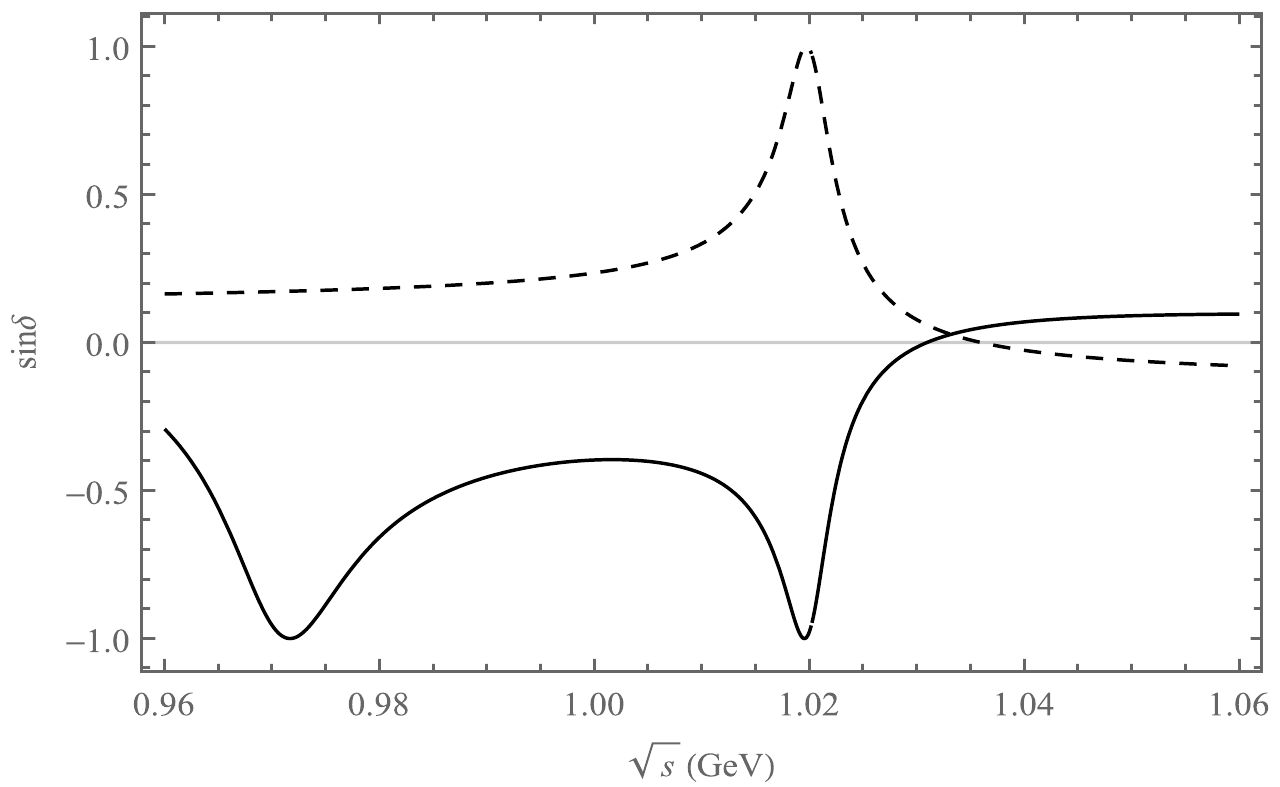
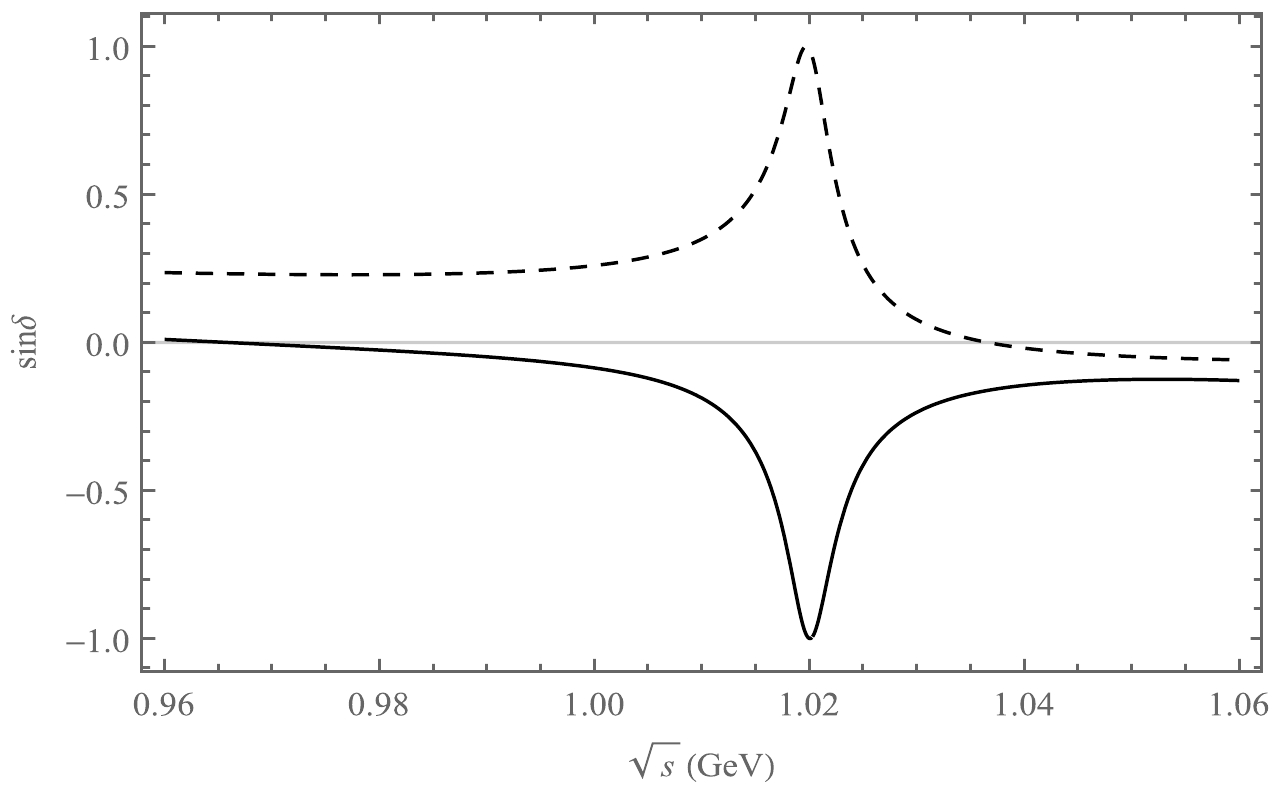
Figure 7.
$ {{\rm{sin}}}\delta $ as a function of$ \sqrt{s} $ , where the solid line is the decay channel$ B^{-}\rightarrow K^{+}K^{-}\pi^{-} $ , and the dotted line refers to the decay channel$ B^{-}\rightarrow K^{+}K^{-}K^{-} $ .
Figure 3.
$A_{ CP}$ as a function of$ \sqrt{s} $ , where the solid line corresponds to the decay channel$ B^{-}\rightarrow K^{+}K^{-}\pi^{-} $ , and the dotted line refers to the decay channel$ B^{-}\rightarrow K^{+}K^{-}K^{-} $ .For the decay mode
$ \bar{B}^{0}\rightarrow K^{+}K^{-}\pi^{0} $ , we find that there are large CP asymmetries, which can reach approximately 82.5% around 1.02 GeV in the ϕ resonance range in Fig. 2. In addition, the CP asymmetry of the$ \bar{B}^{0}\rightarrow K^{+}K^{-} \bar K^{0} $ decay process changes slightly from that of the$ \bar{B}^{0}\rightarrow K^{+}K^{-}\pi^{0} $ process. The CP asymmetry reaches approximately 33.1% around 0.99 GeV in the ϕ resonance range in Fig. 2. The maximum value of the CP asymmetry of the decay channel$ B^{-}\rightarrow K^{+}K^{-}\pi^{-} $ can reach 92.7% around 1.02 GeV in the ϕ resonance range in Fig. 3. Moreover, we find that the CP asymmetry varies, reaching approximately 89.4% in the ϕ resonance range for the decay channel$ B^{-}\rightarrow K^{+}K^{-}K^{-} $ in Fig. 3. The contribution of the resonance effect is obvious under the range of the ϕ mass, which can be seen in Figs. 2 and 3. In summary, the maximum value of CP asymmetry occurs in the range of up to 1.02 GeV for all decay processes.The ratio r of the penguin-level and tree-level contributions affects the CP asymmetry from Eq. (12). We present the relationship between r and
$ \sqrt{s} $ by taking the central parameter value of the CKM matrix elements in Figs. 4 and 5. It is evident that the rangeability of r in the ϕ resonance range is large, especially for the decay mode$ \bar{B}^{0}\rightarrow K^{+}K^{-}\pi^{0} $ , which can have a significant effect on the CP asymmetry.
Figure 4. r as a function of
$ \sqrt{s} $ , where the solid line corresponds to the decay channel$ \bar B^{0}\rightarrow K^{+}K^{-}\pi^{0} $ , and the dotted line refers to the decay channel$ \bar B^{0}\rightarrow K^{+}K^{-} \bar K^{0} $ .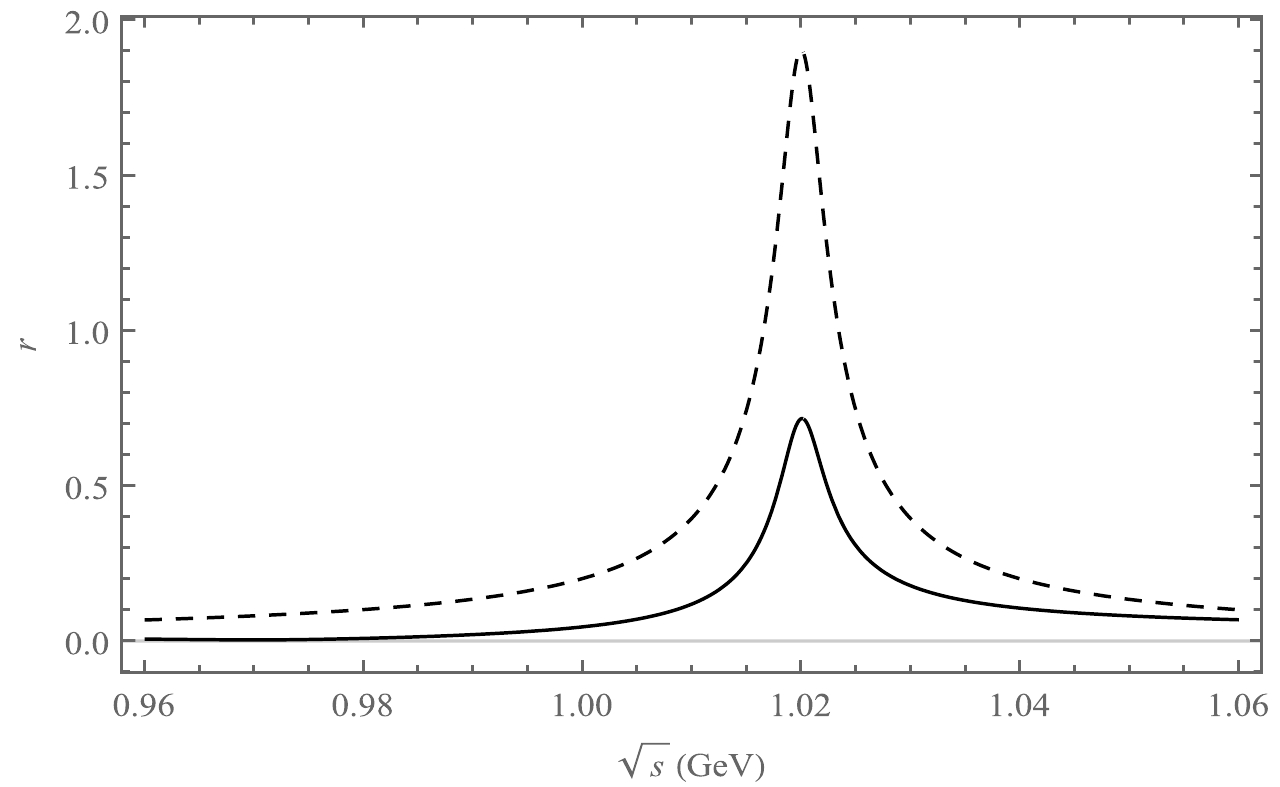
Figure 5. r as a function of
$ \sqrt{s} $ , where the solid line corresponds to the decay channel$ B^{-}\rightarrow K^{+}K^{-}\pi^{-} $ , and the dotted line refers to the decay channel$ B^{-}\rightarrow K^{+}K^{-}K^{-} $ .CP asymmetry also depends on the strong phase via Eq. (12). We show plots of
$ {{\rm{sin}}}\delta $ against$ \sqrt{s} $ in Figs. 6 and 7. Compared with the above plots, for which the main contribution originates from the range of ϕ, from Figs. 6 and 7, we can find that the strong phase has an impact on CP asymmetry. The effect of CP asymmetry for the decay process$ B^{-}\rightarrow K^{+}K^{-}K^{-} $ is larger than that for the decay channel$ \bar B^{0}\rightarrow K^{+}K^{-}\bar K^{0} $ . Meanwhile, the effect of CP asymmetry for the decay process$ B^{-}\rightarrow K^{+}K^{-}\pi^{-} $ is similar to that for the decay channel$ \bar B^{0}\rightarrow K^{+}K^{-}\pi^{0} $ . Therefore, the effect of the strong phase on CP asymmetry is related to the final state meson of the decay channel. In other words, the resonance of vector mesons can affect the CP asymmetry of the three-body decay process. -
The measurement of CP asymmetry in the decay of the B meson has become more accurate owing to the large number of data collected by experiments in recent years. The CP asymmetry from the decay mode
$ \bar B^{0}\rightarrow \phi \bar K^{0}\rightarrow K^{+}K^{-}\bar K^{0} $ was presented by BarBar [28], who described the analysis of time-dependent Dalitz plots and extracted the values of CP asymmetry by considering the complex amplitudes describing the entire$ B^{0} $ and$ \bar B^{0} $ Dalitz plots. Furthermore, the CP asymmetry from the decay mode$ B^{-}\rightarrow \phi K^{-}(\pi^{-}) \rightarrow K^{+}K^{-}K^{-}(\pi^{-}) $ was presented by the LHC [17, 18, 29, 30] and BarBar [19]. Considering the threshold of$ K^+ K^- $ , we calculate the localized CP asymmetry in the region 0.96−1.06 GeV (0.98−1.04 GeV and 1.01−1.03 GeV) in Table 1 , which can provide more accurate measurement of CP asymmetry, and compare it with the experimental results.Decay channel Experimental result $\phi-\rho-\omega$ mixing

(0.96−1.06 GeV)$\phi-\rho-\omega$ mixing

(0.98−1.04 GeV)$\phi-\rho-\omega$ mixing

(1.01−1.03 GeV)$\bar B^{0}\to\phi\pi^{0}\to K^{+}K^{-}\pi^{0}$ 

− 0.197±0.005±0.001 0.286±0.009±0.003 0.536±0.008±0.003 $\bar B^{0}\to\phi \bar K^{0}\to K^{+}K^{-}\bar K^{0}$ 

−0.08±0.18±0.04 BaBar 0.100±0.001±0.005 0.103±0.003±0.002 0.100±0.005±0.001 $(m_{K^+ K^-}<1.1\;{\rm{GeV}})$ [28]

$B^{-}\to\phi\pi^{-}\to K^{+}K^{-}\pi^{-}$ 

−0.141±0.040±0.018 LHC 0.084±0.008±0.006 0.141±0.001±0.001 0.349±0.001±0.008 $(m^2_{K^+ K^-}<1.5\;{\rm{GeV}}^2)$ [18]

$B^{-}\to\phi K^{-}\to K^{+}K^{-}K^{-}$ 

0.128±0.044±0.013 BaBar $(m_{K^+ K^-}<1.04\;{\rm{GeV}})$ [19]

−0.004±0.010±0.007 LHC$(m^2_{K^+ K^-}<1\;{\rm{GeV}}^2)$ [29]

0.187±0.001±0.006 0.278±0.006±0.008 0.482±0.005±0.005 Table 1. Comparison of
$A_{cp}$ from our study with experiments without$\phi-\rho-\omega$ mixingIn our study, we integrate the CP asymmetry for the processes
$ \bar B^{0}\rightarrow K^{+}K^{-}\bar K^{0}(\pi^{0}) $ and$ B^{-} \rightarrow K^{+}K^{-}K^{-}(\pi^{-}) $ when the invariant masses of$ m_{K^{+}K^{-}} $ are in the region 0.96−1.06 GeV (0.98−1.04 GeV and 1.01−1.03 GeV) from the resonances of ϕ, ρ, and ω. The results are presented in Table 1, which indicates the energy intervals of the experimental results. We can easily find that the mixing mechanism changes the values of CP asymmetry compared to the experimental results without mixing for some decay channels from the resonant effects. In particular, the CP asymmetry under$ \phi-\rho-\omega $ mixing is obvious for the range 1.01−1.03 GeV relative to other regions.As shown in Table 1, the decay mode
$ {B}^{-}\to\phi K^{-}(\pi^{-})\rightarrow K^{+}K^{-}K^{-}(\pi^{-}) $ was measured by the LHC and BaBar experiments [18, 19, 29]. We find that there are three uncertainty factors in the experimental result from Table 1. The first uncertainty factor originates from statistics, which indicates that there are errors in the relevant parameters of the CKM matrix, decay constant, form factor, and other values in the calculation. The second is the experimental systematic uncertainty, and the third is due to the CP asymmetry of the$B^{\pm}\to J / \psi K^{\pm}$ reference mode. Meanwhile, in our study, the first uncertainty factor is statistics, the second uncertainty is the form factor and Wolfstein parameters, and the third is due to the phenomenological parameter used to calculate the decay amplitude in the QCDF method under the mixing mechanism of our research. We only list the impacts of the error in the local calculation results because the error has a less than 1% impact on the local results and no significant impact on the image. -
CP asymmetry is affected via the mixing of
$ V\rightarrow K^{+}K^{-} $ $ (V=\phi, \rho, \omega) $ from the decay mode$ B \rightarrow KK\pi(K) $ when the invariant masses of$ K^{+}K^{-} $ pairs are near the ϕ resonance ranges in QCDF. The value of CP asymmetry is enhanced compared to the non-mixing experimental results for the decay mode$ B^{-}\to\phi\pi^{-}(K^{-})\to K^{+}K^{-}\pi^{-}(K^{-}) $ in the certain range. The interferences of$ \phi-\omega $ ,$ \phi-\rho $ , and$ \omega-\rho $ lead to the new generation of the strong phase to influence CP asymmetry from the decay modes$ B \rightarrow KK\pi(K) $ . In the experiment, they can reconstruct the three particles ϕ, ρ, and ω to measure CP asymmetry from the final states of$ KKK(KK\pi) $ from B decay processes.We also calculate the CP asymmetry from the non-interference of ϕ, ρ, and ω for the decay mode
$B^{-}\rightarrow \phi \pi^{-}\rightarrow K^{+}K^{-}\pi^{-}$ to compare with the results of experiments. The CP asymmetry of$ B^{-}\rightarrow \phi\pi^{-}\rightarrow K^{+}K^{-}\pi^{-} $ is –0.141±0.040±0.018 from LHC experiments [18]. Our result is –0.118±0.022±0.014 for the$B^{-}\rightarrow \phi \pi^{-} \rightarrow K^{+}K^{-}\pi^{-}$ decay process without mixing from our framework under the region$ m^2_{K^{+}K^{-}} < 1.5 \; {\rm{GeV}}^2 $ , which is consistent with the experimental results.Except for the above errors in Section IV.B, we must also consider the narrow width approximation (NWA), which includes a factorization relation. In this calculation, we take the method of the quasi-two-body decay process and also consider the resonance effect, where the vector meson can further decay into two hadrons [31]. Hence, the total amplitude form can be considered to be in two parts after taking the quasi-two-body decay process, and the degree of approximation can be connected by the term
$ \eta_{R} $ [32]. The affect of the narrow width in quasi-two-body decay processes can be safely ignored because the widths of ω and ϕ are very small. Considering the large attenuation rate of$ \rho(770) $ , the correction is meaningful. According to QCDF, the correction factor for the quasi-two-body decay process$B^{-}\rightarrow \rho(770)\pi^{-} \rightarrow K^{+}K^{-}\pi^{-}$ is tiny. We can ignore the effect of the NWA for the calculation of CP violation because ηR can be divided out as a constant. Hence, we neglect the effects of this correction in our study. The formalisms of the decay amplitudes contain Breit-Wigner shapes, which depend on the parameters of the invariant mass of$ m_{K^{+}K^{-}} $ associated with the Dalitz plot. We integrate over invariant mass$ m_{K^{+}K^{-}} $ to obtain the localized value of CP asymmetry via quasi-two-body approximation. The introduced CP asymmetry can provide a favorable theoretical support for experimental exploration in the future.
CP asymmetry from the resonance effect of the B meson decay process with π and K final states
- Received Date: 2023-06-25
- Available Online: 2023-11-15
Abstract: We present the novel






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF



















 DownLoad:
DownLoad: