-
Cluster radioactivity refers to a decay process that lies between α decay and spontaneous fission [1−5]. It involves the emission of particles from the nucleus that are heavier than α particles but lighter than the lightest fission fragments [6−8]. This type of decay is commonly known as heavy ion radioactivity. In 1980, cluster radioactivity in heavy nuclei was first predicted by Sandulescu, Poenaru, and Greiner [9]. In 1984, Rose and Jones first observed the phenomenon of cluster radioactivity with the emission of
$ ^{14}\rm{C} $ from$ ^{223}\rm{Ra} $ [10]. Subsequently, Gales et al. [11] and Price et al. [12] definitively confirmed the presence of this distinctive manifestation of radioactivity via experimental investigations. Shortly thereafter, a multitude of clusters heavier than$ ^{14}\rm{C} $ were discovered in trans-lead nuclei, encompassing$ ^{20} \rm{O} $ ,$ ^{23} \rm{F} $ ,$ ^{22,24-26} \rm{Ne} $ ,$ ^{28,30} \rm{Mg} $ , and$ ^{32,34} \rm{Si} $ [13, 14], and these observations highlighted the occurrence of cluster radioactivity, particularly in cases where the daughter nuclei are the doubly magic nucleus$ ^{208} \rm{Pb} $ or its neighboring isotopes [15−19]. This portends that the shell effect plays a vital role in the emission of clusters from heavy nuclei.To comprehend and explain the phenomenon of cluster radioactivity, numerous researchers have proposed diverse theoretical approaches and/or models, which can be broadly classified into two groups: α-like models [5, 20−32] and fission-like models [33−48]. For α-like models, similar to the tunneling theory of α decay [49−51], the process is generally regarded as a non-adiabatic process. It is assumed that the cluster is preformed in the parent nucleus before penetrating the barrier with a certain cluster formation probability, which is determined by the overlapping district between the parent and daughter nucleus before the available radioactive decay energy
$ Q_c $ of the cluster penetrates the barrier. For example, Ren et al. [32] systematically calculated the half-life of cluster radioactivity using a microscopic density-dependent model (DDCM) with the renormalized M3Y nucleon-nucleon interaction, considering the dependence of the preformation probability of clusters on the number of charges. Subsequently, Ni et al. [5] extended the generalized density-dependent cluster model (GDDCM) to study cluster radioactivity by numerically constructing the microscopic cluster-daughter potential [20−23]. For fission-like models, the cluster is considered to form during the adiabatic rearrangement process of the parent nucleus. During this process, the atomic nucleus continuously deforms until it reaches the fission configuration after crossing the potential barrier. For example, Santhosh et al. [52] considered a simple power-law interpolation in the Coulomb and proximity potential (CPPM) model and calculated the probability of cluster formation as the probability of penetration through the interior of the potential barrier. Poenaru et al. [37] used two models of analytic super-asymmetric fission (ASAF) and the universal formula (UNIV) to calculate the half-lives of cluster radioactivity and α decay within superheavy nuclei [39−42]. Furthermore, the phenomenon of cluster radioactivity has been extensively investigated using various empirical formulas, such as a unified formula for α decay and cluster radioactivity proposed by Ni et al. [53], a three-parameter model-independent formula proposed by Balasubramaniam et al. [54], and the universal decay law (UDL) formula proposed by Qi et al. [55, 56]. These formulas can clearly elucidate this bizarre decay mode and provide a reliable theoretical basis for future research.In 2020, based on the Wentzel-Kramers-Brillouin (WKB) approximation and Bohr–Sommerfeld quantization condition, Bayrak [57] proposed a new simple model (HOPM) to study the favored α decay half-lives of 263 nuclei. In this model, there is only one adjustable parameter, that is, the depth of the nucleus potential
$ V_0 $ obtained by fitting the experimental α decay half-lives. Since α decay, cluster radioactivity, and proton radioactivity are analogously described by the quantum mechanical effect. Whether this model can be extended to research on cluster radioactivity is a highly interesting topic. Meanwhile, the cluster preformation probability$ P_c $ is key to calculating cluster radioactivity half-lives. In 1988, Blendowske and Walliser [58] found that$ P_c $ is related to the α preformation probability$ P_\alpha $ via$ \log_{10}P_c= \dfrac{A_c-1}{3}\log_{10}P_\alpha $ , where$ A_c $ is the mass number of the emitted cluster. Recently, Wang et al. [59] modified this relationship between$ P_c $ and$ P_\alpha $ to$ \log_{10}P_c=\dfrac{A_c-1}{3}\log_{10}P_\alpha+ c' $ , where$ c' $ is an adjustable parameter. Based on these two aspects, considering the modified preformation probability$ P_c $ , we extend HOPM to systematically study the cluster radioactivity half-lives of 28 trans-lead nuclei. The calculated results reproduce the experimental data well.This article is organized as follows. A brief introduction to the theoretical framework for the cluster radioactivity half-lives in HOPM and semi-empirical formulas is presented in Sec. II, detailed numerical results and the discussion are given in Sec. III, and a summary is presented in Sec. IV.
-
The cluster radioactivity half-life
$ T_{1/2} $ is generally calculated using [32]$ \begin{equation} T_{1/2} = \frac{\hbar {\rm{ln2}}}{\Gamma} \ , \end{equation} $

(1) where
$ \hbar $ is the reduced Plank constant, and Γ is the cluster radioactivity width, which can be expressed as follows in the framework of HOPM [57]:$ \begin{equation} \Gamma=P_c\,F_c\,\frac{\hbar^2}{4\mu} \,{\rm e}^{-2S_c}, \end{equation} $

(2) where
$\mu=m_d m_c/(m_d+m_c)\approx\ A_d A_c M_{\rm nuc}/(A_d+A_c)$ is the reduced mass of the cluster-daughter nucleus system, with$ A_d $ as the mass number of the daughter nucleus and$M_{\rm nuc}=931.5 \,{\rm MeV}/c^2$ as the nuclear mass unit,$ P_c $ is the preformation probability,$ F_c $ denotes the knocking frequency of the emitted cluster in the potential barrier, and$ S_c $ denotes the action integral. They can be expressed as$ \begin{equation} F_c=\bigg[\,\int_{0}^{r_1}\frac{1}{2k(r)}{\rm d}r \bigg]^{-1}, \end{equation} $

(3) $ \begin{equation} S_c=\int_{r_1}^{r_2}\,k(r){\rm d}r, \end{equation} $

(4) where r represents the distance between the centers of the cluster and daughter nuclei,
$ k(r)=\sqrt{\dfrac{2\mu}{\hbar^2}(V(r)-Q_c)} $ is the wave number, with$ V(r) $ and$ Q_c $ as the total interaction potential and cluster radioactivity decay energy, respectively, and$ r_1 $ and$ r_2 $ denote the classical turning points and satisfy the condition$ V(r_1)=V(r_2)=Q_c $ . The decay energy$ Q_c $ is obtained using [60]$ \begin{equation} Q_c=B(A_c,Z_c)+B(A_d,Z_d)-B(A,Z), \end{equation} $

(5) where
$ B(A_c,Z_c) $ ,$ B(A_d,Z_d) $ , and$ B(A,Z) $ are the binding energies of the emitted cluster, daughter nucleus, and parent nucleus, respectively, taken from AME2020 [61] and NUBASE2020 [62], with$ Z_c $ ,$ Z_d $ , and Z as the proton numbers of the emitted cluster, daughter nucleus, and parent nucleus, respectively, and A is the mass number of the parent nucleus.The total interaction potential
$ V(r) $ between the emitted cluster and daughter nucleus includes the nuclear potential$ V_N(r) $ , Coulomb potential$ V_c(r) $ , and centrifugal potential$ V_l(r) $ . It can be expressed as$ \begin{equation} V(r)=V_N(r)+V_C(r)+V_l(r). \end{equation} $

(6) In this study, we choose
$ V_N(r) $ in the modified harmonic oscillator form, as in [57],$ \begin{equation} V_N(r)=-V_0+V_1\,r^2, \end{equation} $

(7) where
$ V_0 $ and$ V_1 $ are the parameters of the depth and diffusivity of the nuclear potential, respectively. The Coulomb potential$ V_C $ is taken as the potential of a uniformly charged sphere with radius R, which can be expressed as [57]$ V_C(r) = \left\{\begin{array}{*{20}{l}} \dfrac{Z_c Z_d {\rm e}^2}{2R}\left(3-\dfrac{r^2}{R^2}\right), & r\leq r_1, \\ \dfrac{Z_c Z_d {\rm e}^2}{r}, & r > r_1, \end{array}\right. $

(8) where
${\rm e}^2=1.4399652 \; {\rm MeV \cdot fm}$ is the square of the electronic elementary charge, and R is the sharp radius, which is chosen via a semi-empirical formula in terms of mass number,$ R=r_0(A_d^{1/3}+A_c^{1/3}) $ , with$ r_0=1.2249 $ [63]. The centrifugal potential can be generally expressed as$ V_l(r)=\dfrac{\hbar^2\,l\,(l+1)}{2\mu\,r^2} $ , where l is the orbital angular momentum taken away by the emitted cluster. Previous studies [30, 59] have shown that the influence of l on the half-lives of cluster radioactivity is negligible. Furthermore, to simplify this model, we ignore the centrifugal contribution in this study. Then, the total interaction potential$ V(r) $ can be further written as [57]$ V(r) = \left\{\begin{array}{ll} C_0-V_0+(V_1-C_1)r^2, & r\leq r_1 \\ \dfrac{C_2}{r}, & r > r_1 \end{array}\right. $

(9) where
$C_0=\dfrac{3Z_c\,Z_d\,{\rm e}^2}{2R}$ ,$C_1=\dfrac{Z_c\,Z_d\,{\rm e}^2}{2R^3}$ , and$C_2=Z_c\,Z_d{\rm e}^2$ . Using the condition$ V(r_1)=V(r_2)=Q_c $ , we obtain$ r_1=\sqrt{\dfrac{Q_c+V_0-C_0}{V_1-C_1}} $ and$ r_2=\dfrac{C_2}{Q_c} $ .Based on the principles of classical and quantum mechanics, the Bohr-Sommerfeld quantization condition can reduce the freedom of the system, which is also a vital application of the WKB approximation [64]. In this study, we use this condition to reduce the degrees of freedom in the interaction between the daughter nucleus and the emitted cluster. It is expressed as [65, 66]
$ \begin{equation} \int_{0}^{r_1}\sqrt{\frac{2\mu}{\hbar^2}(V(r)-Q_c)}{\rm d}r=(G_c-l+1)\frac{\pi}{2}, \end{equation} $

(10) where
$ G_c $ is the global quantum number, obtained using the relationship$ G_c = \dfrac{G_\alpha A_c}{4} $ [66], where$ G_\alpha $ is the global quantum number of α decay, which is determined using the Wildermuth quantum rule and expressed as [65]$ \begin{eqnarray} G_\alpha & = & \left\{\begin{array}{ll} 22, & N > 126, \\ 20, & 82 < N \leq 126, \\ 18, & N \leq 82. \end{array}\right. \end{eqnarray} $

(11) Then, the relationship between
$ V_0 $ and$ V_1 $ can be expressed as$ \begin{equation} V_1=C_1+\frac{\mu}{2\hbar^2}\bigg(\frac{Q_c+V_0-C_0}{1+G_c}\bigg)^2, \end{equation} $

(12) with the integral conditions
$ C_0<(Q_c+V_0) $ and$ C_1< V_1 $ .Based on Ref. [58], we choose the depth of the nuclear potential between the emitted cluster and daughter nucleus
$ V_0 $ as$V_0=25A_c \; {\rm MeV}$ . Using Eq. (12), the normalization factor$ F_c $ and action integral$ S_c $ can be further written as$ \begin{equation} F_c=\frac{4\,\mu}{\pi\,\hbar^2}\,\frac{(Q_c+V_0-C_0)}{1+G_c}, \end{equation} $

(13) $ \begin{aligned}[b] S_c=&\sqrt{\frac{2\mu}{\hbar^2}}\frac{C_2}{\sqrt{Q_c}}\bigg ({\rm arccos}\bigg (\sqrt{\frac{Q_cr_1}{C_2}}\bigg) \\&- \sqrt{\frac{Q_cr_1}{C_2} - \bigg (\frac{Q_c r_1}{C_2}\bigg)^2}\bigg). \end{aligned} $

(14) Therefore, the cluster radioactivity half-life
$ T_{1/2} $ can be expressed as$ \begin{equation} T_{1/2}= \frac{\pi\, \hbar \,ln2}{P_c} \,\frac{(1+G_c)}{(Q_c+V_0-C_0)}\,{\rm e}^{2S_c}. \end{equation} $

(15) -
In 2009, based on the microscopic mechanism of charged particle emission within α-like R-matrix theory, Qi et al. [56] proposed the UDL, which can be given by
$ {\rm{log}}_{10}T_{1/2}^{\rm{{UDL}}}=a\sqrt{\mathcal{A}}\,Z_c\,Z_d\,Q_c^{-1/2}+b\sqrt{\mathcal{A}\, Z_c\,Z_d\,(A_c^{1/3}+A_d^{1/3})}+c, $

(16) where
$ \mathcal{A}=A_cA_d/(A_c+A_d) $ is the reduced mass of the emitted cluster-daughter nucleus system, measured in units of nucleon mass. The adjustable parameters are$ a=0.4314 $ ,$ b=-0.3921 $ , and$ c=-32.7044 $ . -
In 2004, Balasubramaniam et al. [54] proposed a model-independent formula (MBM) with three parameters by considering the characteristics of exotic cluster decays. It can be expressed as
$ \begin{equation} {\rm{log}}_{10}T_{1/2}^{\rm{{MBM}}}=(aA_c\eta + bZ_c\eta_{z})Q_c^{-1/2}+c, \end{equation} $

(17) where
${\eta=(A_d-A_c)/A}$ and$ \eta_{z}=(Z_d-Z_c)/Z $ represent the mass and charge asymmetry, respectively. The adjustable parameters are$ a=10.603 $ ,$ b=78.027 $ , and$ c=-80.669 $ . -
In 2013, Tavares et al. [67] presented a novel approach (TAM) for estimating the cluster radioactivity half-lives of translead parent nuclei. It can be given by
$ \begin{equation} {\rm{log}}_{10}T_{1/2}^{\rm{{TAM}}}=(aZ_c+b)(Z_d/Q_c)^{1/2}+cZ_c+d, \end{equation} $

(18) where the adjustable parameters are
$ a=12.8717 $ ,$b= -5.1222$ ,$ c=-4.6496 $ , and$d=-73.3326$ . -
Cluster preformation probability
$ P_c $ can be considered as the overlap between the actual ground state configuration and the configuration of clusters coupled to sub-states. In 1988, Blendowske and Walliser [58] first found the relationship between the cluster preformation probability$ P_c $ and mass of the emitted cluster$ A_c $ as$ \log_{10}P_c=\dfrac{A_c-1}{3}\log_{10}P_\alpha $ . To further show this relationship, we plot$ -\log_{10}P_c $ versus$ \dfrac{A_c-1}{3} $ for even-even and odd-A parent nuclei in Figs. 1 and 2, respectively.$ P_c $ is extracted using the relevant experimental data in Eq. (15) and listed in the third column of Table 1. From these figures, we can see that$ -\log_{10}P_c $ and$ \dfrac{A_c-1}{3} $ exhibit a clear linear relationship but have intercepts. This conclusion aligns with that of Wang et al. [59], although the value of$ P_c $ is obtained using different models.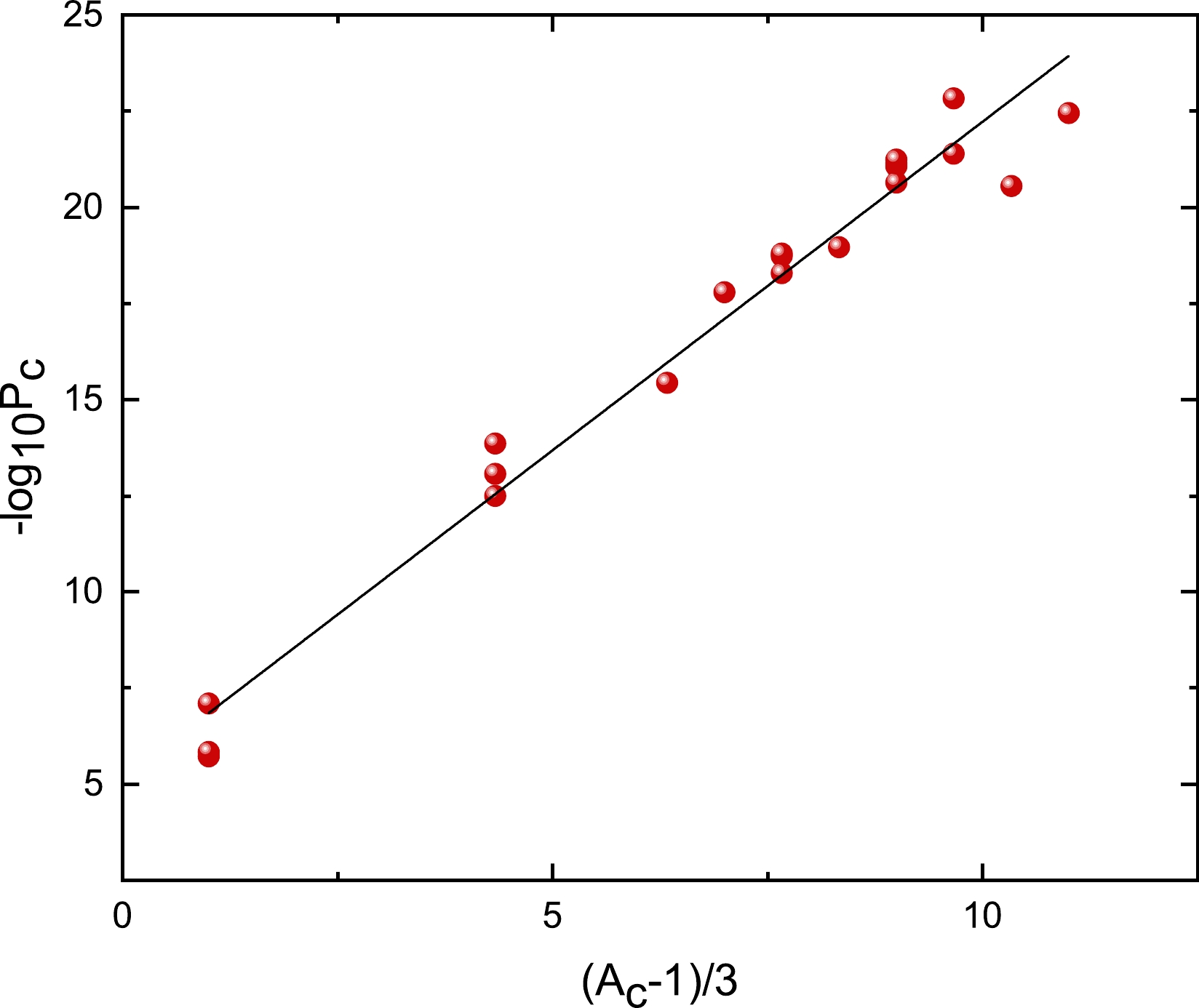
Figure 1. (color online) Negative of the logarithm of the preformation penetrability
$ -\log_{10}P_c $ versus$ (A_c-1)/3 $ for e-e nuclei.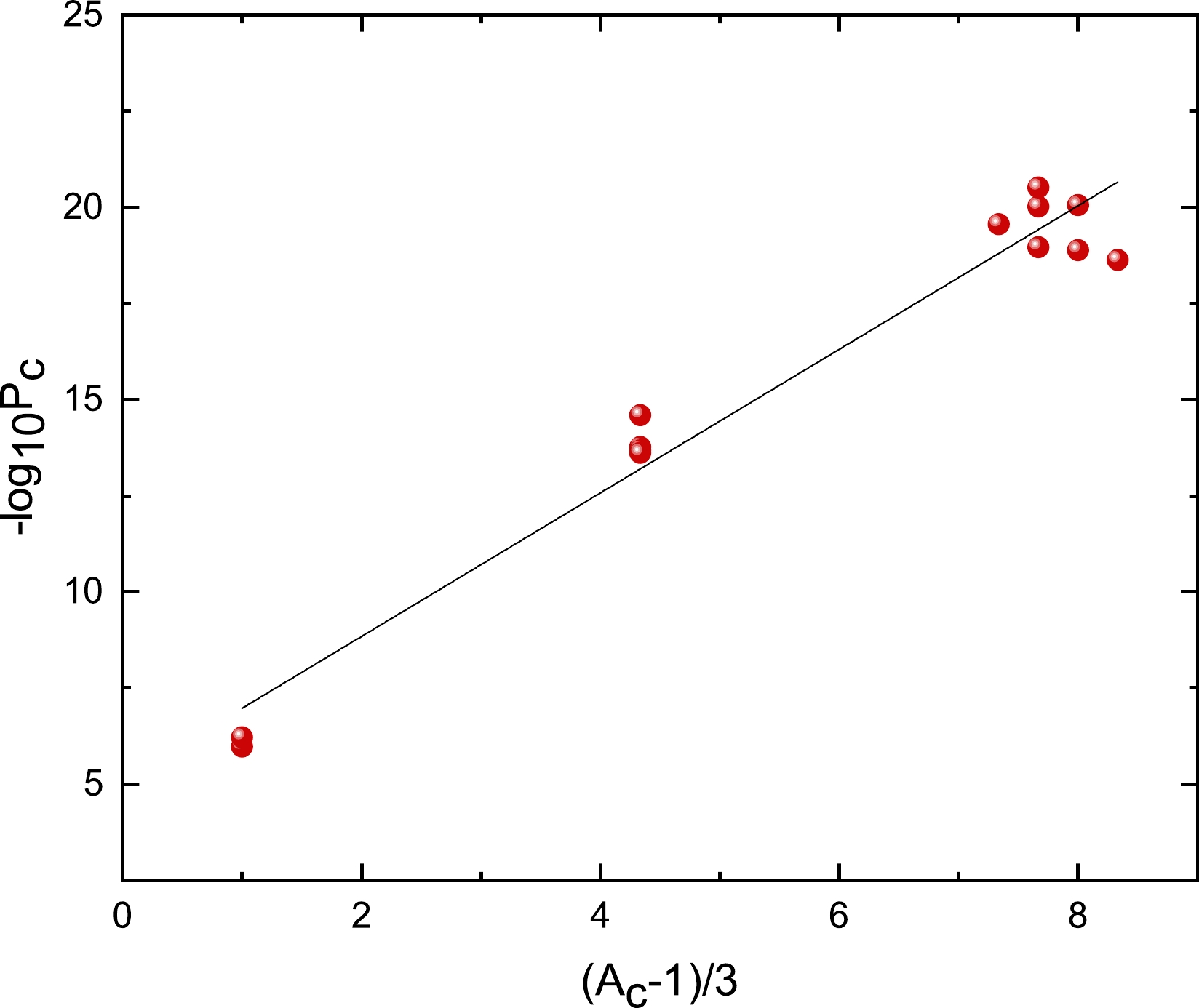
Figure 2. (color online) Same as Fig. 1, but for odd-A nuclei.
Decay ${Q_c}$ /MeV

$ P_c $ 

$ {\rm{log}}_{10}T_{1/2}^{\rm{{Exp}}} $ 

$ {\rm{log}}_{10}T_{1/2}^{\rm{{HOPM}}} $ 

$ {\rm{log}}_{10}T_{1/2}^{\rm{{UDL}}} $ 

$ {\rm{log}}_{10}T_{1/2}^{\rm{{MBM}}} $ 

$ {\rm{log}}_{10}T_{1/2}^{\rm{{TAM}}} $ 

Even-even nuclei $ ^{212} $ Po

$ \to ^{208} $ Pb+

$ ^{4} $ He

8.95 $ 1.908\times10^{-6} $ 

−6.52 −5.397 −13.120 −17.348 −20.213 $ ^{214} $ Po

$ \to ^{210} $ Pb+

$ ^{4} $ He

7.833 $ 1.461\times10^{-6} $ 

−3.78 −2.773 −9.922 −12.978 −15.912 $ ^{238} $ Pu

$ \to ^{234} $ U+

$ ^{4} $ He

5.590 $ 7.900\times10^{-8} $ 

9.59 9.330 4.513 −0.138 1.025 $ ^{222} $ Ra

$ \to ^{208} $ Pb+

$ ^{14} $ C

33.05 $ 3.207\times10^{-13} $ 

11.22 11.266 10.070 12.225 12.351 $ ^{224} $ Ra

$ \to ^{210} $ Pb+

$ ^{14} $ C

30.54 $ 8.606\times10^{-14} $ 

15.92 15.395 15.368 15.998 16.926 $ ^{226} $ Ra

$ \to \; ^{212} $ Pb+

$ ^{14} $ C

28.21 $ 1.369\times10^{-14} $ 

21.19 19.867 20.913 19.941 21.708 $ ^{228} $ Th

$ \to ^{208} $ Pb+

$ ^{20} $ O

44.72 $ 3.629\times10^{-16} $ 

20.72 21.239 21.973 22.228 21.972 $ ^{230} $ U

$ \to \; ^{208} $ Pb+

$ ^{22} $ Ne

61.40 $ 1.603\times10^{-18} $ 

19.57 18.874 20.712 21.335 23.002 $ ^{230} $ Th

$ \to ^{206} $ Hg+

$ ^{24} $ Ne

57.57 $ 1.859\times10^{-19} $ 

24.64 24.147 25.733 25.854 25.867 $ ^{232} $ U

$ \to \; ^{208} $ Pb+

$ ^{24} $ Ne

62.31 $ 5.190\times10^{-19} $ 

20.40 20.353 20.587 22.258 21.955 $ ^{234} $ U

$ \to ^{210} $ Pb+

$ ^{24} $ Ne

58.83 $ 1.593\times10^{-19} $ 

25.25 24.690 26.492 25.317 26.076 $ ^{234} $ U

$ \to ^{208} $ Pb+

$ ^{26} $ Ne

59.47 $ 1.094\times10^{-19} $ 

25.88 26.297 26.902 26.320 25.302 $ ^{234} $ U

$ \to ^{206} $ Hg+

$ ^{28} $ Mg

74.13 $ 8.637\times10^{-22} $ 

25.14 24.594 25.738 25.941 26.010 $ ^{236} $ U

$ \to ^{208} $ Hg+

$ ^{28} $ Mg

71.69 $ 2.254\times10^{-21} $ 

27.58 27.450 29.612 27.811 28.628 $ ^{236} $ Pu

$ \to ^{208} $ Pb+

$ ^{28} $ Mg

79.67 $ 7.260\times10^{-22} $ 

21.67 21.048 20.640 22.817 22.378 $ ^{238} $ Pu

$ \to ^{210} $ Pb+

$ ^{28} $ Mg

75.91 $ 5.719\times10^{-22} $ 

25.70 24.975 26.260 25.417 26.085 $ ^{236} $ U

$ \to ^{206} $ Hg+

$ ^{30} $ Mg

72.51 $ 2.815\times10^{-21} $ 

27.58 28.686 25.472 28.462 25.561 $ ^{238} $ Pu

$ \to ^{208} $ Pb+

$ ^{30} $ Mg

77.00 $ 3.978\times10^{-22} $ 

25.67 25.926 29.533 25.903 27.734 $ ^{238} $ Pu

$ \to ^{206} $ Hg+

$ ^{32} $ Si

91.19 $ 1.479\times10^{-23} $ 

25.28 25.246 25.723 25.626 24.983 $ ^{242} $ Cm

$ \to ^{208} $ Pb+

$ ^{34} $ Si

96.53 $ 3.549\times10^{-23} $ 

23.15 24.636 22.374 24.468 22.941 Odd-A nuclei $ ^{213} $ Po

$ \to ^{209} $ Pb+

$ ^{4} $ He

8.54 $ 1.052\times10^{-6} $ 

−5.37 −4.379 −12.024 −15.843 −18.733 $ ^{215} $ At

$ \to ^{211} $ Bi+

$ ^{4} $ He

8.178 $ 6.108\times10^{-7} $ 

−4.00 −3.244 −10.574 −14.388 −16.937 $ ^{221} $ Fr

$ \to \; ^{207} $ Tl+

$ ^{14} $ C

31.32 $ 1.687\times10^{-14} $ 

14.52 13.941 12.640 14.61 14.732 $ ^{221} $ Ra

$ \to ^{207} $ Pb+

$ ^{14} $ C

32.40 $ 2.071\times10^{-14} $ 

13.39 12.900 11.450 13.138 13.484 $ ^{223} $ Ra

$ \to ^{209} $ Pb+

$ ^{14} $ C

31.83 $ 2.529\times10^{-15} $ 

15.25 13.847 12.564 14.004 14.507 $ ^{225} $ Ac

$ \to ^{211} $ Bi+

$ ^{14} $ C

30.48 $ 2.390\times10^{-14} $ 

17.34 16.913 16.605 16.238 17.761 $ ^{231} $ Pa

$ \to ^{208} $ Pb+

$ ^{23} $ F

51.84 $ 2.755\times10^{-20} $ 

26.02 25.257 24.982 24.699 24.077 $ ^{231} $ Pa

$ \to ^{207} $ Tl+

$ ^{24} $ Ne

60.42 $ 9.430\times10^{-21} $ 

23.38 22.773 22.253 23.585 23.276 $ ^{233} $ U

$ \to \; ^{209} $ Pb+

$ ^{24} $ Ne

60.50 $ 3.036\times10^{-21} $ 

24.82 23.721 23.622 23.815 24.073 $ ^{235} $ U

$ \to ^{211} $ Pb+

$ ^{24} $ Ne

57.36 $ 1.093\times10^{-19} $ 

27.42 27.877 29.168 26.697 27.946 $ ^{233} $ U

$ \to \; ^{208} $ Pb+

$ ^{25} $ Ne

60.75 $ 8.759\times10^{-21} $ 

24.82 24.804 23.864 24.971 23.729 $ ^{235} $ U

$ \to ^{210} $ Pb+

$ ^{25} $ Ne

57.83 $ 1.294\times10^{-19} $ 

27.42 28.573 28.919 27.071 27.434 $ ^{235} $ U

$ \to \; ^{209} $ Pb+

$ ^{26} $ Ne

58.11 $ 2.305\times10^{-19} $ 

27.45 29.476 29.398 27.598 26.99 In the following, based on the modified form of
$ P_c $ of Wang et al. [59], i.e.,$ \log_{10}P_c=\dfrac{A_c-1}{3}\log_{10}P_\alpha+c' $ , and fitting the$ P_c $ listed in the third column of Table 1, we obtain$ P_\alpha=0.0195 $ and$c'=-5.1330$ for even-even parent nuclei and$ P_\alpha=0.0136 $ and$c'=-5.1022$ for odd-A parent nuclei. The values of$ P_\alpha $ are close to those of previous studies [2, 4, 30, 63, 70]. It is crucial to emphasize that the cluster preformation probability$ P_c $ exhibits a strong dependence on the corresponding model. As a result,$ P_c $ can vary considerably over several orders of magnitude [2, 4, 30, 59, 63, 70]. Recently, Delion [47] derived a universal analytical relationship that represents the logarithm of the reduced width squared as a fragmentation potential, which is based on a simple model of Coulomb interactions, including a shifted harmonic oscillator potential. Furthermore, the relationship between the logarithmical form of preformation probability (spectroscopic factor)$ \log_{10}P_c $ and the fragmentation potential$V_{\rm frag}$ is linear, where$V_{\rm frag}$ can be expressed as$ \begin{equation} V_{\rm frag}=\frac{Z_c Z_d {\rm e}^2}{r_1}-Q_c. \end{equation} $

(19) As a verification, we plot the logarithm of the modified form
$ P_c $ versus the fragmentation potential$V_{\rm frag}$ for even-even and odd-A parent nuclei in Fig. 3 (a) and (b), respectively. As shown in this figure, there is a clear linear relationship between$ \log_{10}P_c $ and$V_{\rm frag}$ . This linear relationship may be model-independent.
Figure 3. (color online) Logarithm of the preformation penetrability
$ \log_{10}P_c $ versus the fragmentation potential$V_{\rm frag}$ . (a) and (b) present the cases of e-e and odd-A parent nuclei, respectively.Immediately after, using the modified form of
$ P_c $ with a certain slope$ \log_{10}P_\alpha $ and intercept$ c' $ , we calculate the corresponding$ P_c $ of each emitted cluster. Based on the obtained$ P_c $ , we systematically calculate the cluster radioactivity half-lives of 28 trans-lead nuclei using Eq. (15). For comparison, UDL [56], MBM [54], and TAM [67] are also used. The detailed results are presented in Table 1. In this table, the first and second columns contain the decay process and cluster radioactivity decay energy$ Q_c $ , respectively. The last five columns are the experimental cluster radioactivity half-lives and those calculated using HOPM, UDL [56], MBM [54], and TAM [67] in logarithmic form, denoted as$ {\rm{log}}_{10}T_{1/2}^{\rm{{Exp}}} $ ,$ {\rm{log}}_{10}T_{1/2}^{\rm{{HOPM}}} $ ,$ {\rm{log}}_{10}T_{1/2}^{\rm{{UDL}}} $ ,$ {\rm{log}}_{10}T_{1/2}^{\rm{{MBM}}} $ , and$ {\rm{log}}_{10}T_{1/2}^{\rm{{TAM}}} $ , respectively. It can be easily seen from this table that the calculations from HOPM are essentially consistent with the experimental data.To intuitively compare the experimental and calculated data, we plot the differences between the experimental cluster radioactivity half-lives and those calculated using different formulas in logarithmic form in Fig. 4. In this figure, the pink sphere, green upward triangle, blue downward triangle, and purple five-pointed star represent the results obtained using HOPM, UDL, MBM, and TAM, respectively. As shown in this figure, compared with the other calculated results, the cluster radioactivity half-lives obtained from our study are generally consistent with the experimental data, and the deviations between the experimental and calculated data are within
$ \pm 1.0 $ . To further quantitatively compare the experimental cluster radioactivity half-lives with the results of HOPM, UDL, MBM, and TAM, the standard deviation σ is employed, which is defined as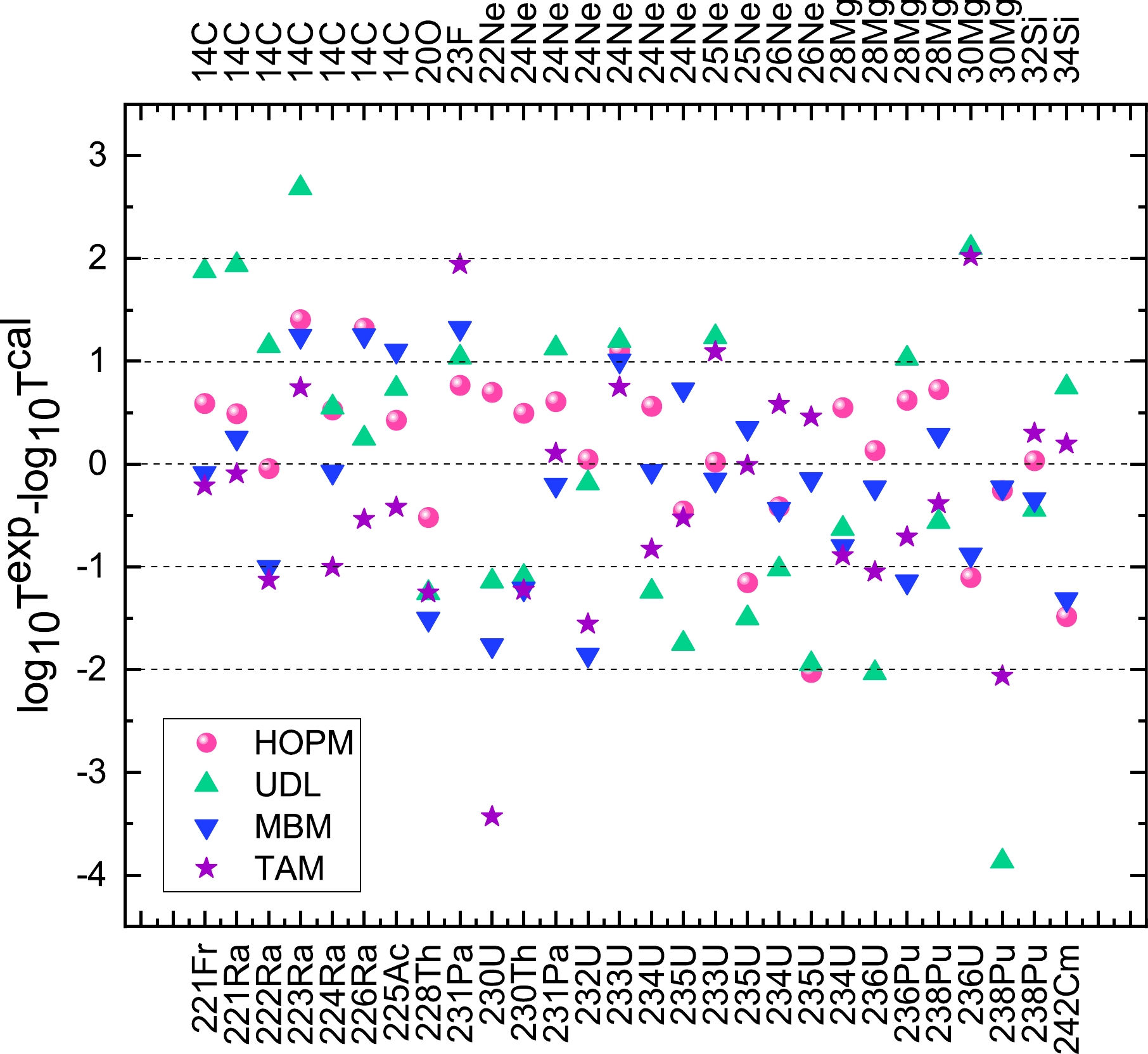
Figure 4. (color online) Comparison of the differences between the experimental cluster radioactivity half-lives and those calculated using the UDL, MBM, TAM, and HOPM in logarithmic form.
$ \begin{equation} \sigma=\sqrt{\frac{1}{n}\sum\limits_{i=1}^{n}\left(\log_{10}{{T^{\rm{exp}}_{1/2_i}}-\log_{10}{T^{\rm{cal}}_{1/2_i}}}\right)^2} \ , \end{equation} $

(20) where
$ \log_{10}{T^{\rm{exp}}_{1/2_i}} $ and$ \log_{10}{T^{\rm{cal}}_{1/2_i}} $ denote the logarithmic form of the experimental and calculated cluster radioactivity half-lives for the i-th nucleus, respectively. The σ values for 28 trans-lead nuclei using HOPM, UDL, MBM, and TAM are listed in Table 2. As shown in this table, σ is 0.696 of HOPM for even-even nuclei, which is smaller than the results from UDL, MBM, and TAM, which are 1.423, 1.025, and 1.369, respectively. For odd-A nuclei, the σ of HOPM, MBM, and TAM are 0.978, 0.758, and 0.787, respectively, which are smaller than the results from MBM with 1.651. σ is 0.818 of HOPM for the total nuclei, which is better than the results obtained using UDL, MBM, and TAM formulas, which are 1.510, 0.930, and 1.176, respectively. It is further shown that HOPM and the modified preformation probability are reliable and can reproduce the calculated cluster radioactivity half-life well.Model $ \rm{HOPM} $ 

$ \rm{UDL} $ 

$ \rm{MBM} $ 

$ \rm{TAM} $ 

even-even(n=17) $ 0.696 $ 

$ 1.423 $ 

$ 1.025 $ 

$ 1.369 $ 

odd-A(n=11) $ 0.978 $ 

$ 1.651 $ 

$ 0.758 $ 

$ 0.787 $ 

total(n=28) $ 0.818 $ 

$ 1.510 $ 

$ 0.930 $ 

$ 1.176 $ 

Considering the good agreement between the cluster radioactivity experimental half-lives and calculated values within HOPM, we further extend this model to predict the cluster radioactivity half-lives of 51 possible cluster radioactive candidates whose cluster radioactivities are energetically allowed or observed but not yet quantified in NUBASE2020 [62]. For comparison, UDL, MBM, and TAM are also used. The detailed predictions are given in Table 3. In this table, the first and second columns are same as in Table 1, and the last four columns are the predicted cluster radioactivity half-lives obtained using HOPM, UDL, MBM, and TAM in logarithmic form, denoted as
$ {\rm{log}}_{10}T_{1/2}^{\rm{{HOPM}}} $ ,$ {\rm{log}}_{10}T_{1/2}^{\rm{{UDL}}} $ ,$ {\rm{log}}_{10}T_{1/2}^{\rm{{MBM}}} $ , and$ {\rm{log}}_{10}T_{1/2}^{\rm{{TAM}}} $ , respectively. As shown in Table 3, our predictions are in good agreement with those of UDL, MBM, and TAM formulas.$Q_{c}$ /MeV

$ {\rm{log}}_{10}T_{1/2}^{\rm{{Exp}}} $ 

$ {\rm{log}}_{10}T_{1/2}^{\rm{{HOPM}}} $ 

$ {\rm{log}}_{10}T_{1/2}^{\rm{{UDL}}} $ 

$ {\rm{log}}_{10}T_{1/2}^{\rm{{MBM}}} $ 

$ {\rm{log}}_{10}T_{1/2}^{\rm{{TAM}}} $ 

$ ^{219} $ Rn

$ \to \; ^{205} $ Hg+

$ ^{14} $ C

28.10 − 18.996 19.079 19.747 20.437 $ ^{220} $ Rn

$ \to \; ^{206} $ Hg+

$ ^{14} $ C

28.54 − 17.496 17.941 18.986 19.496 $ ^{221} $ Fr

$ \to \; ^{206} $ Hg+

$ ^{15} $ N

34.12 − 18.477 21.554 21.322 24.244 $ ^{223} $ Ra

$ \to \; ^{205} $ Hg+

$ ^{18} $ O

40.30 − 24.087 26.453 24.993 27.337 $ ^{225} $ Ra

$ \to \; ^{211} $ Pb+

$ ^{14} $ C

29.47 − 18.021 17.827 17.752 19.052 $ ^{225} $ Ra

$ \to \; ^{205} $ Hg+

$ ^{20} $ O

40.48 − 27.119 28.284 27.008 27.030 $ ^{226} $ Ra

$ \to \; ^{206} $ Hg+

$ ^{20} $ O

40.82 − 25.582 27.455 26.585 26.456 $ ^{223} $ Ac

$ \to \; ^{208} $ Pb+

$ ^{15} $ N

39.47 $> $ 14.76

15.213 12.938 14.503 16.607 $ ^{227} $ Ac

$ \to \; ^{207} $ Tl+

$ ^{20} $ O

43.09 − 22.805 23.942 23.941 23.630 $ ^{229} $ Ac

$ \to \; ^{206} $ Hg+

$ ^{23} $ F

48.35 − 25.524 28.921 27.925 27.246 $ ^{226} $ Th

$ \to \; ^{208} $ Pb+

$ ^{18} $ O

45.73 $> $ 16.76

16.870 18.136 18.955 20.501 $ ^{226} $ Th

$ \to \; ^{212} $ Po+

$ ^{14} $ C

30.55 $> $ 15.36

16.893 17.545 16.268 18.338 $ ^{227} $ Th

$ \to \; ^{209} $ Pb+

$ ^{18} $ O

44.20 − 19.902 21.003 20.685 22.750 $ ^{228} $ Th

$ \to \; ^{206} $ Hg+

$ ^{22} $ Ne

55.74 − 23.863 27.481 25.832 28.240 $ ^{229} $ Th

$ \to \; ^{209} $ Pb+

$ ^{20} $ O

43.40 − 24.282 24.644 23.805 23.973 $ ^{229} $ Th

$ \to \; ^{205} $ Hg+

$ ^{24} $ Ne

57.83 − 24.953 25.327 25.584 25.539 $ ^{231} $ Th

$ \to \; ^{207} $ Hg+

$ ^{24} $ Ne

56.25 − 27.142 28.126 27.127 27.567 $ ^{231} $ Th

$ \to \; ^{206} $ Hg+

$ ^{25} $ Ne

56.80 − 27.696 27.911 27.414 26.851 $ ^{232} $ Th

$ \to \; ^{208} $ Hg+

$ ^{24} $ Ne

54.67 $> $ 29.2

28.245 31.121 28.705 29.682 $ ^{232} $ Th

$ \to \; ^{206} $ Hg+

$ ^{26} $ Ne

55.91 $> $ 29.2

28.993 30.378 29.099 28.014 $ ^{227} $ Pa

$ \to \; ^{209} $ Bi+

$ ^{18} $ O

45.87 − 22.082 19.167 19.003 21.097 $ ^{229} $ Pa

$ \to \; ^{207} $ Tl+

$ ^{22} $ Ne

58.96 − 23.053 23.303 23.157 25.037 $ ^{230} $ U

$ \to \; ^{208} $ Pb+

$ ^{22} $ Ne

61.39 $> $ 18.2

18.885 20.729 21.344 23.014 $ ^{230} $ U

$ \to \; ^{206} $ Pb+

$ ^{24} $ Ne

61.35 $> $ 18.2

21.410 22.346 23.001 23.061 $ ^{232} $ U

$ \to \; ^{204} $ Hg+

$ ^{28} $ Mg

74.32 $> $ 22.26

24.304 25.592 25.734 25.812 $ ^{233} $ U

$ \to \; ^{205} $ Hg+

$ ^{28} $ Mg

74.23 $> $ 27.59

25.835 25.657 25.834 25.906 $ ^{235} $ U

$ \to \; ^{211} $ Pb+

$ ^{24} $ Ne

57.36 $> $ 27.65

27.877 29.168 26.696 27.947 $ ^{235} $ U

$ \to \; ^{210} $ Pb+

$ ^{25} $ Ne

57.68 $> $ 27.65

28.781 29.412 27.211 27.536 $ ^{235} $ U

$ \to \; ^{207} $ Hg+

$ ^{28} $ Mg

72.43 $> $ 28.45

27.936 28.446 27.221 27.821 $ ^{235} $ U

$ \to \; ^{206} $ Hg+

$ ^{29} $ Mg

72.48 $> $ 28.45

29.043 29.025 27.825 27.766 $ ^{236} $ U

$ \to \; ^{212} $ Pb+

$ ^{24} $ Ne

55.95 $> $ 26.27

28.726 31.816 28.069 29.797 $ ^{236} $ U

$ \to \; ^{210} $ Pb+

$ ^{26} $ Ne

56.69 $> $ 26.27

30.267 32.107 28.981 28.818 $ ^{236} $ U

$ \to \; ^{208} $ Hg+

$ ^{28} $ Mg

70.73 $> $ 26.27

28.600 31.255 28.545 29.695 $ ^{236} $ U

$ \to \; ^{206} $ Hg+

$ ^{30} $ Mg

72.27 $> $ 26.27

28.974 29.947 28.644 27.994 $ ^{238} $ U

$ \to \; ^{208} $ Hg+

$ ^{30} $ Mg

69.46 − 32.594 34.783 30.914 31.141 $ ^{231} $ Np

$ \to \; ^{209} $ Bi+

$ ^{22} $ Ne

61.90 − 23.797 21.375 21.179 23.289 $ ^{233} $ Np

$ \to \; ^{209} $ Bi+

$ ^{24} $ Ne

62.16 − 24.926 22.366 22.642 22.990 $ ^{235} $ Np

$ \to \; ^{207} $ Tl+

$ ^{28} $ Mg

77.10 − 23.691 22.816 24.201 23.941 $ ^{237} $ Np

$ \to \; ^{207} $ Tl+

$ ^{30} $ Mg

74.79 $> $ 27.57

27.227 27.530 27.129 26.287 $ ^{237} $ Pu

$ \to \; ^{209} $ Pb+

$ ^{28} $ Mg

77.73 − 24.409 23.489 24.135 24.257 Continued on next page Table 3. Predicted half-lives for possible cluster radioactive nuclei. The values of
$ Q_c $ and the experimental cluster radioactivity half-lives are taken from Ref. [68].Table 3-continued from previous page $Q_{c}$ /MeV

$ {\rm{log}}_{10}T_{1/2}^{\rm{{Exp}}} $ 

$ {\rm{log}}_{10}T_{1/2}^{\rm{{HOPM}}} $ 

$ {\rm{log}}_{10}T_{1/2}^{\rm{{UDL}}} $ 

$ {\rm{log}}_{10}T_{1/2}^{\rm{{MBM}}} $ 

$ {\rm{log}}_{10}T_{1/2}^{\rm{{TAM}}} $ 

$ ^{237} $ Pu

$ \to \; ^{208} $ Pb+

$ ^{29} $ Mg

77.45 − 25.811 24.514 24.949 24.534 $ ^{237} $ Pu

$ \to \; ^{205} $ Hg+

$ ^{32} $ Si

91.46 − 26.548 25.170 25.429 25.319 $ ^{239} $ Pu

$ \to \; ^{209} $ Pb+

$ ^{30} $ Mg

75.08 − 29.614 28.790 27.295 26.941 $ ^{239} $ Pu

$ \to \; ^{205} $ Hg+

$ ^{34} $ Si

90.87 − 29.203 26.824 26.849 25.849 $ ^{237} $ Am

$ \to \; ^{209} $ Bi+

$ ^{28} $ Mg

79.85 − 27.032 22.058 23.016 23.128 $ ^{239} $ Am

$ \to \; ^{207} $ Tl+

$ ^{32} $ Si

94.50 − 26.223 22.648 24.139 23.667 $ ^{241} $ Am

$ \to \; ^{207} $ Tl+

$ ^{34} $ Si

93.96 $> $ 24.41

27.512 24.130 25.507 24.132 $ ^{240} $ Cm

$ \to \; ^{208} $ Pb+

$ ^{32} $ Si

97.55 − 21.854 20.310 22.866 22.095 $ ^{241} $ Cm

$ \to \; ^{209} $ Pb+

$ ^{32} $ Si

95.39 − 25.359 23.191 24.070 23.902 $ ^{243} $ Cm

$ \to \; ^{209} $ Pb+

$ ^{34} $ Si

94.79 − 27.971 24.770 25.472 24.415 $ ^{244} $ Cm

$ \to \; ^{210} $ Pb+

$ ^{34} $ Si

93.17 − 27.849 27.059 26.433 25.825 As is well known, cluster radioactivity is closely related to the shell effect, which has prompted widespread interest in the field of nuclear physics [68, 71, 72]. To verify the shell effect in the cluster radioactivity process, we calculate the cluster radioactivity half-lives of the emitter cluster
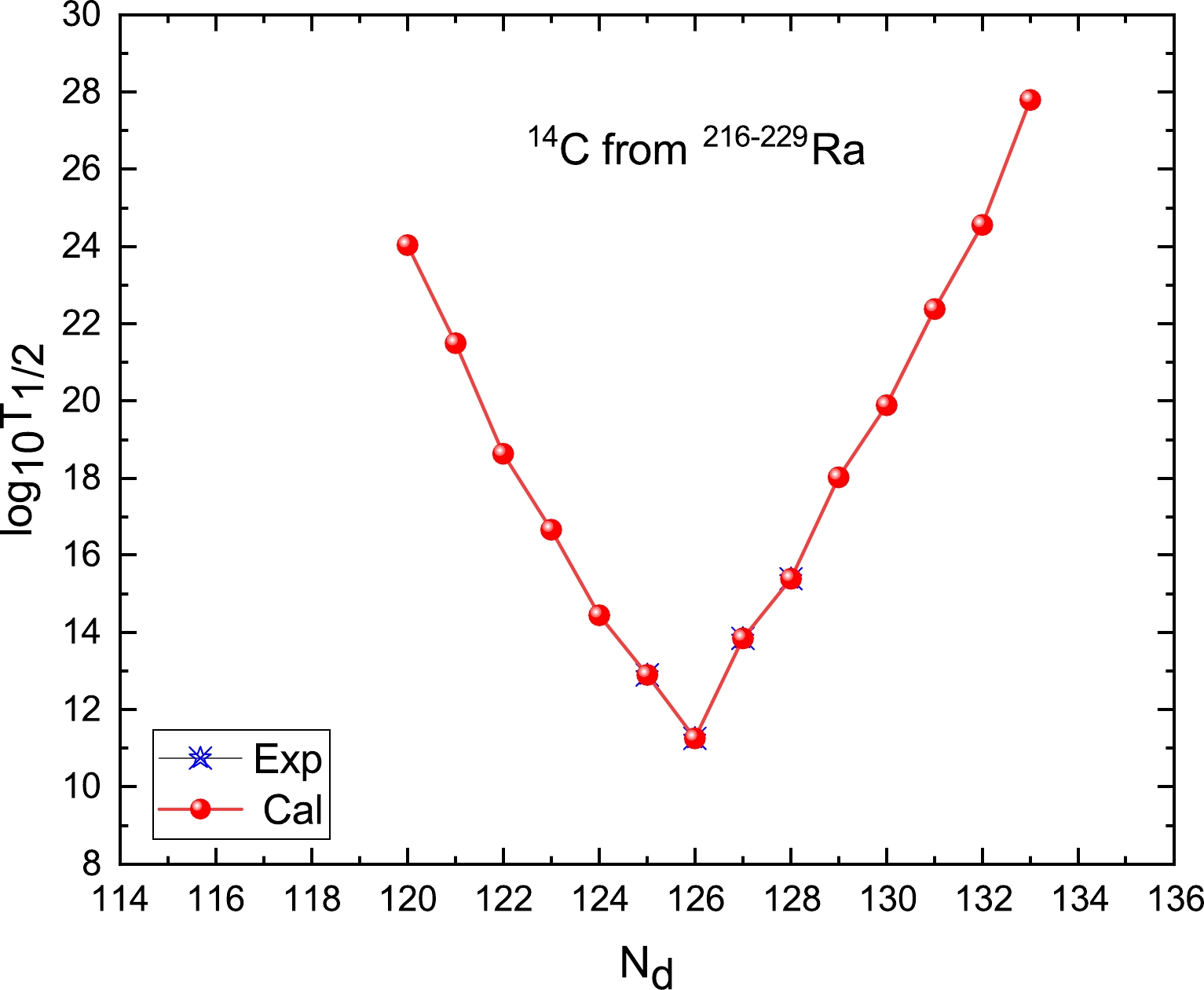
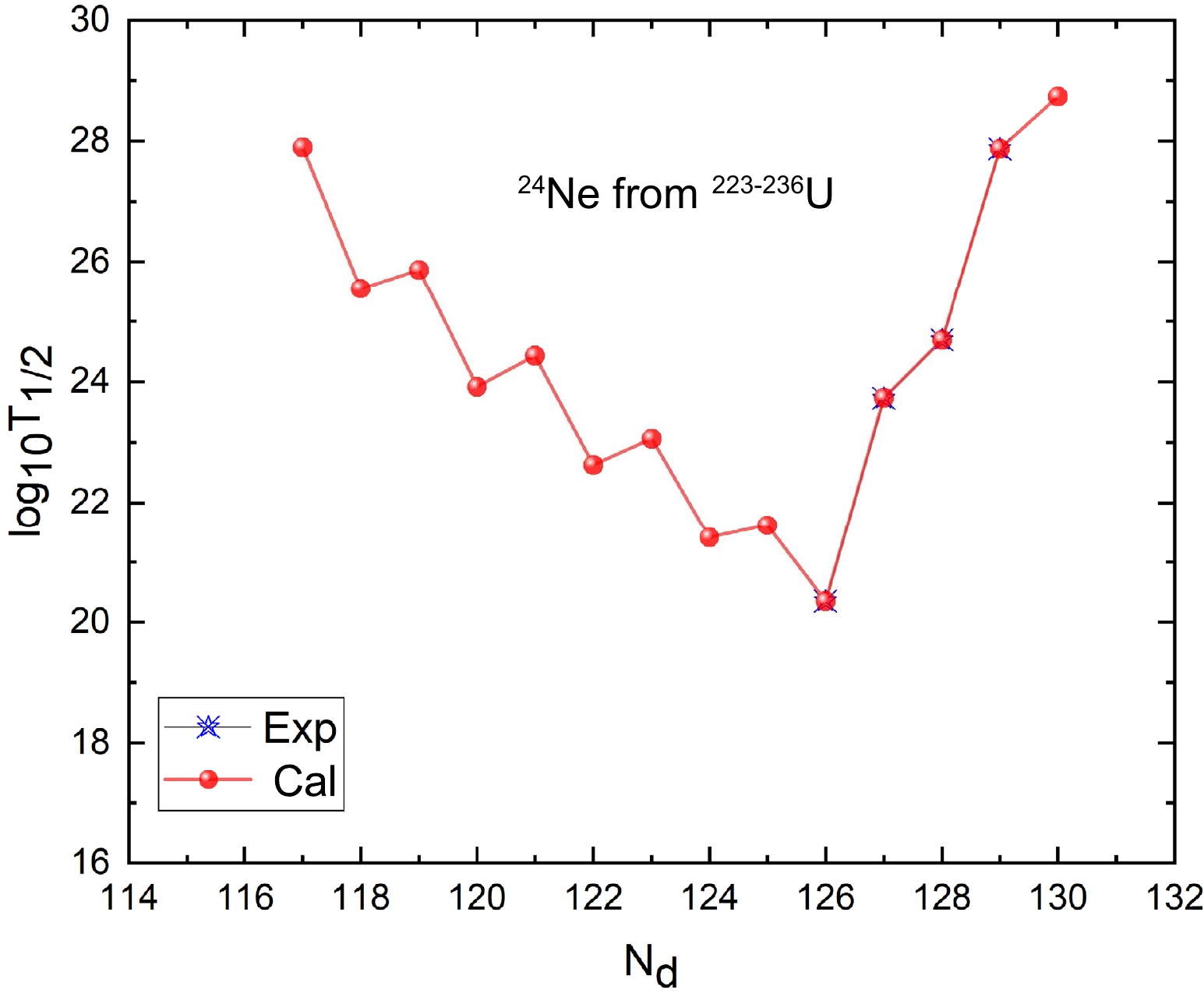
$ \rm{^{14}C} $ from$\rm{^{216-229}Ra}$ isotopes and$ \rm{^{24}Ne} $ from$\rm{^{223-226}U}$ isotopes, which give the daughters$\rm{^{202-215}Pb}$ and$\rm{^{199-212}Pb}$ . The detailed calculated results are listed in Table 4. In this table, the first and fourth columns, second and fifth columns, and third and sixth columns denote the decay process, decay energy$ Q_c $ , and calculated cluster radioactivity half-lives in logarithmic form, respectively. As shown in Table 4, the shortest value of the cluster radioactivity half-life occurs when daughter nuclei are the doubly magic$ \rm{^{208}Pb} $ (Z = 82, N = 126). Meanwhile, the relationship between the experimental and calculated cluster radioactivity half-lives in logarithmic form and the daughter neutron number for the cluster$ \rm{^{14}C} $ from$\rm{^{216-229}Ra}$ isotopes and$ \rm{^{24}Ne} $ from$ \rm{^{223-236}U} $ isotopes is plotted in Figs. 5 and 6, respectively. From these two figures, we can find the minimum logarithmic half-life of the double magic kernel$ \rm {^ {208} Pb} $ (Z=82, N=126). Consequently, this confirms that neutron shell closure plays a crucial role in cluster radioactivity [68, 71, 72]. We hope that these predicted half-lives will be useful for identifying new cluster emissions of the trans-tin region in future measurements.$Q_{c}$ /MeV

$ {\rm{log}}_{10}T_{1/2}^{\rm{{HOPM}}} $ 

Decay $Q_{c}$ /MeV

$ {\rm{log}}_{10}T_{1/2}^{\rm{{HOPM}}} $ 

$ ^{216} $ Ra

$ \to ^{202} $ Pb+

$ ^{14} $ C

26.21 24.035 $ ^{223} $ U

$ \to \; ^{199} $ Pb+

$ ^{24} $ Ne

57.02 27.900 $ ^{217} $ Ra

$ \to ^{203} $ Pb+

$ ^{14} $ C

27.65 21.498 $ ^{224} $ U

$ \to ^{200} $ Pb+

$ ^{24} $ Ne

57.91 25.544 $ ^{218} $ Ra

$ \to \; ^{204} $ Pb+

$ ^{14} $ C

28.74 18.633 $ ^{225} $ U

$ \to ^{201} $ Pb+

$ ^{24} $ Ne

58.59 25.860 $ ^{219} $ Ra

$ \to ^{205} $ Pb+

$ ^{14} $ C

30.14 16.663 $ ^{226} $ U

$ \to ^{202} $ Pb+

$ ^{24} $ Ne

59.21 23.913 $ ^{220} $ Ra

$ \to ^{206} $ Pb+

$ ^{14} $ C

31.04 14.450 $ ^{227} $ U

$ \to ^{203} $ Pb+

$ ^{24} $ Ne

59.76 24.432 $ ^{221} $ Ra

$ \to ^{207} $ Pb+

$ ^{14} $ C

32.4 12.900 $ ^{228} $ U

$ \to ^{204} $ Pb+

$ ^{24} $ Ne

60.29 22.626 $ ^{222} $ Ra

$ \to ^{208} $ Pb+

$ ^{14} $ C

33.05 11.266 $ ^{229} $ U

$ \to ^{205} $ Pb+

$ ^{24} $ Ne

60.93 23.060 $ ^{223} $ Ra

$ \to ^{209} $ Pb+

$ ^{14} $ C

31.83 13.847 $ ^{230} $ U

$ \to ^{206} $ Pb+

$ ^{24} $ Ne

61.35 21.410 $ ^{224} $ Ra

$ \to ^{210} $ Pb+

$ ^{14} $ C

30.54 15.395 $ ^{231} $ U

$ \to ^{207} $ Pb+

$ ^{24} $ Ne

62.21 21.616 $ ^{225} $ Ra

$ \to ^{211} $ Pb+

$ ^{14} $ C

29.47 18.021 $ ^{232} $ U

$ \to ^{208} $ Pb+

$ ^{24} $ Ne

62.31 20.353 $ ^{226} $ Ra

$ \to ^{212} $ Pb+

$ ^{14} $ C

28.2 19.887 $ ^{233} $ U

$ \to ^{209} $ Pb+

$ ^{24} $ Ne

60.49 23.733 $ ^{227} $ Ra

$ \to ^{213} $ Pb+

$ ^{14} $ C

27.34 22.379 $ ^{234} $ U

$ \to ^{210} $ Pb+

$ ^{24} $ Ne

58.83 24.690 $ ^{228} $ Ra

$ \to ^{214} $ Pb+

$ ^{14} $ C

26.1 24.562 $ ^{235} $ U

$ \to ^{211} $ Pb+

$ ^{24} $ Ne

57.36 27.877 $ ^{229} $ Ra

$ \to ^{215} $ Pb+

$ ^{14} $ C

25.06 27.795 $ ^{236} $ U

$ \to ^{212} $ Pb+

$ ^{24} $ Ne

55.94 28.740 -
In summary, based on the WKB approximation and Bohr–Sommerfeld quantization condition and considering a modified preformation probability
$ P_c $ , we verify that the linear relationship between$ \log_{10}P_c $ and$V_{\rm frag}$ is model-independent and extend HOPM to systematically study the cluster radioactivity half-lives of 28 trans-lead nuclei. The results are in good agreement with the experimental data. In addition, we also extend HOPM to predict the cluster radioactivity half-lives of 51 possible cluster radioactive candidates whose cluster radioactivities are energetically allowed or observed but not yet quantified in NUBASE2020. The predicted results are reasonably consistent with those obtained using UDL, MBM, and TAM. Furthermore, the shell effect in the cluster radioactivity process is verified by predicting the emitter cluster$ \rm{^{14}C} $ from$\rm{^{216-229}Ra}$ isotopes and$ \rm{^{24}Ne} $ from$\rm{^{223-236}U}$ isotopes, which may guide future experiments.
Simple model for cluster radioactivity half-lives in trans-lead nuclei
- Received Date: 2023-07-21
- Available Online: 2023-11-15
Abstract: In this study, considering the modified preformation probability





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF




















 DownLoad:
DownLoad: