-
Comprehending the mechanisms of nucleus-nucleus reactions remains a perpetual objective in the field of nuclear physics. In recent years, nuclear reactions involving weakly bound projectiles have garnered significant interest. These reactions exhibit several unique characteristics, distinct from those induced by tightly bound nuclei [1−4]. Owing to the cluster structure and low separation energy in weakly bound nuclei, these exhibit a high probability of breakup. This tendency significantly impacts other relevant observables, including the elastic scattering angular distributions and total reaction cross sections.
The optical potential is an essential tool for calculating elastic scattering angular distributions and total reaction cross sections, providing a straightforward method for prediction. Generally, there are two types of optical potentials. The first is the phenomenological optical potential, which requires parameter adjustments to align with experimental data. The second type is the microscopic optical potential (MOP), theoretically derived from nucleon-nucleon interactions. In the study of nuclear reactions induced by weakly bound nuclei, MOP assumes a crucial role, especially because scattering measurements often do not yield sufficient data to derive a reliable global phenomenological optical potential (GOP).
However, it is usually difficult to build a unified description with unadjusted MOP for the elastic scattering of weakly bound nuclei, as there are strong coupling effects from breakup, transfer, and other reaction channels. For example,
$ ^{6} $ Li can break up into α+d and exhibits a low threshold breakup energy of 1.47 MeV. Hence the breakup mechanisms are crucial in its induced reactions. To date, there have been several measurements for$ ^{6} $ Li elastic scattering, total reaction cross sections, and other observables [5−8]. However, the results are still far from being fully understood. The breakup threshold anomaly [9] has been observed in several experiments for$ ^6 $ Li projectile with a wide range of targets [3], in which the imaginary part of optical potential increases as the energy decreases to well below the Coulomb barrier. This anomaly, arising from the breakup effect, creates a hindrance for both MOP and GOP in accurately describing the elastic scattering angular distributions at energies around the Coulomb barrier.Recently, an analysis [10] of
$ ^6 $ Li+$ ^{90} $ Zr elastic scattering shows that a reduction factor of$ \sim $ 0.5 on the real part of MOP constructed with S$ \tilde{\rm{a}} $ o Paulo potential [11, 12] is required to fit the data at energies below 2$ V_B $ , where$ V_B $ denotes the height of the Coulomb barrier. This suppression is equivalent to adding a repulsive real polarization potential [10], suggesting that the$ ^6 $ Li breakup effect should be considered for elastic scattering calculations.To date, the continuum discretized coupled-channels method (CDCC) [13−16] has been one of the most popular methods to handle the breakup effect and investigate its role in the reactions induced by weakly bound nuclei. In this approach, a two-body model is generally adopted to describe the weakly bound nucleus, which is assumed to be composed of core and valence particles and will break up during the reaction. In early time, Sakuragi et al. [16] presented a comprehensive CDCC study for
$ ^6 $ Li elastic scattering at energies well above the Coulomb barrier with M3Y interaction [17]. They determined that there is no need to adjust the real part of optical potential [17] in CDCC calculations, which is required to be reduced by$ \sim $ 40% in the folding model potential analysis of Satchler and Love [18]. However. given that a few measurements for$ ^6 $ Li scattering at energies around$ V_B $ have been performed recently, it is worthwhile to provide a systematic study for$ ^6 $ Li induced reactions and investigate the effect of the breakup process.Previously, we obtained the nucleon-nucleus MOP based on Skyrme effective nucleon-nucleon interactions [19] and constructed MOPs for
$ ^{2,3} $ H,$ ^{3,4,6} $ He, and$ ^{7} $ Li [20−25] with the folding method. In this study, we will combine our previous reserach of the MOP for light ion projectile with the CDCC method in the calculations of$ ^6 $ Li induced reactions at energies around$ V_B $ . This combination, termed as microscopic CDCC, is not only an exploratory study for examining the validity of our MOP on the heavy ion projectile but also proposes a potential methoed to apply our MOP on other heavier weakly bound projectiles, whose breakup effect is considerable, such as$ ^{11} $ Li and$ ^{11} $ Be.On the other hand, α and d phenomenological optical potentials have been widely adopted in the CDCC analysis for specific
$ ^6 $ Li induced reactions. The adjustment on d optical potential is generally accepted due to the effective suppression of the deuteron-target absorption [26]. However, this adjustment is found to be dependent on the choice of d optical potential. The surface part of d optical potential is removed for$ ^{6} $ Li+$ ^{209} $ Bi reaction in Ref. [27] but that is unchanged for$ ^{6} $ Li+$ ^{159} $ Tb and$ ^{6} $ Li+$ ^{59} $ Co reactions in Ref. [28]. In this study, we perform CDCC calculations with α and d GOPs to ensure consistency on the adjustment of deuteron optical potential and compare their results with those calculated with MOPs to verify the validity of MOPs.Additionally, 1n-stripping process has been found to be a significant contributor to the inclusive α cross sections in
$ ^6 $ Li+$ ^{159} $ Tb [29] and$ ^{6} $ Li+$ ^{112,124} $ Sn [30, 31] reactions. In these cases, a neutron is stripped from$ ^6 $ Li and then$ ^5 $ Li is broken into α+p. It would be interesting to investigate whether we should consider the breakup process of d cluster in$ ^{6} $ Li induced reactions as that in$ (d,p) $ reactions [32−34]. In this study, the breakup effect of d is equivalently treated as a dynamic polarization potential. This approach is integrated into the$ ^{6} $ Li CDCC calculations to examine the effect of d breakup and check the validness of α+d two-body model for$ ^6 $ Li.The paper is organized as follows. The theoretical framework is recapitulated in Sec. II. Furthermore, in Sec. III, we present the calculated results for
$ ^6 $ Li-induced reactions and discuss the breakup effect of$ ^6 $ Li. The breakup probability of d cluster is discussed in Sec. IV. Finally, a summary of the study is provided in Sec. V. -
We recapitulate the three-body CDCC framework for
$ ^6 $ Li scattering from a target nucleus (T). Details can be found in Refs. [13, 16, 35]. Furthermore, α+d two-body model is adopted to describe$ ^6 $ Li. Hence the total wave function of reaction system Ψ with total energy E is determined by the three-body Schr$ \ddot{\rm{o}} $ dinger equation$ \begin{array}{*{20}{l}} \left( H-E \right) \Psi =0, \end{array} $

(1) where H denotes the total Hamiltonian,
$ \begin{array}{*{20}{l}} H=T_R+U_{\alpha}+U_d+H_{\rm{in}}. \end{array} $

(2) $ H_{\rm{in}} $ denotes the internal Hamiltonian of$ ^6 $ Li. Furthermore,$ T_R $ denotes the kinetic energy with respect to the relative coordinate$ {\boldsymbol{R}} $ between$ ^6 $ Li and T. Additionally,$ U_x $ (x=α, d) denotes the optical potential between x and T.In CDCC method, Eq. (1) is solved in the model space spanned by the bound and discretized continuum states, which are all obtained by diagonalizing
$ H_{\rm{in}} $ with square-integrable basis functions. Therefore,$ \begin{array}{*{20}{l}} H_{\rm{in}}\left| \psi _\gamma \right> =\varepsilon _\gamma\left| \psi _\gamma \right> , \end{array} $

(3) where
$ \psi _\gamma $ denotes the γ-th eigenstate with eigenenergy$ \varepsilon_\gamma $ . For$ ^6 $ Li,$ \psi _1 $ represents the ground state and others denote the discretized continuum states.The total wave function Ψ can be expressed as:
$ \Psi =\sum\limits_{\gamma}{\chi _\gamma\left( {\boldsymbol{R}} \right) \left| \psi _\gamma \right \gt}, $

(4) where
$ \chi _\gamma $ denotes the relative motion between T and$ ^6 $ Li in its γ-th state. Furthermore,$ \chi _\gamma $ can be solved with the following coupled equations as follows:$ \left[ T_R+U_{\gamma \gamma}-\left( E-\varepsilon _\gamma \right) \right] \chi _\gamma=-\sum\limits_{\gamma' \ne \gamma}^N{U_{\gamma \gamma'}\chi _{\gamma '}}, $

(5) where the coupling potential matrix can be defined as follows:
$ \begin{array}{*{20}{l}} U_{\gamma \gamma'}=\left< \psi _\gamma \right|U_{\alpha}+U_d\left| \psi _{\gamma '} \right>. \end{array} $

(6) The Lagrange-mesh method is applied to diagonalize
$ H_{\rm{in}} $ . Its basis functions are defined as follows:$ f_i\left( r \right) =\frac{\left( -1 \right) ^i}{\sqrt{hx_i}}\frac{L_N\left( r/h \right)}{r-hx_i}{\rm re}^{-r/2h},\quad i=1,2,...,N, $

(7) where
$ {\boldsymbol{r}} $ denotes the relative coordinate between α and d,$ L_N $ denotes the Laguerre polynomial of degree N, and$ x_i $ denotes the zeros of$ L_N $ , that is$ \begin{array}{*{20}{l}} L_N(x_i)=0, i=1,2,...,N. \end{array} $

(8) Specifically, h denotes a scaling parameter, which is adopted to the typical size of the system. See Refs. [35−37] for details. The interaction between α and d is obtained from Refs. [35, 38].
-
Microscopic optical potentials for α and d clusters are constructed within folding model as
$ \begin{aligned}[b] U\left( {\boldsymbol{R}}_x \right) =&\int{{\rm d}{\boldsymbol{s}}} \left[ U_n\left( \left| {\boldsymbol{R}}_x+{\boldsymbol{s}} \right| \right) \rho _{x,n}\left( {\boldsymbol{s}} \right) \right. \\ & \left. + U_p\left( \left| {\boldsymbol{R}}_x+{\boldsymbol{s}} \right| \right) \rho _{x,p}\left( {\boldsymbol{s}} \right) \right], \end{aligned} $

(9) where
$ {\boldsymbol{R}}_x $ is the relative coordinate between x and T, and$ {\boldsymbol{s}} $ denotes the internal coordinate of x. Furthermore,$ \rho _{x,p} $ and$ \rho _{x,p} $ denote the neutron and proton density distributions of x, respectively.$ U_n $ and$ U_p $ are isospin-dependent nucleon-nucleus MOPs [19] based on Skyrme effective interaction. They are derived from the mass operator of the single-particle Green’s function via the nuclear matter approximation and local density approximation. The real and imaginary parts of nucleon-nucleus MOP are denoted by the first- and imaginary part of the second-order mass operators, respectively. More details can be found in Ref. [19].In this study, the Skyrme interaction SkMP [39] is used to calculate the nucleon-nucleus MOP. Improvements are made on the nucleon density distributions. The proton and neutron density distributions of targets are required for
$ U_n $ and$ U_p $ calculations. Instead of Negele's formula [40] in the original version of MOP [19], they are provided theoretically by an axially-symmetric self-consistent Dirac-Hartree-Bogoliubov mean field approach [41], which has obtained good agreements with ground state masses and charge radii of near-stability nuclei throughout the entire mass table [12]. The proton and neutron density distributions of α are obtained from Ref. [42] (version C in Table 1) and those of d are derived from its bound state wave functions, which is calculated with the n-p Gaussian-type potential$V(r_{np})= -V_0\exp (-r_{np}^{2}/r_{0}^{2})$ .$ V_0 $ =72.25 MeV and$ r_0 $ =1.484 fm. Specifically,$ r_{np} $ denotes the distance between n and p.For comparison, we also perform CDCC calculations with GOPs of α [43] and d [44] and optical potential calculations with a
$ ^6 $ Li GOP [45]. The α GOP of Avrigeanu et al. [43] and d GOP of An et al. [44] have been examined for their validities at low incident energies. They are well-suited for use in the current study. -
In the present study,
$ ^6 $ Li collisions with$ ^{27} $ Al,$ ^{64} $ Zn,$ ^{138} $ Ba, and$ ^{208} $ Pb targets are analysed. The Coulomb barriers in the laboratory system are 8.0, 14.5, 22.0, and 30.6 MeV for these four reaction systems [5−7, 46], respectively. To investigate the breakup effect, we compare the full CDCC results with the one-channel (1ch) calculations, in which the continuum coupling is switched off. -
The first step for the analysis of
$ ^6 $ Li induced reactions involves providing an adequate calculation condition for convergence. In the present study, we adopt parameters N=35 and h=0.5 for the Lagrange-mesh method similar to that in Ref. [38]. Many tests have been performed to ensure that the calculated results are insensitive to N and h.In CDCC calculations, the angular momentum l and energy ε of α-d relative motion must be truncated at certain
$ l_{\max} $ and$ \varepsilon_{\max} $ values, which are selected to be sufficiently large to ensure the convergence of the associated cross sections. Given that$ l_{\max} $ and$ \varepsilon_{\max} $ should be independent of α and d optical potentials, we are able to only examine the convergence of calculations with MOP, and the final calculation condition can be applied to the calculations with GOP directly.Firstly, we perform calculations for
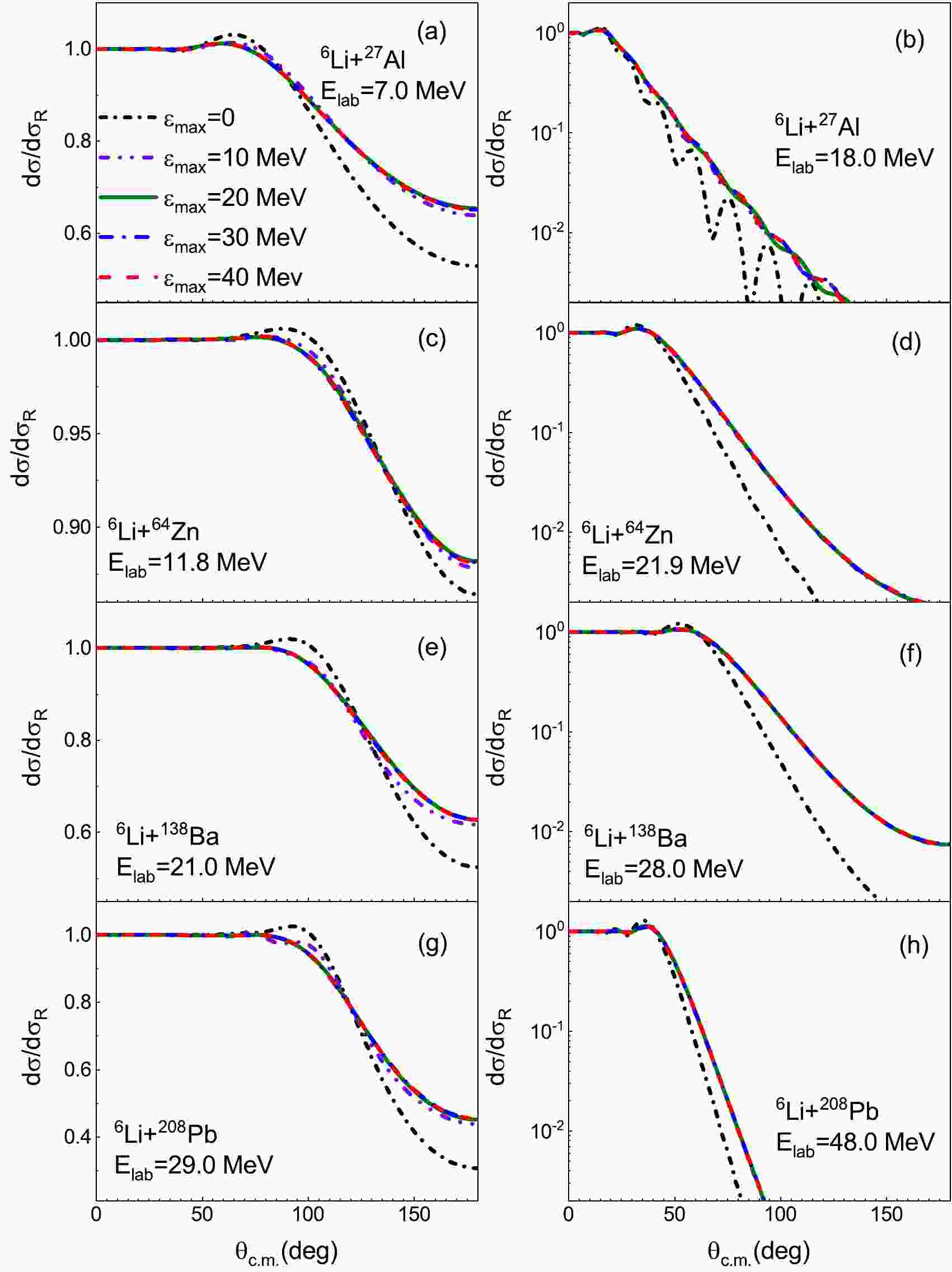
$ ^6 $ Li+$ ^{27} $ Al,$ ^{64} $ Zn,$ ^{138} $ Ba, and$ ^{208} $ Pb systems at incident energies below and above the Coulomb barrier with different values of$ \varepsilon_{\max} $ . Specifically,$ l_{\max} $ =2 is fixed such that important$ 3^+ $ ,$ 2^+ $ , and$ 1^+ $ resonance states are included in CDCC calculations. Figure 1 shows the elastic scattering angular distributions calculated with$ \varepsilon_{\max} $ =0, 10, 20, 30, and 40 MeV. The CDCC calculation with$ \varepsilon_{\max} $ =0 corresponds to the one-channel calculation. It can be observed that the calculated results are almost the same for$ ^{64} $ Zn,$ ^{138} $ Ba, and$ ^{208} $ Pb targets with$ \varepsilon_{\max} \geq $ 10 MeV at incident energies exceeding the Coulomb barrier, while the convergence of elastic scattering angular distribution is reached with$ \varepsilon_{\max} \geq 20$ MeV in the sub-barrier energy region. However, the situation becomes more complicated for$ ^6 $ Li+$ ^{27} $ Al reaction systems. The calculated results are the same with$ \varepsilon_{\max} \geq $ 20 and 30 MeV at$ E_{\rm{lab}} $ =7.0 and 18.0 MeV, respectively. A higher$ \varepsilon_{\max} $ is required for the convergence of$ ^6 $ Li+$ ^{27} $ Al elastic scattering angular distribution at incident energies exceeding the Coulomb barrier.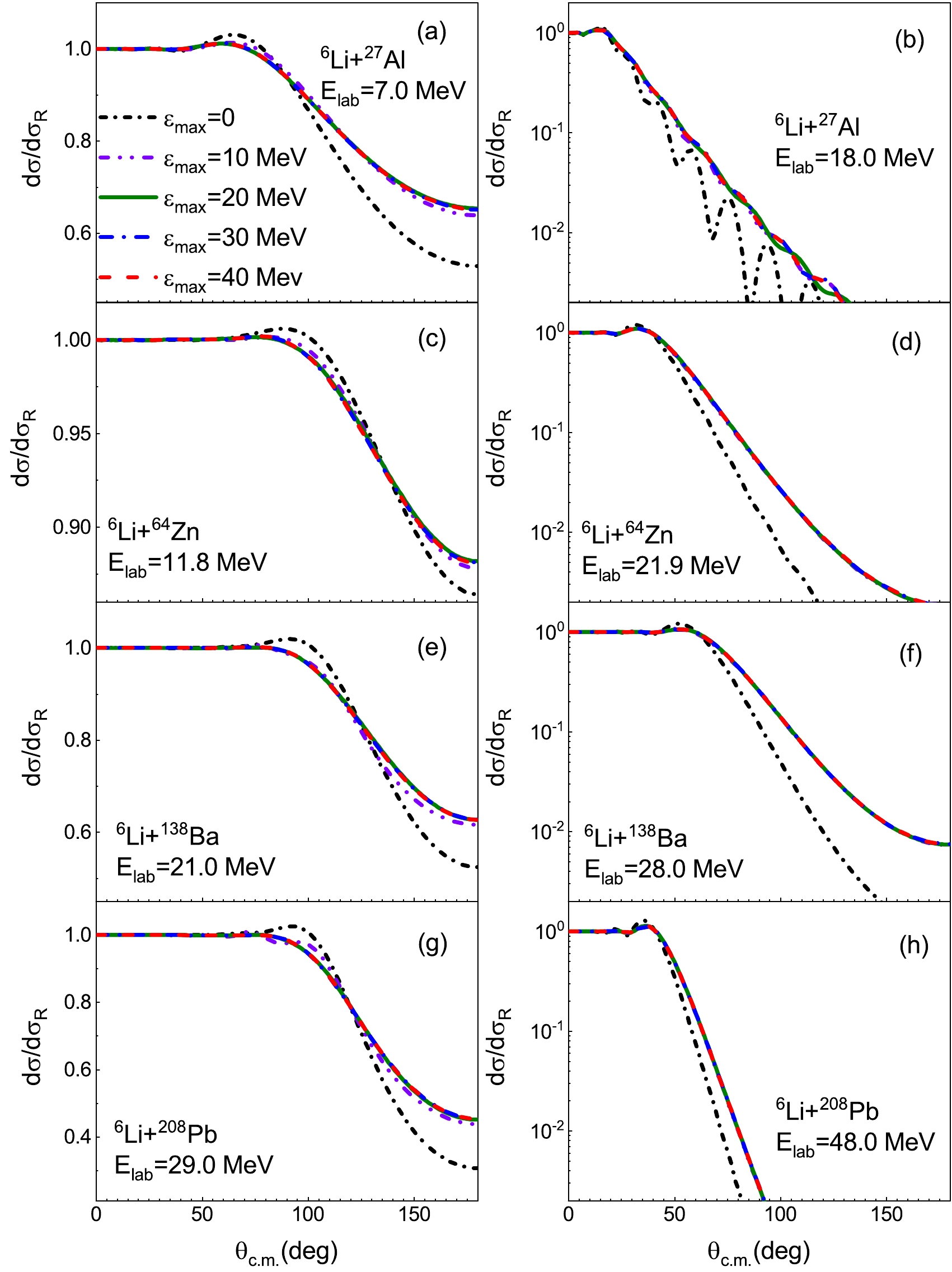
Figure 1. (color online) Elastic scattering angular distributions, as ratios to Rutherford cross sections, for
$ ^6 $ Li+$ ^{27} $ Al,$ ^{64} $ Zn,$ ^{138} $ Ba, and$ ^{208} $ Pb systems at incident energies below and above the Coulomb barrier with respect to different values of$ \varepsilon_{\max} $ .$ l_{\max} $ =2 is fixed. The Coulomb barriers in the laboratory system are 8.0, 14.5, 22.0, and 30.6 MeV for these four reaction systems [5−7, 46], respectively. Black, purple, green, blue, and red lines denote the CDCC calculations with$ \varepsilon_{\max} $ =0, 10, 20, 30, and 40 MeV, respectively. See text for details.We define
$ R_1(\varepsilon_{\max}) $ as:$ R_1(\varepsilon _{\max})=\frac{\sigma _{\rm{TR}} ( \varepsilon _{\max} )}{\sigma _{\rm{TR}} ( \varepsilon _{\max}=40 \, \rm{MeV} )}-1 , $

(10) where
$ \sigma _{\rm{TR}} (\varepsilon _{\max}) $ denotes the total cross section calculated with$ \varepsilon _{\max} $ . Specifically,$ l_{\max} $ =2. Figure 2 shows the value of$ R_1(\varepsilon_{\max}) $ as a function of$ \varepsilon_{\max} $ . For all reaction systems, the absolute values of$ R_1(\varepsilon_{\max}) $ are less than 2% when$ \varepsilon_{\max} \geq $ 20 MeV. The convergence of total reaction cross section requires lower$ \varepsilon_{\max} $ than that of elastic scattering angular distribution. With an overall consideration,$ \varepsilon_{\max} $ =30 MeV is adopted to ensure the convergence of all CDCC calculations in the current study.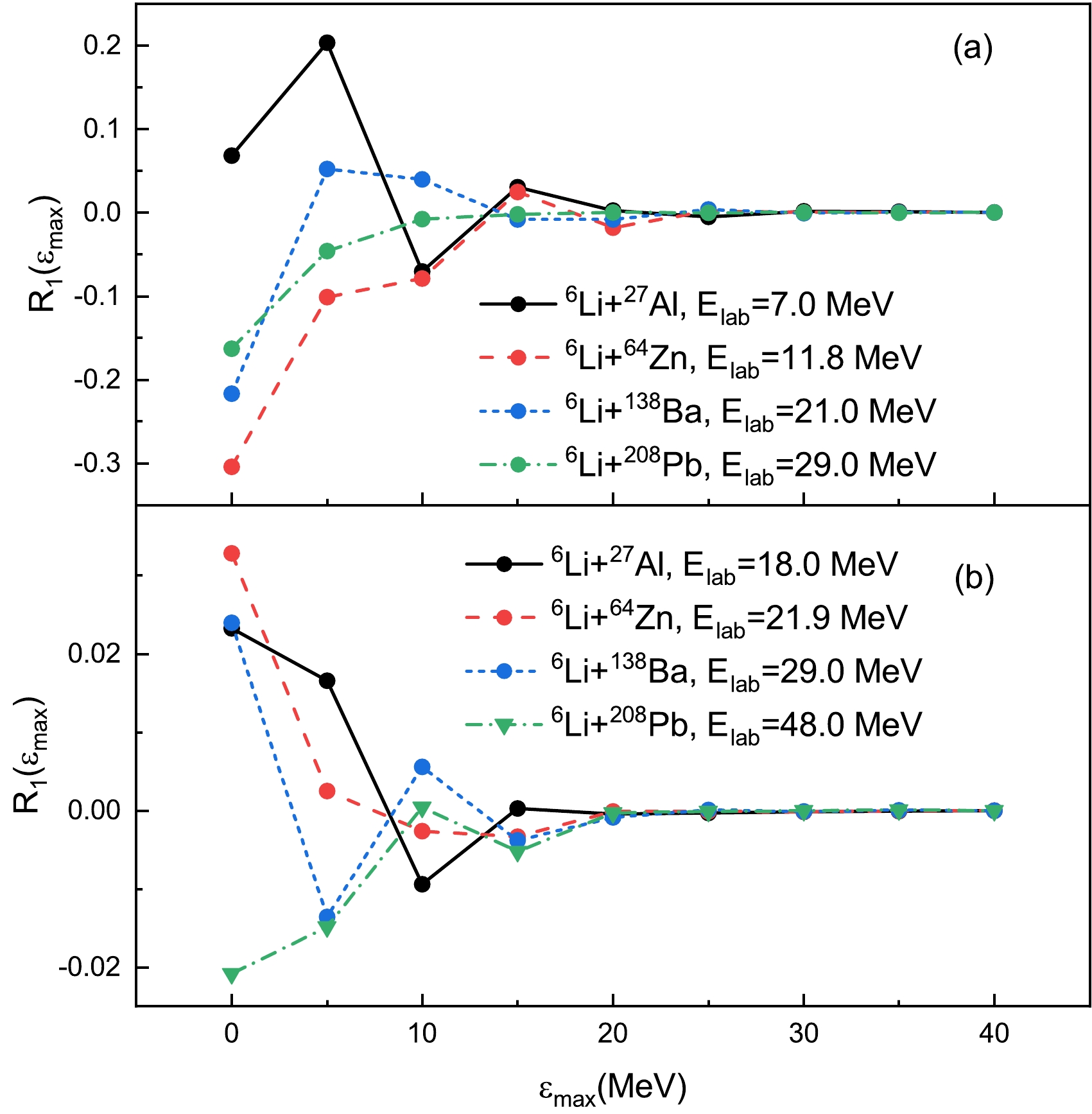
Figure 2. (color online)
$ R_1(\varepsilon_{\max}) $ for$ ^6 $ Li+$ ^{27} $ Al,$ ^{64} $ Zn,$ ^{138} $ Ba, and$ ^{208} $ Pb systems with respect to$ \varepsilon_{\max} $ .$ l_{\max} $ =2 is fixed. (a) Incident energies are below the Coulomb barrier. (b) Incident energies are above the Coulomb barrier. The Coulomb barriers in the laboratory system are 8.0, 14.5, 22.0, and 30.6 MeV for these four reaction systems [5−7, 46], respectively. The solid, dashed, short dashed, and dash-dotted lines denote the CDCC calculations for$ ^6 $ Li+$ ^{27} $ Al,$ ^{64} $ Zn,$ ^{138} $ Ba, and$ ^{208} $ Pb systems, respectively. See text for details.Another important issue is the choice of
$ l_{\max} $ . With fixed$ \varepsilon_{\max} $ =30 MeV, elastic scattering angular distributions are calculated with$ l_{\max} $ =0, 1, 2, and 3 for$ ^6 $ Li+$ ^{27} $ Al,$ ^{64} $ Zn,$ ^{138} $ Ba, and$ ^{208} $ Pb systems at incident energies below and above the Coulomb barrier, as shown in Fig. 3. For all reaction systems, the elastic scattering angular distributions increase in the large scattering angle region as$ l_{\max} $ increases from 0 to 2, while the differences between the calculated results with$ l_{\max} $ =2 and 3 are low.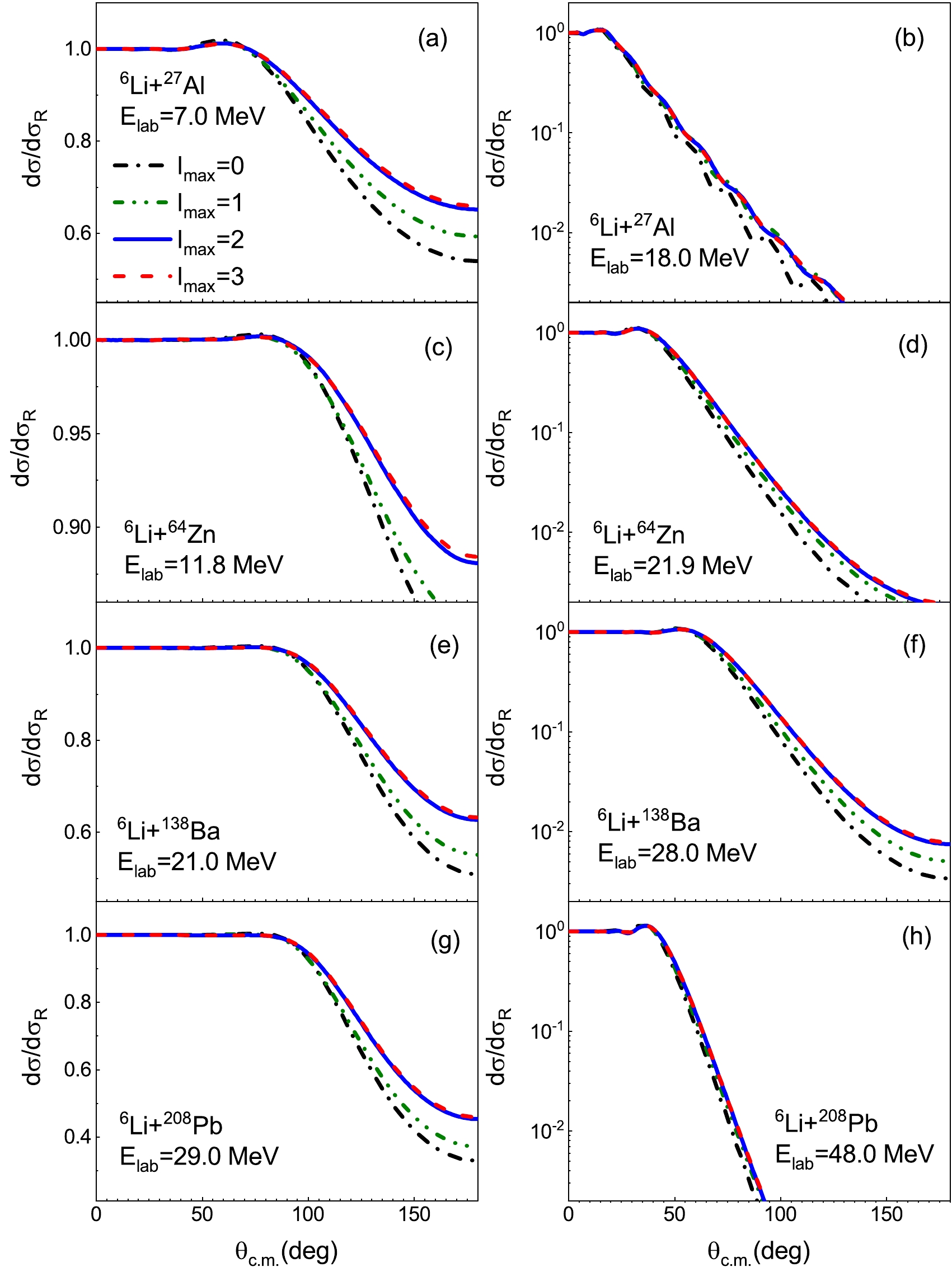
Figure 3. (color online) Same as Fig. 1 but the CDCC calculations are performed with different values of
$ l_{\max} $ .$ \varepsilon_{\max} $ =30 MeV is fixed. The black, green, blue, and red lines denote the CDCC calculations with$ l_{\max} $ =0, 1, 2, and 3, respectively. See text for details.Similar to
$ R_1(\varepsilon_{\max}) $ , we define$ R_2(l_{\max}) $ as follows:$ R_2(l _{\max})=\frac{\sigma _{\rm{TR}} ( l _{\max} )}{\sigma _{\rm{TR}} ( l _{\max}=3 )}-1 , $

(11) where
$ \sigma _{\rm{TR}} (l _{\max}) $ denotes the total cross section calculated with$ l _{\max} $ . Furthermore,$ \varepsilon_{\max} $ =30 MeV is fixed.$ R_2(l_{\max}) $ values are presented in Fig. 4 as a function of$ l_{\max} $ . For all reaction systems, the value of$ R_2(l_{\max}) $ decreases as$ l_{\max} $ increases and it becomes less than 2% at$ l_{\max} $ =2. Hence,$ l_{\max} $ =2 is sufficient to ensure the convergences of elastic scattering angular distribution and total reaction cross section.
Figure 4. (color online) Same as Fig. 2 but for
$ R_2(l_{\max}) $ , shown as a function of$ l_{\max} $ . See text for details.In the following calculations,
$ \varepsilon_{\max} $ =30 MeV and$ l_{\max} $ =2 are used. -
Generally,
$ ^6 $ Li CDCC calculations with α and d phenomenological optical potential require some renormalizations on the optical potentials as a consequence of the effective suppression of the deuteron-target absorption in$ \alpha+d $ two-body model [26, 47]. Given that the parameters of GOP are adjusted to fit various elastic scattering experimental data and total reaction cross sections, the CDCC analysis with GOP is expected to ensure the consistency of the renormalizations and improve reliability.It is found that
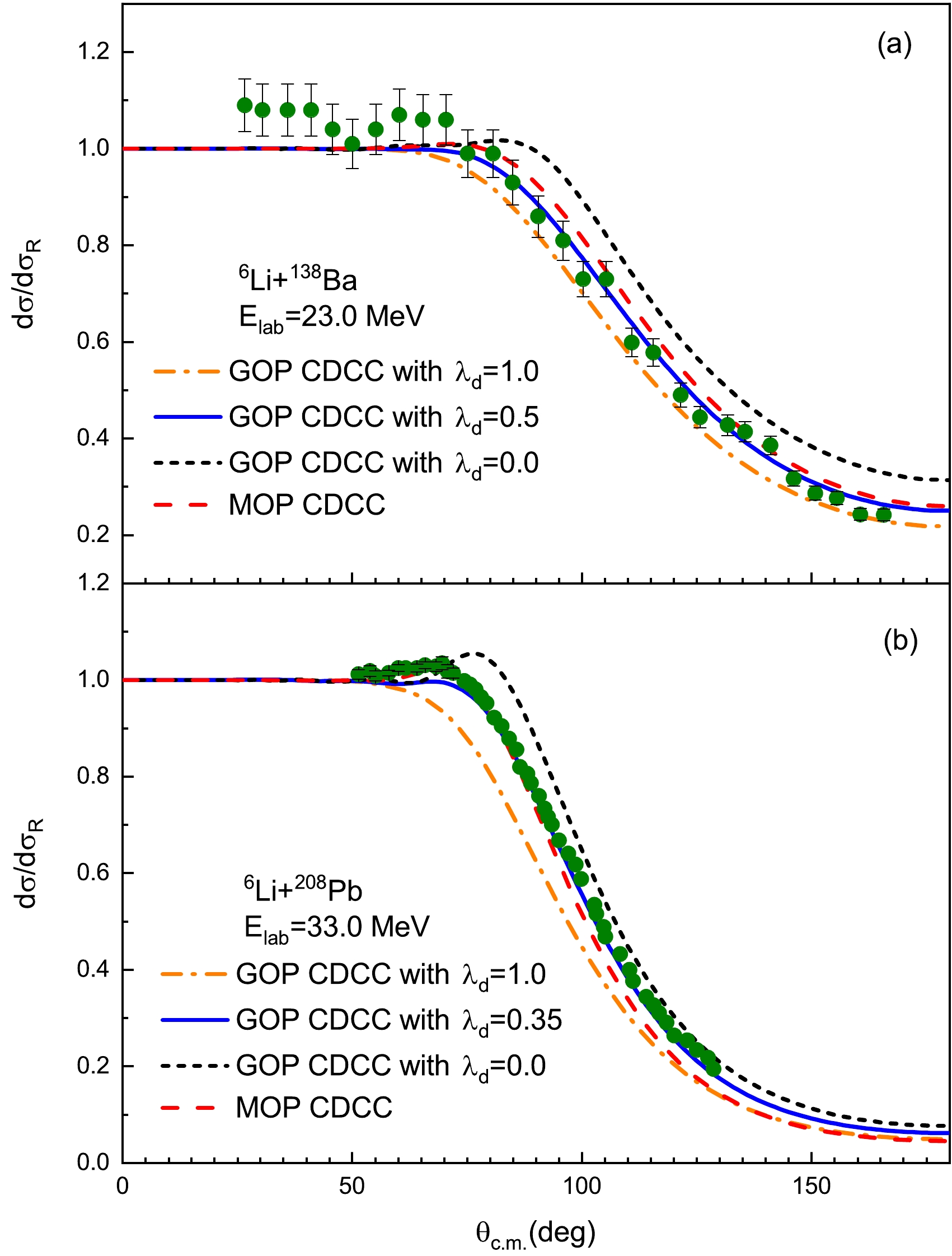
$ ^6 $ Li elastic scattering angular distribution is sensitive to the surface imaginary part of d GOP, which should be multiplied by a reduction factor$ \lambda _d $ to fit the experimental data. Considering the elastic scattering angular distributions and total cross sections simultaneously,$ \lambda _d $ is optimized as 0, 0.45, 0.50, and 0.35 for$ ^6 $ Li+$ ^{27} $ Al,$ ^{64} $ Zn,$ ^{138} $ Ba, and$ ^{208} $ Pb reactions, respectively. These reductions are maintained in the following calculations for$ ^6 $ Li induced reactions with d GOP.Figures 5 and 6 show the CDCC calculations with GOP for
$ ^6 $ Li+$ ^{27} $ Al,$ ^{64} $ Zn,$ ^{138} $ Ba, and$ ^{208} $ Pb reactions at$ E_{\rm{lab}} $ =8.0, 13.6, 23.0, and 33.0 MeV, respectively, when compared with the results calculated with MOP. For$ ^6 $ Li+,$ ^{64} $ Zn,$ ^{138} $ Ba , and$ ^{208} $ Pb reactions, with the decrease of$ \lambda_d $ from 1 to 0, the deuteron-target absorption process is suppressed and the elastic scattering angular distribution increases in the angle region above 70 degrees, leading to a visible Coulomb rainbow [49]. Good agreement between the experimental data [5−7, 48] and CDCC results, calculated with GOP, is obtained with the optimized$ \lambda _d $ , which are no more than 0.5. However, for$ ^6 $ Li+$ ^{27} $ Al reaction, the elastic scattering angular distribution changes moderately as$ \lambda_d $ decreases from 1 to 0. We finally adopt$ \lambda_d $ =0 for this reaction system to fit the total reaction cross sections.
Figure 5. (color online) Elastic scattering angular distributions, as ratios to Rutherford cross sections, for (a)
$ ^6 $ Li+$ ^{27} $ Al reaction at$ E_{\rm{lab}} $ =8.0 MeV and (b)$ ^6 $ Li+$ ^{64} $ Zn reaction at$ E_{\rm{lab}} $ =13.6 MeV. The dash-dotted, solid, and short dashed lines denote the CDCC calculations with GOP, in which the surface imaginary terms of d GOP are multiplied by different values of$ \lambda _d $ , respectively. The dashed lines represent the CDCC results calculated with MOP. Experimental data are obtained from Refs. [5, 6]. See text for details.Unlike the calculations using GOP, the CDCC calculations with MOP successfully replicate the measured values without requiring any adjustments.
-
Figure 7 shows the calculated elastic scattering angular distributions for
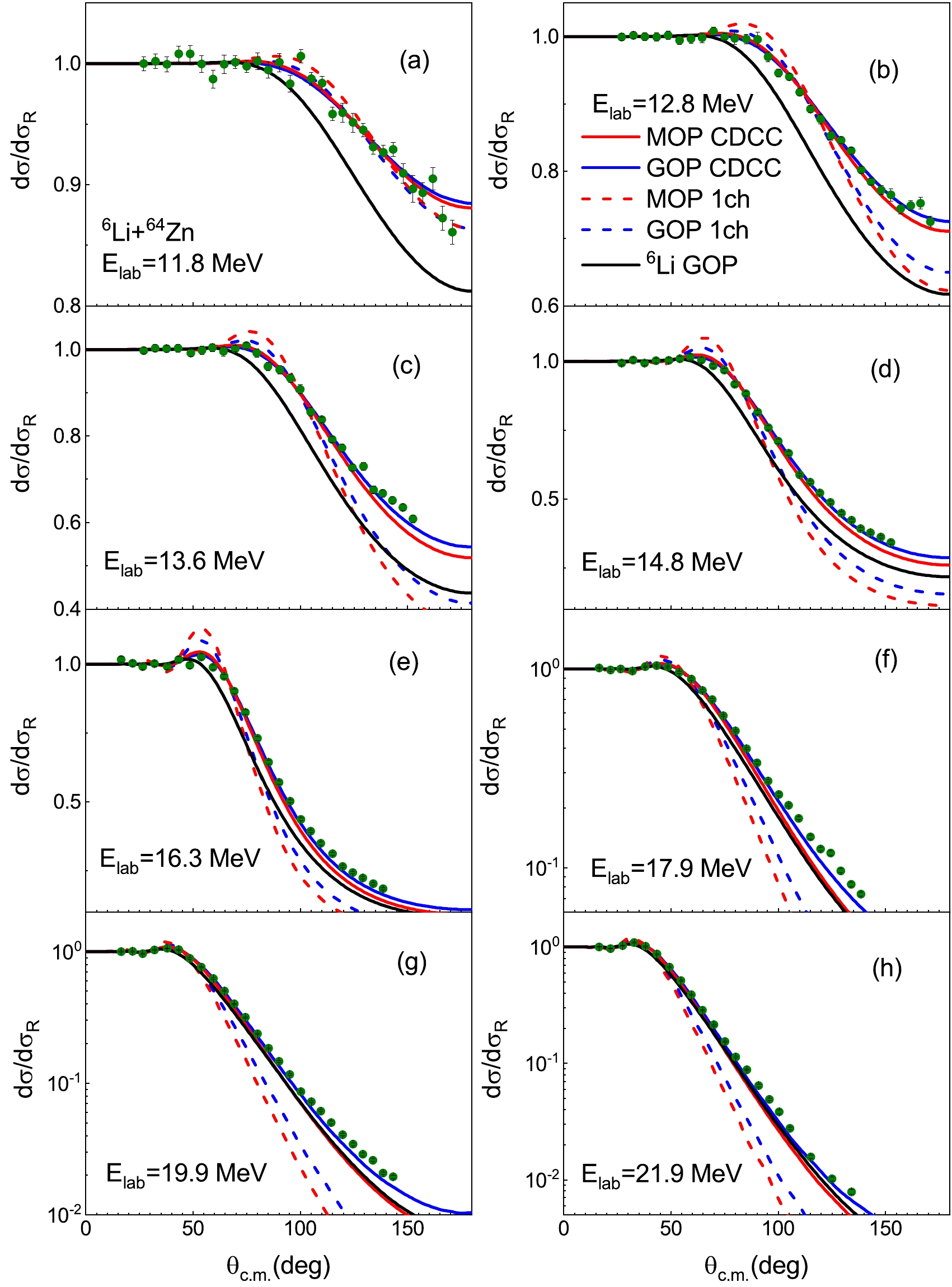
$ ^6 $ Li+$ ^{27} $ Al reactions at incident energies ($ E_{\rm{lab}} $ ) from 7.0 MeV to 18.0 MeV. Compared with one-channel results, continuum state coupling reduces the Coulomb rainbows and increases the angular distributions in the angle region above 70 degrees significantly at$ E_{\rm{lab}}\leq $ 12.0 MeV. More specifically, two types of CDCC calculations provide almost the same results and obtain good agreements with the experimental data [5], with the exception of the underestimations in back angle region at$ E_{\rm{lab}} $ =10.0 and 12.0 MeV. Given that the breakup reaction channel is comprehensively incorporated in CDCC calculations, these underestimations are attributed to the absence of the transfer reaction channel. This channel represents another significant coupling mechanism in reactions induced by weakly bound nuclei [50]. At$ E_{\rm{lab}} $ =18.0 MeV, remarkable oscillations occur in the one-channel results while the CDCC results calculated with MOP are much smoother and are in agreement with the measured value. Additionally, the$ ^6 $ Li GOP [45] significantly underestimates the angular distributions above 50 degrees at$ E_{\rm{lab}}\leq $ 10.0 MeV but provides similar results with CDCC method at higher incident energies.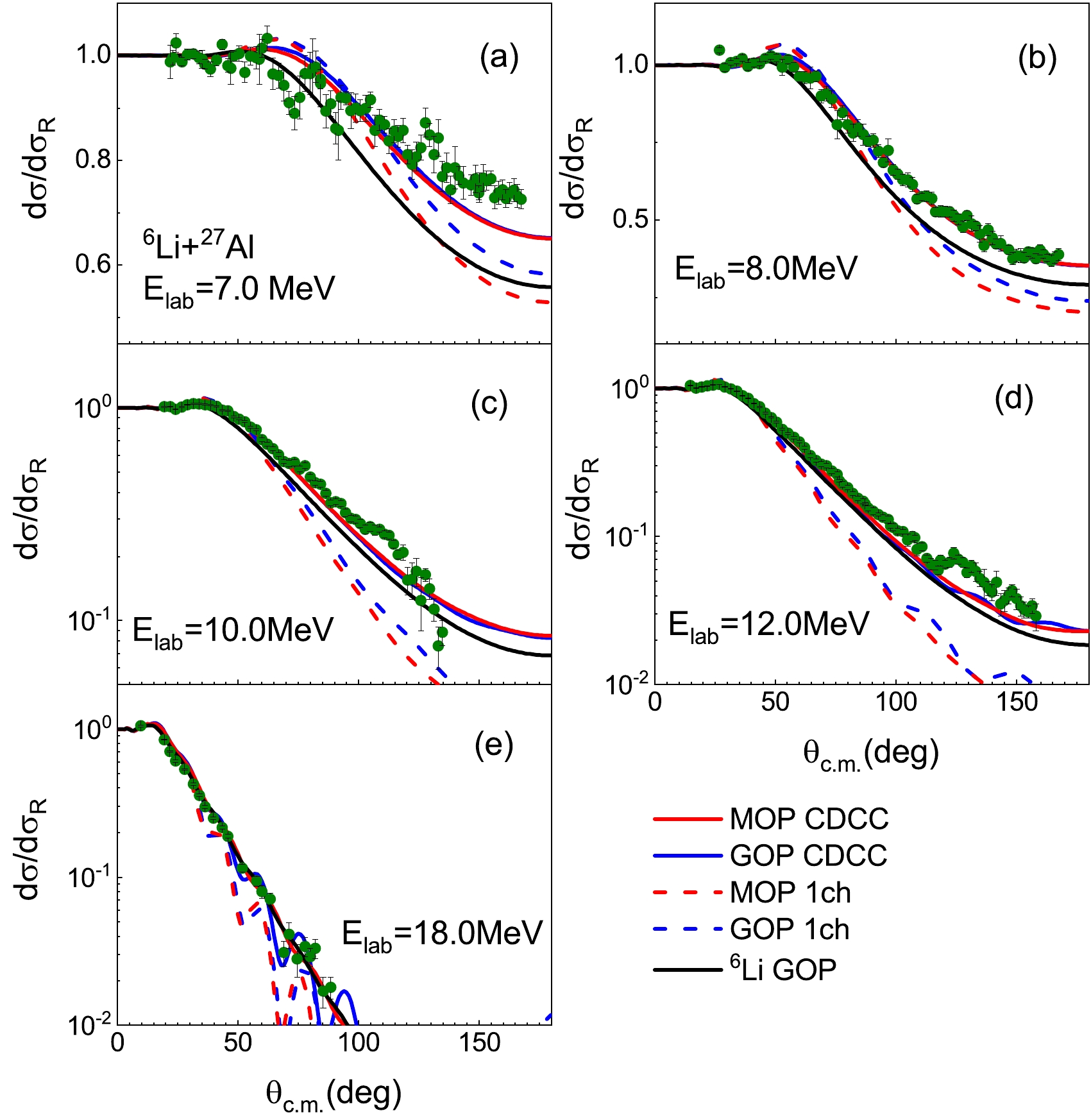
Figure 7. (color online) Elastic scattering angular distributions, as ratios to Rutherford cross sections, for
$ ^6 $ Li+$ ^{27} $ Al reactions. The red solid and blue solid lines denote CDCC calculations with MOP and GOP, respectively. The red dashed and blue dashed lines represent the one-channel calculations with MOP and GOP, respectively. The black lines denote the results calculated with the$ ^6 $ Li GOP [45]. The surface imaginary part of d GOP is multiplied by$ \lambda _d $ =0 in the CDCC and one-channel calculations involving d GOP. Experimental data are obtained from Ref. [5] and represented by green circles. See text for details.The elastic scattering angular distributions for
$ ^6 $ Li+$ ^{64} $ Zn system at$ E_{\rm{lab}} $ =11.8−21.9 MeV are presented in Fig. 8. CDCC results with GOP are the same as those with MOP. However, they become slightly larger in the back angle region, leading to a better agreement with experimental data [6] at$ E_{\rm{lab}} \geq $ 13.6 MeV. Coulomb rainbows are obvious in one-channel calculations but they are negligible in CDCC results, which are strongly reduced by continuum state coupling.Figures 9 and 10 show
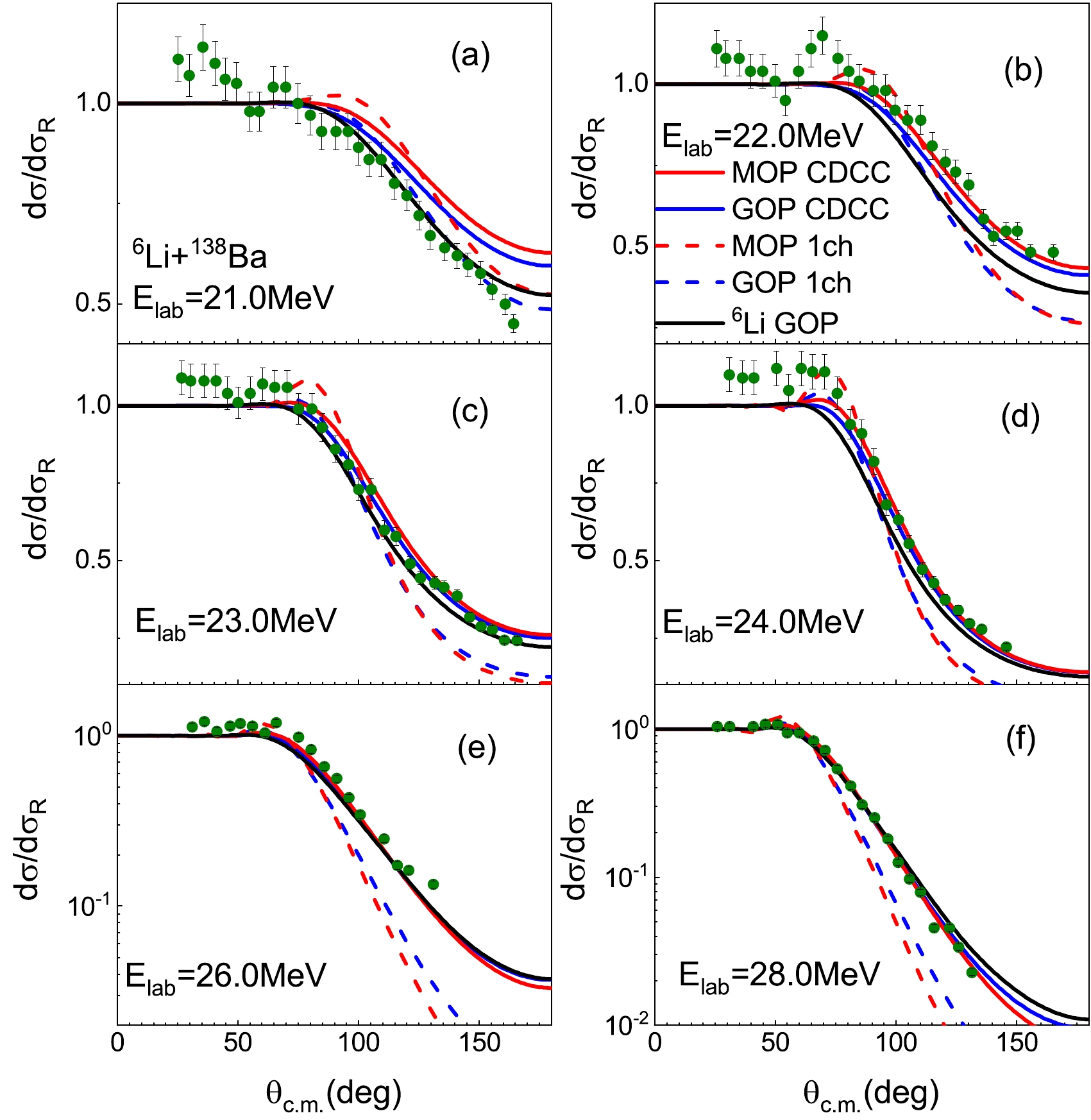
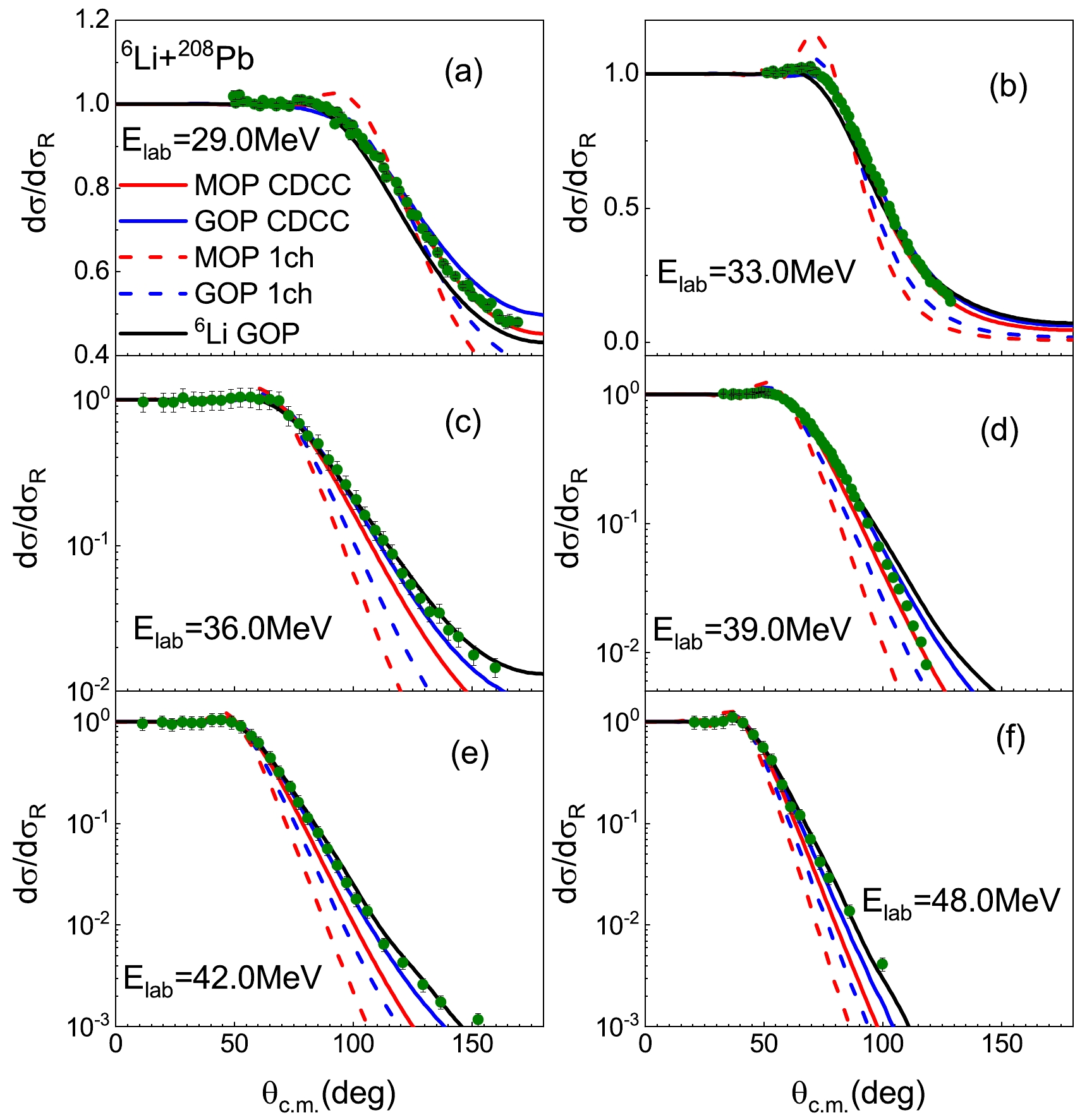
$ ^6 $ Li elastic scattering on$ ^{138} $ Ba and$ ^{208} $ Pb targets. Consistent with the previous two reaction systems, continuum state coupling reduces the Coulomb rainbow and increases the angular distributions in the large angle region. Generally, CDCC results are in good agreement with experimental data [7, 48, 51] with the exception of$ ^6 $ Li+$ ^{138} $ Ba scattering at$ E_{\rm{lab}} $ =21.0 MeV. Additionally, the CDCC calculations with GOP reproduce the measured value better than those with MOP for$ ^6 $ Li+$ ^{208} $ Pb reactions as they provide larger angular distributions in the back angle region.For a clearer understanding of the
$ ^6 $ Li breakup effect on elastic scattering, we compare the elastic scattering S-matrix elements$ S^{J}_{LL'} $ obtained from CDCC and one-channel calculations. Specifically, J denotes the total angular momentum, and L and$ L' $ denote the orbital angular momentums of initial and final channels, respectively, with respect to$ {\boldsymbol{R}} $ . The diagonal elements$ S^{J}_{JJ} $ are plotted in Fig. 11. As J increases, the module value of$ S^{J}_{JJ} $ increases and finally$ S^{J}_{JJ} $ converges to 1 . It can be observed at any J that the real and imaginary parts of$ S^{J}_{JJ} $ are enlarged and reduced by continuum state coupling, respectively, which provides a repulsive correction to the results of one-channel calculations, i.e., the folding potential. This correction is independent of optical potentials and reaction systems, consistent with that in the analysis of Sakuragi et al. [16] at energies significantly above the Coulomb barrier.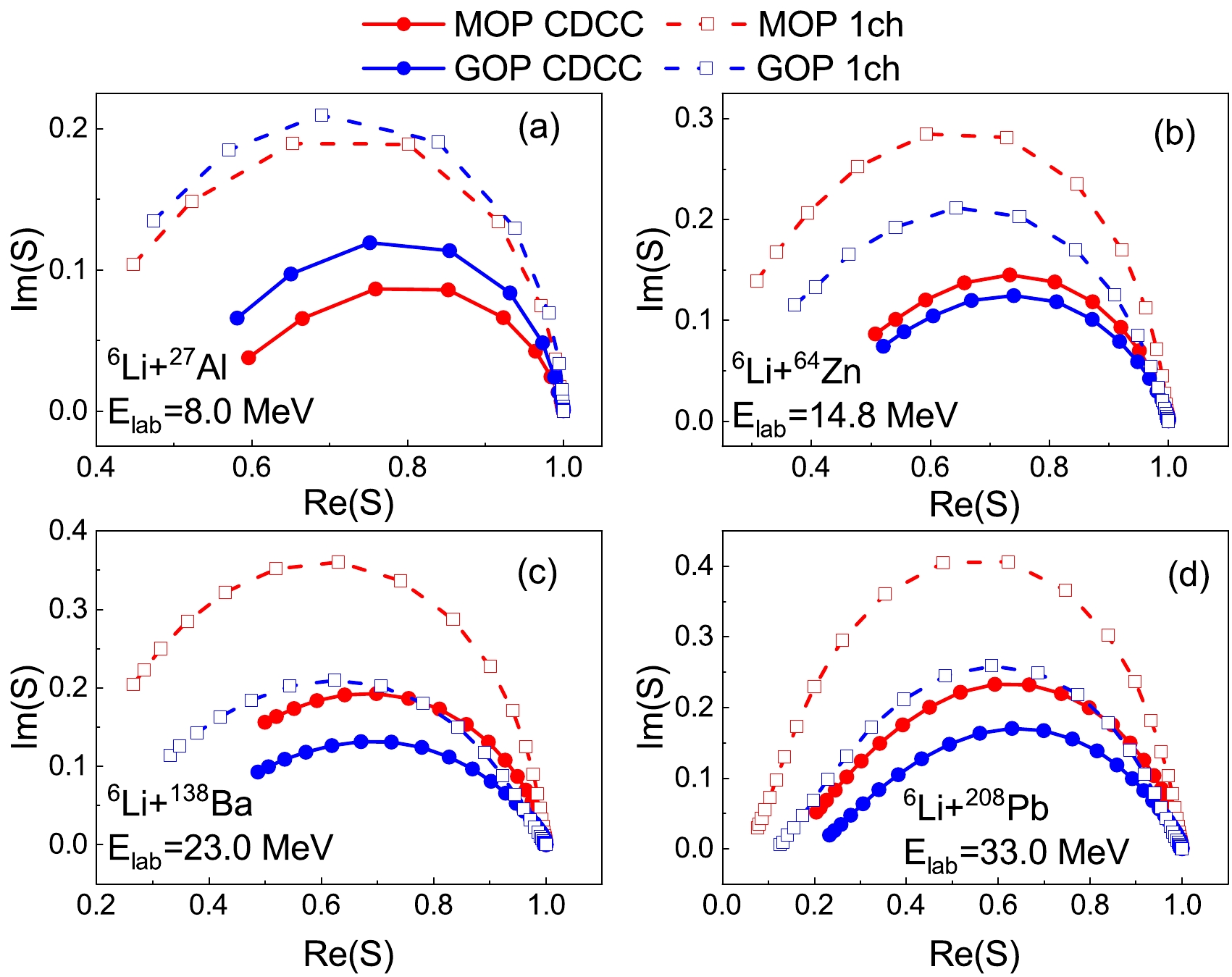
Figure 11. (color online) Elastic scattering S-matrix elements
$ S^{J}_{JJ} $ for$ ^6 $ Li scattering on (a)$ ^{27} $ Al at$ E_{\rm{lab}} $ =8.0 MeV, (b)$ ^{64} $ Ni at$ E_{\rm{lab}} $ =14.8 MeV, (c)$ ^{138} $ Ba at$ E_{\rm{lab}} $ =23.0 MeV, and (d)$ ^{208} $ Pb at$ E_{\rm{lab}} $ =33.0 MeV. Closed circles connected with solid lines and open squares connected with dashed lines denote the results of CDCC and one-channel calculations, respectively. Red and blue scatter lines represent the results obtained with MOP and GOP, respectively. In the CDCC and one-channel calculations involving d GOP, the surface imaginary parts of d GOPs are multiplied by$ \lambda _d $ =0, 0.45, 0.5, and 0.35 for$ ^6 $ Li+$ ^{27} $ Al,$ ^{64} $ Zn,$ ^{138} $ Ba, and$ ^{208} $ Pb systems, respectively. See text for details. -
Comparison between the calculated total reaction cross sections and experimental data [6, 7, 48, 52, 53] are presented in Figs. 12 and 13 for
$ ^6 $ Li+$ ^{27} $ Al,$ ^{64} $ Zn,$ ^{138} $ Ba, and$ ^{208} $ Pb systems. Although the data for$ ^6 $ Li+$ ^{27} $ Al,$ ^{64} $ Zn, and$ ^{138} $ Ba reaction systems are obtained via optical model potential analysis instead of experimental measurement, their values are reliable and can be adopted for comparison. CDCC results obtain satisfactory agreement with experimental data. In the calculations with MOP, continuum state coupling has a weak suppressive effect on$ \sigma_{R}^{} $ for all four reactions at energies above the Coulomb barrier but enlarges$ \sigma_{\rm{TR}}^{} $ considerably in the sub-barrier energy region for$ ^6 $ Li+$ ^{64} $ Zn,$ ^{138} $ Ba, and$ ^{208} $ Pb systems. These properties are maintained in the calculations with GOP. However, the enhancement of$ \sigma_{\rm{TR}} $ at energies below the Coulomb barrier is moderate for$ ^6 $ Li+$ ^{27} $ Al reaction and insignificant for$ ^6 $ Li scattering on heavier targets.
Figure 12. (color online) Total reaction cross sections for (a)
$ ^6 $ Li+$ ^{27} $ Al and (b)$ ^6 $ Li+$ ^{64} $ Zn systems. The red and blue solid lines denote CDCC calculations with MOP and GOP, respectively. The red and blue dashed lines represent the one-channel calculations with MOP and GOP, respectively. The black lines denote the results calculated with the$ ^6 $ Li GOP [45]. In the CDCC and one-channel calculations involving d GOP, the surface imaginary parts of d GOPs are multiplied by$ \lambda _d $ =0 and 0.45 for$ ^6 $ Li+$ ^{27} $ Al and$ ^{64} $ Zn systems, respectively. Experimental data are obtained from Refs. [6, 52, 53] and represented by green circles. The arrows indicate the Coulomb barriers in the laboratory system.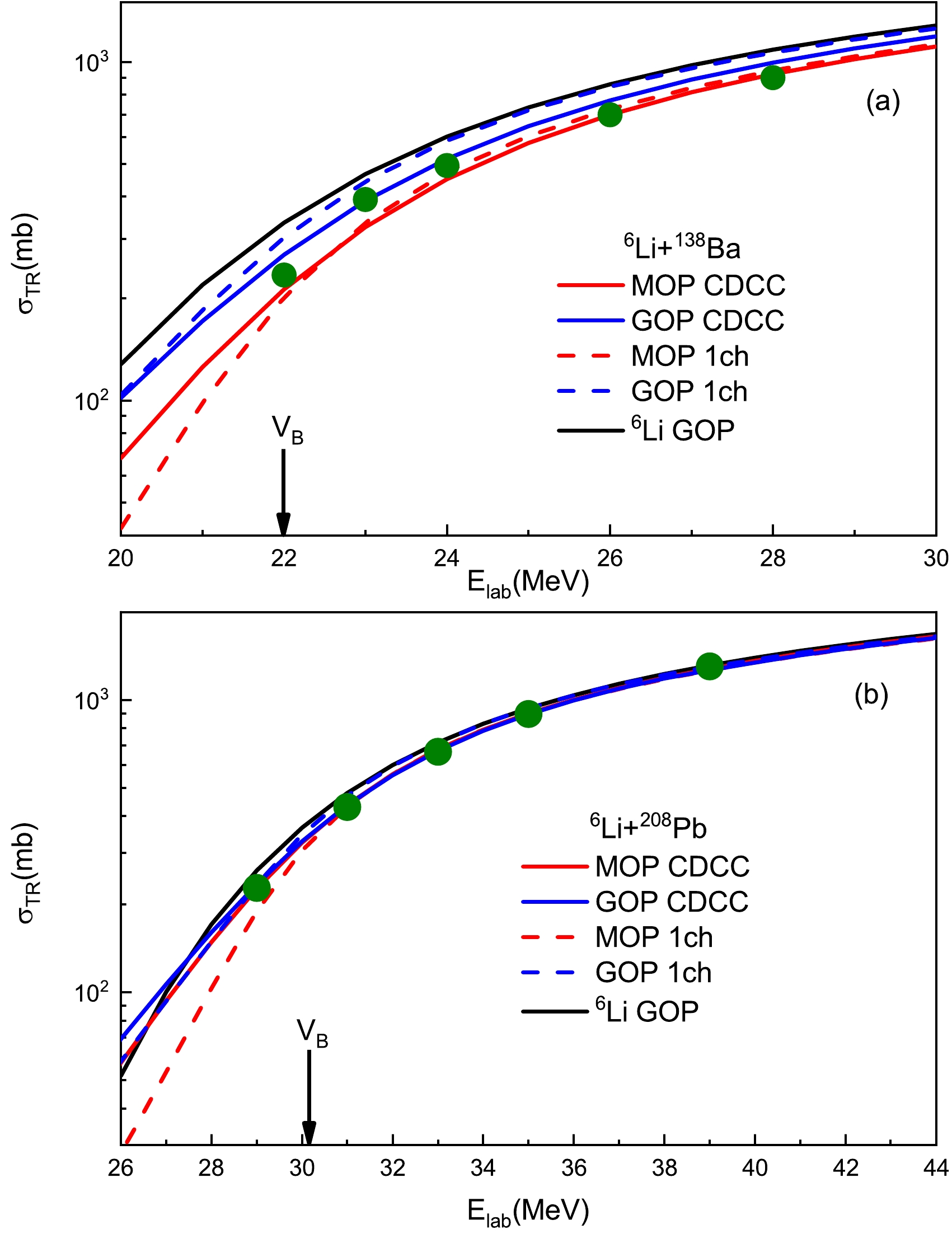
Figure 13. (color online) Same as Fig. 12 but for (a)
$ ^6 $ Li+$ ^{138} $ Ba and (b)$ ^6 $ Li+$ ^{208} $ Pb systems. In the CDCC and one-channel calculations involving d GOP, the surface imaginary parts of d GOPs are multiplied by$ \lambda _d $ =0.5 and 0.35 for$ ^6 $ Li+$ ^{138} $ Ba and$ ^{208} $ Pb systems, respectively. Experimental data are obtained from Refs. [7, 48]. -
As presented in Sec. III, the surface imaginary part of d GOP should be reduced by no less than 50% to fit the data in
$ ^{6} $ Li CDCC calculations with GOP. Hence, this reveals a strong suppression on the d reaction probability. It is well known that breakup and transfer reactions have strong coupling effects in d induced reactions at low incident energies. Their contributions are approximately included in the surface imaginary part of d phenomenological optical potentials, as these reactions mainly occur in the surface region. Hence, it can be inferred that the d cluster in$ ^6 $ Li is not able to break up as easily as that in the free state.Given that the 1n-stripping reaction contributes significantly to the inclusive α cross sections, we wish to investigate whether the breakup process of d cluster should be considered in
$ ^6 $ Li induced reactions. In this study, d breakup effect is treated approximately by means of dynamic polarization potential [16, 54], which provides a correction to the folding model optical potential$ U_d $ =$ U_d^{\rm{fold}} $ .Let us make an extreme hypothesis that α and d clusters in
$ ^{6} $ Li are located close to each other. They move with the same velocity at the beginning and react to the target simultaneously. By ignoring the excitation of target, the breakup process of d can be described by the CDCC method at corresponding incident energy$ E_d $ =$ \frac{1}{3}E_{\rm{lab}} $ . For$ ^6 $ Li+$ ^{208} $ Pb reaction at$ E_{\rm{lab}} $ =33.0 MeV, we perform CDCC calculation for d+$ ^{208} $ Pb reaction at$ E_d $ =11.0 MeV with the microscopic nucleon optical potentials$ U_n $ and$ U_p $ as described in Sec. II.B. The n-p interaction is the Gaussian-type potential as mentioned in Sec. II.B. Furthermore, spins of nucleons are ignored. Following the method of Chau Huu-Tai [55], the n-p continuum states of S, P, and D partial waves in open channels are all considered into CDCC calculations. The Lagrange-mesh method is used to discretize continuum states with parameters N=30 and h=0.4 as suggested in Refs. [35, 37].With this CDCC calculation for d+
$ ^{208} $ Pb reaction, an L-independent polarization potential can be obtained with the method of Thompson et al. [56] as follows:$ U_{d}^{\rm{pol}}=\frac{\sum _L{\left( 2L+1 \right) T_L}\left| \chi _L \right|^2U_{L}^{\rm{pol}}}{\sum _L{\left( 2L+1 \right) T_L}\left| \chi _L \right|^2}, $

(12) where
$ U_L^{\rm{pol}} $ denotes the trivially-equivalent L-dependent polarization potential calculated from the CDCC wave functions [16, 57]. Furthermore,$ T_L $ and$ \chi _L $ denote the transmission coefficient and wave function of d-target relative motion in the elastic channel for the L-th partial wave, respectively.The polarization potential
$ U_{d}^{\rm{pol}} $ , folding model potential$ U_{d}^{\rm{fold}} $ , and their summation are presented in Fig. 14. In the low energy d induced reactions, elastic scattering angular distribution is sensitive to the surface term of the optical potential but nearly independent of the inner part. It can be observed that$ U_{d}^{\rm{pol}} $ provides a repulsion correction to the real part of$ U_d $ around$ R_S $ =8.05 fm, which is the interaction radius of the surface imaginary part of d GOP [44]. Furthermore,$ U_{d}^{\rm{pol}} $ deepens the imaginary part of d optical potentials around$ R_S $ .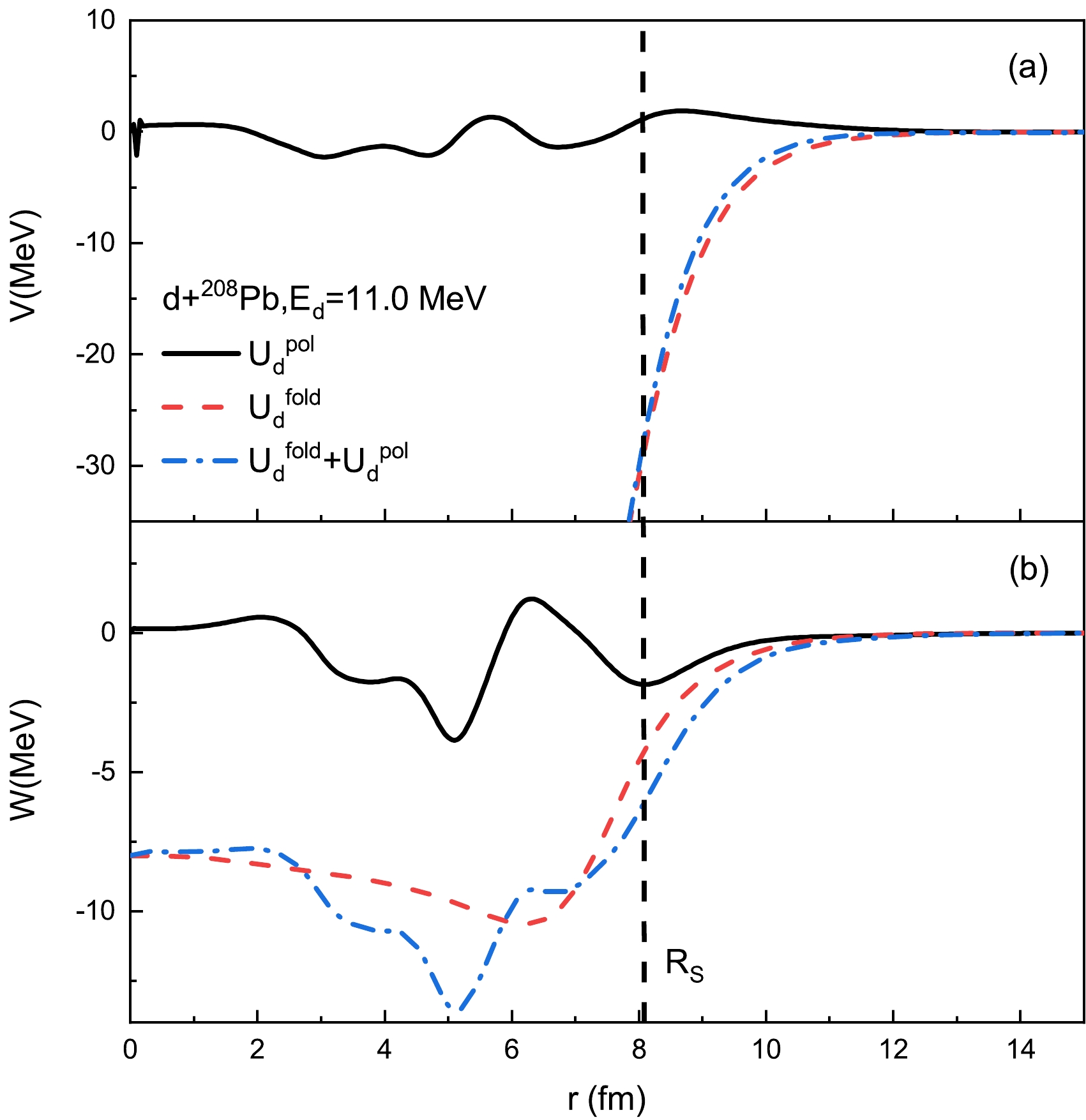
Figure 14. (color online) Polarization potential
$ U_{d}^{\rm{pol}} $ , folding model optical potential$ U_{d}^{\rm{fold}} $ , and their summation for d+$ ^{208} $ Pb reaction at$ E_d $ =11.0 MeV. The solid, dashed, and dash-dotted lines stand for$ U_{d}^{\rm{pol}} $ ,$ U_{d}^{\rm{fold}} $ , and their summation, respectively. The real and imaginary parts of potentials are presented in subfigures (a) and (b), respectively. The dashed vertical line indicates the interaction radius$ R_S $ =8.05 fm of the surface imaginary part of d GOP [44].Figure 15 shows the elastic scattering angular distributions for d+
$ ^{208} $ Pb reaction at$ E_d $ =11.0 MeV. Compared with the results of$ U_{d}^{\rm{fold}} $ , continuum state coupling decreases the angular distributions in 40−80 degrees and increases the results above 80 degrees, improving the agreement with experimental data [58]. Optical potential calculation with$ U_{d}^{\rm{fold}} $ +$ U_{d}^{\rm{pol}} $ provides nearly the same results as those provided by CDCC calculation. Hence$ U_d^{\rm{pol}} $ is sufficient to hold the d breakup effect when d is in a free state.
Figure 15. (color online) Elastic scattering angular distributions, as ratios to Rutherford cross sections, for d+
$ ^{208} $ Pb reaction at$ E_d $ =11.0 MeV. The solid, dashed, dash-dotted lines represent the results of CDCC,$ U_d^{\rm{fold}} $ +$ U_d^{\rm{pol}} $ and$ U_d^{\rm{fold}} $ calculations. Experimental data are taken from Ref. [58]. See text for details.Comparison between the CDCC results with deuteron optical potential
$ U_{d}^{\rm{fold}} $ and$ U_{d}^{\rm{fold}} $ +$ U_d^{\rm{pol}} $ is presented in Fig. 16 for$ ^6 $ Li+$ ^{208} $ Pb reaction at$ E_d $ =33.0 MeV. The α MOP remains unchanged. The angular distributions significantly decrease in 40−90 degrees and slightly increase above 90 degrees when the dynamic polarization potential$ U_d^{\rm{pol}} $ is combined with folding model potential$ U_{d}^{\rm{fold}} $ to be used as deuteron optical potential$ U_d $ . Although the agreement with experimental data [48] in the large scattering angle region is improved, this procedure poorly underestimates the angular distributions in 40−90 degrees, suggesting that$ U_d^{\rm{pol}} $ should not be added into d optical potential. As$ U_{d}^{\rm{fold}} $ is constructed without the consideration of d breakup process, it can be concluded that d cluster behaviors are similar to that of a tight bound nucleus in$ ^6 $ Li induced reactions. Hence, it is not necessary to consider the d cluster breakup.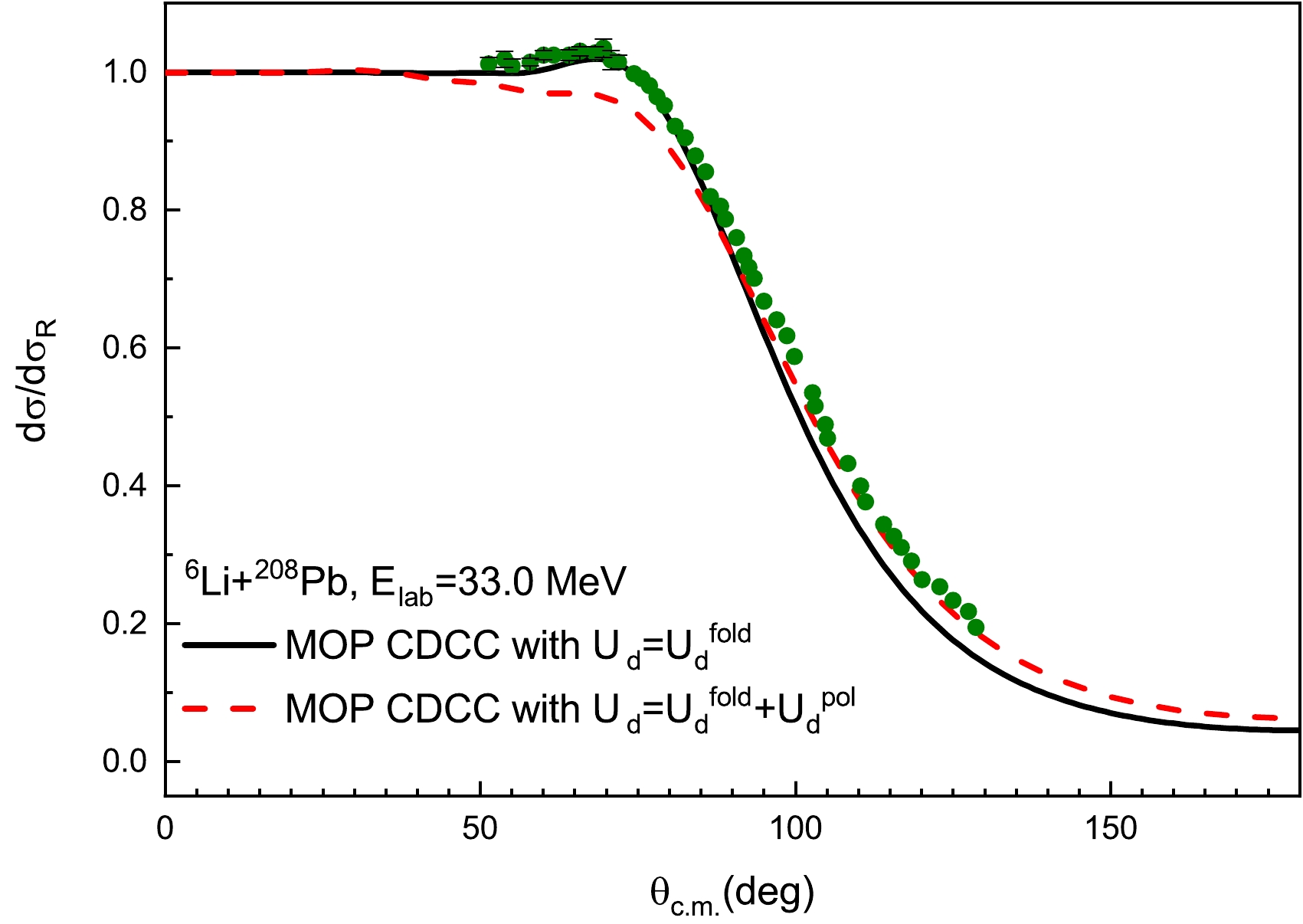
Figure 16. (color online) Elastic scattering angular distributions, as ratios to Rutherford cross sections, for
$ ^6 $ Li+$ ^{208} $ Pb reaction at$ E_{\rm{lab}} $ =33.0 MeV. The solid and dashed lines represent CDCC results with deuteron optical potentials$ U_{d}^{\rm{fold}} $ and$ U_{d}^{\rm{fold}} $ +$ U_d^{\rm{pol}} $ , respectively. Experimental data are obtained from Ref. [48]. See text for details. -
We systematically examined the
$ ^6 $ Li elastic scattering and total reaction cross sections in the vicinity of the Coulomb barrier within the α+d+target three-body framework for$ ^6 $ Li+$ ^{27} $ Al,$ ^{64} $ Zn,$ ^{138} $ Ba, and$ ^{208} $ Pb reaction systems. A combination of α and d MOPs based on the Skyrme nucleon-nucleon effective interaction and CDCC method provides satisfactory agreement with the experimental data without any adjustment on optical potentials. In all cases, the coupling of continuum states visibly reduces the Coulomb barrier and amplifies the elastic scattering angular distributions in regions of large scattering angles by introducing a repulsive correction to the folding model potential. When compared to one-channel calculations where continuum state coupling is deactivated, a modest decrease in the total cross section is noted in CDCC results for all four reaction systems at incident energies above the Coulomb barrier. Conversely, in the sub-barrier energy region, there is a substantial enhancement of the total cross section for$ ^6 $ Li+$ ^{64} $ Zn,$ ^{138} $ Ba, and$ ^{208} $ Pb systems.For comparison, we also performed CDCC calculations with α and d GOPs and optical potential calculations with
$ ^6 $ Li GOP. The surface imaginary part of d GOP should be reduced by no less than 50% to describe the data. CDCC results calculated with MOP and GOP are consistent with each other, suggesting that the MOP combined with the CDCC method is applicable for$ ^6 $ Li induced reactions.The breakup probability of the d cluster is investigated. A local dynamic polarization potential is generated to handle the breakup effect of d and is added to the d MOP to be the d optical potential in
$ ^6 $ Li CDCC calculation. This procedure significantly underestimates the angular distributions in the middle scattering angle region. It reveals that d cluster behaviors are similar to a tightly bound nucleus in$ ^6 $ Li induced reactions, which is consistent with the result of four-body CDCC analysis [26, 47]. This results in the adjustment of the surface imaginary part of d GOP. Hence, it is practical to address the 1n-stripping reaction effectively in Born approximation within the three-body model, rather than conducting a complete four-body computation involving α+n+p+target. Related research is in progress.
Elastic scattering and total reaction cross sections of 6Li examined via a microscopic continuum discretized coupled-channels model
- Received Date: 2023-08-16
- Available Online: 2024-01-15
Abstract: We present a systematic study of 6Li elastic scattering and total reaction cross sections at incident energies around the Coulomb barrier within the continuum discretized coupled-channels (CDCC) framework, where 6Li is treated in an α+d two-body model. Collisions with 27Al, 64Zn, 138Ba, and 208Pa are analyzed. The microscopic optical potentials (MOP) based on Skyrme nucleon-nucleon interaction for α and d are adopted in CDCC calculations and satisfactory agreement with the experimental data is obtained without any adjustment on MOPs. For comparison, α and d global phenomenological optical potentials (GOP) are also used in CDCC analysis and a reduction of no less than 50% on the surface imaginary part of deuteron GOP is required for describing the data. In all cases, the 6Li breakup effect is significant and provides repulsive correction to the folding model potential. The reduction on the surface imaginary part of GOP of deuteron reveals a strong suppression of the reaction probability of deuteron as a component of 6Li when compared with that of a free deuteron. Further investigation is performed by considering the d breakup process equivalently within the dynamic polarization potential approach, and the results show that d behaves in a manner similar to a tightly bound nucleus in 6Li induced reactions.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF













 DownLoad:
DownLoad: