-
Wormholes, hypothetical tunnels in spacetime that potentially connect distant regions of the universe, attract considerable attention from astrophysicists. Understanding the properties, stability, and possible existence of wormholes is essential in theoretical astrophysics. As solutions to Einstein's field equations, wormholes represent intriguing spacetime configurations. Studying wormholes helps elucidate the complex topology of spacetime, providing valuable insights into the fundamental structure of the universe. General relativity forms the foundation for such studies, offering a framework to investigate the theoretical possibility of traversable wormholes.
If traversable, wormholes could enable faster-than-light travel between distant regions of the universe. This has profound implications for space exploration and travel, significantly reducing travel times and expanding our reach in the cosmos. Different astrophysical properties of the traversable wormholes have been studied in Refs. [1–4].
In addition, wormholes could act as crucial conduits, linking different regions of the universe and allowing for a deeper understanding of galaxies, black holes, and dark matter. By investigating wormholes and their behavior within various gravitational theories, one can explore their potential role in the large-scale structure of the universe.
Alternative theories of gravity, which deviate from general relativity, present opportunities to study wormholes in diverse gravitational frameworks. Understanding wormholes within these alternative theories can shed light on the nature of dark energy and dark matter, providing alternative explanations for the enigmatic phenomena that dominate the universe [5, 6].
Overall, theoretical considerations of wormholes challenge our entire understanding of the structure of spacetime. General relativity predictions and alternative theories introduce the possibility of wormholes existing as natural features of the universe.
The study of compact object shadows in astrophysics has emerged as a crucial area of research, offering unique insights into the fundamental properties of compact objects and the nature of spacetime [7–11]. Observations of the shadow of the compact objects at the center of Sgr A* and M87 have provided new opportunities to test gravity theories and different solutions representing astrophysical objects [12, 13]. Particularly, the shadow of a wormhole holds special significance, presenting a theoretical opportunity to probe the structure of the universe in unconventional ways. The shadow of a wormhole, if distinct and distinguishable from other compact objects, could potentially serve as indirect evidence for the existence of these hypothetical tunnels in spacetime. By characterizing and identifying unique features in the wormhole shadow, one can contribute to the ongoing quest for observational confirmation of these exotic cosmic structures. By carefully examining the shape, size, and other characteristics of the wormhole shadow, one can infer valuable information about the wormhole throat size, spin, and potential accretion processes. This could aid in developing a comprehensive understanding of these speculative constructs. The analysis of the shadow of different objects (black holes and wormholes) in different gravity models may be found with and without plasma in Ref. [11–36].
Gravitational lensing is one of the fascinating consequences of the metric theories of gravity. This effect enabled the first direct test of general relativity [37]. Gravitational lensing may provide information regarding a gravitating object and its distance from the source. There has been a lot of work on gravitational lensing around a wormhole for various models [38–48]. Additionally, the study of gravitational weak and strong lensing around compact objects surrounded by plasma can be found in Refs. [49–67].
Weak and strong deflection gravitational lensing and photon motion have been studied around different types of compact objects, e.g., by a charged Horndeski black hole [68], by a renormalization group improved Schwarzschild black hole [69], in Einstein-scalar-Gauss-Bonnet theories [70], by a quantum deformed Schwarzschild black hole [71], in a black-bounce-Reissner-Nordström spacetime [72], for photons coupled to Weyl tensor in a Schwarzschild black hole [73], by a modified Hayward black hole [74], and by a black-bounce, traversable wormhole [75]. The solar system test can also be useful to justify the gravity theories. Such a test has been discussed within
$ f(R) $ gravity [76], quantum corrected gravity [77], a Yukawa parameterization approach [78], and nonlocal gravity [79]. Furthermore, test particle motion around compact objects may play an important role in testing the gravity theories (see, e.g. [80–85]).In this study, we investigated the effect of weak gravitational lensing around the Ellis-Bronnikov wormhole in the presence of a plasma medium and its shadow. The paper is organized as follows. In Sect. II, we review the spacetime surrounding the Ellis-Bronnikov wormhole and study its shadow. Weak gravitational lensing is considered in Sect. III. Image source magnification due to weak lensing is studied in Sect. IV. We draw conclusions based on our obtained results in Sect. V.
-
The Ellis-Bronnikov wormhole spacetime metric can be expressed as [47]
$ \begin{array}{*{20}{l}} {\rm d} s^2=-{\rm e}^{2u(r)}{\rm d}t^2+{\rm e}^{-2u(r)}[{\rm d}r^2+(r^2+a^2) {\rm d} \Omega^2] \ , \end{array} $

(1) where
${\rm d}\Omega^2={\rm d}\theta^2+\sin^2{\theta}{\rm d}\varphi^2$ , r is the radial coordinate running from$ -\infty $ to$ +\infty $ , and$ u(r)=\frac{m}{a}\left(\arctan{\frac{r}{a}}-\frac{\pi}{2}\right). $

(2) m and a are two free parameters. a corresponds to the radius of the wormhole throat located at
$ r=0 $ , and m is the asymptotic mass of the Ellis-Bronnikov wormhole. Eq. (2) accounts for the following asymptotic behavior:$ \begin{aligned}[b] & {\rm e}^{2 u(r)}\Big|_{r\rightarrow + \infty}=\left(1-\frac{2 m}{r}\right)+\mathcal{O}(r^{-2})\ , \\ & {\rm e}^{2 u(r)}\Big|_{r\rightarrow - \infty}={\rm e}^{-\frac{2 \pi m}{a}}\left(1+\frac{2 m}{|r|}\right)+\mathcal{O}(r^{-2})\ . \end{aligned} $

(3) We can see that the spacetime metric in Eq. (1) has two asymptotically flat regions
$ \mathcal{R}_{\pm}: r \rightarrow \pm \infty $ . The asymptotical masses of the$ \mathcal{R}_{+} $ and$ \mathcal{R}_{-} $ regions are equal to$ m_{+}=m $ and$ m_{-}=-m \exp{(-\pi m/a)} $ , respectively. Both masses clearly have different signs and values. Therefore, from the perspective of a distant observer in region$ \mathcal{R}_{-} $ , the Bronnikov-Ellis wormhole appears to have a negative mass. Two asymptotical regions$ \mathcal{R}_{+} $ and$ \mathcal{R}_{-} $ are connected by the throat, with the radius of the throat being$R^2(r)={\rm e}^{-2u(r)}(r^2+a^2)$ , which is the minimum radius of two-dimensional sphere. The minimum value of$ R(r) $ occurs at$ r = m $ and is equal to$ R_0=\exp{\Big[-\frac{m}{a}\Big(\arctan{\frac{m}{a}}-\frac{\pi}{2}\Big)\Big]}(m^2+a^2)^{1/2} . $

(4) If m is equal to zero, then both
$ m_{\pm} $ become zero, and the metric in Eq. (1) reduces to the Ellis metric. -
We now consider the photon motion using the Hamilton-Jacobi equation. One can write the Hamiltonian of a photon around a wormhole surrounded by plasma in the following form [86]:
$ \mathcal H(x^\alpha, p_\alpha)=\frac{1}{2}\left[ g^{\alpha \beta} p_\alpha p_\beta - (n^2-1)( p_\beta u^\beta )^2 \right]\ , $

(5) where
$ x^\alpha $ are the spacetime coordinates, and$ p_\alpha $ and$ u^\beta $ are the four-momentum and four-velocity of the photon, respectively. In Eq. (5), n represents the refractive index ($ n=\omega/k $ , where k is the wave number). For plasma, one can write the refractive index as [87]$ n^2=1- \frac{\omega_{p}^2}{\omega^2}\ , $

(6) with plasma frequency
$ \omega^2_{p}(x^\alpha)=4 \pi e^2 N(x^\alpha)/m_e $ ($ m_e $ and e are the electron mass and charge, respectively, whereas N is the number density of the electrons). The frequency of photon ω is defined by$ \omega^2=(p_\beta u^\beta)^2 $ and$ \omega(r)=\frac{\omega_0}{\sqrt{f(r)}}\ ,\qquad \omega_0=\text{const}\ . $

(7) The lapse function is such that
$ f(r) \to 1 $ as$ r \to \infty $ and$ \omega(\infty)=\omega_0=-p_t, $ which shows the energy of the photon at spatial infinity [88]. Besides, the plasma frequency can be sufficiently smaller than the photon frequency$(\omega_{p}^2\ll \omega^2)$ , which allows the BH shadow to be differentiated from the vacuum case ($\omega_{p}=0$ ).One can now write the Hamiltonian for the light rays in plasma medium as follows [50, 86]:
$ \mathcal{H}=\frac{1}{2}\Big[g^{\alpha\beta}p_{\alpha}p_{\beta}+\omega^2_{p}]\ . $

(8) The components of the four-velocity for the photons in the equatorial plane
$ (\theta=\pi/2,\; p_\theta=0) $ can be written as$ \dot t\equiv\frac{{\rm d}t}{{\rm d}\lambda}=\frac{ {-p_t}}{{\rm e}^{2u(r)}} , $

(9) $ \dot r\equiv\frac{{\rm d}r}{{\rm d}\lambda}=p_r {\rm e}^{2u(r)} , $

(10) $ \dot\phi\equiv\frac{{\rm d}\phi}{{\rm d}\lambda}= p_{\phi} \frac{{\rm e}^{2u(r)}}{r^2+a^2}, $

(11) using the relationship
$ \dot x^\alpha=\partial \mathcal{H}/\partial p_\alpha $ . From Eqs. (10) and (11), one can obtain the following expression for the phase trajectory of light (or photon) in the following form:$ \frac{{\rm d}r}{{\rm d}\phi}=\frac{g^{rr}p_r}{g^{\phi\phi}p_{\phi}}. $

(12) Using the constraint
$ \mathcal H=0 $ , we can rewrite the above expression as [88]$ \frac{{\rm d}r}{{\rm d}\phi}=\sqrt{\frac{g^{rr}}{g^{\phi\phi}}}\sqrt{\gamma^2(r)\frac{\omega^2_0}{p_\phi^2}-1}, $

(13) where
$ \gamma^2(r)\equiv-\frac{g^{tt}}{g^{\phi\phi}}-\frac{\omega^2_p}{g^{\phi\phi}\omega^2_0}\ . $

(14) The circular radius of light, particularly the one which forms the photon sphere of radius
$ r_{\text{ph}} $ , can be determined as the solution of the following equation [88]:$ \frac{{\rm d}(\gamma^2(r))}{{\rm d}r}\bigg|_{r=r_{\text{ph}}}=0\ . $

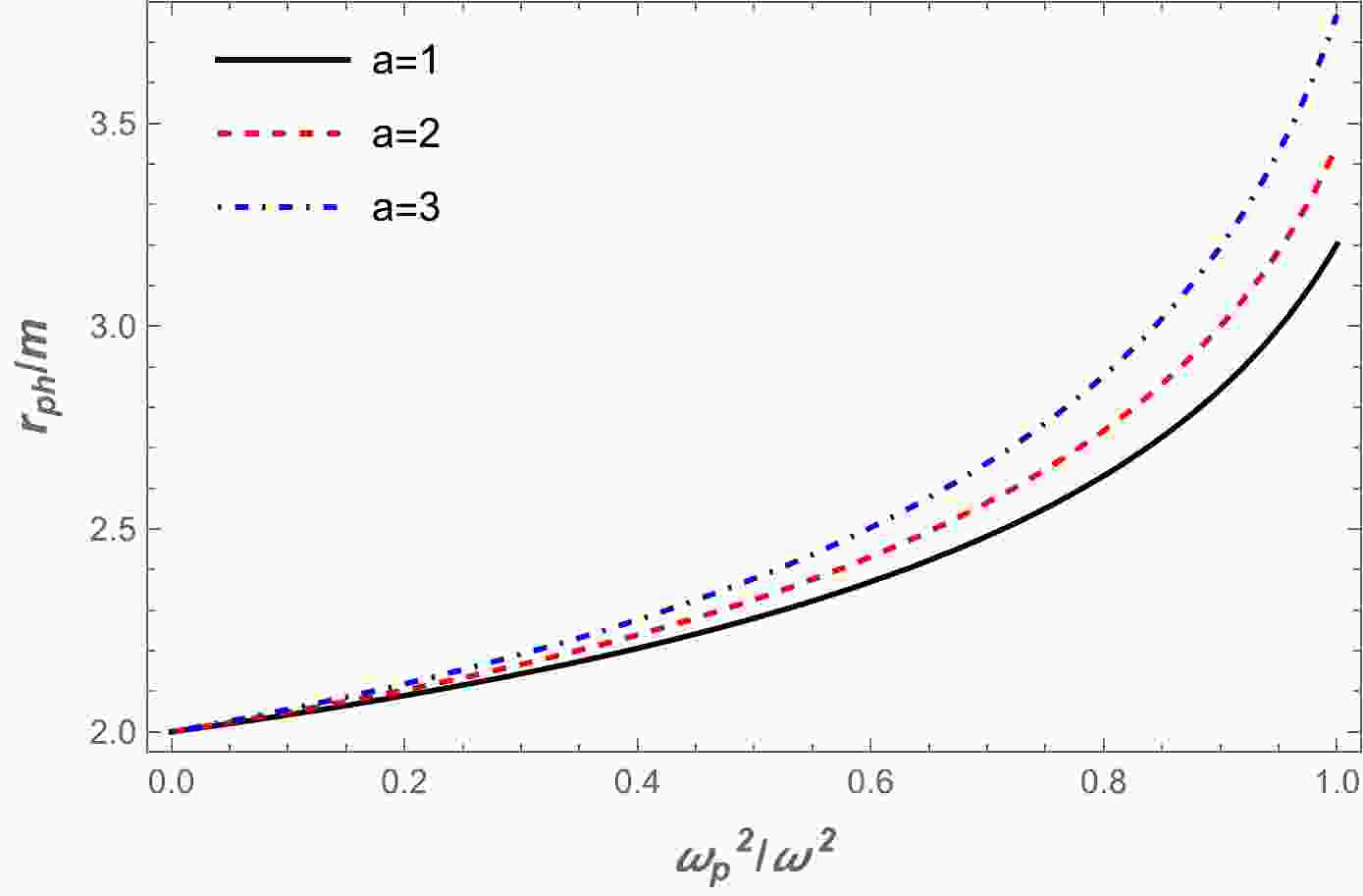
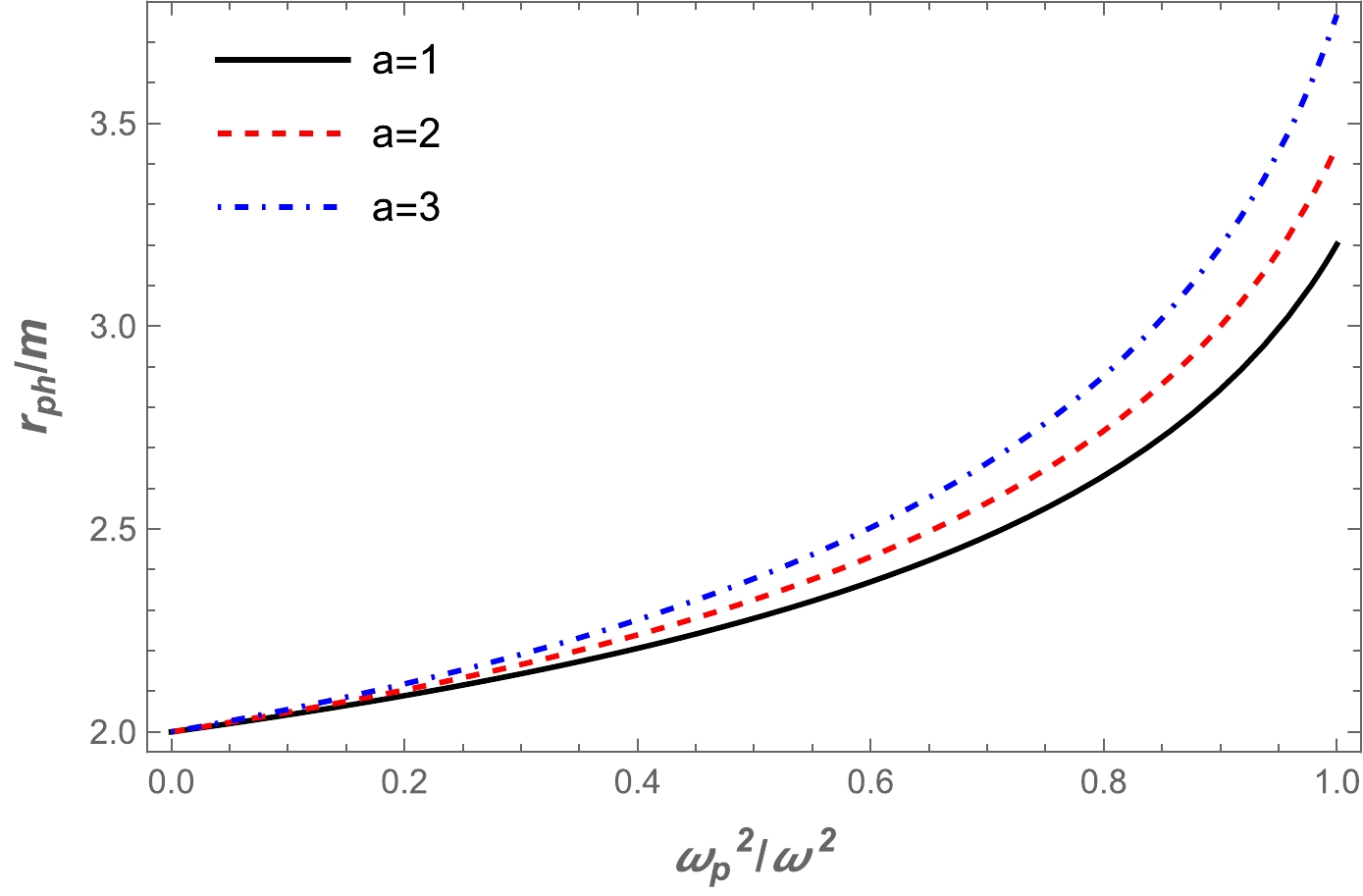
(15) Using Eq. (14), we have solved the above equation numerically. The results are presented graphically in Fig. 1, where we have plotted the dependencies of photon orbits on the plasma frequency. The value of the radius of the photon sphere increased with the increase in plasma frequency. Also, there is a slight increase with the increase in parameter a.
-
Now, we consider the radius of the shadow of the Ellis-Bronnikov wormhole in the presence of plasma. The angular radius
$\alpha_{\rm sh}$ of the wormhole is defined as [88, 89]$ \sin^2 \alpha_{\text{sh}}=\frac{\gamma^2(r_{\text{ph}})}{\gamma^2(r_{\text{o}})}, $

(16) where
$ r_{\text{ph}} $ and$ r_{\text{o}} $ represent the photon sphere and observer locations, respectively. One can now easily find the$\gamma^2(r_{\rm ph})$ and$ \gamma^2(r_{o}) $ from Eq. (14). If the observer is located at a sufficiently large distance from the wormhole, the radius of the wormhole shadow can be approximated using Eq. (16) as [88]$ R_{\text{sh}}\simeq r_{\text{o}} \sin \alpha_{\text{sh}}. $

(17) $R_{\rm sh}$ is calculated numerically, and the radius of the wormhole shadow is depicted for different values of the a parameter in Fig. 2 for a homogeneous plasma with fixed plasma frequencies. Fig. 3 demonstrates the dependence of the wormhole shadow radius on plasma frequencies. These figures show that the size of the wormhole shadow radius decreases with increasing plasma frequency. Accordingly, the BH shadow in the presence of a plasma medium would shrink further, as expected.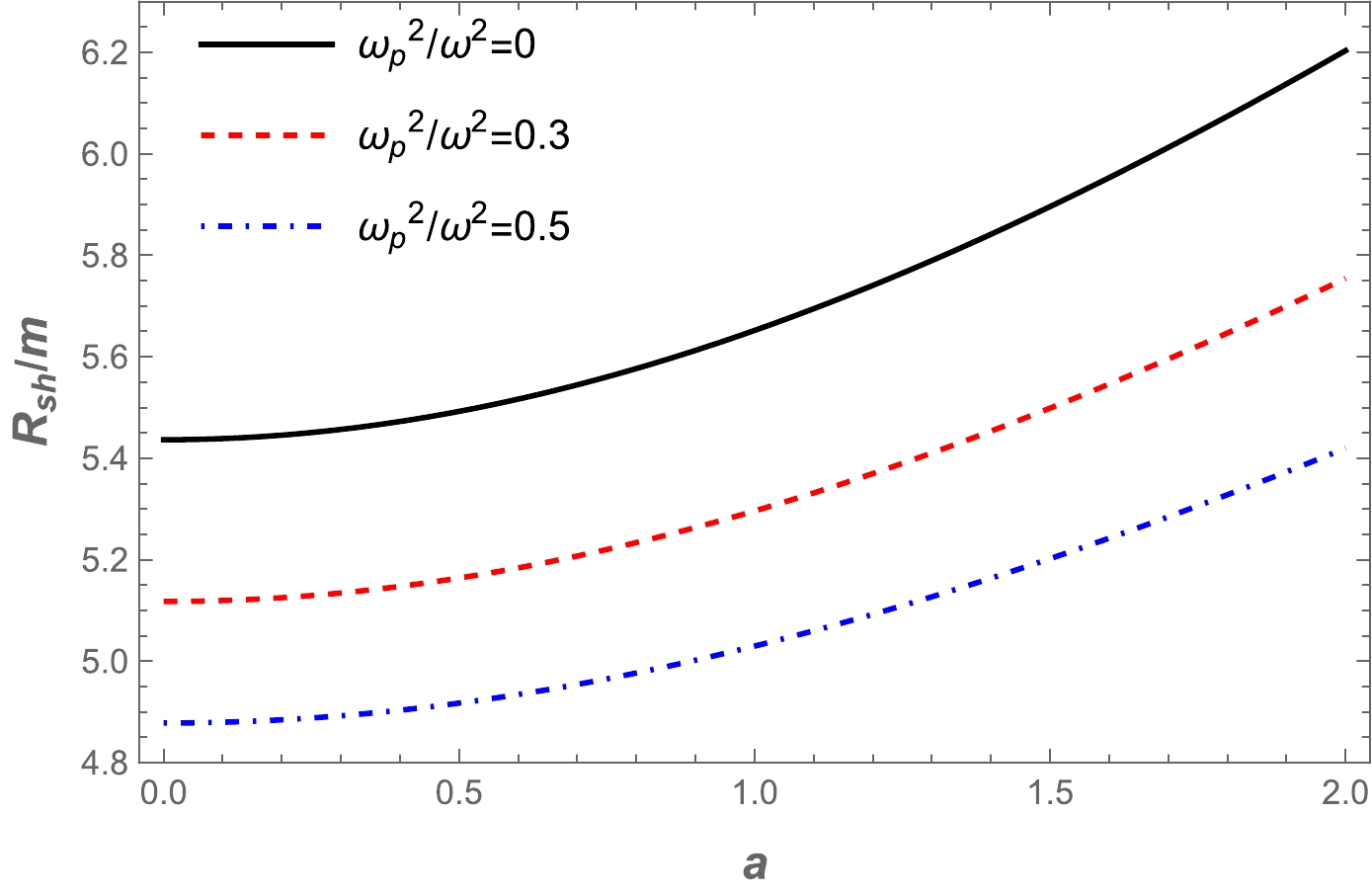
Figure 2. (color online) The dependence of the wormhole shadow radius on the plasma frequency for the different values of parameter a.
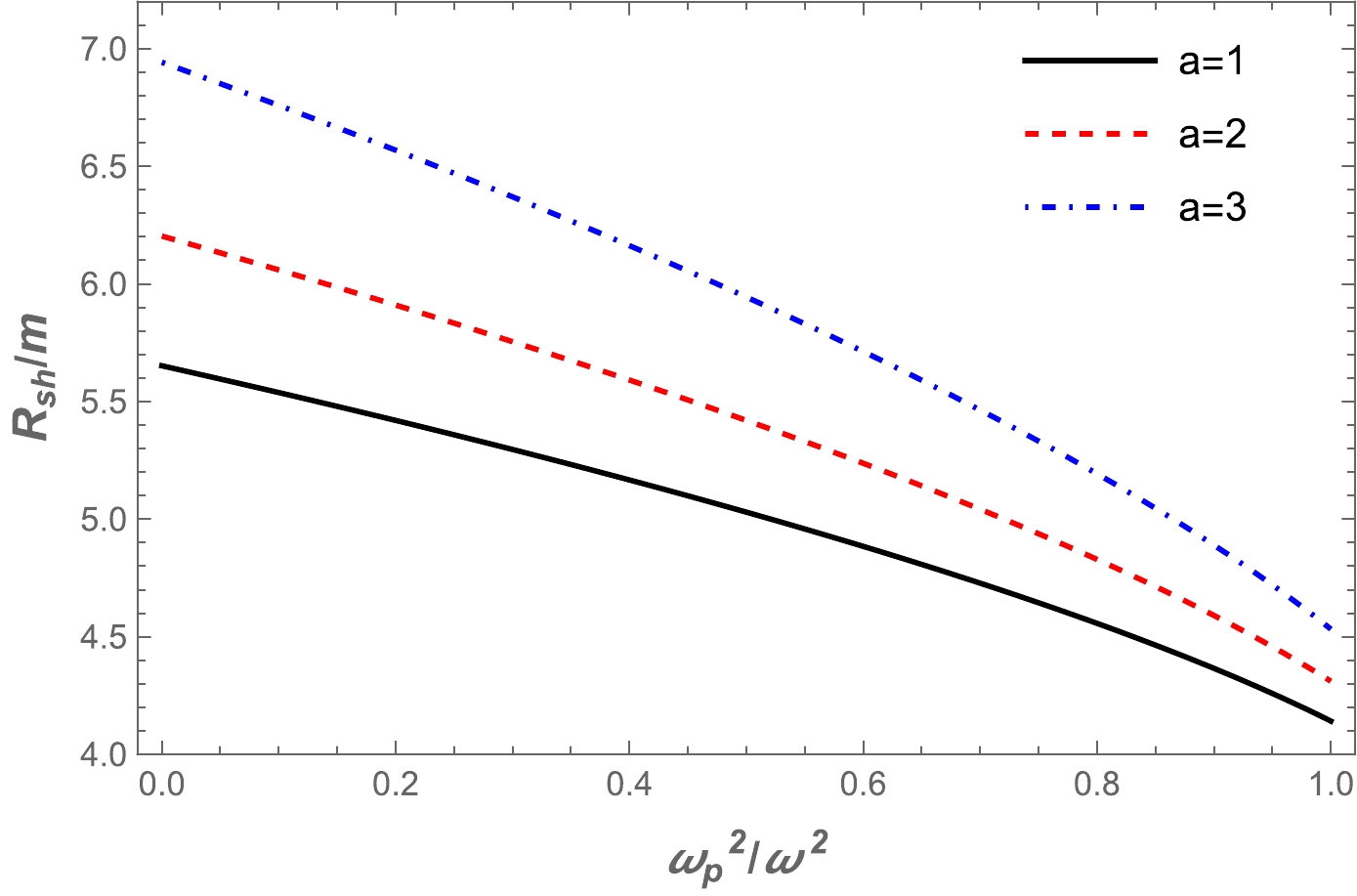
Figure 3. (color online) The dependence of the wormhole shadow radius on the a parameter for different plasma frequency values.
Now, we consider the assumption that the compact objects Sgr A* and M87* are static, spherically symmetric objects in the Ellis-Bronnikov gravity, even though the observation obtained by the EHT collaboration does not support the assumption made here. However, we theoretically investigate the upper limits of the parameter a in the Ellis-Bronnikov wormhole spacetime using the data provided by the EHT collaboration project. The spacetime metric comprises only one parameter, a. Hence, we chose the plasma frequency as the second parameter for the constraint. One can use the observational data provided by the EHT collaboration regarding the shadows of the supermassive black holes Sgr A* and M87* to constrain these two parameters, a and
$ \omega_p/\omega $ . The angular diameter$\theta_{\rm M87*}$ of the BH shadow, the distance from Earth, and the mass of the BH at the center of the M87* are$\theta_{\rm M87*}=42 \pm 3 \mu as$ ,$D= 16.8 \pm 0.8~{\rm M pc}$ , and$M_{\rm M87*} = 6.5 \pm 0.7 \times 10^9 M_{\odot}$ [12], respectively. For Sgr A*, the data provided by the EHT collaboration are$\theta_{\rm Sgr\, A*}=48.7 \pm 7 \mu D=8277 \pm 9 \pm 33~{\rm pc}$ and$M_{\rm Sgr\, A*} = 4.297 \pm 0.013 \times 10^6 M_{\odot}$ (VLTI) [90]. From this information about it, one can calculate the diameter of the shadow caused by the compact object per unit mass as follows$ d_{\rm sh}=\frac{D\theta}{M}\ . $

(18) We know that from the expression
$d_{\rm sh}=2R_{\rm sh}$ , we can easily get the expression for the diameter of the BH shadow. Thus, we obtain the diameters of the BH shadow as$d^{\rm M87*}_{\rm sh}=(11 \pm 1.5)M$ for M87* and$d^{\rm Sgr*}_{\rm sh}=(9.5 \pm 1.4)M$ for Sgr A*. From observational EHT data, we can find the upper limits on parameters a and$ \omega^2_{p}/\omega^2_0 $ for the supermassive BHs at the centers of the galaxies Sgr A* and M87*. Here, we try to theoretically fulfill the constraint for Ellis-Bronnikov wormhole as a BH mimicker. It is demonstrated numerically in Fig. 4. We have demonstrated that the size of the shadow depends on the wormhole and plasma parameters. The upper limits of the a and plasma parameters correspond to the EHT results. Moreover, we estimated the values of the parameter a and the plasma frequency for the supermassive BHs M87* and Sgr A* in Table 1.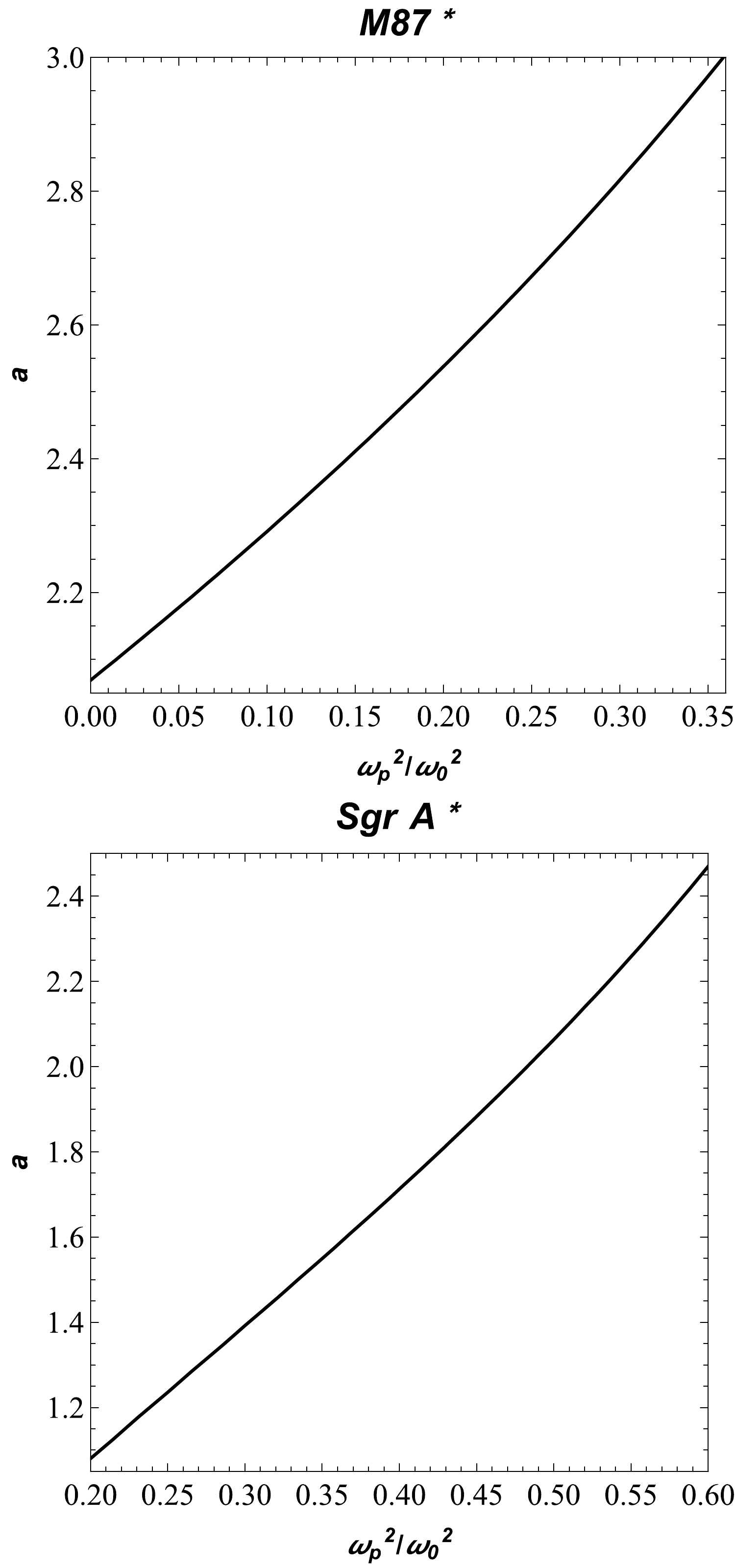
Figure 4. (color online) The values of parameters a and
$ \omega^2_{p}/\omega^2_0 $ for the supermassive BHs in galaxies M87* and Sgr A*. We consider$ m=1 $ for both panels.$\omega^2_{p}/\omega^2$ 

$\rm M87^{*}$ 

$\rm Sgr A^{*}$ 

a a 0.20 2.53 1.08 0.25 2.67 1.24 0.30 2.81 1.39 0.35 2.97 1.55 Table 1. The estimated values of parameters a and
$\omega^2_{p}/\omega^2_0$ for the supermassive BHs: M87* and Sgr A*. -
In this section, we investigate the weak gravitational lensing around the Ellis-Bronnikov wormhole. We will expand metric (1) in the weak-field approximation as follows [49, 54]:
$ \begin{array}{*{20}{l}} g_{\alpha \beta}=\eta_{\alpha \beta}+h_{\alpha \beta}\ , \end{array} $

(19) where
$ \eta_{\alpha \beta} $ and$ h_{\alpha \beta} $ refer to the expressions for flat spacetime and perturbation due to gravity, respectively. The above expressions require the following properties:$ \begin{aligned}[b] & \eta_{\alpha \beta}= {\rm diag} (-1,1,1,1)\ , \\ & h_{\alpha \beta} \ll 1, \quad h_{\alpha \beta} \rightarrow 0 \quad {\rm under} \quad x^{\alpha}\rightarrow \infty \ ,\\ & g^{\alpha \beta}=\eta^{\alpha \beta}-h^{\alpha \beta}, \quad h^{\alpha \beta}=h_{\alpha \beta}. \end{aligned} $

(20) Now, we will study the effect of the plasma on the deflection angle
$ \alpha_k $ in the gravitational field of the Ellis-Bronnikov wormhole. In this paper, we consider two types of plasma:$ \omega_p $ and$ \omega_c $ , representing the frequencies for uniform and non-uniform plasma, respectively. One can write the equation for the deflection angle around the Ellis-Bronnikov wormhole as [49]$ \hat{\alpha }_{b}=\frac{1}{2}\int_{-\infty}^{\infty}\frac{b}{r}\left(\frac{{\rm d}h_{33}}{{\rm d}r}+\frac{1}{1-\omega^2_p/ \omega^2}\frac{{\rm d}h_{00}}{{\rm d}r}-\frac{K_e}{\omega^2-\omega^2_p}\frac{{\rm d}N}{{\rm d}r} \right){\rm d}z , $

(21) where ω represents the frequency of the photon. One can write the line element (1) as
$ {\rm d}s^2 \approx {\rm d}s^2_0+\left(1-{\rm e}^{2u(r)}\right){\rm d}t^2 +\left(1-{\rm e}^{2u(r)}\right){\rm d}r^2\, , $

(22) where
${\rm d}s^2_0=-{\rm d}t^2+{\rm d}r^2+(r^2+a^2)({\rm d}\theta^2+\sin^2\theta {\rm d}\phi^2)$ . Now, we can easily find the components of$ h_{\alpha \beta} $ of metric tensor perturbations in Cartesian coordinates as$ h_{00}=1-{\rm e}^{2u(r)} , $

(23) $ h_{ik}=\left(1-{\rm e}^{2u(r)}\right)n_i n_k , $

(24) $ h_{33}=\left(1-{\rm e}^{2u(r)}\right) \cos^2\chi \, , $

(25) with
$ \cos^2\chi=z^2/(b^2+z^2) $ and$ r^2=b^2+z^2 $ . One may easily calculate the derivative of$ h_{00} $ and$ h_{33} $ as follows:$ \frac{{\rm d}h_{00}}{{\rm d}r}=-\frac{2 m {\rm e}^{2u(r)}}{a^2+r^2}\, , $

(26) $ \frac{{\rm d}h_{33}}{{\rm d}r}=\frac{2 z^2}{r^3}\Big(-1+(1-\frac{m r}{a^2+r^2}){\rm e}^{2 u(r)}\Big) . $

(27) The expression for the deflection angle can be written as [91]
$ \begin{array}{*{20}{l}} \hat{\alpha_b}=\hat{\alpha_1}+\hat{\alpha_2}+\hat{\alpha_3}\ , \end{array} $

(28) with
$ \begin{aligned}[b] \hat{\alpha_1}=&\frac{1}{2}\int_{-\infty}^{\infty} \frac{b}{r}\frac{{\rm d}h_{33}}{{\rm d}r}{\rm d}z\ ,\\ \hat{\alpha_2}=&\frac{1}{2}\int_{-\infty}^{\infty} \frac{b}{r}\frac{1}{1-\omega^2_p/ \omega^2}\frac{{\rm d}h_{00}}{{\rm d}r}{\rm d}z\ ,\\ \hat{\alpha_3}=&\frac{1}{2}\int_{-\infty}^{\infty} \frac{b}{r}\left(-\frac{K_e}{\omega^2-\omega^2_p}\frac{{\rm d}N}{{\rm d}r} \right){\rm d}z\, . \end{aligned} $

(29) Now, we can examine and assess the deflection angle for various plasma density distributions.
-
In this subsection, we consider the uniform plasma distribution, which can be expressed as a sum [91]:
$ \begin{array}{*{20}{l}} \hat{\alpha}_{\rm uni}=\hat{\alpha}_{\rm uni1}+\hat{\alpha}_{\rm uni2}+\hat{\alpha}_{\rm uni3}. \end{array} $

(30) From Eqs. (25), (28), and (29), one can find the expression for
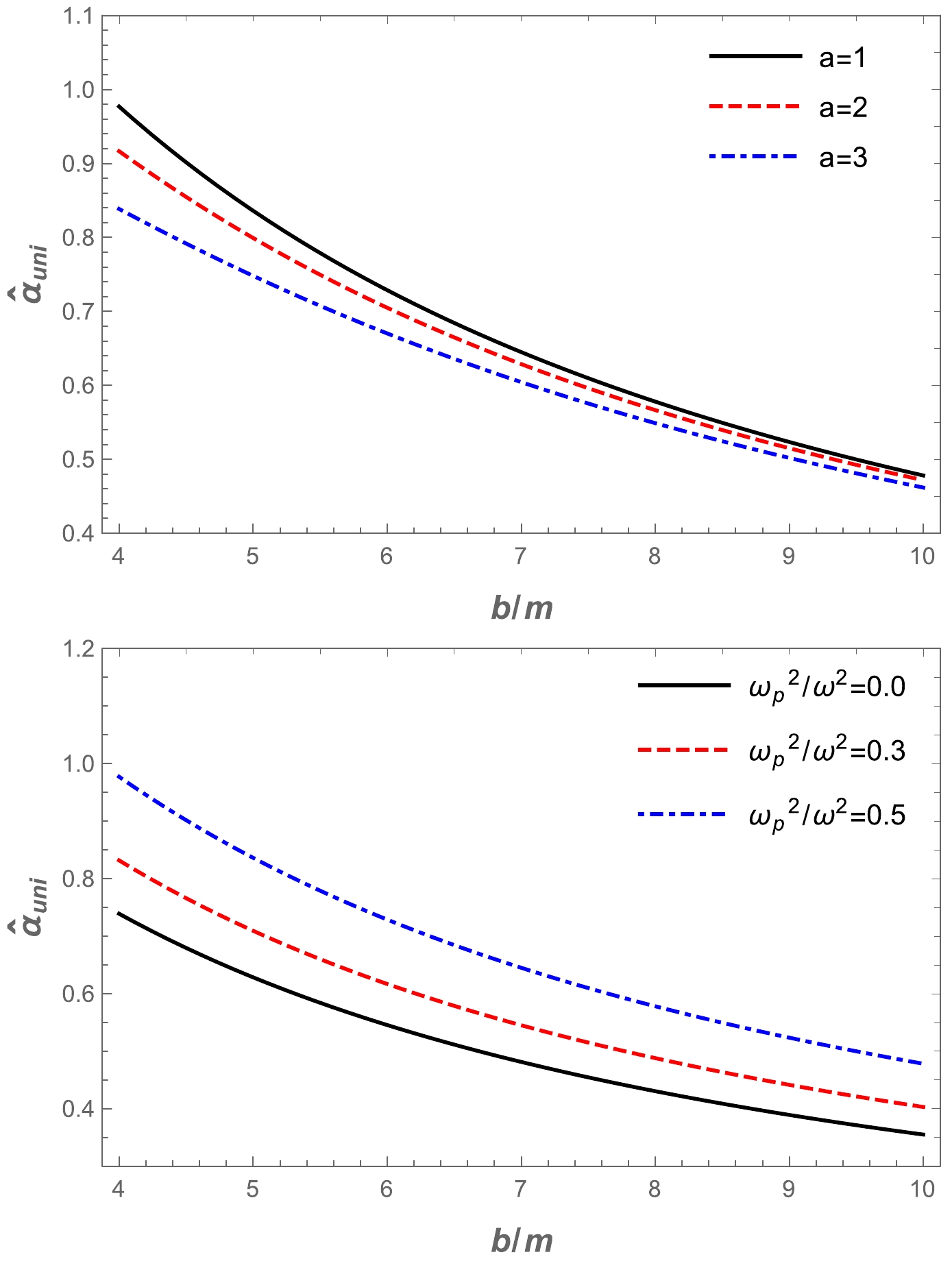
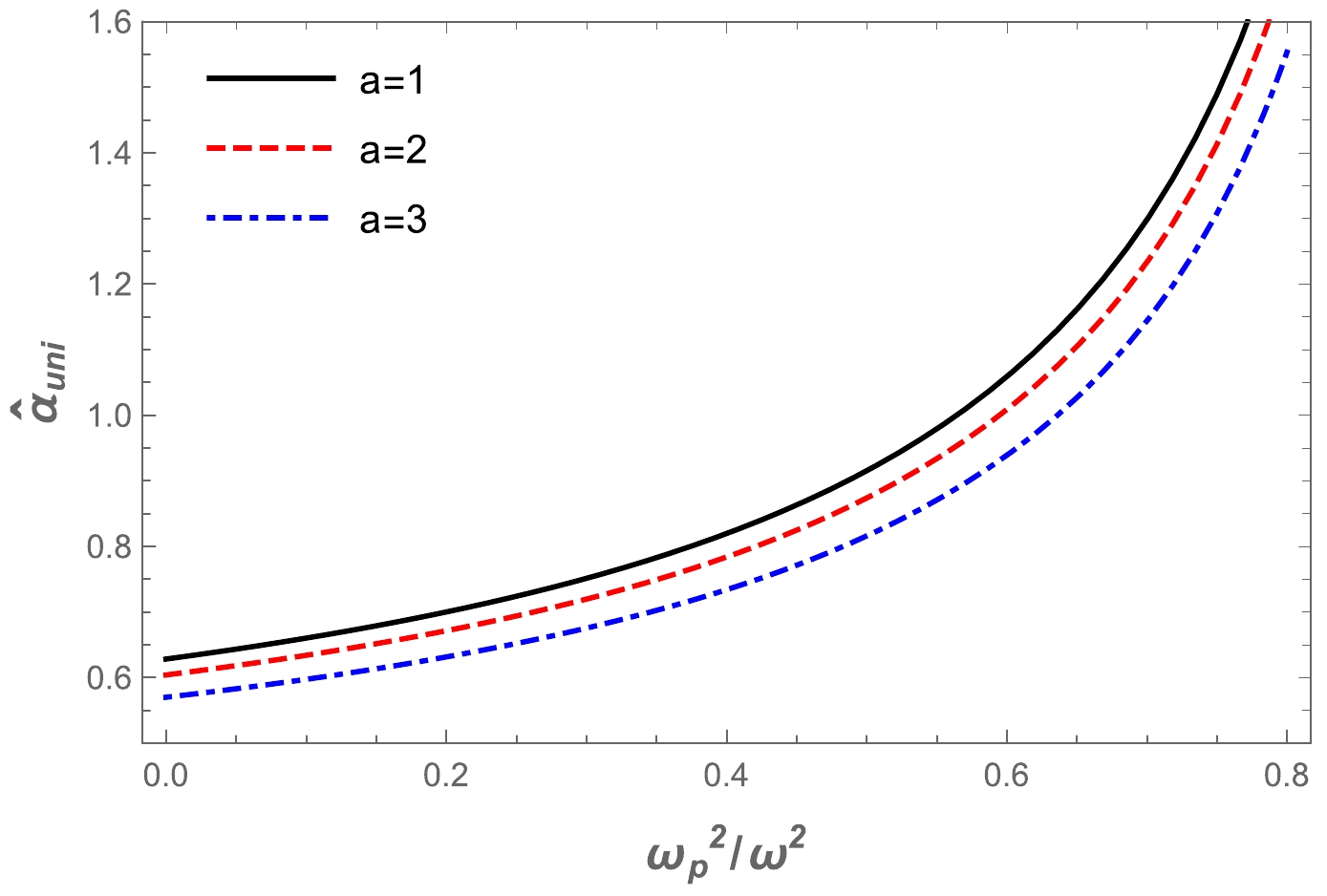
$\hat{\alpha}_{\rm uni}$ . Our metric is complicated, so we cannot find the expression for the deflection angle explicitly. Therefore, we use the numerical method and plot the dependence of the deflection angle on the impact parameter b for different values of the a parameter and plasma parameter$\omega_{p}^2/\omega^2$ in the Ellis-Bronnikov wormhole spacetime. The numerical results are represented graphically in Fig. 5. It can be seen from the graphs that the value of the deflection angle$\alpha_{\rm uni}$ decreased with the increase in the impact parameter for fixed values of the plasma frequency and the a parameter. Moreover, we present the effect of the deflection angle on plasma parameters in Fig. 6. Under the influence of the a parameter, the value of the deflection angle$\alpha_{\rm uni}$ decreases, while the effect of the plasma frequency on the deflection angle is the opposite. -
In this part of our work, we consider the non-singular isothermal sphere (SIS), which represents the most favorable model for understanding the unique characteristics of gravitational weak lensing effects on photons around the wormhole. In general, SIS is a spherical gas cloud characterized by a singularity located at its center, where the density tends to infinity. The density distribution of a SIS is described as follows [49]:
$ \rho(r)=\frac{\sigma^2_{\nu}}{2\pi r^2}\ , $

(31) where
$ \sigma^2_{\nu} $ denotes a one-dimensional velocity dispersion. The analytical expression for the plasma concentration is given as [49]$ N(r)=\frac{\rho(r)}{k m_p}\ , $

(32) where
$ m_p $ represents the mass of a proton, and k is a dimensionless coefficient generally associated with the dark matter universe. The plasma frequency is$ \omega^2_e=K_e N(r)=\frac{K_e \sigma^2_{\nu}}{2\pi k m_p r^2}\ . $

(33) Now, we explore the non-uniform plasma (SIS) effect on the deflection angle in the spacetime of the Ellis-Bronnikov wormhole. One can write the expression of deflection angle around the Ellis-Bronnikov wormhole as [91]
$ \begin{array}{*{20}{l}} \hat{\alpha}_{\rm SIS}=\hat{\alpha}_{\rm SIS1}+\hat{\alpha}_{\rm SIS2}+\hat{\alpha}_{\rm SIS3} \ . \end{array} $

(34) For uniform plasma, we also use the numerical method. These calculations establish a supplementary plasma constant
$ \omega^2_c $ with the following analytic expression [54]:$ \omega^2_c=\frac{K_e \sigma^2_{\nu}}{2\pi k m_p R^2_S}\ . $

(35) We have represented the dependence of the deflection angle on impact parameter b for different values of the a parameter and
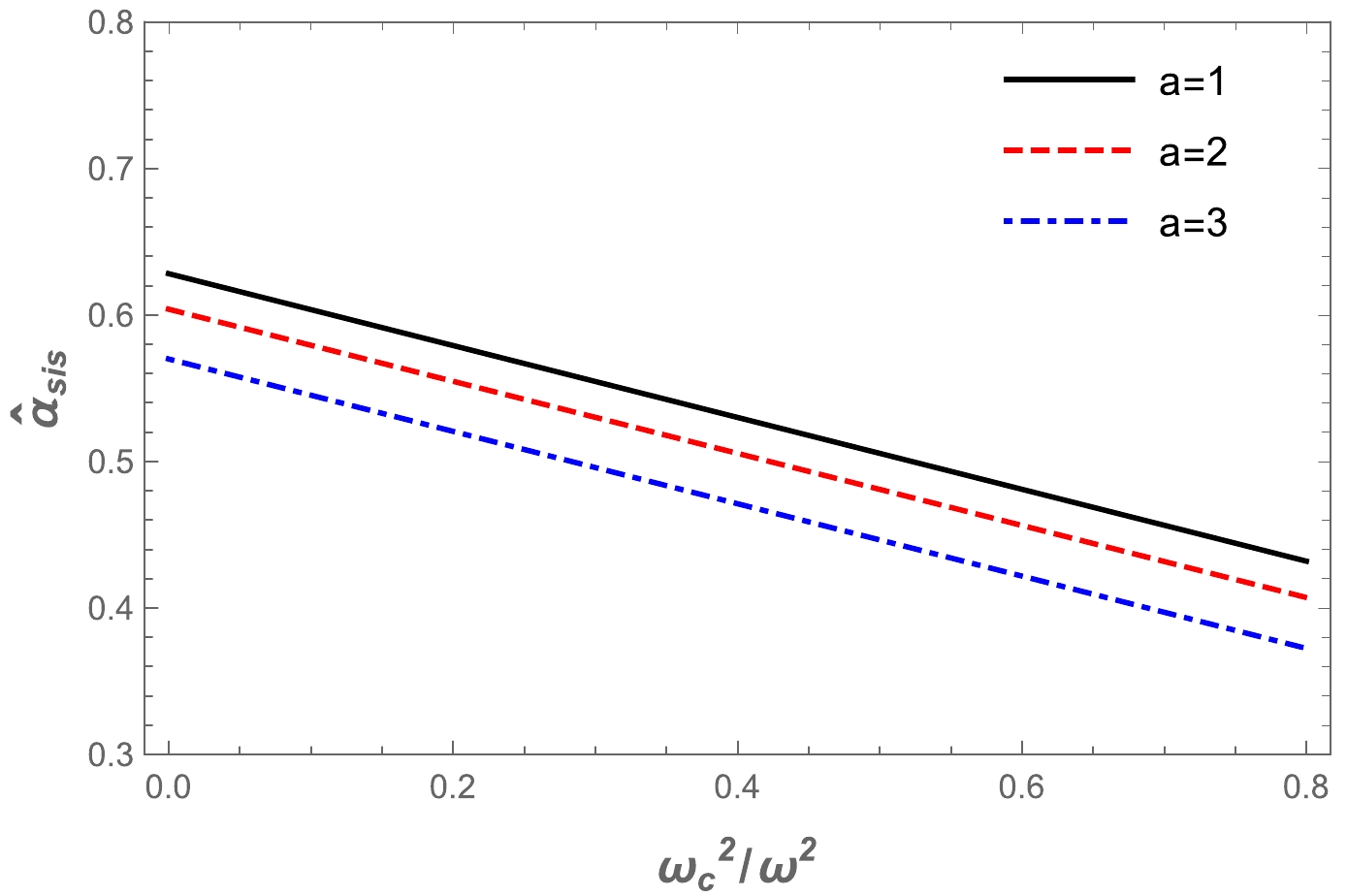
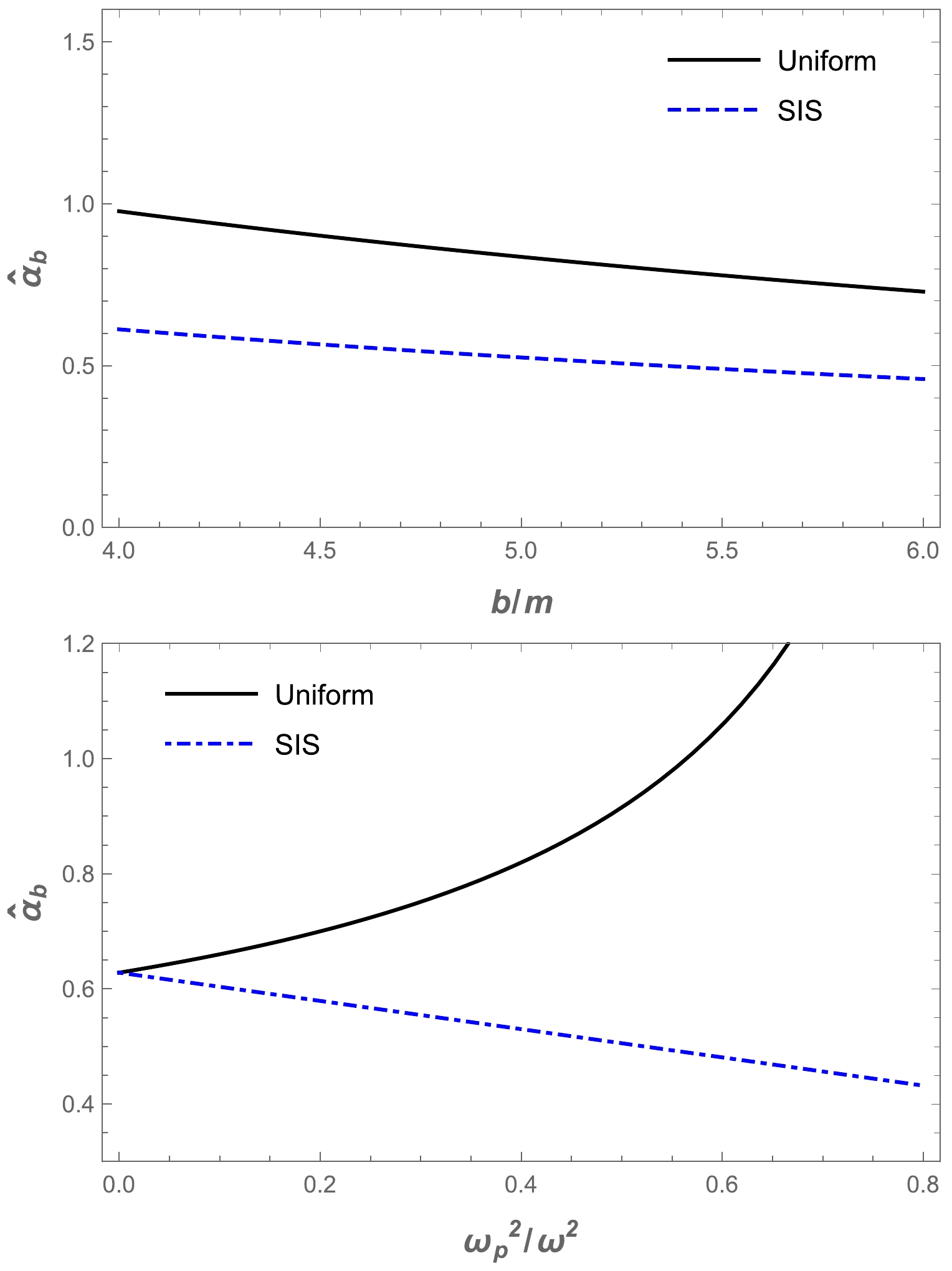
$ \omega_c^2/\omega^2 $ for a non-uniform plasma medium in the Ellis-Bronnikov wormhole spacetime, as shown in Fig. 7. The graphs show that the value of the deflection angle$\alpha_{\rm sis}$ decreased as the impact parameter increased. Then, we demonstrate the dependence of the deflection angle of a light ray around a wormhole in the presence of a non-uniform plasma in Fig. 8. One can easily see from Fig. 8 that the value of the deflection angle$\alpha_{\rm sis}$ decreased under the influence of the plasma and a parameters. In addition, we compared the different effects of plasma on the Ellis-Bronnikov wormhole deflection angle with gravity, as shown in Fig. 9. By comparison, it can be seen that the deflection angle of the light ray for the uniform plasma is greater than that for the non-uniform plasma.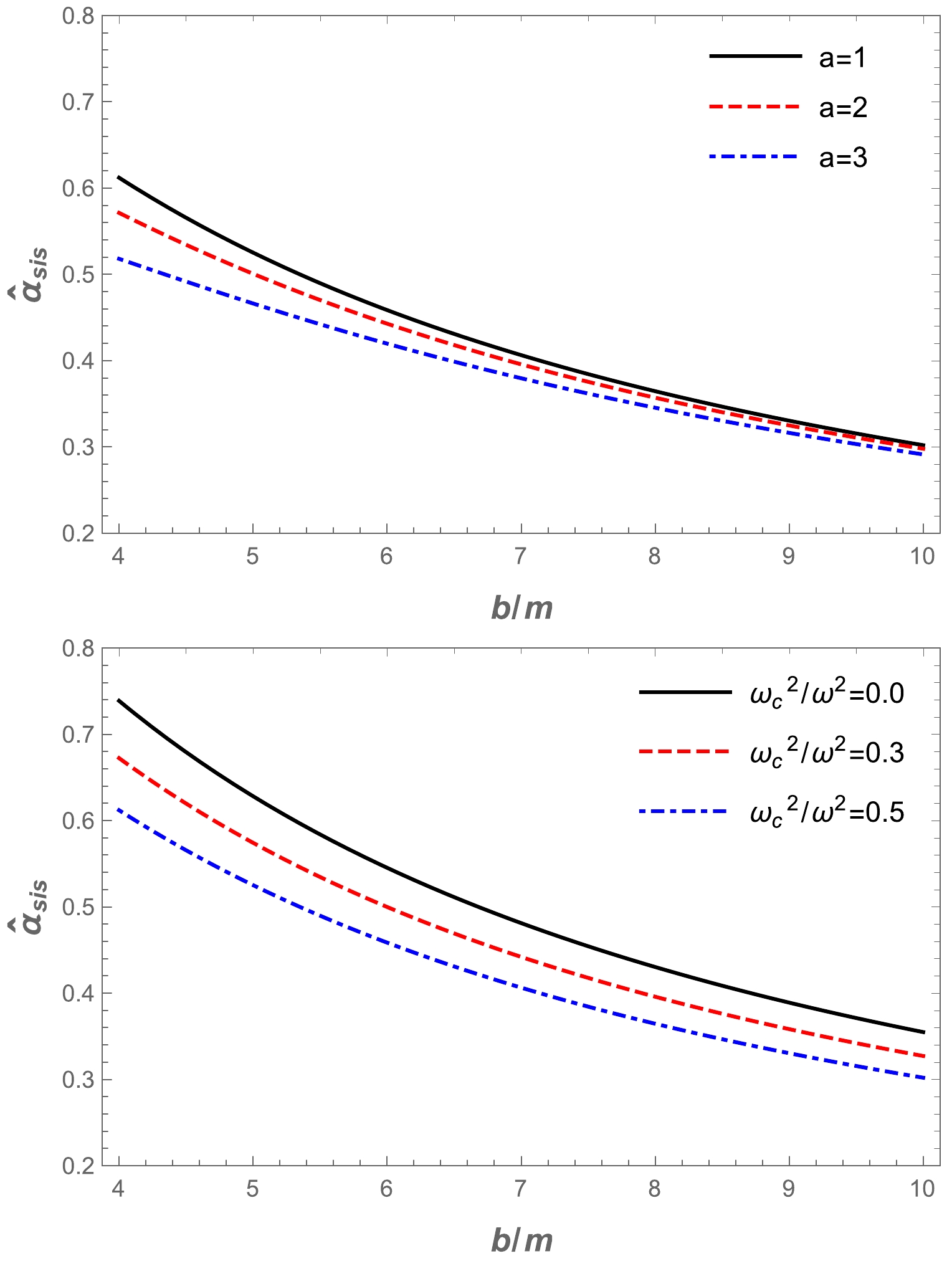
Figure 7. (color online) The dependence of the deflection angle
$ \hat{\alpha }_{\text{sis}} $ on the impact parameter for different values of parameter a (upper panel) and plasma parameters (lower panel). -
Now, we explore the image brightness in the presence of plasma through the angle of deflection of light rays around the Ellis-Bronnikov wormhole. By employing the lens equation, the combination of light angles around the Ellis-Bronnikov wormhole can be written (
$ \hat{\alpha} $ , θ, and β) [51, 54, 92] as$ \begin{array}{*{20}{l}} \theta D_{s}=\beta D_{s}+\hat{\alpha_b}D_{ds}\ , \end{array} $

(36) where
$D_{s}$ ,$D_{d}$ , and$D_{ds}$ are the distances from the source to the observer, lens to the observer, and source to the lens, respectively. In Eq. (36), θ and β denote the angular position of the image and the source, respectively. One can now rewrite the above equation for β as follows:$ \beta=\theta -\frac{D_{ds}}{D_{s}}\frac{\xi(\theta)}{D_m{d}}\frac{1}{\theta} , $

(37) where
$ \xi(\theta)=|\hat{\alpha}_b|b $ , with$ b=D_\mathrm{d}\theta $ , as used in [54].When the image has a ring-like appearance, it is classified as Einstein's ring, with a ring radius defined as
$R_s=D_{d}\theta_E$ . The angular part$ \theta_E $ , arising from the spacetime geometry between the source's images in a vacuum, can be expressed as [51]$ \theta_E=\sqrt{2R_{s}\frac{D_{ds}}{D_{d} D_{s}} }\ . $

(38) Now, we investigate the brightness magnification equation as follows [54]:
$ \mu_{\Sigma}=\frac{I_\mathrm{tot}}{I_*}=\underset{k}\sum\bigg|\bigg(\frac{\theta_k}{\beta}\bigg)\bigg(\frac{{\rm d}\theta_k}{{\rm d}\beta}\bigg)\bigg|, \quad k=1,2, \cdot \cdot \cdot , j\ , $

(39) where
$ I_\mathrm{tot} $ and$ I_* $ are the the total brightness of all images and the unlensed brightness of the source, respectively. The magnification of the source can be expressed as [49, 54]$ \mu^{pl}_\mathrm+=\frac{1}{4}\bigg(\frac{x}{\sqrt{x^2+4}}+\frac{\sqrt{x^2+4}}{x}+2\bigg)\ , $

(40) $ \mu^{pl}_\mathrm-=\frac{1}{4}\bigg(\frac{x}{\sqrt{x^2+4}}+\frac{\sqrt{x^2+4}}{x}-2\bigg)\ , $

(41) where
$ x={\beta}/{\theta_E} $ is a dimensionless quantity [54] and$\mu_{+}^{pl}$ and$\mu_{-}^{pl}$ are the image magnifications. Using equations (40) and (41), we can obtain the expression for the total magnification as follows:$ \mu^{pl}_\mathrm{tot}=\mu^{pl}_++\mu^{pl}_-=\frac{x^2+2}{x\sqrt{x^2+4}}\ . $

(42) Now, we explore the magnification in the presence of plasma with different distributions in the wormhole environment: (i) uniform and (ii) non-uniform cases.
-
Here, we study the effect of uniform plasma on the magnification image. The total magnification
$\mu^{pl}_{\rm tot}$ can be expressed as$ \mu^{pl}_{\rm tot}=\mu^{pl}_++\mu^{pl}_-=\dfrac{x^2_{\rm uni}+2}{x_{\rm uni}\sqrt{x^2_{\rm uni}+4}} , $

(43) The expression for
$ (\theta^{pl}_{E})_{\rm uni} $ is complicated; therefore, we use numerical calculations.$ x_{\rm uni} $ ,$ (\mu^{pl}_+)_{\rm uni} $ , and$ (\mu^{pl}_-)_{\rm uni} $ are defined as$ x_{\rm uni}=\frac{\beta}{(\theta^{pl}_E)_{\rm uni}}. $

(44) The image magnifications can be written as
$ (\mu^{pl}_+)_{\rm uni}=\frac{1}{4}\left(\dfrac{x_{\rm uni}}{\sqrt{x^2_{\rm uni}+4}}+\dfrac{\sqrt{x^2_{\rm uni}+4}}{x_{\rm uni}}+2\right), $

(45) $ (\mu^{pl}_-)_{\rm uni}=\frac{1}{4}\left(\dfrac{x_{\rm uni}}{\sqrt{x^2_{\rm uni}+4}}+\dfrac{\sqrt{x^2_{\rm uni}+4}}{x_{\rm uni}}-2\right). $

(46) The total magnification of the image in the presence of a plasma
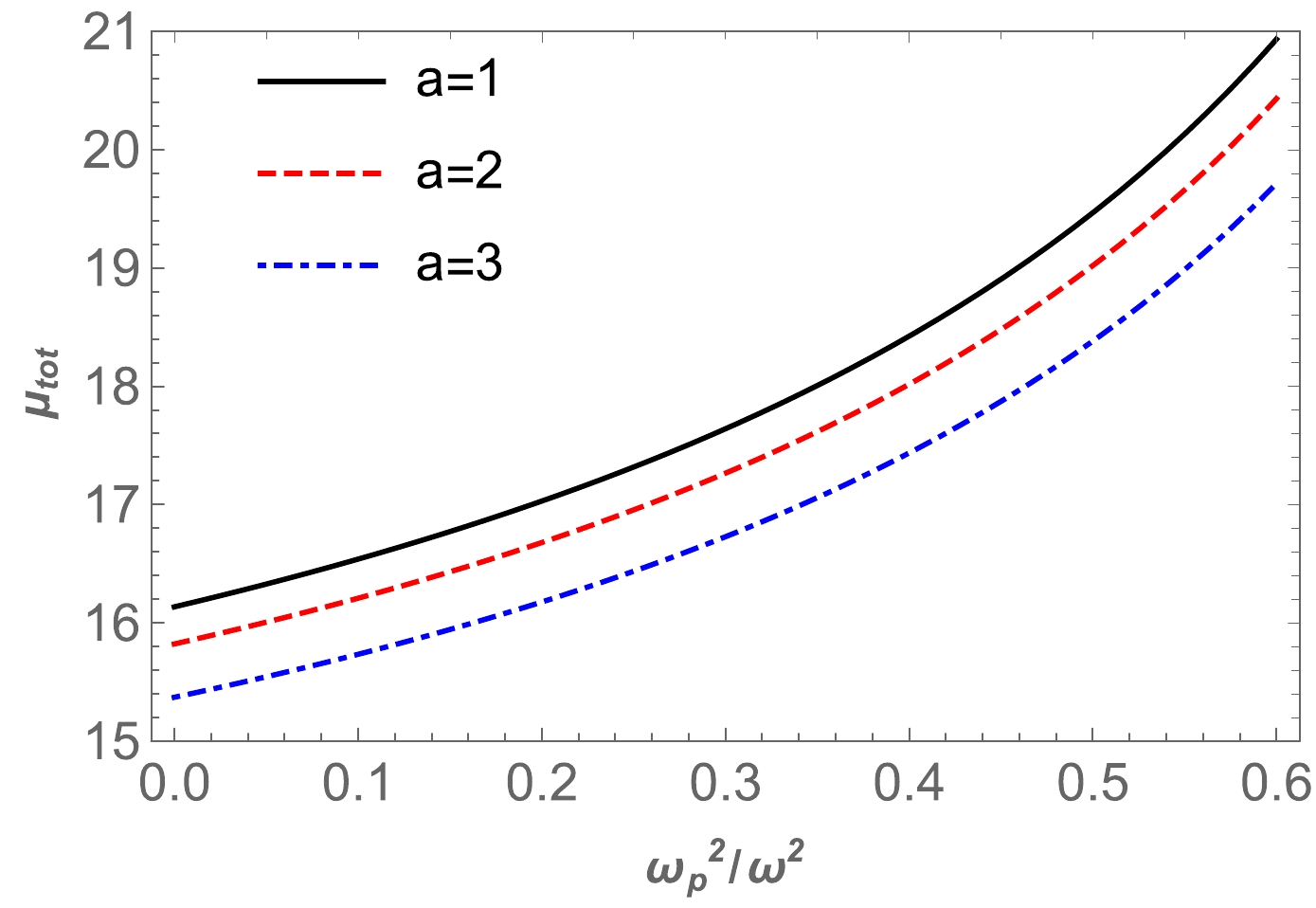
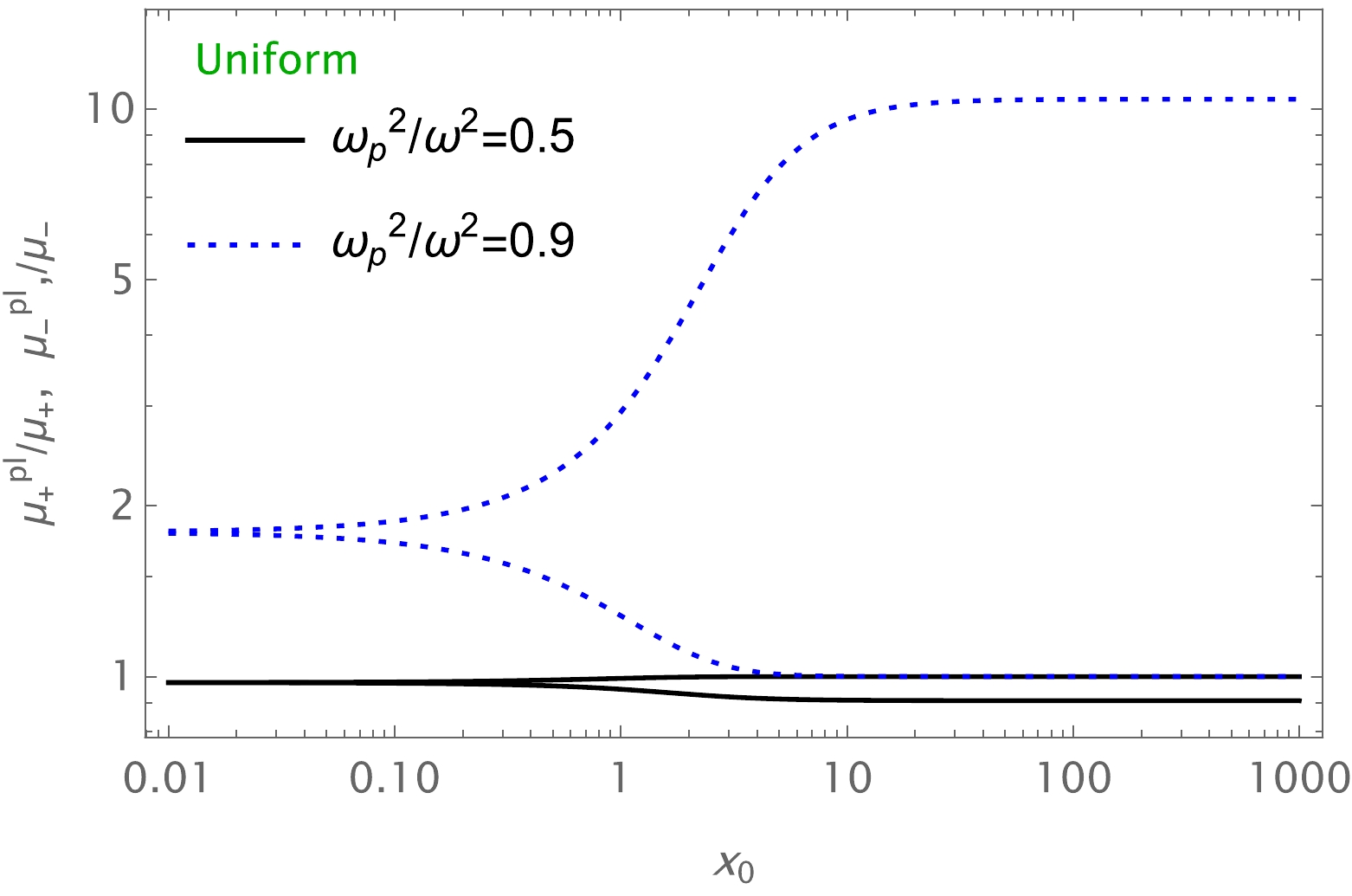
$\mu^{pl}_\mathrm{tot}$ for the Ellis-Bronnikov wormhole is demonstrated in Fig. 10. Fig. 11 shows the dependence of the total magnification on$ x_0 $ in the presence of uniform plasma for different values of the a parameter. These figures clearly indicate that the value of the total magnification of the image for uniform plasma increases with the plasma parameter value. -
In this subsection, we explore the effect of non-uniform plasma on the magnification of the image. We may write the expression for total magnification
$(\mu^{pl}_{\rm tot})_{\rm SIS}$ as$ \begin{array}{*{20}{l}} (\mu^{pl}_{\rm tot})_{\rm SIS}=(\mu^{pl}_+)_{\rm SIS}+(\mu^{pl}_-)_{\rm SIS}=\dfrac{x^2_{\rm SIS}+2}{x_{\rm SIS}\sqrt{x^2_{\rm SIS}+4}} , \end{array} $

(47) with
$ (\mu^{pl}_+)_{\rm SIS}=\frac{1}{4}\left(\dfrac{x_{\rm SIS}}{\sqrt{x^2_{\rm SIS}+4}}+\dfrac{\sqrt{x^2_{\rm SIS}+4}}{x_{\rm SIS}}+2\right) , $

(48) $ (\mu^{pl}_-)_{\rm SIS}=\frac{1}{4}\left(\dfrac{x_{\rm SIS}}{\sqrt{x^2_{\rm SIS}+4}}+\dfrac{\sqrt{x^2_{\rm SIS}+4}}{x_{\rm SIS}}-2\right) , $

(49) $ x_{\rm SIS}=\frac{\beta}{(\theta^{pl}_E)_{\rm SIS}} . $

(50) As with
$(\theta^{pl}_E)_{\rm uni}$ , we use the numerical method for$(\theta^{pl}_E)_{\rm SIS}$ .We can find the dependence of total magnification on the plasma parameter using Eq. (47). From Fig. 12, we can see that the magnification decreased as the plasma parameter increased. Moreover, the plot of the dependence of total magnification on
$ x_{0} $ in the presence of plasma for the fixed values of parameter a is provided in Fig. 13. These figures show that the value of the total magnification of the image for non-uniform plasma decreased as the plasma parameter values increased. Finally, we compared the two cases, i.e., uniform and non-uniform plasma distributions, in Fig. 14.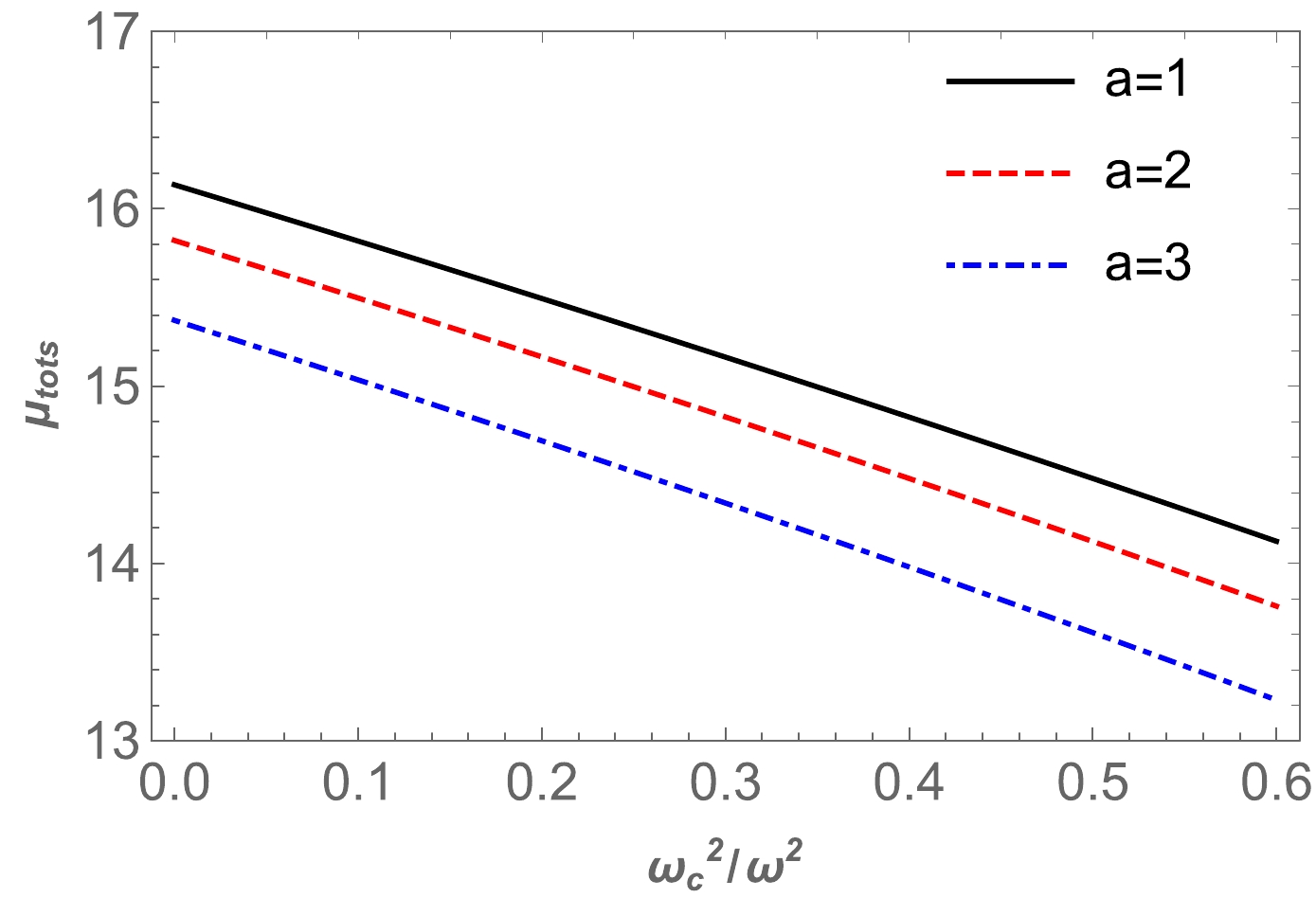
Figure 12. (color online) The total magnification of the images as a function of non-uniform plasma. Here, the impact parameter is set as
$ b = 5M $ .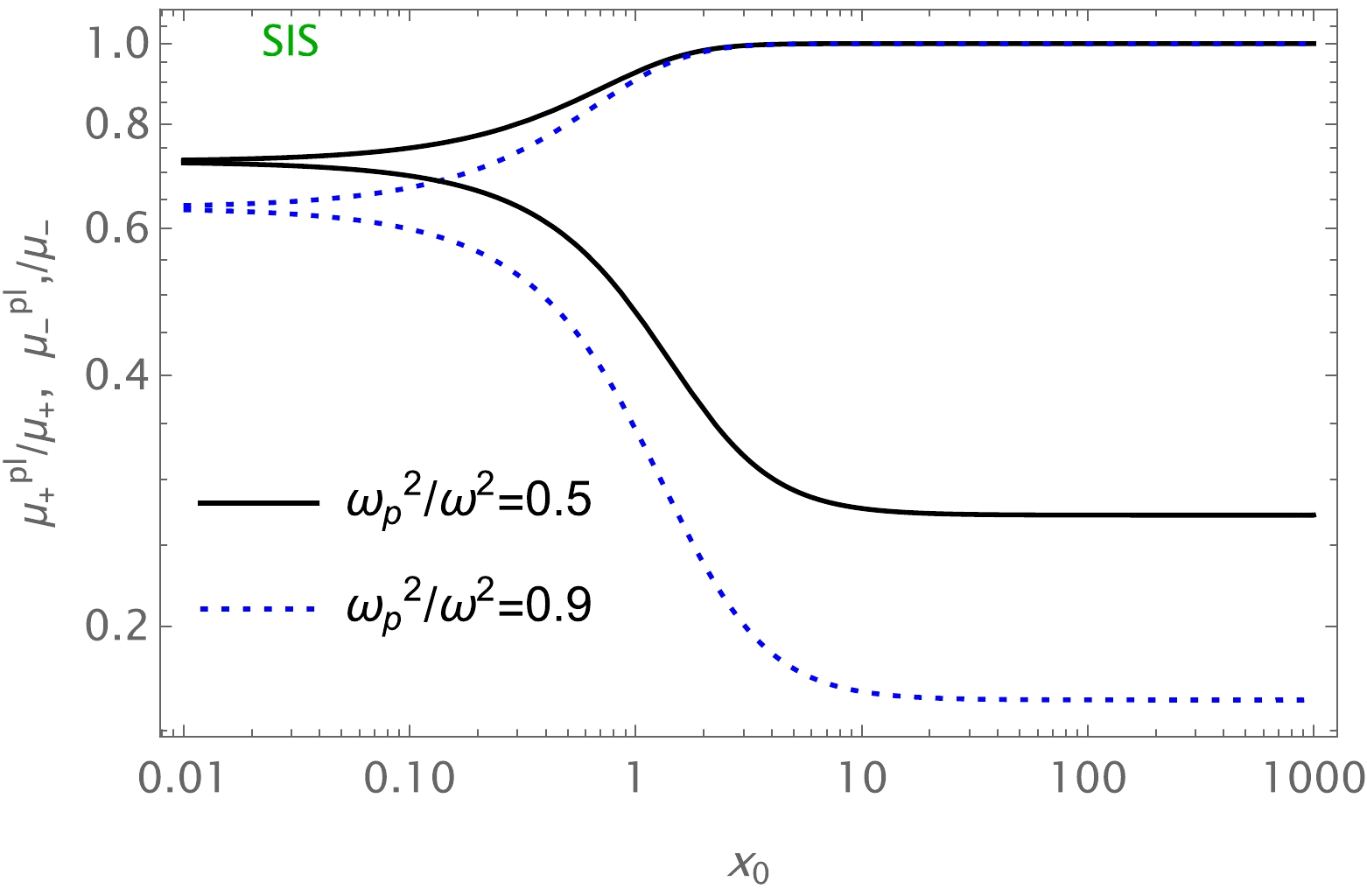
Figure 13. (color online) Image magnification in the presence of SIS. The fixed parameters used are
$ M=1 $ ,$ b=3M $ , and$ a=1 $ .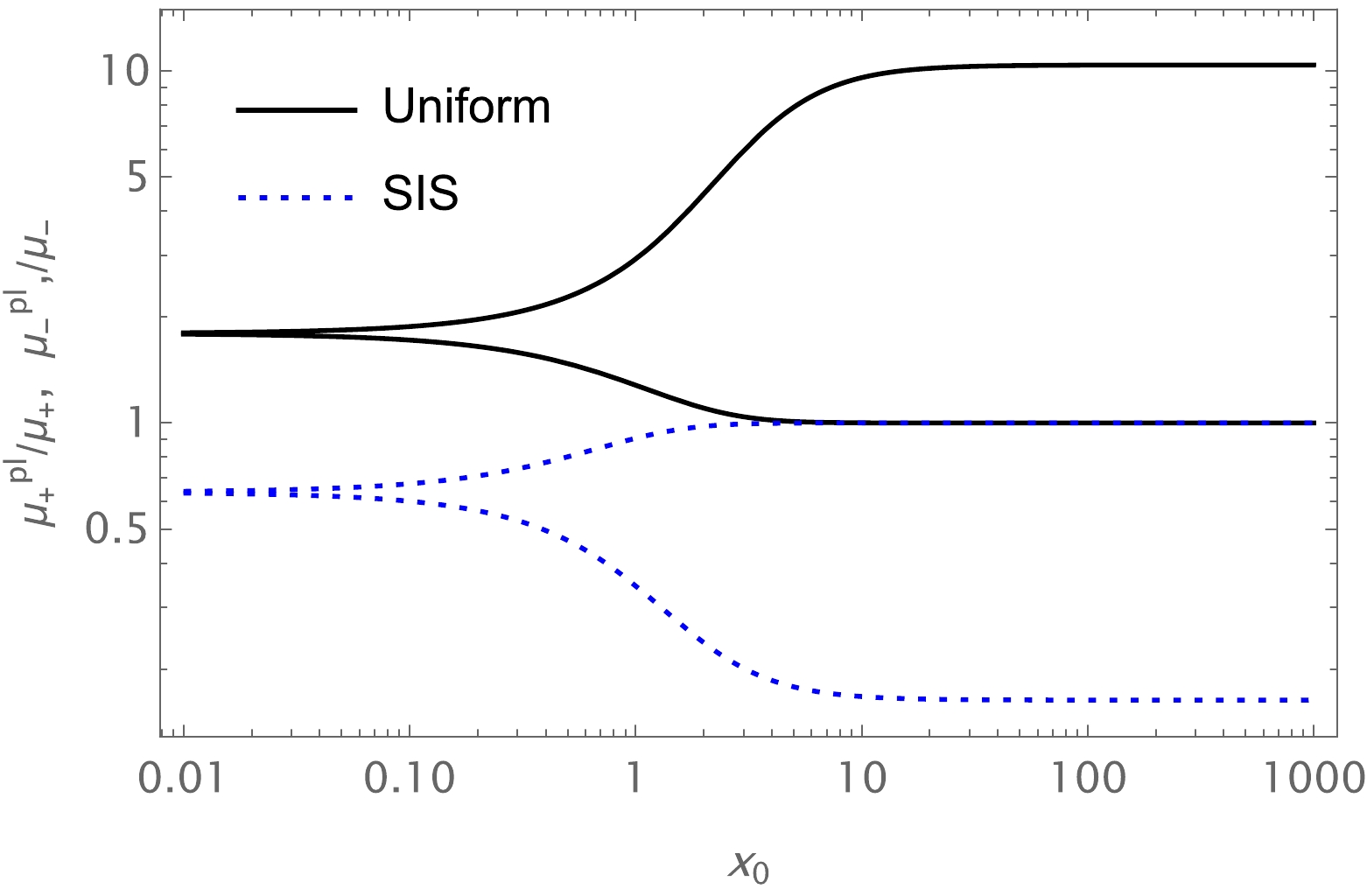
Figure 14. (color online) Image magnifications in the presence of uniform plasma and SIS. The fixed parameters used are
$ M=1 $ ,$ b=3M $ ,$ \frac{\omega^2_p}{\omega^2}=0.9 $ ,$ \frac{\omega^2_c}{\omega^2}=0.9 $ , and$ a=1 $ .The effect of uniform and non-uniform plasma on the total magnification differs; the former increases the total magnification while the latter decreases the total magnification of the images. Also, the image magnification for uniform plasma is greater than that for non-uniform plasma.
-
In this paper, we discussed the optical properties of the Ellis-Bronnikov wormhole. From the performed research, we can summarize our main results as follows:
● We investigated photon motion around a wormhole surrounded by plasma. We obtained numerical results regarding the dependence of the photon sphere radius on the plasma frequency (see Fig. 1). The photon sphere radius increased as the plasma frequency increased.
● We also studied the shadow of the Ellis-Bronnikov wormhole in plasma. The wormhole shadow radius was calculated using the numerical method. The dependencies of the wormhole shadow radius on the plasma frequency and wormhole parameter are demonstrated in Figs. 2 and 3. The figures show that the wormhole shadow radius increased as the a parameter increased, and vice versa for the plasma frequency, as demonstrated in Figs. 2 and 3.
● Since we have demonstrated that the size of the shadow depends on the wormhole and gravity theory parameters, in the future, the obtained results can be applied to the images of Sgr A* and M87* SMBHs to determine the constraints on Ellis-Bronnikov gravity parameters.
● Furthermore, weak gravitational lensing for the Ellis-Bronnikov wormhole was investigated. For this, we considered that the wormhole was surrounded by uniform and non-uniform plasma, and we obtained the deflection angle for each case. The obtained results are illustrated in Figs. 5, 6, 7 and 8. The value of the deflection angle
$ \hat{\alpha}_{\text{uni}} $ decreased as the impact parameter b increased. Under the influence of the uniform plasma frequency, the deflection angle$ \hat{\alpha}_{\text{uni}} $ increased, and vice versa for the a parameter. For uniform plasma, the values of the deflection angle$ \hat{\alpha}_{\text{sis}} $ decreased as the impact parameter b increased. Also, a slight decrease in the deflection angle$ \hat{\alpha}_{\text{sis}} $ was observed under the influence of the a parameter and the non-uniform plasma frequency.● In addition, we compared the deflection angle of light for uniform and non-uniform plasma in Fig. 9. The figure clearly indicates that the deflection angle of the light ray for uniform plasma is greater than that for non-uniform plasma.
● Finally, we studied the total magnification of the images as a function of uniform and non-uniform plasma. The dependencies are plotted in Figs. 10 and 12. From these figures, we can see that the value of the total magnification of the image for uniform plasma increased as the plasma parameter increased, and vice versa for non-uniform plasma. Also, we investigated the image magnification in both cases. The results are demonstrated in Figs. 11 and 13. Moreover, we compared the image magnifications in the presence of uniform plasma and SIS. The image magnification for uniform plasma is greater than that for SIS, as demonstrated in Fig. 14.
The above results demonstrate that plasma changes the optical properties of the Ellis-Bronnikov wormhole and its parameters. Also, we can see that the type of plasma plays an important role in the deflection angle because the deflection angle increases as the uniform plasma frequency increased, and vice versa for non-uniform plasma. In this work, we focused only on the constraint of the BH shadow. In future studies, the observational data of the gravitational lensing in Refs. [93–96] may be further employed to obtain constraints on the spacetime parameters of EB and estimate the plasma characteristics.
Shadow and weak gravitational lensing for Ellis-Bronnikov wormhole
- Received Date: 2023-10-31
- Available Online: 2024-02-15
Abstract: In this study, we investigated the gravitational weak lensing and shadow of the Ellis-Bronnikov wormhole. First, we studied the photon motion in a plasma medium and a wormhole shadow. It was shown that the radius of the photon sphere of the Ellis-Bronnikov wormhole and the size of the wormhole shadow become larger under the influence of the parameter a. The upper limit of the parameter a in the Ellis-Bronnikov wormhole spacetime was obtained. Second, we investigated the weak gravitational lensing for the Ellis-Bronnikov wormhole and calculated the deflection angle for uniform and non uniform plasma cases. The value of the deflection angle for uniform plasma increased with the increase in plasma parameter value, and vice versa for non uniform plasma. We found that, under the influence of the parameter a, the values of the deflection angles for two cases decreased. Finally, we investigated the magnification of image brightness using the deflection angle of the light rays around the wormhole in the Ellis-Bronnikov theory.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF













 DownLoad:
DownLoad: