Proton-neutron symplectic model description of ¹⁰⁶Cd

For over half a century, the conventional paradigm in nuclear structure physics has posited that quadrupole collectivity in atomic nuclei manifests in three main forms: 1) rigid-flow quadrupole rotations in strongly deformed nuclei, 2) quadrupole vibrations in spherical nuclei, and 3) γ-unstable rotor behavior in transitional nuclei. These three forms of quadrupole collectivity have been conceptually well captured by the three exactly solvable limits of the Bohr-Mottelson (BM) collective model. [1]. The latter is based on the quantization of the classical picture of surface vibrations and rotations of nuclear systems [2, 3]. The BM [1] collective model, developed in the early 1950s, is one of the foundational models [4] of nuclear structure and is still used to interpret the structure of nuclei, exhibiting different collective properties. The first exactly solvable limit of the BM model, reported in [2], was the case of the harmonic vibrator (HV), in which the quadrupole vibrations were associated with the vibration of the nuclear surface about a spherical equilibrium shape. Quadrupole vibrations in the HV limit [2] are commonly interpreted in terms of multiphonon excitations, which fall into different families or multiplets of quadrupole states with different angular momenta. The phonon multiplet structure illustrates a horizontal arrangement of nuclear excitations, characterized by the observed near-degeneracy of phonon multiplet states in certain nuclei. The rotor model [5, 6] limit of the BM model, from another side, exploits the vertical organization of the excited nuclear states into rotational bands.

Traditionally, the cadmium isotopes have been considered as textbook (and even as best [7]) examples [1, 4, 8, 9, 10, 11] of vibrational nuclei, primarily based on the excitation energies, and particularly, characterized by the energy ratio $ E_{4^{+}_{1}}/E_{2^{+}_{1}} \simeq 2 $–$ 2.2 $. The latter was first introduced in Ref. [12] and was widely used to classify the nuclei as vibrational. The observation of the anticipated two-phonon triplet of levels at approximately double the energy of one-phonon excitations has served as proof that these nuclei embody vibrational systems. In practice, the multiplets of states observed in nuclear spectra are not degenerate, a phenomenon typically ascribed to "anharmonic effects." The measured $ B(E2) $ transition probabilities in the Cd isotopes reveal notable departures from the idealized harmonic vibrator phonon model. New experimental data, acquired through various spectroscopic techniques, including inelastic scattering of charged and uncharged particles, transfer reactions, β decay, and Coulomb excitation, indicate a breaking of the conventional vibrational model of quadrupole vibrations in spherical nuclei [13−17]. Additionally, the extra $ 0^{+} $ and $ 2^{+} $ levels appear in the region of the two-phonon triplet, which have been observed early on in nuclear physics [18] and have later been interpreted as intruder deformed states. This has led to the consideration of shape coexisting phenomena [19]. It appears that the mixing between the intruder states and phonon states is relatively minor, which does not support the vibrational interpretation of Cd isotopes in terms of vibration-intruder mixing.

Specifically, a systematic study of midshell even-mass $ ^{110,112,114} $Cd isotopes [13−15], based upon the precise lifetime measurments, demonstrated that the transition probabilities in these nuclei are very poorly described by vibrational-type models. The question remained whether the lighter Cd isotopes may still represent examples of near-harmonic quadrupole vibrators. Recently, the structure of neutron-deficient even-even $ ^{102-108} $Cd isotopes was investigated [20] via precise lifetime measurements together with the state-of-the-art beyond-mean-field calculations using the symmetry conserving configuration-mixing (SCCM) approach. Except for the nuclei closed to the neutron shell closures, the SCCM calculations for $ ^{100-130} $Cd predict a well-defined prolate minimum with quadrupole deformation $ \beta \simeq 0.2 $. Assuming an axially symmetric rotor model, the deduced average quadrupole deformations are $ \beta \simeq 0.17 $ and $ \beta \simeq 0.14 $ for $ ^{104-108} $Cd and $ ^{102} $Cd, respectively. For $ ^{106} $Cd, the quadrupole deformation $ \beta \simeq 0.175(2) $ was obtained [20] using the "quadrupole sum rules" method. Additionally, for the axial asymmetry parameter, a value of $ \gamma \simeq 32^{0}(1) $ was obtained, the latter indicating the important role of the γ degrees of freedom in this nucleus. Recently, $ ^{106} $Cd was considered as "an excellent laboratory for studying the emergence of collectivity" [21]. The results of Ref. [21] suggest that the isotopic Cd chain can be described as evolving directly from closed-shell to rotational nuclei, without passing the phase of vibrational or spherical nuclei. The intruders and shape coexistence phenomena appear as well, which become progressively more influential toward the midshells.

A non-zero deformation of the ground states in the Cd nuclei was also recently obtained from the large-scale shell-model calculations of Zuker [22], whose origin was attributed to the pseudo-$S U(3)$ symmetry [23−25] due to the evident quadrupole dominance in the nuclear interaction. These results are consistent with the previous studies, in which these nuclei have been interpreted as deformed rotors [14, 26−30]. A similar behavior is predicted for $ 2^{+}_{1} $ and $ 4^{+}_{1} $ states, with the exception for $ ^{110-118} $Cd nuclei, which presents a second triaxial minimum in their potential energy surfaces. Theoretical and experimental results suggest that the multiple shape-coexistence interpretation, proposed by Garrett et al. [17] for $ ^{110,112} $Cd, can be extended to the neutron-deficient region.

In Ref. [14] the low-energy levels in $ ^{110-116} $Cd were rearranged vertically into quasirotational bands based on the measured $ B(E2) $ transition probabilities. This idea is not new and was proposed already in 1967 and extensively exploited in the 1970s by M. Sakai [26−30]. Particularly, the rearrangement of low-lying energy levels suggests a different mechanism for the vanishing of the previously expected $ \Delta n = 1 $ phonon transitions $ - $these transitions are now interpreted as interband transitions. The suggestion that rotational degrees of freedom underlie the low-energy excitations in the Cd isotopes, along with the smallness of the $ B(E2) $ values for $ 0^{+} $ states, implies that other mechanisms should be considered for the interpretation of excited $ 0^{+} $ states [14]. Some of these states in Cd isotopes are interpreted as intruder states, produced by proton pair excitation across the $ Z = 50 $ shell gap [14, 19]. The question arises that concerns the nature of the other low-lying excited $ 0^{+} $ states in Cd isotopes. Additionally, the rearrangement of the low-energy states into quasirotational bands in Cd isotopes shows a very strong odd-even staggering of γ-unstable type between the collective states of the γ band, revealing the important role of the triaxial degrees of freedom in these nuclei. Furthermore, this is supported by the large collective $ B(E2;2^{+}_{2} \rightarrow 2^{+}_{1}) $ experimental value, characteristic of the $ O(6) $ symmetry [31]. However, it represents only a fraction of $B(E2;2^{+}_{1} \rightarrow 0^{+}_{1})$ as opposed to the factor 2 predicted in the HV limit. Specifically, $ ^{110} $Cd [15] and other mid-shell Cd isotopes [32] were suggested as γ-unstable rotors based on the enhanced $ B(E2;0^{+}_{3} \rightarrow 2^{+}_{2}) $ and almost vanishing $ B(E2;0^{+}_{3} \rightarrow 2^{+}_{1}) $ values, which are characteristic features of γ-unstable Wilets-Jean (WJ) model [33]. Thus, the Cd isotopes, initially interpreted as spherical vibrators in the 1950s, were proposed nearly 60 years later to be γ-unstable rotors, a characteristic observable in numerous Cd nuclei ($ ^{106-126} $Cd, cf., e.g., Figs. 4 and 13 of Refs. [21] and [34], respectively) based on γ band energies.

A simple quantity, pointing to the nonspherical shapes of the atomic nuclei, is provided by the experimentally measured nonzero quadrupole moments (see, e.g., Fig. 11 of Ref. [16]). However, in the HV limit of the BM model (and other vibrational models, like, e.g., the $ U(5) $ dynamical symmetry limit of the IBM [10]), they identically vanish due to the simple selection rule. The quadrupole moments vanish in the γ-unstable WJ limit of the BM as well. This suggests that HV and WJ limits of the BM model, relevant to the structure of Cd isotopes, should be considered just as starting points for further more sophisticated approximations.

Despite extensive experimental studies, the individual theoretical models have not been able to establish a clear physical picture of the observed quadrupole dynamics in even-even Cd isotopes. Evidence for near-harmonic spherical-vibrational properties of Cd isotopes was reported up to three [35] and even up to six [36] quadrupole phonons. Low-energy structure of even-even $ ^{108-116} $Cd isotopes was recently analyzed [37] within the framework of a general collective model based on the relativistic density functional theory. The collective Hamiltonian reproduces the observed quadrupole phonon states of vibrational character, which are based on the moderately deformed equilibrium minimum in the mean-field potential energy surface. The mean-field results for the near midshell nuclei $ ^{112,114} $Cd reveal a coexistence of normal states linked to a weakly deformed prolate or nearly spherical global minimum, and intruder states established on a more deformed, almost prolate-triaxial, local minimum. In Ref. [38] the spherical phonon interpretation has been reinforced and it was demonstrated that the vibrational multiphonon low-lying normal states in $ ^{110} $Cd can be described within the IBM framework with $ U(5) $ partial dynamical symmetry. Specifically, it was shown that most low-lying normal states preserve their spherical-vibrational character, and only a few specific nonyrast collective states do not exhibit good $ U(5) $ symmetry, in accordance with the experimental data.

The diverse model interpretations and significant interest in Cd isotopes over the past decade highlight the fundamental question regarding the emergence and nature of quadrupole collectivity in these nuclei. Another related question seeks to comprehend the development of quadrupole collectivity (rotations) in weakly deformed nuclei, such as the Cd isotopes, from a microscopic shell-model viewpoint. In the case of strongly deformed nuclei, which are far from closed shells, the pronounced deformation clearly dominates their collective behavior, leading us to employ rotor models to describe their rotational dynamics. A recent study by Zuker [22] revealing the dominant role of the quadrupole-quadrupole interaction in Cd nuclei, and the new experimental study of $ ^{106} $Cd isotope [21] suggested as the best experimental laboratory to investigate the appearance of nuclear collectivity and deformation can help to resolve the raised questions.

The microscopic description of the properties of atomic nuclei is a longstanding problem in nuclear structure physics. A general microscopic framework for the study of nuclear collective motion is provided by the nuclear shell model (see, e.g., [39]), which includes all many-particle fermion degrees of freedom and represents the second foundational model [4] of nuclear structure. The shell model provides a general microscopic framework in which other collective models can be embedded.

Recently, a microscopic shell-model version of the BM model was formulated [40, 41] within the framework of the microscopic proton-neutron symplectic model (PNSM) of nuclear collective motion with $ S p(12,R) $ dynamical algebra. This version provides an interesting and relevant shell-model symplectic-based framework to explore the nature of the observed nuclear collective dynamics. In particular, it has already been applied to the microscopic description of the rigid-flow quadrupole collectivity in some strongly deformed [42] and transitional [43] nuclei and as well to the microscopic shell-model description of the irrotational-flow dynamics observed in some weakly deformed nuclei [44, 45]. Thus, the purpose of the present study is to examine the low-lying (normal) collective states in $ ^{106} $Cd, where the latter is suggested as "an excellent laboratory to study the emergence of collectivity" [21], within the microscopic shell-model version of the BM model. Light Cd isotopes, specifically $ ^{106} $Cd, were recently examined by different authors [20−22, 46−52]. In the present study, we exploit the idea of vertical organization of the nuclear excitations into quasibands [14, 17, 20, 21, 26−30], and thus only consider the first three bands in the energy spectrum. The other experimentally observed low-energy levels that are not considered generally can also be represented as members of the appropriate quasibands. The results obtained in present study suggest a different interpretation of the fundamental question concerning the nature of low-energy vibrations and the emergence of deformation and collectivity in atomic nuclei, i.e., the manifestation of the low-energy quadrupole collectivity in the weakly deformed nuclei.

Any shell-model dynamical chain of the PNSM is naturally defined via the the harmonic oscillator creation and annihilation operators

where $ i,j = 1,2,3 $; $ \alpha,\beta = p,n $, and $s = 1,\,2,\ldots,m=A-1$. In Eq. (1), $ x_{is}(\alpha) $ and $ p_{is}(\alpha) $ denote the coordinates and corresponding momenta of the translationally-invariant relative Jacobi vectors of the m-quasiparticle two-component nuclear system and A denotes the number of protons and neutrons. We then consider all bilinear combinations of these operators to obtain the $ S p(12,R) $ dynamical algebra generators [53]:

The operators (4) preserve the number of oscillator quanta, whereas those given by (2) and (3) create and annihilate, respectively, a pair of harmonic oscillator quanta.

The many-particle states in the microscopic shell-model version of the BM model are classified by the following dynamical symmetry chain [40, 41]:

where below the different subgroups are given the quantum numbers that characterize their irreducible representations. The $S U(1,1) \supset U(1)$ quantum numbers $ \lambda_{\upsilon}=\upsilon+5/2 $ and p define the oscillator shell structure. Due to dual pair relationships [54], they are related to the $U(6) \supset S O(6)$ quantum numbers $ E=[E,0,\dots,0]_{6} $ and $ \upsilon \equiv (\upsilon)_{6} = (\upsilon,0,0) $ via the expression $ p=(E-\upsilon)/2 $. Thus, the standard harmonic oscillator basis states $ |n \rangle $ with even (odd) values $ n=2p $ ($ n=2p+1 $) are related [55] to the $S U(1,1)$ basis states $ \{|\lambda_{\upsilon}, p \rangle; p = 0, 1, 2, \ldots\} $ through the expression $ |\lambda_{\upsilon}, p \rangle = |n \rangle $ with $ n=\lambda_{\upsilon} + 2p -6/2 $. The $S U_{pn}(3)$ quantum numbers $ (\lambda,\mu) $ define the deformation of nuclear system and are related to the $S O(6)$ and $S O(2)$ quantum numbers υ and ν by the following expression [40]:

The $S O(3)$ quantum numbers L define the corresponding angular momentum values. q denotes a multiplicity label in the reduction $S U_{pn}(3) \supset S O(3)$ and its values, defining different quasibands, are given by $q =\min(\lambda,\mu), $ $ \min(\lambda,\mu)-2,...,0\; (1) $.

Based on chain (5), the monopole-quadrupole nuclear dynamics splits into radial and orbital motions, and the wave functions of the microscopic SM version of the BM model are as follows [40]:

For more details concerning the structure of these function we refer readers to Ref. [41].

Many Hamiltonians of interest can be expressed by means of the $ S p(12,R) $ algebra generators (2)$ - $(4). Here, we also use such a type of Hamiltonian:

containing three parts having a clear physical meaning. The dynamical symmetry part

is expressed in standard way by Casimir operators of different subgroups only along the chain (5). Particularly, it contains the harmonic oscillator Hamiltonian $ H_{0}= n \hbar\omega $ that defines the shell structure of the nucleus, and a collective potential that is expressed through the second- and third-order Casimir operators of the $S U_{pn}(3)$ group. The collective potential splits different $S U_{pn}(3)$ multiplets and the most deformed irreducible representation is lowered most in energy.

Usually the residual rotor part is expressed as $ H_{rot} = aL^{2}+bX^{a}_{3}+cX^{a}_{4} $ [56], which, in addition to the $S O(3)$ Casimir operator $ L^{2} $ , includes third- and fourth-order $S U(3)$ preserving interactions and represents a shell-model image of the triaxial rotor model Hamiltonian. In this way, we incorporate the quantum rotor dynamics into the shell-model theory and give physical significance to the high-order $S U(3)$ symmetry preserving interactions. However, in the present application, we use the residual rotor part as follows:

where $ X^{a}_{4} = [L\times\widetilde{q}\times\widetilde{q}\times L]^{(0)} $ and the $S U_{pn}(3)$ generators are defined as [40]:

Several studies examined the effect of operators $ X^{a}_{3} $ and $ X^{a}_{4} $ on nuclear spectra, within the broken-$S U(3)$ model [57], the shell model [58], the symplectic $S p(6,R)$ model [59, 60], and the IBM [61−65]. Recently, the role of the high-order $S U(3)$-preserving interactions was reinforced in relation to different nuclear phenomena [66−72]. Studies indicate that the $ X^{a}_{3} $ and $ X^{a}_{4} $ operators introduce an odd-even staggering in the γ band of γ-rigid type [73]. However, Refs. [44, 45] indicate that by modifying them one is able to produce a γ-unstable odd-even staggering pattern for the states of the γ band that is a characteristic of the γ-unstable WJ model (see Fig. 1 for $ ^{106} $Cd). Thus, we follow [44, 45] and use the following parametrization $ c\equiv c(1-(-1)^{L}/\sqrt{2}) $ for the model parameter in Eq. (10).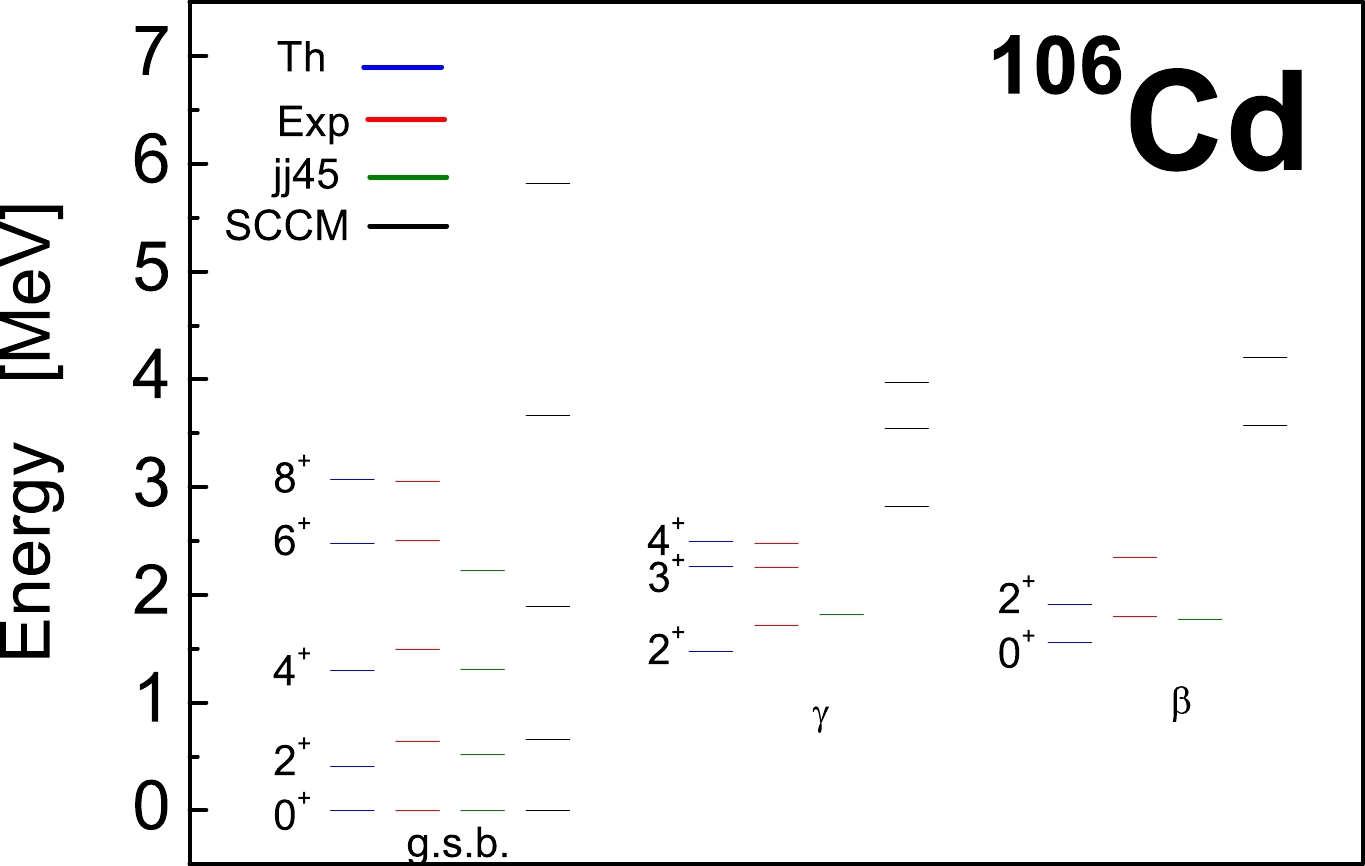

Figure 1.  (color online) Comparison of the excitation energies of the ground, γ, and β quasibands in $ ^{106} $Cd with experiment and predictions of the "jj45" shell-model (extracted from [21]) and the SCCM approach (extracted from [20]). Values of the model parameters (in MeV) are: $ B = -0.075 $, $ C = 0.00045 $, $ c = 0.00114 $, and $ h = -0.187 $.

Finally, the Hamiltonian [55]

introduces a mixing of various $S U_{pn}(3)$ multiplets within the different seniority $S O(6)$ irreps υ. The required matrix elements of (10) and (13) for performing shell-model calculations within the present approach are given in Refs. [56] and [55], respectively.

We use the definitions of Eqs. (2)$ - $(4) to represent the Cartesian components of the mass quadrupole operators $ Q_{ij}(\alpha,\beta)=\sum\limits_{s}x_{si}(\alpha)x_{js}(\beta) $ as follows [53]:

which, as can be seen from (1), are in units of $ b^{2}_{0} $. $ b_{0}=\sqrt{\dfrac{\hbar}{M\omega}} $ denotes the oscillator length parameter and it was also assumed that $ M_{p}=M_{n}=M $. The spherical components of the mass quadrupole operators then become

To obtain the charge quadrupole operators, one needs to multiply the expression (15) by the standard factor $ (eZ/(A-1)) $. Making use of the expression for the harmonic oscillator length $b_{0}=1.010 A^{1/6} \; \; {\rm fm}$ [9], the units of charge quadrupole moments become $e{\rm fm}^{2}$. We note that e is the bare electric charge. The restriction to a single shell leads to the (in-shell) quadrupole operators $ \widetilde{Q}^{2m}(\alpha,\beta) = \sqrt{3}A^{2m}(\alpha,\beta) $. However, to calculate the $ B(E2) $ transition probabilities in the present application of the microscopic shell-model version of the BM model we use the $S U_{pn}(3)$ quadrupole generators (11) as excitation operators, i.e. $ T^{E2} = (eZ/(A-1)) \widetilde{q}^{2m} $, which are a linear combination of $ \widetilde{Q}^{2m}(\alpha,\beta) $. This implies that the quadrupole dynamics in $ ^{106} $Cd is assumed in the present work to be of a rigid-flow type. Only the comparison of the $ B(E2) $ transition strengths with the experimental data can determine if such an assumption is physically justified or not.

The practical application of the PNSM first requires the determination of relevant symplectic representation of its dynamical group $S p(12,R)$. We use the pseudo-$S U(3)$ scheme [23−25] and pairwise fill the pseudo-Nilsson levels with protons at observed quadrupole deformation $ \beta = 0.17 $ [11] to obtain completely filled $ \mathcal{\widetilde{N}}=2 $ pseudo-shell plus 8 protons in the unique-parity level $ g_{9/2} $. Subsequently, the leading proton $S U_{p}(3)$ irrep is the scalar irrep $ (0,0) $. Similarly, for neutrons we obtain completely filled $ \mathcal{\widetilde{N}}=2 $ pseudo-shell plus 6 (or 8) neutrons occupying the $ \mathcal{\widetilde{N}}=3 $ pseudo-shell and 2 (or 0) neutrons in the unique-parity level $ h_{11/2} $. We use available computer codes [74, 75] to obtain the set of Pauli allowed $S U(3)$ states: $ (12,0), (9,3), (6,6), (7,4), (8,2), \ldots $ or $ (10,4), (12,0), (8,5), (9,3), (10,1), (5,8), (6,6), (7,4) $, $ (8,2), \ldots $ by considering 6 or 8 active neutrons, respectively. Further, the proton and neutron irreps should be coupled to obtain the combined proton-neutron $S U_{pn}(3)$ representation of the whole nuclear system. However, given that only the scalar representation for the proton subsystem $ (0,0) $ is admitted, the set of combined proton-neutron multiplets coincides with that of the neutron subsystem since $ (\lambda_{p},\mu_{p})\otimes (\lambda_{n},\mu_{n})= (0,0)\otimes (\lambda_{n},\mu_{n}) \equiv (\lambda,\mu) $. Alternatively, we can use the pseudo-$S U(3)$ scheme [23−25], albeit filling each pseudo-Nilsson level with 4 nucleons based on the supermultiplet spin-isospin scheme. Subsequently, we readily obtain 6 nucleons that fill the last valence $ \mathcal{\widetilde{N}}=3 $ pseudo-shell. The codes [74, 75] produce the set of $S U(3)$ states: $(14,2), (12,3), (13,1), (10,4), (11,2), (12,0), (8,5), \ldots$. We use the Nilsson model ideas [76−79] and select the $S U(3)$ irrep $ (12,0) $, which is contained in the two alternatively obtained sets of Pauli allowed many-particle $S U(3)$ states, and thereby fix the appropriate $S p(12,R)$ irreducible representation 0p-0h $ [12]_{6} $ (or $\langle \sigma\rangle = \langle 27+ m/2, 15+m/2, \ldots, 15+m/2\rangle$ using an equivalent notation) for $ ^{106} $Cd. The $S p(12,R)$ irreducible representation $ \langle \sigma\rangle = \langle 27+m/2, 15+m/2, \ldots, 15+m/2\rangle $ is determined by the lowest-grade $ U(6) $ irrep (or symplectic bandhead) $ \sigma\equiv[\sigma_{1},\ldots,\sigma_{6}]_{6} = [27,15,\ldots,15]_{6}\equiv[12]_{6} $. The relevant irreducible collective space for $ ^{106} $Cd, spanned by the $S p(12,R)$ irreducible representation 0p-0h $ [12]_{6} $, which $S U_{pn}(3)$ basis states are classified according to the chain (5) is given in Table 1. We note that, due to the Pauli principle, only the $S O(6)$ irreducible representations with $ \upsilon \geq \upsilon_{0}=12 $ are retained in the table. If we assume a pure $S U_{pn}(3)$ structure and use the following expression [76]:

N	u/v	$\cdots $	16	14	12	10	8	6	4	2	0	−2	−4	−6	−8	−10	−12	−14	−16	$\cdots $
$\vdots $	$\vdots $	$\ddots $	$\vdots $	$\vdots $	$\vdots $	$\vdots $	$\vdots $	$\vdots $	$\vdots $	$\vdots $	$\vdots $	$\vdots $	$\vdots $	$\vdots $	$\vdots $	$\vdots $	$\vdots $	$\vdots $	$\vdots $	${\mathinner{\mkern2mu\raise1pt\hbox{.}\mkern2mu \raise4pt\hbox{.}\mkern2mu\raise7pt\hbox{.}\mkern1mu}}$
$N_{0}+4$	16		(16,0)	(14,0)	(13,1)	(12,2)	(11,3)	(9,3)	(9,5)	(8,6)	(7,7)	(6,8)	(5,9)	(3,9)	(3,11)	(2,12)	(1,13)	(0,14)	(0,16)
	14			(14,0)	(13,1)	(12,2)	(11,3)	(9,3)	(9,5)	(8,6)	(7,7)	(6,8)	(5,9)	(3,9)	(3,11)	(2,12)	(1,13)	(0,14)
	12				(12,0)	(11,1)	(10,2)	(9,3)	(8,4)	(7,5)	(6,6)	(5,7)	(4,8)	(3,9)	(2,10)	(1,11)	(0,12)
$N_{0}+2$	14			(14,0)	(13,1)	(12,2)	(11,3)	(9,3)	(9,5)	(8,6)	(7,7)	(6,8)	(5,9)	(3,9)	(3,11)	(2,12)	(1,13)	(0,14)
	12				(12,0)	(11,1)	(10,2)	(9,3)	(8,4)	(7,5)	(6,6)	(5,7)	(4,8)	(3,9)	(2,10)	(1,11)	(0,12)
$N_{0}$	12				(12,0)	(11,1)	(10,2)	(9,3)	(8,4)	(7,5)	(6,6)	(5,7)	(4,8)	(3,9)	(2,10)	(1,11)	(0,12)

Table 1.  Relevant $S O(6)$ and $S U_{pn}(3)$ irreducible representations which are contained in the $S p(12,R)$ irreducible collective space 0p-0h $[12]_{6}$ of $^{106}$Cd.

where $ N_{0} = 169.5 $ is the minimal Pauli allowed number of oscillator quanta, we obtain for the quadrupole deformation of the $ (12,0) $ irreducible representation $ \beta \approx 0.21 $, which slightly overestimates the experimental value 0.17 [11]. This suggests the use of a horizontal mixing of different shell-model configurations within the symplectic $S p(12,R)$ bandhead space and our choice for the mixing Hamiltonian (13).

We note that the horizontal sets of $S U(3)$ irreducible representations initially differ from those obtained by the plethysm operation via the reduction$U(d) \supset S U(3)$ [74, 75], where $ d =\dfrac{1}{2}(\mathcal{N}+1)(\mathcal{N}+2) $ for each nuclear shell $ \mathcal{N} $. This is because the many-particle configurations in the PNSM are classified by basis states of the six-dimensional harmonic oscillator instead of the standard three-dimensional one. However, the $S U(3)$ states contained in the $ U(6) $ group structure can be organized in different ways because different choices for the group G in the reduction $U(6) \supset G \supset S U(3)$ are possible. Subsequently, each symplectic shell in the present approach is determined by the corresponding $ U(6) $ representation (or equivalently, by the number of oscillator quanta N), which in turn contains different seniority $S O(6)$ irreducible representations υ (see Table 1). It is further demonstrated that the horizontal set of the remaining $S U(3)$ irreps which are placed to the right from the axially-symmetric multiplet $ (\lambda,0) $, the latter being in the most left position, at each row defined by the corresponding $S O(6)$ irrep υ actually represent many-particle-many-hole (mp-mh) excitations of the nuclear system. The excitations, for even or odd type of the $S U(3)$ representations, are generated by multiple application of the operator $G^{2}(a,a) \cdot F^{2}(b,b)= \dfrac{2}{3}\sqrt{5}[G^{2}(a,a)\times F^{2}(b,b)]^{4}_{-4100}$ of Eq. (13). The latter preserves the number of $ U(6) $ harmonic oscillator quanta N of each symplectic shell and can be considered as a 2p-2h-like operator of the core excitations that creates two oscillator quanta in the shell above and annihilates two oscillator quanta in the shell bellow, i.e., it promotes two oscillator quanta up. For example, the $S U(3)$ multiplet $ (10,2) $ within the maximal $S O(6)$ seniority irrep $ \upsilon_{0} = 12 $ of the symplectic $S p(12,R)$ bandhead, defined by $ N_{0} $ oscillator quanta, can be obtained by promoting two oscillator quanta from the pseudo-shell $ \widetilde{N}=2 $ to $ \widetilde{N}=3 $, i.e., changing the many-particle shell-model configuration $ (\widetilde{2})^{40}(\widetilde{3})^{6} $ to $ (\widetilde{2})^{38}(\widetilde{3})^{8} $, the latter producing the excited $S U(3)$ irrep $ (10,2) $ from $ (12,0) $ of the former configuration. Hence, the $S U(3)$ many-particle shell-model configurations are organized in different way via group $ SO(6) $ through the reduction $U(6) \supset S O(6) \supset S U(3)$ (more precisely, $S p(12,R) \supset U(6) \supset S O(6) \supset S U_{pn}(3) \otimes S O(2)$ for different $ U(6) $ shells) when compared to the standard shell-model plethysm reduction $U(d) \supset S U(3)$, and each horizontal subset of the $S U(3)$ multiplets is characterized by the same value of the $S O(6)$ seniority irrep $ \upsilon=\lambda+\mu $. This is a new feature of the PNSM which arises from the properties of the $S O(6)$ group. We note that the $S U(3)$ content of the symplectic shells defined by the PNSM dynamical chain $S p(12,R) \supset U(6) \supset S U_{p}(3)\otimes S U_{n}(3) \supset S U(3)$ considered, e.g., in Refs. [53, 80], will coincide precisely with that generated first by the separate reductions $ U_{\alpha}(d) \supset SU_{\alpha}(3) $ ($ \alpha=p,n $) with the subsequent coupling of the proton $ (\lambda_{p},\mu_{p}) $ and neutron $ (\lambda_{n},\mu_{n}) $ subsystem representations to the combined proton-neutron $S U(3)$ irreducible representation $ (\lambda,\mu) $, given that the PNSM many-particle $S U(3)$ configurations are organized by means of the group structure $S U_{p}(3)\otimes S U_{n}(3) \supset S U(3)$ within the $ U(6) $ harmonic oscillator shell.

Regarding the calculations of the properties of different Cd isotopes, the particle-hole excitations have been used within the framework of the IBM and other approaches [17, 20, 81−84]. However, we note that the present many-particle-many-hole excitations represented by the different $S U_{pn}(3)$ irreducible representations within the $S O(6)$ irrep $ \upsilon_{0}=12 $ belong to the same $ U(6) $ shell. Their mixing is referred to as a horizontal mixing. The traditional particle-hole excitations within the standard shell-model or the IBM correspond to the vertical mixing of different $S U(3)$ irreducible representations within the PNSM and belong to the higher $ U(6) $ and $S O(6)$ excited representations. The important point in the present application is that the $S p(12,R)$ bandhead, in contrast to the Elliott $S U(3)$ and $S p(6,R)$ shell models, contains many $S U(3)$ multiplets which are appropriate for the description of different collective bands. Hence, the symplectic $S p(12,R)$ bandhead provides us with a microscopic shell-model framework for the simultaneous description of different bands in a manner similar to that of, e.g., the IBM [10]. Thus, the shell-model coupling scheme in the PNSM as defined by the chain $S p(12,R) \supset U(6) \supset S U_{p}(3)\otimes S U_{n}(3) \supset S U(3)$ will produce another $S U(3)$ content, which also can be used for the simultaneous description of different collective bands. We note one more important difference: in the conventional shell model or IBM the particle-hole excitations are associated with the intruder configurations of quite different deformation. The latter in the PNSM can be taken into account by considering the excited $S p(12,R)$ irreducible representations.

We diagonalize the model Hamiltonian (8) in the irreducible collective space of maximal seniority $ \upsilon_{0} = 12 $, belonging to the symplectic bandhead of the $S p(12,R)$ irrep 0p-0h $ [12]_{6} $ as characterized by $ N_{0} $. The results for the low-lying excitation energies of the ground, γ and β bands in $ ^{106} $Cd are shown in Fig. 1, where they are compared with experiment [85] and the predictions of the "jj45" shell-model (extracted from [21]) and the SCCM approach (extracted from [20]). The values of the model parameters are obtained by fitting procedure to the energies and $ B(E2;2^{+}_{1} \rightarrow 0^{+}_{1}) $ value. Their values (in MeV) are as follows: $ B = -0.075 $, $ C = 0.00045 $, $ c = 0.00114 $, and $ h = -0.187 $. As shown in the figure, we observe a good description of the excitation energies for the three bands (up to the bandhead energies) including centrifugal stretching in the ground band for high angular momenta and strong odd-even staggering between the states of the γ band. The description is not perfect but rather good taking into account that the excitation energies are obtained in the microscopic version of the BM model without the use of an adjustable kinetic energy. This is an interesting result obtained for the weakly deformed nuclei. Similar results were obtained for some strongly deformed nuclei within the $S p(6,R)$ model [77, 78, 86] and for some strongly deformed [42] and transitional [43] heavy-mass even-even nuclei within the present microscopic shell-model version of the BM model. To the best of the authors' knowledge, extant studies have not reported results for weakly deformed nuclei, particularly for Cd isotopes.

We effectively obtain the observed moment of inertia in the present calculations without the adjustable kinetic-energy term, and this implies that the quadrupole collective dynamics is correctly captured by the symplectic bandhead of the $S p(12,R)$ irreducible representation 0p-0h $ [12]_{6} $. Fig. 2 shows the results for the intraband $ B(E2) $ transition probabilities between the collective states of the ground band in $ ^{106} $Cd compared with experiment [21, 85], the SCCM approach (SCCM) and the "jj45" shell-model calculations as obtained from Refs. [20] and [21], respectively. As shown in the figure, we observe a typical rigid-flow $S U(3)$-rotor behavior (see Fig. 1 of Ref. [44] and the concerning discussion there). The ground state intraband $ B(E2) $ quadrupole collectivity is slightly underestimated, although the general trend is well described, including the depletion. This behavior of the transition strength $ B(E2;8^{+}_{1} \rightarrow 6^{+}_{1}) $ is also observed for $ ^{102,104,106} $Cd isotopes due to the change in the structure of the yrast states [52]. We note that the intraband $ B(E2) $ transition probabilities between the states of the ground band can be enhanced trivially by introducing an effective charge, or, more naturally $ - $by including also a vertical mixing term to the model Hamiltonian and performing more comprehensive shell-model calculations. Further, in Table 2 , we compare the known experimental $ B(E2) $ values [16, 20, 21, 47, 85, 87] with the theory for the nonyrast states of the γ and β bands in $ ^{106} $Cd. As shown in the table, the observed $ B(E2) $ transition probabilities are in qualitative agreement with the theory. For the quadrupole moments of the excited $ 2^{+}_{1} $ and $ 2^{+}_{2} $ states we obtain $ Q(2^{+}_{1}) = -0.45 $ and $Q(2^{+}_{2}) = +0.35 \; \; \rm eb$, to be compared with the experimental values $ -0.29(13) $ and $+0.61(29) \; \; \rm eb$ [21], respectively. The results indicate that the quadrupole moment for the first excited $ 2^{+} $ state is slightly overestimated by the theory. The same picture is obtained for the SCCM ($Q(2^{+}_{1}) = -0.62 \; \; \rm eb$) and the "jj45" shell-model ($Q(2^{+}_{1}) = -0.60 \; \; \rm eb$) calculations [21]. We note that the quadrupole moments in the pure HV and WJ limits of the BM model are identically zero.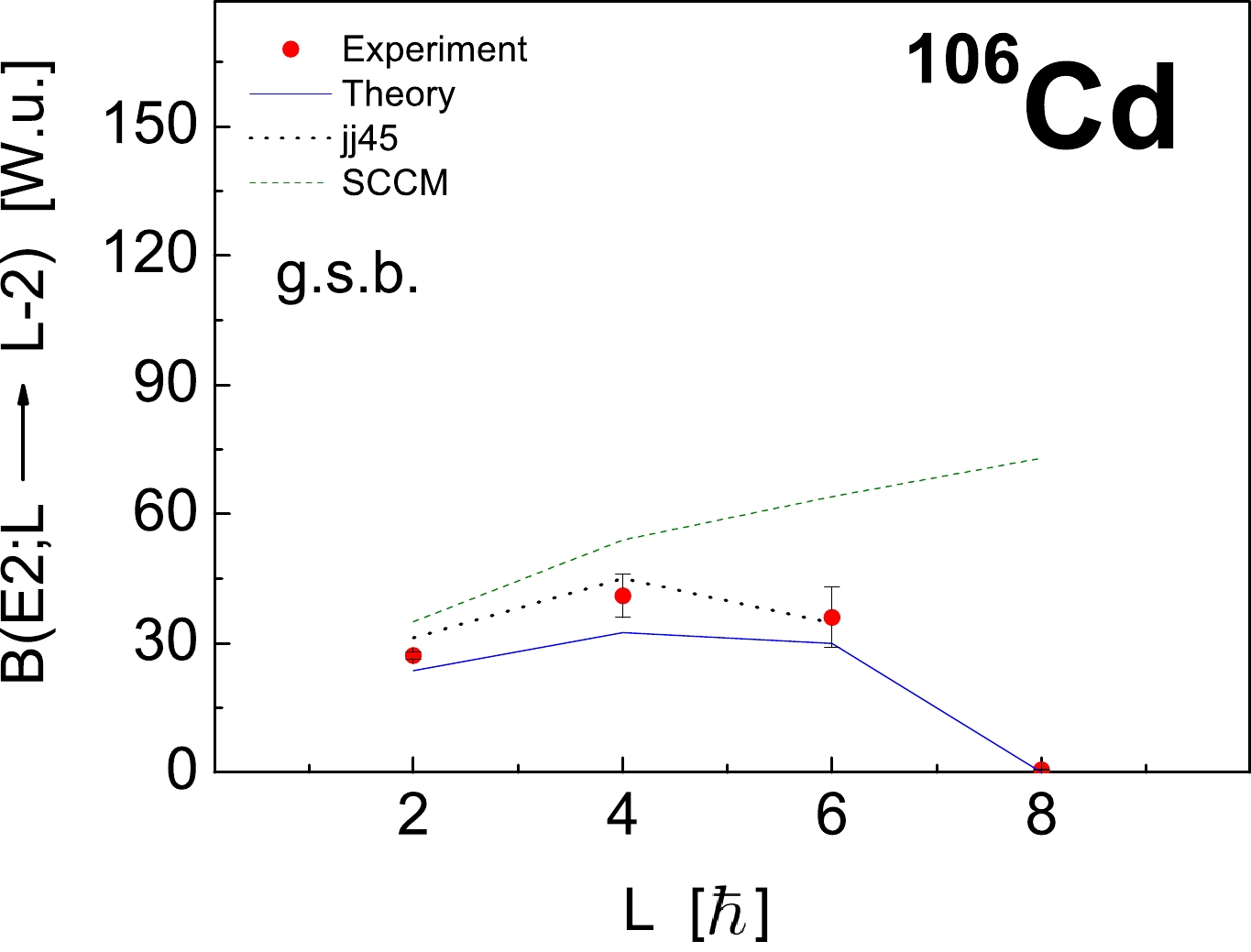

Figure 2.  (color online) Comparison of the experimental [20, 21, 85] and theoretical intraband $ B(E2) $ values in Weisskopf units between the states of the ground band in $ ^{106} $Cd. Theoretical predictions of the SCCM approach (SCCM) and the "jj45" shell-model (jj45) calculations (taken from [20] and [21], respectively) are also given.

i	f	$B(E2;L_{i}\rightarrow L_{f})_{\rm th}$	$ B(E2;L_{i}\rightarrow L_{f})_{\exp } $
$ 2_{2} $	$ 0_{1} $	$ \ \ \ \ \ \ \ 2.4 $	$ \ \ \ \ \ 2.6(5) $
$ 2_{2} $	$ 2_{1} $	$ \ \ \ \ \ \ \ 18.9 $	$ \ \ \ \ \ 13.0(2.2)[11(3)][14(3)] $
$ 3_{1} $	$ 2_{1} $	$ \ \ \ \ \ \ \ 6.9 $	$ \ \ \ \ \ 4.4(_{-1.8}^{+2.9}) $
$ 3_{1} $	$ 4_{1} $	$ \ \ \ \ \ \ \ 8.4 $	$ \ \ \ \ \ 5.2(_{-1.9}^{+3.2}) $
$ 3_{1} $	$ 2_{2} $	$ \ \ \ \ \ \ \ 42.7 $	$ \ \ \ \ \ 83(_{-43}^{+74}) $
$ 4_{2} $	$ 4_{1} $	$ \ \ \ \ \ \ \ 15.9 $	$ \ \ \ \ \ - $
$ 4_{2} $	$ 2_{2} $	$ \ \ \ \ \ \ \ \ 8 $	$ \ \ \ \ \ - $
$ 4_{2} $	$ 2_{1} $	$ \ \ \ \ \ \ \ \ 0.05 $	$ \ \ \ \ \ 0.4(_{-0.06}^{+0.08}) $
$ 0_{2} $	$ 2_{1} $	$ \ \ \ \ \ \ \ \ 2.9 $	$ \ \ \ \ \ 10.4(2.0)[14(6)] $
$ 0_{2} $	$ 2_{2} $	$ \ \ \ \ \ \ \ \ 6.2 $	$ \ \ \ \ \ 14(4) $

Table 2.  Comparison of the theoretical interband or intraband $ B(E2) $ transition probabilities (in Weisskopf units) for the lowest states of the γ and β bands in $ ^{106} $Cd with known experimental data [16, 20, 21, 47, 85, 87]. No effective charge is used in the calculation.

Figure 3 shows the $S U(3)$ decomposition of the wave functions for the collective states of the ground, γ, and β bands in $ ^{106} $Cd for different angular momentum values. As shown in the figure, we observe huge mixing and thus broken $S U(3)$ symmetry. In addition, we obtain certain K-admixtures for the states of the ground and γ bands, produced by the $ X^{a}_{4} $ term. It is a common practice to label the different excited rotational bands by the quantum number $ K \; \; - $ the projection of the total angular momentum on the intrinsic symmetry axis. In the present scheme we use the orthonormal Vergados basis [88], labeled here by q, obtained by Gram-Schmidt orthogonalization of the Elliott states [89]. Practically, to a given K band in the Elliott basis corresponds a $ q\simeq K $ band in the Vergados basis up to small K-admixtures due to the Elliott-Vergados transformation, which are negligible for comparatively large-dimensional $S U(3)$ irreducible representations or/and small angular momenta (the case of the experimentally observed β and γ bands). Despite the K-admixtures seen in Fig. 3 that the observed bands of collective states can still be characterized by the predominant $ q \simeq K $ character of the corresponding band, which is only slightly perturbed by the $ X^{a}_{4} $ operator. It is evident from Fig. 3, the reduction of the ground-state quadrupole collectivity at $ L = 8 $ is due to the change of the structure. The $ L = 8 $ state is obtained in the present calculations with a pure oblate shape, determined by the single $S U(3)$ multiplet $ (0,12) $.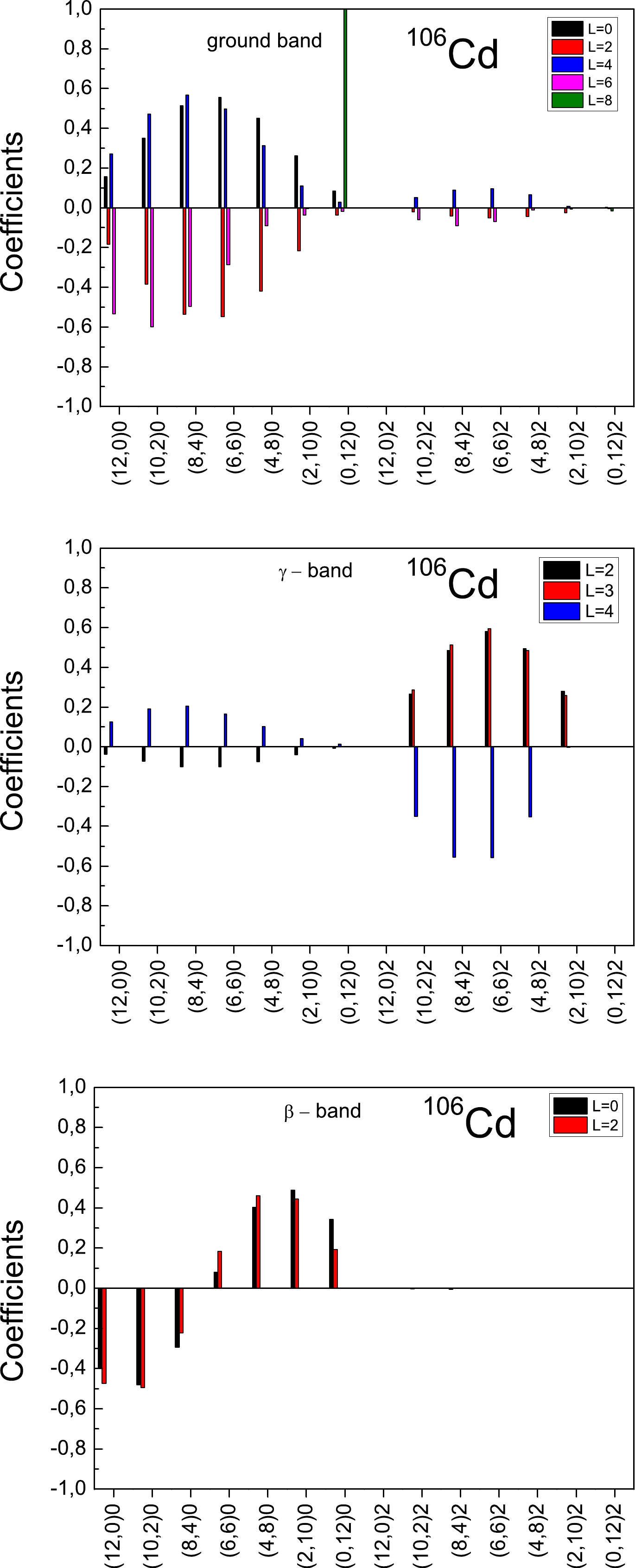

Figure 3.  (color online) $S U(3)$ decomposition of the wave functions for the states of the ground, γ and β bands in $ ^{106} $Cd for different angular momentum values. Used quantum numbers are $ (\lambda,\mu)q $.

Further, considering the correspondence $ (\lambda,\mu) \leftrightarrow (\beta,\gamma) $ [76, 90, 91] between the $S U(3)$ quantum numbers and deformation parameters of the BM model, it is clear that the mixing of different $S U(3)$ multiplets $ (\lambda,\mu) $ corresponds to the mixing of different shapes, characterized by distinct $ (\beta,\gamma) $ values. Thus, within the framework of the PNSM, one naturally obtains the low-energy shape-vibrations $ - $ in contrast to the $ S p(6,R) $ model, which only exhibits high-energy shape-vibrational degrees of freedom within its irreducible collective spaces that are associated with the giant resonance degrees of freedom. We stress that the low-energy vibrations obtained within the present proton-neutron symplectic based shell-model approach are vibrations about a deformed shape that simultaneously performs rigid-flow rotation, contrasting the traditional picture of vibrations about spherical nuclear shape in the HV limit of the original BM model. The obtained results are consistent with the picture of quantum rotor, which can not be truly rigid (with non-square-integrable delta wave functions) and should admit quantal shape fluctuations. The mixing of different $S U(3)$ irreps thus soften the rigidity of the quantum rotor. If the mixing is adiabatic (i.e. highly coherent), this type of rotational motion is sometimes referred to as a "soft-$S U(3)$ rotor" [76]. In this case, despite the larger but highly coherent $S U(3)$ mixing, the quadrupole dynamics preserves its rotor model character, although in a soft-$S U(3)$-rotor model sense in which the complete dynamics can be characterized by an average, quasi-dynamical, $S U(3)$ irrep. As shown in Fig. 3, we observe that the $S U(3)$ decomposition amplitudes are spin-dependent, i.e. $S U(3)$ is not a good quasi-dynamical symmetry [86, 92]. The latter implies that there is no adiabatic decoupling of the rotational and low-energy vibrational degrees of freedom within the PNSM for $ ^{106} $Cd, a situation expected for transitional and weakly deformed nuclei.

Additionally, considering the correspondence $ (\lambda,\mu) \leftrightarrow (\beta,\gamma) $ [76, 90, 91], it is seen from Fig. 3 that the $S U(3)$ multiplets that maximally contribute to the structure of ground (except $ L=8 $ state) and γ bands are those with large values of the triaxial γ deformation. Using the following expression for the γ deformation parameter [76]:

it can be verified that the γ deformation increases gradually from $ \gamma = 0^{0} $ for the $S U(3)$ multiplet $ (12,0) $ (a prolate shape) to the maximal triaxiality value $ \gamma = 30^{0} $ for $ (6,6) $ and then increases further to $ \gamma = 60^{0} $ for $ (0,12) $ (an oblate shape), i.e. we obtain a dynamical γ-unstable behavior consistent with the original WJ [33] model. Thus, the results reported in the present study suggest a differen interpretation of the nature of low-energy quadrupole collectivity observed experimentally in the weakly deformed atomic nuclei. It resembles the adiabatic limit of the original BM model (see, e.g., Sec 2.4 of Ref. [33]) with $ (\beta,\gamma) $ vibrations of the deformed nuclear shape, although, in contrast to the latter, the rotational and low-energy shape vibrational degrees of freedom are strongly coupled (broken adiabatic approximation). Additionally, the rotational motion within the present approach corresponds to a rigid-flow type instead of the originally proposed BM irrotational-flow dynamics.

In the present study, the microscopic structure of low-lying collective states in the weakly deformed $ ^{106} $Cd isotope was examined using the recently proposed microscopic shell-model version of the Bohr-Mottelson model within the framework of the PNSM. This nucleus has been considered in previous studies as most appropriate for studying the emergence of collectivity and deformation in nuclei, and particularly for Cd isotopes. The microscopic structure of the low-lying collective states in$ ^{106} $Cd can be useful in establishing the nature of low-energy quadrupole dynamics in Cd isotopes, which is traditionally considered more than half a century as best examples of harmonic vibrators.

The original BM model considers the atomic nucleus as a deformable liquid drop, which thereby possesses a fundamental quantized surface vibrational mode of spherical equilibrium shape given that there is no rotational degrees of freedom in this case. The nature of vibrational states can be directly associated with the form of the excitation quadrupole operator. Collective excitations corresponding to the original BM surface vibrations and irrotational-flow rotations and related to the giant resonance degrees of freedom are represented within the PNSM by symplectic raising/lowering generators (2)$ - $(3) of $S p(12,R)$ dynamical algebra. The symplectic generators in large dimensional $S p(12,R)$ representations contract [93] to the standard quadrupole phonon operators in the original BM model and the traditional phonon-scheme picture can be naturally obtained. Such irrotational-flow excitation operators are represented by the shear momentum operators of the subgroup $S L(6,R) \subset S p(12,R)$ within the framework of the PNSM and have been used to describe the irrotational-flow rotations and the high-energy vibrations in$ ^{110} $Cd, $ ^{110} $Ru [44] and $ ^{102} $Pd [45].

The original BM model for even-even nuclei admits only one shell-model irreducible representation $ - $namely the scalar representation which only produces irrotational-flow dynamics of Bohr-Mottelson type. In contrast, its microscopic version contains many shell-model representations, which are determined by the underlying fermion structure of the nucleus, and are given by the intrinsic symplectic bandhead structure of the $S p(12,R)$ irrep $ \langle \sigma\rangle $. The scalar $\langle \sigma\rangle = (0) \; \; S p(12,R)$ irreducible representation (and hence a spherical nuclear shape determined by it) is obtained only for doubly closed-shell nuclei for which only the high-energy quadrupole dynamics of BM irrotational-flow type survives. The irreducible representations of $S p(12,R)$ define irreducible collective subspaces $ \mathbb{H}^{(\omega\neq(0))} $ of the many-particle Pauli allowed Hilbert space. The subspaces possess a definite $ O(A-1) $ (or equivalent to it $S p(12,R) \; \; \langle \sigma\rangle \equiv \omega$) symmetry ω, where A denotes the number of protons and neutrons of the nucleus. In addition to ensuring the proper permutational symmetry, the non-scalar $ \langle \sigma\rangle \neq (0) $ representations of $S p(12,R)$ group significantly affect the proton-neutron quadrupole collectivity. We point out also that, in contrast to the $S p(6,R)$ model which contains only the basic rotational and high-energy vibrational degrees of freedom within its irreducible many-particle collective subspaces, the PNSM naturally contains both $ - $ the high- and low-energy vibrational degrees of freedom. The latter as demonstrated in the present work are related to the horizontal (within the $ U(6) $ shells) mixing of different $S U(3)$ multiplets. In the present application, the mixing of $S U(3)$ multiplets was only within the maximal seniority $S O(6)$ irreducible representation $ \upsilon_{0} = 12 $ of the $S p(12,R)$ bandhead. The latter as demonstrated completely governs the quadrupole dynamics in $ ^{106} $Cd, which in turn is determined by the basic rotational and low-energy vibrational degrees of freedom. Hence, the Pauli allowed shell-model representations of $S p(12,R)$ dynamical group support the statement of Ref. [21] (and also of [17]) that a direct transition from closed-shell to rotational nuclei takes place, particularly for Cd chain of isotopes. This is also in agreement with the recent Monte Carlo shell model (MCSM) results for the Sn [94] and Ni isotopes [95−97].

We demonstrated that the low-lying collective states in $ ^{106} $Cd can be described as a result of the coupling of the basic rotational and low-energy shape vibrational degrees of freedom. This type of complex rotation-vibrational quadrupole dynamics is attributed to the (horizontal) mixing of different $S U(3)$ multiplets within the maximal seniority $S O(6)$ irreducible representation $ \upsilon_{0} = 12 $. We note that the latter approach is very close in spirit to the modern state-of-the-art beyond-mean-field (BMF) calculations [20] in which the self-consistent particle-number and angular-momentum projected Hartree-Fock-Bogoliubov (HFB) intrinsic states with different quadrupole (axial and nonaxial) deformations are further mixed within the generator coordinate method. However, within the PNSM, the mixing of various $S U(3)$ states of different quadrupole deformations belonging to a single $S O(6)$ irrep is treated in the laboratory system without the need for performing a particle-number and angular-momentum restoration. The difference from the traditional WJ γ-unstable rotor interpretation is that, in the present approach, the quadrupole dynamics corresponds to the rigid-flow type instead of the irrotational-flow one assumed in the WJ limit of the BM model [1, 2, 33, 44, 45]; both types exhibit the γ-instability as a characteristic feature. As previously mentioned, the difference is easily understood by looking at the form of the excitation quadrupole operators in both traditional WJ and present PNSM approaches$ - $ instead of solely examining the type of γ-band staggering. Thus, the results obtained in the present study suggest a different interpretation of the fundamental question regarding the nature of low-energy quadrupole dynamics in weakly deformed nuclei and its emergence from the shell-model perspective.

A good description of the excitation energies of the lowest ground, γ and β bands or quasibands experimentally observed in $ ^{106} $Cd was obtained without the involvement of an adjustable kinetic energy term. The γ degrees of freedom are shown to play a crucial role in the description of spectroscopy of this nucleus. A modified $S U(3)$-preserving high-order interaction is used to produce a γ-unstable type of odd-even staggering, which is observed experimentally between the states of the quasi-γ band. The present approach allows to describe the observed intraband and interband quadrupole collectivity in $ ^{106} $Cd. The results support the interpretation of quadrupole dynamics of rigid-flow type and the arrangement of the low-lying excited levels in $ ^{106} $Cd into rotational quasibands [20, 21] with strong mixing of different intrinsic $S U(3)$ states/shapes. Similar calculations within the framework of the microscopic shell-model version of the BM model can be performed for the other Cd isotopes and for some of the neighboring Pd, Ru, and Mo weakly deformed nuclei exhibiting a rigid-flow low-energy quadrupole dynamics in their spectra. The corresponding results will be reported elsewhere.