-
The remarkable success of the Standard Model (SM) in accurately describing all current experimental data suggests that the search for deviations from the SM should primarily focus on investigating subtle effects arising from higher energy scales or low-energy observables [1]. Normally, the flavor changing neutral current (FCNC) transitions in the SM are highly suppressed by the Glashow-Iliopoulos-Maiani (GIM) mechanism [2]. This GIM suppression is more effective in the charm sector than on the down-type quarks in the bottom and strange sectors, and is responsible for the relatively small size of charm mixing and
$ C P $ violation in the charm system [3−5]. Thus, the FCNC processes of D-meson decays into charged lepton pairs are always totally overshadowed by long-distance contributions [6, 7]. Nonetheless, when the FCNC process with D-meson decays into final states involving dineutrinos, e.g.,$ D^+\to \pi^+ \nu \bar \nu $ , the short-distance contributions from Z-penguin and box diagrams can become dominant, while the long-distance contributions become insignificant, resulting in a branching fraction at the level of$ 10^{-16} $ in the SM. [8]. Consequently, this FCNC process can provide a unique and clean probe to study the$ C P $ violation in the charm sector [9] and search for new physics beyond the SM [10].On the experimental side, the LHCb Collaboration reported that the breaking of lepton universality appears in bottom-quark FCNC decays to charged dielectrons and dimuons with a significance of 3.1σ [11], implying the possible presence of new physics contributions in the lepton sector [12]. Moreover, in 2021, the BESIII Collaboration explored the FCNC decay process
$ D^0 \to \pi^0 \nu \bar\nu $ and reported that an upper limit of the branching fraction was expected to be$ 2.1\times 10^{-4} $ at 90% confidence level [13]. This value is much larger than the SM prediction from both long and short distances. Non-standard neutrino interactions (NSIs) [14−24], described by four fermion operators of$ (\bar\nu_\alpha\gamma\nu_\beta)(\bar f\gamma f) $ , can narrow the gap between the experimental and SM predictions. It has been reported that the NSIs could be compatible with the oscillation effects along with some new features in various neutrino searches [25−31]. Some studies have also pointed out that the NSIs can well match both the oscillation effects and the new features in neutrino searches [32−38]. Therefore, the branching fraction of$ D^+\to \pi^+ \nu\bar\nu $ is expected to be in the order of$ 10^{-8} $ under the scheme of NSIs. This scheme allows decay processes$ D^+\to \pi^+ \nu \bar{\nu} $ and$ \bar D^0 \to \pi^+ e \bar{\nu}_e $ to establish a direct connection that enables a particular approach, used in this paper, to calculate related physical observables.The
$ D\to \pi $ transition form factors (TFFs) are key components for studying the semileptonic decays$ \bar D^0\to \pi^+ e \bar\nu_e $ . Previous studies addressed$ D\to \pi $ TFFs both experimentally and theoretically. Experimentally, the Belle [39], BESIII [40], Babar [41], and CLEO [42] Collaborations have measured the values of the vector TFFs at the large recoil region$ f_+^{D\to\pi} (0) $ . The Lattice QCD also yields this value [43]. Theoretically, the$ D\to \pi $ TFFs can be calculated using the QCD light-cone sum rule (LCSR) [44, 45], light-front quark model (LFQM) [46], combined heavy mesons, and chiral Lagrangian theory HMχT [47]. The LCSR approach primarily extends the light cone framework, which is expected to be applicable for small and intermediate squared momentum transfers. By extrapolating the TFFs using a suitable series expansion, one can obtain the vector and scalar TFFs across the entire physical region. Subsequently, a comparison with other approaches can be made. In this paper, we predominantly employ the LCSR method to compute the$ D\to \pi $ TFFs.Furthermore, the pion distribution amplitudes (DAs) with different twist structures are key long-distance non-perturbative elements in
$ D\to\pi $ TFFs LCSR expressions describing either contributions of the transverse motion of quarks (antiquarks) in the leading-twist components or contributions of higher Fock states with additional gluons and/or quark-antiquark pairs. Considering the contributions for each twist DA, the leading-twist and twist-3 DAs are dominant. The higher twist DAs contributions are notably suppressed by the energy scale and Borel parameters [48, 49]. Regarding the pion leading-twist DA, various theories can be employed to calculate it, such as the Lattice QCD (LQCD) [50], DS model [51], and QCD/AdS model [52]. The first two Gegenbauer moments are extracted by fitting the LCSR calculation of the pion form factor from experimental data points [53]. For the pion twist-3 DAs, the light-front quark model (LFQM) [54] and QCDSR [55−57] approach can be employed. To obtain a better ending-point behavior of the pion twist-2, 3 DAs, we will calculate the ξ-moments within the QCDSR approach and reconstruct the light-cone harmonic oscillator models.The rest of the paper is organized as follows. In Sec. II, we present the NSIs and branching fraction for
$ D^+\to \pi^+\nu_\ell \bar\nu_{\ell'} $ ,$ D\to \pi $ TFFs, pion twist-2 and twist-3 LCHO model, and ξ-moment within the QCDSR approach. In Sec. III, we conduct a detailed numerical and phenomenological analysis. Finally, a brief summary is provided in Sec. IV. -
According to the approach based on NSIs , one can start with the effective Lagrangian, which has the following form:
$ {\cal L}^{{\rm{NSI}}}_{{\rm{eff}}} = - 2\sqrt{2} G_F \varepsilon^{fP}_{\ell \ell'} (\bar\nu_\ell \gamma_\mu L \nu_{\ell'} ) (\bar f \gamma^{\mu} P f ) , $

(1) where
$ \ell $ and$ \ell' $ denote the light neutrino flavors; f denotes the charged lepton or quark;$ P=(L, R) $ with$ L(R)= (1\mp \gamma_5)/2 $ , which represents the left or right operators; and$ \varepsilon^{fP}_{\ell \ell'} $ is the parameter for NSIs that encodes information about dynamics. The effective Hamiltonian governs the decay process$ D\to \pi \nu\bar\nu $ owing to the$ Z^0 $ -penguin and box-type contributions; it can be expressed as follows: [58]$ \begin{aligned}[b] {\cal H}_{{\rm{eff}}} =\;& \frac{G_F}{\sqrt 2} \frac{\alpha}{2\pi\sin^2\theta_W} \sum\limits_{\ell = e,\mu, \tau}[V_{cs}^*V_{cd} X_{{\rm{NL}}}^\ell + V_{ts}^*V_{td} X(x_t)] \\ &\times (\bar s d)_{V-A}(\bar\nu_\ell \nu_\ell)_{V-A}. \end{aligned} $

(2) In Eq. (2),
$ X_{{\rm{NL}}}^\ell $ is the charm quark contribution and$ X(x_t) $ represents the loop integral of the top quark contribution, i.e.,$ X(x_t) = \eta_X x_t /8 \times [(x_t+2)/(x_t- 1) + (3x_t- 6)/(x_t- 1)^2 \ln x_t] $ with$ x_t = m_t^2/m_W^2 $ ; we apply that$ (\bar f f')_{V-A} = \bar f \gamma_\mu (1- \gamma_5)f' $ . The NSIs in Eq. (1) can induce the transition$ c\to u\nu_\ell \bar\nu_{\ell'} $ at one-loop level with a Feynman diagram, yielding [58]$ \begin{aligned}[b]H^{{\rm{NSI}}}_{c \to u\nu_\ell\bar\nu_{\ell'}}=\;& \frac{G_F}{\sqrt{2}} \left( \frac{\alpha_{{\rm{em}}}}{4\pi \sin^2\theta_W} V_{cd} V^{*}_{ud} \varepsilon^{dL}_{\ell \ell'} \ln \frac{\Lambda}{m_W} \right) \\ &\times (\bar\nu_\ell \nu_{\ell'})_{V-A} (\bar c u)_{V-A}. \end{aligned} $

(3) In Eq. (3),
$ \sin ^2{\theta _W} $ is the Weinberg angle, and$ V_{cd}= 0.225 $ and$ V_{ud}^{*}=0.97370 $ are the CKM matrix elements. The processes are dominated by short-distance contributions; long-distance contributions are almost$ 10^{-3} $ less than short-distance contributions. The up-type quark in the loop will increase the branching fraction of these reactions. Accordingly, the branching fraction for$ D^+ \to \pi^+ \bar\nu_\ell\nu_{\ell'} $ can be expressed as$ \begin{aligned}[b] {\cal B}{(D^+ \to \pi^+ {\nu_\ell }{\bar\nu _{\ell '}})_{{{\rm{NSI}}}}} =\;& \bigg|V_{ud}^* \frac{{{\alpha _{{\rm{em}}}}}}{{4\pi {{\sin }^2}{\theta _W}}}\varepsilon _{\ell {\ell '}}^{dL}\ln \frac{\Lambda }{{{m_W}}}\bigg|^2 \\ &\times {\cal B}(\bar D^0\to \pi^+ e \bar\nu_{e}) \end{aligned} $

(4) To study relevant physical observables, we adopt the explicit expression for the full differential decay width distribution of
$ D\to \pi \ell \bar\nu_\ell $ [59, 60]:$ \begin{aligned}[b] \frac{{\rm d}^2\Gamma(D\to \pi \ell \bar\nu_\ell)}{{\rm d}\cos\theta {\rm d} q^2} =\;& a_{\theta_\ell}(q^2) + b_{\theta_\ell}(q^2) \cos\theta_\ell \\ & + c_{\theta_\ell}(q^2) \cos^2\theta_\ell \end{aligned} $

(5) where the three
$ q^{2} $ -dependent angular coefficient functions have the following expressions:$ \begin{aligned}[b] a_{\theta_\ell}(q^2) =\;& {\cal N}_{{\rm{ew}}} \lambda^{3/2}\bigg(1 - \frac{m_\ell^2}{q^2}\bigg)^2 \bigg[|f^{D\to \pi}_+(q^2)|^2 + \frac{m_\ell^2}{q^2 \lambda} \\ &\times \bigg( 1- { m_\pi^2 \over m_D^2 } \bigg)^2 |f^{D\to \pi}_0 (q^2)|^2\bigg], \end{aligned} $

(6) $ \begin{aligned}[b] b_{\theta_\ell}(q^2)=\;& 2{\cal N}_{{\rm{ew}}} \lambda \bigg(1 - {m_\ell^2 \over q^2}\bigg)^2 {m_\ell^2 \over q^2}\bigg( 1-{m_\pi^2\over m_D^2 } \bigg) \\ &\times {{\rm{Re}}} \left[ f^{D\to \pi}_+(q^2) f^{D\to \pi\ast}_0(q^2) \right], \end{aligned} $

(7) $ c_{\theta_\ell}(q^2)=-{\cal N}_{{\rm{ew}}} \lambda^{3/2} \bigg( 1 - {m_\ell^2 \over q^2} \bigg)^3 |f^{D\to \pi}_+(q^2) |^2. $

(8) From these expressions, we have that the electro-weak normalized coefficients can be expressed as
${\cal N}_{{\rm{ew}}} = {G_F^2 |V_{cd}|^2 m_D^3 }/(256\pi^3)$ and$\lambda(a, b, c) \equiv a^2 + b^2 + c^2 - 2 (ab + ac + bc)$ . For convenience, we use the following shorthand notation:$ \lambda \equiv \lambda (1, m_\pi^2/m_D^2, q^2/m_D^2) $ . In addition, the helicity angle$ \theta_\ell $ is defined as the angle between the$ \ell^- $ direction of flight and the final-state meson momentum in the dilepton rest frame. When ignoring the lepton mass, that is,$ m_\ell = 0 $ , we obtain two interesting algebra relations for the angular functions:$ b_{\theta_\ell}(q^2) =0 $ and$a_{\theta_\ell}(q^2) + c_{\theta_\ell}(q^2) =0$ .The analytical expressions for
$ D\to\pi $ TFFs are calculated next. We use the standard correlator as the starting point and apply an operator product expansion (OPE) close to the light cone near zero. The vacuum-to-pion correlation function used to obtain the LCSR for the form factors of the$ D\to \pi $ transition is defined as follows:$ \Pi_\mu(p,q)={\rm i}\int {\rm d}^4x {\rm e}^{{\rm i} q\cdot x}\langle \pi^+(p)|T\{j_\mu(x), j^\dagger_5(0)\}|0\rangle, $

(9) with the two currents given by
$ j_\mu(x) = \bar u(x)\gamma_\mu c(x) $ and$j^\dagger_5(0) = m_c\bar{c}(0){\rm i}\gamma_5 d(0)$ . After introducing the c-quark propagators into the correlation function and applying the OPE, we obtain the expression for$ D\to\pi $ TFFs. Meanwhile, after inserting hadronic states into the correlator given by Eq. (9), one can isolate the ground-state D-meson contributions using dispersion relations for the two invariant amplitudes:$ \begin{aligned}[b]\Pi^{{\rm{H}}}(p,q) =\;&\frac{2f^{D\to \pi}_+(q^2) m_D^2 f_{D}}{m_c(m_D^2 -(p+q)^2)}+\int_{s_0}^\infty {\rm d}s\frac{\rho(s)}{s-(p+q)^2} \\ &+\text{subtractions}. \end{aligned} $

(10) $ \begin{aligned}[b] \widetilde{\Pi}^{{\rm{H}}}(p,q) =\;&\frac{\tilde f^{D\to \pi}(q^2) m_D^2 f_D}{m_c(m_D^2 -(p+q)^2)}+\int_{\tilde s_0}^\infty {\rm d}s\frac{\tilde\rho(s)}{s-(p+q)^2} \\ &+\text{subtractions}. \end{aligned} $

(11) The
$ D\to \pi $ TFFs entering the residues of the D-meson pole in Eq. (11) are defined as$\langle\pi^+(p)|\bar{u} \gamma_\mu c | \bar D(p+q)\rangle = 2f^{D\to \pi}_+(q^2)p_\mu +\tilde f^{D\to \pi}q_\mu$ ,$\tilde f^{D\to \pi}(q^2) = f^{D\to \pi}_+(q^2) + f^{D\to \pi}_{-}(q^2)$ . Meanwhile,$f_D = \langle D |m_c\bar d {\rm i}\gamma_5 d |0 \rangle/ m_D^2$ is the D-meson decay constant. The effective threshold parameters$ s_0 $ and$ \tilde s_0 $ are introduced with the help of the quark-hadron duality. After making the Borel transformation to the variable$ (p+q)^2 $ , the sum rules for$ D\to \pi $ TFFs can be obtained. The LCSR for the TFFs$ f^{D\to \pi}_+(q^2) $ and$ \tilde f^{D\to \pi}(q^2) $ can be expressed as follows:$ \begin{aligned}[b] f^{D\to \pi}_+(q^2)=\frac{{\rm e}^{m_D^2/M^2}}{2m_D^2 f_D}\Bigg[F_0(q^2,M^2,s_0) +\frac{\alpha_s C_F}{4\pi} F_1(q^2,M^2,s_0)\Bigg], \end{aligned} $

(12) $ \begin{aligned}[b] \tilde f^{D\to \pi}(q^2) = \frac{{\rm e}^{m_D^2/M^2}}{m_D^2 f_D}\Bigg[\tilde F_0(q^2,M^2,s_0) +\frac{\alpha_s C_F}{4\pi} \tilde F_1(q^2,M^2,s_0)\Bigg], \end{aligned} $

(13) where the leading-order (LO) expression for
$ F_0(q^2,M^2,s_0) $ and$ \tilde F_0(q^2,M^2,s_0) $ can be expressed as$ \begin{aligned}[b] F_0(q^2,M^2,s_0)=\;& m_c^2 f_\pi \int_{u_0}^1 {\rm d}u {\rm e}^{-\frac{m_c^2-\bar{u}q^2}{uM^2}}\bigg\{\frac{\phi_{2;\pi} (u,\mu)}u + \frac{\mu_\pi}{m_c} \Bigg[\phi_{3;\pi}^p(u) + \bigg(\frac1{3u}-\frac{m_c^2+q^2}{6(m_c^2-q^2)} \frac {\rm d}{{\rm d}u} \bigg) \times \phi_{3;\pi}^\sigma(u,\mu) \bigg]-2\bigg(\frac{f_{3;\pi}}{m_c f_\pi}\bigg) \frac{I_{3;\pi}(u)}{u} \\&+\frac1{m_c^2-q^2}\bigg[-\frac{m_c^2 u}{4(m_c^2-q^2)} \frac{{\rm d}^2 \phi_{4;\pi}(u)} {{\rm d}u^2} + u\psi_{4;\pi}(u)+ \int_0^u {\rm d}v \psi_{4;\pi}(v)-I_{4;\pi}(u)\bigg]\bigg\} \end{aligned} $ 
(14) $ \tilde F_0(q^2,M^2,s_0)=m_c^2 f_\pi \int_{u_0}^1 {\rm d}u {\rm e}^{-\frac{m_c^2-\bar{u}q^2}{uM^2}}\bigg\{\frac{\mu_\pi}{m_c}\bigg(\frac{\phi_{3;\pi}^p(u)}{u}+ \frac1{6u} \frac{{\rm d}\phi_{3;\pi}^\sigma(u)}{{\rm d}u}\bigg) + \frac1{m_b^2 - q^2} \psi_{4;\pi}(u)\bigg\}. $

(15) where
$ \mu_\pi={m_\pi^2}/{(m_u+m_d)} $ ,$ u_0=(m_c^2-q^2)/(s_0-q^2) $ [61];$ f_D $ and$ f_\pi $ are the decay constants of D- and π-mesons;$ m_c $ is the charm quark mass; and$ \phi_{2;\pi}(u,\mu) $ and$ \phi_{3;\pi}^{(p,\sigma)}(u,\mu) $ are the pionic twist-2, 3 DAs, respectively. The next-leading-order (NLO) correction expressions$ F_1(q^2,M^2,s_0) $ and$ \tilde F_1(q^2,M^2,s_0) $ mainly come from Refs. [62, 63].Additionally, concerning the different pion twist DAs, especially twist-2 and twist-3 DAs, in processes related to the typical scale, we can make use of the Brodsky-Huang-Lepage (BHL) description [64] and the light-cone harmonic oscillator model (LCHO model) of the pion twist-2 and twist-3 wave function (WF) [65, 66]. The WF for the twist-2 DA can be expressed as
$ \Psi_{2;\pi}(x, {k}_\bot) = \sum_{\lambda_1\lambda_2} \chi_{2;\pi}^{\lambda_1\lambda_2}(x, {k}_\bot) \Psi^R_{2;\pi}(x, {k}_\bot) $ , where$ {k}_\bot $ is the pionic transverse momentum, and$ \lambda_1 $ and$ \lambda_2 $ are the helicities of the two constituent quarks.$ \chi_{2;\pi}^{\lambda_1\lambda_2}(x, {k}_\bot) $ replaces the spin-space WF based on the Wigner-Melosh rotation, which exhibits different performances for different values of$ \lambda_1\lambda_2 $ (see Refs. [67−69]). Note also that$\Psi^R_{2;\pi}(x, {k}_\bot) = A_{2;\pi} \varphi_{2;\pi}(x) \exp [-( {k}^2_\bot + m_q^2)/(8\beta_{2;\pi}^2 x\bar x)]$ , where$\bar{x} = (1-x)$ ,$ A_{2;\pi} $ is the normalization constant,$ {k}_\bot $ is the dependence part of the spatial WF$ \Psi^R_{2;\pi}(x, {k}_\bot) $ , which comes from the quark model of the pion and confirms the transverse distribution of the WF through the harmonious parameter$ \beta_{2;\pi} $ . In this paper, we set$ m_q =250\; {{\rm{MeV}}} $ . Let us combine the pionic leading-twist DA and WF through the relationship:$ \phi_{2;\pi}(x,\mu) =\frac{2\sqrt{6}}{16\pi^3f_\pi} \int_{| {\bf{k}}_\bot |^2 \leq \mu^2} {\rm d}^2{\bf{k}}_\bot \Psi_{2;\pi}(x,{\bf{k}}_\bot), $

(16) and taking the spin-space and spatial WFs into Eq. (16), we obtain the full LCHO expression for the pion leading-twist DA:
$ \begin{aligned}[b] \phi_{2;\pi}(x,\mu) =\;& \frac{\sqrt{3} A_{2;\pi} m_q \beta_{2;\pi}}{2\pi^{3/2}f_\pi} \sqrt{x\bar x} \varphi_{2;\pi}(x) \\ &\times \left\{ {\rm{Erf}}\left[ \sqrt{\frac{m_q^2 + \mu^2}{8\beta_{2;\pi}^2 x\bar x}} \right]- {\rm{Erf}}\left[ \sqrt{\frac{m_q^2}{8\beta_{2;\pi}^2 x\bar x}} \right] \right\}. \end{aligned} $

(17) In Eq. (17),
$ \varphi_{2;\pi}(x) = [x\bar x]^{\alpha_{2;\pi}} [1 + \hat{a}^{2;\pi}_2 C_2^{3/2}(\xi)] $ , with$\xi = (2x-1)$ ;${{\rm{Erf}}}(x) = 2\int^x_0 {\rm e}^{-t^2} {\rm d}x/{\sqrt{\pi}}$ is the error function [70];$ \hat{a}^{2;\pi}_2 $ is the second-order Gegenbauer moment; and the parameters$ \alpha_{2;\pi} $ and$ \hat{a}^{2;\pi}_2 $ can be determined by fitting the moments$ \langle\xi^n_{2;\pi}\rangle|_\mu $ directly through the method of least squares.The two pion twist-3 DAs can also be related to its WF as follows:
$ \phi_{3;\pi}^{p,\sigma}(x,\mu) = \frac{1}{16\pi^3} \int_{| {\bf{k}}_\bot |^2 \leq \mu^2} {\rm d}^2{\bf{k}}_\bot \Psi_{3;\pi}^{p,\sigma}(x,{\bf{k}}_\bot), $

(18) where we have applied the LCHO model for the pion twist-3 WF. The basic idea here is that the longitudinal behavior is dominated by the first two Gegenbauer moments and transverse momentum dependence in the BHL prescription. In this approach, the twist-3 DAs will have a better end-point behavior than the asymptotic one. In particular, we found that the transverse momentum dependence is just on the exponential form of the off-shell energy of the constituent quarks, which agrees with Brodsky and Teramond's holographic model obtained by using the Anti-de Sitter (AdS) conformal field theory correspondence [71−73]. A detailed discussion is provided in a previous study of ours [74]. Thus, we obtain
$ \begin{aligned}[b] \phi_{3;\pi}^{p,\sigma}(x,\mu)=\;&\frac{A_{3;\pi}^{p,\sigma} (\beta_{3;\pi}^{p,\sigma})^2}{2\pi^2} \varphi_{3;\pi}^{p,\sigma}(x) {\rm{exp}} \left[ -\frac{m_q^2}{8 (\beta_{3;\pi}^{p,\sigma})^2 x\bar x} \right] \\ &\times \left\{ 1 - {\rm{exp}} \left[ -\frac{\mu^2}{8 (\beta_{3;\pi}^{p,\sigma})^2 x\bar x}\right] \right\}, \end{aligned} $

(19) where
$ \varphi_{3;\pi}^p(x) = 1+B_{3;\pi}^p C^{1/2}_2(\xi) + C_{3;\pi}^p C^{1/2}_4(\xi) $ and$ \varphi_{3;\pi}^\sigma(x) = 1+B_{3;\pi}^\sigma C^{3/2}_2(\xi) + C_{3;\pi}^\sigma C^{3/2}_4(\xi) $ . Next, we address the four free parameters in the LCHO model of pion twist-2 and twist-3 DAs. The first constraint is that the twist-2, 3 DAs must be normalized to 1. The second one is that the average value of the squared transverse momentum is assumed to be$ (\langle{\bf k}_\bot^2\rangle_{2;\pi})^{1/2} = (\langle{\bf k}_\bot^2\rangle_{3;\pi}^{p,\sigma})^{1/2} = 0.35\; {{\rm{GeV}}} $ [75]. Then, to determine the remaining two parameters, we need to calculate the pion DA ξ-moments, which are defined as follows:$ \langle\xi^n_{2;\pi}\rangle|_\mu = \int_0^1 {\rm d}x (2x-1)^n \phi_{2;\pi} (x,\mu), $

(20) $ \langle \xi_{3;\pi}^{(p,\sigma),n}\rangle|_\mu = \int_0^1 {\rm d}x (2x-1)^n \phi_{3;\pi}^{(p,\sigma)}(x,\mu). $

(21) Next, we calculate the moments of the pion twist-2, 3 DAs using the QCD sum rule method.
To derive the ξ-moments of the π-meson twist-2 and twist-3 DAs
$ \phi_{2;\pi}(x) $ and$ \phi_{3;\pi}^{p,\sigma}(x) $ , we use the following correlation functions:$ \begin{aligned}[b] \Pi_{2;\pi} (z,q) &= {\rm i} \int {\rm d}^4 x {\rm e}^{{\rm i}q \cdot x} \langle 0|{{\rm{ T}}} \{J_{2;\pi}^n(x), J_{2;\pi}^{0\dagger} (0) \}| 0\rangle, \\ \Pi_{3;\pi}^{p,\sigma} (z,q) &= -{\rm i} \int {\rm d}^{4} x {\rm e}^{{\rm i}q \cdot x} \langle 0|{{\rm{ T}}} \{J_{3;\pi}^{(p,\sigma),n}(x), J_5^{0\dagger}(0) \}| 0\rangle, \end{aligned} $

(22) where the twist-2 DA currents are
$J_{2;\pi}^n (x) = $ $ \bar{d}(x) / {z}\gamma_{5} ({\rm i} z \cdot \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {D})^{n} u(x)$ and$ J_{2;\pi}^0 (x) = \bar{d}(x) / {z}\gamma_{5} u(x) $ . The twist-3 DA currents are$J_{3;\pi}^{p,n} (x) = \bar{d}(x) \gamma_{5} ({\rm i} z \cdot \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {D})^{n} u(x)$ ,$J_{3;\pi}^{\sigma,n}(x) = \bar{d}(x) \sigma_{\mu\nu} \gamma_5 ({\rm i} z \cdot \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {D})^{n+1} u(x)$ , and$ J_5^{0\dagger}(0) = \bar{u}(0) \gamma_{5} d(0) $ . The correction functions can also be translated into$ \begin{aligned}[b] &\Pi_{2;\pi} (p,q) = (z \cdot q)^{n+2} I^{(n,0)}_{2;\pi} (q^2), \\ &\Pi_{3;\pi}^{p} (p,q) = (z \cdot q)^{n} I^{p,(n,0)}_{3;\pi} (q^2), \\ &\Pi_{3;\pi}^\sigma (p,q) = - {\rm i} (q_\mu z_\nu - q_\nu z_\mu) (z \cdot q)^n I^{\sigma, (n,0)}_{3;\pi} (q^2). \end{aligned} $

(23) After adopting the traditional QCD sum rule approach, we obtain the following analytical expressions for the ξ-moments for twist-2 and twist-3 pion DAs:
$ \begin{aligned}[b]\\[-15pt] \frac{\langle\xi^n_{2;\pi}\rangle|_\mu \langle \xi^0_{2;\pi}\rangle|_\mu f_{\pi}^2}{M^2 {\rm e}^{m_\pi^2/M^2}} =\;& \frac{3}{4\pi^2(n+1)(n+3)} \Big( 1 - {\rm e}^{-s_{2;\pi}/M^2} \Big) + \frac{(m_d + m_u) \langle\bar qq \rangle }{(M^2)^2} + \frac{\langle \alpha_sG^2\rangle }{(M^2)^2} \frac{1 + n\theta(n-2)}{12\pi(n+1)} \\[1ex] &- \frac{(m_d + m_u)\langle g_s\bar q\sigma TGq \rangle }{(M^2)^3}\frac{8n+1}{18} + \frac{\langle g_s\bar qq\rangle ^2}{(M^2)^3} \frac{4(2n+1)}{81} - \frac{\langle g_s^3fG^3\rangle }{(M^2)^3}\frac{n \theta(n-2)}{48\pi^2} \\[1ex] &+ \frac{\langle g_s^2\bar qq\rangle ^2}{(M^2)^3} \frac{2+\kappa^2}{486\pi^2} \Big\{-2(51n+ 25)\Big(-\ln \frac{M^2}{\mu^2} \Big) + 3(17n+35) + \theta(n-2)\Big[ 2n \\ &\times\Big( -\ln \frac{M^2}{\mu^2} \Big) + \frac{49n^2 +100n+56}n - 25(2n+1)\Big[ \psi\Big(\frac{n+1}{2}\Big) - \psi\Big(\frac{n}{2}\Big) + \ln4 \Big] \Big]\Big\}, \end{aligned} $ 
(24) $ \begin{aligned}[b] \frac{ \langle \xi_{3;\pi}^{p,n}\rangle|_\mu \langle \xi_{3;\pi}^{p,0} \rangle|_\mu f^2_\pi \mu_\pi^2}{M^4 {\rm e}^{m^2_\pi / M^2}} =\;&\frac{3}{8 \pi^2} \frac{1}{2n+1}\bigg [ 1 - \bigg( 1 + \frac{s^p_{3;\pi}}{M^2} \bigg) {\rm e}^{-s_{3;\pi}^{p} / M^{2}} \bigg] + \frac{2n-1}{2}\frac{(m_u + m_d) \langle \bar q q \rangle }{M^4} \\ & + \frac{2n+3}{24\pi} \frac{ \langle \alpha_s G^2 \rangle}{M^4} + \frac{16\pi}{81} [21+8n(n+1)] \frac{\langle \sqrt{\alpha_s} \bar q q \rangle^2}{M^6}, \end{aligned} $

(25) $ \begin{aligned}[b] \frac{\langle \xi_{3;\pi}^{\sigma,n}\rangle|_\mu \langle \xi_{3;\pi}^{p,0} \rangle|_\mu f^2_\pi \mu_\pi^2}{M^4 {\rm e}^{m^2_{\pi} / M^2}} =\;& \frac{3}{2n+1}\bigg\{ \frac{3}{8 \pi^2} \frac{1}{2n+3}\bigg[ 1 -\bigg ( 1 + \frac{s^{\sigma}_{3;\pi}}{M^2}\bigg) {\rm e}^{-s^{\sigma}_{3;\pi} / M^{2}} \bigg]+ \frac{2n+1}{2}\frac{(m_u + m_d) \langle \bar q q \rangle}{M^4} \\ & + \frac{2n+1}{24\pi} \frac{ \langle\alpha_s G^2 \rangle}{M^4} + \frac{16\pi}{81} (8n^2 - 2) \frac{\langle \sqrt{\alpha_s} \bar q q \rangle^2}{M^6} \bigg\}. \end{aligned} $

(26) When setting the
$ 0 $ -th order ξ-moment normalized to be 1 directly, which is adopted by many QCD sum rules, there will be an extra deviation to predict$ \langle\xi^n_{2;\pi}\rangle|_\mu $ and$ \langle \xi_{3;\pi}^{(p,\sigma),n}\rangle|_\mu $ . Thus, we keep$ \langle\xi^0_{2;\pi}\rangle|_\mu $ and$ \langle \xi_{3;\pi}^{(p,\sigma),0}\rangle|_\mu $ in Eqs. (24)−(26). The derivation of Eqs. (24)−(26) is detailed in previous studies of ours [70, 74]. -
To perform phenomenological analysis, the following input parameters are required. The pole mass of c-quark is
$ m_c=1.50\pm0.05\; {{\rm{GeV}}} $ [76]. The initial and final meson masses are$ m_D=1869.66\; {{\rm{MeV}}} $ and$m_\pi = 139.57039 \pm 0.00017\; {{\rm{MeV}}}$ , while the pion decay constant is$ f_\pi = 130.2\pm1.2\; {{\rm{MeV}}} $ , according to the Particle Data Group (PDG) [77]. The D-meson decay constant is$ f_D = 0.163^{+0.017}_{-0.021}\; {{\rm{GeV}}} $ . The values of non-perturbative vacuum condensates up to six-dimension are as follows [78−80]:$ \begin{aligned}[b] &\langle \alpha_s G^2 \rangle = 0.038\pm0.011\; {{\rm{GeV}}}^4, \\ &\langle g_s^3fG^3\rangle = 0.045\pm0.007\; {{\rm{GeV}}}^6, \\ &\langle g_s\bar qq\rangle ^2 = (2.082_{-0.697}^{+0.734})\times 10^{-3} \; {{\rm{GeV}}}^6, \\ &\langle g_s^2\bar qq\rangle ^2 = (7.420_{-2.483}^{+2.614})\times 10^{-3}\; {{\rm{GeV}}}^6, \\ &\langle q\bar q\rangle = (-2.417_{-0.114}^{+0.227})\times 10^{-2}\; {{\rm{GeV}}}^3, \\ &\sum {\langle g_s^2\bar qq\rangle ^2} = (1.891_{ - 0.633}^{ + 0.665})\times{10^{ - 2}}\; {{\rm{GeV}}}^6. \end{aligned} $

(27) The quark-gluon mixture condensate is expressed as
$\langle g_s\bar q\sigma TGq\rangle= m_0^2\langle \bar qq\rangle$ , with$ m_0^2 = 0.80 \pm 0.02{{\rm{GeV}}}^2 $ . The typical scale of$ D\to \pi $ processes is$\mu_k = (m_D^2-m_c^2)^{1/2}\sim 1.1\; {{\rm{GeV}}}$ . The renormalization group equations (RGEs) should be utilized to calculate the running of quark masses and each vacuum condensate involved in the BFTSR, spanning from the initial scale$ \mu_0 = 1\; {{\rm{GeV}}} $ to the typical scale$ \mu_k $ . In the QCD sum rule approach, the continuum threshold$ s_0 $ and Borel parameter$ M^2 $ are two important parameters to be determined accurately. In this paper, we apply the following three criteria:● The continuum contributions to the total results are less than 45%.
● The contributions from the dimension-six condensates do not exceed 5%.
● The variations of
$ \langle\xi_{2;\pi}^n\rangle|_\mu $ within the Borel window must be less than 10%Based on the above criteria, we can determine the value of the continuum threshold parameter
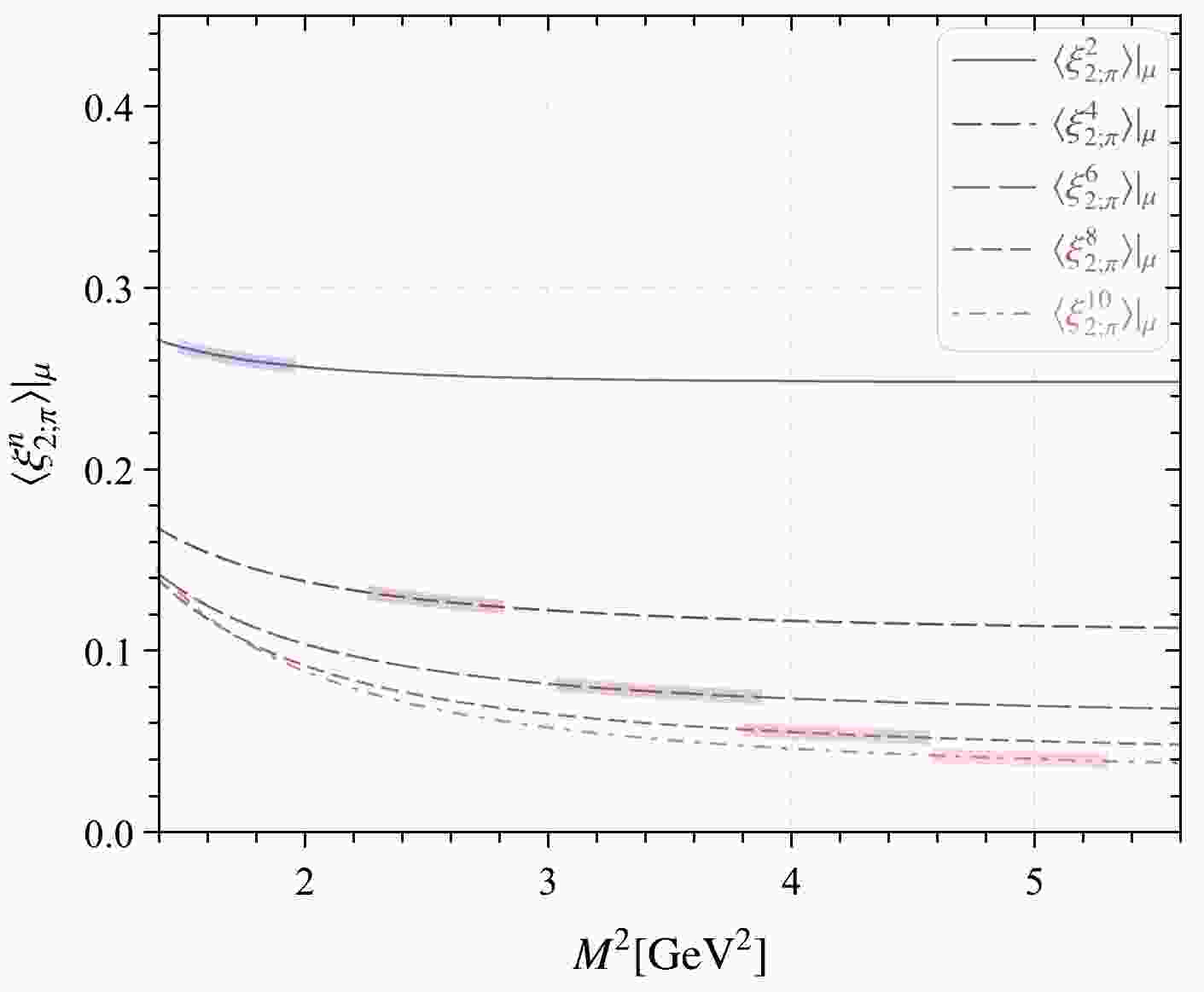
$ s_{0}^\pi $ for the pion leading-twist DA using the normalization of the 0-th-order ξ-moments, i.e.,$ \langle\xi^{0}_{2;\pi}\rangle|_\mu = 1 $ . Therefore, we have$ s_0^\pi=1.05~ {{\rm{GeV^2}}} $ for$ n=(2,4,6,8,10) $ -order moments. The allowable region for Borel parameters (also called Borel window) for each order ξ-moment is presented in Fig. 1, where the shaded region represents the Borel windows. Note that these windows increase with the n-th order, and are always larger than 1. The values of$ \langle\xi_{2;\pi}^n\rangle|_\mu $ decrease with the increase of order n, as reported in a previous study of ours [70]. The first five pion leading-twist DA ξ-moments, i.e.,$ \langle\xi_{2;\pi}^n\rangle|_\mu $ , along with$ n= $ (2, 4, 6, 8, 10) and the contributions of the continuum states and dimension-six condensates are listed in Table 1. When setting$ n= $ (2, 4, 6, 8, 10), the continuum contributions become less than$ 35 $ %,$ 35 $ %,$ 40 $ %,$ 40 $ %,$ 45 $ %, respectively. The contributions of the dimension-six condensates are less than$5$ % for all the orders of$ \langle\xi_{2;\pi}^n\rangle|_\mu $ .
Figure 1. (color online) Moments
$ \langle\xi^{n}_{2;\pi}\rangle|_\mu $ up to$ n=(2,4,\cdots,10) $ -order level versus the Borel parameter$ M^2 $ . The shaded bands represent the corresponding Borel windows.n Con. Six. $ \langle\xi_{2;\pi}^n\rangle|_\mu $ 

2 <35% <5% $ 0.267\pm0.012 $ 

4 <35% <5% $ 0.135\pm0.009 $ 

6 <40% <5% $ 0.085\pm0.008 $ 

8 <40% <5% $ 0.062\pm0.006 $ 

10 <45% <5% $ 0.048\pm0.005 $ 

Table 1. Ratios of the contributions of the continuum states and dimension-six condensates over the total moments of the π-meson twist-2 LCDA
$ \langle\xi_{2;\pi}^n\rangle|_\mu $ with$ n=(2,4,6,8,10) $ within the determined Borel windows. The abbreviations "Con." and "Six." stand for continuum and dimension-six contributions, respectively.Figure 2 shows the relationship between fitting parameters
$ \alpha _{2;{\pi}} $ ,$ B^{2;{\pi}}_{2} $ and the fitting goodness at scale$ \mu_k $ . The shaded bands represent the corresponding Borel windows. The color depth in the shaded band represents the fitting goodness. The deeper the color, the higher the fitting goodness. When the range of fitting goodness is$ 80\% \le P_{\chi^2_{\min}} \le 96\% $ , its effect is maximum. The obtained optimal values of the model parameters$ \alpha_{2;\pi} $ ,$ \hat{a}^{2;\pi}_2 $ , and$ \beta_{2;\pi} $ at scale$ \mu_0 =1\; {{\rm{GeV}}} $ are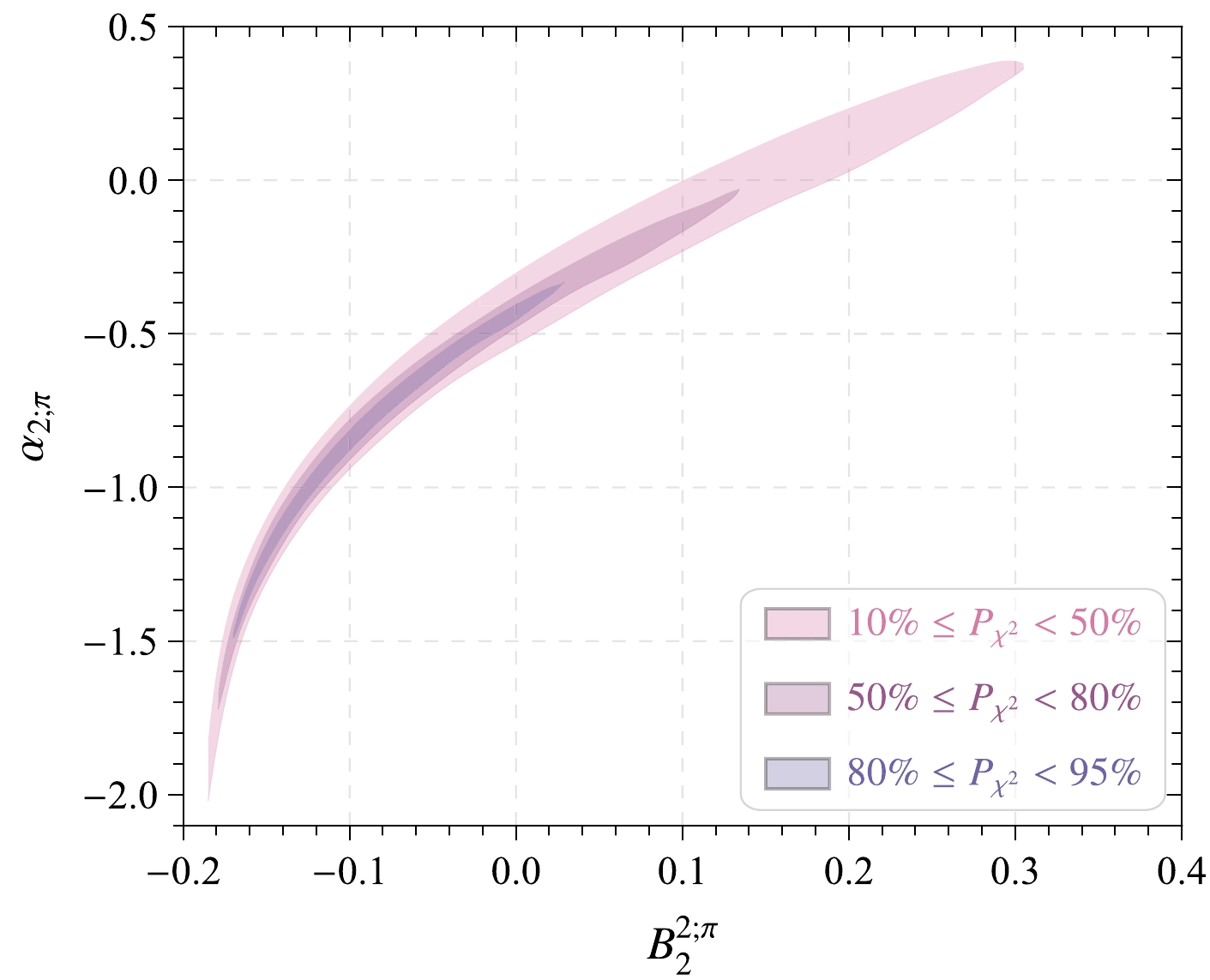
Figure 2. (color online) Relationship curve between parameters
$ \alpha _{2;{\pi}} $ ,$ B^{2;{\pi}}_{2} $ and fitting goodness$ P_{\chi_{\min}^2} $ at factorization scale$ \mu_k $ .$ \begin{aligned}[b] &A_{2;\pi} = 3.659\; {{\rm{GeV}}}^{-1}, \quad\quad \alpha_{2;\pi} = -1.010, \\ & \hat{a}^{2;\pi}_2 = -0.126, \quad\quad \beta_{2;\pi} = 0.727\; {{\rm{GeV}}}. \end{aligned} $

(28) The corresponding behaviors of pion leading-twist DAs
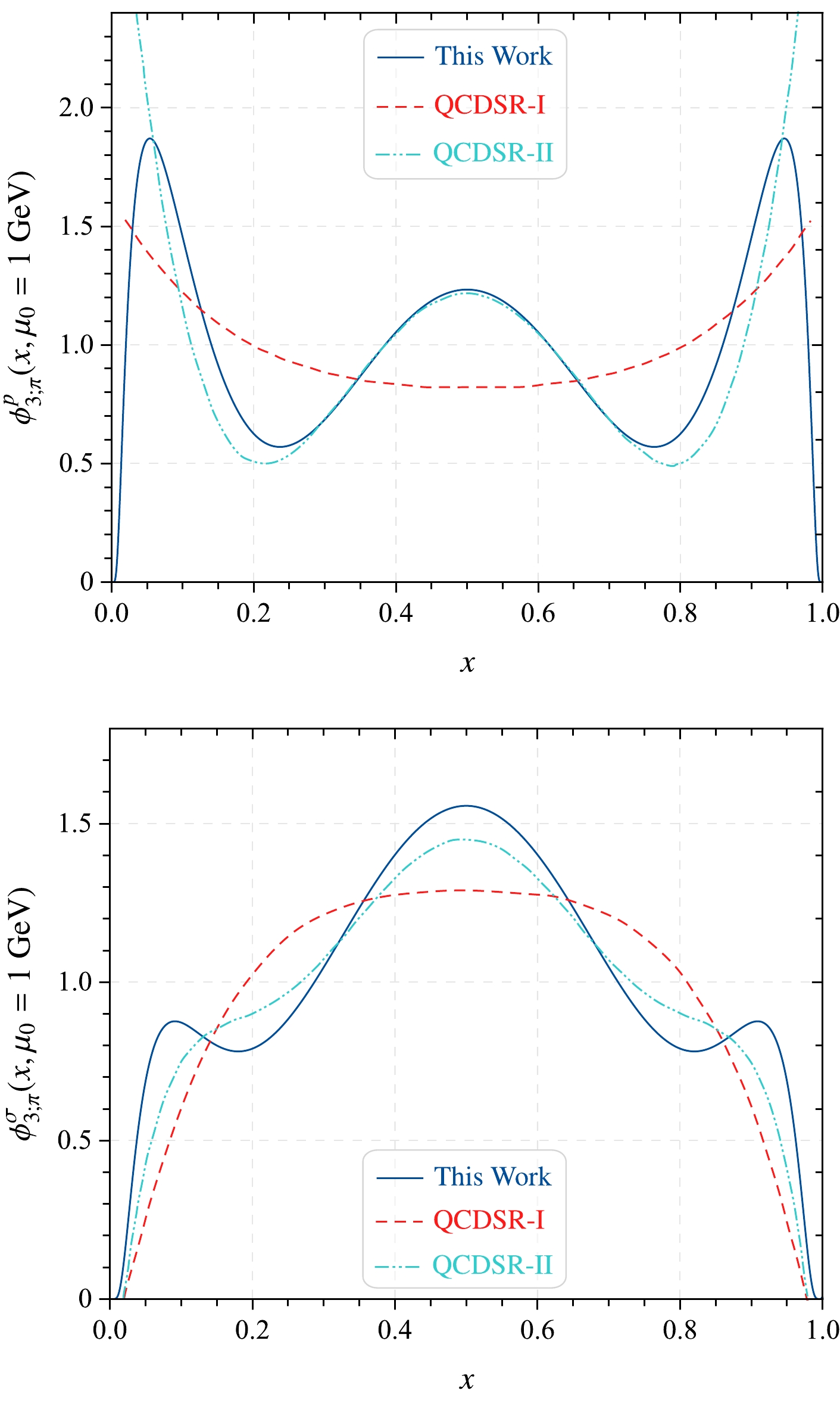
$ \phi_{2;\pi}(x,\mu_0) $ at initial scale$ \mu_0 = 1\; {{\rm{GeV}}} $ for our LCHO prediction are shown in Fig. 3. For comparison, we select models reported in the literature for the π-meson leading-twist DA$ \alpha_{2;\pi} $ such as LQCD [50], DS [51], and QCD/AdS [52]. Figure 3 shows that the present prediction for$ \phi_{2;\pi} $ is close to the DS and QCD/AdS models.Regarding the pion twist-3 DA ξ-moments, we set the continuum threshold
$ s_{3;\pi}^p = s_{3;\pi}^\sigma = 1.69(10)\; {{\rm{GeV}}}^2 $ and$ \langle \xi_{3;\pi}^{p,0} \rangle|_\mu = 1 $ . Using the traditional criteria to determine the Borel window, we can obtain the first two order moments, as reported in a previous study of ours [74]. Using the obtained$ \langle \xi_{3;\pi}^{(p,\sigma),(2,4)}\rangle|_{\mu} $ , we calculated the WF parameters at initial scale$ \mu_0 = 1\; {{\rm{GeV}}} $ :$ \begin{aligned}[b] &A_{3;\pi}^{p} = 78.72\; {{\rm{GeV}}}^{-2}, \quad\quad B_{3;\pi}^{p} = 0.476, \\ & C_{3;\pi}^{p} = 0.943, \quad\quad \beta_{3;\pi}^{p} = 0.608\; {{\rm{GeV}}}, \end{aligned} $

(29) $ \begin{aligned}[b] & A_{3;\pi}^{\sigma} = 160.5 {{\rm{GeV}}}^{-2}, \quad\quad B_{3;\pi}^{\sigma} = -0.027, \\ & C_{3;\pi}^{\sigma} = 0.933, \quad\quad \beta_{3;\pi}^{\sigma} = 0.424\; {{\rm{GeV}}}. \end{aligned} $

(30) The corresponding behaviors of pion twist-3 DAs
$ \phi_{3;\pi}^{(p,\sigma)}(x,\mu) $ for our LCHO predictions are shown in Fig. 4. For comparison, we also present other QCDSR results from the literature for π-meson twist-3 DAs, labeled as QCDSR-I [48] and QCDSR-II [57]. Unlike the twist-2 DA, the pion twist-3 DAs, especially for$ \phi_{3;\pi}^p(x) $ , have a larger discrepancy with other theoretical predictions. As can be seen in the upper panel of Fig. 4, our predictions are in agreement with QCDSR-II in the middle x-region, i.e.,$ 0.3\leq x\leq 0.7 $ . However, there are large differences in the regions$ 0 \leq x < 0.3 $ and$ 0.7 < x \leq 1 $ . For$ \phi_{3;\pi}^\sigma(x) $ , our prediction curve follows the same tendency as that of QCDSR-I. Regarding the twist-4 DAs, we take the expressions and input parameters from Ref. [62].After completing this analysis of pion twist-2 and twist-3 DAs, we can calculate
$ D\to \pi $ TFFs$ f^{D\to \pi}_{+,0} (q^2) $ . The basic input parameters were mentioned at the beginning of this section. The main task is to determine the continuum threshold parameter$ s_0 $ and Borel windows$ M^2 $ . Based on the basic ideas and processes of LCSR, we adopt the following four criteria:● The continuum contributions to the total results are less than 30%.
● The contributions from higher-twist DAs are less than 5%.
● Within the Borel window, the changes of TFFs do not exceed 10%.
● The continuum threshold
$ s_0 $ should be closer to the squared mass of the first excited state D-meson.We set the continuum threshold parameter as
$ s_0^+ = \tilde s_0 = 5.2(3)\; {{\rm{GeV^2}}} $ . The Borel parameters are$M_+^2 = 8.0(5)\;{{\rm{GeV^2}}}$ and$ \tilde M^2=10.0(5)\; {{\rm{GeV^2}}} $ . The Borel mass parameters$ M^2 $ is one of the two significant parameters in the LCSR approach, which is always organized in terms of the$ 1/M^2 $ expansion for the OPE calculations of the vacuum-to-pion or vacuum-to-light meson correlation functions. Let us consider the vector TFF$ f^{D\to\pi}_+(q^2) $ as an example. The choice of intervals for the Borel mass parameters is larger than$ 4.5 \pm 1.0 \, {{\rm{GeV^2}}} $ , according to Refs. [81−83], because of three reasons. (i) Similar to other non-perturbative methods, the LCSR approach is expected to have as little dependence on model parameters as possible. One of the criteria for conventional LCSR is that TFFs should have a stable Borel window. Here, we show the Borel windows for$ f^{D\to\pi}_+(0) $ with respect to Borel mass parameters within the region$M^2 \in [2, 14] {{\rm{GeV^2}}}$ in Fig. 5. From this figure, we conclude that the Borel window is much smoother around$ q^2 = 8\; {{\rm{GeV^2}}} $ than around$ q^2 = 4.5\; {{\rm{GeV^2}}} $ . That is, the TFF changes less with$ M^2 $ around$ 8\; {{\rm{GeV^2}}} $ than around$ 4.5\; {{\rm{GeV^2}}} $ . We also found that the errors/uncertainties in the Borel window near$ 8\; {{\rm{GeV^2}}} $ are smaller than those near$ 4.5\; {{\rm{GeV^2}}} $ . (ii) To ensure the convergence of the calculations, the contribution of the amplitude of the high twist distribution must be as small as possible. In general, the amplitude of the high twist distribution is preceded by a power depression of$ 1/M^2 $ . Therefore, it is more reasonable to choose a larger$ M^2 $ . (iii) The LCSR expression employed in this paper takes the form of a derivative function instead of$ 1/M^2 $ . The Borel mass parameter only appears in the e-index, i.e.,$ {\rm e}^{m_D^2/M^2} $ and$ {\rm e}^{-(m_c^2 -\bar u q^2)/(uM^2)} $ in Eqs. (12)−(15). This approach can reduce the influence of$ M^2 $ to contributions of higher-twist DAs.
Figure 5. (color online) Borel windows for
$ f^{D\to\pi}_+(0) $ with respect to Borel mass parameters within the region$ M^2 \in [2, 14] $ $ {{\rm{GeV^2}}} $ .After considering the errors from all the input parameters, we list the TFFs at the large recoil region, e. g.,
$ f^{D\to \pi}_+ (0) = f^{D\to \pi}_0 (0) $ , in Table 2. The uncertainties in this table are obtained from the squared average of all the mentioned error sources. For comparison, we also present other predictions, such as those from the Belle [39], BESIII [40], BES [84], Babar [41], and CLEO [42] Collaborations for experimental predictions, and those from LQCD [43] and LCSR [85] for theoretical predictions. Our results agree well with the BESIII, Belle, LQCD, Babar, LCSR, and CLEO predictions within errors.References $ f_+^{D\to\pi}(0) $ 

This study $ 0.627^{+0.120} _{-0.080} $ 

Belle [39] $ 0.624\pm 0.020\pm0.030 $ 

BESIII [40] $ 0.637\pm 0.008\pm0.004 $ 

BES [84] $ 0.730\pm 0.14\pm0.0060 $ 

Babar [41] $ 0.610\pm0.020\pm0.005 $ 

CLEO [42] $ 0.640\pm 0.03\pm 0.06 $ 

LQCD [43] $ 0.640\pm0.03\pm0.06 $ 

LCSR [85] $ 0.630\pm0.110 $ 

Table 2. Comparison of theoretical predictions for the form factors
$ f_+^{D\to\pi}(0) $ .The physically allowable range for the
$ D\to \pi $ TFFs is$ 0 \leq q^2\leq 2.993\; {{\rm{GeV^2}}} $ . Theoretically, the LCSR approach for$ D \to \pi {\nu }{\bar\nu } $ TFFs is applied in low and intermediate$ q^2 $ -regions, i.e.,$ 0 \leq q^2\leq 1.4\; {{\rm{GeV^2}}} $ of the π-meson. One can extrapolate this to whole$ q^2 $ -regions via$ z(q^2,t) $ rapidly converging to the simplified series expansion (SSE-I), i.e., the TFFs are expanded as [86]$ f_+^{D\to \pi}(q^2) =\frac{1}{1-q^2/m_D^2}\sum\limits_{k=0,1,2}{\beta _kz^k( q^2,t_0 )}, $

(31) where
$ \beta_k $ are the real coefficients and$ z(q^2,t) $ is the function$ z( q^2,t_0 ) =\frac{\sqrt{t_+-q^2}-\sqrt{t_+-t_0}}{\sqrt{t_+-q^2}+\sqrt{t_+-t_0}}, $

(32) where
$t_{\pm} = (m_{D} \pm m_{\pi})^2$ and the auxiliary parameter$t_0 = t_+ - \sqrt{t_+ - t_-} \sqrt{t_+}$ , which can also be expressed as$ t_0 =t_+ - \sqrt{t_+ - t_-} \sqrt{t_+}. $

(33) Meanwhile, the
$ z(q^2,t) $ -series parameters also converge to the simplified series expansion (SSE-II), which incorporates the desired threshold$ t_+ $ behaviour [53, 87]; the definition for$ t_0 $ is$ t_0 = t_+ - \sqrt{t_+ - t_-}\sqrt{t_+ - q_{{\rm{min}}}^2}. $

(34) The region is defined as
$ q_{{\rm{min}}}^2 < q^2 < q_{{\rm{max}}}^2 $ . Comparing with Eqs. (33) and (34), the difference lies in the term$ q_{{\rm{min}}}^2 $ . In the$ B\to \pi $ decay processes,$ q_{{\rm{min}}}^2 = -6\; {{\rm{GeV^2}}} $ and$ q_{{\rm{max}}}^2 = 12\; {{\rm{GeV^2}}} $ . It is indeed SSE-II which is more constrained to$ t_+ $ . According to the$ B\to \pi $ decay processes with$ -6\; {{\rm{GeV^2}}} < q^2_{B\to \pi} < 12\; {{\rm{GeV^2}}} $ , we perform linear estimation of the$ D\to \pi $ process, that is,$-0.7\; {{\rm{GeV^2}}} < q^2_{D\to \pi} < 1.4\; {{\rm{GeV^2}}}$ with$q_{{\rm{min}}}^2 = -0.7\; {{\rm{GeV^2}}}$ and$q_{{\rm{max}}}^2 = 1.4\; {{\rm{GeV^2}}}$ . Based on LCSR data, we use the two aforementioned methods for analytical continuation. The curves are shown in Fig. 6. SSE-I stands for the z-series parametrization with$ 0 < q^2 < q_{{\rm{max}}}^2 $ in this study. SSE-II is the z-series parametrization with$ q_{{\rm{min}}}^2 < q^2 < q_{{\rm{max}}}^2 $ according to Refs. [87−89], which incorporate the behavior of the threshold$ t_+ $ . Figure 6 shows that (i) the behavior of the two curves in the whole squared momentum transfer is coincident; (ii) in the larger$ q^2 $ region, the two curves are slightly different. Let us take$ q^2 = 2.99\; {{\rm{GeV^2}}} $ as an example. The difference in this case is approximately$ 0.3\ $ %, which is very small and can be safely neglected. Consequently, we only consider SSE-I in this paper.
Figure 6. (color online) Model-independent z-series expansion for
$ f_+^{D\to\pi}(q^2) $ with two types of$ t_+ $ behaviour. SSE-I represents the region$ 0 < q^2 < q_{{\rm{max}}}^2 $ whereas SSE-II represents the region$ q_{{\rm{min}}}^2 < q^2 < q_{{\rm{max}}}^2 $ .The SSE-I method possesses superior merit, which keeps the analytic structure correct in the complex plane and ensures appropriate scaling, i.e.,
$ f_+^{D\to \pi}(q^2)\sim 1/q^2 $ at large$ q^2 $ . The fitting quality parameter Δ allows assessing the result of extrapolation; it is defined as$ \Delta =\frac{\sum _t{| F_i(t) -F_{i}^{\mathrm{fit}}( t ) |}}{\sum _t{| F_i(t) |}}\times 100. $

(35) The fitting quality is less than 1% after extrapolating the TFFs
$ f_+^{D\to \pi}(q^2) $ to the whole physical$ q^2 $ -region. The behaviors of$ D\to\pi $ TFFs in the whole physical region with respect to the squared momentum transfer are represented in Fig. 7. The darker band represents the LCSR results of our prediction, while the lighter band represents the SSE-I predictions. For comparison, we also present theoretical and experimental predictions, such as those from the LQCD [43], Belle [39], Babar [41], CLEO [42], and BESIII [40] collaborations. Our predictions are in good agreement with the experimental collaborations within errors. At the large squared momentum transfer, the predictions from LQCD present a large gap with our results. We also present the TFF$ f_0^{D\to \pi}(q^2) $ in the lower panel of Fig. 7. Furthermore, we present the behaviors of three functions of angular coefficients, namely$ a_{\theta_\ell}(q^2) $ ,$ b_{\theta_\ell}(q^2) $ , and$ c_{\theta_\ell}(q^2) $ , with uncertainties in the order of$ 10^{-17} $ , in Fig. 8. The fact that$ c_{\theta_\ell} $ is negative was established for convenience to compare the three angular coefficients. Note that the absolute values of$ a_{\theta_\ell}(q^2) $ and$ c_{\theta_\ell}(q^2) $ are very close, though with uncertainties, and that the value of$ b_{\theta_\ell}(q^2) $ is smaller than that of$ a_{\theta_\ell}(q^2) $ and$ -c_{\theta_\ell}(q^2) $ .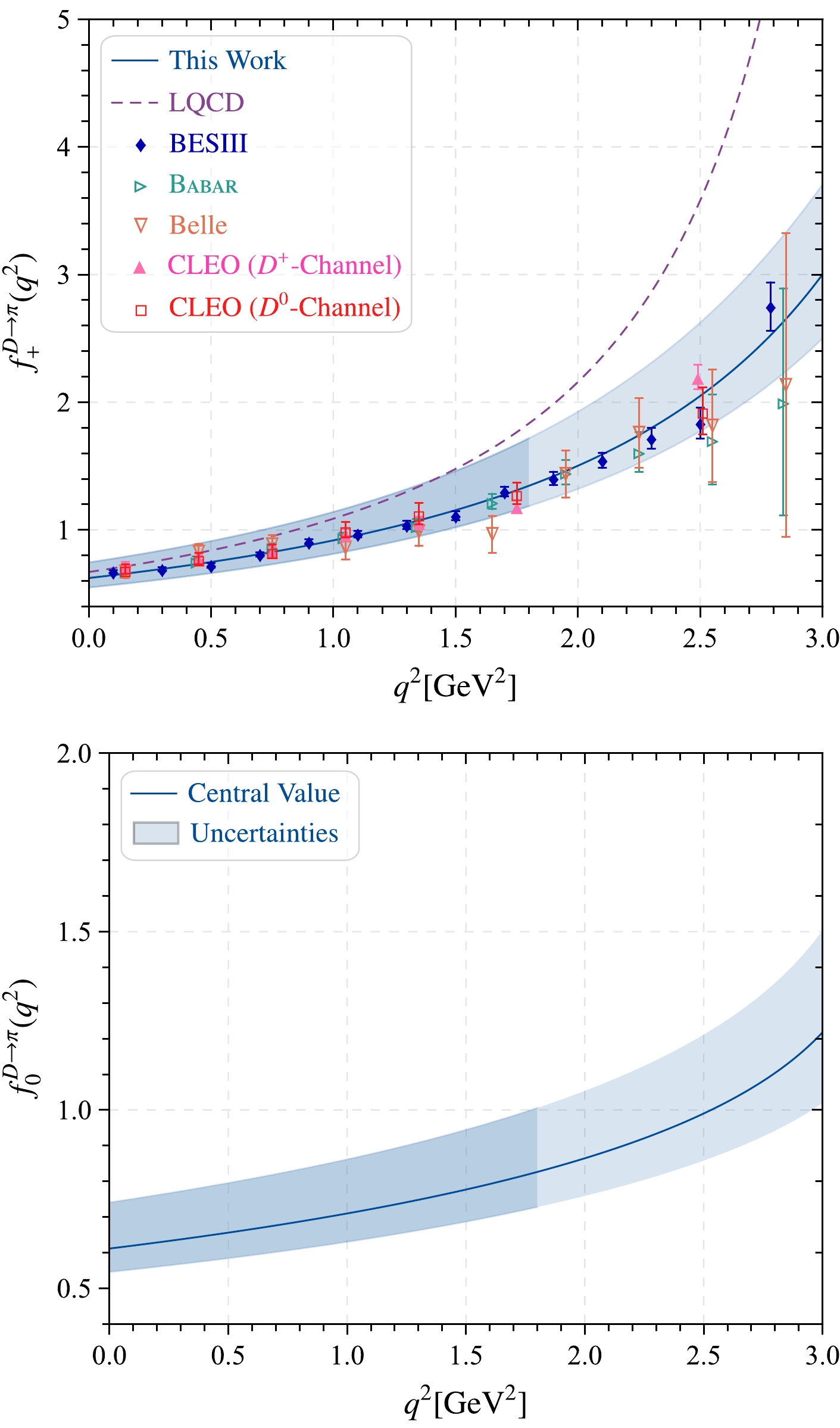
Figure 7. (color online)
$ D\to \pi $ TFFs$ f^{D\to \pi}_+(q^2) $ and$ f^{D\to \pi}_0(q^2) $ in the whole physical region within uncertainties in this study. Other theoretical and experimental predictions from the Belle [39], BESIII [40], BaBar [41], CLEO [42], and LQCD [43] collaborations are also shown for comparison.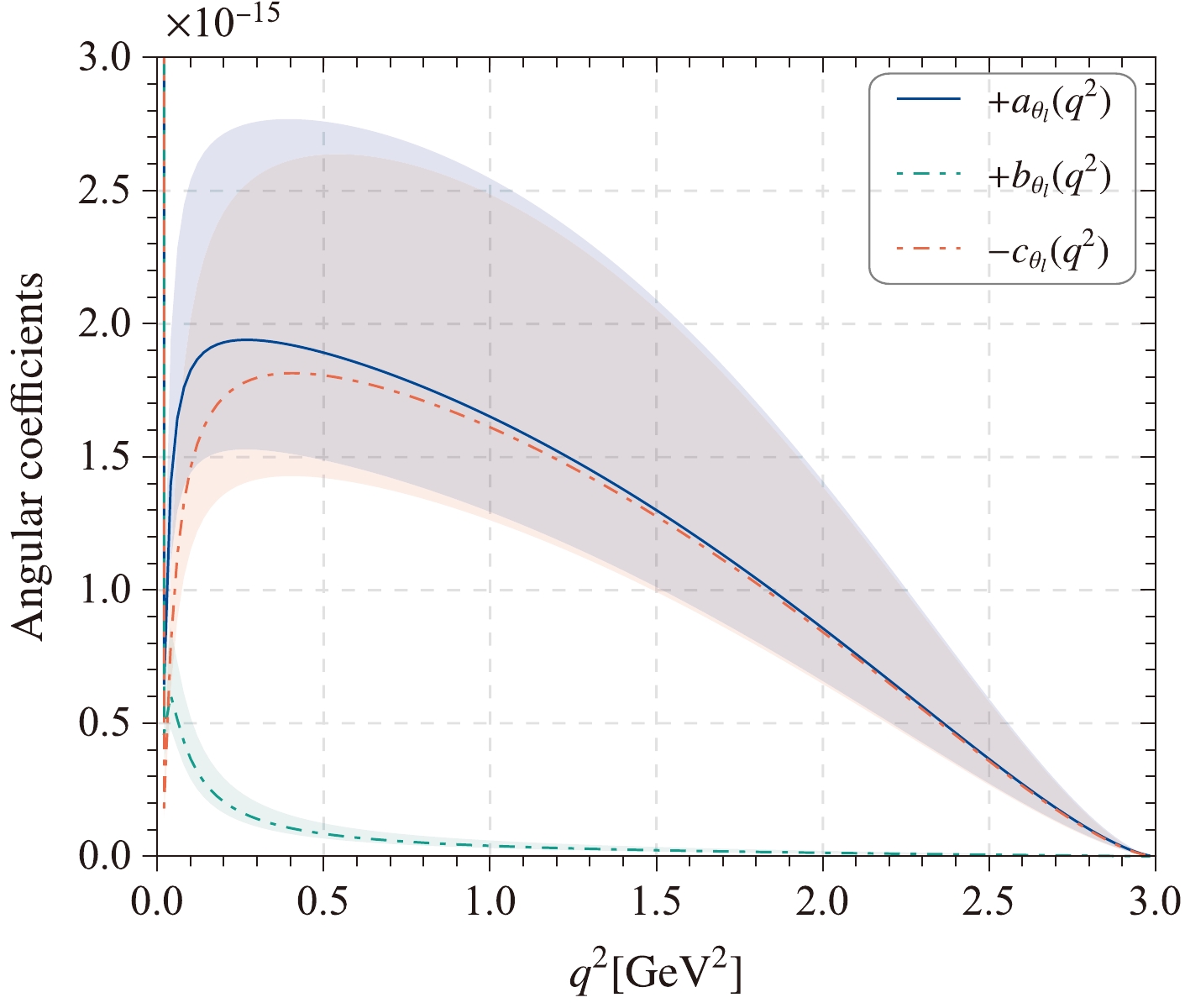
Figure 8. (color online) Distribution of three
$ q^2 $ -dependent angular coefficient functions, namely$ a_{\theta_\ell}(q^2) $ ,$ b_{\theta_\ell}(q^2) $ , and$ c_{\theta_\ell}(q^2) $ (in unit:$ 10^{-15} $ ); the shaded bands represent the uncertainties.Next, we focus on calculating the decay width and branching fraction for the semileptonic decay processes
$ \bar D^0\to \pi^+ e \bar\nu_{e} $ . By taking the$ D\to \pi $ TFFs$ f^{D\to \pi}_{+,0}(q^2) $ or angular coefficient functions$ a_{\theta_\ell}(q^2) $ ,$ b_{\theta_\ell}(q^2) $ ,$ c_{\theta_\ell}(q^2) $ into the expression of decay width, e.g., Eq. (5), we obtain the curves of$ D\to \pi\ell^+\nu_\ell $ differential decay width shown in Fig. 9 (in unit:$ 10^{-15} $ ), where the darker band represents the uncertainties from all the input parameters. For comparison, we also show the predictions from the Belle [39], BESIII [40] Babar [41], CLEO [42] Collaborations and LQCD [43]. Note that the results of our predictions are in agreement with most of the experimental results within uncertainties, especially with those of the BESIII Collaboration.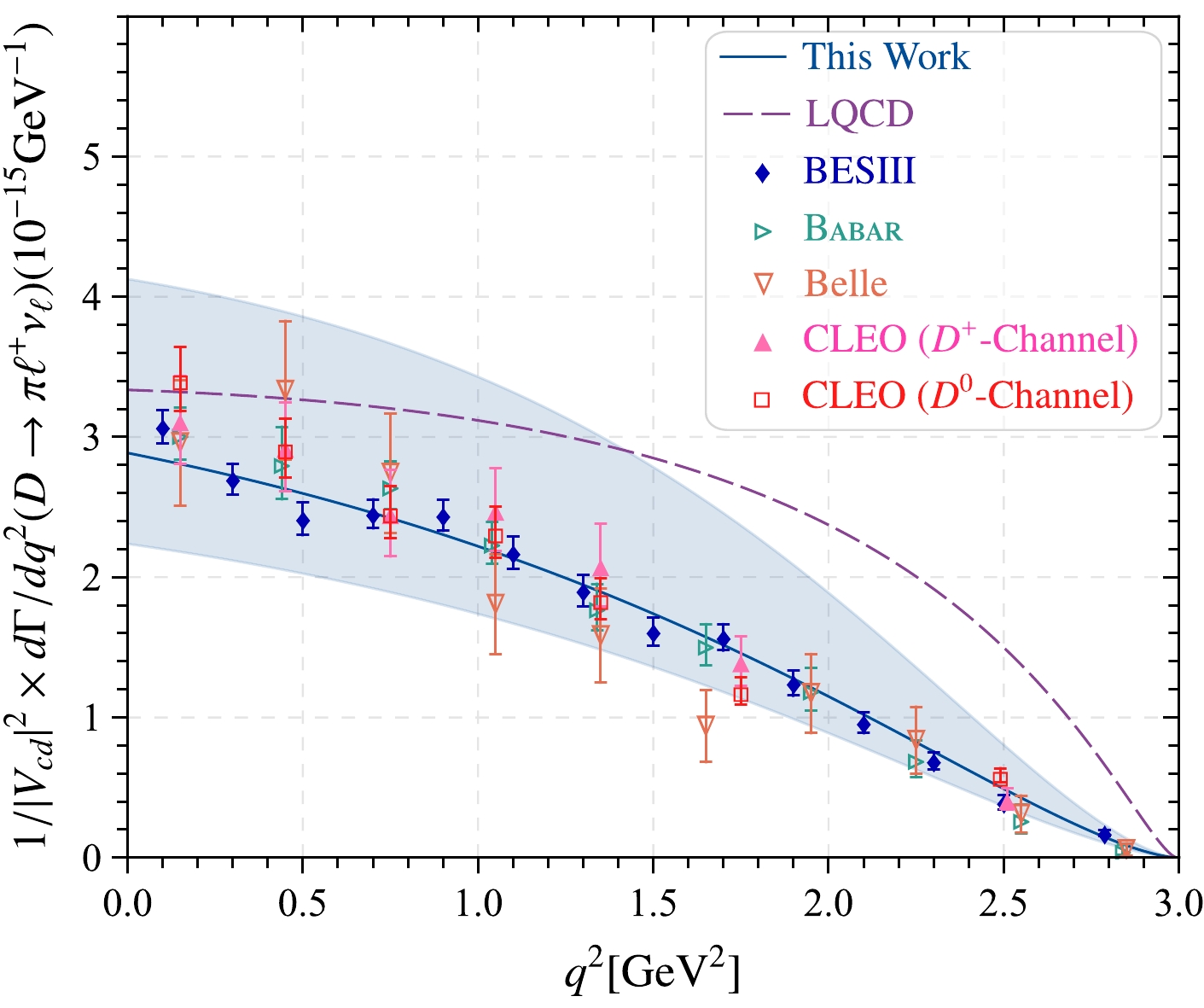
Figure 9. (color online) Predictions from our calculations for the
$ D\to \pi\ell^+\nu_\ell $ differential decay width within uncertainties (in unit:$ 10^{-15} $ ). The results of other experimental groups, such as the Belle [39], BESIII [40] Babar [41], and CLEO [42] Collaborations as well as the LQCD prediction [43] are also presented for comparison.Furthermore, after considering the
$ \bar D^0 $ -meson lifetime$ \tau(\bar D^0) = 0.410(1)\; {{\rm{ps}}} $ from PDG [77] and integrating the squared momentum transfer$ q^2 $ , we can obtain the value of the total branching fraction for$ \bar D^0\to\pi^+ e\bar\nu_e $ , as shown in Table 3. The error of our prediction comes from all input parameters. For comparison, we also present the PDG [58], Belle [39], BESIII [40], BES [84], Babar [41], CLEO [42], and LQCD [43] predictions. The value of our prediction is in agreement with that of BESIII, PDG average, and LQCD results.References Channel Predictions This study $ \bar D^0\to\pi^+e\bar\nu_e $ 

$ 0.308^{+0.155}_{-0.066} $ 

PDG [58] $ \bar D^0\to\pi^+e\bar\nu_e $ 

$ 0.281\pm0.190 $ 

Belle [39] $ D^0\to\pi^- \ell^+\nu_\ell $ 

$ 0.255\pm0.019\pm0.016 $ 

BESIII [40] $ D^0\to\pi^-e^+\nu_e $ 

$ 0.295\pm0.004\pm0.003 $ 

BES [84] $ D^0\to\pi^-e^+\nu_e $ 

$ 0.330\pm0.130\pm0.030 $ 

Babar [41] $ D^0\to\pi^-e^+\nu_e $ 

$ 0.277\pm0.068\pm0.0092\pm0.037 $ 

CLEO [42] $ D^0\to\pi^-e^+\nu_e $ 

$ 0.288\pm0.008\pm0.003 $ 

LQCD [43] $ D^0\to\pi^-\ell^+\nu_\ell $ 

$ 0.316\pm0.025\pm0.062\pm0.033 $ 

Table 3. Our predictions for the branching fraction (in unit
$ 10^{-2} $ ) for semileptonic decay$ \bar D^0\to\pi^+e\bar\nu_e $ . Theoretical and experimental results from other groups are also provided for comparison.Observables such as forward-backward asymmetries,
$ q^2 $ -differential flat terms, and the lepton polarization asymmetry, e.g.,$ {\cal A}_{{\rm{FB}}}^{\bar D^0\to\pi^+ e\bar\nu_e}(q^2) $ ,$ {\cal F}_{{\rm{H}}}^{\bar D^0\to\pi^+ e\bar\nu_e}(q^2) $ , and$ {\cal A}_{\lambda_\ell}^{\bar D^0\to\pi^+ e\bar\nu_e}(q^2) $ , can be obtained by using the resulting three angular coefficients, which were reported in a previous study of ours [90]. The normalized forward-backward asymmetries and$ q^2 $ differential flat terms will vanish in the massless lepton limit to the SM, which is sensitive beyond the SM. Meanwhile, the lepton polarization asymmetry is sensitive to helicity-violating new physics interactions. Therefore, we display the three curves in Fig. 10 in the (a), (b), and (c) panels, respectively. The$ q^2 $ differential flat terms are in the order of$ 10^{-5} $ . The uncertainties of the lepton polarization are very small and almost coincide with the central value. As a next step, we can calculate rare FCNC decays$ D^+ \to \pi^+ \nu \bar{\nu} $ . The input parameters are the Weinberg angle$ \sin ^2{\theta _W}= 0.2312 $ , electromagnetic coupling constant$ \alpha _{{\rm{em}}} $ , running coupling constant$ \alpha_s (1.1{{\rm{GeV}}})= 0.4256 $ , Fermi constant$G_F=1.166\times 10^{-5} \;\; {{\rm{GeV^{-2}}}}$ , and$ C_F=4/3 $ . The curve for differential branching fraction of$ D^+\to \pi^+\nu\bar\nu $ within uncertainties is presented in Fig. 11. Given that other theoretical predictions, such as those of Ref. [58], are in the order of$ 10^{-7} $ , we do not include them in the comparison.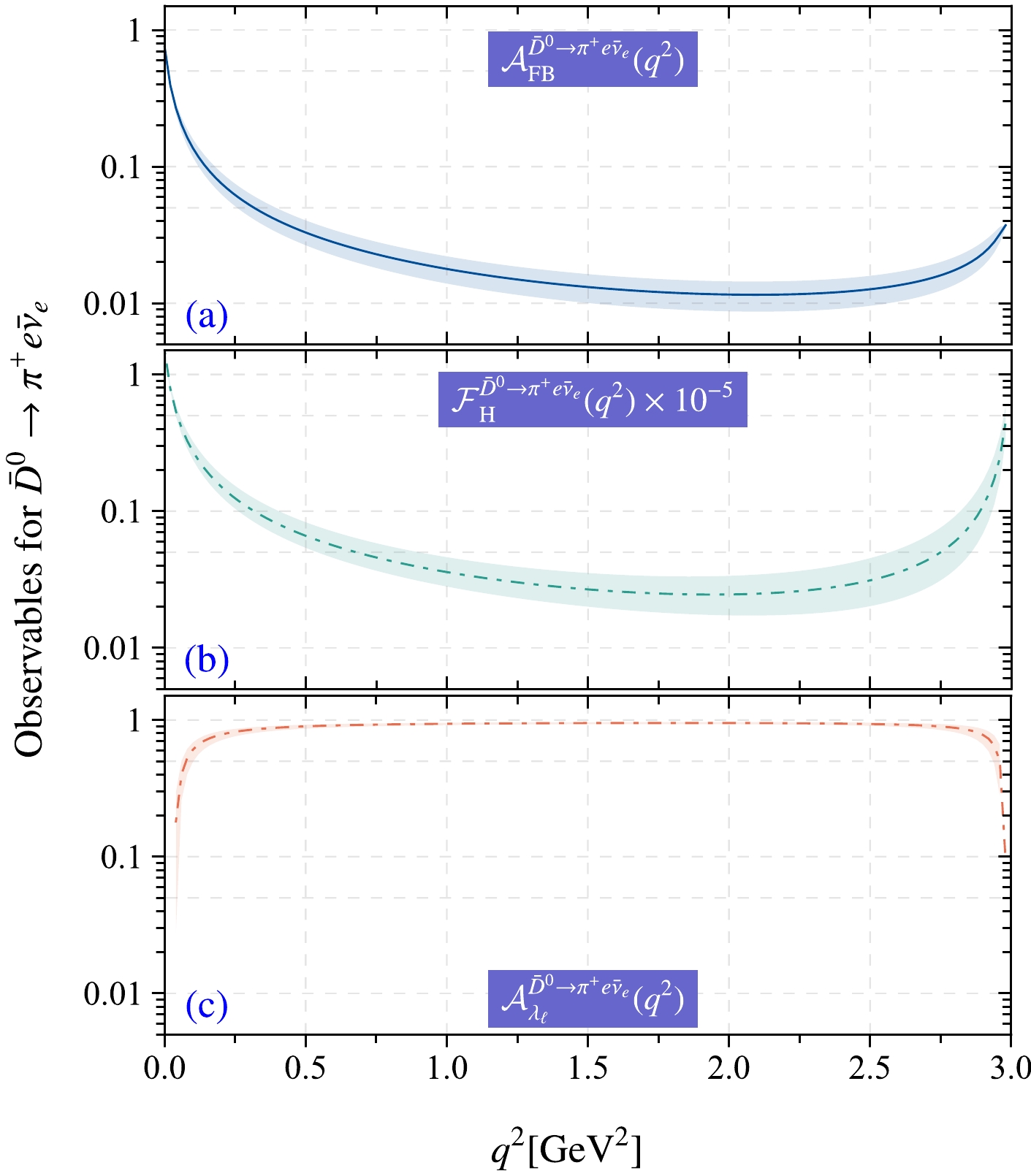
Figure 10. (color online) Theoretical predictions for three angular observables:
$ \mathcal{A}_{\mathrm{FB}}^{ \bar D^0\to\pi^+ e\bar\nu_e}(q^2) $ ,$ \mathcal{F}_{\mathrm{H}}^{\bar D^0\to\pi^+ e\bar\nu_e}(q^2) $ , and$ \mathcal{A}_{\lambda_\ell}^{\bar D^0\to\pi^+ e\bar\nu_e}(q^2) $ . The shaded bands represent uncertainties.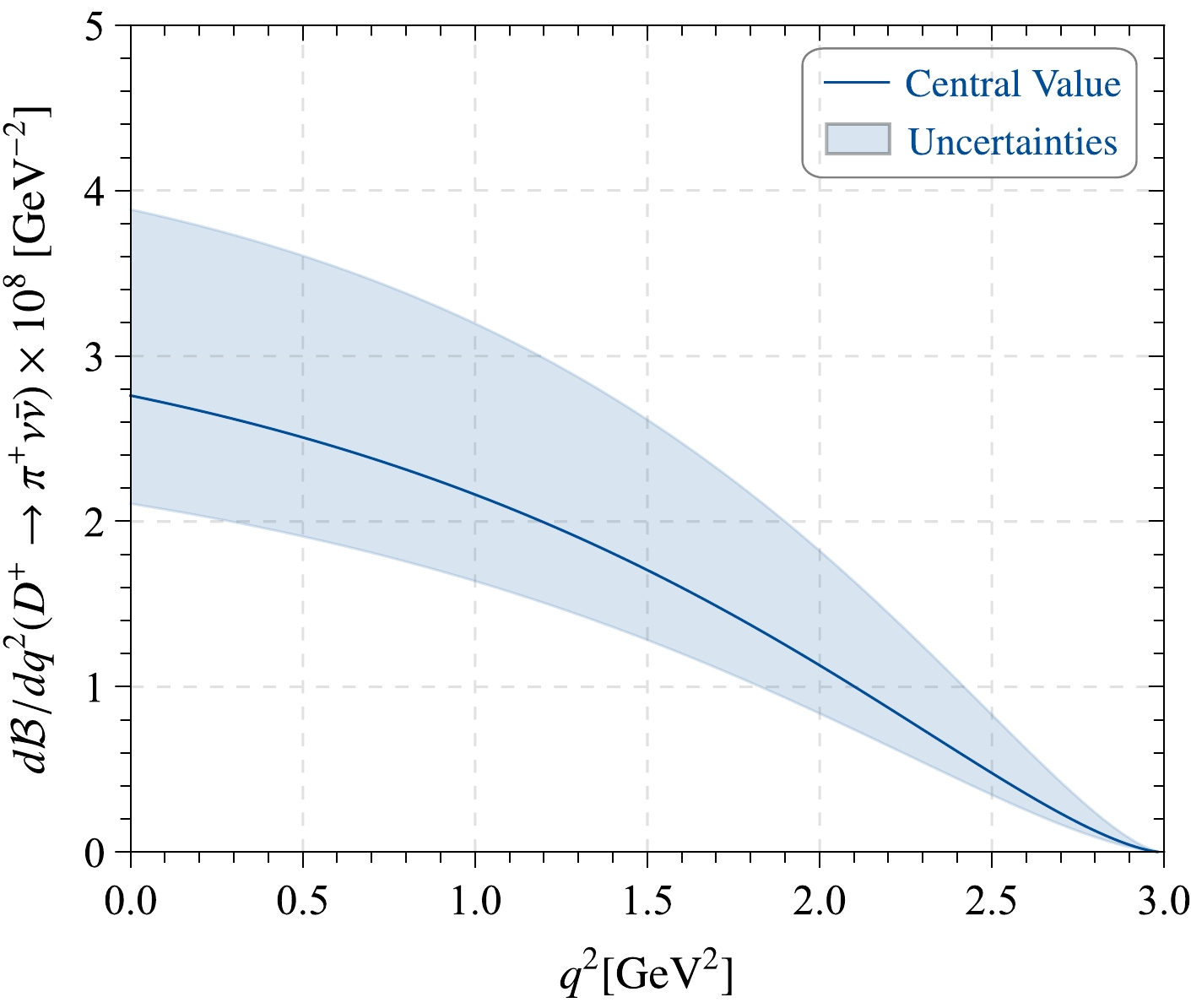
Figure 11. (color online) Predictions of our calculations for the
$ D^+\to \pi^+ \nu\bar\nu $ differential decay width within uncertainties (in unit:$ 10^{-8} $ ). They are consistent with the upper limit of the experimental prediction results of the BESIII [40] Collaboration.Finally, we present the branching fraction of the dineutrino decay mode
$ D\to \pi \nu\bar\nu $ in Table 4 within uncertainties. The NSI [8], SM with long and short distances [91], Lepton Universality (LU), charged Lepton Flavor Conservation (cLFC), and the case with no assumption (General) from Ref. [92] are also included for comparison. Note that our prediction is in the same order as that of NSI, larger than that of the SM, and lower than those of LU, cLFC, and General. Our prediction is also in the same order as that of BESIII.Table 4.
$ D^+ \to \pi^+ {\nu }{\bar\nu} $ branching fraction in this study. The theoretical and experimental results are included for comparison. -
In this paper, the rare decay process of
$ D^+\to \pi^+ \nu\bar\nu $ was studied within the framework of the QCD sum rule approach. First, we derived expressions for the pion twist-2 and twist-3 DAs ξ-moments$ \langle\xi_{2;\pi}^n\rangle|_\mu $ and$ \langle\xi_{3;\pi}^{(p,\sigma),n}\rangle|_\mu $ using the QCD sum rule approach under the background field theory. The first five terms of the twist-2 DA and first two terms of the ξ-moments are given in the process scale$ \mu_k = 1.1\; {{\rm{GeV}}} $ . To avoid the large uncertainties resulting from the Gegenbauer moment$ a_n $ , we constructed the LCHO model for twist-2, 3 LCDAs and determined the parameters using the ξ-moments.Second, we calculated the
$ D\to \pi $ vector and scalar TFFs within the QCD light-cone sum rule approach up to next-to-leading order accuracy. The value of the TFF at the large recoil region$ f^{D\to \pi}_+ (0) $ is presented in Table 2. After extrapolating the TFFs into the whole$ q^2 $ -region via simplified series expansion, we obtained the TFFs shown in Fig. 7. Comparison with other predictions was made. The three$ q^2 $ -dependence angular coefficient functions$ a_{\theta_\ell}(q^2) $ ,$ b_{\theta_\ell}(q^2) $ and$ c_{\theta_\ell}(q^2) $ were also provided.Furthermore, we analyzed the differential decay width for
$ D^+\to \pi^+e\nu_e $ (see Fig. 9) and thoroughly compared with BESIII, Babar, Belle, CLEO, and LQCD predictions. The total branching fraction for$ \bar D^0 \to \pi^+ e\bar\nu_e $ is given in Table 3. Then, we obtained the forward-backward asymmetries,$ q^2 $ differential flat terms, and lepton polarization asymmetry (see Fig. 10). Finally, the differential and total branching fractions of$ D^+\to \pi^+\nu\bar\nu $ were presented in Fig. 11 and Table 4. Our prediction is in the region of the BESIII upper limits. With stable operation of BESIII, the collision energy of the BEPC-II collider will be greatly improved in the following seven years and more results will be reported. We expect that predictions for the$ D^+\to \pi^+\nu\bar\nu $ channel can be reported in the near future.
$ { \boldsymbol D^{\bf +} \boldsymbol\to \boldsymbol\pi^{\bf +} \boldsymbol\nu\bar{\boldsymbol\nu}} $ decay process within the QCDSR approach
- Received Date: 2024-01-09
- Available Online: 2024-06-15
Abstract: In this paper, we investigate the charmed meson rare decay process







 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF









































 DownLoad:
DownLoad: