-
In the standard model of particle physics, three generations of neutrinos, namely,
$ \nu_e, \nu_\mu $ , and$ \nu_\tau $ , are associated with three neutrino flavor eigenstates. The phenomenon of neutrino oscillation provides evidence that the neutrinos are massive [1, 2]. Neutrino mass constraints can be derived from various particle physics experiments; however, the precise value of the neutrino mass remains unclear to date. Among these measurements, the kinematics of tritium decay can provide an upper limit on the neutrino mass [3]. Neutrino oscillation provides an approach to exploring the splittings of the neutrino mass-squared$ \Delta m_{ij} $ . The resulting mass-squared splittings are [4]$ \Delta m_{21}^2 \equiv m_2^2 - m_1^2 \simeq 7.5 \times 10^{-5} \mathrm{eV}^2, $

(1) $ |\Delta m_{31}^2 | \equiv |m_3^2 - m_1^2 | \simeq 2.5 \times 10^{-3} \mathrm{eV}^2, $

(2) where
$ m_1, m_2 $ , and$ m_3 $ are neutrino mass eigenvalues that can be transformed into flavor eigenstates with a neutrino mixing matrix [4]. The sign of$ \Delta m_{31}^2 $ remains undetermined; thus, the above results present two possibilities of neutrino mass hierarchy: the normal hierarchy (NH), characterized by$ m_1<m_2<m_3 $ , and the inverted hierarchy (IH), characterized by$ m_3<m_1<m_2 $ . We denote the sum of the neutrino mass as$ \sum m_\nu $ . In the NH case, there is a lower limit on the total neutrino mass, which is$\sum m_{\nu,\mathrm{NH}} > 0.06 \; {\rm{eV}}$ . Similarly, for the IH case, we have$\sum m_{\nu,\mathrm{IH}} > 0.10\; {\rm{eV}}$ .Cosmological observations can also provide constraints on neutrino mass, particularly the total neutrino mass
$ \sum m_\nu $ [5−9]. In the early universe, massive neutrinos are ultra-relativistic, which can be regarded as radiation. However, in the late-time universe, massive neutrinos become non-relativistic and behave like cold dark matter. The special characteristic of massive neutrinos would have significant implications on cosmological evolution at both background and perturbation levels, consequently leading to a reshaping of the cosmic microwave background (CMB) power spectrum [10−14]. To remain consistent with CMB observations, there is an upper limit on the sum of neutrino masses$ \sum m_\nu $ . Note that the inference of total neutrino mass constraints from the CMB is model-dependent. In concordance$ \Lambda\mathrm{CDM} $ model, it is found that$ \sum m_\nu<0.26 $ eV at the 95% confidence level (C.L.) using Planck 2018 TT, TE, EE+lowE and assuming degeneracy hierarchy ($m_1 = m_2 = m_3$ ), where lowE refers to low-$ \ell $ ($ 2\leqslant \ell \leqslant 29 $ ) EE polarization power spectra [5]. Adding baryon acoustic oscillation (BAO) data results in a more stringent constraint$ \sum m_\nu <0.12 $ eV at the 95% C.L. The neutrino mass hierarchy can be distinguished through strict cosmological constraints derived from cosmological observations. Cosmological constraints on the neutrino mass hierarchy were first proposed in [15]. Subsequently, an updated constraint was derived using Planck 2018 TT, TE, and EE+lowE+BAO, yielding$ \sum m_{\nu,\mathrm{NH}} < $ 0.15 eV and$ \sum m_{\nu,\mathrm{IH}} < $ 0.17 eV at the 95% C.L. [16].The constraints on neutrino mass in alternative cosmological models beyond the standard ΛCDM model have been extensively investigated [17−31]. The new physics in these models may impose distinct constraints on the neutrino mass compared to those derived from the ΛCDM model. In recent years, a multitude of cosmological models have been proposed to alleviate the Hubble tension [32, 33], which refers to the discrepancy between the local distance ladder measurement and the early-time CMB measurement. According to the CMB observations by Planck [34],
$ H_0 = 67.27 \pm 0.60 \;\; $ km s−1Mpc−1 in the ΛCDM model. However, the latest$ H_0 $ measurement by SH0ES yields$ H_0 = 73.04 \pm 1.04 \;\; $ km s−1Mpc−1 [35]. The discrepancy between these two results reaches a$ 5\sigma $ significance level. Therefore, the ΛCDM model may potentially exhibit inconsistencies; thus, we need to constrain the neutrino masses within a consistent cosmological framework. Early dark energy (EDE) is a promising solution to alleviate Hubble tension by increasing the Hubble rate$ H(z) $ prior to recombination. It reduces the sound horizon at recombination while increasing the$ H_0 $ value without shifting the angular scale of the sound horizon. Because the CMB has tight constraints on the angular scale of the sound horizon, introducing EDE can increase the value of$ H_0 $ without violating the fit to the CMB power spectrum. In recent years, several EDE models with different mechanisms have been proposed [36−46], such as the axion-like EDE model (Axi-EDE) [37, 39] and the EDE model with an anti-de Sitter phase around recombination (AdS-EDE) [43]. In this study, we aim to constrain neutrino mass within the Axi-EDE and AdS-EDE models while investigating the preferred hierarchy based on current observational data.This paper is organized as follows. In Sec. II, we introduce the datasets and methods for constraining neutrino mass. Models and their parameters are summarized in Sec. III. The results of parameter constraints and discussions are presented in Sec. IV. Finally, our conclusions are outlined in Sec. V.
-
We use a combination of the following datasets to constrain the neutrino mass and other cosmological parameters:
● CMB
CMB data include the Planck 2018 high-
$ \ell $ $\mathrm{Plik}$ likelihood of the TT power spectrum ($ 30\leqslant\ell \lesssim 2500 $ ), TE cross correlation power spectrum and EE power spectra ($30\leqslant\ell \lesssim 2000$ ) [47], and low-$ \ell $ TT and EE power spectrum ($ 2\leqslant\ell \leqslant 30 $ ) and lensing power spectra [48].● SN Ia
We use the data on the 1048 type Ia supernova in the redshift range
$ 0.01<z<2.3 $ from Pantheon [49], which provides information on the distance modulus versus redshift for each supernova.● BAO
The BAO data include the
$ r_d/D_V $ value of 6dFGS at$ z_\mathrm{eff} = 0.15 $ [50], the$ D_V/r_d $ value of SDSS DR7 at$ z_\mathrm{eff} = 0.15 $ [51], and$ D_A/r_d $ ,$ Hr_d $ at$ z_{\mathrm{eff}} = $ 0.38, 0.51, 0.61 from BOSS DR12 [52], where$ r_d $ is the sound horizon at the baryon drag epoch,$ r_d = \int_{z_d}^{\infty} \dfrac{c_s(z)}{H(z)} \mathrm{d}z, $

(3) and
$ c_s(z) $ is the sound speed of the baryon-photon fluid. The angular diameter distance$ D_A $ is given by$ D_A(z) = \dfrac{1}{1+z} \int_{0}^{z} \dfrac{\mathrm{d} z^\prime}{H(z^\prime)}. $

(4) Then, the definition of
$ D_V $ is$ \begin{array}{*{20}{l}} D_V(z) = \left[(1+z)^2 D_A^2(z) \dfrac{z}{H(z)}\right]^{1/3}. \end{array} $

(5) ●
$ H_0 $ measurementSupernovae and
$ H_0 $ from the Equation of State of dark energy (SH0ES) are measured through a three-step local distance ladder, and the latest$ H_0 $ measurement result is$ H_0 = 73.04 \pm 1.04 $ km s−1Mpc−1 [35]. We adopt the Gaussian prior of$ H_0 $ in our analysis.We perform Markov-chain Monte Carlo (MCMC) sampling using the Python package
$\mathrm{cobaya}$ [53], and the chains is considered converged if the Gelman-Rubin criterion [54]$ R-1 < 0.05 $ is satisfied. -
It is argued that the activation of an axion-like scalar field ϕ around recombination can serve as EDE, potentially resolving the
$ H_0 $ tension [37]. This Axi-EDE can be described by the potential function$ \begin{array}{*{20}{l}} V(\phi) = m^2 f^2 [1-\cos(\phi/f)]^n, \end{array} $

(6) where n is a phenomenological parameter. When
$ n=1 $ , m represents the axion mass and f denotes the axion decay constant. In the context of alleviating$ H_0 $ tension, n is usually chosen to be$ 3 $ . The field is frozen at an initial value owing to Hubble friction and rolls down the potential when the Hubble parameter decreases to a critical level. The field acts as an EDE component before recombination, leading to a reduction the sound horizon at recombination$ r_s(z_*) $ . When the field oscillates around the minimum, its equation of state changes to$w_n = (n-1)/ (n+1)$ . Its energy density dilutes rapidly and hardly affects subsequent cosmological evolution. The fractional energy density of Axi-EDE is defined as$f_{\mathrm{EDE}}(z) \equiv \rho_{\mathrm{EDE}}(z) / \rho_{\mathrm{tot}}(z)$ , and the redshift at which$ f_{\mathrm{EDE}}(z) $ reaches its maximum is denoted as$ z_c $ . For simplicity, we use$ f_{\mathrm{EDE}} $ to represent$ f_{\mathrm{EDE}}(z_c) $ . If m and f are given,$ f_{\mathrm{EDE}} $ and$ z_c $ can be solved numerically. Thus, the Axi-EDE model has 3 additional parameters, namely,$ f_{\mathrm{EDE}}, z_c $ and the initial field value$ \phi_i $ . The robustness of the Axi-EDE model has been evaluated using various datasets [36, 55−57].In [43], the author proposes an EDE model with an AdS phase around recombination to effectively drive the values of
$ f_{\mathrm{EDE}} $ and$ H_0 $ higher. In this model, the potential of the scalar field ϕ is$ \begin{array}{*{20}{l}} V(\phi) = V_0 (\phi/M_{\mathrm{Pl}})^{2n} - V_{\mathrm{AdS}}, \end{array} $

(7) where
$ V_0 $ is a constant,$ V_{\mathrm{AdS}} $ is the depth of the AdS well, and$ M_{\mathrm{Pl}} = 1/\sqrt{8\pi G_N} $ is the reduced Planck mass. The potential function behaves similarly to the Rock ’n’ Roll EDE model (RnR-EDE) [40] when the field is allowed to drop into an AdS phase and climb out of the potential well in the subsequent evolution. The AdS-EDE field is also initially frozen, and$ z_c $ denotes the redshift at which the field begins rolling down. The AdS-EDE model also introduces three extra parameters, namely,$ V_0, \phi_i $ , and$ V_{\mathrm{AdS}} $ . These parameters are typically transformed to$ f_{\mathrm{EDE}} $ ,$ \ln (1+z_c) $ , and$ \alpha_{\mathrm{AdS}} $ . The relationship between$ \alpha_{\mathrm{AdS}} $ and$ V_{\mathrm{AdS}} $ is$ V_{\mathrm{AdS}} \equiv \alpha_{\mathrm{AdS}}[\rho_m(z_c) + \rho_r(z_c)] $ , where$ \rho_m $ and$ \rho_r $ are the densities of matter and radiation, respectively. The AdS-EDE model requires a suitable selection of$ f_{\mathrm{EDE}} $ and$ \ln (1+z_c) $ parameters, i.e.,$ V_{\mathrm{AdS}} $ and$ V_0 $ , to ensure the field does not escape the AdS potential well and prevent a collapsing universe, which is undesirable. This feature will result in a non-zero$ f_{\mathrm{EDE}} $ when constraining AdS-EDE with the CMB alone [58]. It has been shown that the$ H_0 $ value inferred from AdS-EDE with fixed$\alpha_{\mathrm{AdS}} =3.79 \times 10^{-4}$ significantly alleviates the tension [43, 58−60]. Note that the constraints on$ \alpha_{\mathrm{AdS}} $ may be different depending on the datasets used. Therefore, we consider$ \alpha_{\mathrm{AdS}} $ as a free parameter in our analysis.It is commonly assumed that one neutrino has a mass of
$m_\nu = 0.06~{\rm{eV}}$ and the other two neutrinos are massless in cosmological models [5]. We follow this assumption for both the νAxi-EDE and νAdS-EDE base models. However, to constrain the neutrino mass in the NH or IH case, it is necessary to consider three massive neutrino cases in the νAxi-EDE and νAdS-EDE models. To investigate the inclination toward the NH or IH, we also use the neutrino mass hierarchy parameter defined as$ \begin{array}{*{20}{l}} \Delta \equiv \dfrac{m_3 - m_1}{m_1 + m_3}. \end{array} $

(8) With this parameter, we can integrate the NH and IH into a unified model, in which
$ \Delta >0 $ corresponds to the NH and$ \Delta< 0 $ represents the IH. Consequently, the ratio of probabilities between$ \Delta >0 $ and$ \Delta <0 $ can reflect the preference inclination. The neutrino masses can be expressed in terms of Δ [61]:$ m_1 = \dfrac{1-\Delta}{2\sqrt{|\Delta|}} \sqrt{|\Delta m_{31}^2|}, $

(9) $ m_2 = \sqrt{m_1^2 + \Delta m_{21}^2}, $

(10) $ m_3 = \dfrac{1+\Delta}{2\sqrt{|\Delta|}} \sqrt{|\Delta m_{31}^2|}. $

(11) In addition to the 6 parameters in the ΛCDM model, the extra sampling parameters are
$ \{f_{\mathrm{EDE}}, \log_{10}a_c, \phi_i, m_{\min} \} $ for the NH or IH case in the νAxi-EDE model, whereas$ \sum m_\nu $ is a derived parameter. For the νAxi-EDE model with the Δ parameter, the extra sampling parameters are$\{f_{\mathrm{EDE}}, \log_{10}a_c, \phi_i, \Delta \}$ , whereas$ m_{\min} $ and$ \sum m_\nu $ are derived parameters. For the NH or IH case in the νAdS-EDE model, the extra sampling parameters are$\{f_{\mathrm{EDE}}, \; \ln (1+z_c), \alpha_{\mathrm{AdS}},\; m_{\min} \}$ , whereas$ \sum m_\nu $ is a derived parameter. For the νAdS-EDE model with the parameter Δ, the extra sampling parameters are$ \{f_{\mathrm{EDE}}, \ln (1+z_c), \alpha_{\mathrm{AdS}}, \Delta \} $ , whereas$ m_{\min} $ and$ \sum m_\nu $ are derived parameters. To calculate the theoretical prediction of observable quantities, we use modified versions of the$\mathrm{class}$ package for the νAxi-EDE [56]1 and νAdS-EDE models2 . -
We use the
$\mathrm{getdist}$ package [62] to plot the posterior distribution of cosmological parameters and analyze the best-fit parameters. The parameter constraints obtained from MCMC chains are summarized in Table 1. The combination dataset used for analysis is Planck+BAO+Pantheon+SH0ES. The corresponding best-fit values of$ \chi^2 $ are listed in the final line of the table. The one-dimensional posterior distributions of$ m_{\min} $ and$ \sum m_\nu $ for the νAxi-EDE and νAdS-EDE models are shown in Fig. 1. In addition, Fig. 2 shows the posterior of the Δ parameter.νAxi-EDE νAdS-EDE base NH IH base NH IH $ \log(10^{10} A_\mathrm{s}) $ 

$ 3.068\pm 0.015 $ 

$ 3.070^{+0.015}_{-0.016} $ 

$ 3.075\pm 0.016 $ 

$ 3.068\pm 0.015 $ 

$ 3.070\pm 0.015 $ 

$ 3.075\pm 0.015 $ 

$ n_\mathrm{s} $ 

$ 0.9885\pm 0.0063 $ 

$ 0.9898\pm 0.0064 $ 

$ 0.9908\pm 0.0061 $ 

$ 0.9849\pm 0.0056 $ 

$ 0.9854\pm 0.0054 $ 

$ 0.9871\pm 0.0056 $ 

$ \Omega_\mathrm{b} h^2 $ 

$ 0.02284\pm 0.00021 $ 

$ 0.02285\pm 0.00022 $ 

$ 0.02285\pm 0.00021 $ 

$ 0.02303\pm 0.00020 $ 

$ 0.02305\pm 0.00020 $ 

$ 0.02310\pm 0.00020 $ 

$ \Omega_\mathrm{c} h^2 $ 

$ 0.1299\pm 0.0033 $ 

$ 0.1309^{+0.0032}_{-0.0036} $ 

$ 0.1315\pm 0.0035 $ 

$ 0.1284\pm 0.0030 $ 

$ 0.1286\pm 0.0030 $ 

$ 0.1293^{+0.0029}_{-0.0032} $ 

$ \tau_\mathrm{reio} $ 

$ 0.0583^{+0.0069}_{-0.0078} $ 

$ 0.0589^{+0.0072}_{-0.0082} $ 

$ 0.0606^{+0.0071}_{-0.0085} $ 

$ 0.0565\pm 0.0075 $ 

$ 0.0573\pm 0.0076 $ 

$ 0.0589^{+0.0068}_{-0.0078} $ 

$ H_0$ [km s−1Mpc−1]

$ 71.42^{+0.90}_{-0.79} $ 

$ 71.51\pm 0.85 $ 

$ 71.52\pm 0.85 $ 

$ 71.04\pm 0.77 $ 

$ 70.98\pm 0.74 $ 

$ 70.95\pm 0.76 $ 

$ S_8 $ 

$ 0.838\pm 0.012 $ 

$ 0.837\pm 0.013 $ 

$ 0.835\pm 0.013 $ 

$ 0.841\pm 0.013 $ 

$ 0.840\pm 0.013 $ 

$ 0.838\pm 0.013 $ 

$ f_{\mathrm{EDE}} $ 

$ 0.109^{+0.028}_{-0.022} $ 

$ 0.119\pm 0.025 $ 

$ 0.124^{+0.026}_{-0.023} $ 

$ 0.073\pm 0.018 $ 

$ 0.087\pm 0.020 $ 

$ 0.093\pm 0.020 $ 

$ \log_{10}a_c $ 

$ -3.64^{+0.13}_{-0.20} $ 

$ -3.63^{+0.12}_{-0.012} $ 

$ -3.613^{+0.084}_{-0.014} $ 

− − − $ \ln (1+z_c) $ 

− − − $ 8.181^{+0.095}_{-0.11} $ 

$ 8.34\pm 0.10 $ 

$ 8.335\pm 0.094 $ 

$ \alpha_{\mathrm{AdS}} $ 

− − − $< 0.000242 $ 

$< 0.000138 $ 

$< 0.000149 $ 

$m_{\min} /{\rm{ev} }$ 

− $< 0.0429 $ 

$< 0.0437 $ 

− $< 0.0363 $ 

$< 0.0391 $ 

$\sum m_\nu /{\rm{ev} }$ 

− $< 0.152 $ 

$< 0.178 $ 

− $< 0.135 $ 

$< 0.167 $ 

$ \chi^2 $ 

$ 3868.8 $ 

$ 3863.7 $ 

$ 3865.8 $ 

$ 3864.9 $ 

$ 3858.5 $ 

$ 3861.2 $ 

Table 1. Mean values and
$ 1\sigma $ constraints on the cosmological parameters in the base case, considering one massive neutrino, as well as the NH and IH cases of the νAxi-EDE and νAdS-EDE models. The upper limits of$ \alpha_{\mathrm{AdS}} $ ,$ m_{\min} $ , and$ \sum m_\nu $ are at the 95% C.L.
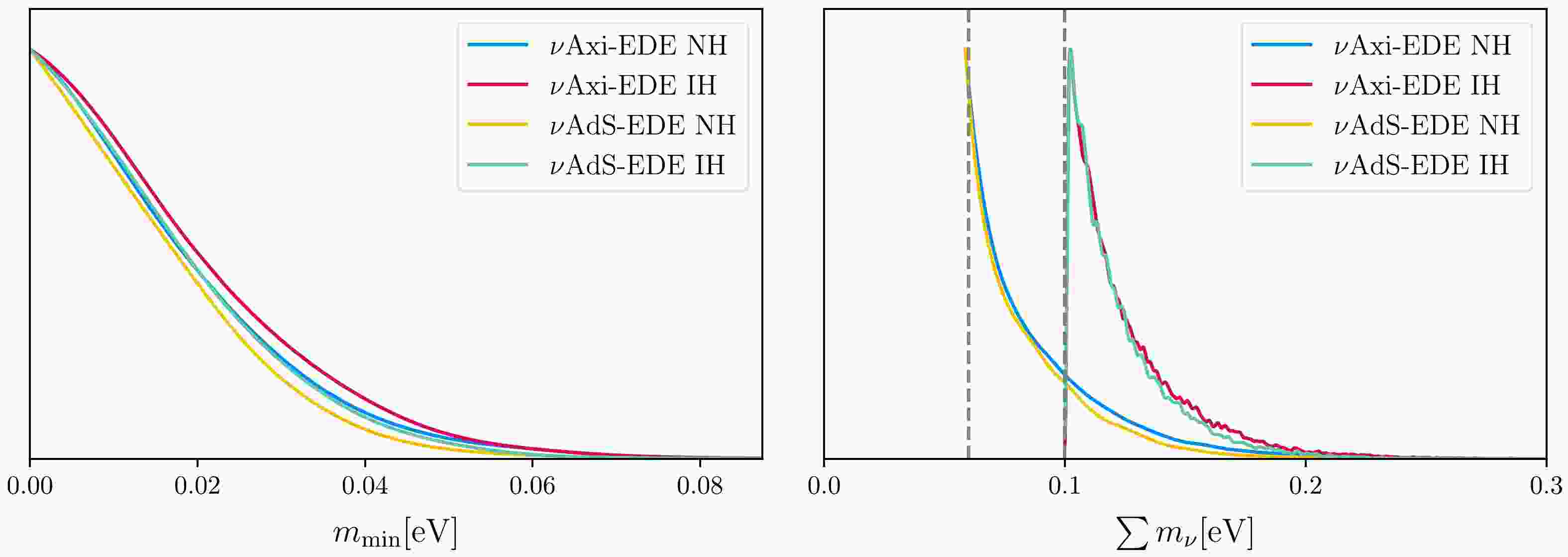
Figure 1. (color online) 1D posterior distribution of
$ m_{\min} $ and$ \sum m_\nu $ for the NH and IH cases in the νAxi-EDE and νAdS-EDE models. The gray dashed lines in the right panel represent the lower limits of$ \sum m_\nu $ in the NH case ($0.06~{\rm{eV}}$ ) and IH case ($0.1~{\rm{eV}}$ ).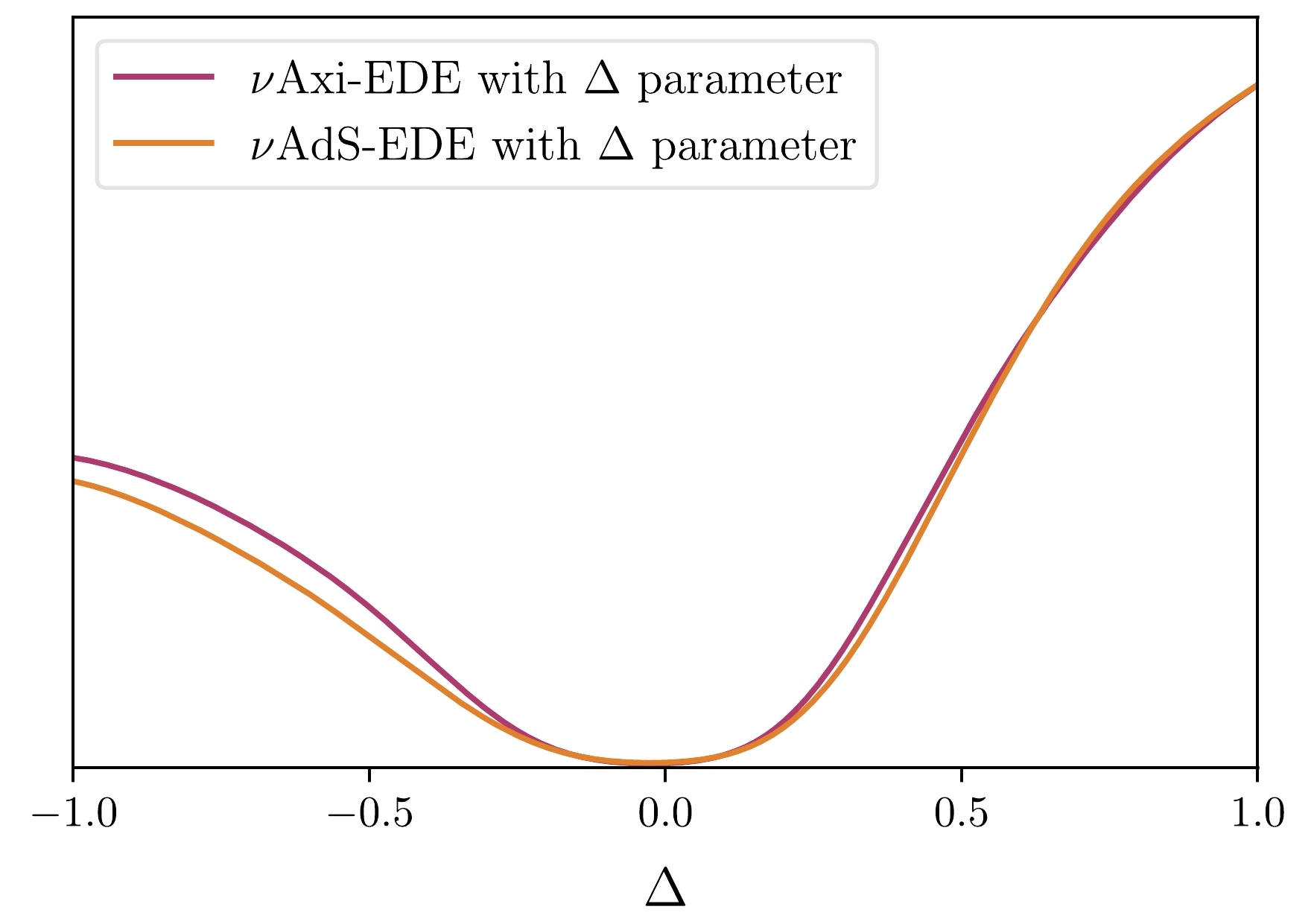
Figure 2. (color online) 1D posterior distribution of the Δ parameter in the νAxi-EDE and νAdS-EDE models.
Axion-like early dark energy (Axi-EDE): For the NH case of the νAxi-EDE model,
$ m_{\min} < 0.0429 $ eV and$ \sum m_\nu < 0.152 $ eV at the 95% C.L., whereas for the IH case,$m_{\min} < 0.0437~{\rm{eV}}$ and$\sum m_\nu < 0.178~ {\rm{eV}}$ at the 95% C.L. Moreover, the constraints on other parameters for the NH or IH case of the νAxi-EDE model exhibit negligible deviations from those in the base case. The NH and IH cases of the νAxi-EDE model exhibit a better fit to the observational datasets, as evidenced by their smaller$ \chi^2 $ values when compared to the base case. Furthermore, the fitting performance of the NH case is better than that of the IH case because$\Delta \chi^2 = \chi^2(\nu\text{Axi-EDE, NH}) - \chi^2 (\nu\text{Axi-EDE, IH}) = -2.1$ .The marginalized probability densities
$ p(\Delta) $ for the NH and IH cases of the νAxi-EDE model with the parameter Δ are plotted in Fig. 2. We can then calculate these two probabilities:$ P(\text{NH}) \equiv P(\Delta > 0) = \int_0^{1} p(\Delta) \mathrm{d}\Delta, $

(12) and
$ P(\text{IH}) \equiv P(\Delta > 0) = \int_{-1}^{0} p(\Delta) \mathrm{d}\Delta. $

(13) The ratio of these two probabilities can be calculated as
$ \begin{array}{*{20}{l}} P(\mathrm{NH}):P(\mathrm{IH}) = 2.11:1 , \end{array} $

(14) indicating that the NH is more favorable than the IH, which aligns with the aforementioned result of the
$ \Delta \chi^2 $ value.Early dark energy with AdS phase (AdS-EDE): The constraints on the minimum neutrino mass in the νAdS-EDE model are
$m_{\min} < 0.0363~{\rm{eV}}$ for the NH case and$m_{\min} < 0.0391~{\rm{eV}}$ for the IH case at the 95% C.L. The constraints on the total neutrino mass are$\sum m_{\nu} < 0.135$ eV for the NH case and$\sum m_{\nu} < 0.167$ eV for the IH case at the 95% C.L. The constraints on parameters other than neutrino parameters in the NH and IH cases of the νAdS-EDE model are not significantly different from those in the base case. Moreover, the NH and IH cases of the νAdS-EDE model fit better than the base case. The discrepancy between the$ \chi^2 $ values in the NH and IH cases is$\Delta\chi^2 =\; \chi^2(\nu\text{AdS-EDE, NH}) - \chi^2\;(\nu\text{AdS-EDE, IH}) \;= -2.7$ . Therefore, the NH case still provides a better fit than the IH case within the framework of νAdS-EDE.For the νAdS-EDE model with the parameter Δ, the ratio of
$ P(\mathrm{NH}) $ and$ P(\mathrm{IH}) $ can be calculated from$ p(\Delta) $ plotted in Fig. 2,$ \begin{array}{*{20}{l}} P(\mathrm{NH}):P(\mathrm{IH})=2.38:1 . \end{array} $

(15) It can be concluded that the NH is more favorable than the IH, which is consistent with the aforementioned result of the
$ \Delta \chi^2 $ value. Comparing the constraints of the neutrino mass and the$ \chi^2 $ values of the above models, we find that the results are congruent. The stringency of the neutrino mass constraints depends on each specific model's characteristics; however, these constraints remain reliable for these two different EDE scenarios. -
In this study, we analyze the constraints on neutrino mass within consistent cosmological models, namely, the νAxi-EDE and νAdS-EDE models. In both models, we assume three massive neutrino mass eigenstates with NH and IH. Additionally, we use the hierarchy parameter Δ in our analysis to evaluate the preference between the NH and IH. We employ a combination of Planck + BAO + Pantheon + SH0ES measurements to constrain the parameters of these models.
The resulting constraint on the minimum neutrino mass in the νAxi-EDE model with the NH is
$m_{\min} < 0.0429 ~ {\rm{eV}}$ at the 95% C.L., and the constraint on the sum of neutrino masses is$\sum m_\nu < 0.152 $ eV. For the νAxi-EDE model with the IH, the neutrino mass constraints are$m_{\min} < 0.0437 ~ {\rm{eV}}$ and$\sum m_\nu < 0.178$ eV both at the 95% C.L. The constraint on the minimum neutrino mass in the νAdS-EDE model with the NH is$m_{\min} < 0.0363$ eV at the 95% C.L., and the constraint on the sum of neutrino masses is$ \sum m_\nu < 0.135 $ eV at the 95% C.L. In the case of νAdS-EDE with the IH, the constraints are$ m_{\min}< 0.0391 $ eV and$ \sum m_\nu < 0.167 $ eV at the 95% C.L.Compared to the νAxi-EDE base model with only one massive neutrino and a total neutrino mass of
$\sum m_\nu = $ 0.06 eV, there is no apparent shift in the constraints on cosmological parameters in the νAxi-EDE models with NH or IH. The$ \chi^2 $ values of the νAxi-EDE model with the NH and IH are both smaller than that of the base case. Additionally, we find that the νAxi-EDE model with the NH fits better with the combination datasets compared to the other two cases. By integrating the probability distribution of the Δ parameter, we find$P(\mathrm{NH}): P(\mathrm{IH}) = 2.11:1$ for νAxi-EDE, indicating a preference for the νAxi-EDE model with the NH over the IH. Similarly, there seems to be no significant deviation of the cosmological parameters in the νAdS-EDE model with the NH or IH compared to those in the base case. The$ \chi^2 $ values of both the NH and IH cases in the νAdS-EDE model are smaller than those in the base case. Furthermore,$P(\mathrm{NH}): P(\mathrm{IH})= 2.38:1$ indicates that the NH case of the νAdS-EDE model provides a better fit to the joint datasets compared to the IH case.By comparing the overall results of the νAxi-EDE and νAdS-EDE models, we find that different hierarchies of three massive neutrino eigenstates give similar results. Thus, it is proved that the parameter constraints of these two EDE models are consistent and reliable.
Cosmological constraints on neutrino mass within consistent cosmological models
- Received Date: 2024-01-29
- Available Online: 2024-06-15
Abstract: Recently, the emergence of cosmological tension has raised doubts about the consistency of the ΛCDM model. To constrain the neutrino mass within a consistent cosmological framework, we investigate three massive neutrinos with normal hierarchy (NH) and inverted hierarchy (IH) in both the axion-like early dark energy (Axi-EDE) and AdS-EDE models. We use joint datasets including the cosmic microwave background power spectrum from Planck 2018, Pantheon of type Ia supernova, baryon acoustic oscillation, and





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF


















 DownLoad:
DownLoad: