Further investigation on the fusion of ⁶Li with ²⁰⁹Bi target at near-barrier energies

Stable weakly-bound nuclei, such as ⁶Li, ⁷Li, and ⁹Be, have low binding energies and strong cluster structures. They frequently undergo a breakup reaction before fusing with the target nucleus, leading to various reaction channels. If the target captures the whole projectile without breakup, it is called direct complete fusion (DCF). If the projectile breakup and all fragments are captured successively by the target, it is regarded as sequential complete fusion (SCF). The complete fusion cross section is the sum of DCF and SCF. Incomplete fusion means that only parts of fragments are captured by the target. Note that the cluster-transfer reaction would lead to the same residuals with ICF, being indistinguishable from the corresponding cross section measurement.

The reaction mechanism induced by weakly bound nuclei has been a hot research topic during recent decades [1, 2], especially in terms of the large number of experiments conducted, such as ⁶Li, ⁷Li, and ⁹Be on ²⁴Mg [3], ²⁸Si [4], ⁹⁶Zr [5],¹⁹⁷Au [6], ¹⁹⁸Pt [7], ²⁰⁹Bi [8, 9], and ²⁰⁸Pb [9] targets. From an experimental point of view, the measurement of ICF cross sections is difficult given that the ICF residues have a significant overlap with that from the CF channel (via evaporation of charged particles). Therefore, one must consider a heavy target nucleus system in which the evaporation of charged particles is typically very small (also predicted by statistical models such as PACE [10−12]). For instance, Dasgupta et al. [13, 14] measured the CF and ICF cross sections for the ⁶Li+²⁰⁹Bi reaction by detecting the α decay events from different residues. Unfortunately, they were unable to obtain an accurate deuteron-captured ICF (d-ICF) reaction cross section. Certain important products cannot be measured in this manner owing to their long lifetime in ground state, such as ²⁰⁹Po, which features a half-life of 102 years. Besides, some products, such as ²¹⁰Po, have a decay chain crossover, resulting in an excessively large cross section. In the present study, CF and ICF cross sections for the ⁶Li+²⁰⁹Bi system were re-measured using in-beam γ-ray measurements. Compared to α decay measurements, this approach provides a more complete deuteron-captured ICF (d–ICF) reaction cross section, which can give rise to a comprehensive description of the reaction mechanism induced by weakly bound projectiles. Furthermore, charged particle measurements can be performed simultaneously with in beam γ-ray measurements, thereby enabling charged particle-γ coincidence measurements and identification of various reaction channels.

From a theoretical point of view, a CDCC-based method was recently proposed to reproduce the CF and ICF cross sections induced by $ ^{6,7} $Li [15, 16] on heavy targets. The fusion process in this method is viewed as the collision between the projectile (P), which consists of two clusters (c1 and c2), and the spherical target (T). To independently handle the interactions between the target and each cluster in the projectile, the CDCC approach is required. This method performs well in the description of CF cross sections of the ⁶Li + ¹²⁴Sn, ¹⁹⁷Au, ¹⁹⁸Pt, and ²⁰⁹Bi systems. However, it lacks experimental data support, especially for ICF data, including the ⁶Li+²⁰⁹Bi system.

This paper is organized as follows. Sec. II introduces the experimental setup. Sec. III elaborates on data analysis and experimental results. Sec. IV demonstrates the theoretical methods whereas Sec. V compares theoretical calculations and experimental data. A summary is provided in Sec. VI.

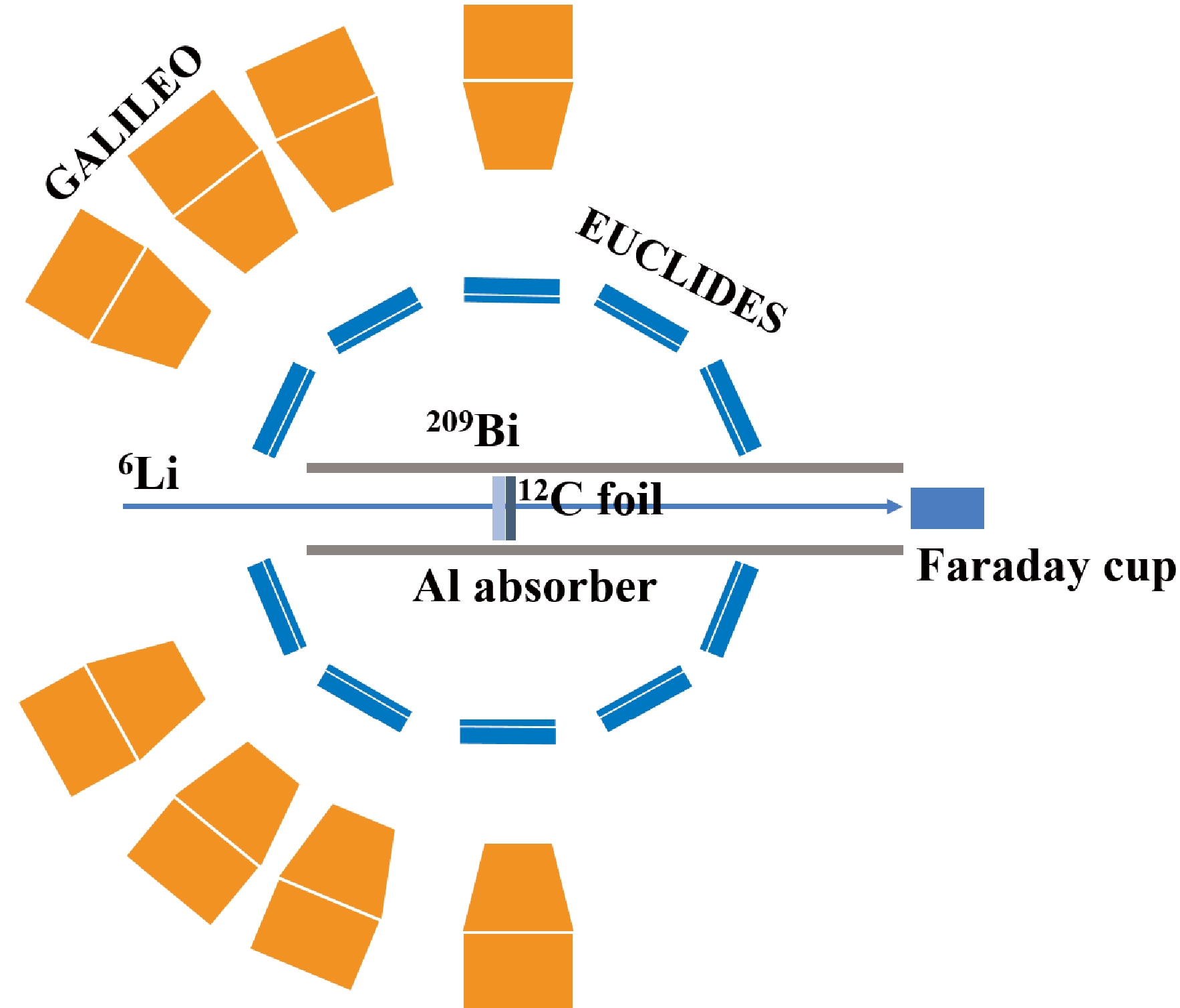
The ⁶Li+²⁰⁹Bi experiment was performed at Legnaro National Laboratories, Italy. A 550-μg/cm$ ^2 \;\; ^{209} $Bi target backed with a 110-μg/cm$ ^2 \;\; ^{12} $C foil was bombarded by the ⁶Li$ ^{3+} $beam with an average intensity of 2.0 enA. The beam energies were 28, 30, and 34 MeV in the laboratory frame, corresponding to approximately 0.99, 1.06, and 1.21 times the Coulomb barrier (derived using the São Paulo potential (SPP) [17, 18]), respectively.

The GALILEO (Gamma Array of Legnaro INFN Laboratories for nuclEar spectrOscopy) array [19] was used to measure the γ transition from different fusion-evaporation residues. The array is composed of 25 Compton-suppressed HPGe tapered detectors organized in four rings at 152°, 129°, 119°, and 90° with respect to the beam direction. There are five detectors in each ring at backward angles, and the last ring at 90° has ten detectors. The distance from the target to the detector is 22.7 cm. The total measured full-energy-peak efficiency was 1.83% at 1408 keV. 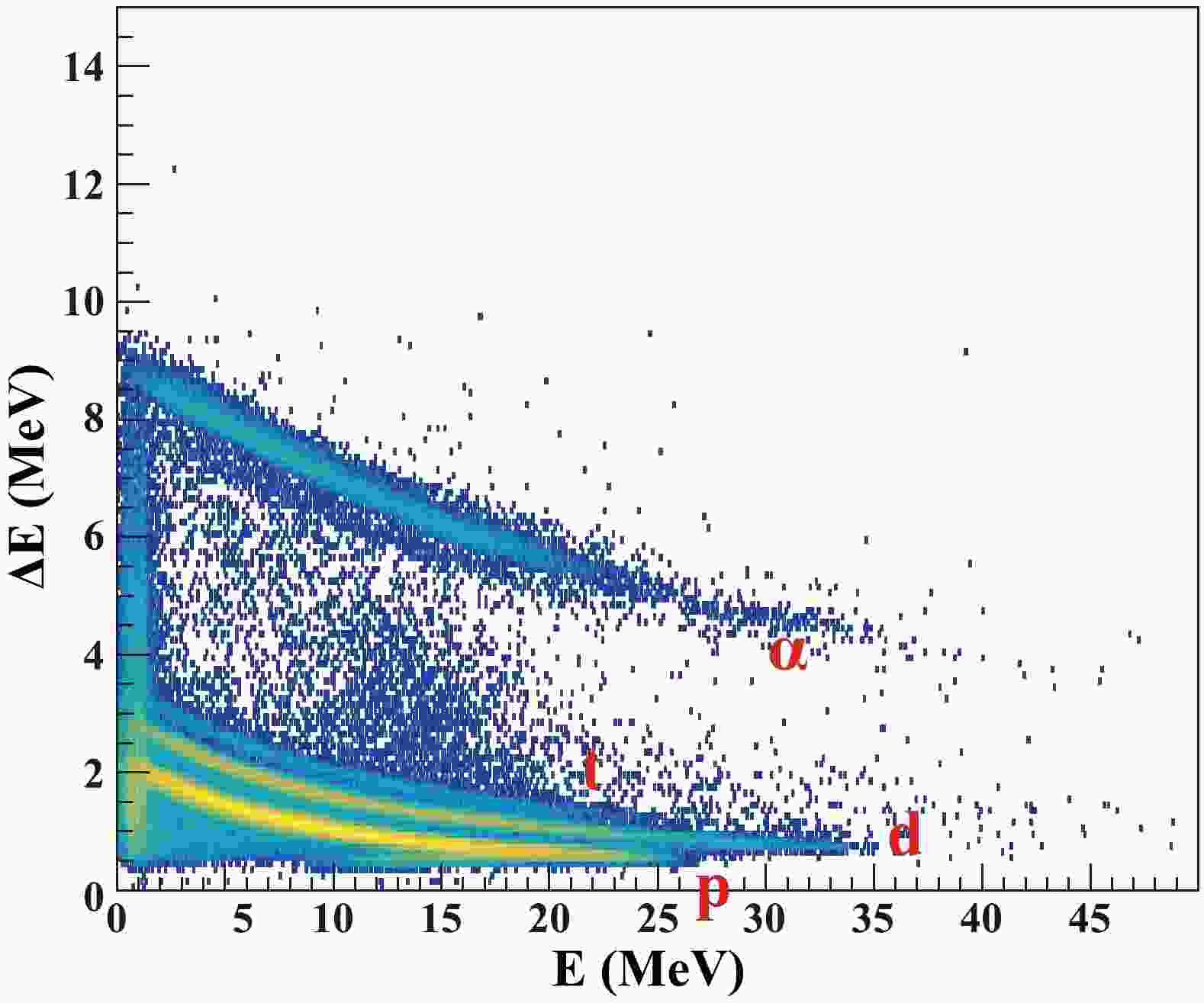The energy resolution was 0.20% at 1408 keV transition of $ ^{152}{\rm{Eu}} $calibration source (FWHM = 2.88 keV). Inside GALILEO, EUCLIDES (EUroball Charged Light particle Identification DEtector Sphere) [20], a ΔE-E telescope array of 40 silicon detectors, is employed for light-charged particle identification. The ΔE and E layers are 130 and 1000 μm thick, respectively. The distance between the ΔE detector and the target is 62 mm. A typical two-dimensional spectrum obtained for the angular ranges covered by the absorber at E$ _{\rm{beam}} $ = 34 MeV is shown in Fig. 1, in which protons, deuterons, tritons, and alphas, labeled as p, d, t, and α, can be clearly identified. To protect the detector from the intense scattering beam, an aluminum cylindrical absorber was inserted inside EUCLIDES along the beam direction. The particle-γ coincidence method was used in this study to identify the different reaction channels. When the beam energy was 34 MeV, the thickness of the cylinder was set to 146 μm, and the backward angles larger than 90° were unshielded by the absorber. In the cases of 30 MeV and 28 MeV, the aluminum absorber covered all angles but with a thickness of 138 μm at 90° and forward angles, and 110 μm at the backward angles. The beam intensity was recorded by a Faraday cup (FC) placed 3 m behind the target. A schematic of the experimental setup is shown in Fig. 2. A detailed description of the experimental setup can be found in Refs. [19, 20].

Figure 1.  (color online) Two-dimensional correlation plot of ΔE vs. E for identification of light charged particles at 30 MeV; p, d, t, and α denote proton, deuteron, triton, and alpha particles, respectively.

Figure 2.  (color online) Schematic of the experimental setup (sectional view). HPGe detectors and ΔE-E telescopes constitute the schematic of part of GALILEO and EUCLIDES arrays, respectively. For further details, see the body text.

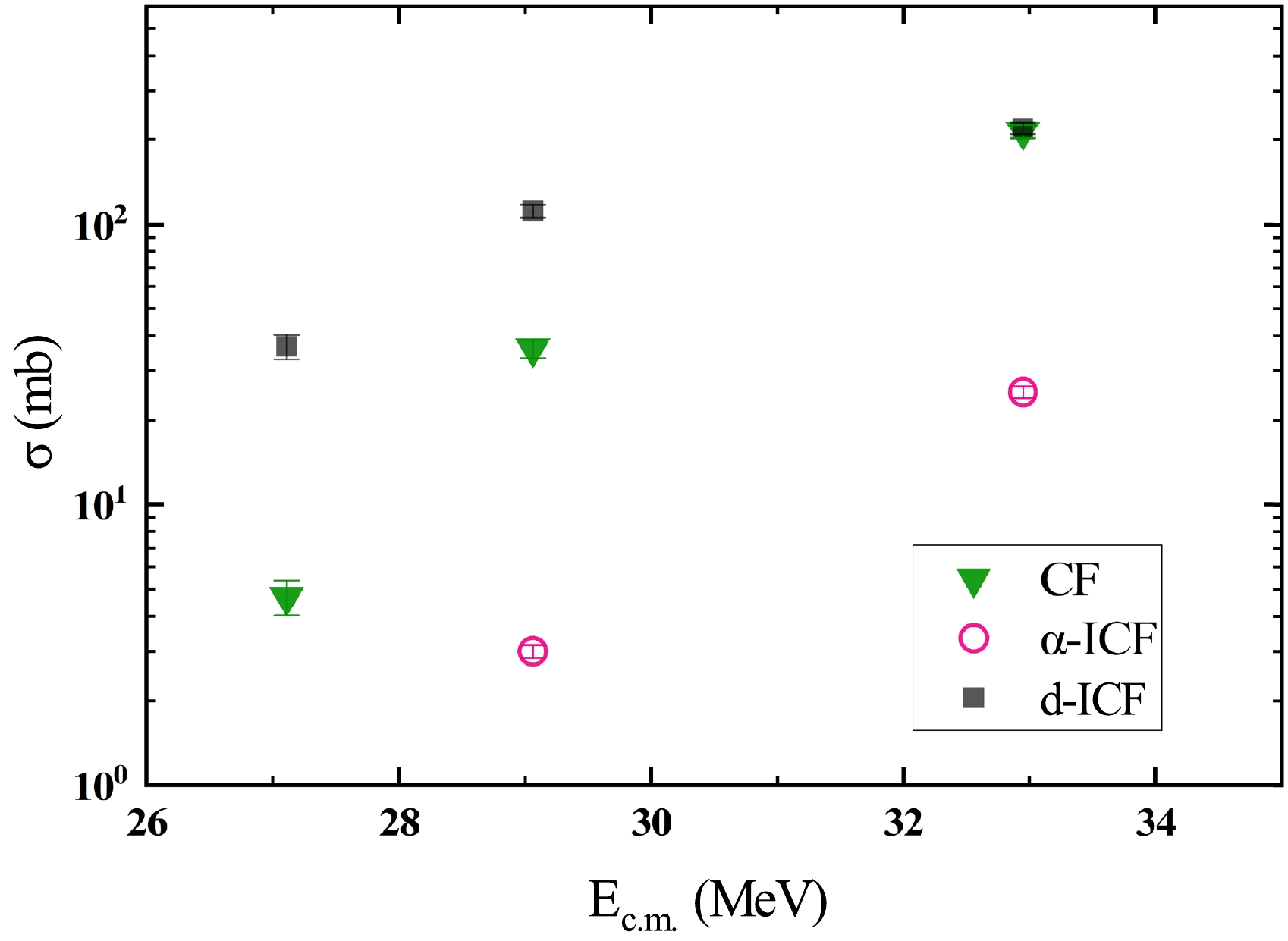
In the ⁶Li+²⁰⁹Bi reaction, the compound nucleus of the complete fusion process is ²¹⁵Rn, producing lighter Rn isotopes by evaporating different numbers of neutrons. Similarly, the products of α-ICF and $ d- $ICF are At and Po isotopes, respectively. The typical in-beam γ-ray spectrum for the ⁶Li+²⁰⁹Bi reaction system at E$ _{\rm{beam}} $ = 34 MeV is shown in Fig. 3 (a), where the identified γ lines for different Rn, At, and Po isotopes are highlighted. The rays used to determine the cross section are marked in blue, whereas the rays of other fusion and transfer products are marked in black. The reaction products of ⁶Li with ¹²C and ²⁷Al are marked in red. The major products of the CF reaction are ²¹²Rn and ²¹¹Rn. For $ d- $ICF, the main products are ²¹⁰Po and ²⁰⁹Po. For α-ICF, the main residues include ²¹²At and ²¹¹At. Figures 3 (b)−(g) show the single γ-ray spectra ((b)−(d), zoom-in parts of (a)) and those gated on deuteron ((e)−(g)) within specific energy regions, respectively. Note that when gated on the measured deuteron, the γ-ray spectra show characteristic γ lines in At isotopes related to the α-capture ICF process. The comparison reveals that, despite being weak, the lower limits of cross section for At isotopes can be determined because several characteristic γ lines are observable in the single γ-ray spectra and, more significantly, in the deuteron gated ones.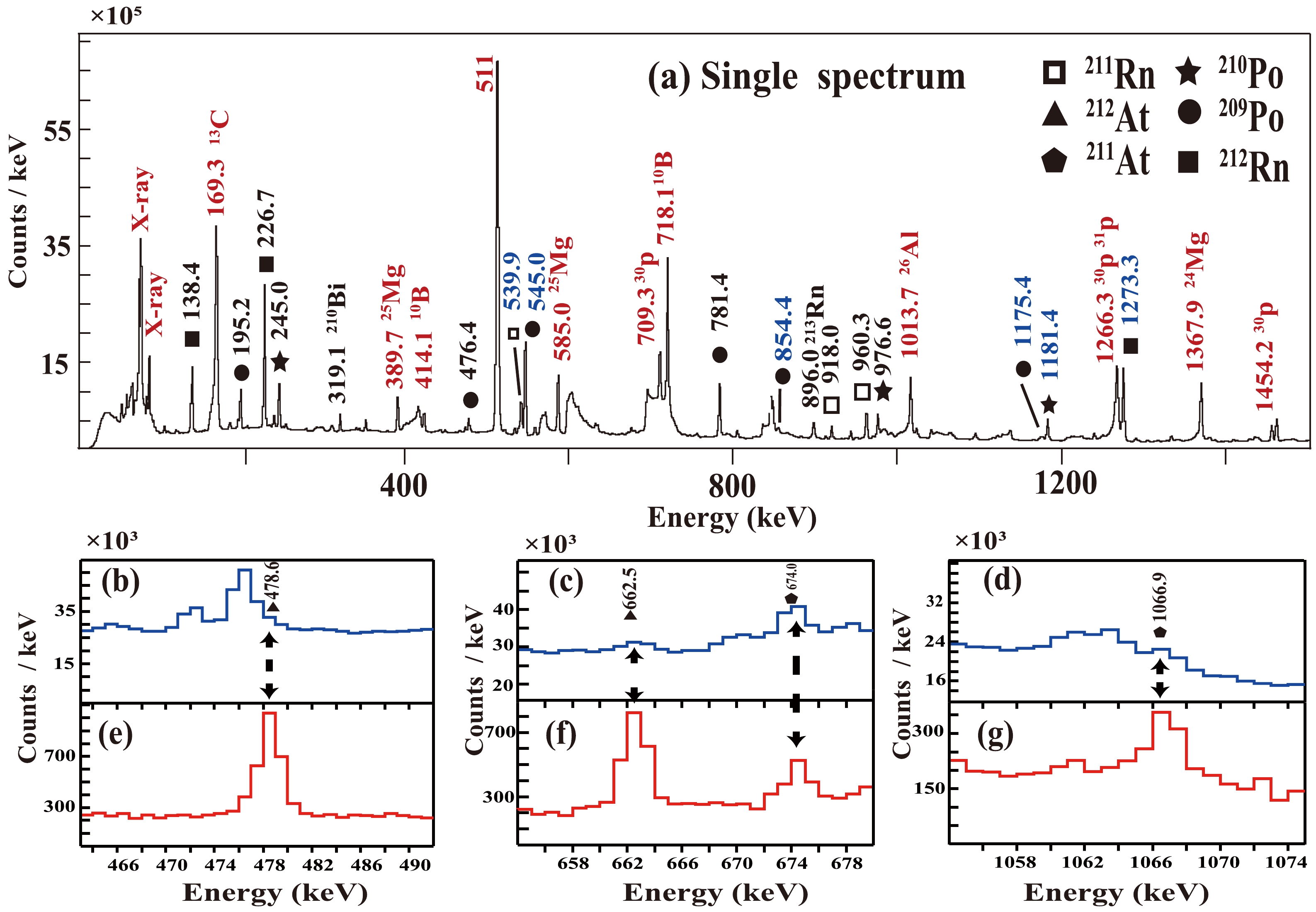

Figure 3.  (color online) (a) In-beam γ-ray spectrum for the ⁶Li+²⁰⁹Bi system at 34 MeV. The rays used to determine the cross section are marked in blue, whereas the rays of other fusion and transfer products are marked in black. The reaction products of ⁶Li with ¹²C and ²⁷Al are marked in red; (b)−(g) compare the single γ-ray spectra ((b)−(d)) with those gated on deuteron ((e)−(g)) within specific energy regions, stressing the fact that, despite being weak, several characteristic γ lines in At isotopes can still be measured in this experiment.

In the present study, all the observed γ transitions feeding (directly) the ground state or long-lived isomers were collected to determine the yield of the specific isotope. Detailed information about the γ transitions and related information in each nucleus is summarized in Table 1 [21−26]. In such a situation, only the production of excited states in the evaporation residues can be measured, and the cross sections can be determined as follows:

Residual channels	Transition	$ E_{\gamma} $/keV
211Rn(CF, 4n)	5/2$ ^- $$ \rightarrow $ 1/2$ ^- $	539.9
212Rn(CF, 3n)	2$ ^+ $$ \rightarrow $ 0$ ^+ $	1273.7
209Po($ d- $ICF, 2n)	5/2$ ^- $$ \rightarrow $ 1/2$ ^- $	545.0
	3/2$ ^- $$ \rightarrow $ 1/2$ ^- $	854.4
	5/2$ ^- $$ \rightarrow $ 1/2$ ^- $	1175.4
210Po($ d- $ICF, 1n)	2$ ^+ $$ \rightarrow $ 0$ ^+ $	1181.4
211At(α-ICF, 2n)	13/2$ ^- $$ \rightarrow $ 9/2$ ^- $	1066.9
	7/2$ ^- $$ \rightarrow $ 9/2$ ^- $	674.0
212At(α-ICF, 1n)	11$ ^+ $$ \rightarrow $ 9$ ^- $	662.5
	10$ ^- $$ \rightarrow $ 9$ ^- $	478.6

Table 1.  Reaction channels and characteristic γ rays counted in the ⁶Li+²⁰⁹Bi system.

Here, n represents the number of γ transitions directly feeding the ground state or long-lived isomer in the same residue; $ A_{E_{\gamma i} } $denotes the counts of measured γ rays with energy $ E_{\gamma i} $; $ \varepsilon _{E_{\gamma i}} $ accounts for the efficiency; $ F_{E_{\gamma i}} $ is the inner conversion electron rate; and $ N_{B} $ and $ N_{T} $ are the numbers of beam particles and target nuclei, respectively. The total uncertainty in the measurement of cross sections comes from (1) statistical errors associated with the yields of γ-rays; (2) errors in the determination of absolute efficiency; (3) the error in the beam intensity normalization process, which includes the experimental error of ²¹²Rn in Ref. [14]; and (4) the uncertainty in the target thickness. The overall error bar ranges from 7% at E$ _{\rm{beam}} $=34 MeV to approximately14% at E$ _{\rm{beam}} $=28 MeV.

However, owing to the existence of dark currents from the Faraday cup, the beam intensity measurement becomes unreliable in this experiment. As mentioned in the introduction, the same ⁶Li+²⁰⁹Bi experiment was previously conducted using a different method [14] in which the beam intensities were measured precisely. In the present study, one specific isotope, ²¹²Rn (the one with the highest cross sections among CF residues for all the energies used in the conducted experiment, see Table 2 in Ref. [14]), was employed for the normalization of the beam intensity. As a result, cross sections for ²¹²Rn identical to those reported in Ref. [14] were obtained in this study (as shown in Table 2) for the same energies. Note that the error bar is independent for each work. All the measured cross sections for each isotope in this experiment are displayed with normalized beam intensity in Table 2 and Fig. 4. This in-beam γ-ray method can only collect the transitions feeding the ground states or long-live isomers, giving rise to a lower limit for the cross section because the part that directly populates the ground state or long-lived excited states cannot be considered.

$ E_{\rm{beam}} $/MeV	28	30	34
$ E_{\rm{c.m.}} $/MeV	27.11	29.06	32.95
$ \sigma_{^{211}{\rm{Rn}}} $/mb	–	–	39.64 $ \pm $ 2.89
$ \sigma_{^{212}{\rm{Rn}}} $/mb	4.70 $ \pm $ 0.68	36.10 $ \pm $ 2.70	175.20 $ \pm $ 12.25
$ \sigma_{{\rm{CF}}} $/mb	4.70 $ \pm $ 0.68	36.10 $ \pm $ 2.70	214.84 $ \pm $ 12.59
$ \sigma_{^{209}{\rm{Po}}} $/mb	19.20 $ \pm $ 2.67	69.54 $ \pm $ 4.85	167.49 $ \pm $ 10.91
$ \sigma_{^{210}{\rm{Po}}} $/mb	17.53 $ \pm $ 2.53	42.14 $ \pm $ 3.15	52.84 $ \pm $ 3.69
$ \sigma_{d-{\rm{ICF}}} $/mb	36.73 $ \pm $ 3.67	111.68 $ \pm $ 5.79	220.33 $ \pm $ 11.51
$ \sigma_{^{211}{\rm{At}}} $/mb	–	0.71 $ \pm $ 0.06	13.73 $ \pm $ 0.91
$ \sigma_{^{212}{\rm{At}}} $/mb	–	2.29 $ \pm $ 0.15	11.47$ \pm $ 0.77
$ \sigma_{\alpha-{\rm{ICF}}} $/mb	–	3.00 $ \pm $ 0.16	25.20 $ \pm $ 1.19

Table 2.  Experimental integrated cross sections of each isotope with incident beam energies of 28, 30, and 34 MeV; E$ _{\rm{c.m.}} $ is corrected for energy losses in the target.

Figure 4.  (color online) Experimental excitation functions of CF and ICF channels.

The CF cross sections are consistent with previous results in Ref. [14], confirming the feasibility of the proposed measurement procedure. However, the $ \alpha- $ICF cross section is the lower bound for this quantity. This is due to the underestimation of the cross section of ²¹²At. The complete measurement of the ²¹²At cross section becomes impossible because many transitions feeding the ground state or long-lived isomers have insufficient intensity during the experiment. In addition, owing to the fact that ²¹²At is an odd-odd nucleus, the level scheme is complicated. Thus, there could be unknown transitions that may feed the ground or long-lived isomeric states in ²¹²At and are not taken into account in the cross section measurement.

For the $ d- $ICF channel, the cross section of ²⁰⁹Po was measured for the first time with a relatively large value, as shown in Table 2. Conversely, the present study also provides a cleaner cross section for ²¹⁰Po populated in the fusion process. The reason is explained below. In the ⁶Li + ²⁰⁹Bi system, the single neutron transfer reaction has an appreciable cross section, producing ²¹⁰Bi, whose ground state undergoes β decay to ²¹⁰Po. Given that the ²¹⁰Bi $ \rightarrow \;\; ^{210} $Po β decay channel has a Q value of 1.16 MeV, which is smaller than the first excited state in ²¹⁰Po (2$ ^{+} $at 1.18 MeV), only one β decay branch can exist, which feeds the ground state in the daughter nucleus. As a result, the measurement of α decay events (de-exciting the ground state of ²¹⁰Po) would be affected by the production of ²¹⁰Bi. In in-beam γ-ray measurements, only γ rays that de-excite the excited states would be collected. Therefore, the existence of ²¹⁰Bi would have no influence at all.

Comparing the observed CF and ICF cross sections shown in Fig. 4, it is evident that for the ⁶Li+²⁰⁹Bi system, CF and ICF are comparable at energies above the Coulomb barrier; however, the CF cross section drops more rapidly as energy decreases. A detailed discussion of these results is provided in Sec. V.

We adopted the theoretical model reported in Ref. [16] to analyze the CF and ICF data. In this model, the projectile is treated as a system of two clusters, $ c_1 $ and $ c_2 $, which, in the case of ⁶Li, are$ ^2{\rm{H}} $ and $ ^4{\rm{He}} $, respectively. These clusters are bound by an energy $ B=1.47 $ MeV. The spectroscopic amplitude for this cluster configuration in the g.s. of ⁶Li was empirically determined in Ref. [16]. The derived value was 0.7 (see Eqs. ($ 16 $) and ($ 18 $) in Ref [16]); it is slightly less than 1.0.

The collision dynamics is determined by the full Hamiltonian of the system:

where $ h({\bf{r}}) $ is the intrinsic Hamiltonian describing the relative motion of the clusters within the projectile, $ \hat{T}_{\bf{R}} $ is the kinetic energy operator associated to the center of mass projectile-target relative motion, and $ \mathbb{V}({\bf{R}},{\bf{r}}) $ is the real part of the projectile-target interaction, represented by

where $ \mathbb{V}^{(i)} $ denotes the interaction between fragment $ c_i $ and the target.

In Eq. (2), $ \mathbb{W}({\bf{R}},{\bf{r}}) $ is the imaginary potential that accounts for the absorption of different fusion processes. To simulate the effects of fusion, note that the imaginary potential, which exhibits a short range, must be very absorptive. This is equivalent to the ingoing-wave boundary condition in barrier penetration model (BPM) calculations, and does not depend on the Woods-Saxon potential [27]. It must ensure total absorption in the inner region of the barrier and vanish elsewhere.

In the coupled channel method, the total wave function of the system undergoes a channel expansion. This expansion must include all channels that are relevant to the collision dynamics. In the case of tightly bound systems, they are labeled by a set of discrete quantum numbers denoted by α. The situation is more complicated in collisions of weakly bound nuclei, where the collision dynamics is strongly influenced by breakup channels. In this case, the channel expansion must also include intrinsic states in the continuum. In this way, α includes a continuous quantum number, ε, corresponding to the relative energy of the clusters. Thus, the coupled channel method would lead to infinite coupled equations. This issue is addressed by applying the continuum discretized coupled channel (CDCC) approach [28, 29], which replaces the infinite set of states in the continuum by a finite set of wave packets ($ {\it bins} $), $\phi_n \,(n=1,\,2,...,N)$, generated by superposing scattering states between fragments with a definite angular momentum in an energy interval, each one centered at one of the energies of the set $\{\varepsilon_{1},\;\varepsilon_{2}$,...., $ \varepsilon_{N} \}$. Then, the total wave function of the system, $ {\rm{\Psi}}^{{\rm{}} (+)}({\bf{R}},{\bf{r}}) $, can be expanded in this new basis of states and expressed as

where $ \Psi_{0}({\bf{R}},{\bf{r}}) $ and $ \Psi_{\rm{bu}}({\bf{R}},{\bf{r}}) $ are the wave functions of the elastic channel and breakup wave function within the CDCC approach, respectively; $ {\bf{R}} $ is the vector joining the centers of mass of the collision partners; and $ {\bf{r}} $ is the vector between the two clusters.

Inserting Eq. (4) into the full Schrödinger equation of the system and taking a scalar product with each of the intrinsic states, the following set of $ N+1 $ coupled equations is obtained:

where $ E_n = E - \varepsilon_n $ is the relative energy in channel n, and $ U_{\rm{nm}}({\bf{R}}) $ are the matrix elements of the total projectile-target interaction. These matrix elements are expressed as follow

where

The expectation value of $ \mathbb{V}({\bf{R}},{\bf{r}}) $ with respect to the ground state of the projectile plays the role of the real part of the optical potential in the elastic channel,

where $ \phi_{0}({\bf{r}}) $ is the ground-state wave function of the projectile. A similar potential is obtained for the other channels by changing the g.s. wave function by the wave function of the corresponding state of the projectile. Throughout this paper, we use the São Paulo potential [17, 18] for the real part of the nuclear interactions between the two clusters and the target ($ \mathbb{V}^{{\rm{}} (1)} $ and $ \mathbb{V}^{{\rm{}} (2)} $).

The imaginary part of the optical potential in Eq. (2), must account for both CF and ICF processes. To satisfy the latter requirement, the imaginary potential within the continuum discretized space must have the general form

Here, $ {r_i}\, (i=1,2) $ is the distance between the cluster $ c_i $ and the target, and the imaginary potential $ \mathbb{W}^{{\rm{}} (i)}(r_i) $ accounts for the absorption of the cluster $ c_i $ by the target. These potentials are parametrized by the short-range Woods-Saxon functions,

where $ W_0 = 50 $ MeV, $ r_{\rm{w}} = 1.0 $ fm, and $ a_{{\rm{}} w} = 0.2 $ fm.

However, it was shown [16] that this potential leads to wrong CF cross sections at sub-barrier energies. The long tail of the g.s. wave function of ⁶Li leads to absorption at large distances that cannot be associated to CF (a detailed discussion on this issue can be found in Ref. [16]). This problem is eliminated by adopting a different potential in the space of bound channels (only the elastic channel in the case of ⁶Li). In this space, we use the imaginary potential,

where $ R_{\rm{w}}=r_{\rm{w}}(A^{1/3}_1 +A^{1/3}_2) $,$ W_0 = 100 $ MeV, $ r_{\rm{w}} = 1.0 $ fm, and $ a_{{\rm{}} w} = 0.2 $ fm. This potential, which is diagonal in the channel space, accounts for the absorption of the whole projectile by the target, ignoring the cluster structure of the projectile.

Thus, we use the imaginary potential of Eqs. (10) and (11) to evaluate matrix elements of the imaginary potential between CDCC bins, and that of Eq. (12) to evaluate the diagonal matrix-element in the elastic channel. As in Refs. [15, 16, 30], we neglect matrix elements of the imaginary potential between bound and unbound channels. This is the approximation of our method. We have no hypothesis for the physical meaning of these couplings concerning the fusion cross sections (they correspond neither to CF nor ICF). For consistency, we do not consider these couplings in the CDCC calculations.

The Hamiltonian of the projectile from Eq. (2) is

where $ \mu_{{\rm{}} 12} = m_0\,A_{{\rm{}} 1} A_{{\rm{}} 2}/\left(A_{{\rm{}} 1} + A_{{\rm{}} 2}\right) $ is the relative motion reduced mass, $ m_0 $ is the nucleon mass, and $ A_{{\rm{}} 1}, A_{{\rm{}} 2} $ are the cluster masses. Concerning the $ v_{{\rm{}} 12}(r) $ potential, the Woods-Saxon function is usually employed for CDCC calculations. Its parameters are varied to reproduce the binding energy of the ground state, as well as the position and width of the main resonances. We adopted the parameters reported in Ref. [16].

The projectile-target interaction was expanded in multipoles, keeping multipolarities up to $ \lambda_{{\rm{max}} } = 4 $. The continuum was discretized using the binning method and considering orbital angular momenta between clusters up to $ l_{{\rm{max}} }=3\hbar $. The discretization was performed in the energy space and finer meshes were used around sharp resonances. The ⁶Li g.s. state is $ 1^+ $ with $ j=1\hbar $ and $ l=0\hbar $. For further details, see Ref. [16].

CDCC calculations yield the following cross sections:

where $\mathcal{P}^{\rm DCF}$ corresponds to the probability of the absorption of whole projectile from g.s. and $ \mathcal{P}^{ (i)} $ is the probability of absorption of fragment $ c_i $ following the breakup. The expressions for these probabilities are given in the appendices of Ref. [30]. Moreover, $ \sigma_{{\rm{}} F}^{{\rm{}} (i)} $ corresponds to the inclusive cross section of fragment $ c_i $, regardless of the state of the other cluster; this does not match with the measurements of the exclusive experiments.

To determine the SCF or ICF cross sections, it is necessary to introduce a model which relates $ \mathcal{P}^{ (1)}(J) $ and $ \mathcal{P}^{ (2)}(J) $ to ICF and SCF probabilities. Following Ref. [16], we treat $ \mathcal{P}^{ (1)}(J) $ and $ \mathcal{P}^{ (2)}(J) $ as probabilities of independent events, and using classical statistics, we introduce

To determine the DCF, SCF, and contribution of each fragment to the ICF cross section, we used CF-ICF computer code (unpublished), which evaluates the projected angular momentum version of the expressions derived in Appendix A of Ref. [30]. These expressions involve intrinsic states of the projectile and scattering wave functions obtained by running the CDCC version of the code FRESCO [31]. The theoretical cross sections for the different fusion processes involving the absorption from continuum states are then given by

The ICF cross section is the sum of the corresponding quantity for each cluster, i.e.,

The CF and TF cross sections are defined by

We used this method in the present study to analyze fusion reactions in collisions of the $ ^{6}{\rm{Li}} $ projectile with the ²⁰⁹Bi target, for which there are experimental data available in Ref. [14]. In addition, new measurements were performed in this study using different experimental techniques.

Next, we apply the theoretical model proposed in Ref. [16] to analyze the data of the present study as well as other fusion data available in the literature for the same system.

Figure 5 shows the CF data of the present study in comparison with the data reported by Dasgupta et al. [14] and the CDCC predicted cross section reported in Ref. [16]. The figure also shows the fusion cross section predicted by the BPM considering the São Paulo potential for the ⁶Li + ²⁰⁹Bi system and neglecting the cluster structure of ⁶Li. Note that the CF data of the present study agree well with the data reported by Dasgupta et al. [14] and with the cross section predicted by CDCC. By contrast, the experimental cross sections are larger than the BPM cross section at sub-barrier energies. However, at energies above the Coulomb barrier, the experimental values are smaller than those of BPM.

Figure 5.  (color online) Theoretical CF cross section in collision of ⁶Li with the target ²⁰⁹Bi. The cross section calculated by our model is compared with the data reported in Refs. [13, 14] (⁶Li $ + ^{209} $Bi) and the measurements performed in this study. Besides, the dashed line represents the results obtained considering the BPM approach.

The validity of the CDCC calculation can also be checked by comparing the theoretical and experimental CF barrier distributions [32],

where E is the collision energy in the center-of-mass frame. In the present study, the theoretical barrier distribution was evaluated by the 3-point formula based on the Taylor expansion of $E\sigma_{\rm CF}(E)$ using the mesh step; the detailed procedure can be found in Ref. [33]. Here, the experimental data were solely taken from Ref. [14] given that the new data obtained in this study only cover three energies, reasonably coinciding with the previous ones.

From the comparison shown in Fig. 6, one observes that the CDCC calculation slightly underestimates the experimentally measured barrier distribution; this is more evident for the high-energy region (beam energy greater than 30 MeV, as shown in Fig. 6). This phenomenon is consistent with the situation in Fig. 5(b) where the CDCC slightly underestimates the measured CF cross sections. The possible reasons could be (1) the barrier (V$ _{00} $ according to Eq. (9)) might be too attractive, especially when assuming that the breakup coupling is considered correctly in the proposed CDCC calculation, or (2) V$ _{00} $ is correct, but the calculated ICF cross section with the same barrier is too large. The second reason seems reasonable only from the perspective of the comparison for ICF cross sections provided in the following subsection. However, a final conclusion cannot be established at the current stage because the obtained cross sections for ICF constitute only the lower bound owing to experimental difficulties, as mentioned in the introduction and the detailed experimental sections. Owing to the limitation of the in-beam γ-ray measurement method, we were unable to obtain the counts of some γ-rays with very weak intensity because they were masked by the background; consequently, it was impossible to calculate their yield. Therefore, the lower limit of cross section is provided. Thus, a more conclusive result demands higher precision of measurements in future studies.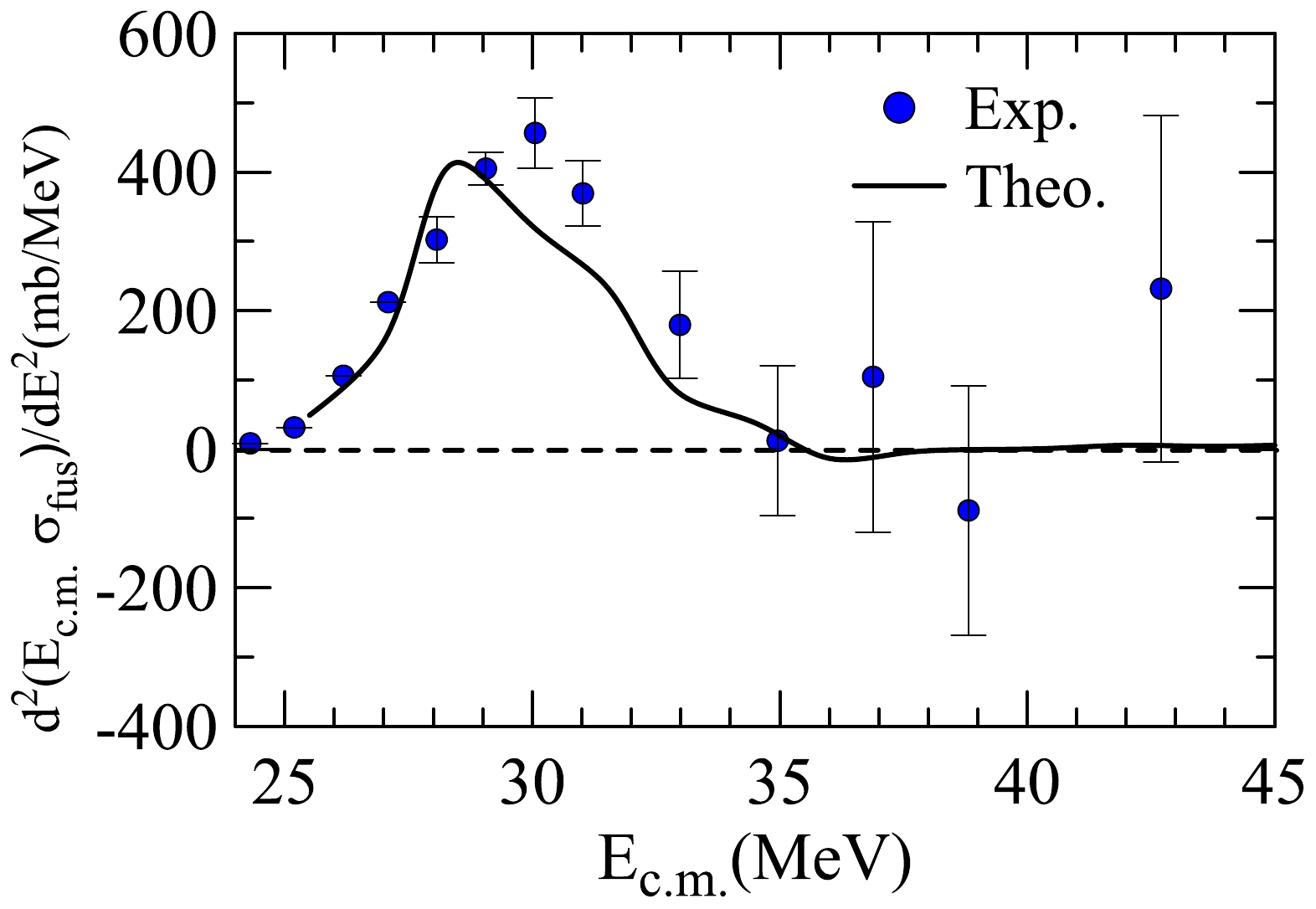

Figure 6.  (color online) Experimental barrier distribution for the ⁶Li+²⁰⁹Bi complete fusion cross section compared with the theoretical one derived from the theoretical CF cross sections considered in this study.

Concerning the comparison with BPM calculation, a crucial issue in the CF of weakly bound projectiles is the question of hindrance or enhancement in collisions of various targets in different energy regimes. The low binding energies of the clusters give rise to a long tail in the g.s. wave function of the projectile. This effect leads to a lower Coulomb barrier, which in turn enhances the fusion cross section at all collision energies. By contrast, the low breakup threshold leads to strong couplings with the breakup channels. These couplings give rise to ICF, suppressing CF. The behavior of the CF data is dictated by the competition of these two opposite tendencies.

Figure 7 shows the Coulomb barriers associated with the nuclear potential that considers the cluster structure of ⁶Li and the one that neglects it. The former, denoted by $ V_{00}(R) $, is the expectation value of the potential of Eq. (3) with respect to the g.s. wave function of ⁶Li (see Eq. (9)). The latter is the standard São Paulo Potential for the ⁶Li + ²⁰⁹Bi system, denoted by $ V_{\rm{PT}}(R) $. The barrier parameters for both potentials are listed in Table 3. In this case, the low binding energy of the clusters leads to barrier lowering: $ \Delta V_{\rm{B}} \equiv V_{\rm{B}}^{\rm{PT}} - V_{\rm{B}}^{00} = 1.6 $ MeV.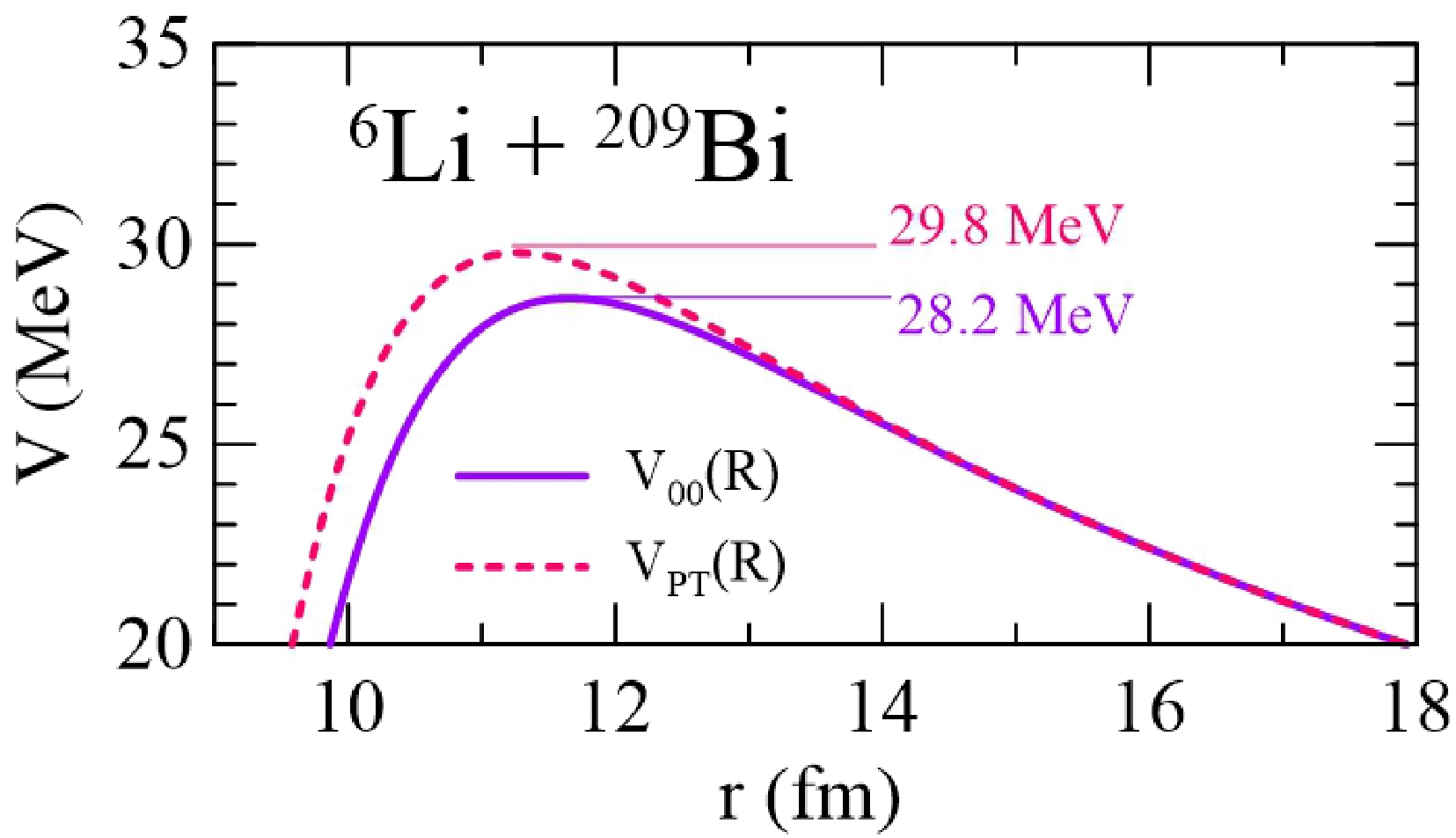

Figure 7.  (color online) Coulomb barriers of the potentials $ V_{{\rm{PT}} }(R) $ and $ V_{00}(R) $ obtained for the ⁶Li $ + ^{209} $Bi system.

Potential/Parameter	$ R_{\rm B} $/fm	$ V_{\rm B} $/MeV	$ \hbar \omega $/MeV
$ V_{{\rm{PT}} }(R) $	11.3	29.8	4.8
$ V_{00}(R) $	11.8	28.2	4.4

Table 3.  Barrier parameters for the potentials $ V_{{\rm{}} 00}(R) $ and $ V_{{\rm{PT}} }(R) $ for the system analyzed in this study.

Systematic studies of suppression and enhancement of CF in collisions of weakly bound projectiles are usually carried out in terms of reduced cross sections. The reduction procedure aims at eliminating trivial differences in the cross sections arising from the charges and sizes of the collision partners (a review of these methods can be found in Ref. [34]). We adopt here the fusion function reduction method proposed by Canto et al. [35, 36]. This method consists of the following transformations:

where $ R_{{\rm{B}} },V_{{\rm{B}} } $, and $ \hbar\omega $ are the parameters of the parabolic approximation to the Coulomb barrier. The reduced cross section $ F(x) $ is the fusion function associated with the cross section $ \sigma_{\rm{F}} $. In an ideal situation in which there are no channel coupling effects and the one-channel fusion cross section is well described by the Wong formula [37], $ F(x) $ reduces to the universal fusion function (UFF):

Thus, $ F(x) $ deviations with respect to the UFF may indicate that channel couplings influence the fusion cross section. However, they may also indicate that the Wong formula is invalid in the corresponding energy region. It is well known (see for instance Refs. [1, 36]) that the Wong formula overestimates the one-channel cross section of light and intermediate-mass systems ($ Z_{\rm{P}}\times Z_{\rm{T}} < $ 500) at sub-barrier energies. To reach any reliable conclusion about the influence of nuclear structure properties, this possibility must be discarded. This can be achieved by replacing $ F(x) $ with a renormalized fusion function defined as

To evaluate the renormalized fusion function associated with the experimental cross section, denoted as $ {\overline F}_{\rm{exp}}(x) $, a reference potential must be selected. This potential yields the barrier parameters appearing in Eq. (27) and the BPM cross section in Eq. (29). The first possibility is to use the standard São Paulo potential for the ⁶Li + ²⁰⁹Bi system, $ V_{\rm{PT}}(R) $. Another possibility is to adopt the potential $ V_{00}(R) $. The fusion functions evaluated with these potentials are denoted as $ {\overline F}_{\rm{exp}}^{\,\rm PT}(x) $ and $ {\overline F}_{\rm{exp}}^{\,\rm 00}(x) $, respectively. A detailed discussion of these fusion functions is presented below.

Given that the potential $ V_{\rm{PT}}(R) $ completely ignores the cluster structure of ⁶Li, comparing $ {\overline F}_{\rm{exp}}^{\,\rm PT}(x) $ with the UFF, we can assess the net effect of the low binding energy of the clusters in ⁶Li, that is, the result of two opposing trends: the enhancement arising from the barrier lowering and the suppression resulting from breakup couplings. The results are shown in logarithmic (Fig. 8(a)) and linear (Fig. 8(b)) scales. The first scale is more appropriate for showing the coupling effects below the Coulomb barrier, while the second is more suitable for the energy regime above this barrier, where the hindrance due to the breakup is usually studied. Compared to UFF, $ {\overline F}_{\rm{exp}}^{\,\rm PT}(x) $ is enhanced below the Coulomb barrier and suppressed at energies above this barrier. In the lower energy region, the fusion function gets close to the curve corresponding to the UFF multiplied by the factor 0.6, represented by the dashed line in the linear plot. This indicates that the fusion function is suppressed by 40% when using $ V_{\rm{PT}}(R) $, which is a result similar to that obtained in Ref. [14], in which the experimental barrier was used in the theoretical calculations. Therefore, it is not unexpected that the $ V_{\rm{PT}}(R) $ gets close to the measured barrier (30.0 $ \pm $ 0.3 MeV in Ref. [14]) given that the experimental barrier has to consider all the coupling effects. As mentioned before, the opposing trends of clustering (lowering barrier) and breakup couplings (increasing barrier) might almost cancel their difference.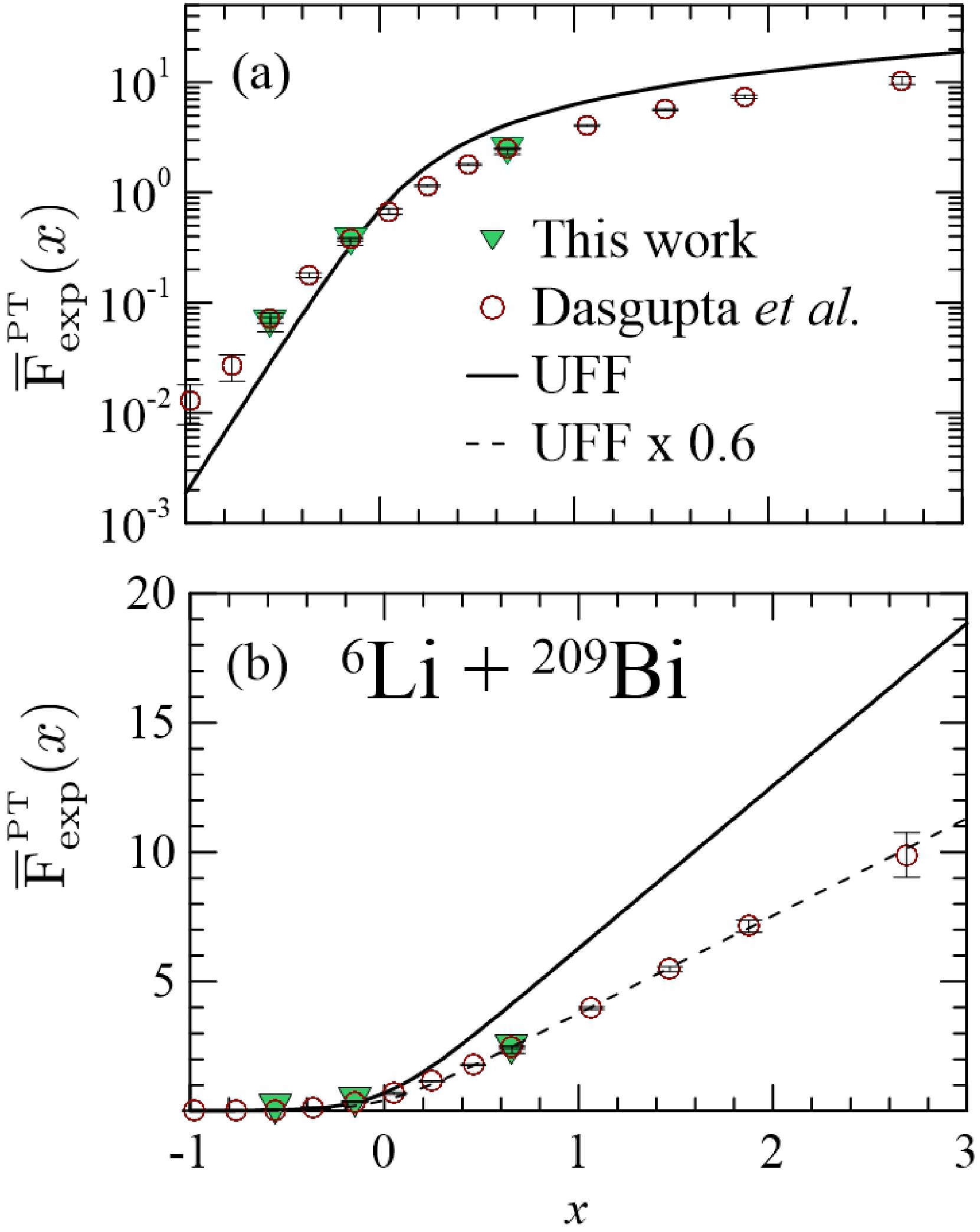

Figure 8.  (color online) Fusion function in the collision of the ⁶Li projectile on a ²⁰⁹Bi target corresponding to data reported in Ref. [14] and the measurements performed in this study. The barrier parameters were derived from the $ V_{{\rm{PT}} }(R) $ nuclear potential (see the body text for further details).

Next, we consider the fusion function $ {\overline F}_{\rm{exp}}^{\,\rm 00}(x) $. Given that the barrier-lowering effects are already contained in the potential $ V_{00}(R) $, deviations concerning the UFF result exclusively from the dynamic effects of the breakup couplings. Figure 9 compares this fusion function with the UFF. As in the previous figure, the results are shown in logarithmic (Fig. 9(a)) and linear (Fig. 9(b)) scales. It is supposed that under this condition, only the suppression arising from breakup couplings remains in the comparison. Thus, the fusion function is suppressed at all collision energies. Above the Coulomb barrier, the fusion function gets close to the UFF multiplied by 0.45 (dashed line in the Fig. 9(b)). Thus, there is a suppression of 55%. As expected, the suppression is larger than that exhibited by $ {\overline F}_{\rm{exp}}^{\,\rm PT}(x) $, which keeps the barrier-lowering effects. This also implies that the real part of the dynamic polarization potential produced by the breakup channels is repulsive in the whole energy interval (see Ref. [2] and references therein). It has to be stressed here that we are not suggesting to change the value of the suppression factor; however, the proposed analysis can help distinguish the contributions from different coupling effects.

Figure 9.  (color online) Same as Fig. 8 but using $ V_{00}(R) $ to derive barrier parameters (see the body text for further details).

In Ref. [38], a systematic study of breakup effects on complete fusion at energies above the Coulomb barrier was performed. A suppression factor was obtained for experimental CF involving several weakly bound projectiles. The CF was reduced using the fusion function method and the São Paulo potential for the nuclear interaction to derive barrier parameters. The systematic value of the reduction coefficient for reactions induced for the ⁶Li projectile was 0.6, in agreement, as expected, with the value obtained in the present study when the São Paulo potential was used. To have a larger value for the CF suppression factor when $ V_{00} $ is used is only an apparent contradiction. In this last case, the cluster structure of the projectile was considered, allowing for complete isolation of the static effect of breakup on the CF cross section.

To finish this sub-section, we emphasize that although it is not possible to experimentally separate the DCF and SCF, theoretically, this can be done using Eqs. (14) and (20). We do not show the plots of these two contributions because it would contribute in a very limited manner to our knowledge of the breakup-fusion reaction mechanism. For that, an extensive study using different targets and projectiles is mandatory. This is out of the scope of the present study.

Figure 10 shows the ICF data of the conducted experiment, together with the contribution from the capture of each fragment ($ d $-ICF and $ \alpha $-ICF). They are compared with the corresponding theoretical cross sections obtained in the calculations reported in Ref. [16]. The solid blue line is the same ICF cross section reported in Ref. [16] (dotted line in panels (g) and (h) in Fig. 6 of that paper). The dashed black line and dashed-dotted red lines correspond to the theoretical d-ICF and α-ICF cross sections, respectively. These results were not reported in that paper because this type of data was unavailable then. The experimental method adopted by Dasgupta et al. [14] was appropriate for measuring the ICF cross section, but only works when the α decay half-lives of the residues are not so long as mentioned in the introduction.

Figure 10.  (color online) Comparison of the experimental data for the incomplete functions of the deuteron and α-particle ($ d $-ICF and α-ICF) with the theoretical results for the ⁶Li $ + ^{209} $Bi reaction.

By comparing the CF and ICF cross sections in Fig. 5 and Fig. 10, we found that the ICF cross section is equivalent to the CF cross section at energies above the Coulomb barrier but exceeds the CF cross section below the Coulomb barrier and dominates the TF cross section. In Fig. 2 of Ref. [39], the NEB (non-elastic breakup) cross section, which contains ICF and transfer, similarly exceeds the CF section in the near-barrier energies, which proves the rationality of our results.

Comparing the experimental $ d $-ICF cross section with the dashed line, one concludes that the theoretical model describes the data to a great extent. Conversely, the theoretical prediction of the α-ICF cross section (dash-dotted line) is much larger than the data. However, this comparison is inconclusive. As we pointed out previously, the experimental α-ICF data in this study are just a lower bound for the real cross section.

Before discussing the TF, we mention that ICF, considered an absorption, is distinguished from cluster transfer from a theoretical point of view. Cluster transfer is one of the contributors to experimental ICF because the products are indistinguishable depending on the possible fragments produced in the reaction. Fusion is understood as a short-range absorption, while transfer is a more peripheral process, so the mechanism should differ. Consequently, specific reaction calculations may or may not explicitly include transfer channels. The CDCC method used in this study is an example of the latter. Likewise, other models, such as the coupled reaction channel [31] or the Ichimura-Austern-Vincent model [39], include transfer explicitly. Although this is the general case, it was shown in Ref. [16] that the deuteron cluster transfer cross section is much smaller than d-ICF in the whole energy interval analyzed in the present study. Nevertheless, deuteron cluster transfer was found to be a relevant mechanism for ⁶Li + ¹⁹⁷Au at energies below the Coulomb barrier.

Figure 11 compares the theoretical TF cross section with the TF cross section experimentally obtained in the present study and the one measured by Dasgupta et al.. Note that the theoretical curve is systematically higher than the data points. As mentioned before, our experiment missed parts of α–ICF events that should also contribute to the TF cross section. By contrast, the measurements reported in Ref. [14] missed the contribution from the α-decay of a long-life isotope, which, according to estimates made by the code PACE [10−12], is important in the whole energy interval of the experiment. Nevertheless, in the case of the experiment conducted in this study, the contribution of $ \alpha $-ICF to the TF at the two lower energies is small, showing a good agreement between theory and experiment. We further emphasize that the theoretical TF cross section obtained in this study is the one already reported in Ref. [16].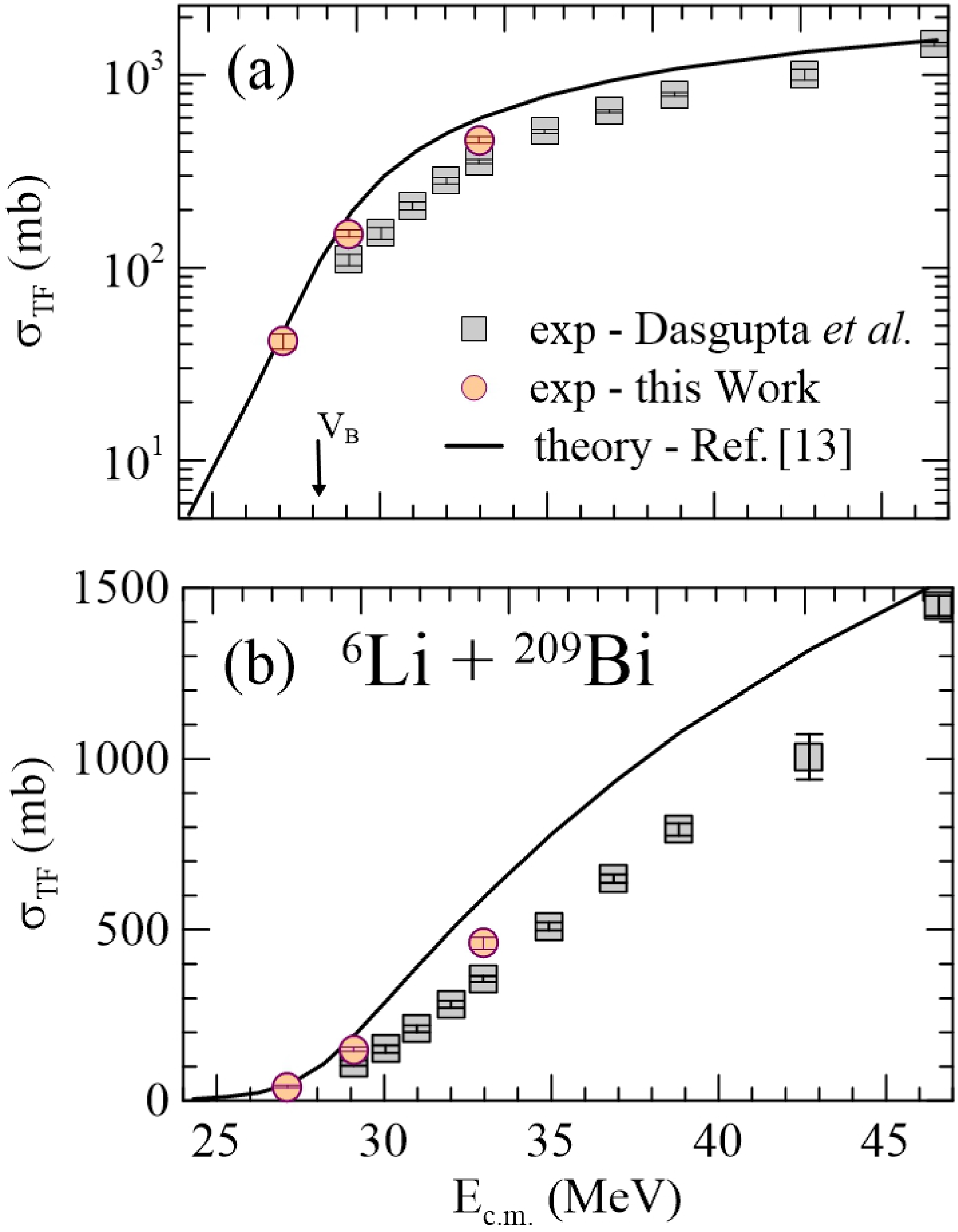

Figure 11.  (color online) Comparison of the theoretical TF cross section for the ⁶Li $ + ^{209} $Bi system with the available experimental data.

In addition to incomplete data for the ICF cross section, it should be stressed here that the discrepancy between experiment and theory shown in Figs. 10 and 11 could also partly come from the ill-definition of total fusion given that the cluster transfer and proton transfer reaction can also contribute to the ICF and TF cross sections. Thus, a more comprehensive study, including new complete measurements compared with a more sophisticated model, is required to address this problem in the future.

The experiment ⁶Li+²⁰⁹Bi was performed at the Tandem-XTU accelerator of INFN-LNL, Italy. The CF and ICF cross sections for the ⁶Li+²⁰⁹Bi system at near-Coulomb barrier energies were obtained by in-beam γ measurements. The experimental results demonstrate that the ICF cross section is of the same order as the CF cross section above the Coulomb barrier, and dominates at energies around and below the Coulomb barrier.

A theoretical approach based on the CDCC method was employed to describe the same system, and the calculated CF cross sections agree well with the experimental results, especially for the d-ICF ones. The fusion function method was employed to assess the impact of breakup on the fusion process. It was found that the CF reduction factor is greatly influenced by the choice of potential and related barrier parameters, demanding more accurate data for the total fusion cross section.

It is also relevant to point out that above a certain threshold, the deuteron can break up, and the ⁶Li projectile would be more reasonably described by the $ \alpha+n+p $ configuration. This configuration is not accessible at low beam energies but could be relevant at higher energies. It would be interesting to check this possibility within the four-body CDCC calculations above the $ n+p $ threshold. Another possibility would be a sequential breakup of the projectile. Thus, the ⁶Li first breaks up into $ \alpha +d $, and in a second step, the deuteron breaks up into $ n+p $. These are some of our plans for developing a theoretical model in the future.

We are grateful to the INFN-LNL staff for providing a stable ⁶Li beam throughout the conducted experiment.