-
An intriguing puzzle within the field of nuclear structure physics pertains to the single-particle composition of heavy and superheavy elements (SHE). This poses a significant challenge for both theoretical frameworks and experimental investigations. Experimental endeavors predominantly concentrate on determining the specific location and scope of the "island of stability." The emergence of SHE is attributed to shell effects, as the liquid-drop model predicts the non-existence of such nuclei due to substantial Coulomb repulsions. An essential question in this pursuit involves the exploration of magic numbers beyond
$ Z=82 $ and$ N=126 $ in SHE, representing a crucial aspect for both theoretical frameworks and experimental inquiries. The identification of new magic numbers is intricately linked to the single-particle structure. Theoretical predictions suggest that nuclei in close proximity to$N=184 $ and$ Z =114 $ may indicate the presence of an island of stability [1]. Currently, the availability of detailed spectroscopy data for$ Z\approx100 $ opens up a new realm for systematically studying the evolution of single-particle states [2]. The exploration of super-heavy elements (SHE) is constrained by narrow cross-sections, resulting in a scarcity of experimental data to corroborate theoretical predictions. The experimental approaches for studying SHE can be broadly categorized into two types: in-beam and decay spectroscopies [3]. The in-beam spectroscopic technique is pivotal in examining rotational bands and the single-particle structure, even for faint channels. Despite its complexity, in-beam conversion electron spectroscopy is highly valuable, as it establishes rotational bands and extracts crucial information about the alignments of protons and neutrons, even with a few dozen gamma rays. Decay spectroscopy is instrumental in analyzing single-particle levels through alpha decay chains. Alpha decay in odd-mass nuclei typically removes pairs of protons and neutrons, leaving behind an unpaired nucleon in the mother nucleus. The state populated in the daughter nucleus and the ground state of the mother nucleus possess the same single-particle configuration. The daughter nucleus's excited state decays to the ground state, emitting secondary gamma rays and conversion electrons, which aid in determining the excitation energy of single-particle states. At present, the most substantial spectroscopic information available is for the heaviest nuclei, particularly the transfermium elements, such as californium, fermium, and nobelium [4−7]. Although these deformed nuclei, with$ Z\approx100 $ and$ N\approx150-160 $ , are not strictly classified as SHE, they represent a threshold of the SHE region. The increasing sensitivity of experimental setups at facilities such as ANL (Argonne), GSI (Darmstadt), JYFL (Jyvaskyla), GANIL (Caen), and FLNR (Dubna) has made it feasible to measure$ \alpha-\gamma $ or α conversion-electron coincidences [8−14].One of the most essential quantities is moment of inertia (MoI), which characterizes the nuclear rotational bands. MoI has been widely studied and is the most fundamental observable for illustrating the structure of the nuclei. To describe the high spin phenomena of the rotational bands, two types of MoI are typically used: kinematic (
$ \Im^{(1)} $ ) and dynamic ($ \Im^{(2)} $ ) MoI.The calculation of dynamic MoI is advantageous over that of kinematic MoI, as it does not necessitate knowledge of the spins. Systematic studies of MoI have uncovered some remarkable features in the
$ A\sim250 $ mass region. Specifically, an investigation into the MoI systematics of plutonium isotopes revealed distinct behaviors between lighter isotopes ($ A\sim 238-240 $ ) and heavier ones ($ A\geq241 $ ). Lighter isotopes do not exhibit the upbending in MoI that is observed in the heavier counterparts [15]. In the lightest isotopes, strong octupole correlations are present, which are believed to be responsible for the absence of significant proton alignment, a feature observed in heavier Pu isotopes [15]. For$ ^{240} $ Pu, the lack of alignment has been interpreted in terms of phonon condensation [16]. In the case of Cm isotopes, the dynamic MoI exhibits an extraordinary pattern: initially, there is a smooth up-bend, followed by a downturn in the ground band. This behavior was suggested to be a result of the interplay between$ j_{15/2} $ neutrons and$ i_{13/2} $ protons [17, 18].Here, we systematically studied the rotational bands in
$ ^{244} $ Pu and$ ^{248} $ Cm with perturbed$S U_{sdg}(3)$ symmetry and the perturbation holding$S O_{sdg}(5)$ symmetry, which has been very successful in reproducing the changing behaviour of dynamic MoI [19−25]. In Sec. II, a short description of the model is presented, and an extension to the previous model is proposed by incorporating new parameters in the previously defined Arima coefficient. In Sec. III, the calculated results are presented for even-even$ ^{244} $ Pu and$ ^{248} $ Cm nuclei. Finally, a summary is given in Sec. IV. -
The Hamiltonian of the variable moment of inertia (VMI) inspired interacting boson model (IBM) is [19]
$ H=E_{0}+\kappa \hat{Q}^{(2)}\cdot \hat{Q}^{(2)}+\frac{C_{0}}{1+f\hat{L} \cdot \hat{L}}\hat{L} \cdot \hat{L} , $

(1) where
$ \hat{Q}^{(2)} $ and$ \hat{L} $ are the quadrupole and angular momentum operator, respectively. The parameter f is known as the Arima coefficient, which was introduced in IBM-1. The parameter f is a spin dependent term that was introduced in the denominator of the Hamiltonian to increase the MoI. Phenomenological studies proposed that the spin dependent term$ f\hat{L}.\hat{L} $ in the IBM Hamiltonian includes the anti-pairing effect at high spins [26]. However, in the superdeformed bands (SD) of the$ A\sim150,190 $ mass region, a turnover in the dynamic MoI is observed. It was emphasised that the extending Arima coefficient is important to describe the changing feature of the dynamic MoI. Following the VMI model, the Arima coefficient f was extended as$ f=f_1+f_2 [I(I+1)] $ . Hence, the energy expression in the framework of the VMI model can be written as [19]$ \begin{aligned}[b] E=\; & E_{0}(N_{B},N_{F}) \\ & +\frac{C_{0}}{1+f_{1}I(I+1)+f_{2}I^{2}(I+1)^{2}}I(I+1). \end{aligned} $

(2) Here,
$ N_B $ and$ N_F $ represent the boson and fermion numbers, respectively. This expression is for a core with$S U(3)$ symmetry plus a pseudospin S. The 2 generates the rotational band, which reproduces the global turnover of the dynamic MoI relatively well. However, the calculated dynamic MoI changes very smoothly with rotational frequency such that the weak$ \Delta I=2 $ staggering is completely ignored. To describe the$ \Delta I=4 $ bifurcation, the$S U $ (3) symmetry must be broken, and the interaction$S U_{sdg}(5)$ symmetry as a perturbation was taken into account [20]. Hence, the energy of the state can be written as$ \begin{aligned}[b] E =\;& E_{0}(N_{B}, N_{F}) \\ & + A \biggl[ n_{1}(n_{1}+4) + n_{2}(n_{1}+2) \\ &+ n_{3}^{2} + n_{4}(n_{4}-2) - \frac{1}{5}(n_{1}+n_{2}+n_{3}+n_{4})^{2} ] \\ & + B[\tau_{1}(\tau_{1}+3) + \tau_{2}(\tau_{2}+1)] \\ &+ \frac{C_{0}}{1+f_{1}I(I+1)+f_{2}I^{2}(I+1)^{2}} I(I+1). \end{aligned} $

(3) The perturbed
$ S U$ (3) limit of the$ sdg $ IBM can describe the rotational bands. Moreover, the$S U_{sdg}(5)$ limit of the$ sdg $ IBM is relevant for deformed nuclei, as is the$S U_{sdg}$ (3) limit. The calculation of the hexadecupole deformation parameter$ \beta_{4} $ , two-nucleon transfer cross section, and energy spectra demonstrated that the$S U_{sdg}(5)$ limit has almost the same properties in describing deformed rotational nuclear spectra as the$S U_{sdg}(3)$ limit does. This implies that the$S U_{sdg}(5)$ symmetry of the$ sdg $ IBM incorporates a shape coexistence and shape phase transformation that is directed by the hexadecupole deformation and angular momentum. Due to the irreducible representation (irrep) ($ \lambda,\mu $ ), the irrep$ [n_{1},n_{2},n_{3},n_{4}] $ of$S U_{sdg}(5)$ contributes nothing to the excitation energy of the states in the band. Hence, only the contribution of the perturbation to the energy of the SD bands has$S O_{sdg}(5)$ symmetry. Now, Eq. (3) can be rewritten as$ \begin{aligned}[b] E =\;&E_{0}(N_{B},N_{F})\\ & +B[\tau_{1}(\tau_{1}+3)+\tau_{2}(\tau_{2}+1)]\\ & +\frac{C_{0}}{1+f_{1}I(I+1)+f_{2}I^{2}(I+1)^{2}}I(I+1), \end{aligned} $

(4) where
$ I=I-i,~(\tau_{1},\tau_{2}) $ is the irrep of the$S O $ (5) group. In more realistic calculation, irrep$ (\tau_{1},\tau_{2}) $ is given as$ \begin{align} (\tau_{1}, \tau_{2}) = \begin{cases} \begin{aligned} &\biggl(\dfrac{L}{2}, 0), \\ &\text{if } L = 4k, 4k + 1 \quad (k = 0, 1, \ldots) \end{aligned} \\ \begin{aligned} &\biggl(\dfrac{L}{2} - 1, 2), \\ &\text{if } L = 4k + 2, 4k + 3 \quad (k = 0, 1, \ldots) \end{aligned} \end{cases} \end{align} $

(5) Here,
$ [L/2] $ denotes the integer part of L, and B,$ C_{0} $ ,$ f_{1} $ , and$ f_{2} $ are the free parameters. Building upon the foundational concepts presented in previous studies [19−28], which advocate for the necessity of higher-order terms in Arima coefficients to incorporate effects that promote either the pairing or anti-pairing favouring effect, this research introduces an additional independent variable,$ f_3 $ , to more accurately represent the rotational bands within the nuclear mass region around$ A\sim250 $ . Consequently, the formulation of the Arima coefficient f is revised to encompass a more complex structure, expressed as$f= f_1+f_2 [I(I+1)]+f_3 [I(I+1)]^2$ . Utilizing this refined approach, key nuclear properties, such as the energy of$ E_2 $ transition γ-rays, kinematic, and dynamic MoI, are calculated. -
Here, we focus on two even-even nuclei,
$ ^{244} $ Pu and$ ^{248} $ Cm, as subjects of our study. Both nuclei exhibit rotational bands characterized by notable variations, including back-bending, up-bending, and downturn, in the kinematic/dynamic MoI at higher frequency regions [3, 29]. These distinct features render$ ^{244} $ Pu and$ ^{248} $ Cm ideal candidates for investigating the effectiveness of the VMI-inspired IBM within the higher$ A\sim250 $ mass region.The irrep is determined by Eq. (5). Illustratively, with the branching rules of the irreps, we obtain
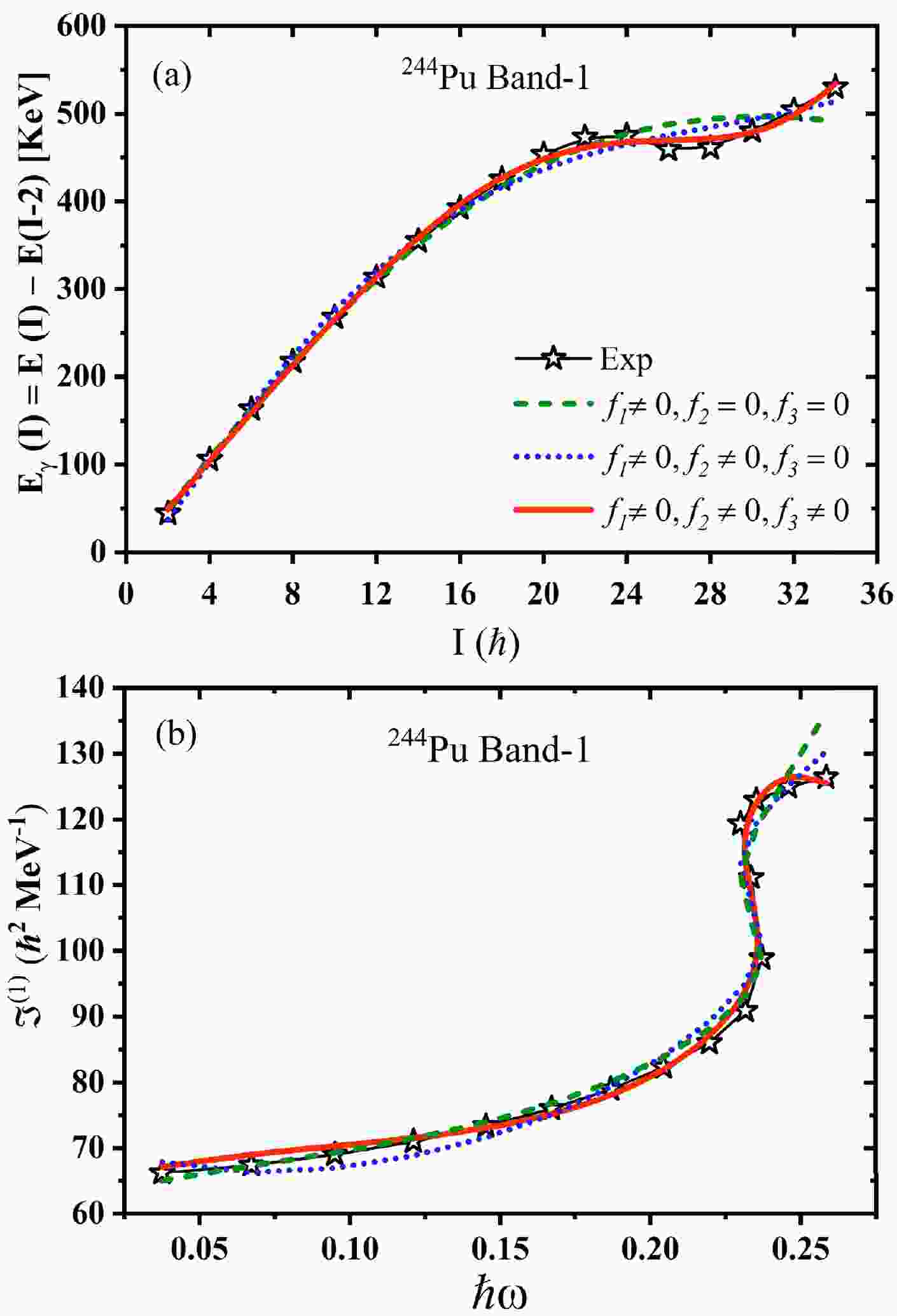
$(\tau_1, \tau_2)=$ $ (16,\; 2),\; (16,\; 0),\; (14,\; 2),\; (14,\; 0), \ldots$ for$ ^{244} $ Pu band-1 with level sequence$I = 34, 32, 30, 28, \ldots$ [2]. The$ E_2 $ transitions are taken from Ref. [2]. After a non-linear least squares fitting of the experimental intraband$ \gamma $ -transition, the respective parameters and calculated intraband$ \gamma $ -transitions are obtained. The best fitting parameters obtained for$ ^{244} $ Pu and$ ^{248} $ Cm are listed in Table 1. For every band, three sets of parameters are deduced in this study. In the current analysis, three separate parameter sets are derived for each rotational band studied. Set A is formulated based on the sole influence of the coefficient$ f_1 $ . Set B is expanded to include the effects of two parameters,$ f_1 $ and$ f_2 $ . In contrast, Set C is the most inclusive, encompassing the combined contributions of$ f_1 $ ,$ f_2 $ , and$ f_3 $ . The table also lists the root-mean-square (RMS) deviation obtained in all the cases mentioned. The results clearly indicate that, among the three parameter sets examined in this study, Set C consistently yields the lowest RMS deviation between the calculated and experimental$ E_2 $ values across all the bands considered. This observation emphasizes the improved precision of Set C in accurately representing the details of the$ E_2 $ transitions within these bands. Figure 1(a) presents a graphical representation of the intraband$ \gamma $ -transition energies in$ ^{244} $ Pu for band-1, incorporating both experimental observations and theoretical calculations. This particular rotational band is henceforth designated as$ ^{244} $ Pu(1), and similar nomenclature will be followed for subsequent bands. In the same figure, three distinct theoretical curves are depicted, each corresponding to a different calculation scenario. In the first scenario, labeled as Case-I, the computation utilizes solely the parameter$ f_1 $ while setting$ f_2 $ and$ f_3 $ to zero. Case-II extends this model by incorporating both$ f_1 $ and$ f_2 $ parameters in the calculation. Finally, Case-III advances the model further by employing an extrapolation of the Arima coefficient and integrating the$ f_3 $ parameter, in conjunction with$ f_1 $ and$ f_2 $ . Figure 1(a) clearly indicates that, in Cases I and II, where the parameter$ f_3 $ is set to zero, there is a notable discrepancy between the calculated and experimental$ \gamma $ -transition energies for$ ^{244} $ Pu(1), particularly in the region of higher spin ($ I\geq20\hbar $ ). Conversely, the introduction of a non-zero$ f_3 $ parameter significantly enhances the agreement with the experimental data, leading to an excellent reproduction of the$ \gamma $ -transitions. Furthermore, a careful examination of the parameters pertaining to$ ^{244} $ Pu(1), as listed in Table 1, reveals that the RMS deviation reaches its minimum value with Set C. Additionally, it is observed that incorporating the$ f_2 $ parameter into the calculation results in an increase in RMS deviation, which increases from$ 46.6 \times 10^{-3} $ to$ 49.5 \times 10^{-3} $ . This indicates that the inclusion of the$ f_2 $ parameter, rather than enhancing the accuracy of the model, actually leads to a slight decrease in precision in reproducing the experimental data. Figure 1(b) displays the kinematic MoI,$ \Im^{(1)} $ , for$ ^{244} $ Pu(1). The data presented in this figure clearly demonstrate that the inclusion of a non-zero parameter$ f_3 $ significantly improves the model's ability to describe the backbending phenomenon observed in$ ^{244} $ Pu(1). In contrast, Cases I and II, which do not account for$ f_3 $ , fail to accurately replicate the experimental curve in the higher frequency region. The dynamic MoI,$ \Im^{(2)} $ , for the band$ ^{244} $ Pu(2) is depicted in Fig. 2 (a), showcasing a distinctive downturn at higher rotational frequencies. From this figure, it is evident that Cases I and II, which exclude the$ f_3 $ parameter, inadequately reproduce this downturn and instead exhibit a monotonic increase in$ \Im^{(2)} $ with rotational frequency. In stark contrast, Case III, with the inclusion of$ f_3\neq0 $ , effectively mirrors the observed behavior, satisfactorily replicating the downturn in the dynamic MoI. Additionally, the parameter dynamics for$ ^{244} $ Pu(2) show similarities to those of$ ^{244} $ Pu(1), as detailed in Table 1. Notably, the RMS deviation reaches its lowest value with Set C. Furthermore, the introduction of the$ f_2 $ parameter into the model results in an increase in the RMS deviation compared to that of Set B, suggesting a less optimal fit for the dynamic MoI of$ ^{244} $ Pu(2) when$ f_2 $ is included.Nucleus(Band) Set B $C_{0}$ 

$f_1$ 

$f_2$ 

$f_3$ 

$\chi \times 10^{-3}$ 

244Pu(1) $\left\{\begin{array}{l}\text{A} \\\text{B} \\\text{C}\end{array}\right.$ 

0.0213 7.290 3.732×10−4 46.6 −0.0452 8.495 6.234×10−4 −1.073×10−7 49.5 0.0238 6.920 2.682×10−5 5.519×10−7 −2.608×10−10 29.8 244Pu(2) $\left\{\begin{array}{l}\text{A}: \\\text{B}: \\\text{C}:\end{array}\right.$ 

−0.1865 6.845 3.015×10−4 6.40 −0.2680 7.362 3.869×10−4 −4.473×10−8 7.06 0.0784 4.923 −3.804×10−4 9.289×10−7 −5.008×10−10 1.85 244Pu(3) $\left\{\begin{array}{l}\text{A}: \\\text{B}: \\\text{C}:\end{array}\right.$ 

−0.1490 7.019 2.343×10−4 7.07 0.2047 4.970 −2.098×10−4 2.899×10−7 2.49 −0.1358 5.952 5.952×10−4 −8.602×10−7 6.767×10−10 0.91 244Pu(4) $\left\{\begin{array}{l}\text{A}: \\\text{B}: \\\text{C}:\end{array}\right.$ 

−0.1047 6.641 1.916×10−4 2.60 0.001 5.968 −5.790×10−5 2.227×10−7 1.07 −0.1912 7.310 5.267×10−4 −6.626×10−7 4.978×10−10 0.71 248Cm(1) $\left\{\begin{array}{l}\text{A}: \\\text{B}: \\\text{C}:\end{array}\right.$ 

0.0400 6.675 2.682×10−4 40.8 −0.0119 7.449 4.747×10−4 −1.138×10−7 11.4 2.99×10−3 7.159 3.341×10−4 8.416×10−8 −9.807×10−11 1.60 248Cm(2) $\left\{\begin{array}{l}\text{A}: \\\text{B}: \\\text{C}:\end{array}\right.$ 

0.0254 5.326 1.275×10−4 4.39 −0.260 7.142 3.616×10−4 −9.266×10−8 0.71 −0.159 6.400 2.259×10−4 2.569×10−8 −4.601×10−11 0.60 248Cm(3) $\left\{\begin{array}{l}\text{A}: \\\text{B}: \\\text{C}:\end{array}\right.$ 

−0.2180 7.244 3.762×10−4 8.14 −0.2860 7.712 4.605×10−4 −4.893×10−8 8.50 0.0567 5.087 −4.502×10−4 1.239×10−6 −7.309×10−10 5.70 248Cm(4) $\left\{\begin{array}{l}\text{A}: \\\text{B}: \\\text{C}:\end{array}\right.$ 

−0.2465 6.233 1.813×10−4 3.27 −0.1419 5.618 4.762×10−5 8.556×10−8 1.30 −0.0188 4.787 −2.800×10−4 5.706×10−7 −2.903×10−10 0.34 Table 1. Parameters obtained using least-squares fitting method for rotational bands in
$ ^{244} $ Pu and$ ^{248} $ Cm. B and$ C_0 $ are in keV, and χ represents the RMS deviation between calculated and experimental$ E_\gamma $ transitions. Here,$ 1,2,.. $ in parentheses represent band 1, band 2..., respectively.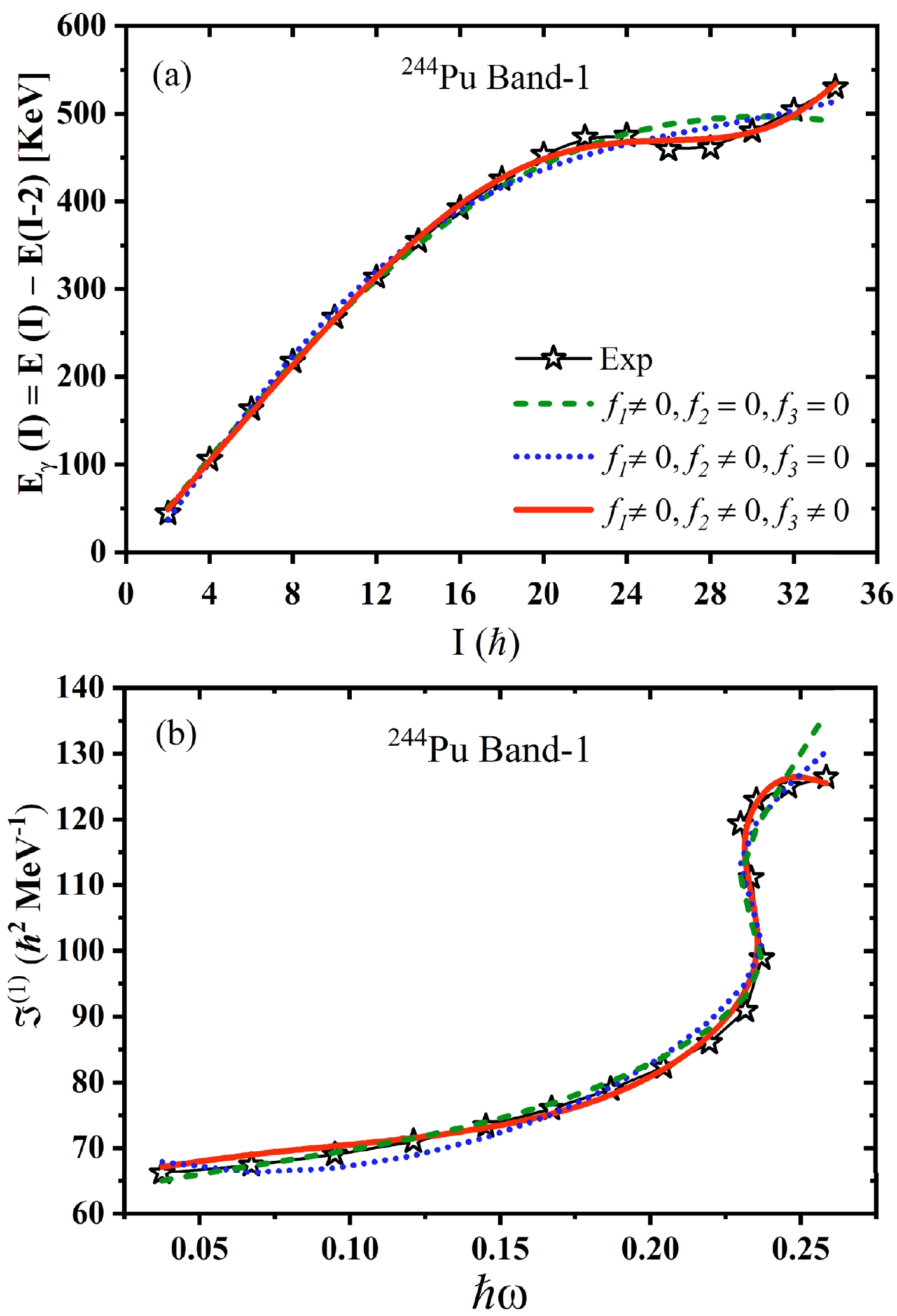
Figure 1. (color online) (a) Comparative analysis between the experimental and calculated intraband gamma-transition energies (
$ E_\gamma(I) $ ) plotted against spin. (b) Relationship between the kinematic moment of inertia ($ \Im^{(1)} $ ) and rotational frequency ($ \hbar\omega $ ) for the isotope$ ^{244} $ Pu(1).Figures 2(b) and 2(c) illustrate the dynamic MoI for the bands
$ ^{244} $ Pu(3) and$ ^{244} $ Pu(4), respectively. Contrary to the previous band, these two do not exhibit a downturn in their dynamic MoI. Instead, they exhibit an upbending phenomenon at a rotational frequency of approximately$ \hbar\omega \approx 0.22 $ MeV. Initially, one might conjecture that incorporating the parameter$ f_{1} $ alone could adequately reproduce this upbending in the dynamic MoI, particularly because$ f_{1} $ , when positive, accounts for the anti-pairing effect. However, a closer examination of Fig. 2 reveals that, in Cases I and II, where the calculation includes only$ f_{1} $ or both$ f_{1} $ and$ f_{2} $ but excludes$ f_{3} $ , the magnitude of the dynamic MoI at the highest rotational frequencies is underestimated. It is only in Case III, which integrates the$ f_{3} $ parameter, that the dynamic MoI for these bands is reproduced with satisfactory accuracy.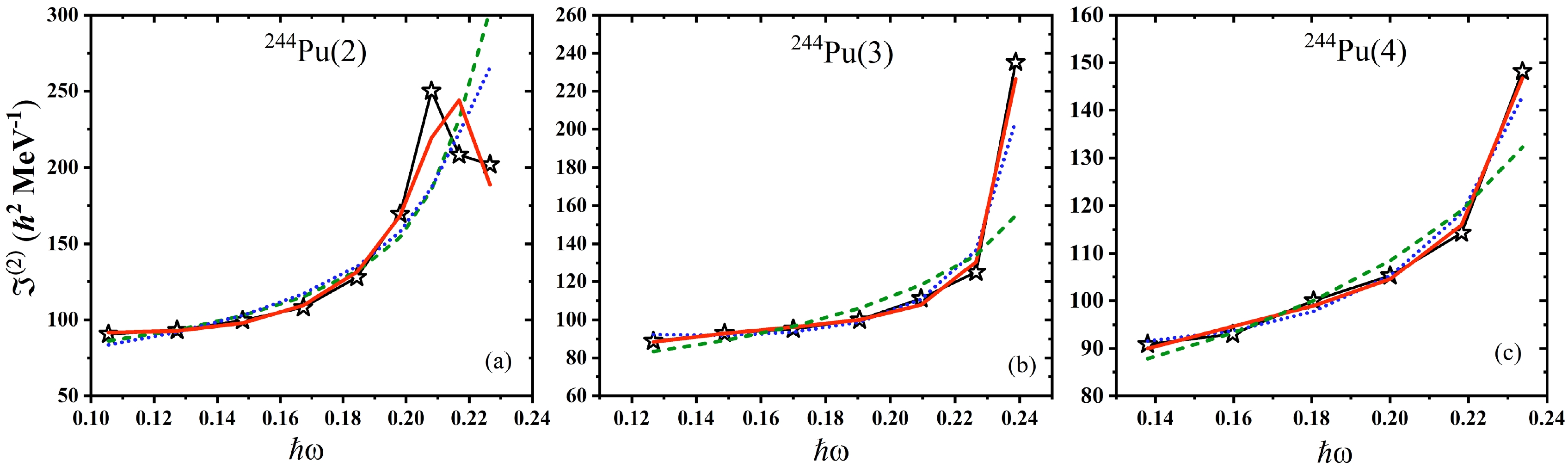
Figure 2. (color online) Comparison of experimental and calculated dynamic moment of inertia (
$ \Im^{(2)} $ )$ vs. $ rotational frequency$ \hbar\omega $ for rotational bands in$ ^{244} $ Pu.The methodology utilized for
$ ^{244} $ Pu has been similarly applied to the$ ^{248} $ Cm nucleus. Within$ ^{248} $ Cm, bands 1, 2, and 3 exhibit a downturn in their dynamic MoI, while band 4 is distinguished by an upbending, as illustrated in Figs. 3(a)–(d). These figures indicate that Case III, which incorporates the$ f_3 $ parameter, accurately reflects the experimental values for the dynamic MoI in$ ^{248} $ Cm bands 1, 2, and 4. For$ ^{248} $ Cm(3), Case III can reproduce the overall trend of the dynamic MoI, albeit with less precision. Notably, in$ ^{248} $ Cm(2), the downturn in the dynamic MoI is not as pronounced as in bands 1 and 3. In this scenario, both Case II and Case III provide satisfactory representations of the dynamic MoI. However, Case III achieves a closer match to the experimental data. This pattern is also evident in$ ^{248} $ Cm(4). Here, the experimental data are better represented by Case III as opposed to Cases II and I. This consistency in accurately modeling the dynamic MoI across various bands of$ ^{244} $ Pu and$ ^{248} $ Cm underscores the importance and effectiveness of including the$ f_3 $ parameter, especially for capturing detailed phenomena such as backbending, downturn, and up-bending in the dynamic MoI.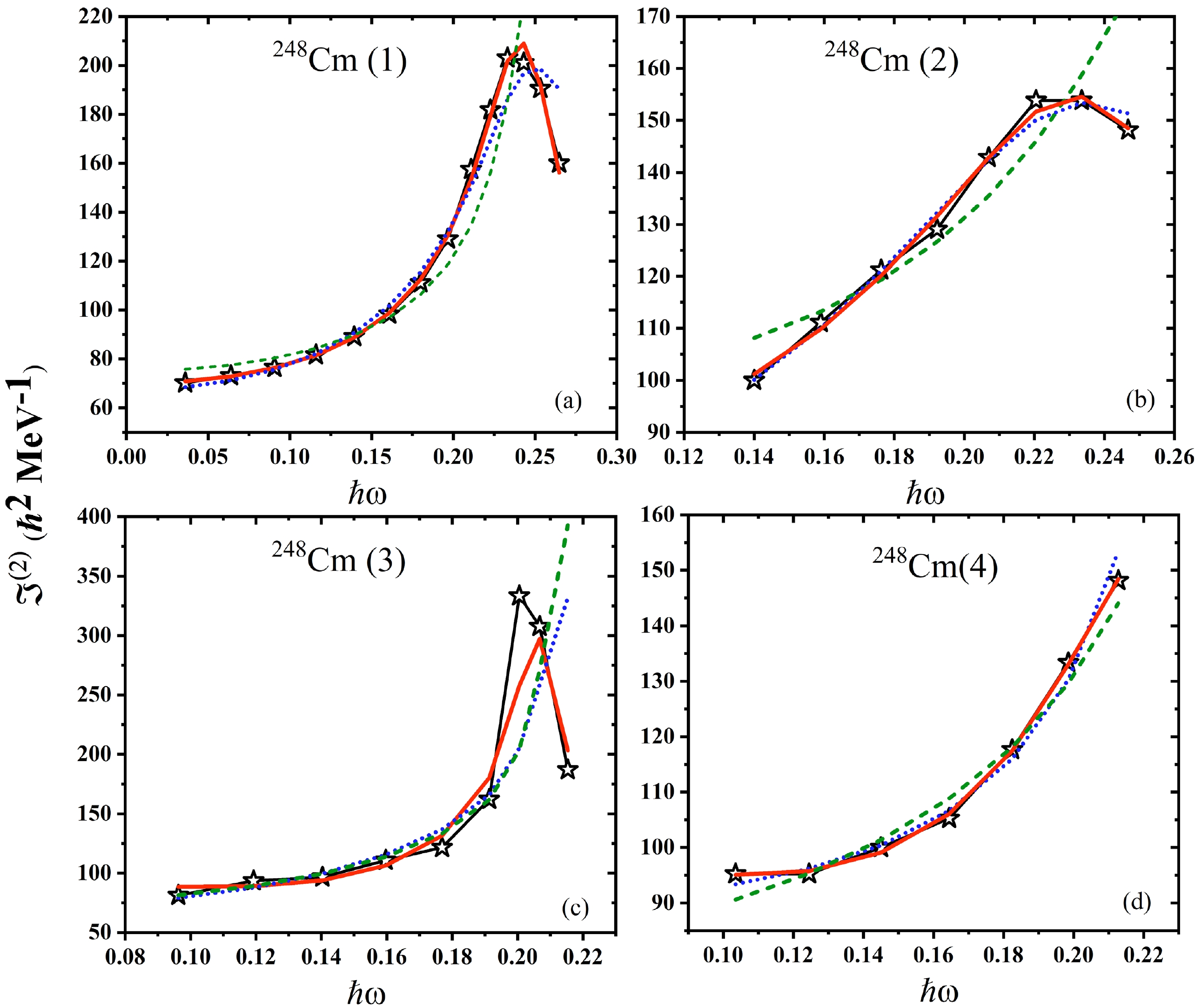
Figure 3. (color online) Comparison of experimental and calculated dynamic moment of inertia (
$ \Im^{(2)} $ )$ vs. $ rotational frequency$ \hbar\omega $ for rotational bands in$ ^{248} $ Cm.As outlined in Ref. [26], the incorporation of the
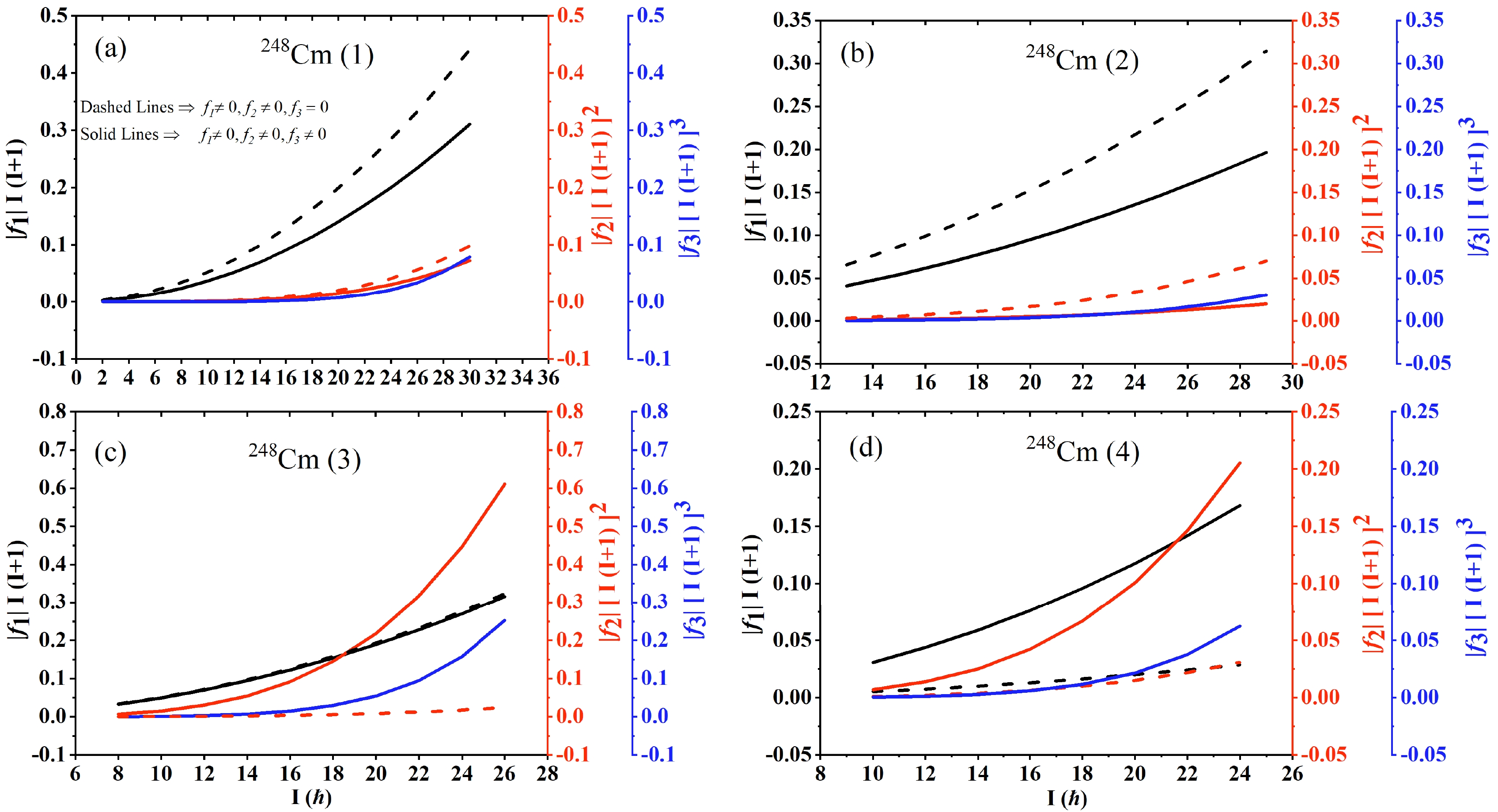
$ f_1 $ parameter in the Hamiltonian is pivotal for modeling pairing and anti-pairing effects in nuclear systems. Specifically, a positive$ f_1 $ ($ f_1>0 $ ) induces an anti-pairing effect, whereas a negative$ f_1 $ ($ f_1<0 $ ) facilitates a pairing effect. Extending this concept, it has been recognized that the anti-pairing effect is intensified when both$ f_1 $ and$ f_2 $ are positive ($ f_1>0, f_2>0 $ ); conversely, the pairing effect is strengthened when both parameters are negative ($ f_1<0, f_2<0 $ ). When$ f_1 $ and$ f_2 $ assume opposite signs (either$ f_1<0, f_2>0 $ or$ f_1>0, f_2<0 $ ), both anti-pairing and pairing effects become influential in determining the evolution of the dynamic MoI with rotational frequency. In scenarios where$ f_1>0 $ and$ f_2<0 $ , there is a shift from an anti-pairing-dominated regime (where angular momentum is the driving factor) to one favoring pairing (characterized by a restraining influence) as the angular momentum increases. Conversely, when$ f_1<0 $ and$ f_2>0 $ , the system transitions from a pairing-dominated regime (restraining) to one favoring anti-pairing (angular momentum driving) with increasing angular momentum. This intricate interplay and the resulting shifts between pairing and anti-pairing effects, dictated by the values of$ f_1 $ and$ f_2 $ , have been extensively discussed in literature [19−25]. The pairing effects play a vital role before the turnover appears in the dynamic MoI. To further explore the contribution of the parameters$ f_1 $ and$ f_2 $ and the importance of the inclusion of parameter$ f_3 $ in reproducing the dynamic MoI of the$ A\sim250 $ mass region, we plot the variation in parameters with spin. For$ ^{244} $ Pu(1), Fig. 4(a) shows the variations in$ |f_1|I(I+1)| $ ,$ |f_2|[I(I+1)]^{2} $ , and$ |f_3|[I(I+1)]^3 $ with spin. The analysis clearly shows that$ |f_1| $ is significantly larger than$ |f_2| $ , which in turn is considerably larger than$ |f_3| $ , indicated by the relationships$ |f_1|\gg|f_2|\gg|f_3| $ (see Table 1). This disparity in magnitudes reveals that the contributions of$ f_2 $ and$ f_3 $ become notably significant only at higher spin levels.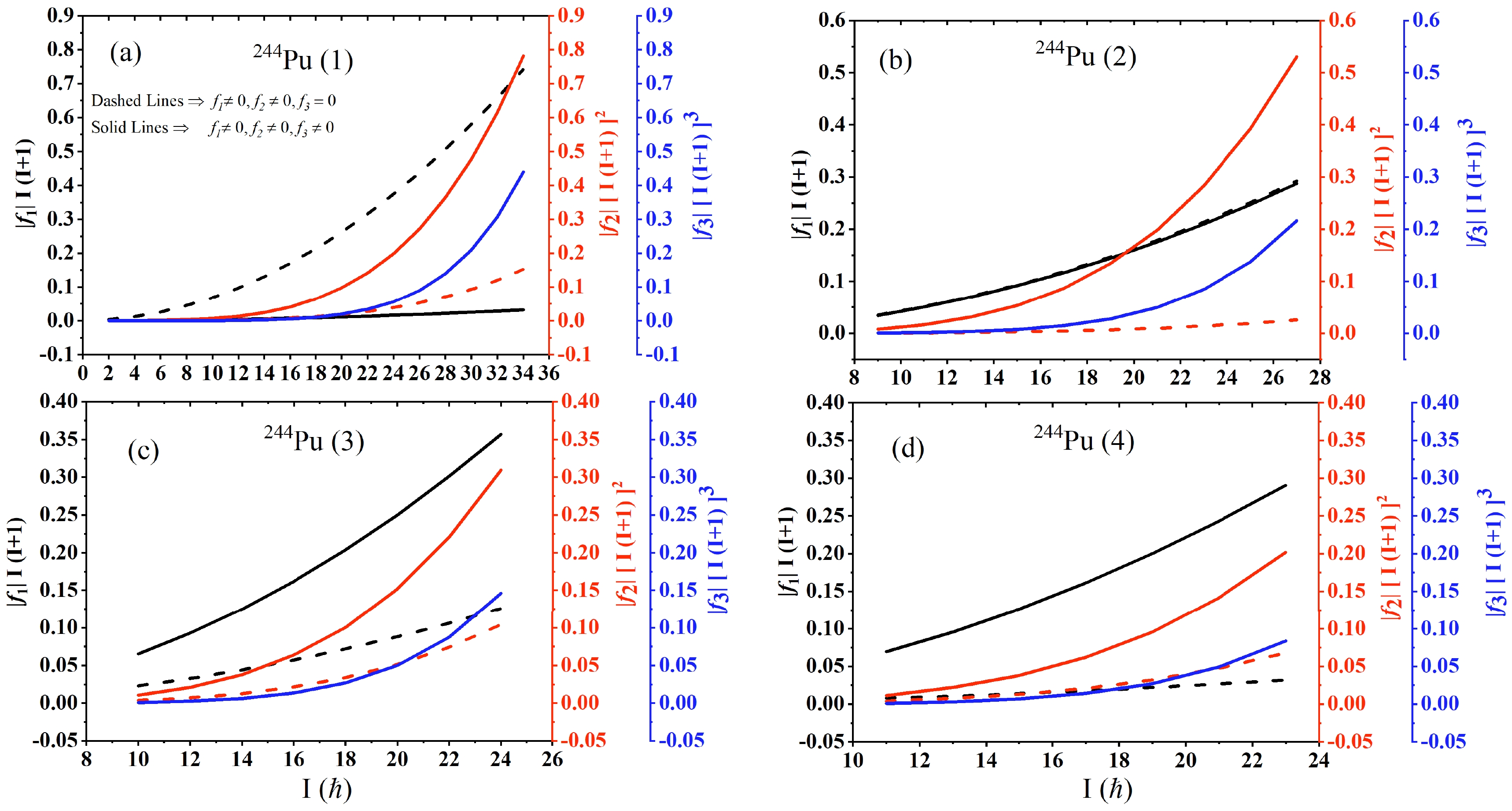
Figure 4. (color online) Comparative analysis of the spin-dependent variations in the parameters
$ |f_{1}|[I(I+1)] $ ,$ |f_{2}|[I(I+1)]^2 $ , and$ |f_{3}|[I(I+1)]^3 $ associated with the rotational bands of$ ^{244} $ Pu, depicted on the black, red, and blue Y-axes, respectively.In Fig. 4, the parameters are differentiated by the style and color of the lines. The solid lines represent the calculated parameters when the
$ f_3 $ factor is included, whereas the dashed lines indicate the variations in these parameters under the condition that$ f_3=0 $ . In terms of color, the black and red lines, both solid and dashed, correspond to the contributions from the parameters$ f_1 $ and$ f_2 $ , respectively. The solid blue line exclusively represents the contribution from$ f_3 $ . To show a direct comparison of these parameters on a unified scale, their absolute values are plotted while deliberately omitting the signs. This approach allows for a clear visual comparison of the magnitude of each parameter's contribution. However, it is important to note that the actual values of parameters$ f_1 $ ,$ f_2 $ , and$ f_3 $ can be positive or negative, depending on the specific dynamics of the MoI being analyzed, as detailed in Table 1. In the analysis of$ ^{244} $ Pu(1), the roles of parameters$ f_1 $ ,$ f_2 $ , and$ f_3 $ in determining nuclear dynamics, especially in terms of anti-pairing and pairing effects, are evident from the data presented in Fig. 4(a). The$ f_1 $ term, associated with the anti-pairing effect, shows a negligible contribution across the entire range of spins, suggesting its minimal influence on the nuclear behavior in$ ^{244} $ Pu(1). Conversely, the$ f_2 $ parameter, another anti-pairing favoring term, demonstrates a negligible contribution up to approximately$ 10\hbar $ and becomes significantly more influential at higher spin values. This indicates a growing impact of the anti-pairing effect as the spin increases. Meanwhile, the$ f_3 $ term, which favors pairing, only becomes significant after the spin exceeds$ 20\hbar $ . This implies that the pairing favoring effect is particularly crucial at higher spin states. At the maximum spin value of$ 34\hbar $ , the magnitude of the pairing favoring term reaches approximatley half that of the anti-pairing favoring terms combined, underscoring the substantial role of pairing effects at extreme spin values. Furthermore, a comparison between scenarios with and without the inclusion of$ f_3 $ reveals distinct dynamics. When$ f_3 $ is set to zero, the dominance of the$ f_1 $ parameter over$ f_2 $ suggests a prevailing anti-pairing effect. The positive and negative values of$ f_1 $ and$ f_2 $ , respectively, are detailed in Table 1. However, including the$ f_3 $ parameter significantly alters this balance, emphasizing the increased importance of the pairing favoring term in accurately reproducing the experimental data for$ ^{244} $ Pu(1). The contribution of each parameter thus emerges as not only dependent on its magnitude but also intricately linked to the spin range.For
$ ^{244} $ Pu(2), an analysis based on the presented figures, particularly Fig. 4(b), reveals insightful dynamics about the interplay of anti-pairing and pairing effects. When the$ f_3 $ parameter is set to zero, the system is predominantly influenced by the anti-pairing favoring effect, with the pairing favoring effect being almost negligible throughout the spin range. This dominance of the anti-pairing effect is reflected in the calculated dynamic MoI, which shows a monotonous increase with rotational frequency. However, when$ f_3 $ is not equal to zero, there is a noticeable shift in dynamics. Both$ f_1 $ and$ f_3 $ parameters contribute toward enhancing the pairing effect. This implies that, for an accurate global reproduction of the experimental data, the contributions from pairing favoring terms must be significantly higher. This finding underscores the importance of considering the$ f_3 $ parameter in the model to capture the nuanced behavior of$ ^{244} $ Pu(2). The behavior observed in$ ^{244} $ Pu(3) and$ ^{244} $ Pu(4) demonstrates similar parameter systematics, as indicated in Table 1. In the scenarios where$ f_3=0 $ , the parameters$ f_1 $ and$ f_2 $ exhibit negative (pairing favoring) and positive (anti-pairing favoring) values, respectively. In contrast, when$ f_3 $ is included (i.e.,$ f_3\neq0 $ ), both$ f_1 $ and$ f_3 $ are positive, while$ f_2 $ remains negative. This configuration suggests a balanced contribution from both anti-pairing and pairing effects in the evolution of the dynamic MoI with rotational frequency, indicating a competition between these two effects. Particularly for$ ^{244} $ Pu(3), the inclusion of the$ f_3 $ parameter seems to strengthen the anti-pairing effect compared to the results obtained when$ f_3=0 $ .In the nuclear structure of
$ ^{248} $ Cm, specifically in bands 1 and 2, the systematic examination of the parameters listed in Table 1 reveals notable trends. In scenarios where$ f_3 $ is not considered ($f_3=0$ ),$ f_1 $ exhibits a positive value, while$ f_2 $ is negative, indicating an interplay of effects. However, the introduction of non-zero$f_3$ ($f_3\neq0$ ) results in both$ f_1 $ and$ f_2 $ maintaining their positive values but with$ f_3 $ assuming a negative value. This adjustment, as discernible from Figs. 5(a) and (b), leads to a marked reduction in the anti-pairing favoring term, highlighting the critical role of$ f_3 $ in the model. The impact of these parameters becomes even more pronounced in$ ^{248} $ Cm(3). In the absence of$ f_3 $ , the anti-pairing effect predominates, leading to a continuous increase in the dynamic MoI, as observed in Fig. 5(c). However, the integration of a non-zero$ f_3 $ shifts the balance, bringing a significant contribution from the pairing favoring term. This results in a complex interplay between the pairing and anti-pairing effects, which is pivotal in the evolution of the dynamic MoI. For$ ^{248} $ Cm(4), with$ f_3 $ set to zero, both$ f_1 $ and$ f_2 $ parameters are positive, suggesting an amplified anti-pairing effect. The incorporation of the$ f_3 $ term, however, not only aligns the calculated data more closely with experimental data but also introduces a notable pairing favoring term. -
A systematic investigation of the dynamic moment of inertia (MoI) in rotational bands of even-even nuclei
$ ^{244} $ Pu and$ ^{248} $ Cm was conducted using a refined approach of the variable moment of inertia model, inspired by the interacting boson model. This approach incorporated a perturbed$S U_{sdg}(3)$ symmetry integrated with an interaction upholding$S O_{sgd}(5)$ ($S U_{sdg}(5)$ ) symmetry. A significant advancement was made by extending the Arima coefficients to include three parameters:$ f_1 $ ,$ f_2 $ , and$ f_3 $ . This extension allowed the intraband γ-transition energies to be depicted by a five-parameter formula, consisting of two terms. The first term,$ B[\tau_1(\tau_1 +3)+\tau_2(\tau_2 +1)] $ , retained the$S O_{sdg}(5)$ symmetry, while the second term,$ C_{0}/[1+f_{1}I(I+1)+f_{1}I^2(I+1)^2+f_{3}I^3(I+1)^3] I(I+1) $ , exhibited$S O(3)$ symmetry, incorporating many-body interactions.In these nuclei, the rotational bands demonstrated various changes in MoI, including back-bending, up-bending, and downturn. A closer analysis of the dynamic MoI revealed that the inclusion of only the
$ f_1 $ parameter yielded results significantly lower than experimental data. The introduction of the$ f_2 $ parameter enhanced the results beyond those achieved with the exclusive use of the$ f_1 $ model. Nevertheless, it could not accurately replicate the experimental variations observed in MoI. This limitation was addressed by introducing the$ f_3 $ parameter, which effectively replicated the experimental trends. The inclusion of$ f_1 $ and$ f_2 $ alone in the model accounted for pairing and anti-pairing effects. However, with the addition of$ f_3 $ , these effects were considerably amplified, with the pairing effects becoming more pronounced in rotational bands where the dynamic MoI experienced a downturn at higher rotational frequencies. Conversely, anti-pairing effects were intensified in bands exhibiting up-bending in the dynamic MoI. Given that the parameters satisfied the relationship$ |f_1|\gg |f_2|\gg |f_3| $ , it became evident that the impact of$ |f_3| $ was particularly significant at higher spin values. In conclusion, the introduction of the$ f_3 $ parameter led to the identification of three distinct phenomena in the rotational bands of$ ^{244} $ Pu and$ ^{248} $ Cm. In the bands$ ^{244} $ Pu(1,2) and$ ^{248} $ Cm(3), an enhancement in the pairing effect was observed. For the bands$ ^{244} $ Pu(3,4), dominance of the anti-pairing effect became evident. Meanwhile, in the bands$ ^{248} $ Cm(1,2,4), there was a noticeable decrease in the anti-pairing effect. This comprehensive analysis underscores the significance of the$ f_3 $ parameter in capturing the complex interplay of correlations within the nucleus, crucial for understanding the rotational behavior in heavy nuclei.
Description of moment of inertia and the interplay between anti-pairing and pairing correlations in 244Pu and 248Cm
- Received Date: 2024-05-06
- Available Online: 2024-10-15
Abstract: A variable moment of inertia (VMI) inspired interacting boson model (IBM), which includes many-body interactions and a perturbation possessing





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF


















 DownLoad:
DownLoad: