-
The story of Einstein introducing the cosmological constant is well known. The key takeaway from this story is that Einstein valued physical reality more than his theory itself. In other words, the inclusion or exclusion of a cosmological constant in the theory should be guided by physical evidence. Since the discovery of the accelerating expansion of our Universe, it has become clear that a cosmological constant is necessary in the Einstein equation.
$ \begin{array}{*{20}{l}} G_{\mu\nu}+\Lambda g_{\mu\nu}=8\pi T_{\mu\nu}. \end{array} $

(1) Corresponding to the accelerating expansion of our Universe, we have
$ \Lambda>0 $ . Consequently the term$ \Lambda g_{\mu\nu} $ in the aforementioned Einstein equation mimics an ideal fluid with negative energy and negative pressure. Hence, the cosmological term has been considered to represent dark energy.The concept of dark matter is inspired by galaxy rotation curves. Typically, the observed rotation velocity at relatively large distances from the center of the galaxy is greater than what is predicted by Newtonian gravity. This discrepancy suggests the presence of additional matter that provides extra gravitational attraction.
If the cosmological constant is related to dark energy, it would provide a repulsive force rather than an attractive one, which contrasts with the behavior of dark matter. As a result, few scientists consider the cosmological constant problem and the dark matter problem as a single issue. One interesting and somewhat mysterious fact is that, through data fitting using modified Newtonian dynamics (MOND) [1−3], galaxy rotation curves reveal a characteristic acceleration scale
$ a_0\approx10^{-10} $ ms$ {}^{-2} $ (with international system of units)$ \approx10^{-18} $ s$ {}^{-1} $ (with geometric units)$ \approx\sqrt{\Lambda} $ [4]. Some authors have suggested that this phenomenon may be related to the quantum nature of gravity [5] or to alternative gravity theories beyond those of Newton and Einstein [6−10].If general relativity were to break down, the related equivalence principle or the general covariance principle would have to be violated. To date, there is no definitive evidence of such a breakdown at either the galaxy scale or the cosmological scale [11−17]. Unlike previous studies, we would like to pose the following question: Is it possible to relate the cosmological constant Λ to the characteristic acceleration scale
$ a_0 $ completely within the theory of general relativity?To relate the cosmological constant Λ to the phenomenological MOND theory, we must first investigate the gravitational force associated with the cosmological constant. In general relativity, the concept of gravitational force does not exist in the traditional sense. To discuss whether the gravitational force is attractive or repulsive, the Newtonian limit must be considered.
In this study, we highlight the subtleties involved in deriving the Newtonian limit of the Einstein equation with the cosmological constant. A careless reduction can lead to a modified Newtonian gravity with a repulsive gravitational force correction, but our analysis will show that this result is incorrect. A careful reduction instead leads to a modified Newtonian gravity with an attractive gravitational force correction.
The analysis of the modified Newtonian gravity equation in this work indicates that the cosmological constant Λ does contribute to an attractive gravitational force. But the correction is approximately
$ H^2r^2 $ , where H denotes the Hubble parameter and r denotes the distance to the force center. In typical galaxy scenarios, this correction is negligibly small. As a result, the cosmological constant Λ does not significantly affect galaxy rotation curves.Through the entire paper, geometric units are used, where the speed of light and the gravitational constant are set to one
$ c=G=1 $ . Thise paper is organized as follows: In the next section, we outline the initial reduction of the Newtonian limit of the Einstein equation with a cosmological constant and then highlight the mistakes involved. In Section III, we accurately deduce the Newtonian limit of the Einstein equation with a cosmological constant. Following this, we analyze the modified Newtonian gravity equation derived in Section III and estimate the resulting corrections. Finally, we conclude the paper with a summary and some discussions in the last section. -
In the traditional approach to deducing the Newtonian limit of the Einstein equation, it is common to assume that the metric is a perturbation of the Minkowski spacetime.
$ \begin{array}{*{20}{l}} g_{\mu\nu}=\eta_{\mu\nu}+h_{\mu\nu}. \end{array} $

(2) Regarding the gravitational source, the mass density ρ is the leading term, while the velocity-dependent terms are subleading or higher-order. Therefore, when considering only the leading order for the Newtonian limit, the stress-energy tensor for the gravitational source reads as follows:
$ \begin{array}{*{20}{l}} T_{\mu\nu}=\begin{pmatrix}\rho&0&0&0\\ 0&0&0&0\\ 0&0&0&0\\ 0&0&0&0\end{pmatrix}. \end{array} $

(3) As usual, we introduce the trace-inverse tensor of
$ h_{\mu\nu} $ $ \bar{h}_{\mu\nu}\equiv h_{\mu\nu}-\frac{1}{2}h\eta_{\mu\nu}, $

(4) where h denotes the trace of
$ h_{\mu\nu} $ . To the linear order of$ h_{\mu\nu} $ , the Einstein tensor of$ g_{\mu\nu} $ can be expressed as:$ G_{\mu\nu}=\frac{1}{2}\left[\bar{h}_{\mu\lambda,\nu}{}^{,\lambda}+\bar{h}_{\nu\lambda,\mu}{}^{,\lambda}-\bar{h}_{\mu\nu,\lambda}{}^{,\lambda}-\eta_{\mu\nu}\bar{h}_{\rho\lambda}{}^{,\rho,\lambda}\right]. $

(5) As is customary, we apply the harmonic gauge condition:
$ \begin{array}{*{20}{l}} \bar{h}_{\mu\alpha}{}^{,\alpha}=0. \end{array} $

(6) Consequently, we have:
$ G_{\mu\nu}=-\frac{1}{2}\bar{h}_{\mu\nu,\lambda}{}^{,\lambda}. $

(7) Then, the Einstein equation (1) becomes:
$ \begin{array}{*{20}{l}} \Box\bar{h}_{\mu\nu}=-16\pi T_{\mu\nu}+2\Lambda g_{\mu\nu}, \end{array} $

(8) where
$ \Box $ denotes the usual d'Alembert operator. Given the fact that the speed of light is multiplied to time t, the time derivative is higher order than the spatial derivative with respect to the Newtonian limit. Hence, the above equation becomes:$ \begin{array}{*{20}{l}} \nabla^2\bar{h}_{\mu\nu}=-16\pi T_{\mu\nu}+2\Lambda g_{\mu\nu}, \end{array} $

(9) where
$ \nabla^2 $ denotes the usual Laplace operator.Furthermore, it is reasonable to assume Λ is a small quantity. Hence,
$ \Lambda h_{\mu\nu} $ are high order terms and can be neglected. Consequently, Eq. (9) becomes:$ \begin{array}{*{20}{l}} \nabla^2\bar{h}_{\mu\nu}=-16\pi T_{\mu\nu}+2\Lambda \eta_{\mu\nu}. \end{array} $

(10) The 00 component of Eq. (10) takes the form:
$ \begin{array}{*{20}{l}} \nabla^2\bar{h}_{00}=-16\pi\rho-2\Lambda. \end{array} $

(11) Compared to the Newtonian potential φ satisfies:
$ \begin{array}{*{20}{l}} \nabla^2\varphi=4\pi\rho, \end{array} $

(12) Hence, we obtain solution of Eq. (11) [6]
$ \begin{array}{*{20}{l}} \bar{h}_{00}=-4\varphi-\frac{\Lambda}{3}r^2, \end{array} $

(13) where r denotes the distance to the source center.
Hence, ii component of Eq. (10) becomes:
$ \begin{array}{*{20}{l}} \nabla^2\bar{h}_{ii}=2\Lambda. \end{array} $

(14) Corresponding to solution (13), we obtain the following solution [6]:
$ \bar{h}_{ii}=\frac{\Lambda}{3}r^2. $

(15) In summary, we obtain:
$ \begin{array}{*{20}{l}} \bar{h}_{\mu\nu}=\begin{pmatrix}-4\varphi-\dfrac{\Lambda}{3}r^2&0&0&0\\ 0&\dfrac{\Lambda}{3}r^2&0&0\\ 0&0&\dfrac{\Lambda}{3}r^2&0\\ 0&0&0&\dfrac{\Lambda}{3}r^2\end{pmatrix}. \end{array} $

(16) Correspondingly,
$ \begin{array}{*{20}{l}} &h_{\mu\nu}=\\ &\begin{pmatrix}-2\varphi+\dfrac{\Lambda}{3}r^2&0&0&0\\ 0&-2\varphi-\dfrac{\Lambda}{3}r^2&0&0\\ 0&0&-2\varphi-\dfrac{\Lambda}{3}r^2&0\\ 0&0&0&-2\varphi-\dfrac{\Lambda}{3}r^2\end{pmatrix}. \end{array} $

(17) Compared to the usual Newtonian limit of Einstein equation without the cosmological constant, we can determine that the correction term of the cosmological constant to the Newtonian potential is:
$ -\frac{\Lambda}{6}r^2. $

(18) This correction term results in an effective force
$ \frac{\Lambda}{3}r\hat{e}_r, $

(19) which behaves as a repulsive force.
At first glance, this result seems consistent with the expectation that dark energy should produce a repulsive gravitational force. Due to this incorrect sign of Λ, it is often concluded that the cosmological constant cannot be related to dark matter.
However, the aforementioned analysis reveals a fatal problem. Matter
$ T_{\mu\nu} $ is the source to the result in perturbation$ h_{\mu\nu} $ . In this sense, when$ T_{\mu\nu} $ vanishes,$ h_{\mu\nu} $ should vanish too. However, this is not true.I can be argued that this nonvanishing
$ h_{\mu\nu} $ is due to the small but nonvanishing Λ. Approximately, this argument makes sense. However, a subtle problem continues to exist. When$ T_{\mu\nu} $ vanishes, (11) and (14) become:$ \begin{array}{*{20}{l}} \nabla^2\bar{h}_{00}=-2\Lambda, \end{array} $

(20) $ \begin{array}{*{20}{l}} \nabla^2\bar{h}_{ii}=2\Lambda. \end{array} $

(21) Now the entire system is uniform and isotropic. Similar to the famous Neumann-Zeeliger problem, the above equations have no solutions that correspond to the isotropic symmetry the equations admit. This fact presents a significant issue when applying the result of Equation (19) to a galaxy. The galaxy in question is accounted for by Equation (19), but what about other galaxies far away? According to Equation (19), the farther the galaxy, the stronger the force, which leads to a paradoxical situation.
We can observe the contradiction further through Eq. (11). Effectively, Λ term acts as a form of matter:
$ \rho_{\rm eff}=\frac{\Lambda}{8\pi}, $

(22) which is positive
$ \rho_{\rm eff}>0 $ as usual matter. This implies that it should contribute an attractive gravitational force. Additionally, it does not correspond to dark energy.Mathematically, this issue is related to fact that the partial differential equation
$ \begin{array}{*{20}{l}} \nabla^2u=2\Lambda \end{array} $

(23) does not admit an unique solution without a suitable boundary condition. The solution (15) is just one of many possible solutions.
Given that there is no resolution to the aforementioned critical issue, we conclude that the previously derived result of a repulsive force associated with Λ is incorrect..
-
The discussion in the previous section suggests that there may be no Newtonian limit for the Einstein equation. This observation aligns with the famous Neumann-Zeeliger problem, which implies that Newtonian gravity cannot describe cosmology. However, interestingly, general relativity can indeed describe cosmology. Specifically, when small-scale matter is absent, Equation (1) admits a cosmological solution, the Friedman-Robertson-Walker (FRW) metric.
As in the previous section, we can again assume that matter introduces a perturbation to the metric, which disappears when matter is absent. Following this approach, we find that the background metric should be the FRW metric, rather than the Minkowski metric used in the previous section.
$ \begin{array}{*{20}{l}} g_{\mu\nu}=\gamma_{\mu\nu}+h_{\mu\nu}, \end{array} $

(24) where
$ \gamma_{\mu\nu} $ denotes the FRW metric corresponding to the cosmology solution. In the following, we always use the background metric$ \gamma_{\mu\nu} $ to raise and lower the indexes. For an example, the trace of$ h_{\mu\nu} $ implies:$ \begin{array}{*{20}{l}} h\equiv\gamma^{\mu\nu}h_{\mu\nu}. \end{array} $

(25) Along with this assumption, we have the Christoffel symbol of
$ g_{\alpha\beta} $ $ \begin{array}{*{20}{l}} \Gamma^{\mu}_{ \ \alpha\beta}=\hat{\Gamma}^{\mu}_{\ \alpha\beta}+{\Gamma^{(1)\mu}_{\ \ \ \ \alpha\beta} }+O(h^2), \end{array} $

(26) $ \Gamma^{(1)\mu}_{\ \ \ \ \alpha\beta}=\frac{1}{2}(\hat{\nabla}_\beta h_{\alpha}^{\ \mu}+\hat{\nabla}_{\alpha}h_{\beta}^{\ \mu}-\gamma^{\mu\rho}\hat{\nabla}_{\rho}h_{\alpha\beta}). $

(27) Here
$ \hat{\nabla}_{\alpha} $ denotes the covariant derivative associated with the FRW metric$ \gamma_{\alpha\beta} $ . Furthermore, the Riemann curvature tensor of$ g_{\mu\nu} $ is as follows:$ \begin{array}{*{20}{l}} R_{\mu\nu\sigma}^{\ \ \ \ \rho}=\hat{R}_{\mu\nu\sigma}^{\ \ \ \ \rho}+\hat{\nabla}_{\nu}\Gamma^{(1)\rho}_{\ \ \ \ \mu\sigma}-\hat{\nabla}_{\mu}\Gamma^{(1)\rho}_{\ \ \ \ \nu\sigma}+O(h^2), \end{array} $

(28) where
$ \hat{R}_{\mu\nu\sigma}^{\ \ \ \ \rho} $ denotes the Riemann curvature tensor of$ \gamma_{\mu\nu} $ . Accordingly, the Ricci tensor of$ g_{\mu\nu} $ reads$ \begin{array}{*{20}{l}} R_{\mu\sigma}=\hat{R}_{\mu\sigma}+R^{(1)}_{\mu\sigma}+O(h^2), \end{array} $

(29) where
$ \hat{R}_{\mu\sigma} $ denotes the Ricci tensor of$ \gamma_{\mu\nu} $ and$ R^{(1)}_{\mu\sigma}= \dfrac{1}{2}\bigg(-\hat{\nabla}_{\rho}\hat{\nabla}^{\rho}h_{\mu\sigma}-\hat{\nabla}_{\mu}\hat{\nabla}_{\sigma}h+\hat{\nabla}_{\rho}\hat{\nabla}_{\sigma}h_{\mu}^{\ \rho}+\hat{\nabla}_{\rho}\hat{\nabla}_{\mu}h_{\sigma}^{\ \rho}\bigg). $

(30) The Einstein tensor of
$ g_{\mu\nu} $ reads:$ \begin{array}{*{20}{l}} G_{\mu\sigma}=\hat{G}_{\mu\sigma}+G_{\mu\sigma}^{(1)}+O(h^2), \end{array} $

(31) $ \hat{G}^{(1)}_{\mu\sigma}= R^{(1)}_{\mu\sigma}-\frac{1}{2}(\gamma^{\alpha\beta}R^{(1)}_{\alpha\beta})\gamma_{\mu\sigma}- \frac{1}{2}\hat{R}h_{\mu\sigma}+\frac{1}{2}(h^{\alpha\beta}\hat{R}_{\alpha\beta})\gamma_{\mu\sigma}, $

(32) where
$ \hat{G}_{\mu\sigma} $ and$ \hat{R} $ denote the Einstein tensor and scalar curvature of$ \gamma_{\mu\nu} $ , respectively.Given that
$ \hat{R}_{\mu\nu}-\frac{1}{2}\hat{R}\gamma_{\mu\nu}+\Lambda \gamma_{\mu\nu}=8\pi \hat{T}_{\mu\nu}, $

(33) where
$ \hat{T}_{\mu\nu} $ denotes the cosmological scale matternto linear order of$ h_{\mu\nu} $ , the Einstein equation (1) leads to:$ \begin{aligned}[b]& R^{(1)}_{\mu\sigma}-\frac{1}{2}(\gamma^{\alpha\beta}R^{(1)}_{\alpha\beta})\gamma_{\mu\sigma}- \frac{1}{2}\hat{R}h_{\mu\sigma}+\frac{1}{2}(h^{\alpha\beta}\hat{R}_{\alpha\beta})\gamma_{\mu\sigma}\\ &+\Lambda h_{\mu\sigma}=8\pi T_{\mu\sigma}. \end{aligned} $

(34) Here,
$ T_{\mu\nu} $ denotes the small-scale matter.By combining all of these results, we obtain the following:
$ \begin{aligned}[b]& -\frac{1}{2}\hat{\nabla}_{\rho}\hat{\nabla}^{\rho}h_{\mu\sigma}-\frac{1}{2}\hat{\nabla}_{\mu}\hat{\nabla}_{\sigma}h+\frac{1}{2}\gamma_{\mu\sigma}\hat{\nabla}_{\rho}\hat{\nabla}^{\rho}h+{\Lambda}h_{\mu\sigma}\\ =\;&+\frac{1}{2}\hat{\nabla}_{\sigma}\hat{\nabla}_{\rho}h_{\mu}^{\ \rho}+\frac{1}{2}\hat{\nabla}_{\mu}\hat{\nabla}_{\rho}h_{\sigma}^{\ \rho}-\frac{1}{2}(\hat{\nabla}_{\alpha}\hat{\nabla}_{\rho}h^{\alpha\rho})\gamma_{\mu\sigma}\\& +\frac{1}{2}\hat{R}_{\rho\sigma\mu\alpha}h^{\alpha\rho}+\frac{1}{2}\hat{R}_{\rho\mu\sigma\alpha}h^{\alpha\rho}+\frac{1}{2}\hat{R}_{\sigma\alpha}h_{\mu}^{\ \alpha}+\frac{1}{2}\hat{R}_{\mu\alpha}h_{\sigma}^{\ \alpha}\\& -\frac{1}{2}\hat{R}h_{\mu\sigma}+\frac{1}{2}(h^{\alpha\beta}\hat{R}_{\alpha\beta})\gamma_{\mu\sigma}=8\pi T_{\mu\sigma}. \end{aligned} $

(35) Using the same trick as in the last section, we can use the trace-inverse tensor of
$ h_{\mu\nu} $ $ \bar{h}_{\mu\nu} \equiv h_{\mu\nu}-\frac{1}{2}h\gamma_{\mu\nu}, $

(36) to simplify the aforementioned equation, and the result is as follows:
$ \begin{aligned}[b]& -\frac{1}{2}\hat{\nabla}_{\rho}\hat{\nabla}^{\rho}\bar{h}_{\mu\sigma}+\Lambda\bar{h}_{\mu\sigma}-\frac{\Lambda}{2}\bar{h}\gamma_{\mu\sigma}\\&+\frac{1}{2}\hat{\nabla}_{\sigma}B_{\mu}+\frac{1}{2}\hat{\nabla}_{\mu}B_{\sigma}-\frac{1}{2}(\hat{\nabla}_{\alpha}B^{\alpha})\gamma_{\mu\sigma}\\& +\hat{R}_{\rho\mu\sigma\alpha}\bar{h}^{\alpha\rho}+\frac{1}{2}\hat{R}_{\sigma\alpha}\bar{h}_{\mu}^{\ \alpha}+\frac{1}{2}\hat{R}_{\mu\alpha}h_{\sigma}^{\ \alpha}\\&-\frac{1}{2}\hat{R}\bar{h}_{\mu\sigma}+\frac{1}{2}(\bar{h}^{\alpha\beta}\hat{R}_{\alpha\beta})\gamma_{\mu\sigma}=8\pi T_{\mu\sigma}. \end{aligned} $

(37) Furthermore, we use harmonic gauge in the last section as follows:
$ \begin{array}{*{20}{l}} B_{\mu}\equiv\hat{\nabla}^{\rho}\bar{h}_{\rho\mu}=0. \end{array} $

(38) Then, the aforementioned equation can be simplified to:
$ \begin{aligned}[b] \hat{\nabla}_{\rho}\hat{\nabla}^{\rho}\bar{h}_{\mu\sigma}=\;&-16\pi T_{\mu\sigma} +2\Lambda\bar{h}_{\mu\sigma}-\Lambda\bar{h}\gamma_{\mu\sigma} +2\hat{R}_{\rho\mu\sigma\alpha}\bar{h}^{\alpha\rho}\\&+\hat{R}_{\sigma\alpha}\bar{h}_{\mu}^{\ \alpha}+\hat{R}_{\mu\alpha}h_{\sigma}^{\ \alpha} -\hat{R}\bar{h}_{\mu\sigma}+(\bar{h}^{\alpha\beta}\hat{R}_{\alpha\beta})\gamma_{\mu\sigma}. \end{aligned} $

(39) Corresponding to the cosmology background, we use Friedman-Robertson-Walker (FRW) coordinate:
$ \begin{array}{*{20}{l}}\gamma_{\mu\nu}{\rm d}x^\mu {\rm d} x^\nu=-{\rm d} t^2+a(t)^2{\rm d}x^i{\rm d}x^j. \end{array} $

(40) The 'Cartesian' coordinate
$ (x,y,z) $ corresponds to the dimensionless coordinate with respect the size of current universe$ a_0 $ . In this viewpoint, which is the focus of the current paper, variables$ (x,y,z) $ are considerd as small values, with$ x,y,z\ll1 $ . It should be noted that$ a_0\sim\dfrac{1}{H_0} $ , where$ H_0 $ denotes the Hubble constant and$ x,y,z\sim H_0r $ , where r denotes the size we are interested in.For the FRW metric, we have the following nonzero curvature components as follows:
$ R_{0i0j}=-\frac{\ddot{a}}{a}\gamma_{ij},\ R_{ijkl}=\frac{\dot{a}^2}{a^2}(\gamma_{ik}\gamma_{jl}-\gamma_{il}\gamma_{jk}), $

(41) $ \hat{R}_{00}=-3\frac{\ddot{a}}{a},\;\hat{R}_{ij}=\frac{2\dot{a}^2+a\ddot{a}}{a^2}\gamma_{ij}, $

(42) $ \hat{R}=6\frac{\dot{a}^2+a\ddot{a}}{a^2}. $

(43) Corresponding to the left hand side of (39), we obtain the following.
$ \begin{aligned}[b]\hat{\nabla}_{\rho}\hat{\nabla}^{\rho}\bar{h}_{00}=\;&-\frac{\partial^2}{\partial t^2}\bar{h}_{00}+\frac{1}{a^2}\sum\limits_{j=1}^3\frac{\partial^2}{\partial (x^j)^2}\bar{h}_{00}-3H\frac{\partial}{\partial t}\bar{h}_{00}\\& +8H^2\bar{h}_{00}-4H\frac{1}{a}\sum\limits_{j=1}^3\frac{\partial}{\partial x^j}\frac{\bar{h}_{0j}}{a}+2H^2\bar{h}, \end{aligned} $

(44) $ \begin{aligned}[b] \hat{\nabla}_{\rho}\hat{\nabla}^{\rho}\bar{h}_{ii}=\;&-\frac{\partial^2}{\partial t^2}\bar{h}_{ii}+\frac{1}{a^2}\sum\limits_{j=1}^3\frac{\partial^2}{\partial (x^j)^2}\bar{h}_{ii}+H\frac{\partial}{\partial t}\bar{h}_{ii}\\ &+2H^2\bar{h}_{ii}+2\frac{\ddot{a}}{a}\bar{h}_{ii}-4H\frac{\partial}{\partial x^i}\bar{h}_{0i}+2\dot{a}^2\bar{h}_{00}, \end{aligned} $

(45) $ \begin{aligned}[b] \hat{\nabla}_{\rho}\hat{\nabla}^{\rho}\bar{h}_{0i}=\;&-\frac{\partial^2}{\partial t^2}\bar{h}_{0i}+\frac{1}{a^2}\sum\limits_{j=1}^3\frac{\partial^2}{\partial (x^j)^2}\bar{h}_{0i} -H\frac{\partial}{\partial t}\bar{h}_{0i}\\&+7H^2\bar{h}_{0i}+\frac{\ddot{a}}{a}\bar{h}_{0i}-2H\frac{\partial}{\partial x^i}\bar{h}_{00}\\& -2H\frac{1}{a}\sum\limits_{j=1}^3\frac{\partial}{\partial x^j}\frac{\bar{h}_{ij}}{a}, \end{aligned} $

(46) $ \begin{aligned}[b] \hat{\nabla}_{\rho}\hat{\nabla}^{\rho}\bar{h}_{ij}=\;&-\frac{\partial^2}{\partial t^2}\bar{h}_{ij}+\frac{1}{a^2}\sum\limits_{k=1}^3\frac{\partial^2}{\partial (x^k)^2}\bar{h}_{ij} +H\frac{\partial}{\partial t}\bar{h}_{ij}\\&-2H\frac{\partial}{\partial x^i}\bar{h}_{0j}-2H\frac{\partial}{\partial x^j}\bar{h}_{0i} +2\frac{\ddot{a}}{a}\bar{h}_{ij}\\&+H^2\bar{h}_{ij},i\neq j \end{aligned} $

(47) where
$ H\equiv\dfrac{\dot{a}}{a} $ denotes the Hubble parameter.We change the dimensionless coordinate
$ (x,y,z) $ to an appropriate length coordinate$ (x',y',z')=(ax,ay,az) $ and introduce auxiliary variables as follows:$ \begin{array}{*{20}{l}} \chi_{00}=h_{00},\;\;\bar\chi_{00}=\bar{h}_{00}, \end{array} $

(48) $ \chi_{0i}=\frac{h_{0i}}{a},\;\;\bar\chi_{0i}=\frac{\bar{h}_{0i}}{a}, $

(49) $ \chi_{ij}=\frac{h_{ij}}{a^2},\;\;\bar\chi_{ij}=\frac{\bar{h}_{ij}}{a^2}, $

(50) $ \begin{array}{*{20}{l}} \chi\equiv\eta^{\mu\nu}\chi_{\mu\nu}=h, \end{array} $

(51) $ \begin{array}{*{20}{l}} \bar{\chi}\equiv\eta^{\mu\nu}\bar\chi_{\mu\nu}=\bar{h}. \end{array} $

(52) Then, Eqs. (44)−(47) become:
$ \begin{aligned}[b] \hat{\nabla}_{\rho}\hat{\nabla}^{\rho}\bar{h}_{00}=\;&\Box\bar{\chi}_{00}-3H\dot{\bar{\chi}}_{00} +8H^2\bar{\chi}_{00}\\&-4H\sum\limits_{j=1}^3\frac{\partial}{\partial x'^j}\bar{\chi}_{0j}+2H^2\bar{\chi}, \end{aligned} $

(53) $ \begin{aligned}[b] \hat{\nabla}_{\rho}\hat{\nabla}^{\rho}\bar{h}_{ii}=\;&a^2\Box\bar{\chi}_{ii}-3a\dot{a}\dot{\bar{\chi}}_{ii} +2\dot{a}^2\bar{\chi}_{ii}\\&-4a\dot{a}\frac{\partial}{\partial x'^i}\bar{\chi}_{0i}+2\dot{a}^2\bar{\chi}_{00}, \end{aligned} $

(54) $ \begin{aligned}[b] \hat{\nabla}_{\rho}\hat{\nabla}^{\rho}\bar{h}_{0i}=\;&a\Box\bar{\chi}_{0i}-3\dot{a}\dot{\bar\chi}_{0i}+6H^2a\bar{\chi}_{0i}-2\dot{a}\frac{\partial}{\partial x'^i}\bar{\chi}_{00}\\& -2\dot{a}\sum\limits_{j=1}^3\frac{\partial}{\partial x'^j}\bar{\chi}_{ij}, \end{aligned} $

(55) $ \begin{aligned}[b] \hat{\nabla}_{\rho}\hat{\nabla}^{\rho}\bar{h}_{ij}=\;&a^2\Box\bar{\chi}_{ij}-3a\dot{a}\dot{\bar{\chi}}_{ij}+\dot{a}^2\bar{\chi}_{ij}\\& -2a\dot{a}\frac{\partial}{\partial x'^i}\bar{\chi}_{0j}-2a\dot{a}\frac{\partial}{\partial x'^j}\bar{\chi}_{0i},i\neq j \end{aligned} $

(56) Here, operator
$ \Box $ implies:$ \Box\equiv-\frac{\partial^2}{\partial t^2}+\frac{\partial^2}{\partial x'^2}+\frac{\partial^2}{\partial y'^2}+\frac{\partial^2}{\partial z'^2}. $

(57) Plugging the aforementioned results in (39) and considering the Newtonian limit (3) of
$ T_{\mu\sigma} $ , we obtain:$ \begin{aligned}[b] \Box\bar{\chi}_{00}=\;&-16\pi\rho+3H\dot{\bar{\chi}}_{00}+4H\sum\limits_{j=1}^3\frac{\partial}{\partial x'^j}\bar{\chi}_{0j}\\& +(2\Lambda-16H^2+4\frac{\ddot{a}}{a})\bar{\chi}_{00}+(\Lambda-4H^2+\frac{\ddot{a}}{a})\bar{\chi}, \end{aligned} $

(58) $ \begin{aligned}[b] a^2\Box\bar{\chi}_{ii}=\;&3a\dot{a}\dot{\bar{\chi}}_{ii}+(2\Lambda-4\frac{\ddot{a}}{a})a^2\bar{\chi}_{ii}+4a\dot{a}\frac{\partial}{\partial x'^i}\bar{\chi}_{0i}\\& -3a\ddot{a}\bar{\chi}_{00}-(\Lambda-2H^2-2\frac{\ddot{a}}{a})a^2\bar{\chi}, \end{aligned} $

(59) $ \begin{aligned}[b] a\Box\bar{\chi}_{0i}=\;&3\dot{a}\dot{\bar\chi}_{0i}+(2\Lambda-10H^2)a\bar{\chi}_{0i}+2\dot{a}\frac{\partial}{\partial x'^i}\bar{\chi}_{00}\\& +2\dot{a}\sum\limits_{j=1}^3\frac{\partial}{\partial x'^j}\bar{\chi}_{ij}, \end{aligned} $

(60) $ \begin{aligned}[b] a^2\Box\bar{\chi}_{ij}=\;&3a\dot{a}\dot{\bar{\chi}}_{ij}+(2\Lambda+H^2-4\frac{\ddot{a}}{a})a^2\bar{\chi}_{ij}+2a\dot{a}\frac{\partial}{\partial x'^i}\bar{\chi}_{0j}\\& +2a\dot{a}\frac{\partial}{\partial x'^j}\bar{\chi}_{0i},i\neq j \\[-10pt]\end{aligned} $

(61) Once again, given that the speed of light is multiplied by the time t, the time derivative is of higher order than the spatial derivative in the context of the Newtonian limit. Therefore, the aforementioned Eqs. (58)–(61) simplify to:
$ \begin{aligned}[b] \nabla^2\bar{\chi}_{00}=\;&-16\pi\rho+4H\sum\limits_{j=1}^3\frac{\partial}{\partial x'^j}\bar{\chi}_{0j}\\ &+(2\Lambda-16H^2+4\frac{\ddot{a}}{a})\bar{\chi}_{00}+(\Lambda-4H^2+\frac{\ddot{a}}{a})\bar{\chi}, \end{aligned} $

(62) $ \begin{aligned}[b] \nabla^2\bar{\chi}_{ii}=\;&(2\Lambda-4\frac{\ddot{a}}{a})\bar{\chi}_{ii}+4H\frac{\partial}{\partial x'^i}\bar{\chi}_{0i}\\ &-3\frac{\ddot{a}}{a}\bar{\chi}_{00}-(\Lambda-2H^2-2\frac{\ddot{a}}{a})\bar{\chi}, \end{aligned} $

(63) $ \begin{aligned}[b] \nabla^2\bar{\chi}_{0i}=\;&(2\Lambda-10H^2)\bar{\chi}_{0i}+2H\frac{\partial}{\partial x'^i}\bar{\chi}_{00}\\ &+2H\sum\limits_{j=1}^3\frac{\partial}{\partial x'^j}\bar{\chi}_{ij}, \end{aligned} $

(64) $ \begin{aligned}[b] \nabla^2\bar{\chi}_{ij}=\;&(2\Lambda+H^2-4\frac{\ddot{a}}{a})\bar{\chi}_{ij}+2H\frac{\partial}{\partial x'^i}\bar{\chi}_{0j}\\& +2H\frac{\partial}{\partial x'^j}\bar{\chi}_{0i},i\neq j \end{aligned} $

(65) Here, operator
$ \nabla^2 $ implies:$ \nabla^2\equiv \frac{\partial^2}{\partial x'^2}+\frac{\partial^2}{\partial y'^2}+\frac{\partial^2}{\partial z'^2}. $

(66) The current observation facts indicate that
$ \dfrac{\ddot{a}}{a}\sim H^2 $ and$ H\sim\sqrt{\Lambda} $ , which is a small quantity [18, 19]. The aforementioned Eqs. (62)–(65) lead to:$ \begin{array}{*{20}{l}} \bar{\chi}_{00}\sim O(H^0), \end{array} $

(67) $ \begin{array}{*{20}{l}} \bar{\chi}_{0i}\sim O(H), \end{array} $

(68) $ \begin{array}{*{20}{l}} \bar{\chi}_{ij}\sim O(H^2). \end{array} $

(69) In the following, we use perturbation method to solve Eqs. (62)−(65). Up to
$ O(H^0) $ , we obtain:$ \begin{array}{*{20}{l}} \nabla^2\bar{\chi}_{00}=-16\pi\rho, \end{array} $

(70) $ \begin{array}{*{20}{l}} \nabla^2\bar{\chi}_{\mu\nu}=0,\text{ other }\mu, \nu. \end{array} $

(71) Accordingly, we obtain:
$ \begin{array}{*{20}{l}} \bar{\chi}_{00}=-4\varphi, \end{array} $

(72) $ \begin{array}{*{20}{l}}\bar{\chi}_{\mu\nu}=0,~\text{ other }~~ \mu, \nu, \end{array} $

(73) where φ denotes the Newtonian potential satisfying
$ \begin{array}{*{20}{l}} \nabla^2\varphi=4\pi \rho. \end{array} $

(74) Up to
$ O(H) $ , we obtain:$ \begin{array}{*{20}{l}} \nabla^2\bar{\chi}_{00}=-16\pi\rho, \end{array} $

(75) $ \nabla^2\bar{\chi}_{0i}=-8H\frac{\partial\varphi}{\partial x'^i}, $

(76) $ \begin{array}{*{20}{l}} \nabla^2\bar{\chi}_{ij}=0. \end{array} $

(77) Accordingly, we obtain:
$ \begin{array}{*{20}{l}} \bar{\chi}_{00}=-4\varphi, \end{array} $

(78) $ \bar{\chi}_{0i}=-8H\frac{\partial\psi}{\partial x'^i}, $

(79) $ \begin{array}{*{20}{l}} \bar{\chi}_{ij}=0, \end{array} $

(80) where ψ is determined through:
$ \begin{array}{*{20}{l}} \nabla^2\psi=\varphi. \end{array} $

(81) Up to
$ O(H^2) $ , we obtain:$ \nabla^2\bar{\chi}_{00}=4(4H^2-\Lambda-3\frac{\ddot{a}}{a})\varphi-16\pi\rho, $

(82) $ \nabla^2\bar{\chi}_{ii}=-32H^2\frac{\partial^2\psi}{\partial x'^{i2}}+4(2H^2-\Lambda+5\frac{\ddot{a}}{a})\varphi, $

(83) $ \nabla^2\bar{\chi}_{0i}=-8H\frac{\partial\varphi}{\partial x'^i}, $

(84) $ \nabla^2\bar{\chi}_{ij}=-32H^2\frac{\partial^2\psi}{\partial x'^i\partial x'^j},i\neq j $

(85) The corresponding solution of
$ \bar{\chi}_{00} $ is:$ \bar{\chi}_{00}=-4\varphi+4(4H^2-\Lambda-3\frac{\ddot{a}}{a})\psi. $

(86) Furthermore, we obtain:
$ \begin{aligned} \sum\limits_{i=1}^3\nabla^2\bar{\chi}_{ii}&=-32H^2\sum\limits_{i=1}^3\frac{\partial^2\psi}{\partial x'^{i2}}+12(2H^2-\Lambda+5\frac{\ddot{a}}{a})\varphi\\ &=-32H^2\varphi+12(2H^2-\Lambda+5\frac{\ddot{a}}{a})\varphi\\ &=4(15\frac{\ddot{a}}{a}-3\Lambda-2H^2)\varphi, \end{aligned} $

(87) $ \sum\limits_{i=1}^3\bar{\chi}_{ii}=4(15\frac{\ddot{a}}{a}-3\Lambda-2H^2)\psi. $

(88) Consequently, we obtain:
$ \begin{aligned} \bar{\chi}=-\bar{\chi}_{00}+\sum\limits_{i=1}^3\bar{\chi}_{ii} =4\varphi-8(3H^2+\Lambda-9\frac{\ddot{a}}{a})\psi, \end{aligned} $

(89) $ \begin{aligned}[b] h_{00}&=\bar{h}_{00}+\frac{1}{2}\bar{h}=\bar{\chi}_{00}+\frac{1}{2}\bar{\chi}\\ &=-2\varphi+4(H^2-2\Lambda+6\frac{\ddot{a}}{a})\psi. \end{aligned} $

(90) Concerning the motion of a test particle in the curved spacetime described by the metric in (24), we have the geodesic equation:
$ \frac{{\rm d}^2x^\mu}{{\rm d}s^2}=-\Gamma^\mu{}_{\sigma\tau}\frac{{\rm d}x^\sigma}{{\rm d}s}\frac{{\rm d}x^\tau}{{\rm d}s} $

(91) $ =-\hat\Gamma^\mu{}_{\sigma\tau}\frac{{\rm d}x^\sigma}{{\rm d}s}\frac{{\rm d}x^\tau}{{\rm d}s}-\Gamma^{(1)\mu}{}_{\sigma\tau}\frac{{\rm d}x^\sigma}{{\rm d}s}\frac{{\rm d}x^\tau}{{\rm d}s}. $

(92) Here, s denotes an affine parameter.
Similar to the usual treatment of Newtonian limit of Einstein equation without cosmological constant, we consider both the velocity of test particle v and perturbation metric coefficient
$ \chi_{\mu\nu} $ as small quantities with the same order. Accordingly, for time component, we obtain:$ \frac{{\rm d}^2t}{{\rm d}s^2}=0 $

(93) up to the first order of small quantities. Hence, we can use t to replace s as the Newtonian limit for Einstein equation without cosmological constant.
Then, for the spatial components of (92), we obtain:
$ \frac{{\rm d}^2x^i}{{\rm d}t^2}=-2H\frac{{\rm d}x^i}{{\rm d}t}+\frac{1}{2a^2}h_{00,i}. $

(94) Given that
$ \ddot{x'}=\frac{{\rm d}^2}{{\rm d}t^2}(ax) $

(95) $ \begin{array}{*{20}{l}} ~=\ddot{a}x+2\dot{a}\dot{x}+a\ddot{x} \end{array} $

(96) $ =\frac{\ddot{a}}{a}x'+\frac{1}{2}\frac{\partial}{\partial x'}h_{00}, $

(97) a change to appropriate length coordinate
$ (x',y',z') $ leads to acceleration:$ \vec{a}=2(H^2-2\Lambda+6\frac{\ddot{a}}{a})\nabla\psi+\frac{\ddot{a}}{a}\vec{r}-\nabla\varphi. $

(98) Compared to the usual Newtonian dynamics, we obtain extra-corrected acceleration
$ \vec{a}_{\rm cor}=2(H^2-2\Lambda+6\frac{\ddot{a}}{a})\nabla\psi+\frac{\ddot{a}}{a}\vec{r}, $

(99) where ψ is determined through (81).
The current observation [18] indicates that
$ \begin{aligned}[b] H_0&\approx67.4\text{kms}^{-1}\text{Mpc}^{-1}\\ &\approx2.19\times10^{-18}\text{s}^{-1}\text{ in geometric units}, \end{aligned}$

(100) $ \begin{aligned}[b] \Lambda&\approx4.24\times10^{-66}\text{eV}^2\text{ in natural units}\\ &\approx9.54\times10^{-36}\text{s}^{-2}\text{ in geometric units} \end{aligned} $

(101) $ \begin{array}{*{20}{l}} ~\approx1.99H_0^2, \end{array} $

(102) $ \frac{\ddot{a}}{a}\approx0.55H_0^2. $

(103) This implies we have the following corresponding to the current universe.
$ \begin{array}{*{20}{l}} \vec{a}_{\rm cor}\approx H_0^2\left[0.32\nabla\psi+0.55\vec{r}\right]. \end{array} $

(104) Given that the Newtonian potential is negative, the correction described in (81) behaves like a gravitational force produced by positive matter. Hence, we can observe that the correction term
$2(H^2-2\Lambda+6\dfrac{\ddot{a}}{a})\nabla\psi \sim 0.32H_0^2\nabla\psi$ yields an attractive force. Additionally, the correction term$ \dfrac{\ddot{a}}{a}\vec{r}\sim 0.55H_0^2\vec{r} $ results in a repulsive force for an increasingly expansion universe. -
As an example, we consider a point mass M distribution ρ which results in
$ \varphi=-\dfrac{M}{r} $ . Then, Eq. (81) becomes:$ \nabla^2\psi=-\frac{M}{r}. $

(105) The solution is:
$ \psi=-\frac{1}{2}Mr. $

(106) Apparently, the extra gravitational force introduced by ψ is:
$ 2(H^2-2\Lambda+6\frac{\ddot{a}}{a})\nabla\psi\approx-0.16H_0^2M\hat{e}_r, $

(107) which is an attractive force. Based on the point mass case and circular orbit of test particle, we obtain:
$ v\approx\sqrt{M}\sqrt{\left|\frac{1}{r}+0.16H_0^2r\right|}. $

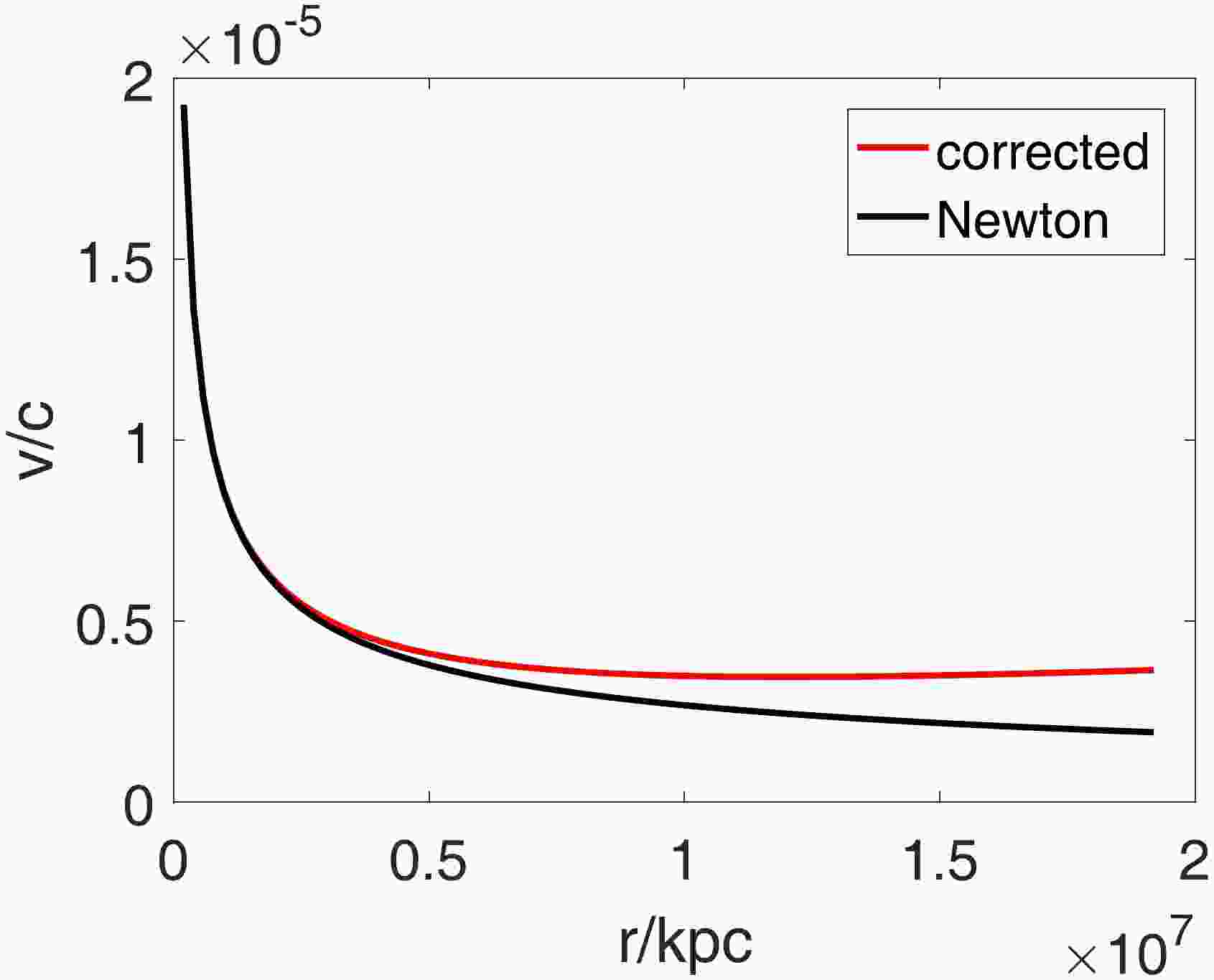
(108) Using our milky way galaxy as an example, we plot the corrected velocity when compared to standard Newtonian gravity prediction with a point mass model in Fig. 1.

Figure 1. (color online) We use our Milky Way galaxy as an example to demonstrate the effect of the correction in Equation (108). We assume a point mass distribution model for the Milky Way galaxy with a total mass of
$ M=1.5\times10^{12} $ M$ {}_\odot $ . Furthermore, we consider$ H_0\approx1\times10^{-23} $ M$ {}^{-1}_\odot $ . Qualitatively, we can observe an asymptotic relic velocity, which results from the correction. However, quantitatively, it is too small to explain the observed rotation curve [20].If we further consider the effect of the universe's expansion, we obtain the following:
$ \begin{aligned}[b] v&\sim\sqrt{|r(\nabla\varphi-0.32H_0^2\nabla\psi-0.55H_0^2r)|}\\ &\approx\sqrt{M}\sqrt{\left|\frac{1}{r}+0.16H_0^2r-0.55\frac{H_0^2r^2}{M}\right|}. \end{aligned} $

(109) Quantitatively, we can estimate the ratio between the corrected v and velocity predicted by Newtonian dynamics
$ v_{\rm N} $ $ \frac{v}{v_{\rm N}}=\sqrt{\left|\frac{1}{H_0r}-(0.55\frac{r}{M}-0.16)H_0r\right|}/\sqrt{\frac{1}{H_0r}}. $

(110) We plot
$ \log_{10}\left|\dfrac{v}{v_{\rm N}}-1\right| $ with respect to$ H_0r $ in Fig. 2. The size of usual galaxy is approximately$ H_0r\sim10^{-6} $ . The mass of usual galaxy is approximately$ H_0M\sim10^{-12} $ . Hence, in galaxy scale, we obtain that the correction is approximately$ 10^{-6} $ .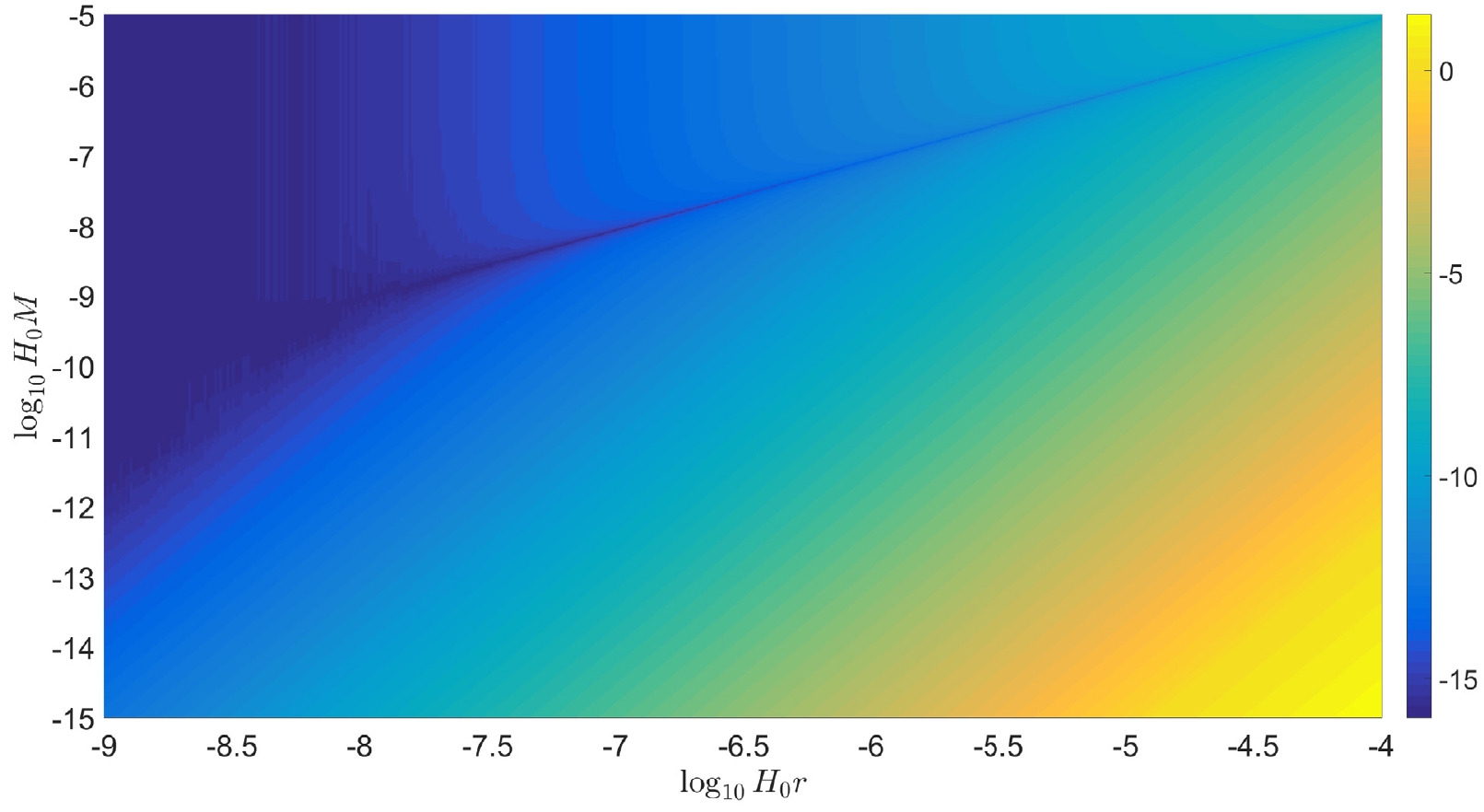
Figure 2. (color online) Ratio between the corrected velocity v by cosmological constant and velocity predicted by Newtonian dynamics
$ v_{\rm N} $ ,$ \log_{10}\left|\dfrac{v}{v_{\rm N}}-1\right| $ , with respect to different space scale$ H_0r $ and galaxy mass scale$ H_0M $ .Typically, we consider a general power law mass distribution model of galaxy
$ \begin{array}{*{20}{l}} \rho=Cr^{\alpha}. \end{array} $

(111) Physically, the mass distribution should be a decreasing function with respect to r such that
$ \alpha<0 $ . The aforementioned mass distribution results in:$ \varphi=\frac{C}{(2+\alpha)(3+\alpha)}r^{2+\alpha}, $

(112) $ -\nabla\varphi=-\frac{C}{3+\alpha}r^{1+\alpha}\hat{e}_r. $

(113) The corresponding circular orbit test particle velocity is:
$ v_N\sim\sqrt{r|\nabla\varphi|}=\sqrt{\left|\frac{C}{3+\alpha}\right|}r^{1+\frac{\alpha}{2}}. $

(114) The observed velocity does not increase along with r. This implies that
$ \alpha<-2 $ . Given that the observations show that the resulted gravitational force is attractive, we obtain$ \alpha>-3 $ . Altogether, we obtain the following:$ \begin{array}{*{20}{l}} -3<\alpha<-2. \end{array} $

(115) Then, Eq. (81) becomes:
$ \nabla^2\psi=\frac{C}{(2+\alpha)(3+\alpha)}r^{2+\alpha}. $

(116) The solution is:
$ \psi=\frac{C}{(2+\alpha)(3+\alpha)(4+\alpha)(5+\alpha)}r^{4+\alpha}. $

(117) Interestingly, we determine that the corrected gravitational force introduced by ψ is attractive when
$ -3<\alpha<-2 $ and is repulsive when$ \alpha>-2 $ or$ \alpha<-3 $ . For real galaxy, an attractive corrected force is expected.Again we consider circular orbit of test particle, so we have
$ \begin{aligned}[b] v&\sim\sqrt{|r(\nabla\varphi-0.32H_0^2\nabla\psi-0.55H_0^2r)|}\\ &\approx\sqrt{\frac{C}{3+\alpha}r^{2+\alpha}}\sqrt{1-\frac{0.32H_0^2r^2}{(2+\alpha)(5+\alpha)}-\frac{0.55(3+\alpha)H_0^2r^2}{Cr^{2+\alpha}}}. \end{aligned} $

(118) Hence, the corresponding correction can be estimated as:
$ \frac{v}{v_N}-1\approx-\left(\frac{0.16}{(2+\alpha)(5+\alpha)}+\frac{0.28(3+\alpha)}{Cr^{2+\alpha}}\right)H_0^2r^2. $

(119) For typical galaxy
$ H_0r\sim10^{-6} $ , the correction is approximately$ 10^{-12} $ , which is ignorably small.When
$ \alpha=-2 $ , the aforementioned correction appears to diverge. Hence,$ \alpha=-2 $ corresponds to the Singular Isothermal Sphere (SIS) mass distribution model of galaxy. Usually, SIS model is used to describe dark matter. We should consider this case individually. For SIS, we obtain:$ \rho=\frac{\sigma^2}{4\pi r^2}, $

(120) $ \begin{array}{*{20}{l}} \varphi=\sigma^2\ln r, \end{array} $

(121) $ \psi=\frac{\sigma^2}{6}r^2\left(\ln r-\frac{5}{6}\right), $

(122) where parameter σ corresponds to the asymptotic velocity in the rotation curves of galaxies. In this case, the corrected force is repulsive. The velocity correction for circular orbit test particle is approximately:
$ \frac{v}{v_N}-1\sim H_0^2r^2, $

(123) which is approximately
$ 10^{-12} $ , ignorably small, for a typical galaxy$ H_0r\sim10^{-6} $ . -
The acceleration of the expanding universe has been confirmed by several independent observations. This phenomenon can be explained by the Einstein equation with a cosmological constant. Alternatively, some prefer to explain it with dark energy, which is characterized by negative energy and negative pressure. Due to these properties, it is often concluded that the cosmological constant might contribute to a repulsive gravitational force.
We would like to emphasize that the concept of gravitational force is valid only within the framework of Newtonian dynamics. For dark energy, a repulsive gravitational force is a natural consequence of its negative energy. However, for the cosmological constant, this is not as straightforward.
To address the behavior of the gravitational force associated with the cosmological constant, we investigate the Newtonian limit of the Einstein equation with a cosmological constant. We argue that the approach based on perturbations of Minkowski spacetime is incorrect. Instead, perturbations should be applied to the FRW spacetime.
Based on the analysis of FRW metric perturbation, we observe two effective gravitational forces contributed by the cosmological constant Λ. Specifically,
$ \dfrac{\ddot{a}}{a}\vec{r} $ , which is repulsive but proportional to the distance to the center of the galaxy in question. The another gravitational force is due to the nonlinear behavior of matter's gravitational force$2\left(H^2-2\Lambda+6\dfrac{\ddot{a}}{a}\right)\nabla\psi\sim0.32H_0^2\nabla\psi$ with$ \begin{array}{*{20}{l}} \nabla^2\psi=\varphi. \end{array} $

(124) If only the Newton potential φ of the matter is negative, then this effective gravitational force introduced by the cosmological constant is attractive.
Quantitatively, the effective gravitational force introduced by the cosmological constant is
$ H_0^2r^2 $ . For dark energy model, the average density of dark energy is approximately$ H_0^2 $ . The gravitational force potential acted by dark energy is approximately$ \sim\dfrac{H_0^2r^3}{r}=H_0^2r^2 $ , which is comparable to the effective gravitational force introduced by the cosmological constant. However, there is an essential difference between these two forces. The force of dark energy is repulsive while the force of cosmological constant is attractive. Hence, in principle, we can use this feature to distinguish the two different theoretical models for the accelerating expansion universe.
Newtonian limit of Einstein equation with a cosmological constant
- Received Date: 2024-05-13
- Available Online: 2024-10-15
Abstract: Traditionally, the cosmological constant has been viewed as dark energy that mimics matter with negative energy. Given that matter with negative energy provides a repulsive force, which fundamentally differs from typical gravitational forces, it has been believed that the cosmological constant effectively contributes a repulsive force. However, it is important to note that the concept of gravitational force is valid only within the framework of Newtonian dynamics. In this study, we demonstrate that the traditional understanding of the gravitational force contributed by the cosmological constant is not entirely correct. Our approach involves investigating the Newtonian limit of the Einstein equation with a cosmological constant. The subtleties involved in this analysis are discussed in detail. Interestingly, we find that the effect of the cosmological constant on Newtonian gravity is an attractive force rather than a repulsive one for ordinary matter. As expected, this corrective force is negligibly small. However, our findings may offer a way to distinguish between dark energy and the cosmological constant, as one contributes a repulsive force while the other contributes an attractive force.





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF













 DownLoad:
DownLoad: