-
Since the first interpretation of the nuclear fission by the barrier penetration [1], it has become one of the most significant topics in nuclear physics, which plays a key role in the studies of superheavy synthesis and astrophysical r-process nucleosynthesis. It has attracted significant attention from both nuclear theoretical studies and experimental investigations at large-scale facilities worldwide. The inner fission barrier is a critical factor, as a 1-MeV variance in height can result in several orders of magnitude difference in the fission half-life. However, to date, very little experimental data has been obtained, making the corresponding theoretical studies particularly important.
Many theoretical models have been used to study fission barriers, such as the macroscopic-microscopic (MM) model [2−8], extended Thomas-Fermi plus Strutinsky integral (ETFSI) method [9, 10], and the density functional theories in non-relativistic framework [11−15] and relativistic framework [16−24]. Further theoretical research of nuclear fission has been reported in a recent review paper [25] and references therein. Currently, the covariant density functional theory (CDFT) has garnered significant attention due to its inherent advantages, particularly its preservation of Lorentz symmetry[26−28]. Furthermore, CDFT has achieved significant success in describing a variety of nuclear properties in a microscopic manner [28−32], such as nuclear masses and radii [33−37], half-lives [38−40], nuclear magicity [41−43], pseudospin symmetry [44−47], spin symmetry in antinucleon spectrum [48], nuclear rotations [49−52], shape coexistence and shape transition [53, 54], level density [55, 56], low-lying spectrum [57, 58], and single-particle resonances [59−61], as well as hypernuclear properties [62−65]. Focusing on the fission study, both the static fission properties [16−20] and fission dynamics [21−24] have been widely investigated by CDFT. Specifically, a systematic survey of fission paths and barriers for a broad range of superheavy nuclei has been examined with the restriction of axially symmetric shapes [16]. The impact of pairing correlations on the fission barriers has been investigated in Ref. [17]. Subsequently, considering the multidimensional constrained relativistic mean field (MDC-RMF) model, different roles of various shape degrees of freedom on the inner and outer fission barriers have been systematically examined [18, 19]. All the studies show that the triaxial and octupole degrees of freedom play significant roles for description on inner and outer fission barriers.
In recent years, starting from the CDFT, the deformed relativistic Hartree-Bogoliubov theory in continuum (DRHBc) has been developed, which can simultaneously consider the deformation, pairing correlations, and continuum effects [66, 67]. To date, it has been successfully applied to study stable and weakly-bound nuclei across the nuclear chart for many interesting topics, such as the prediction of shape-decoupling phenomenon in deformed halo nuclei [66−70], solution of the puzzles concerning the radius and neutron configuration in
$ ^{22} $ C [71], number of particles in the classically forbidden regions for magnesium isotopes [72], dependence of the multipole expansion order [73], deformation effects on the neutron drip line [74], shape evolution, shape coexistence and prolate-shape dominance [75−79], evolution of shell closures [43, 80], stability peninsulas beyond the neutron drip line [81−83], one-proton emission from$ ^{148-151} $ Lu [84], optimization of Dirac Woods-Saxon (DWS) basis [85], rotational excitations of exotic nuclei with angular momentum projection [86, 87], reaction and charge-changing cross sections of light nuclei with the Glauber model [88−90], and dynamical correlation with a two-dimensional collective Hamiltonian method [91]. Recently, efforts have been made to construct a DRHBc mass table that considers both deformation and continuum effects [35, 36, 92, 93]. However, to date, it does not exist for the application of DRHBc theory in the study of fission barrier.In this study, shape evolution and the inner fission barrier for even-even uranium isotopes from the proton drip line to the neutron drip line will be examined based on the DRHBc theory. In principle, to extract the height of the fission barrier
$ B_{\rm f} $ , i.e., the energy difference between the global ground state and the respective saddle, calculations should be performed in the multidimensional deformation space. In addition to the most important axial quadrupole deformation$ \beta_{2} $ , degrees of freedom, such as triaxial deformation γ and octupole deformation$ \beta_{3} $ , are also indispensable. For the inner fission barrier, it was determined by various models that the inclusion of triaxial deformation can reduce its height up to a few MeVs [7, 94−100]. As the DRHBc theory is limited to the axial symmetry, in this study, to evaluate the triaxial effect, the triaxial relativistic mean field calculations in combination with a simple BCS (RMF+BCS) method for pairing will also be performed. With this type of triaxial correction, the inner fission barrier heights will be compared with the available empirical data and results of FRLDM [7], ETFSI [10], HFB-14 [12], and MDC-RMF [20] models.The paper is organized as follows: Sec. II briefly introduces the theoretical framework of DRHBc; Sec. III presents the results and discussion; and Sec. IV provides a brief summary and perspective.
-
Detailed formalism of the DRHBc theory can be found in Refs. [66, 67, 92]. Here, a brief introduction is presented. In the DRHBc theory, the relativistic Hartree-Bogoliubov (RHB) equation that treats the mean field and pairing correlations self-consistently can be expressed as [101]:
$ \begin{align} \left(\begin{array}{cc} h_D-\lambda & \Delta \\ -\Delta^* & -h_D^*+\lambda \end{array}\right)\left(\begin{array}{c} U_k \\ V_k \end{array}\right)=E_k\left(\begin{array}{c} U_k \\ V_k \end{array}\right), \end{align} $

(1) where
$ E_k $ ,$ h_D $ , λ, and$(U_k, V_k)^{\rm T}$ denote the quasiparticle energy, Dirac Hamiltonian, Fermi energy, and quasiparticle wave function, respectively. The Dirac Hamiltonian$ h_D $ can be expressed as:$ \begin{align} h_D={\boldsymbol{\alpha}} \cdot {\boldsymbol{p}}+\beta(M+S({\boldsymbol{r}}))+V({\boldsymbol{r}}), \end{align} $

(2) where
$ S({\boldsymbol{r}}) $ and$ V({\boldsymbol{r}}) $ denote the scalar and vector potentials, respectively. The pairing potential for particle-particle channel can be expressed as:$ \begin{align} \Delta_{k k^{\prime}}\left({\boldsymbol{r}}, {\boldsymbol{r}}^{\prime}\right)=-\sum_{\tilde{k} \tilde{k}^{\prime}} V_{k k^{\prime}, \tilde{k} \tilde{k}^{\prime}}^{p p}\left({\boldsymbol{r}}, {\boldsymbol{r}}^{\prime}\right) \kappa_{\tilde{k} \tilde{k}^{\prime}}\left({\boldsymbol{r}}, {\boldsymbol{r}}^{\prime}\right), \end{align} $

(3) with the pairing tensor
$\kappa=V^* U^{\rm T}$ and density-dependent zero-range pairing interaction:$ \begin{align} V^{p p}\left({\boldsymbol{r}}, {\boldsymbol{r}}^{\prime}\right)=\frac{V_0}{2}\left(1-P^\sigma\right) \delta\left({\boldsymbol{r}}-{\boldsymbol{r}}^{\prime}\right)\left(1-\frac{\rho({\boldsymbol{r}})}{\rho_{\text{sat}}}\right), \end{align} $

(4) where
$ \rho_{\text{sat}} $ denotes the nuclear saturation density and$ V_0 $ denotes the pairing strength.In the DRHBc theory, the potentials and densities are expanded in terms of the Legendre polynomials as follows:
$ \begin{align} f({\boldsymbol{r}})=\sum_\lambda f_\lambda(r) P_\lambda(\cos \theta), \quad \lambda=0,2,4, \cdots \end{align} $

(5) Meanwhile, to appropriately consider the continuum effect, especially for nuclei close to drip lines, the deformed RHB Eq. (1) is solved using a spherical DWS basis [102], whose wave functions exhibit proper asymptotic behavior at large coordinates. After solving the RHB equation self-consistently, the total binding energy
$ E_{\rm tot} $ , radius, intrinsic multipole moments$ Q_\lambda $ along with the deformation parameters can be calculated. -
The numerical details of the present DRHBc calculations for the ground states of uranium isotopes follow those of the DRHBc mass table construction [35]. The point-coupling density functional PC-PK1 [103] is adopted. The size of the coordinate space is
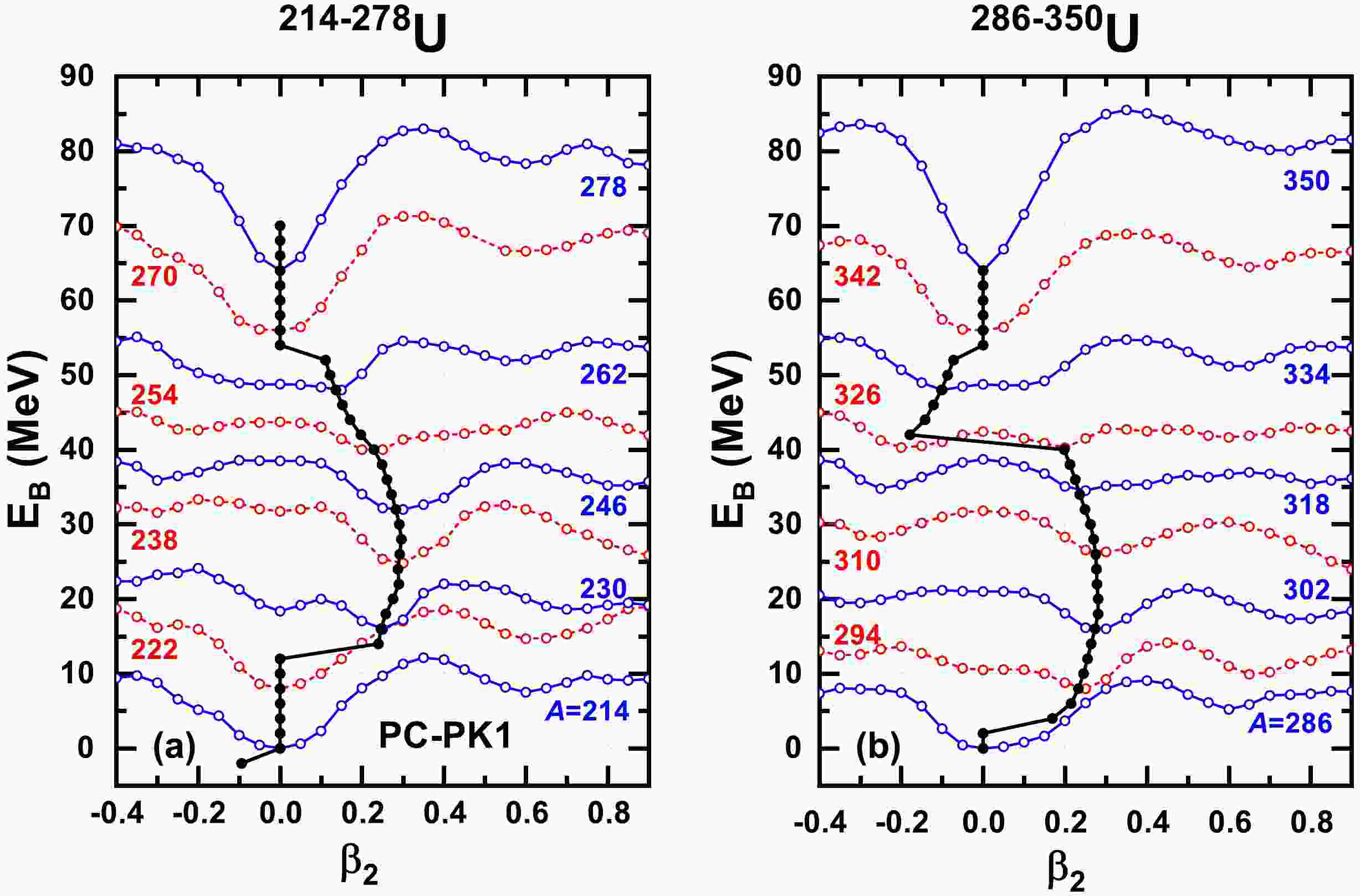
$ R_{\rm box} = 20 $ fm, the cutoffs for the energy and angular momentum in the DWS basis are$ E_{\rm cut} = 300 $ MeV and$ J_{\rm max} = 23/2\hbar $ , and Legendre expansion truncation order in Eq. (5) is$ \lambda_{\rm max}=8 $ . The pairing strength is$ V_0=-325\; \rm {MeV\; fm}^3 $ along with the pairing window of 100 MeV. However, with respect to the present calculations of potential energy curves (PECs) for examining the fission barrier, where large quadrupole deformation is involved, a larger$ \lambda_{\rm max}=10 $ [73] and larger$ J_{\rm max}=31/2 \hbar $ are found to be necessary. Correspondingly, as the zero-range pairing interaction is used, a weaker pairing strength is required to yield an appropriate pairing gap [92]. It is determined that$V_0= -300 {\rm {MeV\; fm}^3}$ combined with$ J_{\rm max}=31/2 \hbar $ are suitable for the odd-even mass differences of calcium and lead isotopes [104], and they can reproduce the ground state energies of uranium isotopes.Figure 1 shows the PECs obtained by the constrained DRHBc calculations for the uranium isotopes from
$ A= $ 214 to 350 with an interval of$ \Delta A=8 $ . The ground state deformations obtained in the unconstraint calculations are also shown for all even-even isotopes from the proton drip line$ ^{212} $ U to the neutron drip line$ ^{350} $ U predicted by DRHBc in Ref. [35]. It can be observed that these ground states correspond precisely with all the global minima on the individual PECs, confirming the accuracy of the constrained calculations. It should be noted that the predicted ground state deformations for$ ^{230,232,234,236,238} $ U are in good agreement with the empirical data extracted from experimental$ B(E2) $ values, and they are 0.246, 0.258, 0.276, 0.290, and 0.288, while they correspond to 0.260, 0.264, 0.266, 0.274, and 0.274 for empirical data [105]. A periodic-like pattern is exhibited for the shape evolution with neutron number, i.e., for closed shells$ N= $ 126,184, and 258, ground states of$ ^{218,276,350} $ U, and their neighbors are spherical; away from$ N= $ 126 to the next closure$ N= $ 184, the ground states experience spherical, prolate, and to spherical shape again; and away from$ N= $ 184 to the next closure$ N= $ 258, they experience spherical, prolate, oblate, and then back to spherical shape. It should be noted that the prominent shape transition from prolate to oblate occurs from$ ^{326} $ U ($ \beta_2=0.198 $ ) to$ ^{328} $ U ($ \beta_2= -0.179 $ ). Particularly for the PEC of$ ^{326} $ U, the prolate and oblate minima have very close energies with a difference of 0.05 MeV and low barrier with a height of 2.18 MeV located between them, which indicates potential shape coexistence.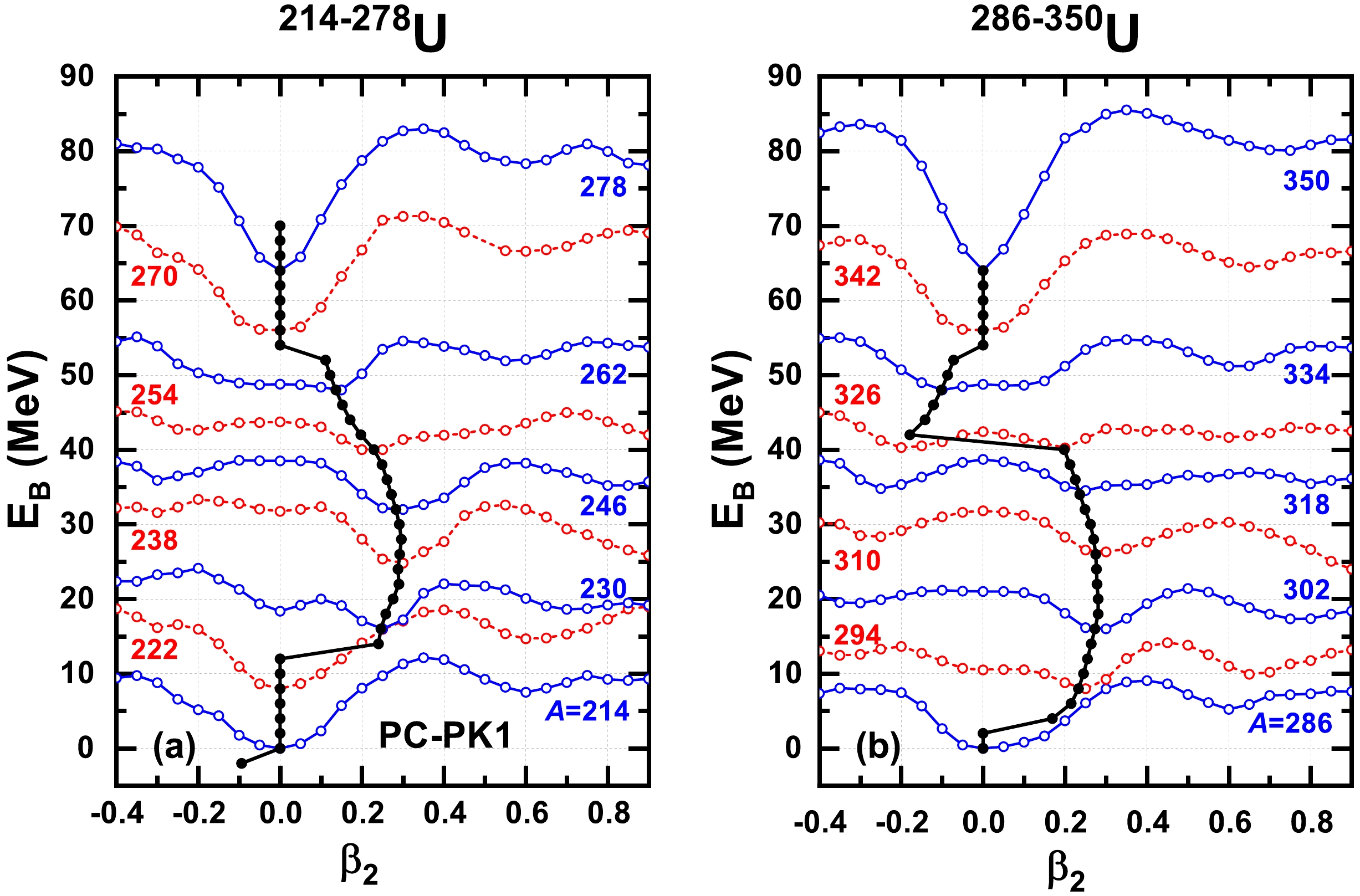
Figure 1. (color online) PECs of
$ ^{214-278} $ U (a) and$ ^{286-350} $ U (b) denoted by open circles by the constrained DRHBc calculations with PC-PK1. For comparison, the ground state deformations are shown as solid circles obtained by unconstraint calculations. In each panel, the PECs of$ ^{214} $ U and$ ^{286} $ U are renormalized to their ground states, and others are each shifted upward by 8 MeV.In Fig. 2, the inner fission barrier heights
$ B_{\rm f} $ obtained in the axially deformed case by DRHBc are shown, which is considered as the energy difference between the ground state and top of the first barrier. Analogous to the ground state shape evolutions, the fission barrier height$ B_{\rm f} $ also manifests a distinct pattern. Specifically,$ B_{\rm f} $ shows pronounced peaks ($ \approx 20 $ MeV) when the neutron numbers are at the shell closures, i.e.,$ N= $ 126, 184, and 258 while in the mid-shell,$ B_{\rm f} $ is lowered dramatically with a minimum of 2.44 MeV at$ ^{318} $ U. For comparison, the available empirical fission barriers obtained by fitting experimental fission cross sections [106] are also shown. It can be observed that the fission barrier heights extracted for$ ^{232,234,236,238} $ U from the DRHBc theory are approximately 2 MeV higher than the empirical values. The main reason for this is believed to be triaxial effect.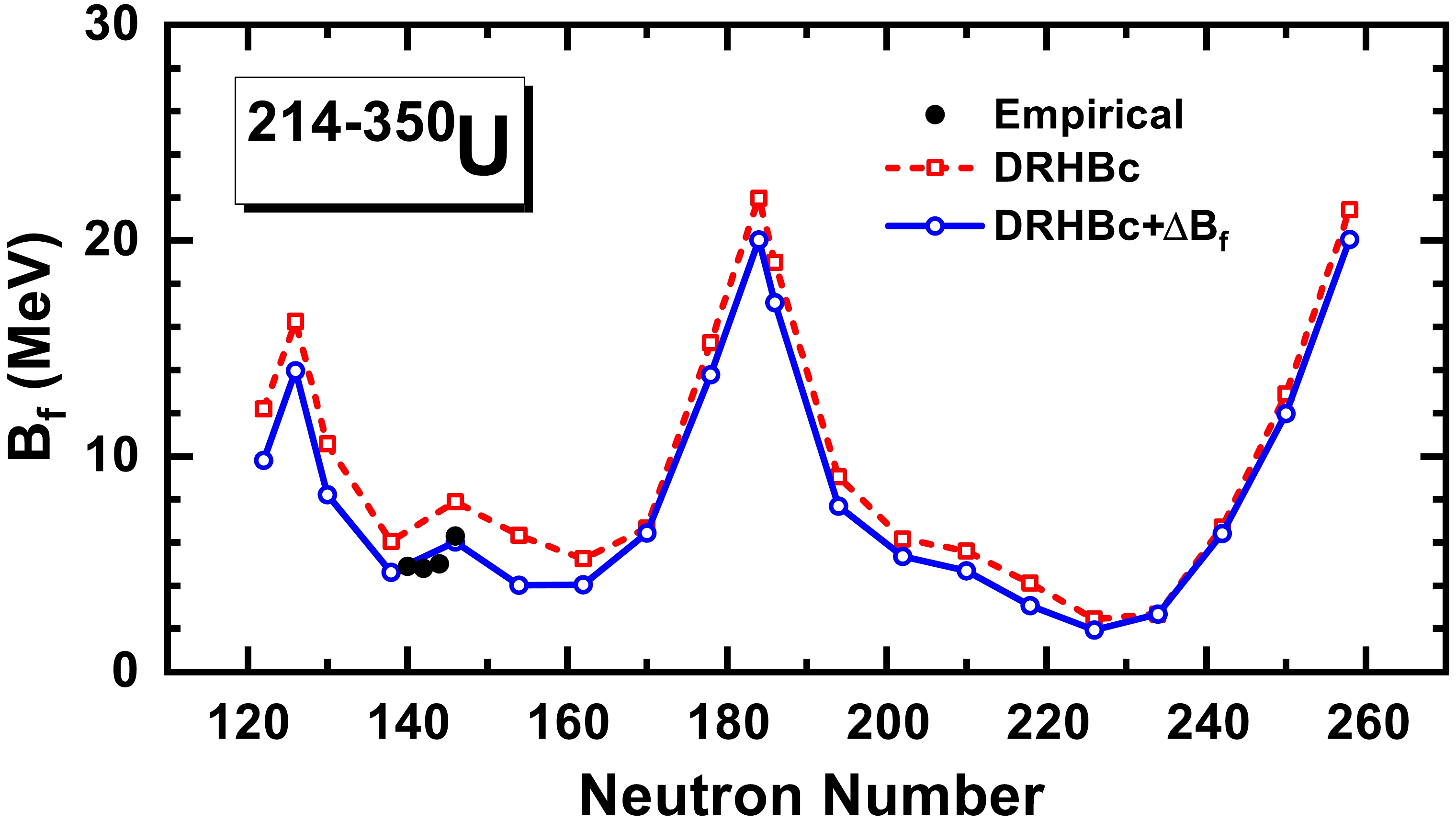
Figure 2. (color online) Inner fission barrier heights
$ B_{\rm f} $ in the DRHBc calculations for even-even U isotopes when compared with the empirical data [106]. The results with the triaxial correction$ \Delta B_{\rm f} $ are also shown.According to the previous studies, the importance of triaxiality to reduce the inner fission barrier height has been emphasized [7, 94−100]. In principle, we explicitly consider the triaxial effect for examining the inner barrier height by considering models such as triaxial relativistic Hartree-Bogoliubov theory (TRHB) [107]. However, we encountered the challenge of extensive computational demands. To address this, we adopted a simpler model — RMF+BCS in the harmonic oscillator basis — to extract the triaxial effect in this work. To maintain consistency with the DRHBc calculations, we used the same density functional, PC-PK1. The harmonic oscillator basis is
$ N_{\rm f}=16 $ while the parameters of the separable pairing force G = 728 MeV fm$ ^3 $ and a = 0.644 fm are considered from Ref. [108].In Fig. 3, the potential energy surfaces (PESs) in the (
$ \beta_2 $ , γ) plane obtained by the constrained RMF + BCS calculations are shown for$ ^{214-342} $ U with$ \Delta A=16 $ . It can be determined that the ground states of U isotopes, denoted by red dots, are all spherical or axially deformed, which verifies the appropriateness of the ground state deformation obtained in the DRHBc calculations presented in Fig. 1. Specifically, for$ ^{326} $ U, where the prolate and oblate minima are very close in energy in Fig. 1, the triaxial RMF + BCS calculations also predict a prolate minimum at$ \beta_2 \sim 0.20 $ and an oblate minimum at$ \beta_2 \sim -0.20 $ with a tiny energy difference of 200 keV. This implies that the prediction of shape coexistence in$ ^{326} $ U still holds with the triaxial degree of freedom considered. Please note that there is a second local minimum at$ \beta_2 = $ 0.56, which is much higher than the ground state. In Fig. 3, we also indicate the position of the saddle point for each nucleus by red stars. It can be shown that$ \beta_2 $ values of these saddle points are located between 0.4 and 0.8, while the corresponding γ values are located between 0$ ^\circ $ and 20$ ^\circ $ . It is clear that the saddle point is lower than the peak with axial symmetry, and the consideration of the triaxial degree of freedom does reduce the height of the inner fission barrier for the uranium isotopes.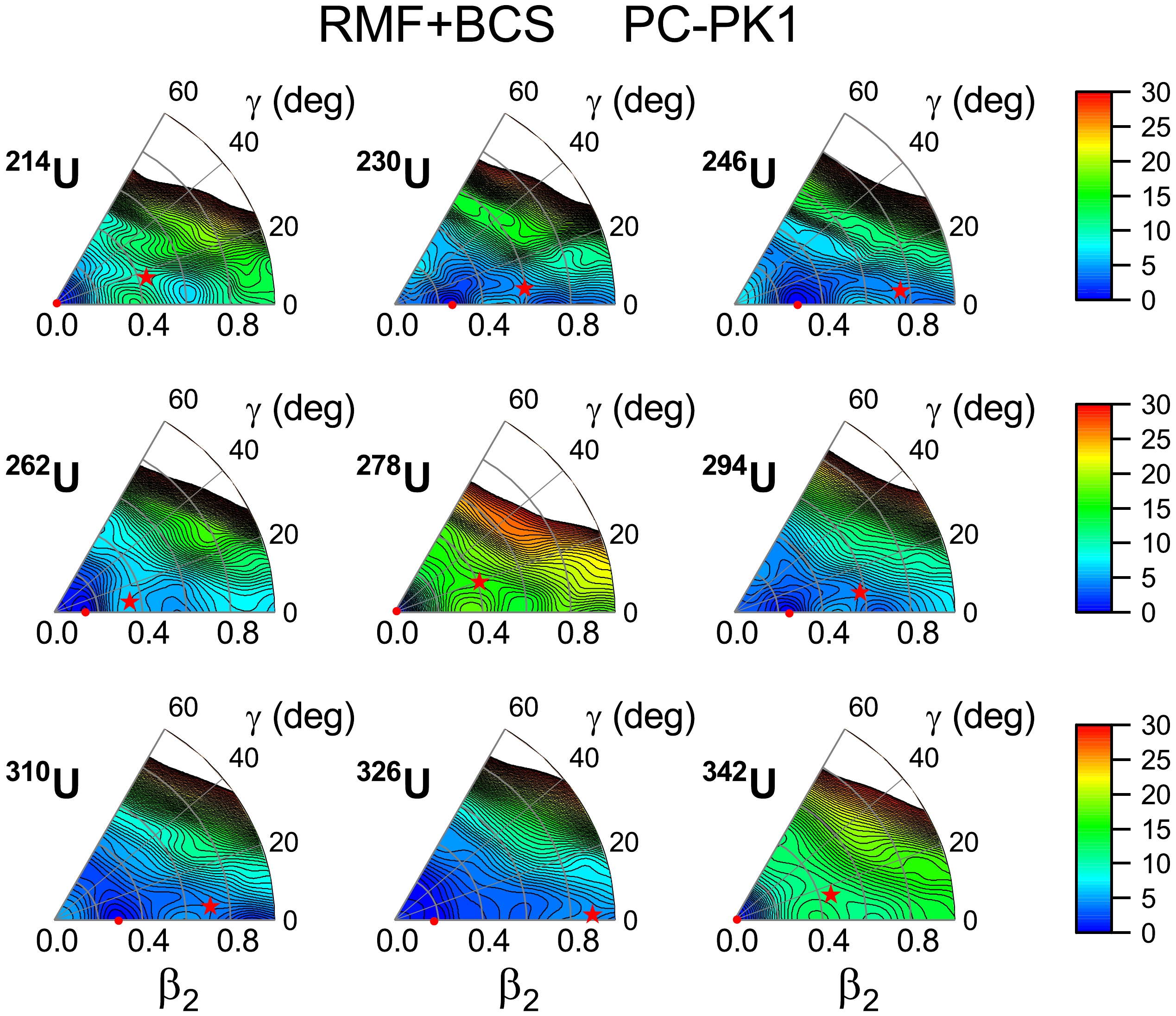
Figure 3. (color online) PESs in the
$ (\beta_2,\gamma) $ plane for$ ^{214-342} $ U isotopes with$ \Delta A $ =16, calculated by the RMF + BCS model. For each nucleus, the global minimum and saddle point are represented by the red dots and stars, respectively. The energy separation between contour lines is 0.5 MeV.Based on the RMF+BCS calculations, the reduction of the fission barrier by triaxial effect is defined as
$ \Delta B_{\rm f}=B_{\rm f}^{\rm BCS}({\rm triaxial})-B_{\rm f}^{\rm BCS}({\rm axial}) $ , where$ B_{\rm f}^{\rm BCS}({\rm triaxial}) $ denotes the height of the fission barrier in the PES determined by the triaxial calculations and$ B_{\rm f}^{\rm BCS}({\rm axial}) $ denotes the corresponding height under the restriction of axial symmetry. Considering$ ^{238} $ U as an example, Fig. 4 illustrates the PECs obtained by the DRHBc and triaxial RMF + BCS calculations. For the latter, the PEC along the fission path (blue solid line) and the path under the axial symmetry (blue dash-dotted line) have been plotted. In general, the PEC by the DRHBc is in good agreement with the one by the RMF + BCS under the axial symmetry with the exception of the perceptible differences in regions of$\beta_2 \leqslant 0.10$ and$\beta_2 \geqslant 0.75$ . Obvious triaxial effects are found in the range of$0.40 \leqslant \beta_2 \leqslant 0.65$ , which significantly reduce the fission barrier by an amount of$ -\Delta B_{\rm f}=1.87 $ MeV. After superimposing$ \Delta B_{\rm f} $ to the fission barrier height obtained by the DRHBc calculation, the corrected barrier height denoted by the red square becomes very close to the empirical value.
Figure 4. (color online) PECs of
$ ^{238} $ U by DRHBc (red dotted line), RMF+BCS under axial symmetry (blue dash-dotted line), and triaxial RMF+BCS (blue solid line) calculations. The triaxial correction is determined by$ \Delta B_{\rm f}=B_{\rm f}^{\rm BCS}({\rm triaxial})- $ $ B_{\rm f}^{\rm BCS}({\rm axial}) $ . The black dashed line denotes the empirical barrier.Considering the prescription shown in Fig. 4, triaxial corrections
$ \Delta B_{\rm f} $ in the fission barrier have been estimated for$ ^{214-350} $ U isotopes plotted as a function of neutron number in Fig. 5(a). Significant variations in triaxiality are shown for uranium isotopes, e.g., correction$ -\Delta B_{\rm f} $ can be as high as 2.5 MeV for$ ^{214} $ U while almost zero for$ ^{326} $ U. With respect to$ ^{214} $ U, as shown in Fig. 3, the saddle point denoted by the red star includes a large triaxial deformation, which implies that the static fission path in$ (\beta_2, \gamma) $ plane is far away from the axial symmetric path, leading to a remarkable triaxial effect. However, for$ ^{326} $ U, the saddle point and fission path are with the axial symmetry. Hence, the triaxial effect is zero. It is interesting to show the evolution of γ values of the fission barriers, which may be correlated with$ \Delta B_{\rm f} $ . As shown in Fig. 5(b), γ values display synchronized evolution with$ \Delta B_{\rm f} $ in general except for$ ^{254} $ U, which is related to the steepness of PES in γ direction around the saddle points. By superimposing$ \Delta B_{\rm f} $ to the barrier height obtained by the DRHBc theory, in Fig. 2, a good agreement with the empirical fission barriers of$ ^{232,234,236,238} $ U is obtained. Furthermore, the triaxial effect does not change the global trend of the barrier height.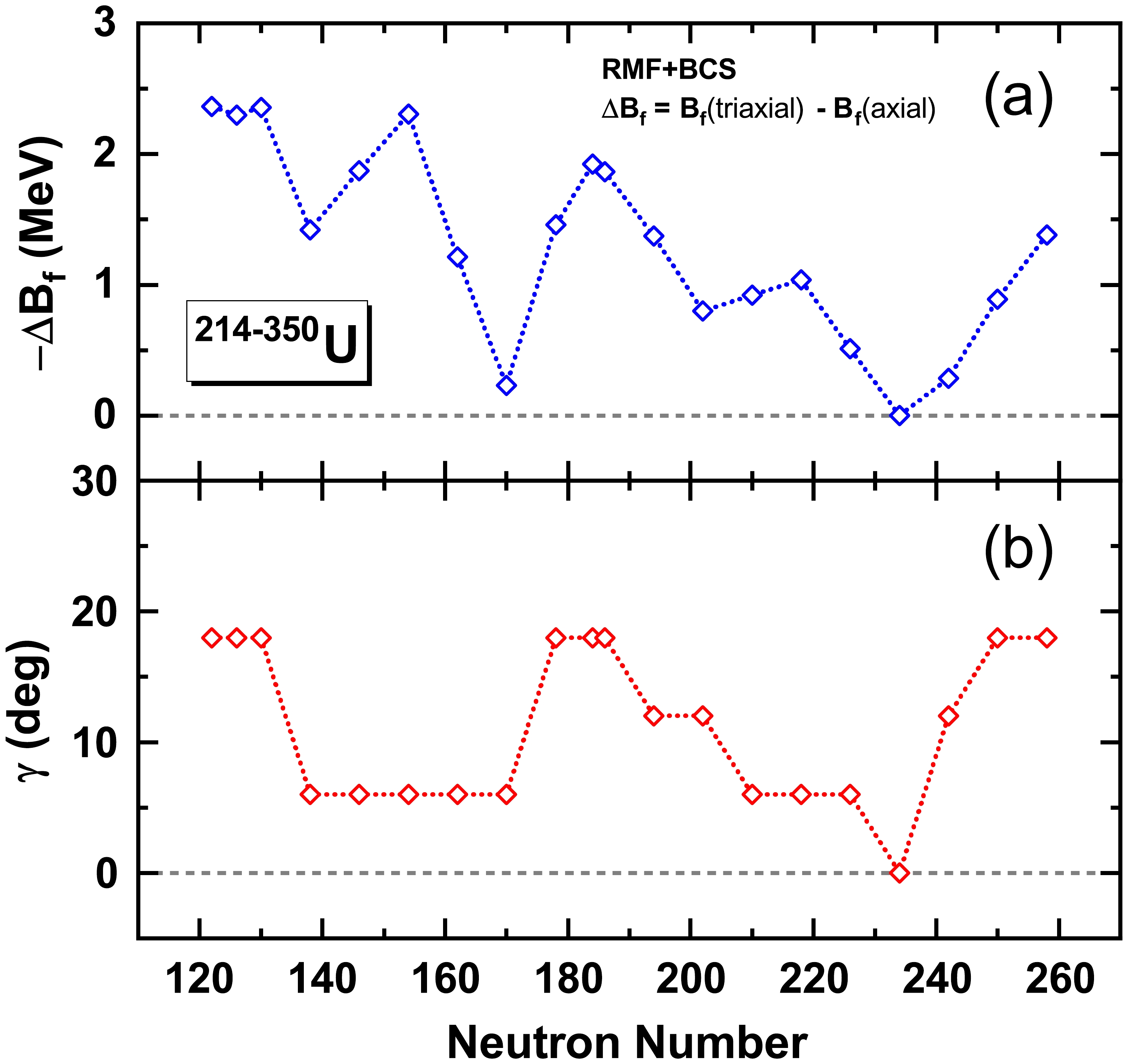
Figure 5. (color online) (a) Triaxial correction
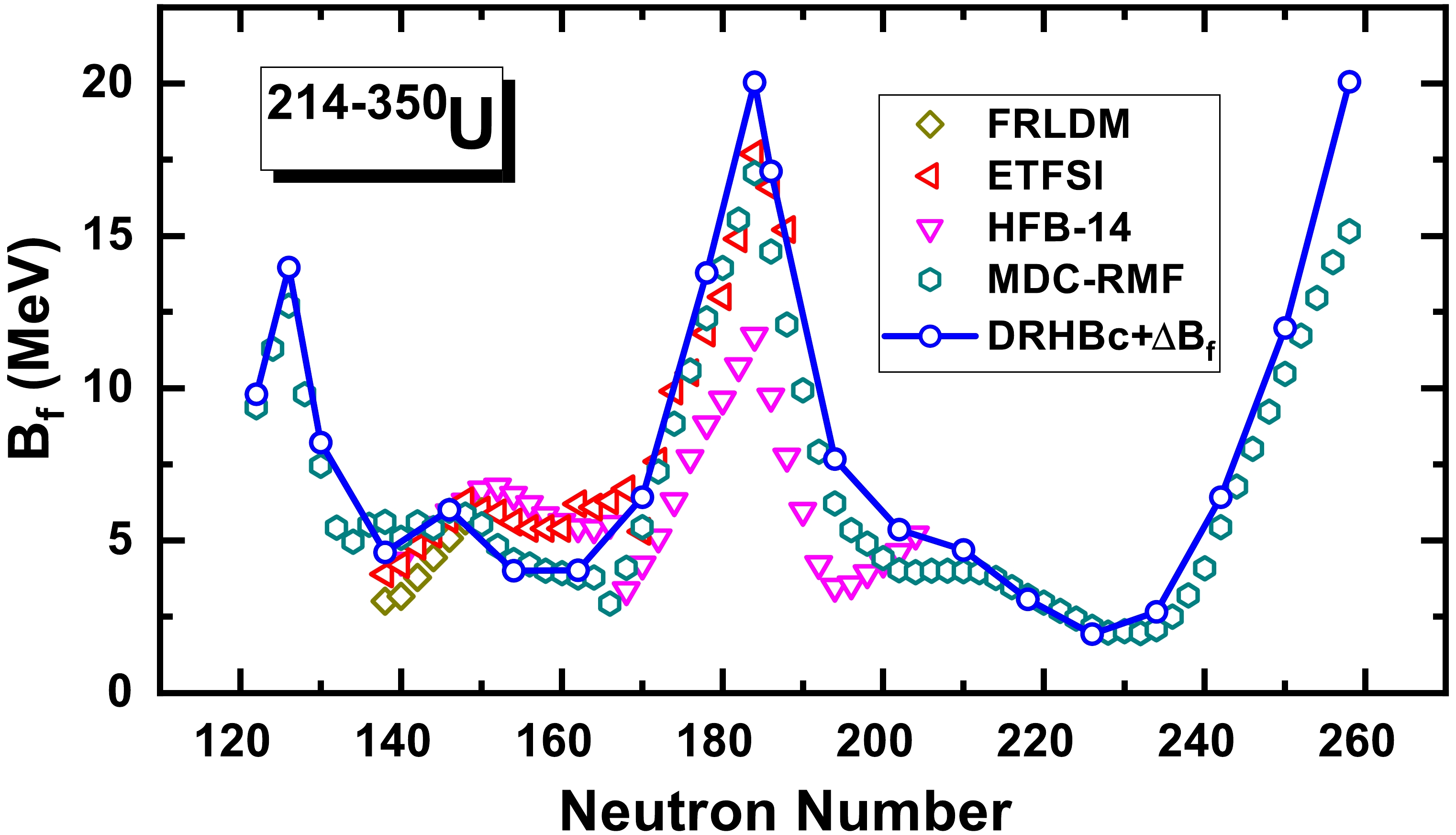
$ -\Delta B_{\rm f} $ for the inner fission barrier and (b) γ values of the saddle points by the RMF+BCS model as a function of the neutron number.Finally, in Fig. 6, inner fission barriers by the DRHBc theory with the triaxial correction
$ \Delta B_{\rm f} $ are compared with the results by FRLDM [7], ETFSI [10], HFB-14 [12], and MDC-RMF [20] models. For isotopes with$ 138 \leqslant N \leqslant 194 $ , the evolutions of the fission barrier heights, given by these theories, are analogous to each other. For the peak at$ N=184 $ , the DRHBc provides the largest barrier height, HFB-14 provides the lowest one, and ETFSI and MDC-RMF are in between. Drastic different evolutions of the barrier heights appear around$ N \geqslant 194 $ , i.e., results by the HFB-14 [12] increase with neutron number N while those by the MDC-RMF [20] and DRHBc decrease with N. However, from the proton drip line to the neutron drip line, the DRHBc and MDC-RMF results show significant consistency. It is further noted that a flat valley is shown around the neutron-rich nucleus$ ^{318} $ U with a barrier height of as low as 1.9 MeV, indicating a large probability in spontaneous or induced fission, which may play an important role in the astrophysical r-process nucleosynthesis [109]. -
In this study, we investigate the shape evolution and inner fission barriers of the even-even uranium isotopes from the proton to the neutron drip line with the deformed relativistic Hartree-Bogoliubov theory in continuum. The obtained ground state deformations of
$ ^{230,232,234,236} $ U are in good agreement with the empirical data. A periodic-like evolution is shown for the ground state shape with respect to the neutron number: it evolves from spherical at the closed shell$ N = 126 $ to prolate at the mid-shell, then back to spherical near the next closed shell$ N = 184 $ . Subsequently, it further undergoes spherical to prolate to oblate transitions, and finally becomes spherical again near the next possible closed shell$ N = 258 $ . From the PECs obtained through DRHBc calculations, the inner fission barriers of uranium isotopes have been extracted. The triaxial correction to these inner fission barriers was further evaluated using the triaxial RMF + BCS method. Including the triaxial correction results in good consistency with available empirical data on inner barrier heights. Additionally, the evolutionary trend from the proton to the neutron drip line aligns with results from the MDC-RMF theory. Notably, a flat valley in the fission barrier height is predicted around the neutron-rich nucleus$ ^{318} $ U, indicating that a possible fission intends to occur easily. This can play a key role in the astrophysical r-process nucleosynthesis.In the future, a self-consistent multidimensional constraint relativistic Hartree-Bogoliubov (MDC-RHB) theory will be developed to study both the inner and outer fission barriers, incorporating axial, triaxial, and higher-order deformations. However, for certain specific potential energy surfaces, the true saddle point may be misrepresented by the conventional constrained method due to the limitations in the dimensionality of the calculations. In Refs. [5, 7], Möller et al. discussed the difficulty of the commonly used minimization techniques in identifying the real saddle point and indicated that the immersion method [7] can solve it unambiguously. In the future, we may incorporate this type of method to determine the saddle point in the framework of MDC-RHB theory.
-
The authors are grateful to Dr. Xiangquan Deng for providing us the inner fission barriers of uranium nuclei with the MDC-RMF calculations. Helpful discussions with members of the DRHBc Mass Table Collaboration are highly appreciated.
Inner fission barriers of uranium isotopes in the deformed relativistic Hartree-Bogoliubov theory in continuum
- Received Date: 2024-04-15
- Available Online: 2024-10-15
Abstract: The inner fission barriers of the even-even uranium isotopes from the proton to the neutron drip line are examined using the deformed relativistic Hartree-Bogoliubov theory in continuum. A periodic-like evolution for the ground state shapes is shown with respect to the neutron number, i.e., spherical shapes at shell closures





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF















 DownLoad:
DownLoad: