-
For several decades, the enigmatic nature of dark matter (DM), despite its dominance in the mass budget of galaxies, has puzzled the scientific community. One compelling explanation is the hypothesis that DM comprises weakly interacting massive particles (WIMPs) (See Ref.[1, 2] for detail). This hypothesis arises from the intriguing coincidence between the interaction strength required for early-universe relics to possess the correct cosmological density and electroweak interaction strength. WIMPs encompass a diverse class of DM candidates, ranging from scalar particles to fermions, with significant variations in the couplings between DM and ordinary matter across different models. Over the past few decades, various strategies have been proposed to detect WIMPs through space-based observations [3], and particle accelerators [4], with the aim of complementing direct detection techniques [5–7].
Direct detection experiments, primarily focused on searching for non-relativistic DM-nucleus scattering events [8, 9], play a crucial role in testing the WIMP hypothesis. These experiments are conducted in low-background environments located deep underground, aiming to measure the energy spectrum and direction of nuclear recoils resulting from interactions between DM and ordinary matter. However, challenges arise from irreducible neutrino backgrounds [10–14] that can mimic the DM signal, necessitating effective background removal techniques. Furthermore, direct detection experiments face the challenge of insensitivity to the spin of DM.
Recent advancements in direct detection research have proposed a variation, termed as polarized-target DM scattering, to address these challenges [15–19]. This innovative approach offers a promising solution by simultaneously addressing the background mimicry issue and providing insights into the particle nature of WIMPs, including their spin. By measuring the polarization dependence of scattering angle distributions, it is possible to distinguish backgrounds and shed light on crucial aspects of WIMPs upon detection. Notably, recent studies explored the potential of direct detection experiments to discern the spin of DM, differentiating between fermionic and bosonic spins and higher spin states [18].
From an experimental perspective, an intriguing approach emerges from the observation that the Earth's movement through the galactic dark matter (DM) halo may create a preferred direction for nuclear recoil events. This suggests that valuable insights can be gained not only by examining the differential recoil rate as a function of energy but also by considering the double differential recoil rate, which accounts for the angular dependence of scattering. Polarized detectors [20–28] leverage spin-dependent interactions between DM particles, such as WIMPs, and polarized nuclei. Key components include the choice of materials such as polarized noble gases [29, 30] (xenon or helium-3) or solid-state targets (lithium fluoride), and achieving high polarization through methods such as optical pumping or dynamic nuclear polarization. These detectors operate at cryogenic temperatures with stable magnetic fields to maintain polarization and reduce noise.
Moreover, extant studies have largely overlooked the potential impact of nonvanishing mass splitting in DM [31–44] on the energy deposition spectrum within the detector (dubbed as Inelastic Dark Matter), particularly in relation to polarized targets. This omission is particularly pertinent in light of the constraints imposed by the Cosmic Microwave Background (CMB) [45–48]. Measurements of the CMB contradict the presence of light Dirac fermion DM, especially if it is capable of undergoing annihilation during the recombination era. However, the introduction of a pseudo-Dirac fermion [49] allows for the circumvention of these CMB constraints, as long as only the ground state exhibits a significant abundance. Consequently, viable models involving light DM necessitate the presence of both a ground state and an excited state, along with a mediator in the form of a light dark photon that connects to the Standard Model.
The investigation of inelastic DM continues to be a dynamic and thriving research field [50–53]. In this study, we direct our attention toward the exploration of inelastic signatures with polarized target, an area that has not been thoroughly investigated, to date. The primary objective of our research is to establish a connection between these two distinct aspects and elucidate the emergence of distinctive observables resulting from their synergistic combination.
Furthermore, an additional aspect of inelasticity in the interaction between DM and nuclei arises from the Migdal effect. Although the understanding of electron emission from an atom following the sudden perturbation of its nucleus has been documented since the early 1940s [54], the DM community has recently recognized its broader implications in direct detection searches [55–75]. Despite the usual suppression of electromagnetic signal production, when compared to conventional elastic nuclear scattering rates, the domain of sub-GeV DM presents a unique opportunity. In this regime, the nuclear recoil energy falls below the threshold, rendering it unobservable, while the electromagnetic signal remains detectable. By capitalizing on this characteristic, numerous experiments have successfully constrained the parameter space associated with sub-GeV DM [76–80].
In our study, we conduct a thorough investigation of the inelastic behavior observed in dark matter (DM)-nucleus scattering. In the case of heavy DM, elastic scattering predominates, making the exclusion of the Migdal effect necessary. However, in light-DM scenarios, challenges arise due to detection thresholds that hinder the observation of nuclear recoil. Therefore, incorporating the Migdal effect is crucial for enhancing sensitivity in these cases. Although the Migdal effect has been explored in direct detection literature, its application to inelastic DM detection with polarized detectors is still in its early stages. We provide a comprehensive analysis of the Migdal effect within this novel framework, enabling a more detailed understanding of its experimental implications and potential observables. Our aim is to identify significant shifts in the distribution of scattering angles and recoil energy as mass splitting varies, which can be readily observed in upcoming direct detection experiments.
This paper is organized as follows: Section II introduces our general dark photon model featuring pseudo-Dirac fermion DM. We explicitly demonstrate the matching procedure from quarks to nucleons/nuclei. By employing pseudo-Dirac fermions, we naturally attain inelastic DM with a tiny mass splitting. In section III, we present the computational framework for both the inelastic scattering and Migdal effect. Section IV showcases the results involving the inelastic scattering and Migdal effect, employing various benchmark values. The distinctive angular and recoil energy distribution provides insights into determining the mass splitting.
-
We propose a generic model that establishes a connection between a dark photon, denoted as
$ A^{\prime} $ , and standard model quarks f, as well as DM, represented by χ. In this model, the Lagrangian is as follows:$ {\cal{L}}=g_{A^{\prime}} \sum\limits_f \bar{f}\left(x_f^V \gamma^\mu+x_f^A \gamma^\mu \gamma^5\right) f A^{\prime}_\mu +{\cal{L}}_{\chi}, $

(1) which denotes the interaction between dark photon and standard model quarks and DM. The product
$ g_{A^{\prime}}\times x_f^{V(A)} $ denotes the strength of the vector (axial) interaction. To account for the polarized target, we extend beyond the minimal dark photon model [81–83] by including the axial interaction$ x_f^A $ [84]. For simplicity, we focus on the isovector form of both the vector and axial vector interactions, described by the Lagrangian:$ -{\cal{L}}_{f}=g_{A^{\prime}}x_f^V(\bar{u} \gamma^\mu u-\bar{d} \gamma^\mu d) A_{\mu}^{\prime}+g_{A^{\prime}}x_f^A(\bar{u} \gamma^\mu \gamma_5 u-\bar{d} \gamma^\mu \gamma_5 d)A_{\mu}^{\prime}. $

(2) In our analysis of DM-nucleus scattering, it is crucial to derive the DM-nucleon interaction from the DM-quark level interaction. The matching between quarks and nucleons is straightforward, and the nucleon coupling for the vector interaction, denoted as
$ {\cal{L}}_{A^{\prime} n}=c_n^V A^{\prime}_\mu \bar{n} \gamma^\mu n $ , can be easily identified. Specifically, n denotes both protons and neutrons, and$ c_p^V=g_{A^{\prime}}x_f^V $ and$ c_n^V=-g_{A^{\prime}}x_f^V $ . Thus, we can readily match the proton to the nucleus (N) in the case of a vector interaction:$ \langle N\left(p^{\prime}\right)\left|\bar{n} \gamma^\mu n\right| N(p)\rangle=\overline{N}\left(\gamma^\mu F\left(q^2\right)+\frac{\sigma^{\mu \nu} q_\nu}{2 m_{N}} F_1\left(q^2\right)\right) N. $

(3) In the aforementioned equation, the transfer four-momentum
$ q=p^{\prime}-p $ is defined by the four-momenta of the incoming and outgoing nucleus, denoted as p and$ p^{\prime} $ , respectively. We assume equality between the form factors for the proton and neutron, denoted as$ F_n(q^2) = F(q^2) $ , and adopt the Helm form factor. Additionally, we consider the form factor$ F_1(q^2) $ , which accounts for the electric and magnetic form factors governing the magnetic moment interaction. However, in this specific process, the contribution of$ F_1(q^2) $ can be neglected due to its suppression by$ {\cal{O}}(q/m_{N}) $ , where$ m_{N} $ denotes the mass of the nucleus.Matching for the axial vector follows a similar process. At the hadron level, the nucleon matrix element of the isovector axial-vector current can be decomposed into two Lorentz-invariant isovector form factors: the axial form factor
$ G_A(Q^2) $ and induced pseudoscalar form factor$ G_P(Q^2) $ ,$ \begin{aligned}[b] &\langle N(p^\prime) | (\bar{u} \gamma_\mu\gamma_5 u - \bar{d} \gamma_\mu\gamma_5 d) | N(p) \rangle \\ =\;& \bar{N}(p^\prime) \left[ \gamma_\mu G_A(Q^2) - \frac{Q_\mu}{2m_n} G_P(Q^2) \right] \gamma_5N(p). \end{aligned} $

(4) Here,
$ Q^2 = -q^2 $ , and the pseudoscalar form factor is commonly neglected, similar to the vector case. It is widely accepted in the literature that the effective Lagrangian, specifically formulated as Eq. (5), adequately captures the rate calculation [17]:$ -{\cal{L}}_{{\rm{int}}}=h_3\bar{N}\gamma^\mu{N}A^{\prime}_\mu+h_4\bar{N}\gamma^\mu\gamma^5{N}A^{\prime}_\mu. $

(5) Deriving values of
$ h_3 $ and$ h_4 $ from the microscopic Lagrangian after matching is straightforward:$ \begin{aligned}[b] h_3 &= Z g_{A^{\prime}} x_V F(q^2), \\ h_4 &= g_{A^{\prime}} x_A G_A(Q^2). \end{aligned} $

(6) In the extant studies, it is customary to set
$ h_3 = -h_4 = 1/2 $ to realize maximal parity violation. The interactions between the dark sector are described by the Lagrangian,$ {\cal{L}}_\chi = \bar{\chi}\left({\rm i} \gamma^{\mu} D_{\mu}-m_{\chi}\right) \chi-\frac{\delta_{{\rm{DM}}}}{4}\left(\bar{\chi}^c \chi+{\rm { h.c. }}\right). $

(7) The interaction between DM χ and dark photon is minimally realized by the covariant derivative,
$D_\mu \equiv \partial_\mu+ {\rm i} g_D A_\mu^{\prime}$ . To capture the polarization effect, we also extend the minimal coupling$ g_D $ as shown in:$ -{\cal{L}}_{\chi}= \lambda_3 \bar{u}_{\chi}\gamma^{\mu} u_{\chi}A_{\mu}^{\prime}+\lambda_4 \bar{u}_{\chi}\gamma^{\mu}\gamma_5 u_{\chi}A_{\mu}^{\prime}. $

(8) In a similar way, we also set
$ \lambda_3 = -\lambda_4 = 1/2 $ to realize maximal parity violation.The DM mass splitting originates primarily from the Majorana mass term, generated through χ and
$ \chi^{c} $ Yukawa couplings within the framework of the Higgs mechanism. Hence, these dark sector interactions facilitate the decomposition of the Dirac fermion into two closely degenerate Majorana mass eigenstates,$ \begin{aligned}[b] & \chi_1=\frac{1}{\sqrt{2}}\left(\chi-\chi^c\right),~~ m_{\chi_1}=m_\chi-\frac{\delta_{{\rm{DM}}}}{2}, \\ & \chi_2=\frac{1}{\sqrt{2}}\left(\chi+\chi^c\right),~~ m_{\chi_2}=m_\chi+\frac{\delta_{{\rm{DM}}}}{2}, \end{aligned} $

(9) where
$ {\chi}_1 $ and$ {\chi}_2 $ denote DM particles with masses$ m_{\chi_1} $ and$ m_{\chi_2} $ , respectively,$ \delta_{{\rm{DM}}}=m_{\chi_2}-m_{\chi_1} $ stands for the actual mass splitting.Hence, we investigate the inelastic aspects of the interaction between DM and atomic nuclei in two distinct scenarios. Firstly, we explore the impact of mass splitting (
$ \delta_{{\rm{DM}}} $ ) on the scattering of polarized nucleus and DM when the DM has a heavy mass (taken 100 GeV as a benchmark value), disregarding electron ionization energy ($ \delta_{{\rm{EM}}} $ ). In the second scenario, which pertains to DM with a smaller mass (sub-GeV), we delve into Migdal effect. This effect emerges when the low mass of DM interacts with nucleus, resulting in an experimental signal that is highly insensitive and challenging to observe. However, we can detect DM by analyzing the electromagnetic signal emitted by the electrons surrounding the nucleus. Consequently, our primary focus in this scenario centers on the impact of mass splitting ($ \delta_{{\rm{DM}}} $ ) of DM on the scattering of DM-polarized nucleus.Regarding the constraints from the CMB and BBN, the authors of Ref. [85] demonstrated that joints CMB and BBN constraints exclude dark matter masses below
$ 4{\rm{MeV}} $ at a$ 95\% $ confidence level for all dark matter spins and dark photon mediator masses. Our model considers two representative dark matter masses: heavy dark matter ($ m_{\chi}=100,{\rm{GeV}} $ ) and light dark matter ($ m_{\chi}=1,{\rm{GeV}} $ ), both of which are not excluded by the joint constraints from CMB and BBN. -
To emphasize the impact of polarization-dependent effects on physical observable and facilitate a comparison between different DM mass splitting, we introduce a fundamental quantity that solely relies on target polarization:
$ \frac{{\rm d} \Delta R}{{\rm d} E_R {\rm d} \Omega}=\frac{1}{2}\left(\frac{{\rm d}^3 R(\vec{s})}{{\rm d} E_R {\rm d} \Omega}-\frac{{\rm d}^3 R(-\vec{s})}{{\rm d} E_R {\rm d} \Omega}\right). $

(10) Here,
$ \vec{s} $ denotes the polarization vector of the target nuclei, as defined by$ \vec{s}=2\vec{S}_N $ , where$ \vec{S}_N $ denotes the nuclear spin operator, and${\rm d}^3R/{\rm d} E_R {\rm d}\Omega$ denotes the triple differential rate of DM-nucleus scattering events per unit detector mass,$ \frac{{\rm d}^3 R}{{\rm d} E_R {\rm d}{\Omega}} = \frac{\rho_{\chi}}{m_{\chi}m_N} \int{{\rm d}^3v vf(\vec{v})}\frac{{\rm d}\sigma}{{\rm d}E_R {\rm d}{\Omega}}. $

(11) Here,
$ \rho_{\chi}= 0.4{\rm{GeV}}/{\rm{cm}}^{3} $ ,$ m_{\chi} $ denotes the mass of the DM particle,$ m_N $ denotes the mass of the nucleus,$ f(\vec{v}) $ denotes Maxwell-Boltzmann velocity distribution,$ \vec{v} $ signifies the incoming velocity of the DM, and${\rm d}\sigma/{\rm d}E_R/{\rm d}\Omega$ corresponds to the triple differential scattering cross section.At low DM masses, the nuclear recoil falls below the detector threshold, making it undetectable by the experiment, even if there is a significant cross-section between the DM and nucleus. The Migdal effect allows for the efficient capture of ionized electrons, thereby maintaining the ability to detect light DM. In the case of contact interaction, the Migdal effect can be factorized into the elastic scattering between the nucleus and DM, along with the probability of electron ionization.
$ \frac{{\rm d}^4 R}{{\rm d} E_{{\rm{EM}}} {\rm d} E_R {\rm d} \Omega}=\frac{{\rm d}^3 R}{{\rm d} E_R {\rm d}\Omega} \times \frac{1}{2 \pi} \sum\limits_{n, \ell} \frac{{\rm d}}{{\rm d} E_{{\rm{EM}}}} p_{q_e}^c\left(n, \ell \rightarrow E_e\right). $

(12) This study presents the ionization probability
$ p_{q_e}^c $ for xenon, with specific values available in [55]. The deposited energy spectrum is determined by summing the contributions from nuclear recoil ($ E_R $ ) and electromagnetic energy ($ E_{{\rm{EM}}}=\delta_{{\rm{EM}}} $ ).$ E_{{\rm{EM}}} $ includes the energy of the ejected electron ($ E_e $ ) and atomic de-excitation energy ($ E_{nl} $ ). Given that the nuclear recoil falls below the observable threshold, it must be integrated out by considering${\rm d}\Omega$ and${\rm d}E_R$ to generate the physical differential event rate as follows:$ \begin{aligned}[b] \frac{{\rm d}R}{{\rm d} E_{{\rm{det}}}}=\;&\int {\rm d}\Omega \int_{E_R^{\min}}^{E_R^{\max}} {\rm d} E_R\frac{{\rm d}^3 R}{{\rm d} E_R{\rm d}\Omega} \times \frac{1}{2 \pi} \\&\sum\limits_{n, \ell} \frac{{\rm d}}{{\rm d} E_{{\rm{EM}}}} p_{q_e}^c\left(n, \ell \rightarrow E_e\right) \times \delta\left(E_{{\rm{det}}}-{\cal{Q}} E_R-E_{{\rm{EM}}}\right), \end{aligned} $

(13) where
$ E_{R}^{\min} $ and$ E_R^{\max} $ are determined in kinematics, and$ E_{{\rm{det}}} $ stands for the detected electron energy,$ E_{{\rm{det}}}={\cal{Q}} E_R+E_{{\rm{EM}}}, $

(14) where
$ {\cal{Q}} $ denotes the quenching factor. -
Consider the inelastic collision between DM and a nucleus in the detector. The scattering process can be represented as
$ {\chi}_1N\longrightarrow{\chi}_2 N $ , and N represents the Xenon nucleus with a mass of$ m_N = 122\; {\rm{GeV}} $ .In the three-dimensional coordinate system depicted in Fig. 1, let
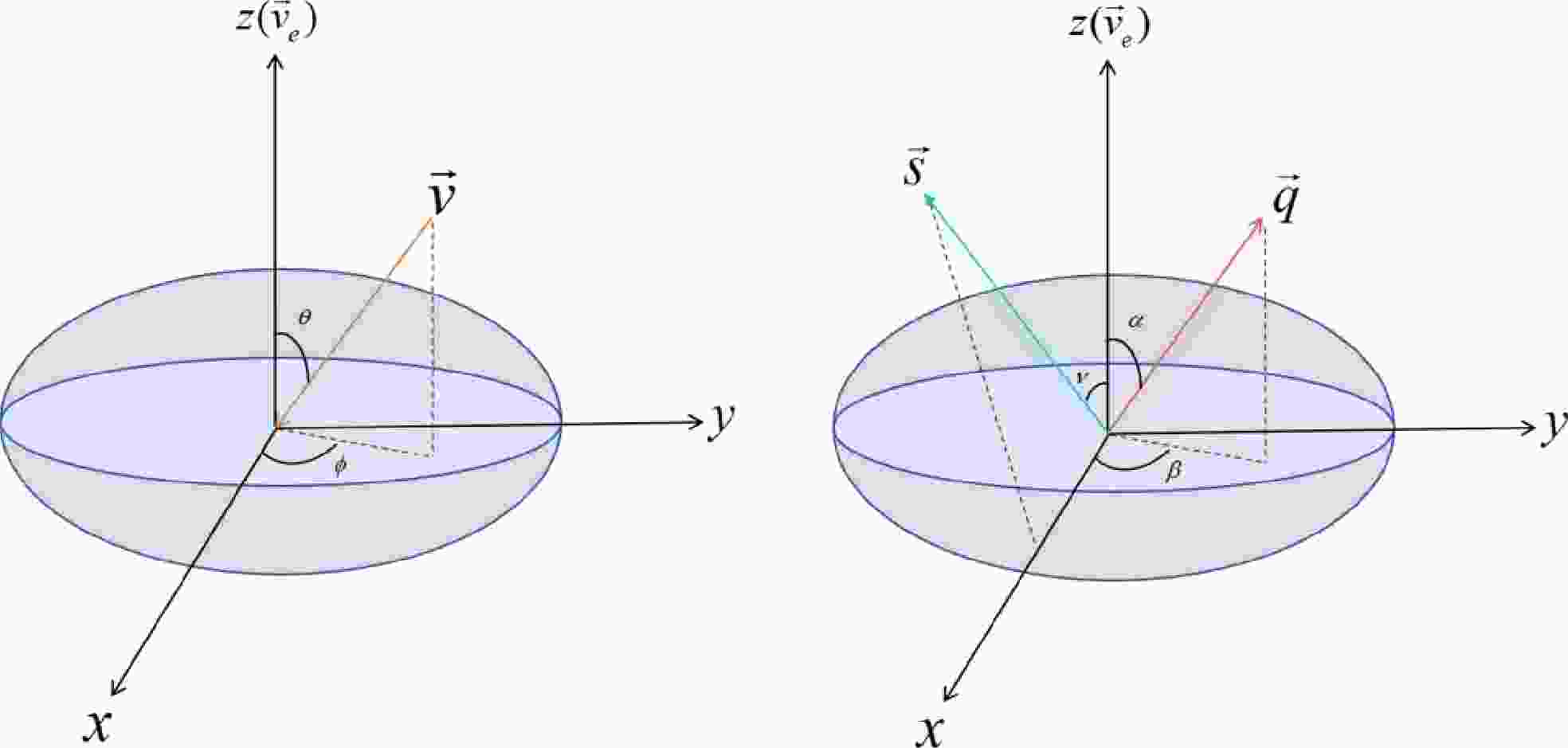
$ \vec{v} $ denote the incoming velocity of DM particle at the detector, and$ \vec{v}^\prime $ represents the outgoing velocity of the DM. As illustrated in Fig. 1, the unit vector$ \hat{v} $ is defined as$ (\sin \theta \cos \phi, \sin \theta \sin \phi, \cos \theta) $ . The unit vector of transferred momentum is denoted as$ \hat{q} $ and provided by$ (\sin \alpha \cos \beta,~ \sin \alpha \sin \beta,~ \cos \alpha) $ . To facilitate the discussion and explicitly showcase the angle dependence, let us begin by considering a specific scenario where$ \alpha=\theta={\pi}/{2} $ and$ \phi=0 $ . This simplification enables us to treat the inelastic collision between DM and nucleus as occurring on a two-dimensional plane. However, it is crucial to note that the entire scattering process can still be reconstructed in a three-dimensional plane. The conservation of energy and momentum leads to the following relationships:
Figure 1. (color online) Three-dimensional coordinate system with the earth velocity direction in the Z-axis direction is constructed to calculate the triple differential rate of DM scattering and nucleus scattering. Among them, the direction of orange arrow is the direction of the incident velocity of DM, the direction of the indigo blue arrow is the direction of the polarization of the nucleus, and red denotes the direction of recoil of the nucleus.
$ \begin{aligned}[b] m_{\chi_1}+\frac{1}{2}m_{\chi_1}v^2&=m_{\chi_2}+\frac{1}{2}m_{\chi_2}v^{\prime 2}+\frac{q^2}{2m_N}, \\ m_{\chi_1} v &=m_{\chi_2}v^{\prime}\cos{\phi_1}+q\cos{\beta}, \\ 0&=q\sin{\beta}-m_2v^{\prime}\sin{\phi_1}, \end{aligned} $

(15) where
$ \phi_1 $ denotes the out-going DM direction. By applying energy and momentum conservation, we determine:$ q=2\mu v \cos{\beta}-\frac{\Delta}{\cos{\beta}v}. $

(16) In this equation,
$ \Delta=\delta_{{\rm{DM}}}+\delta_{{\rm{EM}}} $ , in the inelastic collision between DM and the nucleus. The DM-target reduced mass$ \mu=\dfrac{m_Nm_{\chi}}{m_N+m_{\chi}} $ . The triple differential scattering cross-section${\rm d}\sigma/{\rm d}E_R {\rm d}\Omega$ for the scattering of DM on a polarized target can be expressed within the energy-momentum conservation as follows:$ \frac{{\rm d}{\sigma}}{{\rm d}E_R {\rm d}\Omega}=\frac{{\rm d}{\sigma}}{2{\pi}{\rm d} E_R}\delta\left(\cos{\beta}-\frac{q}{2{\mu}v}-\frac{\Delta}{qv}\right). $

(17) Recall that equation (17) simplify δ function, we have
$ \begin{align} \frac{{\rm d}{\sigma}}{2{\pi}{\rm d}E_R}{\delta}\left(\cos{\beta}-\frac{q}{2{\mu}v}-\frac{\Delta}{qv}\right) &=\frac{{\rm d}{\sigma}v}{2{\pi}{\rm d}E_R}{\delta}\left(\vec{v}\cdot \hat{q}-\frac{q}{2{\mu}}-\frac{\Delta}{q}\right) \\&=\frac{{\rm d}{\sigma}v}{2{\pi}{\rm d}E_R}\frac{{\delta}(v-\bar{v})}{|\hat{v}\cdot\hat{q}|}, \end{align} $

(18) where
$ \bar{v} = q/(2{\mu}(\hat{v}\cdot\hat{q}))+\Delta/q(\hat{v}\cdot\hat{q}) $ and$ \hat{v} $ denotes a unit vector in the direction of the incoming DM velocity,$ \vec{v}=v\hat{v} $ . The velocity distribution of DM can significantly affect the rates of direct detection. The Maxwell-Boltzmann distribution is commonly used as a simple analytic approximation for the velocity distribution of DM. Within the frame of the Galaxy, this velocity distribution is$ f(\vec{v})=\frac{1}{{\cal{N}}}{\rm e}^{-(\vec{v}+\vec{v_e})^2/{v_0}^2}\Theta({v_{{\rm{esc}}}-|\vec{v}+\vec{v_e}|}), $

(19) with a galactic escape velocity of
$ v_{{\rm{esc}}}=544\;{\rm{km/s}} $ . Furthermore, the distribution is cut off at the local escape speed, and a most probable speed is provided by the circular speed of the local standard of rest of$ v_0=220 {\rm{ km/s}} $ . The Earth's velocity in the galactic rest frame,$ \vec{v_e} $ , is$ 232,{\rm{km/s}} $ . Furthermore, Θ denotes the Heaviside step function, and$ {\cal{N}} $ is a normalization constant as follows:$ {\cal{N}}=\pi{v_0}^2\left(\sqrt{\pi}v_0{\rm{Erf}}\left(\frac{v_{{\rm{esc}}}}{v_0}\right)-2v_{{\rm{esc}}} {\rm e}^{-{v_{{\rm{esc}}}}^2/{v_0}^2}\right). $

(20) The velocity range considered is
$ v\in[v_{\min},v_{\max}] $ , where$ v_{\min}=\sqrt{{m_NE_R}/{2\mu^2}} $ and$ v_{\max}=v_{{\rm{esc}}} $ , with$ m_N $ denoting the mass of the target nucleus,$ E_R $ denotes the recoil energy, and μ denotes the reduced mass of the DM-nucleus system. The problem requires$ v_{{\rm{esc}}}-|\vec{v}+\vec{v_e}|>0 $ , which implies$ \cos\theta<({v_{{\rm{esc}}}^2-v^2-v_e^2})/ {2 v v_e} $ . The range of$ \cos\theta $ is therefore$ [-1,{(v_{{\rm{esc}}}^2-v^2-v_e^2)}/ {2 v v_e}] $ . However, this range over-counts the available parameter space as$ |\vec{v}+\vec{v_e}| $ is smaller than$ v_{{\rm{esc}}} $ by definition. Consequently,$ \cos\theta $ can cover the entire parameter space$ \cos\theta\in[-1,1] $ . The maximum value of$ |\vec{v}+\vec{v_e}| $ occurs when$ \vec{v} $ is parallel to$ \vec{v_e} $ . Thus, the corresponding ranges of v and$ \cos\theta $ are$ v\in[v_{\min},v_{{\rm{esc}}}-v_e] $ and$ \cos\theta\in[-1,1] $ . Another phase space exists where$ \cos\theta\in[-1, (v_{{\rm{esc}}}^2-v^2-v_e^2)/{2 v v_e}] $ and$v\in [v_{{\rm{esc}}}-v_e,v_{{\rm{esc}}}+v_e]$ . Thus, the velocity integral becomes:$ \begin{aligned}[b] \int {\rm d}^3v =\;& \int_{v_{\min}}^{v_{{\rm{esc}}}-v_e}{\rm d}v v^2\int_{-1}^{+1}{\rm d}\cos\theta\int_0^{2\pi}{\rm d}\phi \\ &+\int_{v_{{\rm{esc}}}-v_e}^{v_{{\rm{esc}}}+v_e}{\rm d}v v^2\int_{-1}^{\frac{{v_{{\rm{esc}}}}^2-v^2-{v_e}^2}{2vv_e}}{\rm d}\cos\theta\int_0^{2\pi}{\rm d}\phi. \end{aligned} $

(21) Performing the velocity integral defined in Eq. (21) while respecting energy-momentum conservation, as described in Eq. (18), determines the triple differential event rate, which is the cornerstone of the calculation:
$ \begin{aligned}[b] \frac{{\rm d}^3 R}{{\rm d}E_R {\rm d}{\Omega}}=\;&\frac{\rho_\chi}{64\pi^2m_{\chi}^3m_N^2{\cal{N}}}\sum\limits_{l=1}^2\int_{-1}^{+1}{\rm d}\cos\theta\int_0^{2\pi}{\rm d}\phi \\&\frac{\bar{v}^{2}}{|\hat{v}\cdot\hat{q}|}{\rm e}^{-(\bar{v}^{2}+v_e^2+2\bar{v}^{\prime}v_e\cos{\theta})/v_0^2}|\overline{M}|^2\Theta_l. \end{aligned} $

(22) In Migdal scattering, the incoming and outgoing states exhibit slight deviations from the elastic scattering process involving a DM particle, an ionized atom, and an unbound electron. The incoming DM is treated as a plane wave, representing an energy eigenstate and a momentum eigenstate. Similarly, the incoming atom, initially at rest in the lab frame, is considered both an energy eigenstate and a momentum eigenstate with respect to the total momentum of the atom. Consequently, the entire atom experiences recoil with a velocity
$ v_A $ and possesses momentum$ p_A = m_A v_A $ , where$ m_A = m_N $ given the negligible electron mass. In the case where the atom is considered as a composite system comprising electrons and a nucleus with multiple internal energy levels, conservation laws dictate the energy and momentum in DM-atom interactions. For DM with mass$ m_\chi $ , an incoming velocity v and an outgoing momentum$ p_{\chi}^\prime $ , the conservation of energy and momentum results in the following relationship:$ E_R=\frac{\mu^2}{m_A} v^2\left[1-\frac{\Delta}{\mu v^2}-\sqrt{1-\frac{2 \Delta}{\mu v^2}} \cos \theta_{{\rm{cm}}}\right], $

(23) with
$ E_{R}^{\min} $ and$ E_R^{\max} $ correspond to$ \cos\theta_{{\rm{cm}}}=\pm 1 $ . -
The square of the matrix element,
$ |M|^2 $ , encapsulates the underlying physics of the scattering process and is contingent on the particular DM model being investigated. In this study, we only consider fermionic DM as the object of study. To describe the scattering amplitude, particularly in situations that involve heavy mediators with a significantly larger mass ($ m_{A^{\prime}} $ ) when compared to the momentum transfer (q), we can utilize the Lagrangian presented in Equation (5) along with its corresponding Feynman rule as follows:$ \begin{aligned}[b] {\rm i} M=\;& \frac{\rm -i}{{m_{A^{\prime}}}^2}\bar{u}_{\chi_2}(p^{\prime},s^{\prime})\gamma^\mu(\lambda_3+\lambda_4\gamma_5)u_{\chi_1}(p,s)\\& \times \bar{u}_{N}(k^{\prime},r^{\prime})\gamma_\mu(h_3+h_4\gamma_5)u_{N}(k,r). \end{aligned} $

(24) In this context, the symbols
$ \bar{u}_{\chi_2} $ ,$ u_{\chi_1} $ ,$ \bar{u}_{N} $ , and$ u_{N} $ represent the solutions derived from the Dirac equation. Variables s and$ s^{\prime} $ (r and$ r^{\prime} $ ) correspond to the initial and final spins of the DM particle and target nucleus, respectively. When considering the non-relativistic limit, the spinor bilinears can be expressed as follows [86]:$ \bar{u}_{\chi_2}(p^{\prime},s^{\prime})\gamma^{\mu}u_{\chi_1}(p,s) = \left( \begin{array}{c} (2m_{\chi}+\Delta)\delta^{s^{\prime}s}\\ \vec{P}\delta^{s^{\prime}s}-2{\rm i}\vec{q}\times\vec{S}_{\chi}^{s^{\prime}s} \end{array} \right). $

(25) $ \bar{u}_{\chi_2}(p^{\prime},s^{\prime})\gamma^{\mu}\gamma_5u_{\chi_1}(p,s) = \left( \begin{array}{c} 2\vec{P}\cdot\vec{S}_{\chi}^{s^{\prime}s}\\ (4m_{\chi}+2\Delta)\vec{S}_{\chi}^{s^{\prime}s} \end{array} \right) . $

(26) $ \bar{u}_N(k^{\prime},r^{\prime})\gamma^{\mu}u_N(k,r) = \left( \begin{array}{c} 2m_{N}\delta^{r^{\prime}r}\\ -\vec{K}\delta^{r^{\prime}r}-2{\rm i}\vec{q}\times\vec{S}_{N}^{r^{\prime}r} \end{array} \right) . $

(27) $ \bar{u}_N(k^{\prime},r^{\prime})\gamma^{\mu}\gamma_5u_N(k,r) = \left( \begin{array}{c} 2\vec{K}\cdot\vec{S}_{N}^{r^{\prime}r}\\ -4m_{N}\vec{S}_{N}^{r^{\prime}r} \end{array} \right) . $

(28) It should be noted that for process
$ {\chi}_1N\longrightarrow{\chi}_2 N $ , we only consider that the mass of the DM changes in the initial state and the final state, while the mass of the nucleus remains unchanged in the initial state and the final state. Hence, the bilinear spinor of the DM above has mass splitting, while the bilinear spinor of the nucleus does not have mass splitting. Here , we define$ \vec{P}=\vec{p}+\vec{p}^{\prime} $ ,$\vec{K}= \vec{k}+\vec{k}^{\prime}$ ,$ \vec{S}_{N}^{r^{\prime}r}=\xi^{r^{\prime}\dagger}(\vec{\sigma_N}/2)\xi^{r} $ ,$ \vec{S}_{\chi}^{s^{\prime}s}=\xi^{s^{\prime}\dagger}(\vec{\sigma_{\chi}}/2)\xi^{s} $ ,$ \xi^{s^{\prime}\dagger}\xi^{s}=\delta^{s^{\prime}s} $ ,$\xi^{r^{\prime}\dagger}\xi^{r}= \delta^{r^{\prime}r}$ , and the two-component spinor ξ can be normalized as usual. Hence, we obtain the amplitude from equation (24):$ \begin{aligned}[b] {\rm i} M=\;&\frac{\rm -i}{{m_{A^{\prime}}}^2}\{ \lambda_3h_3[4m_Nm_{\chi}\delta^{s^{\prime}s} \delta^{r^{\prime}r}+2m_N\Delta\delta^{s^{\prime}s} \delta^{r^{\prime}r}] \\ +&\lambda_3h_4[-8m_Nm_{\chi}\delta^{s^{\prime}s}\vec{v}^{\perp}\cdot\vec{S}_{N}^{r^{\prime}r} \\ +&8{\rm i}m_N \vec{S}_{\chi}^{s^{\prime}s}\cdot(\vec{S}_{N}^{r^{\prime}r}\times\vec{q})+2\Delta\delta^{s^{\prime}s}\vec{K}\cdot\vec{S}_{N}^{r^{\prime}r}] \\ +&\lambda_4h_3[8m_Nm_{\chi}\delta^{r^{\prime}r}\vec{v}^{\perp}\cdot\vec{S}_{\chi}^{s^{\prime}s}\\ +&4{\rm i}(2m_{\chi}+\Delta) \vec{S}_{\chi}^{s^{\prime}s}\cdot(\vec{S}_{N}^{r^{\prime}r}\times\vec{q})-2\Delta\delta^{r^{\prime}r}\vec{K}\cdot\vec{S}_{\chi}^{s^{\prime}s}] \\ +&\lambda_4h_4[-16m_Nm_{\chi}\vec{S}_{\chi}^{s^{\prime}s}\cdot\vec{S}_{N}^{r^{\prime}r}-8m_N\Delta\vec{S}_{\chi}^{s^{\prime}s}\cdot\vec{S}_{N}^{r^{\prime}r}] \}, \end{aligned} $

(29) where the transverse relative velocity vector is as follows:
$ 2\vec{v}^{\perp}=\vec{v}+\vec{v}^{\prime}+\frac{m_\chi}{m_N}\left(\vec{v}^{\prime}-\vec{v}\right). $

(30) We proceed to calculate
$ |\overline{M}|^2 $ , which represents the squared amplitude for DM-nucleus scattering. This calculation involves summing over the final spin states of DM and nucleus, and averaging over the initial spin configurations of the DM. Finally, we apply the following spin summation rules as follows:$ \begin{aligned}[b]&|\overline{M}|^2=\frac{1}{2}\sum\limits_{ss^{\prime}}\sum\limits_{r^{\prime}}|M|^2,\\& \sum\limits_{r^{\prime}}\vec{S}_{N}^{r^{\prime}r}\times\vec{S}_{N}^{rr^{\prime}} =\frac{\rm i}{2}\vec{s},\\& \sum\limits_{r^{\prime}}\vec{S}_{N}^{r^{\prime}r}\cdot\vec{S}_{N}^{rr^{\prime}}=\frac{3}{4},\\& \sum\limits_{ss^{\prime}}(\vec{a}\cdot\vec{S}_{\chi}^{ss^{\prime}})(\vec{b}\cdot\vec{S}_{\chi}^{s^{\prime}s})=\frac{1}{2}\vec{a}\cdot\vec{b}. \end{aligned} $

(31) In this analysis, we only consider terms that are linear or lower order in
$ \vec{q} $ and$ \vec{v}^{\perp} $ . Consequently, we neglect terms such as$ \vec{q} \vec{v}^{\perp} $ ,$ \vec{v}^{2\perp} $ , and$ \vec{q}^2 $ . It is determined that$ |\overline{M}|^2 $ can be simplified to yield (see Appendix A for details):$ |\overline{M}|^2= \frac{16m_N^2m_{\chi}^2}{{m_{A^{\prime}}}^4}\{A-B\vec{v}\cdot \vec{s}-C\vec{v}'\cdot \vec{s} \}, $

(32) with
$ \begin{aligned}[b] A=\;&\lambda_3^2h_3^2(1+\frac{\Delta}{m_{\chi}})+3\lambda_4^2h_4^2(1+\frac{\Delta}{m_{\chi}}), \\ B=\;&\lambda_3^2h_3h_4(1-\frac{m_{\chi}}{m_N}+\frac{\Delta}{4m_{\chi}}(1-\frac{m_{\chi}}{m_N})-\frac{\Delta}{4m_N})\\ &+\lambda_4^2h_3h_4(2-3(1-\frac{m_{\chi}}{m_N})-\frac{\Delta}{2m_{\chi}}(1-\frac{m_{\chi}}{m_N})+\frac{\Delta}{2m_N})\\ &+2\lambda_{3}\lambda_{4} h_{4}^{2}(1+\frac{\Delta}{2m_{\chi}}), \\ C=\;&\lambda_3^2h_3h_4(1+\frac{m_{\chi}}{m_N}+\frac{\Delta}{4m_{\chi}}(1+\frac{m_{\chi}}{m_N})+\frac{\Delta}{4m_N})\\&+\lambda_4^2h_3h_4(2-3(1+\frac{m_{\chi}}{m_N})-\frac{\Delta}{2m_{\chi}}(1+\frac{m_{\chi}}{m_N})-\frac{\Delta}{2m_N})\\ &-2\lambda_3\lambda_4h_4^2(1+\frac{\Delta}{2m_{\chi}}). \end{aligned} $

(33) It is evident that the squared matrix element remains invariant under the limit of small mass splitting
$\Delta/m_{\chi} \rightarrow 0$ . Therefore, the deviation from elastic scattering is based on the kinematics, which will be explicitly presented in the next section. Furthermore, to maximize the polarization effect, we adopt a specific value$ \lambda_3=h_3=1/2 $ and$ \lambda_4=h_4=-1/2 $ for the coupling of the interaction. As a consequence, we observe that only the term corresponding to B in the polarization dependent part of Eqs. (32) and (33) remains, while the contributions of A are nullified. Additionally, C term simplifies to zero. -
In the context of scattering between heavy DM and polarized nuclei, with a benchmark value of
$ m_{\chi}= $ 100 GeV, the squared matrix element is expressed as a function of$ \delta_{{\rm{DM}}}/m_{\chi} $ . This implies that a small mass splitting during the scattering of DM with nucleus does not affect the calculation of the scattering amplitude. Therefore, the presence of mass splitting in DM only affects the kinematics, specifically the phase space integral, while leaving the elastic scattering amplitude unaffected. We analyze the magnitude of the scattering rate for heavy DM in three different directions defined by angles α, β, and the nucleus polarization angle ν (the unit of all angles is radian). By considering the conservation of energy Eq. (15) in the center-of-mass frame and recoil energy of the nucleus, we find that the mass splitting falls within the range of$ \delta_{{\rm{DM}}} \leq {{\mu}v^2}/{2} $ for heavy DM-polarized nucleus scattering. Considering$ m_{\chi}= $ 100 GeV,$ m_N= $ 122 GeV, and$ v\sim10^{-3} $ as benchmark values, the resulting mass splitting is$ \delta_{{\rm{DM}}} \leq 50\; {\rm{keV}} $ . For the negative mass splitting, we denote that the dominant role of recoil energy increases with larger mass splitting, albeit leading to a suppression in event rates due to the exponential dependence. Consequently, we adopted a conservative approach by setting a fixed value of mass splitting at$ 40 \;{\rm{keV}} $ . Therefore, we focus on mass splittings within the range of$\delta_{{\rm{DM}}} \in [-40, 40]$ keV for the figures presented. Similarly, based on the relationship$ E_{R}^{\max}=\dfrac{1}{2}m_Nv_{\max}^2 $ , we set$ E_{R}^{\max} $ to be$ 100 \; {\rm{keV}} $ . Thus, our primary focus is on the recoil energy of the nucleus, which ranges from$ E_{R} = 0 $ to$ 100\; {\rm{keV}} $ in the depicted figures.Figure 2 depicts the increasing trend of the maximum scattering rate's position along the direction angle α with an increase in mass splitting. This trend occurs due to the correlation between an increase in
$ \delta_{{\rm{DM}}} $ and a corresponding increase in$ \bar{v} $ . Hence, the integral value increases across the entire phase space. The azimuth angle α is determined by$ \hat{v}\cdot\hat{q} $ , and to maintain the same scattering rate,$ \hat{v}\cdot\hat{q} $ must increase as the phase space integral increases. Consequently, as$ \delta_{{\rm{DM}}} $ increases, the region of α angle with the local maximum scattering rate shifts toward larger values. However, as$ \delta_{{\rm{DM}}} $ increases, the phase space integral expands, while the minimum value of$ v_{\min} $ also increases, resulting in a contraction of the integral range. Consequently, after reaching the local maximum, the scattering rate decreases as$ \delta_{{\rm{DM}}} $ increases. Conversely, when$ \delta_{{\rm{DM}}} < 0 $ , the local maximum transitions to a negative value, indicating the predominance of the spin-flip component. Therefore, we can utilize the trend in α to differentiate between the mass splitting case and elastic scattering.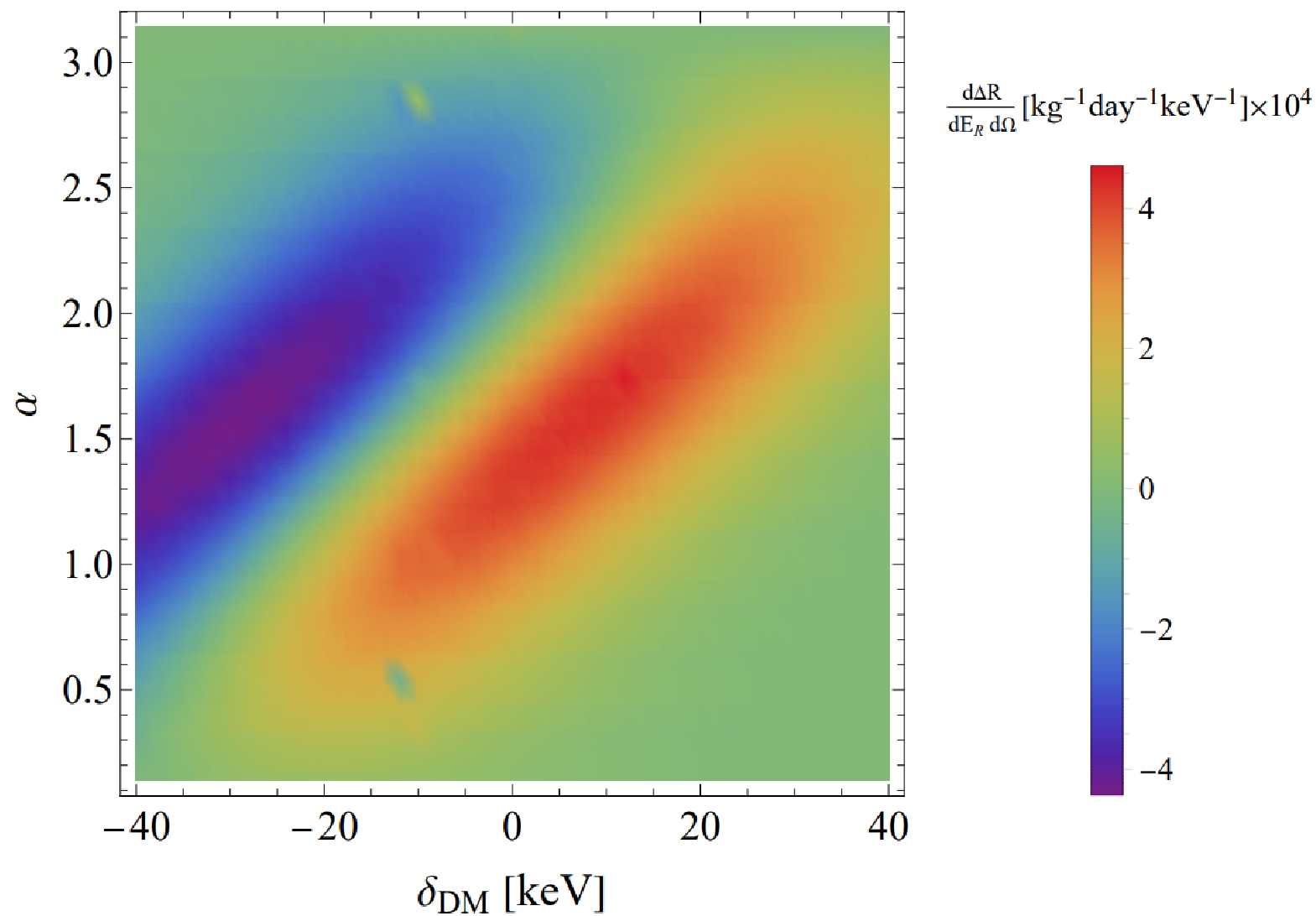
Figure 2. (color online) Differential rate of scattering events, especially the purely polarization-dependent component, is plotted against the polar recoil angle α for various mass splittings. The recoil energy
$ E_{R} $ is fixed at 5$ {\rm{keV}} $ , and the polarization angle is set to$ \nu = \pi/2 $ with$ \beta = 0 $ .Regarding the distribution on
$ \delta_{{\rm{DM}}}-\beta $ plane shown in Fig. 3, our focus is on the phase space integral, which incorporates β through$ \hat{v}\cdot\hat{q} $ , enabling us to observe periodic variations in the angular distribution. Notable instances of DM and nucleus scattering take place at$ \beta=0,\pi/2,\pi $ , regardless of the positive or negative value of the mass splitting. However, the positions of the maxima interchange for positive and negative$ \delta_{{\rm{DM}}} $ values.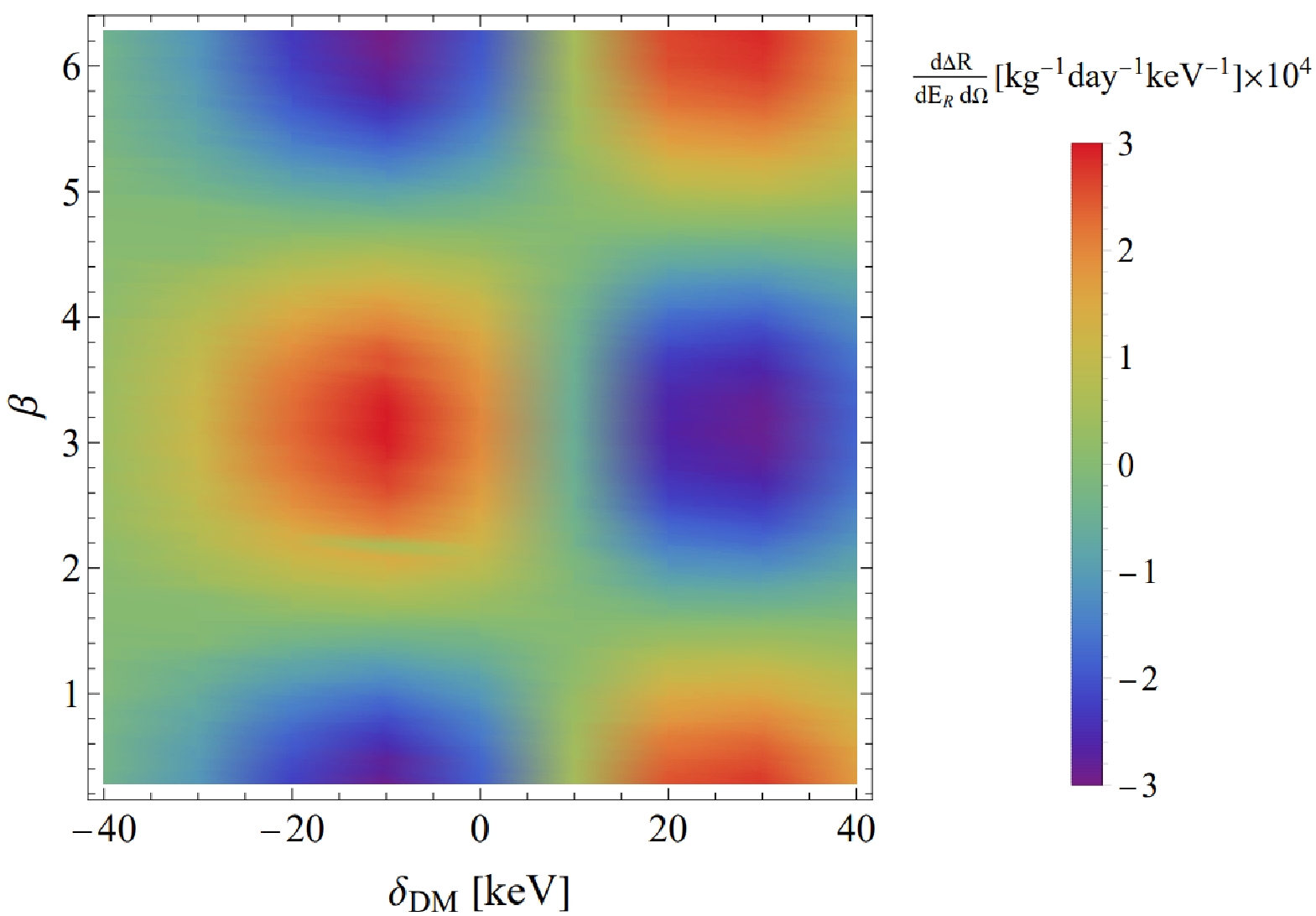
Figure 3. (color online) Polarization-dependent component of the differential scattering event rate is plotted with respect to the polar recoil angle β for various mass splittings. The recoil energy
$ E_R $ is fixed at$ 5\; {\rm{keV}} $ , and the polarization angle is set to$ \nu = {\pi}/2 $ , while the polar angle is fixed at$ \alpha = 3\pi/4 $ .The distribution on the
$ \delta_{{\rm{DM}}}-\nu $ plane, depicted in Fig. 4, reveals a substantial number of events when the mass splitting$ \delta_{{\rm{DM}}} $ is positive, while the number of cases is negligible for negative mass splitting. As we selected the z-axis direction of our coordinate system to align with velocity$ \vec{v_e} $ of the Earth in the galactic rest frame, it results in incident velocity$ \vec{v} $ of the DM being initially opposite to the polarization direction$ \vec{s} $ . Consequently, we observe a local maximum value of ν in the opposite direction within the range of$ \nu \in [0, \pi/2] $ . Furthermore, as the angle ν increases, the scattering rate decreases and reaches$ 0 $ at$ \nu = \pi/2 $ . When ν lies within the range of$ \nu \in [0, \pi/2] $ ,$ \vec{s} $ aligns with the DM incident velocity$ \vec{v} $ , resulting in a local maximum in the correct direction. Equation (22) reveals the presence of$ \bar{v} $ ,$ \vec{v} \cdot \vec{s} $ , which encompass the variables in Figure$ \delta_{{\rm{DM}}}-\nu $ , namely the mass splitting$ \delta_{{\rm{DM}}} $ and polarization angle ν. As for the remaining values in the equation, we assign specific parameters to simplify Eq. (22) for calculating the scattering rate, resulting in a simplified function of form$(0.00035 + x/35000)^3 \exp [-(0.00035 + x/35000)^2]$ . Here, variable x corresponds to variable$ \delta_{\rm DM} $ in the equation. Given our mass splitting value,$ \delta_{{\rm{DM}}} $ , falls within the range of$ [-40, 40]\; {\rm{keV}} $ , our figure of$ \delta_{{\rm{DM}}}-\nu $ only represents the number of cases where$ \delta_{{\rm{DM}}} $ is positive.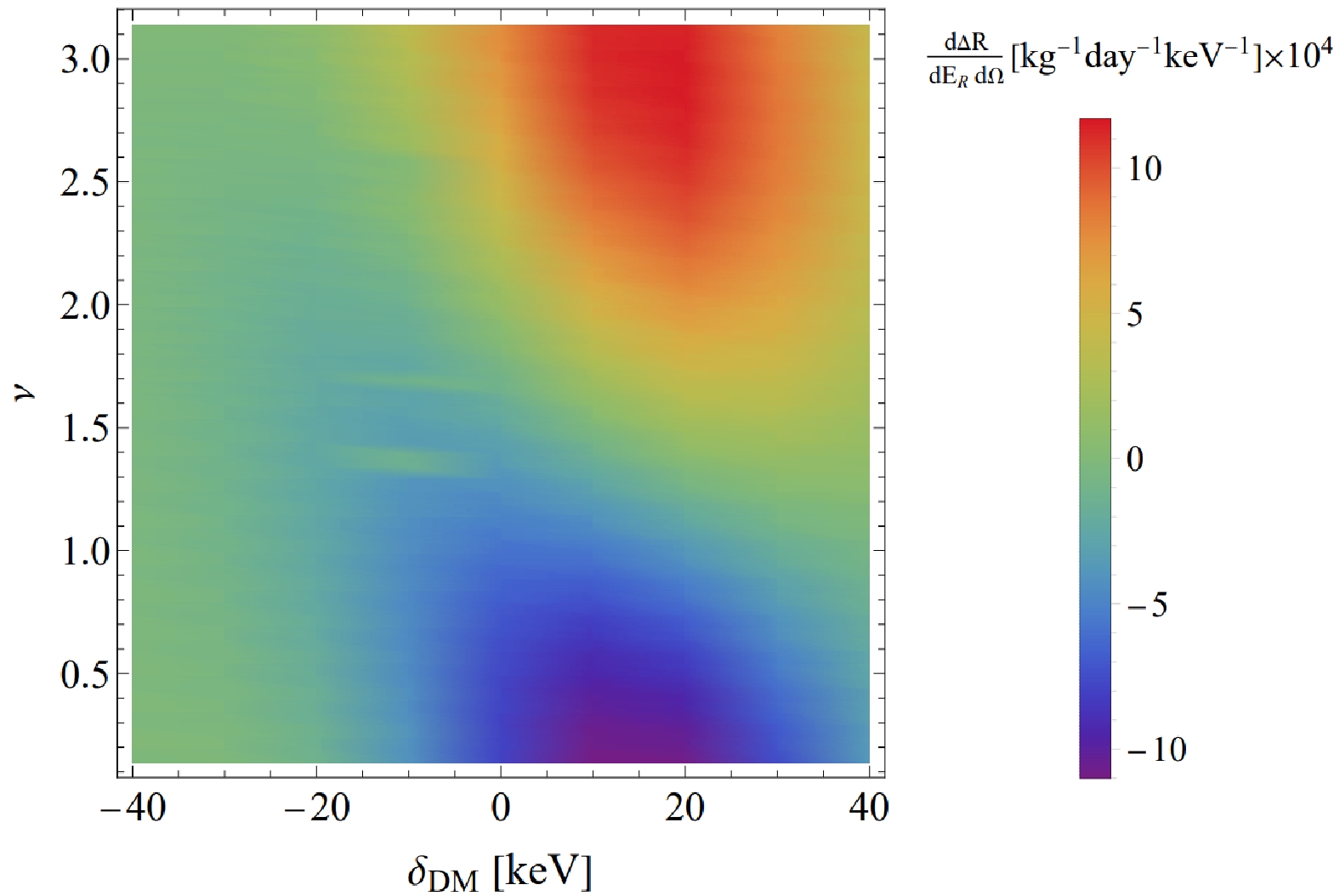
Figure 4. (color online) Polarization-dependent component of the differential scattering event rate is plotted against the polar recoil angle ν for various mass splittings. The recoil energy
$ E_{R} $ is fixed at 5$ {\rm{keV}} $ , and the polarization angle is fixed at$ \beta = 0 $ , while the polar angle is fixed at$ \alpha = 3\pi/4 $ .To further investigate the effect of the mass splitting, we generate a figure of
$ \alpha-\beta $ in Fig. 5 while holding$ E_R $ constant at$ 5\; {\rm{keV}} $ and ν at$ \pi/2 $ . Furthermore, notable occurrences can be observed at$ \beta=0,\pi/2,\pi $ , and when$ \delta_{{\rm{DM}}} $ is positive or negative, the positions of the positive maximum and negative maximum values are reversed, aligning precisely with the$ \beta-\delta_{{\rm{DM}}} $ diagram. Similarly, we note that for$ \alpha>\pi/2 $ , a local maximum value is observed when$ \delta_{{\rm{DM}}} $ is negative, while for$ \alpha=\pi/2 $ , a local maximum value is observed when$ \delta_{{\rm{DM}}} $ is zero, and for$ \alpha>\pi/2 $ , a local maximum value is observed when$ \delta_{{\rm{DM}}} $ is positive. Therefore, in the presence of a mass splitting, the local maximum value is accompanied by an increase in the angle α, which is reflected in the$ \alpha-\delta_{{\rm{DM}}} $ plot.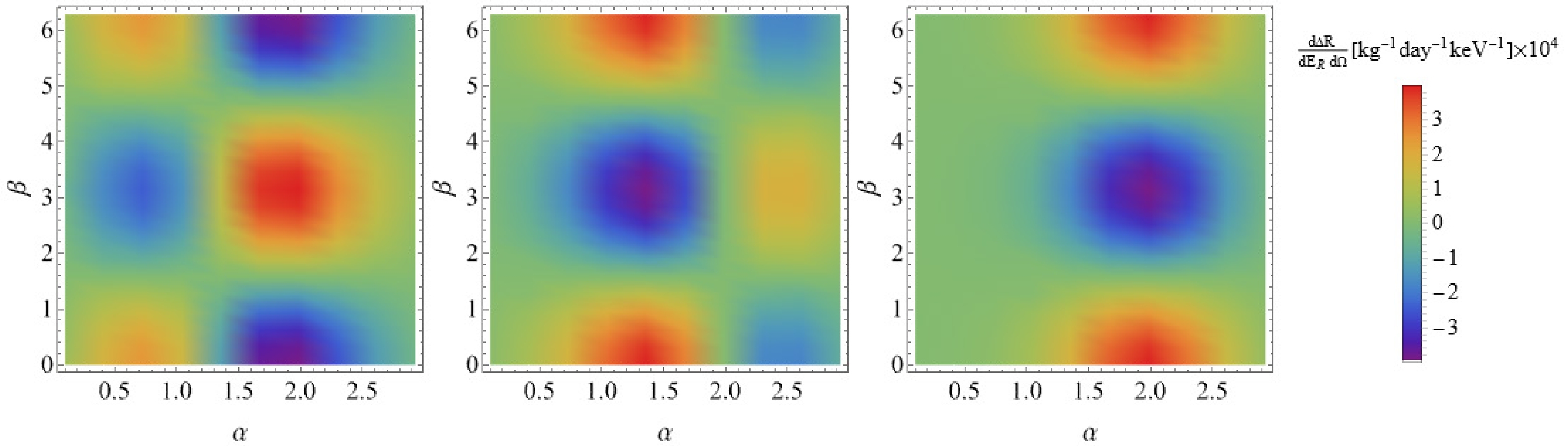
Figure 5. (color online) Purely polarisation dependent part of the differential rate of scattering events plotted against the polar recoil angle α with the azimuthal angle β. The recoil energy
$ E_{R} $ is set to 5 keV and polarisation angle is fixed to$ \nu = \pi/2 $ , left image shows the mass split as$ \delta= -20\; {\rm{keV}} $ , middle image shows the mass split as$ \delta= 0 \;{\rm{keV}} $ , and bright image shows the mass split as$ \delta= 20\;{\rm{keV}} $ .We then generated a plot illustrating the correlation between the recoil energy of the nucleus and scattering rate, considering the presence of mass splitting. Clearly, an increase in the mass splitting leads to higher values for both the position of the local maximum and recoil energy. Figure 6 displays the distribution on the
$ E_{R}-\delta_{{\rm{DM}}} $ plane. Across the entire plane distribution, an increase in$ \delta_{{\rm{DM}}} $ leads to a higher value of$ \bar{v} $ . Hence, the phase space integral approaches its maximum value, allowing an earlier observation of the maximum local scattering rate at a low-energy position. When$ \delta_{{\rm{DM}}} $ is negative,$ \bar{v} $ decreases accordingly, indicating that a higher energy is required to reach the maximum local scattering rate. However, simultaneously,$ v_{\min} $ decreases, leading to an increased phase space integral. Consequently, we observe a higher abundance of DM at low-energy positions in the opposite direction of polarization. Remarkably, in contrast to elastic scattering, the event rate does not decrease as the recoil energy increases. This phenomenon can be attributed to the enhanced$ \delta_{{\rm{DM}}} $ .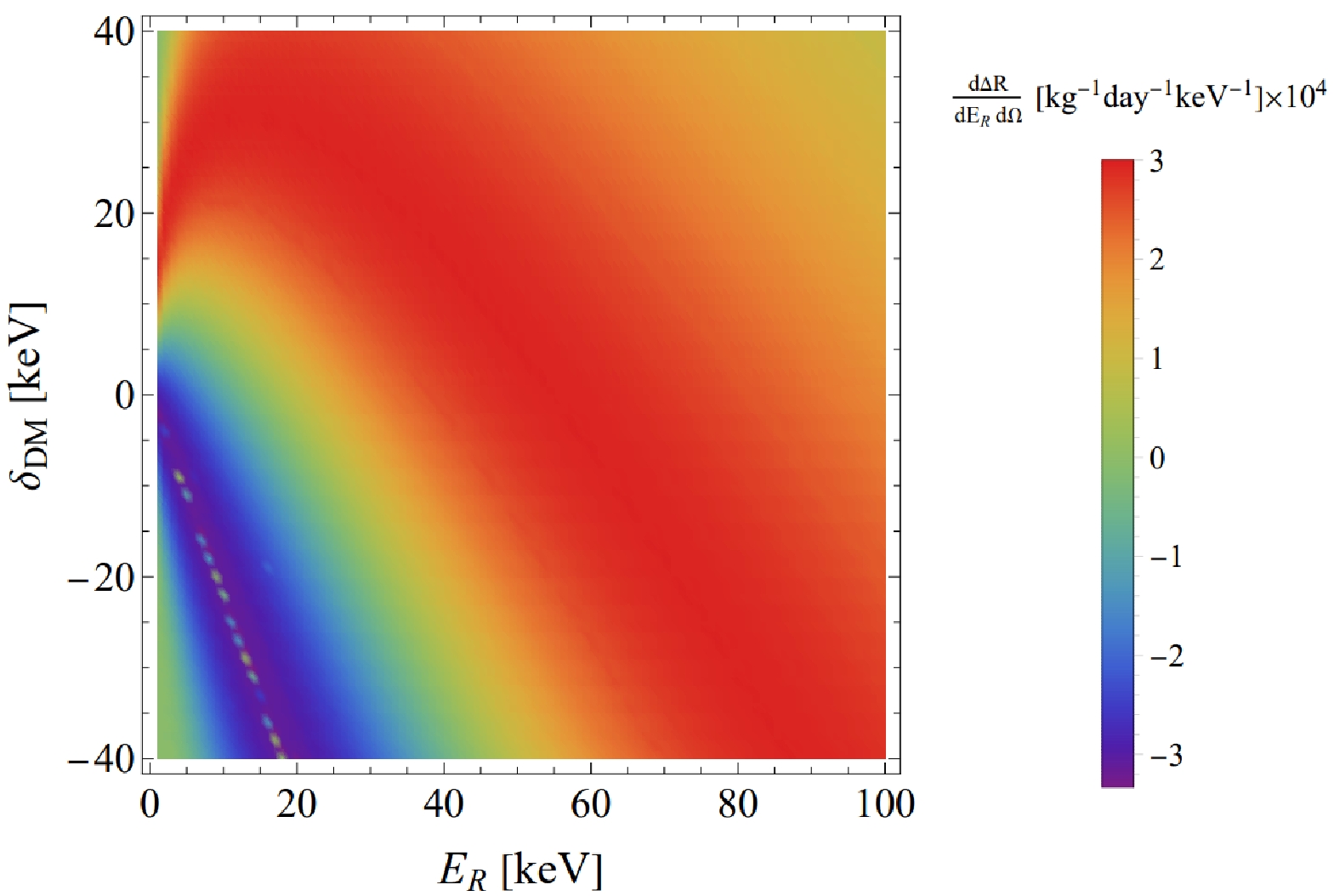
Figure 6. (color online) Pure polarization dependent part of the differential rate of scattering events corresponding to energy and mass splitting. The polarization angle is set to
$ \alpha = 3\pi/4, $ $ \beta=0, \nu = \pi/2 $ .The preceding discussion was aimed at examining the inelastic mass splitting through the angular distribution of α and β. We now proceed to investigate the polarization effect on the recoil energy, by integrating over the angular distribution. In Fig. 7, the mass splitting difference of the left panel is
$ 1\;{\rm{keV}} $ , the mass splitting difference of the middle panel is$ 5\;{\rm{keV}} $ , and the mass splitting difference of the right panel is$ 20\;{\rm{keV}} $ . Each panel shows a blue line with a mass splitting difference of$ 0\;{\rm{keV}} $ , a green line corresponding to a positive mass splitting difference, and a yellow line corresponding to a negative mass splitting difference. By construction, these three lines are independent of the recoil direction. These three diagrams illustrate an important result: even without directional information, it is possible to observe the mass splitting effect in dark matter scattering with polarized nucleons. Furthermore, we determine that when the mass splitting difference is very small, we cannot distinguish the effect of mass splitting on the total rate. Meanwhile, when compared with elastic scattering with mass splitting difference of$ 0\;{\rm{keV}} $ , inelastic scattering with mass splitting difference of$ 5\;{\rm{keV}} $ has a peak value. Furthermore, as the mass splitting difference increases, the peak value becomes more obvious. This is because$E_R\sim|\delta_{\rm DM}|$ . Additionally, for negative mass splitting, the value of total velocity increases with the increase in mass splitting value. For positive mass splitting, with the increase in mass splitting value, the value of total velocity also decreases. Therefore, we can determine the positive and negative mass splitting by comparing it with the total rate of elastic scattering. Ultimately, the event rate between the polarized and unpolarized scenarios can be discerned by the absolute value of the event rate, with the polarized one being comparatively smaller.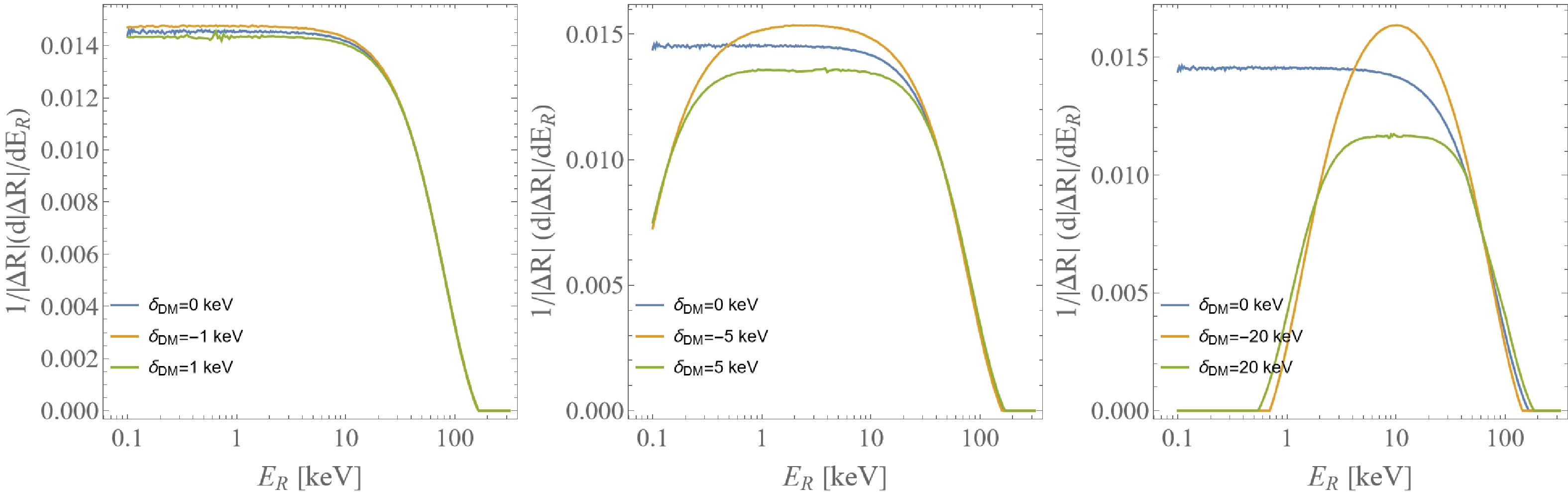
Figure 7. (color online) Triple differential event rate, integrated over all nuclear recoil angles, α and β, as a function of the recoil energy. The blue line indicates that the mass splitting is
$ 0\;{\rm{keV}} $ , yellow line indicates that the mass splitting is negative, and green line indicates that the mass splitting is positive. -
For light DM with
$ m_{\chi}=1\; {\rm{GeV}} $ , information about recoiling electrons is obtained through the Migdal effect since the recoil of the nucleus cannot be observed. By integrating all recoil directions of the nucleus, our focus lies solely on the impact of the polarization direction angle ν and electron recoil energy on the scattering rate for various DM mass splitting.Similarly to heavy DM, the same distribution of DM can be observed in the polarization direction angle ν, as depicted in Fig. 8. Analyzing Fig. 8, we observe that the number of events is noticeable only when the mass splittings are negative. This is because
$ \Delta=\delta_{{\rm{DM}}}+\delta_{{\rm{EM}}} $ , and$ \delta_{{\rm{EM}}} $ is non-zero under the Migdal effect due to$ E_{{\rm{det}}} $ . Consequently,$ \bar{v}\sim \Delta/q $ becomes significantly larger than$ v_{{\rm{esc}}} $ in most parameter space. Therefore, the contribution of$ \delta_{{\rm{EM}}} $ must be counterbalanced by the negative$ \delta_{{\rm{DM}}} $ to achieve a smaller$ \bar{v} $ . Consequently, we only observe a number of cases when$ \delta_{{\rm{DM}}} $ is negative. We conclude that the Migdal effect tends to have sizeable event rate in negative mass splitting for the same dark matter mass. Given that the signature of the Migdal effect involves probing the electron as opposed to the nucleus, the angle distributions α and β are thus integrated. Consequently, the significance of the polarized effect is diminished in scenarios involving light dark matter, making it highly analogous to the findings presented in [65]. -
This study presents the novel application of spin-polarized direct detection to explore the inelastic signatures of DM, with a specific emphasis on the mass splitting and Migdal effect for heavy and light DM, respectively. Our comprehensive analyses unequivocally demonstrate the invaluable utility of the polarized triple-differential event rate as a powerful investigative tool for studying inelastic DM, owing to its ability to capture angular and energy dependencies. Notably, in the case of pseudo-Dirac fermion DM, the angular dependence allows for the discrimination between positive and negative mass splitting, thereby offering a distinguishing characteristic. Moreover, an intriguing observation emerges, whereby the maxima of the event rate manifests at higher recoil energies
$ E_R $ as the mass splitting increases. These salient features strongly indicate that the angular and energy dependencies of the recoil rate provide complementary information for accurately determining mass splitting. Therefore, distinguishing between different mass splittings becomes feasible through a meticulous analysis of the event rate's shape. -
We are grateful to Shu-Yuan Guo and Liangliang Su for the valuable discussions.
-
For the DM scattering process of
$ {\chi}_1N\longrightarrow{\chi}_2N $ , the squared amplitude$ |\overline{M}|^2 $ has nine terms. The first term is:$ \begin{aligned}[b] &\frac{1}{{m_{A^{\prime}}}^4} (256h_4^2\lambda_4^2m_N^2m^2\vec{S}_{\chi}^{ss^{\prime}}\cdot\vec{S}_{N}^{rr^{\prime}}\vec{S}_{\chi}^{s^{\prime}s}\cdot\vec{S}_{N}^{r^{\prime}r} +256h_4^2\lambda_4^2m_N^2m\Delta\vec{S}_{\chi}^{ss^{\prime}}\cdot\vec{S}_{N}^{rr^{\prime}}\vec{S}_{\chi}^{s^{\prime}s}\cdot\vec{S}_{N}^{r^{\prime}r} +64h_4^2\lambda_4^2m_N^2\Delta^2\vec{S}_{\chi}^{ss^{\prime}}\cdot\vec{S}_{N}^{rr^{\prime}}\vec{S}_{\chi}^{s^{\prime}s}\cdot\vec{S}_{N}^{r^{\prime}r}) \\ =\;&\frac{16m_N^2m^2}{{m_{A^{\prime}}}^4}(16h_4^2\lambda_4^2\vec{S}_{\chi}^{ss^{\prime}}\cdot\vec{S}_{N}^{rr^{\prime}}\vec{S}_{\chi}^{s^{\prime}s}\cdot\vec{S}_{N}^{r^{\prime}r} +16h_4^2\lambda_4^2\frac{\Delta}{m}\vec{S}_{\chi}^{ss^{\prime}}\cdot\vec{S}_{N}^{rr^{\prime}}\vec{S}_{\chi}^{s^{\prime}s}\cdot\vec{S}_{N}^{r^{\prime}r}) =\frac{16m_N^2m^2}{{m_{A^{\prime}}}^4}(3h_4^2\lambda_4^2+3\frac{\Delta}{m}h_4^2\lambda_4^2), \end{aligned} $

(A1) where
$ \Delta^2\simeq0 $ . The second term is$ \begin{aligned}[b] &\frac{1}{{m_{A^{\prime}}}^4}4h_4^2\lambda_3^2 [\Delta\vec{K}\cdot\vec{S}_{N}^{rr^{\prime}}\delta^{ss^{\prime}}+4{\rm i}m_N\vec{S}_{\chi}^{ss^{\prime}}\cdot(\vec{S}_{N}^{rr^{\prime}}\times\vec{q})+4m_Nm\delta^{ss^{\prime}}\vec{v}^{\perp}\cdot\vec{S}_{N}^{rr^{\prime}}] [\Delta\vec{K}\cdot\vec{S}_{N}^{r^{\prime}r}\delta^{s^{\prime}s} +4{\rm i}m_N\vec{S}_{\chi}^{s^{\prime}s}\cdot(\vec{S}_{N}^{r^{\prime}r}\times\vec{q})-4m_Nm\delta^{s^{\prime}s}\vec{v}^{\perp}\cdot\vec{S}_{N}^{r^{\prime}r}] \\ =\;&\frac{h_4^2\lambda_3^2}{{m_{A^{\prime}}}^4} [64{\rm i}m_N^2\vec{S}_{\chi}^{ss^{\prime}}\cdot(\vec{S}_{N}^{rr^{\prime}}\times\vec{q})\vec{S}_{\chi}^{s^{\prime}s}\cdot(\vec{S}_{N}^{r^{\prime}r}\times\vec{q}) +64{\rm i}m_N^2m\delta^{ss^{\prime}}\vec{v}^{\perp}\cdot\vec{S}_{N}^{rr^{\prime}}\vec{S}_{\chi}^{s^{\prime}s}\cdot(\vec{S}_{N}^{r^{\prime}r}\times\vec{q})-64{\rm i}m_N^2m\vec{S}_{\chi}^{ss^{\prime}}\cdot(\vec{S}_{N}^{rr^{\prime}}\times\vec{q})\delta^{s^{\prime}s}\vec{v}^{\perp}\cdot\vec{S}_{N}^{r^{\prime}r} \end{aligned} $

$ \begin{aligned}[b] &-64m_N^2m^2\delta^{ss^{\prime}}\vec{v}^{\perp}\cdot\vec{S}_{N}^{rr^{\prime}}\delta^{s^{\prime}s}\vec{v}^{\perp}\cdot\vec{S}_{N}^{r^{\prime}r} -4\Delta^2\vec{K}\cdot\vec{S}_{N}^{rr^{\prime}}\vec{K}\cdot\vec{S}_{N}^{r^{\prime}r}\delta^{s^{\prime}s}\delta^{ss^{\prime}} +16{\rm i}m_N\Delta\vec{K}\cdot\vec{S}_{N}^{r^{\prime}r}\vec{S}_{\chi}^{ss^{\prime}}\cdot(\vec{S}_{N}^{rr^{\prime}}\times\vec{q})\delta^{s^{\prime}s} \\ &-16{\rm i}m_N\Delta\vec{K}\cdot\vec{S}_{N}^{rr^{\prime}}\vec{S}_{\chi}^{s^{\prime}s}\cdot(\vec{S}_{N}^{r^{\prime}r}\times\vec{q})\delta^{ss^{\prime}}-16m_Nm\Delta\vec{v}^{\perp}\cdot\vec{S}_{N}^{r^{\prime}r}\vec{K}\cdot\vec{S}_{N}^{rr^{\prime}}\delta^{s^{\prime}s}\delta^{ss^{\prime}} +16m_Nm\Delta\vec{v}^{\perp}\cdot\vec{S}_{N}^{rr^{\prime}}\vec{K}\cdot\vec{S}_{N}^{r^{\prime}r}\delta^{s^{\prime}s}\delta^{ss^{\prime}}] =0. \end{aligned} $

(A2) The third item is:
$ \begin{aligned}[b] &\frac{1}{{m_{A^{\prime}}}^4}16\lambda_3\lambda_4h_4^2m_N[-4{\rm i}m_N\Delta\vec{S}_{\chi}^{s^{\prime}s}\cdot(\vec{S}_{N}^{r^{\prime}r}\times\vec{q})\vec{S}_{\chi}^{ss^{\prime}}\cdot\vec{S}_{N}^{rr^{\prime}} +4{\rm i}m_N\vec{S}_{\chi}^{ss^{\prime}}\cdot(\vec{S}_{N}^{rr^{\prime}}\times\vec{q})(2m\vec{S}_{\chi}^{s^{\prime}s}\cdot\vec{S}_{N}^{r^{\prime}r}+\Delta\vec{S}_{\chi}^{s^{\prime}s}\cdot\vec{S}_{N}^{r^{\prime}r}) \\ &+8m^2m_N\vec{v}^{\perp}\cdot\vec{S}_{N}^{rr^{\prime}}\vec{S}_{\chi}^{s^{\prime}s}\cdot\vec{S}_{N}^{r^{\prime}r}\delta^{ss^{\prime}} +4mm_N\Delta\vec{v}^{\perp}\cdot\vec{S}_{N}^{rr^{\prime}}\vec{S}_{\chi}^{s^{\prime}s}\cdot\vec{S}_{N}^{r^{\prime}r}\delta^{ss^{\prime}}\\ &+4mm_N\Delta\vec{v}^{\perp}\cdot\vec{S}_{N}^{r^{\prime}r}\vec{S}_{\chi}^{ss^{\prime}}\cdot\vec{S}_{N}^{rr^{\prime}}\delta^{s^{\prime}s} -2m\Delta\vec{K}\cdot\vec{S}_{N}^{rr^{\prime}}\vec{S}_{\chi}^{s^{\prime}s}\cdot\vec{S}_{N}^{r^{\prime}r}\delta^{ss^{\prime}} -\Delta^2\vec{K}\cdot\vec{S}_{N}^{rr^{\prime}}\vec{S}_{\chi}^{s^{\prime}s}\cdot\vec{S}_{N}^{r^{\prime}r}\delta^{ss^{\prime}} \\ &-\Delta^2\vec{K}\cdot\vec{S}_{N}^{r^{\prime}r}\vec{S}_{\chi}^{ss^{\prime}}\cdot\vec{S}_{N}^{rr^{\prime}}\delta^{s^{\prime}s} -2m\vec{S}_{\chi}^{ss^{\prime}}\cdot\vec{S}_{N}^{rr^{\prime}}(4{\rm i}m_N\vec{S}_{\chi}^{s^{\prime}s}\cdot(\vec{S}_{N}^{r^{\prime}r}\times\vec{q}) -4mm_N\vec{v}^{\perp}\cdot\vec{S}_{N}^{r^{\prime}r}\delta^{s^{\prime}s}+\Delta\vec{K}\cdot\vec{S}_{N}^{r^{\prime}r}\delta^{s^{\prime}s}))] \\ =\;&\frac{1}{{m_{A^{\prime}}}^4}\lambda_3\lambda_4h_4^2[\vec{S}_{\chi}^{s^{\prime}s}\cdot\vec{S}_{N}^{r^{\prime}r}({\rm i}128m_N^2m)\vec{S}_{\chi}^{ss^{\prime}}\cdot(\vec{S}_{N}^{rr^{\prime}}\times\vec{q}) +\vec{S}_{\chi}^{ss^{\prime}}\cdot\vec{S}_{N}^{rr^{\prime}}(-{\rm i}128m_N^2m)\vec{S}_{\chi}^{s^{\prime}s}\cdot(\vec{S}_{N}^{r^{\prime}r}\times\vec{q}) \\ &+\vec{S}_{\chi}^{s^{\prime}s}\cdot\vec{S}_{N}^{r^{\prime}r}({\rm i}64m_N^2\Delta)\vec{S}_{\chi}^{ss^{\prime}}\cdot(\vec{S}_{N}^{rr^{\prime}}\times\vec{q}) +\vec{S}_{\chi}^{ss^{\prime}}\cdot\vec{S}_{N}^{rr^{\prime}}(-{\rm i}64m_N^2\Delta)\vec{S}_{\chi}^{s^{\prime}s}\cdot(\vec{S}_{N}^{r^{\prime}r}\times\vec{q})] \\ =\;&\frac{1}{{m_{A^{\prime}}}^4}16m_N^2m^2[-2\lambda_3\lambda_4h_4^2\vec{v}\cdot\vec{s}+2\lambda_3\lambda_4h_4^2\vec{v}^\prime\cdot\vec{s} -\frac{\Delta}{m}\lambda_3\lambda_4h_4^2\vec{v}\cdot\vec{s}+\frac{\Delta}{m}\lambda_3\lambda_4h_4^2\vec{v}^\prime\cdot\vec{s}], \end{aligned} $

(A3) where
$ \vec{K}=-\vec{q}=-m(\vec{v}^\prime-\vec{v}) $ . The fourth item is:$ \begin{aligned}[b] &\frac{1}{{m_{A^{\prime}}}^4}4\lambda_4^2h_3^2(2(2m+\Delta)\vec{S}_{\chi}^{ss^{\prime}}\cdot(\vec{S}_{N}^{rr^{\prime}}\times\vec{q}) +{\rm i}(4mm_N\vec{v}^{\perp}\cdot\vec{S}_{\chi}^{ss^{\prime}}\delta^{rr^{\prime}}-\Delta\vec{K}\cdot\vec{S}_{\chi}^{ss^{\prime}}\delta^{rr^{\prime}})) \\ &\times (2(2m+\Delta)\vec{S}_{\chi}^{s^{\prime}s}\cdot(\vec{S}_{N}^{r^{\prime}r}\times\vec{q}) -i4mm_N\vec{v}^{\perp}\cdot\vec{S}_{\chi}^{s^{\prime}s}\delta^{r^{\prime}r}+{\rm i}\Delta\vec{K}\cdot\vec{S}_{\chi}^{s^{\prime}s}\delta^{r^{\prime}r}) =0. \end{aligned} $

(A4) The fifth term is:
$ \begin{aligned}[b] &\frac{1}{{m_{A^{\prime}}}^4}\lambda_4^2h_3h_4[-128{\rm i}m^2m_N\vec{S}_{\chi}^{ss^{\prime}}\cdot\vec{S}_{N}^{rr^{\prime}}\vec{S}_{\chi}^{s^{\prime}s}\cdot(\vec{S}_{N}^{r^{\prime}r}\times\vec{q}) +128{\rm i}m^2m_N\vec{S}_{\chi}^{s^{\prime}s}\cdot\vec{S}_{N}^{r^{\prime}r}\vec{S}_{\chi}^{ss^{\prime}}\cdot(\vec{S}_{N}^{rr^{\prime}}\times\vec{q}) +128m_N^2m^2\vec{v}^{\perp}\cdot\vec{S}_{\chi}^{ss^{\prime}}\vec{S}_{\chi}^{ss^{\prime}}\cdot\vec{S}_{N}^{r^{\prime}r}\delta^{rr^{\prime}} \\ &+128m_N^2m^2\vec{v}^{\perp}\cdot\vec{S}_{\chi}^{s^{\prime}s}\vec{S}_{\chi}^{s^{\prime}s}\cdot\vec{S}_{N}^{rr^{\prime}}\delta^{r^{\prime}r} -32mm_N\Delta\vec{K}\cdot\vec{S}_{\chi}^{s^{\prime}s}\vec{S}_{\chi}^{ss^{\prime}}\cdot\vec{S}_{N}^{rr^{\prime}}\delta{r^{\prime}r} +32mm_N\Delta\vec{K}.\vec{S}_{\chi}^{ss^{\prime}}\vec{S}_{\chi}^{s^{\prime}s}.\vec{S}_{N}^{r^{\prime}r}\delta{rr^{\prime}} \\ &-16m_N\Delta^2\vec{K}\cdot\vec{S}_{\chi}^{s^{\prime}s}\vec{S}_{\chi}^{ss^{\prime}}\cdot\vec{S}_{N}^{rr^{\prime}}\delta{r^{\prime}r} +16m_N\Delta^2\vec{K}\cdot\vec{S}_{\chi}^{ss^{\prime}}\vec{S}_{\chi}^{s^{\prime}s}\cdot\vec{S}_{N}^{r^{\prime}r}\delta{rr^{\prime}} +32{\rm i}m_N\Delta^2\vec{S}_{\chi}^{s^{\prime}s}\cdot(\vec{S}_{N}^{r^{\prime}r}\times\vec{q})\vec{S}_{\chi}^{ss^{\prime}}\cdot\vec{S}_{N}^{rr^{\prime}} \\ &-32{\rm i}m_N\Delta^2\vec{S}_{\chi}^{ss^{\prime}}\cdot(\vec{S}_{N}^{rr^{\prime}}\times\vec{q})\vec{S}_{\chi}^{s^{\prime}s}\cdot\vec{S}_{N}^{r^{\prime}r} +64m_N^2m\Delta\vec{v}^{\perp}\cdot\vec{S}_{\chi}^{ss^{\prime}}\vec{S}_{\chi}^{s^{\prime}s}\cdot\vec{S}_{N}^{r^{\prime}r}\delta^{rr^{\prime}} +64m_N^2m\Delta\vec{v}^{\perp}\cdot\vec{S}_{\chi}^{s^{\prime}s}\vec{S}_{\chi}^{ss^{\prime}}\cdot\vec{S}_{N}^{rr^{\prime}}\delta^{r^{\prime}r} \\ &+128{\rm i}mm_N\Delta\vec{S}_{\chi}^{ss^{\prime}}\cdot(\vec{S}_{N}^{rr^{\prime}}\times\vec{q})\vec{S}_{\chi}^{s^{\prime}s}\cdot\vec{S}_{N}^{r^{\prime}r} -128{\rm i}mm_N\Delta\vec{S}_{\chi}^{s^{\prime}s}\cdot(\vec{S}_{N}^{r^{\prime}r}\times\vec{q})\vec{S}_{\chi}^{ss^{\prime}}\cdot\vec{S}_{N}^{rr^{\prime}}] \\ =\;&\frac{16\lambda_4^2h_3h_4m_N^2m^2}{{m_{A^{\prime}}}^4}[(2-3(1-\frac{m}{m_N})-\frac{\Delta}{2m}(1-\frac{m}{m_N})+\frac{\Delta}{2m_N})\vec{v}\cdot\vec{s}+(2-3(1+\frac{m}{m_N})-\frac{\Delta}{2m}(1+\frac{m}{m_N})-\frac{\Delta}{2m_N})\vec{v}^\prime\cdot\vec{s}]. \end{aligned} $

(A5) The sixth term is:
$ \frac{1}{{m_{A^{\prime}}}^4}16\lambda_3^2h_3^2(m_N^2m^2\delta^{r^{\prime}r}\delta^{rr^{\prime}}\delta^{ss^{\prime}}\delta^{s^{\prime}s} +16m_N^2m\Delta\delta^{r^{\prime}r}\delta^{rr^{\prime}}\delta^{ss^{\prime}}\delta^{s^{\prime}s} +4m_N^2\Delta^2\delta^{r^{\prime}r}\delta^{rr^{\prime}}\delta^{ss^{\prime}}\delta^{s^{\prime}s}) =\frac{16m_N^2m^2\lambda_3^2h_3^2}{{m_{A^{\prime}}}^4}(1+\frac{\Delta}{m}). $

(A6) The seventh term is:
$ \begin{aligned}[b] &\frac{1}{{m_{A^{\prime}}}^4}\lambda_3^2h_3h_4[-32{\rm i}mm_N^2\vec{S}_{\chi}^{s^{\prime}s}\cdot(\vec{S}_{N}^{r^{\prime}r}\times\vec{q})\delta^{rr^{\prime}}\delta^{ss^{\prime}} +32{\rm i}mm_N^2\vec{S}_{\chi}^{ss^{\prime}}\cdot(\vec{S}_{N}^{rr^{\prime}}\times\vec{q})\delta^{r^{\prime}r}\delta^{s^{\prime}s} +32m_N^2m^2\vec{v}^{\perp}\cdot\vec{S}_{N}^{r^{\prime}r}\delta^{rr^{\prime}}\delta^{ss^{\prime}}\delta^{s^{\prime}s} \\ &+32m_N^2m^2\vec{v}^{\perp}\cdot\vec{S}_{N}^{rr^{\prime}}\delta^{r^{\prime}r}\delta^{s^{\prime}s}\delta^{ss^{\prime}} -8m_Nm\Delta\vec{K}\cdot\vec{S}_{N}^{r^{\prime}r}\delta^{rr^{\prime}}\delta^{ss^{\prime}}\delta^{s^{\prime}s} -8m_Nm\Delta\vec{K}\cdot\vec{S}_{N}^{rr^{\prime}}\delta^{r^{\prime}r}\delta^{s^{\prime}s}\delta^{ss^{\prime}} \\ &-4m_N\Delta^2\vec{K}\cdot\vec{S}_{N}^{r^{\prime}r}\delta^{rr^{\prime}}\delta^{ss^{\prime}} -4m_N\Delta^2\vec{K}\cdot\vec{S}_{N}^{rr^{\prime}}\delta^{r^{\prime}r}\delta^{s^{\prime}s} -16{\rm i}m_N^2\Delta\vec{S}_{\chi}^{s^{\prime}s}\cdot(\vec{S}_{N}^{r^{\prime}r}\times\vec{q})\delta^{rr^{\prime}}\delta^{ss^{\prime}} +16{\rm i}m_N^2\Delta\vec{S}_{\chi}^{ss^{\prime}}\cdot(\vec{S}_{N}^{rr^{\prime}}\times\vec{q})\delta^{r^{\prime}r}\delta^{s^{\prime}s} \end{aligned} $

$ \begin{aligned}[b] &+16mm_N^2\Delta\vec{v}^{\perp}\cdot\vec{S}_{N}^{r^{\prime}r}\delta^{rr^{\prime}}\delta^{ss^{\prime}}\delta^{s^{\prime}s} +16mm_N^2\Delta\vec{v}^{\perp}\cdot\vec{S}_{N}^{rr^{\prime}}\delta^{r^{\prime}r}\delta^{s^{\prime}s}\delta^{ss^{\prime}}] \\ =&\frac{16\lambda_3^2h_3h_4m_N^2m^2}{{m_{A^{\prime}}}^4}[(1-\frac{m}{m_N}+\frac{\Delta}{4m}(1-\frac{m}{m_N})-\frac{\Delta}{4m_N})\vec{v}\cdot\vec{s} +(1+\frac{m}{m_N}+\frac{\Delta}{4m}(1+\frac{m}{m_N})+\frac{\Delta}{4m_N})\vec{v}^\prime\cdot\vec{s}]. \end{aligned} $

(A7) The eighth term is:
$ \begin{aligned}[b] &\frac{1}{{m_{A^{\prime}}}^4}4\lambda_3\lambda_4h_3^2m_N(2{\rm i}(2m+\Delta)\vec{S}_{\chi}^{s^{\prime}s}\cdot(\vec{S}_{N}^{r^{\prime}r}\times\vec{q})\delta^{rr^{\prime}}(2m\delta^{ss^{\prime}}+\Delta\delta^{ss^{\prime}}) +4mm_N\vec{v}^{\perp}\cdot\vec{S}_{\chi}^{s^{\prime}s}\delta^{rr^{\prime}}\delta^{r^{\prime}r}(2m\delta^{ss^{\prime}}+\Delta\delta^{ss^{\prime}}) \\ &+\delta^{r^{\prime}r}(-2{\rm i}(2m+\Delta)\vec{S}_{\chi}^{ss^{\prime}}\cdot(\vec{S}_{N}^{rr^{\prime}}\times\vec{q})(2m\delta^{s^{\prime}s}+\Delta\delta^{s^{\prime}s})+4mm_N\vec{v}^{\perp}\cdot\vec{S}_{\chi}^{ss^{\prime}}\delta^{rr^{\prime}}(2m\delta^{s^{\prime}s}+\Delta\delta^{s^{\prime}s}) \\ &-\delta^{rr^{\prime}}(\Delta\vec{K}\cdot\vec{S}_{\chi}^{s^{\prime}s}(2m\delta^{ss^{\prime}}+\Delta\delta^{ss^{\prime}}) +\Delta\vec{K}\cdot\vec{S}_{\chi}^{ss^{\prime}}(2m\delta^{s^{\prime}s}+\Delta\delta^{s^{\prime}s})))) =0. \end{aligned} $

(A8) The ninth term is:
$ \begin{aligned}[b] &\frac{1}{{m_{A^{\prime}}}^4}4\lambda_3\lambda_4h_3h_4[16{\rm i}m^2m_N\vec{v}^{\perp}\cdot\vec{S}_{N}^{rr^{\prime}}\vec{S}_{\chi}^{s^{\prime}s}\cdot(\vec{S}_{N}^{r^{\prime}r}\times\vec{q})\delta^{ss^{\prime}} +8{\rm i}mm_N\Delta\vec{v}^{\perp}\cdot\vec{S}_{N}^{rr^{\prime}}\vec{S}_{\chi}^{s^{\prime}s}\cdot(\vec{S}_{N}^{r^{\prime}r}\times\vec{q})\delta^{ss^{\prime}} \\ &+16m^2m_N^2\vec{v}^{\perp}\cdot\vec{S}_{N}^{rr^{\prime}}\vec{v}^{\perp}\cdot\vec{S}_{\chi}^{s^{\prime}s}\delta^{ss^{\prime}}\delta^{r^{\prime}r} +4{\rm i}m_N\Delta\vec{K}\cdot\vec{S}_{\chi}^{ss^{\prime}}\vec{S}_{\chi}^{s^{\prime}s}\cdot(\vec{S}_{N}^{r^{\prime}r}\times\vec{q})\delta^{rr^{\prime}} \\ &+16m^2m_N^2\vec{S}_{\chi}^{s^{\prime}s}\cdot\vec{S}_{N}^{r^{\prime}r}\delta^{rr^{\prime}}\delta^{ss^{\prime}}+ 8mm_N^2\Delta\vec{S}_{\chi}^{s^{\prime}s}\cdot\vec{S}_{N}^{r^{\prime}r}\delta^{rr^{\prime}}\delta^{ss^{\prime}} \\ &-4mm_N\Delta\vec{v}^{\perp}\cdot\vec{S}_{N}^{r^{\prime}r}\vec{K}\cdot\vec{S}_{\chi}^{ss^{\prime}}\delta^{rr^{\prime}}\delta^{s^{\prime}s} -4mm_N\Delta\vec{v}^{\perp}\cdot\vec{S}_{N}^{rr^{\prime}}\vec{K}\cdot\vec{S}_{\chi}^{s^{\prime}s}\delta^{r^{\prime}r}\delta^{ss^{\prime}} \\ &+16m^2m_N^2\vec{S}_{\chi}^{ss^{\prime}}\cdot\vec{S}_{N}^{rr^{\prime}}\delta^{r^{\prime}r}\delta^{s^{\prime}s} +8mm_N^2\Delta\vec{S}_{\chi}^{ss^{\prime}}\cdot\vec{S}_{N}^{rr^{\prime}}\delta^{r^{\prime}r}\delta^{s^{\prime}s} \\ &-4{\rm i}m\Delta\vec{K}\cdot\vec{S}_{N}^{rr^{\prime}}\vec{S}_{\chi}^{s^{\prime}s}\cdot(\vec{S}_{N}^{r^{\prime}r}\times\vec{q})\delta^{ss^{\prime}} -2{\rm i}\Delta^2\vec{K}\cdot\vec{S}_{N}^{rr^{\prime}}\vec{S}_{\chi}^{s^{\prime}s}\cdot(\vec{S}_{N}^{r^{\prime}r}\times\vec{q})\delta^{ss^{\prime}} \\ &-4mm_N\Delta\vec{v}^{\perp}\cdot\vec{S}_{\chi}^{s^{\prime}s}\vec{K}\cdot\vec{S}_{N}^{rr^{\prime}}\delta^{ss^{\prime}} \delta^{r^{\prime}r} +\Delta^2\vec{K}\cdot\vec{S}_{N}^{rr^{\prime}}\vec{K}\cdot\vec{S}_{\chi}^{s^{\prime}s}\delta^{ss^{\prime}} \delta^{r^{\prime}r} \\ &+\Delta^2\vec{K}\cdot\vec{S}_{N}^{r^{\prime}r}\vec{K}\cdot\vec{S}_{\chi}^{ss^{\prime}}\delta^{s^{\prime}s} \delta^{rr^{\prime}} +4mm_N\vec{v}^{\perp}\cdot\vec{S}_{\chi}^{ss^{\prime}}\delta^{rr^{\prime}}(-4{\rm i}m_N\vec{S}_{\chi}^{s^{\prime}s}\cdot(\vec{S}_{N}^{r^{\prime}r}\times\vec{q}) \\ &+4mm_N\vec{v}^{\perp}\cdot\vec{S}_{N}^{r^{\prime}r}\delta^{s^{\prime}s}-\Delta\vec{K}\cdot\vec{S}_{N}^{r^{\prime}r}\delta^{s^{\prime}s}) -2{\rm i}\vec{S}_{\chi}^{ss^{\prime}}\cdot(\vec{S}_{N}^{rr^{\prime}}\times\vec{q})(-8(2m+\Delta){\rm i}m_N\vec{S}_{\chi}^{s^{\prime}s}\cdot(\vec{S}_{N}^{r^{\prime}r}\times\vec{q}) \\ &-8mm_N^2\vec{v}^{\perp}\cdot\vec{S}_{\chi}^{s^{\prime}s}\delta^{r^{\prime}r}+8m^2m_N\vec{v}^{\perp}\cdot\vec{S}_{N}^{r^{\prime}r}\delta^{s^{\prime}s} +4mm_N \Delta\vec{v}^{\perp}\cdot\vec{S}_{N}^{r^{\prime}r}\delta^{s^{\prime}s} +2m_N\Delta\vec{K}\cdot\vec{S}_{\chi}^{s^{\prime}s}\delta^{r^{\prime}r} \\ &-2m\Delta\vec{K}\cdot\vec{S}_{N}^{r^{\prime}r}\delta^{s^{\prime}s}-\Delta^2\vec{K}\cdot\vec{S}_{N}^{r^{\prime}r}\delta^{s^{\prime}s}) +8mm_N^2\Delta\vec{S}_{\chi}^{s^{\prime}s}\cdot\vec{S}_{N}^{r^{\prime}r}\delta^{ss^{\prime}}\delta^{rr^{\prime}} +4m_N^2\Delta^2\vec{S}_{\chi}^{s^{\prime}s}\cdot\vec{S}_{N}^{r^{\prime}r}\delta^{ss^{\prime}}\delta^{rr^{\prime}} \\ &+8mm_N^2\Delta\vec{S}_{\chi}^{ss^{\prime}}\cdot\vec{S}_{N}^{rr^{\prime}}\delta^{s^{\prime}s}\delta^{r^{\prime}r}+4m_N^2\Delta^2\vec{S}_{\chi}^{ss^{\prime}}\cdot\vec{S}_{N}^{rr^{\prime}}\delta^{s^{\prime}s}\delta^{r^{\prime}r}]=0. \end{aligned} $

(A9)
Probing inelastic signatures of dark matter detection via polarized nucleus
- Received Date: 2024-06-08
- Available Online: 2024-10-15
Abstract: We investigate the inelastic signatures of dark matter-nucleus interactions, explicitly focusing on the ramifications of polarization, dark matter splitting, and the Migdal effect. Direct detection experiments, crucial for testing the existence of dark matter, encounter formidable obstacles, such as indomitable neutrino backgrounds and elusive determination of dark matter spin. To overcome these challenges, we explore the potential of polarized-target dark matter scattering, examining the impact of nonvanishing mass splitting, and the role of the Migdal effect in detecting dark matter. Our analysis demonstrates the valuable utility of the polarized triple-differential event rate as an effective tool for examining inelastic dark matter. It enables us to investigate angular and energy dependencies, providing valuable insights into the scattering process.






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: