Form factor for Dalitz decays from J/ψ to light pseudoscalars

The electromagnetic (EM) Dalitz decay of a hadron A, namely, $ A\to B\gamma^*\to B l^+l^- $, refers to the decay process where A decays into B by emitting a time-like photon that then converts to a lepton pair $ l^+l^- $. The differential partial decay width with respect to the invariant mass $ q^2\equiv m^2_{l^+l^-} $ of the lepton pair can be expressed by ${\rm d}\Gamma(q^2)/{\rm d}q^2= ({\rm d}\Gamma(q^2)/{\rm d}q^2)_\mathrm{point-like} |f_{AB}(q^2)|^2$ [1], where $({\rm d}\Gamma(q^2)/{\rm d}q^2)_\mathrm{point-like}$ can be calculated exactly in QED for point-like particles A and B; $ f_{AB}(q^2) $ is called the transition form factor (TFF) of the transition $ A\to B $ and is an important probe to the EM structure of the $ AB\gamma $ vertex as well as the internal structure of the hadron A (and B if it is also structured). Experimentally, the TFF $ f_{AB}(q^2) $ can be derived by taking the ratio $[{\rm d}\Gamma(q^2)/{\rm d}q^2]/\Gamma(A\to B\gamma)\propto |f_{AB}(q^2)|^2/|f_{AB}(0)|^2\equiv |F_{AB}(q^2)|^2$ with the normalization $ F_{AB}(0)=1 $, where many systematic uncertainties cancel. The Dalitz decays of light hadrons, such as $ \phi\to \pi^0 e^+e^- $ [2, 3], $ \phi\to \eta e^+e^- $ [4], $ \omega\to \pi^0 e^+e^- $ [5], and $ \omega\to \pi^0 \mu^+\mu^- $ [6], have been widely studied in experiments. It should be noted that experimental studies on Dalitz decays usually require large statistics, as they are rare decays for a hadron.

The BESIII Collaboration (BESIII) has accumulated more than $ 10^{10} $ $ J/\psi $ events [7], based on which the Dalitz decays of $ J/\psi $ to light hadrons can be researched. Meanwhile, the light pseudoscalars (P), such as $\eta,\;\eta', \eta(1405/1475)$ and $ X(1835) $, are observed to have large production rates on the $ J/\psi $ radiative decays [8]. Thus, it is expected that the Daltiz decays $ J/\psi \to Pl^+l^- $ can be investigated to a high precision. Actually, BESIII has performed experimental studies on the processes $ J/\psi\to e^+e^-(\eta,\eta',\pi^0) $ [9], $ J/\psi\to e^+e^-\eta $ [10], $ J/\psi\to e^+e^-\eta' $ [11, 12], $ J/\psi\to e^+e^- \eta(1405) $ [13], and $J/\psi\to e^+e^-(X(1835), X(2120),\;X(2370)$ [14]. With the large $ \psi(3686) $ data ensemble, BESIII also studied the process $\psi(3686)\to e^+e^- \eta_c$. The TTFs $ F_{\psi p}(q^2) $ are extracted for the processes $J/\psi\to \eta,\;\eta',\;\eta(1405),\;X(1835)$, and $ \psi(3686)\to \eta_c $, and the $ q^2 $-dependence can be described by the single-pole model

based on the vector meson dominance (VMD) [1, 15, 16]. The pole parameter Λ varies in the range of 1.7 to 3.8 GeV.

Intuitively, the Dalitz and radiative decays of charmonium into light pseudoscalars happens through the annihilation of the charm quark and antiquark. According to the OZI rule, the dominant contribution comes from the initial state radiation of the virtual and real photons from the charm (anti)quark (strictly speaking, the initial state radiation can also take place through light sea quarks; however, although the intermediate gluons can be soft such that the OZI rule is not conceptually justified, the approximate flavor SU(3) symmetry leads to a cancellation among the contributions from $ u,d,s $ quarks due to their electric charges). In this sense, the TFF of $ J/\psi $ to pseudoscalars should reflect the electromagnetic properties of $ J/\psi $. Therefore, for the same initial vector charmonium, Dalitz decays are insensitive to the properties of the final state light hadrons. A theoretical derivation of $ F_{\psi P}(q^2) $ from QCD is desirable but is still challenging because $ F_{\psi P}(q^2) $ is obviously in the non-perturbative regime of QCD. Phenomenological studies of $ F_{\psi \eta^{(')}}(q^2) $ can be found in Ref. [17], where the analysis is carried out in the full kinematic region based on QCD models, and in Ref. [18], where the $ J/\psi\to\gamma^* P $ is discussed within the framework of the effective Lagrangian approach and $ \eta_c-\eta-\eta' $ mixing is considered.

Lattice QCD may take the mission to give reliable predictions of TFF of $ J/\psi $ to light hadrons. A recent $ N_f=2 $ lattice QCD calculation confirms the large production rate of the flavor singlet pseudoscalar meson $ \eta_{(2)} $ in the $ J/\psi $ radiative decay [19]. In that work, the EM form factor was obtained at numerous values of time-like $ q^2 $, from which the on-shell form factor at $ q^2=0 $ was obtained through a polynomial interpolation. By assuming the $ \mathrm{U}_A(1) $ anomaly dominance and using the $ \eta-\eta' $ mixing angle, this on-shell form factor results in the branching fractions of $ J/\psi\to\gamma\eta $ and $ J/\psi \to \gamma \eta' $ that are close to the experimental values. Actually, the $ q^2 $ dependence of this decay form factor is described better by the single-pole model in Eq. (1) below.

Recently, we generated a large gauge ensemble with $ N_f=1 $ strange sea quarks. The $ N_f=1 $ QCD is a well defined theory and simplified version of QCD. It has no chiral symmetry breaking, but the $ \mathrm{U}_A(1) $ anomaly has a close relation with the unique light pseudoscalar meson $ \eta_{(1)} $. Thus, we will revisit the production rate of $ \eta_{(1)} $ in the $ J/\psi $ radiative decays. We will test the $ \mathrm{U}_A(1) $ anomaly dominance in this process by looking at the $ N_f $ dependence of the partial decay width, as the $ \mathrm{U}_A(1) $ anomaly is proportional to $ N_f $. In the meantime, we will explore the $ q^2 $-dependence of the related TFF and its sensitivity to the light pseudoscalar mass since our sea quark is much heavier than that in Ref. [19]. The related calculations necessarily involve the annihilation effect of strange quarks, which are dealt with using the distillation method [20].

The remainder of this paper is organized as follows. The numerical procedures and results are presented in Section II. Section III is devoted to the discussion and physical implications of our results. Section IV gives the summary of this work.

We generate gauge configurations with $ N_f=1 $ dynamical strange quarks on an $ L^3\times T=16^3\times 128 $ anisotropic lattice. We use the tadpole-improved Symanzik's gauge action for anisotropic lattices [21, 22] and the tadpole-improved anisotropic clover fermion action [23, 24]. The RHMC algorithm implemented in Chroma software [25] is used to generate the $ N_f=1 $ gauge configurations. The parameters in the action are tuned to give the anisotropy $ \xi=a_s/a_t\approx 5 $, where $ a_t $ and $ a_s $ are the temporal and spatial lattice spacings, respectively. The scale setting takes the following procedure. Experimentally, there is an interesting relation between pseudoscalar meson masses $ m_{PS} $ and the vector meson masses $ m_V $ of the quark configuration $ q_l\bar{q} $:

where $ q_l $ represents the u, d, s quarks, and q represents $ u,d,s,c $ quarks. The masses of these vector and pseudoscalar mesons from PDG [8] are listed in Table 1 along with their mass squared differences. Similar to the scale setting in Ref. [26], we assume the relation of Eq. (2) is somewhat general for light mesons and use it to set the scale parameter $ a_t $. We make the least squares fitting to the mass squared differences over the $ n\bar{n} $, $ n\bar{s} $, $ n\bar{c} $, and $ s\bar{c} $ systems, where n refers to the $ u,d $ quarks, and get the mean value $ \overline{\Delta m^2}=0.568(8) $ $ \mathrm{GeV}^2 $, which serves as an input to give the lattice scale parameter $ a_t^{-1}=6.66(5) $ GeV. As the HPQCD collaboration determined the $ s\bar{s} $ pseudoscalar meson mass to be $ m_{\eta_s}=0.686(4) $ GeV from the connected quark diagram [27], we use the ratio $ m_\phi/m_{\eta_s}= $ 1.487(9) to set the bare mass parameters of strange quarks. Although $ \eta_s $ is not a physical state, the mass squared difference $m_\phi^2-m_{\eta_s}^2\approx 0.570 \; \mathrm{GeV}^2$ also satisfies the empirical relation of Eq. (2). Finally, we obtain $ m_{\eta_s}=693.1(3)(6.0) $ MeV, $ m_\phi=1027.2(5)(7.7) $ MeV, and $ m_\phi^2-m_{\eta_s}^2=0.570\; \mathrm{GeV}^2 $ on our gauge ensemble. This serves as a self-consistent check of our lattice setup. The details of the gauge ensemble are given in Table 2. For the valence charm quark, we use the same fermion action as the strange sea quarks, and the charm quark mass parameters are tuned to give $ (m_{\eta_c}+3m_{J/\psi})/4=3069 $ MeV.

$ q_l\bar{q} $	$ m_V $/GeV	$ m_{PS} $/GeV	$m_V^2-m_{PS}^2 /\mathrm{GeV}^2$
$ n\bar{n} $	0.775	0.140	0.581
$ n\bar{s} $	0.896	0.494	0.559
$ s\bar{s} $	1.020	0.686 [27]	0.570
$ n\bar{c} $	2.010	1.870	0.543
$ s\bar{c} $	2.112	1.968	0.588
$ n\bar{b} $	5.325	5.279	0.481
$ s\bar{b} $	5.415	5.367	0.523

Table 1.  Experimental values of the masses of the pseudoscalar (P) and vector mesons (V) of quark configurations $ n\bar{n} $, $ n\bar{s} $, $ n\bar{c} $, $ s\bar{c} $, $ n\bar{b} $, and $ s\bar{b} $ [8] , where n refers to the $ u,d $ quarks. The rightmost column lists the $ m_V^2-m_{PS}^2\; (\mathrm{GeV}^2) $ values. In the row of $ s\bar{s} $ states, the mass of the $ s\bar{s} $ pseudoscalar $ \eta_s $ is determined by the HPQCD collaboration from lattice QCD calculations [27].

$ L^3 \times T $	$ \beta $	$ a_t^{-1} $/GeV	$ \xi $	$ m_{\eta_s} $/MeV	$ m_\phi $ /MeV	$ N_\mathrm{cfg} $
$ 16^3 \times 128 $	2.0	$ 6.66(5) $	$ \sim 5.0 $	$ 693(5) $	$ 1027(8) $	$ 1547 $

Table 2.  Parameters of the gauge ensemble.

The quark propagators are calculated in the framework of the distillation method [20]. Let $\{V_i,\;i=1, 2,\ldots, 70\}$ be the set of the $ N_V=70 $ eigenvectors (with smallest eigenvalues) of the gauge covariant Laplacian operator on the lattice. We use these eigenvectors to calculate the perambulators of strange and charm quarks, which are encoded with the all-to-all quark propagators and facilitate the treatment of quark disconnected diagrams. In the meantime, these eigenvectors provide a smearing scheme for quark fields, namely, $ \psi^{(s)}=V^\dagger V \psi $, where $ \psi^{(s)} $ is the smeared quark field of $ \psi $, and V is a matrix with each column being an eigenvector. All the meson interpolation operators in this work are built from the smeared charm and strange quark fields.

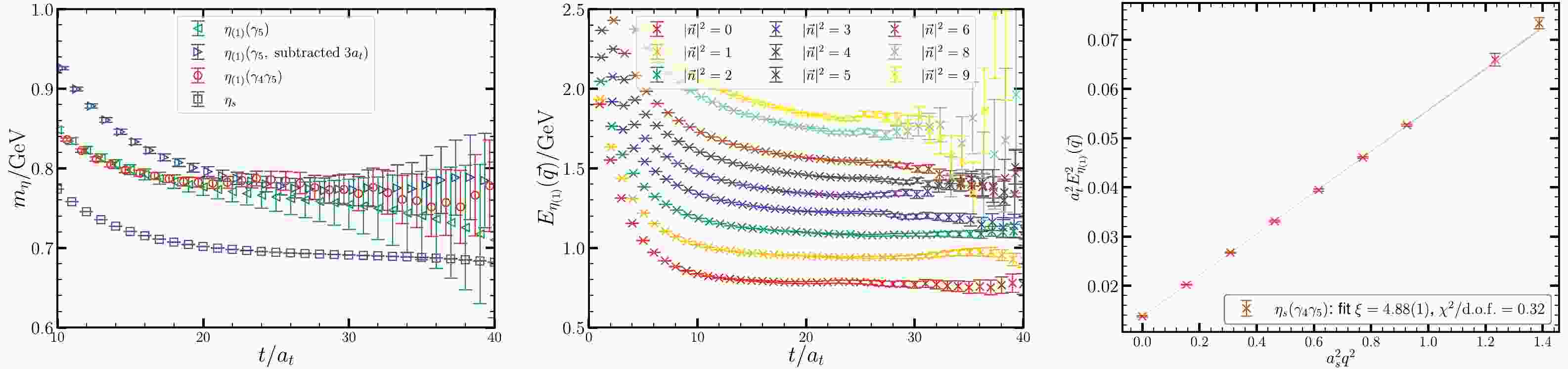
We use two interpolation operators for $ \eta_{(1)} $, namely, $ \mathcal{O}_{\gamma_5}=\bar{s}^{(s)}\gamma_5 s^{(s)} $ and $ \mathcal{O}_{\gamma_4\gamma_5}=\bar{s}^{(s)}\gamma_4\gamma_5 s^{(s)} $, to calculate the correlation functions $ C_{\gamma_5\gamma_5}(t) $ and $ C_{(\gamma_4\gamma_5)(\gamma_4\gamma_5)}(t) $. $ C_{\gamma_5\gamma_5}(t) $ has a finite volume artifact that approaches a nonzero constant when t is large, as shown in Fig. 1. This artifact comes from the topology of QCD vacuum and can be approximately expressed as $ a^5(\chi_\mathrm{top} + Q^2/V)/T $, where a is the lattice spacing (in the isotropic case), $ \chi_\mathrm{top} $ is the topological susceptibility, Q is the topological charge, V is the spatial volume, and T is the temporal extension of the lattice [28−30]. In contrast, $ C_{(\gamma_4\gamma_5)(\gamma_4\gamma_5)}(t) $ damps to zero for large t, which is the normal large t behavior. The constant term of $ C_{\gamma_5\gamma_5}(t) $ can be subtracted by taking the difference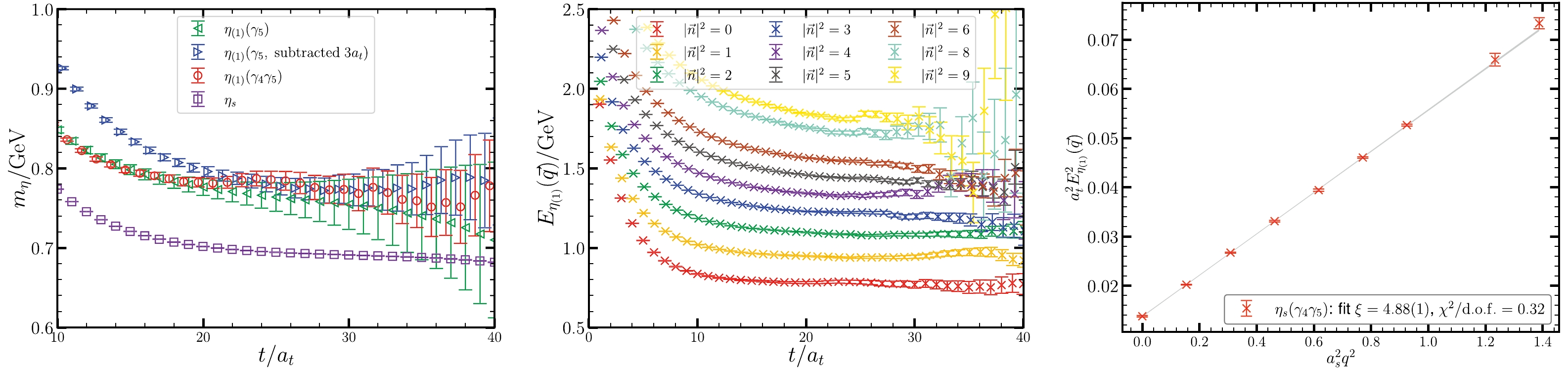

Figure 1.  (color online) Lattice results of the energies of $ \eta_{(1)} $. Left panel: effective mass of two-point correlation functions of $ \eta_{(1)} $ and $ \eta_{s} $, where $ \eta_{(1)} $ uses the operators $ \mathcal{O}_{\gamma_5} $ and $ \mathcal{O}_{\gamma_4\gamma_5} $. The green points are from the original two-point function of $ \mathcal{O}_{\gamma_5} $, the blue points are from the subtracted two-point function in Eq. (3) with $ t_0=3 a_t $, and the red points are from the two-point function of $ \mathcal{O}_{\gamma_4\gamma_5} $. The plateau regions of red and blue points merge together in the large $ t/a_t $ range. The purple points represent unphysical $ \eta_s $, which only include connected diagram. Middle panel: effective energies $ E_{\eta_{(1)}}^{(\vec{q})}(t) $ with momentum mode $ \vec{n} $ of $ \vec{q} $ up to $ |\vec{n}|^2=9 $, where the data points are from the correlation functions of $ \mathcal{O}_{\gamma_4\gamma_5}(\vec{q}) $. The fitted $ E_{\eta_{(1)}}^{(\vec{q})} $ values are given in Table 3. Right panel: dispersion relation of $ \eta_{(1)} $. The grey band illustrates the dispersion relation in Eq. (9) with the fitted $ \xi=4.88(1) $ and $ \chi^2 $ per degree of freedom $\chi^2/{d.o.f}=0.32$.

and we take $ t_0=3 a_t $ in practice. The effective mass functions $ m_\mathrm{eff}(t)=\ln \frac{C_{\Gamma\Gamma}^{(')}(t)}{C_{\Gamma\Gamma}^{(')}(t+1)} $ of the two correlations are shown in Fig. 1, where one can see that notable mass plateaus appear when $ t/a_t>15 $ and agree with each other. The effective masses of the connected parts of the two correlation functions are also shown for comparison. Their plateaus correspond to the mass $ m_{\eta_s} $ of $ \eta_s $. The data analysis gives the results

Here, $ m_{\eta_s} $ is the mass parameter from the connected diagram and is consistent with the value $ m_{\eta_s}=686(4) $ obtained by HPQCD at the physical strange quark mass [27]. This indicates that our sea quark mass parameter is tuned to be almost at the strange quark mass. $ m_{\eta_{(1)}} $ is determined from the correlation function that includes the connected diagram and quark annihilation diagram and is therefore the mass of the well-defined pseudoscalar meson $ \eta_{(1)} $.

The transition matrix element $ \mathcal{M} $ for the process $ J/\psi \to \gamma^* \eta_{(1)} $ can be expressed in terms of one form factor $ M(q^2) $, namely,

where $ q^2=(p_\psi-p_{\eta})^2 $ is the virtuality of the photon, $ \epsilon_\sigma(p_{J/\psi},\lambda) $ is the polarization vector of $ J/\psi $, and $ j_\mathrm{em}^\mu=\bar{c}\gamma^\mu c $ is the electromagnetic current of charm quark (we only consider the initial state radiation and ignore photon emissions from sea quarks and the final state). The matrix element $ \mathcal{M} $ is encoded in the following three-point functions:

with $ \vec{q}=\vec{p'}-\vec{p} $, where $ \mathcal{O}_{\eta}(\vec{p'},t) $ and $ \mathcal{O}_{\psi}^{i}(\vec{p},t) $ are the interpolating field operators for $ \eta_{(1)} $ and $ J/\psi $ with spatial momenta $ \vec{p'} $ and $ \vec p $, respectively. For $ t\gg t' $, $ t'\gg 0 $, and in the rest frame of $ J/\psi $ ($ \vec{p}=0 $), the explicit spectral expression of $ C^{\mu i}_{(3)}(\vec{q};t,t') $ reads

where $ V_3 $ is the spatial volume, $ Z_\eta(\vec{q})=\langle \Omega|\mathcal{O}_{\eta_{(1)}}(\vec{q})|{\eta_{(1)}}(\vec{q})\rangle $and $ Z_{\psi}\epsilon^i(\vec{0},\lambda)=\langle \Omega|\mathcal{O}_{\psi}^i(\vec{0})|J/\psi(\vec{0},\lambda)\rangle $. Note that $ Z_\eta $ has a $ \vec{q} $ dependence due to the smeared operator $ \mathcal{O}_{\eta} $ [31]. The parameters $ m_\psi $, $ E_\eta(\vec{q}) $, $ Z_\psi $, and $ Z_\eta(\vec{q}) $ can be derived from the two-point correlation functions

Thus, we can extract the matrix element $ \langle \eta_{(1)}|j_\mathrm{em}^\mu|J/\psi\rangle $ through Eqs. (7) and (8).

Therefore, the major numerical task is the calculation of $ C_{(3)}^{\mu i}(\vec{q};t,t') $. The local EM current $ j_\mathrm{em}^\mu(x)=[\bar{c}\gamma^\mu c](x) $ mentioned above (the charm quark field c and $ \bar{c} $ are the original field, which are not smeared) is not conserved anymore on the finite lattice and should be renormalized. We determine the renormalization factors $ Z_V^{t}=1.147(1) $ and $ Z_V^s=1.191(2) $ for the temporal and spatial components of $ j_\mathrm{em}^\mu(x) $, respectively, by calculating the relevant electromagnetic form factors of $ \eta_c $ [32, 33]. In practice, only $ Z_V^{s} $ is involved and is incorporated implicitly in $ j_\mathrm{em}^\mu(x) $. We use the operator $ \mathcal{O}_{\gamma_4\gamma_5}=\bar{s}^{(s)}\gamma_4\gamma_5 s^{(s)} $ for $ \mathcal{O}_\eta $, and $ \mathcal{O}_{\psi}^i $ takes the form $ \bar{c}^{(s)}\gamma^i c^{(s)} $ in Eq. (6). The three-point function $ C_{(3)}^{\mu i}(\vec{q};t,t') $ is calculated in the rest frame of $ J/\psi $ ($ \vec{p}=0 $) such that $ \eta_{(1)} $ moves with spatial momentum $ \vec{p}'=\vec{q} $. The right panel of Fig. 1 shows the dispersion relation of $ \eta_{(1)} $

where $ \vec{n} $ represents the momentum mode of $ \vec{q}=\dfrac{2\pi}{La_s} \vec{n} $. It can be seen that $ E_{\eta}^2(\vec{q}) $ exhibits a perfect linear behavior in $ |\vec{q}|^2 $ up to $ |\vec{n}|^2=9 $ and the fitted slope gives $ \xi=4.88(1) $, which deviates from the renormalized anisotropy $ \xi\approx 5.0 $ by less than 3%.

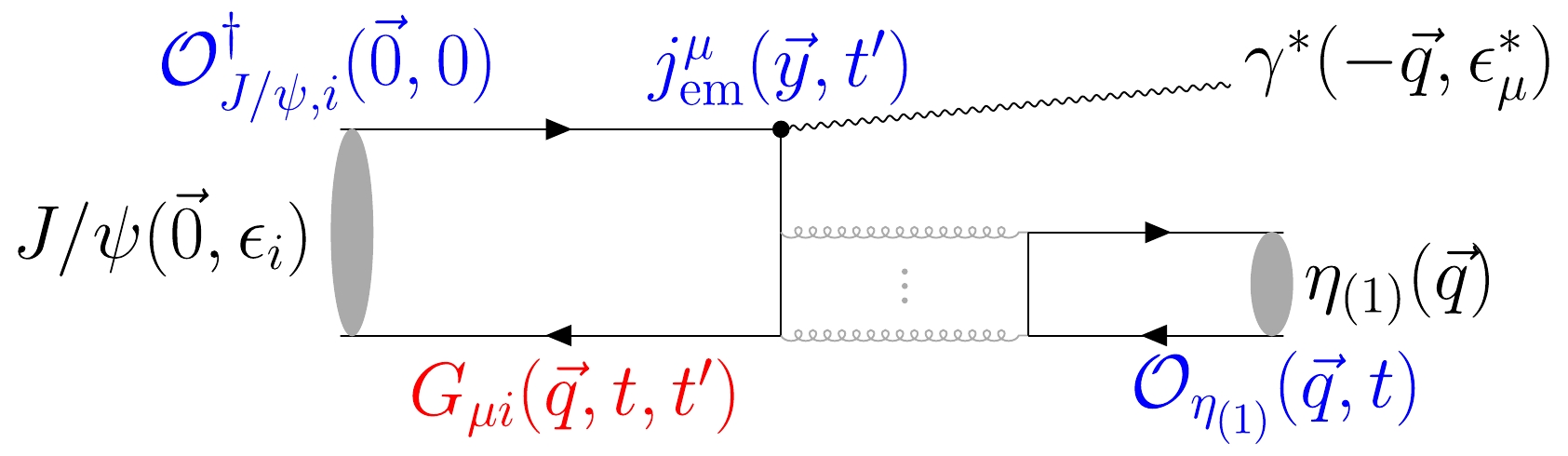
After the Wick's contractions, the three-point function $ C^{\mu i}_{(3)} $ is expressed in terms of quark propagators, and the schematic quark diagram is illustrated in Fig. 2. There are two separated quark loops connected by gluons. The strange quark loop on the right-hand side can be calculated in the framework of the distillation method. The left part $ G^{\mu i} $ comes from the contraction of $ \mathcal{O}_{\psi}^i $ and the current $ j^\mu_\mathrm{em} $, namely,

Figure 2.  (color online) Schematic diagram for the process $ J/\psi\to \gamma^* \eta_{(1)} $.

and is dealt with by the distillation method [34]. Considering $\mathcal{O}_{\psi}^i(\vec{p},t)=\sum\limits_{\vec{y}} {\rm e}^{-{\rm i}\vec{p}\cdot\vec{y}}[\bar{c}^{(s)}\gamma_i c^{(s)}](\vec{y},t)$, the explicit expression of $ G^{\mu i} $ at the source time slice $ \tau=0 $ is

where $ S_c=\langle c\bar{c}\rangle_U $ is the all-to-all propagator of charm quark for a given gauge configuration U , and $ D(\vec{p}) $ is a $ 3L^3\times 3L^3 $ diagonal matrix with diagonal elements $\delta_{ab} {\rm e}^{{\rm i}\vec{p}\cdot\vec{y}}$ ($ \vec{y} $ labels the column or row indices, and $ a,b=1,2,3 $ refer to the color indices). The $ \gamma_5 $-hermiticity $ S_c=\gamma_5 S_c^\dagger\gamma_5 $ implies $ [V^\dagger(0)S_c](\vec{x},t)=\gamma_5 [S_cV(0)]^\dagger(\vec{x},t)\gamma_5 $, such that only $ S_c V(0) $ is required, while $ S_c V(0) $ can be obtained by solving the system of linear equations

where $ M[U;m_c] $ is the fermion matrix in the charm quark action (the linear system solver defined by $ M[U;m_c]x=b $ is applied $ 4N_V $ times for Dirac indices $ \alpha=1,2,3,4 $ and all columns of $ V(0) $). To increase the statistics, the above procedure runs over the entire time range, say, $ \tau\in[0,T-1] $. Averaging over $ \tau\in [0,T-1] $ improves the precision of the calculated $ C^{\mu i}_{(3)} $ drastically.

It is observed that the$ J/\psi $ contribution dominates $ C^{\mu i}_{(3)} (\vec{q};t,t') $ when $ t'>40 $. Combining Eqs. (5), (7), and (8), we have the expression

for fixed $ t'/a_t=40 $, from which we obtain $ M(q^2,t-t') $ for each $ q^2 $. Figure 3 shows the $ t-t' $ dependence of $ M(q^2,t-t') $ at several $ q^2 $ close to $ q^2=0 $. It can be seen that a plateau region appears beyond $ t-t'>10 $ for each $ q^2 $, where $ M(q^2) $ is obtained through a constant fit. The grey bands illustrate the fitted values and fitting time ranges, along with the jackknife errors. We also test the fit function form $M(q^2,t-t')=M(q^2)+c(q^2) {\rm e}^{-\delta E (t-t')}$, with the exponential term being introduced to account for the higher state contamination. The fitted values of $ M(q^2) $ in this way are consistent with those in the constant fit but have much larger errors. Therefore, we use the results from the constant fit for the values of $ M(q^2) $. The derived $ M(q^2) $ up to $ q^2=4.3\; \mathrm{GeV}^2 $ data points are listed in Table 3.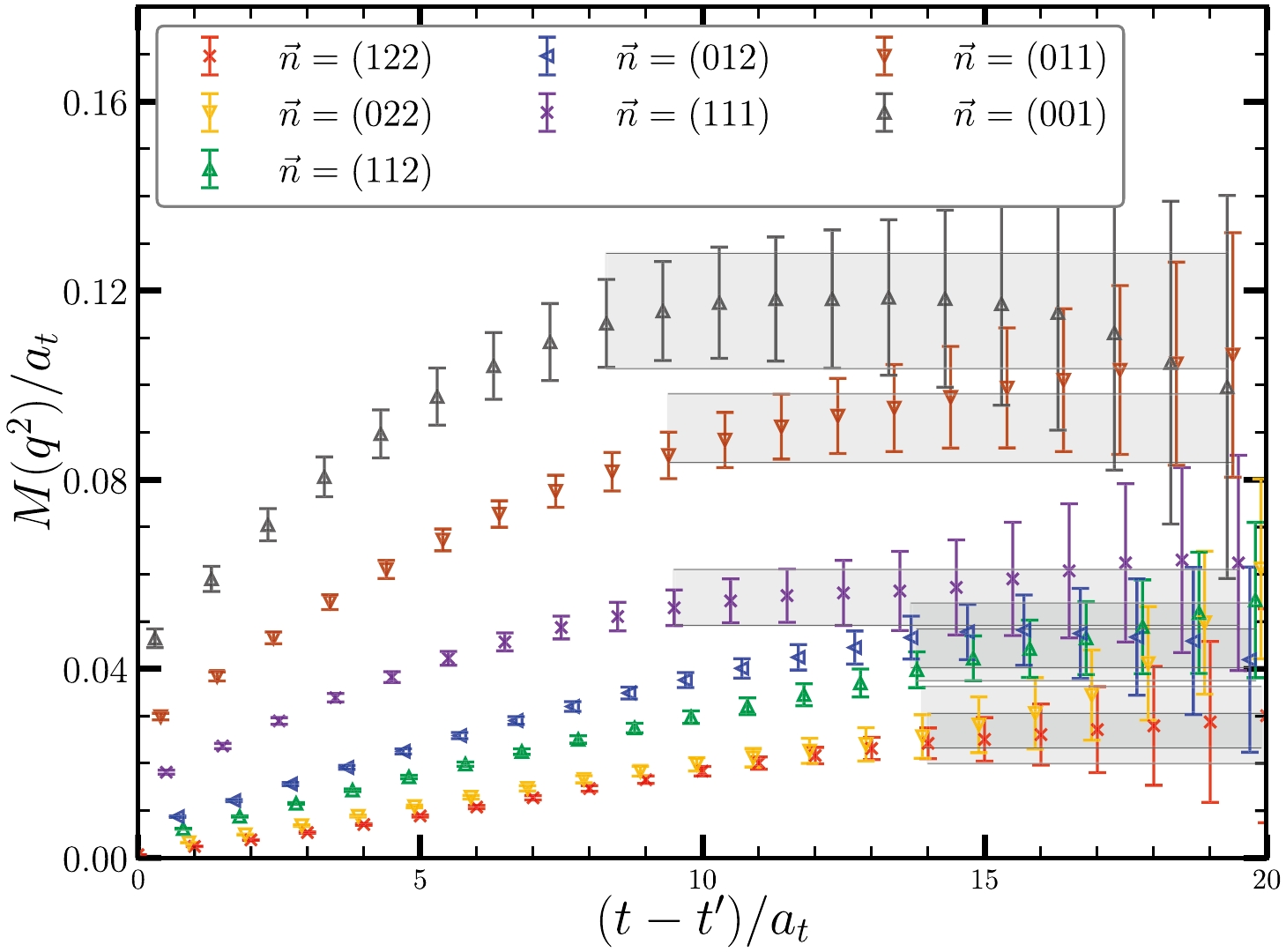

Figure 3.  (color online) Fit of form factor $ M(q^2) $ for $J/\psi\to $$ \gamma^* \eta_{(1)}$. The lattice data are plotted as data points, and the grey bands show the fit by constants to the plateau regions. The fitted $ M(q^2) $ values are given in Table 3.

mode $ \vec{n} $ of $ \vec{q} $	$ (1, 2, 2) $	$ (0, 2, 2) $	$ (1, 1, 2) $	$ (0, 1, 2) $	$ (1, 1, 1) $	$ (0, 1, 1) $	$ (0, 0, 1) $
$ q^2/ \mathrm{GeV}^{2} $	$ - $0.6800(66)	$ - $0.1869(73)	0.8777(91)	1.459(10)	2.756(14)	3.499(16)	4.337(20)
$ E_{\eta_{(1)}}^{(\vec{q})} / \mathrm{GeV} $	1.803(14)	1.710(17)	1.5279(29)	1.4291(24)	1.2119(29)	1.0886(20)	0.9466(18)
$ M(q^2) / \mathrm{GeV}^{-1} $	0.00380(80)	0.00447(97)	0.00645(82)	0.0071(10)	0.00828(89)	0.0137(11)	0.0174(18)

Table 3.  Fit values of $ \eta_{(1)} $ form factor $ M(q^2) $. The momentum modes $ \vec{n} $ represent the relation $ \vec{q} = \frac{2\pi}{L} \vec{n} $. The two-point function $ C_{\Gamma\Gamma}(t) $ and three-point ratio function $ R^{\mu i}(\vec{q};t,t') $ corresponding to the same momentum mode $ \vec{n} $ have been averaged for increasing signal of the energy $ E_{\eta_{(1)}}^{(\vec{q})} $ and form factor $ M(q^2) $, respectively.

Instead of a polynomial function form used by Ref. [19], we use the single-pole model to describe the $ q^2 $ dependence of $ M(q^2) $

As indicated by the red band in Fig. 4, the model fits the overall behaviors of $ M(q^2) $ very well with the parameters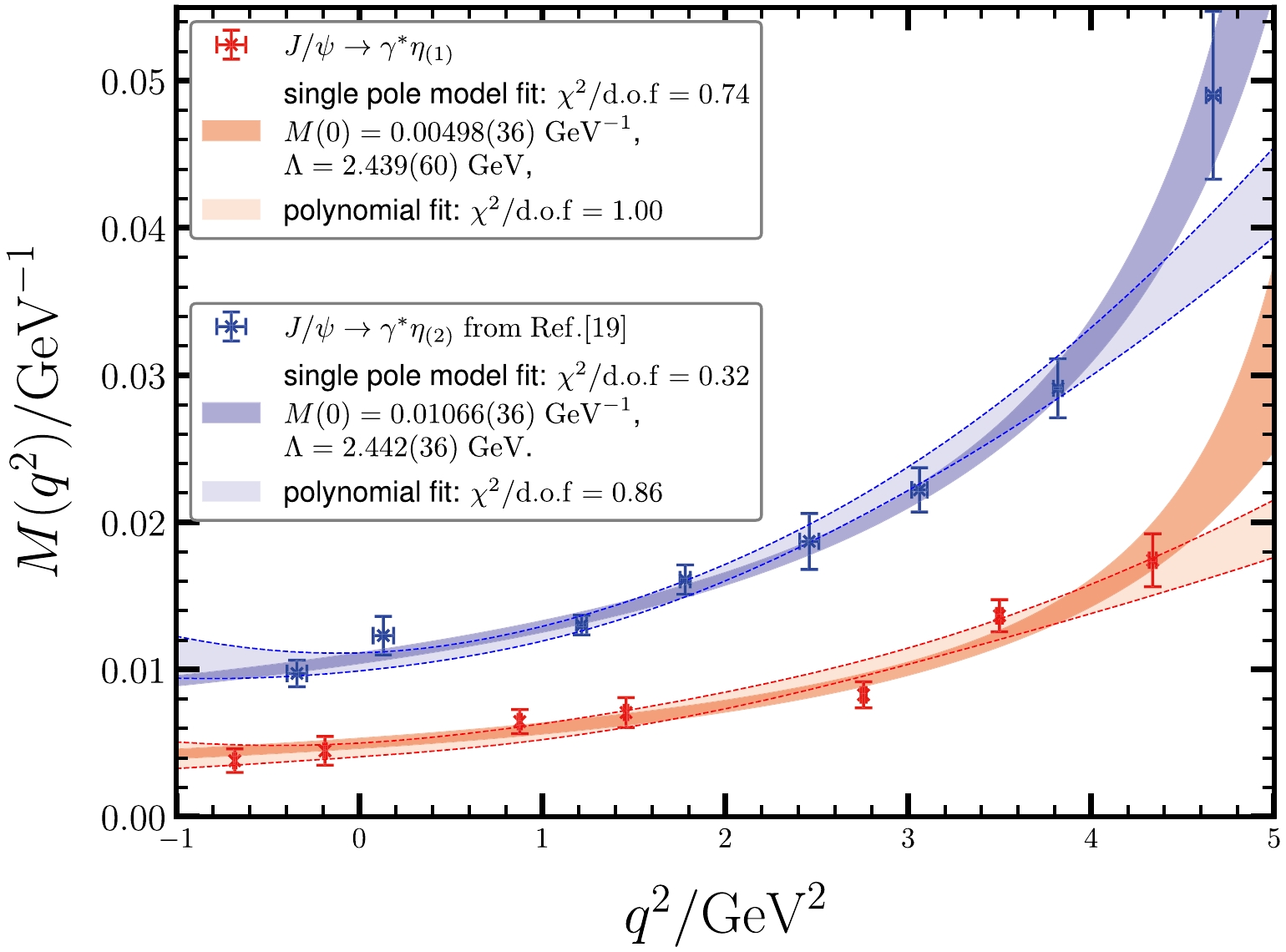

Figure 4.  (color online) The form factor $ M(q^2) $ for $J/\psi\to $$ \gamma^* \eta_{(1,2)}$. The data points are the lattice QCD results, and the shaded bands illustrate the fit model $ M(q^2)=\frac{M(0)}{1-q^2/\Lambda^2} $ with the best fit parameters $ M(0)=0.01066(36)\; \text{GeV}^{-1} $ for $ N_f=1 $ and $ \Lambda=2.442(36)\; \text{GeV} $ for $ N_f=2 $. The $ M(q^2) $ data of $ J/\psi\to\gamma^*\eta_{(2)} $ are the same as those in Table II of Ref. [19], and the fit is performed using the jackknife method on the original data sample. The light-shaded bands are the comparison with the polynomial fit $ M(q^2) = M(0) + a q^2 + b q^4 $.

The partial decay width $ \Gamma(J/\psi\to \gamma \eta_{(1)}) $ is dictated by the on-shell form factor $ M(q^2=0) $ through the relation

where the electric charge of charm quark $ Q=+2e/3 $ has been incorporated, $\alpha\equiv {e^2}/({4\pi})=1/134$ is the fine structure constant at the charm quark mass scale, and $ |\vec{p}_\gamma|=(m_\psi^2-m_{\eta_{(1)}}^2)/2m_\psi $ is the on-shell momentum of the photon. Using the value of $ M(0) $ in Eq. (15), the partial decay width and corresponding branching fraction are predicted as

where the experimental value $ \Gamma_{J/\psi}=92.6\; \mathrm{keV} $ is used. Obviously, $ \mathrm{Br}(J/\psi\to\gamma\eta_{(1)}) $ is four or five times smaller than $ \mathrm{Br}(J/\psi\to \gamma \eta_{(2)})=4.16(49)\times 10^{-3} $ in the $ N_f=2 $ case of $ m_\pi\approx 350\; \mathrm{MeV} $ [19] and the experimental value $ \mathrm{Br}(J/\psi\to \gamma \eta')=5.25(7)\times 10^{-3} $ [8].

This large difference can be attributed to the dependence of quark masses and the flavor number $ N_f $. The decay process $ J/\psi\to \gamma\eta_{(N_f)} $ takes place in the procedure that the $ c\bar{c} $ pair annihilates into gluons (after a photon radiation), which then convert into $ \eta_{(N_f)} $. There are two mechanisms for gluons to couple to $ \eta_{(N_f)} $. The first is the $ \mathrm{U}_A(1) $ anomaly manifested by the anomalous axial vector current relation (in the chiral limit)

where $ j_5^\mu=\dfrac{1}{\sqrt{N_f}}\sum\limits_{k=1}^{N_f} \bar{q}_k\gamma_5\gamma^\mu q_k $ is the flavor singlet axial vector current for $ N_f $ flavor quarks, and $ q(x) $ is the topological charge density. The ${\rm U}_A(1)$ anomaly induces the anomalous gluon-$ \eta $ coupling with the strength described by the matrix element $ \langle 0|q(0)|\eta_{(N_f)}\rangle $, which has been discussed extensively in theoretical studies [35−42]. With the matrix element $ \langle 0|\partial_\mu j_5^\mu(0)|\eta_{(N_f)}\rangle=f_{\eta_{(N_f)}}m_{\eta_{(N_f)}}^2 $, from Eq. (18), one has the relation

in the chiral limit. According to the Witten and Veneziano mechanism [43, 44] for the mass of $ \eta_{(N_f)} $, $m_{\eta_{(N_f)}}^2= \dfrac{4N_f}{f_\pi^2} \chi_\mathrm{top}$, where $ \chi_\mathrm{top} $ is the topological susceptibility of the SU(3) pure Yang-Mills theory, one has $\langle 0| q(0) |\eta_{(N_f)}\rangle\propto \sqrt{N_f}/f_{\eta_{(N_f)}}$ in the chiral limit. Consequently, if the ${\rm U}_A(1)$ anomaly dominates the production of $ \eta_{(N_f)} $ in the process $ J/\psi\to\gamma \eta_{(N_f)} $, then one expects the $ N_f $ dependence for the partial decay width

This kind of $ N_f $ dependence can be tested in a $ N_f=3 $ lattice QCD calculation. Note that $ f_{\eta_{(N_f)}} $ has quark mass dependence for massive quarks and becomes larger when quark mass increases. Thus, Eq. (20) partially explains the small value of $ \Gamma(J/\psi\to \gamma \eta_{(1)}) $ we obtain at the strange quark mass in $ N_f=1 $ QCD.

There may be also other sources for the quark mass dependence. First, an additional term $\dfrac{1}{\sqrt{N_f}}\sum_{k=1}^{N_f} 2 {\rm i} m_k \bar{q}_k\gamma_5 q_k$ appears on the right-hand side of Eq. (18) when the quark masses $ m_k\neq 0 $. Secondly, the coupling of perturbative gluons to $ \eta_{(N_f)} $ is proportional to quark mass [45, 46]. However, it is nontrivial to theoretically deduce a precise quark mass dependence for the decay process we are considering. This issue can be explored by the lattice QCD calculations at different light quark masses in the future.

The form factor $ M(q^2) $ in Eq. (14) is actually the TFF for the Dalitz decay $ J/\psi\to\eta_{(1)} l^+l^- $ when $ q^2>4m_l^2 $, which is seen to be well described by the single pole model with $ \Lambda={2.439(60)}\; \mathrm{GeV} $. In Ref. [19], the Dalitz TFF $ M(q^2) $ is also obtained in the $ N_f=2 $ lattice QCD at $ m_\pi\approx 350\; \mathrm{MeV} $, and the value $ M(0) $ is interpolated using a polynomial function form, namely, $ M(q^2) = M(0) + a q^2 + b q^4 $. We refit the $ q^2 $-dependence of $ M(q^2) $ in Ref. [19] using the same single-pole model and present the result in Fig. 4, where the polynomial fits to both the $ N_f=1 $ data in this work and the $ N_f=2 $ data in Ref. [19] are also shown for comparison. In both cases, the pole model (only two parameters) fit gives smaller values (0.74 for $ N_f=1 $ and $ 0.32 $ for $ N_f=2 $) of $\chi^2/{d.o.f}$ than the polynomial fit (1.00 for $ N_f=1 $ and 0.86 for $ N_f=2 $), even though the latter has one more parameter. Especially for the $ N_f=2 $ case, the pole model with $ \Lambda=2.442(36)\; \mathrm{GeV} $ describes the whole $ q^2 $ range very well. This indicates that the single-pole model is suitable for describing the Dalitz decay TFFs of $ J/\psi $ to light pseudoscalar mesons P.

In experiments, the TFF $ F_{\psi P} $ is extracted from the ratio

where $ A(q^2) $ is a known kinematic factor [1, 15, 16]

derived from the QED calculation. BESIII has measured many Dalitz decay processes of $ J/\psi\to P e^+e^- $ with $ P=\eta $ [9, 10], $ \eta' $ [9, 11, 12], $ \eta(1405) $ [13], and $(X(1835),~X(2120), X(2370))$ [14]. For some of these processes, the TFF are obtained and fitted through the single-pole model (along with resonance terms if experimental data are precise enough [10]) in Eq. (1), and the fitted values of Λ are listed in Table 4, where the values of Λ derived from lattice QCD are also presented in the last two rows for comparison. Although the values of Λ for the $ J/\psi\to \eta,\eta' $ Dalitz decays are compatible with the lattice values, the values of Λ for $ J/\psi\to \eta(1405), X(1835) $ are substantially smaller. Thus, it is possible that Λ depends on the mass of the final state pseudoscalar meson.

$ V\to e^+ e^- P $	$\Lambda /\text{GeV}$	Ref.
$ J/\psi\to e^+e^- \eta $	$ 2.56\pm 0.04\pm 0.03 $	[10]
$ J/\psi\to e^+e^- \eta' $	$ 3.1 \pm 1.0 $	[9]
$ J/\psi\to e^+e^- \eta(1405) $	$ 1.96\pm 0.24\pm 0.06 $	[13]
$ J/\psi\to e^+e^- X(1835) $	$ 1.75\pm 0.29\pm 0.05 $	[14]
$ J/\psi\to \gamma^* \eta_{(2)}(718) $	$ 2.44\pm 0.04 $	[19]
$ J/\psi\to \gamma^* \eta_{(1)}(783) $	$ {2.44\pm 0.06} $	this work

Table 4.  Values of the pole parameter Λ of the TFF for different Dalitz decays $ J/\psi\to P e^+ e^- $. The $ N_f=1,2 $ lattice QCD results of Λ are also shown in the bottom two rows for comparison.

In principle, the production of each light pseudoscalar P in the $ J/\psi $ radiative decay or Dalitz decay undergoes the same procedure that the $ c\bar{c} $ pair emits a photon of the virtuality $ q^2 $ and then annihilates into gluons, whose invariant mass squared is labelled as s. As the single-pole model describes $ M(q^2) $ very well while the $ q^2 $ and s in the $ J/\psi-\gamma^*(q^2)-(gg\cdots)^*(s) $ vertex are correlated, one expects the s-dependence of Λ. We assume an empirical linear function for $ \Lambda(s) $, namely,

and then use the experimental values of Λ at different $ s=m_P^2 $ in Table 4 to determine the parameters $ \Lambda_1 $ and $ \Lambda_2 $. Finally, we get

with $\chi^2/ {d.o.f}=0.26$. The fit result is illustrated in Fig. 5 by a shaded blue band. It can be seen that the lattice QCD data at $ N_f=1,2 $ reside almost entirely on the fitting curve. Actually, the function in Eq. (23) with fitted parameters $ \Lambda_{1,2} $ gives the interpolated values $ \Lambda(s= m_{\eta_{(1)}}^2)=2.465(40) $ and $ \Lambda(s=m_{\eta_{(2)}}^2)=2.495(42) $, which are in good agreement with the lattice QCD results $ 2.44(4) $ GeV and $ 2.44(6)\; \mathrm{GeV} $ .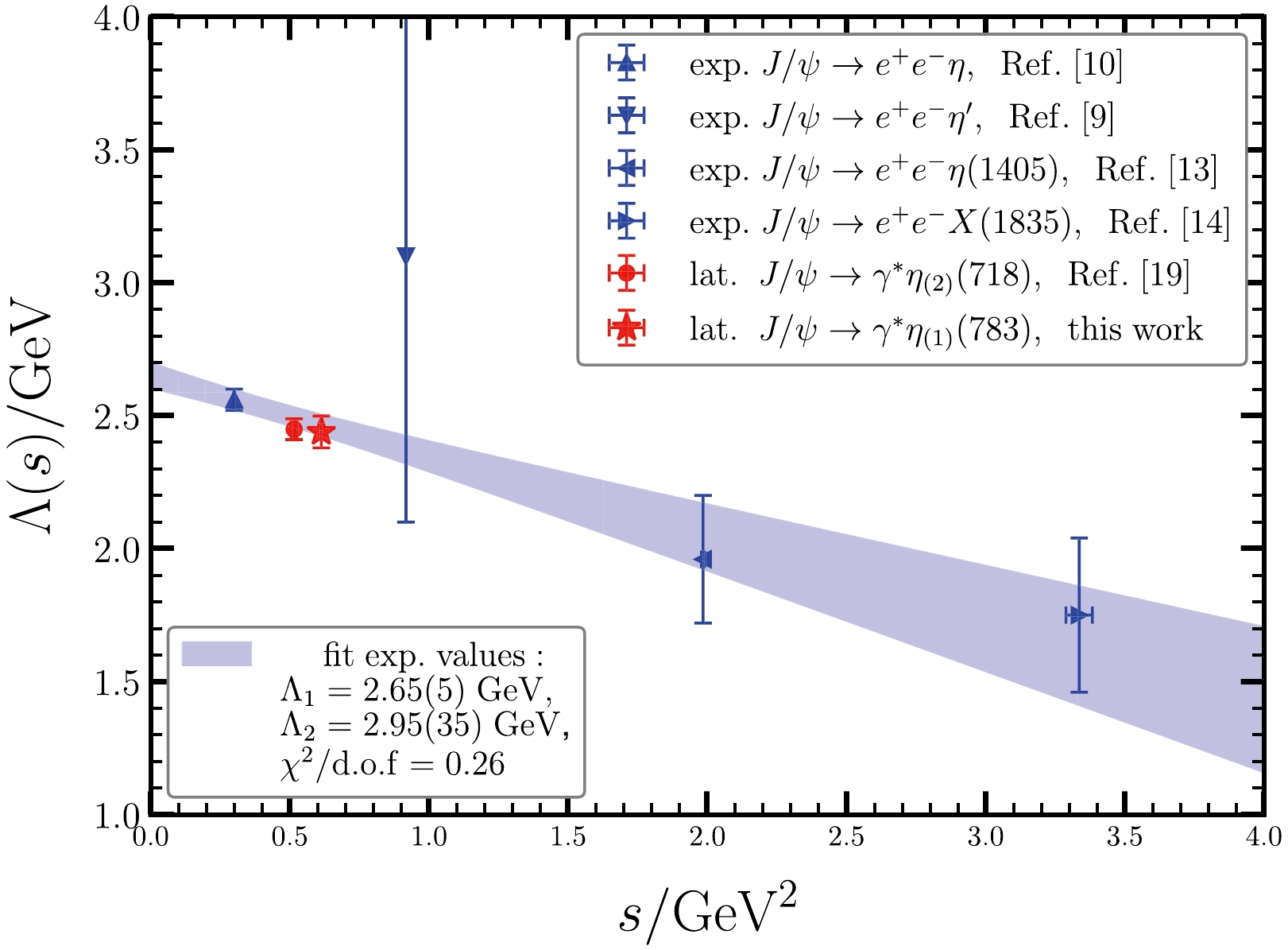

Figure 5.  (color online) The s dependence of the pole parameter Λ. The data points indicate the experimental (blue points) and lattice result (red points) of Λ at different values of $ s=m_P^2 $ (listed in Table 4), where $ m_P $ is the mass of the psuedoscalar meson in the process $ J/\psi\to P\gamma^* $. The shaded blue band shows the fitting of the experimental data using the model $ \Lambda(s) = \Lambda_1(1 - \frac{s}{\Lambda_2^2}) $ with fitted parameters $ \Lambda_1 = {2.65(5)}\; \mathrm{GeV} $ and $ \Lambda_2 = {2.90(35)}\; \mathrm{GeV} $. The $\chi^2 / {d.o.f}$ of the fit is 0.26.

The values of $ \Lambda_{1,2} $ in Eq. (24) can give inputs for theoretical and experimental studies. Taking the process $ J/\psi\to \eta' e^+e^- $ for instance, the experimental value of Λ has huge uncertainties, but the model in Eq. (23) with the parameters in Eq. (24) gives a more precise prediction

Then, according to Eq. (21) and using the experimental result of $ \mathrm{Br}(J/\psi\to\gamma \eta')=5.25(7)\times 10^{-3} $, the branching fraction of $ J/\psi\to \eta' e^+e^- $ is estimated to be $ {6.04(4)(8)}\times 10^{-5} $, which is compatible with the BESIII result $ 6.59(7)(17)\times 10^{-5} $ [12]. When the $ \rho $ resonance contribution is included, as it was by BESIII for $ J/\psi\to \eta e^+e^- $ in Ref. [10], $ |F_{\psi\eta'}(q^2)|^2 $ reads

where $ A_\rho $ is the coupling constant of the $ \rho $ meson, and $ A_\Lambda $ is the coupling constant of the non-resonant contribution. For $ J/\psi\to\eta e^+e^- $, BESIII determines $ A_\rho=0.23(4) $ and $ A_\Lambda=1.05(3) $ [10], which give $|F_{\psi\eta}(q^2\approx 0)|^2=1.11\pm 0.07\pm 0.07$. If we take the same value for $ A_\rho=0.23(4) $ and assume $ A_\Lambda=1 $ for the case of $ \eta' $ (the $ |F_{\psi\eta'}(q^2)|^2 $ at $ q^2\approx 0 $ in Ref. [9] is consistent with one within errors), then using the PDG values of $ m_\rho $ and $ \Gamma_\rho $ [47], we get

where the first error is due to the uncertainty of $ A_\rho $, the second is from that of Λ, and the third is from that of the experimental value of $ \mathrm{Br}(J/\psi\to\gamma\eta') $. This value agrees with the experimental value better.

We generate a large gauge ensemble with $ N_f=1 $ dynamical strange quarks on an anisotropic lattice with the anisotropy $ a_s/a_t\approx 5.0 $. The pseudoscalar mass is measured to be $ m_{\eta_s}=693.1(3)\; \mathrm{MeV} $ without considering the quark annihilation effect, and $ m_{\eta_{(1)}}=783.0(5.5)\; \mathrm{MeV} $ with the inclusion of quark annihilation diagrams. We calculate the EM form factor $ M(q^2) $ for the decay process $ J/\psi\to \gamma^*(q^2) \eta_{(1)} $ with $ q^2 $ being the virtuality of the photon. By interpolating $ M(q^2) $ to the value at $ q^2=0 $ through the VMD-inspired single-pole model in Eq. (14), the decay width and branching fraction of $ J/\psi\to \gamma \eta_{(1)} $ are predicted to be $ \Gamma(J/\psi\to \gamma\eta_{(1)})={0.087(13)}\; \mathrm{keV} $ and $ \mathrm{Br}(J/\psi\to \gamma\eta_{(1)})= {0.93(14)} \times 10^{-3} $, respectively, which are much smaller than those from previous $ N_f=2 $ lattice QCD results [19] and the experimental results for $ J/\psi\to\gamma\eta' $. This large difference can be attributed in part to the $ N_f $ dependence owing to the $ \mathbf{U}_A(1) $ anomaly and quark mass dependence.

It is interesting to see that $ M(q^2) $ in both $ N_f=1,2 $ is well described by the single-pole model $ M(q^2)=M(0)/ (1-q^2/\Lambda^2) $. By assuming an empirical $ s=m_P^2 $ dependence $ \Lambda(m_P^2)=\Lambda_1(1-m_P^2/\Lambda_2^2) $, the parameters $ \Lambda_{1,2} $ are determined to be $ \Lambda_1={2.65(5)}\; \mathrm{GeV} $ and $ \Lambda_2={2.90(35)}\; \mathrm{GeV} $ by using the experimental results of the Dalitz decays $ J/\psi\to Pe^+e^- $ with P being light pseudoscalar mesons. This parameterization of $ \Lambda(m_P^2) $ gives a consistent result with lattice QCD data at the same $ m_P $ and may provide meaningful inputs for future theoretical and experimental studies on Dalitz decays $ J/\psi\to Pe^+e^- $. As a direct application, this $ m_P $ dependence expects a pole parameter $ \Lambda(s=m_{\eta'}^2)={{2.37(5)}}\; \mathrm{GeV} $, which is more precise than the value $ 3.1(1.0)\; \mathrm{GeV} $ measured by BESIII [9] and provides a more precise prediction for $ \mathrm{Br}(J/\psi\to \eta'e^+e^-) $.