Analytical formula for the cross section of hadron production from e⁺e⁻ collisions around the narrow charmouinum resonances

The parameters (e.g., mass M, total width Γ, leptonic widths $ \Gamma_{ee} $, and $ \Gamma_{ \mu^{+} \mu^{-}} $) of narrow resonances like $ J/\psi $ and $ \psi(2S) $ have been extensively discussed in theoretically and experimentally. These resonances are often referred to as the "hydrogen atom" in QCD. Theoretical predictions of these parameters can be made using different potential models or lattice QCD, as well as be measured from experiments with $ e^{+} e^{-} $ colliders, such as BABAR, CLEO, KEDR, and BESIII. With the availability of large datasets from experiments, the determination of these parameters has entered a precison era.

Moreover, the branching fraction ($ {\cal{B}} $) or partial decay width ($ \Gamma_{f} $) of a specific hadron final state plays a critical role in understanding the mechanism of quarkonium decays and contributes to uncovering the patterns and properties of the quarkonium decays. In experimental measurements, the interference between the strong and electromagnetic amplitudes of $1^{--}$ resonance decays has to be considered [1]. However, the interference is usually not considered, and full positive or negative interference has been subtracted in many of the past experiements. In fact, the interference pattern or relative phase (Φ) between strong ($ A_{g} $) and electromagnetic ($ A_{\gamma} $) amplitudes could be indirectly measured by comparing decay branching ratios based on SU(3) symmetry [2]. The Feynman diagrams for $ A_{g} $ and $ A_{\gamma} $ from quarkonium decays are depicted in Fig. 1 (a) and (b), respectively. It has been conjectured that Φ is a universal quantity, holding a constant value for quarkounium decays [3], such as ϕ, $ J/\psi $, $ \psi(2S) $, and Υ. On the contrary, the practical extraction of Φ from decays of ϕ, $ J/\psi $, and $ \psi(2S) $ do not always yield consistent results [4−9]. The relative phase has drawn interest from both theoretical and experimental perspectives, as it plays a crucial role in almost every branching ratio measurement and in exotic searches [10−13]. A direct measurement could be achieved by scanning experiment, which introduces another electromagnetic amplitude from the continuum, denoted as $ A_{\rm{cont}} $, as illustrated in Fig. 1 (c) [14, 15].

Figure 1.  (color online) (a) $e^+e^-\to \psi(nS) \to$ hadrons via strong mechanism; (b) $e^+e^-\to\psi(nS) \to$ hadrons via EM mechanism; (c) non-resonant $e^+e^-\to$ hadrons via a virtual photon.

Experimentally, the Born cross section for a certain hadronic decay can be expressed as the sum of three diagrams, as depicted in Fig. 1:

Here, the relative phase between $ A_{\gamma} $ and $ A_{\rm{cont.}} $ is zero according to QED [16], as confirmed by numerous experiments [17−19]. All decay parameters (M, $\Gamma_{\rm tot}$, $ \Gamma_{ee} $, $ \Gamma_{ \mu^{+} \mu^{-}} $, $ {\cal{B}} $, and Φ) can be determined from the production cross section lineshape of $ \psi(nS) $ decays to hadronic final states. In the current experiemtal study, the regression procedure of parameters from the cross section lineshape must be accompanied with a fomula that considers the Born cross section ($ \sigma^{0} $) convolving the initial state radiation (ISR, $ F(x,S) $) and beam energy spread ($ GS(W-W^{\prime\prime}) $). The observed production cross section could be expressed as

where $ \sqrt{s} $ is the energy of the center of mass system (CMS) of $ e^{+} e^{-} $, and $ \Pi_{0}(s) $ represents the vacuum polarization operator [17, 18]. The function $ F(x,s) $ represents the ISR function, which was first proposed in Refs. [20, 21]:

where $t = \dfrac{2\alpha}{\pi} \left(\ln \dfrac{s}{m^{2}_{e}}-1\right)$, $1+\delta = 1+\dfrac{\alpha}{\pi}\left(\dfrac{\pi^2}{3}-\dfrac{1}{2}\right)+\dfrac{3}{4}t+ t^2 \left(\dfrac{9}{32}-\dfrac{\pi^2}{12}\right)$, $x = 1-\dfrac{s^{\prime}}{s}$, and $ \sqrt{s^\prime} $ is the experimentally invariant mass of the final state f after losing energy due to radiation. The upper limit $ x_{f} $ for x corresponds to the case when $ \sqrt{s^{\prime}} $ reaches its minimum $\sqrt{s^{\min}_{f}}$ and the radiation energy reaches its largest value. For example, $\sqrt{s^{\min}_{f}}$ could be the mass threshold of a given final state or the experimental cutoff. The beam energy spread caused by the $ e^{+} e^{-} $ colliders is typically modeled as a Gaussian distribution $ GS(\sqrt{s}-\sqrt{s^{\prime}}) $, expressed as

where ∆ represents the standard deviation of the Gaussian distribution. This reflects the total energy spread of the collider and detector and must be determined by experiment. For instance, in the BESIII experiment [22], ∆ is approximately $ 0.9 $ MeV for the $ J/\psi $ resonance region and approximately 1.3 MeV for the $ \psi(2S) $ resonance region. In a narrow energy interval, it could be treated as a constant.

It is evident that the cross-section calculations involve the two fold integration (DTFI) of Eq. (2). This can significantly slow down the regression process of experimental analysis. In this paper, we introduce an analytical approximation formula (AAF) of the integrations of initial state radiation over the Born production cross section around a narrorw resonance in the τ-charm energy region. It should be noted that there were some papers published more than 20 years ago that presented a similar analytical formula [23−25]. However, the previous papers focused on the leptonic and inclusive decays, without considering the interference between the strong and EM amplitudes in a specific hadronic decay. Therefore, we present the full formula in this paper for the convenience of researchers who are conducting or will conduct analysis of a single narrow resonance (such as $ J/\psi $ or $ \psi(2S) $) scanning at BESIII or other $ e^{+} e^{-} $ collision experiments, especially for the measurement of the phase between strong and EM mechanisms.

The comparison results demonstrate a satisfactory level of consistency between our AAF and DTFI, meeting the current experimental precision requirements. However, it is worth noting that the computing speed has been significantly enhanced with the AAF implementation. Throughout this paper, we use ψ to represent $ J/\psi $ and $ \psi(2S) $ narrow resonances for brevity.

We begin with the calculation of the deduction for the AAF of the cross section in Section II. Comparison between the AAF and DTFI and between the AAF and Monte Carlo generator are presented in Section III. Finally, a summary is given in Section IV.

The Born cross section for the $ \mu^{+} \mu^{-} $ final state near a resonance is

In the formula, $ \Gamma^{0}_{ee} $ and $ \Gamma^{0}_{\mu\mu} $ are the "bare" electronic and muonic widths, respectively. Considering the VP effect, the dressed cross section is usually used, which is part of the core of integrand of Eq. (2):

Here, $ \Pi_{0}(s) $ takes a similar meaning to that of $ \Pi_0(s) $ in Refs. [17, 18], which contains the contribution from lepton pairs ($ \Pi_{ee}+\Pi_{\mu\mu}+\Pi_{\tau\tau} $), hadronic decays from continuum ($\Pi_{\rm had.}$), and other resonances ($ \Pi_{R} $) except ψ resonance. The contribution from ψ resonance production is included by the BW in Eq. (5). With definations of $ \Gamma_{ee} = \Gamma^{0}_{ee}/|1-\Pi_{0}|^2 $ and $ \Gamma_{\mu\mu} = \Gamma^{0}_{\mu\mu}/|1-\Pi_{0}|^2 $, the dressed cross section is transformed as follows:

$ \Gamma_{ee} $ and $ \Gamma_{\mu\mu} $ are the so called experimental parital widths recommended for use by the Particle Data Group [26]. In some literatures, $ \Gamma_{ee} $ and $ \Gamma_{\mu\mu} $ are refered to as $\Gamma^{\rm exp}_{ee}$ and $\Gamma^{\rm exp}_{\mu\mu}$, respectively.

Similarly, for a specific hadronic final state f, the dressed cross section of the hadronic production in $ e^{+} e^{-} $ collision near a resonance is

where the parameter $ {\cal{C}} $ represents the ratio between $ |A_{g}| $ and $ |A_{\gamma}| $. The dressed continuum amplitude $ A_{\rm{cont.}} $ contributes as follows:

In the above formulas, $\, \beta^{2l+1} $ represents the phase space factor, and β is the velocity of the final state particles. For two-body decays, l denotes the orbital angular momentum number between the final state particles. For example, $ l = 1 $ for $ K^{+} K^{-} $, and $ l = 0 $ for $ p \bar{p} $. The term $ {\cal{F}}^{2}/s^{n} $ represents the form factor for $ e^{+} e^{-} $ annihilating to the hadronic final state f. From a fit on the experimental data [27−33], the value of n is set as 1 for meson pair and 2 for bayron pair. Usually, two form factors, $ G_E $ for electric and $ G_M $ for magnetic, are needed to describe the cross section of baryon pair production. The ratio between them reaches unity in our region of interest, the charmonium resonance region, which is far away from the threshold of baryon pairs [30−33]. Thus, only one form factor is sufficient in this case.

Comparing the partial width of $ \psi\to \mu^{+} \mu^{-} $, the experimental partial decay width of $ \psi\to f $ should be the value on the resonance peak ($ \sqrt{s} = M $):

The branching ratio for $ \psi\to f $ can be extracted as follows:

Considering the lepton universality in QED, $ \Gamma_{ee} $ is used to substitute the term for $ \sqrt{\Gamma_{ee}\Gamma_{\mu\mu}} $. Defining $A = \dfrac{4\pi\alpha^{2}}{3}$, $ B = \dfrac{3\Gamma_{ee}}{\alpha M} $, Eq. (8) for hadronic production in the absolute sign is expanded as follows:

Considering ISR, the CMS energy squared s is changed to $ s(1-x) $, and the first integrand of Eq. (2) results in the cross section after radiation:

where

The function $ F(x,s) $ has a singularity at $ x = 0 $ due to the term $ x^{t-1} $, with $ t \approx 0.07 $ at the charmonium energy region. Therefore, the integral is dominated by the value of the integrand with x close to 0. In the integrand, besides the BW formula, factors such as $ 1/|1-\Pi_{0}| $, phase space, and form factor are all slowly varying functions of s. Thus, these factors can be approximated by their values at $ x = 0 $. The $ 1/|1-\Pi_{0}| $ factor is calculated with a program developed in Ref. [34] and without considering the contribution of ψ resonance, as explained in Eq. (6) and shown in Fig. 2. This increases the cross section by approximately 3%−4% at the charmonium region, which was clarified in Ref. [35]. The terms $ C_{1} $ and $ C_{2} $ are defined as follows:

Figure 2.  (color online) Distribution of $1/|1-\Pi_{0}|^{2}$ variation with $\sqrt{s}$ below $4.2$ GeV.

In Eq. (14), the first part is contribution from continuum cross section. The terms with $ AB^{2} $ in $ C_{1} $ in Eq. (15) and $ C_{2} $ in Eq. (16) represent the resonace part, while the term with $ 2AB $ represents the interference contribution. For our purpose, $ F(x,s) $ could be rewritten as Eq. (17) based on the approximations of $ x^{t} = 1+t \ln x $ and $ \ln(1-x) = -x-x^2/2 $ [23]. With Eq. (17), we can derive an analytical expression for the resonances and an interference with continuum contribution.

To proceed, some equlities must be introduced with contour integration from Ref. [36]:

With these equlities, one can obtain

Note that this approximation only works for $ \nu<2 $, so $ \dfrac{\infty^{\nu-2}}{\nu-2}\sim 0 $. Based on Eq. (20), one can obtain

where

Based on the equalities above and ignoring the small contribution from higher orders, each term in the resonance and interference part in Eq. (14) integrated with terms in Eq. (17) can be calculated, and the cross section considering only the ISR function is written as follow:

where each term is described below and can be calculated with the help of Eq. (21). In the following, $ R_{2} = -2a\cos\theta $ and $ R_{3} = a^{2}(4\cos^{2}\theta-1) $.

The approximations in $ \sigma^{\rm{int4}} $ and $ \sigma^{\rm{int5}} $ have potential because they only contribute no more than 1.5% in the charmonium region. The integration in $ \sigma^{\rm{int4}} $ and $ \sigma^{\rm{int5}} $ could be done with simple calculus:

By considering the ISR effect, the QED part $ \sigma^{\rm{cont,ISR}} $ is described as:

For the contribution from the continuum prosess, the beam energy spread $ GS(\sqrt{s}-\sqrt{s^{\prime}}) $ has little effect on $ \sigma^{\rm{cont}} $ as it is almost flat in our region of interest. Finally, the total observed cross section could be summarized as follows:

So far, we have derived the full AAF for the cross section of hadron production from $ e^{+} e^{-} $ collisions around the charmouinum resonances. In this way, the two folds of integration are reduced to one fold. To verify the accuracy of the AAF, we compare the cross sections calculated by the AAF with those by the DTFI. Meanwhile, the comparison between the cross sections from AAF and Monte Carlo simulation is shown in Section III.

Traditionally, cross sections are calculated using the DTFI, but it has been found that the DTFI takes a long time to calculate. For example, Table 1 shows the time consumed if the cross section values for ten energy points are calculated, and it is approximately 36 s. In experimental analysis, physical parameters are extracted by a $ \chi^{2} $ fit or likelihood fit, which means hundreds of thousands of iterations may be required. If the initial parameters are not proper for a converged result, the regression process should be repeated. Thus, the computing speed must be improved to meet practical requirements.

$N_{\rm points}$	$T_{\rm{DTFI}}$ (second)	$T_{\rm{AAF}}$ (second)
$10$	35.9	0.3
$100$	385.3	0.7
$500$	1721.4	2.0
$1000$	3988.5	3.9

Table 1.  Comparison of computing time with the DTFI and AAF. The first column is the number of energy points computed $N_{\rm points}$, the second column is the time consumption of the DTFI ($T_{\rm{DTFI}}$), and the third column is that of the AAF ($T_{\rm{AAF}}$).

The comparison of the computing time with the DTFI and AAF is shown in Table 1. The first column of Table 1 is the number of energy points computed, the second column is the computing time of the DTFI, and the third column is that of the AAF. It is obvious that the computing time with the analytical form of the cross section is greatly reduced. This makes it possible for the regression process on a production cross section lineshape to be finished in several minutes.

It is also necessary to compare the cross section calculated by the AAF and DTFI to assess the level of precision achieved. Figure 3 shows the comparison between the two forms with the parameters of the $\psi(2S)\to K^{+} K^{-}$ process as an example, with results under different asumptions of Φ: (a) $ \Phi = 0^\circ $, (b) $ \Phi = 90^\circ $, (c) $ \Phi = 180^\circ $. The red and blue dots represent for the results of the cross section calculated using the DTFI and AAF, respectively. The difference is calculated as $\delta = \dfrac{(\sigma^{\rm{DTFI}}-\sigma^{\rm{AAF}})}{(\sigma^{\rm{DTFI}}+\sigma^{\rm{AAF}})/2.0}$ and presented at the bottom of each figure. Here, $ \sigma^{\rm{DTFI}} $ represents the cross section calculated using the DTFI, while $ \sigma^{\rm{AAF}} $ denotes the cross section calculated using the AAF. From comparison, the difference between the two forms is less than 1% under different assumptions of Φ.

Figure 3.  (color online) Comparisons of cross sections calculated with the analytic form and DTFI in the cases of (a) $\Phi=0^\circ$, (b) $\Phi=90^\circ$, and (c) $\Phi=180^\circ$. The red dots represent the results of the cross section calculated with the DTFI and blue dots the results of the cross section using the AAF. The bottom plots show the ratio between two results under different Φ assumptions.

To gain a deeper understanding of the differences between DTFI and AAF, a careful comparison with $ n = 1 $ for a meson pair is implemented. The $ {\cal{C}} $ and $ {\cal{F}} $ parameters are changed under different assumptions of Φ. The largest difference between DTFI and AAF in range of $ (3.67,3.70) $ GeV is highlighted in color and shown in Fig. 4. The comparison with $ n = 2 $ for a bayron pair is shown in Fig. 5. From the comparison, we observe that the difference for $ n = 1 $ is no more than 1.5%, while it is 5% for $ n = 2 $. This is probably caused by the different position of form factor in the DTFI and AAF. In DTFI, the form factor is merged directly in the Born cross section, while in AAF, the form factor is multiplied after the ISR and Gauss resolution integrations. From Figs. 4 and 5, it is evident that the influence of $ {\cal{C}} $ is much larger than that of $ {\cal{F}} $. This may be due to the fact that the cross section changes dramatically around the resonance according to $ {\cal{C}} $, while it changes relatively slowly according to $ {\cal{F}} $.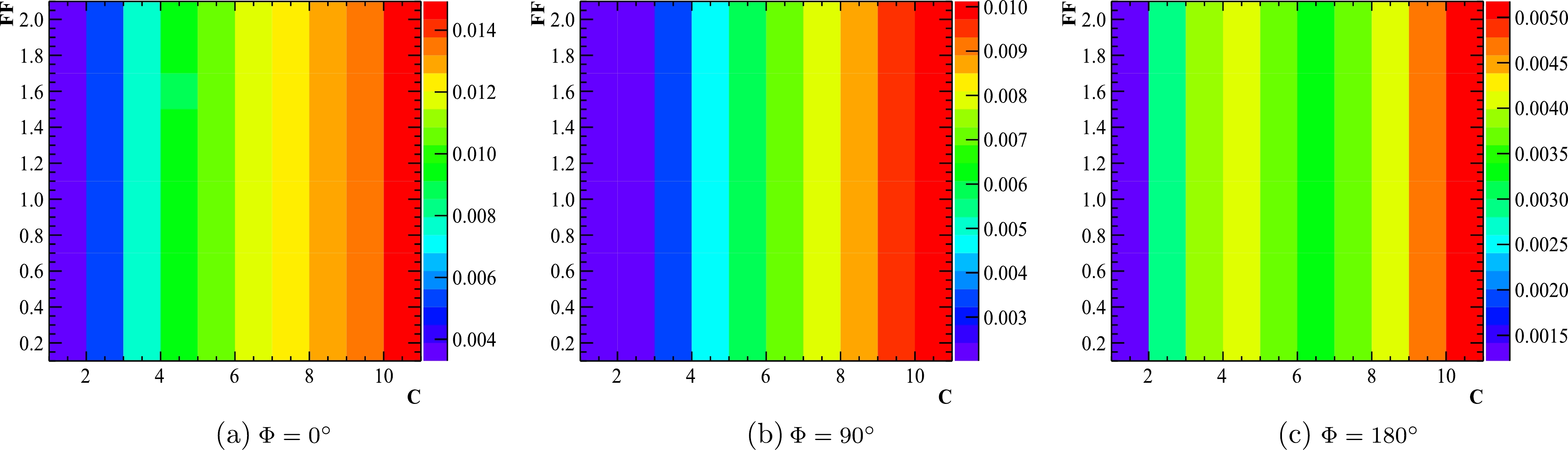

Figure 4.  (color online) Difference between DTFI and AAF with $n=1$ under different assumptions of ${\cal{C}}$, ${\cal{F}}$, and Φ. The color in each box represents the largest difference from $3.67$ to $3.70$ GeV.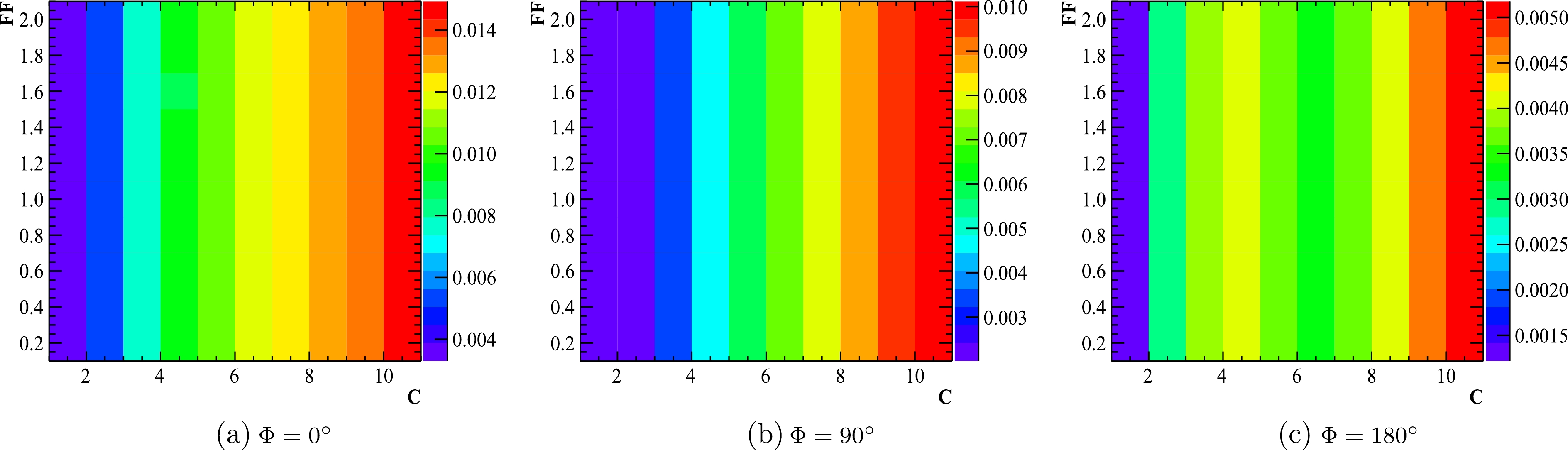

Figure 5.  (color online) Difference between DTFI and AAF with $n=2$ in different assumptions of ${\cal{C}}$, ${\cal{F}}$, and Φ. The color in each box represents the largest difference from $3.67$ to $3.70$ GeV.

There might be a concern about the influence from the difference between the DTFI and AAF for parameter determination in experiments. An input-output (IO) check is implemented with DTFI cross section values at nine energy points around $ \psi(2S) $, which decays to $ K^{+} K^{-} $ and $ p \bar{p} $ final states. The regression procedure is finished with AAF. The total uncertainty is set at 5% for all energy points, which is less than or roughly equal to the current practical experimental data around resonance. The output values for each parameters are listed in Table 2. From the IO check, no bias is observed within the uncertainty.

$K^+K^-$ Parameter	Input	Output
		$\Phi=0^{\circ}$	$\Phi=90^{\circ}$	$\Phi=180^{\circ}$
${\cal{C}}$	$3.0$	$2.96\pm0.32$	$2.94\pm0.21$	$3.01\pm0.81$
${\cal{F}}$	$0.5$	$0.509\pm0.008$	$0.509\pm0.009$	$0.507\pm0.008$
Φ	$-$	$-5.9\pm55.2$	$89.7\pm7.8$	$185.3\pm126.7$
$\chi^2/ndf$	$-$	$0.08/6$	$0.00/6$	$0.02/6$
$p\bar p$ Parameter	Input	Output
		$\Phi=0^{\circ}$	$\Phi=90^{\circ}$	$\Phi=180^{\circ}$
${\cal{C}}$	$15$	$15.12\pm0.35$	$14.97\pm0.59$	$14.89\pm0.78$
${\cal{F}}$	$2.5$	$2.49\pm0.04$	$2.51\pm0.07$	$2.51\pm0.07$
Φ	$-$	$-1.2\pm25.7$	$88.5\pm6.2$	$169.2\pm38.6$
$\chi^2/ndf$	$-$	$0.67/6$	$0.32/6$	$0.08/6$

Table 2.  Input-output check results with $K^+K^-$ and $p\bar p$ pair parameters under different assumptions of $\Phi$.

As the experimental analysis is performed with regression and simulation, it is necessary to check the consistency between them. Otherwise, the parameters from the analysis will never converge no matter how many iterations are performed. At BESIII, the ConExc generator was developed to take into account the ISR effect up to the next-leading-order [37]. It is widely used with at least seventy hadronic decay modes implemented with effective center-of-mass energy coverage from the two pion mass threshold up to approximately 6 GeV. The accuracy achieved for the ISR correction reaches the level achieved by the KKMC generator [38]. Furthermore, the ConExc is used for the R-value and light meson resonance measurements at BESIII. The cross section with ISR calculated by the ConExc Monte Carlo generator is written as

where

The mass threshold for hadronic final states is $M_{\rm th}$, and the integral is composed of two parts, which are separated by a point $ M_0 $ = $\sqrt{s-2\sqrt{s}E^{\rm cut}_{\gamma}}$ with an energy cut $E^{\rm cut}_{\gamma}$ on the ISR photon, and b is a small value, $ b\ll 1 $. In practice, $E^{\rm cut}_{\gamma}$ is set to the energy sensitivity of photon detection. Here, since the ConExc only considers the ISR effect,$ \sigma^0 $ must be the cross section after convolving the Gaussian resolution to consider both beam energy spread and ISR effects. The radiative function $ W(x,s) $ is expressed as

which has some difference with Eq. (3) or (17). β takes the same defination as t in Eq. (3) or (17). The ∆ is in a different representation from $ 1+\delta $ in Eq. (3) or (17). The order of convolutions of ISR and beam energy spread in the AAF is exactly the opposite to that in the ConExc generator. In Ref. [39], it was pointed out that the order of convolutions does not affect the results in a narrow energy range and with a small $ x_{f} $. A test is performed with different orders around $ \psi(2S) $ resonance with $ x_{f} = 0.1 $. The difference between two orders is no more than 0.05% with the same parameterizations as those used for Figs. 4 and 5.

In contrast to the AAF, the ConExc generator computes the cross section using a sampling method. Additionally, the radiative function $ W(x,s) $ in theConExc generator is slightly different from $ F(x,s) $ in the AAF. It is necessary to compare the analytic form with the ConExc Monte Carlo generator under different assumptions of Φ. Figure 6 shows the results of the cross section calculated using the ConExc generator and the AAF in the cases of $ \Phi = 0^\circ $,$ \Phi = 90^\circ $, and $ \Phi = 180^\circ $ for the $ e^{+} e^{-}\to K^{+} K^{-} $ channel. The red and blue dots represent the results of the cross section calculated by using the ConExc generator and AAF, respectively. Moverover, the ratio of two cross sections is calculated as $ R = \dfrac{\sigma^{\rm{ConExc}}}{\sigma^{\rm{AAF}}} $ and presented in Fig. 6. Here, $ \sigma^{\rm{ConExc}} $ is the cross section calculated using the ConExc Monte Carlo generator, while $ \sigma^{\rm{AAF}} $ denotes the cross section calculated using the AAF. The comparison result shows that the difference between the two cross section values is no more than 1% under different assumptions of Φ for the $ K^{+} K^{-} $ pair.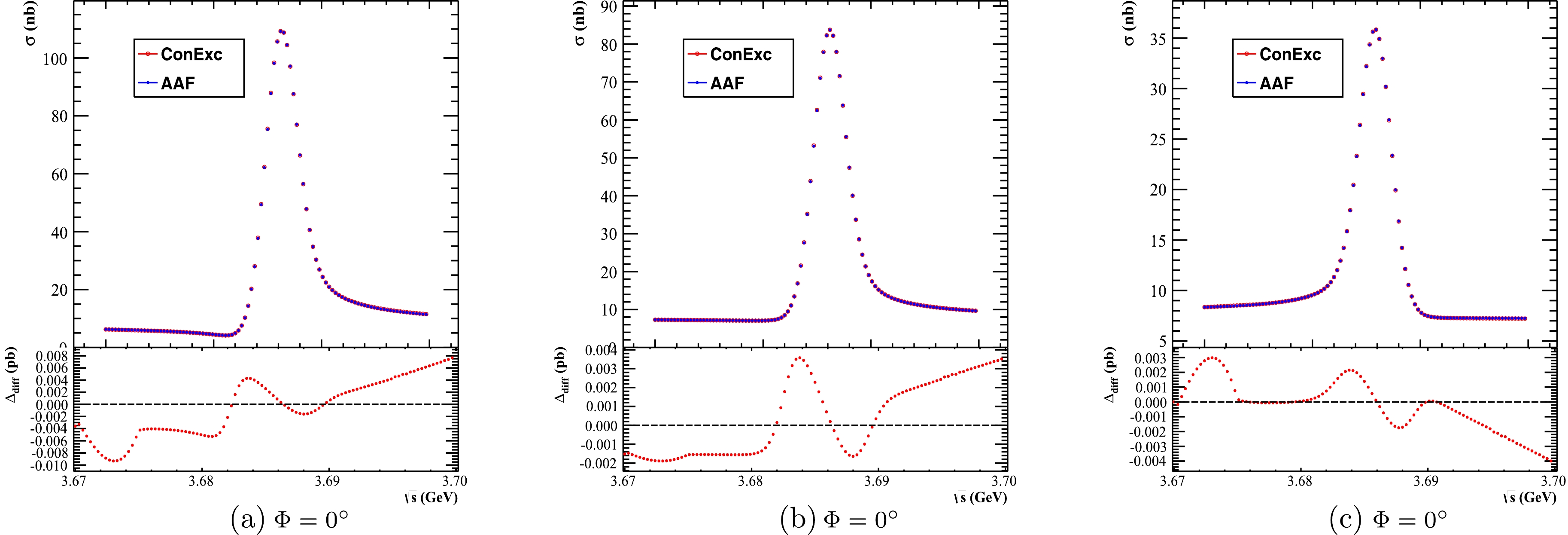

Figure 6.  (color online) Comparisons of the analytic form and ConExc generator in the cases of (a) $\Phi=0^\circ$, (b)$\Phi=90^\circ$, and (c) $\Phi=180^\circ$. The red dots represent the results of the cross section calculated with the ConExc generator, and blue dots the results of the cross section using the analytic form. The bottom plots show the ratio between two results under different Φ assumptions.

In summary, the analytical formula for the cross section of hadron production from $ e^{+} e^{-} $ collisions around the narrow charmouinum resonances in the τ-charm energy region has been presented. Comparisons between the analytical formula and direct two fold integration shows good accuracy, with the difference between the two cross section results for meson pairs being no more than 1.5%, and that for baryon pairs no more than 5%. Based on the IO check, the observed difference will not introduce any bias in parameter determination for experiments involving cross sections with a 5% uncertainty. Users are advised to conduct the IO check independently for the specific physical channel in question. Additionally, the comparison in the cross section between the analytical formula and ConExc generator also shows good consistency. Most importantly, the analytical formula can greatly shorten the computing time, which is of great significance for experiments to extract the parameters of narrow charmonium resonances and helpful for efficient determinations for each branching ratio. Finally, for those interested in the AAF, more information can be found at the link https://github.com/yakuma320/phase_measurement/blob/main/AAF.C.

The authors would like to express their gratitude to the staff of BESIII and the IHEP computing center for their strong support. We are grateful to Prof. Changzhang Yuan for his suggestion as well as Prof. Xiaohu Mo for their kind help and benificial discussions.