Photonuclear reactions on ⁵⁹Co at bremsstrahlung end-point energies of 40–130 MeV

The photon-induced reaction cross sections of ⁵⁹Co are important for designing conventional reactors, fast reactors, and accelerator-driven systems (ADSs). The high-energy photon-induced reactions of ⁵⁹Co can be used for production of important medical isotopes, such as ⁵⁵Co, ⁵⁶Co, ⁵⁷Co, and ⁵⁸Co, owing to their suitable decay characteristics. Moreover, ⁵⁹Co is often used as a monitor target during the study of photonuclear reactions to determine the photon of gamma rays or the accelerator current.

The ⁵⁹Co(γ, xn)^58-56Co reaction cross sections already covered in Refs. [1–5] are only for monoenergetic photons in the energy range from 9.65 to 36.504 MeV. The flux-averaged cross-sections for the ⁵⁹Co(γ, xn)^58-55Co reaction were measured using the method of activation at the bremsstrahlung end-point energies of 15 MeV [6], 22 MeV [7], 25 MeV [8], 30 MeV [9], 65, and 75 MeV [10]. In Ref. [11], the yields of the reactions (γ, 2n), (γ, 3n), (γ, 4n), and ⁵⁹Co(γ, 1n2p)⁵⁶Mn, relative to the yield of the reaction (γ, n), were determined using the measurements of gamma-ray activities induced when irradiating ⁵⁹Co with the 35- and 54-MeV bremsstrahlung. In Ref. [12], the ⁵⁹Co(γ, 1n2p)⁵⁶Mn reaction was investigated in the energy range of 30–260 MeV, and differential effective cross sections were calculated from yield curves using the photon difference method. In Refs. [13, 14], data for photospallation yields were presented in units of mb per equivalent photon from a ⁵⁹Co target measured at the bremsstrahlung end-point energies of 30 to 1050 MeV.

The present study aimed at obtaining new nuclear data for bremsstrahlung-induced photonuclear reactions on ⁵⁹Co in the energy range of 40–130 MeV and comparing these data with data reported in the literature [7–10] and theoretical values computed with the program package TALYS1.96 [15].

The experiment was carried out with electron beams at energies in the range of 40–130 MeV. A tungsten plate with a size of 4.5 × 4.5 cm and a thickness of 0.5 cm was used as a converter. In the experiments (E_e = 60, 80, 105, and 130 MeV), cobalt metal samples were irradiated with a bremsstrahlung flux formed in the tungsten converter. To compare the results of experiments performed under different conditions at an energy of 40 MeV, the target was directly irradiated with the electron beam. The main parameters of the experiments are given in Table 1.

The electron linac was operated in the stable mode with a beam pulse width of 2 μs and a repetition rate of 10 Hz. The electron current was measured with a high-sensitivity inductive current sensor [16]. After irradiation, the target was transferred to the test room, where the induced activity in the irradiated target was measured using a high-purity germanium detector (HPGe detector). The spectra of γ-quanta of irradiated targets in the energy range from 50 keV to 3.7 MeV were measured using a CANBERRA GC3018 HPGe detector with a volume of 145 cm³. We used the HPGe γ-detector with resolutions of 0.8 keV at 122 keV and of 1.76 keV at 1332 keV in combination with standard measurement electronics and a 8K ADC/MCA (Multiport II Multichannel Analyzer). The relative efficiency of this detector is 34.7%. For γ-activity measurements, the activated sample were placed at 56 and 130 mm from the detector surface to maintain the detector dead time at approximately 5% and reduce counting losses due to the coincidence summing effect. Compton background was missed at approximately 3 hours after irradiation, so the targets were located 10 mm from the detector surface for measuring γ-rays of long-lived isotopes in the target.

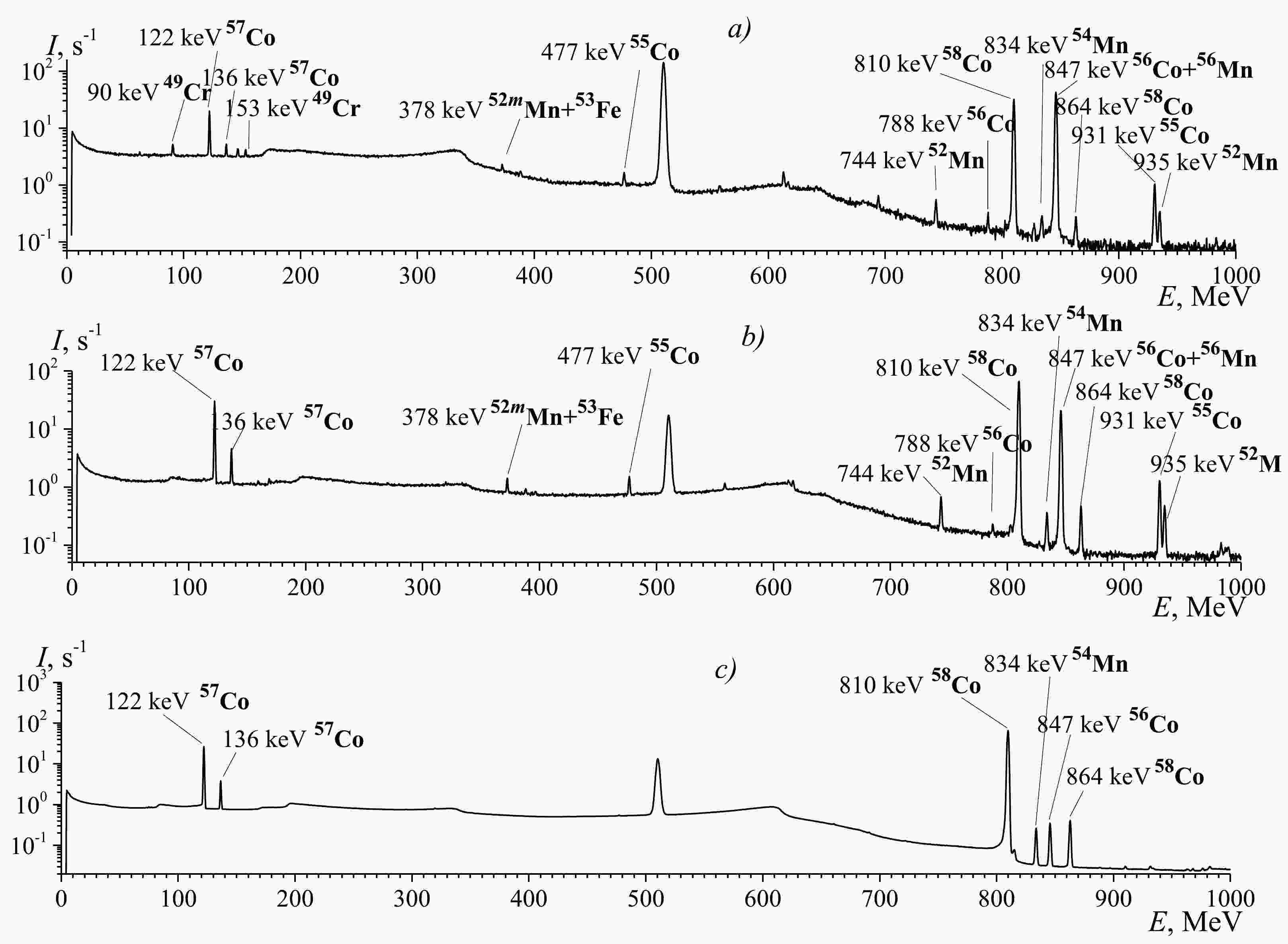
Energy and efficiency calibrations of the HPGe detector were carried out using the standard gamma-ray sources ²²Na, ⁵⁴Mn, ⁵⁷Co, ⁶⁵Zn, ⁸⁸Y, ¹¹³Sn, ¹³³Ba, ¹³⁹Ce, ¹⁵²Eu, ²⁰⁷Bi, and ²⁴¹Am. The gamma-ray spectra were processed using the program DEIMOS32 [17], which fits the count area of the full-energy peaks with a Gaussian function. The processed peaks were identified on the basis of gamma-ray energy and intensity and the half-life of generated residual nuclei. Typical γ-ray spectra of reaction products from irradiated cobalt with a bremsstrahlung end-point energy of 130 MeV are shown in Fig. 1.

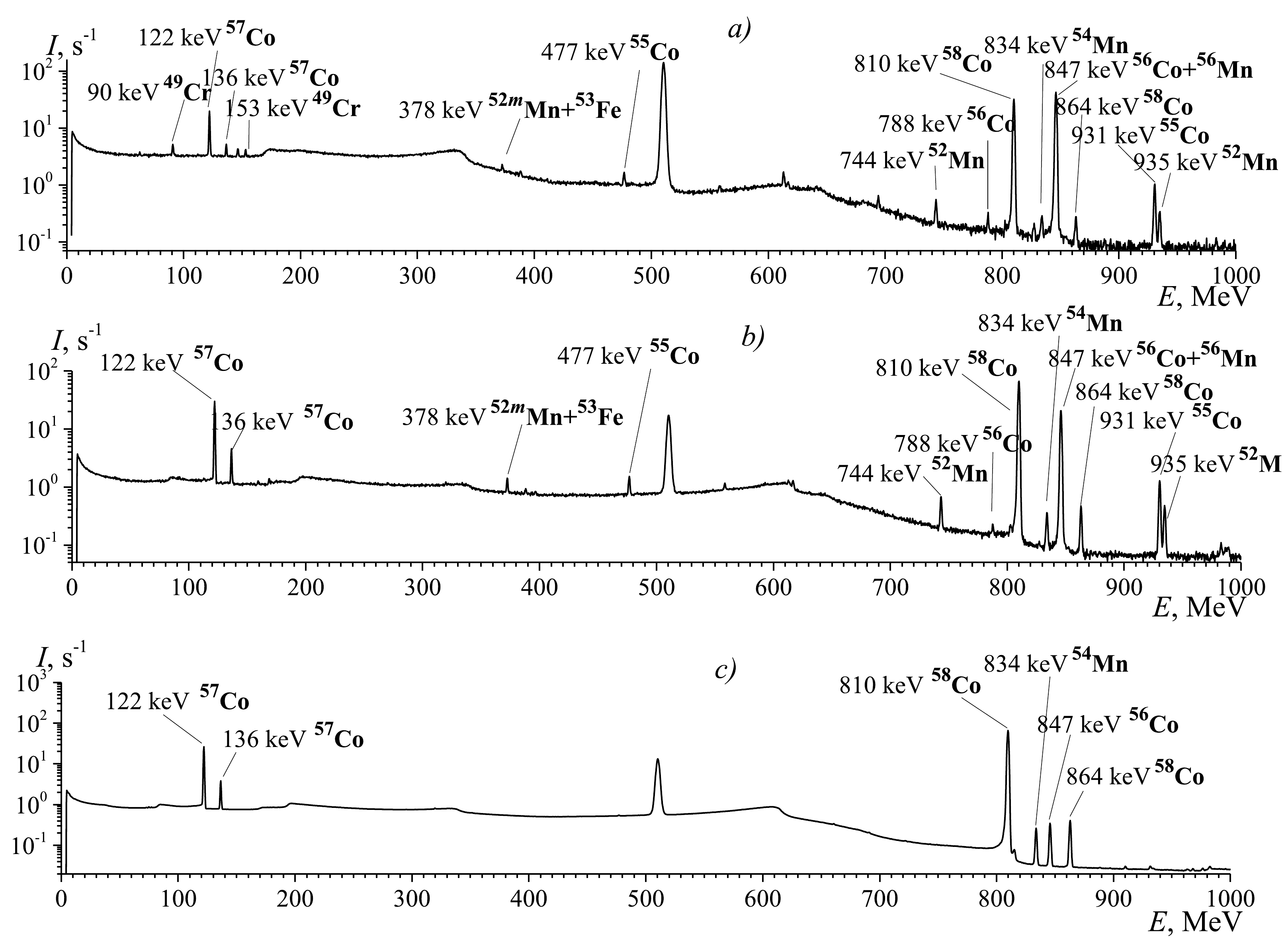
Figure 1.  Spectra of residual activity of the irradiated sample of ⁵⁹Co (top-to-bottom) at 2 h (a), 6 h (b), and 40 days (c) after irradiation. The spectra measurement duration was 10 min (a), 1 h (b), and 7 days (c), respectively. The bremsstrahlung end-point energy used for the irradiation was 130 MeV.

The experimental yields of the reactions Y_exp were normalized to one electron of the accelerated beam incident on the bremsstrahlung target and calculated using the following formula:

where $ {S}_{p} $ is the full-energy-peak area; $ \epsilon $ is the full-energy-peak detector efficiency; $ {I}_{\gamma } $ is the gamma emission probability; ${C}_{\rm abs}$ is the correction for self-absorption of gamma rays in the sample; ${t}_{\rm real}$ and ${t}_{\rm live}$ are the real and live times of the measurement, respectively; $ N $ is the number of atoms in the activation sample; $ {N}_{e} $ is the integral number of incident electrons; $ \lambda $ is the decay constant; ${t}_{\rm cool}$ is the cooling time; and ${t}_{\rm irr}$ is the irradiation time. The main γ-ray energies and intensities used to determine the yield of reaction products are listed in Table 2. The nuclear data in Table 2 were extracted from Ref. [18].

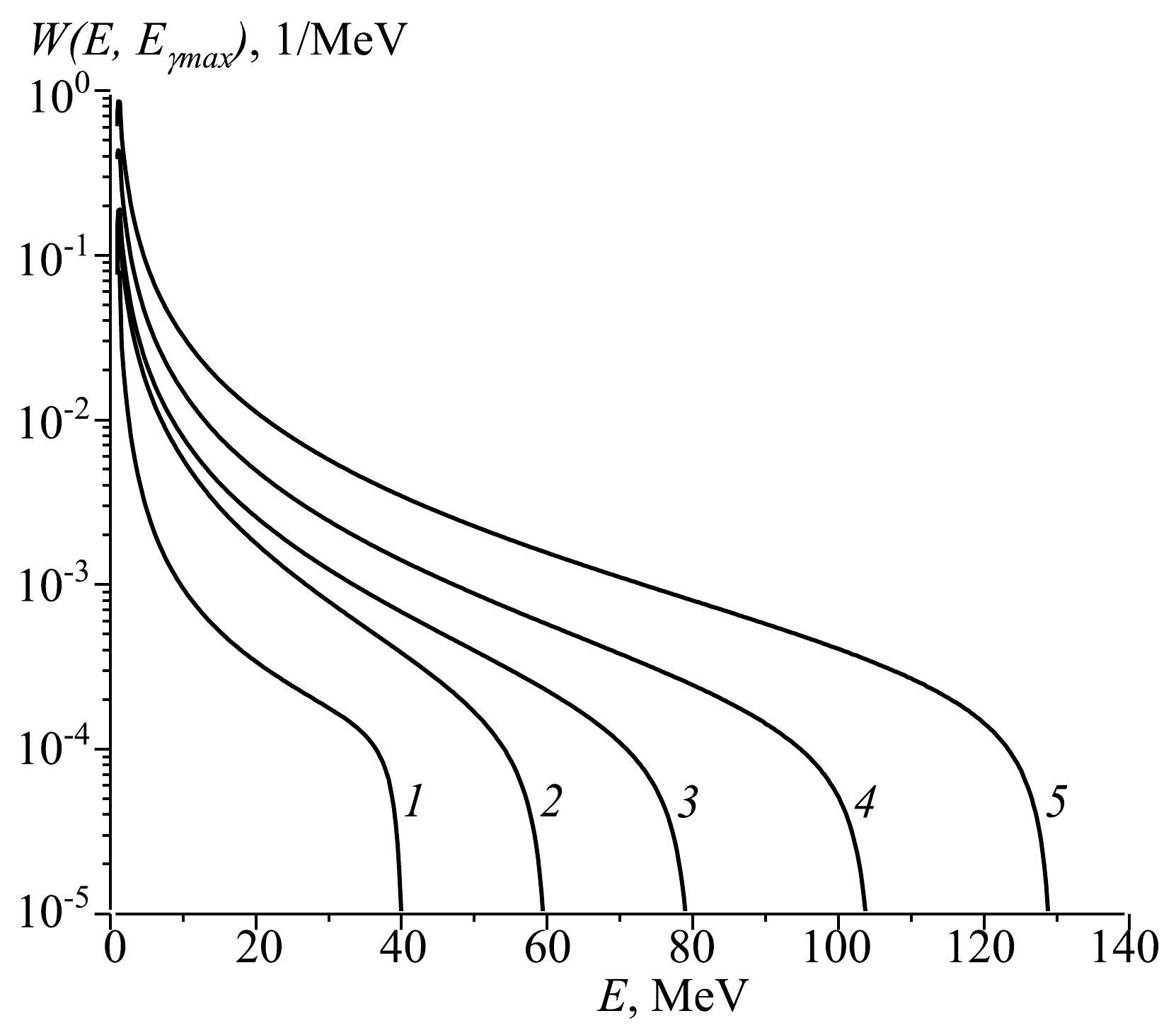
The yields Y_theor of photonuclear reactions representing the convolution of the photonuclear reaction cross section σ(E) and distribution density of the number of bremsstrahlung photons over energy per one electron of the accelerator W(E, E_γmax) were determined as a result of the experiment. For the yield measurement of a natural mixture of isotopes, the result is the yield of isotope production in all possible reactions on the natural mixture:

where E_γmax is the kinetic energy of electrons hitting the tungsten radiator, E is the energy of bremsstrahlung photons produced on the radiator, and E_th is the threshold of the studied photonuclear reaction.

The use of the relative yields makes it possible to obtain the dependence of the probability of photonuclear reactions on the maximum energy of bremsstrahlung under different experimental conditions. The calibration with respect to the yield of the most probable reaction excludes the influence of the total photon absorption cross section. In our case, the ⁵⁹Co(γ, n)^58m+gCo reaction was chosen as a dominant reaction because of its wide application in this capacity. The half-lives of the isotopes ^58mCo and ^58gCo are 9.10 hours and 70.86 days, respectively. ^58mCo decays by IT with a branching fraction of 100%. Given that ^58mCo has the single gamma line with E_γ = 24.89 keV, it is not possible to experimentally determine the yield of this isotope by the usual method from the peak in the residual activity spectrum; the detector used detects γ-quanta starting from 50 keV. We could determine only the cumulative yield of ^58m+gCo. Thus, the net photopeak counts of ^58gCo from different spectra were taken after the decay of more than ten half-lives of ^58mCo.

Theoretical values of the relative yields can be calculated using the following formula:

Owing to the assumption on the unchanged shape of the bremsstrahlung spectrum, the bremsstrahlung photon production cross section σ(E, E_γmax) must be taken as the function W (E, E_γmax):

where σ(E, E_γmax) is calculated based on the Zeltzer-Berger tables [19].

The total and partial cross sections σ(E) of the ⁵⁹Co(γ, xnyp) reaction were computed for monochromatic photons with the TALYS code. The phenomenological models used below are generally parameterized in terms of Lorentzian forms with giant resonance parameters:

• σ_Xl: strength of the giant resonance,

• E_Xl: energy of the giant resonance,

• Г_Xl: width of the giant resonance.

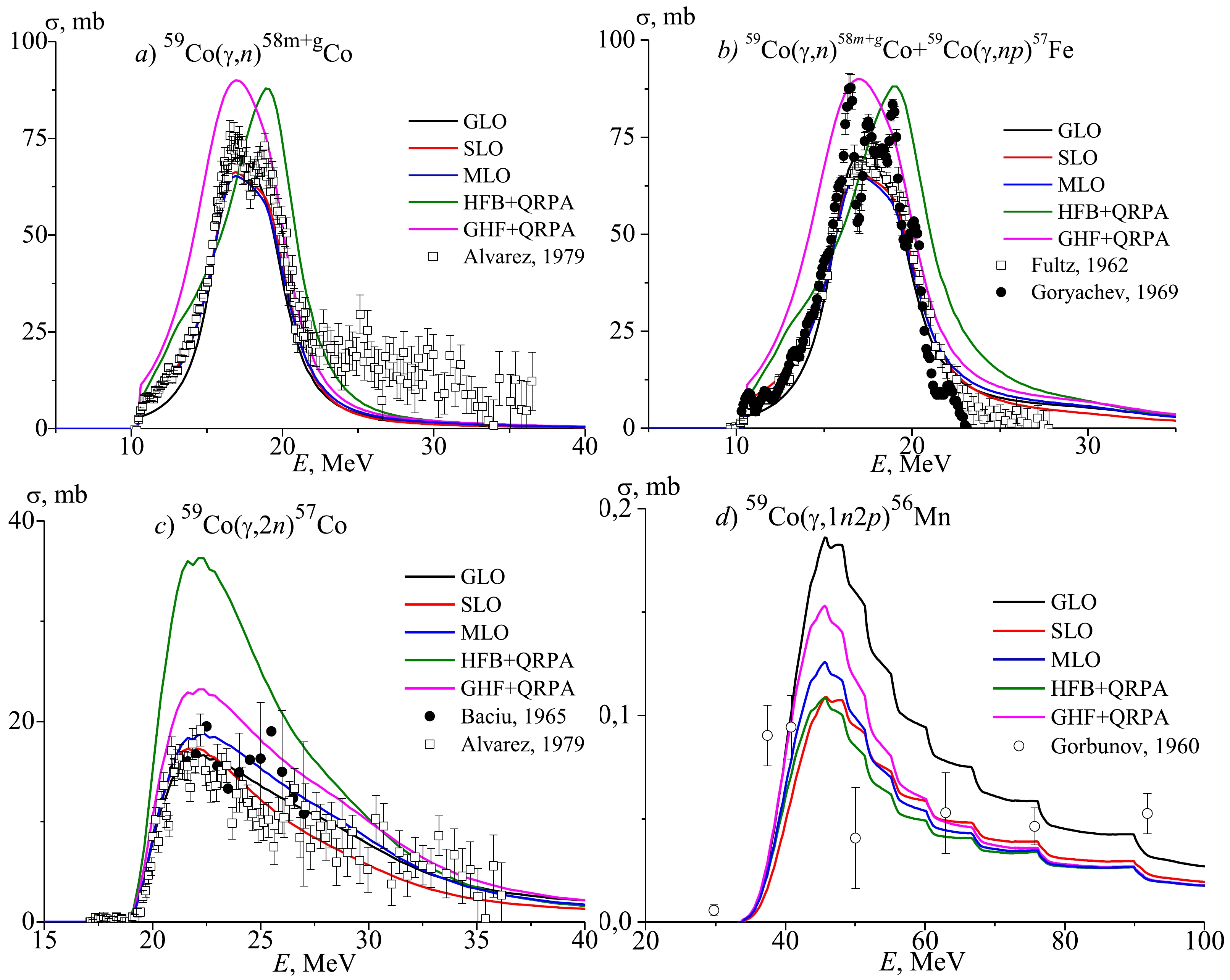
The photoreaction cross section data were compared to theoretical calculations on the basis of three standard models of the γSF, namely the Kopecky-Uhl generalized Lorentzian model (GLO) [20], Brink-Axel standard Lorentzian model (SLO) [21, 22], and simplified modified Lorentzian model (MLO) [23]. In addition to these phenomenological models (GLO, SLO, and MLO), two microscopic models, namely the Skyrme-Hartree-Fock-Bogoliubov model with QRPA, proposed by Goriely et al. (HFB+QRPA) [24], and the Gogny-Hartree-Fock-Bogoliubov model with QRPA, proposed by Goriely et al. (GHF+QRPA) [25], were used. This approach is natural, because it involves the use of a single-particle nuclear level scheme, which means that the individual properties of each nucleus are considered.Fig. 2 shows experimental data and results of TALYS models on the cross section of reactions (γ, n), (γ, 2n), (γ, n)+ (γ, np), and (γ, 1n2p) on ⁵⁹Co.

Figure 2.  (color online) Experimental data and results of TALYS models on the cross section of reactions (γ, n) [3], (γ, 2n) [3, 7], (γ, n)+ (γ, np) [4, 9], and (γ, 1n2p) [12] on ⁵⁹Co.

GLO was suggested to predict the correct behavior of the E1 γ-strength functions in the low-energy range by adopting the temperature-dependent width along with the non-zero limiting value as E_γ goes to zero. We used SLO for all multipoles higher than 1. The MLO model was developed to provide an improved estimate of the E1 and M1 PSFs for all nuclei. The HFB+QRPA model is based on the Skyrme force. In this model, some phenomenological corrections are introduced to take into account the damping of the collective motion as well as the deformation effects. The GHF+QRPA model allows for a consistent description of axially symmetric deformations; it phenomenologically includes the impact of multiparticle multihole configuration as a function of their densities.

The photon flux in the sample was simulated using Geant4 [26]. The energy spectrum of bremsstrahlung in the location of cobalt samples is shown in Fig. 3. In the experiments at 60 and 80 MeV, the shape of the electron beam was round, setting a diameter of 5.5 mm. In the experiments at 40, 105, and 130 MeV, the shape of the electron beam was a rectangle with a size of 2 mm × 20 mm.

Figure 3.  Distribution density of the number of bremsstrahlung photons at energies of 40 (1), 60 (2), 80 (3), 105 (4), and 130 MeV (5).

The relative yields Y_rel of the photonuclear reactions measured in the bremsstrahlung end-point energy range of 40–130 MeV from the conducted experiment are given in Table 3 and Figs. 4–7.

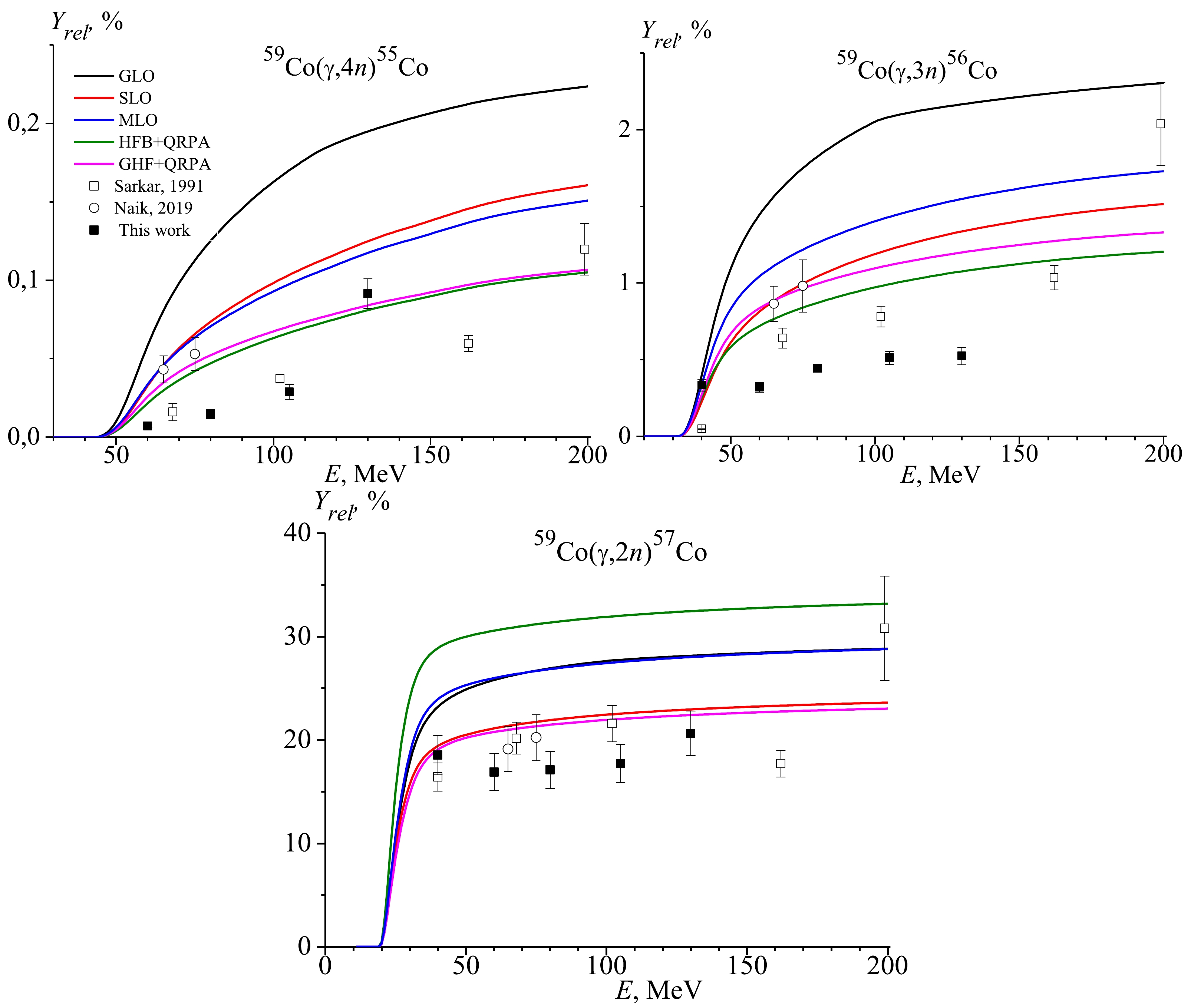
Figure 4.  (color online) Relative yields of the ⁵⁹Co(γ, xn)^57,56,55Co reactions as a function of the bremsstrahlung end-point energy from the present study (solid squares) and literature data, [4] (open triangles), [10] (open circles), and [13] (open squares), as well as theoretically calculated values using different models for the E1 gamma-ray strength function in TALYS values.

Figure 5.  (color online) Relative yields of the ⁵⁹Co(γ, xn1p)^52,53Fe reactions as a function of the bremsstrahlung end-point energy from the present work (solid squares) and literature data [4] (open triangles), [10] (open circles), and [13] (open squares), as well as the theoretically calculated values using different models for the E1 gamma-ray strength function in TALYS values.

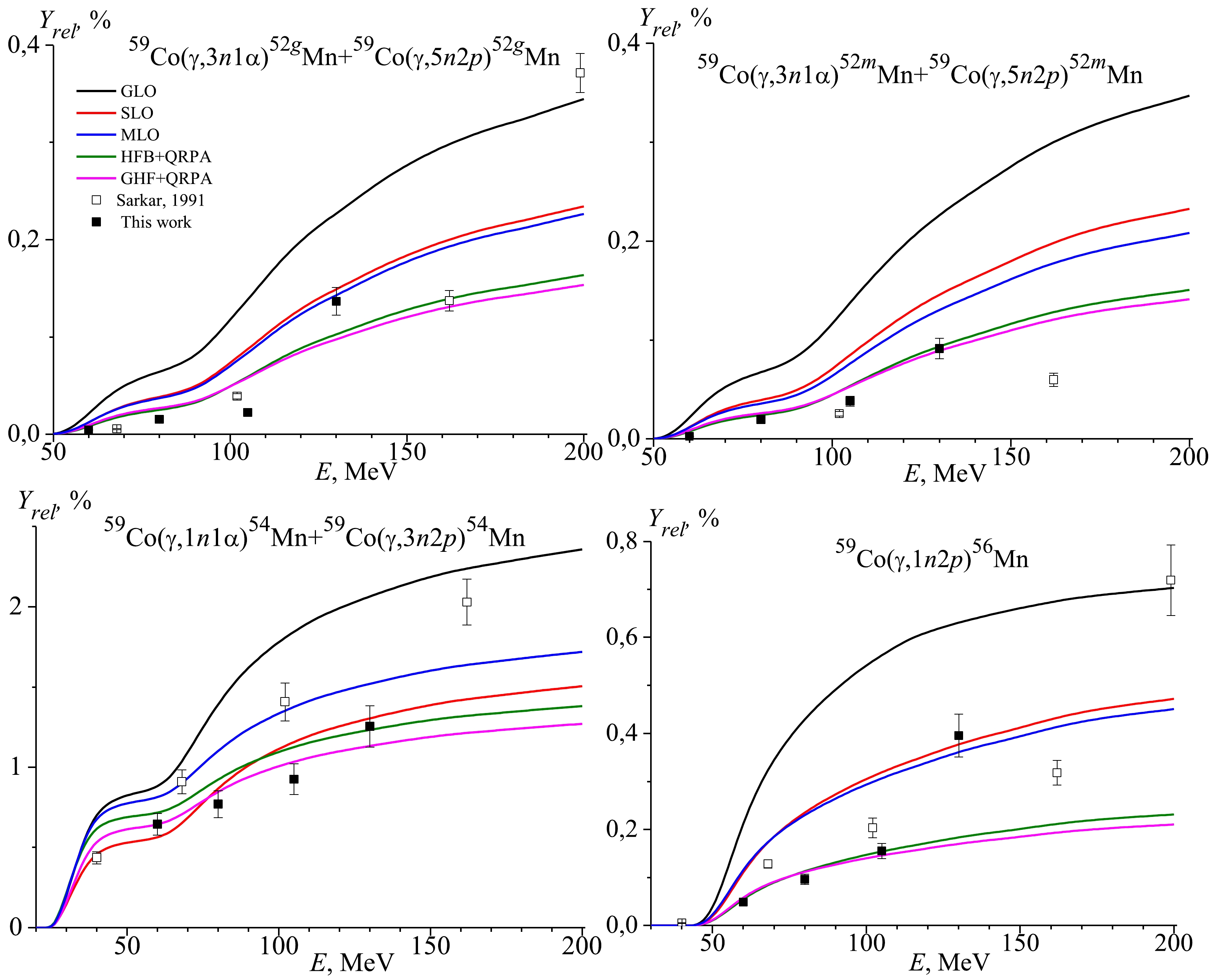
Figure 6.  (color online) Relative yields for the production of ^{52g,52m,54,56}Mn from reactions ⁵⁹Co(γ, xn1α) and ⁵⁹Co(γ, xn2p) as a function of the bremsstrahlung end-point energy from the present study (solid squares), literature data [13] (open squares), and the theoretically calculated values using different models for the E1 gamma-ray strength function in TALYS values.

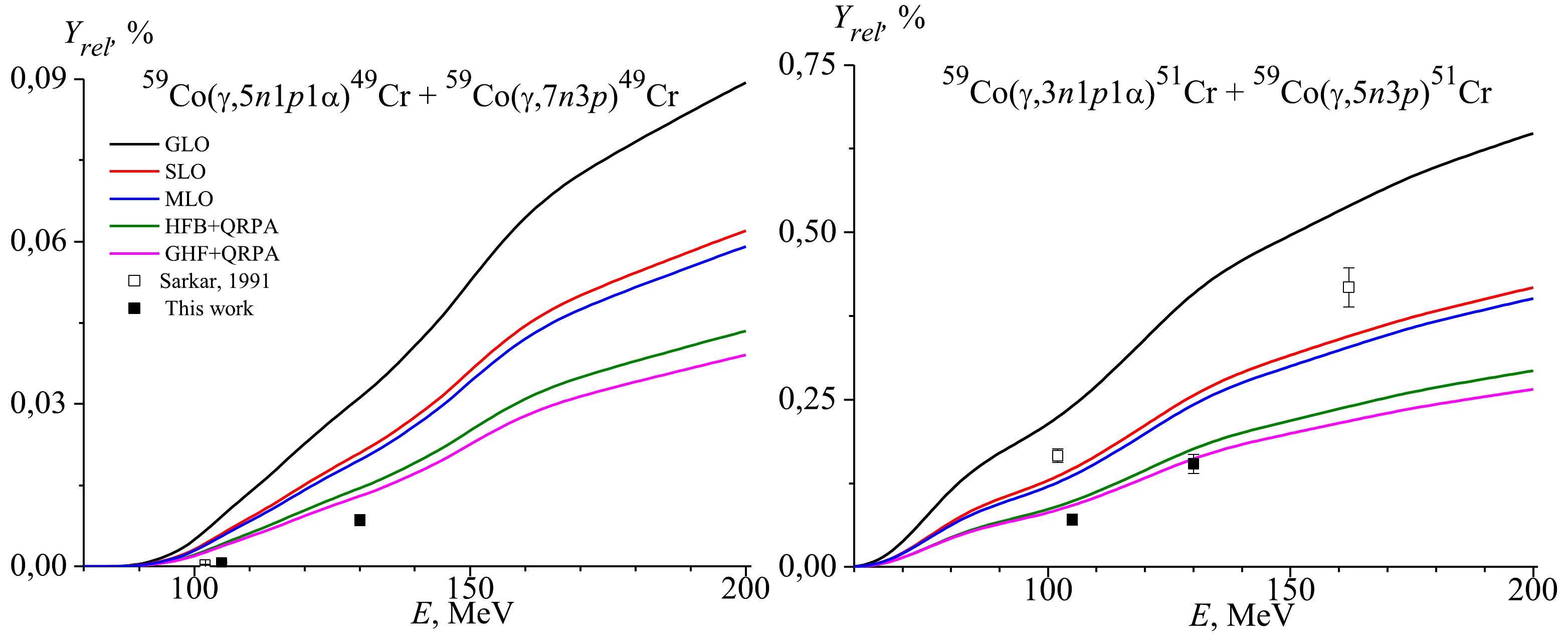
Figure 7.  (color online) Relative yields for the production of ^49,51Cr from reactions ⁵⁹Co(γ, xn1p1α) and ⁵⁹Co(γ, xn3p) as a function of the bremsstrahlung end-point energy from the present study (solid squares), literature data [13] (open squares), as well as theoretically calculated values using different models for the E1 gamma-ray strength function in TALYS values.

Figure 4 shows relative yields of the ⁵⁹Co(γ, xn)^57,56,55Co reactions. Within the limits of error, our results on relative yields of the ⁵⁹Co(γ, 2n)⁵⁷Co reaction in 40 MeV agree well with calculations based on models GLO, SLO and MLO, and with literature data [13]. The experimental points at 60, 67 [13], and 80 MeV are located at lower positions than the calculated data. Our results on the relative yield of the ⁵⁹Co(γ, 3n)⁵⁶Co reaction in 40 MeV agree well with calculations based on model SLO. The experimental points at 40 [13], 60, 67 [13], and 80 MeV are located at lower positions than the calculated data. The experimental points on the relative yield of the ⁵⁹Co(γ, 4n)⁵⁵Co reaction are also located at lower positions than the calculated data. Given that there are not sufficient experimental points in this area, we cannot draw clear conclusions on the cross sections.

It can be seen from Fig. 5 that the experimentally obtained relative yields for the ⁵⁹Co(γ, 6n1p)⁵²Fe reaction at energies of 162 and 200 MeV in previous studies [13] are not in agreement with the values simulated with TALYS, according to different models. The experimental points at 130 MeV are in agreement with the calculated values based on different models without GLO.

It can be seen from Fig. 5 that the experimentally obtained relative yields for the ⁵⁹Co(γ, 5n1p)⁵³Fe reaction at energy 102 MeV [13] is not in agreement with the values simulated with TALYS, according to different models. The experimental points at 105 MeV are in agreement with the calculated values based on model HFB+QRPA.

It can be seen from Fig. 6 that the experimentally obtained relative yields for the production of ^52gMn at the bremsstrahlung end-point energies of 60, 80, and 105 MeV are in agreement with the values simulated with TALYS, according to different models (SLO and MLO). Fig. 6 also shows that the experimentally obtained relative yields for the production of ^52mMn at the bremsstrahlung end-point energies of 60, 80, and 105 MeV are in agreement with the values simulated with TALYS, according to models SLO and MLO. Literature data [13] are located at much lower positions than the calculated curves.

Figure 6 shows that the experimentally obtained relative yields for the production of ⁵⁴Mn at the bremsstrahlung end-point energy of 40 MeV are in agreement with the values simulated with TALYS, according to model GLO. Fig. 6 also shows that the relative yields for the production of ⁵⁴Mn are an order of magnitude greater than those for the reaction ⁵⁹Co(γ, 1n2p)⁵⁶Mn.

Figure 6 shows that the experimentally obtained relative yields for the ⁵⁹Co(γ, 1n2p)⁵⁶Mn reaction at the bremsstrahlung end-point energies of 40–100 MeV that are not in agreement with the values simulated with TALYS.

Finally, according to Fig. 6, it is clear that relative yields for reactions producing ⁵⁴Mn, ^52gMn, and ^52mMn are not constantly increasing functions. This is due to the fact that in the initial energy region, the main channels for the formation of the ⁵⁴Mn, ^52gMn, and ^52mMn isotopes are reactions with the emission of an alpha-particle. Near the energies of the reaction threshold, the ⁵⁹Co(γ, xn2p)^54,52g,52mMn reaction is accompanied with the release of alpha-particles. Consequently, its cross sections decrease. A further increase in the relative yields is associated with the reactions ⁵⁹Co(γ, xn2p)^54,52g,52mMn.

It can be seen from Fig. 7 that the experimentally obtained relative yields for the production of ⁴⁹Cr at an energy of 102 MeV reported in previous studies [13] are not in agreement with the values simulated with TALYS based on different models. However, our experimental points are in agreement with the simulated values based on TALYS with models MLO and HFB+QRPA. Fig. 7 also shows that the experimentally obtained relative yields for the production of ⁵¹Cr at energies of 102 and 162 MeV reported in the literature [13] are not in agreement with simulated values based on TALYS with different models.

Furthermore, Fig. 7 shows that the relative yields for reactions producing ⁵¹Cr and ⁴⁹Cr are not constantly increasing functions. This is due to the fact that in the initial energy region, the main channels for the formation of ⁵¹Cr and ⁴⁹Cr isotopes are reactions with emission of alpha-particles. At energies close to the threshold of the reactions ⁵⁹Co(γ, 5n3p)⁵¹Cr and ⁵⁹Co(γ, 7n3p)⁴⁹Cr, the cross sections for reactions with the emission of alpha-particles decrease. Therefore, in this energy region in Fig. 7, a decrease in values was observed.

The E1 photon absorption by isotopes of the ⁵⁹Co (J ^π = 7/2^–) nucleus leads to the excitation of the giant dipole resonance. Upon the decay of the giant dipole resonance via a reaction involving the emission of an alpha particle and three neutrons, a ⁵²Mn nucleus arises in the ground or excited state. Cascades of gamma transitions from excited states lead to the production of the isomeric or ground state of ⁵²Mn. The ^52mMn isomeric state decays through electron capture or the isomer transition channel. The probability p for isomer transition to the ground state is 1.75%. Usually, the isomeric and ground states strongly differ in spins. Therefore, the isomeric ratio is represented in most cases through the yields of high- to low-spin states. In the case of ^52m,gMn, the spin of the isomeric state of ^52mMn is 2⁺ (low-spin state, l) and that of the unstable ground state of ^52gMn is 6⁺ (high-spin state, h). Therefore, the isomeric ratio of ^52m,gMn was computed as the ratio of the high- to low-spin states.

The isomeric ratios for the production of ^52m,gMn from reactions ⁵⁹Co(γ, 3n1α) and ⁵⁹Co(γ, 5n2p) at different bremsstrahlung end-point energies are plotted in Fig. 8. The measured isomeric yield ratios for the pairs ^52m,gMn at 80, 105, and 130 MeV are 0.79 ± 0.18, 0.90 ± 0.14, and 1.03 ± 0.16, respectively. Fig. 8(a) shows that the experimentally obtained isomeric ratio for the pairs ^52m,gMn at the bremsstrahlung end-point energies of 80–130 MeV are in agreement with the values simulated with TALYS on the basis of GLO and SLO.Fig. 8(b) shows that our data on isomeric ratio complement the missing experimental data in the literature [10, 13]. Fig. 8(b) includes lines to guide the analysis of literature data [10] (blue dashed line) and [13] (red dashed line). The red line shows exponential growth in the region of 50−600 MeV and further saturation. The blue line coincides with an unchanged linear function surrounded by an isomer ratio value of 0.84. It is necessary to conduct experiments in the energy region of 130−300 MeV to obtain accurate information.

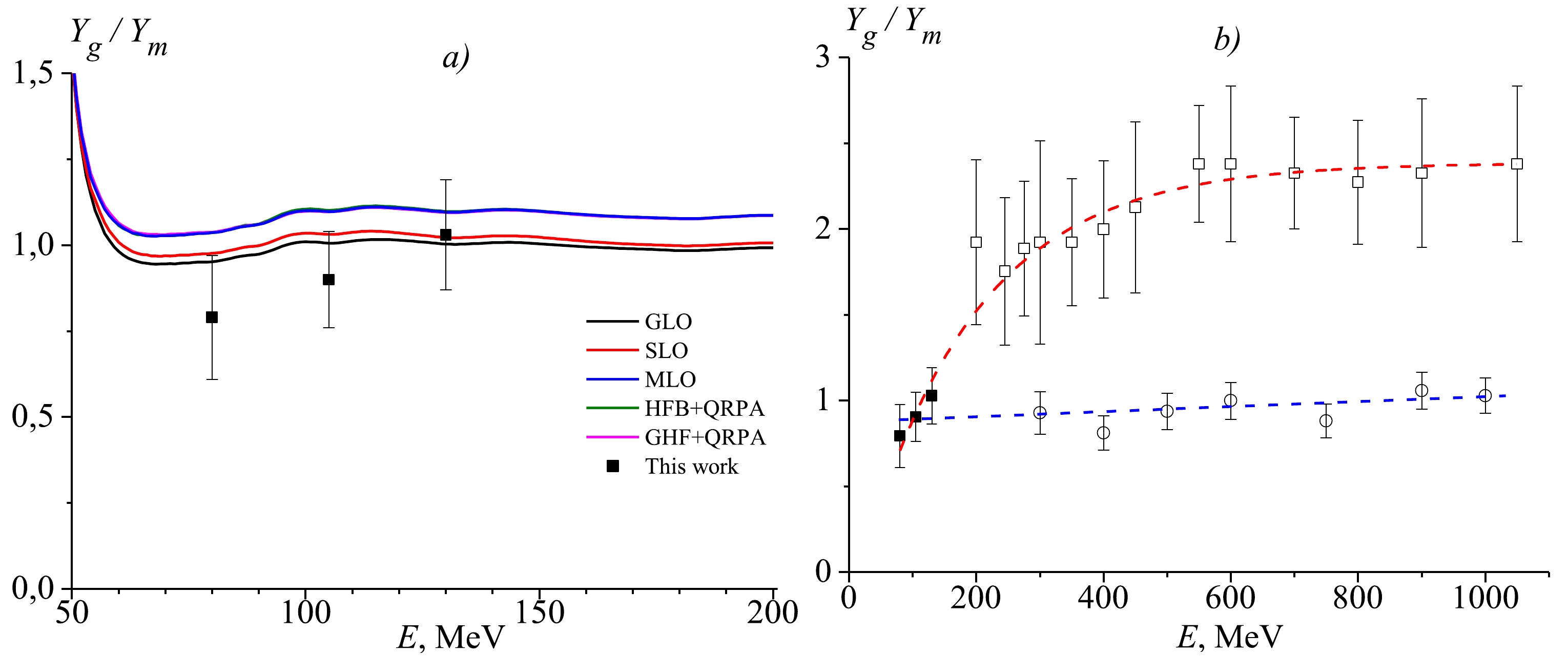
Figure 8.  (color online) Isomeric yield ratios of the pairs ^52m,gMn produced in ⁵⁹Co(γ, 3n1α) and ⁵⁹Co(γ, 5n2p) reactions as a function of the bremsstrahlung end-point energy from the present study (solid squares), literature data [10] (open circles), [13] (open squares), and the theoretically calculated values using different models for the E1 gamma-ray strength function in TALYS values.

Relative yields of the ⁵⁹Co(γ, xn; x = 1−4)^58-55Co, ⁵⁹Co(γ, 2pxn; x = 1−5)^56-52Mn, and ⁵⁹Co(γ, 3pxn; x = 5− 7)^51,49Cr reactions at different bremsstrahlung end-point energies were obtained on the basis of the values simulated with TALYS. The data reported in this study along with those in the literature were found to be in good agreement with the simulated values. The relative yields for reactions producing ^54,52g,52mMn and ^49,51Cr are not constantly increasing functions. This is due to the fact that in the initial energy region, the main channels for the formation of the ^54,52g,52mMn and ^49,51Cr isotopes are reactions with the emission of an alpha-particle. Near the energies of the reaction threshold, the ⁵⁹Co(γ, xn2p)^54,52g,52mMn and ⁵⁹Co(γ, xn3p)^49,51Cr reactions are accompanied by the release of alpha-particles; consequently, its cross sections decrease. The experimentally obtained isomeric ratio for the pairs ^52m,gMn at the bremsstrahlung end-point energies of 80–130 MeV complement the missing experimental data in the literature.