-
The pairing phase transition is widely recognized as essential for comprehending the thermodynamic properties of atomic nuclei [1]. Through precise measurements of level densities at low excitation energies, thermodynamic quantities have been deduced within the canonical ensemble framework, thereby confirming the S-shaped curve of heat capacity as a function of temperature [2−5]. The significance of this S-shaped curve has been extensively explored across various theoretical models, including the nuclear shell model [6−8], mean field model [9−13], among others [14, 15]. The occurrence of S-shaped curve is considered to be the hallmark of the pairing phase transition. However, in the superfluid phase, particle number conservation is violated by the BCS theory or the Bogoliubov transformation within the mean field model. The importance of conservation laws in studying phase transitions of finite systems has been elucidated in Refs. [16−18]. To address these drawbacks, we employed the shell-model-like approach, which ensures particle number conservation and accurately deals with the blocking effect [19−21]. Additionally, the covariant density functional theory (CDFT) has effectively described numerous nuclear phenomena [22−25]. The shell-model-like approach has been integrated within the CDFT framework [21]. Previous studies have examined the thermodynamic properties of even-even nuclei and odd-A nuclei using CDFT and the shell-model-like approach [26, 27].
Although the pairing and pairing phase transition have been extensively investigated [28−31], few studies have focused on the order of these transitions, which remains to be more clearly defined. The initial classification of general types of phase transitions, introduced by Paul Ehrenfest in 1933, has played a pivotal role in the thermodynamic study of critical phenomena [32]. Subsequently, Lee and Yang proposed a theorem on the distribution of roots of the grand partition function, predicting its broad applicability even in small systems [33]. In Refs. [34, 35], a classification scheme for phase transitions in finite systems was proposed. This scheme is based on the distribution of zeros (DOZ) of the canonical partition function in complex temperature. This method has been successfully applied to determine the order of phase transitions in
$ ^{162}\text{Dy} $ [36]. To the best of our knowledge, the order of the pairing phase transition in odd-A nuclei has not been studied yet.This study aimed to further investigate the microscopic mechanism underlying the S-shaped heat capacity curve. We examined whether its appearance entirely corresponds to the occurrence of pairing phase transitions. If a pairing phase transition does occur, the order of the transition in odd-A nuclei remains unclear, and the influence of the blocking effect on the phase transition needs to be studied. Additionally, this study explored whether and how the strength of the pairing correlation affects the pairing phase transition, an aspect that has not been addressed in previous studies.
In this study, we used
$ ^{161} \text{Dy} $ as an example. By employing the shell-model-like approach and CDFT, combined with the effective interaction PC-PK1 [37], we investigated the thermodynamic properties and influence of the blocking effect on the pairing phase transition. The order of this transition was determined according to a classification scheme based on the DOZ of the pairing partition function in the complex temperature plane. Furthermore, we constructed an ideal odd system and an ideal even system to explore the impact of pairing correlation strength on the pairing phase transition, as evidenced by changes in the order of the transition.This paper is organized as follows. In
$\text{Sec. II}$ , we briefly introduce the theoretical framework.$\text{Sec. III}$ presents the results and discussion. Finally,$\text{Sec. IV}$ presents a summary. -
In this section, we briefly introduce the basic formalism of the CDFT theory, which was summarizedin Ref. [37]. CDFT begins with a Lagrangian. Fromthis Lagrangian, the Dirac equation for nucleons with local scalar
$ S({\boldsymbol{r}}) $ and vector$ V^{\mu}({\boldsymbol{r}}) $ potentials can be deduced as$ \left[ \gamma_{\mu} (\mathrm{i} \partial^{\mu} - V^{\mu}) - (m + S) \right] \psi_{\xi} = 0,$

(1) where
$ S({\boldsymbol{r}}) = \Sigma_{S}, V({\boldsymbol{r}}) = \Sigma^{\mu} + \boldsymbol{\tau} \cdot \boldsymbol{\Sigma}^{\mu}_{TV}, $

(2) and
$ \psi_{\xi} $ is the Dirac spinor.In this study, SLAP was applied within the CDFT framework to deal with pairing correlations by diagonalizing the Hamiltonian in the multi-particle configurations (MPCs) space, which is constructed from the single-particle levels obtained through the CDFT method. The total Hamiltonian reads
$\begin{aligned}[b] H =\;& H_{\rm s.p.} + H_{\rm pair} \\ =\;& \sum\limits_{i}\varepsilon_{i}a^+_{i}a_{i} -G\sum\limits^{i\neq j}_{i,j>0} a^+_{i}a^+_{\bar{i}}a_{\bar{j}}a_{j}, \end{aligned} $

(3) where
$ \varepsilon_{i} $ is the single-particle energy gained from the Dirac equation (Eq. (1)),$ \bar i $ is the time-reversal state of i, and G represents constant pairing strength.For a system with an odd particle number
$ N = 2n+1 $ , it is necessary to block the state occupied by the odd nucleons. The MPCs for s = 0 states can be expressed as$ |c_bc_1\bar{c}_1\cdots c_n\bar{c}_n\rangle=a_b^+(a_{c_1}^+a_{\bar{c}_1}^+\cdots a_{c_n}^+a_{\bar{c}_n}^+)|0\rangle, $

(4) where b denotes the single-particle level blocked by the odd nucleon.
During the calculation process, a cutoff energy
$ E_c $ is needed to truncate the MPCs space. The configurations with energies$ E_m-E_0 \leqslant E_c $ are used to diagonalize the Hamiltonian (Eq. (3)), where$ E_m $ and$ E_0 $ are the energies of the m-th and ground-state configurations, respectively.After the diagonalization of the Hamiltonian (Eq. (3)), the nuclear many-body wave function is
$ \begin{aligned}[b] |\psi_\beta\rangle =\;&\sum\limits_{c_{1}\cdots c_{n}}{v_{\beta,\,c_1\cdots c_n}}|c_1\bar{c}_1\cdots c_n\bar{c}_n\rangle \\ & +\sum\limits_{i,j}{\sum\limits_{c_{1}\cdots c_{n-1}}{v_{\beta(ij),\,c_1\cdots c_{n-1}}}|i\bar{j}c_1\bar{c}_1\cdot\cdot\cdot c_{n-1}\bar{c}_{n-1}\rangle} + \cdots, \end{aligned} $

(5) where
$ \beta = 0 $ corresponds to the ground state,$\beta = 1, 2, 3, \cdots$ denotes the excited states with excitation energy$ E_{\beta} $ , and$ v_{\beta} $ denotes the coefficient after diagonalization.Moreover, the pairing gap can be calculated as [38−40]
$ \Delta_\beta=G\left[-\frac{1}{G}\langle\Psi_\beta|H_{\text{p}}|\Psi_\beta\rangle\right]^{1/2}, $

(6) and the thermodynamic quantities of the pairing interaction are calculated in the canonical ensemble [41]. The partition function Z can be calculated as
$ Z = \sum\limits^{\infty}_{\beta=0}\eta(E_{\beta})\,{\rm e}^{-E_{\beta}/T}. $

(7) where
$ E_{\beta} $ is the excitation energy that could be acquired through the CDFT + SLAP method, and the corresponding level density$ \eta (E_{\beta}) $ is taken as$ 2^s $ , i.e., the degeneracy of each state.The classification scheme for phase transitions relies completely on Ref. [42]. Only the main formulas of the classification scheme are provided below. Specifically, the scheme relies on the DOZ of the canonical partition function in the complex temperature plane.
The inverse complex temperature is defined as
$ {\cal{B}} = \beta + {\rm i}\tau, $

(8) where
$ \beta=1/T $ , and τ corresponds to the imaginary part of the inverse complex temperature, measured in$ \text{MeV}^{-1} $ . The zeros of the canonical partition function typically line up on curves in the complex temperature plane. The zeros are denoted by$ (\beta_{j},\tau_{j}) $ . If there are n zero points, we have that j = 1, 2,$\cdots,$ n, and j increases with the distance from the real axis.If the first three zeros closest to the real axis have been determined, the average inverse distance between zeros can be calculated as
$ \Phi(\widetilde{\tau}_j)=\dfrac{1}{d_j}, $

(9) where
$ \tilde{\tau}_{j}=(\tau_{j}+\tau_{j+1})/2 $ ,$ d_{j}=\sqrt{(\beta_{j+1}-\beta_{j})^{2}+(\tau_{j+1}-\tau_{j})^{2}} $ . The function Φ can then be approximated in the vicinity of the real axis by a power law of$ \tau_{j} $ only,$ \Phi(\tau_j)\propto\tau_j^\alpha, $

(10) and α can be calculated as
$ \alpha=\dfrac{\ln\Phi(\tau_3)-\ln\Phi(\tau_2)}{\ln\tau_3-\ln\tau_2}. $

(11) According to the definition in Ref. [42], when α
$ < $ 0, the system displays a first-order phase transition. When 0$ < $ α$ < $ 1, the phase transition is of second order. When α$ > $ 1, a higher-order phase transition occurs. -
For neutrons and protons, 16 single-particle levels and 9 valence nucleons were selected to construct a multi-particle configuration space, including 5 levels on and below the Fermi surface and 11 energy levels above the Fermi surface. PC-PK1 was chosen as the effective interaction. For neutrons, the Fermi surface is occupied by a single particle, and the maximum seniority number s is 8. The span of the upper and lower energy levels of the model space is 7.56
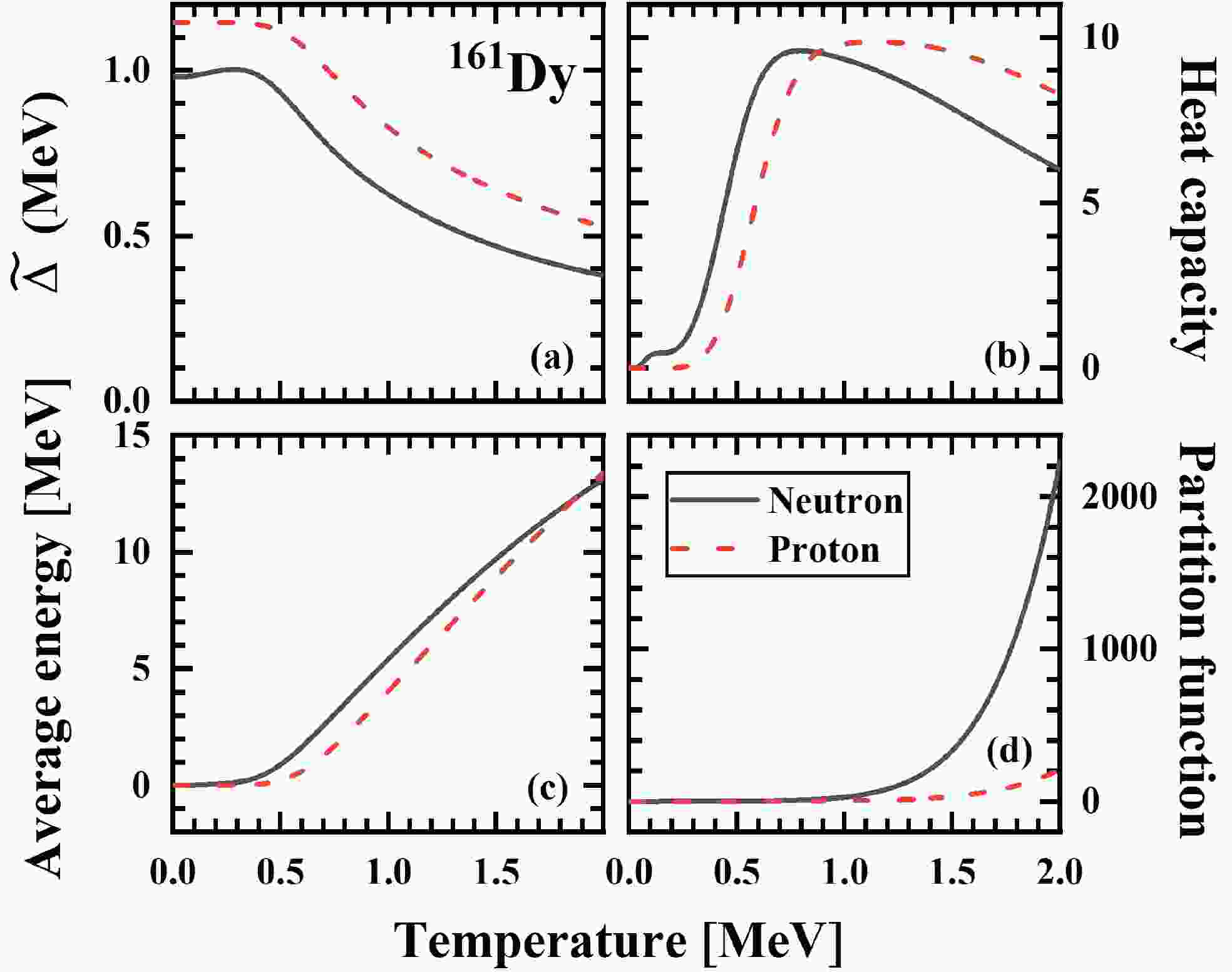
$ \text{MeV} $ . The corresponding pairing strengths of neutrons and protons are 0.29 and 0.32 MeV, which can reproduce the experimental odd-even mass differences well. In this study, the treatment of blocking was consistent with the method reported in Ref. [27]. "Bk1" corresponds to the blocking of the Fermi surface, while "bkn" corresponds to the blocking of the (n-1)th energy level above the Fermi surface.Figure 1 illustrates the behavior of the pairing gap (a), heat capacity (b), average energy (c), and partition function (d) of neutrons (indicated by black solid lines) and protons (represented by red dashed lines) in
$ ^{161} \text{Dy} $ as functions of temperature. Figure 1 (a) shows an evident increase in the neutron curve at temperatures below 0.3 MeV, contrasting with the almost constant trend observed in the proton curve within this temperature range. This behavior in the neutron curve indicates the pairing re-entrance phenomenon, wherein the pairing correlation in nuclei with an odd number of neutrons or protons is promoted as temperature rises. This enhancement is primarily attributed to the influence of the single-particle level structure near the level occupied by the odd nucleons, which weakens the blocking effect and reinforces the pairing correlation. Regarding heat capacity, both protons and neutrons exhibit an S-shaped curve. The initial turning point occurs at approximately 0.3 MeV for protons and 0.2 MeV for neutrons, aligning with the turning points of the pairing gap and average excitation energy. A second turning point emerges at around 1 MeV for protons and 0.7 MeV for neutrons, corresponding to the critical temperature of the phase transition. Additionally, the neutron curve demonstrates fluctuations in the low-temperature region. In the average energy diagram (Figure 1 (c)), both curves take nearly zero values at low temperatures (around 0.25 MeV for neutrons and 0.3 MeV for protons), gradually increasing almost linearly thereafter.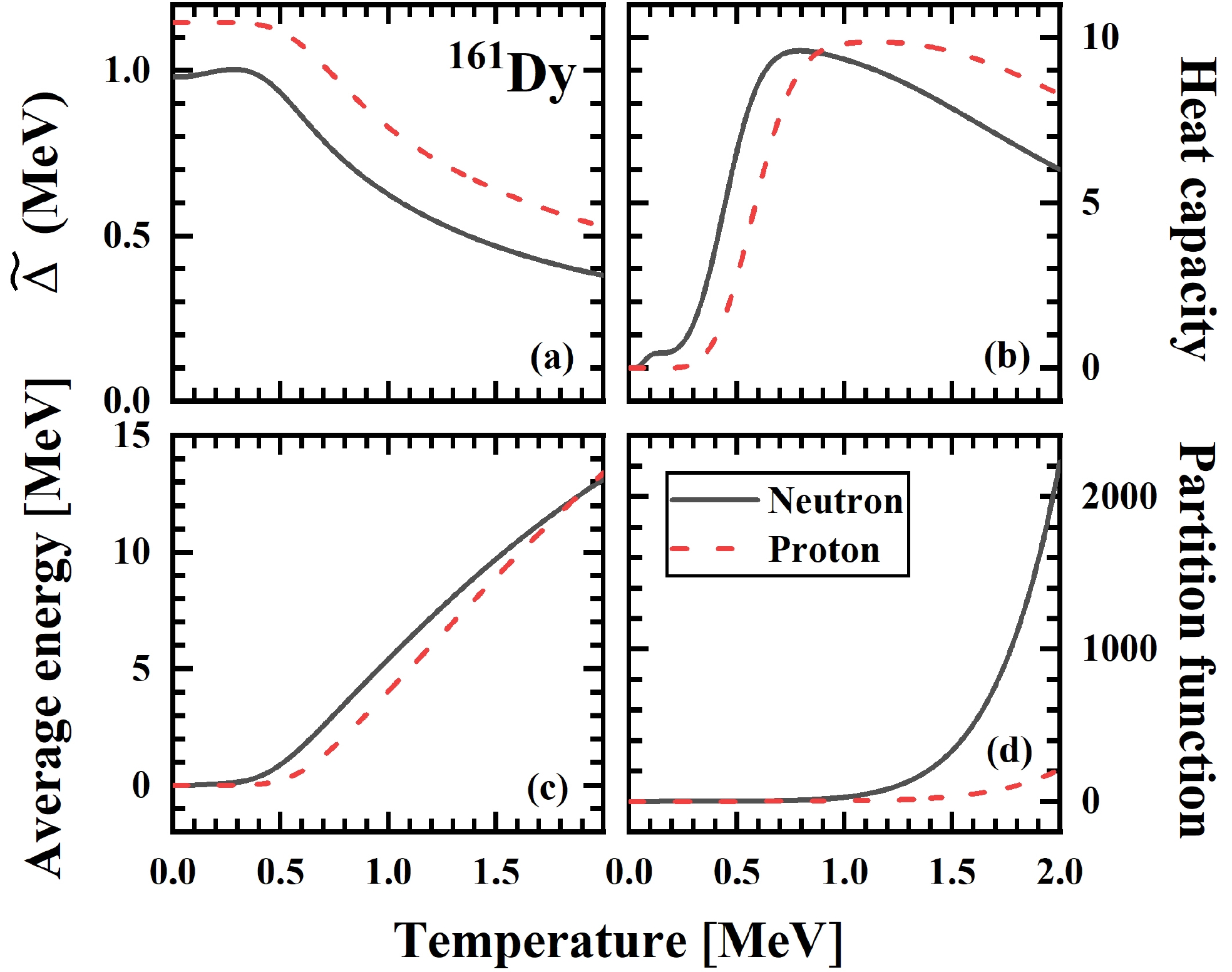
Figure 1. (color online) Pairing gap (a), heat capacity (b), average energy (c), and partition function (d) of neutrons (black solid lines) and protons (red dashed line) for
$ ^{161} \text{Dy} $ as functions of temperature.Figure 2 (a) displays the heat capacity of neutrons in
$ ^{161} \text{Dy} $ as functions of temperature, considering total and different blocking scenarios. The fluctuations observed at low temperatures primarily stem from the contribution of "bk1", which can be attributed to the single-particle level structure. In the case of "bk2", corresponding to the blocking of the first level above the Fermi surface, Fig. 2(b) shows that no levels exist around this energy level. Consequently, an energy input is required to excite nucleons, resulting in near-zero heat capacity at low temperatures. Subsequent blockings involve energy levels occupied by odd nucleons, which have less impact on the shape of the heat capacity curve. Hence, accurate treatment of Fermi surface blocking and its neighboring levels is crucial for investigating the relevant properties of odd-A nuclei.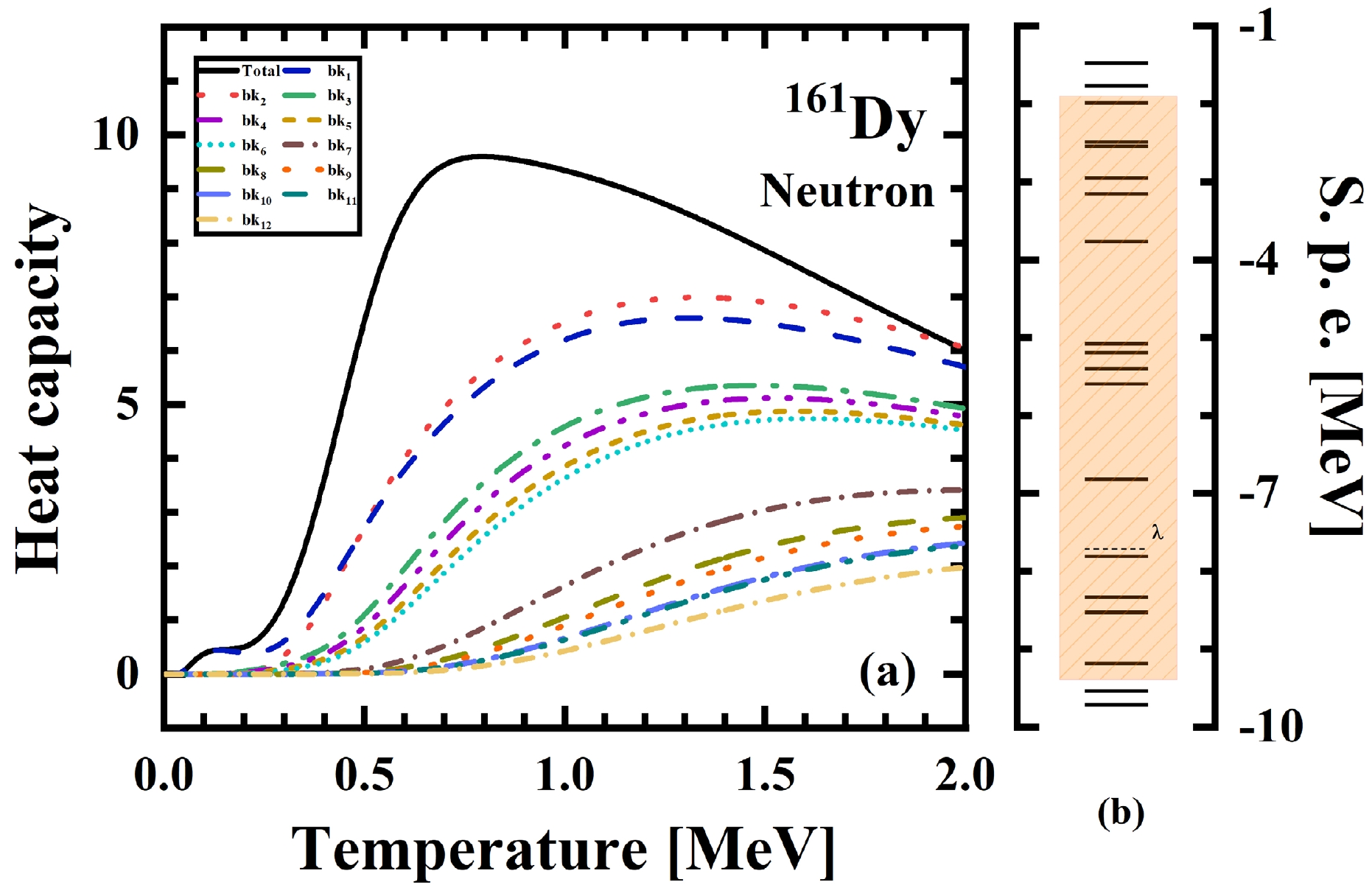
Figure 2. (color online) (a) Heat capacity of neutrons in
$ ^{161} \text{Dy} $ as functions of temperature with total and different levels blocked; (b) single-particle levels of neutrons for$ ^{161} \text{Dy} $ . The levels in the orange area are used to construct the SLAP MPCs; λ corresponds to the Fermi surface.For further microscopic understanding of the nuclear pairing transition, it is valuable to examine the number of Cooper pairs that become broken with increasing temperature in
$ ^{161} \text{Dy} $ . In this analysis, we followed the definition of the seniority component outlined in Ref. [26]:$ \chi_s=Z^{-1}\sum_{\beta\in\{s\}}\eta(E_\beta){\rm e}^{-E_\beta/T}. $

(12) The seniority component represents the contribution of excited states with specific seniority numbers to the total average energy. Figure 3 presents the seniority components as functions of temperature for different seniority numbers: s = 0, 2, 4, 6, 8 for neutrons (a) and s = 0, 2, 4, 6, 8, 10 for protons (b) in
$ ^{161} \text{Dy} $ . Note that s = 0 states contribute nearly 100% below$T \approx 0.3 $ MeV for protons and 0.2 MeV for neutrons, aligning with the vanishing heat capacity shown in Fig. 1. As the temperature exceeds 0.3 MeV for protons and 0.2 MeV for neutrons, the contribution of s = 0 states begins to decrease. Simultaneously, the curve for s = 2 states starts to rise, corresponding to the first turning point in the heat capacity curve and the temperature at which the pairing gap curve begins to decline and the average energy curve begins to rise. The curves for s = 2 reach their maximum at 0.8 MeV for neutrons and 1 MeV for protons, corresponding to the second turning point of the heat capacity curve. This indicates the pairing phase transition from the superfluid phase to the normal phase. This transition is responsible for the S-shape of the heat capacity curve. Furthermore, around T$ \approx $ 0.5 MeV, the contribution of s = 4 states begins to increase.
Figure 3. (color online) Seniority components as functions of temperature for different seniority numbers: s = 0, 2, 4, 6, 8 for neutrons (a) and s = 0, 2, 4, 6, 8, 10 for protons (b) in
$ ^{161} \text{Dy} $ .The level density serves as a valuable tool for characterizing pairing transitions in hot nuclei. To further elucidate the microscopic mechanisms underlying the S-shaped heat capacity curve, we investigated the number of excited states of nuclei in terms of different seniority contributions. Figure 4 shows the level densities as functions of excitation energies for different seniority numbers: s = 0, 2, 4, 6, 8 for neutrons (a) and s = 0, 2, 4, 6, 8, 10 for protons (b) in
$ ^{161} \text{Dy} $ . These curves show distinct and evident protuberances for s = 2, 4, 6, and 8 for neutrons, and s = 2 and 4 for protons. Notably, these protuberances are absent at higher seniority numbers. This observation suggests that the initial fluctuations around 4$ \text{MeV} $ are primarily attributed to the contribution of one-pair-broken states. The number of excited states increases rapidly owing to the emergence of one-pair-broken states with increasing excitation energies. However, when$ T \geqslant $ 4$ \text{MeV} $ , the growth rate of the curves diminishes because no additional one-pair-broken states can be formed. This phenomenon corresponds to the first S-shaped feature in the heat capacity curve. Subsequently, with the emergence of the second fluctuation, the appearance of two-pair-broken states leads to rapid increase, followed by a decline after an excitation energy of 8$ \text{MeV} $ for neutrons and 7$ \text{MeV} $ for protons. Other protuberances may indicate additional S-shaped features in the heat capacity curve at higher energies.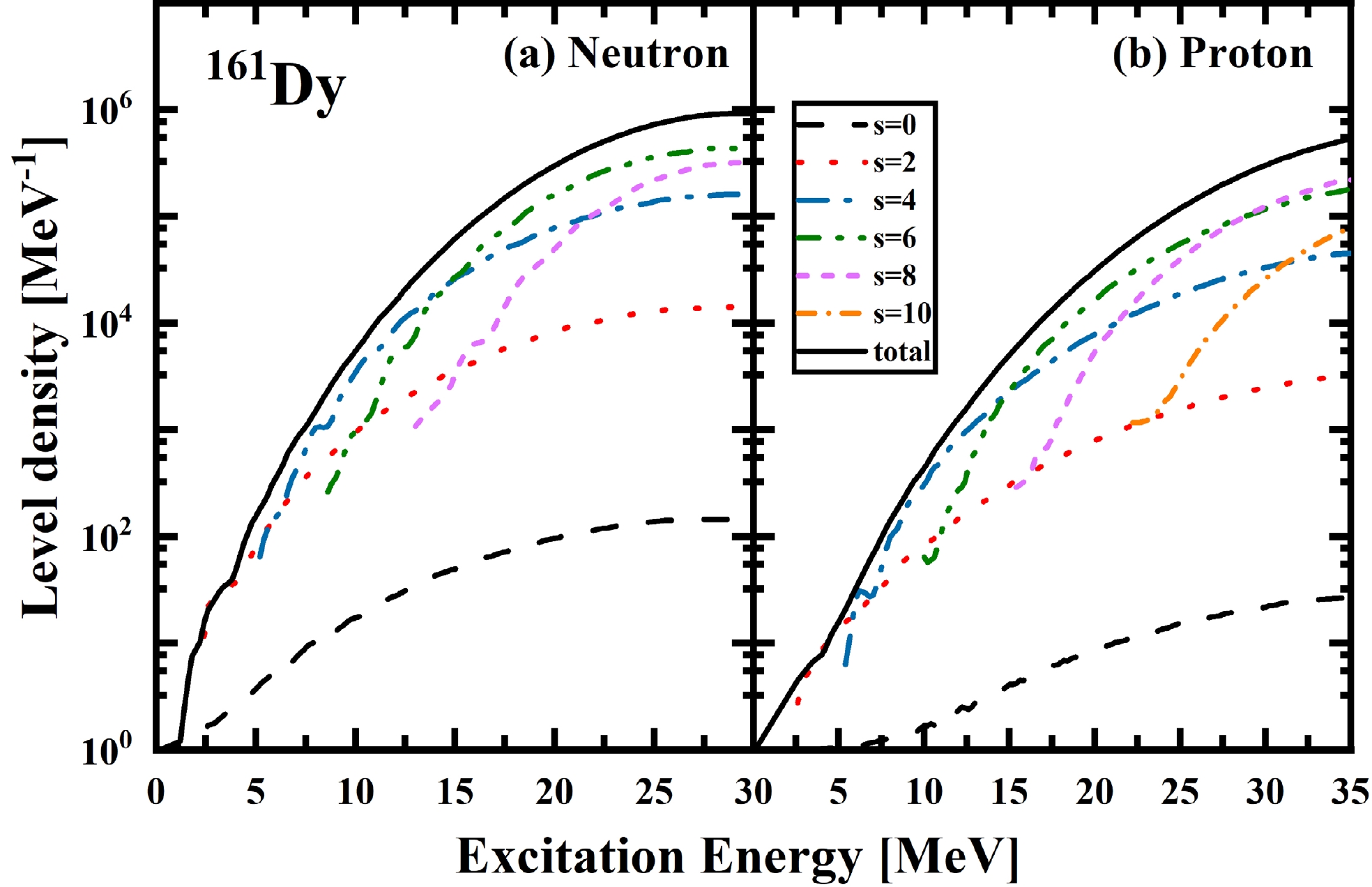
Figure 4. (color online) Level densities as functions of excitation energies for different seniority numbers: s = 0, 2, 4, 6, 8 for neutrons (a) and s = 0, 2, 4, 6, 8, 10 for protons (b) in
$ ^{161} \text{Dy} $ .Figure 5 shows contour plots of the partition function of neutrons and protons in the complex temperature plane. Zero points at
$ \beta \approx 1.05 \; \text{MeV}^{-1} $ for protons and 1.3$ \text{MeV}^{-1} $ for neutrons effectively reflect the critical temperature of the phase transition. The corresponding critical temperature of protons and neutrons are 0.95 and 0.77 MeV, and the experimental value for$ ^{161} \text{Dy} $ is 0.52 MeV [2]. The contour plots of the partition function of neutrons for$ ^{161} \text{Dy} $ under different blocking scenarios in the complex temperature plane are presented in Fig. 6. It is evident that the partition functions of "bk1" and "bk2" contribute the most to the overall partition function. Conversely, patterns of blocking higher energy levels are similar, contributing minimally to the overall partition function. This observation aligns with earlier discussions regarding the effects of different blocking scenarios on heat capacity. Furthermore, in cases of blocking higher energy levels, the partition function predominantly occupies the zero-point domain. This suggests weakening of the nuclear superfluidity, with the nucleus primarily existing in the normal phase.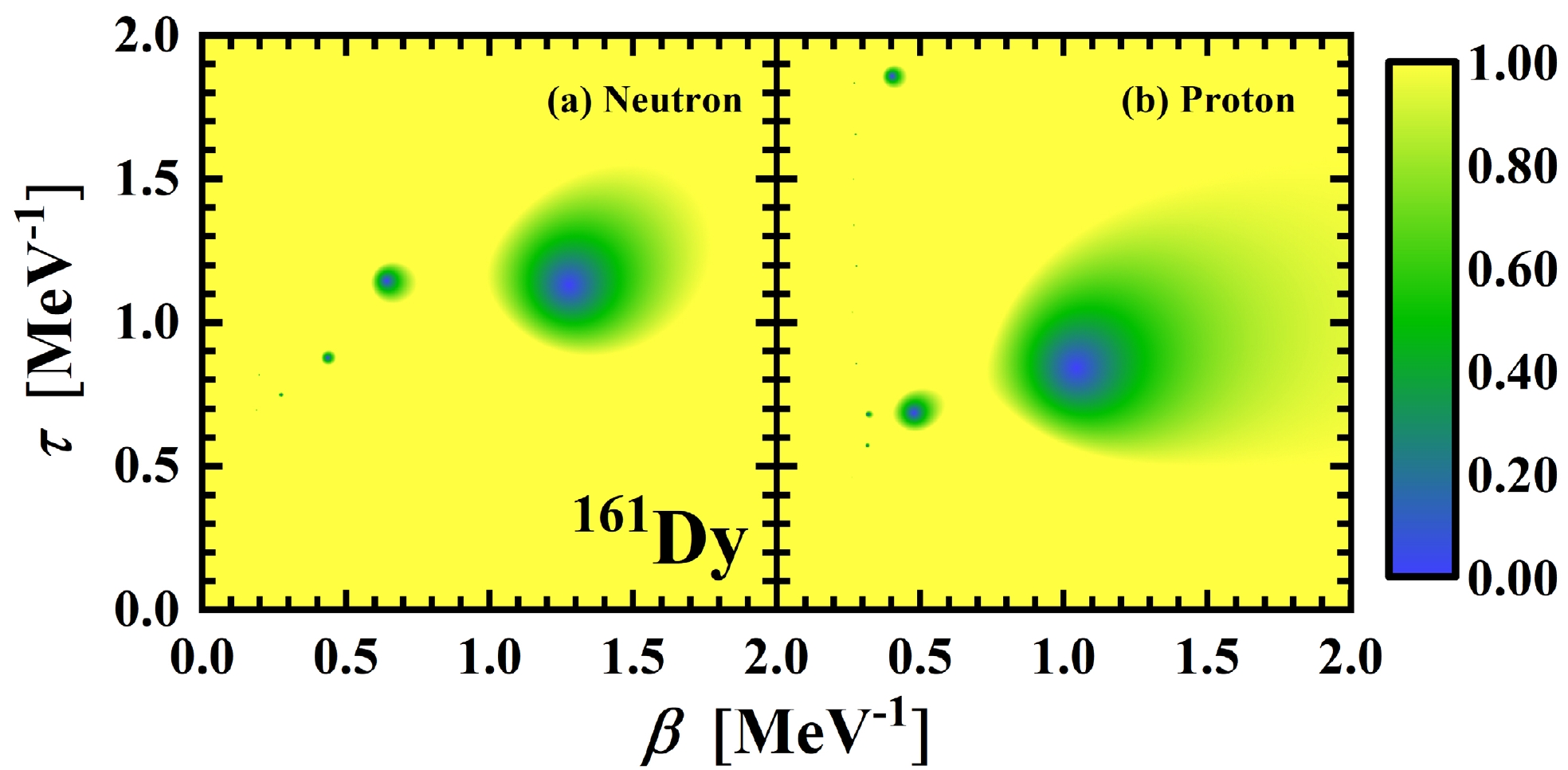
Figure 5. (color online) Contour plots of the partition function of neutrons and protons for
$ ^{161} \text{Dy} $ in the complex temperature plane.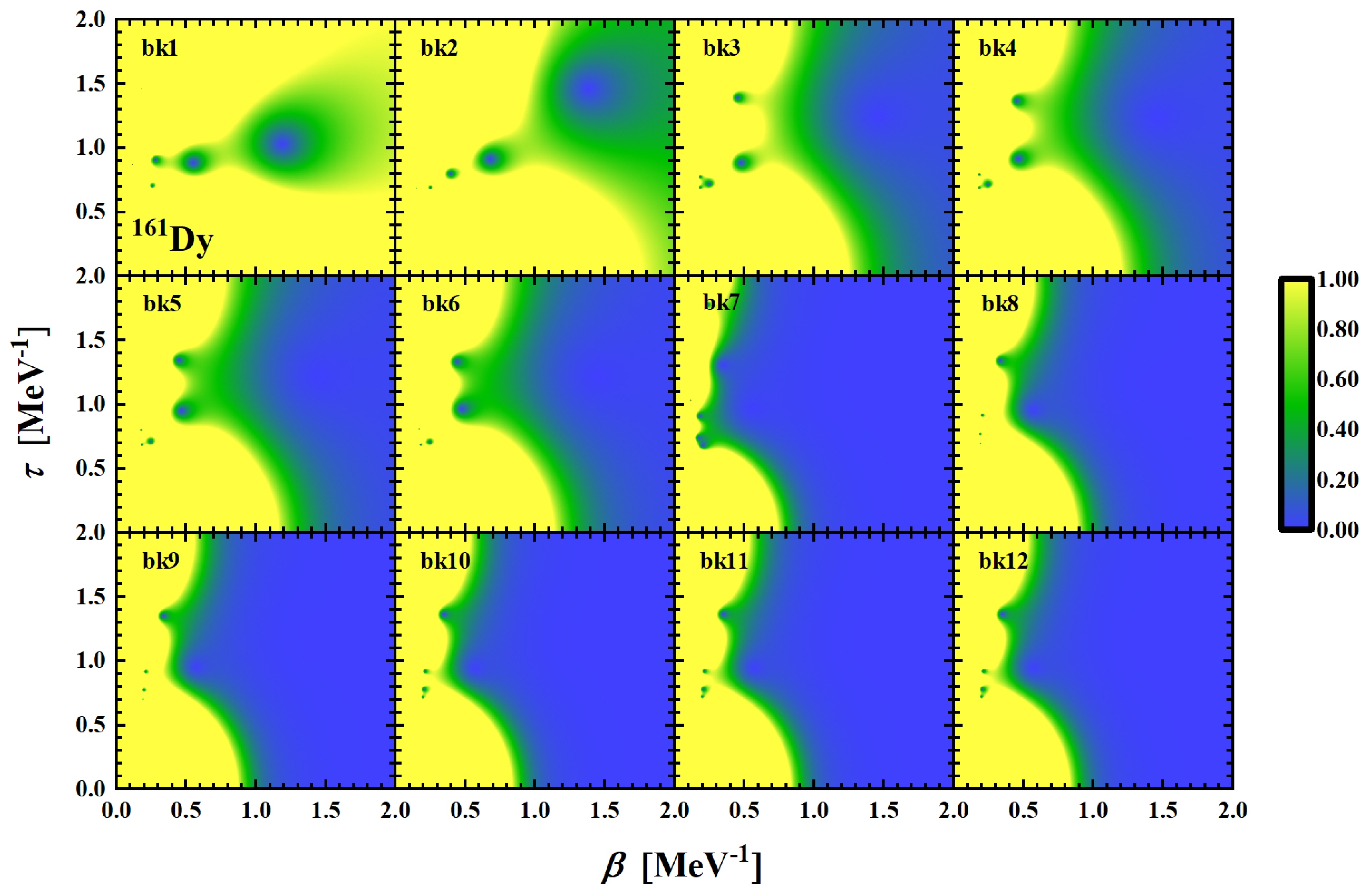
Figure 6. (color online) Contour plots of the partition function of neutrons for
$ ^{161} \text{Dy} $ under different blocking scenarios in the complex temperature plane.According to Fig. 5, the minima are iteratively determined as the zero points of the partition function. The distributions of zero points of the partition function for neutrons and protons in the complex temperature plane are displayed in Fig. 7, where the zero points of the pairing phase transition are indicated by the solid line. By calculation using Eq. (11), the α values corresponding to the neutrons and protons of
$ ^{161} \text{Dy} $ are –2.04 and –5.66, respectively. Based on the phase transition classification method, this indicates a first-order phase transition.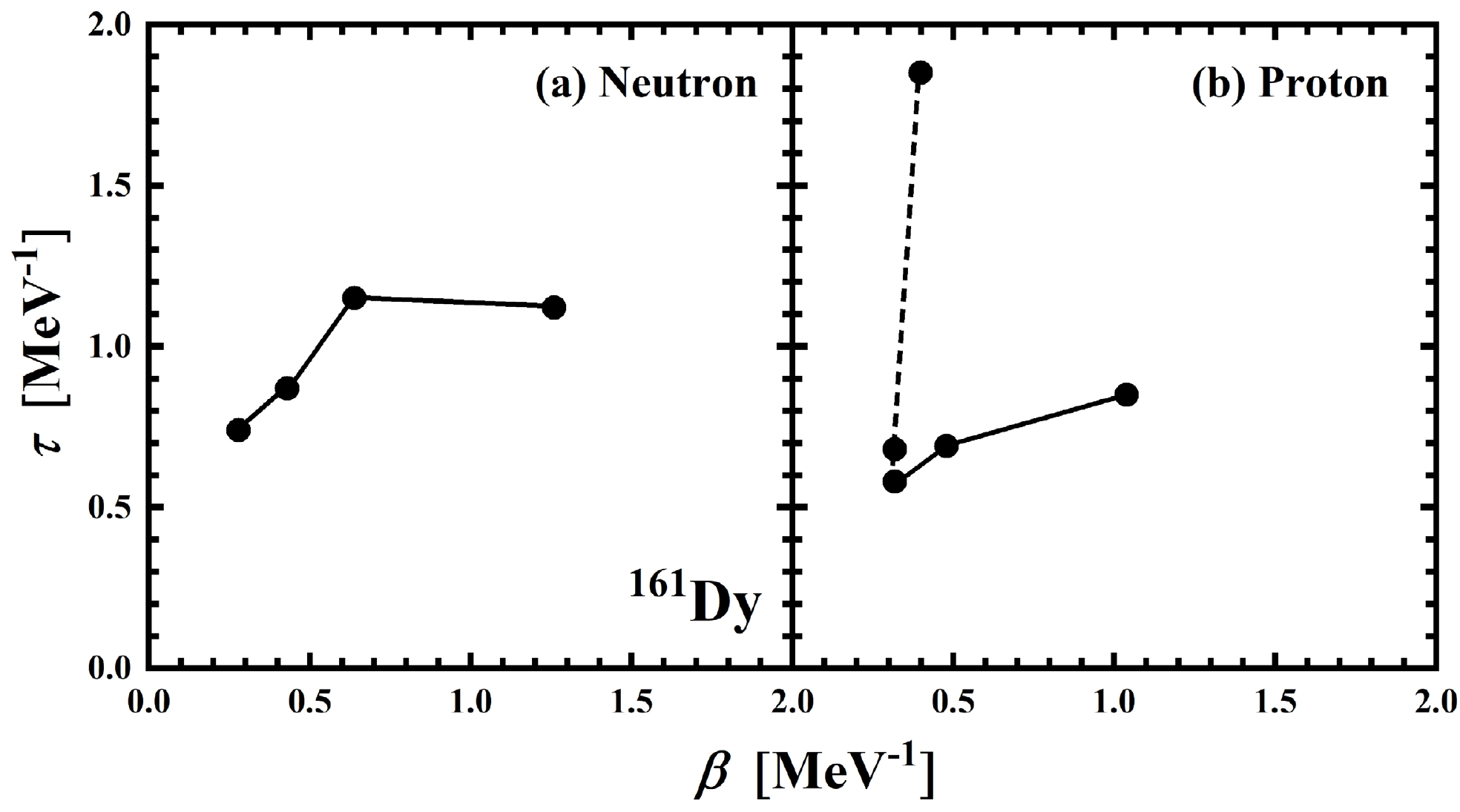
Figure 7. DOZ of the partition function of the neutrons (a) and protons (b) for
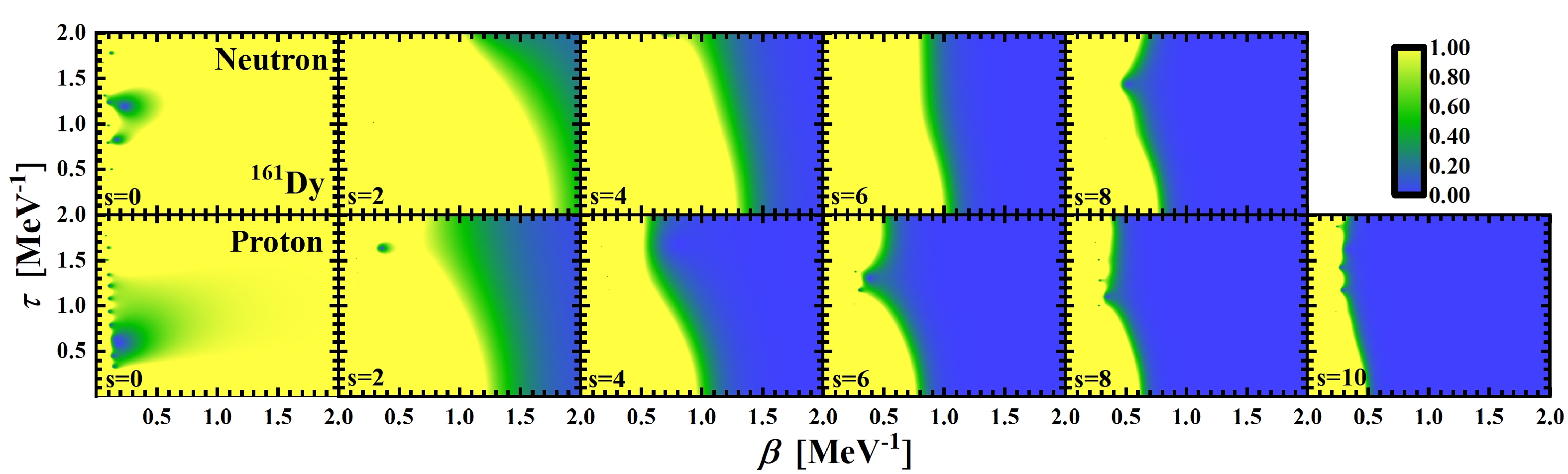
$ ^{161} \text{Dy} $ in the complex temperature plane. The solid and dashed lines represent two types of phase transitions.Figure 8 shows the contour plots of the partition function for
$ ^{161}\text{Dy} $ in the complex temperature plane for different seniority numbers, namely s = 0, 2, 4, 6, 8, and 10, where the upper and lower lines correspond to neutrons and protons, respectively. In the first column of the seniority number, that is, for s = 0 (fully paired states), zero points exist only in the region where β is very small. Additionally, there are no zero points in the region from 0 to 2$ \text{MeV} $ (β$ > $ 0.5$ \text{MeV}^{-1} $ ), indicating that the nucleus is entirely in the superfluid phase. As we move to s = 2 (one pair broken) state, the zero point domain begins to appear with a clear boundary, signifying the coexistence of the superfluid and normal phases. Subsequently, differences emerge between neutrons in odd systems and protons in even systems. The zero domain for neutrons is smaller than that for protons in the s = 2 state, primarily due to the blocking effect of the odd nucleon hindering the evolution of the pairing phase transition. With increasing seniority number, the zero point domain gradually expands, and the normal phase gradually dominates. The evolution of the pairing phase transition can still be effectively demonstrated. By the time we reach the seniority number, that is, for s = 8 or 10 (completely broken) state, the image is nearly entirely covered by the zero point domain, indicating that the nucleus is entirely in the normal phase. -
From the analysis presented above, we found that the structure of single-particle levels affects the heat capacity curve. Under the SLAP framework, single-particle levels are derived using Eq. (1). In fact, it may be affected by many factors, such as nuclear deformation and shell structure. Given that this study only focused on the influence of pairing correlation, it was necessary to remove the influence of other factors to establish an ideal model. In this study, ideal models with odd and even particles were constructed with controllable pairing strength, and thermodynamic quantities were investigated under the same framework. For the even system, a configuration space with 10 levels and 10 particles was established, with five levels above the Fermi surface. The energy levels ranged from 1 to 10 MeV, and the pairing strength varied from 0 to 2 MeV in increments of 0.1 MeV. The cut-off energy was set to 45 MeV, resulting in a configuration space dimension of
$ 10^4 $ . In the case of the odd system, a configuration space with 10 levels and 11 particles was chosen, with four levels above the Fermi surface. The single-particle levels, pairing strength, and cut-off energy were consistent with the even system. The configuration space dimension was$ 1.4\times10^4 $ . By employing these ideal models, we aimed to investigate the thermodynamic quantities under the same framework, thus allowing for clearer understanding of the sole influence of the pairing correlation on the system.Figure 9 shows the heat capacity with varying pairing strengths for both the ideal even system (a) and ideal odd system (b) as functions of temperature. As the pairing strength G increases, the temperatures corresponding to the first and second turning points of the curves, as well as the peak values of the curves, also increase. In Fig. 9 (b), fluctuations are observed in the low-temperature region, similar to the situation discussed for
$ ^{161}\text{Dy} $ . These fluctuations are primarily attributed to the pairing re-entrance phenomenon in the odd-nucleon system.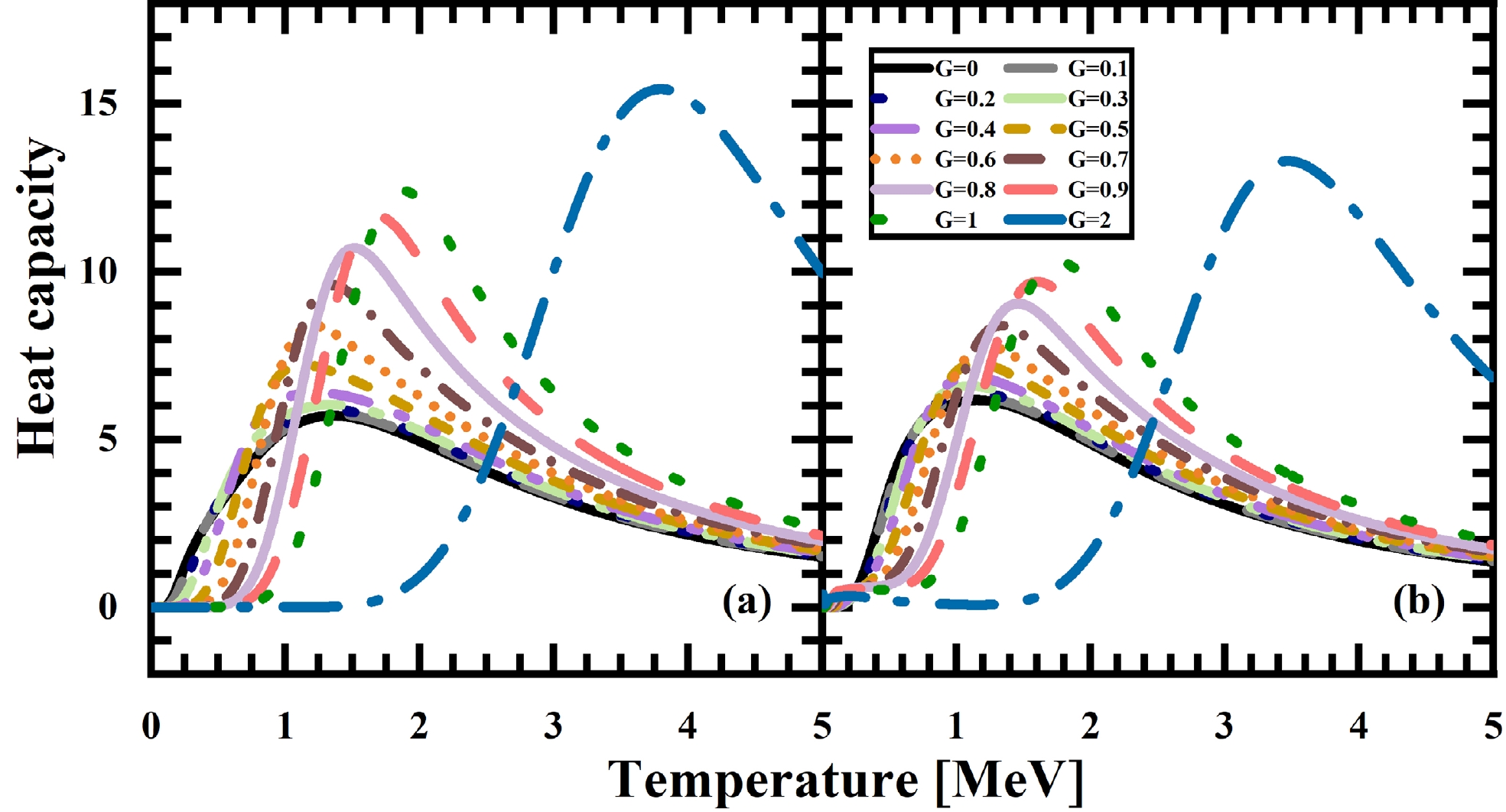
Figure 9. (color online) Heat capacity with different pairing strengths for the ideal even system (a) and ideal odd system (b) as functions of temperature.
According to the contour plots of the partition function with varying pairing strengths for the ideal even system in the complex temperature plane, the DOZ of the partition function is shown in Fig. 10. When the pairing strength is 0.1, a zero point is observed outside the plotted range, as indicated in the inset figure. In contrast, when the pairing strength is 0 (indicating no pairing correlation), there is no zero point in the corresponding β region. However, the heat capacity curve for G = 0 still exhibits an S shape, suggesting that the appearance of an S-shaped heat capacity curve does not solely correspond to the pairing phase transition. As the pairing strength G increases, the branch of zero points near the real axis undergoes significant changes. The zero point corresponding to the peak value of the heat capacity curves gradually shifts to the region of smaller values of β owing to the increasing temperature.
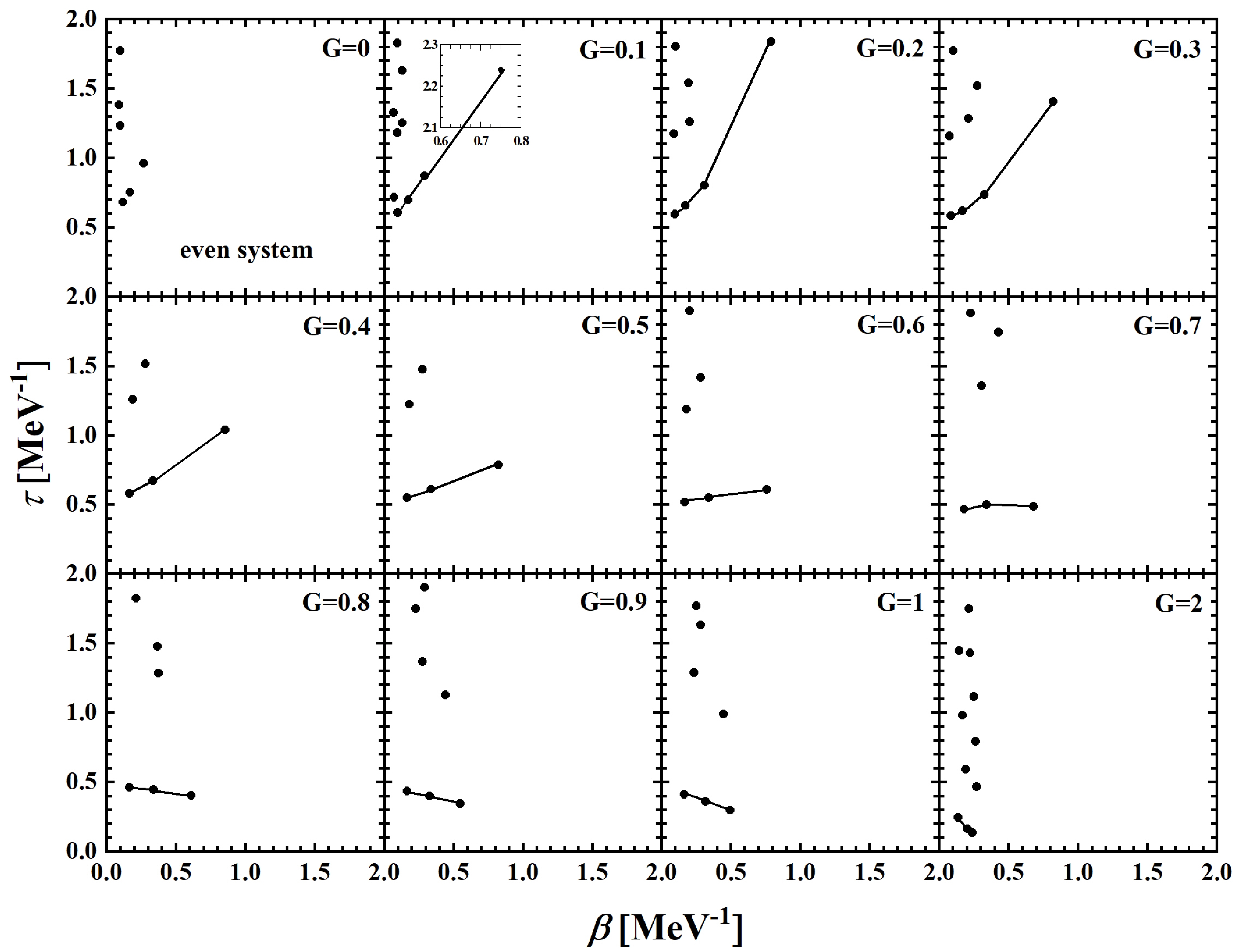
Figure 10. DOZ of the partition function for different pairing strengths for the ideal even system in the complex temperature plane.
The corresponding α values are presented in Table 1. For pairing strengths G
$ \leqslant $ 0.7, a first-order phase transition is observed. When G is between 0.8 and 0.9, a higher-order phase transition is identified. Finally, for G = 1, a second-order phase transition is observed. This analysis reveals a nonlinear relationship between the pairing strength and the order of the pairing phase transition, consistent with the results reported in Ref. [41].G / $\text{MeV}$ 

0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 α −3.98 −4.73 −5.45 −3.86 −5.46 −10.49 −39.3 7.1 2.69 0.94 Table 1. Values of α for different pairing strengths for the ideal even system.
Figure 11 shows the DOZ of the partition function with varying pairing strength for the ideal odd system in the complex temperature plane. Notably, a branch is observed when the pairing strength is 0. The presence of this branch is primarily attributed to changes in the zero point distribution caused by the blocking effect, and it does not correspond to a real pairing phase transition. This behavior contrasts with the case of even systems.

Figure 11. DOZ of the partition function with different pairing strengths for the ideal odd system in the complex temperature plane.
Based on the zero distribution depicted in Fig. 11, the corresponding α values are presented in Table 2. For pairing strengths G
$ \leqslant $ 0.7, a first-order phase transition is identified. However, for values of G between 0.8 and 1, a higher-order phase transition is observed. This analysis demonstrates that the pairing strength also influences the pairing phase transition in the odd system.G / $ \text{MeV} $ 

0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 α −3.4 −3.66 −3.98 −4.66 −4.61 −8.37 −18.59 35.01 7.2 3.2 Table 2. Values of α for different pairing strengths for the ideal odd system.
-
In this study, we investigated the pairing phase transition in the odd-A nucleus
$ ^{161}\text{Dy} $ using the CDFT and the shell-model-like approach. Thermodynamic quantities were evaluated within the canonical ensemble theory, and the phase transition order was determined using a classification scheme based on the DOZ of the partition function in the complex temperature plane. The impact of different pairing strengths on the pairing phase transition was also examined.The heat capacity curve of
$ ^{161} \text{Dy} $ exhibits an S shape, indicating a pairing phase transition from the superfluid phase to the normal phase. Extending the calculations to the complex temperature plane revealed that the pairing phase transition is of first order. Blocking the Fermi surface and the first level above significantly contributes to the total partition function, highlighting the importance of considering the blocking of the nearest levels above the Fermi surface in the study of odd-A nuclei. The contour plots of the partition function with different seniority show that the blocking effect of the odd nucleon hinders the evolution of the pairing phase transition.Furthermore, ideal models with odd and even particles were constructed to explore the influence of different pairing strengths on the pairing phase transition in the complex temperature plane. In the ideal even system, the absence of pairing correlation does not lead to a zero point corresponding to the critical temperature in the large β region, yet the heat capacity curve still exhibits an S shape. This suggests that the appearance of an S-shaped heat capacity curve does not exclusively indicate a pairing phase transition. Conversely, in the ideal odd system, the presence of a zero point branch in the partition function plot is due to the blocking effect. The analysis also demonstrates that the pairing strength has a nonlinear influence on the pairing phase transition. In the ideal even system, the phase transition order changes from first order to higher order and then to second order as the pairing strength increases. For the ideal odd system, the phase transition order changes from first order to higher order with increasing pairing strength. In the near future research, we will focus on the experimental spectroscopic properties, among others, to study pairing.
Pairing phase transition in the odd-A nuclei: identification and classification
- Received Date: 2024-07-02
- Available Online: 2024-12-15
Abstract: Research on the pairing phase transition in the odd-A nucleus





 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF














 DownLoad:
DownLoad: