The thermodynamic stability and phase structure of the Einstein-Euler-Heisenberg-AdS black holes

As solutions to the Einstein equations theoretically and being accepted as compact objects for testing general relativity, the black holes have received significant attentions for decades [1−5]. The Event Horizon Telescope (EHT) collaboration proceeded with the detections of the candidates of black holes such as supermassive ones at the centers of the galaxy M$ 87^{\ast} $ and the Milky Way [6−13]. The black holes have their own characteristics relating to their structures and environments [1]. The black holes in the background with a negative cosmological constant can be thought of as a gauge-gravity duality in the boundary of Anti-de Sitter (AdS) spacetime [14].

According to the astronomical observations, the compact objects immersed in the magnetic fields produce pair conversion and vacuum polarization [15, 16], so the influence from the electromagnetic fields can not be neglected. When the strength of electromagnetic fields is strong enough, the vacuum seems to act as a material medium due to the electromagnetic self-interactions for the vacuum polarization like the light-light scattering or electron-positron creation [17−19]. The self-interactions can also rewrite the metric of the compact celestial bodies and leave an imprint in the background structure around the black holes. More achievements have been made on the nonlinear electromagnetic effects in the experiments [20−23]. Within the frame of Euler-Heisenberg theory with vacuum polarization to one loop, the system Lagrangian with the Lorentz and gauge invariants is expanded up to the second-order in the fine structure constant [24, 25]. The Euler-Heisenberg theory coupling with gravitation leads a static and spherically symmetric solution for a black hole with electric or magnetic charge [26−29]. It is interesting to wonder how the effects from the Euler-Heisenberg theory affect the structure of spacetime around the black hole. As the possible phenomenon of birefringence, the two light trajectories were studied in the background of Einstein-Euler-Heisenberg black hole and the null geodesics governed by the two optical metrics relating to the light polarization respectively [30]. The authors of Ref. [30] also researched on the quasinormal modes of this kind of black holes characterized by a strong field nearby. It is significant to generalize the discussion on the Einstein-Euler-Heisenberg-AdS black holes.

The black hole thermodynamics has attracted a lot of attentions of physical community for more than twenty years [1]. There has also been much interest in the investigations of black hole in the AdS spacetime [1]. The occurrence of phase transition between two thermodynamically stable black holes and the thermal radiation from black holes in the AdS world were put forward, which is known as the Hawking-Page phase transition [31]. The existence of phase transition between the thermodynamically stable large black hole and the thermal radiation in the AdS universe was shown nearly forty years ago [31]. The Hawking-Page phase transition can also be interpreted as a confinement/deconfinement process of gauge field under the AdS/CFT correspondence [14]. It is inevitable that the black hole thermodynamics may be explored in a new direction with negative cosmological constant thought as a thermodynamic variable while the thermodynamic potential enthalpy considered [32−34]. In this process, the first law of thermodynamics for the Schwarzschild and Reissner-Nordstrom black holes in an anti-de Sitter universe originated, and the cosmological constant acts as a vacuum pressure $P=-\dfrac{\Lambda}{8\pi}$ conjugating to a thermodynamic volume $V=\dfrac{4}{3}\pi r_{+}^{3}$ with horizon radius $ r_{+} $ [32−39]. The efforts have been made that the phase structures subject to the thermodynamics of Reissner-Nordstrom-AdS black holes were discussed [40, 41]. The Hawking-Page-like phase transitions between the AdS black holes were explored [42−55]. The extension was performed to the P-V phase transitions of the same kinds of ones [36, 39, 56−62]. In order to gain insights into the special topic of black hole thermodynamics, we aim to analyze the thermodynamic stability and phase structure of AdS black holes [40, 41, 63−66]. It is fundamental to derive and calculate the basic quantities such as the Hawking temperature and entropy [40, 41]. Further the free energy and the heat capacity of the black hole in the background with negative cosmological constant are discussed in the canonical ensemble with fixed charge and the grand canonical ensemble with fixed potential respectively [40, 41]. The dependence of the free energy on temperature shows the phase structure of AdS black hole' phase structure [40, 41]. The nature of the heat capacity decides the stability of the AdS black hole [40, 41]. More efforts have been made to the several kinds of AdS black holes. The thermodynamic stability of the black holes constructed in the general relativity and Gauss-Bonnet gravity respectively was considered [63]. Both in the canonical ensembles and the grand canonical ensembles, the analysis of black holes' thermodynamical properties in de Rham, Gabadadze and Tolley (dRGT) massive gravity was performed [64]. Chaturvedi et.al. considered the thermodynamic geometry including the phase structure and critical phenomena for four-dimensional Reissner-Nordstrom-AdS and Kerr-AdS black holes in the canonical ensemble [65]. In the two kinds of ensembles, the author of Ref. [67] derived and computed the thermodynamic quantities of phantom AdS black holes to show the Hawking-Page phase transition and the sign of heat capacity graphically [67].

It is necessary to scrutinize the thermodynamic characteristics of Einstein-Euler-Heisenberg-AdS (EEH-AdS) black hole under different conditions of fixed charge or fixed potential. The self-interaction-corrected black holes need to be probed with several respects. In addition to the motion of the particles with the description of geodesics specified by the corrected black holes, it is useful to study the thermodynamic quantities and stability of the compact sources. We follow the procedure of Refs. [40, 41] research on the EEH-AdS black holes with considerable corrections from electromagnetic self-interactions. We aim to understand whether the electromagnetic self-interaction exerts the nonlinear influence on the black holes just brings about some shifts on the quantities or change the thermodynamic features of system greatly. We derive the Hawking temperature, Helmholtz free energy, Gibbs potential and entropy and then plot the dependence of the quantities on the temperature under the nonlinear influence to display the quantity difference evidently. The phase transition appear and the black hole's stability can be confirmed. The discussion and conclusion are listed in the end.

Within the framework of Euler-Heisenberg theory, the Lagrangian with Lorentz and gauge invariants was constructed as [24, 25],

where μ is the parameter demonstrating the electromagnetic self-interactions,

and α is the fine structure constant, $ m_{e} $ being electron mass. It is noted that $ ^{\ast}F^{\mu\nu}=\dfrac{1}{2\sqrt{-g}}\varepsilon_{\mu\nu\rho\sigma} F^{\rho\sigma} $ is dual of $ F_{\mu\nu} $, the electromagnetic field tensor [24, 25]. The μ-term in the Lagrangian (1) involves the square of the electromagnetic field tensor, leading the appearance of nonlinear term for gauge field in the field equation [24, 25].

The four-dimensional action of general relativity coupled to the nonlinear electromagnetic field can be expressed as [24−26],

resulting in the field equations, the Einstein-Euler-Heisenberg equations [26, 30]. Here g is the determinant of the metric tensor and R is the Ricci scalar. As a solution to the field equations, the metric in a static spherically symmetric form for Euler-Heisenberg-AdS black hole surrounded by the strong electromagnetic field is [26, 28, 29],

with the metric function,

where M is the mass of the black hole and Q is its electric charge. Here l is the AdS radius corresponding to the cosmological constant like $ \Lambda=-\dfrac{3}{l^{2}} $. It is noted that μ is the Euler-Heisenberg parameter [26, 28, 29]. With $ \mu=0 $, the metric (4) with its component (5) reduces to be Reissner-Nordstrom ones [26, 28, 29]. The nonlinear effect mainly appeared as μ-term with the fourth power of electric charge and the negative sixth power of the radial coordinate in the spacetime metric is due to the vacuum polarization, leading the compact object more gravitationally attractive than the Reissner-Nordstrom-AdS black hole [26, 28, 29]. According to the figures showing the behaviors of the metric functions of the Einstein-Euler-Heisenberg black hole and Reissner-Nordstrom black hole from Ref. [30], the shapes of the curves beyond the outer horizons belonging to the two kinds of black holes respectively are similar. Maybe the motion of test particles or lights around the gravitational sources may not exhibit the subtle difference between the black holes with or without the additional corrections owing to the electromagnetic self-interactions clearly. It is probable to compare the thermodynamic properties of the Einstein-Euler-Heisenberg-AdS black holes with those of the corresponding celestial bodies without nonlinear effect. We also wonder whether the own features of the internal constitutions of the nonlinear effect-corrected black holes may bring about their evolution. It is indispensable to further the research on the black holes under the nonlinear electrodynamics in the thermodynamics direction. The horizon radii can be thought as real roots of the equation like $ f(r)=0 $ [1]. Here we can let the external horizon $ r_{+} $ satisfy the condition as follows [30],

By combining the Eqs. (5) and (6), the black hole mass can be denoted as [30, 31],

According to the definition [31], the Hawking temperature for this kind of black holes,

while the entropy of black hole introduces [68],

also written as $ S=\dfrac{A}{4} $ where $ A=4\pi r_{+}^{2} $ is the area of horizon [68]. The Hawking temperature versus the horizon is depicted in the Fig. 1. The asymptotic behavior of the temperature are $\mathop\lim\limits_{r_{+}\longrightarrow 0}T=\dfrac{1}{4\pi r_{+}}\dfrac{\mu Q^{4}}{4r_{+}^{6}}>0 $ and $\mathop\lim\limits_{r_{+}\longrightarrow\infty}T= \dfrac{1}{4\pi r_{+}}\dfrac{3r_{+}^{2}}{l^{2}} > 0$ which corresponding to the curves in the Fig. 1. The Fig. 1 also demonstrates that the curves with larger factor μ locate above the ones under the weaker nonlinear effect in the small horizon scope and the curves of Hawking temperature with different values of μ seem to coincide in the case of huge black holes. Within the region with small $ r_{+} $, the temperature keeps positive, which is different from Reissner-Nordstrom metric [40, 41]. It is manifest that the curves of temperature function $ T(r_{+}) $ is concave in view of the Fig. 1. The condition equations are given in[40, 41],

Figure 1.  The solid, dotted and dashed curves corresponding to the dependence of Hawking temperature of Einstein-Euler-Heisenberg-AdS black holes in the canonical ensemble on the horizon for nonlinear factors $ \mu=0.08, 0.1, 0.14 $ respectively.

Substituting the temperature (8) into the Eq. (10) and Eq. (11), we obtain the minimum of Hawking temperature, charge and horizon radius at the extreme point of temperature as follows,

For the sake of the real quantities, the condition $\mu\leq{l^{2}}/{7}$ must be obeyed. It is obvious that the results from Eqs. (7), (8), (12)−(14) will recover to be those in Refs. [40, 41, 67] when $ \mu=0 $. The equation $T(r_{+})= T_{0} > T_{c}$ has two roots in contrast to the Fig. 1.

Now we must investigate the specific thermal characteristics of Einstein-Euler-Heisenberg-AdS black holes. It should be pointed out that the gravitational sources involve the charges and the sources evolve under different conditions [24−26, 28, 29]. We start to discuss the thermodynamic stability and phase structure of the black holes in the canonical ensemble where the charge is invariant. According to the approach of Refs. [40, 41] and with the help of Eqs. (7)−(9), the Helmholtz free energy $ F=M-TS $ is expressed as,

We connect the free energy (15) with the temperature (8) to plot the curves with the self-interaction coupling μ in the Fig. 2. The shapes of curves with different values of parameter μ are similar. There exists a point on the each curve as the dependence of Helmholtz free energy on the Hawking temperature and the free energy as a function of temperature is not derivable at the point. The Helmholtz free energy is a multiple valued function of Hawking temperature according to the Fig. 2. When the temperature is higher than the ones at the underivable point, a series of curves for small free energy due to several valued μ are nearly identical. The underivable point of the Helnholtz free energy can be thought as the critical point and certainly the relevant temperature is the critical temperature denoted as $ T_{c} $.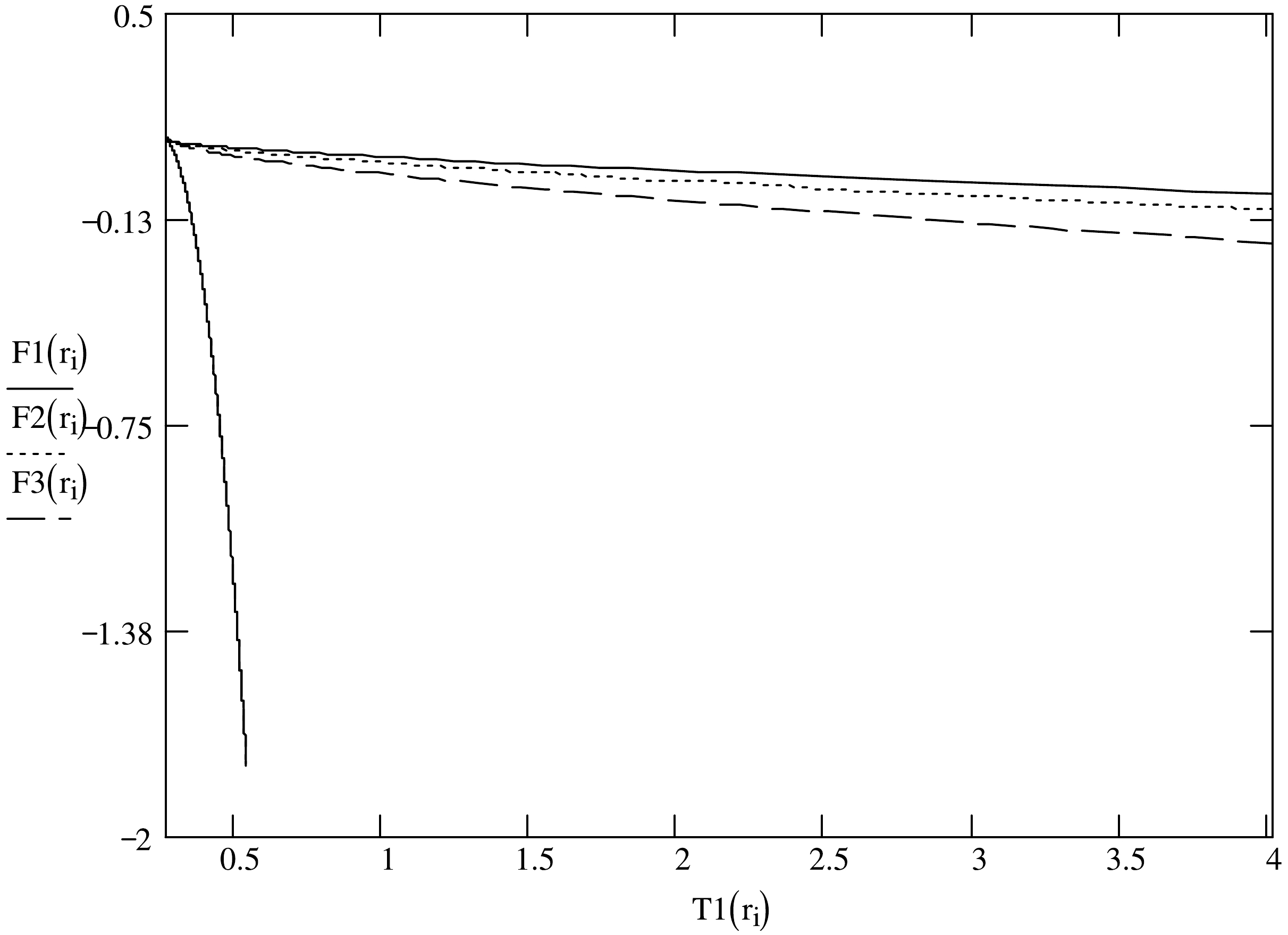

Figure 2.  The solid, dotted and dashed curves of the Helmholtz free energy of Einstein-Euler-Heisenberg-AdS black holes in the canonical ensemble as functions of the temperature for nonlinear factors $\mu=0.08,\; 0.1, \;0.14$ respectively.

It is also noted that the black hole satisfies the first law of thermodynamics [69],

where

is the electric potential. The corollary for the free energy can be written as [69]:

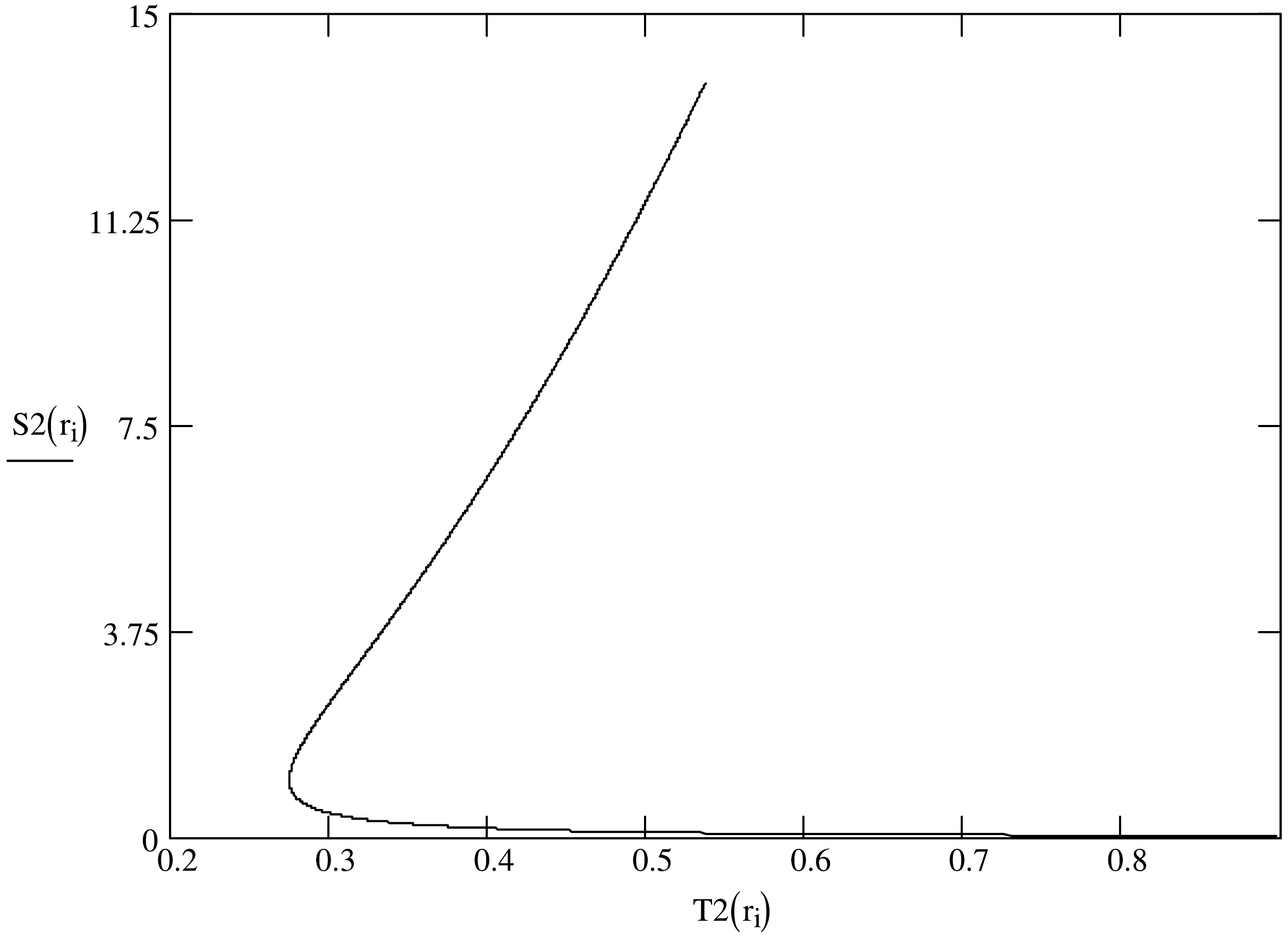
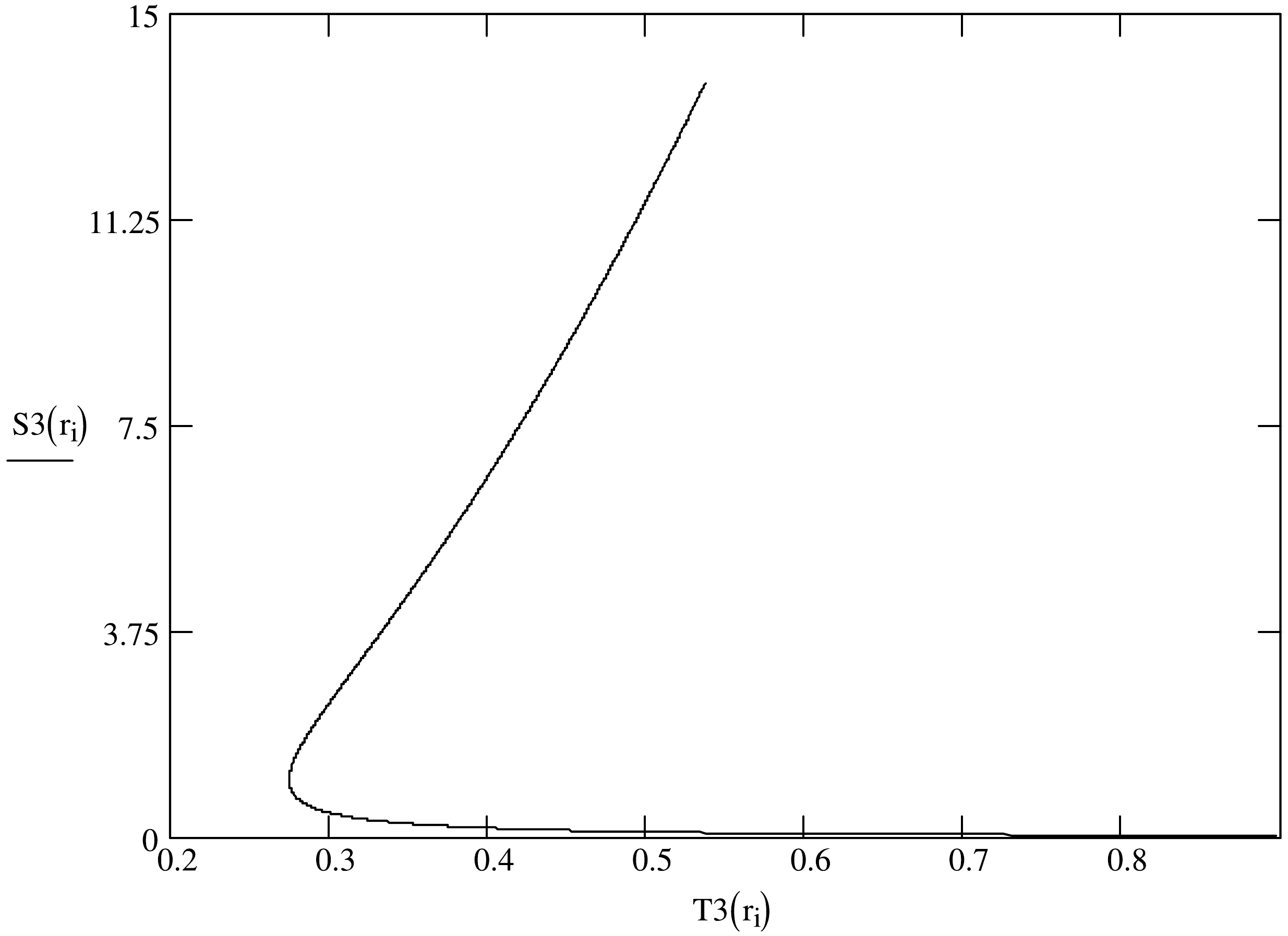
In the ensemble with fixed charge, the entropy of the black hole is shown as [69]:

In view of the temperature (8) and free energy (15), the entropy of black hole like Eq. (9) can be varied again [68]. Because of the Eq. (8) and Eq. (19), the relation between the entropy and temperature of the charged black holes within the frame of nonlinear electrodynamics can be depicted in the Figs. 3−5 with $ \mu= $ 0.08, 0.1, 0.14 respectively. The profiles of curves based on each diagram also resemble each other. If the temperature approaches the critical value $ T_{c} $, the entropy (19) will become $ \mathop\lim\limits_{T\longrightarrow T_{c}}S_{Q}=-{\mathop\lim\limits_{T\longrightarrow T_{c}}\bigg(\dfrac{\partial F}{\partial r_{+}}\bigg)_{Q}}\Big/{\mathop\lim\limits_{T\longrightarrow T_{c}}\bigg(\dfrac{\partial T}{\partial r_{+}}\bigg)_{Q}}\longrightarrow\infty $$ because of the condition (10) [40, 41]. It is discovered that the tangent line of the entropy function at the critical point $ T_{c} $ is perpendicular to the T-axis in the figures. The critical point $ T_{c} $ can be thought as the common boundary. To each figure, we find that the entropy curve starts to divide into two branches at the common boundary. In addition the sufficiently high surface temperature of black hole like $ T>T_{c} $ corresponds to two values of the entropy. Further the slopes of tangent lines for the upper branch keep positive and the lower part reflects the decreasing function of temperature with negative slopes. According to the black hole entropy (9) from Ref. [68], the upper parts of entropies describe the large black holes and the lower branch refers to the source with small size.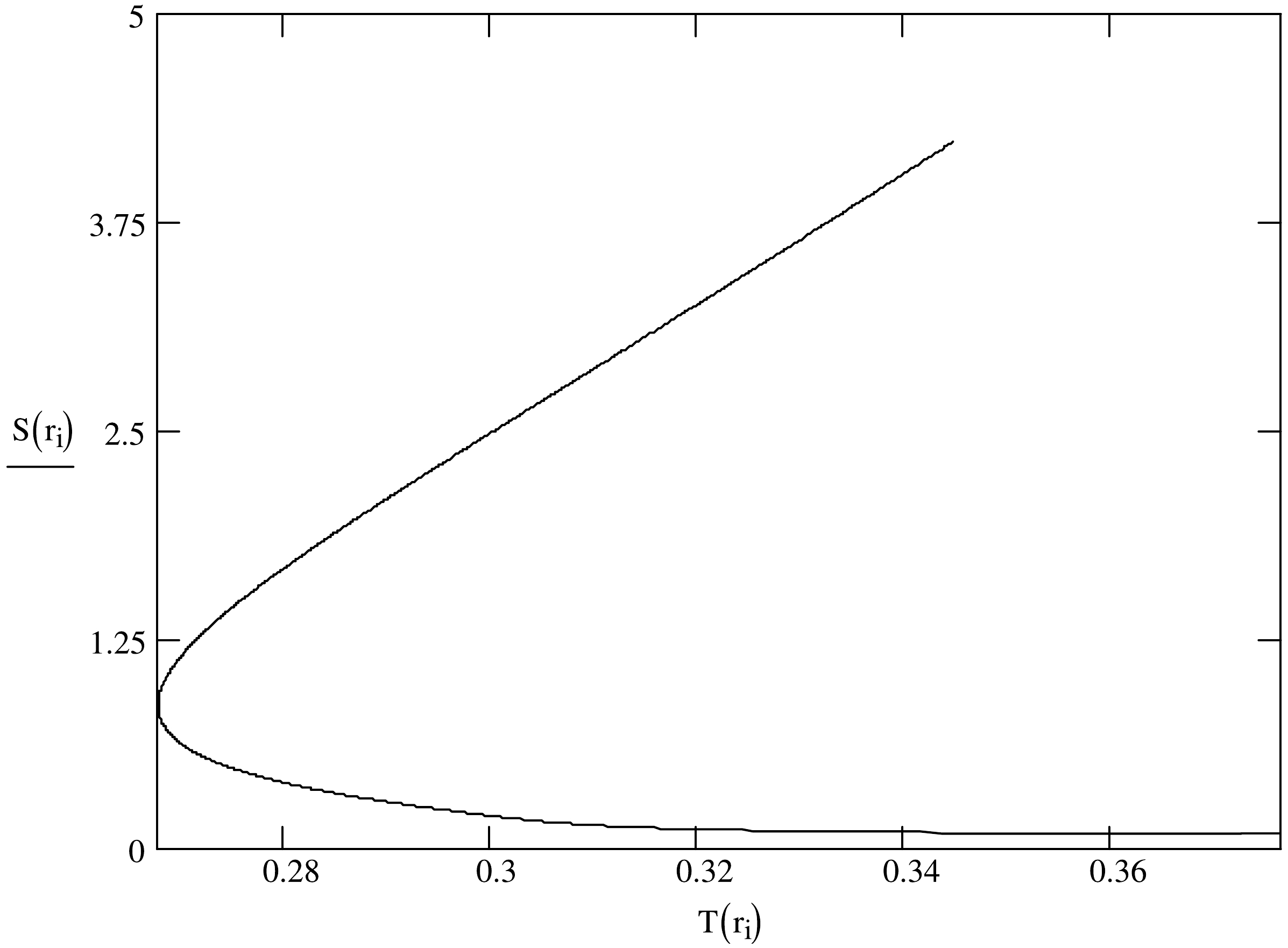

Figure 3.  The curves of the entropy of Einstein-Euler-Heisenberg-AdS black holes in the canonical ensemble as functions of the temperature for nonlinear factors $ \mu=0.08 $.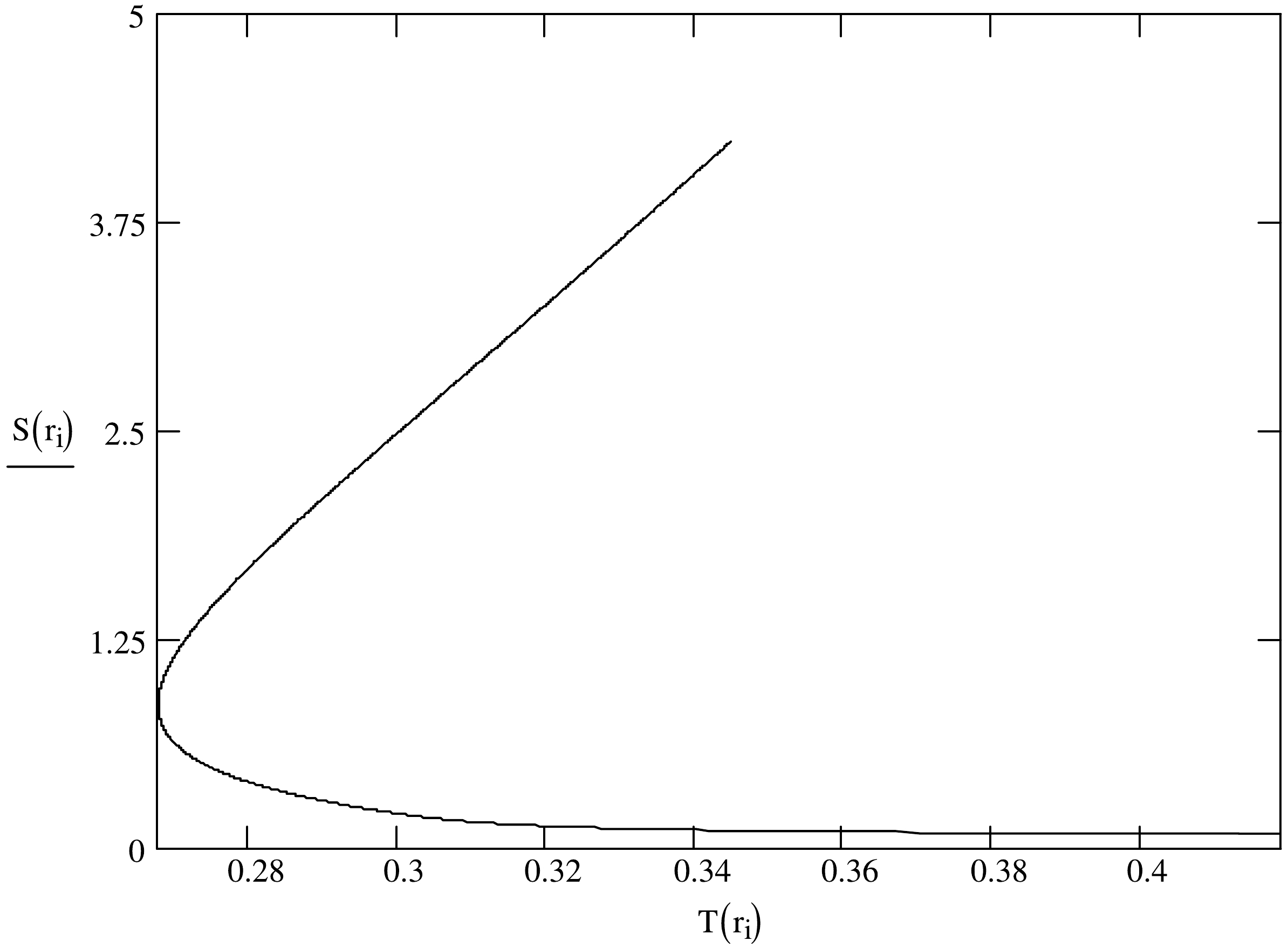

Figure 4.  The curves of the entropy of Einstein-Euler-Heisenberg-AdS black holes in the canonical ensemble as functions of the temperature for nonlinear factors $ \mu=0.1 $.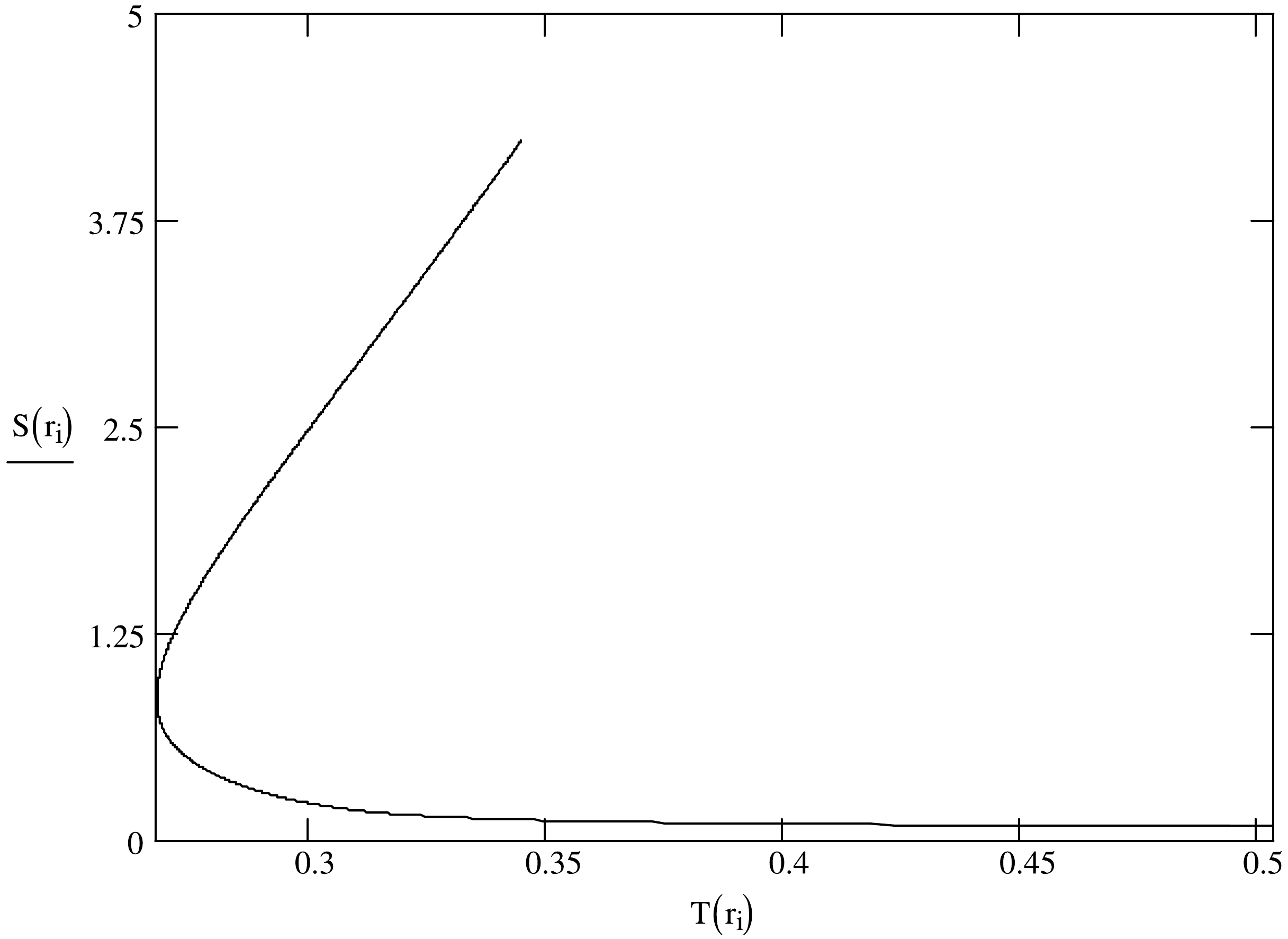

Figure 5.  The curves of the entropy of Einstein-Euler-Heisenberg-AdS black holes in the canonical ensemble as functions of the temperature for nonlinear factors $ \mu=0.14 $.

Based on the analysis above, we continue analyzing the heat capacity of the Einstein-Euler-Heisenberg black holes in the ensemble. According to the thermodynamics of black holes [1, 31, 40, 41, 68], the heat capacity at fixed charge is given by:

From Figs. 3−5, it is clear that the temperature region formed with $ T\geq T_{c} $ means that the temperature keeps positive. The slopes of tangent lines of the upper entropy curves are positive while the slopes of lower part is negative. We can argue that large Einstein-Euler-Heisenberg-AdS black holes with positive heat capacity are thermodynamically stable, while the smaller ones with negative heat capacity will evaporate.

The stability of a black hole needs to be investigated in a systematic way. The possibility for the fragmentation of a black hole claimed that the black hole entropy must increase owing to the second law of thermodynamics during its evolution [70]. Now we wonder whether the charged black holes under the influence from the self-interaction can break into pieces. The original black hole can be thought as the initial state and certainly the final state may consist of two black holes subject to the conservation of mass and charge in the process of fragmentation. During this fragmentation, the mass and charge of the homogeneous source will be rewritten as [70]:

and

respectively. The ratio is limited as $ 0\leq\varepsilon\leq 1 $ [71]. After splitting, one Einstein-Euler-Heisenberg-AdS black hole has its metric as:

where

with mass $ \varepsilon M $ and charge $ \varepsilon Q $. The metric function $ f_{2}(r) $ replaces $ f_{1}(r) $ in the metric (23) and the metric of the other part possessing mass $ (1-\varepsilon)M $ and charge $ (1-\varepsilon)Q $ is obtained as:

The metric with component function $ f_{2}(r) $ belongs to the background of the new Einstein-Euler-Heisenberg AdS black hole that has mass $ (1-\varepsilon)M $ and charge $ (1-\varepsilon)Q $. The entropy difference between the initial black hole and the two fragmented parts can be expressed as [70]:

The fragmented black holes have their own horizons $ r_{1} $ and $ r_{2} $ satisfying $ f_{1}(r_{1})=0 $ and $ f_{2}(r_{2})=0 $ respectively. The entropy difference between the initial Einstein-Euler-Heisenberg-AdS black hole and the final system including two black holes is shown graphically in the Fig. 6. Figure 6 shows that the difference keeps negative no matter how considerable the nonlinear effect is. In the ensemble, the division of this kind of AdS black holes can not happen spontaneously. The nonlinear effect factor just adjust the magnitude of the entropy difference within its region like $ \varepsilon\in[0, 1] $, but the sign of the difference remains negative. Therefore, charged AdS black holes involving electromagnetic self-interactions will not split according to the second law of thermodynamics. We can argue that the self-interactions may make the curves for the dependence of entropy difference on the ratio ε different a little, but the nonlinear influence can not change the curves greatly. Within the region of ratio ε, the entropy differences keep negative.

Figure 6.  The solid, dashed and dotted curves of entropy difference between the initial Einstein-Euler-Heisenberg-AdS black holes and the fragmented bodies in the canonical ensemble as functions of the ration ε for nonlinear factors $\mu=0.08, \;0.1, \;0.14$ respectively.

It is necessary to discuss the stability and phase structure of charged black holes revised by the self-interactions when the potential is invariant. By substituting the definition of electric potential like Eq. (17) into the black hole's mass (17) and the temperature (8), the corresponding thermodynamic variables like the black hole's mass and its Hawking temperature are:

and

When the potential Φ is fixed, the asymptotic behavior of the temperature is $\mathop\lim\limits_{r_{+}\longrightarrow 0}T=\dfrac{\mu\Phi^{4}}{16\pi r_{+}^{3}} > 0$ for larger values under stronger μ influence and $\mathop\lim\limits_{r_{+}\longrightarrow\infty}T=\dfrac{3}{4\pi l^{2}r_{+}} > 0$ which is equal to the asymptotic ones in the canonical ensemble as discussed earlier. The Hawking temperatures depending on the black hole horizon under the influence of electromagnetic self-interactions are depicted in the Fig. 7. It should be pointed out that the curves shapes involving some properties in the Fig. 7 resemble those in the Fig. 1. The temperature curves are also concave, which is similar to the works of the black holes in the fixed-charge ensembles. With the further investigations on the Hawking temperature relating to the horizon, the minimum temperature at the point is listed as follows,

Figure 7.  The solid, dotted and dashed curves corresponding to the dependence of Hawking temperature of Einstein-Euler-Heisenberg-AdS black holes in the grand canonical ensemble on the horizon for nonlinear factors $ \mu=0.08, 0.1, 0.14 $ respectively.

with

There are two valued $ r_{+} $ to support the equation $T(r_{+}) > T_{\rm min}$, one $ r_{+} $ for smaller black hole and the other for the larger one.

In the grand canonical ensembles, the Gibbs free energy is defined as [40, 41],

From the first law of thermodynamics for black holes in Eq. (16), the Gibbs potential function can be demonstrated as [40, 41],

In virtue of the mass (22) and temperature (23), the Gibbs free energy is obtained,

We plot the Gibbs potential of the nonlinear-effect-corrected black holes involving charges as function of temperature graphically with a fixed electric potential. Having investigated the curves with allowed values of nonlinear factor μ, we find that the shapes of the Gibbs potential curves for different values of μ resemble each other. The curve of Gibbs function with $ \mu=0.1 $ is shown in Fig 8. It should be noted that the point of Gibbs free energy at the minimum temperature is non-derivable, which is similar to the Helmholtz free energy in the canonical ensemble discussed earlier.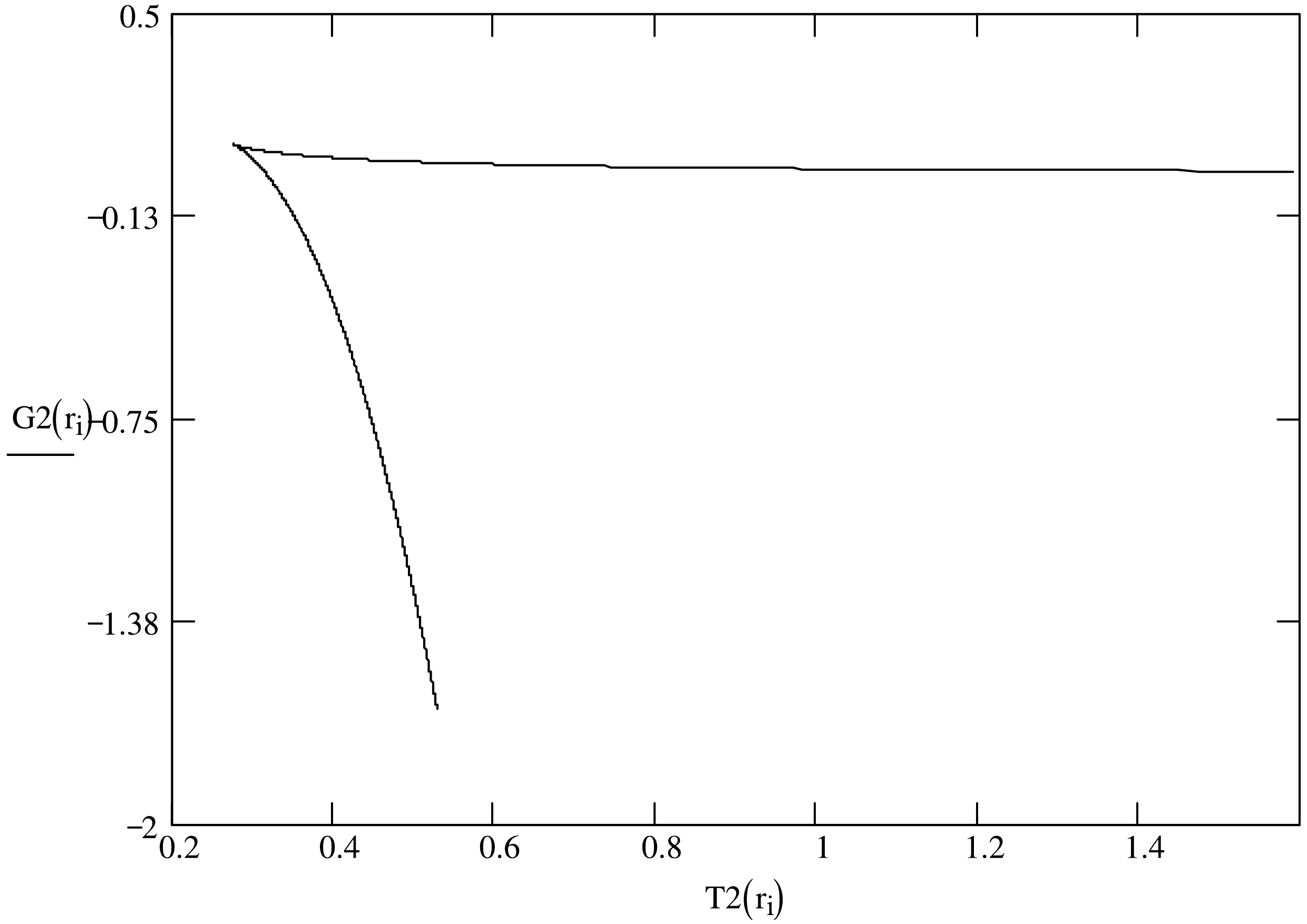

Figure 8.  The curves of the Gibbs potential of Einstein-Euler-Heisenberg-AdS black holes in the grand canonical ensemble as functions of the temperature for nonlinear factors $ \mu=0.1 $.

We use the differential expression (Eq.32) to obtain the entropy of the nonlinear-corrected and charged black hole [40, 41],

Using the temperature (28) and the Gibbs potential (Eq. 33), we plot the entropy function with various values of μ to specify the nonlinear effects in the three diagrams numbered as Fig. 9−11. A series of entropy curves are similar although the parameter of self-interactions μ has different values. It is interesting that the upper portion of the entropy stands for the large black hole and the lower one belongs to the compact object with small size. The phase transition will happen at the joint of the two parts of entropy curves relating to the temperature. The critical temperature $ T_{c} $ for the underivable point of Gibbs potential is related to the nonlinear effect factor μ. It is shown that the slopes of tangent lines for the upper curves of entropy keep positive, meaning that the relatively large charged black hole under nonlinear influence is stable. The smaller black holes with negative heat capacity will evaporate.

Figure 9.  The curves of the entropy of Einstein-Euler-Heisenberg-AdS black holes in the grand canonical ensemble as functions of the temperature for nonlinear factors $ \mu=0.08 $.

Figure 10.  The curves of the entropy of Einstein-Euler-Heisenberg-AdS black holes in the grand canonical ensemble as functions of the temperature for nonlinear factors $ \mu=0.1 $.

Figure 11.  The curves of the entropy of Einstein-Euler-Heisenberg-AdS black holes in the grand canonical ensemble as functions of the temperature for nonlinear factors $ \mu=0.14 $.

The thermodynamic quanties such as Hawking temperature, Helmholtz free energy, Gibbs potential, entropy and heat capacity of the Einstein-Euler-Heisenberg-AdS black holes are discussed in the canonical ensembles and grand canonical ensembles respectively. The black hole surface temperatures have the minimum value associated with the horizon. The self-interactions of the electromagnetic fields have an influence not to be ignored on the smallest temperature. The phase transition may happen at the lowest point. When the temperature exceeds the minimum, the heat capacities of the relatively large black holes are positive and the smaller black holes have negative heat capacities. The tiny black holes with negative heat capacity evaporate and will disappear through evaporation. The huge ones remain and the evolution proceeds. Most of black holes are enveloped in the electromagnetic fields where the intensities have something to do with the backgrounds like in the vicinity of the centers of galaxies or neutron stars. The fields approaching the critical strengths characterize the charged black holes [71]. The charged black holes with self-interaction are universal and their evolution and outcome need to be scrutinized. The expressions of Hawking temperature at fixed-charge point or fixed-potential point contain the parameter μ viewed as the self-interaction of electromagnetic fields, so the self-interaction certainly brings about the modifications to the thermodynamic quantities such as Helmholtz free energy, Gibbs potential, entropy, heat capacity. Our investigations show that these modifications due to nonlinear effects result in the distinct corrections to the thermodynamic characteristics and phase structure of the Einstein-Euler-Heisenberg-AdS black holes in contrast to the Reissner-Nordstrom-AdS black holes, but the influences from nonlinear effect with allowed values of factor μ can not change the evolution and the thermodynamic properties fundamentally. This kind of huge black holes will exist instead of evaporating and splitting.