Unraveling the early universe’s equation of state and primordial black hole production with PTA, BBN, and CMB observations

Recently, multiple data releases of pulsar timing arrays (PTAs) showed significant evidence for a stochastic gravitational-wave background in the nanohertz band [1−4]. The signal has been interpreted to arise from scalar-induced gravitational waves (SIGWs) by the authors of Refs. [5−22]. Although this scenario fits the PTA data better than other scenarios, it results in an issue of overproduction of primordial black holes (PBHs) [23, 24]. In these works, the authors assumed that SIGWs were produced during an epoch of radiation domination with the equation of state (EoS) $ w = 1/3 $. However, the EoS of the early Universe might deviate from the radiation domination [25−39]. We wonder if the overproduction issue can be resolved via considering an arbitrary EoS of the early Universe during an epoch between the end of inflation and the onset of radiation domination.

It is well known that SIGWs could be nonlinearly produced by linear cosmological curvature perturbations, when the latter reentered the Hubble horizon after the end of inflation [40−45]. The energy-density spectrum of SIGWs would be significantly affected by the EoS of the Universe at their production time [28, 39, 45−52]. The corresponding imprints may be left on the PTA signal because the Universe is transparent to the gravitational waves [53]. Therefore, we anticipate that SIGWs are an effective probe of the early-Universe physics, particularly for the EoS parameter.

It is also known that PBHs were produced due to the gravitational collapse of these perturbations if the latter excessed a critical overdensity when they reentered the Hubble horizon [54]. The mass function of PBHs, and thereby the abundance, would also be significantly impacted by the EoS of the Universe at their formation time [51, 55−57]. Therefore, the issue of PBH overproduction might be resolved taking into account an appropriate EoS of the early Universe.

In this work, we study a scenario of SIGWs produced during the epoch with an arbitrary EoS between the end of inflation and the onset of radiation domination. Differing from studies assuming that all of SIGWs were produced during the w-domination before the onset of radiation domination [49, 52], we consider that SIGWs were produced during both epochs. Our scenario is inspired by an enhancement mechanism for SIGWs caused by a sudden transition from the early-matter domination to the radiation domination [46, 47]. We expect that a similar enhancement mechanism can also exist in our scenario. By fitting the North American Nanohertz Observatory for Gravitational Waves (NANOGrav) 15-year data release [3] to our scenario, we study whether varying the EoS of the early Universe can improve the ability of SIGWs to interpret the PTA signal. Meanwhile, we propose that the enhancement of the SIGW spectrum can be significantly constrained by further taking into account the big-bang nucleosynthesis (BBN) [58] and cosmic microwave background (CMB) [59] data. It is worth noting that our results would be different from those of Refs. [23, 24], where the authors only considered the SIGWs produced during the radiation domination and only analyzed PTA data. Moreover, we study the production process of PBHs during the w-dominated epoch. We show that the PBH abundance is significantly changed, probably leading to a resolution of the PBH-overproduction issue.

The remaining of this paper is arranged as follows. In Sec. II, we develop the scenario of SIGWs by taking into account an arbitrary EoS of the early Universe. In Sec. III, we demonstrate the method of data analysis and show the inferred parameter region. In Sec. IV, we study the formation of PBHs in our scenario and the issue of PBH overproduction. In Sec. V, we present our conclusions and discussion.

It has been known that a sudden transition from the early-matter domination to the radiation domination can result in a significant enhancement of the energy-density spectrum of SIGWs [46, 47]. In this work, we replace the early-matter domination with an epoch dominated by “matter” with an arbitrary EoS parameter $ w \in [0,1] $, following the research method of Refs. [48, 49, 52]. However, we still consider the sudden transition because, in general, it is too complicated to study a finite duration of the transition, which is left to future works. We study the imprints of such a scenario on the energy-density spectrum of SIGWs. In fact, several mechanisms can generate the sudden transition from the early-matter domination to the radiation domination [29, 30, 39, 47, 57, 60−65].

We adopt a sudden transition of the scale factor a, i.e., [47]

where η is the conformal time. We introduce $ a_{\text{R}} $ with $ \eta_\text{R} $ at the occasion of transition, i.e.,

where $g\ast$ is an effective number of relativistic species as a function of the cosmic temperature $ T_\text{R} $ corresponding to $ \eta_\text{R} $, $ H_0 $ is the Hubble constant, $\Omega_{m,0}$ is the present-day energy-density fraction of dark matter, and $ a_{\mathrm{eq}} $ denotes the scalar factor at the epoch of matter-radiation equality. The conformal Hubble parameter $ {\cal{H}} = a'/a $ is

where the prime denotes a derivative with respect to η.

The equation of motion for SIGWs is presented as [40−45]

where $ h_{ij} $ is the strain of SIGWs, $ \Lambda^{ab}_{ij} $ is the transverse-traceless operator, and $ {\cal{S}}_{ab} $ denotes the source term consisting of nonlinear couplings between the linear cosmological perturbations ψ, namely, $ {\cal{S}}_{ab}\sim \psi^2 $. Analytic formulas of $ {\cal{S}}_{ab} $ can be explicitly obtained via calculating the non-linear cosmological perturbations with $ \mathrm{xpand}$ [66].

The energy-density fraction spectrum of SIGWs for the sub-horizon modes ($ k\eta \gg 1 $) is given by [44, 45]

where k is a wavenunber, and $ {\cal{P}}_h (k,\eta) $ and $ \bar{{\cal{P}}}_h (k,\eta) $ stand for the two-point correlators of $ h_{ij} $ and $ h_{ij}' $, respectively, defined as

In fact, Eq. (8) is redundant because it can be derived from Eq. (7), but it lets us express Eq. (6) in a simple form. Semi-analytic formulas for $ h_{i j, {\boldsymbol{k}}} $ and $ {h'_{i j, {\boldsymbol{k}}}} $ can be obtained explicitly. According to Eq. (5), the stochastic nature of $ h_{i j, {\boldsymbol{k}}} $ is attributed to that of $ \Psi_{{\boldsymbol{k}}} $, i.e., the initial conditions of ψ. The two-point correlator of $ \Psi_{{\boldsymbol{k}}} $ is defined as

where $ {\cal{P}}_{\zeta} (k) $ is a power spectrum of primordial curvature perturbations ζ, and we related ψ to ζ. For simplicity, we consider a monochromatic spectrum, i.e., ${\cal{P}}_\zeta = A k_\ast\delta(k-k_\ast)$, with $ k_\ast $ being a reference wavenumber. Such a spectrum may be related to the formation of PBHs [67−69], and it has been extensively studied in the literature (see reviews in Refs. [70, 71] and references therein). It would be interesting to study a finite-width spectrum [72,73], which may change parts of our results. However, such a study is left to future works.

In Fig. 1, we show the energy-density fraction spectra of SIGWs for several different sets of model parameters. We take $ k = 2\pi f $ and $ k_\ast = 2\pi f_\ast $ throughout this work. For a small w, i.e., $ w\rightarrow{0} $, the spectrum experiences an enhancement due to the sudden transition. In other words, when the early Universe transits from the almost early-matter domination to the radiation domination, the SIGWs produced during the radiation domination dominates the spectrum.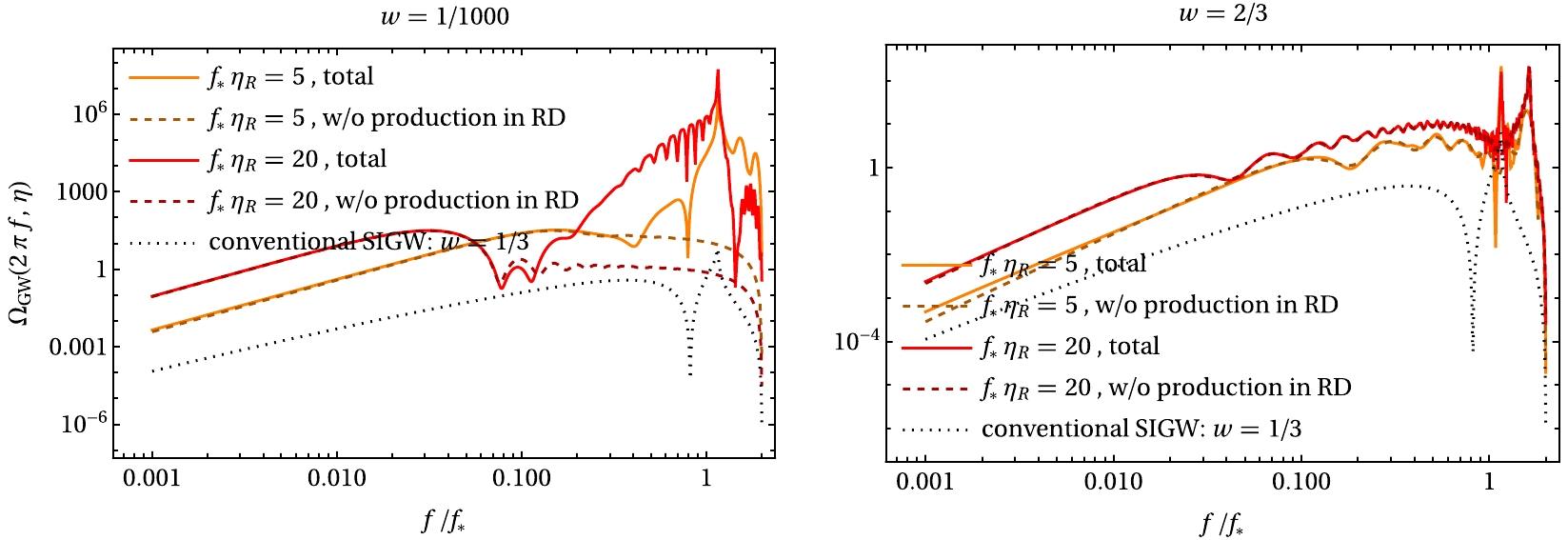

Figure 1.  (color online) Energy-density fraction spectrum of SIGWs produced during the w-domination (dashed) versus the total spectrum (solid). For comparison, we show the conventional scenario of SIGWs (dotted).

This result is consistent with the enhancement mechanism proposed in Refs. [46, 47], where the authors considered a sudden transition from the early-matter domination to the radiation domination.

To compare the theoretical results with the observations, we should know the energy-density fraction spectrum of SIGWs in the present Universe, i.e.,

where $ \Omega_{\mathrm{GW}} $ has been shown in Eq. (6), and the physical energy-density fraction of radiations in the present-day Universe is $ h^{2}\Omega_{\mathrm{r},0} \simeq 4.2\times10^{-5} $ with the dimensionless Hubble constant being $ h = 0.6766 $, as measured by the Planck satellite [74].

Besides the above SIGW component, the PTA signal may be contributed by an astrophysical component arising from binary supper-massive black holes (SMBHs). The corresponding energy-density spectrum is parameterized as a power-law [24, 75]

where $ A_{\mathrm{BHB}} $ is the spectral amplitude, $ \gamma_{\mathrm{BHB}} $ is the spectral index, and $ f_{\mathrm{yr}} $ is a pivot frequency corresponding to one year. Therefore, the total spectrum is expressed as a sum of Eq. (10) and Eq. (11).

Using the same statistical tools used by the PTA collaborations, we analyze the NANOGrav 15-year data [3] using the publicly-available $ \mathrm{PTArcade}$ [76, 77], which implements the Bayes parameter inferences for PTA data by providing a wrapper of $ \mathrm{ENTERPRISE}$ [78] and $ \mathrm{Ceffyl}$ [79]. Here, the total spectrum would be fitted to the PTA data during our data analysis.

We take the BBN [58] and CMB [59] constraints on the effective number of relativistic species into account, which can further pin down the parameter space of SIGWs. In terms of the integrated energy-density fraction, as defined by $\int_{k_{\mathrm{min}}}^{\infty}{\rm d}\ln k \ h^{2}\Omega_{\mathrm{SIGW}}(k)$, the upper limits at 95% confidence level are given as $ 1.3\times10^{-6} $ for BBN [58] and $ 2.9\times10^{-7} $ for CMB [59]. The lower bound of the integral is denoted as $ k_{\rm{min}} = 2 \pi f_{\rm{min}} $, where $ f_{\rm{min}} $ is $ 1.5\times10^{-11}\mathrm{Hz} $ for BBN and $ 3\times10^{-17} $ for CMB [80]. The BBN and CMB data have also been considered in studies of SIGWs [16] and phase-transition gravitational waves [81]. Here, we take each of them into account by assuming that the integrated energy-density spectrum follows a Gaussian distribution, whose variance is given by one-half of the aforementioned upper limit. Therefore, we adopt a modified version of $ \mathrm{Ceffyl}$ [79] via adding two likelihoods to account for the BBN and CMB constraints, respectively.

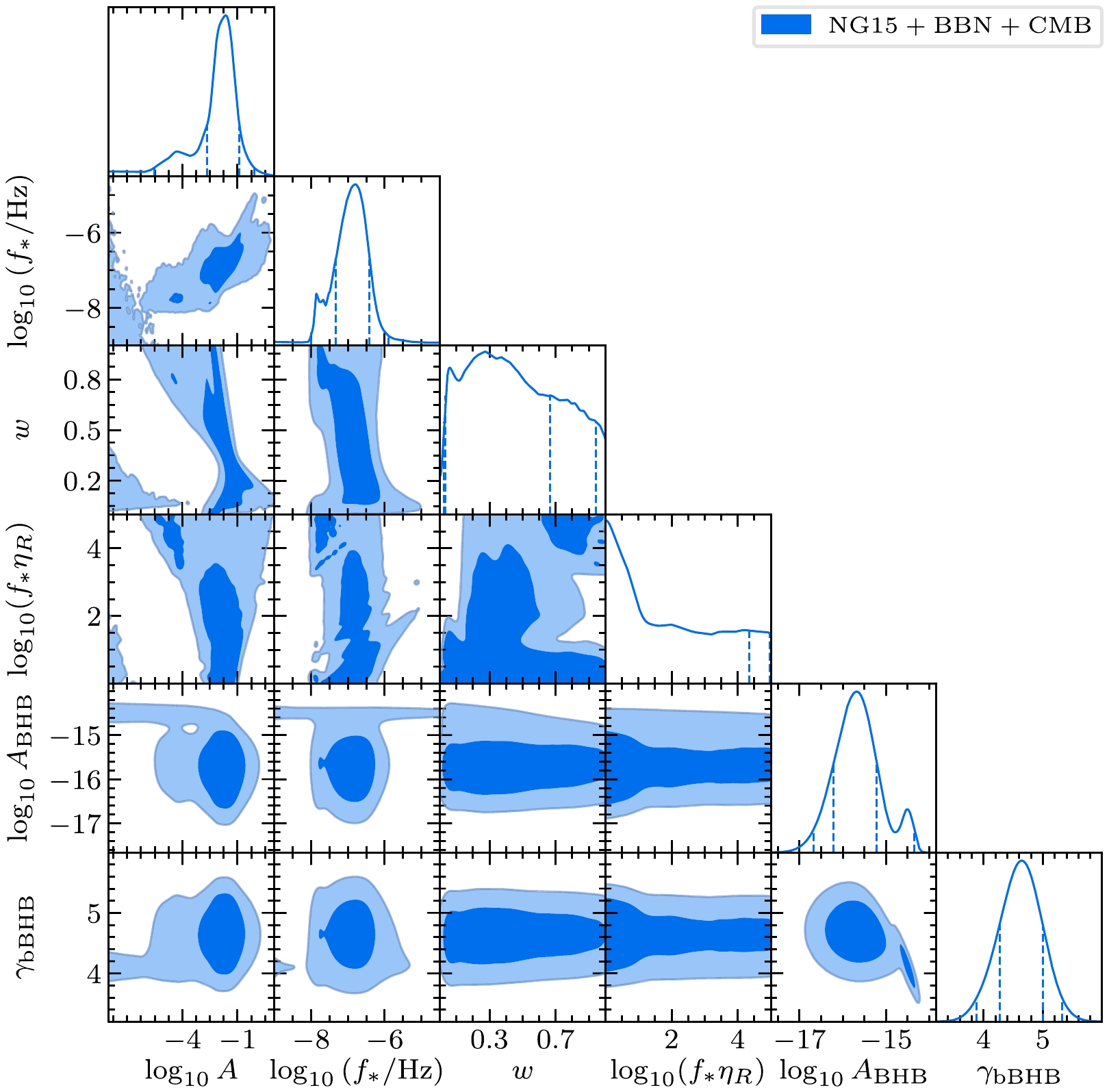
The parameter space under investigation is spanned by $ \log_{10}A $, $ \log_{10}(f_\ast/\mathrm{Hz}) $, w, $ \log_{10}(f_\ast\eta_R) $, $ \log_{10}A_{\mathrm{BHB}} $, and $ \gamma_{\mathrm{BHB}} $. We adopt the uniform priors for the SIGW parameters, i.e., $ \log_{10} A\in {\cal{U}}[-8,1] $, $ \log_{10}(f_\ast/\mathrm{Hz})\in{\cal{U}}[-9,-4.5] $, $ w\in{\cal{U}}[0,1] $, and $ \log_{10}(f_\ast \eta_\text{R}) \in {\cal{U}}[0,5] $. The priors for the last two parameters indicate a prior for $ \eta_{\text{R}} $ within $ [10^{9},10^{14}] $ s. According to Eq. (3), this prior promises $ T_{\text{R}} $ to be higher than $ \sim5 $ MeV, i.e., a temperature at which the w-domination should transition to the radiation domination, as suggested in Refs. [82−84]. In addition, the priors for the SMBH parameters, i.e., $ \log_{10}A_{\mathrm{BHB}} $ and $ \gamma_{\mathrm{BHB}} $, are the same as those of Ref. [23], which follow a bivariate Gaussian distribution, as wrapped in $ \mathrm{PTArcade}$.

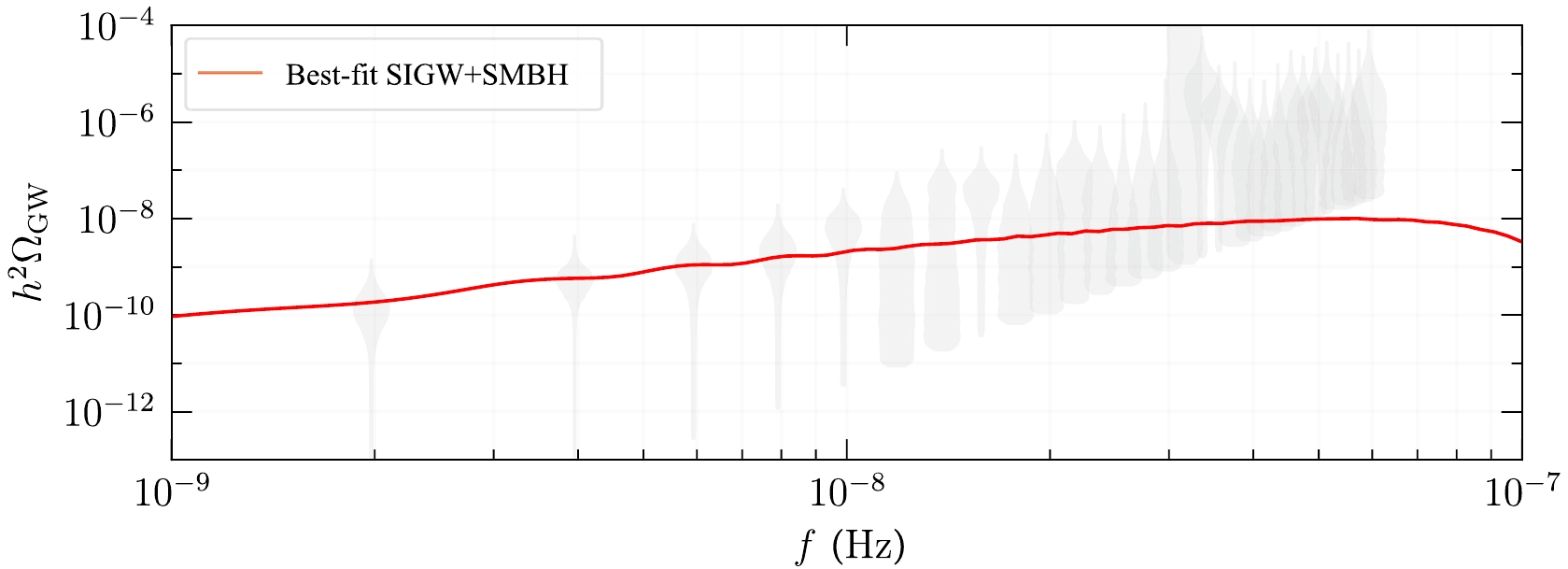
We depict the posteriors of six independent parameters in Fig. 2. Compared with Ref. [23], which analyzed the NANOGrav data only, we combine the NANOGrav data with the BBN and CMB data. Hence, the inferred posteriors in our work are changed significantly. In particular, we find that at 95% confidence level, A is bounded from the upper, but not from the lower, i.e., $ A\leq0.39 $, and $ f_{\ast} $ is within $ 1.2\times10^{-8}-1.9\times10^{-6} $ Hz. In contrast, we obtain looser constraints on w and $ f_\ast\eta_R $. We find that most of the considered EoSs fit the joint dataset just as well as $ w = 1/3 $ within a 95% confidence interval. In addition, our constraints on $ A_{\mathrm{BHB}} $ and $ \gamma_{\mathrm{BHB}} $ are compatible with those of Ref. [23]. We summarize the information of priors and posteriors in Table 1. Furthermore, we compare the best-fit spectrum with the observed signal in Fig. 3.

Figure 2.  (color online) Posteriors of six independent parameters.

Parameter	Prior	Posterior
$ \log_{10} A $	$ {\cal{U}}[-8,1] $	$ -1.92^{+1.50}_{-4.32} $
$ \log_{10} (f_{\star}/{\rm{Hz}}) $	$ {\cal{U}}[-9,-4.5] $	$ -6.89^{+1.16}_{-1.03 } $
w	$ {\cal{U}}[0,1] $	$ 0.44^{+0.52 }_{-0.40 } $
$ \log_{10} (f_{\ast}\eta_\text{R}) $	$ {\cal{U}}[0,5] $	$ 1.74^{+3.09 }_{-1.68} $
$ \log_{10} A_{\mathrm{BHB}} $	Same as Ref. [23]	$ -15.68^{+1.24 }_{-1.00} $
$ \gamma_{\mathrm{BHB}} $	Same as Ref. [23]	$ 4.63^{+0.69}_{-0.75} $

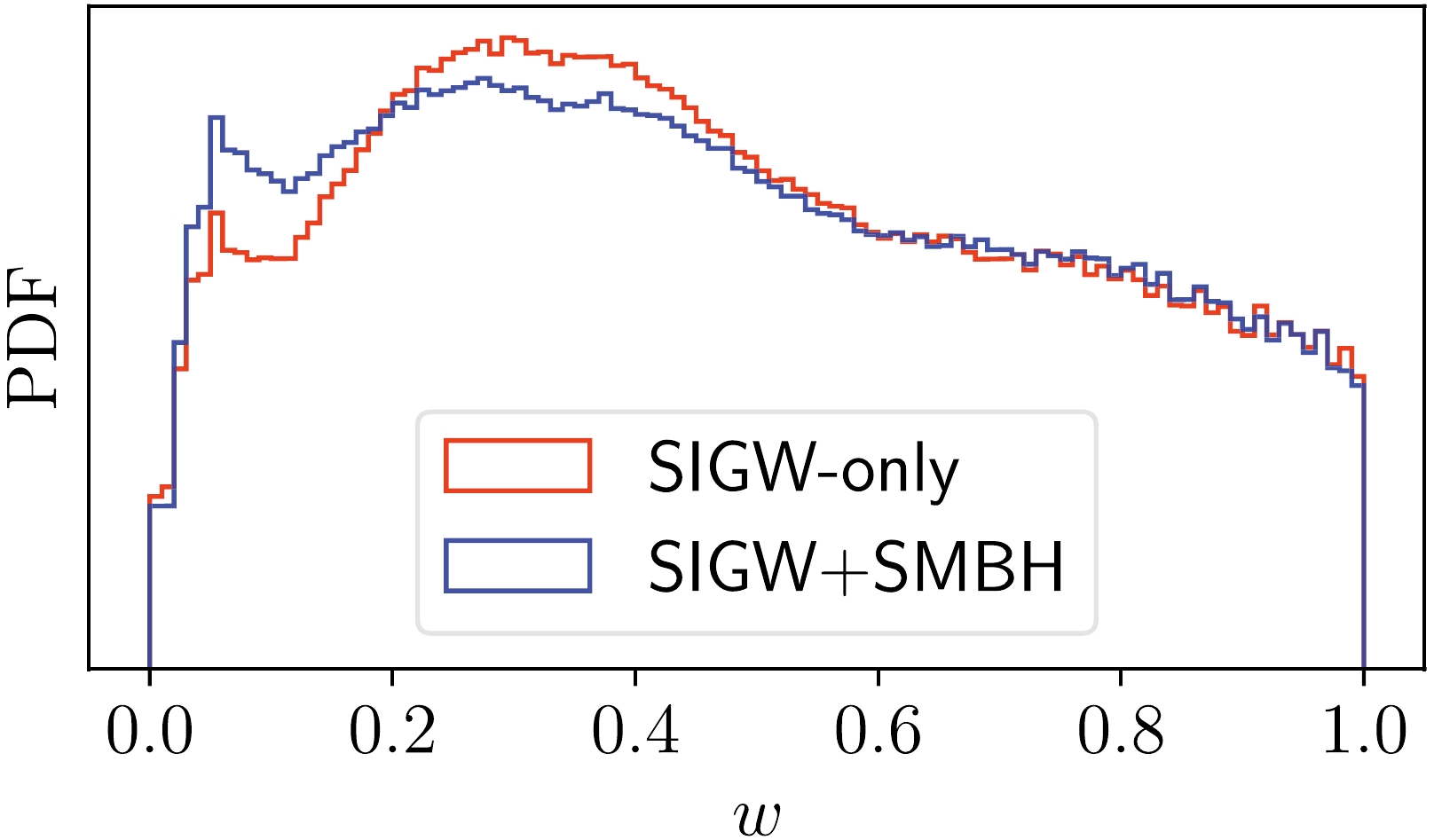
Table 1.  Posterior and prior distributions for the parameters in the analysis. Here, $ {\cal{U}} $ denotes the uniform distribution. We show the results at 95% confidence level.

Figure 3.  (color online) Comparison between the best-fit spectrum and the NANOGrav signal.

Following the same approach mentioned above, we perform an additional analysis of the SIGW-only model, meaning that we consider the SIGW parameters only and disregard the SMBH parameters. In Fig. 4, we compare the inferred probability distribution functions of w between the SIGW-only model (red curve) and the combined SIGW+SMBH model (blue curve). We find that they are compatible with each other.

Figure 4.  (color online) Comparison of the probability distribution functions of the EoS parameter w between the SIGW-only model (red) and the SIGW+SMBH model (blue).

The PBH formation during the radiation domination results in the overproduction of PBHs [23, 24]. In contrast, we expect that PBHs were produced during an epoch instead of the radiation domination. The PBH abundance can be changed to some extent, possibly leading to avoidance of the overproduction issue.

When the k modes reentered into the Hubble horizon, i.e., $ k\simeq{\cal{H}} = 2/[(1+3w)\eta] $, and collapsed to form PBHs, the PBH fraction of dark matter is given by [71]

where H is the Hubble parameter, and we have $ \gamma = 0.356 $ [23], $ \Omega_{m,0} = 0.3089 $, and $ \Omega_\text{CDM} = 0.2589 $ [85]. The probability of PBH production is defined as [86]

where the critical overdensity for gravitational collapse is $ \delta_c = [{3(1+w)}/{(5+3w)}]\sin^2\left[ {(\pi\sqrt{w})}/{(1+3w)}\right] $ [55]. The coarse-grained overdensity is defined as

where $ W(k,R) = \exp[-(k R)^2/2] $ is a window function, and the power spectrum of overdensity is related to that of primordial curvature perturbations ζ, i.e., $ {\cal{P}}_\delta = [{2(1+w)}/ {(5+3w)}]^2(k/{\cal{H}})^4 T^2(k\eta){\cal{P}}_{\zeta}(k) $ with $ T(k\eta) $ being the transfer function of ψ. One should note that the transfer function for the case of $ w\neq1/3 $ is different from that for the radiation domination.

To define the PBH abundance, we should derive a relation between the PBH mass $ M_{\text{PBH}} $ and k via evaluating $ k/k_\ast = {\cal{H}}/{\cal{H}}_\ast $ by making use of $ M_\text{PBH} = \gamma M_H = $ $\gamma (4\pi/3)\rho {{H}}^{-3} $ and Eq. (1). Such a relation is

where $ M_{\text{PBH},\ast} $ corresponds to $ k_\ast $. Finally, the PBH abundance is defined as [23, 87]

where $ M_\text{PBH,R} $ corresponds to the k modes reentering the Hubble horizon at $ \eta_\text{R} $.

In Fig. 5, we show to what extent we could resolve the issue of PBH overproduction via comparing $ f_{\mathrm{PBH}} = 1 $, as predicted by our scenarios, with the inferred posteriors. As suggested in Ref. [23], where only the PTA data was analyzed, the issue of PBH overproduction is inevitable in the case of $ w = 1/3 $. Although being changed significantly, as shown in Sec. III, the posteriors associated with the combination of PTA, BBN, and CMB still can not avoid the PBH overproduction. In this sense, we pay attention to scenarios of the varying EoS in the early Universe. It was surprising to find that the scenarios of $ w\sim{\cal{O}}(10^{-2}) $, which are allowed by our joint dataset, can alleviate the overproduction issue.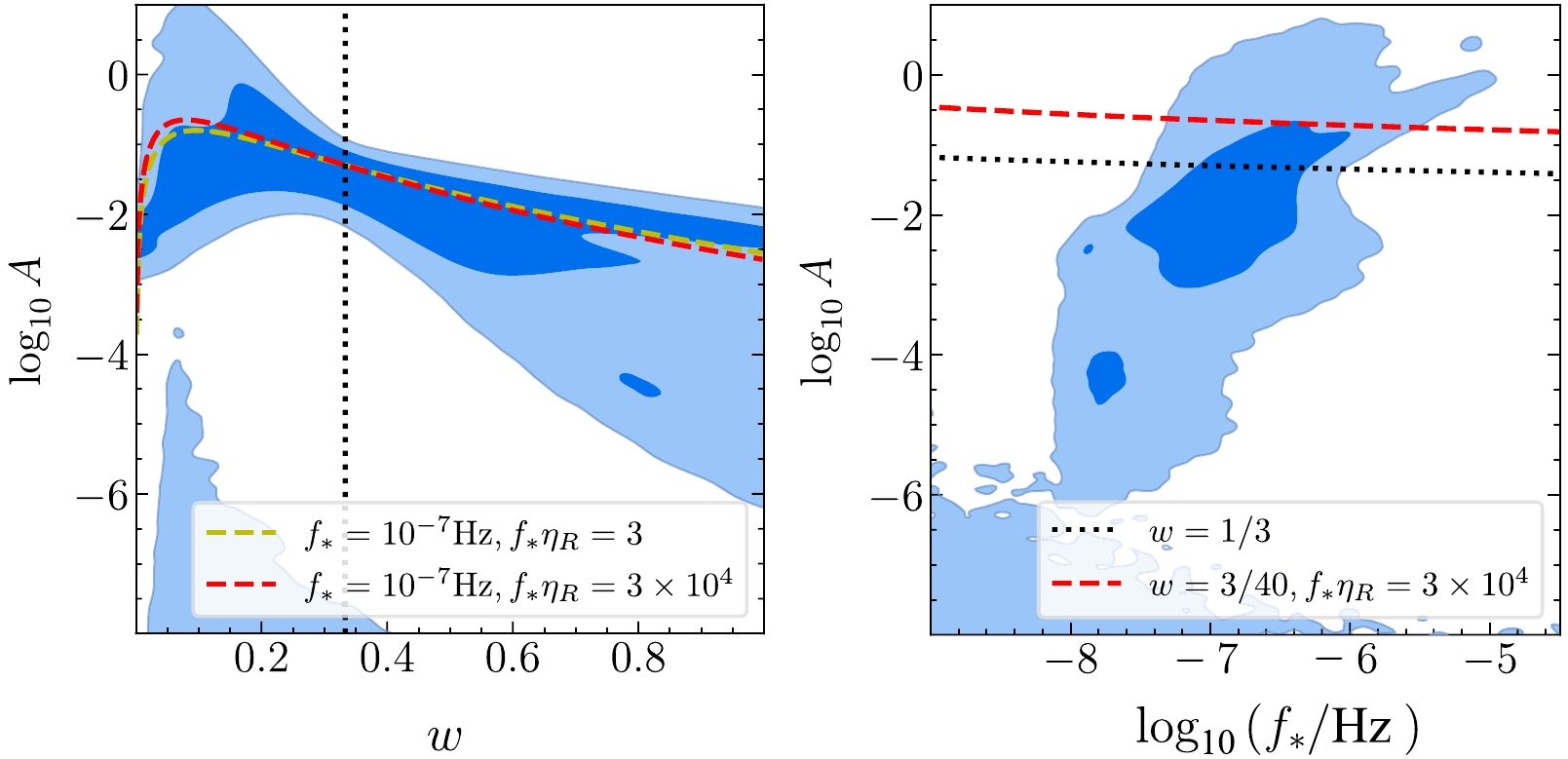

Figure 5.  (color online) The PBH overproduction versus the SIGW scenario with a sudden transition from the epoch of $ w\neq1/3 $ to the radiation domination. We denote $ f_{\mathrm{PBH}} = 1 $ as dashed curves, above which PBHs are over-produced. For comparison, posteriors are shown as shaded regions. In the left panel, $ w = 1/3 $ is shown in the dotted line. In the right panel, $ f_{\mathrm{PBH}} = 1 $ for $ w = 1/3 $ is also shown in the dotted curve.

In this work, we studied the influence of the EoS of the early Universe on the production of SIGWs, and further interpreted the recent PTA data releases as well as the overproduction issue of PBHs. Via generalizing the scenario of Refs. [45−47] and following the method of Refs. [48, 49, 52], we computed the energy-density fraction spectrum of SIGWs for a sudden transition of the early Universe from an arbitrary EoS $ w\in[0,1] $ to the radiation domination $ w = 1/3 $. We showed that the SIGW spectrum exhibits a notable enhancement as the parameter w approaches zero, as shown in Fig. 1. To obtain precise constraints on the model parameters, we analyzed the data combination incorporating the NANOGrav 15-year PTA data with the BBN and CMB data. To our knowledge, this is the first time that Bayes data analysis is performed for the considered topic. It is also the first time that PTA data are combined with BBN and CMB data for the Bayes data analysis. The posteriors of model parameters are presented in Table 1. In addition, studying the PBH production in the w-dominated epoch, we found that the PBH-overproduction issue can be alleviated to some extent, as demonstrated by Fig. 5.

In fact, the production of SIGWs in the early Universe with an arbitrary EoS was studied in Refs. [48−50, 52]. In these works, the gravitational waves were produced during the w-domination, without further production during the subsequent radiation domination. However, it was shown that for SIGWs produced during both the early-matter domination and subsequent radiation domination, the SIGW spectrum could be significantly enhanced due to a sudden transition of EoS [46, 47]. We found a similar enhancement mechanism for our scenario.

We propose that the SIGW spectrum is tightly constrained by the PTA data and the total energy-density fraction by the BBN and CMB data. In Table 1, we present the allowed parameter region, e.g., the spectral amplitude $ A\leq0.39 $, spectral peak frequency $ f_\ast\sim10^{-8}- 10^{-6} $ Hz, and EoS $ w = 0.44_{-0.40}^{+0.52} $. Compared with those of Ref. [23], the posteriors have been significantly changed owing to the combination of PTA data with BBN and CMB data, and the consideration of different scenarios of SIGWs. We revealed the importance of BBN and CMB for data analysis. Our results can be further tested with future observations. Other works relevant to the background EoS can be found in Ref. [88].

By exploring the production of PBHs during the epoch of w-domination, we found that our scenario of $ w\sim{\cal{O}}(10^{-2}) $ can suppress the abundance of PBHs, leading to alleviation of the overproduction issue [23, 24]. It should be noted that we derived systematic formulas for the PBH abundance, implying a consistent study of PBH production. In addition, the speed of transition from the w-domination to the radiation domination is another issue to investigate. Introducing a finite speed of transition into our model may change our results [57, 89]. However, it is extremely complicated to take the effect of transition speed into account following the existing research approach. To our knowledge, no works have adopted this research direction until now. We think that this warrants further study, which is left to future work.

We acknowledge Zucheng Chen, Shi Pi and Yan-Heng Yu for helpful discussion.

In conformal Newtonian gauge, the perturbed spatially-flat Friedmann-Robertson-Walker (FRW) metric is

where η is a conformal time, a is a scale factor of the Universe, both ϕ and ψ are the linear cosmological scalar perturbations, and $ h_{ij} $ denotes the second-order tensor perturbations, i.e., SIGWs. In the absence of anisotropic stress, we have $ \psi = \phi $, exactly. Here, the evolution of ψ is determined by the master equation,

where $ ' $ denotes the derivative with respect to η, and we adopted an adiabatic sound speed $ c_s^2 = w $ with $ 0\leq w \leq 1 $ for a phenomenological study. By solving Eq. (18), we obtain the Fourier modes of ψ in the w-domination and radiation domination, respectively, namely,

where the superscripts (w) denote the w-domination, and we introduce $ \eta_{w} = \eta-(1-3w)\eta_\text{R}/2 $. $ \Psi_{{\boldsymbol{k}}} $ stands for a random variable related to the primordial curvature perturbations, and $ _0 F_1 $ is the confluent hypergeometric function. According to the continuity and differentiability of $ \psi_{\boldsymbol{k}} $, we can determine $ \psi_{{\boldsymbol{k}}}^{(\text{A})} $ and $ \psi_{{\boldsymbol{k}}}^{(\text{B})} $ as follows:

where we introduced $ y = k\eta_w $.

The equation of motion for SIGWs is presented in Eq. (5) in the main text, where the source term $ {\cal{S}}_{a b} $ consisting of the linear perturbations is given by

Therefore, in the Fourier space, we obtain the subhorizon modes of $ h_{i j,{\boldsymbol{k}}} $ based on Eq. (5) in the main text, namely,

where $ {\cal{S}}_{ab,{\boldsymbol{k}}} $ stands for the Fourier mode of $ {\cal{S}}_{ab} $ with the wavevector $ {\boldsymbol{k}} $. Due to the continuity and differentiability of $ h_{ij,{\boldsymbol{k}}} $, the time-independent quantities $ h_{i j, {\boldsymbol{k}}}^{(\text{A})} $ and $ h^{(\text{B})}_{i j, {\boldsymbol{k}}} $ can be determined by SIGWs produced during the w-domination (denoted as $ h_{i j, {\boldsymbol{k}}}^{(w)}) $, namely,

where we define

and we introduce $ \alpha = - 3 (1 - w) / [2 (1 + 3 w)] $. $ Y_{\alpha}(x) $ is the Bessel function of second kind, and $ J_{\alpha}(x) $ is the Bessel function of first kind.