-
Describing baryons in the AdS/QCD bottom approach is similar to describing meson states. We start with an action for bulk fields dual to baryons at the conformal boundary. However, confinement is performed slightly differently from that in the meson scenario. Confinement is understood in these bottom-up scenarios as a localization process, where the non-normalizable bulk modes become normalizable by appropriately adding an energy scale. This energy scale later fixes the Regge slope. This localization mechanism can be performed via two possible alternatives: cutting off or deforming the AdS geometry, i.e., breaking conformal invariance in the bulk.
Space cutoff leads to the so-called hardwall [1–3] and softwall models [4]. The former is achieved by placing a D-brane into the AdS space. The locus of the brane defines the energy scale as
$ \Lambda_\text{QCD} = 1/z_c \propto M_0 $ , where$ M_0 $ is the lightest hadron on the Regge trajectory. The mass spectrum usually behaves as$ M_n \propto n $ , which is unexpected from light-unflavored hadron phenomenology. Quantum mechanically, this model behaves like an infinite square well. The softwall model case includes a dilaton field that can be static [4] or dynamically generated [5], breaking conformal invariance smoothly. The net effect of this dilaton is the emergence of linear confinement [4] when considering quadratic dilaton profiles, leading to Regge-like behavior,$ M_n^2\propto n $ , with n defined as the excitation number, which is expected for unflavored light hadrons. In terms of quantum mechanics, these holographic potentials defined with quadratic dilatons behave as harmonic oscillators in the polar plane.The softwall model proposal has proven successful in describing the spectroscopy of light-unflavored hadrons [6–17], form factors [18–20], structure functions [21], and deep inelastic scattering [12, 22]. It has been extended to the light-front case [23–25], opening an area of active research on wave functions [26, 27], form factors [28, 29], and spectroscopy [30].
However, despite all its success in the light sector, it cannot properly describe heavy mesons because their Regge trajectories are not linear. From the Bethe-Salpeter perspective, by including the quark constituent, mass linearity is lifted, i.e.,
$ M_n^2\propto n^{\nu} $ , where ν depends on the constituent mass [31–33]. This induces another issue related to the mesonic decay constants. For bottom-up models, the decay constants do not match the phenomenologically expected behavior; mesonic decay constants (in units of MeV) are expected to decrease with the excitation number. For hardwall, they increase, and for softwall, they are degenerate. Attempts to preserve quadratic behavior and obtain acceptable phenomenological decays have been conducted in the past [34, 35]. However, as noted in Ref. [36], decay constants also depend on the low-z behavior of the dilaton field. This situation is precisely the scenario proposed in Ref. [37] for heavy vector quarkonia.Regarding the heavy-spectroscopy issue, Ref. [38] extended the softwall model to include non-linear Regge trajectories by promoting the quadratic dilaton
$ \kappa^2\,z^2 $ to be deformed as$ (\kappa\,z)^{2-\alpha} $ by a parameter that accounts for constituent mass effects. This proposal has also been successful in describing non-$ q\bar{q} $ states such as hadroquarkonium, hadronic molecules, and hybrid mesons, as shown in Ref. [39], where configurational entropy was used as a tool to test the feasibility of the proposed holographic structures.Reference [40] originally proposed the deformation of AdS space in the context of gauge/string duality applied to describe OPE expansion for a two-point function. In their study, the author proved how quadratic deformations in the AdS
$ _5 $ sector caused Regge-like behavior. This observation led to Ref. [41], where the authors extended this idea to compute Regge trajectories for mesons and baryons. Subsequently, the geometric deformation was used in Ref. [42] to describe glueballs and light baryons. In all these studies, deformations in the AdS geometry induced locality by transforming bulk modes into normalizable ones to realize confinement, and this fact translated into the emergence of confining terms in the holographic potential. In this sense, deformations and softwall models are equivalent. However, the analytical behavior of eigenmodes is completely different. In this framework, it is possible to describe proton structure functions [43], and electromagnetic form factors for nucleons [44] and pions [45].Another tool, known as configurational entropy (CE), has gained importance within the holographic approaches developed to describe hadrons. The original proposal [46–48] addresses the connection between the information and physical solutions of a given system, which relates to how energy is localized in such solutions. This localization of energy is related to the emergence of order structures. Thus, CE can be understood as a entropic measure of how system constituents are organized in space. Holographically, CE has been extended in studies such as [49, 50] to describe black hole stability in AdS and heavy quarkonia. In particular, the authors found the connection between decay constants and CE: when the former decreases with excitation number, the latter increases. This observation can be considered an insight into hadronic stability via holographic tools. In this line of research, several studies have enriched the literature, for example, Refs. [51–55].
In this study, we consider an approach to heavy baryons involving the deformed dilaton proposal in both softwall and deformed geometry models. We also consider CE as a tool to test hadronic stability in these models.
This paper is organized as follows. Section II summarizes the bottom-up description of baryons. Section III uses geometric deformations and static dilaton within the context of non-linear Regge trajectory to describe Σ baryons. Section IV presents a detailed calculation of the CE for these fermionic systems. Finally, in Sec. V, we present our conclusions.
-
Let us consider the AdS
$ _5 $ space defined by the Poincar$ \rm{\acute{e}} $ line element as$ {\rm d}S^2={\rm e}^{2\,A(z)}\,\left[{\rm d}z^2+\eta_{\mu\nu}\,{\rm d}x^\mu\,{\rm d}x^\nu\right], $

(1) where the warp factor is defined as
$ A(z)=\log(R/z)+h(z) $ , with R as the radius of the AdS curvature. The function$ h(z)\in \mathcal{C}^{\infty} $ is the geometric deformation, which is fixed at zero for the softwall model case. We use Latin indices for five-dimensional bulk objects and Greek indices for four-dimensional boundary objects.Baryons, as standard in AdS/QCD, are described by bulk fermionic fields. However, this is not a straightforward task compared to that for mesons, where the effect of a dilaton field (static or dynamically generated) enters directly into the holographic potential owing to the coupling of the dilaton field with bulk fields dual to mesons. In the case of baryons, the dilaton field is factorized out from the equation of motion. Thus, different mechanisms must be considered to model these states. This situation can be avoided when geometric deformations are considered, because confinement information is condensed in the warp factor. The main objection now arises because the background is flavor-dependent.
We describe fermionic fields in AdS backgrounds with deformation and dilaton fields, following the prescription defined in [13, 42].
Let us focus on baryons with dilaton fields. Refs. [13, 56] noted that the dilaton field can be introduced as an anomalous dimension that modifies the fermion bulk mass as
$ \tilde{M}_5(z)=M_5+\frac{\Phi(z)}{R}. $

(2) This modification ensures that the bulk modes become normalizable when considering dilaton-based models.
-
For
$ 1/2 $ baryons, the bulk action is written in the standard Dirac form as follows:$ I=\frac{1}{\mathcal{K}}\int{{\rm d}^5x\,\sqrt{-g}\left[\frac{1}{2}\bar{\psi}\,\Gamma^r\,\overset{\leftrightarrow}{D}_r\,\psi-M_5(z)\,\bar{\psi}\,\psi\right]}, $

(3) where
$ \Gamma^r=e^r_a\,\gamma^a $ represents the Dirac gamma matrices in curved space,$ \mathcal{K} $ is a constant that fixes the units in the action, and the covariant spin-connected derivative operator$ D_m $ is defined as$ D_m\,\psi = \partial_m\,\psi+\omega^{ab}_m\,\sigma_{ab}\,\psi/{4}, $

(4) where
$ \omega^{ab}_m $ is the spin connection, and$ \sigma^{ab} $ is the flat gamma matrix commutator. The equations of motion for these fields are as follows:$ \begin{eqnarray} \left(\Gamma^m\, \overset{\rightarrow }{D}_m-M_5\right)\,\psi(z,x^\mu)=0, \end{eqnarray} $

(5) $ \begin{eqnarray} \bar{\psi}(z,x^\mu) \left(\Gamma^m\, \overset{\leftarrow}{D}_m+M_5\right)=0. \end{eqnarray} $

(6) For AdS
$ _5 $ , the frame field is$ e^a_m=\delta^a_m\,{\rm e}^{A(z)} $ , where Latin indices$a,b,c,\cdots$ denote the flat frame indices. Thus, for the spin-affine connection, the non-zero components are$ \omega^{5\,b}_\mu=-A'\left(z\right)\,\delta^b_\mu. $

(7) Therefore, the Dirac equation for the bulk spinor
$ \psi(z,x^\mu) $ can be written as$ \left[ \gamma^{5}\,\partial_z+ \eta^{\mu \nu}\,\gamma_\mu\,\partial_\nu+2\,A'\left(z\right)\gamma_{5}-M_{5}(z)\,{\rm e}^{A\left(z\right)}\right]\psi\left(z,x^\mu\right)=0. $

(8) A similar expression can be found for the adjoint bulk spinor
$ \bar{\psi}(z,x^\mu) $ . Next, we introduce the chiral components for the bulk spinors as$ \psi(z,x^\mu)=\psi_L(z,x^\mu)+\psi_R(z,x^\mu). $

(9) $ \psi_{L/R}(z,q)=\frac{1\pm\gamma_5}{5}\,\psi(z,q). $

(10) Using this definition and after transforming to the Fourier space, the Dirac equation is written as
$ \left[\mp\partial_z\mp2\,A'\left(z\right)-M_{5}(z)\,{\rm e}^{A(z)}\right]\psi_{L/R} +m\,\psi_{L/R}=0, $

(11) $ \left[\partial_z+2\,A'\left(z\right)\pm M_{5}(z)\,{\rm e}^{A(z)}\right]\psi_{L/R} \mp m\,\psi_{L/R}=0. $

(12) In the last equation, we use the boundary Dirac equation in Fourier space to introduce the baryonic mass m.
To decouple these equations, we take the second derivative, and after some algebra, we obtain the Sturm-Liouville form of the Dirac equation:
$ \begin{aligned}[b]& \psi''_{L/R} +4\,A'\,\psi'_{L/R}+\left\{4\,A'^2+2\,A''\right.\\ &\quad \left.\pm \left[M_{5}(z)\,A'+M_{5}'(z)\right]\,\,{\rm e}^A-M_{5}^2(z)\,{\rm e}^{2\,A}\,\right\}\psi_{L/R}+m^2\,\psi_{L/R}=0. \end{aligned} $

(13) At this step, confinement emerges from the holographic potential
$ V(z) $ . This potential is defined using the Bogoliubov transformation,$ \psi_{L/R}\left(z\right)={\rm e}^{-2\,A\left(z\right)}\,\phi_{L/R}\left(z\right), $

(14) and we obtain the Schrödinger-like form of the bulk equations of motion:
$ -\phi_{L/R}''+V(z)\,\phi_{L/R}=m_n^2\,\phi_{L/R}, $

(15) with
$ p^2=-m_n^2 $ . The potential has the following structure:$ V(z)=M_{5}^2(z)\,{\rm e}^{2\,A(z)}\mp \left[M_{5}(z)\,A'(z)+M_{5}'(z)\right]\,{\rm e}^{A(z)}. $

(16) The eigenvalues of this potential correspond to the spin
$ 1/2 $ baryon masses at the boundary. A similar behavior is found for the adjoint spinor solutions. Both left and right solutions have the same eigenvalue mass$ m_n^2 $ . Thus, following [42], we choose right-spinors to be dual to baryons at the boundary. The final component we must fix is the bulk mass to define the baryonic identity. We discuss this topic in the next section.In the next sections, we apply the non-quadratic dilaton and deformed geometry to this formalism.
-
Let us consider spin 3/2 baryons defined using a Rarita-Schwinger bulk field. The bulk action in this case is given by [13]
$ \begin{aligned}[b] I=\;&-\frac{1}{2\,\mathcal{K}}\int{{\rm d}^5x\,\sqrt{-g}\,g^{mn}} \left[\bar{\psi}_{m}\,\Gamma^r\,\overset{\leftrightarrow}{\nabla}_r\,\psi_{n}-M_5(z)\,\bar{\psi}_{m}\,\psi_{n}\right], \end{aligned} $

(17) where
$ \psi_m(z,x^\mu) $ is a bulk vector spinor, and the covariant derivative is defined as$ \nabla_m\,\psi_{n}=D_m\,\psi_{n}-\Gamma^r_{m n}\,\psi_{r}, $

(18) with
$ \Gamma^r_{mn} $ as the Levi-Civita affine connection in AdS$ _5 $ , which has the following non-zero components:$ \Gamma^z_{zz}=A'\left(z\right), $

(19) $ \Gamma^z_{\mu\nu}=-A'\left(z\right)\,\eta_{\mu\nu}, $

(20) $ \Gamma^\mu_{z\nu}=A'\left(z\right)\,\delta^\mu_\nu. $

(21) From the action principle (17), we obtain the following bulk equations of motion:
$ \left[g^{nm}\,\Gamma_m\,\nabla_n-M_{5}(z)\right]\,\psi_{m}=0. $

(22) We now consider gauge fixing. Because no holographic information should be explicitly written at the boundary, i.e., no dependence on the holographic coordinate z is expected, we impose
$ \psi_{z}(z,x^\mu)=0. $

(23) As a consequence, we have the following set of transverse conditions:
$ \Gamma^m\,\psi_{m}(z\,x^\mu)=0, $

(24) $ g^{mn}\,\nabla_m\,\psi_{n}(z,x^\mu)=0. $

(25) Condition (25) considers the product of the antisymmetric products of the Dirac matrices
$ \Gamma^{mnr} $ with the symmetric spinor tensor field, i.e.,$ \begin{eqnarray} \Gamma^{mnr}\,\nabla_m\,\psi_{r}+M_{5}(z)\,\Gamma^{mn}\,\psi_{m}=0, \end{eqnarray} $

(26) which is equivalent to the Dirac equation. Using the first transverse condition leads to the second one [57].
After the gauge fixing process, and using the expressions for the covariant derivative in AdS
$ _5 $ , we write the equations of motion for the bulk vector spinor as$ \left[\gamma^{5}\,\partial_z+\gamma^\mu\,\partial_\mu+2\,A'\left(z\right)\,\gamma_{5}-M_{5}(z)\,{\rm e}^{A\left(z\right)}\right] \psi_{m}=0, $

(27) which is the equation for spin 1/2 bulk fermions. The main difference is the bulk mass
$ M_5(z) $ because the operators that define spin 3/2 baryons have a different scaling dimension than those of spin 1/2 baryons.Therefore, following the same procedure used for the spin 1/2 bulk spinor, we obtain the Schrödinger-like equation of motion:
$ -\phi_{L/R}''+U\left(z\right)\,\phi_{L/R}=m_n^2\,\phi_{L/R}, $

(28) with the holographic potential
$ U(z) $ defined as$ U(z)=M_{5}^2(z)\,{\rm e}^{2\,A(z)}\mp \left[M_{5}(z)\,A'(z)+M_{5}'(z)\right]\,{\rm e}^{A(z)}. $

(29) As in the spin 1/2 case, we consider baryons defined by right-vector spinors. In the next sections, we solve the eigenvalue problem for the non-quadratic and deformed geometry models.
-
In this section, we apply the aforementioned machinery to describe the Σ baryon spectrum.
These Σ baryons were initially observed in cosmic ray experiments during the 1950s and have since been extensively studied in particle accelerators. These states are compounded by a pair of light quarks with an s quark. They play a crucial role in understanding the strong force that binds quarks and the composition of protons and neutrons within atomic nuclei.
Here, we focus on neutral Σ baryons with
$I(J^P)= 1(1/2^+)$ and$ I(J^P)=1(3/2^+) $ . The experimental masses are listed in Tables 1 and 2. Neutral Σ baryons, aside from$ \Sigma^0(1/2) $ , predominantly decay into neutral kaons.$ I(J^P)=1(1/2^+) $ states

n $ M_\text{{th}} $ /MeV

$ M_\text{Exp} $ /MeV

%M 1 1135.22 1192.6±0.02 4.81 2 1431.32 1585±20 9.70 3 1717.22 1820—1940 8.66 Table 1. Masses of the
$ \Sigma(1/2) $ trajectory using a non-quadratic deformed background with$ k_{1/2}=239 $ MeV and$ \alpha_{1/2}=0.16 $ . The ground state is represented by$ n=1 $ . The last column shows the relative error. For the mass intervals, we choose the average between the interval extremes. The experimental masses are taken from the particle data group [59].$ I(J^P)=1(3/2^+) $ states

n $ M_\text{th} $ /MeV

$ M_\text{Exp} $ /MeV

%M 1 1401.37 1382.83±0.34 1.28 2 1675.77 1730—1830 5.86 3 1942.61 1920—1960 0.13 4 2203.36 2060—2120 5.42 5 2459.06 2240±27 10.07 In previous studies (see [58] and the references therein), the Regge trajectory has been found to depend on the constituent mass of quarks. Thus, if a hadron contains an s or a heavy quark, the linearity of the trajectory ceases. Motivated by this observation, we employ the non-quadratic softwall model [38] to address neutral Σ spectroscopy.
In the standard AdS/CFT prescription, baryonic states, created by boundary operators such as
$ \hat{\mathcal{O}}\sim \epsilon_{ijk}\, \hat{q}_i \,\hat{q}_j\,\hat{q}_k $ with$ \text{dim}\,\bar{\mathcal{O}}=\Delta $ , are dual to bulk normalizable fermionic modes that scale as$ z^\Delta $ . This matching is a consequence of the so-called field/operator duality. These bulk fields obey the dynamics governed by action densities, such as (3) and (17). The information regarding the hadronic identity, i.e., the dimension of$ \bar{\mathcal{O}} $ , is condensed in the fermionic bulk mass$ M_5 $ . In general, for a given hadron, we can write the conformal dimension as a combination of the contribution from constituent quarks (twist) and the total orbital angular momentum L:$ \Delta_{\rm baryon}=\Delta_{q}+L. $

(30) In the case of baryons, the above expression becomes useful for dealing with high fermionic spin. Higher spin contributions can be written with L. For Σ with spin 1/2 and 3/2, their L values are 0 and 1, respectively.
Because a baryonic state has three quarks, each with a scaling dimension of
$ 3/2 $ , the constituent scaling dimension is$ \Delta_{q}=9/2 $ . By substituting these data into Eq. (30), we can easily obtain the conformal dimensions$ \Delta_{1/2}=9/2 $ and$ \Delta_{3/2}=11/2 $ for the Σ trajectories.From the AdS/CFT dictionary, we find the following relationship for the fermion bulk mass
$ M_{5} $ and its baryon conformal dimension:$ \left|M_5\right|=\Delta_{\rm baryon}-2. $

(31) Therefore, according to Eq. (30), for the Σ baryons, we obtain
$ M_{5}=5/2 $ and$ M_{5}=7/2 $ for$ \Sigma(1/2) $ and$ \Sigma(3/2) $ , respectively. -
This model is a variation of the proposal presented in [42], where quadratic deformations of the AdS warp factor, in Poincar
$ \rm{\acute{e}} $ coordinates, describe light hadrons. For strange baryons, we propose$ h(z)= {1}/{2}\,\left(k\,z\right)^{2-\alpha} $ and fix the dilaton to be zero. Thus, we can write the following expression for the warp factor in the AdS metric:$ A\left(z\right)=\log \left(\frac{R}{z}\right)+\frac{1}{2}\,\left(k\,z\right)^{2-\alpha}. $

(32) The effect of the geometric deformation
$ h(z) $ is placing confinement. For fermions in the AdS space, bulk modes are unbounded. However, the deformation$ h(z) $ causes the emergence of bounded states dual to baryons at the conformal boundary. Because we choose$ \Phi(z)=0 $ , the bulk mass reduces to the standard value of$ M_5 $ given by Eq. (31).After these definitions, we obtain the Schrödinger-like equation for both the right and left bulk fermions as
$ -\phi_{L/R}^{\prime \prime}(z)+\left[M_5^2 \,{\rm e}^{2\,A(z)} \mp M_5 \,{\rm e}^{A(z)} A^{\prime}(z)\right] \phi_{L/R}(z) =m^2_n\,\phi_{L/R}(z), $

(33) where
$ m_{n} $ is the four-dimensional fermion mass.We perform a regression process using the Σ family mass data, which allows us to find the parameter set that minimizes the RMS error. After performing this procedure, we set the parameters for the geometric deformation
$ h(z) $ , given in Eq. (32), as$ k_{1/2}=239 $ MeV,$ k_{3/2}=219 $ MeV, and$ \alpha_{1/2}=\alpha_{3/2}=0.16 $ for each baryonic trajectory. By substituting these parameters into Eq. (33), we calculate a baryonic mass spectrum that is consistent with the$ \Sigma(1/2) $ and$ \Sigma(3/2) $ trajectories, as indicated in Tables 1 and 2.We construct
$ (n, m^2) $ Chew-Frautschi plots using data from Tables 1 and 2, as shown in Figs. 1 and 2. The figures show that the discrepancies between the calculated baryon masses and experimentally measured mass data are below 10%.
Figure 1. (color online)
$ (n,m^2) $ Chew-Frautschi plot depicting the Regge trajectory for the$ \Sigma(1/2) $ baryon system computed from the non-quadratic deformed background.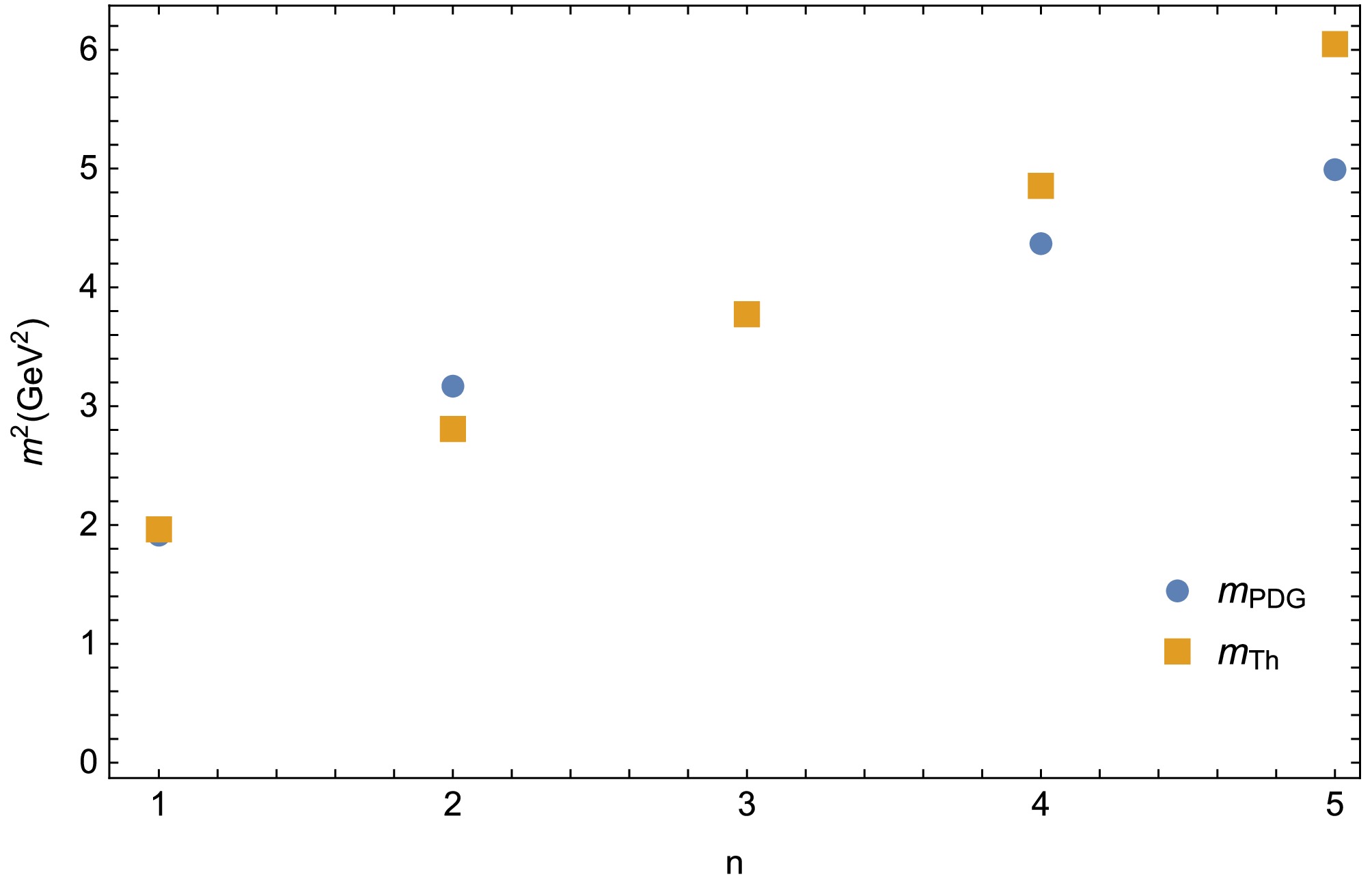
Figure 2. (color online)
$ (n,m^2) $ Chew-Frautschi plot depicting the Regge trajectory for the$ \Sigma(3/2) $ baryon system computed from the non-quadratic deformed background.Additionally, we calculate the overall RMS error using the following definition:
$ \delta_{\text{RMS}}=\sqrt{\frac{1}{N-N_p} \sum\limits_{i=1}^N\left(\frac{\delta O_i}{O_i}\right)^2} \times 100, $

(34) where N is the number of experimental measurements, and
$ N_p $ is the number of parameters. For the deformed gravity approach, we have three parameters (two k and one α) describing eight baryonic states. From Eq. (34), we find that$ \delta_{\text{rms}}=8.5 $ % for Σ trajectories using the deformed background.The set of parameters
$ \{k_{1/2},\,k_{3/2},\,\alpha\} $ is obtained by regression over the experimental data. Having a single α for both models is consistent with both baryonic families with the same quark content, as we would expect from the Bethe-Salpeter analysis [31] -
This proposal is an extension of the non-quadratic dilaton idea developed for isovector mesons and non-
$ q\bar{q} $ states [38, 39]. In the case of fermionic bulk fields, the dilaton field factors out from the equations of motion. However, confinement is addressed by inserting an anomalous dimension into the dilaton, as we explain in Section II.In this prescription, we set
$ h(z)=0 $ , implying that the warp factor$ A(z) $ and dilaton field$ \Phi(z) $ can be written as$ A(z)=\log \left(\frac{R}{z}\right), $

(35) $ \Phi(z)=\frac{1}{R}(\kappa\,z)^{2-\alpha}. $

(36) Then, using Eq. (2), we obtain a Schrödinger-like equation:
$ \begin{aligned}[b]& -\phi_{L/R}^{\prime \prime}(z)+\left\{\left[M_5+\Phi(z)\right]^2 {\rm e}^{2 A(z)} \mp \right.\\ &\quad \left.\left[(M_5+\Phi) {\rm e}^{A(z)}\right]^{\prime}\right\} \phi_{L/R}(z)=m^2_n\, \phi_{L/R}(z). \end{aligned} $

(37) Note that the bulk mass
$ M_{5} $ used here remains the same as in the deformed case. As in the geometric deformation case, after performing a regression on the experimental Σ mass data, we obtain$ \kappa_{1/2}=\kappa_{3/2}=0.423 $ and$ \alpha_{1/2}=\alpha_{3/2}=0.17 $ and substitute them into Eq. (37). The resulting data is displayed in Tables 3 and 4.$ I(J^P)=1(1/2^+) $ states

n $ M_{\rm th} $ /MeV

$ M_{\rm PDG} $ /MeV

%M 1 1377.51 1192.6±0.02 15.50 2 1555.77 1585±20 1.84 3 1712.28 1820—1940 8.92 Table 3. Mass spectrum for the
$ \Sigma(1/2) $ trajectory within the non-quadratic dilaton model. We use$ \kappa=0.423 $ MeV and$ \alpha=0.17 $ . The ground state is represented by$ n=1 $ . As customary, %M is the relative error. For the mass intervals, we choose the average between the interval extremes. The experimental masses are taken from the PDG [59].$ I(J^P)=1(3/2^+) $ states

n $ M_{\rm th} $ /MeV

$ M_{\rm PDG} $ /MeV

%M 1 1571.94 1382.83±0.34 13.60 2 1726.75 1730—1830 3.00 3 1866.39 1920—1960 3.79 4 1994.45 2060—2120 4.57 5 2113.28 2240±27 5.40 We generate
$ (n, m^2) $ Chew-Frautschi plots based on the data presented in Tables 3 and 4, as shown in Figs. 3 and 4. The non-quadratic dilaton accurately matches the high excited states, i.e., the relative errors are below 6%. However, the ground state is not well-fitted. This is unsurprising because the ground state strongly depends on the dilaton slope κ.
Figure 3. (color online)
$ (n,m^2) $ Chew-Frautschi plot for the$ \Sigma(1/2) $ trajectory using the non-quadratic dilaton.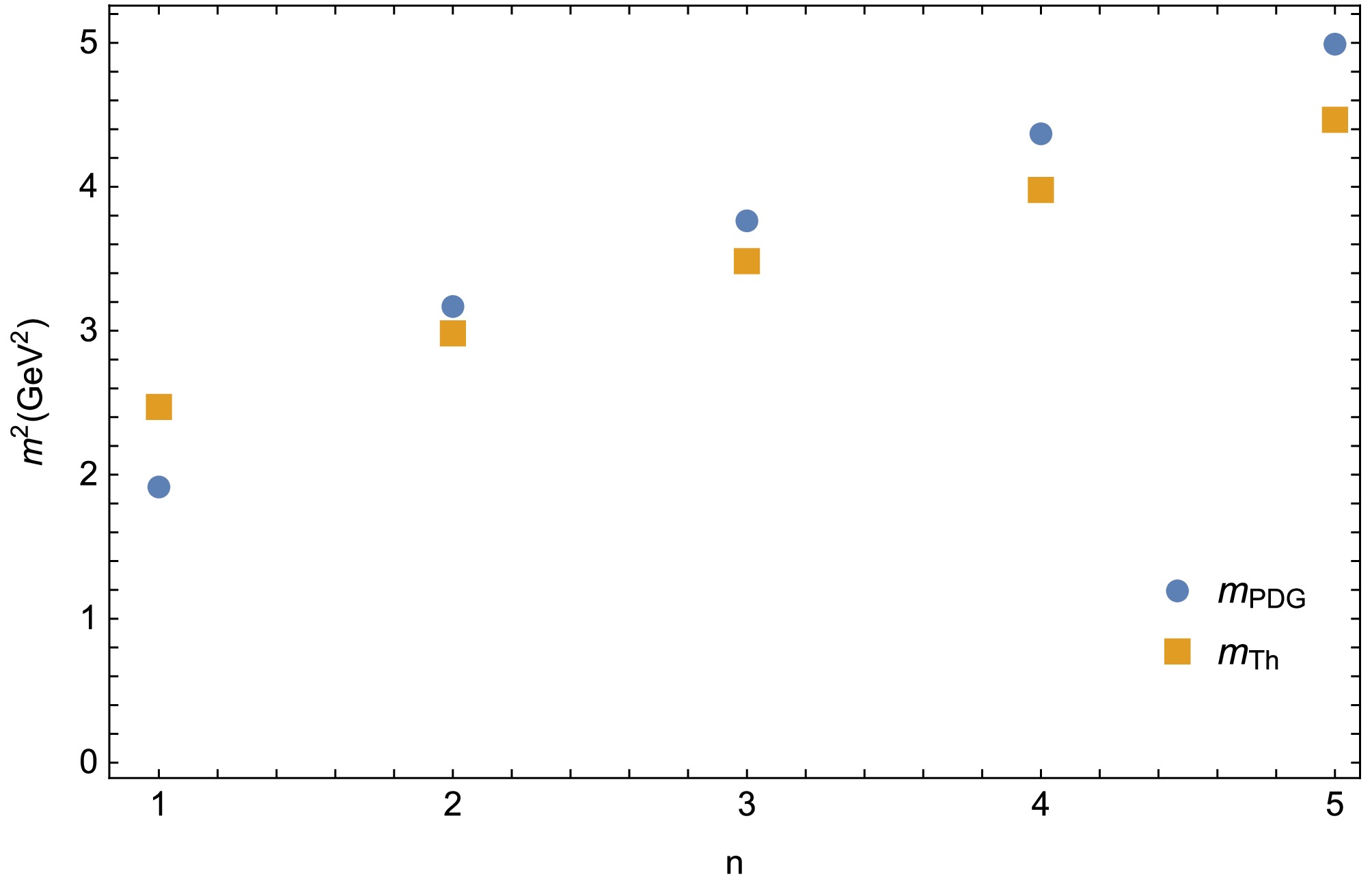
Figure 4. (color online)
$ (n,m^2) $ Chew-Frautschi plot for the$ \Sigma(3/2) $ trajectory using the non-quadratic dilaton.Finally, we compute the total RMS error. It is important to note that we employ identical parameters for Σ with different spins, which is expected from dilaton-based models, where the dilaton field carries information about the nature of strong interactions inside hadrons. Thus, for
$ \Sigma(1/2) $ and$ \Sigma(3/2) $ to have the same value of κ is consistent. In this scenario, parameters are reduced to two, i.e.,$ N_{p}=2 $ . From Eq. (34), we find$ \delta_{\mathrm{rms}}=9.84 $ % for the Σ family with eight baryonic states.To test the reliability of this nonquadratic dilaton approach, by taking advantage of the same parameter space for Σ baryons in this model, we can calculate the mass for the
$ I(J^P)=(5/2^+) $ Σ baryon. This state has a mass of$ 1908\pm7 $ MeV [60]. We have$ M_5=9/2 $ for this state, implying that the theoretical mass ($ 1S $ ) is$ 1741.01 $ MeV, which indicates a deviation of 8%. -
The inspiration behind CE [46–48] comes from Shannon's information entropy [61], a measure that quantifies the amount of uncertainty in a random variable [62]. For a variable that can take
$ N_{d} $ discrete possible values, with probabilities given by$ p_{i} $ , it is defined by$ S_{\text {info }}=-\sum\limits_{i=1}^{N_d} p_i \ln p_i. $

(38) In the original formulation within information theory, CE can be understood as a measure of the information required to describe localized functions. Generally, these functions are dynamical solutions emerging from an action, and CE measures the information available in these solutions.
CE characterizes the complexity of a given physical system. Thus, states with higher CE require more energy for their occurrence in nature compared to states with lower CE. Higher energy levels also imply more modes conforming to such physical states, implying a measure of complexity.
For unstable systems, we can also argue that CE brings a measure of stability. In general, for hadrons, the hadronic mass can be written as an increasing function of CE. From Heisenberg's uncertainty principle, we can define the decay width Γ with the hadron mass as [55]
$ \Gamma\sim M_n\sim s_{CE}^\gamma. $

where
$ \gamma>0 $ . The fact that CE can be written as an increasing function of the hadron mass follows experimental evidence: excited states decay into lower energy states, implying that CE should increase with mass. Thus, increasing the mass will lead to a larger decay width for unstable particles. Therefore, for hadronic states, we expect that higher excited states should have increasing CE. In this sense, we expect a holographic model describing hadrons to have increasing CE with excitation number n.In the cases at hand, when computing CE for the Σ family, from a bottom-up perspective, we connect bulk localization of the dual fermionic modes with the stability at the boundary. This is consistent with the observation that heavier states decay faster than light states. Thus, we expect CE to increase with excitation level n.
Therefore, we can state that holographic CE indirectly measures the complexity of constituent spatial arrangements in the Σ baryon family. A high CE in the Σ system implies that the microscopic particle arrangement exhibits a high degree of randomness and disorder, potentially making the system more susceptible to decay. In contrast, a low CE suggests a more compact and orderly microscopic particle arrangement, often indicative of a more stable system.
In recent years, numerous studies have focused on CE, including investigations into compact objects [63], many body systems [64], and holographic AdS/QCD models [49, 50, 55, 65–69], among other diverse systems. These studies, which were approached from various angles, consistently demonstrated a parallel relationship between changes in CE and stability. In this study, we perform holographic calculations of CE for baryons using the different holographic models discussed in the previous section.
To achieve this, we compute the differential CE (DCE) for a given physical system by performing the following calculations for each model. First, we obtain the localized solutions to the equations of motion. Then, we evaluate the on-shell energy density. Next, we transform the on-shell energy density into momentum space. Finally, we calculate the modal fraction and evaluate the DCE integral based on the results.
-
The key component for DCE arises from the on-shell energy-momentum tensor
$ T_{mn} $ for bulk fields, defined as$ T_{mn}=-\frac{2}{\sqrt{-g}}\frac{\delta\,I}{\delta\,g^{mn}}. $

(39) For DCE, this definition is sufficient because gravity is not affected by the fermionic fields. However, variations must be performed using the frame fields
$ e^a_m $ instead of the metric tensor. Thus, we follow the prescription in Ref. [70]. From action (3), we obtain the following for spin$ 1/2 $ $ T_{mn}=\frac{1}{2\,\mathcal{K}}\bar{\psi}\left(\Gamma_m\,\overset{\leftrightarrow}{D}_n+\Gamma_n\,\overset{\leftrightarrow}{D}_m\right)\psi, $

(40) and for spin
$ 3/2 $ , from action (17), we have$ \begin{aligned}[b] T_{mn}=\;&-\frac{1}{2\,\mathcal{K}}\,\bar{\psi}^{r p}\left(\Gamma_m\,\overset{\leftrightarrow}{\nabla}_n+\Gamma_n\,\overset{\leftrightarrow}{\nabla}_m\right)\psi_{rp}\\& +\frac{1}{\mathcal{K}}\left[\bar{\psi}_m^{p}\,\Gamma^r\,\overset{\leftrightarrow}{\nabla}_r\,\psi_{n\, p}-M_5(z)\,\bar{\psi}_m^{l}\psi_{n l}\right]. \end{aligned} $

(41) The energy density in both cases is extracted from the
$ T_{00} $ component. For the spin$ 1/2 $ field, after Fourier transform, we find$ \rho_{1/2}(z)=\frac{1}{\mathcal{K}}{\rm e}^{A(z)}\,m_n\,\left(\phi_{L,n}^2+\phi_{R,n}^{2}\right)\,\mathcal{A}_0, $

(42) where
$ \mathcal{A}_0 $ is a polarization factor. The energy density for the spin$ 3/2 $ field is$ \begin{aligned}[b] \rho_{3/2}(z)=\;& -\frac{1}{\mathcal{K}}\,{\rm e}^{-A(z)}\left[m_n\left(2\,\mathcal{A}_1-\mathcal{A}_2\,{\rm e}^{2\,A(z)}\right)\right.\\& \left.+\,M_5\,\mathcal{A}_2\,{\rm e}^{2\,A(z)}\right]\left(\phi_{L,n}^2+\phi_{R,n}^{2}\right), \end{aligned} $

(43) where
$ \mathcal{A}_1 $ and$ \mathcal{A}_2 $ are polarization factors that appear from the contraction of the indices. For simplicity, we choose$ \mathcal{A}_1=\mathcal{A}_2=\mathcal{A}_0 $ . Subsequently, we perform a Fourier transform on the energy density and express it as$ \bar{\rho}(k)=\int_0^{\infty} {\rm d} \zeta {\rm e}^{- {\rm i} k \zeta} \rho(\zeta). $

(44) The modal fraction, which describes how localized the information is in a given mode, is defined as
$ f(k)=\frac{|\bar{\rho}(k)|^2}{\int {\rm d} k|\bar{\rho}(k)|^2}. $

(45) For the case of continuous variables, we use the DCE defined as
$ S_{D C E}=-\int {\rm d} k \tilde{f}(k) \log \tilde{f}(k), $

(46) where
$ \tilde{f}(k)=f(k) / f(k)_{\operatorname{Max}} $ , and$ f(k)_{\operatorname{Max}} $ is the maximum value assumed by$ f(k) $ .Recall that
$ \rho(z)\in L^2(\mathbb{R}) $ has information on how energy is localized in the bulk. Thus, it indirectly measures how well normalizable modes are localized in the AdS space. In hadronic terms, this localization measure is also a signal of confinement, because a bounded state should be localized. Therefore, DCE becomes a clear test for holographic models that mimic hadrons.We calculate the DCE for the
$ \Sigma(1/2) $ and$ \Sigma(3/2) $ trajectories using both bottom/up approaches and summarize our findings in Figs. 5 and 6.
Figure 5. (color online) Differential configurational entropy (DCE) for the two holographic models describing the
$\Sigma(1/2)$ trajectory as a function of excitation number n. The blue circles represent non-quadratic geometric deformation, and the orange squares represent the non-quadratic dilaton.
Figure 6. (color online) Differential configurational entropy (DCE) for the two holographic models describing the
$\Sigma(3/2)$ trajectory as a function of the excitation number n. The blue circles represent non-quadratic geometric deformation, and the orange squares represent the non-quadratic dilaton.As expected from the localization and stability hypothesis, Fig. 5 shows that as n increases,
$ S_\text{DCE} $ increases for the$ \Sigma(1/2) $ trajectory in both models. However, for the$ \Sigma(3/2) $ trajectory in Fig. 6, DCE only increases with n in non-quadratic dilaton approach. In the deformed background approach, this increase is only observed for the first excited state. Higher excitations decrease the DCE.The local maximum in the
$ \Sigma(3/2) $ CE plot for the geometric deformation is inherent in the model because it depends on the bulk modes. Recall that the bulk modes depend on the holographic potential$ U(z) $ structure for each model, which can be inferred from Eq. (29). Assuming the CE stability hypothesis, these higher states become more stable. This conclusion is not possible from the hadronic phenomenology. Thus, the deformed background approach is not suitable for describing the$ \Sigma(3/2) $ states. -
This study develop two models: the first has a non-quadratic deformed background with the warp factor set as
$A\left(z\right)=\log \left({R}/{z}\right)+\,\left(k\,z\right)^{2-\alpha}/2$ , and the second assume a non-quadratic dilaton$\Phi(z)=(\kappa\,z)^{2-\alpha}/R$ . Using standard bottom-up techniques, we test these models as alternatives to describe Σ baryon spectroscopy. Each model has two parameters associated with the Regge slope and linearity deviation. In both cases, experimental data are properly fitted, with RMS errors smaller than 10%. The next stage in choosing a suitable model is DCE analysis.We observe that ground states are not well-fitted in either model regarding the mass spectrum. In other bottom-up models, the ground state mass sets the Regge slope. However, in this non-quadratic scenario, the slope and deformation are fitted via regression over the entire trajectory. Ground states are strongly related to the behavior of the one-gluon exchange term in hadronic potentials. These terms originate from perturbative analysis, which does not capture the dilaton or deformations. Recall that this bottom-up confinement attempts to mimic the confinement part in the Cornell-like potentials that control higher excitations. Further improvements in determining the intercept (which would lead to a better ground state mass) are required. For further details, see [71] for an interesting discussion and review of how hadronic spectroscopy can be captured in bottom-up models.
CE measures how well a mode is localized in the solution space. Thus, it may have information about confinement, considering that the emergence of bounded colorless states is a consequence of color confinement. Thus, DCE can be used to address whether a given holographic approach is suitable for describing hadrons from the stability perspective. However, DCE is not the only test available. Thermal analysis [45] of the two-point spectral function also considers stability.
For the models discussed here, we observe that the deformed background appears inconsistent with the hypothesis of stability/DCE, at least for the
$ \Sigma(3/2) $ trajectory. As a hypothesis, if we analyze the behavior of the Schrödinger modes in the deformed background, we find that they are highly suppressed in the bulk; owing to the structure of the holographic potential, i.e., the exponential factor in Eq. (16), the modes are spatially confined. For excited modes, they oscillate in small bulk regions. Because these solutions do not tend to smear out into the bulk, DCE does not decrease. This hypothesis must be tested with other similar geometric approaches.In its original motivation, DCE describes how constituents are distributed among different states or configurations in a given system. It allows us to quantify the degree of disorder or randomness of these constituent arrangements, providing insights into the probabilities of various particle configurations. Thus, DCE is related to how constituents interact with each other. Therefore, DCE is considered a probe to test how confinement is realized in holographic models. However, there is still considerable room to discuss the nature of the constituent arrangements inside hadrons because the modeling of these systems in such holographic models requires improvement.
A higher DCE indicates more possible particle arrangements, implying greater disorder or freedom of movement. Conversely, a lower DCE suggests a more ordered particle arrangement or more significant constraints on the configuration. The calculation results for the two models are shown in Figs. 5 and 6. As shown in the figures, the overall data increase with mass, and the values of CE also increase. By comparing the results of the two models, it is found that the model incorporating the dilaton field obtains lower CE in the
$ \Sigma (1/2) $ and$ \Sigma (3/2) $ calculations.The relationship between CE and the mass spectrum of Σ baryons is highly significant. CE is an indirect measure of the intricacy of the structure in Σ baryons. Meanwhile, the mass spectrum characterizes the distribution of masses corresponding to different energy levels and combinations of constituent particles within Σ baryons. Higher CE in Σ baryons signifies a broader range of arrangements and degrees of freedom. This observation can also be interpreted in terms of transition probabilities. A higher DCE is associated with smaller decay widths. Thus, the smallest DCE is expected to belong to the ground state with the highest decay width. We will explore this idea in further investigations.
Holographic bottom-up approach to Σ baryons
- Received Date: 2024-07-26
- Available Online: 2025-01-15
Abstract: In this study, we discuss the description of neutral Σ baryons with






 Abstract
Abstract HTML
HTML Reference
Reference Related
Related PDF
PDF















 DownLoad:
DownLoad: