Spectroscopy of excited quarkonium states in the light-front quark model

Quantum Chromodynamics (QCD) [1, 2] provides us an understanding of the intricacies of the strong interactions that occur in our universe. QCD explains how a parent hadron comprises the fundamental particles, namely the quarks, gluons, and sea quarks, as well as the interactions that exist among each of them. In the recent years, understanding the multi-dimensional structure of hadrons has become an interesting topic [3−23]. To visualize the partonic content and its behavior within a parent hadron, different mathematical constructs are employed, such as the parton distribution functions (PDFs) [11−16], which give us a one dimensional (1-D) picture of the hadron and describe the likelihood of finding a parton carrying the parent hadron's longitudinal momentum fraction (x). However, PDFs do not carry any information about other degrees of freedom of the parton. To obtain the two-dimensional (2-D) representation of a hadron, one can study the form factors (FFs), giving us information regarding the charge distribution inside a hadron. Further, one can achieve deeper insights into to spatial and transverse structure of a hadron by investigating its three dimensional (3-D) structure using the transverse momentum-dependent parton distributions (TMDs) [3−10] and the generalized parton distributions (GPDs) [16−23].

The distribution amplitude (DA) provides detailed information on the strength of the coupling between quark and anti-quark pairs within a hadron. It quantifies the probability amplitude for finding these constituent particles bound together, thereby indicating the effectiveness of their interaction in forming the hadronic structure. In quantum field theory, these non-perturbative and scale-dependent functions can be thought of as the closest relatives of quantum mechanical wave functions [24]. In the limit of zero transverse momentum, represented by the leading-twist DAs, the leading Fock-state contribution to its light-front wave function is considered. Because particle number is conserved in this frame, the light-front formulation of a wave function permits a probability interpretation of partons that is not easily available in an infinite-body field theory.

Light-front dynamics (LFD) plays a crucial role in understanding the theory of strong interactions. It is a dynamical theory where the dynamical variables correspond to the physical conditions on a front $ x^{+} = 0 $ [25]. In particular, because of its unique characteristics of rational energy-momentum dispersion relation, LFD is discovered to offer an efficient means of handling the relativistic effects. With a maximum number of seven kinematic (or interaction-independent) generators, it requires less dynamic effort to obtain QCD solutions that fully reflect Poincaré symmetries [26]. In this study, we adopted the light-front quark model (LFQM) [27−32], which describes a hadron's composition as a bound state between its active quark and anti-quark spectator. LFQM focuses on a hadron's valence quarks, i.e., the fundamental elements responsible for the overall structure and behavior. Because both the light-front transverse and longitudinal boost operators are kinematic, the light-front wave function is independent of the external momentum.

Although LFQM has already been used to successfully explain the various characteristics of the ground state mesons [33−50], the attributes of the radially excited states are still pending investigation given that, in contrast to the ground states, their nature is currently unknown and less understood. Radially excited states of hadrons in particular provide complementary information to the orbitally excited states, making them crucial to comprehending the strong interactions. The Particle Data Group (PDG) [39] states that a few of them have not yet been verified, but they have been seen in the light and heavy quark sectors of hadrons. One more important point to note is the coupled-channel effects, which have been introduced to account for exotic charmonia. The coupled channel effect is responsible for the coupling between two-quark cs bound states and two-meson continuum states of DK [40]. This connection has two noteworthy effects. The first causes cs bound state configuration mixing and mass shifts. The second presents large peaks above the threshold of cs resonance states [41, 42]. Hoewever, our LFQM assumes that the main contributions to the bound state properties come from the quark-antiquark interaction, rather than from meson loops or other intermediate channels. This assumption works well for charmonium because the heavy charm quark mass leads to relatively suppressed decay widths into open-charm channels for many higher excited states, reducing the impact of coupled-channel effects. In this study, we investigated the wave functions of the ground state (1S), radially excited states (2S and 3S), and orbitally excited state (1P) of bottomonia ($ b\bar b $) and charmonia ($ c\bar c $) for spin-0 and spin-1 mesons within the LFQM regime. We discussed various characteristics related to them, such as the DAs, PDFs, decay constants, electromagnetic form factors (EMFFs) [43, 44], and charge radii. It is important to note here that these meson attributes have been studied previously for the ground state [33, 45, 46] and radially excited state 2S [47] but are yet to be investigated for the 3S and 1P states. We compare our results obtained between the pseudo-scalar and vector mesons for their various excited states. Therefore, the major goal of our work is to examine these features and assess how they differ from heavy quarkonia in the ground state. We believe that our results will help to obtain a better understanding of the excited states of mesons in the future.

The paper is arranged as follows. In Sect. II, we quantitatively present the LFQM, which is the primary model we consider in this study. In Sect. III, we present our chosen input parameters and theorize various structural properties of the studied meson. Further, we discuss the numerical results obtained for the various excited states of the heavy quarkonia meson systems. We also present plots showing the nature of different wave functions that we have considered here. Finally, we summarize our results in Sect. IV.

The minimal hadron Fock-state wave function based on light-front quantization in the form of quark-antiquark is expressed as [32, 48]

where $ |M(P, J, J_{z})\rangle $ is the meson eigenstate with $P= (P^+,P^-,P_{\perp})$ being the four-vector total momentum of the hadron, $ (J, J_{z}) $ is the total angular momentum, ${k}= (k^+,k^-,{k}_{\perp})$ is the momentum of the active quark, $ x=\frac{k^+}{P^+} $ is the longitudinal momentum fraction carried by the active quark, and $ \lambda_{q (\bar q)} $ is the helicity of quark (anti-quark).

The light-front wave function $ \psi_{\lambda_q,\lambda_{\bar q}}^{J J_{z}} $ for pseudo-scalar and vector mesons is defined as follows:

where $\phi_{nS(nP)}\left(x, \boldsymbol{k}_{\perp}\right)$ is the radial (orbital) wave function, and $ \mathcal{X}_{\lambda_{q} \lambda_{\bar{q}}}^{J J_{z}} $ is the spin-orbit wave function obtained by the interaction-independent Melosh transformation [49]. $ n S (n P) $ refers to the various radially (orbitally) excited states, and in this work, we considered $ n=1,2,3 $ for the S state and $ n=1 $ for the P state. Covariant forms of $ \mathcal{X} $ for pseudo-scalar and vector mesons are respectively presented as [50]

where $ \mathcal{M} \equiv \sqrt{M_{0}^{2}-\left(m_{q}-m_{\bar{q}}\right)^{2}} $. The polarisation vectors $ \epsilon^{\mu}\left(J_{z}\right)=\left(\epsilon^{+}, \epsilon^{-}, \boldsymbol{\epsilon}_{\perp}\right) $ of the vector meson are given by

where

We define the radial wave function $\phi_{nS(nP)} (x, {\boldsymbol{k}_{\perp}})$ in Eq. (2) for the 1S, 2S, 3S, and 1P states as [51, 52]

where $ (k_{m = \pm 1} = \mp (k_{\perp 1} \pm \iota k_{\perp 2})/ \sqrt{2} $ and $ k_{m = 0} = k_{z}) $, and m denotes the magnetic quantum number obtained from the spherical harmonics. For this paper, we consider only the $ m = 0 $ form of the wave function. β is a variational parameter that we use in our model later in this paper. The radial wave functions of $ \phi_{1S} $, $ \phi_{2S} $, $ \phi_{3S} $, and $ \phi_{1P} $ can be normalized as

We define the mass of the meson invariant under the influence of boost as

The three-momentum ${\boldsymbol{k}} = (k_{z}, {\boldsymbol{k}_{\perp}})$ can be expressed as ${\boldsymbol{k}} = (x, \boldsymbol{k}_{\perp})$ [50] using the following relation:

Consequently, the transformation of variables $[k_{z}, {\boldsymbol{k}_{\perp}}]$ $ \rightarrow $ $[x, {\boldsymbol{k}_{\perp}}]$ is connected to the Jacobian variable in the following manner:

In the LFQM, the parameters required for our calculations are the quark masses $ (m_{c}, m_{b}) $ and two variational harmonic parameters $ (\beta_{c \bar c}, \beta_{b \bar b}) $. We adopt the model parameters from the work of Arifi et al. [50], who obtained the input parameters using the variational principle. They evaluated $ \langle \Psi | [H_{0} + V_{0}] \Psi \rangle $ while using a trial wave function depending on the values of m and β by further varying their values till they reached a minimum of the expectation value. These model parameters are presented in Table 1. These parameters yield good results for numerous attributes of the meson, such as mass spectra, EMFFs, DAs, and other related metrics.

$m_{c}/\mathrm{GeV}$	$m_{b}/\mathrm{GeV}$	$ \beta_{c\overline{c}} $	$ \beta_{b\overline{b}} $
1.68	5.10	0.699	1.376

Table 1.  Model parameters for LFQM [50].

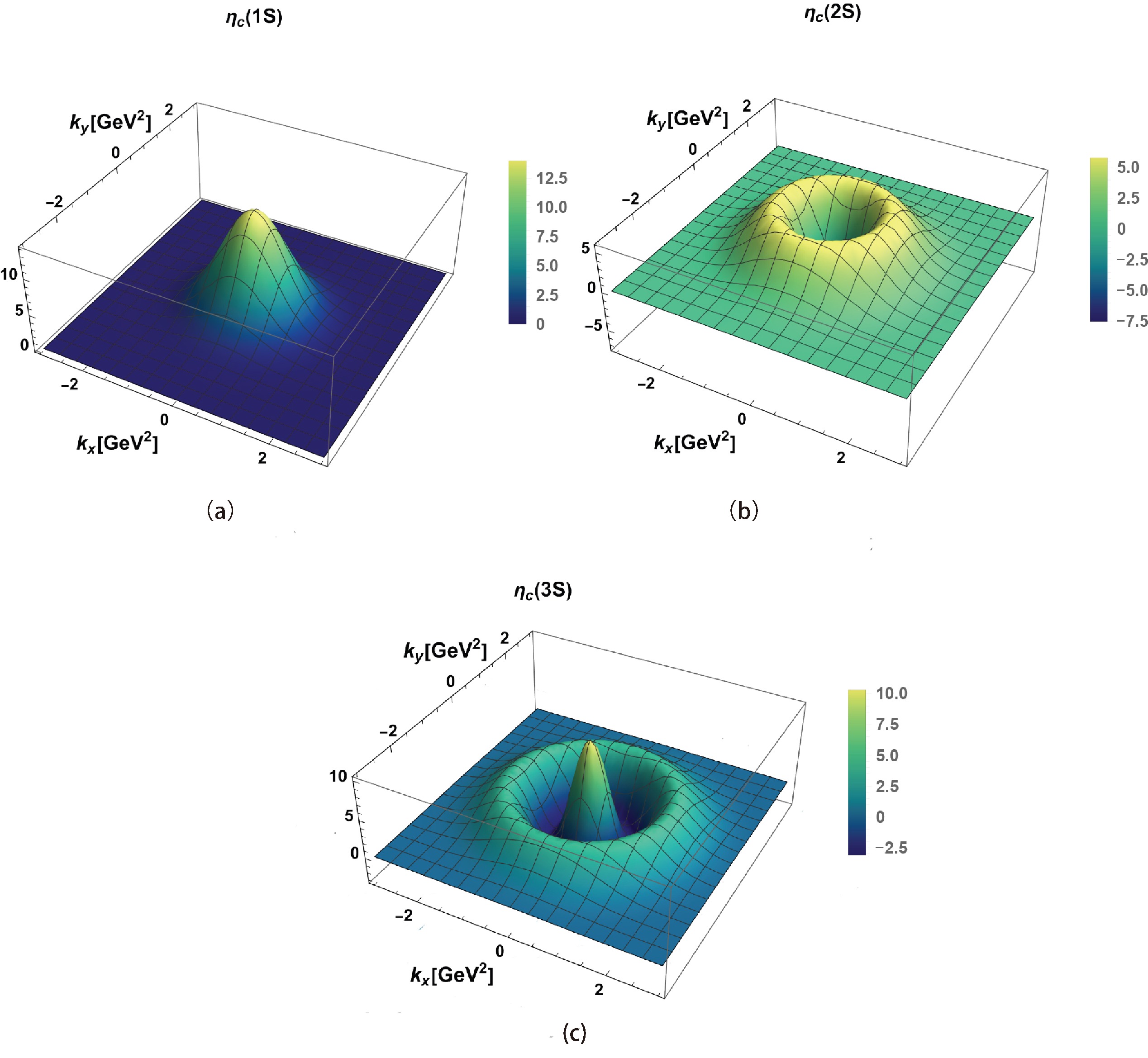
In Fig. 1, we show the momentum space wave functions for the states (defined in Sec. II) as a function of the longitudinal momentum fraction x at a fixed transverse quark momenta ${\boldsymbol{k}}_{\perp}^{2} = 0.1$ GeV² for the charmonium and bottomonium mesons. We considered only the quark distributions here because the quark and anti-quark masses are similar. These mesons tend to have a symmetric distribution in terms of the quark distributions with their anti-quark distributions being identical. For a more intuitive understanding of the wave functions, we provide 3-D representations of the wave functions as functions of $ k_{x} $ and $ k_{y} $, where ${\boldsymbol{k}}_{\perp} = \sqrt{k^{2}_{x} + k^{2}_{y}}$. We present these plots in Fig. 2. We have excluded the plot for the 1P state because its behavior is not very reflective of its wave nature. These plots portray a very beautiful understanding of the nodal structure of the wave functions. We notice that the 1S state has no nodes and a Gaussian distribution, which is as expected from its wave function construction. Similarly, for the 2S state, we have a singular node, whereas for the 3S state, we have two subsequent nodes, which are well represented in the figure. As we go to higher excited states, each state follows the trend of $ (n-1) $ nodes, where n is the principle quantum number of the given state.

Figure 1.  (color online) 2-D visualization of the excited state wave functions for spin-0 charmonium ($ c \bar c $) (left side) and bottomonium ($ b \bar b $) (right side) systems.

Figure 2.  (color online) 3-D visualization of the nodal structure contained within the radially excited states 1S, 2S, and 3S of the $ \eta_{c} $ meson ((a), (b), and (c) respectively).

The decay constants for a pseudo-scalar meson $ \mathcal{P} $ can be defined from the axial-vector current's matrix components, whereas for a vector meson $ \mathcal{V} $, it can be defined from the vector current element. They are respectively expressed as [50, 53]

The explicit form of these current components for the case of pseudo-scalar mesons is denoted as $ f^{(\pm)}_{\mathcal{P}} $ and expressed as

where $ \mathcal{A} = (1 - x) m_{q} + x m_{\overline{q}} $ and

with $ \mathcal{A}^{\prime}=\mathcal{A}\left(m_{q} \leftrightarrow m_{\bar{q}}\right) $. For the case of pseudo-scalar mesons, the ''+'' and ''−'' current components correspond to the generators for the decay constants of ground state (1S) and first excited state (2S) state mesons [50, 53] (previously proven to be identical). We extend this study to the cases of pure 3S and 1P states.

Similarly, for the vector meson case, the ''+'' current component with longitudinal polarization ϵ (0) is equivalent to the ⊥ current component carrying transverse polarization ϵ (±), and they have also proven to be completely identical [54]. We denote the vector decay constant $ f_{\mathcal{V}} $ for the ⊥ and ''+'' current components as $ f^{\perp}_{\mathcal{V}} $ and $ f^{+}_{\mathcal{V}} $, respectively. We express them quantitatively as

where

and $ G_{LF} = M_{0} + m_{q} + m_{\bar q} $. The decay constants $ f^{+}_{\mathcal{V}} $ and $ f^{\perp}_{\mathcal{V}} $ computed using the basis light-front quantization (BLFQ) technique [55] differ based on the current components considered in their work, which was attributed to the model's violation of its rotational symmetry. However, in LFQM, we were able to successfully calculate that $ f_{\mathcal{P}} $ = $ f^{+}_{\mathcal{P}} $ = $ f^{-}_{\mathcal{P}} $ and $ f_{\mathcal{V}} $ = $ f^{+}_{\mathcal{V}} $ = $ f^{\perp}_{\mathcal{V}} $ for all the radially excited states of the mesons.

In Table 2, we have presented our theoretical calculations for decay constants of heavy pseudo-scalar mesons, $ \eta_{c} $ and $ \eta_{b} $, along with heavy vector mesons $ J /\psi $ and $\Upsilon$ for their ground state and excited states. For the sake of comparison, we provide the available experimental data along with some other theoretical calculations, such as the lattice simulations [56−60] and QCD sum rules [61]. Because we have adopted the model parameters from Ref. [50], our results for the 1S and 2S states are identical. From our calculations, it is observed that the decay constants have an increasing trend as we consider the higher radially excited states for a particular meson. For the case of $ \phi_{nS} $, the decay constants follow the trend $f_{1 S} < f_{2 S} < f_{3 S}t; f_{3 S}$, which is in violation of the empirical hierarchy discussed in Ref. [50] stating that $ f_{1 S} > f_{2 S} $. This is due to the fact that they have mixed the 1S and 2S states to satisfy the hierarchy. This further makes us believe that mixing even higher excited states would help us obtain better results and uphold the empirical hierarchy.

	$ f_{\eta_{c}(1 S)} $ /MeV	$ f_{J / \psi(1 S)} $ /MeV	$ f_{\eta_{b}(1 S)} $ /MeV	$ f_{\Upsilon(1 S)} $ /MeV
Our results	356	403	648	688
Expt. [39]	$ 335 \pm 75 $	$ 407 \pm 5 $	−	$ 689 \pm 5 $
Lattice [56−60]	$ 394.7 \pm 2.4 $	$ 405 \pm 6 $	$ 667_{-2}^{+6} $	$ 649 \pm 31 $
RQM Sum rules [62]	$ 387 \pm 7 $	$ 418 \pm 9 $	−	−
BS [63]	$ 292 \pm 25 $	$ 459 \pm 28 $	−	$ 496 \pm 20 $
BS [64]	385	−	709	−
LFQM (CJ) [65]	326	360	507	529
LFQM (CJ2) [66]	353	361	605	611
	$ f_{\eta_{c}(2 S)} $ /MeV	$ f_{{\psi(2 S)}} $ /MeV	$ f_{\eta_{b}(2 S)} $ /MeV	$ f_{\Upsilon(2 S)} $ /MeV
Our calculation	318	420	671	771
Expt. [39]	−	$ 294(5) $	−	$ 497(5) $
Lattice [59]	−	−	−	$ 481(39) $
BLFQ [67] $ { }^{a} $	298	312	525	520
LFD [68]	−	$ 288(6) $	−	−
	$ f_{\eta_{c}(3 S)} $ /MeV	$ f_{{\psi(3 S)}} $ /MeV	$ f_{\eta_{b}(3 S)} $ /MeV	$ f_{\Upsilon(3 S)} $ /MeV
Our calculation	239	357	586	724
Expt. [69]		238 (5)
RHCM [70]	420	−	711	−
BS [71]	−	375	−	−
	$ f_{h_{c}(1P)} $ /MeV	$ f_{\chi_{c0}(1 P)} $ /MeV	$ f_{h_{b}(1P)} $ /MeV	$ f_{\chi_{b0}(1 P)} $ /MeV
Our calculation	373	421	701	745
Sum rules [72]	$ 490 $	−	657	−
BS [71]	−	239	−	−

Table 2.  Decay constants of heavy quarkonia for various radially and orbitally excited states. We compare our results with available theoretical and experimental data.

In LFQM, one can extract the DA $ \phi_{\mathcal{P (V)}}(x, \mu) $ of a meson from its LF wave function by integrating over the transverse momenta $ {\boldsymbol{k}}_{\perp} $ of the quarks in the meson. DAs provide the probability amplitudes for locating the hadron in a state with a minimal transverse momentum separation and minimum amount of Fock elements, identified by an ultraviolet (UV) cutoff of $ \mu \gtrsim 1 $ GeV. The QCD evolution equation [73] provides the μ-scale dependence, which can be determined perturbatively. However, the DAs can be extracted using contributions from the non-perturbative regimes of the LFQM at certain low-scale values. Moreover, LFQM includes a damping Gaussian component that allows the computation of indefinite integrals with no loss in accuracy. Pseudo-scalar and vector meson quark DAs are correlated with decay constants derived from the “+” current constituents according to the relation [74]

We define the normalized quark DA as $ {\phi''}_{\mathcal{P(V)}} (x, \mu)= $ $ \left(2 \sqrt{6} / f_{\mathcal{P(V)}}^{(+)}\right) \phi_{\mathcal{P(V)}} (x, \mu) $ so that

It is typically possible to expand the quark DAs using Gegenbaur polynomials $ C_{n}^{3/2} $ as $ {\phi''}(x, \mu)={\phi''}_{\text {asym}}(x) \left[1+\sum_{n=1}^{\infty} e_{n}(\mu) C_{n}^{3 / 2}(\xi)\right] $, where the asymptotic DA is defined as $ {\phi''}_{\text {asym}}(x) = 6 x (1-x) $, and $ e_{n}(\mu) $ are the Gegenbaur moments [73−76]. With $ n > 0 $, the Gegenbauer moments describe the DAs' divergence from the asymptotic form. As an alternative, the longitudinal momentum's expectation value intricately connected to $ e_{n}(\mu) $ can be defined as [74]

where $ \xi=x-(1-x)=2 x-1 $.

In Fig. 3, we compare the DAs of spin-0 and spin-1 mesons for the radially and orbitally excited states separately. In the left panel, we show the comparisons for the states of the bottomonia ($ b \bar{b} $) system, and in the right panel, we compare the charmonia ($ c \bar{c} $) systems. We choose the convention where the quark carries the longitudinal momentum fraction x and the anti-quark carries the fraction $ 1-x $. Because we are considering the charmonia ($ c \bar c $) and bottomonia ($ b \bar b $) systems, our quark and anti-quark pair have identical masses. The plot indicates that the vector mesons in the LFQM model and the pseudo-scalar mesons in the 1S state are relatively comparable. However, when we consider higher excited states, we have observed that the pseudo-scalar and vector meson DAs have a more pronounced difference in their amplitudes. This discrepancy seems to increase as we go to higher excited states. The DA structure for the bottomonia is narrower than for charmonia even though both the heavy quarkonia DAs are symmetric under $ x \rightarrow 1-x $. We also observed that the amplitude for the bottomonium DA is larger than that for charmonium. This difference, in our view, results from the enormous mass of the b quark and its significantly larger β parameter compared to the $ c \bar c $ system. For the 1P state, we observed that the wave function has two amplitude peaks, and they tend to have a minimum at $ x = 0.5 $. This is because our chosen wave function has a $ x - {1}/{2} $ term in the numerator when we substitute the explicit form of $ k_{z} $ into the orbital wave function.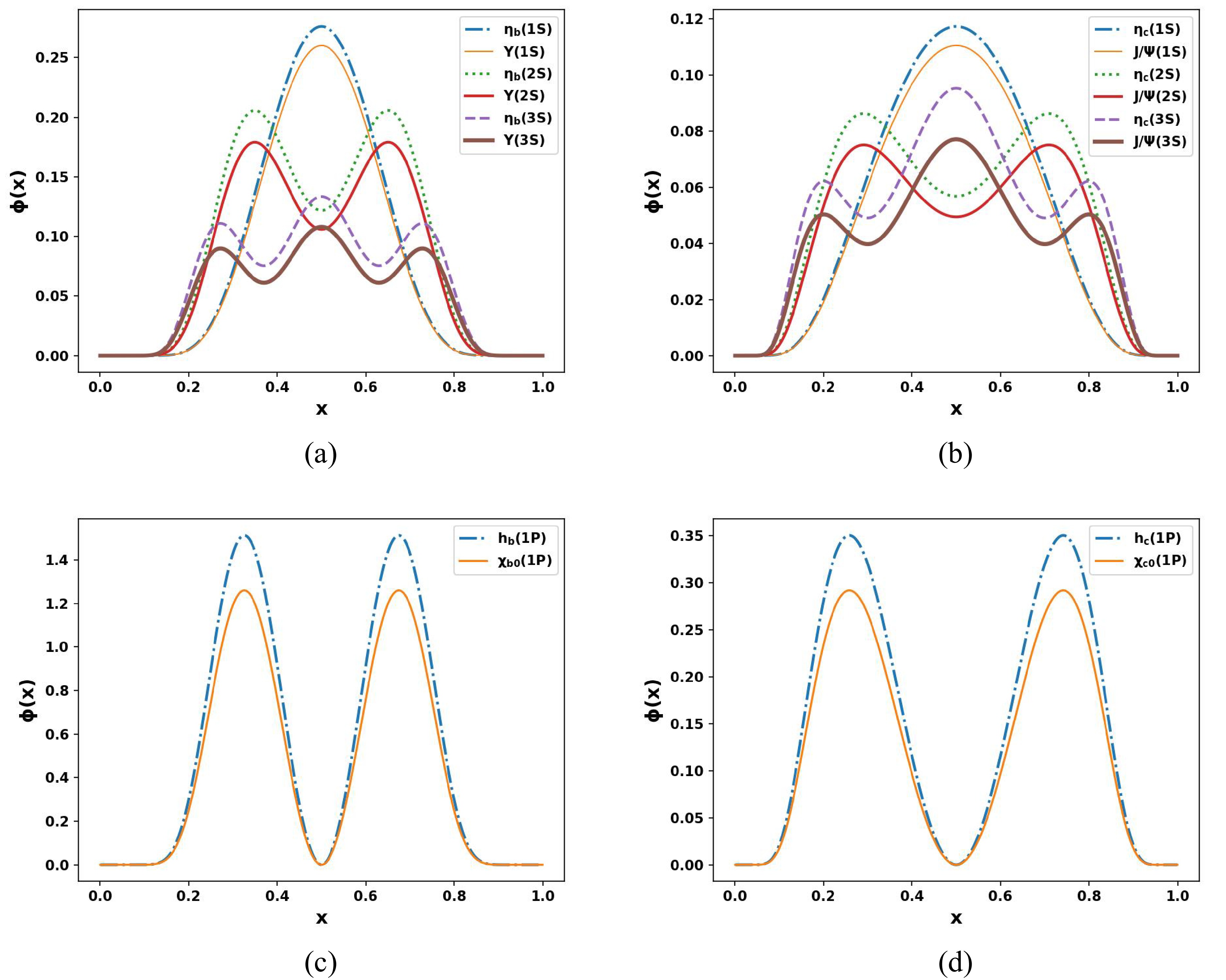

Figure 3.  (color online) Comparison of DAs of the different excited states for the pseudo-scalar and vector bottomonia ($ b \bar b $) and charmonia ($ c \bar c $) systems. The radially excited states are compared in the upper panel, and the orbitally excited state (1P) in the lower panel.

The DAs for the heavy quarkonia can be normalized and rewritten as

where $\psi''_{\mathcal{P(V)}} (x, {\boldsymbol{k}}_{\perp})$ is the LF wave function associated with $ {\phi''}_{\mathcal{P(V)}} (x, \mu) $. In Fig. 4, we presente the 3-D plots for $\psi''_{\eta_{c}} (x, {\boldsymbol{k}}_{\perp})$ and $\psi''_{\eta_{b}} (x, {\boldsymbol{k}}_{\perp})$ of their respective excited states. It is inferred from Eq. (27) that the normalized DAs $ {\phi''}_{\mathcal{P(V)}} (x, \mu) $ shown in Fig. 3 are calculated by integrating $\psi''_{\mathcal{P(V)}} (x, {\boldsymbol{k}}_{\perp})$ over the transverse momentum ${\boldsymbol{k}}_{\perp}$. We find that the UV cutoffs or energy scale μ correlate to $| {\boldsymbol{k}}_{\perp}| \rightarrow \infty$ in LFQM using the Gaussian wave functions. They are approximately equal to 2 GeV for $ \eta_{c} $ and 4 GeV for $ \eta_{b} $. This clearly indicates that the wave functions for the heavy-heavy systems have longer transverse momentum tails compared to the light-heavy systems. This was also concluded in Ref. [50]. Meanwhile, the wave functions for systems with a heavy quark and light anti-quark pair exhibit larger negative troughs than those for systems with a heavy quark and anti-quark pair. This characteristic of the LF wave function explains the presence of negative areas exclusively in the DAs for the higher excited state heavy-light system.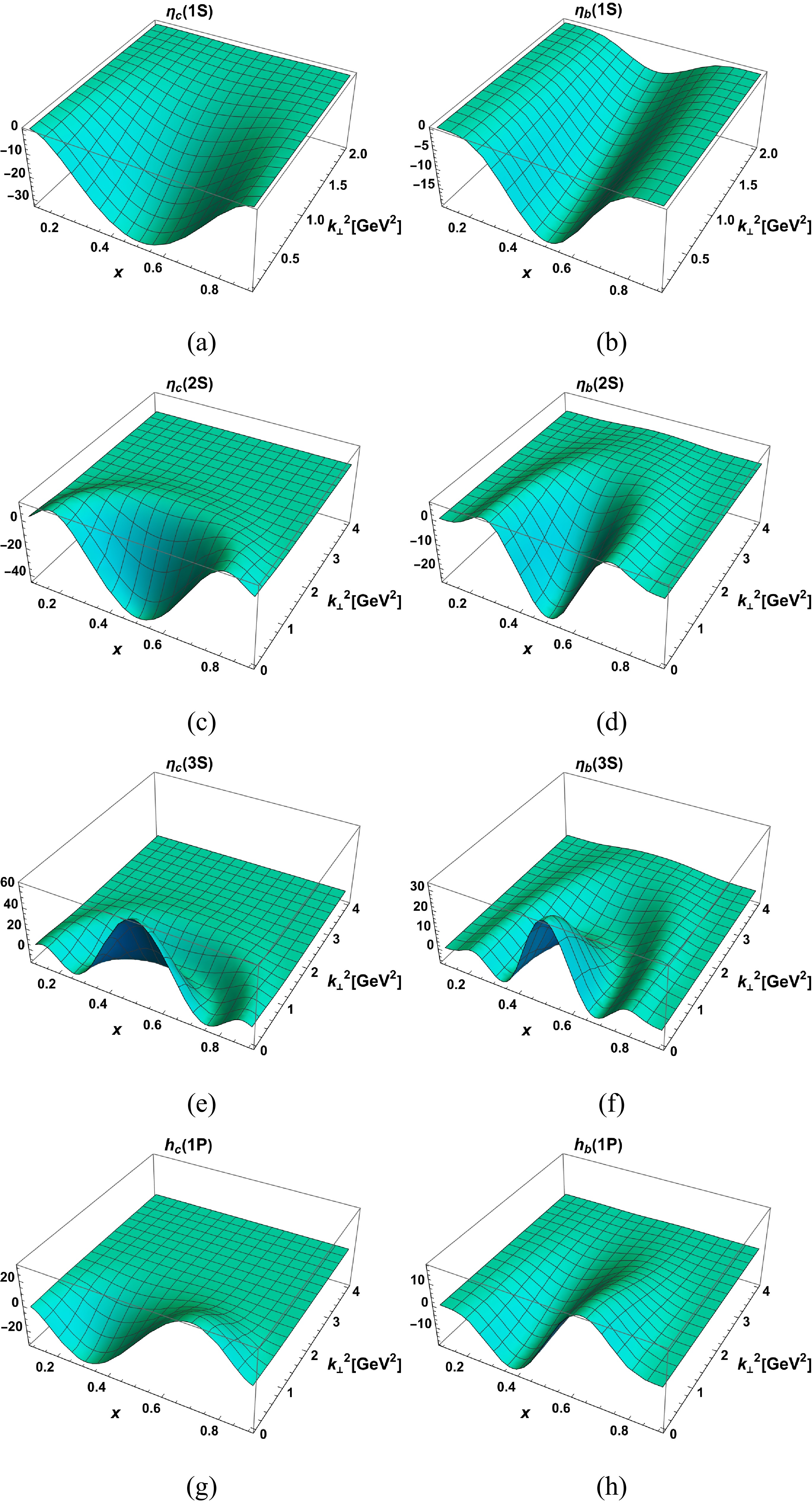

Figure 4.  (color online) 3D plots of $\Psi_{\eta_{c}} (x, {\boldsymbol{k}}_{\perp})$ and $\Psi_{\eta_{b}} (x, {\boldsymbol{k}}_{\perp})$ for the radially and orbitally excited states of $ \eta_{c} $ meson (left panel) and $ \eta_{b} $ meson (right panel).

In Table 3, we present the ξ-moments for various excited states of the heavy quarkonia using the relation defined in Eq. (26). For our charmonia ($ c \bar c $) and bottomonia ($ b \bar b $) cases, the odd moments vanish due to their DAs having a symmetric waveform. Therefore, we provide the results only for the even moments upto $ n = 6 $. We note that our choice is due to the reasoning provided in Ref. [77], where the authors noted that there is a larger contribution from the end points ($ x \sim 0 $ and $ x \sim 1 $) as we consider higher powers of the moment. At these points in space, the mobility of the quark-antiquark pair becomes relativistic and we cannot consider potential models to properly explain their behavior. Hence, it is not possible to calculate the higher powers of the moment within our potential model. Therefore, we chose only the moments up to $ n = 6 $. For brevity, we compare some of our results with other available theoretical models, as summarized in Table 4.

(1S)	$ \eta_{c} $	$ J/\psi $	$ \eta_{b} $	$\Upsilon$
$ \langle \xi^{2} \rangle $	0.089	0.089	0.051	0.051
$ \langle \xi^{4} \rangle $	0.019	0.019	0.006	0.007
$ \langle \xi^{6} \rangle $	0.0056	0.0056	0.0013	0.0013
(2S)	$ \eta_{c} $	ψ	$ \eta_{b} $	$\Upsilon$
$ \langle \xi^{2} \rangle $	0.168	0.167	0.105	0.105
$ \langle \xi^{4} \rangle $	0.049	0.050	0.020	0.020
$ \langle \xi^{6} \rangle $	0.018	0.018	0.005	0.005
(3S)	$ \eta_{c} $	ψ	$ \eta_{b} $	$\Upsilon$
$ \langle \xi^{2} \rangle $	0.169	0.169	0.066	0.13
$ \langle \xi^{4} \rangle $	0.059	0.059	0.016	0.031
$ \langle \xi^{6} \rangle $	0.025	0.025	0.005	0.009
(1P)	$ h_{c} $	$ \chi_{c0} $	$ h_{b} $	$ \chi_{b0} $
$ \langle \xi^{2} \rangle $	0.166	0.089	0.091	0.051
$ \langle \xi^{4} \rangle $	0.045	0.019	0.016	0.006
$ \langle \xi^{6} \rangle $	0.015	0.005	0.004	0.0013

Table 3.  ξ-moment upto $ n=6 $ for the excited states of pseudo-scalar and vector quarkonia.

		LFQM	NRQCD [78]	QCDSR [77−80]	DSE [81]	BLFQ [67]	Buchmuller-Tye model [82]
	$ \langle \xi^{2} \rangle $	0.089	0.075	0.070	0.10	0.096	0.086
$ \eta_{c} (1S) $	$ \langle \xi^{4} \rangle $	0.019	0.010	0.012	0.032	0.019	0.020
	$ \langle \xi^{6} \rangle $	0.0056	0.0017	0.0032	0.015	0.0036	0.0066
	$ \langle \xi^{2} \rangle $	0.168	0.22	0.18		0.157	0.16
$ \eta_{c} (2S) $	$ \langle \xi^{4} \rangle $	0.049	0.085	0.051		0.043	0.042
	$ \langle \xi^{6} \rangle $	0.018	0.039	0.017		0.013	0.015
	$ \langle \xi^{2} \rangle $	0.089	0.075	0.070	0.039	0.096	0.086
$ J/\psi (1S) $	$ \langle \xi^{4} \rangle $	0.019	0.010	0.012	0.038	0.021	0.020
	$ \langle \xi^{6} \rangle $	0.0056	0.0017	0.0031	7.3×10−4	0.0060	0.0066
	$ \langle \xi^{2} \rangle $	0.051			0.070	0.052
$ \eta_{b} (1S) $	$ \langle \xi^{4} \rangle $	0.006			0.015	0.081
	$ \langle \xi^{6} \rangle $	0.0013			0.042	0.0020
	$ \langle \xi^{2} \rangle $	0.105				0.082
$ \eta_{b} (2S) $	$ \langle \xi^{4} \rangle $	0.020				0.013
	$ \langle \xi^{6} \rangle $	0.005				0.003
	$ \langle \xi^{2} \rangle $	0.051			0.014	0.047
$ \Upsilon (1S) $	$ \langle \xi^{4} \rangle $	0.007			4.3×10−4	0.0066
	$ \langle \xi^{6} \rangle $	0.0013			4.4×10−5	0.0014

Table 4.  Comparison of some of our LFQM ξ-moment results in the 1S and 2S states with different theoretical models and sum rules.

The charge radii and EMFFs of heavy pseudo-scalar mesons have also been computed in our model. We followed the Drell-Yan-West frame ($ q^{+} = 0 $) with $\boldsymbol{q}_{\perp}^{2}= Q^{2}=-q^{2}$ [50]. Owing to the existence of several formulations for exact FFs in the light-front regime, we believe that this is a clear benefit in the LFQM. For the ''+''-component of the current $ J^{\mu} $, the pseudo-scalar meson's charge FF can be represented as [36]

where $ e_{q}\left(e_{\bar{q}}\right) $ is the electric charge of quark (anti-quark), and

where $\boldsymbol{k}_{\perp}^{\prime}=\boldsymbol{k}_{\perp}+(1-x) \boldsymbol{q}_{\perp}$. The charge radius is thus given as

In Fig. 5, we compare the EMFFs of $ \eta_{c} $ and $ \eta_{b} $ for the various excited states. As the form factors of heavy quarkonia derived from the combined quark and anti-quark contributions disappear, we only present the quark portion of the contribution. We compared our results for the 1S and 1P state $ \eta_{c} $ meson with the lattice B1 and C1 simulation data [83], and the results are in good agreement. We find that the form factors for the $ \eta_{b} $ meson are generally steeper than those for the $ \eta_{c} $ meson, and the curves saturate at much larger $ Q^{2} $ values. Because we have identical quark and anti-quark masses in our quarkonia system, the contributions from both the quark and anti-quark are almost equally responsible for the distribution in the $ Q^{2} $ region.

Figure 5.  (color online) Form factors of $ \eta_{c} $ (orange solid line) and $ \eta_{b} $ (red dashed line) for 1S, 2S, 3S, and 1P states. The $ \eta_{c} $ 1S state is compared to the Lattice B1 and Lattice C1 simulation data [83].

In Table 5, we present the calculated charge radii $ \langle r^{2} \rangle $ of the heavy quarkonia excited states. We compared our calculations with the theoretical results of the lattice simulations [83] and BLFQ [84], as we lack any experimental data regarding this topic. We find that our results agree well with the lattice calculations. As per our understanding of charge radii, the heavy quark is seated near to the meson's core, while the light quark is traveling and its mobility in a heavy-light system primarily determines the corresponding meson's charge radius. For our case of the heavy-heavy system, both the heavy quarks are situated close to the center of the meson with little to no mobility; hence, we obtain very low values of the charge radii. This is evident when comparing the outcomes of LFQM from Ref. [34].

	$ \langle r^{2} \rangle_{\eta_{c}(1 S)} $	$ \langle r^{2} \rangle_{\eta_{b}(1 S)} $
Our results	0.041	0.010
BLFQ [84]	0.038(5)	0.0146(8)
DSE [85]	0.048(4)
Lattice, B1 [83]	0.052(4)
Lattice, C1 [83]	0.044(4)
	$ \langle r^{2} \rangle_{\eta_{c}(2 S)} $	$ \langle r^{2} \rangle_{\eta_{b}(2 S)} $
Our results	0.089	0.020
BLFQ [84]	0.1488(5)	0.0510(8)
	$ \langle r^{2} \rangle_{\eta_{c}(3 S)} $	$ \langle r^{2} \rangle_{\eta_{b}(3 S)} $
Our results	0.107	0.037
	$ \langle r^{2} \rangle_{h_{c}(1 P)} $	$ \langle r^{2} \rangle_{h_{b}(1 P)} $
Our results	0.126	0.056

Table 5.  Charge radii (in fm²) of heavy quarkonia in comparison to other theoretical models.

PDFs give us a 1-D picture of the hadron and describe the likelihood of finding a parton carrying the parent hadron's longitudinal momentum fraction (x). Using the LF approach, the PDFs of a hadron state can be determined by integrating the transverse momentum of the wave function overlaps. The unpolarized quark's PDF for spin-0 mesons is defined as

We normalize this PDF to unity in our model as follows:

For the spin-1 mesons, there are four T-even distributions for the twist-2 case, which are $ f_{1}(x) $, $ f_{1 LL}(x) $, $ h_{1}(x) $, and $ g_{1} (x) $, depending on the relative polarization of both the quark and its respective meson. We can simply integrate the T-even TMDs over the transverse momentum $\boldsymbol{k}_{\perp}$ to obtain the analytical form for the spin-1 PDFs. In the present work, we only considered the unpolarized PDF $ f_{1}(x) $, which describes the distribution of the unpolarized quark in the unpolarized spin-1 meson.

For the heavy vector mesons, the overlap form of the LFWFs with respect to the LF helicity amplitudes with quark-antiquark helicities and their polarizations can be written as [10]

where Λ is the spin projection of the spin-1 meson. For the unpolarized T-even TMD, the explicit overlap form in terms of helicity amplitudes is expressed as [10]

As a result, we can obtain the analytical form for the unpolarized $ f_{1} (x) $ PDF from its corresponding $ f_1\left(x, \boldsymbol{k}_{\perp}^2\right) $ TMD as [10]

where

In Fig. 6, we present the unpolarized PDFs as a function of longitudinal momentum fraction x for the various excited states of the spin-0 and spin-1 mesons. The plots are symmetric about $ x = 0.5 $, which is representative of their similar quark and anti-quark masses. Similar to the DAs, we observe here that the bottomonia ($ b \bar b $) PDFs have a narrower waveform along with a higher amplitude peak compared to the charmonia ($ c \bar c $) PDFs. As we go to higher excited states, the PDFs tend to have ridges along their curves due to their nodal wave structure. We also notice that the 1P state has a double amplitude, which we believe arises due to the $ k_{z} $ factor present in the orbital wave function that we have considered. We conclude that when the quarks reach higher orbital states, they tend to carry a very high percentage of the momentum fraction x inside the parent hadron.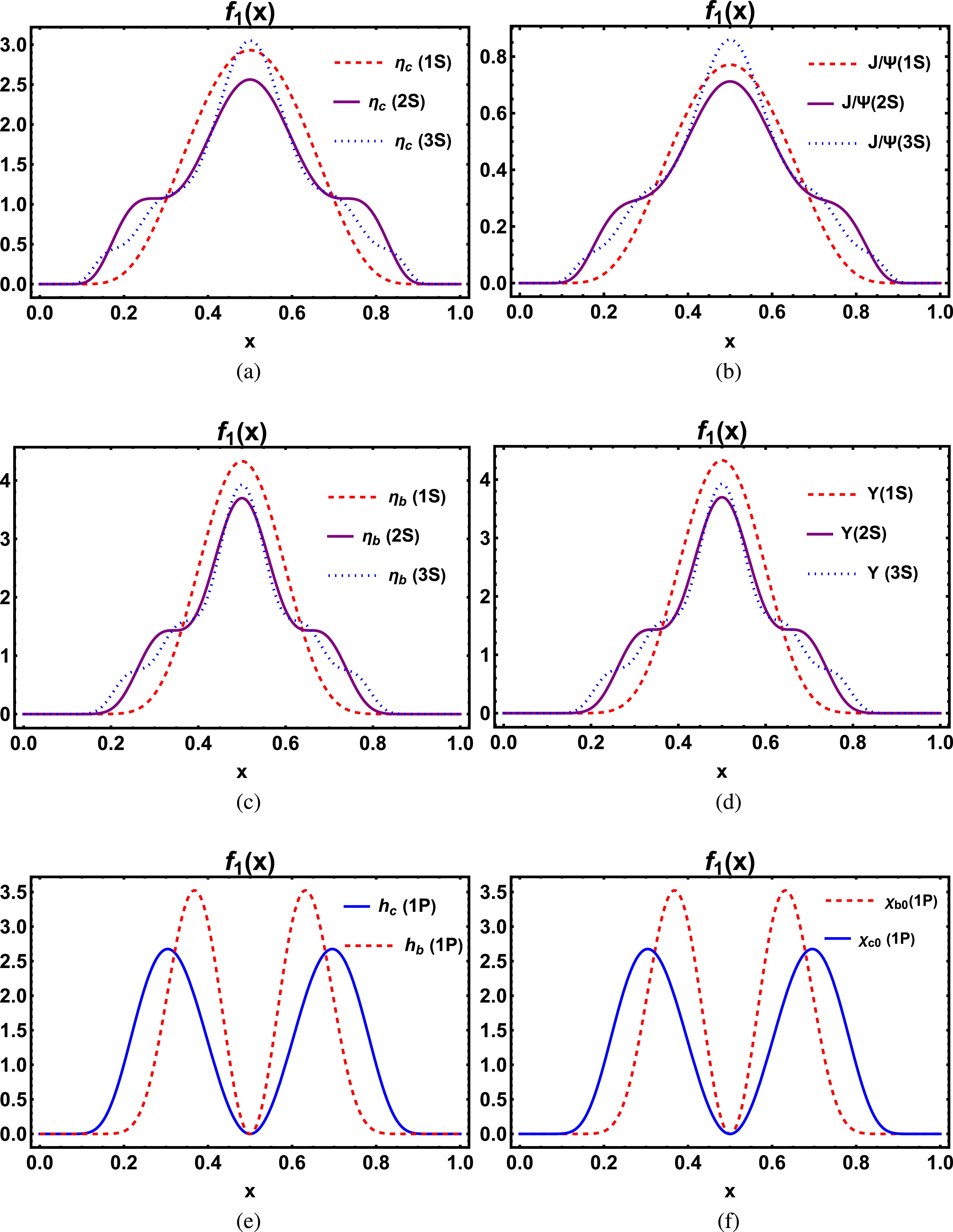

Figure 6.  (color online) $ f_{1} (x) $ PDFs plotted as a function of x for the radially excited states of the $ \eta_{c} $, $ J/\psi $, $ \eta_{b} $, and $\Upsilon$ ((a), (b), (c), and (d) respectively). A comparison of the orbitally excited state for $ h_{c} $and $ h_{b} $ is shown in (e), whereas comparison of $ \chi_{c0} $ and $ \chi_{b0} $ is shown in (f).

PDFs for the charmonia ($ c \bar c $) and bottomonia ($ b \bar b $) have been studied in detail in other theoretical formulations, such as BLFQ. We compare our results for the 1S state of the $ \eta_{c} $ meson, 3S state of the $ \eta_{b} $ meson, 1S state of the $ J/\psi $ meson, and 1P state of $ \chi_{c0} $ to those calculated by the BLFQ method [86, 67] in Fig. 7. Our results are in relatively good agreement in most of the cases, except in the 3S and 1P states, which vary mostly in their amplitudes. This difference is again due to different model assumptions and input parameters.

Figure 7.  (color online) $ f_{1} (x) $ PDFs for the 1S state $ \eta_{c} $ meson and 3S state $ \eta_{b} $ meson (left panel), along with 1S state for $ J/\psi $ and 1P state for $ \chi_{c0} $ (right panel) compared with the BLFQ data [86, 67].

In the present work, we studied the ground state 1S, radially excited states 2S and 3S, orbitally excited state 1P for the heavy quarkonia in both spin-0 and spin-1 mesons in the LFQM. The results obtained for the decay constants are in good agreement with the experimental data and lattice simulations for the 1S state, but the similarities deviate as we go to higher excited states. This contradicts the empirical hierarchy that the decay constants should decrease with increasing excitation of the hadrons. The introduction of mixing effects to the 1S and 2S states has already been studied, and mixing of higher radially excited states in the present study further gives required results for the decay constants. For the case of DAs, our results are in good agreement with the lattice simulations. We note that for the 1S state, there is no visible difference between the pseudo-scalar and vector DAs, but the differences become more pronounced and prominent as we go to the higher excited states. We also observed that the DAs for the bottomonium systems have a narrower shaped wave form compared to the charmonium systems. In addition, the 3-D plots presented for the $ \eta_{c} $ meson for all the excited states give a better visualization of the wave functions we employed in this work. The PDFs considered in this work give us a more precise understanding of the internal structure of the hadron. No nodes were observed for the 1S and 1P states, whereas nodes exist for the 2S and 3S states. In this case, the bottomonium systems also have a narrower shaped wave form compared to the charmonium systems. The results of EMFFs and charge radii computed for $ \eta_{c} $ and $ \eta_{b} $ mesons for their excited states are in good agreement with the available lattice simulation data. We mainly addressed the heavy-heavy meson sector in the framework of LFQM in this work. Nevertheless, a collective investigation of the heavy and light meson sectors is equally crucial to examine how closely physical quantities depend on quark masses. Accurate measurements of the physical characteristics of heavy mesons and findings of yet unidentified heavy meson states in the future will be crucial to evaluate phenomenological notions about the heavy meson structure.